Effect of Quantum Noise on Teleportation of an Arbitrary Single-Qubit State via a Triparticle W State

Abstract

Using a three-particle W state as the quantum channel, we investigate the teleportation of an arbitrary single-qubit state in noisy environments. The influence of different noises on the process of teleporation of an arbitrary single-qubit state with a three-particle W state is considered by analytically derivation and calculations of the fidelities of the teleportation. The single-qubit teleportation fidelity was derived and computed numberically in the case of teleportation through a triparticle W state in which the sender’s entangled qubit is interacted to environment during the process of entanglement distribution and the receiver’s entangled particle is rotated to optimize the teleportation fidelity. It is shown that the fidelity of single-qubit teleportation through a strong bit flipping or bit-phase flipping environment can be enhanced by rotating the entangled particle about x-axis or y-axis. While such effect does not appear in quantum teleportation when rotating an entangled particle of Bell state under a strong bit-phase flipping environment.

1 Introduction

Multi-qubit entangled states have been utilized extensively in quantum computation [1], quantum secure direct communication [2,3,4,5], quantum teleportation [6,7,8,9,10], quantum entanglement concentration and quantum entanglement purification [11,12,13,14,15], quantum entanglement swapping [16,17,18], blind quantum computation [19], quantum remote state preparation [20, 21], quantum remote control [22,23,24,25,26,27,28] and so on. There are two LU-inequivalent types of the maximally entangled states, called Greenberger-Horne-Zeilinger(GHZ) [29] and W [30] states. Differently from GHZ state, a three-qubit W state has the maximal bipartite entanglement among all three-qubit states, so that it can maximally symmetrically robust against loss of any single qubit and can be effectively used in quantum secure communication [31]. Joo et al. [32] investigated two schemes of QT with a W state as quantum channel. In one scheme the W state is shared by three parties one of whom, called a sender, performs a Bell measurement. While in other scheme the sender takes two particles of the W state and performs positive operator valued measurements. They showed the average fidelity of the former cannot exceed that of the latter.

In practical QT, the influence of noises on the process of teleporation is unavoidable. With noises introduced into quantum channel, the literatures [7, 9, 10] have compared the teleportation fidelity of GHZ state with that of W state. Jung et al. [7] showed, by solving analytically a master equation in the Lindbald form, that GHZ state is always more robust than W state if the noisy channel is (L_2,x,L_3,x,L_4,x)-type, while reverse case occurs if the noises are (L_2,y,L_3,y,L_4,y)-type, for (L_2,z,L_3,z,L_4,z)-type noises which is more robust relies on the noisy parameter κ. Methodologically same to [10], Hu found that the GHZ state is always more robust than the W state when subject to zero temperature, and the reverse situation appears when the channel is subject to infinite temperature or dephasing environment. All works mentioned above aimed at obtaining a faithful teleportation fidelity with different entangled states acting as quantum channel, wherein the noises served as busters.

Recently, effects of quantum noise on quantum state transmitting have been attached much interest [33,34,35,36,37,38,39,40,41,42,43,44,45, 47]. Oh et al investigate quantum teleportation through quantum channel subjected to different type of noises by solving the master equation in Lindblad form [33]. Espoukeh and Pedram studied teleportation of an arbitrary single-qubit state through noisy channel for multi-qubit GHZ state [34]. Guan et al study joint remote preparation of an arbitrary two-qubit state through a six-qubit cluster state suffering from the amplitude-damping noise and the phase-damping noise [35]. Liang analyzes the effects of noises on joint remote state preparation via a GHZ-class channel [36]. Li et al investigate joint remote preparation of an arbitrary two-qubit state by using four Einstein-Podolsky-Rosen(EPR) states as the quantum channel in the present of noisy environments [37]. Wang and Qu examine the effect quantum channel noise on deterministic joint remote preparation of a single-qubit state $\vert \varphi \rangle =a_{0}e^{i\theta _{0}}\vert 0\rangle +a_{1}e^{i\theta _{1}}\vert 1\rangle$ with a GHZ state $\vert \phi \rangle =\frac {1}{\sqrt {2}}(\vert 000\rangle +\vert 111\rangle )$ [38].

Interestingly, local noises enhancing the teleportation fidelity have been reported. It is worth to be particularly noted that after they first proposed QT, Bennett et al. soon investigated the faithful QT Via noisy channels [46]. They showed that by performing local unitary operations such as rotations and measurements on the shared entangled pairs, an arbitrary unknown single-qubit state can be teleported with high fidelity from sender to receiver through noisy environments. Badziag et al. [47] and Bandy- opadhyay [48] obtained a family of entangled two-qubit mixed states whose teleportation fidelity can be enhanced by subjecting one of the qubits to dissipative interaction with the environment via an amplitude damping channel. Soon after, Yeo [49] discovered a dissipative interaction with the local environment via a pair of time-correlated amplitude damping channels can enhance fidelity of entanglement teleportation for a class of entangled four-qubit mixed states. One knows that QT via Multi-qubit entangled state is more complex than QT via Bell state, and it not always successful in recovering the unknown state using W state as quantum channel [50]. Therefore, exploration of QT advantage using W state is of importance. This determines the necessity of QT with W state as channel. To our knowledge, it is still an open question as how to enhance the teleportation fidelity via a W state interacting with various environments (in particular the interaction is very strong) by using local noises or local operations.

In this paper, the effect of quantum noise on teleportation through a three-particle W state under various environments is investigated, primarily aiming how to enhance the teleportation fidelity in a strong noisy channel by rotating the entangled particle. We will show that under a strong bit-phase flipping environment, the average fidelity of single-qubit teleportation can be enhanced by rotating the entangled particle of W state about x-axis or y-axis, while there is not such effect when rotating the entangled particle of Bell state. The paper is arranged as follows: Secttion 2 presents the protocol of single-qubit teleportation via the triparticle W state, wherein a qubit is rotated by a magnetic field and a qubit passes through a noisy channel, such as through bit flipping, phase flipping, bit-phase flipping, amplitude damping, phase damping and depolarzing channel. The teleportation fidelity formulae, considering the combinative influences of the noise channel and the qubit rotated by the magnetic field, are derived. In Section 3 we numerically compute the average teleportation fidelities via W state. In contrast with the case of Bell state, the enhanced teleportation fidelities using W state as quantum channel are discussed. Finally, we summarize our work in Section 4.

2 Teleportation of an Arbitrary Single-Qubit State in Ideal Situation

To present the protocol explicitly, we first rewrite the protocol for teleportation of single-qubit state in ideal situation with W state via density operators representation, then discuss the effect of various quantum noise on teleportation of an arbitrary single-qubit state via W state and the method to enhance the fidelity of single-qubit teleportation via w state in noisy situation.

An arbitrary single-qubit state can be written as [25, 26]

$$ \begin{array}{@{}rcl@{}} \vert\psi_{\chi}\rangle=cos\frac{\theta}{2}\vert 0\rangle+sin\frac{\theta}{2}e^{-i\phi}\vert 1\rangle, \end{array} $$

(1)

where 𝜃,ϕ are arbitrary real numbers.

Since the pure state may evolves to mixed state in noisy situation. It is more convenient to rewrite the arbitrary single-qubit state in the form of density operator [45]

$$ \begin{array}{@{}rcl@{}} \rho_{\chi}=&&(cos\frac{\theta}{2}\vert 0\rangle+sin\frac{\theta}{2}e^{-i\phi}\vert 1\rangle)(cos\frac{\theta}{2}\langle 0\vert+sin\frac{\theta}{2}e^{i\phi}\langle 1\vert)\\ =&&cos^{2}\frac{\theta}{2}\vert 0\rangle\langle 0\vert+cos\frac{\theta}{2}sin\frac{\theta}{2}e^{i\phi}\vert 0\rangle\langle 1\vert+sin\frac{\theta}{2}cos\frac{\theta}{2}\\ &&e^{-i\phi}\vert 1\rangle\langle 0\vert+sin^{2}\frac{\theta}{2}\vert 1\rangle\langle 1\vert, \end{array} $$

(2)

Similar to Ref. [50], the sender Alice and the receiver Bob share a three-particle W state as the quantum channel.

$$ \begin{array}{@{}rcl@{}} \rho_{ABC}=&&\frac{1}{3}(\vert 001\rangle+\vert 010\rangle+\vert 100\rangle)(\langle 001\vert+\langle 010\vert+\langle 100\vert)\\ =&&\frac{1}{3}(\vert 001\rangle\langle 001\vert+\vert 001\rangle\langle 010\vert+\vert 001\rangle\langle 100\vert+\\ &&\vert 010\rangle\langle 001\vert+\vert 010\rangle\langle 010\vert+\vert 010\rangle\langle 100\vert+\vert 100\rangle\langle 001\vert\\ &&+\vert 100\rangle\langle 010\vert+\vert 100\rangle\langle 100\vert). \end{array} $$

(3)

Here particle A belongs to Alice and particles B,C belong to Bob.

To teleport the arbitrary single-qubit state ρ_χ via three-particle W state ρ_ABC, Bob performs single-qubit project measurement on particle C. Alice performs Bell state measurement on his particles χ and A. Bob can reconstruct the original state by performing corresponding operation on particle B. The single-qubit measurement can be described as

$$ \begin{array}{@{}rcl@{}} P_{0}=\vert0\rangle\langle0\vert, P_{1}=\vert1\rangle\langle1\vert. \end{array} $$

(4)

The state of particles A,B becomes ρ_χAB if the single-qubit measurement result is P₀.

$$ \begin{array}{@{}rcl@{}} \rho_{AB}=&&tr_{C}[\frac{P_{0}*\rho_{ABC}*P_{0}^{\dagger}}{tr(P_{0}^{\dagger}*P_{0}*\rho_{ABC})}]\\ =&&\frac{1}{2}(\vert 01\rangle\langle01\vert+\vert 01\rangle\langle10\vert+\vert 10\rangle\langle01\vert+\\ &&\vert 10\rangle\langle10\vert. \end{array} $$

(5)

The Bell state measurement can be described as

$$ \begin{array}{@{}rcl@{}} M_{00}=\frac{1}{2}(\vert00\rangle\langle00\vert+\vert00\rangle\langle11\vert+\vert11\rangle\langle00\vert+\vert11\rangle\langle11\vert),\\ M_{01}=\frac{1}{2}(\vert00\rangle\langle00\vert-\vert00\rangle\langle11\vert-\vert11\rangle\langle00\vert+\vert11\rangle\langle11\vert),\\ M_{10}=\frac{1}{2}(\vert01\rangle\langle01\vert+\vert01\rangle\langle10\vert+\vert10\rangle\langle01\vert+\vert10\rangle\langle10\vert),\\ M_{11}=\frac{1}{2}(\vert01\rangle\langle01\vert-\vert01\rangle\langle10\vert-\vert10\rangle\langle01\vert+\vert10\rangle\langle10\vert). \end{array} $$

(6)

The state of particles B collapses to ρ_B if Alice’s Bell state measurement result is M₀₀.

$$ \begin{array}{@{}rcl@{}} \rho_{B}=&&tr_{\chi A}[\frac{M_{00}*\rho_{\chi AB}*M_{0}^{\dagger}}{tr(M_{00}^{\dagger}*M_{00}*\rho_{\chi AB})}]\\ =&&cos^{2}\frac{\theta}{2}\vert 1\rangle\langle 1\vert+cos\frac{\theta}{2}sin\frac{\theta}{2}e^{i\phi}\vert 1\rangle\langle 0\vert+sin\frac{\theta}{2}cos\frac{\theta}{2}\\ &&e^{-i\phi}\vert 0\rangle\langle 1\vert+sin^{2}\frac{\theta}{2}\vert 0\rangle\langle 0\vert. \end{array} $$

(7)

Bob can reconstruct the original state ρ_χ by performing corresponding unitary operation σ_x.

$$ \begin{array}{@{}rcl@{}} \rho_{B}(out)=\sigma_{x}\rho_{B}\sigma_{x}^{\dagger}, \end{array} $$

(8)

where

$$ \begin{array}{@{}rcl@{}} \sigma_{x}=\vert 0\rangle\langle1\vert+\vert 1\rangle\langle0\vert. \end{array} $$

(9)

For the the case, Bob can recovery the original state ρ_χ by performing corresponding unitary operation σ_zσ_x, I or σ_z on particle B if Alice’s Bell state measurement result is M₀₁, M₁₀ or M₁₁, respectively. Here I is the identify matrix and σ_z = |0〉〈0|−|1〉〈1|.

The fidelity of teleportation of single-qubit state via W state in ideal situation is 1.

$$ \begin{array}{@{}rcl@{}} F^{I}=\langle\psi\vert\rho_{B}(out)\vert\psi\rangle. \end{array} $$

(10)

3 Teleportation of an Arbitrary Single-Qubit State in Noisy Situation

In practical application, quantum noise, an unavoidable factor in quantum teleportation, may effect the fidelity of quantum teleportation. We discuss the effect of various quantum noise on the fidelity teleportation of an arbitrary single-qubit state via W state and the method to enhance the fidelity via local operation.

3.1 Effect of Quantum Noise on the Fidelity of Single-Qubit Teleportation via W State

There are six types of quantum noises which may encountered in practical application of quantum teleportation, namely bit flipping, phase flipping, bit-phase flipping, depolarzing, amplitude damping and phase damping noise. We discuss fidelity of single-qubit quantum teleportation in six types of quantum noises via W state below.

Similar to the case for teleportation of an arbitrary single-qubit state via W state in ideal situation, the receiver Bob prepares a three-qubit W state ρ_ABC, sends qubit A to Alice and keeps particles B, C in his hand. The quantum channel shared by Alice and Bob evolves to $\rho ^{\prime }$ after particle A passes the noisy channel.

$$ \begin{array}{@{}rcl@{}} \rho^{\prime}=\sum\limits_{j}E_{j}^{(A)}\rho_{ABC}E_{j}^{(A)^{\dagger}}, \end{array} $$

(11)

where $E_{j}^{(A)}$(j = 0,1) represent different noise operators act on qubit A.Similar to the teleportation in ideal situation, Bob performs single-qubit projection measurement on qubit C, Alice performs Bell state measurement on particles χ, A. The receiver Bob can prepare the target state ρ_out by performing corresponding unitary operation on qubit B.

The state of qubits A,B after the projective measurement can be calculated as:

$$ \begin{array}{@{}rcl@{}} \rho_{AB}^{\prime}=&&tr_{C}[\frac{P_{0}*\rho^{\prime}*P_{0}^{\dagger}}{tr(P_{0}^{\dagger}*P_{0}*\rho^{\prime}}]. \end{array} $$

(12)

After the Bell state measurement, the state of qubit B evolves to:

$$ \begin{array}{@{}rcl@{}} \rho_{B}^{\prime}=&&tr_{\chi A}[\frac{M_{00}*\rho_{\chi AB}^{\prime}*M_{0}^{\dagger}}{tr(M_{00}^{\dagger}*M_{00}*\rho_{\chi AB})'}]. \end{array} $$

(13)

Similar to the case of teleportation in ideal situation, Bob can prepare the target state ρ_C(out)^′ by performing corresponding unitary operation σ_x on qubit B if the Bell state measurement result is M₀₀.

$$ \begin{array}{@{}rcl@{}} \rho_{B}(out)'=\sigma_{x}\rho_{B}^{\prime}\sigma_{x}^{\dagger}. \end{array} $$

(14)

The fidelity of teleportation in noisy situation can be calculated as:

$$ \begin{array}{@{}rcl@{}} \mathcal{F}^{N}=\langle\psi\vert\rho_{B}(out)'\vert\psi\rangle. \end{array} $$

(15)

3.1.1 The Bit Flipping Noise

• 1. The bit flipping noise

The Kraus operators of the bit flipping noise can be described as [44, 45]

$$ \begin{array}{@{}rcl@{}} E_{0}=\sqrt{p}\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right), E_{1}=\sqrt{1-p}\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), \end{array} $$

(16)

where p ∈{0,1} is the noise parameter, and 1 − p represent the probability that the noise flip the state.

In bit flipping noise, the output state is

$$ \begin{array}{@{}rcl@{}} \rho_{B}(out)'=&&[p cos^{2}\frac{\theta}{2}+(1-p)sin^{2}\frac{\theta}{2}]\vert 0\rangle\langle 0\vert+[pcos\frac{\theta}{2}\\ &&sin\frac{\theta}{2}e^{i\phi}+(1-p)cos\frac{\theta}{2}sin\frac{\theta}{2}e^{-i\phi}]\vert 0\rangle\langle 1\vert+\\ &&[pcos\frac{\theta}{2}sin\frac{\theta}{2}e^{-i\phi}++(1-p)cos\frac{\theta}{2}sin\frac{\theta}{2}e^{i\phi}]\\ &&\vert 1\rangle\langle 0\vert+[p sin^{2}\frac{\theta}{2}+(1-p)cos^{2}\frac{\theta}{2}]\vert 0\rangle\langle 0\vert \end{array} $$

(17)

We can get the fidelity of teleportation in bit flipping noise

$$ \begin{array}{@{}rcl@{}} F^{BF}=p+(1-p)sin^{2}\theta cos^{2}\phi. \end{array} $$

(18)

The fidelity is related to noise parameter, the amplitude and phase factors of the original state ρ_χ. For the strongest noise (i.e., p = 0), if we set ϕ = 0, the maximally fidelity is 1 when $\theta =\pm \frac {\pi }{2}$.

3.1.2 The Phase Flipping Noise

The Kraus operators of the phase flipping noise can be written as

$$ \begin{array}{@{}rcl@{}} E_{0}=\sqrt{p}\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right), E_{1}=\sqrt{1-p}\left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right), \end{array} $$

(19)

where p ∈{0,1} is the noise parameter, and 1 − p represent the probability that the noise flip the state |1〉 to state −|1〉.

Similar to the case for teleportation in bit flipping noise, we can calculate the fidelity of teleportation in phase flipping noise.

$$ \begin{array}{@{}rcl@{}} F^{PF}=p+(1-p)cos^{2}\theta. \end{array} $$

(20)

The fidelity of teleportation in phase flipping noise is related to noise parameter p and the amplitude factor $cos\frac {\theta }{2}$, not related to the phase factor ϕ. For the strongest noise, the maximally fidelity is 1 when 𝜃 = 0 or 𝜃 = π.

3.1.3 The Bit-Phase Flipping Noise

The Kraus operators of the bit-phase flipping noise is

$$ \begin{array}{@{}rcl@{}} E_{0}=\sqrt{p}\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right), E_{1}=\sqrt{1-p}\left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array} \right), \end{array} $$

(21)

where p ∈{0,1}. The bit-phase flipping noise flips state |0〉 to i|1〉 and flips |1〉 to − i|0〉 with probability 1-p.

We can calculate the fidelity of teleportation in bit-phase flipping noise.

$$ \begin{array}{@{}rcl@{}} F^{BPF}=p. \end{array} $$

(22)

The fidelity of teleportation in phase flipping noise is related to noise parameter p, but not related to the amplitude factor $cos\frac {\theta }{2}$ and phase factor ϕ.

3.1.4 The Depolarizing Noise

The Kraus operators of the depolarizing noise is

$$ \begin{array}{@{}rcl@{}} E_{0}=\sqrt{1-\frac{3p}{4}}\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right), E_{1}=\sqrt{\frac{p}{4}}\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right),\\ E_{2}=\sqrt{\frac{p}{4}}\left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array} \right), E_{3}=\sqrt{\frac{p}{4}}\left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right), \end{array} $$

(23)

where $p\in \{0,\frac {4}{3}\}$.

The fidelity of teleportation in depolarzing noise is

$$ \begin{array}{@{}rcl@{}} F^{D}=1-\frac{3p}{4}+\frac{p}{4}sin^{2}\theta cos^{2}\phi+\frac{p}{4}cos^{2}\theta. \end{array} $$

(24)

3.1.5 The Amplitude Damping Noise

The amplitude damping noise can be written as

$$ \begin{array}{@{}rcl@{}} E_{0}=\left( \begin{array}{cc} 1 & 0 \\ 0 & \sqrt{1-\gamma} \end{array} \right), E_{1}=\left( \begin{array}{cc} 0 & \sqrt{\gamma} \\ 0 & 0 \end{array} \right), \end{array} $$

(25)

where γ ∈{0,1}.

The fidelity of single-qubit teleportation in amplitude damping noise via W state is

$$ \begin{array}{@{}rcl@{}} F^{AD}=\frac{{\Gamma}^{AD}}{4(\gamma cos\theta+1)}, \end{array} $$

(26)

where

$$ \begin{array}{@{}rcl@{}} {\Gamma}^{AD} &=& (\gamma+2\sqrt{1-\gamma}cos2\phi)sin^{2}\theta+(2-\gamma)(1+cos^{2}\theta) + 2\gamma cos\theta \end{array} $$

(27)

The fidelity F^AD is relevant to the noise parameter λ, amplitude factor $cos\frac {\theta }{2}$ and the phase factor ϕ. For the strongest amplitude damping noise (γ = 1), the fidelity equals $\frac {1}{2}$ if ϕ = 0.

3.1.6 The Phase Damping Noise

The phase damping noise can be written as

$$ \begin{array}{@{}rcl@{}} E_{0}=\left( \begin{array}{cc} 1 & 0 \\ 0 & \sqrt{1-\gamma} \end{array} \right), E_{1}=\left( \begin{array}{cc} 0 & 0 \\ 0 & \sqrt{\gamma} \end{array} \right), \end{array} $$

(28)

where γ ∈{0,1}.

The fidelity of single-qubit teleportation in phase damping noise is

$$ \begin{array}{@{}rcl@{}} F^{PD}=\frac{1+cos^{2}\theta+\sqrt{1-\gamma}sin^{2}\theta cos2\phi}{2} \end{array} $$

(29)

The fidelity F^PD is relevant to the noise parameter λ, amplitude factor $cos\frac {\theta }{2}$ and the phase factor ϕ.

3.2 Effect of Quantum Noise on the Fidelity of Single-Qubit Teleportation via W State

We have calculate the teleportation fidelity for single-qubit teleportation in six types of quantum noises. Now, let us discuss the effect of quantum noise on the fidelity of single-qubit teleportation via W state. It is shown that local operation can enhance the teleportation fidelity for single-qubit state in the strong noisy situation.

Similar to the case for teleportation in ideal situation, the receiver Bob prepares a three-qubit W state ρ_χ, and shares the three-qubit W state with the sender Alice. After setting up the quantum channel, Bob first performs a rotation operation on qubit C, then performs the single-qubit projective measurement on qubit C. Alice makes Bell state measurement on her qubits χ, A. Bob can prepare the output state by performing corresponding operation on qubit B in accordance with Alice’s measurement result. It is shown that the teleportation fidelity can be enhanced in strong noisy situation by the rotation of qubit C.

The rotation of qubit C by local magnetic field can be characterized with the rotation operator R_k(α) about k-axis, where α ∈ [0,2π] and k = 1,2,3 standing for x,y and z,respectively [27]. It reads with $\hbar =1$ as

$$ \begin{array}{@{}rcl@{}} R_{k}(\alpha)=e^{-i\alpha S_{k}}=\cos\frac{\alpha}{2} I-i\sin\frac{\alpha}{2} \sigma_{k}, \end{array} $$

(30)

where $S_{k}=\frac {\hbar }{2}\sigma _{k}$ is the k-axis angular momentum component operator, σ_k is Pauli operator. The rotation angle α is determined by the strength of magnetic field and the time of interaction between the magnetic field and particle C.

3.2.1 The Bit Flipping Noise

To show the QT fidelity influenced by noise and the rotation of the qubit C, we now, as an example, derive in detail the QT fidelity which is influenced by a bit flipping environment and a rotation of qubit C about x-axis.To set up the quantum channel, Bob prepares the three-qubit W state ρ_ABC and sends qubit A to Alice. With a bit flipping noise introduced to particle A, the quantum channel shared by Alice and Bob becomes a state expressed by a density operator as

$$ \begin{array}{@{}rcl@{}} \rho_{ABC}(p)=&&\sum\limits_{j=0}^{1}E_{j}^{(A)}\rho_{ABC}E_{j}^{(A)^{\dagger}}\\ =&&\frac{p}{3}(\vert 001\rangle\langle 001\vert+\vert 001\rangle\langle 010\vert+\vert 001\rangle\langle 100\vert+\\ &&\vert 010\rangle\langle 001\vert+\vert 010\rangle\langle 010\vert+\vert 010\rangle\langle 100\vert+\\ &&\vert 100\rangle\langle 001\vert+\vert 100\rangle\langle 010\vert+\vert 100\rangle\langle 100\vert)+\\ &&\frac{1-p}{3}(\vert 101\rangle\langle 101\vert+\vert 101\rangle\langle 110\vert+\vert 101\rangle\langle 000\vert\\ &&+\vert 110\rangle\langle 101\vert+\vert 110\rangle\langle 110\vert+\vert 110\rangle\langle 000\vert+\\ &&\vert 000\rangle\langle 101\vert+\vert 000\rangle\langle 110\vert+\vert 000\rangle\langle 000\vert). \end{array} $$

(31)

Here $\{E_{j}^{(A)}\}$ (j = 0,1) are operators implemented on particle A and act as the influences of noise. For bit flipping noise, $E_{0}^{(A)}=\sqrt {p}(|0_{1}\rangle \langle 0_{1}|+|1_{1}\rangle \langle 1_{1}|)$ and $E_{1}^{(A)}=\sqrt {1-p}(|0_{1}\rangle \langle 1_{1}|+|1_{1}\rangle \langle 0_{1}|)$. The parameter 0 ≤ p ≤ 1 quantifies the strength of noise. ρ_ABC(p) is the state of the particles A, B, C after particle A passes through noise channel.

After set up the quantum channel, Bob first rotates particle C about x-axis, then performs single-qubit projective measurement on particle C. The state of qubit A,B,C becomes ρ_ABC(α,p) after Bob rotates particle C about x-axis.

$$ \begin{array}{@{}rcl@{}} \rho_{ABC}(\alpha,p)=&&R_{x}(\alpha)\rho_{ABC}(p)R_{x}(\alpha)^{\dagger}\\ =&&\frac{1}{3}\{[p \sin^{2}\frac{\alpha}{2}+(1-p)\cos^{2}\frac{\alpha}{2}]\vert 00\rangle\langle 00\vert-\\ &&i\frac{p}{2}\sin\alpha+i\frac{1-2p}{2}\sin\alpha\vert 00\rangle\langle 10\vert+\\ &&(1-p) \cos^{2}\frac{\alpha}{2}\vert 00\rangle\langle 11\vert+i\frac{p}{2}\sin\alpha\vert 01\rangle\langle 00\vert\\ &&+p \cos^{2}\frac{\alpha}{2}\vert 01\rangle\langle 01\vert+p \cos^{2}\frac{\alpha}{2}\vert 01\rangle\langle 10\vert-i\\ &&\frac{1-2p}{2}\sin\alpha\vert 10\rangle\langle 00\vert+p \cos^{2}\frac{\alpha}{2}\vert 10\rangle\langle 01\vert+\\ &&[(1-p) \sin^{2}\frac{\alpha}{2}+p\cos^{2}\frac{\alpha}{2}]\vert 10\rangle\langle 10\vert-i\frac{1-p}{2}\\ &&\sin\alpha\vert 10\rangle\langle 11\vert+(1-p)\cos^{2}\frac{\alpha}{2}\vert 11\rangle\langle 00\vert+i\\ &&\frac{1-p}{2}\sin\alpha\vert 11\rangle\langle 10\vert+(1-p) \cos^{2}\frac{\alpha}{2}\vert 11\rangle\langle 11\vert\}\\ &&\otimes\vert 0\rangle\langle 0\vert+\cdots \end{array} $$

(32)

Here ⋯ represents terms that particle C is not in state |0〉.

Bob performs single-qubit projective measurement {P₀,P₁} on qubit C. The state of particles A,B becomes ρ_AB(α,p) if the single qubit projective measurement result is P₀. The state of particles A,B can be described in the matrix form.

$$ \begin{array}{@{}rcl@{}} \rho_{AB}(\alpha,p)=\frac{1}{1+\cos^{2}\frac{\alpha}{2}}\left( \begin{array}{cccc} (1-p)\cos^{2}\frac{\alpha}{2}+p\sin^{2}\frac{\alpha}{2}&-i\frac{p}{2}\sin\alpha&i\frac{1-2p}{2}\sin\alpha&(1-p)\cos^{2}\frac{\alpha}{2}\\ i\frac{p}{2}\sin\alpha&p\cos^{2}\frac{\alpha}{2}&p\cos^{2}\frac{\alpha}{2}&0 \\ -i\frac{1-2p}{2}\sin\alpha&p\cos^{2}\frac{\alpha}{2}&(1-p)\sin^{2}\frac{\alpha}{2}+p\cos^{2}\frac{\alpha}{2}&-i\frac{1-p}{2}\sin\alpha\\ (1-p)\cos^{2}\frac{\alpha}{2}&0&i\frac{1-p}{2}\sin\alpha&(1-p)\cos^{2}\frac{\alpha}{2} \end{array} \right). \end{array} $$

(33)

One can find that ρ_AB(α,p)(α = 0,p = 0) is just the Bell state $\frac {1}{\sqrt {2}}(\vert 01\rangle +\vert 10\rangle )$. Up to now, together with the teleported state ρ_χ, Alice and Bob share the three-particle state which reads ρ_χAB = ρ_χ ⊗ ρ_AB(α,p).

The state of particle B becomes ρ_B(out) after Alice’s Bell state measurement and Bob’s recovery operation.

$$ \begin{array}{@{}rcl@{}} \rho_{B}(out)=\frac{1}{2AP_{x}^{BF}}\left( \begin{array}{cc} b_{1}&b_{2}\\ b_{2}^{*}&b_{3} \end{array} \right), \end{array} $$

(34)

where

$$ \begin{array}{@{}rcl@{}} A=&&1+\cos^{2}\frac{\alpha}{2};\\ P_{x}^{BF}=&&\frac{1}{4A}\{2\cos^{2}\frac{\alpha}{2}+[1+(2p-1)\cos\theta]\sin^{2}\frac{\alpha}{2}\\ &&-(1-2p)\sin\theta\sin\phi\sin\alpha\};\\ b_{1}=&&p\cos^{2}\frac{\theta}{2}\cos^{2}\frac{\alpha}{2}+(1-p)\sin^{2}\frac{\theta}{2}\cos^{2}\frac{\alpha}{2};\\ b_{2}=&&\frac{ip\cos^{2}\frac{\theta}{2}}{2}\sin\alpha +p\cos\frac{\theta}{2}\sin\frac{\theta}{2}e^{i\phi}\cos^{2}\frac{\alpha}{2}+\\ &&(1-p)\cos\frac{\theta}{2}\sin\frac{\theta}{2}e^{-i\phi}\cos^{2}\frac{\alpha}{2}+\sin\alpha\\ &&\frac{i(1-p)\sin^{2}\frac{\theta}{2}}{2};\\ b_{3}=&&\cos^{2}\frac{\theta}{2}[(1-p)\cos^{2}\frac{\alpha}{2}+p\sin^{2}\frac{\alpha}{2}]+\sin^{2}\frac{\theta}{2}\\ &&[(1-p)\sin^{2}\frac{\alpha}{2}+p\cos^{2}\frac{\alpha}{2}]-(1-2p)\\ &&\cos\frac{\theta}{2}\sin\frac{\theta}{2}\sin\phi\sin\alpha. \end{array} $$

(35)

As same as the derivation process of QT fidelity F^I, we have derived the teleportation fidelities which are influenced by the rotation of particle C and various environments (noisy channels), such as bit flipping, phase flipping, bit-phase flipping, amplitude damping, phase damping and depolarzing channel [44]. One can finds that rotation of particle C about z-axis and measuring it with projection operator {P₀,P₁} only introduces a global phase to the output state ρ_B(out)^′. This means that rotating particle C about z-axis does not affect the teleportation fidelity. While for the cases of rotation about x-axis and y-axis, the teleportation fidelities under various noises are computed.

The fidelity of single-qubit teleportation via W state in bit flipping noise with the rotation of qubit C about x-axis is

$$ \begin{array}{@{}rcl@{}} F_{x}^{BF}=\frac{\eta^{BF}+2p\xi_{x}}{8P_{x}^{BF}(1+\cos^{2}\frac{\alpha}{2})}. \end{array} $$

(36)

Here

$$ \begin{array}{@{}rcl@{}} \eta^{BF}=&&2p(1+\cos^{2}\theta)\cos^{2}\frac{\alpha}{2}+(2\cos^{2}\frac{\alpha}{2}+p\sin^{2}\frac{\alpha}{2})\\ &&\sin^{2}\theta+2(1-p)\sin^{2}\theta\cos2\phi\cos^{2}\frac{\alpha}{2}+(1-p)\\ &&(1-\cos\theta)^{2}\sin^{2}\frac{\alpha}{2};\\ \xi_{x}=&&\sin\theta\sin\phi\sin\alpha. \end{array} $$

(37)

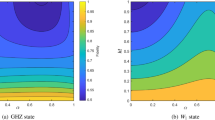
As shown in Fig. 1a, in strong bit flipping noise (p = 0), the fidelity of teleportation via W state can be enhanced via rotation of qubit C about x-axis when ϕ = 0.

Fig. 1

Fidelities of the output state in various strong noise environments with or without the rotation of qubit C about the x-axis when ϕ = 0. F^BF,F^PF,F^BPF,F^D,F^AD and F^PD represent fidelities in bit flipping, phase flipping, bit-phase flipping, depolarizing, amplitude damping and phase damping noise without rotation of qubit C. $F_{x}^{BF},F_{x}^{PF},F_{x}^{BPF},{F_{x}^{D}},F_{x}^{AD}$ and $F_{x}^{PD}$ represent fidelities in bit flipping, phase flipping, bit-phase flipping, depolarizing, amplitude damping and phase damping noise with rotation of qubit C about x-axis. a$F^{BF},F_{x}^{BF}$ with respect to $\cos \limits \frac {\theta }{2}$ in strong bit flipping noise when p = 0. b$F^{PF},F_{x}^{PF}$ with $\cos \limits \frac {\theta }{2}$ in strong phase flipping noise when p = 0. c$F^{BPF},F_{x}^{BPF}$ with respect to $\cos \limits \frac {\theta }{2}$ in strong bit-phase flipping noise when p = 0. d$F^{D},{F_{x}^{D}}$ with respect to $\cos \limits \frac {\theta }{2}$ in strong depolarizing noise when $p=\frac {4}{3}$. e$F^{AD},F_{x}^{AD}$ with respect to $\cos \limits \frac {\theta }{2}$ in strong amplitude noise when γ = 1. f Fidelities F^PD, $F_{x}^{PD}$ in phase amplitude noise with respect to $\cos \limits \frac {\theta }{2}$ when γ = 1

As same as the derivation process of QT fidelity $F_{x}^{BF}$, we can get the fidelity of single-qubit teleportation in bit flipping noise with the rotation of qubit C about y-axis

$$ \begin{array}{@{}rcl@{}} F^{BF}(y)=\frac{\eta^{BF}-2[1-(1-p)\cos\theta]\xi_{y}}{8P_{y}^{BF}(1+\cos^{2}\frac{\alpha}{2})}. \end{array} $$

(38)

Here

$$ \begin{array}{@{}rcl@{}} P_{y}^{BF}=&&\frac{1}{4A}\{2\cos^{2}\frac{\alpha}{2}+[1+(2p-1)\cos\theta]\sin^{2}\frac{\alpha}{2}\\ &&-\sin\theta\cos\phi\sin\alpha\};\\ \xi_{y}=&&\sin\theta\cos\phi\sin\alpha. \end{array} $$

(39)

3.2.2 The Phase Flipping Noise

Similar to the case for fidelity in bit flipping noise, the fidelity in phase flipping noise with rotation about x-axis is

$$ \begin{array}{@{}rcl@{}} F_{x}^{PF}=\frac{\eta^{PF}+2[p+(1-p)\cos\theta]\xi_{x}}{8P_{x}^{PF}(1+\cos^{2}\frac{\alpha}{2})}, \end{array} $$

(40)

where

$$ \begin{array}{@{}rcl@{}} \eta^{PF}=&&2(1+\cos^{2}\theta)\cos^{2}\frac{\alpha}{2}+[2(2p-1)\cos^{2}\frac{\alpha}{2}+p\\ &&\sin^{2}\frac{\alpha}{2}]\sin^{2}\theta;\\ P_{x}^{PF}=&&\frac{1}{4A}[2\cos^{2}\frac{\alpha}{2}+(1+\cos\theta)\sin^{2}\frac{\alpha}{2}+(2p-1)\\ &&\xi_{x}]. \end{array} $$

(41)

Figure 1b shows F^PF, $F_{x}^{PF}$ with $\cos \limits \frac {\theta }{2}$ in strong phase flipping when ϕ = 0.

The fidelity in phase flipping noise with rotation about y-axis is

$$ \begin{array}{@{}rcl@{}} F_{y}^{PF}=\frac{\eta^{PF}-2[p+(1-p)\cos\theta]\xi_{x}}{8P_{y}^{PF}(1+\cos^{2}\frac{\alpha}{2})}, \end{array} $$

(42)

where

$$ \begin{array}{@{}rcl@{}} P_{y}^{PF}=&&\frac{1}{4A}[2\cos^{2}\frac{\alpha}{2}+(1+\cos\theta)\sin^{2}\frac{\alpha}{2}-(2p-1)\\ &&\xi_{y}]. \end{array} $$

(43)

3.2.3 The Bit-Phase Flipping Noise

In bit-phase flipping noise, the fidelity of teleportation with rotation of qubit C about x-axis is

$$ \begin{array}{@{}rcl@{}} F_{x}^{BPF}=\frac{\eta^{BPF}+[1-(1-p)\cos\theta]2\xi_{x}}{8P_{x}^{BPF}(1+\cos^{2}\frac{\alpha}{2})}, \end{array} $$

(44)

where

$$ \begin{array}{@{}rcl@{}} \eta^{BPF}=&&2p(1+\cos^{2}\theta)\cos^{2}\frac{\alpha}{2}+(2\cos^{2}\frac{\alpha}{2}+p\sin^{2}\frac{\alpha}{2})\\ &&\sin^{2}\theta+2(1-p)\sin^{2}\theta\cos2\phi\cos^{2}\frac{\alpha}{2};\\ P_{x}^{BPF}=&&\frac{1}{4A}[2\cos^{2}\frac{\alpha}{2}+[1+(2p-1)\cos\theta]\sin^{2}\frac{\alpha}{2}+\\ &&\xi_{x}]. \end{array} $$

(45)

As shown in Fig. 1c, the fidelity is enhanced by rotation of qubit C about x-axis in strong bit-phase flipping noise.

The fidelity of teleportation in bit-phase flipping with rotation about y-axis is

$$ \begin{array}{@{}rcl@{}} F_{y}^{BPF}=\frac{\eta^{BPF}+[1-(1-p)\cos\theta]2\xi_{x}}{8P_{x}^{BPF}(1+\cos^{2}\frac{\alpha}{2})}, \end{array} $$

(46)

where

$$ \begin{array}{@{}rcl@{}} P_{y}^{BPF}=&&\frac{1}{4A}[2\cos^{2}\frac{\alpha}{2}+[1+(2p-1)\cos\theta]\sin^{2}\frac{\alpha}{2}+\\ &&\xi_{y}]. \end{array} $$

(47)

3.2.4 The Depolarizing Noise

In depolarizing noise, the fidelity of teleportation via rotation about x-axis is

$$ \begin{array}{@{}rcl@{}} {F_{x}^{D}}=\frac{\eta^{D}+2(1-\frac{p}{2})\xi_{x}}{8{P_{x}^{D}}(1+\cos^{2}\frac{\alpha}{2})}, \end{array} $$

(48)

where

$$ \begin{array}{@{}rcl@{}} \eta^{D}=&&2(1-\frac{p}{2})(1+\cos^{2}\theta)\cos^{2}\frac{\alpha}{2}+(1-\frac{p}{2})(1+\\ &&\cos^{2}\frac{\alpha}{2})\sin^{2}\theta+\frac{p}{2}(1-\cos\theta)^{2}\sin^{2}\frac{\alpha}{2};\\ {P_{x}^{D}}=&&\frac{1}{4A}\{2\cos^{2}\frac{\alpha}{2}+[1+(1-p)\cos\theta]\sin^{2}\frac{\alpha}{2}+\\ &&(1-p)\xi_{x}\}. \end{array} $$

(49)

In strong depolarizing noise, F^D, ${F_{x}^{D}}$ with $cos\frac {\theta }{2}$ for ϕ = 0 is shown in Fig. 1d. It is shown that the fidelity in strong depolarizing noise can be enhanced via rotation of qubit C.

The fidelity of teleportation with rotation about y-axis can be written as

$$ \begin{array}{@{}rcl@{}} {F_{y}^{D}}=\frac{\eta^{D}-2(1-\frac{p}{2})\xi_{y}}{8{P_{y}^{D}}(1+\cos^{2}\frac{\alpha}{2})}, \end{array} $$

(50)

where

$$ \begin{array}{@{}rcl@{}} {P_{y}^{D}}=&&\frac{1}{4A}\{2\cos^{2}\frac{\alpha}{2}+[1+(1-p)\cos\theta]\sin^{2}\frac{\alpha}{2}-\\ &&(1-p)\xi_{x}\}. \end{array} $$

(51)

3.2.5 The Amplitude Damping Noise

In amplitude damping noise, the fidelity of teleportation via rotation about x-axis is

$$ \begin{array}{@{}rcl@{}} F_{x}^{AD}=\frac{\eta^{AD}+[(1+\sqrt{1-\gamma})+(1-\sqrt{1-\gamma})\cos\theta]\xi_{x}}{8P_{x}^{AD}(1+\cos^{2}\frac{\alpha}{2})},\\ \end{array} $$

(52)

where

$$ \begin{array}{@{}rcl@{}} \eta^{AD}=&&[\sin^{2}\frac{\alpha}{2}+(\gamma+2\sqrt{1-\gamma})\cos^{2}\frac{\alpha}{2}]\sin^{2}\theta+\\ &&[(2-\gamma)(1+\cos^{2}\theta)+2\gamma\cos\theta]\cos^{2}\frac{\alpha}{2};\\ P_{x}^{AD}=&&\frac{1}{4A}[2\cos^{2}\frac{\alpha}{2}+2\gamma\cos\theta\cos^{2}\frac{\alpha}{2}+(1+\cos\theta)\\ &&\sin^{2}\frac{\alpha}{2}+\sqrt{1-\gamma}\xi_{x}]. \end{array} $$

(53)

Figure 1e shows F^AD, $F_{x}^{AD}$ with respect to amplitude factor $cos\frac {\theta }{2}$ when ϕ = 0 in strong amplitude damping noise.

The fidelity of teleportation via rotation about y-axis is

$$ \begin{array}{@{}rcl@{}} F_{y}^{AD}=\frac{\eta^{AD}-[(1+\sqrt{1-\gamma})+(1-\sqrt{1-\gamma})\cos\theta]\xi_{y}}{8P_{y}^{AD}(1+\cos^{2}\frac{\alpha}{2})},\\ \end{array} $$

(54)

where

$$ \begin{array}{@{}rcl@{}} P_{y}^{AD}=&&\frac{1}{4A}[2\cos^{2}\frac{\alpha}{2}+2\gamma\cos\theta\cos^{2}\frac{\alpha}{2}+(1+\cos\theta)\\ &&\sin^{2}\frac{\alpha}{2}-\sqrt{1-\gamma}\xi_{y}]. \end{array} $$

(55)

3.2.6 The Phase Damping Noise

In phase damping noise, the fidelity of teleportation with rotation about x-axis can be written as

$$ \begin{array}{@{}rcl@{}} F_{x}^{PD}=\frac{\eta^{PD}+[(1+\sqrt{1-\gamma})+(1-\sqrt{1-\gamma})\cos\theta]\xi_{x}}{8P_{x}^{PD}(1+\cos^{2}\frac{\alpha}{2})},\\ \end{array} $$

(56)

where

$$ \begin{array}{@{}rcl@{}} \eta^{PD}=&&2(1+\cos^{2}\theta)\cos^{2}\frac{\alpha}{2}+(\sin^{2}\frac{\alpha}{2}+2\sqrt{1-\gamma}\\ &&\cos^{2}\frac{\alpha}{2})\sin^{2}\theta;\\ P_{x}^{PD}=&&\frac{1}{4A}[2\cos^{2}\frac{\alpha}{2}+(1+\cos\theta)\sin^{2}\frac{\alpha}{2}+\sqrt{1-\gamma}\xi_{x}].\\ \end{array} $$

(57)

As shown in Fig. 1f, the fidelity is enhanced by rotation of qubit C about x-axis.

The fidelity of teleportation with rotation about y-axis is

$$ \begin{array}{@{}rcl@{}} F_{y}^{PD}=\frac{\eta^{PD}-[(1+\sqrt{1-\gamma})+(1-\sqrt{1-\gamma})\cos\theta]\xi_{y}}{8P_{y}^{PD}(1+\cos^{2}\frac{\alpha}{2})},\\ \end{array} $$

(58)

and

$$ \begin{array}{@{}rcl@{}} P_{y}^{PD}=&&\frac{1}{4A}[2\cos^{2}\frac{\alpha}{2}+(1+\cos\theta)\sin^{2}\frac{\alpha}{2}-\sqrt{1-\gamma}\xi_{y}].\\ \end{array} $$

(59)

4 Discussion and Summary

To compare the antinoise capacity of the protocol for teleportation via W state with antinoise capacity of the protocol for teleportation via Bell state, we compute and compare the channel fidelities in such two schemes under the influence of noise and local operation. Similar to the case for teleportation via W state, in scheme of Bell state the noise is assumed to be interact with the entangled particle A during distributed from Bob to Alice. In teleportation via Bell state, the Bell state $\vert \psi \rangle _{AB}=\frac {1}{\sqrt {2}}(\vert 01\rangle +\vert 10\rangle )$ (i.e., the shared state of particle A and particle B) becomes a decoherence state and consequently shrink the QT fidelity with it as a quantum channel.

It is shown that enhancing QT fidelity by rotation of entangled particle is essentially increasing the fidelity of the shared state of particle A and particle B, i.e., making the quantum channel very near to be the Bell state |ψ〉_AB. Following, we analyze and compute the quantum channel fidelities in the present of interaction of particle ‘1’ with noise and rotation of an entangled particle. Afterwards QT fidelities are computed and discussed. Similar to the fidelity of single-qubit teleportation in noise environment, the quantum channel fidelity under the influence of noise and local operation is

$$ \begin{array}{@{}rcl@{}} F_{channel}=\langle\psi_{AB}\vert\rho^{\prime}_{AB}(\alpha, p)\vert\psi_{AB}\rangle, \end{array} $$

(60)

where $\rho ^{\prime }_{AB}(\alpha , p)$ can be the decoherence state of Bell state |ψ〉_AB in QT using Bell state as channel and can also be the decoherence state ρ_AB(α,p) in QT using W state. We derived the channel fidelities F_Bell and F_W under various noises. It is noted that these channel fidelities in the case of rotating particle about x-axis are equal to those rotating about y-axis.In phase flipping noise, the channel fidelities for Bell state and W state after the distribution of qubit A and the rotation of entangled qubit are

$$ \begin{array}{@{}rcl@{}} F_{Bell}^{PF}=&&p\cos^{2}\frac{\alpha}{2};\\ F_{W}^{PF}=&&2p\cos^{2}\frac{\alpha}{2}/(1+\cos^{2}\frac{\alpha}{2}). \end{array} $$

(61)

In amplitude damping noise, the channel fidelities for Bell state and W state after the distribution of qubit A and the rotation of entangled qubit are

$$ \begin{array}{@{}rcl@{}} F_{Bell}^{AD}=&&\frac{1}{2}[\frac{\gamma}{2}+(1-\gamma+\sqrt{1-\gamma})\cos^{2}\frac{\alpha}{2}];\\ F_{W}^{AD}=&&\frac{\cos^{2}\frac{\alpha}{2}(1+\sqrt{1-\gamma}-\frac{\gamma}{2})}{1+\cos^{2}\frac{\alpha}{2}}. \end{array} $$

(62)

In phase damping noise, the fidelities are

$$ \begin{array}{@{}rcl@{}} F_{Bell}^{PD}=&&\frac{(1+\sqrt{1-\gamma})\cos^{2}\frac{\alpha}{2}}{2};\\ F_{W}^{PD}=&&\frac{(1+\sqrt{1-\gamma})\cos^{2}\frac{\alpha}{2}}{1+\cos^{2}\frac{\alpha}{2}}. \end{array} $$

(63)

In bit flipping noise, the fidelities are

$$ \begin{array}{@{}rcl@{}} F_{Bell}^{BF}=&&1-p+(2p-1)\cos^{2}\frac{\alpha}{2};\\ F_{W}^{BF}=&&\frac{1-p+(5p-1)\cos^{2}\frac{\alpha}{2}}{2(1+\cos^{2}\frac{\alpha}{2})}. \end{array} $$

(64)

In bit-phase flipping noise, the fidelities can be computed as

$$ \begin{array}{@{}rcl@{}} F_{Bell}^{BPF}=&&p\cos^{2}\frac{\alpha}{2};\\ F_{W}^{BPF}=&&\frac{1-p+(5p-1)\cos^{2}\frac{\alpha}{2}}{2(1+\cos^{2}\frac{\alpha}{2})}. \end{array} $$

(65)

In depolarizing noise, the fidelities are

$$ \begin{array}{@{}rcl@{}} F_{Bell}^{D}=&&\frac{\frac{p}{2}+(2-\frac{5p}{2})\cos^{2}\frac{\alpha}{2}}{2};\\ {F_{W}^{D}}=&&\frac{\frac{p}{2}+(4-\frac{p}{2})\cos^{2}\frac{\alpha}{2}}{2(1+\cos^{2}\frac{\alpha}{2})}. \end{array} $$

(66)

From the above formulae for channel fidelities, it is shown that the channel fidelity of Bell state in phase flipping noise can not be enhanced by the rotation of entangled qubit. However, the channel fidelity of W state in the phase flipping noise can be enhanced when $\alpha \in \{0,\frac {\pi }{2}\}$. As shown in (61), the channel fidelity of W state after the rotation of the entangled particle is higher than that of Bell state in phase flipping noise.

In case of bit flipping noise, taking the derivative of $1-p+(2p-1)\cos \limits ^{2}\frac {\alpha }{2}$ and $1-p+(5p-1)\cos \limits ^{2}\frac {\alpha }{2}$ with respect to the rotation angle α, it shows that F_Bell increases when noise parameter 0 ≤ p < 0.5 and F_W increases observably when 0 ≤ p < 0.2, with augment of α. The detailed calculation results are shown in Fig. 1. The enhancement effect of channel fidelity by rotating entangle particle arise under a stronger bit flipping noise, for the strongest noise (i.e., p = 0) F_Bell increases from 0 to 1 while F_W increases from 0 to $\frac {1}{\sqrt {2}}$ when α increases from 0 to π.