1 Introduction

Quantum entanglement plays an important role in modern quantum information theory. It is widely used for implementation of quantum communication protocols, like quantum teleportation(QT) [1, 2] and remote state preparation(RSP) [3–7]. Compared with the standard QT, RSP is a transportation of a known state. Meanwhile, the classical information and entanglement costs are invariable in QT, but in RSP it is possible to have a trade-off between entanglement cost and classical information cost [5, 8]. Recently, RSP has attracted many attentions, and a lot of interesting RSP protocols have been proposed one after another, such as oblivious RSP [9], low-entanglement RSP [10], continuous variable RSP [11], joint RSP [12–14], controlled RSP [15], and deterministic RSP [16–18]. Moreover, some RSP protocols have been experimentally implemented [19–21] by using linear optical elements and nuclear magnetic resonance technology.

However, to date most of the previous RSP protocols are considered in close quantum systems which do not suffer from any unwanted interactions with the realistic environment. In fact, a real quantum communication system will unavoidably interact with its surrounding world. These unwanted interactions are generally considered as noises in quantum information processing. In recent years, some RSP protocols in noisy environments have been discussed both theoretically and experimentally. In 2005, Xiang et al. [19] presented a RSP protocol for mixed state in depolarizing and dephasing channel. They experimentally realized the RSP protocol by using spontaneous parametric down-conversion. In 2006, Chen et al. [22] investigated remote preparation of an entangled state through a mixed-state channel in nonideal conditions. And in 2011 Liang et al. [23] considered the RSP of a qubit state and an entangled state via a partially entangled noisy channel. We note that almost all the transmitted states in these previous studies are considered only the single qubit or some special entangled states. If the initial quantum state to be transmitted is a general multiple quantum state and there are more than one information carriers involving in the processing, then what will happen to the noisy RSP scheme? As far as we know, there are few studies involving with these questions. In this paper we consider joint remote preparation of an arbitrary two-qubit state in noisy environments.

In an open quantum system, the noise source is mainly derived from the decoherence effect, which is caused by the interaction with its environment. Under the assumption of Markov and Born approximations, the time evolution of an open quantum system can be described by a master equation in the Lindblad form [24] for the density operator ρ(t) [19, 22, 23]. On the other hand, in a RSP protocol, the senders and the receivers need to share a quantum state as communication channel to complete the preparation. All of the ideal RSP protocols do not care how the channel sate to be shared. But in a realistic situation, the channel state must be prepared by one side, then the generator distributes the corresponding qubits to their owners through the outside noisy environment. This process will convert the pure channel state into a mixed one. In this paper, we no longer pay attention to the time evolution of an open system in the RSP process, but to the noisy influence on the process of distributing the channel qubits. We use Kraus operators to describe the noisy effect and analyze two specific kinds of noises, the amplitude-damping noise and the phase-damping noise. We use fidelity to describe how close the final state with the original state are, and how much information has been lost in the RSP process. Interestingly, studies show in these two cases, if the initial state is sucessfully prepared, the fidelities will only depend on the amplitude factor of the initial state and decoherence rate, but have nothing to do with the phase information. Finally, we will make some discussions between the two cases to show which will lose more information in the transmission of quantum state.

This paper is organized as follows. In Sect. 2, we introduce the joint remote preparation of an arbitrary two-qubit state using a six-qubit cluster state in ideal condition. In Sect. 3, we analyze the case that the channel qubits are distributed through amplitude-damping noisy environment. In Sect. 4, we consider the situation that the channel qubits are distributed through phase-damping noisy environment. Finally, we give some discussions and a brief conclusion for these two cases in Sect. 5.

2 Review of Wang’s Joint Remote Preparation of an Arbitrary Two-Qubit State

Need to declare that we no longer pay attention to the ideal JRSP, and many work has been done in this area. We take out one of them as example to utilize. In 2011, Wang et. al. [25] introduced a JRSP protocol utilizing a six-qutbit cluster state to prepare an arbitrary two-qubit state. Based on their works, we will make a study on its noisy situation.

Firstly we briefly describe their scheme. Suppose two participants Alice and Bob want to help the remote receiver Charlie prepare an arbitrary two-qubit quantum state described as

$$ | T \rangle= a_0 e^{i\theta_0 }| {00} \rangle+ a_1 e^{i\theta_1 }| {01} \rangle+ a_2 e^{i\theta_2 }| {10} \rangle+ a_3 e^{i\theta_3 }| {11} \rangle, $$
(1)

where the coefficients a s (s=0,1,2,3) are real with the normalization condition \(a_{0} ^{2} + a_{1} ^{2} + a_{2} ^{2} + a_{3} ^{2} = 1\), and θ t ∈[0,2π](t=0,1,2,3). The information of |T〉 state is shared by Alice and Bob. Alice owns the amplitude information a s , while Bob knows the phase information θ t .

In order to transmit the initial state to remote receiver Charlie, they need to share a quantum state as communication channel, as follows [26]

$$ | C_6 \rangle= \frac{1}{2}(| {000000} \rangle+ | {000111} \rangle+ | {111000} \rangle- | {111111} \rangle)_{123456}. $$
(2)

Here, Alice holds particles (1,4). Bob owns particles (2,5). And particles (3,6) belong to receiver Charlie.

Then Alice and Bob choose orthogonal measurement bases to measure their local qubits, respectively. The form of Alice’s and Bob’s measurement bases are shown as follows:

Alice chooses {|φ 1〉14,|φ 2〉14,|φ 3〉14,|φ 4〉14} as her local measurement basis:

$$ \left\{ { \begin{aligned} | {\varphi^1} \rangle_{14} &= a_0 | {00} \rangle+ a_1 | {01} \rangle+ a_2 | {10} \rangle- a_3 | {11} \rangle\\ | {\varphi^2} \rangle_{14} &= a_1 | {00} \rangle- a_0 | {01} \rangle- a_3 | {10} \rangle- a_2 | {11} \rangle\\ | {\varphi^3} \rangle_{14} &= a_2 | {00} \rangle+ a_3 | {01} \rangle- a_0 | {10} \rangle+ a_1 | {11} \rangle\\ | {\varphi^4} \rangle_{14} &= a_3 | {00} \rangle- a_2 | {01} \rangle+ a_1 | {10} \rangle+ a_0 | {11} \rangle \end{aligned} } \right. $$
(3)

And Bob chooses {|ϕ 1〉25,|ϕ 2〉25,|ϕ 3〉25,|ϕ 4〉25} as her basic measurement basis:

$$ \left\{ { \begin{aligned} | {\phi^1} \rangle_{25} &= \frac{1}{2} (e^{ - i\theta_0 }| {00} \rangle+ e^{ - i\theta_1 }| {01} \rangle+ e^{ - i\theta _2 }| {10} \rangle+ e^{ - i\theta_3 }| {11} \rangle) \\ | {\phi^2} \rangle_{25} &= \frac{1}{2} (e^{ - i\theta_0 }| {00} \rangle- e^{ - i\theta_1 }| {01} \rangle+ e^{ - i\theta _2 }| {10} \rangle- e^{ - i\theta_3 }| {11} \rangle) \\ | {\phi^3} \rangle_{25} &= \frac{1}{2} (e^{ - i\theta_0 }| {00} \rangle- e^{ - i\theta_1 }| {01} \rangle- e^{ - i\theta _2 }| {10} \rangle+ e^{ - i\theta_3 }| {11} \rangle) \\ | {\phi^4} \rangle_{25} &= \frac{1}{2} (e^{ - i\theta_0 }| {00} \rangle+ e^{ - i\theta_1 }| {01} \rangle- e^{ - i\theta _2 }| {10} \rangle- e^{ - i\theta_3 }| {11} \rangle) \end{aligned} } \right. $$
(4)

Under these two sets of bases, the quantum system |C 6〉 can be rewritten as

$$\begin{aligned} | C_6 \rangle &= \frac{1}{2}(| {000000} \rangle+ | {000111} \rangle+ | {111000} \rangle- | {111111} \rangle)_{123456} \\ &= \frac{1}{4}| {\varphi^1} \rangle_{14} [| {\phi^1} \rangle_{25} (a_0 e^{i\theta_0 }| {00} \rangle+ a_1 e^{i\theta_1 }| {01} \rangle + a_2 e^{i\theta_2 }| {10} \rangle+ a_3 e^{i\theta_3 }| {11} \rangle )_{36} \\ & \qquad\qquad\ \ + | {\phi^2} \rangle_{25} (a_0 e^{i\theta_0 }| {00} \rangle- a_1 e^{i\theta_1 }| {01} \rangle+ a_2 e^{i\theta_2 }| {10} \rangle- a_3 e^{i\theta_3 }| {11} \rangle)_{36} \\ & \qquad\qquad\ \ + | {\phi^3} \rangle_{25} (a_0 e^{i\theta_0 }| {00} \rangle- a_1 e^{i\theta_1 }| {01} \rangle- a_2 e^{i\theta_2 }| {10} \rangle+ a_3 e^{i\theta_3 }| {11} \rangle)_{36} \\ & \qquad\qquad\ \ + | {\phi^4} \rangle_{25} (a_0 e^{i\theta_0 }| {00}\rangle+ a_1 e^{i\theta_1 }| {01} \rangle- a_2 e^{i\theta_2 }| {10} \rangle- a_3 e^{i\theta_3 }| {11} \rangle)_{36} ] \\ &\quad{}+ \frac{1}{4}| {\varphi^2} \rangle_{14} [| {\phi^1} \rangle_{25} (a_1 e^{i\theta_0 }| {00} \rangle- a_0 e^{i\theta_1 }| {01} \rangle - a_3 e^{i\theta_2 }| {10} \rangle+ a_2 e^{i\theta_3 }| {11} \rangle )_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^2} \rangle_{25} (a_1 e^{i\theta_0 }| {00} \rangle+ a_0 e^{i\theta_1 }| {01} \rangle- a_3 e^{i\theta_2 }| {10} \rangle- a_2 e^{i\theta_3 }| {11} \rangle)_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^3} \rangle_{25} (a_1 e^{i\theta_0 }| {00} \rangle+ a_0 e^{i\theta_1 }| {01} \rangle+ a_3 e^{i\theta_2 }| {10} \rangle+ a_2 e^{i\theta_3 }| {11} \rangle)_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^4} \rangle_{25} (a_1 e^{i\theta_0 }| {00} \rangle- a_0 e^{i\theta_1 }| {01} \rangle+ a_3 e^{i\theta_2 }| {10} \rangle- a_2 e^{i\theta_3 }| {11} \rangle)_{36} ] \\ &\quad{}+ \frac{1}{4}| {\varphi^3} \rangle_{14} [| {\phi^1} \rangle_{25} (a_2 e^{i\theta_0 }| {00} \rangle+ a_3 e^{i\theta_1 }| {01} \rangle - a_0 e^{i\theta_2 }|{10} \rangle- a_1 e^{i\theta_3 }| {11} \rangle )_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^2} \rangle_{25} (a_2 e^{i\theta_0 }| {00} \rangle- a_3 e^{i\theta_1 }| {01} \rangle- a_0 e^{i\theta_2 }| {10} \rangle+ a_1 e^{i\theta_3 }| {11} \rangle)_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^3} \rangle_{25} (a_2 e^{i\theta_0 }| {00} \rangle- a_3 e^{i\theta_1 }| {01} \rangle+ a_0 e^{i\theta_2 }| {10} \rangle- a_1 e^{i\theta_3 }| {11} \rangle)_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^4} \rangle_{25} (a_2 e^{i\theta_0 }| {00} \rangle+ a_3 e^{i\theta_1 }| {01} \rangle+ a_0 e^{i\theta_2 }| {10} \rangle+ a_1 e^{i\theta_3 }| {11} \rangle)_{36} ] \\ &\quad{}+ \frac{1}{4}| {\varphi^4} \rangle_{14} [| {\phi^1} \rangle_{25} (a_3 e^{i\theta_0 }| {00} \rangle- a_2 e^{i\theta_1 }| {01} \rangle + a_1 e^{i\theta_2 }| {10} \rangle- a_0 e^{i\theta_3 }| {11} \rangle )_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^2} \rangle_{25} (a_3 e^{i\theta_0 }| {00} \rangle+ a_2 e^{i\theta_1 }| {01} \rangle+ a_1 e^{i\theta_2 }| {10} \rangle+ a_0 e^{i\theta_3 }| {11} \rangle)_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^3} \rangle_{25} (a_3 e^{i\theta_0 }| {00} \rangle+ a_2 e^{i\theta_1 }| {01} \rangle- a_1 e^{i\theta_2 }| {10} \rangle- a_0 e^{i\theta_3 }| {11} \rangle)_{36} \\ & \qquad\qquad\quad\ \ + | {\phi^4} \rangle_{25} (a_3 e^{i\theta_0 }| {00} \rangle- a_2 e^{i\theta_1 }| {01} \rangle- a_1 e^{i\theta_2 } | 10 \rangle+ a_0 e^{i\theta_3 } | 11 \rangle)_{36} ]. \end{aligned}$$
(5)

From (4), we can see that if Alice’s measurement result is |φ 1〉14, then Charlie will have a chance to recover the original state by performing a unitary transformation on particles (3, 6) in accordance with the Bob’s help. When Alice and Bob’ measurement results are in other situations, Charlie can not reconstruct the original state. We will list all the successful recover transformations in Table 1.

Table 1 In this table we list Charlie’s recover transformations accompanied with the other two participants’ measurement outcomes. Here, we only consider the successful situations that Alice’s measurement outcome is |φ 1〉14
Full size table

Then, we will generalize the above ideal protocol to a realistic situation. In the above JRSP scheme, the three participants will share the state |C 6〉 with each other before the communication. However, in a realistic situation, it needs one participant, for example, the Charlie to generate the |C 6〉 state in his laboratory at first. Then he keeps particles (3, 6) with him, and send the (1, 4) and (2, 5) particles to Alice and Bob via the noisy channel, respectively. Due to the interaction with the environment, the |C 6〉 state will do some changes. Here we will consider the case of amplitude damping noise and phase-damping noise, respectively. We use fidelity to describe how close the final state and the original state are. We also make a discussion between these two cases to show that in which noisy environment more information will be lost.

3 Joint Remote Preparation of an Arbitrary Two-Qubit State Via Amplitude-Damping Noisy Environment

In this section, we consider the amplitude-damping noise as noisy model. Amplitude-damping noise is one of the most important decoherence noise that it can be used to describe the energy-dissipation effects due to loss of energy from a quantum system. The action of amplitude-damping noise is shown by a set of Kraus operators [27], which are given as follows:

$$ E_{0}^a = \left[ \begin{array}{c@{\quad}c} 1 & 0 \\ 0 & \sqrt{1 - \eta_{a}} \end{array} \right], \qquad E_{1}^a = \left[ \begin{array}{c@{\quad}c} 0 & \sqrt{ \eta_{a} } \\ 0 & 0 \end{array} \right], $$
(6)

where η a (0<η a <1) is the decoherence rate to describe the error probability when the quantum states pass through the amplitude-damping noisy environment.

Without loss of generality, we assume Charlie prepares the |C 6〉 state in his laboratory. Then, he will send the particles (1, 4) and (2, 5) to Alice and Bob via the amplitude-damping noisy environment, respectively. We describe the effect of amplitude damping noise on the shared state |C 6〉 as

$$ \xi(\rho) = \sum_{i,j}E_{i}^{a1}E_{i}^{a4} E_{j}^{a2}E_{j}^{a5} \rho {E_{i}^{a1}}^{\dagger}{E_{i}^{a4}}^{\dagger} {E_{j}^{a2}}^{\dagger }{E_{j}^{a5}}^{\dagger}, $$
(7)

where the subscripts i,j∈{0,1} represent which Kraus operator will be chosen from (6) to preform, and the superscripts (1,2,4,5) represent the operator E act on which qubit. Also, the ρ=|C 6〉〈C 6| is the density matrix of shared state |C 6〉 in the above JRSP protocol, and ξ denotes a quantum operation which maps from ρ to ξ(ρ) due to the noise.

Then, Alice measures particles (1, 4) with basis {|φ 1〉14,|φ 2〉14,|φ 3〉14,|φ 4〉14}, and broadcasts her measurement result to Charlie via classical communication. Meanwhile, Bob will also measure particles (2, 5) with basis {|ϕ 1〉25,|ϕ 2〉25,|ϕ 3〉25,|ϕ 4〉25}, and send the classical result to Charlie. Finally, according to Alice and Bob’s measurement results, Charlie will carry out appropriate operations on his own qubits to recover the original state.

We know that in Wang’s JRSP scheme, only when Alice’s measurement result is |φ 1〉14, Charlie can successfully recover the original state. While in other cases, Charlie will not do any recover operators, but directly to give up the final state in his side. Then the communication scheme will fail. The same is true in noisy environments. Charlie will not perform any recover operators on the final state of the failing cases. It means the final state in the failing cases is not a actual output state, but in some sense is a random qubit for the initial prepared state. Therefore, we will not take into account the case in failure, but only to analyze the fidelity in successful preparation.

Afterwards, the density matrix of the final state at Charlie’s side can be expressed as

$$ \rho_{out} = \operatorname{Tr}_{14,25}\{U_{0} \xi(\rho) U_{0}^\dagger\}, $$
(8)

where \(\operatorname{Tr}_{14,25}\) is the partial trace over particles (1, 4) and (2, 5), and U 0 is a untiary operator to describe the JRSP process, which is shown in the previous part of our paper. We know that if the JRSP is ideal, the density-matrix ρ out is identical to the original state to be transmitted up to the normalization factor. To analyse the influence of noise on the JRSP precess, here we only take into account the cases of the successful preparation. So the U 0 is given by

$$ U_{0} = (I_{14} \otimes I_{25} \otimes\sigma^k_{36})(I_{14} \otimes| {\phi^k} \rangle_{25} \langle{\phi^k} |_{25} \otimes I_{36})(| {\varphi^1} \rangle_{14} \langle{\varphi^1} |_{14} \otimes I_{25} \otimes I_{36}). $$
(9)

Here, k∈{1,2,3,4}, and \(\sigma^{1}_{36} = I_{1} \otimes I_{4}, \sigma^{2}_{36} = I_{1} \otimes\sigma_{z}, \sigma^{3}_{36} = \sigma_{z} \otimes\sigma_{z}, \sigma^{4}_{36} = \sigma_{z} \otimes I_{4}\).

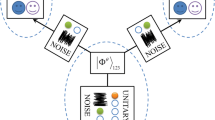
In order to describe the process more clearly, we will show it in Fig. 1. The top line belongs to Charlie, the middle line belongs to Bob, and the bottom line belongs to Alice. The dotted box denotes the noisy environment which affect on Alice’s and Bob’s particles, but not on Charlie’s particles. It means that the channel state is prepared on Charlie’side. After receiving the measurement results, Charlie will perform some operators to recover the original state.

Fig. 1
figure 1

The top line belongs to Charlie, the middle line belongs to Bob, and the bottom line belongs to Alice. Charlie firstly prepares the channel state C 6 in his laboratory, then distributes particles(1, 4) and (2, 5) to Alice and Bob, respectively. The dotted box denotes the noisy environment which affect on Alice’s and Bob’s particles in the distribution process. M 1=|φ 1〉14〈φ 1|14 denotes Alice’s measurement operator on his own particles (1, 4) (here we only consider the case of successful preparation). M 2=|φ k〉25〈φ k|25 denotes Bob’s measurement operators on his own particles (2, 5). \(\sigma^{k}_{36}\) is Charlie’s recover operator, which depends on Bob’s measurement result k. The dotted arrows represent classical communication form Alice and Bob to Charlie. After receiving the measurement results, Charlie will perform some operators to recover the original state

Full size image

In Charlie’s side, how close the final state with the original state are? We use fidelity to answer this question. The state we want to prepare is \(| T \rangle= a_{0} e^{i\theta_{0} }| {00} \rangle+ a_{1} e^{i\theta_{1} }| {01} \rangle+ a_{2} e^{i\theta_{2} }|{10} \rangle+ a_{3} e^{i\theta_{3} }| {11} \rangle\), so the fidelity can be expressed as

$$ F = \langle T | \rho_{out} | T \rangle, $$
(10)

which is the square of the usual fidelity \(F(\rho, \sigma) = \operatorname{Tr} \sqrt {\rho^{1/2} \sigma\rho^{1/2}}\). Thus F=1 means the perfect communication. If F becomes smaller and smaller, it indicates that we have lost more and more information in this process.

Now we detail our noisy JRSP protocol via the amplitude damping noisy environment. From the above discussion, we know that the shared state, influenced by the environment noise, will become a mixed state after the distribution of particles

$$\begin{aligned} \xi(\rho) &= \frac{1}{4}\{[| 000000 \rangle+ (1 - \eta_{a})| 000111 \rangle+ (1 - \eta_{a})| 111000 \rangle- (1 - \eta_{a})^{2}| 111111 \rangle] \\ &\quad{}\times[\langle000000 | + (1 - \eta_{a})\langle000111 | + (1 - \eta_{a})\langle111000 | - (1 - \eta_{a})^{2}\langle111111 |] \\ & \quad{} + (1 - \eta_{a})^2 \eta_{a}^2 | 101101 \rangle\langle101101 | + (1 - \eta_{a})^2 \eta_{a}^2 | 011011 \rangle\langle011011 | \\&\quad{} + \eta _{a}^4 | 001001 \rangle\langle001001 |\}. \end{aligned}$$
(11)

Here, three participants take their particles in their own sides, respectively. Then, according to (8) and (9), it can be easy to get the resultant state ρ out in Charlie’s side. From (9), we can intuitively see that the ρ out is related to Bob’s measurement result k. However, after calculation we get that Charlie’s output state ρ out is independent of k. And the ρ out is shown as follows

$$\begin{aligned} \rho_{out} &= [a_0 e^{i\theta_0 }| {00} \rangle+ (1 - \eta_{a}) a_1 e^{i\theta_1 }| {01} \rangle+ (1 - \eta_{a}) a_2 e^{i\theta_2 }| {10} \rangle+ (1 - \eta_{a})^2 a_3 e^{i\theta_3 }| {11} \rangle] \\ &\quad{}\times[a_0 e^{-i\theta_0 }\langle{00} | + (1 - \eta_{a}) a_1 e^{-i\theta_1 }\langle{01} | + (1 - \eta_{a}) a_2 e^{-i\theta_2 }\langle{10} | + (1 - \eta_{a})^2 a_3 e^{-i\theta_3 }\langle{11} |] \\ &\quad{} + a_3^2 (1-\eta_{a})^2 \eta_{a}^2 | 11 \rangle\langle11 | + a_0^2 (1-\eta_{a})^2 \eta_{a}^2 | 11 \rangle\langle11 | + a_0^2 \eta _{a}^4 | 11 \rangle\langle11 |. \end{aligned}$$
(12)

Then we calculate the fidelity to describe how much information has been lost in this process. From (10) and (12), we can get that

$$\begin{aligned} F &= [a_0^2 + (1 - \eta_{a}) a_1^2 + (1 - \eta_{a}) a_2^2 + (1 - \eta _{a})^2 a_3^2]^2 + a_3^4 (1-\eta_{a})^2 \eta_{a}^2 \\&\quad{}+ a_0^2 a_3^2 (1-\eta _{a})^2 \eta_{a}^2 + a_0^2 a_3^2 \eta_{a}^4. \end{aligned}$$
(13)

Interestingly, we note that the fidelity F for amplitude-damping noise only depends on the amplitude factor of the prepared state a s and the decoherence rat η, but has nothing to do with the phase parameter θ t . In particular, for maximal entangled state to be prepared \(a_{0} = a_{1} = a_{2} = a_{3} = \frac{1}{2}\), \(F = [\frac{1}{4} + \frac{1}{2}(1 - \eta_{a}) + \frac{1}{4} (1 - \eta_{a})^{2} ]^{2} + \frac {1}{8} (1-\eta_{a})^{2} \eta_{a}^{2} + \frac{1}{16} \eta_{a}^{4} \); for \(\eta _{a} = 1, F = a_{0}^{4} + a_{0}^{2}a_{3}^{2}\); and for η a =0,F=1, that is the perfect JRSP.

4 Joint Remote Preparation of an Arbitrary Two-Qubit State Via Phase-Damping Noisy Environment

In this section we would like to repeat the calculation of preceding section while replacing the amplitude-damping noise by phase-damping noise. Compared with the amplitude-damping noise, the phase-damping noise describes more about the loss of quantum information but without the energy dissipation. Before we begin our calculation, we firstly show the Kraus operators [27] description of phase-damping noise

$$ E_{0}^p = \sqrt{1 - \eta_{p}} I, \qquad E_{1}^p = \sqrt{\eta_{p}} \left[ \begin{array}{cc} 1 & \ \ 0 \\ 0 & \ \ 0 \end{array} \right], \qquad E_{2}^p = \sqrt{\eta_{p}} \left[ \begin{array}{cc} 0 & \ \ 0 \\ 0 & \ \ 1 \end{array} \right], $$
(14)

where η p (0<η p <1) is the decoherence rat of phase-damping noise.

Now we first describe the noisy effect on the communication channel |C 6〉. Just like the preceding protocol, in this case we similarly assume that Charlie prepares the |C 6〉 in his laboratory, and respectively distribute the particles to remote participants through phase-damping noisy environment. After this process, we know the shared state will become a mixed state due to the noisy effects, as follows

$$ \xi(\rho) = \sum_{i,j}E_{i}^{p1}E_{i}^{p4} E_{j}^{p2}E_{j}^{p5} \rho {E_{i}^{p1}}^{\dagger}{E_{i}^{p4}}^{\dagger} {E_{j}^{p2}}^{\dagger }{E_{j}^{p5}}^{\dagger}, $$
(15)

where the subscripts i,j∈{0,1,2} denote which Karus operator in (14) will be performed, and the superscripts (1,2,4,5) represent the operator E will act on which qubit.

In this case, the ξ(ρ) becomes

$$\begin{aligned} \xi(\rho) &= \frac{1}{4}\{(1 - \eta_{p})^4(| 000000 \rangle+ | 000111 \rangle+ | 111000 \rangle- | 111111 \rangle) (\langle000000 | \\&\quad{}+ \langle000111 | + \langle111000 | - \langle111111 |) \\&\quad{} + 2(1 - \eta_{p})^2 \eta_{p}^2 (| 000000 \rangle\langle000000 | + | 111111 \rangle\langle111111 |) \\&\quad{}+ \eta_{p}^4 (| 000000 \rangle \langle000000 | + | 111111 \rangle\langle111111 |) \}. \end{aligned}$$
(16)

Then, three participants will remotely prepare the state T through the ξ(ρ) channel similarly as the ideal JRSP protocol. And this process has been described in (9). Therefore, according to (8) and (9), Charlie can get the output state as

$$\begin{aligned} \rho_{out} &= (1 - \eta_p)^4 (a_0 e^{i\theta_0 }| {00} \rangle+ a_1 e^{i\theta_1 }| {01} \rangle+ a_2 e^{i\theta_2 }| {10} \rangle+ a_3 e^{i\theta_3 }| {11} \rangle) \\ &\quad{}\times(a_0 e^{-i\theta_0 }\langle{00} | + a_1 e^{-i\theta _1 }\langle{01} | + a_2 e^{-i\theta_2 }\langle{10} | + a_3 e^{-i\theta_3 }\langle{11} |) \\ &\quad{} + [2(1-\eta_{p})^2 \eta_{p}^2 + \eta_{p}^4]( a_0^2| 00 \rangle \langle00 | + a_3^2 | 11 \rangle\langle11 |). \end{aligned}$$
(17)

Same as above mentioned, in this case the ρ out is also independent of Bob’s measurement result k. Meanwhile, in order to depict how much information is lost through the phase-damping channel, it is quite useful to calculate the fidelity between ρ out and the initial state T, which is defined by (10). And according to (10), we can get the fidelity

$$ F = (1 - \eta_p)^4 + [2(1 - \eta_p)^2 \eta_p^2 + \eta_p^4](a_0^4 + a_3^4). $$
(18)

The same as the former case, we find that the fidelity here is also independent of the phase parameter θ t . In particular, for the maximal entangled state to be prepared, \(a_{0} = a_{1} = a_{2} = a_{3} = \frac {1}{2}\), \(F = (1 - \eta_{p})^{4} + \frac{1}{8}[2(1 - \eta_{p})^{2} \eta_{p}^{2} + \eta_{p}^{4}] \); for \(\eta_{p} = 1, F = a_{0}^{4} + a_{3}^{4}\); and for η p =0,F=1, that is the ideal JRSP.

5 Discussions and Conclusions

Now we turn our attention to analyze the fidelities for these two cases. Interestingly, we find if the initial state has been successfully prepared, the fidelities for both of the two cases only depend on amplitude parameter of the initial state and the decoherence rate, but not on the phase parameter of the prepared state.

In Fig. 2, we plot the fidelity with noise parameter η in the condition that the prepared state is maximal entangled state, i.e., \(a_{0} = a_{1} = a_{2} = a_{3} = \frac{1}{2}\). From the figure, we can find the fidelity influenced by amplitude-damping noise decreases as η becomes larger, but the fidelity for phase-damping noise decreases first, then increasing. When η=0, the fidelity for these two cases have the same maximal value, F=1; while η=1, the two fidelities also get the same value, F=1/8, which is the minimal value for amplitude-damping noise, but not for the phase-damping noise. Moreover, the plot shows that the fidelity for amplitude-damping noise is always larger than the phase-damping channel, which implies that the state transferred through phase-damping noise environment will lose more information than amplitude-damping noise environment.

Fig. 2
figure 2

The fidelities of amplitude-damping noise and phase-damping noise in the condition that the prepared state is maximal entangled state. The solid line stands for the phase-damping noise, the dashed line for the amplitude-damping noise. The plot shows in this condition that F for amplitude-damping noise is always larger than phase-damping noise, which implies that the state transferred through phase-damping noise environment will lose more information than amplitude-damping noise environment

Full size image

In summary, we present a practical joint remote preparation scheme of a general two-qubit state under the influence of two important decoherence noises, the amplitude-damping noise and the phase-damping noise. The effects of these two noises are discussed by the state fidelity. Studies show the fidelities for both of the two cases depend on the amplitude parameter of the prepared state and the decoherence rate η, but not on the phase parameter. Meanwhile, the decoherence rate η get more close to 0, the fidelity will be more close to 1. When η=1, the fidelity get the maximal value F=1 for both two cases, which means the perfect JRSP. Furthermore, in some special conditions such as the prepared state is maximal entangled state, the effects of amplitude-damping noise on the state transmission is relatively stronger than that of the phase-damping noise.

In this paper, we have investigated the effect of noisy environment for RSP. Compared with previous works, we consider the situation that the scheme involves more than one participants, and the state to be prepared is not single qubit but an arbitrary two-qubit state. However, how to reduce, further more, to eliminate the influence of these noises to improve the transmission efficiency should be a more important thing, and it is our future work.