1 Introduction

Quantum entanglement plays a central role for some applications in quantum information science [1]. Also high-dimensional entanglement is very important physical resource in quantum information processing. With the realization of preparing a high-dimensional quantum state [2], during the last few years, the high-dimensional aspects of various topics in a quantum information system have been proposed, such as superdense coding [3], quantum key distribution [4], and quantum teleportation [5,6,7,8,9,10,11,12,13,14,15,16], and so on. Compared with qubits, high-dimensional quantum systems are better suited for certain purposes. For instance, Braß and Macchiavello [17] showed that, in the presence of noise, qudit schemes for quantum cryptography are more secure than protocols using qubit states. Klimov et al. [18] pointed out that the quantum computation with qutrits instead of a qubit is the exponential increase of the available Hilbert space with the same amount of physical resources. Therefore, extending the local implementation of the nonlocal quantum operation to a high-dimensional system is important.

As is known to all, quantum teleportation, proposed by Bennett et al [19] is one of the most important aspects of quantum information science. Since then, teleportation has always interested a lot of researchers in both theoretical and experimental respects [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. Recently, Zha et al. [39] presented the original bidirectional controlled quantum teleportation (BCQT) scheme. In their scheme, two users can simultaneously exchange their single qubit states. Since then, several different works for BCQT have been proposed by using different kinds of entangled states as the quantum channel [40,41,42,43,44,45,46,47,48]. However, one can notice easily that all of above schemes for BCQT [39,40,41,42,43,44,45,46,47,48] have dealt with problem by using a qubit system. We find that so far no scheme has been reported for BCQT with high-dimensional systems. In this paper, we propose a new scheme for BCQT with three-dimensional system. In this scheme, two distant parties, Alice and Bob, are not only senders but also receivers, and Alice wants to transmit an unknown state of single qutrit to Bob, and at the same time Bob wishes to transmit another unknown state of single qutrit to Alice. It is shown that, only if the two users and the controller collaborate with each other, the BCQT can be completed successfully.

2 Generalized Bell Basis and Five-qutrit Entangled Quantum Channel

Let us first review the generalized Bell basis (GBB). The GBB of the Hilbert space of two particles with three dimensions is [10]

$$ |{\Psi}_{nm}\rangle={\Sigma}_{j} e^{2\pi ijn}|j\rangle\otimes |j+m \ \texttt{mod} \ 3 \rangle/\sqrt{3}, $$
(1)

where n, m, j = 0, 1, 2. More explicitly

$$\begin{array}{@{}rcl@{}} &&|{\Psi}_{00}\rangle=\frac{1}{\sqrt{3}}(|00\rangle+|11\rangle+|22\rangle), \\ &&|{\Psi}_{10}\rangle=\frac{1}{\sqrt{3}}(|00\rangle+e^{2\pi i/3}|11\rangle+e^{4\pi i/3}|22\rangle), \\ &&|{\Psi}_{20}\rangle=\frac{1}{\sqrt{3}}(|00\rangle+e^{4\pi i/3}|11\rangle+e^{2\pi i/3}|22\rangle), \\ &&|{\Psi}_{01}\rangle=\frac{1}{\sqrt{3}}(|01\rangle+|12\rangle+|20\rangle), \\ &&|{\Psi}_{11}\rangle=\frac{1}{\sqrt{3}}(|01\rangle+e^{2\pi i/3}|12\rangle+e^{4\pi i/3}|20\rangle), \\ &&|{\Psi}_{21}\rangle=\frac{1}{\sqrt{3}}(|01\rangle+e^{4\pi i/3}|12\rangle+e^{2\pi i/3}|20\rangle), \\ &&|{\Psi}_{02}\rangle=\frac{1}{\sqrt{3}}(|02\rangle+|10\rangle+|21\rangle), \\ &&|{\Psi}_{12}\rangle=\frac{1}{\sqrt{3}}(|02\rangle+e^{2\pi i/3}|10\rangle+e^{4\pi i/3}|21\rangle), \\ &&|{\Psi}_{22}\rangle=\frac{1}{\sqrt{3}}(|02\rangle+e^{4\pi i/3}|10\rangle+e^{2\pi i/3}|21\rangle). \end{array} $$
(2)

Through simple calculation, it can be shown that the single-body operation

$$\begin{array}{@{}rcl@{}} &&U_{00}=\left( \begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right), \\ &&U_{10}=\left( \begin{array}{lll} 1 & 0 & 0 \\ 0 & e^{2\pi i/3} & 0 \\ 0 & 0 & e^{4\pi i/3} \end{array}\right), \\ &&U_{20}=\left( \begin{array}{lll} 1 & 0 & 0 \\ 0 & e^{4\pi i/3} & 0 \\ 0 & 0 & e^{2\pi i/3} \end{array}\right), \\ &&U_{01}=\left( \begin{array}{lll} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right), \\ &&U_{11}=\left( \begin{array}{lll} 0 & 0 & e^{4\pi i/3} \\ 1 & 0& 0 \\ 0 & e^{2\pi i/3} & 0 \end{array}\right), \\ &&U_{21}=\left( \begin{array}{lll} 0 & 0 & e^{2\pi i/3} \\ 1 & 0& 0 \\ 0 & e^{4\pi i/3} & 0 \end{array}\right), \\ &&U_{02}=\left( \begin{array}{lll} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array}\right), \\ &&U_{12}=\left( \begin{array}{lll} 0 & e^{2\pi i/3} & 0 \\ 0 & 0 & e^{4\pi i/3} \\ 1 & 0 & 0 \end{array}\right), \\ && U_{22}=\left( \begin{array}{lll} 0 & e^{4\pi i/3} & 0 \\ 0 & 0 & e^{2\pi i/3} \\ 1 & 0 & 0 \end{array}\right) \end{array} $$
(3)

will transform |Ψ00〉 into the corresponding states in Eq. (1), respectively,

$$ U_{nm}|{\Psi}_{00}\rangle=|{\Psi}_{nm}\rangle. $$
(4)

In order to realize the BCQT with three-dimensional system, now we prepare a five-qutrit quantum channel composed of the direct product of a three-qutrit entangled state and a two-qutrit pair. Supposing a state preparer Victor has a two-qutrit pair and a three-qutrit entangled state, which are given by

$$\begin{array}{@{}rcl@{}} |r_{1}\rangle_{12}=\frac{1}{\sqrt{3}}(|00\rangle+|11\rangle+|22\rangle)_{12}, \end{array} $$
(5)

and

$$\begin{array}{@{}rcl@{}} |r_{2}\rangle_{345}=\frac{1}{\sqrt{3}}(|000\rangle+|111\rangle+|222\rangle)_{345}, \end{array} $$
(6)

The direct product state |R〉 can be described as

$$\begin{array}{@{}rcl@{}} |R\rangle&&=|r_{1}\rangle_{12}\otimes |r_{2}\rangle_{345} \\ &&=\frac{1}{3}(|00000\rangle+|00111\rangle+|00222\rangle+|11000\rangle+|11111\rangle \\ &&\ \ \ \ +|11222\rangle+|22000\rangle+|22111\rangle+|22222\rangle)_{12345}. \end{array} $$
(7)

To achieve the five-qutrit entangled quantum channel, Victor can perform three three-dimensional C-NOT gates C25, C35 and C45 on his qutrits 2, 3, 4, 5 successively. Here operation C i j acts on a pair of qutrits i and j in the following manner [4].

$$\begin{array}{@{}rcl@{}} C_{ij}|k, l\rangle_{ij}=|k,\ k+l\rangle_{ij}, \end{array} $$
(8)

and C i j denotes that i as control qutrit and j as target one. After that, the direct product state |R〉 (see Eq. (7)) will become a five-qutrit entangled state, which is given by

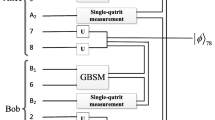
$$\begin{array}{@{}rcl@{}} |Q\rangle&&= \frac{1}{3}(|00000\rangle+|00110\rangle+|00220\rangle+|11001\rangle+|11111\rangle \\ &&\ \ \ \ +|11221\rangle+|22002\rangle+|22112\rangle+|22222\rangle)_{12345}. \end{array} $$
(9)

To help users Alice, Bob and controller Charlie complete the BCQT. Victor distributes the qutrits 1 and 3 to Alice, qutrits 2 and 4 to Bob, and qutrit 5 to Charlie, respectively. Thus, the five-qutrit entangled channel shared by Alice, Bob and Charlie has been achieved.

3 The BCQT with Three-dimensional Systems

Supposed that Alice has an unknown single-qutrit state

$$ |p_{0}\rangle_{A}=(\alpha_{0}|0\rangle+\alpha_{1}|1\rangle+\alpha_{2}|2\rangle)_{A}, $$
(10)

and that Bob has an unknown single-qutrit state

$$ |q_{0}\rangle_{B}=(\beta_{0}|0\rangle+\beta_{1}|1\rangle+\beta_{2}|2\rangle)_{B}, $$
(11)

where α0, α1, α2, β0, β1 and β2 are complex numbers, and

$$\begin{array}{@{}rcl@{}} &&|\alpha_{0}|^{2}+|\alpha_{1}|^{2}+|\alpha_{2}|^{2}= 1, \\ &&|\beta_{0}|^{2}+|\beta_{1}|^{2}+|\beta_{2}|^{2}= 1. \end{array} $$
(12)

Now Alice wants to teleport the state of the qutrit A to Bob, and at the same time, Bob wants to teleport the state of the qutrit B to Alice. As described above in section 2, the quantum channel shared by Alice, Bob and controller Charlie is the state |Q〉 (see Eq. (9)), and qutrits 1 and 3 belong to Alice, qutrits 2 and 4 to Bob, and qutrit 5 to Charlie. Thus the compound state of total system may be expressed as

$$\begin{array}{@{}rcl@{}} |P\rangle=|p_{0}\rangle_{A}\otimes |q_{0}\rangle_{B}\otimes |Q\rangle. \end{array} $$
(13)

In order to complete the BCQT, Alice and Bob should employ their own measurement. Alice has to perform generalized Bell state measurement (GBSM) on her qutrit pair (A, 1) by using the GBB |Ψ n m 〉 (see Eq. (11)). At the same time, Bob should make GBSM on his qutrits B and 2. After those measurements, Alice (Bob) should inform Bob (Alice) and Charlie of the measurement result by classical channel. If Charlie like to help Alice and Bob with the BCQT, he can perform a single-qutrit measurement on his qutrit 5 under the projective measurement basis (PMB) {|Φ k 〉}(k = 0, 1, 2), which is given by

$$\begin{array}{@{}rcl@{}} &&|{\Phi}_{0}\rangle=H_{(3)}|0\rangle=\frac{1}{\sqrt{3}}(|0\rangle+|1\rangle+|2\rangle), \\ &&|{\Phi}_{1}\rangle=H_{(3)}|1\rangle=\frac{1}{\sqrt{3}}(|0\rangle+e^{2\pi i/3}|1\rangle+e^{4\pi i/3}|2\rangle), \\ &&|{\Phi}_{2}\rangle=H_{(3)}|2\rangle=\frac{1}{\sqrt{3}}(|0\rangle+e^{4\pi i/3}|1\rangle+e^{2\pi i/3}|2\rangle), \end{array} $$
(14)

where H(3) is the Hadamard operator in three dimensional Hilbert space. After that, Charlie should inform Alice and Bob of his outcome of measurement. Then, Alice and Bob can make the suitable unitary operations on the qutrits at hand, the BCQT can be successfully completed.

Now we discuss this scheme in more detail below. For example, without loss of generality, we assume that the result of Alice’s GBSM is |Ψ00〉A1, the state of qutrits B, 2, 3, 4, 5 will collapse into

$$\begin{array}{@{}rcl@{}} |P_{1}\rangle=_{A1}\langle{\Psi}_{00}|P\rangle&&=\frac{1}{3\sqrt{3}}(\alpha_{0}\beta_{0}|00000\rangle+\alpha_{0}\beta_{0}|00110\rangle+\alpha_{0}\beta_{0}|00220\rangle \\ &&+\alpha_{0}\beta_{1}|10000\rangle+\alpha_{0}\beta_{1}|10110\rangle+\alpha_{0}\beta_{1}|10220\rangle \\ &&+\alpha_{0}\beta_{2}|20000\rangle+\alpha_{0}\beta_{2}|20110\rangle+\alpha_{0}\beta_{2}|20220\rangle \\ &&+\alpha_{1}\beta_{0}|01001\rangle+\alpha_{1}\beta_{0}|01111\rangle+\alpha_{1}\beta_{0}|01221\rangle \\ &&+\alpha_{1}\beta_{1}|11001\rangle+\alpha_{1}\beta_{1}|11111\rangle+\alpha_{1}\beta_{1}|11221\rangle \\ &&+\alpha_{1}\beta_{2}|21001\rangle+\alpha_{1}\beta_{2}|21111\rangle+\alpha_{1}\beta_{2}|21221\rangle \\ &&+\alpha_{2}\beta_{0}|02002\rangle+\alpha_{2}\beta_{0}|02112\rangle+\alpha_{2}\beta_{0}|02222\rangle \\ &&+\alpha_{2}\beta_{1}|12002\rangle+\alpha_{2}\beta_{1}|12112\rangle+\alpha_{2}\beta_{1}|12222\rangle \\ &&+\alpha_{2}\beta_{2}|22002\rangle+\alpha_{2}\beta_{2}|22112\rangle+\alpha_{2}\beta_{2}|22222\rangle)_{B2345}. \end{array} $$
(15)

Meanwhile, Bob performs GBSM on his qutrits B and 4 under the GBB (1). After that, the state (15) can be rewritten as

$$\begin{array}{@{}rcl@{}} |P_{1}\rangle=&&{~}_{A1}\langle{\Psi}_{00}|P\rangle \\ &&=\frac{1}{9\sqrt{3}}(|{\Psi}_{00}\rangle_{B4}|q_{0}\rangle_{3}+|{\Psi}_{10}\rangle_{B4}|q_{1}\rangle_{3}+|{\Psi}_{20}\rangle_{B4}|q_{2}\rangle_{3} \\ &&\ \ \ \ \ \ \ \ +|{\Psi}_{01}\rangle_{B4}|q_{3}\rangle_{3}+|{\Psi}_{11}\rangle_{B4}|q_{4}\rangle_{3}+|{\Psi}_{21}\rangle_{B4}|q_{5}\rangle_{3} \\ &&\ \ \ \ \ \ \ \ +|{\Psi}_{02}\rangle_{B4}|q_{6}\rangle_{3}+|{\Psi}_{12}\rangle_{B4}|q_{7}\rangle_{3}+|{\Psi}_{22}\rangle_{B4}|q_{8}\rangle_{3})|s\rangle_{25}, \end{array} $$
(16)

where

$$\begin{array}{@{}rcl@{}} |s\rangle_{25}=|p_{0}\rangle_{2}|{\Phi}_{0}\rangle_{5}+|p_{1}\rangle_{2}|{\Phi}_{1}\rangle_{5}+|p_{2}\rangle_{2}|{\Phi}_{2}\rangle_{5}, \end{array} $$
(17)

and

$$\begin{array}{@{}rcl@{}} &&|p_{0}\rangle=\alpha_{0}|0\rangle+\alpha_{1}|1\rangle+\alpha_{2}|2\rangle, \\ &&|p_{1}\rangle=\alpha_{0}|0\rangle+\alpha_{1}e^{4\pi i/3}|1\rangle+\alpha_{2}e^{2\pi i/3}|2\rangle, \\ &&|p_{2}\rangle=\alpha_{0}|0\rangle+\alpha_{1}e^{2\pi i/3}|1\rangle+\alpha_{2}e^{4\pi i/3}|2\rangle, \end{array} $$
(18)

and

$$\begin{array}{@{}rcl@{}} &&|q_{0}\rangle=\beta_{0}|0\rangle+\beta_{1}|1\rangle+\beta_{2}|2\rangle, \\ &&|q_{1}\rangle=\beta_{0}|0\rangle+\beta_{1}e^{4\pi i/3}|1\rangle+\beta_{2}e^{2\pi i/3}|2\rangle, \\ &&|q_{2}\rangle=\beta_{0}|0\rangle+\beta_{1}e^{2\pi i/3}|1\rangle+\beta_{2}e^{4\pi i/3}|2\rangle, \\ &&|q_{3}\rangle=\beta_{0}|1\rangle+\beta_{1}|2\rangle+\beta_{2}|0\rangle, \\ &&|q_{4}\rangle=\beta_{0}|1\rangle+\beta_{1}e^{4\pi i/3}|2\rangle+\beta_{2}e^{2\pi i/3}|0\rangle, \\ &&|q_{5}\rangle=\beta_{0}|1\rangle+\beta_{1}e^{2\pi i/3}|2\rangle+\beta_{2}e^{4\pi i/3}|0\rangle, \\ &&|q_{6}\rangle=\beta_{0}|2\rangle+\beta_{1}|0\rangle+\beta_{2}|1\rangle, \\ &&|q_{7}\rangle=\beta_{0}|2\rangle+\beta_{1}e^{4\pi i/3}|0\rangle+\beta_{2}e^{2\pi i/3}|1\rangle, \\ &&|q_{8}\rangle=\beta_{0}|2\rangle+\beta_{1}e^{2\pi i/3}|0\rangle+\beta_{2}e^{4\pi i/3}|1\rangle, \end{array} $$
(19)

and |Φ0〉, |Φ1〉 and |Φ2〉 are still in the PMB {|Φ k 〉}(k = 0, 1, 2) (see Eq. (14)). From Eqs. (16)–(19), if Bob’s measurement result is |Ψ21〉B4, the state of qutrits 2, 3, 5 can be expressed as

$$\begin{array}{@{}rcl@{}} |w\rangle_{235}=\frac{1}{9\sqrt{3}}|q_{5}\rangle_{3}(|p_{0}\rangle_{2}|{\Phi}_{0}\rangle_{5}+|p_{1}\rangle_{2}|{\Phi}_{1}\rangle_{5} +|p_{2}\rangle_{2}|{\Phi}_{2}\rangle_{5}). \end{array} $$
(20)

Then Alice (Bob) tells the measurement result to Bob (Alice) and Charlie by classical channel. If Charlie would like to help them with the BCQT, he can measure his qutrit 5 under the basis {|Φ k 〉}(k = 0, 1, 2) and transfer the measurement outcome to Alice and Bob by classical channel. From Eq. (20), it is clear that, if the result of Charlie is |Φ0〉, or |Φ1〉, or |Φ2〉, the qutrits 2 and 3 will collapse into the state

$$\begin{array}{@{}rcl@{}} |\eta\rangle=\frac{1}{9\sqrt{3}}&&(\alpha_{0}|0\rangle+\alpha_{1}|1\rangle+\alpha_{2}|2\rangle)_{2} \\\otimes &&(\beta_{0}|1\rangle+\beta_{1}e^{2\pi i/3}|2\rangle+\beta_{2}e^{4\pi i/3}|0\rangle)_{3}, \end{array} $$
(21)

or

$$\begin{array}{@{}rcl@{}} |\eta^{\prime}\rangle=\frac{1}{9\sqrt{3}}(\alpha_{0}|0\rangle+\alpha_{1}e^{4\pi i/3}|1\rangle+\alpha_{2}e^{2\pi i/3}|2\rangle)_{2} \\\otimes(\beta_{0}|1\rangle+\beta_{1}e^{2\pi i/3}|2\rangle+\beta_{2}e^{4\pi i/3}|0\rangle)_{3}, \end{array} $$
(22)

or

$$\begin{array}{@{}rcl@{}} |\eta^{\prime\prime}\rangle=\frac{1}{9\sqrt{3}}(\alpha_{0}|0\rangle+\alpha_{1}e^{2\pi i/3}|1\rangle+\alpha_{2}e^{4\pi i/3}|2\rangle)_{2} \\\otimes(\beta_{0}|1\rangle+\beta_{1}e^{2\pi i/3}|2\rangle+\beta_{2}e^{4\pi i/3}|0\rangle)_{3}. \end{array} $$
(23)

Then Bob and Alice can employ appropriate unitary operations (U00)2(U22)3, or (U10)2(U22)1, or (U20)2(U22)3 on their own qutrits 2 and 3, respectively. After these operations, Alice and Bob can recover the desired states |q0〉 and |p0〉, respectively. That is, in this situation, the BCQT has been completed successfully. The relation of GBSM results |Ψ00〉A1 performed by Alice, |Ψ n m 〉(n, m = 0, 1, 2) by Bob, measurement outcomes |Φ k 〉(k = 0, 1, 2) of Charlie and the unitary transformations U A performed by Alice and U B by Bob are given in Table 1. If Alice’s measurement result is any one of other 8 cases (see Eqs. (1) and (2)), Bob and Charlie can apply the same method as above, then Alice and Bob can choose suitable unitary operations on their own qutrits respectively, after that, their desired states can be reconstructed successfully.

Table 1 The relation of GBSM results |Ψ00〉A1 performed by Alice, |Ψ n m 〉(n, m = 0, 1, 2) by Bob, measurement outcomes |Φ k 〉(k = 0, 1, 2) of Charlie and the unitary transformations U A performed by Alice and U B by Bob
Full size table

4 Conclusion

In conclusion, we have presented a new scheme for bidirectional controlled teleportation in three-dimension system. In this scheme, Alice and Bob are not only senders but also receivers, and Alice wishes to teleport an unknown single-qutrit state to Bob, at the same time, Bob wants to teleport an another unknown single-qutrit state at distant Alice’s site under the control of the supervisor Charlie. In the scheme, a five-qutrit entangled state is considered as the quantum channel. Firstly, Alice should preform a GBSM on her qutrits, meanwhile, Bob must employ a GBSM on his qutrits. Then Charlie can make a single-qutrit measurement on his qutrit. After that, Alice and Bob can perform the respective suitable unitary operations on own qutrits to achieve the BCQT.