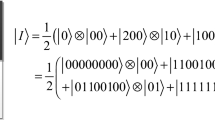1 Introduction

With the rapid development of quantum communication network, in order to achieve safe and efficient transmission of quantum image information in quantum communication network, people began to study using quantum states to store and transmit digital image information in the decades. Copyright protection [1, 2] of quantum images is one of the research fields in quantum information hiding [3,4,5], which is an important branch of information security in quantum networks. With widespread applications of quantum image in quantum communication network, quantum watermark has emerged to protect copyright of quantum image, which is fulfilled by embedding watermark image consisting of the information related to copyright owner into carrier image. So far, quantum image representation methods and quantum watermark algorithms have made a lot of achievements.

At present, many achievements of quantum image representation methods, i.e., Qubit Lattice [6], Entangled Image [7], Real Ket [8], flexible representation of quantum images (FRQI) [9], novel enhanced quantum representation (NEQR) [10], quantum log-polar image (QUALPI) [11] and novel quantum representation of color digital images (NCQI) [12], have been proposed. Among of them, quantum images of QUALPI representation can easily perform some complex geometric transformations, such as rotation and scaling. In the aspect of quantum watermark algorithms, some watermark algorithms for quantum images based on quantum Fourier transform [13], quantum wavelet transform [14] and Hadamard transform [15] have been respectively proposed in recent years. The least significant bit (LSB [16]) modification is one of widely used methods for classical digital watermarking technology, which has advantages of easy implementation and large payload. In 2016, a least significant qubit (LSQb) algorithm for quantum image based on NCQI representation [17] was proposed by Sang Jianzhi et al..

With the further research of quantum watermark algorithms, people began to analyze algorithm’s robustness. In 2014, Jiang Nan et al., proposed a novel strategy for quantum image steganography based on Moire pattern [18]. They discussed the influence of Cropping attack and analyzed the robustness of quantum image. In 2015, LSB based quantum image steganography algorithm [19] was also proposed by Jiang Nan et al.. The advantage of their algorithm is that analyzes the robustness of quantum image from the Bit Error Rate (BER) and the Normalized Correlation (NC). In 2016, Miyake et al., proposed a quantum watermarking scheme using simple and small-scale quantum circuits [20] to correct and recover watermark image from the extracted watermark image affected by salt and pepper noise.

So far, most of algorithms [13,14,15,16,17,18,19,20] have not yet begun to discuss the influence of geometric attacks to the robustness of watermark image. In view of widespread applications and universality of geometric attacks in quantum image processing, most of watermark images are invulnerable to resist geometric attacks. In order to make up for the drawbacks of existing quantum watermark algorithms, this paper proposes a novel robust quantum watermark algorithm based on QUALPI representation. By combining QUALPI representation with the LSQb modification technique, the new algorithm enables to effectively resist geometric attacks, so as to better protect copyright of quantum image.

The rest of the paper is organized as follows. Section 2 introduces the preliminary knowledge related to the new algorithm, including QUALPI representation model, quantum rotation transformation of QUALPI representation model and quantum bit comparator. In Section 3, embedding process and extracting process of the new robust watermark algorithm are presented in detail, along with designed quantum circuits to implement those processes. The simulation results and related performance analysis are given in Section 4. Finally, a conclusion and the future work are provided in Section 5.

2 Preliminaries

2.1 Quantum Representation for Log-polar Images

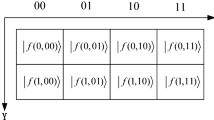
In 2013, quantum log-polar image (QUALPI) [11], a novel quantum image representation, was proposed by Zhang Yi et al.. In QUALPI, the sampling resolutions of the log-radius and the angular orientations of a log-polar image are assumed to be 2m and 2n respectively. For this image, the quantum image representation can be expressed as shown in the following equation:

$$ \left|I\right\rangle = \frac{1}{{\sqrt {{2^{m + n}}} }}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left( {\left|{g\left( {\rho, \theta}\right)}\right\rangle \otimes \left|\rho\right\rangle \otimes \left|\theta\right\rangle}\right)} } $$
(1)

The position information of a pixel is represented by (ρ,𝜃), where ρ denotes the log-radius and 𝜃 denotes the angular position. The gray scale of the corresponding pixel is represented by g(ρ,𝜃). The gray range of this image is assumed to be 2q. Thus the gray scale can be encoded by binary sequence C q−1 C q−2⋯C 1 C 0 as follow:

$$ g\left( {\rho, \theta}\right) = {C_{q - 1}}{C_{q - 2}} {\cdots} {C_{1}}{C_{0}},g\left( {\rho, \theta}\right) \in \left[ {0,{2^{q - 1}}}\right] $$
(2)

In addition, the process of quantum image preparation of QUALPI is described in detail in Ref [11].

2.2 Quantum Rotation Transformation of QUALPI Representation Model

Ref [11] discusses quantum rotation transformation of QUALPI representation model. Let’s assume that a rotation transformation for QUALPI will be operated and the rotation angle R x can be encoded by binary sequence r n−1 r n−2⋯r 1 r 0:

$$ {R_{x}} = {r_{n - 1}}{r_{n - 2}} {\cdots} {r_{1}}{r_{0}},{r_{i}} \in \{ 0,1\} ,{R_{x}} \in \left[{0,{2^{n}} - 1}\right] $$
(3)

Thus, when rotation angle R x is performed, the procedure can be divided into n sub-operations. If r i = 0, none of operations will be done for the i-th sub-operation. Otherwise, a transformation \({R_{{2^{i}}}}\) of rotation angle 2i will be performed on quantum image.

Next, let’s discuss the transformation \({U_{{2^{k}}}}\) of rotation angle 2k on QUALPI. This operation will add the angular positions of every pixel by 2k (mod 2n). Specifically, this operation aims at making a unit shift for the highest (n − k) qubits of the angular sequence |𝜃〉 in QUALPI.

The quantum rotation operation \({U_{{2^{k}}}}\) is defined as seen in the following equation:

$$\begin{array}{@{}rcl@{}} {U_{{2^{k}}}}\left( {\left|I\right\rangle}\right) &= &{U_{{2^{k}}}}\left( {\frac{1}{{\sqrt {{2^{m + n}}}}}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left|{g\left( {\rho, \theta}\right)}\right\rangle \otimes \left|\rho\right\rangle \otimes \left|\theta\right\rangle}}}\right)\\ &=& \frac{1}{{\sqrt {{2^{m + n}}}}}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left( {\left|{g\left( {\rho, \theta}\right)}\right\rangle \otimes \left|\rho\right\rangle \otimes \left|{\left( {\theta + {2^{k}}}\right)\bmod {2^{n}}}\right\rangle}\right)}}\\ &=& \frac{1}{{\sqrt {{2^{m + n}}}}}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left( {\left|{g\left( {\rho, \theta}\right)}\right\rangle}\right.}} \otimes \left|\rho\right\rangle\\ &&\left.{ \otimes \left|{\left( {{\theta_{n - 1}}{\theta_{n - 2}} {\cdots} {\theta_{k}} + 1}\right)\bmod {2^{n - k}}}\right\rangle \otimes \left|{{\theta_{k - 1}}{\theta_{k - 2}} {\cdots} {\theta_{0}}}\right\rangle}\right) \end{array} $$
(4)

Therefore, an arbitrary rotation can be decomposed into n rotation operations at most and the total time complexity of the arbitrary rotation transformation is no more than O(n 3).

Image registration is one of the most important topics in image processing which can obtain the correspondence of two different images for a same scene or object from different circumstances. In order to find the unknown rotation difference between two log-polar images, Zhang Yi et al., presented a fast quantum image registration algorithm based on QUALPI representation model in Ref [11]. Their proposed algorithm can achieve an approximately quartic speedup in time complexity compared with that of the classical brute-force image registration algorithm.

2.3 Quantum Bit Comparator

In order to embed watermark image into carrier image by using the LSQb modification technique, it is necessary to compare the state of the last qubit of a pixel in the same position of those two images by using quantum bit comparator. According to the results of quantum bit comparator, the corresponding unitary operation will be performed on carrier image. Consequently, this section describes a specific quantum bit comparator.

In 2012, Wang Dong et al., proposed a quantum bit comparator to judge whether two qubits are same or not in Ref [21]. As shown in Fig. 1, |a〉 and |b〉 are the input qubits, while |c〉 and |d〉 denote the outputs of the corresponding states.

Fig. 1
figure 1

Two qubit comparator

Full size image

If |c〉|d〉 = |1〉|0〉 or |c〉|d〉 = |0〉|1〉, then quantum state |a〉 is not equal to quantum state |b〉. If |c〉|d〉 = |0〉|0〉, then quantum state |a〉 is equal to quantum state |b〉.

3 A Robust Quantum Watermarking Algorithm

In this section, the detailed steps of the new algorithm including the process of embedding watermark and extracting watermark are given. The embedding process is mainly based on QUALPI representation and the LSQb modification technique, and the extracting process is the inverse of the embedding process.

3.1 The Process of Embedding Watermark

In this paper, the size of carrier image is equal to the size of watermark image. The flow chart of the embedding process is shown in Fig. 2 and steps of the embedding process are given as follows.

Step1 :

At first, two classical log-polar images including carrier image and watermark image, will be prepared by QUALPI representation. As a result, the QUALPI expressions of carrier image and watermark image are shown in (5) and (6), respectively:

$$ \left|C\right\rangle = \frac{1}{{\sqrt {{2^{m + n}}}}}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left|{{c_{q - 1}}{c_{q - 2}} {\cdots} {c_{1}}{c_{0}}}\right\rangle}} \left|{\rho \theta}\right\rangle $$
(5)
$$ \left|W\right\rangle = \frac{1}{{\sqrt {{2^{m + n}}}}}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left|{{w_{0}}}\right\rangle \left|{\rho \theta}\right\rangle}} $$
(6)
Step2 :

\(\left |{{c_{{0_{ji}}}}}\right \rangle \) and \(\left |{{w_{{0_{ji}}}}}\right \rangle \) denote the state of the last qubit of the (ρ j ,𝜃 i ) pixel in carrier image and watermark image, respectively, which are used into quantum bit comparator as the inputs. According to the results of quantum bit comparator, the corresponding unitary operation is performed on carrier image to complete the LSQb modification technique. The related steps in detail are given as follows.

  1. (1)

    If the outputs from quantum bit comparator are equal, then nothing will be done for carrier image. In this case, the following unitary transformation will be performed.

    $$ {U_{{s_{ji}}}} = {I^{\otimes q}} \otimes \left( {\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left|{\rho \theta }\right\rangle \left\langle {\rho \theta }\right|} } } \right) $$
    (7)
  2. (2)

    However, if the outputs are different, the following unitary transformation will be performed on the state of carrier image.

    $$ {U_{{D_{ji}}}} = {I^{\otimes q - 1}} \otimes U \otimes \left|{ji}\right\rangle \left\langle {ji} \right| + {I^{\otimes q}} \otimes \left( {\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0,\rho \theta \ne ji}^{{2^{n}} - 1} {\left|{\rho \theta }\right\rangle \left\langle {\rho \theta }\right|} }}\right) $$
    (8)
    $$ U = {\sigma_{X}} = \left[{\begin{array}{*{20}{c}} 0 & 1 \\ 1 & 0 \\ \end{array}}\right] $$
    (9)

    It is obvious that the unitary U is CNOT gate. Next, the concrete derivation process of \({U_{{D_{ji}}}}\) is given by (10) and (11).

    $$\begin{array}{@{}rcl@{}} {U_{{D_{ji}}}}\left( {\left|C\right\rangle}\right) &=& \left( {{I^{\otimes q - 1}} \otimes U \otimes \left| {ji}\right\rangle \left\langle {ji}\right| + {I^{\otimes q}} \otimes \sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0,\rho \theta \ne ji}^{{2^{n}} - 1} {\left|{\rho \theta}\right\rangle \left\langle {\rho \theta}\right|}}}\right)\\ &&\left( {\frac{1}{{\sqrt {{2^{m + n}}}}}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left|{{c_{q - 1}}{c_{q - 2}} {\cdots} {c_{1}}{c_{0}}}\right\rangle}} \left|{\rho \theta}\right\rangle}\right) \\ &=& \!\frac{1}{{\sqrt {{\!2^{m + n}}}}}\left( {{I^{\otimes q - 1}} \otimes U \otimes \left|{ji}\right\rangle \left\langle {ji}\right| \,+\, {I^{\otimes q}} \otimes \sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0,\rho \theta \ne ji}^{{2^{n}} - 1} {\left|{\rho \theta}\right\rangle \left\langle {\rho \theta}\right|}}}\!\!\right)\\ &&\!\!\left( \!\! {\left|{c_{q - 1}^{ji}c_{q - 2}^{ji} {\cdots} c_{1}^{ji}c_{0}^{ji}}\right\rangle \left| {ji}\right\rangle \,+\,\! \sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0,\rho \theta \ne ji}^{{2^{n}} - 1} {\left|{{c_{q - 1}}{c_{q - 2}} {\cdots} {c_{1}}{c_{0}}}\right\rangle \left|{\rho \theta}\right\rangle}}}\!\!\right)\\ &=& \frac{1}{{\sqrt {{2^{m + n}}}}}\left( {\left|{c_{q - 1}^{ji}c_{q - 2}^{ji} {\cdots} c_{1}^{ji}\overline c_{0}^{ji}}\right\rangle}\right.\left|{ji}\right\rangle \\&&+ \left.{\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0,\rho \theta \ne ji}^{{2^{n}} - 1} {\left|{{c_{q - 1}}{c_{q - 2}} {\cdots} {c_{1}}{c_{0}}}\right\rangle}} \left|{\rho \theta}\right\rangle}\right) \\ \end{array} $$
    (10)
    $$ \left|{\overline c_{0}^{ji}}\right\rangle = \left\{ \begin{array}{l} \left|0\right\rangle ,\left|{c_{0}^{ji}}\right\rangle = 1 \\ \left|1\right\rangle ,\left|{c_{0}^{ji}}\right\rangle = 0 \\ \end{array}\right. $$
    (11)

By repeating Step1 and Step2 above, watermark image can be embedded into carrier image by the LSQb modification technique to get stego image.

Assuming that carrier image with size 2m × 2n is a gray image which the gray value of the pixel is represented by a 8 bit binary sequence, and watermark image with size 2m × 2n is a binary image represented by a 1 bit binary sequence. Inspired by the quantum circuit of embedding watermark designed by Qu Zhiguo et al. [22], Fig. 3 gives a quantum circuit to implement the process of embedding watermark. In Fig. 3, \({C_{j}^{i}}\), where superscript denotes the i-th pixel and subscript denotes the j-th significant bit of the 8 bit binary sequence, is the gray value of carrier image, and \({W_{0}^{i}}\) is the gray value of the i-th pixel of watermark image.

Step3 :

Finally, as it is described in Section 2.2, stego image will be made a rotation transformation R x . The rotation angle can be determined according to the key, named as K, shared by two parties of communication in advance. Figure 4 gives a quantum circuit of rotation transformation for stego image with size 2q × 2m × 22 based on the key (K = k 3 k 2 k 1 k 0).

Fig. 2
figure 2

The flow chart of the embedding process

Full size image
Fig. 3
figure 3

Quantum circuit of the process of embedding watermark

Full size image
Fig. 4
figure 4

Quantum circuit of rotation transformation for stego image with size 2q × 2m × 22 based on K = k 3 k 2 k 1 k 0

Full size image

3.2 The Process of Extracting Watermark

The flow chart of the extracting process is shown as Fig. 5. Its main steps can be described as follows.

Step1 :

The first step is to perform another rotation transformation for rotated stego image to recover the original stego image. According to the K, two parties of communication will share another key, named as M. K and M satisfies the following relationship:

$$ {\left( K\right)_{d}} + {\left( M\right)_{d}} = {2^{n}} $$
(12)

The subscript d denotes decimalist, n is the number of angular sequence 𝜃. For example, if n = 4 and K = 0110, then M = 1010.

The design principle of a quantum circuit of inverse rotation transformation is the same as that of Fig. 4, and no longer repeated here.

Step2 :

It is clear that the LSQb of stego image is a complex vector in Hilbert space which the size is 2q + m + n. So let decompose the vector into the direct product of color and correspondingly position. Taking a 21 × 22 log-polar image with gray rang 2q as an example, stego image vector is Q. Then the disintegrated vector Q is given as the following form:

$$ Q = {a_{0}} \otimes \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \\ {\vdots} \\ 0 \\ 0 \\ \end{array}}\right) + {a_{1}} \otimes \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 0 \\ {\vdots} \\ 0 \\ 0 \\ \end{array}}\right) + {\cdots} + {a_{6}} \otimes \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ {\vdots} \\ 1 \\ 0 \\ \end{array}}\right) + {a_{7}} \otimes \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ {\vdots} \\ 0 \\ 1 \\ \end{array}}\right) $$
(13)

Obviously, this step can be realized because the vector Q and the binary encoding of position are known. After converting every first part (color information) of the direct product to binary data, the number of binary bit is equivalent to the number of bits of stego image’s color encoding. In this example, it means converting \({a_{0}},{a_{1}}, {\cdots } ,{a_{6}},{a_{7}}\) to the appropriate binary data \({a_{{0_{b}}}},{a_{{1_{b}}}}, \cdots ,{a_{{6_{b}}}},{a_{{7_{b}}}}\). The \({a_{{i_{b}}}}\) stands for the gray’s binary sequence of the i-th pixel in stego image.

Step3 :

The last step is to extract the last bit of every binary data. According to the preparation of QUALPI in Ref [11], the information of these bits could be restored to the original watermark image.

Fig. 5
figure 5

The flow chart of the extracting process

Full size image

In order to make the extracting process more executable and efficient, Fig. 6 gives an efficient quantum circuit of the process of extracting watermark. Here, \({S_{j}^{i}}\), where superscript denotes the i-th pixel and subscript denotes the j-th significant bit of the 8 bit binary sequence, is the gray value of stego image.

Fig. 6
figure 6

Quantum circuit of the process of extracting watermark

Full size image

In general, the process of extracting watermark is an inverse process of embedding watermark.

4 The Simulation Results and Performance Analysis

This section gives some simulation-based experiments of the proposed quantum watermark algorithm. All experiments are simulated on the MATLAB R2012a.

There are three factors of performance evaluation for quantum watermark algorithms, including robustness, transparency and capacity, respectively. Robustness shows that watermark image can be extracted effectively from stego image after various attacks. Transparency represents the similarity between carrier image and stego image. Capacity is the maximum amount of watermark information embedded into carrier image without affecting its normal use. It can be represented by the number of bits of watermark information contained in the unit carrier image pixel. Three images Baboon, Cameraman and Lena are used in experiments as carrier images. Four images Eagle, Recycling, Thumbs-up and HTC are used as watermark images. The image sizes for carrier and watermark are the same as 27 × 28.

4.1 Robustness

In order to defend various geometric attacks, the new algorithm effectively utilizes two important properties of log-polar sampling, including rotation and scale invariances. These invariances make watermark image extracted having a good robustness when stego image was subjected to various geometric attacks, such as rotation, horizontal axisymmetry, vertical axisymmetry and scaling.

In order to prove the above argument, Figs. 7, 8, 9 and 10 are given respectively to represent above-mentioned geometric attacks. The simulation results show that watermark image can be extracted effectively after a variety of geometric attacks, and has a high image quality. In other words, it means that the new algorithm has a good robustness.

Fig. 7
figure 7

Rotation attack. a The stego image attacked by rotation, (b) The stego image restored by the quantum image registration algorithm, (c) The watermark image extracted from (b)

Full size image
Fig. 8
figure 8

Horizontal axisymmetry. a The stego image attacked by horizontal axisymmetry, (b) The stego image restored, (c) The watermark image extracted from (b)

Full size image
Fig. 9
figure 9

Vertical axisymmetry. a The stego image attacked by vertical axisymmetry, (b) The stego image restored, (c) The watermark image extracted from (b)

Full size image
Fig. 10
figure 10

Scaling attack. a The stego image attacked by scaling, (b) The stego image restored, (c) The watermark image extracted from (b)

Full size image

4.1.1 Rotation Attack

Log-polar coordinates is a well-known sampling method in the field of image processing. Araujo and Dias [23] introduced the fundamental theory of log-polar sampling and analyzed two important properties, i.e., rotation and scale invariances. For the peculiar properties, log-polar sampling is more suitable for some complex image transformations such as rotation and scaling.

As is mentioned in Section 3.1, watermark image is embedded into carrier image by using the LSQb modification technology. However, in order to prevent the third party extracting watermark image from the original stego image, the new algorithm utilizes the rotation invariance of QUALPI representation to make an arbitrary rotation transformation on the original stego image. This method enables to make the most information of watermark image extracted effectively once the original stego image was damaged. Therefore, the rotation invariance of QUALPI representation improves the robustness of watermark image.

In Fig. 7, (a) is the rotated stego image. It is easy to restore the original stego image in the light of Step3 of Section 3.1 as well as Step1 of Section 3.2, as shown in (b). And (c) is the extracted watermark image from (b).

4.1.2 Flip Attack

Axisymmetry transformation is a kind of important flip transformation, including horizontal axisymmetry and vertical axisymmetry. For classical images, the position information of all pixels needs to be modified during axisymmetry transformations. Therefore, the time requirements of these classical image operations are unacceptable when the sampling resolution is large. But in QUALPI representation model, all pixels are stored in a quantum superposition and can be operated on simultaneously during transforming. In Ref [11], Zhang Yi et al., proposed quantum horizontal axisymmetry and quantum vertical axisymmetry for QUALPI.

In Fig. 8, (a) shows stego image attacked by horizontal axisymmetry transformation. Using the proposed method in Ref [11], (a) will be recovered to the original stego image, as shown in (b). And (c) is the extracted watermark image from (b). Correspondingly, stego image attacked by vertical axisymmetry is shown in Fig. 9.

4.1.3 Scaling Attack

Ref [23] illustrated the scaling invariance of QUALPI representation. Thus, scaling operations on QUALPI can be restored to the original QUALPI. In Fig. 10, (a) gives the stego image attacked by scaling. (b) is the original stego image. (c) is the extracted watermark image from (b).

4.1.4 Translation Attack

Before analyzing the influence of translation attack to original stego image, let discuss quantum translation transformation of QUALPI representation model. Because all pixels of QUALPI can be simultaneously operated, quantum translation transformation will be faster and more flexible.

Firstly, quantum unit translation of QUALPI representation model is discussed. For QUALPI, it will add the log-radius positions of every pixel by 1 (mod 2m). The quantum unit translation operation is defined as T 1 in the following equation:

$$\begin{array}{@{}rcl@{}} {T_{1}}\left|I\right\rangle &=& {T_{1}}\left( {\frac{1}{{\sqrt {{2^{m + n}}} }}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left|{g\left( {\rho, \theta}\right)}\right\rangle } } \otimes \left| \rho\right\rangle \otimes \left|\theta\right\rangle}\right)\\ &=& \frac{1}{{\sqrt {{2^{m + n}}} }}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left( {\left|{g\left( {\rho, \theta}\right)}\right\rangle \otimes \left|{\left( {\rho + 1}\right)\bmod {2^{m}}}\right\rangle \otimes \left|\theta\right\rangle}\right)} } \end{array} $$
(14)

From (14), it is obvious that the log-radius positions of all pixels will be shifted by one unit. Thus, a quantum circuit of quantum operation T 1 is shown in Fig. 11.

Fig. 11
figure 11

Quantum circuit of T 1 for a 2m × 2n log-polar image with gray range 2q. The qubit \(\left |{{\rho _{j}}}\right \rangle \) will be overturned only when |ρ j−1 ρ j−2⋯ρ 1 ρ 0〉 = |11⋯11〉

Full size image

Next, quantum arbitrary translation of QUALPI representation model is focused on. Referring to quantum arbitrary rotation of QUALPI representation model, the translation length T y can be encoded by binary sequence t m−1 t m−2⋯t 1 t 0:

$$ {T_{y}} = {t_{m - 1}}{t_{m - 2}} {\cdots} {t_{1}}{t_{0}},{t_{j}} \in \{ 0,1\} ,{T_{y}} \in \left[{0,{2^{m}} - 1}\right] $$
(15)

Thus, when translation length T y is performed, the procedure can be divided into m sub-operations. If t j = 0, none operation will be done for the j-th sub-operation. Otherwise, a transformation \({T_{{2^{j}}}}\) of translation length 2j will be performed on quantum image.

Then, let’s discuss the transformation \({T_{{2^{j}}}}\) of translation length 2j on QUALPI. This operation will add the log-radius positions of every pixel by 2k(mod 2m). Specifically, this operation aims to make a unit shift for the highest (m − k) qubits of the log-radius sequence |ρ〉 in QUALPI.

The quantum arbitrary translation operation \({T_{{2^{k}}}}\) is defined as seen in the following equation.

$$\begin{array}{@{}rcl@{}} {T_{{2^{k}}}}\left( {\left|I\right\rangle}\right) &=& {T_{{2^{k}}}}\left( {\frac{1}{{\sqrt {{2^{m + n}}} }}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left|{g\left( {\rho, \theta}\right)}\right\rangle \otimes \left|\rho\right\rangle \otimes \left|\theta\right\rangle}}}\right)\\ &= &\frac{1}{{\sqrt {{2^{m + n}}} }}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left( {\left|{g\left( {\rho, \theta}\right)}\right\rangle \otimes \left|{\left( {\rho + {2^{k}}}\right)\bmod {2^{m}}}\right\rangle \otimes \left|\theta\right\rangle}\right)} }\\ &=& \frac{1}{{\sqrt {{2^{m + n}}} }}\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left( {\left|{g\left( {\rho, \theta}\right)}\right\rangle }\right.} } \otimes \left|{\left( {{\rho_{m - 1}}{\rho_{m - 2}} {\cdots} {\rho_{k}} + 1}\right)\bmod {2^{m - k}}}\right\rangle \\ &&\left.{ \otimes \left|{{\rho_{k - 1}}{\rho_{k - 2}} {\cdots} {\rho_{0}}}\right\rangle \otimes \left| \theta\right\rangle}\right) \end{array} $$
(16)

The quantum circuit of this operation \({T_{{2^{k}}}}\) is shown in Fig. 12.

Fig. 12
figure 12

Quantum circuit of \({T_{{2^{k}}}}\) for a \({2^{m}} \times {2^{n}}\) log-polar image with gray range 2q. The lowest k qubits in the log-radius sequence \(\left |\rho \right \rangle \) will not be modified in this quantum operation

Full size image

Finally, the original stego image attacked by translation is also discussed. According to quantum translation operation of QUALPI representation model presented above, a reversible quantum translation operation T r0 can be always performed to restore the original stego image when stego image operated a quantum translation operation T 0.

Because there are not effective simulation of translation for log-polar images in the classical computer, it theoretically proves that the new algorithm can resist translation attack by using quantum translation operation.

4.2 Transparency

At present, there is no specific evaluation standard for visual quality index of the quantum image. Therefore, in this paper, the classical PSNR (Peak Signal-to-Noise Ratio) is applied to evaluate transparency of quantum watermark image.

It’s assumed that there are two 2m × 2n images I and J with gray range 2q(I is the original carrier image, J is the embedded carrier image). I(ρ,𝜃) and J(ρ,𝜃) represents the values of the (ρ,𝜃) pixels in two images. MSE (Mean Squared Error) and PSNR are defined as the (17) and (18), respectively.

$$ MSE = \frac{1}{{mn}}{\sum\limits_{\rho = 0}^{{2^{m}} - 1} {\sum\limits_{\theta = 0}^{{2^{n}} - 1} {\left[{I\left( {\rho, \theta}\right) - J\left( {\rho, \theta}\right)}\right]} }^{2}} $$
(17)
$$ PSNR = 20 \times {\log_{10}}\left( {\frac{{MA{X_{I}}}}{{\sqrt {MSE} }}}\right) $$
(18)

Here, M A X I is the maximum possible pixel value of the image I.

From the experimental results in Fig. 13, it is easy to know that the embedded carrier image and the original carrier image are incapable to be identified by the naked eye of human being.

Fig. 13
figure 13

In three groups of pictures, the left are the original carrier images, the middle are the watermark images, the right are the embedded carrier images

Full size image

Table 1 lists out the PSNR values of stego images obtained by embedding four different watermark images into three different carrier images, respectively. And Fig. 14 shows the curve graph of PSNR values of Table 1. It can be found that the PSNR values of stego images are much higher than the image quality standard of 38dB, which proves that stego images have high image qualities. Therefore, the new algorithm can obtain good transparency.

Table 1 PSNR values of stego images in our simulation
Full size table
Fig. 14
figure 14

The curve graph of PSNR values of Table 1

Full size image

4.3 Capacity

Capacity can be accurately calculated by the embedding rate, which is denoted by the number of bits embedded divided by all the least significant qubits of carrier image in this paper. It is easy to know the embedding rate of the new algorithm is equal to 1. Furthermore, based on the LSQb modification technology in our algorithm, the modifying rate of the new algorithm is 0.5, which means that half of qubits need to be modified, and the other half is not. Comparing with the previous achievements, the embedding rate and the modifying rate of our algorithm is also good.

5 Conclusion

In this paper, a novel robust watermark algorithm is proposed. By combining QUALPI representation with the LSQb modification technique, the new algorithm enables to effectively resist geometric attacks, so as to better protect the copyright of quantum image. The new algorithm designs quantum circuits for embedding and extracting watermark image, which are very practical. The simulation results based on MATLAB show that the new algorithm has good performances on robustness and transparency. On the basis of the capacity analysis to the new algorithm, the embedding rate of our algorithm is 1 and the modification rate is 0.5.

The robustness of quantum watermark image against geometric attacks has been improved in this paper. But it does not discuss more complex attacks, such as filtering and compression, etc. Therefore, the next research will be focused on the research of robust quantum watermark algorithm to deal with these complex attacks in the future.