Gravity-modulated Rayleigh–Bénard convection in a Newtonian liquid bounded by rigid–free boundaries: a comparative study with other boundary conditions

Abstract

Effect of different boundaries on the gravity-modulated Rayleigh–Bénard convection has been investigated with an emphasis on rigid–free boundaries. Small-amplitude and large-amplitude modulations are studied using the linear stability analysis. The modified Venezian approach is used to study small-amplitude modulations using different modes of perturbations and the superposition principle. The existence of subharmonic motions for the case of large-amplitude modulations was explored using the Mathieu equation arising from the linear stability analysis. Floquet theory was used together with Hill’s infinite determinant method to compute the critical Rayleigh number for the case of large-amplitude modulations. Weakly non-linear analysis is performed leading to the cubic Stuart–Landau equation from the Lorenz system. Heat transport was quantified using the Nusselt number and the mean Nusselt numbers for different amplitudes and frequencies. It was found that gravity modulation has, in general, a stabilizing effect on the convection process in all three boundary types, and the heat transport was found to be an increasing function of amplitude. Another important outcome of the study is that the critical Rayleigh number for the onset of convection for rigid–free boundaries lies between those of the corresponding values of the free–free and rigid–rigid boundaries in the case of both harmonic and subharmonic motions which could be exploited in controlling convection.

1 Introduction

In recent decades, work on natural convective instability has garnered much attention due to its vast application to geophysics, oceanography, meteorology, and engineering. An early concise review of the available studies on Rayleigh–Bénard convection towards the end of the nineteenth century can be found in Getling [1]. Today, there are many variations of the thermal convective problem accounting for different types of working fluid, boundary conditions, modulations, column dimensions, and a number of other factors that are significant in altering dynamics in a Rayleigh–Bénard setup. There is also a greater demand from industries time-to-time for controlling the onset of instabilities, especially in the area of crystal growth. Many modulation techniques are used to control the onset of convection based on the industrial needs, such as

• 1. gravity modulation,

• 2. temperature modulation,

• 3. rotational modulation,

• 4. magnetic-field modulation,

• 5. heat-source modulation,

and others. The use of the modulation technique to control the onset of stability dates back to the experimental works of Donnelly [2], where he has shown that rotational modulation can be effectively used to inhibit the onset of the instability in a Taylor–Couette flow between two cylinders. There are numerous studies concerning various other modulation effects on the Rayleigh–Bénard convection following the pioneering work of Venezian [3], who investigated the effects of boundary temperature modulations on thermal convection. Theoretically. Biringen and Danabasoglu [4] made a computational study of convective flow with gravity modulation in rectangular cavities. Wheeler [5] also concluded similar results in his investigation of the onset of solutal convection during directional solidification subject to high-frequency modulation. Saunders et al. [6] have studied the effect of gravity modulation on double-diffusive convection and concluded that modulation may stabilize an unstable base solution or destabilize a stable base solution based on the frequency of modulation. Siddheshwar and Pranesh [7] studied the effect of temperature and gravity modulations on the onset of magnetoconvection in a weak electrically conducting medium considering the internal angular momentum of suspended particles. They observed that while temperature modulation influences the stability of the system and causes sub-critical movement for variation of different parameter values, under the stated conditions, gravity modulation on the system causes a delay in convection. Li [8] studied stability of modulated-gravity-induced thermal convection in magnetic fields and extended the study to include multi-frequency modulations. Aniss et al. [9] studied the effect of modulations of imposed magnetic field on the onset of convection of a magnetic liquid layer heated from above, bounded by isothermal, non-magnetic boundaries. The Galerkin method of solution was used by them to explore the possible competition between the subharmonic and harmonic modes at the point of instability. Using a cubic Ginzburg–Landau model, Bajaj [10, 11] investigated the effects of gravity modulation (with one or two frequency modulation) on the convective instability of a ferrofluid in the presence of a vertical magnetic field. Singh et al. [12] investigated the time-periodic temperature-modulated state of the Rayleigh–Bénard convection in a horizontal thin fluid layer. Siddheshwar et al. [13, 14] have investigated the effect of imposed modulations of boundary temperature and gravity on the heat transport by a magneto-convective Newtonian liquid layer. Kanchana et al. [15] have considered the effect of three types of modulations, namely, gravity, boundary temperature, and rotation, on the heat transport by a Rayleigh–Bénard system, delineated by the Nusselt number. They found that in the case of gravity and rotational modulations specifically, the frequency of modulation has a greater impact than amplitude in regulating convection as compared to the case of boundary temperature modulation. Kanchana et al. [16] too concluded that gravity modulation has a stabilizing effect (for all three mediums considered) in their work on the effect of time-periodic gravity modulation with trigonometric sine, triangular, and square waves-forms on Rayleigh–Bénard convection in water–alumina nanoliquids and water–alumina–copper hybrid nanoliqiuds. Pranesh et al. [17] analyzed linear and non-linear triple diffusive convection in the presence of sinusoidal/non-sinusoidal gravity modulation. Recently, Meenakshi and Siddheshwar [18] carried out a comparative study of controlling Rayleigh–Bénard magnetoconvection in Newtonian nanoliquids using different modulations such as rotational, gravitational, and temperature modulations.

Most of the studies mentioned above deal with controlling instabilities of flow in various geometries by modulating one or many parameters using idealistic conditions of no shear stress on the bounding surfaces which are commonly known as stress-free boundary conditions. The rigid boundaries are the realistic ones and among the modulations, gravity modulation has applications in melting/solidification processing systems under extra-terrestrial conditions. Quite generally, however, when a system whose temperature and density gradients are well established due to non-uniform heating, the buoyancy forces within the medium and the external modulatory forces give rise to an interesting relationship in time and space. In other words, gravity modulation can significantly impact the convective stability of the system by disrupting its equilibrium. Apart from microgravity/g-jitter situations seen in space, gravity modulation is encountered quite naturally due to mechanical vibrations (in pumps and motors). It should be mentioned that microgravity/g-jitter is a non-uniform phenomenon where randomness can be seen in time and with an alignment to the gravity. However, researchers have adapted uniform periodic modulations which are represented by one or many harmonics of a Fourier series for the ease of mathematical analysis. Similar considerations are noted in other types of modulations mentioned above. Thermal convection under microgravity/g-jitter situations is greatly impacted by the frequency and amplitudes of vibrations, and the direction of the gravity vector.

Here we mention works concerning gravity-modulation effects on thermal convection involving rigid boundaries. Gresho and Sani [19] studied the effects of gravity modulation on the stability of a heated fluid layer. Gershuni et al. [20] investigated convective stability in the presence of periodically varying parameters such as modulation of the equilibrium temperature gradient and modulation of the external force field. Murray et al. [21] investigated the effect of gravity modulation on solutal convection during directional solidification. Clever et al. [22] investigated two-dimensional oscillatory convection in a gravitaty-modulated fluid layer. Farooq and Homsy [23] investigated linear and non-linear dynamics of a differentially heated slot with gravity modulation. Chen and Chen [24] investigated the effect of gravity modulation on the stability of convection in a vertical slot. Christov and Homsy [25] studied non-linear dynamics of two-dimensional convection in a vertically stratified slot with and without gravity-modulation effect.

Studies concerning convection in porous media are also important from an engineering point of view and there have been numerous works concerning gravity-modulated thermal convection in porous media. In their investigation of the impact of gravity modulation on the onset of convection in a fluid porous layer, Malashetty and Padmavathi [26] highlighted that gravity modulation has a stabilizing effect on the system for moderate Prandtl numbers. This was concluded based on the assumption that the amplitude of modulation is small and that the non-linear effects be neglected. They also concluded that gravity modulation stabilizes the medium for a densely packed porous medium. Other important works on gravity-modulated thermal convection in fluid-saturated porous media include, Bardan and Mojtabi [27], Govender [28, 29], Saravanan and Purusothaman [30], Sivakumar and Saravanan [31], Saravanan and Sivakumar [32], Malashetty and Swamy [33], Siddheshwar et al. [34], Bhadauria et al. [35] Bhadauria and Kiran [36], Matta et al. [37] and Suthar et al. [38].

We observe from the literature survey mentioned so far that the gravity-modulation effects on Rayleigh–Bénard convection with rigid–free (rigid lower surface and stress-free upper surface) boundaries are sparsely studied. With the exception of Skarda [39] considering gravity-modulation effects and Or and Kelly [40] considering boundary temperature-modulation effects on the onset of thermal convection involving rigid–free boundaries by taking surface tension effects into consideration. Singh et al. [41, 42] also investigated the effect of two-frequency modulation of boundary temperatures on the onset of natural convection in a layer of fluid. The thermal convection in layers bounded by rigid–free boundaries is most prevalent in nature and in many practical situations and surface tension effects can be a key factor in controlling the dynamics in such situations. The surface tension effects are predominant in liquid metals like Mercury and are usually small in most liquids, especially in organic liquids. It also tends to decrease with temperature and hence we propose to study the effect of gravity modulation on thermal convection in a region bounded by a lower rigid and upper free surface by neglecting the surface tension effect. The study mainly aims to compare the results of rigid–free boundaries with those of free–free and rigid–rigid boundaries. This study is of particular importance as it seeks to investigate how the onset of harmonic and subharmonic motions of fluid under gravity modulated conditions vary with the choice of bounding surfaces. Although highly theoretical, this study gives perspective on the variety of boundary conditions that exist naturally and how gravity modulation uniquely influences the state and onset of convection for each scenario.

We have observed that quite a bit of work has been done on the area of gravity modulation and its effect on convection which gives even further room for exploration on how this external time-dependent body force may impact the onset of convection in a number of fluid media. What is unexplored, however, is a comparative study of time-dependent gravity-modulation effects on the onset of convection in a Rayleigh–Bénard system with free–free, rigid–rigid, and rigid–free boundaries. The linear and non-linear analysis done by Kanchana et al. [16] complements this study very well as we seek to add insight to the aforementioned work by considering small-amplitude vibrations. We propose to use the perturbation method highlighted by Venezian [3] to deal with harmonic motions which are observed for small-amplitude modulations. Floquet theory-based Mathieu equation (see, Jordan and Smith [43]) will be solved using Hill’s infinite determinant method in exploring subharmonic regimes of the said study. Finally, heat transport will be quantified by the Nusselt number arising from the numerical solution of the Stuart–Landau equation that is based on slow time-scale expansions.

2 Mathematical Formulation

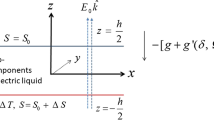
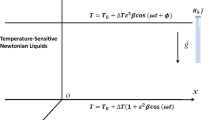
A horizontal layer of a Newtonian fluid in a Rayleigh–Bénard situation is subjected to time-periodic vertical oscillations and therefore the gravity term has an additional time-dependent component, $g_{m}(\Omega ,t)$, with $\Omega$ being the frequency of modulation. The horizontal layer is of height h, and the lower and upper boundaries $z=-\dfrac{h}{2}$ and $z=\dfrac{h}{2}$ which are, respectively, maintained at constant temperatures (isothermal) $T_{0}+\Delta T$ $(\Delta T>0)$ and $T_{0}$. Here $\Delta T$ represents the difference in temperature between the two horizontal boundaries. Three different boundaries conditions, namely; free-isothermal-free-isothermal (FIFI), rigid-isothermal-rigid-isothermal (RIRI), and free-isothermal-rigid-isothermal (FIRI) are considered for the horizontal bounding surfaces.

The governing equations are as follows:

$$\begin{aligned} \nabla \cdot \vec {q}= & {} 0, \end{aligned}$$

(1)

$$\begin{aligned} \rho _{0}\left[ \frac{\partial \vec {q}}{\partial t}+(\vec {q}\cdot \nabla )\vec {q}\right]= & {} -\nabla p+\mu \nabla ^{2}\vec {q}+\rho \vec {g}, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial T}{\partial t}+(\vec {q}\cdot \nabla )T= & {} \kappa \nabla ^{2}T, \end{aligned}$$

(3)

where

$$\begin{aligned} \rho (T)={{\rho _{0}\left[ 1-\alpha (T-T_{0})\right] ,} }\left( \alpha >0\right) \end{aligned}$$

(4)

and

$$\begin{aligned} \vec {g}=-g_{0}\left[ 1+\epsilon \cos (\Omega t)\right] \hat{k}. \end{aligned}$$

(5)

In the basic state, the fluid is assumed to be at rest and therefore the pressure and temperature vary with z only. The basic state equations are given by

$$\begin{aligned} \vec {q}_{b}=0,\qquad T_{b}=T_{b}(z),\qquad \rho _{b}=\rho _{b}(z),\qquad p_{b}=p_{b}(z). \end{aligned}$$

(6)

In the basic state, equation (2) takes the form

$$\begin{aligned} \frac{dp_{b}}{dz}=-\rho _{0}g_{0}[1-\alpha (T_{b}-T_{0})], \end{aligned}$$

(7)

where use has been made of equation (4), and equation (3) takes the form

$$\begin{aligned} \frac{d^{2}T_{b}}{dz^{2}}=0. \end{aligned}$$

(8)

The solution of equation (8) subject to the condition $T_{b}=T_{0}+\Delta T$ at $z=-\dfrac{h}{2}$ and $T_{b}=T_{0}$ at $z=\dfrac{h}{2}$ is as follows:

$$\begin{aligned} T_{b}(z)=T_{0}+\Delta T\left( \frac{1}{2}-\frac{z}{h}\right) . \end{aligned}$$

(9)

We now subject the basic state to a perturbation as follows:

$$\begin{aligned} \vec {q}=\vec {q}_{b}+\vec {q}\,'(x,z,t),\qquad p=p_{b}(z)+p'(x,z,t),\qquad T=T_{b}(z)+T'(x,z,t). \end{aligned}$$

(10)

Here, $\vec {q}\,'$, $p'$, and $T'$ are small perturbations whose evolution dictates the stability of the considered Rayleigh–Bénard system. Using equation (10) in equations (1)-(5), and using the basic state equations (7) and (8), we set up the following equations governing the perturbations $\vec {q}\,'$, $p'$, and $T'$:

$$\begin{aligned} \nabla \cdot \vec {q}\,'= & {} 0, \end{aligned}$$

(11)

$$\begin{aligned} \rho _{0}\left[ \frac{\partial \vec {q}\,'}{\partial t}+(\vec {q}\,'\cdot \nabla )\vec {q}\,'\right]= & {} -\nabla p+\mu \nabla ^{2}\vec {q}\,' \nonumber \\{} & {} +\,\rho _{0}\alpha g_{0}\left[ 1+\epsilon \cos (\Omega t)\right] T' \hat{k}-\bar{g}(t,z)\hat{k} \end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial T'}{\partial t}+(\vec {q}\,'\cdot \nabla )T'+w'\frac{dT_{b}}{dz}= & {} \kappa \nabla ^{2}T', \end{aligned}$$

(13)

where the term

$$\begin{aligned} \bar{g}(t,z)=\rho _0g_0\epsilon \cos (\Omega t)[1-\alpha (T_b-T_0)], \end{aligned}$$

on the right-hand side of (12) arises due to the fact that there is no modulation of the basic state. In other words, we imply that gravity modulation is brought into play at the time of onset. We restrict the analysis to two-dimensional longitudinal rolls for which all the physical quantities are independent of y. Eliminating the pressure from equation (12) by rewriting equation (12) in component-form and cross-differentiation, we get

$$\begin{aligned}{} & {} \rho _{0}\left[ \frac{\partial }{\partial t}+u'\frac{\partial }{\partial x}+w'\frac{\partial }{\partial z}\right] \left( \frac{\partial u'}{\partial z}-\frac{\partial w'}{\partial x}\right) =\mu \left( \frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial z^{2}}\right) \left( \frac{\partial u'}{\partial z}-\frac{\partial w'}{\partial x}\right) \nonumber \\{} & {} \quad -\rho _0g_{0}\alpha [1+\epsilon \cos (\Omega t)]\frac{\partial T'}{\partial x}. \end{aligned}$$

(14)

We now introduce the stream function, $\psi$, in the form

$$\begin{aligned} u'=-\frac{\partial \psi }{\partial z}\qquad \text {and} \qquad w'=\frac{\partial \psi }{\partial x}, \end{aligned}$$

(15)

which satisfy the continuity equation (11). Now, equations (14) and (13) may be written as follows:

$$\begin{aligned} \rho _{0}\left[ \frac{\partial }{\partial t}\left( \nabla ^{2}\psi \right) +\frac{\partial \left( \psi ,\nabla ^{2}\psi \right) }{\partial \left( x,z\right) }\right]= & {} \mu \nabla ^{4}\psi +\rho _0g_{0}\alpha [1+\epsilon \cos (\Omega t)]\frac{\partial T'}{\partial x}. \end{aligned}$$

(16)

$$\begin{aligned} \frac{\partial T'}{\partial t} + \frac{\partial \left( \psi ,T'\right) }{\partial \left( x,z\right) } -\frac{\partial \psi }{\partial x}\frac{\Delta T}{h}= & {} \kappa \nabla ^{2}T'. \end{aligned}$$

(17)

We now non-dimensionalize equations (16) and (17) using the following scaling:

$$\begin{aligned} \left( x^{*},z^{*}\right) =\left( \frac{x}{h},\frac{z}{h}\right) , \qquad t^*=\frac{t\kappa }{h^{2}}, \qquad \psi ^*=\frac{\psi }{\kappa }, \qquad T^*=\frac{T'}{\Delta T}. \end{aligned}$$

(18)

Using the scaling (18) in equations (16) and (17) and on dropping the asterisks for simplicity we get

$$\begin{aligned} \frac{1}{Pr}\left[ \frac{\partial }{\partial t}\left( \nabla ^{2}\psi \right) +\frac{\partial \left( \psi ,\nabla ^{2}\psi \right) }{\partial \left( x,z\right) }\right]= & {} \nabla ^{4}\psi +Ra\left[ 1+\epsilon \cos (\omega t)\right] \frac{\partial T}{\partial x}, \end{aligned}$$

(19)

$$\begin{aligned} \frac{\partial T}{\partial t}+\frac{\partial \left( \psi ,T\right) }{\partial \left( x,z\right) }= & {} \nabla ^{2} T+\frac{\partial \psi }{\partial x}, \end{aligned}$$

(20)

in which $Pr=\dfrac{\mu }{\kappa \rho _{0}}$ is the Prandtl number, $Ra=\dfrac{\rho _{0}\alpha g_{0}h^{3}\Delta T}{\mu \kappa }$ is the Rayleigh number, and $\omega =\dfrac{\Omega h^2}{\kappa }$ is the scaled frequency.

To solve equations (19) and (20) we make use of three different boundary conditions, namely, free–free, rigid–rigid, and rigid–free boundaries. The stress-free boundaries are characterized by vanishing shear stress and the fluid is free to move any direction, whereas in the case of rigid boundaries are characterized by adhesive forces between the molecules of the bounding surface and those of fluids. The velocity of the fluid in the latter case will be same as that of the solid surface and this condition is commonly known as ‘no-slip’ condition. Rigid boundaries are practically realizable, whereas free boundaries are hypothetical and are interesting from the point of theoretical interest alone. Combination of these two boundaries are important as they exist quite naturally in many practical situations (encountered more than rigid boundaries). In fact, the experimental studies of Bénard considers a layer of fluid with rigid–free boundaries. With this view point, gravity-modulated thermal convection in a Newtonian fluid bounded by rigid–free boundaries forms a focal point of the present study and a comparison of the results of the same is done with those of the other combinations.

2.1 Boundary Condition

The three boundary conditions to be separately considered in the paper are given below:

Free-Isothermal-Free-Isothermal (FIFI)

$$\begin{aligned} \frac{\partial \psi }{\partial x}=\frac{\partial ^{2}}{\partial z^{2}}\left( \frac{\partial \psi }{\partial x}\right) =T=0\qquad \text {at} \quad z=\pm \frac{1}{2}. \end{aligned}$$

(21)

Rigid-Isothermal-Rigid-Isothermal (RIRI)

$$\begin{aligned} \frac{\partial \psi }{\partial x}=\frac{\partial }{\partial z}\left( \frac{\partial \psi }{\partial x}\right) = T =0\qquad \text {at} \quad z=\pm \frac{1}{2}. \end{aligned}$$

(22)

Rigid-Isothermal-Free-Isothermal (RIFI)

$$\begin{aligned}{} & {} \frac{\partial \psi }{\partial x}=\frac{\partial }{\partial z}\left( \frac{\partial \psi }{\partial x}\right) =T=0\qquad \text {at} \quad z=-\frac{1}{2}, \end{aligned}$$

(23)

$$\begin{aligned}{} & {} \frac{\partial \psi }{\partial x}=\frac{\partial ^{2}}{\partial z^{2}}\left( \frac{\partial \psi }{\partial x}\right) =T=0\qquad \text {at} \quad z=\frac{1}{2}. \end{aligned}$$

(24)

2.2 Derivation of the non-autonomous Lorenz System with quadratic non-linearities

For small-scale convective motion, equations (19) and (20) take the form

$$\begin{aligned} \frac{1}{Pr}\frac{\partial }{\partial t}\left( \nabla ^{2}\psi \right)= & {} \nabla ^{4}\psi +Ra\left[ 1+\epsilon \cos (\omega t)\right] \frac{\partial T}{\partial x}, \end{aligned}$$

(25)

$$\begin{aligned} \frac{\partial T}{\partial t}= & {} \nabla ^{2}T+\frac{\partial \psi }{\partial x}\left( 1-\frac{\partial T}{\partial z}\right) +\frac{\partial \psi }{\partial z}\frac{\partial T}{\partial x}. \end{aligned}$$

(26)

The solution to equations (25) and (26) may be assumed in the form

$$\begin{aligned} \left. \begin{array}{c} \psi (t,x,z)=A(t)\sin \left( kx\right) F(z), \\ T(t,x,z)=B(t)\cos \left( kx\right) G(z)+C(t)H(z), \end{array}\right\} \end{aligned}$$

(27)

where the forms of F(z) and G(z) depend on the three boundary conditions considered. One may consider different modes of disturbances characterized by the number n as shown in Table 1. Further, Table 1 also gives the critical Rayleigh number and wave number corresponding to the least mode of $n=1$. The characteristic values $\mu _n$ and $\lambda _n$ corresponding to even and odd modes, respectively, are tabulated in Table 2 and compared, respectively, with the members of the sequences $\left\{ \left( 2n+\frac{1}{2}\right) \pi \right\} _{n=0}^\infty$ and $\left\{ \left( 2n-\frac{1}{2}\right) \pi \right\} _{n=0}^\infty$.

Table 1 The z-dependent part of the eigenfunction of different boundary conditions

For the weakly non-linear stability analysis, we take $H(z)=\sin (2\pi z)$ which characterizes the non-linear interaction between the velocity and the temperature fields in an isothermal situation. It is evident the eigenfunctions $E_F(x,z)=F(z)\sin \left( kx\right)$, $E_G(x,z)=G(z) \textrm{cos} (kx)$, and $E_H(z)=H(z)$ satisfy the orthogonality conditions. Multiplying (25) by $F(z)\sin \left( kx\right)$ and (26) by $G(z) \textrm{cos} \left( kx\right)$, respectively, substituting the solution (27) into resulting equations and integrating over a pair of counter-rotating Bénard cells gives us the following Lorenz system:

$$\begin{aligned} \frac{1}{Pr}\frac{dA}{dt}= & {} -p_1A+Ra\left[ 1+\epsilon \cos (\omega t)\right] p_2 B, \end{aligned}$$

(28)

$$\begin{aligned} \frac{dB}{dt}= & {} p_3 A-p_4 B+p_5 AC, \end{aligned}$$

(29)

$$\begin{aligned} \frac{dC}{dt}= & {} -p_6 C + \frac{p_7}{2} AB, \end{aligned}$$

(30)

in which

$$\begin{aligned} p_1= & {} -\frac{\left\langle F,F^{''''}-2k^{2}F^{''}+k^{4}F\right\rangle }{\left\langle F,F''-k^{2}F\right\rangle }, \qquad p_2 =-\frac{k\left\langle F,G\right\rangle }{\left\langle F,F''-k^{2}F\right\rangle },\\ p_3= & {} k\frac{\left\langle G,F\right\rangle }{\left\langle G,G\right\rangle },\qquad p_4=-\frac{\left\langle G,G''-k^{2}G\right\rangle }{\left\langle G,G\right\rangle },\qquad p_5=-k\frac{\left\langle G,FH'\right\rangle }{\left\langle G,G\right\rangle },\\ p_6= & {} -\frac{\left\langle H,H^{''}\right\rangle }{\left\langle H,H\right\rangle }, \qquad p_7=\frac{\left\langle H,FG'+F'G\right\rangle }{\left\langle H,H\right\rangle }. \end{aligned}$$

In the above expressions for the Lorenz coefficients, the angular brackets denote integration with respect to z over $\left[ -\frac{1}{2},\frac{1}{2}\right]$. We now perform the linear and weakly non-linear stability analyses based on the Lorenz system (28)–(30). We choose appropriate eigenfunctions F(z) and G(z) to perform the linear stability analysis for small-scale and large-scale modulations.

Table 2 Eigenvalues for the respective even and odd functions

3 Linear Stability Analysis

3.1 Small-amplitude modulation $(\epsilon<<1)$

We assume the gravity modulation to be of order $\epsilon$ where $\epsilon$ is a very small quantity and the eigenfunctions F(z) and G(z) will be functions of mode of perturbation n, i.e., $F(z)=F_n(z)$ and $G(z)=G_n(z)$. As a result the Lorenz coefficients $p_i,\,i=1,2,3,4$ in the linear terms will be functions of n. We now assume the following expansion for the amplitudes A and B, and the Rayleigh number Ra:

$$\begin{aligned} \left[ \begin{array}{c} A \\ B\\ Ra \end{array}\right] = \left[ \begin{array}{c} A_0\\ B_0\\ Ra_0 \end{array}\right] +\epsilon \left[ \begin{array}{c} A _1\\ B_1\\ Ra_1 \end{array}\right] +\epsilon ^{2} \left[ \begin{array}{c} A_2 \\ B_2\\ Ra_2 \end{array}\right] . \end{aligned}$$

(31)

Substituting expansion (31) into the linearized Lorenz system (27)–(28) (noting that the equation (30) for the amplitude C will be decoupled in the linearized Lorenz system) and equating the coefficients of various powers of $\epsilon$ on either side of the resulting equations gives us the following:

$$\begin{aligned} O(\epsilon ^0): \qquad{} & {} \mathcal {L} \left[ \begin{array}{c} A_0\\ B_0 \end{array}\right] = \left[ \begin{array}{c} 0\\ 0 \end{array}\right] , \end{aligned}$$

(32)

$$\begin{aligned} O(\epsilon ^1): \qquad{} & {} \mathcal {L}\left[ \begin{array}{c} A_1\\ B_1 \end{array}\right] = \left[ \begin{array}{c} -p_2PrB_{0}\left\{ Ra_{1}+Ra_{0}\cos (\omega t)\right\} \\ 0 \end{array}\right] , \end{aligned}$$

(33)

$$\begin{aligned} O(\epsilon ^2): \qquad{} & {} \mathcal {L}\left[ \begin{array}{c} A_2\\ \\ ~~ B_2 \end{array}\right] = \left[ \begin{array}{c} -p_2Pr\left[ B_{0}\left\{ Ra_{2}+Ra_{1}\cos (\omega t)\right\} \right. \\ \qquad \left. +B_{1}\left\{ Ra_{1}+Ra_{0}\cos (\omega t)\right\} \right] \\ \\ 0 \end{array}\right] , \nonumber \\{} & {} \qquad \vdots \end{aligned}$$

(34)

where the differential operator $\mathcal {L}$ is defined as follows:

$$\begin{aligned} \mathcal {L}=\left[ \begin{array}{cc} -\dfrac{\mathrm{{d}}}{\mathrm{{d}}t}- p_1Pr &{} p_2PrRa_0 \\ p_3 &{} -\dfrac{\mathrm{{d}}}{\mathrm{{d}}t}-p_4 \end{array}\right] . \end{aligned}$$

For marginal stationary stability, from equation (32), we get

$$\begin{aligned} \left[ \begin{array}{cc} -p_1Pr &{} p_2PrRa_0\\ p_3 &{} -p_4 \end{array}\right] \left[ \begin{array}{c} A_{0}\\ B_{0} \end{array}\right] =\left[ \begin{array}{c} 0\\ 0 \end{array}\right] . \end{aligned}$$

(35)

Using the condition for a non-trivial solution to equation (35) we require

$$\begin{aligned} Ra_{0}=\frac{p_1p_4}{p_2p_3}. \end{aligned}$$

(36)

At $O\left( \epsilon ^{1}\right)$, using solvability condition which states that the non-homogeneous time-independent part should be orthogonal to the solution of the homogeneous part, $\left[ \begin{array}{c} A_{1H} \\ B_{1H}\end{array}\right]$, we get

$$\begin{aligned} \left[ \begin{array}{c} A_{1H}\\ B_{1H} \end{array}\right] \cdot \left[ \begin{array}{c} -p_2PrB_0Ra_1\\ 0 \end{array}\right] =0. \end{aligned}$$

(37)

From equation (37), we obtain the following:

$$\begin{aligned} Ra_1=0. \end{aligned}$$

As the Rayleigh number is always positive, it should be independent of the sign of $\epsilon$ and this will result in

$$\begin{aligned} Ra_3=Ra_5=\cdots =0. \end{aligned}$$

The solution of equation (33) with $Ra_1=0$ can be assumed in the form

$$\begin{aligned} \left[ \begin{array}{c} A_1\\ B_1 \end{array}\right] =\left[ \begin{array}{c} A_{10}\left( \omega ^*\right) e^{i\omega ^*t}\\ B_{10}\left( \omega ^*\right) e^{i\omega ^*t} \end{array}\right] , \end{aligned}$$

where $\omega ^*$ is the natural frequency of the system. Now, equation (33) at the first order can be written as

$$\begin{aligned} \left[ \begin{array}{cc} -i\omega ^*-p_1Pr &{} p_2PrRa_0\\ p_3 &{} -i\omega ^*-p_4 \end{array}\right] \left[ \begin{array}{c} A_{10}\left( \omega ^*\right) e^{i \omega ^*t}\\ B_{10}\left( \omega ^*\right) e^{i\omega ^*t} \end{array}\right] =\left[ \begin{array}{c} -p_2PrRa_0B_0\cos (\omega t)\\ 0 \end{array}\right] \end{aligned}$$

which gives

$$\begin{aligned} \left[ \begin{array}{c} A_1\\ \\ B_1 \end{array}\right] =\frac{-PrRa_0\cos (\omega t)B_0}{\left\{ PrRa_0-\dfrac{\left( i\omega ^*+p_1Pr\right) \left( i\omega ^*+p_4\right) }{p_2p_3}\right\} } \left[ \begin{array}{c} \dfrac{i\omega ^*+p_4}{p_3}\\ \\ 1 \end{array}\right] . \end{aligned}$$

(38)

Again, using the solvability condition at $O\left( \epsilon ^{2}\right)$ we get

$$\begin{aligned} Ra_2=\Re \left[ \sum _{n=1}^{\infty } \left( \frac{-PrRa_0^2}{2\left\{ PrRa_0-\dfrac{\left( i\omega +p_1Pr\right) \left( i\omega +p_4\right) }{p_2p_3}\right\} }\right) \right] . \end{aligned}$$

(39)

For the existence of solution we have considered the natural frequency of the system to be equal to the applied frequency, i.e., $\omega ^*=\omega$.

The Rayleigh number can be calculated as

$$\begin{aligned} Ra=Ra_0+\epsilon ^2 Ra_2. \end{aligned}$$

Here it is to be noted that the Rayleigh number, Ra, depends on the wave number k which is present in the integrals $p_i$, $i=1,\ldots ,4$. By expanding the wavenumber as

$$\begin{aligned} k=k_0+\epsilon k_1+\epsilon ^2 k_2+\ldots \end{aligned}$$

and following Venezian [3] it can be shown that $k_1$ is negligibly small and so are $k_2$, $k_3$, ... and hence the wave number for the evaluation of the correction Rayleigh number, $Ra_2$, must be $k_0$ which is the same used in the evaluation of $Ra_0$. Further, higher-order corrections like $k_2$ become important when we seek corrections $Ra_4$ or beyond. The analysis performed here is valid for small-amplitude modulations where the dynamics is usually of the harmonic type. For not-so-small-amplitude modulations there is a possibility of subharmonics motions and the perturbation analysis cannot highlight the same. To explore the subharmonic type instability we use the Floquet theory and derive the Mathieu equation. The following subsection highlights the same including the solution procedure for the Mathieu equation.

3.2 Large-amplitude modulation $(\epsilon>>1)$

We note that the analysis presented in the previous subsection which is valid for small-scale modulations details only on the synchronous motions and does not depict the existence of subharmonic motions. In this subsection, we explore the possibility of subharmonic motions with the help of Mathieu equations. To this end, we consider the linearized version of equations (28)–(30). Making amplitude A the subject of equation (29), and eliminating A from equation (28) gives the damped Mathieu equation in the form

$$\begin{aligned} \frac{\mathrm{{d}}^{2}B}{\mathrm{{d}}{t}^{2}}+c_{1}\frac{\mathrm{{d}}B}{\mathrm{{d}}t}+c_{2}\left( Ra_{0}-Ra\left[ 1+\epsilon \cos ({\omega }{t})\right] \right) B=0, \end{aligned}$$

(40)

in which the time t is scaled by $\dfrac{1}{\sqrt{Pr}}$ and the frequency $\omega$ is scaled by $\sqrt{Pr}$. Here, $c_{1}=\left( \dfrac{p_{4}}{\sqrt{Pr}}+p_{1}\sqrt{Pr}\right)$ and $c_{2}=p_{3}p_{2}$ are the coefficients of the Mathieu equation, and $Ra_{0}=\dfrac{p_{1}p_{4}}{p_{2}p_{3}}$ is the Rayleigh number of the non-modulated system. One can recover the Mathieu equation reported by Saravanan [32] for clear fluid (for $\lambda =0$ in their paper) in the domain $z\in [0,1]$ by choosing appropriate eigenfunctions F(z) and G(z) in equation (40). By taking $F(z)=G(z)=\sin \left( \pi z\right)$ we obtain the Mathieu equation reported by Saravanan [32] corresponding to the free boundaries with coefficients

$$\begin{aligned} c_{1}= & {} \frac{k^{2}+\pi ^{2}}{\sqrt{Pr}}+\sqrt{Pr}\left( k^{2}+\pi ^{2}\right) ,\\ c_{2}= & {} \frac{k^{2}}{k^{2}+\pi ^{2}},\\ Ra_{0}= & {} \frac{(k^{2}+\pi ^{2})^{3}}{k^{2}}, \end{aligned}$$

and by taking $F(z)=z^{2}\left( 1-z\right) ^{2}$ and $G(z)=z\left( 1-z\right) \left( 1+z-z^{2}\right)$ we obtain the Mathieu equation reported by Saravanan [32] corresponding to the rigid boundaries with coefficients

$$\begin{aligned} c_{1}= & {} \frac{1}{P}\left( k^{2}+\frac{306}{31}\right) +P\left( \frac{k^{4}+24k^{2}+504}{k^{2}+12}\right) ,\\ c_{2}= & {} \frac{121k^{2}}{124\left( k^{2}+12\right) },\\ Ra_{0}= & {} \frac{4\left( k^{4}+24k^{2}+504\right) \left( 31k^{2}+306\right) }{121k^{2}}. \end{aligned}$$

We now highlight the evaluation of the Rayleigh number using the Mathieu equation (40).

3.2.1 Hill’s infinite determinant method

Firstly, we rewrite equation (40) using $2\zeta =c_{1}.$ We next introduce the solution of the form $B(t)=e^{-\zeta t}F(t)$ and let $2\tau =\omega t$. We now arrive at the canonical form of the Mathieu equation in the form

$$\begin{aligned} F''+\left[ D_{1}-2D_{2}\cos \left( 2\tau \right) \right] F=0, \end{aligned}$$

(41)

where prime indicates differentiation with respect to $\tau$ and the coefficients are given by

$$\begin{aligned} D_{1}= & {} \dfrac{4}{\omega ^{2}}\Big (c_{2}\left( Ra_{0}-Ra\right) -\zeta ^{2}\Big ),\\ D_{2}= & {} -\left( \dfrac{4}{\omega ^{2}}\right) \dfrac{c_{2}\epsilon Ra}{2}. \end{aligned}$$

Following the Floquet theory, we assume the general solution of the equation (41) in the form $F(\tau )=e^{\xi \tau }\mathcal {F}(\tau )$ where $\xi$ is the Floquet exponent and $\mathcal {F}(\tau )$ is a periodic function with period $\pi .$ As such, the solution of equation (41) can be written as

$$\begin{aligned} B(t)=e^{-\zeta t}F(t)=e^{\left( \frac{\xi \omega }{2}-\zeta \right) t}\mathcal {F}(t). \end{aligned}$$

(42)

For stability, it is required that $\dfrac{\xi \omega }{2}\le \zeta$. Therefore, the corresponding marginal stability condition is $\dfrac{\xi \omega }{2}=\zeta$. The solution of equation (41) may be written in the form of a Fourier series as follows:

$$\begin{aligned} F=e^{\xi \tau }\sum _{n=-\infty }^{+\infty }a_{n}e^{i(2n+p)\tau }. \end{aligned}$$

(43)

If $p=0$, then we would have a solution of synchronous type (S) with period $\pi$ and a solution of subharmonic type (SH) if $p=1$ with period $2\pi$. Substituting equation (43) corresponding to S mode in equation (41) gives the linear system:

$$\begin{aligned} \gamma _{n}a_{n-1}+a_{n}+\gamma _{n}a_{n+1}=0,\quad n=...,-2,-1,0,1,2,... \end{aligned}$$

(44)

where $\gamma _{n}(\xi )=\dfrac{D_{2}}{\left[ \left( 2n-i\xi \right) ^{2}-D_{1}\right] }$. For the existence of non-trivial solution, the characteristic determinant of the coefficient matrix of the linear system (41) must vanish. In general this determinant is a function of $\xi$, $D_1$ and $D_2$ but it can be shown to depend only on $\xi$ and $D_1$. Therefore, we get

$$\begin{aligned} \Delta \left( D_1, \xi \right) =\left\| \begin{array}{ccccccccc} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} \gamma _{-2} &{} 1 &{} \gamma _{-2} &{} 0 &{} 0 &{} 0 &{} 0 &{} .\\ . &{} 0 &{} \gamma _{-1} &{} 1 &{} \gamma _{-1} &{} 0 &{} 0 &{} 0 &{} .\\ . &{} 0 &{} 0 &{} \gamma _{0} &{} 1 &{} \gamma _{0} &{} 0 &{} 0 &{} .\\ . &{} 0 &{} 0 &{} 0 &{} \gamma _{1} &{} 1 &{} \gamma _{1} &{} 0 &{} .\\ . &{} 0 &{} 0 &{} 0 &{} 0 &{} \gamma _{2} &{} 1 &{} \gamma _{2} &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . \end{array}\right\| =0, \end{aligned}$$

(45)

Here the determinant $\Delta \left( D_1,\xi \right)$ is known as the Hill’s infinite determinant. According to Morse and Feshback [44], this infinite determinant may be written in terms of a succinct equation as

$$\begin{aligned} \cosh (\xi \pi )= & {} 1-2\Delta (D_1,0)\sin ^{2}\left( \frac{\pi \sqrt{D_{1}}}{2}\right) , \nonumber \\= & {} 1+2\Delta (D_1,0)\sinh ^{2}\left( \frac{\pi \sqrt{-D_{1}}}{2}\right) , \end{aligned}$$

(46)

from which the value of Ra can be evaluated. However, one must first consider the computation of $\Delta (D_1,0)$ (Hill’s infinite determinant evaluated at $\xi =0$). Conveniently, $\Delta (D_1,0)$ can be computed using the following recurrence relations between the determinants of orders differing by two at each step, beginning with the mid-determinant [43]:

$$\begin{aligned} \left. \begin{array} {l} \Delta _{0}=1,\\ \Delta _{1}=1-2\gamma _{0}\gamma _{1},\\ \Delta _{2}=\left( 1-\gamma _{1}\gamma _{2}\right) ^{2}-2\gamma _{0} \gamma _{1}\left( 1-\gamma _{1}\gamma _{2}\right) ,\\ \qquad \vdots \\ \Delta _{n+2}=\left( 1-\gamma _{n+1}\gamma _{n+2}\right) \Delta _{n+1}-\gamma _{n+1}\gamma _{n+2}\left( 1-\gamma _{n+1}\gamma _{n+2}\right) \Delta _{n} \\ \qquad \qquad +\;\gamma _{n}^{2}\gamma _{n+1}^{3}\gamma _{n+2}\Delta _{n-1}.\\ \qquad \vdots \end{array} \right\} \end{aligned}$$

(47)

The sequence $\{\Delta _n\}_{n=0}^\infty$ converges to the value $\Delta (D_1,0)$. In the same way, one may obtain the corresponding characteristic equation for the SH mode as follows:

$$\begin{aligned} \cosh (\xi \pi )= & {} -1+2\Delta (D_1,0)\sin ^{2}\left( \frac{\pi \sqrt{D_{1}}}{2}\right) \nonumber \\= & {} -1-2\Delta (D_1,0)\sinh ^{2}\left( \frac{\pi \sqrt{-D_{1}}}{2}\right) . \end{aligned}$$

(48)

The characteristic equations (46) and (48) are solved numerically for Ra by first calculating the Floquet exponent $\xi$ by using marginal stability conditions and then fixing values of $\omega$, k, and other parameters. The recurrence relation converges quite rapidly, leading to Ra values which are exact to two or three decimal places. It converges even more quickly for large $\omega$ values. The discussion of computational results will follow in the succeeding sections. Having explored instability aspects for cases of small- and large-amplitude modulations we now move on to discuss the heat transport.

4 Weakly non-linear stability analysis

4.1 Derivation of the non-autonomous Stuart–Landau Equation with cubic non-linearity

We use a small time-scale $\tau =\delta ^{2}t$, where $\delta<<1$ in view of marginal stability onset and assume that the gravity modulation is of order $\delta ^{2}$, that is, $\epsilon \thickapprox \epsilon _{1}\delta ^{2}$. The small time-scale version of the Lorenz system (28)–(30) is now given by

$$\begin{aligned} \frac{\delta ^{2}}{Pr}\dfrac{\mathrm{{d}}A}{\mathrm{{d}}\tau }= & {} -p_{1}A+Ra\left[ 1+\epsilon _{1}\delta ^{2}\cos (\omega _1\tau )\right] p_{2}B, \end{aligned}$$

(49)

$$\begin{aligned} \delta ^{2}\dfrac{\mathrm{{d}}B}{\mathrm{{d}}\tau }= & {} p_{3}A-p_{4}B+p_{5}AC, \end{aligned}$$

(50)

$$\begin{aligned} \delta ^{2}\dfrac{\mathrm{{d}}C}{\mathrm{{d}}\tau }= & {} -p_{6}C+\frac{p_{7}}{2}AB, \end{aligned}$$

(51)

where $\omega _1=\dfrac{\omega }{\delta ^{2}}$ is the rescaled frequency. Now we expand the amplitudes A, B, C, and Ra in powers of $\delta$ as follows:

$$\begin{aligned} \left. \begin{array}{c} A=\delta A_{1}+\delta ^{2}A_{2}+\delta ^{3}A_{3}+..., \\ B=\delta B_{1}+\delta ^{2}B_{2}+\delta ^{3}B_{3}+..., \\ C=\delta C_{1}+\delta ^{2}C_{2}+\delta ^{3}C_{3}+..., \\ Ra=Ra_{0}+\delta ^{2}Ra_{2}+\delta ^{4}Ra_{4}+... \end{array}\right\} . \end{aligned}$$

(52)

For the sake of convenience, we define the operators $L_{2}$ and $V_{i}$ as follows:

$$\begin{aligned} L_{2}=\left[ \begin{array}{ccc} -p_{1}\quad &{} Ra_{0}p_{2}\quad &{} 0\\ p_{3} &{} -p_{4} &{} 0\\ 0 &{} 0 &{} -p_{6} \end{array}\right] \qquad \text {and} \qquad V_{i}=\left[ \begin{array}{c} A_{i}\\ B_{i}\\ C_{i} \end{array}\right] ,\quad i=1,2,3 \end{aligned}$$

(53)

Substituting equation (52) in equation (49) - (51) and comparing the various powers of $\delta$ gives

$$\begin{aligned} O(\delta ^{1}):\qquad{} & {} L_{2}V_{1}=0, \end{aligned}$$

(54)

$$\begin{aligned} O(\delta ^{2}):\qquad{} & {} L_{2}V_{2}=\left[ \begin{array}{ccc} R_{21}\quad&R_{22}\quad&R_{23}\end{array}\right] ^{Tr}, \end{aligned}$$

(55)

$$\begin{aligned} O(\delta ^{3}):\qquad{} & {} L_{2}V_{3}=\left[ \begin{array}{ccc} R_{31}\quad&R_{32}\quad&R_{33}\end{array}\right] ^{Tr}, \end{aligned}$$

(56)

where

$$\begin{aligned} \left. \begin{array}{l} R_{21}=0,\\ R_{22}=p_{5}A_{1}C_{1},\\ R_{23}=-\dfrac{p_{7}}{2}A_{1}B_{1} \\ R_{31}=\dfrac{1}{Pr}\dfrac{dA_{1}}{d\tau }-p_{2}B_{1}\left[ Ra_{2}-\epsilon _{1}Ra_{0}\cos (\omega _1\tau )\right] , \\ R_{32}=\dfrac{dB_{1}}{d\tau }+p_{5}\left( A_{1}C_{2}+A_{2}C_{1}\right) , \\ R_{33}=\dfrac{dC_{1}}{d\tau }-\dfrac{p_{7}}{2}\left( A_{1}B_{2}+A_{2}B_{1}\right) , \end{array}\right\} . \end{aligned}$$

(57)

The non-trivial solution of the problem at $O(\delta ^{1})$ is given by

$$\begin{aligned} V_{1}=\left[ \begin{array}{ccc} A_{1}\quad&\dfrac{p_{3}}{p_{4}}A_{1}\quad&0\end{array}\right] ^{Tr}. \end{aligned}$$

(58)

The solution of the problem at $O(\delta ^{2})$ is given by

$$\begin{aligned} V_{2}=\left[ \begin{array}{ccc} 0\quad&0\quad&\dfrac{p_{7}p_{3}}{2p_{4}P_{6}}A_{1}^{2}\end{array}\right] ^{Tr}. \end{aligned}$$

(59)

For solvability the non-homogeneous part of the problem at $O(\delta ^{3})$ must be orthogonal to the solution $\left[ \begin{array}{ccc} A_{1}\quad&\quad \dfrac{p_{3}A_{1}}{A_{4}}\quad&\quad 0\end{array}\right] ^{Tr}$,

$$\begin{aligned} \text {i.e.,} \quad A_{1}R_{31}+B_{1}R_{32}+C_{1}R_{33}=0. \end{aligned}$$

Substituted for $B_{1}$ and $C_{2}$, into the above equation, we get

$$\begin{aligned} \frac{\mathrm{{d}}A_{1}}{\mathrm{{d}}\tau }=Q_{1}\left[ Ra_{2}-Ra_{0}\epsilon _{1}\cos \left( \omega _1\tau \right) \right] A_{1}-Q_{2}A_{1}^{3}, \end{aligned}$$

(60)

where, $Q_{1}=\dfrac{Prp_{2}p_{3}p_{4}}{Prp_{3}^{2}+p_{4}^{2}}$, and $Q_{2}=\dfrac{Prp_{3}^{2}p_{5}p_{7}}{2p_{6}\left( Prp_{3}^{2}+p_{4}^{2}\right) }$. The non-linear amplitude equation (60) is the non-autonomous Stuart–Landau equation. For more discussion on the Stuart–Landau equation, please refer to the work by Siddheshwar [45], which outlines an unabridged method of solution of the same and its application to continuum mechanics. We find the numerical solution using the Runge–Kutta–Fehlberg (RKF45) method to seek temporal variation of heat transfer at the boundary. The bifurcation analysis is beyond the scope of the present study.

4.1.1 Estimation of the heat transport in terms of Nusselt number

The thermal Nusselt number, $Nu\left( \tau \right)$, is defined as follows:

$$\begin{aligned} Nu\left( \tau \right)= & {} 1+\frac{\text {Heat transport by convection}}{\text {Heat transport by conduction}}\nonumber \\= & {} 1+\left[ \frac{\displaystyle \int _{0}^{\frac{2 \pi }{k}}\left( \dfrac{\partial T}{\partial z}\right) \mathrm{{d}}x}{\displaystyle \int _{0}^{\frac{2 \pi }{k}}\left( \dfrac{\mathrm{{d}} T_{b}}{\mathrm{{d}} z}\right) \mathrm{{d}}x}\right] _{z=-\frac{1}{2}} \end{aligned}$$

(61)

According to equation (9), $T_{b}=\dfrac{1}{2}-z$, in which $T_{b}$ and z are in their non-dimensional form. Substituting the second equation of (27) into (61) and making use of equations (58) and (59) gives

$$\begin{aligned} Nu\left( \tau \right)= & {} 1+H'\left( -\frac{1}{2}\right) \delta ^{2}\frac{p_{7}p_{3}}{2p_{4}p_{6}}A_{1}^{2} \nonumber \\= & {} 1-2\pi \delta ^{2}\frac{p_{7}p_{3}}{2p_{4}p_{6}}A_{1}^{2}. \end{aligned}$$

(62)

We now present the results concerning the effect of frequency and amplitude on the gravity-modulated thermal convection obtained using linear and weakly non-linear stability analyses.

5 Results and discussion

The effect of gravity modulation on the onset of convection in a horizontal Newtonian fluid layer was studied. Three types of isothermal boundaries, namely, free–free, rigid–rigid, and rigid–free are considered and effects are comparatively analyzed, with emphasis on rigid–free boundaries. Linear stability analysis was done with small-scale modulation as reported by Kanchana, et.al. [16], and with large-scale modulation, as reported by Saravanan and Sivakumar [32]. Results on the heat transport are obtained under the influence of gravity modulation, and are explained in the subsections to come. We begin the discussion with the accuracy of results of the linear theory.

5.1 Accuracy of results

The value of Ra obtained from the perturbation analysis ($\epsilon<<1$) and the Floquet theory ($\epsilon>>1$) quantifies the onset of convection within the medium, and the procedure to find Ra makes use of F(z) and G(z) as the corresponding eigenfunctions. The choice of eigenfunctions F(z) and G(z) decides the accuracy of results in both the cases. We have made appropriate choices for the two cases that are considerably accurate (to be discussed a little later) and assist the mathematical analysis.

From the perturbation analysis valid for small-amplitude modulations the Rayleigh number is obtained as

$$\begin{aligned} Ra=Ra_0+\epsilon ^2Ra_2, \end{aligned}$$

where $Ra_0$ and $Ra_2$ are evaluated at the critical wave number corresponding to critical value of $Ra_0$. It should be noted that the correction Rayleigh number $Ra_2$ is a function of frequency of modulation alone, as seen in equation (39). The procedure gives the exact value of Ra for the free–free boundaries, whereas for rigid–rigid and rigid–free boundaries it is a highly accurate single-term Galerkin method. We have used even and odd functions of Chandrashekar as tabulated in Tables 1 and 2 in unison with the superposition principle for the computation of $Ra_0$ and $Ra_2$ in the case of rigid-rigid and rigid–free boundaries. Of course, one has to scale the Rayleigh number obtained for rigid–rigid boundaries using the odd Chandrashekar function by 16 to get the Rayleigh number for rigid–free boundaries. Similarly, the wave number has to be scaled by 2. We observe an absolute relative error of 1.2 % and 2.9 % in the computation of $Ra_0$ in the cases of rigid–rigid and rigid–free boundaries, respectively.

Table 3 Comparison of $Ra_{c}$ values calculated using Chandrashekar functions and polynomial eigenfunctions

To extract Ra from the Mathieu equation valid for all amplitudes we have used eigenfunctions

$$\begin{aligned} F(z)= & {} (z-1)\left( z-\dfrac{1}{2}\right) \left( z+\dfrac{1}{2}\right) ^2,\\ G(z)= & {} \left( z^2-\dfrac{1}{4}\right) \left( \dfrac{5}{4}-z^2\right) ^2. \end{aligned}$$

The reason being these eigenfunctions produce the unmodulated Rayleigh number with an absolute relative error of 2.2% which is much less compared to the odd Chandrashekar functions for rigid–rigid boundaries and subsequent scaling. These errors would therefore be propagated throughout the numerical calculations of $Ra_c$, and so we avoided the odd Chandrashekar functions of the rigid–rigid boundaries as in this case the error in the computation of Ra would amplify with the scaling used for rigid–free boundaries. Table 3 highlights the actual differences in $Ra_c$ values calculated. It is observed that the $Ra_c$ values calculated using the odd Chandrashekar function deviate drastically from those computed using polynomial eigenfunctions for the cases of (i) small frequencies corresponding to small-amplitude modulations and (ii) large frequencies corresponding to large-amplitude modulations. Here, it is shown that the odd Chandrashekar functions produce inconsistent errors in the case of rigid–free boundaries, in comparison to the even Chandrashekar functions for rigid–rigid boundaries. It is worth noting here that the values obtained using the polynomial trial functions are more consistent with that obtained by Saravanan [32].

To arrive at the most accurate values, we would need to pursue analytical solutions to the Mathieu equation, which is beyond the scope of this study. With the decision on the choice of appropriate eigenfunctions for the computation of Ra we now present the results concerning the effect of frequency and amplitude of modulations in the said two cases.

Fig. 1

$Ra_2$ as a function of $\omega$ for different Prandtl numbers Pr when gravity is modulated

5.2 Effect of frequency of modulation on the onset of convection

5.2.1 Results from Linear Theory

Figures 1 and 2  project the effect of modulating frequency on the correction Rayleigh number $Ra_2$ and the Rayleigh number Ra, respectively. It is shown in Fig. 1 (a) that $Ra_2$ tends to 0 as the frequency of oscillation increases infinitely. For free boundaries, it is shown that small-frequency modulations marginally stabilize the medium as it delays the onset of convection when $Pr=1$ and $Pr=10$ since $Ra_2$ tends to 0 from above. However, for larger values of Pr, one notes that for small-frequency modulations $Ra_2$ tends to 0 from below which means that convection is advanced, marginally destabilizing the medium. In the cases of rigid–rigid and rigid–free boundaries, Figs. 1 (b) and (c) show that small-frequency gravity modulation destabilizes the medium and expedites the onset of convection, for all the values of Pr considered, since $Ra_2$ tends to 0 from below as frequency increases. It can also be seen that in the case of small-frequency gravity modulation, the effect of large Prandtl number on the system is to destabilize the system in all cases as seen in Fig. 1 (a), (b), and (c), for which the correction Rayleigh number $Ra_2$ assumes negative values. However, the effect of the Prandtl number on the system is insignificant for large frequencies. Similar trends are observed in the case of Ra versus $\omega$ from Fig. 2. The Rayleigh number values level off to those corresponding to the respective unmodulated case for large frequencies in the three types of boundaries considered. These results are consistent with the ones already reported in the literature.

Fig. 2

Ra as a function of $\omega$ for different Prandtl numbers Pr when gravity is modulated

We now delineate the effect of the frequency of modulation on the onset of Rayleigh–Bénard convection subjected to large-amplitude modulations computed using the Floquet solution of the Mathieu equation (40). The effect of frequency of modulation was studied and shown using marginal stability curves. The marginal and critical stability curves are considered in the case of rigid–free boundaries alone as qualitatively similar curves are exhibited for free–free and rigid–rigid boundaries by Saravanan and Sivakumar [32].

Fig. 3

Marginal curves for rigid–free boundaries with harmonic and subharmonic modes for different values of $\epsilon$ and $\omega$ with $Pr=1$

Figure 3 depicts the marginal curves constructed as a function of modulation frequency and amplitude. The value of the Prandtl number was kept constant at $Pr=1$. These plots are done using the solution obtained from the Hill infinite determinant solution of the Mathieu equation, which differ from the traditional stability curves. The curves exhibit an array of alternate subharmonic (SH) and harmonic (H) loop-shaped branches in which the lower of the two loops decides the mode of onset of convection within the medium at the specified conditions. Each loop has a critical Rayleigh number which quantifies where the stable region transitions to convective instability, and the smaller of the array indicates the type of convective motion. For small frequency, the loops are thinner, and also have the critical Rayleigh number $Ra_c$ with harmonic mode. However, this is not permanent and the variations of $\epsilon$ and $\omega$ give scenarios in which $Ra_c$ is transferred between modes, H or SH. It is also evident that the difference between the local minimum, that is, the critical Rayleigh number, of each loop increases with increasing frequency of modulation, where the loops for large frequency are pushed further up and are wider with bigger wave number k. Therefore, we note that, in general, increasing the frequency of modulation delays convection, therefore, stabilizing the medium. However, with a microscopic view, we can see that the coupled effect of amplitude and frequency introduces inconsistencies in such a trend, and one observes a transition between harmonic and subharmonic modes.

Fig. 4

a $Ra_c$ and b $k_c$ against $\omega$ for rigid–free boundaries with harmonic and subharmonic modes for different values of $\epsilon$ with $Pr=1$

Figures 4 (a) and (b) depict the critical Rayleigh number, $Ra_c$, and the critical wave number, $k_c$, respectively, versus frequency, $\omega$, for different values of the amplitude $\epsilon$ for $Pr=1$. As stated before, the effect of frequency is to generally stabilize the medium, but we see in Fig. 4 (a) that for frequencies of the order less than 100 there are regions, where $Ra_c$ oscillates with alternating bands of SH and H modes as frequency increases. This is the general trend for modulation with amplitude $\epsilon >1$. Therefore, in the situations of engineering interests, one would need to consider specific ratios of frequency and amplitude to attain desired results. Figure 4 (b) shows that $k_c$ is an increasing function of $\omega$ for both modes of SH and H. We observe a drastic drop in the values of $k_c$ whenever the mode switches from SH to H or vice versa. We note three such transitions at lower frequencies similar to the case of rigid–rigid boundaries which are actually one more than those observed in the free–free boundaries case as reported by Saravanan and Sivakumar [32].

Table 4 Comparison of the critical Rayleigh number, $Ra_c$, and corresponding wavenumber $k_c$ obtained numerically using Hill’s Determinant method, for different boundaries

Table 4 shows how $Ra_c$ and $k_c$ vary with changes for all three boundary conditions considered. Generally, for each specified value of $\omega$, it is observed that $Ra_c$ is smallest for free boundaries, and largest for rigid–rigid boundaries, with rigid–free boundaries sitting in between. However, for high frequency, $Ra_c$ is less for rigid–rigid boundaries than that of rigid–free. It is also noted that $k_c$ at which the onset occurs for both these cases is significantly higher than that of lower frequency.

5.2.2 Results from Non-linear Theory

A weakly non-linear stability analysis is performed to investigate the effect of gravity modulation on the heat transport for the three types of boundaries considered. The expression representing the Nusselt number Nu was obtained using the solution of the Stuart–Landau equation for and is given by equation (62). Figure 6 shows the effect of $\omega$ on heat transport. It is observed that increasing $\omega$ reduced the Nusselt number, therefore causing a reduction in the heat transport. The mean Nusselt number, $\overline{Nu}$, documented in Table 5 also shows this result in which $\omega$ reduces the heat transport. Table 5 also shows that the effect of increasing the frequency on heat transport is more significant for rigid–rigid boundaries than it is for free–free and rigid–free boundaries since the differences between each $\overline{Nu}$ at different frequencies are greater. It must also be noted that due to modulatory effects, $\overline{Nu}$ oscillates about the respective values of the unmodulated case, that is, when $\epsilon _1=0$.

5.3 Effect of amplitude of modulation on onset of convection

5.3.1 Results from Linear Theory

We now turn our attention to the effects of the amplitude of modulation on convection. Though some aspects (especially having to do with the coupling effects with frequency) were previously stated, the significant observations must now be mentioned.

As mentioned earlier, the linear stability analyses were carried out considering both small- and large-amplitude modulations within which the amplitudes were further varied. It should be noted that for small-amplitude $\epsilon<<1$, the correction Rayleigh number $Ra_2$ is independent of $\epsilon$ and therefore Ra is unaffected by the amplitude of modulations. In the cases of large-amplitude $\epsilon>> {1}$, there are significant effects to be noted. From the marginal curves in Fig. 3, one notes that varying amplitude does not cause $Ra_c$ to be transferred between the modes of onset of convection, whether H or SH, at a constant frequency. For example, for $\omega$ held constant at 10, all the amplitudes considered support $Ra_c$ by harmonic mode and subharmonic mode for $\omega =200$. However, for large frequency and large amplitude, there begins inconsistencies in the aforementioned trend. Therefore, the mode of onset of convection is determined by the frequency at which the external gravity force is modulated.

Generally, increasing the amplitude of modulation destabilizes the system for relatively small frequency (up to $\omega$ of order 1000, as depicted in Fig. 4). For larger frequencies of modulation, the effect of amplitude diminishes as $Ra_c$ approaches that of the unmodulated case. For $\epsilon =1$, the unstable region is predominantly H mode as no SH mode is observed. However, there are alternate regions of H and SH modes of onset of convection at each of the other amplitudes $\epsilon$ considered. That is, for $\epsilon =100$, the onset of convection is by the SH mode at very low frequencies until $\omega$ gets to 16 where it transitions to H until $\omega =25.7$. Again, the mode transitions to SH where $Ra_c$ increases significantly, from a region of decrease, with an increase in frequency. Here, we also see that SH mode spreads over the widest range of $\omega$, before making the next transition. Finally, as $\omega$ passes through 2060, the mode transitions to H where $Ra_c$ decreases asymptomatically to the unmodulated case. This is observed for all the cases of $\epsilon =10,50,100$.

Table 4 also shows how the critical Rayleigh number $Ra_c$ and corresponding wave number $k_c$ vary with changes in amplitude of modulation for all three boundary conditions. The table supports the fact that generally, the amplitude of modulation may have stabilizing/destabilizing effect based on the frequency of modulation. At lower frequencies, for example, $\omega =20$ it has destabilizing effect as $Ra_c$ decreases with $\epsilon$. At moderate frequencies, for example, $\omega =200$ it has stabilizing effect until the mode switches from H to SH at large amplitudes. Such inconsistencies are observed in all three types of boundary conditions considered.

5.3.2 Results from Non-linear Theory

Much can be said also about how the amplitude of induced modulations impacts heat transport. It was assumed that the amplitude of modulation was small and was of order $\delta ^{2}$. This assumption aided in deriving the Stuart–Landau equation using perturbation analysis and slow time-scale approximations. The amplitudes of modulation $\epsilon _{1}$ considered were $\epsilon _{1}=0, 0.05, 0.08, 0.1$ since they were considered small. Figure 5 displays the effect of amplitude on heat transport, for fixed $\omega _1=2$. It is shown that as amplitude increases, so does the displacement of the Nusselt number from the unmodulated case. In other words, increasing the amplitude of gravity modulation increases heat transport within the system. This is observation is true for all three types of boundaries considered. The mean Nusselt numbers $\overline{Nu}$ reflected in Table 6 for each of the cases considered are consistent with the previous observation, in which increasing amplitude amplifies heat transport. This result becomes particularly important when the heat transport capabilities of the considered cell are applied to other engineering phenomena. One such example is as reported by Yikun et al. [46] in which entropy is generated by the transport of heat from the convective processes of Rayleigh–Bénard convection. The oscillatory nature of the mean Nusselt number may act to control the output of heat in such a scenario, wherein the roles of amplitude and frequency of modulation would be pivotal.

Fig. 5

Variation of Nusselt number Nu with time $\tau$ for different frequencies $\omega _1$ with $\epsilon _{1}=0.05$

Fig. 6

Variation of Nusselt number Nu with time $\tau$ for different amplitudes $\epsilon _1$ with $\omega _1=2$

Table 5 Values of mean Nusselt number $\overline{Nu}$ for amplitude $\epsilon _{1}=0.05$ and $Pr=1$ for different boundaries at different frequencies $\omega _1$

Table 6 Values of mean Nusselt number $\overline{Nu}$ for frequency $\omega _1=2$ and $Pr=1$ for different boundaries at different amplitudes $\epsilon _{1}$

5.4 Comparison of results

It is well known for the unmodulated case that the critical Rayleigh number and the corresponding critical wave number of the rigid–free boundaries lie in between those corresponding to the free–free boundaries and rigid–rigid boundaries, i.e.,

$$\begin{aligned}{} & {} {Ra_0}_c^{\text {free--free}}<{Ra_0}_c^{\text {rigid--free}}<{Ra_0}_c^{\text {rigid--rigid}}, \\{} & {} {k_0}_c^{\text {free--free}}<{k_0}_c^{\text {rigid--free}}<{k_0}_c^{\text {rigid--rigid}}. \end{aligned}$$

When the convective mode is of the harmonic type (small-amplitude case) similar results are true as depicted by small-amplitude analysis

$$\begin{aligned}{} & {} {Ra_\text {H}}_c^{\text {free--free}}<{Ra_\text {H}}_c^{\text {rigid--free}}<{Ra_\text {H}}_c^{\text {rigid--rigid}}, \\{} & {} {k_\text {H}}_c^{\text {free--free}}<{k_\text {H}}_c^{\text {rigid--free}}<{k_\text {H}}_c^{\text {rigid--rigid}}, \end{aligned}$$

where H stands for harmonic motions. This can be attributed to the fact that in the case of rigid–rigid boundaries the fluid adheres to two surfaces and consumes more energy for the buoyancy force to overcome the adhesive forces so that the convection sets in. In the case of rigid–free boundaries, there is only one rigid boundary as a result the system consumes less energy in comparison with rigid–rigid boundaries for the onset of convection. It can go without saying that the system with free–free boundaries consumes the least energy as for obvious reasons. For moderate amplitudes and frequencies when the subharmonic mode is prevalent in all three cases following results hold:

$$\begin{aligned}{} & {} {Ra_\text {SH}}_c^{\text {free--free}}<{Ra_\text {SH}}_c^{\text {rigid--free}}<{Ra_\text {SH}}_c^{\text {rigid--rigid}}, \\{} & {} {k_\text {SH}}_c^{\text {free--free}}<{k_\text {SH}}_c^{\text {rigid--free}}<{k_\text {SH}}_c^{\text {rigid--rigid}}, \end{aligned}$$

where SH stands for subharmonic motions. For large amplitudes and frequencies, we observe a deviation from the above inequalities as we observe the delayed onset of convection in rigid–free boundaries as compared to rigid–rigid boundaries. Even though the large-amplitude modulations are physically unrealistic one would be curious to know the unexpected behavior of the rigid–free system. Further investigation is warranted in this direction. It can also be observed for all the three types of considered boundary combinations that

$$\begin{aligned}{} & {} Ra_c^{\text {with-modulation}}>Ra_c^{\text {without-modulation}}, \\{} & {} k_c^{\text {with-modulation}}<k_c^{\text {without-modulation}}, \\{} & {} \overline{Nu}^{\text {with-modulation}}>\overline{Nu}^{\text {without-modulation}}, \end{aligned}$$

and

$$\begin{aligned} \overline{Nu}^{\text {free--free}}<\overline{Nu}^{\text {rigid--free}}<\overline{Nu}^{\text {rigid--rigid}}. \end{aligned}$$

The above inequality essentially means that gravity modulation can effectively be used to alter the onset of convection. Attention is drawn to the work of Krishna et al. [47] who developed a device that uses Rayleigh–Bénard convection to carry out polymerase chain reaction (PCR) amplification of DNA. Instead of controlling the temperature of the thermocyclers externally, Rayleigh–Bénard cells are constructed through which fluid is cycled and the ideal reaction conditions are regulated by varying Ra. Under such situations, one can use gravity modulation to regulate the temperature of the thermocyclers by exercising optimum frequency and amplitude of modulation. It goes without saying that under the conditions of gravity modulation, key attention would need to be taken to understand the ideal frequency and amplitude of modulation to be used to achieve desired results.

6 Conclusion

A comparative study on the effect of gravity modulation on the Rayleigh–Bénard convection bounded by three different surfaces was carried out. Effects of small-amplitude modulations were studied using the modified perturbation approach of Venezian [3] and those of large-amplitude modulations using the Floquet solution of the Mathieu equation. An appropriate choice of eigenfunctions for the computation of Ra was made for both the cases of small- and large-amplitude modulations. The following are the important outcomes of the present study:

• 1. Modulation has a stabilizing effect on the system in all three boundary types. The Rayleigh number corresponding to the onset of convection for rigid–free boundaries lies between free–free and rigid–rigid counterparts for both harmonic and subharmonic modes observed at lower and moderate amplitudes of modulations. This implies that gravity-modulated Rayleigh–Bénard convection can be adapted in practical situations to control convection.

• 2. The amplitude of modulation dictates the transitions between harmonic and subharmonic types of motions.

• 3. Large-amplitude large-frequency modulations which are physically not realistic deviated from the expected behavior.