Amplitude Equation and Heat Transport for Rayleigh–Bénard Convection in Newtonian Liquids with Nanoparticles

Abstract

Rayleigh–Bénard convection in liquids with nanoparticles is modelled as a single phase system with liquid properties like density, viscosity, thermal expansion coefficient, heat capacity and thermal conductivity modified by the presence of the nanoparticles. Expressions for the thermophysical properties are chosen from earlier works. The tri-modal Lorenz model is derived under the assumptions of Boussinesq approximation and small-scale convective motions. Ginzburg–Landau equation is arrived at from the generalized Lorenz model. The amplitudes of convective modes required for estimating the heat transport are determined analytically. A table is prepared documenting the actual values of the thermophysical properties of water, ethylene-glycol, engine-oil and glycerine with different nanoparticles, namely copper, copper oxide, titania, silver and alumina, and Nusselt number is calculated. Enhanced thermal conductivity being the reason for the enhancement of heat transport due to the presence of the nanoparticles is shown. Detailed discussion is made on the percentage increase of heat transport in twenty Newtonian nanoliquids compared to that in Newtonian liquids without nanoparticles.

Introduction

Nanoliquid comprises of a carrier liquid such as water or ethylene-glycol or engine-oil or glycerine with a dilute concentration of nanoparticles such as metallic or metallic oxide particles (Cu, CuO, $\hbox {TiO}_2$, Ag, $\hbox {Al}_2\hbox {O}_3$), having dimensions from 1 to 100 nm. It was Choi [10] who first proposed this term “Nanoliquid”. A significant feature of nanoliquids is thermal conductivity enhancement, a phenomenon which was first reported by Masuda et al. [29]. Eastman et al. [16] reported an increase of 40 % in the effective thermal conductivity of ethylene-glycol with 0.3 % volume of copper nanoparticles of 10nm diameter. Further 10–30 % increase of the effective thermal conductivity in alumina/water nanoliquids with 1–4 % of alumina was reported by Das et al. [12]. These reports led Buongiorno and Hu [8] to suggest the possibility of using nanoliquids in advanced nuclear systems.

A comprehensive review on thermal transport in nanoliquids was made by Eastman et al. [17] who concluded that despite several attempts, a satisfactory explanation for the abnormal enhancement in thermal conductivity and viscosity in nanoliquids is yet to be found. Buongiorno [7] conducted an extensive study of convective transport in nanoliquids but focused on explaining the further heat transfer enhancements observed during convective situations. Ruling out dispersion, turbulence and particle rotation as significant agents for heat transfer enhancements, Buongiorno [7] suggested a new model based on the mechanics of nanoparticles/carrier-liquid relative velocity. He observed that the absolute velocity of nanoparticles can be taken as the sum total of the carrier-liquid velocity and a slip velocity. He considered seven slip mechanisms- inertia, Brownian diffusion, thermophoresis, diffusophoresis, Magnus effects, liquid drainage and gravity settling. He studied each one of these and concluded that in the absence of turbulent effects, Brownian diffusion and thermophoresis would dominate. Based on these two effects, he derived the conservation equations. With the help of the transport equations of Buongiorno [7], Tzou [36, 37] studied the onset of convection in a horizontal layer of a nanoliquid heated uniformly from below and found that as a result of Brownian motion and thermophoresis of nanoparticles, the critical Rayleigh number was found to be much lower, by one to two orders of magnitude, than that of an ordinary liquid. Kim et al. [26–28] also investigated the onset of convection in a horizontal nanoliquid layer and modified the three quantities, namely the thermal expansion coefficient, the thermal diffusivity and the kinematic viscosity that appear in the definition of the Rayleigh number. The role of thermophoresis in laminar natural convection in a Rayleigh–Bénard cell filled with a water-based CuO nanoliquid was studied by Eslamian et al. [15].

Apart from the papers discussed above, there are other related works on this problem [4, 13, 14]. All the above works are based on the two-phase model with both the liquid and solid phases playing a distinct role in the heat transfer process. Khanafer et al. [25] and Jou and Tzeng [24] have argued in favour of modelling nanoliquids as a single-phase model on the reason that as of now there is no concrete theoretical ground on which enhanced heat transfer in nanoliquids can be explained. It thus becomes clear that in seeking to explain enhanced heat transfer, an alternate way of studying thermoconvective motion in nanoliquids in the form a single-phase model can be quite naturally considered. In this model the liquid and solid phases are in local thermal equilibrium and flow with the same local velocity. This signifies that the nanoparticles and the liquid particles have similar properties so far as flow is concerned but have different thermal properties. Thus in this model nanoliquid behaves more as a liquid rather than as a solid–liquid mixture as in the conventional two-phase model. Since in the single-phase model, properties of nanoliquids have contributions from the solid and liquid phases, the density, thermal expansion coefficient, specific heat, thermal conductivity of the two phases, viscosity of carrier liquid and nanoparticle concentration contribute to the nanoliquid properties. In addition, based on the experimental observation that heat transport is enhanced only when nanoparticle concentration is dilute, nanoparticle volume fraction has to be assumed quite small. It needs to be emphasized here that this paper only estimates heat transport in nanoliquids using the single-phase model discussed in Khanafer et al. [25] and Tiwari and Das [35]. Simo et al. [34] studied Rayleigh–Bénard convection in a cube with perfectly conducting lateral walls using the Galerkin spectral method. They analysed the stability properties and bifurcations of fixed point and also discussed about chaotic motions. The effect of nanoparticles on chaotic convection in a liquid layer heated from below was studied by Hashim et al. [23]. Corcione [11] in his paper on Rayleigh–Bénard convection of nanoliquids assumed a single-phase model for nanoliquid. In this paper two empirical equations are adopted from earlier works [11, 25, 35] for the evaluation of the effective value of nanoliquid thermal conductivity and dynamic viscosity based on a wide variety of experimental data reported in the literature. The other effective properties are evaluated by the traditional mixing theory. Park [31] investigated Rayleigh–Bénard convection of nanoliquids using a single-phase continuum model but with thermophysical properties assumed to be that of nanoliquids rather than that of carrier liquids. The study predicts enhancement of heat transfer. A good account of many aspects of enhanced heat transfer in nanoliquids is discussed in the books by Bianco et al. [5] and Bergman et al. [3]. In the absence of experimental works on heat transport in nanoliquids, it remains to be seen whether the single-phase or the two-phase model is best suited as a mathematical model for natural convection in nanoliquids.

Carrier liquids with a range of thermal conductivity from weakly thermally conducting to reasonably well conducting liquids has been chosen for investigation in combination with nanoparticles whose thermal conductivity ranges from very well conducting to extremely well conducting solids. Such combinations gave rise to a wide spectrum of Prandtl numbers for investigation. The above consideration led to the choice of the twenty nanoliquids chosen for investigation in the paper. Curiosity as to whether high thermal conductivity in nanoparticles leads to high thermal conductivity in nanoliquids and thereby to enhanced heat transport in nanoliquids is the reason for our considering in the paper comparison of heat transports in twenty nanoliquids. In the paper we study Rayleigh–Bénard convection in liquids with nanoparticles modelled as a single phase system with liquid properties like density, viscosity, thermal expansion coefficient, heat capacity and thermal conductivity modified by the presence of the nanoparticles. Thermal convection in nanoliquids has mainly been studied between two vertical plates with differential temperature or natural convection in nanoliquids due to a hot vertical plate. Natural convection in the Rayleigh–Bénard configuration has been very less studied in most nanoliquids in enclosures. This is the reason why the classical problem of Rayleigh–Benard in nanoliquids has been undertaken in the current study.

Mathematical Formulation

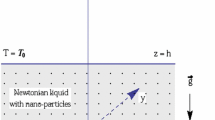
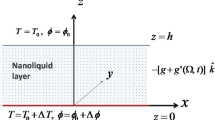
An infinite extent horizontal nanoliquid layer of thickness, h, whose lower and upper bounding planes are at $z = 0$ and $z = h$ respectively is considered (see Fig. 1). The nanoliquid is assumed to be a viscous, Newtonian liquid. The upper and lower boundaries are maintained at constant temperatures $T_0$ and $T_0 + {\Delta } T$ (${\Delta } T > 0$ ) respectively. For mathematical tractability we confine ourselves to two-dimensional longitudinal rolls so that all physical quantities are independent of y, a horizontal co-ordinate. The region of interest is $R=\{(x,z)/-\infty <x<\infty , 0\le z\le h\}$. The boundaries are assumed to be stress-free and isothermal. In this paper we assume the dynamic coefficient of viscosity of the nanoliquid, $\mu _{nl}$ , and thermal diffusivity of the nanoliquid, $\alpha _{nl}$, to be constants. However, these vary with the nanoparticle volume fraction, $\chi$, the thermal conductivity of the carrier liquid, $k_l$, the thermal conductivity of the nanoparticle, $k_{np}$, the density of the carrier liquid, $\rho _l$, the density of the nanoparticle, $\rho _{np}$, the heat capacity of the carrier liquid, $(Cp)_l$, and the heat capacity of the nanoparticle, $(Cp)_{np}$. We assume that the Oberbeck–Boussinesq approximation is valid and that there is thermal equilibrium between the Newtonian carrier liquid and the nanoparticles. The governing equations describing the Rayleigh–Bénard instability situation in a Newtonian nanoliquid with constant viscosity are:

Fig. 1

Physical configuration

Conservation of Mass

$$\begin{aligned} \nabla \cdot {\mathbf {q}} = 0, \end{aligned}$$

(1)

Conservation of Momentum

$$\begin{aligned} \rho _{nl}\left[ \dfrac{\partial \mathbf {q}}{\partial t}+(\mathbf {q} \cdot \nabla ) \mathbf {q}\right] =-\nabla p+\mu _{nl} \nabla ^2 \mathbf {q} +\left[ \rho _{nl}-\left( \rho \beta \right) _{nl}(T-T_0)\right] \mathbf {g} , \end{aligned}$$

(2)

Conservation of Energy

$$\begin{aligned} \dfrac{\partial T}{\partial t}+(\mathbf {q} \cdot \nabla )T = \alpha _{nl} \nabla ^2 T, \end{aligned}$$

(3)

where the nanoliquid properties are obtained from either phenomenological laws or mixture theory as given below [6, 19]:

• a. Phenomenological laws:

  $$\begin{aligned} \dfrac{\mu _{nl}}{\mu _l}= & {} \dfrac{1}{(1-\chi )^{2.5}} \quad \hbox {(Brinkman model) [6]}, \end{aligned}$$

  (4)
  $$\begin{aligned} \dfrac{k_{nl}}{k_l}= & {} \frac{\left( \dfrac{k_{np}}{k_l}+2\right) -2\chi \left( 1-\dfrac{k_{np}}{k_l}\right) }{\left( \dfrac{k_{np}}{k_l}+2\right) +\chi \left( 1-\dfrac{k_{np}}{k_l}\right) }\nonumber \\&\hbox {(Hamilton--Crosser model for stagnant conditions) [19]} \end{aligned}$$

  (5)

• b. Mixture theory:

  $$\begin{aligned} \left. \begin{array}{rcl} \alpha _{nl}&{}=&{}\dfrac{k_{nl}}{(\rho C_p)_{nl}}\\ \dfrac{\rho _{nl}}{\rho _{l}}&{}=&{}(1-\chi )+\chi \dfrac{\rho _{np}}{\rho _{l}}\\ \dfrac{(\rho C_p)_{nl}}{(\rho C_p)_l}&{}=&{}(1-\chi )+\chi \dfrac{(\rho C_p)_{np}}{(\rho C_p)_l}\\ \dfrac{(\rho \beta )_{nl}}{(\rho \beta )_l}&{}=&{}(1-\chi )+\chi \dfrac{(\rho \beta )_{np}}{(\rho \beta )_l}\\ \end{array} \right\} . \end{aligned}$$

  (6)

In the Eqs. (1–6), $q=(u, 0, w)$ is the velocity vector, u is horizontal component of velocity, w is vertical component of velocity, x is horizontal coordinate, z is vertical coordinate, $\rho _{nl}$ is the density of the nanoliquid at $T=T_0$, t is the time, p is the total pressure, $\mu _{nl}$ is the dynamic coefficient of viscosity of the nanoliquid, $\beta _{nl}$ is the coefficient of thermal expansion of the nanoliquid, T is the dimensional temperature, $\mathbf {g}=(0,0,-g)$ is the acceleration due to gravity, $\alpha _{nl}$ is the thermal diffusivity of the nanoliquid, $\mu _{l}$ is the dynamic coefficient of viscosity of the carrier liquid, $k_{nl}$ is the thermal conductivity of the nanoliquid, $(Cp)_{nl}$ is the heat capacity of the nanoliquid, $\beta _{l}$ is the coefficient of thermal expansion of the carrier liquid and $\beta _{np}$ is the coefficient of thermal expansion of the nanoparticle.

The expression for effective viscosity and effective thermal conductivity is applicable for spherical-particles suspended in a carrier liquid. These models are discussed in detail by Khanafer et al. [25]. Taking the velocity, temperature and density fields in the quiescent basic state to be $q_b (z)=(0,0)$, $T_b (z)$ and $\rho _b (z)$, we obtain the quiescent state solution in the form:

$$\begin{aligned} \left. \begin{array}{c} q_b =(0,0)\\ T_b = T_0+{\Delta } T f\left( \frac{z}{h}\right) \\ p_b=-\int \rho _b \left( \frac{z}{h}\right) g dz +C \end{array} \right\} , \end{aligned}$$

(7)

where $f\left( \dfrac{z}{h}\right) =\left( 1-\dfrac{z}{h}\right)$ and C is the constant of integration. The quiescent basic state is motionless and, in fact, the initial state of the system. On the quiescent basic state we superimpose perturbation in the form:

$$\begin{aligned} \left. \begin{array}{c} q = q_b+q'\\ T = T_b \left( \frac{z}{h}\right) +T'\\ \rho = \rho _b \left( \frac{z}{h}\right) +\rho '\\ p = p_b\left( \frac{z}{h}\right) +p' \end{array} \right\} , \end{aligned}$$

(8)

where the prime indicates a perturbed quantity. Since we consider only two-dimensional disturbances, we introduce stream function as follows:

$$\begin{aligned} u'=-\dfrac{\partial \psi '}{\partial z},\quad w'=\dfrac{\partial \psi '}{\partial x}, \end{aligned}$$

(9)

where $\psi$ is the dimensional stream function. These satisfy Eq. (1) in the perturbed state. Eliminating the pressure in Eq. (2), incorporating the quiescent state solution and non-dimensionalizing the resulting equations as well as Eq. (3) using the following definition

$$\begin{aligned} (X,Z)=\left( \dfrac{x}{h}, \dfrac{z}{h}\right) ,\quad \tau =\dfrac{\alpha _l}{h^2}t,\quad {\varPsi }=\frac{\psi '}{\alpha _l},\quad {\varTheta }=\frac{T '}{{\Delta } T}, \end{aligned}$$

(10)

we obtain the dimensionless form of the vorticity and heat transport equations as follows :

$$\begin{aligned} \dfrac{1}{Pr_{nl}}\dfrac{\partial }{\partial \tau }(\nabla ^2{\varPsi })= & {} a_1\nabla ^4 {\varPsi } +a_1^2R_{nl} \dfrac{\partial {\varTheta }}{\partial X}- \dfrac{1}{Pr_{nl}} J({\varPsi },\nabla ^2 {\varPsi }),\end{aligned}$$

(11)

$$\begin{aligned} \dfrac{\partial {\varTheta }}{\partial \tau }= & {} \dfrac{\partial {\varPsi }}{\partial X} + a_1 \nabla ^2 {\varTheta } - J({\varPsi } , {\varTheta }), \end{aligned}$$

(12)

where X is the non-dimensional horizontal coordinate, Z is the non-dimensional vertical coordinate, $\tau$ is non-dimensional time, ${\varPsi }$ is the non-dimensional stream function, ${\varTheta }$ non-dimensional temperature and

$$\begin{aligned} \left. \begin{array}{rcl} a_1&{} =&{}\dfrac{\left[ 1-\dfrac{3\chi \left( 1-\frac{k_{np}}{k_l}\right) }{\left( \dfrac{k_{np}}{k_l}+2\right) +\chi \left( 1-\dfrac{k_{np}}{k_l}\right) }\right] }{(1-\chi )+\chi \dfrac{(\rho C_p)_{np}}{(\rho C_p)_{l}}}\\ Pr_{nl}&{} =&{}\dfrac{\mu _{nl}}{\rho _{nl}\alpha _{nl}} \quad (\text {nanoliquid Prandtl number})\\ R_{nl}&{} =&{}\dfrac{(\rho \beta )_{nl}g{\Delta } Th^3}{\alpha _{nl}\mu _{nl}}\quad (\text {nanoliquid Rayleigh number})\\ J({\varPsi },\ldots )&{} =&{}\left| \begin{array}{c@{\quad }c} \dfrac{\partial {\varPsi }}{\partial X} &{} \dfrac{\partial {\varPsi }}{\partial Z} \\ \dfrac{\partial }{\partial X}(\ldots ) &{} \dfrac{\partial }{\partial Z}(\ldots ) \\ \end{array} \right| \end{array} \right\} . \end{aligned}$$

(13)

Equations (11–12) are solved using the boundary/periodicity conditions

$$\begin{aligned} {\varPsi }= & {} \frac{\partial ^2}{\partial Z^2}\left( \dfrac{\partial {\varPsi }}{\partial X}\right) = {\varTheta } = 0 \quad \mathtt {at} \quad Z = 0,1, \nonumber \\ {\varPsi }\left( X\pm \dfrac{2\pi }{\pi \kappa _c},Z\right)= & {} {\varPsi }(X,Z), \quad {\varTheta }\left( X\pm \dfrac{2\pi }{\pi \kappa _c},Z\right) ={\varTheta }(X,Z), \end{aligned}$$

(14)

where $\pi \kappa _c$ is the critical wave number. In the next section we discuss the linear stability analysis of the system which is of great utility in the local nonlinear stability analysis to be discussed further on.

Linear Stability Analysis

It can easily be proved that the principle of exchange of stabilities (PES) is valid in the problem and hence we consider only the marginal stationary state. In order to make a linear stability analysis we consider the linear and steady-state version of Eqs. (11–12) and assume the solutions to be periodic waves of the form [9]:

$$\begin{aligned} {\varPsi }(X,Z)= & {} {\varPsi }_0\sin (\pi \kappa X)\sin (\pi Z),\end{aligned}$$

(15)

$$\begin{aligned} {\varTheta } (X,Z)= & {} {\varTheta }_0\cos (\pi \kappa X)\sin (\pi Z), \end{aligned}$$

(16)

The quantities ${\varPsi }_0$ and ${\varTheta }_0$ are, respectively, amplitudes of the stream function and temperature and $\pi \kappa$ is the wave number. The normal mode solutions of Eqs. (15) and (16) satisfy the boundary conditions in Eq. (14). In Eqs. (15) and (16), $\pi \kappa$ is the horizontal wave number.

Following standard procedure, we can obtain the expression for the critical Rayleigh number in the form:

$$\begin{aligned} R_{nlc} =\dfrac{\eta _1^6}{\pi ^2\kappa _c^2}=\frac{27\pi ^4}{4}, \end{aligned}$$

(17)

where the critical wave number $\pi \kappa _c=0.707\pi$ and $\eta _1^2=\pi ^2 (\kappa _c^2+1)=\frac{3\pi ^2}{2}.$ The critical Rayleigh number, $R_{nlc},$ indicates transition from linear to nonlinear instability. More on this is discussed further on in the section on “Results and Discussion”.

The linear theory predicts only the condition for the onset of convection and is silent about the heat transport. We now embark on a weakly non-linear analysis by means of a truncated representation of Fourier series for streamfunction and temperature fields to find the effect of various parameters on finite-amplitude convection and to know the amount of heat transfer.

Local Nonlinear Stability Analysis

The first effect of nonlinearity is to distort the temperature field through the interaction of ${\varPsi }$ and ${\varTheta }$. The distortion of temperature field will correspond to a change in the horizontal mean, i.e., a component of the form $\sin (2 \pi z)$ will be generated. Substituting a minimal double Fourier series which describes the unsteady finite-amplitude convection in a Newtonian nanoliquid given by

$$\begin{aligned} {\varPsi }(X,Z,\tau )= & {} \dfrac{\sqrt{2}\eta _1^2}{\pi ^2\kappa }A_1(\tau )\sin (\pi \kappa _c X)\sin (\pi Z),\end{aligned}$$

(18)

$$\begin{aligned} {\varTheta }(X,Z,\tau )= & {} \dfrac{R_{nlc}}{R_{nl}\pi }\left[ \sqrt{2}B_1(\tau )\cos (\pi \kappa _c X)\sin (\pi Z)-C_1(\tau )\sin (2\pi Z)\right] , \end{aligned}$$

(19)

into Eqs. (11–12) and adopting the standard orthogonalization procedure for the Galerkin expansion, the following nonlinear autonomous system (generalized tri-modal Lorenz model) of differential equations is obtained:

$$\begin{aligned} \dfrac{dA_1}{d\tau _1}= & {} a_1Pr_{nl}[a_1B_1-A_1],\end{aligned}$$

(20)

$$\begin{aligned} \dfrac{dB_1}{d\tau _1}= & {} r_{nl}A_1-a_1B_1-A_1C_1,\end{aligned}$$

(21)

$$\begin{aligned} \dfrac{dC_1}{d\tau _1}= & {} -a_1bC_1+A_1B_1, \end{aligned}$$

(22)

where

$$\begin{aligned} \tau _1=\eta _{1}^{2}\tau ,\quad r_{nl}=\dfrac{R_{nl}}{R_{nlc}},\quad b=\dfrac{4 \pi ^2}{\eta _1^2} \end{aligned}$$

(23)

and $A_1, B_1$ are amplitudes in normal mode solution and $C_1$ is the amplitude of convective mode. It is well known in the problems as these that the trajectories of the solution of the Lorenz model in phase-space remain within a bounded region. In the next section we show that this trapping region is, in fact, a sphere for the current problem.

Trapping Region

Multiplying Eqs. (20) and (21) by $A_1$ and $B_1$ respectively, we get

$$\begin{aligned} A_1\dfrac{dA_1}{d\tau _{1}}= & {} -a_1Pr_{nl}A_1^2+a_1^2Pr_{nl}A_1B_1,\end{aligned}$$

(24)

$$\begin{aligned} B_1\dfrac{dB_1}{d\tau _{1}}= & {} r_{nl}A_1B_1-a_1B_1^2-A_1B_1C_1. \end{aligned}$$

(25)

Adding Eqs. (24) and (25), we get

$$\begin{aligned} A_1\dfrac{dA_1}{d\tau _{1}}+B_1\dfrac{dB_1}{d\tau _{1}}=-a_1Pr_{nl}A_1^2-a_1B_1^2+A_1B_1\left[ a_1^2Pr_{nl}+r_{nl}-C_1\right] . \end{aligned}$$

(26)

To get an equation of a sphere from Eqs. (22) and (26), we multiply Eq. (22) by $(C_1-a_1^2Pr-r_{nl})$ and add the resulting equation to Eq. (26). This gives us

$$\begin{aligned} \dfrac{dE}{d\tau _{1}}=A_1\dfrac{dA_1}{d\tau _{1}}+B_1\dfrac{dB_1}{d\tau _{1}}+(C_1-a_1^2Pr_{nl}-r_{nl})\dfrac{d}{d\tau _{1}}\left( C_1-a_1^2Pr_{nl}-r_{nl}\right) . \end{aligned}$$

(27)

Integrating the above equation, we get the trapping region in the form

$$\begin{aligned} E=\dfrac{1}{2}\left[ A_1^2+B_1^2+(C_1-a_1^2Pr_{nl}-r_{nl})^2\right] . \end{aligned}$$

(28)

The post-onset trajectories of the Lorenz system (20–22) enter and stay within a sphere with center $(0,0,a_1^2Pr_{nl}+r_{nl})$ and radius $\sqrt{2}$ given by

$$\begin{aligned} A_1^2+B_1^2+(C_1-a_1^2Pr_{nl}-r_{nl})^2=(\sqrt{2})^2. \end{aligned}$$

(29)

Noting that the Lorenz model is, in general, not analytically tractable we now move on to derive the analytically tractable Ginzburg–Landau equation from the tri-modal Lorenz model.

Ginzburg–Landau Amplitude Equation from the Lorenz Model

From the Eqs. (20) and (21), $B_1$ and $C_1$ can be obtained in terms of $A_1$ as:

$$\begin{aligned}&\displaystyle B_1 =\dfrac{1}{a_1}\left[ \dfrac{1}{a_1Pr_{nl}}\dfrac{dA_1}{d\tau _1}+A_1\right] ,\end{aligned}$$

(30)

$$\begin{aligned}&\displaystyle C_1 =\dfrac{1}{A_1}\left[ (r_{nl}-1)A_1-\left( \dfrac{1}{Pr_{nl}a_1}+\dfrac{1}{a_1}\right) \dfrac{dA_1}{d\tau _1}-\dfrac{1}{Pr_{nl}a_1^2}\dfrac{d^2A_1}{d\tau _1^2}\right] . \end{aligned}$$

(31)

Substituting Eqs. (30) and (31) in Eq. (22), we get a third order differential equation in $A_1$. Neglecting terms of the type $\left( \dfrac{d^3A_1}{d\tau _1^3}\right) , \left( \dfrac{dA_1}{d\tau _1}\right) ^2, \left( \dfrac{dA_1}{d\tau _1}\right) \left( \dfrac{d^2A_1}{d\tau _1^2}\right) ,$ and $A_1\left( \dfrac{d^2A_1}{d\tau _1^2}\right)$, we get the Ginzburg–Landau model in the form

$$\begin{aligned} \dfrac{dA_1}{d\tau _1}=\left( \dfrac{Pr_{nl}}{1+Pr_{nl}}\right) \left( \dfrac{1}{b}\right) \left[ a_1b(r_{nl}-1)A_1-\dfrac{1}{a_1}A_1^3\right] . \end{aligned}$$

(32)

Equation (32) is a Bernoulli equation in $A_1$ which can be solved using an initial condition $A(0)=A_0$ and the solution is given by

$$\begin{aligned} A_1(\tau _1)=\dfrac{A_0a_1\sqrt{b(r_{nl}-1)}\exp \left( \frac{Pr_{nl}a_1(r_{nl}-1)\tau _1}{1+Pr_{nl}}\right) }{\sqrt{A_0^2\exp \left( \frac{2Pr_{nl}a_1(r_{nl}-1)\tau _1}{1+Pr_{nl}}\right) +a_1^2b(r_{nl}-1)-A_{0}^{2}}}. \end{aligned}$$

(33)

It is one of the intentions of the paper to study the pre-onset and post-onset critical points of the tri-modal Lorenz model. The same is discussed below.

Steady Finite Amplitude Convection

We note that the nonlinear system of autonomous differential equations (20–22) is not amenable to analytical treatment for the general time-dependent variables and it is to be solved by means of a numerical method. However, in the case of steady motions, these equations can be solved in closed form.

The solution of the system (20–22) with left hand sides omitted is

$$\begin{aligned} (0,0,0), (\pm a_1\sqrt{b(r_{nl}-1)},\pm \sqrt{b(r_{nl}-1)},(r_{nl}-1)). \end{aligned}$$

(34)

These are the post-onset critical points of the dynamical system (20–22). The solution $A_1=B_1=C_1=0$ of the Lorenz model represents the state of no convection and non-zero values represent the convective state. Following standard procedure with the linear system of autonomous differential equations, it can be easily shown that the only pre-onset critical point is (0, 0, 0) which is a saddle point. In the next section we quantify the heat transport in terms of the Nusselt number within a wave-length distance in the horizontal direction at the lower boundary.

Nano-Particle-Enhanced Heat Transport in a Newtonian Liquid

The horizontally-averaged Nusselt number, $Nu_{nl}$, for the stationary mode of convection (the preferred mode in this problem) in a nanoliquid evaluated at the lower boundary $z=0$ for a single wave-length is given by

$$\begin{aligned} Nu_{nl}= & {} \dfrac{\text {Heat transport by conduction + Heat transport by convection}}{\text {Heat transport by conduction}}. \end{aligned}$$

(35)

From Fourier law, we know that

$$\begin{aligned} \text {Heat transport by conduction}= & {} \left[ k_l\int _{0}^{\frac{2\pi }{\pi \kappa _c}}\dfrac{d{\varTheta }_b}{dZ}dX\right] _{Z=0},\end{aligned}$$

(36)

$$\begin{aligned} \text {Heat transport by convection}= & {} \left[ k_{nl}\int _{0}^{\frac{2\pi }{\pi \kappa _c}}\dfrac{\partial {\varTheta }}{\partial Z}dX\right] _{Z=0}, \end{aligned}$$

(37)

where ${\varTheta }_b=\dfrac{T_b-T_0}{{\Delta } T}.$ Using Eqs. (36) and (37) in Eq. (35) and simplifying, we get

$$\begin{aligned} Nu_{nl}= & {} 1+\dfrac{k_{nl}}{k_l}\left[ \dfrac{\int _{0}^{\frac{2}{\kappa _c}}\left( \dfrac{\partial {\varTheta }}{\partial Z}\right) dX}{\int _{0}^{\frac{2}{\kappa _c}}\left( \dfrac{d{\varTheta }_b}{dZ}\right) dX}\right] _{Z=0}. \end{aligned}$$

(38)

In the conduction state there will be equilibrium between the liquid and solid phases and thus thermal conductivity can be taken to be that of the liquid phase. In the convective state the thermal conductivity of the nanoliquid is to be assumed. It is on this reason that the ratio $\dfrac{k_{nl}}{k_l}$ appears in the expression for the Nusselt number in Eq. (38).

Substituting Eqs. (7) and (19) in Eq. (38) and completing the integration, we get

$$\begin{aligned} Nu_{nl}(\tau _1)=1+\dfrac{2}{r_{nl}}\left[ a_1a_2\right] C_1(\tau _1), \end{aligned}$$

(39)

where

$$\begin{aligned} a_2=(1-\chi )+\chi \dfrac{(\rho C_p)_{np}}{(\rho C_p)_l} \end{aligned}$$

(40)

and $C_1(\tau _1)$ is obtained as follows. Substituting $\dfrac{dA_1}{d\tau _1}$ and its derivative from Eq. (32) in Eq. (31), we get $C_1$ in terms of $A_1$ as:

$$\begin{aligned} C_1(\tau _1)=-\dfrac{1}{\left[ 1+Pr_{nl}\right] ^2}\left[ P_1+P_2A_{1}^{2}+P_3A_{1}^{4}\right] , \end{aligned}$$

(41)

where

$$\begin{aligned} P_1= & {} Pr_{nl}(r_{nl}-1)^2,\end{aligned}$$

(42)

$$\begin{aligned} P_2= & {} -\left[ \dfrac{4[r_{nl}-1]Pr_{nl}+\left[ 1+Pr_{nl}\right] ^2}{a_{1}^{2}b}\right] ,\end{aligned}$$

(43)

$$\begin{aligned} P_3= & {} \dfrac{3Pr_{nl}}{a_{1}^{4}b^2}. \end{aligned}$$

(44)

For steady, finite-amplitude convection, we get $C_1$ in the form

$$\begin{aligned} C_1=r_{nl}-1. \end{aligned}$$

(45)

With this the expression (39) takes the form

$$\begin{aligned} Nu_{nl}(\infty )=1+2\left[ a_1a_2\right] \left[ 1-\dfrac{1}{r_{nl}}\right] . \end{aligned}$$

(46)

With the necessary background for analysing the results prepared in the previous sections, in what follows we discuss the results obtained and make a few conclusions.

Results and Discussion

Rayleigh–Bénard convection in nanoliquids is usually studied using one of the following two models:

• 1. Buongiorno [7] two-phase model and

• 2. Khanafer–Vafai–Lightstone [25] single-phase model.

There are good number of papers dealing with convective heat transfer in nanoliquids using Buongiorno [7] two-phase model. An alternative to studying heat transfer in nanoliquids is provided by Khanafer–Vafai–Lightstone [25] single-phase model. The present paper uses the latter model.

Table 1 Thermophysical properties of four carrier liquids at $300\,^{\circ }\hbox {K}$

Table 2 Thermophysical properties of five nanoparticles at $300\,^{\circ }\hbox {K}$

Table 3 Thermophysical properties of twenty nanoliquids

Table 4 Values of the factor, F, for twenty nanoliquids

The definition of the nanoliquid Rayleigh number as used in the paper is based on combined properties of the carrier liquid and the nanoparticles. To interpret the results in the case of real nanoliquids it becomes necessary to have information about the actual value of the thermophysical quantities of the carrier liquids and the nanoparticles under consideration in the study. Tables 1 and 2 document information on the thermophysical quantities culled out from the papers of other investigators. Using the phenomenological laws and the mixture theory, for calculating various thermophysical quantities of the nanoliquids as taken in Eqs. (4–6), and the values documented in Tables 1 and 2, the contents of Table 3 were arrived at. Also $\beta _{nl}$ and $(Cp)_{nl}$ were calculated using the following expressions:

$$\begin{aligned} \beta _{nl}=\dfrac{(\rho \beta )_{nl}}{\rho _{nl}}, \quad (Cp)_{nl}=\dfrac{(\rho Cp)_{nl}}{\rho _{nl}}. \end{aligned}$$

From Tables 1, 2 and 3 the following is apparent:

$$\begin{aligned} \rho _l<\rho _{nl}<\rho _{np},\quad \beta _l>\beta _{nl}>\beta _{np}, \quad Cp_l>Cp_{nl}>Cp_{np}\quad \hbox { and }\quad k_l<k_{nl}\ll k_{np}. \end{aligned}$$

From the values of the above thermophysical quantities it is clear that the most significant change in these quantities is seen for dilute concentrations and this is an experimentally observed fact as well. We use the above information in making the right conclusions from the result obtained on onset of convection. To understand the implication of the linear stability results, one may rewrite $R_{nl}$ as follows:

$$\begin{aligned} R_{nl}=\left[ \dfrac{(\rho \beta )_{nl}}{\rho _l\beta _{l}}\dfrac{\alpha _l}{\alpha _{nl}}\dfrac{\mu _l}{\mu _{nl}}\right] R_l, \end{aligned}$$

Fig. 2

Phase-plane trajectories in the AB, AC and BC planes respectively, for volume fraction, $\chi =0.1,$ Prandtl number, $Pr_{nl}=4.55523,$ for water–titania nanoliquid

Fig. 3

Phase-plane trajectories in the AB, AC and BC planes respectively, for $\chi =0.1,$ $Pr_{nl}=4.49345,$ for water–alumina nanoliquid

where $R_l=\dfrac{\rho _l\beta _{l}g{\Delta } Th^3}{\mu _l \alpha _l}$. On computation, it is found that the factor, F,  multiplying $R_{l}$ decreases with increase in $\chi$. These results are shown in Table 4. From the above reasoning we conclude that the critical nanoliquid Rayleigh number is less than that of the carrier liquid without nanoparticles, viz., $R_{lc}$. Thus, we may conclude that onset of convection is advanced by the addition of nanoparticles.

Fig. 4

Phase-plane trajectories in the AB, AC and BC planes respectively, for $\chi =0.1,$ $Pr_{nl}=3.81111,$ for water–copper-oxide nanoliquid

Fig. 5

Phase-plane trajectories in the AB, AC and BC planes respectively, for $\chi =0.1,$ $Pr_{nl}=3.24396,$ for water–copper nanoliquid

Fig. 6

Phase-plane trajectories in the AB, AC and BC planes respectively, for $\chi =0.1,$ $Pr_{nl}=2.91189,$ for water–silver nanoliquid

In what follows we discuss the results of a local nonlinear stability analysis of “Local Nonlinear Stability Analysis” section. For such an analysis the linear stability results are important. The critical point of the linear autonomous system is (0, 0, 0) which can only be a saddle point.

Fig. 7

The streamlines of unsteady convection at two different times for $\chi =0.1,$ $Pr_{nl}=4.55523,$ for water–titania nanoliquid. a $\tau _1=0.05$. b $\tau _1=0.1$

Fig. 8

The streamlines of unsteady convection at two different times for $\chi =0.1,$ $Pr_{nl}=3153.47,$ for engine-oil–silver nanoliquid. a $\tau _1=0.05$. b $\tau _1=0.1$

From Table 3 we note that except water-based nanoliquids all other nanoliquids have high Prandtl number, $Pr_{nl}$. In the context of the Lorenz model of Eqs. (20–22), $Pr_{nl}>>1$ would mean the following:

$$\begin{aligned} \left. \begin{array}{rcl} B_1&{}=&{}\dfrac{A_1}{a_1},\\ \dfrac{dA_1}{d\tau _1}&{}=&{}a_1[(r_{nl}-1)A_1-A_1C_1],\\ \dfrac{dC_1}{d\tau _1}&{}=&{}\dfrac{A_1^2}{a_1}-a_1bC_1. \end{array} \right\} . \end{aligned}$$

(47)

In the system of Eq. 47, the second and third equations are solved for $A_1$ and $C_1$ and then the first equation is solved for $B_1$.

The point $(a_1\sqrt{b(r_{nl}-1)},\sqrt{b(r_{nl}-1)},r_{nl}-1)$ is the only critical point and hence the trajectories are around this point (see Figs. 2, 3, 4, 5 and 6). In general, only one half of the butterfly diagram normally seen in the case of the Lorenz model for Newtonian liquid without nanoparticles, can be realized in the case of the carrier liquids that we have considered here for investigation. This is due to the fact that the Prandtl numbers of these liquids are quite large except for water which is 6.1.

Similar to the case of the classical Lorenz model we note from the proceedings of “Trapping Region” section that the trapping region of the post-onset trajectories of the Lorenz system is a sphere with center at $(0,0,a_1^2Pr_{nl}+r_{nl})$ and of radius $\sqrt{2}.$ From Eq. (47), it is evident that in the absence of the nonlinear term and for $r_{nl}>1,$ the amplitude $A_1$ grows exponentially. We also know that the trajectories remain within the finiteness of a sphere (trappping region). These two observations clearly point to the fact that the nonlinear term $A_1C_1$ is responsible for altering the exponentially increasing nature of the trajectories and bringing it back to the confines of a sphere.

Fig. 9

Isotherms of unsteady convection at two different times for $\chi =0.1,$ $Pr_{nl}=4.55523,$ for water–titania nanoliquid. a $\tau _1=0.05$. b $\tau _1=0.1$

Fig. 10

Isotherms of unsteady convection at two different times for $\chi =0.1,$ $Pr_{nl}=3153.47,$ for engine-oil–silver nanoliquid. a $\tau _1=0.05$. b $\tau _1=0.1$

Fig. 11

Variation of nanoliquid Nusselt number, $Nu_{nl},$ with $\tau _1$ for different values of $\chi$, for engine-oil–silver and water–titania nanoliquids

Fig. 12

Variation of nanoliquid Nusselt number, $Nu_{nl},$ with $\tau _1$ for different $r_{nl}$, for engine-oil–silver and water–titania nanoliquids

Table 5 Values of nanoliquid Nusselt number, $Nu_{nl},$ in the steady state for $\chi =0.1, R_{nlc}=657.511,$ with $Nu_l=2$ for $R_{nl}=2R_{nlc}$ and $Nu_l=2.3333$ for $R_{nl}=3R_{nlc}$

In “Ginzburg–Landau Amplitude Equation from the Lorenz Model” section the Ginzburg–Landau amplitude equation is derived from the Lorenz model. This result is important when we recognize the fact that Lorenz model is, in general, not analytically tractable but Ginzburg–Landau equation is. This helps us in obtaining an analytical expression for the amplitude and thereby the Nusselt number. We are mainly interested in quantifying heat transport in nanoliquids by steady finite-amplitude convection and also in analysing the essential difference between the trajectories of nanoliquids and carrier liquids without nanoparticles. To that end “Steady Finite Amplitude Convection” section reports critical points of the Lorenz model. This essentially gives us the solution for the amplitudes in the steady state.

Further on we note that water–titania transports least heat while engine-oil–silver transports maximum heat amongst the twenty nanoliquids under investigation. In Figs. 7, 8, 9 and 10 we have included the plots of streamlines and isotherms only for these two nanoliquids. Figure 7 is a plot of the streamlines of unsteady convection for water–titania nanoliquid at two different times, $\tau _1=0.05$ and $\tau _1=0.1$. Quite clearly there is more vigour in the cell activity as time progresses. This observation is true in the case of engine-oil–silver also. Water–titania and engine-oil–silver are two representative nanoliquids chosen from the twenty nanoliquids under investigation. So the above observation is true of the other eighteen nanoliquids also. Comparing the convective activity of all twenty nanoliquids we found that engine-oil–silver has convective activity in a major part of the Bénard cell.

Figure 9 is a plot of the isotherms of water–titania nanoliquid at two different times, $\tau _1=0.05$ and $\tau _1=0.1$ in a single Rayleigh–Bénard cell having counter rotating circulations. One can easily see that as time progresses heat is distributed to more parts of the Rayleigh–Bénard cell. This observation on the distribution of heat is applicable to engine-oil–silver nanoliquid also. Compared to water–titania, the heat distribution in engine-oil–silver is in a wider expanse of the Rayleigh–Bénard cell. As water–titania and engine-oil–silver are representative liquids we can make similar observation for all other eighteen nanoliquids. In the case of engine-oil–silver we note from Figs. 7, 8, 9 and 10 that the convective activity is seen in a major part of the Bénard cell as is to be expected. The streamlines and isotherms in these figures depict this fact.

We now proceed to make comments on the proceedings of “Nano-Particle-Enhanced Heat Transport in a Newtonian Liquid” section. The results of nonlinear stability analysis in this section are depicted in Figs. 11 and 12 and Table 5. Theoretical explanation for the enhanced heat transfer situation in nanoliquids is definitely the main issue in the current paper. Natural convection in nanoliquids with dilute concentrations of nanoparticles is known to be the preferred working medium in most heat transfer studies aiming enhanced heat transfer. Further, since the Nusselt number depends on the square of the amplitude, $A_{1}^{2}(\tau )$ , in Fig. 11 we have chosen the Nusselt number variation with change in volume fraction, $\chi$ , rather than the variation of the amplitude of convection with change in $\chi$. In the context of Fig. 11 which is a plot of Nusselt number versus scaled thermal Rayleigh number for three different values of volume fraction, $\chi ,$ we need to emphasise that Prandtl number, $Pr_{nl},$ varies with $\chi ,$ and the same can be understood from Eqs. (4), (5) and the Prandtl number expression in Eq. (13). These clearly indicate that there is enhanced heat transport in all nanoliquids in comparison with that in carrier liquids without nanoparticles. Table 5 provides explanation on the reason for the enhancement of heat transfer in nanoliquids compared to that in Newtonian liquids without nanoparticles. We find in general that there is a decrease in the critical Rayleigh number of nanoliquids with increase in $\chi$ and thereby increase in $Nu_{nl}$ with increase in $\chi$. Also, $Nu_{nl}$ increases with increase in scaled thermal Rayleigh number, $r_{nl}$ (see Figs. 11, 12). Enhanced thermal conductivity of nanoliquids is clearly the reason for enhanced heat transport [see also factor $a_1a_2$ which is greater than unity in the convective part of the Nusselt number expression (46)].

Conclusion

The following general conclusions can be made from the study:

• 1. Thermodynamically correct results have been obtained in the study and this lends credence to the fact that the choice of expression for the thermophysical parameters of nanoliquids is a correct choice. The values of the critical Rayleigh number and the Nusselt number obtained in the study are to be treated as estimates at best. This observation is made considering the fact that the phenomenological laws used in the study are based on static conditions. Corcione [11] has made a very apt comment on this aspect.

• 2. $R_{lc}^\mathrm{nanoparticle}<R_{lc}^{ \text {no nanoparticle}}$ for all values of parameters and for all twenty nanoliquids.

  $R_{lc}$ refers to carrier liquid critical Rayleigh number and the phrase in the superscripts refer to the presence or absence of nanoparticles.

• 3. Due to high Prandtl number in most nanoliquids considered in the study only one half of the butterfly diagram can be obtained as the trajectory of the solution of the Lorenz model. This is unlike the case of carrier liquids without nanoparticles.

• 4. Convective activity in the case of nanoliquids is seen in regions quite interior to the cell. This is much more than what is seen in the case of carrier liquids without nanoparticles.

• 5. Amongst the twenty nanoliquids considered, it is found, in general, that engine-oil–silver has the most enhanced heat transport while water–titania has the least. However, all nanoliquids transport more heat compared to a Newtonian liquid without nanoparticles. Thus the following is true:

  $Nu_{nl}>Nu_{l}$.

• 6. Enhanced thermal conductivity in nanoliquids is the reason for enhanced heat transport.

• 7. Most experimental investigations [1, 20, 30, 32, 33] on natural convection in nanoliquids do not pertain to a Rayleigh–Bénard set-up. In the absence of experimental works on heat transport in nanoliquids by Rayleigh–Bénard convection, it remains to be seen whether the single-phase or the two-phase model is best suited as a mathematical model for studying heat transfer in nanoliquids.