1 Introduction

In a horizontal layer of a Newtonian liquid the convective instability of a liquid owing to time-dependent gravity is of practical significance. From an application perspective the regulation of convection is very important and thermogravitational vibration which is also called gravity modulation or g-jitter is now understood to be an efficient way of controlling instabilities. Specifically, in the instance of smaller scale gravity condition, for example, in space labs even the vibrations of extremely small amplitudes are observed to have a significant say on the threshold of the convective flow and on the amount of heat transport [1,2,3]. The time-dependent gravitational field plays a very important role in the large-scale convection of the atmosphere. Mechanical vibration is also a known tool for enhancing the rate of heat transfer and this has gained lot of consideration in the past few years ([4,5,6,7,8] and references therein). For the purpose of taking examples for situations involving electric fields and fluids, we find that pumps, generators and image-processing devices come handy. Oscillating water column devices placed in onshore or in deeper waters offshore are examples pertaining to double-diffusive systems in a dielectric fluid involving time-periodic oscillations [9, 10]. In these practical devices study on convection and heat and mass transports are important and is the motivation for the present problem.

It was Gershuni et al. [11] who first provided a theoretical framework for studying the effect of time-dependent sinusoidally modulated gravitational field on thermoconvective instability using free boundaries. A mechanical analogy for the gravity modulated thermoconvective instability was reported by Gresho and Sani [12]. The effect of sinusoidally modulated gravity on the convective system for physically realistic free-top and rigid-bottom boundaries was investigated by Gresho and Sani [12]. The influence of gravity modulation when one of the parameters of the conduction state depends on time was reported by Gershuni and Zhukhovitskii [13] who used time-periodic oscillations. In addition to sinusoidal modulation, the effect of random modulation on the stability of the system was reported by Biringen and Peltier [14]. Venezian [15] performed a linear stability analysis for a thermally modulated system using a perturbation method and he reported an expression for threshold which had in it the influence of gravity modulation parameters. Siddheshwar [16] showed that the gravity modulated convective system could have a series solution of the Ginzburg–Landau equation with a time-periodic coefficient. Recently, Siddheshwar and Kanchana [17] and Siddheshwar and Meenakshi [18] studied effect of three different wave-forms of gravity modulation on Rayleigh-Bénard convective system in nanoliquids. An ultimate conclusion from these aforementioned works is that the effect of gravity modulation is to regulate onset of convection and heat transfer.

Controlling thermal convection and regulating heat transfer in a system having a dielectric liquid as a working medium is also a problem of utmost importance. In literature, thermal convective system in a dielectric liquid is called electro-convection (EC) and this problem can throw light on many engineering applications. Turnbull [19] showed that in the system of electro-convection stationary convection is preferred mode of onset. There are many other works that are deal with dielectric liquids [20,21,22,23,24,25,26,27,28] under different circumstances. The stabilizing influence of gravity modulation in a dielectric liquid was reported by Siddheshwar and Revathi [29].

A double-diffusive convection is one that describes a form of convection that is driven by the presence of two different substances which have different rates of diffusion. An example of double-diffusive convection is heat and salt in water. The sources of this field of study are in oceanography, yet its applications are in the fields such as growing crystals, convection in the sun and the dynamics of magma chambers. The main point to consider this type of instability is that heat diffuses into water faster than salt. Two different types of fluid motions that exists are “diffusive” type and “finger” type depending on whether the component with the highest diffusivity has a stratification that is stable or unstable. These two components affect the density stratification in opposite senses. This means that convection may occur even though overall net density is stably stratified. Many interesting convective phenomena occur when such two components of different diffusivities are present in a fluid layer. Situations as these are not possible in a single-component fluid.

An excellent review of the studies related to double-diffusive convection has been reported by Turner [30,31,32], Huppert and Turner [33] and Platten and Legros [34]. Yu et al. [35] studied the effect of gravity modulation on the stability of a horizontal double-diffusive Newtonian fluid layer heated from below and showed that the gravity modulation destabilizes the system slightly when solutal Rayleigh number is increased at the onset. In literature there are many other works that deal with effect of gravity modulation on double-diffusive convection in Newtonian liquid ([36, 37] and references therein). There is no such study involving a two-component dielectric liquid. A literature survey shows that the works on convection in dielectric liquids involve problems mainly of Rayleigh–Benard thermoconvection with no modulation of any sort. These invariably consider the artificial free boundaries and not the realistic rigid boundaries.

In this paper we consider double-diffusive convection in a dielectric liquid in the presence of time-periodic gravity modulation. Diffusive type of fluid motion is assumed and hence the highest diffusivity (solutal) has a stratification that is stable. It is to be mentioned here that the finger type of fluid motion that results in a destabilizing density profile is excluded in the present study. Further, the study of sub-harmonic is excluded in the present paper. The primary motto of the present paper is to study the impact of time-periodic oscillations of the Rayleigh-Bénard configuration on heat and mass transports in a two-component dielectric liquid using linear, weakly-nonlinear and local-nonlinear stability analyses. We first derive the generalized Lorenz model using a weakly nonlinear stability analysis. Using a linearized version of this equation a linear stability analysis is made and threshold Rayleigh number is determined in the modulated problem. The analytically-intractable generalized Lorenz model is then reduced to the analytically-intractable Ginzburg–Landau equation using a local nonlinear analysis. Focusing on stationary convection and using the numerical solution of this simpler non-autonomous equation (compared to the non-autonomous generalized Lorenz model) the impact of gravity modulation on heat and mass transports is studied for the cases of free-free and rigid-rigid boundaries.

2 Mathematical formulation

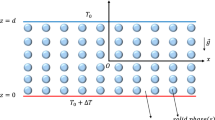
We consider two infinite horizontal and parallel planes at \(z =-\frac{h}{2}\) and \(z =\frac{h}{2}\) and between these two planes an electrically conducting liquid of depth, h, is confined. We have taken Cartesian coordinates with z-axis vertically upwards and the origin at the center of the layer. The layer is heated and salted from below to maintain a constant temperature gradient, \(\varDelta T\), and a constant solutal gradient, \(\varDelta S\), across the layer. The infinite extent horizontal layer is subjected to time-periodic gravity-aligned oscillations, and thus the gravity term has an additional time-dependent term, \(g'(\delta ,\varOmega ,t)\), where \(\delta\) is the amplitude, \(\varOmega\) is the frequency and t is the time. The paper is restricted to low frequency gravity modulation. The objective of the paper is to study the influence of the frequency and the amplitude on gravity modulation on the stability of convection and heat and mass transports of the double-diffusive system in a dielectric liquid. The physical arrangement of the problem with gravity modulation is shown in Fig. 1.

Fig. 1
figure 1

Physical configuration of the problem

Full size image

For the study of stationary convection in an dielectric liquid with gravity modulation the dimensional governing equations are

$$\begin{aligned}&\nabla \cdot \mathbf {q}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\rho _{0}\left( \frac{\partial \mathbf {q}}{\partial t}+(\mathbf {q}\cdot \nabla )\mathbf {q}\right) =-\nabla p \, -\rho [g + g'(\delta , \varOmega ,t)] {\hat{k}} \nonumber\\ &\quad+\,(\mathbf {P}\cdot \nabla )\mathbf {E}+\mu \nabla ^{2}\mathbf {q}, \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial T}{\partial t}+(\mathbf {q}\cdot \nabla )T=\alpha _{T}\nabla ^{2}T, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial S}{\partial t}+(\mathbf {q}\cdot \nabla )S=\alpha _{S}\nabla ^{2}S, \end{aligned}$$
(4)

where \(\rho\) represents the density and using the Boussinesq approximation this is written as:

$$\begin{aligned} \rho =\rho _{0}\left[ 1-\beta _1(T-T_{0})+\beta _2(S-S_{0})\right] . \end{aligned}$$
(5)

The electrical field equations for a dielectric liquid under an AC electric field are

$$\begin{aligned} \nabla \times \mathbf {E}=0, \quad \nabla \cdot \mathbf {D}=0, \end{aligned}$$
(6)

where

$$\begin{aligned} \mathbf {D}&=\mathbf {P}+\varepsilon _{0}\mathbf {E},\; \mathbf {P}\nonumber\\ &=\varepsilon _{0}\mathbf {E}(\varepsilon _{r}-1) \text { and } \varepsilon _{r}=\varepsilon _{r}^{0}-(T-T_{0})e, \end{aligned}$$
(7)

In the Eqs. (1)–(7) the physical quantities that are mentioned have their definition as given in the nomenclature. The electrical field, \(\mathbf {E}\), is assumed to be in sufficiently high oscillation rate and this leads to the body force of free charges in the liquid unimportant. It is convenient to write \(\varepsilon _{r}^{0}\) in terms of the electric susceptibility, \(\chi _e\), as \(\varepsilon _{r}^{0}=(1+\chi _{e})\) so that \(\mathbf {P}=\varepsilon _{0}\chi _{e}\mathbf {E}\) when \(e = 0\). Thus, in Eq. (7), we replace \(\varepsilon _{r}^{0}\) by \((1+\chi _{e})\). In the paper we consider a two-dimensional analysis in the \(xz-\) plane and hence the physical quantities are independent of y-coordinate. It is thus imperative that we are limiting ourselves to the study of longitudinal rolls as a preferred pattern at onset.

The governing equations (1)–(7) are subjected to the following boundary conditions in the basic state:

  1. Case 1:

    Stress-free, isothermal and iso-solutal concentration boundary condition

    $$\begin{aligned} \left. \begin{aligned} (u,w)=(0,0),\iota _{xz}=0,T=T_0+\varDelta T,\;S=S_0+\varDelta S \text { at } z=-\dfrac{h}{2} \\ (u,w)=(0,0),\iota _{xz}=0,T=T_0,\;S=S_0 \text { at } z=\dfrac{h}{2}\\ \end{aligned} \right\} , \end{aligned}$$
    (8)
  2. 1

    Rigid, isothermal and iso-solutal concentration boundary condition

    $$\begin{aligned} \left. \begin{aligned} (u,w)=(0,0),\dfrac{\partial u}{\partial x}=0,\dfrac{\partial w}{\partial z}=0,T=T_0+\varDelta T,\;S=S_0 +\varDelta S \text { at } z=-\dfrac{h}{2} \\ (u,w)=(0,0),\dfrac{\partial u}{\partial x}=0,\dfrac{\partial w}{\partial z}=0, T=T_0,\;S=S_0 \text { at } z=\dfrac{h}{2}\\ \end{aligned} \right\} , \end{aligned}$$
    (9)

where u and w are the x- and z- components of velocity vector, \(\mathbf {q}\), and \(\iota _{xz}=\mu \left( \dfrac{\partial u}{\partial z}+\dfrac{\partial w}{\partial x}\right)\). Coming to the boundary condition on the electrical field, it is assumed that the normal component of the electric displacement, \(\mathbf {D}\), and the tangential component of the electric field, \(\mathbf {E}\), are continuous across the boundaries.

At the basic state the components of velocity, pressure, temperature, solutal concentration, polarization and electric field are considered to be:

$$\begin{aligned} \left. \begin{aligned} \mathbf {q}_b=(0,0),\;p=(p_b(x),p_b(z)),\;T=(0,T_b(z)),\;S=(0,S_b(z))\\ \mathbf {P}=(0,P_{b}(z)),\; \mathbf {E}=(0,E_{b}(z)) \end{aligned} \right\} , \end{aligned}$$
(10)

Substituting Eq. (10) into the governing equations (1)–(7) and using the temperature and concentration boundary conditions, we get the following quiescent state solution:

$$\begin{aligned} \left. \begin{aligned} \mathbf {q}_{b}=0,\;p_b(z)=-\rho _0 g\left[ 1-\beta _1\varDelta T \left( \dfrac{1}{2}-\dfrac{z}{h}\right) +\varDelta S \beta _2\left( \dfrac{1}{2}-\dfrac{z}{h}\right) \right] z+c, \\ T_b(z)=T_0+\varDelta T\left( \dfrac{1}{2}-\dfrac{z}{h}\right) ,\;S_b(z)=S_0+\varDelta S\left( \dfrac{1}{2}-\dfrac{z}{h}\right) ,\\ \mathbf {P}_{b}=\left[ 1-\frac{1}{(1+\chi _{e}) + \left( \dfrac{1}{2}-\dfrac{z}{h}\right) \varDelta T + \left( \dfrac{1}{2}-\dfrac{z}{h}\right) \varDelta S}\right] (1 + \chi _{e})\varepsilon _{0}E_{0}{\hat{k}},\\ \mathbf {E}_{b}=\left[ \frac{(1+\chi _{e})E_{0}}{(1+\chi _{e})+e\left( \dfrac{1}{2}-\dfrac{z}{h}\right) \varDelta T+e\left( \dfrac{1}{2}-\dfrac{z}{h}\right) \varDelta S}\right] {\hat{k}} \end{aligned} \right\} , \end{aligned}$$
(11)

where c is an integration constant.

We superpose finite-amplitude perturbations on the basic state in the form:

$$\begin{aligned} \left. \begin{aligned} \mathbf {q}=\mathbf {q_{b}}+(u'(t,x,z),w'(t,x,z)),\;p=p_{b}(x,z) + p'(t,x,z),\\ T = T_{b}(z) + T'(t,x,z),\; S = S_{b}(z)+S(t,x,z)',\\ \mathbf {P}=\mathbf {P_{b}}(z) + (P_{1}'(t,x,z),P_{3}'(t,x,z)),\; \mathbf {E}=\mathbf {E_{b}}(z) + (E_{1}'(t,x,z),E_{3}'(t,x,z)) \end{aligned}\right\} . \end{aligned}$$
(12)

Using Eq. (12) and (7) becomes

$$\begin{aligned} P_{1}'=\varepsilon _{0}\chi _{e}E_{1}'-e\varepsilon _{0}T'E_{1}',\qquad P_{3}'=\varepsilon _{0}\chi _{e}E_{3}'-e\varepsilon _{0}T'E_{0}'-e\varepsilon _{0}T'E_{3}'. \end{aligned}$$
(13)

Here it is assumed that \(e\varDelta T \ll (1+\chi _{e})\).

Substituting Eq. (12) into the governing equations (1)–(7) and using the basic state solution (11), we get the governing equations concerning perturbations. Introducing the stream function, \(\psi '\), as

$$\begin{aligned} u'=-\frac{\partial \psi '}{\partial z}, \; w'= \frac{\partial \psi '}{\partial x}, \end{aligned}$$
(14)

and the perturbed electric potential, \(\varPhi '\), as

$$\begin{aligned} \mathbf {E'}=\nabla \varPhi ' \end{aligned}$$
(15)

into the resulting governing equations, eliminating pressure term in the linear momentum equation and non-dimensionalizing the equations using the following definition:

$$\begin{aligned} \left( x^{*}, z^{*}\right)= & {} \left( \frac{x}{h},\frac{z}{h}\right) ,\; \varPsi ^{*}=\frac{\psi '}{\alpha _T}, \; t^{*}=\frac{\alpha _T t}{h^{2}}, \; \varPhi ^{*}=\frac{(1+\chi _{e})}{eE_{0}\varDelta T h}\varPhi ', \;\nonumber \\ T^{*}= & {} \frac{T'}{\varDelta T},\;S^{*}=\frac{S'}{\varDelta S}, \end{aligned}$$
(16)

we get the governing equations in the dimensionless form as

$$\begin{aligned} \frac{1}{Pr}\frac{\partial }{\partial t}(\nabla ^{2}\varPsi )= & {} [R(1+g_m)+R_{E}] \dfrac{\partial T}{\partial x}-R_{s}(1+g_m)\frac{\partial S}{\partial x}\nonumber \\&-R_{E}\frac{\partial ^{2} \varPhi }{\partial x \partial z}+\nabla ^{4}\varPsi - R_{E}J\left( T, \frac{\partial \varPhi }{\partial z}\right) , \end{aligned}$$
(17)
$$\begin{aligned} \frac{\partial T}{\partial t}= & {} \nabla ^{2}T+\frac{\partial \varPsi }{\partial x}-J(\varPsi ,T), \end{aligned}$$
(18)
$$\begin{aligned} \frac{\partial S}{\partial t}= & {} \frac{1}{Le}\nabla ^{2} S +\frac{\partial \varPsi }{\partial x}-J(\varPsi ,S), \end{aligned}$$
(19)
$$\begin{aligned} \nabla ^{2}\varPhi +\frac{\partial T}{\partial z}= & {} 0, \end{aligned}$$
(20)

where \(Pr = \frac{\mu }{\rho _{0}\alpha _T}\) is the Prandtl number, \(R = \frac{\beta _1 \rho _{0}g \varDelta T h^{3}}{\mu \alpha _T}\) is the thermal Rayleigh number, \(R_{E}=\frac{\varepsilon _{0}(E_{0}e\varDelta T h)^{2}}{\mu \alpha _T (1+\chi _{e})}\) is the electrical Rayleigh number, \(R_{S} = \frac{\beta _2 \rho _0 g \varDelta S h^{3}}{\mu \alpha _{T}}\) is the solutal Rayleigh number, \(Le = \frac{\alpha _{T}}{\alpha _{S}}\) is the Lewis number and \(g_m=\dfrac{g'(\delta ,\varOmega ,t)}{g}\).

In writing the momentum equation (17) we have neglected the term (\(\mathbf {q}\cdot \nabla \mathbf {q}\)) by assuming the small-scale convective motion. In the paper we have considered the trigonometric sine wave type of gravity modulation with small amplitude, \(\delta\), and hence we take \(g_m(t)=\delta \sin (\varOmega t)\).

The boundary conditions now take the form:

  1. Case 1:

    Stress-free, isothermal and iso-soluatal concentration boundary condition

    $$\begin{aligned} \varPsi =\frac{\partial ^{2}\varPsi }{\partial z^{2}}=T= S= \frac{\partial \varPhi }{\partial z}=0 \; \text {at} \; z = \pm \dfrac{1}{2}. \end{aligned}$$
    (21)
  2. 1

    Rigid, isothermal and iso-soluatal concentration boundary condition

    $$\begin{aligned} \varPsi =\frac{\partial \varPsi }{\partial z}=T= S= \frac{\partial \varPhi }{\partial z}=0 \; \text {at} \; z = \pm \dfrac{1}{2}. \end{aligned}$$
    (22)

It is also assumed to have periodicity in the x-direction which leads to the following periodicity condition:

$$\begin{aligned} \left. \begin{aligned} \varPsi \left( x\pm \dfrac{2\pi }{\kappa _c},z,t\right) =\varPsi \left( x,z,t\right) \\ T\left( x\pm \dfrac{2\pi }{\kappa _c},z,t\right) =T\left( x,z,t\right) \\ S\left( x\pm \dfrac{2\pi }{\kappa _c},z,t\right) =S\left( x,z,t\right) \\ \varPhi \left( x\pm \dfrac{2\pi }{\kappa _c},z,t\right) =\varPhi \left( x,z,t\right) \end{aligned}\right\} , \end{aligned}$$
(23)

where \(\kappa _c\) is the critical wave number of the convecting cell and is determined using the linear stability analysis.

2.1 Weakly nonlinear stability analysis—derivation of the generalized Lorenz system

Consider the following minimal mode Fourier–Galerkin expansions to describe the nonlinear interaction of the stream function, temperature, solutal and electrical potential:

$$\begin{aligned} \varPsi= & {} \dfrac{\sqrt{2}\eta ^2}{\pi \kappa }A(t)\sin (\kappa _c x) \;f_1(z), \end{aligned}$$
(24)
$$\begin{aligned} T= & {} \dfrac{\sqrt{2}}{\pi }B(t)\cos (\kappa _c x) \;f_2(z)-\dfrac{1}{\pi }C(t)\;f_3(z) , \end{aligned}$$
(25)
$$\begin{aligned} S= & {} \dfrac{\sqrt{2}}{\pi } L(t)\cos (\kappa _c x) \;f_2(z)+\dfrac{1}{\pi }M(t)\;f_3(z), \end{aligned}$$
(26)
$$\begin{aligned} \varPhi= & {} I_1 \cos (\kappa _c x) \;\texttt {D}f_2(z)+ I_2 \; \texttt {D}f_3(z), \end{aligned}$$
(27)

where \(\eta =\sqrt{\kappa ^2+\pi ^2}\), \(\texttt {D}=\dfrac{d}{dz}\), \(f_2(z)=\sin \left( \pi z+\dfrac{\pi }{2}\right)\) and \(f_3(z)=\sin (2\pi z+\pi )\).

The choice of \(f_1(z)\) depends on the velocity boundary condition.

  1. (i)

    For free boundaries, \(f_1(z)= \sin \left( \pi z+\dfrac{\pi }{2}\right)\) and

  2. (ii)

    For rigid boundaries, \(f_1(z) =\dfrac{\cosh (\mu _1 z)}{\cosh \left( \frac{\mu _1}{2}\right) } -\dfrac{\cos (\mu _1 z)}{\cos \left( \frac{\mu _1}{2}\right) }\) where \(\mu _1=4.73004074\) .

Substituting Eqs. (24)–(27) into the governing equations (17)–(20) and using the orthogonality condition with eigenfunctions, we get the following non-autonomous system of equations called as the generalized Lorenz model:

$$\begin{aligned} \dfrac{dA}{d\tau }= & {} \dfrac{Pr}{\texttt {p}_1} \left[ -\texttt {p}_2A+r \texttt {p}_3(1+g_m)B -r_S \texttt {p}_3(1+g_m)L\right. \nonumber \\&\left. +\,r_E b_1 \texttt {p}_4 B-r_E b_1 \texttt {p}_5 BC\right] , \end{aligned}$$
(28)
$$\begin{aligned} \dfrac{dB}{d\tau }= & {} \dfrac{1}{\texttt {p}_6}\left[ \texttt {p}_7 A-\texttt {p}_8B -\texttt {p}_9 AC \right] , \end{aligned}$$
(29)
$$\begin{aligned} \dfrac{dC}{d\tau }= & {} \dfrac{1}{\texttt {p}_{10}}\left[ -\texttt {p}_{11}b_2 C +\texttt {p}_{12} AB \right] , \end{aligned}$$
(30)
$$\begin{aligned} \dfrac{dL}{d\tau }= & {} \dfrac{1}{\texttt {p}_6}\left[ \texttt {p}_7 A -\dfrac{\texttt {p}_8}{Le} L+\texttt {p}_9 AM \right] , \end{aligned}$$
(31)
$$\begin{aligned} \dfrac{dM}{d\tau }= & {} \dfrac{1}{\texttt {p}_{10}}\left[ -\dfrac{\texttt {p}_{11}}{Le} b_2 M-\texttt {p}_{12} AL \right] , \end{aligned}$$
(32)

where \(\tau =\eta ^2 t\), \(b_1=\dfrac{\eta ^2}{\kappa _c^2}\) and \(b_2=\dfrac{4\pi ^2}{\eta ^2}\).

The coefficients, \(\texttt {p}_i\)’s are given by

$$\begin{aligned} \left. \begin{aligned} \texttt {p}_1=<-\kappa _c^2f_1^2+f_1\texttt {D}^2f_1>,\;\texttt {p}_2=-\dfrac{1}{\eta ^2}<\kappa _c^4f_1^2-2\kappa _c^2f_1\texttt {D}^2f_1+f_1\texttt {D}^4f_1>,\\ \texttt {p}_3=-\eta ^2<f_1f_2>,\; \texttt {p}_4=-\dfrac{\eta ^2}{b_1}\left[<f_1f_2>-\dfrac{<f_1(\texttt {D}f_2)^2\texttt {D}^2f_2>}{<-\kappa _c^2(\texttt {D}f_2)^2+\texttt {D}f_2\texttt {D}^3f_3>}\right] ,\\ \texttt {p}_5=\dfrac{\eta ^2}{\pi b_1}\left[ \dfrac{<f_1f_2(\texttt {D}f_3)^2\texttt {D}^3f_3>}{<\texttt {D}f_3\texttt {D}^3f_3>}-\dfrac{<f_1(\texttt {D}f_2)^2\texttt {D}^2f_2\texttt {D}f_3>}{<-\kappa _c^2(\texttt {D}f_2)^2+\texttt {D}f_2\texttt {D}^3f_2>}\right] ,\\ \texttt {p}_6=\eta ^2<f_2^2>,\;\texttt {p}_7=\eta ^2<f_1f_2>,\;\texttt {p}_8=-<-\kappa _c^2f_2^2+f_2\texttt {D}^2f_2>,\\ \texttt {p}_9=-\dfrac{\eta ^2}{\pi }<f_1f_2\texttt {D}f_3>,\;\texttt {p}_{10}=\eta ^2<f_3^2>,\;\texttt {p}_{11}=-\dfrac{1}{b_2}<f_3\texttt {D}^2f_3>,\\ \texttt {p}_{12}=\dfrac{2\eta ^2}{\pi }\left[<f_1f_3\texttt {D}f_1>+<\sec ^2 (\kappa _c x) \;f_1f_3 \texttt {D}f_2>\right] \end{aligned} \right\} . \end{aligned}$$
(33)

We first use the linearized version of the generalized Lorenz model (28)–(32) in making a linear stability analysis and then use the full system (28)–(32) to make a local nonlinear analysis with the sole aim of obtaining a numerical solution of a first-order equation rather the fifth-order one of the generalized Lorenz model.

2.2 Linear stability analysis—expressions for the critical Rayleigh number and its correction using the modified Venezian approach

Expressions for the critical Rayleigh number and its correction are determined by performing a linear stability analysis. The linear stability analysis involves infinitesimal amplitudes and hence the nonlinear terms in the Eqs. (28)–(32) are neglected. This gives us the following system of equations:

$$\begin{aligned} \dfrac{dA}{d\tau }&= \dfrac{Pr}{\texttt {p}_1} \left[ -\texttt {p}_2A+ \texttt {p}_3r(1+\overline{g_m(\tau )})B\right.\nonumber \\&\left.-\,\texttt {p}_3r_S(1+\overline{g_m(\tau )})L+\texttt {p}_4b_1 r_E B\right] , \end{aligned}$$
(34)
$$\begin{aligned} \dfrac{dB}{d\tau }= & {} \dfrac{1}{\texttt {p}_6}\left[ \texttt {p}_7 A-\texttt {p}_8B \right] , \end{aligned}$$
(35)
$$\begin{aligned} \dfrac{dL}{d\tau }= & {} \dfrac{1}{\texttt {p}_6}\left[ \texttt {p}_7 A -\dfrac{\texttt {p}_8}{Le} L \right] . \end{aligned}$$
(36)

The over line on \(g_m\) denotes the time-average in \(\left[ 0, \dfrac{2\pi }{\varOmega }\right]\).

The Venezian [15] approach involved a linear stability analysis using the system of partial differential equations as in Eqs. (17)–(20). We use a modified approach on the linearized Lorenz model (28)–(32). Following the modified Venezian [17] approach, we assume the gravity modulation to be of first-order in \(\epsilon _1\) and so we expand the amplitudes A, B and L, and the scaled thermal Rayleigh number, r, of Eqs. (34)–(36) in terms of \(\epsilon _1\) as shown below:

$$\begin{aligned} \left. \begin{aligned} A&= A_0+\epsilon _1 A_1+\epsilon _1^2 A_2+\cdots ,\\ B&= B_0+\epsilon _1 B_1+\epsilon _1^2 B_2+\cdots ,\\ L&= L_0+\epsilon _1 L_1+\epsilon _1^2 L_2+\cdots ,\\ r&= r_0+\epsilon _1^2 r_2+\epsilon _1^4 r_4 +\cdots , \end{aligned}\right\} \end{aligned}$$
(37)

Substituting Eq. (37) into Eqs. (34)–(36), we get a system of equations involving \(\epsilon _1\) and its higher powers. Equating terms independent of \(\epsilon _1\) on either side of the resulting equations, we get

$$\begin{aligned} \texttt {I} \mathtt {V}_0 =0, \end{aligned}$$
(38)

where

$$\begin{aligned} \texttt {I}=\left[ \begin{matrix} -\left( \dfrac{\texttt {p}_2}{\texttt {p}_1}+\dfrac{1}{Pr}\dfrac{d}{d\tau }\right) &{} &{} r_0 \dfrac{\texttt {p}_3}{\texttt {p}_1}+r_E b_1 \dfrac{\texttt {p}_4}{\texttt {p}_1}&{} &{} -r_S \dfrac{\texttt {p}_3}{\texttt {p}_1} \\ \dfrac{\texttt {p}_7}{\texttt {p}_6} &{}&{} -\left( \dfrac{\texttt {p}_8}{\texttt {p}_6} +\dfrac{d}{d\tau }\right) &{}&{} 0 \\ \dfrac{\texttt {p}_7}{\texttt {p}_6}&{}&{} 0 &{} &{} -\left( \dfrac{\texttt {p}_8}{\texttt {p}_6}+\dfrac{1}{Le}\dfrac{d}{d\tau }\right) \end{matrix} \right] \text { and } \\ \mathtt {V}_0= & {} [A_0,\;\; B_0, \;\; L_0]^{Tr}. \end{aligned}$$

At the marginal stability the time derivative does not appear leading to the following solution to Eq. (38):

$$\begin{aligned} \mathtt {V}_0=\left[ A_0, \;\; \dfrac{\texttt {p}_7}{\texttt {p}_8} A_0,\;\; \dfrac{\texttt {p}_7}{\texttt {p}_8}\dfrac{1}{Le} A_0\right] ^{Tr}. \end{aligned}$$
(39)

The condition for the occurrence of the above solution is

$$\begin{aligned} r_0=\dfrac{\texttt {p}_2\texttt {p}_8}{\texttt {p}_3\texttt {p}_7}+r_SLe - \dfrac{\texttt {p}_4}{\texttt {p}_3}b_1 r_E. \end{aligned}$$
(40)

The above Eq. (40) is the expression for the critical Rayleigh number of the non-modulated system.

On equating terms involving \(\epsilon _1\) on either side of the Eqs. (34)–(36) and also substituting (37) in them, we get

$$\begin{aligned} \texttt {I} \mathtt {V}_1 =[\texttt {N}_1,\;\;0,\;\;0], \end{aligned}$$
(41)

where \(\mathtt {V}_1=[A_1,\;\; B_1, \;\; L_1]^{Tr}\) and \(\texttt {N}_1=-\dfrac{\texttt {p}_3}{\texttt {p}_1}\overline{g_m(\tau )}(r_0B_0-r_S L_0)\).

To determine \(\mathtt {V}_1\) we note that time variations occur as \(e^{-i \varOmega \tau }\) and hence \(\texttt {I}(\tau )\) now becomes:

$$\begin{aligned} \texttt {I}(\varOmega )=\left[ \begin{matrix} -\left( \dfrac{\texttt {p}_2}{\texttt {p}_1}+\dfrac{1}{Pr}i \varOmega \right) &{} &{} r_0 \dfrac{\texttt {p}_3}{\texttt {p}_1}+r_E b_1 \dfrac{\texttt {p}_4}{\texttt {p}_1}&{} &{} -r_S \dfrac{\texttt {p}_3}{\texttt {p}_1} \\ \dfrac{\texttt {p}_7}{\texttt {p}_6} &{}&{} -\left( \dfrac{\texttt {p}_8}{\texttt {p}_6} +i \varOmega \right) &{}&{} 0 \\ \dfrac{\texttt {p}_7}{\texttt {p}_6}&{}&{} 0 &{} &{} -\left( \dfrac{\texttt {p}_8}{\texttt {p}_6}+\dfrac{1}{Le}i \varOmega \right) \end{matrix} \right] \end{aligned}.$$
(42)

Using column operations one can easily show that \(\texttt {I}\) is self-adjoint. Solving Eq. (41) using the zeroth-order solution (39) and the matrix (42), we get

$$\begin{aligned} \left. \begin{aligned} A_1=\dfrac{1}{{\mathcal {L}}}\dfrac{\texttt {p}_3 \texttt {p}_7}{\texttt {p}_8}Pr \left( \dfrac{r_S}{Le}-r_0\right) \overline{g_m}\;A_0,\\ B_1 = \left( \dfrac{\texttt {p}_7}{\texttt {p}_8+i\varOmega \texttt {p}_6 }\right) A_1,\\ L_1= \left( \dfrac{\texttt {p}_7 Le}{\texttt {p}_8+i\varOmega \texttt {p}_6 Le}\right) A_1 \end{aligned} \right\} , \end{aligned}$$
(43)

where

$$\begin{aligned} {\mathcal {L}}= & {} -\left( \texttt {p}_2 +\dfrac{\texttt {p}_1}{Pr} i \varOmega \right) +\dfrac{\texttt {p}_7(\texttt {p}_3r_0+\texttt {p}_4 r_E b_1)}{\texttt {p}_8 +i\varOmega \texttt {p}_6}-\dfrac{\texttt {p}_3\texttt {p}_7 r_S Le}{\texttt {p}_8+i \varOmega \texttt {p}_6 Le}. \end{aligned}$$
(44)

Using the zeroth- and first-order solutions, we determine the correction Rayleigh number, \(r_2\). To do so we equate the order of \(\epsilon _1^2\) on either side of the Eqs. (34)–(36) after substituting (37), we get

$$\begin{aligned} \texttt {I}\mathtt {V}_2 =[\texttt {N}_2,\;\;0,\;\;0], \end{aligned}$$
(45)

where \(\mathtt {V}_2=[A_2,\;\; B_2, \;\; L_2]^{Tr}\) and \(\texttt {N}_2=-\dfrac{\texttt {p}_3}{\texttt {p}_1}\left[ r_2 B_0+\overline{g_m}(r_0B_1-r_S L_1)\right]\).

In order to obtain the expression for the correction Rayleigh number we make use of the following theorem (the Fredholm-solvability condition):

Theorem 1

Consider \(\texttt {I}\mathtt {V}_2 =[\texttt {N}_2,\;\;0,\;\;0]\) on the interval \(\left[ -\frac{1}{2} \;\;\frac{1}{2}\right]\) subject to \(A_2(0)=B_2(0)=L_2(0)=0\) then there exist a solution to the non-homogeneous system (45) provided there exist a non-trivial solution to \(\texttt {I}\mathtt {V}_0=0\) and the following condition is true

$$\begin{aligned} \texttt {N}_2 {\hat{A}}_0 =0, \end{aligned}$$
(46)

where \({\hat{A}}_0\) is the solution of the self-adjoint system of Eq. (39).

Substituting \(\texttt {N}_2\) into the Eq. (46) and rearranging, we get the expression for the scaled correction Rayleigh number as:

$$\begin{aligned} r_2= & {} \texttt {p}_3\texttt {p}_8 Pr \left( r_0 - \dfrac{r_S}{Le}\right) \overline{g_m} \;Re \left[ \dfrac{1}{{\mathcal {S}}}\left( \dfrac{r_0}{\texttt {p}_8+i\varOmega \texttt {p}_6}-\dfrac{r_S Le}{\texttt {p}_8+i\varOmega \texttt {p}_6 Le}\right) \right] , \end{aligned}$$
(47)

where Re means the real part.

2.3 Local nonlinear stability analysis—derivation of the Ginzburg–Landau equation from the generalized Lorenz system

We now derive the one-dimensional Ginzburg–Landau amplitude equation from the fifth-order generalized Lorenz system (28)–(32) by using the method of multiscales ([38], [39]). To do so we assume

  1. (a)

    A small time-scale, i.e., \(\tau _1=\epsilon _2^2 \tau\),

  2. (b)

    Gravity modulation to be of order \(\epsilon _2^2\) and

  3. (c)

    The following regular perturbation expansion for amplitudes and scaled thermal Rayleigh number:

    $$\begin{aligned} \left. \begin{aligned} A= & {} \epsilon _2 A_1+\epsilon _2^2 A_2+\epsilon _2^3 A_3\ldots ,\\ B= & {} \epsilon _2 B_1+\epsilon _2^2 B_2+\epsilon _2^3 B_3\ldots ,\\ C= & {} \epsilon _2 C_1+\epsilon _2^2 C_2+\epsilon _2^3 C_3\ldots ,\\ L= & {} \epsilon _2 L_1+\epsilon _2^2 L_2+\epsilon _2^3 L_3\ldots ,\\ M= & {} \epsilon _2 M_1+\epsilon _2^2 M_2+\epsilon _2^3 M_3\ldots ,\\ r= & {} r_0+\epsilon _2^2 r_2+\epsilon _2^4 r_4+\cdots \\ \end{aligned}\right\} . \end{aligned}$$
    (48)

where \(\epsilon _2\) is a small amplitude which is different from \(\epsilon _1\) and concerns finite amplitude convection.

Using the above small time scale, small amplitudes and Eq. (48) in Eqs. (28)–(32), we arrive at the system of equations involving amplitude, \(\epsilon _2\). Equating the like powers of \(\epsilon _2\) on either side of the resulting equations, we get the following system of homogeneous/non-homogeneous equations at various orders:

At o(\(\epsilon _2\))::
$$\begin{aligned} \texttt {J}{} \texttt {W}_1=0, \end{aligned}$$
(49)

where

$$\begin{aligned} \texttt {J}= & {} \left[ \begin{matrix} -\texttt {p}_2 &{} &{} (\texttt {p}_3r_0 +\texttt {p}_4b_1 r_E ) &{} &{} 0 &{} &{} -r_S \texttt {p}_3 &{}&{} 0 \\ \texttt {p}_7 &{}&{} -\texttt {p}_8 &{}&{} 0 &{}&{} 0 &{}&{} 0 \\ 0 &{}&{} 0 &{}&{} \texttt {p}_{11}b_2 &{}&{} 0 &{} &{} 0 \\ \texttt {p}_7 &{}&{} 0 &{}&{} 0 &{}&{} -\dfrac{\texttt {p}_8}{Le} &{}&{} 0 \\ 0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} -\dfrac{\texttt {p}_{11}}{Le}b_2 \\ \end{matrix} \right] \text { and } \\ \mathtt {W}_1= & {} [A_1,\;\; B_1, \;\;C_1,\;\; L_1,\;\;M_1]^{Tr}. \end{aligned}$$
At o(\(\epsilon _2^2\))::
$$\begin{aligned} \texttt {J}{} \texttt {W}_2=[0,\;\;0,\;\;N_{23},\;\;0,\;\;N_{25}]^{Tr}, \end{aligned}$$
(50)

where

$$\begin{aligned} \mathtt {W}_2= & {} [A_2,\;\; B_2, \;\;C_2,\;\; L_2,\;\;M_2]^{Tr},\;\;\nonumber \\ N_{23}= & {} -\texttt {p}_{12} A_1B_1 \text { and } \, N_{25}=\texttt {p}_{12} A_1L_1. \end{aligned}$$
(51)
At o(\(\epsilon _2^3\))::
$$\begin{aligned} \texttt {J}{} \texttt {W}_3=[N_{31},\;\;N_{32},\;\;0,\;\;N_{34},\;\;0]^{Tr}, \end{aligned}$$
(52)

where

$$\begin{aligned} \left. \begin{aligned} \mathtt {W}_3=[A_3,\;\; B_3, \;\;C_3,\;\; L_3,\;\;M_3]^{Tr},\\ N_{31}=\dfrac{\texttt {p}_1}{Pr}\dfrac{dA}{d\tau _1}-\texttt {p}_{3} \left[ r_2B_1-\overline{g_m}(r_0B_1-r_SL_1)\right] ,\\ N_{32}=\texttt {p}_{6}\dfrac{dB_1}{d\tau _1}+\texttt {p}_{9}A_1C_2,\\ N_{34}=\texttt {p}_{6}\dfrac{dL_1}{d\tau _1}-\texttt {p}_{9}A_1M_2 \end{aligned} \right\} . \end{aligned}$$
(53)

On solving systems (48) and (50), we get the following solutions:

$$\begin{aligned} \left. \begin{aligned} \texttt {W}_1=\left[ A_1,\;\;\dfrac{\texttt {p}_7}{\texttt {p}_8}A_1,\;\;0,\;\; \dfrac{\texttt {p}_7}{\texttt {p}_8}Le A_1,\;\;0\right] ^{Tr},\\ \texttt {W}_2=\left[ 0,\;\;0,\;\;\dfrac{\texttt {p}_7\texttt {p}_{12}}{\texttt {p}_8 \texttt {p}_{11}}\dfrac{1}{b_2}A_1^2,\;\;0,\;\;\dfrac{\texttt {p}_7 \texttt {p}_{12}}{\texttt {p}_8\texttt {p}_{11}}\dfrac{1}{b_2}Le^2A_1^2\right] ^{Tr} \end{aligned}\right\} . \end{aligned}$$
(54)

Here \(A_1\) corresponds to the linear convective mode at threshold whereas \(A_2\) concerns the nonlinear convective mode and hence has to be zero.

In order to determine the amplitude, \(A_1\), we use the aforementioned Theorem 1 which leads to the following condition for the occurrence of the solution of Eq. (52):

$$\begin{aligned} N_{31}{\hat{A}}_1+N_{32}{\hat{B}}_1+N_{34}{\hat{L}}_1=0, \end{aligned}$$
(55)

where \({\hat{A}}_1=1, {\hat{B}}_1=\dfrac{1}{\texttt {p}_8}(r_0\texttt {p}_3+\texttt {p}_4 r_E b_1)\) and \({\hat{L}}_1=-\dfrac{\texttt {p}_3}{\texttt {p}_8}r_S Le\) are the solution of the self-adjoint system of Eq. (49).

Using Eqs. (54) and (55), we get the Ginzburg–Landau equation in the form:

$$\begin{aligned} \dfrac{dA_1}{d\tau _1}=\dfrac{Q_1}{Q_3}A_1-\dfrac{Q_2}{Q_3}A_1^3, \end{aligned}$$
(56)

where

$$\begin{aligned} \left. \begin{aligned} Q_1 = \dfrac{\texttt {p}_3\texttt {p}_7}{\texttt {p}_8}Pr\left[ r_2+g_m(r_0-r_SLe)\right] ,\\ Q_2= \dfrac{\texttt {p}_7\texttt {p}_9\texttt {p}_{12}}{\texttt {p}_8^2\texttt {p}_{11}} \dfrac{1}{b_2}Pr[\texttt {p}_3(r_0-r_SLe^3)+\texttt {p}_4r_E b_1],\\ Q_3 = \texttt {p}_1+\dfrac{\texttt {p}_6\texttt {p}_7}{\texttt {p}_8^2}Pr [\texttt {p}_3(r_0-r_SLe^2)+\texttt {p}_4r_E b_1] \end{aligned}\right\} , \end{aligned}$$
(57)

where \(r_0\) and \(r_2\) are given by Eqs. (40) and (47). The numerical solution of the Ginzburg–Landau equation (56) with a time-periodic coefficient is obtained using the initial condition \(A_1(0)=0.5\) and this solution is used to quantify the heat and mass transports in the system.

3 Estimation of heat and mass transports at the lower boundary

The heat and mass transports are quantified using the Nusselt and Sherwood numbers respectively. The horizontally-averaged Nusselt (Nu) and Sherwood (Sh) numbers for the stationary double-diffusive convection are given as:

$$\begin{aligned} Nu(\tau _1)&= 1+\left[ \dfrac{\int _{0}^{\frac{2\pi }{\kappa _c}} \left( \dfrac{\partial T}{\partial z}\right) dx }{\int _{0}^{\frac{2\pi }{\kappa _c}} \left( \dfrac{d T_b}{d z}\right) dx}\right] _{z=-\dfrac{1}{2}} \text { and }\nonumber \\ Sh(\tau _1)&= 1+\left[ \dfrac{\int _{0}^{\frac{2\pi }{\kappa _c}} \left( \dfrac{\partial S}{\partial z}\right) dx }{\int _{0}^{\frac{2\pi }{\kappa _c}} \left( \dfrac{d S_b}{d z}\right) dx}\right] _{z=-\dfrac{1}{2}}. \end{aligned}$$
(58)

Substituting the non-dimensional form of the basic state solution of temperature and solute from Eq. (11), and the Eqs. (25), (26) and (54) in Eq. (58), we get

$$\begin{aligned} Nu(\tau _1)&=1+\left( \dfrac{\texttt {p}_7\texttt {p}_{12}}{\texttt {p}_8\texttt {p}_{11}} \right) \dfrac{2\epsilon _2^2}{b_2}A_1^2 \text { and } \nonumber \\ Sh(\tau _1)&=1+Le^2[Nu(\tau _1)-1]. \end{aligned}$$
(59)

4 Results and discussion

The focus of the paper is on studying the influence of gravity modulation, second diffusing component, AC electric field and the effect of free and rigid boundaries on

  1. (i)

    Onset of convection,

  2. (ii)

    Heat transport and

  3. (iii)

    Mass transport.

The modified Venezian approach [17] is used to perform a linear stability analysis and expressions for the threshold values of the scaled thermal Rayleigh number and its correction are arrived at. Using these expressions the combined effect of parameters arising from gravity modulation and those arising due to the dielectric nature of the liquid are discussed in the paper for both free and rigid boundaries. Fourier–Galerkin expansion is used to derive the fifth-order generalized Lorenz system. The method of multiscales is employed to derive the non-autonomous Ginzburg–Landau equation from the fifth-order, non-autonomous generalized Lorenz system. We note that both the systems are non-autonomous due to the presence of a time-periodic coefficient but the procedure to obtain the numerical solution of the former one is much simpler. The solution of the Ginzburg-Landau model is used in quantifying the heat and mass transports in terms of the Nusselt and the Sherwood numbers.

We now present the results and their discussion under two headings: (a) results from linear theory and (b) results from nonlinear theory.

4.1 Results from linear stability analysis

Equations (40) and (47) represent respectively, the expressions for the scaled thermal Rayleigh number and its correction. It is clear from these expressions that the influence of gravity modulation comes only through the correction Rayleigh number. Using these two equations one can write down the expression for the thermal Rayleigh number as

$$\begin{aligned} R_T=\dfrac{\eta ^6}{\kappa ^2} (r_0+\epsilon _1^2 r_2). \end{aligned}$$
(60)

Minimizing the above expression with respect to wave number, \(\kappa\), we get the critical thermal Rayleigh number as a function of \(R_S\), \(R_E\), Le, Pr, \(\delta\) and \(\varOmega\). Tables 1 and 2 respectively document values of the critical wave number and the thermal Rayleigh number for different values of the aforementioned parameters in the absence and presence of gravity modulation.

Table 1 Values of the critical wave and thermal Rayleigh numbers for different values of parameters for both free and rigid isothermal boundaries in the absence of gravity modulation(\(\delta =0\))
Full size table
Table 2 Values of the critical wave and thermal Rayleigh numbers for different values of parameters for both free and rigid isothermal boundaries in the presence of gravity modulation (\(\delta =0.1\))
Full size table

The values of the thermal Rayleigh and wave numbers corresponding to parameter values \(Le=R_S=R_E=0\) denote that of the classical Rayleigh-Bénard convection in a Newtonian liquid [34] (single-component thermo-convection). Thus, in the limiting case, i.e., classical Rayleigh-Bénard convection in a Newtonian liquid, the values of the critical thermal Rayleigh number coincide with the values reported by Siddheshwar et al. [40] and Kanchana et al. [41] for free-isothermal and rigid-isothermal boundary conditions. Further, it is obvious from these tables that in the presence/absence of gravity modulation and in the limiting case, the following result is true:

$$\begin{aligned} (R_T)_c^{FF}<(R_T)_c^{RR}, \end{aligned}$$
(61)

where FF and RR denote the free and rigid boundaries respectively.

From the Tables 1 and 2 it is apparent that the effect of increasing Lewis and solutal Rayleigh numbers is to stabilize the system irrespective of the boundaries being rigid or free. In the double-diffusive system, increase in Lewis number essentially means that the thermal diffusivity dominates over solutal diffusivity results in a delay in the onset of convection. Solutal Rayleigh number concerns the buoyancy force and the dissipative terms. Increase in solutal Rayleigh number means the buoyancy force is less vigorous and thus a dominant viscous force and hence the system approaches stability.

The nondimensional parameters \(R_E\) and Pr characterize liquid properties and the effect of electrical field is characterized by electrical Rayleigh number, \(R_E\) . The Tables 1 and 2 clearly show that the effect of an increase in the strength of the AC electric liquid is to promote early onset of convection. As we notice from Tables 1 and 2 there is no significant influence of Pr on onset of modulated/non-modulated convection.

As far as gravity modulation is concerned, on comparing the values of the critical Rayleigh numbers between the Tables 1 and 2 (wherein Table 1 corresponds to no modulation case and Table 2 corresponds to problem with gravity modulation) it is clear that there is a slight forward shift in threshold value due to gravity modulation. Thus, the present study essentially reiterates the findings of the experimental and numerical works of Gresho and Sani [12], Biringen and Peltier [14] and Yu et al. [35]. It is to be noted that the influence of the gravity modulation is seen only as a positive correction to the thermal Rayleigh number and appears thus as a forward shift in the critical Rayleigh number.

Fig. 2
figure 2

Plots of critical scaled correction Rayleigh number versus frequency of modulation for different values of Le, \(R_S\), \(R_E\) and \(\delta\) and for fixed values \(Le=2\), \(R_S=20\), \(R_E=50\), \(Pr=10\), \(\delta =0.1\), \(\varOmega =10\) and \(A_0=0.5\)

Full size image

This result essentially means that the influence of modulation is to suppress the double-diffusive electro-convection. In some applications which involve the fluid flow and electric field (cases of water column devices and image processing devices) one can suppress the convection by imposing gravity modulation. However, the values of amplitude and the frequency of modulation play a greater role in the further suppressing convection and the same is discussed using Figs. 2 and 3.

The influence of frequency of gravity modulation can be explained using the plots pertaining to the critical scaled correction Rayleigh number versus the frequency of modulation for different values of the parameters Le, \(R_S\), \(R_E\), \(\delta\) and Pr (see Figs. 2 and 3). It is clear from these figures that the effect of increasing \(R_E\) is to enhance convection whereas the effect of increasing Le, \(R_S\) and \(\delta\) is to suppress convection. Tuning of amplitude (increase) and frequency (decrease) increases the critical Rayleigh number leading to further suppression of double diffusive electro-convection. Thus, gravity modulation can be considered as a regulating mechanism in the double-diffusive electro-convective system.

From Figs. 2 and 3 it is apparent that though the critical thermal Rayleigh number is large for rigid boundaries compared to that for free boundaries (see Eq. (61)), the scaled correction Rayleigh number is small for rigid boundaries. This is because the gravity modulation significantly influences the boundaries and as we have mentioned earlier it is only in the correction Rayleigh number that the influence of gravity modulation appears. The magnitude of the scaled, correction Rayleigh number is, however, small compared to the scaled, critical Rayleigh number of the non-modulated system obtained using the fundamental mode and hence the to-be-expected result of (61).

The influences of Le, \(R_S\), \(R_E\) on the scaled correction Rayleigh number are similar to their influence on the critical Rayleigh number obtained by the fundamental mode. The effect of increasing amplitude/frequency of gravity modulation is to increase/decrease the correction Rayleigh number. The effect of Pr on the onset of convection comes through only the correction Rayleigh number. From (3) it is clear that as we increase Pr, the critical scaled correction Rayleigh number decreases. Since the magnitude of correction Rayleigh number is very small compared to the Rayleigh number obtained using the normal mode, it must be said that the overall effect of Pr on onset is quite negligible.

Fig. 3
figure 3

Plots of critical scaled correction Rayleigh number versus frequency of modulation for different values of Pr and for fixed values \(Le=2\), \(R_S=20\), \(R_E=50\), \(Pr=10\), \(\delta =0.1\), \(\varOmega =10\) and \(A_0=0.5\)

Full size image
Fig. 4
figure 4

Plots of Nusselt number versus time for different values of Le, \(R_S\), \(R_E\) and Pr and for fixed values \(Le=2\), \(R_S=20\), \(R_E=50\), \(Pr=10\), \(\delta =0.1\), \(\varOmega =10\) and \(A_0=0.5\)

Full size image

4.2 Results from weakly-nonlinear/local-nonlinear stability analyses

Nusselt and Sherwood numbers are used to study heat and mass transports of the double-diffusive system in a dielectric liquid. Figures 4 and 5 concerning heat transport. It is evident from the Fig. 4 that the effect of increasing Le and \(R_S\) is to enhance heat transport whereas the effect of increasing \(R_E\) is to diminish the same. Though we notice that an increase in Pr is to increase the Nusselt number at short time, at large times its influence is negligible.

As we mentioned earlier, Lewis number represents the relative magnitude of thermal diffusivity and mass diffusivity which are essentially the properties of the two-component dielectric liquid. A value of Lewis number greater than unity means that thermal diffusion dominates over solutal diffusion and hence results in an enhanced heat transfer situation.

A similar explanation can be provided for the observed influence of the buoyancy force due to solute on the heat transport. The effect of increase in the electrical Rayleigh number is to diminish the heat transport. Influence of amplitude of gravity modulation on convection can be studied using Fig. 5. It is clear from the Fig. 5 that the effect of increase in the amplitude of modulation is to decrease the Nusselt number and thereby to diminish the heat transport.

As far as boundary condition is concerned it is observed from Figs. 4 and 5 that

$$\begin{aligned} Nu(\tau _1)^{FF}>Nu(\tau _1)^{RR}, \end{aligned}$$
(62)

irrespective of gravity modulation being present or absent. The above result is in concurrence with the result mentioned in (61). We may summarize the results by saying that the parameters’ influence on onset of convection and heat transport is unaltered by gravity modulation and boundary condition.

From the expression of the Sherwood number in Eq. (59), it is clear that the Sherwood number is always greater than the Nusselt number. Computation also shows that the influence of non-dimensional parameters/gravity modulation/boundaries on the Sherwood number is similar to their influence on the Nusselt number and hence the plots pertaining to Sherwood number are omitted in the paper due to redundance.

Fig. 5
figure 5

Plots of Nusselt number versus time for different values of \(\delta\) and fixed values of parameters as taken in the other plots

Full size image

5 Conclusion

Based on the results and their discussion, we have the following conclusion to make:

  1. 1

    The study of onset of double-diffusive convection and heat and mass transports using free boundaries is qualitatively similar to that using rigid boundaries.

  2. 2

    The influence of gravity modulation has less impact on the Rayleigh number compared to that on the heat and mass transports.

  3. 3

    The effect of increase in the values of Le and \(R_{S}\) is to stabilize the system whereas the effect of increase in \(R_E\) is to destabilize it.

  4. 4

    The effect of increase in the value of the amplitude of modulation is to stabilize the system whereas the effect of increase in frequency of modulation is to destabilize it.

  5. 5

    The effect of increase in the values of Le and \(R_{S}\) is to enhance heat and mass transports whereas the effect of increase in \(R_E\) is to diminish the same.

  6. 6

    Pr has negligible influence on onset of convection as well as on heat and mass transports.

  7. 7

    The effect of increase in values of amplitude of modulation is to diminish the heat and mass transports.