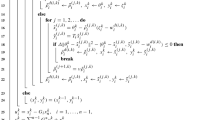Abstract
This work describes a new variant of projective splitting for solving maximal monotone inclusions and complicated convex optimization problems. In the new version, cocoercive operators can be processed with a single forward step per iteration. In the convex optimization context, cocoercivity is equivalent to Lipschitz differentiability. Prior forward-step versions of projective splitting did not fully exploit cocoercivity and required two forward steps per iteration for such operators. Our new single-forward-step method establishes a symmetry between projective splitting algorithms, the classical forward–backward splitting method (FB), and Tseng’s forward-backward-forward method. The new procedure allows for larger stepsizes for cocoercive operators: the stepsize bound is \(2\beta\) for a \(\beta\)-cocoercive operator, the same bound as has been established for FB. We show that FB corresponds to an unattainable boundary case of the parameters in the new procedure. Unlike FB, the new method allows for a backtracking procedure when the cocoercivity constant is unknown. Proving convergence of the algorithm requires some departures from the prior proof framework for projective splitting. We close with some computational tests establishing competitive performance for the method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Problem statement
For a collection of real Hilbert spaces \(\{\mathcal {H}_i\}_{i=0}^n\) consider the finite-sum convex minimization problem:
where every \(f_i:\mathcal {H}_i\rightarrow (-\infty ,+\infty ]\) and \(h_i:\mathcal {H}_i\rightarrow \mathbb {R}\) is closed, proper, and convex, every \(h_i\) is also differentiable with \(L_i\)-Lipschitz-continuous gradients, and the operators \(G_i:\mathcal {H}_0\rightarrow \mathcal {H}_i\) are linear and bounded. Under appropriate constraint qualifications, (1) is equivalent to the monotone inclusion problem of finding \(z\in \mathcal {H}_0\) such that
where all \(A_i:\mathcal {H}_i\rightarrow 2^{\mathcal {H}_i}\) and \(B_i:\mathcal {H}_i\rightarrow \mathcal {H}_i\) are maximal monotone and each \(B_i\) is \(L_i^{-1}\)-cocoercive, meaning that it is single-valued and
for some \(L_i\ge 0\). (When \(L_i=0\), \(B_i\) must be a constant operator, that is, there is some \(v_i\in \mathcal {H}_i\) such that \(B_i x = v_i\) for all \(x\in \mathcal {H}_i\). ) In particular, if we set \(A_i = \partial f_i\) (the subgradient map of \(f_i\)) and \(B_i = \nabla h_i\) (the gradient of \(h_i\)) then the solution sets of the two problems coincide under a special case of the constraint qualification of [8, Prop. 5.3].
Defining \(T_i = A_i + B_i\) for all i, problem (2) may be written as
This more compact problem statement will be used occasionally in our analysis below.
1.2 Background
Operator splitting algorithms are an effective way to solve structured convex optimization problems and monotone inclusions such as (1), (2), and (3). Their defining feature is that they decompose a problem into a set of manageable pieces. Each iteration consists of relatively easy calculations confined to each individual component of the decomposition, in conjunction with some simple coordination operations orchestrated to converge to a solution. Arguably the three most popular classes of operator splitting algorithms are the forward–backward splitting (FB) [10], Douglas/Peaceman-Rachford splitting (DR) [24], and forward-backward-forward (FBF) [37] methods. Indeed, many algorithms in convex optimization and monotone inclusions are in fact instances of one of these methods. The popular Alternating Direction Method of Multipliers (ADMM), in its standard form, can be viewed as a dual implementation of DR [18].
Projective splitting is a relatively recent and currently less well-known class of operator splitting methods, operating in a primal-dual space. Each iteration k of these methods explicitly contructs an affine “separator” function \(\varphi _k\) for which \(\varphi _k(p) \le 0\) for every p in the set \(\mathcal {S}\) of primal-dual solutions. The next iterate \(p^{k+1}\) is then obtained by projecting the current iterate \(p^k\) onto the halfspace defined by \(\varphi _k(p) \le 0\), possibly with some over-relaxation or under-relaxation. Crucially, \(\varphi _k\) is obtained by performing calculations that consider each operator \(T_i\) separately, so that the procedures are indeed operator splitting algorithms. In the original formulations of projective splitting [16, 17], the calculation applied to each operator \(T_i\) was a standard resolvent operation, also known as a “backward step”. Resolvent operations remained the only way to process individual operators as projective splitting was generalized to cover compositions of maximal monotone operators with bounded linear maps [1]—as in the \(G_i\) in (3)—and block-iterative (incremental) or asynchronous calculation patterns [9, 15]. Convergence rate and other theoretical results regarding projective splitting may be found in [20, 21, 26, 27].
The algorithms in [19, 36] were the first to construct projective splitting separators by applying calculations other than resolvent steps to the operators \(T_i\). In particular, [19] developed a procedure that could instead use two forward (explicit or gradient) steps for operators \(T_i\) that are Lipschitz continuous. However, that result raised a question: if projective splitting can exploit Lipschitz continuity, can it further exploit the presence of cocoercive operators? Cocoercivity is in general a stronger property than Lipschitz continuity. However, when an operator is the gradient of a closed proper convex function (such as \(h_i\) in (1)), the Baillon–Haddad theorem [2, 3] establishes that the two properties are equivalent: \(\nabla h_i\) is \(L_i\)-Lipschitz continuous if and only if it is \(L_i^{-1}\)-cocoercive.
Operator splitting methods that exploit cocoercivity rather than mere Lipschitz continuity typically have lower per-iteration computational complexity and a larger range of permissible stepsizes. For example, both FBF and the extragradient (EG) method [23] only require Lipchitz continuity, but need two forward steps per iteration and limit the stepsize to \(L^{-1}\), where L is the Lipschitz constant. If one strengthens the assumption to \(L^{-1}\)-cocoercivity, one can instead use FB, which only needs one forward step per iteration and allows stepsizes bounded away from \(2L^{-1}\). One departure from this pattern is the recently developed method of [29], which only requires Lipschitz continuity but uses just one forward step per iteration. While this property is remarkable, it should be noted that its stepsizes must be bounded by \((1/2)L^{-1}\), which is half the allowable stepsize for EG or FBF and just a fourth of FB’s stepsize range.
Much like EG and FBF, the projective splitting computation in [19] requires Lipschitz continuity,Footnote 1 two forward steps per iteration, and limits the stepsize to be less than \(L^{-1}\) (when not using backtracking). Considering the relationship between FB and FBF/EG leads to the following question: is there a variant of projective splitting which converges under the stronger assumption of \(L^{-1}\)-cocoercivity, while processing each cocoercive operator with a single forward step per iteration and allowing stepsizes bounded above by \(2L^{-1}\)?
This paper shows that the answer to this question is “yes”. Referring to (2), the new procedure analyzed here requires one forward step on \(B_i\) and one resolvent for \(A_i\) at each iteration. In the context of (1), the new procedure requires one forward step on \(\nabla h_i\) and one proximal operator evaluation on \(f_i\). When the resolvent is easily computable (for example, when \(A_i\) is the zero map and its resolvent is simply the identity), the new procedure can effectively halve the computation necessary to run the same number of iterations as the previous procedure of [19]. This advantage is equivalent to that of FB over FBF and EG when cocoercivity is present. Another advantage of the proposed method is that it allows for a backtracking linesearch when the cocoercivity constant is unknown, whereas no such variant of general cocoercive FB is currently known.
The analysis of this new method is significantly different from our previous work in [19], using a novel “ascent lemma” (Lemma 17) regarding the separators generated by the algorithm. The new procedure also has an interesting connection to the original resolvent calculation used in the projective splitting papers [1, 9, 16, 17]: in Section 2.2 below, we show that the new procedure is equivalent to one iteration of FB applied to evaluating the resolvent of \(T_i = A_i+B_i\). That is, we can use a single forward–backward step to approximate the operator-processing procedure of [1, 9, 16, 17], but still obtain convergence.
The new procedure has significant potential for asynchronous and incremental implementation following the ideas and techniques of previous projective splitting methods [9, 15, 19]. To keep the analysis relatively manageable, however, we plan to develop such generalizations in follow-up work. Here, we will simply assume that every operator is processed once per iteration.
1.3 The optimization context
For optimization problems of the form (1), our proposed method is a first-order proximal splitting method that “fully splits” the problem: at each iteration, it utilizes the proximal operator for each nonsmooth function \(f_i\), a single evaluation of the gradient \(\nabla h_i\) for each smooth function \(h_i\), and matrix-vector multiplications involving \(G_i\) and \(G_i^*\). There is no need for any form of matrix inversion, nor to use resolvents of composed functions like \(f_i \circ G_i\), which may in general be much more challenging to evaluate than resolvents of the \(f_i\). Thus, the method achieves the maximum possible decoupling of the elements of (1). There are also no assumptions on the rank, row spaces, or column spaces of the \(G_i\). Beyond the basic resolvent, gradient, and matrix-vector multiplication operations invoked by our algorithm, the only computations at each iteration are a constant number of inner products, norms, scalar multiplications, and vector additions, all of which can all be carried out within flop counts linear in the dimension of each Hilbert space.
Besides projective splitting approaches, there are a few first-order proximal splitting methods that can achieve full splitting on (1). The most similar to projective splitting are those in the family of primal-dual (PD) splitting methods; see [7, 11, 12, 32] and references therein. In fact, projective splitting is also a kind of primal-dual method, since it produces primal and dual sequences jointly converging to a primal-dual solution. However, the convergence mechanisms are different: PD methods are usually constructed by applying an established operator splitting technique such as FB, FBF, or DR to an appropriately formulated primal-dual inclusion in a primal-dual product space, possibly with a specially chosen metric. Projective splitting methods instead work by projecting onto (or through) explicitly constructed separating hyperplanes in the primal-dual space.
There are several potential advantages of our proposed method over the more established PD schemes. First, unlike the PD methods, the norms \(\Vert G_i\Vert\) do not effect the stepsize constraints of our proposed method, making such constraints easier to satisfy. Furthermore, projective splitting’s stepsizes may vary at each iteration and may differ for each operator. In general, projective splitting methods allow for asynchronous parallel and incremental implementations in an arguably simpler way than PD methods (although we do not develop this aspect of projective splitting in this paper). Projective splitting methods can incorporate deterministic block-iterative and asynchronous assumptions [9, 15], resulting in deterministic convergence guarantees, with the analysis being similar to the synchronous case. In contrast, existing asynchronous and block-coordinate analyses of PD methods require stochastic assumptions which only lead to probabilistic convergence guarantees [32].
1.4 Notation and a simplifying assumption
For the definition of maximal monotone operators and their basic properties, we refer to [4]. For any maximal monotone operator A and scalar \(\rho > 0\), we will use the notation \(J_{\rho A} \triangleq (I+\rho A)^{-1},\) to denote the resolvent operator, also known as the backward or implicit step with respect to A. Thus,
the x and a satisfying this relation being unique. Furthermore, \(J_{\rho A}\) is defined everywhere and \(\text {range}(J_A) = \text {dom}(A)\) [4, Prop. 23.2]. If \(A = \partial f\) for a closed, convex, and proper function f, the resolvent is often referred to as the proximal operator and written as \(J_{\rho \partial f}={\text {prox}}_{\rho f}\). Computing the proximal operator requires solving
Many functions encountered in applications to machine learning and signal processing have proximal operators which can be computed exactly with low computational complexity. In this paper, for a single-valued maximal monotone operator A, a forward step (also known as an explicit step) refers to the direct evaluation of Ax (or \(\nabla f(x)\) in convex optimization) as part of an algorithm.
For the rest of the paper, we will impose the simplifying assumption
As noted in [19], the requirement that \(G_n = I\) is not a very restrictive assumption. For example, one can always enlarge the original problem by one operator, setting \(A_n=B_n=0\).
2 A new form of projective splitting
2.1 Projective splitting basics in detail
Returning attention to the compact form of the problem written in (3), the goal of our algorithm will be to find a point in
It is clear that \(z^*\) solves (3) if and only if there exist \(w_1^*,\ldots ,w_{n-1}^*\) such that \((z^*,w_1^*,\ldots ,w_{n-1}^*)\in \mathcal {S}\). Under reasonable assumptions, the set \(\mathcal {S}\) is closed and convex; see Lemma 2. \(\mathcal {S}\) is often called the Kuhn-Tucker solution set of problem (3), and essentially consists of all primal-dual solution pairs for the problem.
At each iteration k, projective splitting algorithms work by using a decomposition procedure to construct a halfspace \(H_k \subset \varvec{\mathcal {H}} \triangleq \mathcal {H}_0\times \mathcal {H}_1\times \cdots \times \mathcal {H}_{n-1}\) that is guaranteed to contain \(\mathcal {S}\). Each new iterate \(p^{k+1} \in \varvec{\mathcal {H}}\) is obtained by projecting the previous iterate \(p^k = (z^{k},w_1^{k},\ldots ,w_{n-1}^{k}) \in \varvec{\mathcal {H}}\) onto \(H_k\), with possible over-relaxation or under-relaxation.
With \(\mathcal {S}\) as in (5), the separator formulation presented in [9] constructs the halfspace \(H_k\) using the function \(\varphi _k:\varvec{\mathcal {H}}\rightarrow \mathbb {R}\) defined as
for some auxiliary points (\(x_i^k,y_i^k) \in \mathcal {H}_i^2\). These points (\(x_i^k,y_i^k\)) will be specified later and must be chosen at each iteration in a specific manner guaranteeing the validity of the separator and convergence to \(\mathcal {S}\). Among other properties, they must be chosen so that \(y^k_i\in T_i x^k_i\) for \(i = 1,\ldots ,n\). Under this condition, it follows readily that \(\varphi _k\) has the promised separator properties:
Lemma 1
The function \(\varphi _k\) defined in (6) is affine, and if \(y^k_i\in T_i x^k_i\) for all \(i = 1,\ldots ,n\), then \(\varphi _k(z,w_1,\ldots ,w_{n-1}) \le 0\) for all \((z,w_1,\ldots ,w_{n-1}) \in \mathcal {S}\).
Proof
That \(\varphi _k\) is affine is clear from its expression in (7). Now suppose that \(y^k_i\in T_i x^k_i\) for all \(i = 1,\ldots ,n\) and \(p = (z,w_1,\ldots ,w_{n-1}) \in \mathcal {S}\). Then
where \(w_n \triangleq -\sum _{i=1}^{n-1} G_i^* w_i.\) From \((z,w_1,\ldots ,w_{n-1}) \in \mathcal {S}\) and the definition of \(\mathcal {S}\), one has that \(w_i \in T_i z\) for all \(i=1,\ldots ,n-1\), as well as \(w_n \in T_n z\). Since \(y_i \in T_i x_i\) for \(i=1,\ldots ,n\), it follows from the monotonicity of \(T_1,\ldots ,T_n\) that every inner product displayed in (8) is nonnegative, and so \(\varphi _k(p) \le 0\). \(\square\)
Properties of the hyperplane \(\left\{ p\in \varvec{\mathcal {H}} \; \left| \;\; \varphi _k(p) = 0 \right. \right\}\) obtained from the affine function \(\varphi _k\). This hyperplane is the boundary of the halfspace \(H_k\), and it always holds that \(\varphi _k(p^*) \le 0\) for every \(p^*\in \mathcal {S}\). When \(\varphi _k(p^k) > 0\) (as shown), the hyperplane separates the current point \(p^k\) from the solution set \(\mathcal {S}\)
The basic operation of the method. Each iteration k constructs a separator \(\varphi _k\) as shown in Fig. 1 and then obtains the next iteration by projecting onto the halfspace \(H_k = \left\{ p\in \varvec{\mathcal {H}} \; \left| \;\; \varphi _k(p) \le 0 \right. \right\}\), within which the solution set \(\mathcal {S}\) is known to lie
Figure 1 presents a rough depiction of the current algorithm iterate \(p^k = (z^{k},w_1^{k},\ldots ,w_{n-1}^{k})\) and the separator \(\varphi _k\) in the case that \(\varphi _k(p^k) > 0\). The basic iterative cycle pursued by projective splitting methods is:
-
1
For each operator \(T_i\), identify a pair \((x_i^k,y_i^k)\in {{\,\mathrm{gra}\,}}T_i\). These pairs define an affine function \(\varphi _k\) such that \(\varphi _k(p) \le 0\) for all \(p\in \mathcal {S}\), using the construction (6) (or related constructions for variations of the basic problem formulation).
-
2
Obtain the next iterate \(p^{k+1}\) by projecting the current iterate \(p^k\) onto the halfspace \(H_k \triangleq \left\{ p \; \left| \;\; \varphi _k(p) \le 0 \right. \right\}\), with possible over—or under-relaxation.
Figure 2 presents a rough depiction of two iterations of this process in the absence of over-relaxation or under-relaxation. The projection operation in part 2 of the cycle is a straightforward application of standard formulas for projecting onto a halfspace. For the particular formulation (3), the necessary calculations are derived in [19] and displayed in Algorithm 3 below. This projection is a low-complexity operation involving only inner products, norms, matrix multiplication by \(G_i\), and sums of scalars. For example, when \(\mathcal {H}_i=\mathbb {R}^d\) for \(i=1,\ldots ,n\) and each \(G_i=I\), then the projection step has computational complexity \({{\,\mathrm{O}\,}}(nd)\).
The key question in the design of algorithms in this class therefore concerns step 1 in the cycle: how might one select the points \((x_i^k,y_i^k)\in {{\,\mathrm{gra}\,}}T_i\) so that convergence to \(\mathcal {S}\) may be established? The usual approach has been to choose \((x^k_i,y^k_i)\in {{\,\mathrm{gra}\,}}T_i\) to be some function of \((z^k,w_i^k)\) such that \(\varphi _k(p^k)\) is positive and “sufficiently large” whenever \(p^k \not \in \mathcal {S}\). Then projecting the current point onto this hyperplane makes progress toward the solution and can be shown to lead (with some further analysis) to overall convergence. In the original versions of projective splitting, the calculation of \((x^k_i,y^k_i)\) involved (perhaps approximately) evaluating a resolvent; later [19] introduced the alternative of a two-forward-step calculation for Lipschitz continuous operators that achieved essentially the same sufficient separation condition.
Here, we introduce a one-forward-step calculation for the case of cocoercive operators. A principal difference between this analysis and earlier work on projective splitting is that processing all the operators \(T_1,\ldots ,T_n\) at iteration k need not result in \(\varphi _k(p^k)\) being positive. Instead, we establish an “ascent lemma” that relates the values \(\varphi _k(p^{k})\) and \(\varphi _{k-1}(p^{k-1})\) in such a way that overall convergence may still be proved, even though it is possible that \(\varphi _k(p^k) \le 0\) at some iterations k. In particular, \(\varphi _k(p^k)\) will be larger than the previous value \(\varphi _{k-1}(p^{k-1})\), up to some error term that vanishes as \(k\rightarrow \infty\).
When \(\varphi _k(p^k) \le 0\), projection onto \(H_k = \left\{ p \; \left| \;\; \varphi _k(p) \le 0 \right. \right\}\) results in \(p^{k+1} = p^k\). In this case, the algorithm continues to compute new points \((x_i^{k+1},y_i^{k+1})\), \((x_i^{k+2},y_i^{k+2}),\ldots\) until, for some \(\ell \ge 0\), it constructs a hyperplane \(H_{k+\ell }\) such that the \(\varphi _{k+\ell }(p^k) > 0\) and projection results in \(p^{k+\ell +1} \ne p^{k+\ell } = p^k\).
2.1.1 Additional notation for projective splitting
For an arbitrary \((w_1,w_2,\ldots ,w_{n-1}) \in \mathcal {H}_1\times \mathcal {H}_2\times \ldots \times \mathcal {H}_{n-1}\) we use the notation
as in the Proof of Lemma 1. Note that when \(n=1\), \(w_1=0\). Under the above convention, we may write \(\varphi _k:\varvec{\mathcal {H}}\rightarrow \mathbb {R}\) in the more compact form
We also use the following notation for \(i=1,\ldots ,n\):
Note that \(\varphi _k(z,w_1,\ldots ,w_{n-1})=\sum _{i=1}^n \varphi _{i,k}(z,w_i)\).
2.2 The new procedure
Recall the original problem of interest (2), which is related to (3) via \(T_i = A_i + B_i\). At each iteration k and for each block \(i=1,\ldots ,n\), we propose to find a pair \((x_i^k,y_i^k)\in {{\,\mathrm{gra}\,}}T_i = {{\,\mathrm{gra}\,}}(A_i+B_i)\) conforming to the conditions
where \(\alpha _i\in (0,1)\), \(\rho _i\le 2(1-\alpha _i)/L_i\), and \(b_i^0 = B_i x_i^0\). Condition (9) is readily satisfied by some simple linear algebra calculations and a resolvent calculation involving \(A_i\). In particular, referring to (4), one may see that (9) is equivalent to computing
Following this resolvent calculation, (10) requires only an evaluation (forward step) on \(B_i\), and (11) is a simple vector addition.
The parameter \(\rho _i\) plays the role of the stepsize in the resolvent calculation. It also plays the role of a forward (gradient) stepsize, since it multiplies \(-b_i^{k-1}\) in (9), and \(b_i^{k-1}=B_i x_i^{k-1}\) by (10). From the assumptions on \(\alpha _i\) and \(\rho _i\) immediately following (11), it follows that \(\rho _i\) may be made arbitrarily close to \(2/L_i\) by setting \(\alpha _i\) close to 0. However, in practice it may be better to use an intermediate value, such as \(\alpha _i=0.1\), since doing so causes the update to make significant use of the information in \(z^k\), a point computed more recently than \(x_i^{k-1}\).
Computing \((x_i^k,y_i^k)\) as proposed in (9)–(11) does not guarantee that the quantity \(\varphi _{i,k}(z^k,w_i^k)\) is positive. In the remainder of this section, we give some intuition as to why (9)–(11) nevertheless leads to convergence to \(\mathcal {S}\).
In the projective splitting literature preceeding [19], the pairs \((x_i^k, y_i^k)\) are solutions of
for some \(\rho _i>0\), which—again following (4)—is a resolvent calculation. Since the stepsize \(\rho _i\) in (12) can be any positive number, let us replace \(\rho _i\) with \(\rho _i/\alpha _i\) for some \(\alpha _i\in (0,1)\) and rewrite (12) as
The reason for this reparameterization will become apparent below.
In this paper, \(T_i = A_i+B_i\), with \(B_i\) being cocoercive and \(A_i\) maximal monotone. For \(T_i\) in this form, computing the resolvent as in (12) exactly may be impossible, even when the resolvent of \(A_i\) is available. With this structure, \(x_i^k\) in (13) satisfies:
which can be rearranged to \(0\in A_i x_i^k +\tilde{B}_i x_i^k,\) where
Since \(B_i\) is \(L_i^{-1}\)-cocoercive, \(\tilde{B}_i\) is \((L_i+\alpha _i/\rho _i)^{-1}\)-cocoercive [4, Prop. 4.12]. Consider the generic monotone inclusion problem \(0\in A_i x +\tilde{B}_i x\): \(A_i\) is maximal and \(\tilde{B}_i\) is cocoercive, and thus one may solve the problem with the forward–backward (FB) method [4, Theorem 26.14]. If one applies a single iteration of FB initialized at \(x_i^{k-1}\), with stepsize \(\rho _i\), to the inclusion \(0\in A_i x +\tilde{B}_i x\), one obtains the calculation:
which is precisely the update (9). So, our proposed calculation is equivalent to one iteration of FB initialized at the previous point \(x_i^{k-1}\), applied to the subproblem of computing the resolvent in (13). Prior versions of projective splitting require computing this resolvent either exactly or to within a certain relative error criterion, which may be time consuming. Here, we simply make a single FB step toward computing the resolvent, which we will prove is sufficient for the projective splitting method to converge to \(\mathcal {S}\). However, our stepsize restriction on \(\rho _i\) will be slightly stronger than the natural stepsize limit that would arise when applying FB to \(0\in A_i x +\tilde{B}_i x\).
3 The algorithm
3.1 Main problem assumptions and preliminary results
Assumption 1
Problem (2) conforms to the following:
-
1
\(\mathcal {H}_0 = \mathcal {H}_n\) and \(\mathcal {H}_1,\ldots ,\mathcal {H}_{n-1}\) are real Hilbert spaces.
-
2
For \(i=1,\ldots ,n\), the operators \(A_i:\mathcal {H}_{i}\rightarrow 2^{\mathcal {H}_{i}}\) and \(B_i:\mathcal {H}_i\rightarrow \mathcal {H}_i\) are monotone. Additionally, each \(A_i\) is maximal.
-
3
Each operator \(B_i\) is either \(L_i^{-1}\)-cocoercive for some \(L_i>0\) and \({{\,\mathrm{dom}\,}}B_i = \mathcal {H}_i\), or \(L_i = 0\) and \(B_ix = v_i\) for all \(x\in \mathcal {H}_i\) and some \(v_i\in \mathcal {H}_i\) (that is, \(B_i\) is a constant function).
-
4
Each \(G_i:\mathcal {H}_{0}\rightarrow \mathcal {H}_i\) for \(i=1,\ldots ,n-1\) is linear and bounded.
-
5
Problem (2) has a solution, so the set \(\mathcal {S}\) defined in (5) is nonempty.
Problem (1) will be equivalent to an instance of Problem (2) satisfying Assumption 1 if each \(f_i\) and \(h_i\) is closed, convex, and proper, each \(h_i\) has \(L_i\)-Lipschitz continuous gradients, and a special case of the constraint qualification in [8, Prop. 5.3] holds.
Lemma 2
Suppose Assumption 1holds. The set \(\mathcal {S}\) defined in (5) is closed and convex.
Proof
By [4, Cor. 20.28] each \(B_i\) is maximal. Furthermore, since \({{\,\mathrm{dom}\,}}(B_i)=\mathcal {H}_i\), \(T_i=A_i+B_i\) is maximal monotone by [4, Cor. 25.5(i)]. The rest of the proof is identical to [19, Lemma 3]. \(\square\)
Throughout, we will use \(p =(z,\mathbf{w}) = (z,w_1,\ldots , w_{n-1})\) for a generic point in \(\varvec{\mathcal {H}}\), the collective primal-dual space. For \(\varvec{\mathcal {H}}\), we adopt the following (standard) norm and inner product:
Lemma 3
[19, Lemma 4] Let \(\varphi _k\) be defined as in (6). Then:
-
1
\(\varphi _k\) is affine on \(\varvec{\mathcal {H}}\).
-
2
With respect to inner product \(\langle \cdot ,\cdot \rangle\) on \(\varvec{\mathcal {H}}\), the gradient of \(\varphi _k\) is
$$\begin{aligned} \nabla \varphi _k = \left( \sum _{i=1}^{n-1} G_i^* y_i^k+ y_n^k, x_1^k - G_1 x_{n}^k,x_2^k - G_2 x_{n}^k,\ldots ,x_{n-1}^k - G_{n-1} x_{n}^k\right) . \end{aligned}$$
3.2 Abstract one-forward-step update
We sharpen the notation for the one-forward-step update introduced in (9)–(11) as follows:
Definition 1
Suppose \(\mathcal {H}\) and \(\mathcal {H}'\) are real Hilbert spaces, \(A:{\mathcal {H}}\rightarrow 2^{{\mathcal {H}}}\) is maximal-monotone with nonempty domain, \(B:\mathcal {H}\rightarrow \mathcal {H}\) is \(L^{-1}\)-cocoercive, and \(G:\mathcal {H}'\rightarrow \mathcal {H}\) is bounded and linear. For \(\alpha \in [0,1]\) and \(\rho >0\), define the mapping \(\mathcal {F}_{\alpha ,\rho }(z,x,w;A,B,G):\mathcal {H}'\times \mathcal {H}^2\rightarrow \mathcal {H}^2\), with additional parameters A, B, and G, as
To simplify the presentation, we will also use the notation
With this notation, (9)–(11) may be written as \((x_i^k,y_i^k) = \mathcal {F}^i(z^k,x_i^{k-1},w_i^k).\)



3.3 Algorithm definition
Algorithms 1–3 define the main method proposed in this work. They produce a sequence of primal-dual iterates \(p^k = (z^k,w_1^k,\ldots ,w_{n-1}^k)\in \varvec{\mathcal {H}}\) and, implicitly, \(w_n^k \triangleq -\sum _{i=1}^{n-1} G_i^* w_i^k\). Algorithm 1 gives the basic outline of our method; for each operator, it invokes either our new one-forward-step update with a user-defined stepsize (through line 6) or its backtracking variant given in Algorithm 2 (through line 4). Together, Algorithms 1–2 specify how to update the points \((x_i^k,y_i^k)\) used to define the separating affine function \(\varphi _k\) in (6). Algorithm 3, called from line 7 of Algorithm 1, defines the projectToHplane function that performs the projection step to obtain the next iterate.
Taken together, Algorithms 1–3 are essentially the same as Algorithm 2 of [19], except that the update of \((x_i^k,y_i^k)\) uses the new procedure given in (9)–(11). For simplicity, the algorithm also lacks the block-iterative and asynchronous features of [9, 15, 19], which we plan to combine with Algorithms 1–3 in future research.
The computations in projectToHplane are all straightforward and of relatively low complexity. They consist of matrix multiplies by \(G_i\), inner products, norms, and sums of scalars. In particular, there are no potentially difficult minimization problems involved. If \(G_i=I\) and \(\mathcal {H}_i = \mathbb {R}^d\) for \(i=1,\ldots ,n\), then the computational complexity of projectToHplane is \({{\,\mathrm{O}\,}}(nd)\).
3.4 Algorithm parameters
The method allows two ways to select the stepsizes \(\rho _i\). One may either choose them manually or invoke the backTrack procedure. If one decides to select the stepsizes manually, the upper bound condition \(\rho _i\le 2(1-\alpha _i)/L_i\) is required whenever \(L_i>0\). However, it may be difficult to ensure that this condition is satisfied when the cocoercivity constant is hard to estimate. The global cocoercivity constant \(L_i\) may also be conservative in parts of the domain of \(B_i\), leading to unnecessarily small stepsizes in some cases. We developed the backtracking linesearch technique for these reasons. The set \(\mathcal {B}\) holds the indices of operators for which backtracking is to be used.
For a trial stepsize \(\tilde{\rho }_{j}\), Algorithm 2 generates candidate points \((\tilde{x}_{j},\tilde{y}_{j})\) using the single-forward-step procedure of (15). For these candidates, Algorithm 2 checks two conditions on lines 10–11. If both of these inequalities are satisfied, then backtracking terminates and returns the successful candidate points. If either condition is not satisfied, the stepsize is reduced by the factor \(\delta \in (0,1)\) and the process is repeated. These two conditions arise in the analysis in Sect. 5.
The parameter \(\hat{\rho }\) is a global upper bound on the stepsizes (both backtracked and fixed) and must be chosen to satisfy Assumption 2. In backTrack, one must choose an initial trial stepsize within a specified interval (line 5 of Algorithm 2). This interval arises in the analysis (see Lemmas 16 and 17). Written in terms of the parameters passed into backTrack in the call on line 4 of Algorithm 1, and assuming the global upper bound \(\hat{\rho }\) is sufficiently large to not be active on line 5, the interval is
An obvious choice is to set the initial stepsize to be at the upper limit of the interval. In practice we have observed that \(\Vert y_i^k - w_i^k\Vert\) and \(\Vert \hat{y}_i^k - w_i^k\Vert\) tend to be approximately equal, so this allows for an increase in the trial stepsize by up to a factor of approximately \(1+\alpha _i\) over the previous stepsize.
Note that backTrack returns the chosen stepsize \(\tilde{\rho }_j\) as well as the quantity \(\eta\) which are needed to compute the available interval in the call to backTrack during the next iteration.
In the analysis it will be convenient to let \(\tilde{\rho }^{(i,k)}\) be the initial trial stepsize chosen during iteration k of Algorithm 1, when backTrack has been called through line 4 for some \(i\in \mathcal {B}\).
We call the stepsize returned by backTrack \(\rho _i^k\). Assuming that backTrack always terminates finitely (which we will show to be the case), we may write for \(i\in \mathcal {B}\)
The only difference between the update for \(i\in \mathcal {B}\) on line 6 and this update for \(i\notin \mathcal {B}\) is that in the former, the stepsize \(\rho _i^k\) is discovered by backtracking, while in the latter it is directly user-supplied.
The backTrack procedure computes several auxiliary quantities used to check the two backtracking termination conditions. The point \(\hat{y}_{j}\) is calculated to be the same as \(\hat{y}\) given in Definition 2. The quantity \(\varphi _j^+ = \langle G z - \tilde{x}_{j},\tilde{y}_{j} - w\rangle\) is the value of \(\varphi _{i,k}(z^k,w_i^k)\) corresponding to the candidate points \((\tilde{x}_{j},\tilde{y}_{j})\). The quantity \(\varphi\) computed on line 3 is equal to \(\varphi _{i,k-1}(z^k,w_i^k) = \langle G_i z^k - x_i^{k-1},y_i^{k-1} - w_i^k\rangle\). Typically, we want \(\varphi _j^+\) to be as large as possible to get a deeper cut with the separating hyperplane, but the condition checked on line 11 will ultimately suffice to prove convergence.
Algorithm 1 has several additional parameters.
- \((\hat{\theta }_i,\hat{w}_i)\):
-
these are used in the backtracking procedure for \(i\in \mathcal {B}\). An obvious choice which we used in our numerical experiments was \((\hat{\theta }_i,\hat{w}_i) = (x_i^0,y_i^0)\), i.e. the initial point.
- \(\gamma >0\)::
-
allows for the projection to be performed using a slightly more general primal-dual metric than (14). In effect, this parameter changes the relative size of the primal and dual updates in lines 10–11 of Algorithm 3. As \(\gamma\) increases, a smaller step is taken in the primal and a larger step in the dual. As \(\gamma\) decreases, a smaller step is taken in the dual update and a larger step is taken in the primal. See [17, Sec. 5.1] and [16, Sec. 4.1] for more details.
In Algorithm 1, the averaging parameters \(\alpha _i\) and user-selected stepsizes \(\rho _i\) are fixed across all iterations. In the preprint version of this paper [22], we instead allow these parameters to vary by iteration, subject to certain restrictions. Doing so complicates the notation and the analysis, so for relative simplicity we consider only fixed values of these parameter here. This simplification also accords with the parameter choices in our computational tests below. For the full, more complicated analysis, please refer to [22].
As written, Algorithm 1 is not as efficient as it could be. On the surface, it seems that we need to recompute \(B_i x_i^{k-1}\) in order to evaluate \(\mathcal {F}\) on line 6. However, \(B_i x_i^{k-1}\) was already computed in the previous iteration and can obviously be reused, so only one evaluation of \(B_i\) is needed per iteration. Similarly, within backTrack, each invocation of \(\mathcal {F}\) on line 7 may reuse the quantity \(B x = B_i x_i^{k-1}\) which was computed in the previous iteration of Algorithm 1. Thus, each iteration of the loop within backTrack requires one new evaluation of B, to compute \(B\tilde{x}_j\) within \(\mathcal {F}\).
We now precisely state our stepsize assumption for the manually chosen stepsizes, as well as the stepsize upper bound \(\hat{\rho }\).
Assumption 2
For \(i\notin \mathcal {B}\): If \(L_i>0\), then \(0<\rho _i\le 2(1-\alpha _i)/L_i,\) otherwise \(\rho _i>0\). The parameter \(\hat{\rho }\) must satisfy
Note that if \(L_i>0\), Assumption 2 effectively limits \(\alpha _i\) to be strictly less than 1, otherwise the stepsize \(\rho _i\) would be forced to 0, which is prohibited. In this case \(\alpha _i\) must be chosen in (0, 1). On the other hand, if \(L_i=0\), there is no constraint on \(\rho _i\) other than that it is positive and nonzero, and in this case \(\alpha _i\) may be chosen in (0, 1].
3.5 Separator-projector properties
Lemma 4 details the key results for Algorithm 1 that stem from it being a seperator-projector algorithm. While these properties alone do not guarantee convergence, they are important to all of the arguments that follow.
Lemma 4
Suppose that Assumption 1holds. Then for Algorithm 1
-
1
The sequence \(\{p^k\}=\{(z^k,w_1^k,\ldots ,w_{n-1}^k)\}\) is bounded.
-
2
If the algorithm never terminates via line 9, \(p^k - p^{k+1}\rightarrow 0\). Furthermore \(z^k - z^{k-1}\rightarrow 0\) and \(w_i^k - w_i^{k-1}\rightarrow 0\) for \(i=1,\ldots n\).
-
3
If the algorithm never terminates via line 9 and \(\Vert \nabla \varphi _k\Vert\) remains bounded for all \(k\ge 1\), then \(\limsup _{k\rightarrow \infty }\varphi _k(p^k)\le 0\).
Proof
Parts 1–2 are proved in lemmas 2 and 6 of [19]. Part 3 can be found in Part 1 of the proof of Theorem 1 in [19]. The analysis in [19] uses a different procedure to construct the pairs \((x_i^k,y_i^k)\), but the result is generic and not dependent on that particular procedure. Note also that [19] establishes the results in a more general setting allowing asynchrony and block-iterativeness, which we do not analyze here. \(\square\)
4 The special case \(n=1\)
Before starting the analysis, we consider the important special case \(n=1\). In this case, we have by assumption that \(G_1=I\), \(w_1^k=0\), and we are solving the problem \(0\in A z + B z,\) where both operators are maximal monotone and B is \(L^{-1}\)-cocoercive. In this case, Algorithm 1 reduces to a method which is similar to FB. Let \(x^k\triangleq x_1^k\), \(y^k\triangleq y_1^k\), \(\alpha \triangleq \alpha _1\), and \(\rho \triangleq \rho _1\). Assuming for simplicity that \(\mathcal {B}=\{\emptyset \}\), meaning backtracking is not being used, then the updates carried out by the algorithm are
If \(\alpha =0\), then for all \(k\ge 2\), the iterates computed in (18) reduce simply to
which is exactly FB. However, \(\alpha =0\) is not allowed in our analysis. Thus, FB is a forbidden boundary case which may be approached by setting \(\alpha\) arbitrarily close to 0. As \(\alpha\) approaches 0, the stepsize constraint \(\rho \le 2(1-\alpha )/L\) approaches the classical stepsize constraint for FB: \(\rho \le 2/L-\epsilon\) for some arbitrarily small constant \(\epsilon >0\). A potential benefit of Algorithm 1 over FB in the \(n=1\) case is that it does allow for backtracking when L is unknown or only a conservative estimate is available.
5 Main proof
The core of the proof strategy will be to establish (19) below. If this can be done, then weak convergence to a solution follows from part 3 of Theorem 1 in [19].
Lemma 5
Suppose Assumption 1holds and Algorithm 1 produces an infinite sequence of iterations without terminating via Line 9. If
then there exists \((\overline{z},\overline{\mathbf{w}})\in \mathcal {S}\) such that \((z^k,\mathbf{w}^k)\rightharpoonup (\overline{z},\overline{\mathbf{w}})\). Furthermore, we also have \(x_i^k\rightharpoonup G_i {\bar{z}}\) and \(y_i^k\rightharpoonup \overline{w}_i\) for all \(i=1,\ldots ,n-1\), \(x_{n}^k\rightharpoonup {\bar{z}}\), and \(y_n^k\rightharpoonup -\sum _{i=1}^{n-1}G_i^* \overline{w}_i\).
Proof
Equivalent to part 3 of the Proof of Theorem 1 in [19].\(\square\)
In order to establish (19), we start by establishing certain contractive and “ascent” properties for the mapping \(\mathcal {F}\), and also show that the backtracking procedure terminates finitely. Then, we prove the boundedness of \(x_i^k\) and \(y_i^k\), in turn yielding the boundedness of the gradients \(\nabla \varphi _k\) and hence the result that \(\limsup _{k\rightarrow \infty }\{\varphi _k(p^k)\}\le 0\) by Lemma 4. Next we establish a “Lyapunov-like” recursion for \(\varphi _{i,k}(z^k,w_i^k)\), relating \(\varphi _{i,k}(z^k,w_i^k)\) to \(\varphi _{i,k-1}(z^{k-1},w_i^{k-1})\). Eventually this result will allow us to establish that \(\liminf _k\varphi _k(p^k)\ge 0\) and hence that \(\varphi _k(p^k)\rightarrow 0\), which will in turn allow an argument that \(y_i^k-w_i^k\rightarrow 0\). The proof that \(G_i z^k - x_i^k\rightarrow 0\) will then follow fairly elementary arguments.
The primary innovations of the upcoming proof are the ascent lemma and the way that it is used in Lemma 18 to establish \(\varphi _k(p^k)\rightarrow 0\) and \(y_i^k-w_i^k\rightarrow 0\). This technique is a significant deviation from previous analyses in the projective splitting family. In previous work, the strategy was to show that \(\varphi _{i,k}(z^k,w_i^k)\ge C\max \{\Vert G_i z^k - x_i^k\Vert ^2,\Vert y_i^k - w_i^k\Vert ^2\}\) for a constant \(C>0\), which may be combined with \(\limsup \varphi _k(p^k)\le 0\) to imply (19). In contrast, in the algorithm of this paper we cannot establish such a result and in fact \(\varphi _{i,k}(z^k,w_i^k)\) may be negative.
We begin by stating three elementary results on sequences, which may be found in [33], and a basic, well known nonexpansivity property for forward steps with cocoercive operators.
Lemma 6
[33, Lemma 1, Ch. 2] Suppose that \(a_k\ge 0\) for all \(k\ge 1\), \(b\ge 0\), \(0\le \tau <1\), and \(a_{k+1}\le \tau a_k+b\) for all \(k\ge 1\). Then \(\{a_k\}\) is a bounded sequence.
Lemma 7
[33, Lemma 3, Ch. 2] Suppose that \(a_k\ge 0, b_k\ge 0\) for all \(k \ge 1\), \(b_k\rightarrow 0\), and there is some \(0\le \tau <1\) such that \(a_{k+1}\le \tau a_k + b_k\) for all \(k\ge 1\). Then \(a_k\rightarrow 0\).
Lemma 8
Suppose that \(0\le \tau <1\) and \(\{r_k\},\{b_k\}\) are sequences in \(\mathbb {R}\) with the properties \(b_k\rightarrow 0\) and \(r_{k+1}\ge \tau r_k + b_k\) for all \(k\ge 1\). Then \(\lim \inf _{k\rightarrow \infty } \{ r_k \} \ge 0\).
Proof
Negating the assumed inequality yields \(-r_{k+1}\le \tau (-r_k)- b_k\). Applying [33, Lemma 3, Ch. 2] then yields \(\lim \sup \{ -r_k\}\le 0\).\(\square\)
Lemma 9
Suppose B is \(L^{-1}\)-cocoercive and \(0\le \rho \le 2/L\). Then for all \(x,y\in {{\,\mathrm{dom}\,}}(B)\)
Proof
Squaring the left hand side of (20) yields
\(\square\)
5.1 Foundations: contractive and “ascent” properties of \(\mathcal {F}\)
Lemma 10
Suppose \((x^+,y^+) = \mathcal {F}_{\alpha ,\rho }(z,x,w;A,B,G)\), where \(\mathcal {F}_{\alpha ,\rho }\) is given in Definition 1. Recall that B is \(L^{-1}\)-cocoercive. If \(L=0\) or \(\rho \le 2(1-\alpha )/L\), then
for any \(\hat{\theta }\in {{\,\mathrm{dom}\,}}(A)\) and \(\hat{w}\in A \hat{\theta }+B\hat{\theta }\).
Proof
Select any \(\hat{\theta }\in {{\,\mathrm{dom}\,}}(A)\) and \(\hat{w} \in A\hat{\theta } + B\hat{\theta }\). Let \(\hat{a} = \hat{w} - B\hat{\theta } \in A\hat{\theta }\). It follows immediately from the definition of \(J_{\rho A}=(I+\rho A)^{-1}\) that
Therefore, (15) and (22) yield
To obtain (a), one uses the nonexpansivity of the resolvent [4, Prop. 23.8(ii)]. To obtain (b), one regroups terms and adds and subtracts \(B\hat{\theta }\). Then (c) follows from the triangle inequality. Finally we consider (d): If \(L>0\), apply Lemma 9 to the first term on the right-hand side of (23) with the stepsize \(\rho /(1-\alpha )\) which by assumption satisfies
Alternatively, if \(L=0\), implying that B is a constant-valued operator, then \(B x=B\hat{\theta }\) and (d) is just an equality.\(\square\)
Lemma 11
Suppose \((x^+,y^+) = \mathcal {F}_{\alpha ,\rho }(z,x,w;A,B,G)\), where \(\mathcal {F}_{\alpha ,\rho }\) is given in Definition 1. Recall B is \(L^{-1}\)-cocoercive. Let \(y\in Ax+Bx\) and define \(\varphi \triangleq \langle G z-x,y-w\rangle\). Further, define \(\varphi ^+\triangleq \langle G z - x^+,y^+ - w\rangle\), t as in (15), and \(\hat{y}\triangleq \rho ^{-1}(t-x^+)+B x\). If \(\alpha \in (0,1]\) and \(\rho \le 2(1-\alpha )/L\) whenever \(L>0\), then
Proof
Since \(y\in Ax+Bx\), there exists \(a\in Ax\) such that \(y=a+Bx\). Let \(a^+ \triangleq \rho ^{-1}(t-x^+)\). Note by (4) that \(a^+\in A x^+\). With this notation, \(\hat{y} = a^++B x\).
We may write the \(x^+\)-update in (15) as
which rearranges to
Adding Gz to both sides yields
Substituting this equation into the definition of \(\varphi ^+\) yields
We now focus on the second term in (26). Assume for now that \(L>0\) (we will deal with the \(L=0\) case below). We write
To derive (27) we substituted \((y^+,y) =(a^+ + B x^+,a+Bx)\) and for the following inequality we used the monotonicity of A and \(L^{-1}\)-cocoercivity of B (recall that \(a\in A x\) and \(a^+\in A x^+\)). Substituting the resulting inequality back into (26) yields
Subtracting \((1-\alpha )\varphi ^+\) from both sides of the above inequality produces
Using (25) once again, this time to the third term on the right-hand side of (29), we write
Substituting this equation back into (29) yields
We next use the identity \(\langle x_1,x_2\rangle = \frac{1}{2}\Vert x_1\Vert ^2+\frac{1}{2}\Vert x_2\Vert ^2-\frac{1}{2}\Vert x_1-x_2\Vert ^2\) on both inner products in (31), as follows:
and
Here we have used the identities
Using (32)–(33) in (31) yields
Consider this last expression: since \(\alpha \le 1\), the coefficient \((1-\alpha )\rho /2\) multiplying \(\Vert a^+ - a\Vert ^2\) is nonnegative. Furthermore, since \(\rho \le 2(1-\alpha )/L\), the coefficient multiplying \(\Vert B x^+ - B x\Vert ^2\) is positive. Therefore we may drop these two terms from the above inequality and divide by \(\alpha\) to obtain (24).
Finally, we deal with the case in which \(L = 0\), which implies that \(B x = v\) for some \(v\in \mathcal {H}\) for all \(x\in \mathcal {H}\). The main difference is that the \(\Vert B x^+ - Bx\Vert ^2\) terms are no longer present since \(B x^+ = B x\). The analysis is the same up to (26). In this case \(B x^+ = v\) so instead of (28) we may deduce from (27) that
Since \(B x^+=B x=v\) is constant we also have that
Thus, instead of (29) in this case we have the simpler inequality
The term \(\langle G z - x^+,w - y\rangle\) in (34) is dealt with just as in (29), by substitution of (25). This step now leads via (30) to
Once again using \(\langle x_1,x_2\rangle = \frac{1}{2}\Vert x_1\Vert ^2+\frac{1}{2}\Vert x_2\Vert ^2 - \frac{1}{2}\Vert x_1-x_2\Vert ^2\) on the second term on the right-hand side above yields
We can lower-bound the \(\Vert y^+ - y\Vert ^2\) term by 0. Dividing through by \(\alpha\) and rearranging, we obtain
Since \(y^+=\hat{y}\) in the \(L=0\) case, this is equivalent to (24).\(\square\)
5.2 Finite termination of backtracking
In all the following lemmas in Sects. 5.2 and 5.3 regarding algorithms 1–3, Assumptions 1 and 2 are in effect and will not be explicitly stated in each lemma. We start by proving that backTrack terminates in a finite number of iterations, and that the stepsizes it returns are bounded away from 0.
Lemma 12
For \(i\in \mathcal {B}\), Algorithm 2 terminates in a finite number of iterations for all \(k\ge 1\). There exists \(\underline{\rho }_i>0\) such that \(\rho _i^k\ge \underline{\rho }_i\) for all \(k\ge 1\), where \(\rho _i^k\) is the stepsize returned by Algorithm 2 on line 4. Furthermore \(\rho _i^k\le \hat{\rho }\) for all \(k\ge 1\).
Proof
Assume we are at iteration \(k\ge 1\) in Algorithm 1 and backTrack has been called through line 4 for some \(i\in \mathcal {B}\). The internal variables within backTrack are defined in terms of the variables passed from Algorithm 1 as follows: \(z=z^k\), \(x = x_i^{k-1}\), \(w=w_i^k\), \(y=y_i^{k-1}\), \(\rho = \rho _i^{k-1}\) and \(\eta = \eta _i^{k-1}\). Furthermore \(\alpha =\alpha _i\), \(\hat{\theta }=\hat{\theta }_i\), \(\hat{w}=\hat{w}_i\), \(A=A_i\), \(B=B_i\), and \(G=G_i\). The calculation on line 3 of Algorithm 2 yields \(\varphi = \varphi _{i,k-1}(z^k,w_i^k)\). In the following argument, we mostly refer to the internal name of the variables within backTrack without explicitly making the above substitutions. With that in mind, let \(L=L_i\) be the cocoercivity constant of \(B=B_i\).
Recall that \(\tilde{\rho }^{(i,k)}\) is the initial trial stepsize \(\tilde{\rho }_1\) chosen on line 5 of backTrack. We must establish that the interval on line 5 is always nonempty and so a valid initial stepsize can be chosen. Since \(\eta \alpha \ge 0\), this will be true if \(\hat{\rho }\ge \rho =\rho _i^{k-1}\), which we will prove by induction. Note that by Assumption 2, \(\hat{\rho }\ge \rho _i^0\) for all \(i\in \mathcal {B}\). Therefore for \(k=1\), \(\hat{\rho }\ge \rho =\rho _i^0\). We will prove the induction step below.
Observe that backtracking terminates via line 13 if two conditions are met. The first condition,
is identical to (21) of Lemma 10, with \(\tilde{x}_j\) and \(\tilde{\rho }_j\) respectively in place of \(x^+\) and \(\rho\). The initialization step of Algorithm 2 provides us with \(\hat{w}\in A\hat{\theta }+B\hat{\theta }\) for some \(\hat{\theta }\in {{\,\mathrm{dom}\,}}(A)\). Furthermore, since
the findings of Lemma 10 may be applied. In particular, if \(L > 0\) and \(\tilde{\rho }_j\le 2(1-\alpha )/L\), then (35) will be met. Alternatively, if \(L=0\), (35) will hold for any value of the stepsize \(\tilde{\rho }_j>0\).
Next, consider the second termination condition,
This relation is identical to (24) of Lemma 11, with \((\tilde{y}_j,\hat{y}_j,\tilde{\rho }_j)\) in place of \((y^+,\hat{y},\rho )\). However, to apply the lemma we must show that \(y=y_i^{k-1}\in A x_i^{k-1}+B x_i^{k-1}=A x+B x\). We will also prove this by induction.
For \(k=1\), \(y=y_i^{k-1}\in A x_i^{k-1}+B x_i^{k-1}=A x+B x\) holds by the initialization step of Algorithm 1. Now assume that at iteration \(k\ge 2\) it holds that \(y=y_i^{k-1}\in A x_i^{k-1}+B x_i^{k-1}=A x+B x\) and furthermore that \(\hat{\rho }\ge \rho =\rho _i^{k-1}\), therefore the interval on line 5 is nonempty. We may then apply the findings of Lemma 11 to conclude that if \(L > 0\) and \(\tilde{\rho }_j\le 2(1-\alpha )/L\), then condition (36) is satisfied. Or, if \(L=0\), condition (36) is satisfied for any \(\tilde{\rho }_j>0\).
Combining the above observations, we conclude that if \(L > 0\) and \(\tilde{\rho }_j\le 2(1-\alpha )/L\), backtracking will terminate for that iteration j of backTrack via line 13. Or, if \(L=0\), it will terminate in the first iteration of backTrack. The stepsize decrement condition on line 14 of the backtracking procedure implies that \(\tilde{\rho }_j\le 2(1-\alpha )/L\) will eventually hold for large enough j, and hence that the two backtracking termination conditions must eventually hold.
Let \(j^*\ge 1\) be the iteration at which backtracking terminates when called for operator i at iteration k of Algorithm 1. For the pair \((x_i^k,y_i^k)\) returned by backTrack on line 1 of Algorithm 1, we may write
Thus, by the definition of \(\mathcal {F}\) in (15), \(y_i^k\in A_i x_i^k + B_i x_i^k\). Therefore, induction establishes that \(y_i^k\in A_i x_i^k + B_i x_i^k\) holds for all \(k\ge 1\).
Now the returned stepsize must satisfy \(\rho _i^k=\tilde{\rho }_{j^*}\le \tilde{\rho }^{(i,k)}\le \hat{\rho }\). In the next iteration, \(\rho =\rho _i^{k}\le \hat{\rho }\). Thus we have also established by induction that \(\hat{\rho }\ge \rho =\rho _i^k\) and therefore that the interval on line 5 is nonempty for all iterations \(k\ge 1\). Finally, we now also infer by induction that backTrack terminates in a finite number of iterations for all \(k\ge 1\) and \(i\in \mathcal {B}\).
Now \(\tilde{\rho }^{(i,k)}\) must be chosen in the range
Since we have established that this interval remains nonempty, it holds trivially that \(\tilde{\rho }^{(i,k)}\ge \rho _i^{k-1}\). For all \(k\ge 1\) and \(i\in \mathcal {B}\), the returned stepsize \(\rho _i^k=\tilde{\rho }_{j^*}\) must satisfy
Therefore for all \(k\ge 1\) and all \(i\in \mathcal {B}\) such that \(L_i > 0\), one has
where the first inequality uses (37) and \(\tilde{\rho }^{(i,k)}\ge \rho _i^{k-1}\), the second inequality recurses, and the final inequality is just (37) for \(k=1\). If \(L_i=0\), the argument is simply
\(\square\)
5.3 Boundedness results and their direct consequences
Lemma 13
For all \(i=1,\ldots ,n\), the sequences \(\{x_i^k\}\) and \(\{y_i^k\}\) are bounded.
Proof
To prove this, we first establish that for \(i=1,\ldots ,n\) and \(k\ge 1\)
For \(i\in \mathcal {B}\), Lemma 12 establishes that backTrack terminates for finite \(j\ge 1\) for all \(k\ge 1\). For fixed \(k\ge 1\) and \(i\in \mathcal {B}\), let \(j^*\ge 1\) be the iteration of backTrack that terminates. At termination, the following condition is satisfied via line 10:
Into this inequality, now substitute in the following variables from Algorithm 1, as passed to and from backTrack: \(x_i^k = \tilde{x}_{j^*}\), \(\hat{\theta }_i=\hat{\theta }\), \(\alpha _i=\alpha\), \(x_i^{k-1}=x\), \(G_i=G\), \(z^k = z\), \(\rho _i^k = \tilde{\rho }_{j^*}\), \(w_i^k = w\), and \(\hat{w}_i = w\). Further noting that \(\rho _i^k\le \hat{\rho }\), the result is (38).
For \(i\notin \mathcal {B}\), we note that line 6 of Algorithm 1 reads as
and since Assumption 2 holds, we may apply Lemma 10. Further noting that by Assumption 2\(\rho _i\le \hat{\rho }\) we arrive at yield (38).
Since \(\{z^k\}\), and \(\{w_i^k\}\) are bounded by Lemma 4 and \(\Vert G_i\Vert\) is bounded by Assumption 1, boundedness of \(\{x_i^k\}\) now follows by applying Lemma 6 with \(\tau =1-\alpha _i<1\) to (38).
Next, boundedness of \(B_i x_i^k\) follows from the continuity of \(B_i\). Since Lemma 12 established that backTrack terminates in a finite number of iterations we have for any \(k \ge 2\) that
where for \(i\notin \mathcal {B}\) \(\rho _i^k \triangleq \rho _i\). Expanding the \(y^+\)-update in the definition of \(\mathcal {F}\) in (15), we may write
Since \(G_i\), \(z^k\), and \(w_i^k\) are bounded, for \(i\in \mathcal {B}\) \(\rho _i^k\le \hat{\rho }\), and \(\rho _i^k\ge \underline{\rho }_i\) (using Lemma 12 for \(i\in \mathcal {B}\)), and for \(i\notin \mathcal {B}\) \(\rho _i^k=\rho _i\) is constant, we conclude that \(y_i^k\) remains bounded.\(\square\)
With \(\{x_i^k\}\) and \(\{y_i^k\}\) bounded for all \(i=1,\ldots ,n\), the boundedness of \(\nabla \varphi _k\) follows immediately:
Lemma 14
The sequence \(\{\nabla \varphi _k\}\) is bounded. If Algorithm 1 never terminates via line 9, \(\limsup _{k\rightarrow \infty }\varphi _k(p^k)\le 0\).
Proof
By Lemma 3, \(\nabla _z\varphi _k = \sum _{i=1}^n G_i^* y_i^k\), which is bounded since each \(G_i\) is bounded by assumption and each \(\{y_i^k\}\) is bounded by Lemma 13. Furthermore, \(\nabla _{w_i}\varphi _k= x_i^k - G_i x_n^k\) is bounded using the same two lemmas. That \(\limsup _{k\rightarrow \infty }\varphi _k(p^k)\le 0\) then immediately follows from Lemma 4(3).\(\square\)
Using the boundedness of \(\{x_i^k\}\) and \(\{y_i^k\}\), we can next derive the following simple bound relating \(\varphi _{i,k-1}(z^k,w_i^k)\) to \(\varphi _{i,k-1}(z^{k-1},w_i^{k-1})\):
Lemma 15
There exists \(M_1,M_2\ge 0\) such that for all \(k\ge 2\) and \(i=1,\ldots ,n\),
Proof
For each \(i\in \{1,\ldots ,n\}\), let \(M_{1,i},M_{2,i}\ge 0\) be respective bounds on \(\big \{\Vert G_i z^{k-1}-x_i^{k-1}\Vert \big \}\) and \(\big \{\Vert y_i^{k-1}-w_i^k\Vert \big \}\), which must exist by Lemma 4, the boundedness of \(\{x_i^k\}\) and \(\{y_i^k\}\), and the boundedness of \(G_i\). Let \(M_1 = \max _{i=1,\ldots ,m} \{ M_{1,i}\}\) and \(M_2 = \max _{i=1,\ldots ,m} \{ M_{2,i}\}\). Then, for any \(k \ge 2\) and \(i\in \{1,\ldots ,n\}\), we may write
where the last step uses the Cauchy-Schwarz inequality and the definitions of \(M_1\) and \(M_2\).\(\square\)
5.4 A Lyapunov-like recursion for the hyperplane
We now establish a Lyapunov-like recursion for the hyperplane. For this purpose, we need two more definitions.
Definition 2
For all \(k\ge 1\), since Lemma 12 establishes that Algorithm 2 terminates in a finite number of iterations, we may write for \(i=1,\ldots ,n\):
where for \(i\notin \mathcal {B}\) \(\rho _i^k=\rho _i\) are actually fixed. Using (4) and the \(x^+\)-update in (15), there exists \(a_i^k\in A_i x_i^k\) such that
Define \(\hat{y}_i^k\triangleq a_i^k+B_i x_i^{k-1}\).
Definition 3
For \(i\notin \mathcal {B}\) we will use \(\rho _i^k\triangleq \rho _i\), even though these stepsizes are fixed, so that we can use the same statements as for \(i\in \mathcal {B}\). Similarly we will use \(\underline{\rho }_i\triangleq \rho _i\) for \(i\notin \mathcal {B}\).
Lemma 16
For all \(k\ge 1\), and \(i=1,\ldots ,n\)
Proof
For \(i\in \mathcal {B}\), recall that \(\tilde{\rho }^{(i,k)}\) is the initial trial stepsize chose on line 5 of backTrack at iteration k for some \(i\in \mathcal {B}\). The condition on line 5 of backTrack guarantees that
Multiplying through by \(\alpha _i^{-1}\Vert y_i^k - w_i^k\Vert ^2\) and noting that \(\rho _i^{k+1}\le \tilde{\rho }^{(i,k+1)}\) proves the lemma.
For \(i\notin \mathcal {B}\) the expression holds trivially because \(\rho _i^{k+1}=\rho _i^k=\rho _i\). \(\square\)
Lemma 17
For all \(k\ge 2\) and \(i=1,\ldots ,n\),
and
Proof
Take any \(i\in \mathcal {B}\). Lemma 12 guarantees the finite termination of backTrack. Now consider the backtracking termination condition
Fix some \(k\ge 2\), and let \(j^*\ge 1\) be the iteration at which backTrack terminates. In the above inequality, make the following substitutions for the internal variables of backTrack by those passed in/out of the function: \(\varphi _{i,k}(z^k,x_i^k) = \varphi _{j^*}^+\), \(\rho _i^k = \tilde{\rho }_{j^*}\), \(\alpha _i = \alpha\), \(y_i^k = \tilde{y}_j\), \(w_i^k = w\), \(\varphi _{i,k-1}(z^k,w_i^k) = \varphi\). Furthermore, \(\hat{y}_i^k = \hat{y}_{j^*}\) where \(\hat{y}_i^k\) is defined in Definition 2. Together, these substitutions yield (40). We can then apply Lemma 16 to get (41).
Now take any \(i \in \{1,\ldots ,n\} \backslash \mathcal {B}\). From line 6 of Algorithm 1, Assumption 2, and Lemma 11, we directly deduce (40). Combining this relation with (39) we obtain (41).\(\square\)
5.5 Finishing the proof
We now work toward establishing the conditions of Lemma 5. Unless otherwise specified, we henceforth assume that Algorithm 1 runs indefinitely and does not terminate at line 9. Termination at line 9 is dealt with in Theorem 1 to come.
Lemma 18
For all \(i=1,\ldots ,n\), we have \(y_i^k-w_i^k\rightarrow 0\) and \(\varphi _k(p^k)\rightarrow 0\).
Proof
Fix any \(i\in \{1,\ldots ,n\}\).
First, note that for all \(k\ge 2\),
where \(d_i^k \triangleq M_3\Vert w_i^k-w_i^{k-1}\Vert + \Vert w^k_i - w^{k-1}_i\Vert ^2\) and \(M_3\ge 0\) is a bound on \(2\Vert y_i^{k-1}-w_i^{k-1}\Vert\), which must exist because both \(\{y_i^k\}\) and \(\{w_i^k\}\) are bounded by Lemmas 4 and 13. Note that \(d_i^k\rightarrow 0\) as a consequence of Lemma 4.
Second, recall Lemma 15, which states that there exists \(M_1,M_2\ge 0\) such that for all \(k\ge 2\),
Now let, for all \(k\ge 1\),
so that
Using (42) and (43) in (41) yields
where
Note that \(\rho _i^k\) is bounded, \(0<{\alpha _i}\le 1\), \(\Vert G_i\Vert\) is finite, \(\Vert z^{k}-z^{k-1}\Vert \rightarrow 0\) and \(\Vert w_i^k - w_i^{k-1}\Vert \rightarrow 0\) by Lemma 4, and \(d_i^k\rightarrow 0\). Thus \(e_i^k\rightarrow 0\).
Since \(0<{\alpha _i}\le 1\), we may apply Lemma 8 to (46) with \(\tau = 1-{\alpha _i}<1\), which yields \(\liminf _{k\rightarrow \infty } \{r^k_i\}\ge 0\). Therefore
On the other hand, \(\limsup _{k\rightarrow \infty } \varphi _k(p^k)\le 0\) by Lemma 14. Therefore, using (45) and (48),
Therefore \(\lim _{k\rightarrow \infty }\big \{\varphi _k(p^k)\big \} = 0\). Consider any \(i\in \{1,\ldots ,n\}\). Combining \(\lim _{k\rightarrow \infty }\big \{\varphi _k(p^k)\big \} = 0\) with \(\liminf _{k\rightarrow \infty } \sum _{i=1}^n r_i^k\ge 0,\) we have
Since \(\rho _i^k\ge \underline{\rho }_i>0\) (using Lemma 12 for \(i\in \mathcal {B}\)) we conclude that \(y_i^k-w_i^k\rightarrow 0\).\(\square\)
We have already proved the first requirement of Lemma 5, that \(y_i^k - w_i^k\rightarrow 0\) for all \(i\in \{1,\ldots ,n\}\). We now work to establish the second requirement, that \(G_i z^k - x_i^k\rightarrow 0\). In the upcoming lemmas we continue to use the quantity \(\hat{y}_i^k\) which is given in Definition 2.
Lemma 19
For all \(i=1,\ldots ,n\), \(\hat{y}_i^k - w_i^k\rightarrow 0\).
Proof
Fix any \(k\ge 1\). For all \(i= 1,\ldots ,n\), repeating (40) from Lemma 17, we have
where we have used \(r_i^k\) defined (44) along with (42)–(43) and \(e_i^k\) is defined in (47). This is the same argument used in Lemma 18, but now we apply (42)–(43) to (40), rather than (41), so that we can upper bound the \(\Vert \hat{y}_i^k - w_i^k\Vert ^2\) term. Summing over \(i=1,\ldots ,n\), yields
Since \(\varphi _k(p^k)\rightarrow 0\), \(e_i^k\rightarrow 0\), \(\liminf _{k\rightarrow \infty } \{r_i^k\}\ge 0\), and \(\rho _i^k\ge \underline{\rho }_i>0\) for all k, the above inequality implies that \(\hat{y}_i^k - w_i^k\rightarrow 0\).\(\square\)
Lemma 20
For \(i=1\ldots ,n, x_i^k - x_i^{k-1}\rightarrow 0\).
Proof
Fix \(i\in \{1,\ldots ,n\}\). Using the definition of \(a_i^k\) in Definition 2, we have for \(k\ge 1\) that
Using the definition of \(\hat{y}_i^k\), also in Definition 2, this implies that
Subtracting the second of these equations from the first yields, for all \(k\ge 2\),
Taking norms and using the triangle inequality yields, for all \(k\ge 2\), that
where
Since \(\rho _i^{k}\) is bounded from above, \(\tilde{e}_i^k\rightarrow 0\) using Lemma 19, the finiteness of \(\Vert G_i\Vert\), and Lemma 4. Furthermore, \({\alpha _i}>0\), so we may apply Lemma 7 to (50) to conclude that \(x_i^k - x_i^{k-1}\rightarrow 0\).\(\square\)
Lemma 21
For \(i=1,\dots ,n, G_i z^k - x_i^k\rightarrow 0\).
Proof
Recalling (49), we first write
Lemma 20 implies that the first term on the right-hand side of (51) converges to zero. Since \(\{\rho _i^k\}\) is bounded, Lemma 19 implies that the second term on the right-hand side also converges to zero. Since \({\alpha _i}>0\), we conclude that \(\Vert G_i z^k-x_i^k\Vert \rightarrow 0\). \(\square\)
Finally, we can state our convergence result for Algorithm 1:
Theorem 1
Suppose that Assumptions 1–2hold. If Algorithm 1 terminates by reaching line 9, then its final iterate is a member of the extended solution set \(\mathcal {S}\). Otherwise, the sequence \(\{(z^k,\mathbf{w}^k)\}\) generated by Algorithm 1 converges weakly to some point \(({\bar{z}},\overline{\mathbf{w}})\) in the extended solution set \(\mathcal {S}\) of (2) defined in (5). Furthermore, \(x_i^k\rightharpoonup G_i {\bar{z}}\) and \(y_i^k\rightharpoonup \overline{w}_i\) for all \(i=1,\ldots ,n-1\), \(x_{n}^k\rightharpoonup {\bar{z}}\), and \(y_n^k\rightharpoonup -\sum _{i=1}^{n-1}G_i^* \overline{w}_i\).
Proof
For the finite termination result we refer to Lemma 5 of [19]. Otherwise, Lemmas 18 and 21 imply that the hypotheses of Lemma 5, hold, and the result follows.\(\square\)
6 Numerical experiments
All our numerical experiments were implemented in Python (using numpy and scipy) on an Intel Xeon workstation running Linux with 16 cores and 64 GB of RAM. The code is available via github at https://github.com/projective-splitting/coco. We compared this paper’s backtracking one-forward-step projective splitting algorithm given in Algorithm 1 (which we call ps1fbt) with the following methods, selected for their similarities in features (especially the ability to “fully split” problems and having deterministic convergence guarantees), applicability, and implementation effort:
-
The two-forward-step projective splitting algorithm with backtracking we developed in [19] (ps2fbt). This method requires only Lipschitz continuity of single-valued operators, as opposed to cocoercivity.
-
The adaptive three-operator splitting algorithm of [31] (ada3op) (where “adaptive” is used to mean “backtracking linesearch”); this method is a backtracking adaptation of the fixed-stepsize method proposed in [13]. This method requires \(G_i = I\) in problem (2) and hence can only be readily applied to two of the three test applications described below.
-
The backtracking linesearch variant of the Chambolle-Pock primal-dual splitting method [28] (cp-bt).
-
The algorithm of [11]. This is essentially Tseng’s method applied to a product-space “monotone + skew” inclusion in the following way: Assume \(T_n\) is Lipschitz monotone, problem (3) is equivalent to finding \(p\triangleq (z,w_1,\ldots ,w_{n-1})\) such that \(w_i\in T_i G_i z\) (which is equivalent to \(G_iz\in T_i^{-1}w_i\)) for \(i=1,\ldots ,n-1\), and \(\sum _{i=1}^{n-1}G_i^* w_i=-T_n z\). In other words, we wish to solve \(0\in \tilde{A}p + \tilde{B} p\), where \(\tilde{A}\) and \(\tilde{B}\) are defined by
$$\begin{aligned} \tilde{A}p&= \{0\} \times T_1^{-1}w_1 \times \cdots \times T_{n-1}^{-1}w_{n-1} \end{aligned}$$(52)$$\begin{aligned} \tilde{B}p&= \left[ \begin{array}{c} T_n z\\ 0\\ \vdots \\ 0 \end{array} \right] + \left[ \begin{array}{ccccc} 0&{}G_1^*&{}G_2^*&{}\ldots &{}G_{n-1}^*\\ -G_1&{}0&{} \ldots &{} \ldots &{} 0\\ \vdots &{}\vdots &{} \ddots &{} \ddots &{} \vdots \\ -G_{n-1} &{} 0 &{} \ldots &{} \ldots &{} 0 \end{array} \right] \left[ \begin{array}{c} z\\ w_1\\ \vdots \\ w_{n-1} \end{array} \right] . \end{aligned}$$(53)\(\tilde{A}\) is maximal monotone, while \(\tilde{B}\) is the sum of two Lipshitz monotone operators (the second being skew linear), and therefore also Lipschitz monotone. The algorithm in [11] is essentially Tseng’s forward-backward-forward method [37] applied to this inclusion, using resolvent steps for \(\tilde{A}\) and forward steps for \(\tilde{B}\). Thus, we call this method tseng-pd. In order to achieve good performance with tseng-pd we had to incorporate a diagonal preconditioner as proposed in [38].
-
The recently proposed forward-reflected-backward method [29], applied to this same primal-dual inclusion \(0\in \tilde{A}p + \tilde{B} p\) specified by (52)–(53). We call this method frb-pd.
6.1 Portfolio selection
Consider the optimization problem:
where \(Q\succeq 0\), \(r>0\), and \(m\in \mathbb {R}^d_+\). This model arises in Markowitz portfolio theory. We chose this particular problem because it features two constraint sets (a general halfspace and a simplex) onto which it is easy to project individually, but whose intersection poses a more difficult projection problem. This property makes it difficult to apply first-order methods such as ISTA/FISTA [5] as they can only perform one projection per iteration and thus cannot fully split the problem. On the other hand, projective splitting can handle an arbitrary number of constraint sets so long as one can compute projections onto each of them. We consider a fairly large instance of this problem so that standard interior point methods (for example, those in the CVXPY [14] package) are disadvantaged by their high per-iteration complexity and thus not generally competitive with first-order methods. Furthermore, backtracking variants of first-order methods are preferable for large problems as they avoid the need to estimate the largest eigenvalue of Q.
To convert (54) to a monotone inclusion, we set \(A_1 = N_{C_1}\) where \(N_{C_1}\) is the normal cone of the simplex \(C_1 = \{x\in \mathbb {R}^d:\sum _{i=1}^d x_i=0,x_i\ge 0\}\). We set \(B_1 = 2Qx\), which is the gradient of the objective function and is cocoercive (and Lipschitz-continuous). Finally, we set \(A_2 = N_{C_2}\), where \(C_2 = \{x:m^\top x\ge r\}\), and let \(B_2\) be the zero operator. Note that the resolvents of \(N_{C_1}\) and \(N_{C_2}\) (that is, the projections onto \(C_1\) and \(C_2\)) are easily computed in \({{\,\mathrm{O}\,}}(d)\) operations [30]. With this notation, one may write (54) as the the problem of finding \(z\in \mathbb {R}^d\) such that
which is an instance of (2) with \(n=2\) and \(G_1=G_2=I\).
To terminate each method in our comparisons, we used the following common criterion incorporating both the objective function and the constraints of (54):
where \(F^*\) is the optimal value of the problem. Note that \(c(x)=0\) if and only if x solves (54). To estimate \(F^*\), we used the best feasible value returned by any method after 1000 iterations.
We generated random instances of (54) as follows: we set \(d=10,000\) to obtain a relatively large instance of the problem. We then generated a \(d\times d\) matrix \(Q_0\) with each entry drawn from \(\mathcal {N}(0,1)\). The matrix Q is then formed as \((1/d)\cdot Q_0 Q_0^\top\), which is guaranteed to be positive semidefinite. We then generate the vector \(m\in \mathbb {R}^d\) of length d to have entries uniformly distributed between 0 and 100. The constant r is set to \(\delta _r\sum _{i=1}^d m_i/d\) for various values of \(\delta _r>0\). We solved the problem for \(\delta _r\in \{0.5,0.8,1,1.5\}\).
All methods were initialized at the same point \([1~1~\ldots ~1]^\top /d\). For all the backtracking linesearch procedures except cp-bt , the initial stepsize estimate is the previously discovered stepsize; at the first iteration, the initial stepsize is 1. For cp-bt we allowed the stepsize to increase in accordance with [28, Algorithm 4], as performance was poor otherwise. The backtracking stepsize decrement factor (\(\delta\) in Algorithm 2) was 0.7 for all algorithms.
For ps1fbt and ps2fbt, \(\rho _1^k\) was discovered via backtracking. We also set the other stepsize \(\rho _2^k\) equal to \(\rho _1^k\) at each iteration. While this is not necessary, this heuristic performed well and eliminated \(\rho _2^k\) as a separately tunable parameter. For the averaging parameters in ps1fbt, we used \(\alpha _1=0.1\) and \(\alpha _2=1\) (which is possible because \(L_2=0\)). For ps1fbt we set \(\hat{\theta }_1 = x_1^0\) and \(\hat{w}_1 =2 Q x_1^0\).
For tseng-pd and frb-pd, we used the following preconditioner:
where U is used as in [38, Eq. (3.2)] for tseng-pd (\(M^{-1}\) on [29, p. 7] for frb-pd). In this case, the “monotone + skew” primal-dual inclusion described in (52)–(53) features two d-dimensional dual variables in addition to the d-dimensional primal variable. The parameter \(\gamma _{pd}\) changes the relative size of the steps taken in the primal and dual spaces, and plays a similar role to \(\gamma\) in our algorithm (see Algorithm 3). The parameter \(\beta\) in [28, Algorithm 4] plays a similar role for cp-bt. For all of these methods, we have found that performance is highly sensitive to this parameter: the primal and dual stepsizes need to be balanced. The only method not requiring such tuning is ada3op, which is a purely primal method. With this setup, all the methods have one tuning parameter except ada3op , which has none. For each method, we manually tuned the parameter for each \(\delta _r\); Table 1 shows the final choices.
We calculated the criterion c(x) in (55) for \(x_1^k\) computed by ps1fbt and ps2fbt, \(x_t\) computed on Line 3 of [31, Algorithm 1] for ada3op, \(y^{k}\) computed in [28, Algorithm 4] for cp-bt, and the primal iterate for tseng-pd and frb-pd. Table 2 displays the average number iterations and running time, over 10 random trials, until c(x) falls (and stays) below \(10^{-5}\) for each method. Examining the table,
-
For all four problems, ps1fbt outperforms ps2fbt. This behavior is not suprising, as ps1fbt only requires one forward step per iteration, rather than two. Since the matrix Q is large and dense, reducing the number of forward steps should have a sizable impact.
-
For \(\delta _r<1\), ps1fbt is the best-performing method. However, for \(\delta _r\ge 1\), ada3op is the quickest.
6.2 Sparse group logistic regression
Consider the following problem:
where \(a_i\in \mathbb {R}^d\) and \(y_i\in \{\pm 1\}\) for \(i=1,\ldots ,n\) are given data, \(\lambda _1,\lambda _2\ge 0\) are regularization parameters, and \(\mathcal {G}\) is a set of subsets of \(\{1,\ldots ,d\}\) such that no element is in more than one group \(g\in \mathcal {G}\). This is the non-overlapping group-sparse logistic regression problem, which has applications in bioinformatics, image processing, and statistics [34]. It is well understood that the \(\ell _1\) penalty encourages sparsity in the solution vector. On the other hand the group-sparse penalty encourages group sparsity, meaning that as \(\lambda _2\) increases more groups in the solution will be set entirely to 0. The group-sparse penalty can be used when the features/predictors can be put into correlated groups in a meaningful way. As with the portfolio experiment, this problem features two nonsmooth regularizers and so methods like FISTA cannot easily be applied.
Problem (57) may be treated as a special case of (1) with \(n=2\), \(G_1=G_2=I\), and
Since the logistic regression loss has a Lipschitz-continuous gradient and the \(\ell _1\)-norm and non-overlapping group-lasso penalties both have computationally simple proximal operators, all our candidate methods may be applied.
We applied (57) to two bioinformatics classification problems with real data. Following [34], we use the breast cancer dataset of [25] and the inflammatory bowel disease (IBD) dataset of [6].Footnote 2 The breast cancer dataset contains gene expression levels for 60 patients with estrogen-positive breast cancer. The patients were treated with tamoxifen for 5 years and classified based on whether the cancer recurred (there were 28 recurrences). The goal is to use the gene expression values to predict recurrence. The IBD data set contains gene expression levels for 127 patients, 85 of which have IBD. The IBD data set actually features three classes: ulcerative colitis (UC), Crohn’s disease (CD), and normal, and so the most natural goal would be to perform three-way classification. For simplicity, we considered a two-way classification problem of UC/CD patients versus normal patients.
For both datasets, as in [34], the group structure \(\mathcal {G}\) was extracted from the C1 dataset [35], which groups genes based on cytogenetic position data.Footnote 3 Genes that are in multiple C1 groups were removed from the dataset.Footnote 4 We also removed genes that could not be found in the C1 dataset, although doing so was not strictly necessary. After these steps, the breast cancer data had 7,705 genes in 324 groups, with each group having an average of 23.8 genes. For the IBD data there were 19,836 genes in 325 groups, with an average of 61.0 genes per group. Let A be the data matrix with each row is equal to \(a_i^\top \in \mathbb {R}^{d}\) for \(i=1,\ldots ,n\); as a final preprocessing step, we normalized the columns of A to have unit \(\ell _2\)-norm, which tended to improve the performance of the first-order methods, especially the primal-dual ones.
For simplicity we set the regularization parameters to be equal: \(\lambda _1=\lambda _2\triangleq \lambda\). In practice, one would typically solve (57) for various values of \(\lambda\) and then choose the final model based on cross-validation performance combined with other criteria such as sparsity. Therefore, to give an overall sense of the performance of each algorithm, we solved (57) for three values of \(\lambda\): large, medium, and small, corresponding to decreasing the amount of regularization and moving from a relatively sparse solution to a dense solution. For the breast cancer data, we selected \(\lambda \in \{0.05,0.5,0.85\}\) and for IBD we chose \(\lambda \in \{0.1,0.5,1\}\). The corresponding number of non-zero entries, non-zero groups, and training error of the solution are reported in Table 3. Since the goal of these experiments is to assess the computational performance of the optimization solvers, we did not break up the data into training and test sets, instead treating the entire dataset as training data.
We initialized all the methods to the 0 vector. As in the portfolio problem, all stepsizes were initially set to 1. Since the logistic regression function does not have uniform curvature, we allowed the initial trial stepsize in the backtracking linesearch to increase by a factor of 1.1 multiplied by the previously discovered stepsize. The methods ps1fbt, cp-bt, and ada3op have an upper bound on the trial stepsize at each iteration, so the trial stepsize was taken to be the minimum of 1.1 multiplied by the previous stepsize and this upper bound.
Otherwise, the setup was the same as the portfolio experiment. tseng-pd and frb-pd use the same preconditioner as given in (56). For ps1fbt and ps2fbt we set \(\rho _2^k\) to be equal to the discovered backtracked stepsize \(\rho _1^k\) at each iteration. For ps1fbt we again set \(\hat{\theta }_1 = x_1^0\), \(\hat{w}_1 =\nabla h_1(x_1^0)\), and \(\alpha _1^k\) fixed to 0.1. As such, all methods (except ada3op) have one tuning parameter which was hand-picked for each method; the chosen values are given in Table 4.
Results for (57) applied to bioinformatics classification problems. The top row shows breast cancer data with left: \(\lambda =0.05\); middle: \(\lambda =0.5\); right: \(\lambda =0.85\). The bottom row shows IBD data with left: \(\lambda =0.1\); middle: \(\lambda =0.5\); right: \(\lambda =1.0\). The y-axis is relative objective error: \(\big (F(x_0,x)-F^*\big )/F^*\) and the x-axis is elapsed running time in seconds
Figure 3 shows the results of the experiments, plotting \((F(x_0,x)-F^*)/F^*\) against time for each algorithm, where F is the objective function in (57) and \(F^*\) is the estimated optimal value. To approximate \(F^*\), we ran each algorithm for 4,000 iterations and took the lowest value obtained. Overall, ps1fbt and ada3op were much faster than the other methods. For the highly regularized cases (the right column of the figure), ps1fbt was faster than all other methods. For middle and low regularization, ps1fbt and ada3op are comparable, and for \(\lambda =0.05\) ada3op is slightly faster for the the breast cancer data. The methods ps1fbt and ada3op may be succesful because they exploit the cocoercivity of the gradient, while ps2fbt, tseng-pd,and frb-pd only treat it as Lipschitz continuous. cp-bt also exploits cocoercivity, but its convergence was slow nonetheless. We discuss the performance of ps1fbt versus ps2fbt more in Sect. 6.4.
6.3 Rare feature selection
In [40], the problem of utilizing rare features in machine learning problems was studied. In many applications, certain features are rarely nonzero, making it hard to estimate their coefficients accurately. Despite this, these features can be highly informative, and the standard practice of discarding them is wasteful. The technique in [40] overcomes this difficulty by making use of an auxiliary tree data structure \(\mathcal {T}\) describing the relatedness of features. Each leaf of the tree is a feature and two features’ closeness on the tree measures how “related” they are. Closely related features can then be aggregated (summed) so that more samples are captured, increasing the accuracy of the estimate for a single coefficient for the aggregated features.
To solve this aggregation and fitting problem automatically, [40] introduced the following generalized regression problem:
where \(X\in \mathbb {R}^{n\times d}\) is the data matrix, \(y\in \mathbb {R}^n\) is the target (response) vector, \(\varvec{\beta }\in \mathbb {R}^d\) are the feature coefficients, \(e\in \mathbb {R}^n\) has all elements equal to 1, and \(\beta _0\in \mathbb {R}\) is an offset. Each \(\varvec{\gamma }_i\) is associated with a node of the similarity tree \(\mathcal {T}\) and \(\varvec{\gamma }_{-r}\) means all nodes except the root. The matrix \(H\in \mathbb {R}^{d\times |\mathcal {T}\,|}\) contains a 1 in positions i, j for which feature i corresponds to a leaf of \(\mathcal {T}\) that is descended from node j, and elsewhere contains zeroes. H thus fuses coefficients together in the following way: if \(\varvec{\gamma }_i\) is nonzero for a node i and all descendants of \(\varvec{\gamma }_i\) in \(\mathcal {T}\) are 0, then all coefficients on the leaves which are descendant from \(\varvec{\gamma }_i\) are equal (see [40, Sec. 3.2] for more details). The \(\ell _1\) norm on \(\varvec{\gamma }\) enforces sparsity of \(\varvec{\gamma }\), which in turn fuses together coefficients in \(\varvec{\beta }\) associated with similar features. The \(\ell _1\) norm on \(\varvec{\beta }\) itself additionally enforces sparsity on these coefficients, which is also desirable.
In [40], (58) is solved by a specialized application of the ADMM. The implementation involves precomputing the SVDs of X and H, and so does not fall within the scope of the methods considered in our experiments (it does not fully split the problem). Instead, we solve (58) by simply eliminating \(\varvec{\beta }\), so that it becomes
This problem may be formulated as a special case of (1) with
Note that \(h_2\) is Lipschitz differentiable and \(f_1\) (and \(f_2\)) have easily-computed proximal operators. Because of the presence of the matrix \(G_1 = H\), ada3op cannot easily be applied to this problem, since the proximal operator of the function \(\varvec{\gamma }\mapsto \Vert H\varvec{\gamma }\Vert _1\) cannot be computed in a simple way. All other methods, namely ps1fbt, ps2fbt, cp-bt, tseng-pd, and frb-pd, may still be applied.
We apply this model to the TripAdvisor hotel-review dataset developed in [39] and [40].Footnote 5 The response variable was the overall hotel review, in the set \(\{1,2,3,4,5\}\). The features were the counts of certain adjectives in the review. Many adjectives were very rare, with 95% of the adjectives appearing in less than 5% of the reviews. The authors of [40] constructed a similarity tree using information from word embeddings and emotion lexicon labels. In the end, there were \(7,\!573\) adjectives from the \(209,\!987\) reviews and the tree \(\mathcal {T}\) had \(15,\!145\) nodes. They withheld \(40,\!000\) examples for a test set. The \(169,\!987\times 7,\! 573\) design matrix X was sparse, having only 0.32% nonzero entries. The \(7,\! 573\times 15,\!145\) matrix H arising from the similarity tree \(\mathcal {T}\) was also sparse, having 0.15% nonzero entries. In our implementation, we used the sparse matrix package sparse in scipy.
In practice, one typically would solve (59) for many values of \((\mu ,\lambda )\) and then choose the final model based on cross validation. To assess the computational performance of the tested methods, we solve three representative examples corresponding to sparse, medium, and dense solutions. For simplicity, we fixed \(\mu =0.5\). The chosen values for \(\lambda\) were \(\{10^{-5},10^{-2},10^{-1}\}\).
The setup for the algorithms was the same as in the previous two examples, except for a few differences. For backtracking, we simply set the trial stepsize at each iteration equal to the previously discovered stepsize, as increasing it at each iteration did not provide any empirical benefit. However cp-bt performed better with increasing trial stepsize so we used the same scheme as before. For ps1fbt and ps2fbt, setting \(\rho _1^k\) equal to the discovered backtracking stepsize for the other operator from the previous iteration: \(\rho _2^{k-1}\), did not work well on this model. So instead we fixed \(\rho _1^k=1\) for ps1fbt and \(\rho _1^k=10\) for ps2fbt, which gave the best performance across the three examples. Each tested method then has one additional tuning parameter which we hand-picked for each of the three examples. The final values are given in Table 5.
Results for (59) applied to TripAdvisor data. From left to right, the values of \(\lambda\) are \(\lambda =10^{-5},\) \(\lambda =10^{-2},\) and \(\lambda =10^{-1}\); \(\mu =0.5\) in all cases. The y-axis is relative objective error \(\big (F(\varvec{\gamma },\beta _0)-F^*\big )/F^*\), where \(F(\varvec{\gamma },\beta _0)\) is the objective function in (59), and the x-axis is elapsed running time in seconds
The results are shown in Fig. 4. For the plots, the optimal objective value \(F^*\) was estimated by running ps1fbt for \(100,\!000\) iterations, while the plots are shown only for the first \(20,\!000\) iterations of ps1fbt. The x-axis is running time excluding the time taken to actually compute the function values for the graph. Overall, there is not a large gap between the methods. However, ps1fbt and cp-bt are slightly faster for \(\lambda =10^{-5}\), ps2fbt is slightly faster for \(\lambda =10^{-2}\), and ps1fbt is slightly faster for \(\lambda =10^{-1}\). Since ps1fbt is either fastest, tied fastest, or in close second position, it is arguably the best performing algorithm overall. We suspect that the performance of ps1fbt (and ps2fbt) could greatly improve if we were to break the loss function up into blocks and use the greedy subproblem selection scheme we proposed in [19]. We plan to develop this generalization for ps1fbt — along with general asynchrony and block-iterativeness — in future work.
6.4 Final comments: ps1fbt versus ps2fbt
On the portfolio and rare feature problems, ps1fbt and ps2fbt have fairly comparable performance, with ps1fbt being slightly faster. However, for the group logistic regression problem, ps1fbt is significantly faster. Given that both methods are based on the same projective splitting framework but use different forward-step procedures to update \((x_1^k,y_1^k)\), this difference may be somewhat surprising. Since ps1fbt only requires one forward step per iteration while ps2fbt requires two, one might expect ps1fbt to be about twice as fast as ps2fbt. But for the group logistic regression problem, ps1fbt significantly outpaces this level of performance.
Examining the stepsizes returned by backtracking for both methods reveals that ps1fbt returns much larger stepsizes for the logistic regression problem, typically 2-3 orders of magnitude larger; see Fig. 5. For the portfolio problem and the rare feature problem, where the performance of the two methods is more similar, this is not the case: the ps1fbt stepsizes are typically about twice as large as the ps2fbt stepsizes, in keeping with their theoretical upper bounds of \(1/L_i\) and \(2(1-\alpha _i)/L_i\), respectively.
Note that the portfolo and rare features problem both have a smooth function which is quadratic and hence has the same curvature everywhere, while group logisitic regression does not. We hypothesize that the backtracking scheme in ps1fbt does a better job adapting to nonuniform curvature. A possible reason for this behavior is that the termination criterion for the backtracking search in ps1fbt may be weaker than for ps2fbt. For example, while ps2fbt requires \(\varphi _{i,k}\) to be positive at each iteration k and operator i, ps1fbt does not.
Notes
If backtracking is used, then all three of these methods can converge under weaker local continuity assumptions.
The breast cancer dataset is available at https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE1379. The IBD dataset is available at https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE3365.
The C1 dataset is available at http://software.broadinstitute.org/gsea/index.jsp.
Overlapping group norms can also be handled with our method, but using a different problem formulation than (57).
TripAdvisor data is available at https://github.com/yanxht/TripAdvisorData or through our repository at https://github.com/projective-splitting/coco.
References
Alotaibi, A., Combettes, P.L., Shahzad, N.: Solving coupled composite monotone inclusions by successive Fejér approximations of their Kuhn–Tucker set. SIAM J. Optim. 24(4), 2076–2095 (2014)
Baillon, J.B., Haddad, G.: Quelques propriétés des opérateurs angle-bornés \(n\)-cycliquement monotones. Isr. J. Math. 26(2), 137–150 (1977)
Bauschke, H.H., Combettes, P.L.: The Baillon-Haddad theorem revisited. J. Convex Anal. 17(3–4, SI), 781–787 (2010)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd edn. Springer, Berlin (2017)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18(11), 2419–2434 (2009)
Burczynski, M.E., Peterson, R.L., Twine, N.C., Zuberek, K.A., Brodeur, B.J., Casciotti, L., Maganti, V., Reddy, P.S., Strahs, A., Immermann, F., et al.: Molecular classification of Crohn’s disease and ulcerative colitis patients using transcriptional profiles in peripheral blood mononuclear cells. J. Mol. Diagn. 8(1), 51–61 (2006)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)
Combettes, P.L.: Systems of structured monotone inclusions: duality, algorithms, and applications. SIAM J. Optim. 23(4), 2420–2447 (2013)
Combettes, P.L., Eckstein, J.: Asynchronous block-iterative primal-dual decomposition methods for monotone inclusions. Math. Program. 168(1–2), 645–672 (2018)
Combettes, P.L., Pesquet, J.C.: Proximal splitting methods in signal processing. In: Fixed-Point Algorithms for Inverse Problems in Science and Engineering, pp. 185–212. Springer, Berlin (2011)
Combettes, P.L., Pesquet, J.C.: Primal-dual splitting algorithm for solving inclusions with mixtures of composite, Lipschitzian, and parallel-sum type monotone operators. Set-Valued Var. Anal. 20(2), 307–330 (2012)
Condat, L.: A primal-dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 158(2), 460–479 (2013)
Davis, D., Yin, W.: A three-operator splitting scheme and its optimization applications. Set-Valued Var. Anal. 25(4), 829–858 (2017)
Diamond, S., Boyd, S.: CVXPY: a Python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 17(83), 1–5 (2016)
Eckstein, J.: A simplified form of block-iterative operator splitting and an asynchronous algorithm resembling the multi-block alternating direction method of multipliers. J. Optim. Theory Appl. 173(1), 155–182 (2017)
Eckstein, J., Svaiter, B.F.: A family of projective splitting methods for the sum of two maximal monotone operators. Math. Program. 111(1), 173–199 (2008)
Eckstein, J., Svaiter, B.F.: General projective splitting methods for sums of maximal monotone operators. SIAM J. Control Optim. 48(2), 787–811 (2009)
Gabay, D.: Applications of the method of multipliers to variational inequalities. In: Fortin, M., Glowinski, R. (Eds.) Augmented Lagrangian Methods: Applications to the Solution of Boundary Value Problems, chap. IX, pp. 299–340. North-Holland, Amsterdam (1983)
Johnstone, P.R., Eckstein, J.: Projective splitting with forward steps. Math. Program. (2020). https://doi.org/10.1007/s10107-020-01565-3
Johnstone, P.R., Eckstein, J.: Projective splitting with forward steps only requires continuity. Optim. Lett. 14(1), 229–247 (2020)
Johnstone, P.R., Eckstein, J.: Convergence rates for projective splitting. SIAM J. Optim. 29(3), 1931–1957 (2019)
Johnstone, P.R., Eckstein, J.: Single-forward-step projective splitting: exploiting cocoercivity. arXiv preprint arXiv:1902.09025 (2019)
Korpelevich, G.: Extragradient method for finding saddle points and other problems. Matekon 13(4), 35–49 (1977)
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16(6), 964–979 (1979)
Ma, X.J., Wang, Z., Ryan, P.D., Isakoff, S.J., Barmettler, A., Fuller, A., Muir, B., Mohapatra, G., Salunga, R., Tuggle, J.T., et al.: A two-gene expression ratio predicts clinical outcome in breast cancer patients treated with tamoxifen. Cancer Cell 5(6), 607–616 (2004)
Machado, M.P.: On the complexity of the projective splitting and Spingarn’s methods for the sum of two maximal monotone operators. J. Optim. Theory Appl. 178(1), 153–190 (2018)
Machado, M.P.: Projective method of multipliers for linearly constrained convex minimization. Comput. Optim. Appl. 73(1), 237–273 (2019)
Malitsky, Y., Pock, T.: A first-order primal-dual algorithm with linesearch. SIAM J. Optim. 28(1), 411–432 (2018)
Malitsky, Y., Tam, M.K.: A forward-backward splitting method for monotone inclusions without cocoercivity. SIAM J. Optim. 30(2), 1451–1472 (2020)
Michelot, C.: A finite algorithm for finding the projection of a point onto the canonical simplex of \(\mathbb{R}^n\). J. Optim. Theory Appl. 50(1), 195–200 (1986)
Pedregosa, F., Gidel, G.: Adaptive three-operator splitting. In: Proceedings of the 35th International Conference on Machine Learning (ICML-18), pp. 4085–4094 (2018)
Pesquet, J.C., Repetti, A.: A class of randomized primal-dual algorithms for distributed optimization. J. Nonlinear Convex Anal. 16(12), 2453–2490 (2015)
Polyak, B.T.: Introduction to Optimization. Optimization Software Inc., Publications Division, New York (1987)
Simon, N., Friedman, J., Hastie, T., Tibshirani, R.: A sparse-group lasso. J. Comput. Graph. Stat. 22(2), 231–245 (2013)
Subramanian, A., Tamayo, P., Mootha, V.K., Mukherjee, S., Ebert, B.L., Gillette, M.A., Paulovich, A., Pomeroy, S.L., Golub, T.R., Lander, E.S., et al.: Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. 102(43), 15545–15550 (2005)
Tran-Dinh, Q., Vũ, B.C.: A new splitting method for solving composite monotone inclusions involving parallel-sum operators. Preprint arXiv:1505.07946 (2015)
Tseng, P.: A modified forward–backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 38(2), 431–446 (2000)
Vũ, B.C.: A variable metric extension of the forward–backward–forward algorithm for monotone operators. Numer. Funct. Anal. Optim. 34(9), 1050–1065 (2013)
Wang, H., Lu, Y., Zhai, C.: Latent aspect rating analysis on review text data: a rating regression approach. In: Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 783–792 (2010)
Yan, X., Bien, J.: Rare Feature Selection in High Dimensions. J. Am. Stat. Assoc. (2020). https://doi.org/10.1080/01621459.2020.1796677
Acknowledgements
We thank Xiaohan Yan and Jacob Bien for kindly sharing their data for the TripAdvisor reviews problem in Sect. 6.3. This research was supported by the National Science Foundation Grant CCF-1617617.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Johnstone, P.R., Eckstein, J. Single-forward-step projective splitting: exploiting cocoercivity. Comput Optim Appl 78, 125–166 (2021). https://doi.org/10.1007/s10589-020-00238-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-020-00238-3