1 Introduction

For a collection of real Hilbert spaces \(\{\mathcal {H}_i\}_{i=0}^{n}\), consider the problem of finding \(z\in \mathcal {H}_{0}\) such that

$$\begin{aligned} {0\in \sum _{i=1}^{n} G_i^* T_i(G_i z),} \end{aligned}$$
(1)

where \(G_i:\mathcal {H}_{0}\rightarrow \mathcal {H}_i\) are linear and bounded operators, and \(T_i:\mathcal {H}_i \rightarrow 2^{\mathcal {H}_i}\) are maximal monotone operators. We suppose that \(T_i\) is continuous with \({{\,\mathrm{dom}\,}}(T_i)=\mathcal {H}_i\) for each i in some subset \(\mathcal {I}_{{{\,\mathrm{F}\,}}}\subseteq \{1,\ldots ,n\}\). A key special case of (1) is

$$\begin{aligned} {\min _{x\in \mathcal {H}_{0}} \sum _{i=1}^{n}f_i(G_i x),} \end{aligned}$$
(2)

where every \(f_i:\mathcal {H}_i\rightarrow \mathbb {R}\) is closed, proper and convex, with some subset of the functions also being Fréchet differentiable everywhere. Under appropriate constraint qualifications, (1) and (2) are equivalent.

A relatively recently proposed class of operator splitting algorithms which can solve (1) is projective splitting [1,2,3,4]. In [5], we showed that it is possible for projective splitting to process Lipschitz-continuous operators using a pair of forward steps rather than the customary resolvent (backward, proximal, implicit) step. In general, the stepsize must be bounded by the inverse of the Lipschitz constant, but a backtracking linesearch procedure is available when this constant is unknown. See also [6] for a similar approach to using forward steps in a more restrictive projective splitting context, without backtracking.

The purpose of this work is to show that this Lipschitz assumption is unnecessary. It demonstrates that, when the Hilbert spaces \(\mathcal {H}_i\) in (1) are finite dimensional for \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\), the two-forward-step procedure with backtracking linesearch yields weak convergence to a solution assuming only simple continuity and full domain of the operators \(T_i\).Footnote 1 A new argument is required beyond those in [5] since the stepsizes resulting from the backtracking linesearch are no longer guaranteed to be bounded away from 0.

Theoretically, this result aligns projective splitting with two related monotone operator splitting and variational inequality methods which utilize (at least) two forward steps per iteration, backtracking, and only require continuity in finite dimensions. These are the forward–backward–forward method of Tseng [7] and the extragradient method of Korpelevich [8], along with its later extensions [9, 10]. Tseng’s method applies to the special case of Problem (1) with \(n=2\), \(\mathcal {I}_{{{\,\mathrm{F}\,}}}=\{1\}\), and \(G_1=G_2=I\), while the extragradient method applies to a more restrictive variational inequality setting. Tseng’s method was also extended in [11] to include more general problems such as (3) by applying it to the appropriate primal–dual product space inclusion.

All of these methods can be viewed in contrast with the classical forward–backward splitting algorithm [12, 13]. This method utilizes a single forward step at each iteration but requires a cocoercivity assumption which is in general stricter than Lipschitz continuity. Also disadvantageous is that the choice of stepsize depends on knowledge of the cocoercivity constant and no backtracking linesearch is known to be available. Progress was made in a very recent paper [14] which modified the forward–backward method so that it can be applied to (locally) Lipschitz continuous operators with backtracking for unknown Lipschitz constant. The locally Lipschitz continuous assumption is stronger than the mere continuity assumption considered here and in [7, 9, 10], and for known Lipschitz constant the stepsize constraint is more restrictive.

As in [5], we will work with a slight restriction of problem (1), namely

$$\begin{aligned} 0\in \sum _{i=1}^{n-1} G_i^* T_i(G_i z) +T_n(z). \end{aligned}$$
(3)

In terms of problem (1), we are simply requiring that \(G_n\) be the identity operator and thus that \(\mathcal {H}_n = \mathcal {H}_0\). This is not much of a restriction in practice, since one could redefine the last operator as \(T_{n}\leftarrow G^*_{n} \circ T_{n} \circ G_{n}\), or one could simply append a new operator \(T_n\) with \(T_n(z) = \{0\}\) everywhere.

The rest of the paper is organized as follows: in Sect. 2, we precisely state the projective splitting algorithm and our assumptions, and collect some necessary results from [5]. Section 3 proves the main result. Finally, Sect. 4 provides some numerical examples on the fused \(L_p\) regression problem.

Notation Define \(\mathcal {I}_{{{\,\mathrm{B}\,}}}\triangleq \{1,\ldots ,n\}\backslash \mathcal {I}_{{{\,\mathrm{F}\,}}}\), the set of indices of operators for which our algorithm will utilize resolvents. We will use a boldface \(\mathbf{w}= (w_1,\ldots ,w_{n-1})\) for elements of \(\mathcal {H}_1\times \cdots \times \mathcal {H}_{n-1}\). To ease the presentation, we use the following notation throughout, where I denotes the identity operator:

$$\begin{aligned} G_{n}:\mathcal {H}_{n}\rightarrow \mathcal {H}_{n} \triangleq I \quad (\forall \,k\in \mathbb {N}) \quad w_{n}^k \triangleq -{\sum _{i=1}^{n-1} G_i^*w_i^k}. \end{aligned}$$
(4)

For a maximal monotone operator \(T_i\) we use the following notation \(J_{T_i} \triangleq (I+T_i)^{-1}\) for the corresponding resolvent map (also know as the proximal, backward, or implicit step). Note that computing \(J_{T_i}(a)\) is equivalent to finding the unique \((x,y)\in \text {gra } T_i\) s.t. \(x+y = a\) [15, Props. 23.2 and 23.10].

2 Algorithm, principal assumptions, and preliminary analysis

2.1 Separator-projection methods

Let \(\varvec{\mathcal {H}} = \mathcal {H}_0\times \mathcal {H}_1\times \cdots \times \mathcal {H}_{n-1}\) and \(\mathcal {H}_n = \mathcal {H}_0\). In this primal–dual space, our algorithm produces a sequence of iterates denoted by \(p^k = (z^k,w_1^k,\ldots ,w_{n-1}^k)\in \varvec{\mathcal {H}}\). Define the extended solution set or Kuhn–Tucker set of (3) to be

$$\begin{aligned} \mathcal {S}\triangleq \left\{ (z,\mathbf{w}) \in \varvec{\mathcal {H}} \,\Big |\, w_i\in T_i(G_i z),\, i=1,\ldots ,n-1, -\sum _{i=1}^{n-1} G_i^* w_i \in T_n(z) \right\} . \end{aligned}$$
(5)

Clearly \(z\in \mathcal {H}_{0}\) solves (3) if and only if there exists \(\mathbf{w}\in \mathcal {H}_1 \times \cdots \times \mathcal {H}_{n-1}\) such that \((z,\mathbf{w})\in \mathcal {S}\).

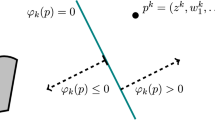
Our algorithm is a special case of a general seperator-projection method for finding a point in a closed and convex set. At each iteration the method constructs an affine function \(\varphi _k:\mathcal {H}^n\rightarrow \mathbb {R}\) which separates the current point from the target set \(\mathcal {S}\) defined in (5). In other words, if \(p^k\) is the current point in \(\varvec{\mathcal {H}}\) generated by the algorithm, \(\varphi _k(p^k)>0\), and \(\varphi _k(p)\le 0\) for all \(p\in \mathcal {S}\). The next point is then the projection of \(p^k\) onto the hyperplane \(\{p:\varphi _k(p)=0\}\), subject to a relaxation factor \(\beta _k\). What makes projective splitting an operator splitting method is that the hyperplane is constructed through individual calculations on each operator \(T_i\), either resolvent calculations or forward steps.

The hyperplane is defined in terms of the following affine function:

$$\begin{aligned} \varphi _k(z,w_1,\ldots ,w_{n-1})&\triangleq \sum _{i=1}^{n-1}\langle {G_i z-x^k_i},{y^k_i-w_i}\rangle +\left\langle {z-x_i^n},{y_i^n + \sum _{i=1}^{n-1} G_i^* w_i}\right\rangle \nonumber \\&= \sum _{i=1}^n \langle G_i z - x_i^k,y_i^k - w_i^k\rangle . \end{aligned}$$
(6)

To derive (6), we used the notational conventions in (4). See [5, Lemma 4] for the relevent properties of \(\varphi _k\). This function is parameterized by points \((x_i^k,y_i^k)\in \text {gra }T_i\) for \(i=1,\ldots ,n\). These points must be chosen in such a way that projection of \(p^k\) onto the hyperplane \(\{p:\varphi _k(p)=0\}\) makes sufficient progress towards the solution set \(\mathcal {S}\) that one can guarantee overall convergence. Our work in [5] makes this choice using a two-forward-step procedure in the case of Lipschitz-continuous operators, whereas all prior work on the topic employed only resolvent-based calculations. In this work, we show that the two-forward-step procedure, combined with backtracking, works with Lipschitz continuity relaxed to mere continuity.

As in [5], we use the following inner product and norm for \(\varvec{\mathcal {H}}\), for an arbitrary scalar \(\gamma > 0\):

$$\begin{aligned} \left\langle {(z^1,\mathbf{w}^1)},{(z^2,\mathbf{w}^2)}\right\rangle _\gamma&\triangleq \gamma \langle z^1,z^2\rangle + {\sum _{i=1}^{n-1}\langle w^1_i,w^2_i\rangle }\\ \left\| (z,\mathbf{w})\right\| _\gamma ^2&\triangleq \left\langle {(z,\mathbf{w})},{(z,\mathbf{w})}\right\rangle _\gamma . \end{aligned}$$

Note that with this inner product it was shown in [5, Lemma 4] that

$$\begin{aligned} \nabla \varphi _k = \left( \frac{1}{\gamma }\left( \sum _{i=1}^{n-1} G_i^* y_i^k+ y_n^k\right) \!\!,\; x_1^k - G_1 x_{n}^k,x_2^k - G_2 x_{n}^k,\ldots ,x_{n-1}^k - G_{n-1} x_{n}^k\right) . \end{aligned}$$
(7)

The scalar \(\gamma >0\) controls the relative emphasis on the primal and dual variables in the projection update in lines 37–38.

2.2 The algorithm

Algorithm 1 presents the algorithm analyzed in this paper. It is essentially the block-iterative and asynchronous projective splitting algorithm as in [5], but directly incorporating a backtracking linesearch procedure. It has the following parameters:

  • For each iteration \(k\ge 1\), a subset \(I_k\subseteq \{1,\ldots ,n\}\) of activated operators to be processed.

  • For each \(k\ge 1\) and \(i=1,\ldots ,n\), a positive scalar stepsize \(\rho _{i}^{k}\). For \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\), \(\rho _i^{k}\) is the initial stepsize tried in the backtracking linesearch, while \(\hat{\rho }_i^{k}\) is the accepted stepsize returned by the linesearch. Note that \(\hat{\rho }_i^k\) on line 22 is not actually used within the algorithm, but is defined to simplify the notation in the analysis to come. The stepsizes \(\tilde{\rho }_i^{(j,k)}\) are the intermediate stepsizes tested during iteration j of the linesearch.

  • A constant \(\varDelta >0\) for the backtracking linesearch and a constant \(\nu \in (0,1)\) controlling how much the stepsize is decreased at each iteration of the backtracking linesearch.

  • For each iteration \(k\ge 1\) and \(i=1,\ldots ,n\), a delayed iteration index \(d(i,k)\in \{1,\ldots ,k\}\) which allows the subproblem calculations to use outdated information.

  • For each iteration \(k\ge 1\), an overrelaxation parameter \(\beta _k\in [\underline{\beta },\overline{\beta }]\) for some constants \(0<\underline{\beta }\le \overline{\beta }<2\).

We remark that the exact resolvent computation on lines 5–7 of the algorithm may be relaxed to an inexact calculation satisfying a relative error criterion. This technique was introduced in [2, 4] and is also used in [5, 16, 17]. To simplify the analysis in this paper, we only consider exact resolvent computations here. The reader may refer to [2, 4, 5, 16, 17] for a detailed treatment of employing inexact computation of resolvents within projective splitting.

There are many ways in which Algorithm 1 could be implemented in various parallel computing environments. We refer to [5] for a more thorough discussion. The delay parameters d(i, k) might seem confusing. Of course one can always simply set \(d(i,k)=k\) which corresponds to a fully synchronous implementation, but we allow for \(d(i,k)\le k\) so that we can model asynchronous block-iterative (incremental) implementations. Conditions on these delays are given in the next section.

The advantage of separating the linear operators from each \(T_i\) in (3) is clear from lines 5–7 of the algorithm, at least for \(i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\). For these i, even when the resolvent of \(T_i\) has a simple closed form or is otherwise computationally feasible, computing the resolvent of \(G_i^*\circ T_i\circ G_i\) is often difficult. Algorithm 1 does not require this resolvent and only computes resolvents of \(T_i\) and matrix multiplies by \(G_i\) and \(G_i^*\).

On the other hand, for \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\), the advantage of separating \(T_i\) and \(G_i\) is less obvious, since a forward evaluation \(G_i^*\circ T_i\circ G_i\) has essentially the same complexity as performing the matrix multiplies and forward evaluations of \(T_i\) separately. However there are a number possible advantages: first, in our previous work [5] we showed that if \(T_i\) is \(L_i\)-Lipschitz continuous, then the stepsize constraint is \(\rho _i<1/L_i\) and is unaffected by the linear operator norm \(\Vert G{}_i\Vert \) (unlike some primal–dual methods [11]). If instead forward evaluations were to be applied to \(G_i^*\circ T_i\circ G_i\), then the norm of \(G_i\) would effect the stepsize constraint, possibly leading to smaller stepsizes and more backtracking (when it is necessary).

Second, the operators \(G_i\) do not appear within the backtracking loop on lines 15–21 of the algorithm, so separating \(T_i\) and \(G_i\) keeps matrix multiplications from being needed within the backtracking procedure; if we were to replace \(T_i\) with \(G_i^*\circ T_i\circ G_i\), backtracking would have to perform such multiplications.

Finally, if \(G_i\) is a “wide matrix” with fewer rows than columns, then the dimension of \((x_i^k,y_i^k)\) would be smaller than \(z^k\). Thus splitting up the problem in this way would lead to a smaller memory footprint. Ultimately, the decision on how to split up the problem will depend on the details of the implementation and projective splitting offers fairly unparalleled flexibility in this respect.

In [17, Sec. 9] we considered some simple special cases of Algorithm 1 in which \(n=1\) and there is no asynchrony or block-iterativeness (i.e. \(I_k \equiv \{1,\ldots ,n\}\) and \(d(i,k)\equiv 0\)), which may be of interest to the reader. In the special case of \(n=1\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\), we showed that projective splitting reduces to the proximal point method [15, Thm. 23.41]. If \(n=1\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\), then the method essentially reduces to the backtracking variant of the extragradient method proposed in [9].

figure a

2.3 Main assumptions and preliminary analysis

Our main assumptions regarding (3) are as follows:

Assumption 1

Problem (3) conforms to the following:

  1. 1.

    \(\mathcal {H}_0 = \mathcal {H}_n\) and \(\mathcal {H}_1,\ldots ,\mathcal {H}_{n-1}\) are real Hilbert spaces.

  2. 2.

    For \(i=1,\ldots ,n\) the operators \(T_i:\mathcal {H}_{i}\rightarrow 2^{\mathcal {H}_{i}}\) are monotone.

  3. 3.

    For all i in some subset \(\mathcal {I}_{{{\,\mathrm{F}\,}}}\subseteq \{1,\ldots ,n\}\), \(\mathcal {H}_i\) is finite-dimensional, the operator \(T_i\) is continuous with respect to the metric induced by \(\Vert \cdot \Vert \) (and thus single-valued), and \(\text {dom}(T_i) = \mathcal {H}_i\).

  4. 4.

    For \(i \in \mathcal {I}_{{{\,\mathrm{B}\,}}}\triangleq \{1,\ldots ,n\} \backslash \mathcal {I}_{{{\,\mathrm{F}\,}}}\), the operator \(T_i\) is maximal monotone and the map \(J_{\rho T_i}:\mathcal {H}_i\rightarrow \mathcal {H}_i\) can be computed.

  5. 5.

    Each \(G_i:\mathcal {H}_{0}\rightarrow \mathcal {H}_i\) for \(i=1,\ldots ,n-1\) is linear and bounded.

  6. 6.

    The solution set \(\mathcal {S}\) defined in (5) is nonempty.

Our assumptions regarding the parameters of Algorithm 1 are as follows, and are the same as used in [4, 5, 16].

Assumption 2

For Algorithm 1, assume:

  1. 1.

    For some fixed integer \(M\ge 1\), each index i in \(1,\ldots ,n\) is in \(I_k\) at least once every M iterations, that is, \( \bigcup _{k=j}^{j+M-1}I_k = \{1,\ldots ,n\} \) for all \(i=1,\ldots ,n\) and \(j \ge 1\).

  2. 2.

    For some fixed integer \(D\ge 0\), we have \(k-d(i,k)\le D\) for all i, k with \(i\in I_k\).

We also use the following additional notation from [16]: for all i and k, define

$$\begin{aligned} S(i,k)&= \{j\in \mathbb {N}:j\le k,i\in I_j \}&s(i,k)&= \left\{ \begin{array}{ll} \max S(i,k),&{}\quad \text {when } S(i,k)\ne \emptyset \\ 0,&{}\quad \text {otherwise.} \end{array} \right. \end{aligned}$$

Essentially, s(i, k) is the most recent iteration up to and including k in which the index-i information in the separator was updated. Assumption 2 ensures that \(0\le k-s(i,k)< M\). For all \(i=1,\ldots ,n\) and iterations k, also define \( l(i,k) = d(i,s(i,k)), \) the iteration in which the algorithm generated the information \(z^{l(i,k)}\) and \(w_{i}^{l(i,k)}\) used to compute the current point \((x_i^k,y_i^k)\). Regarding initialization, we set \(d(i,0) = 0\); note that the initial points \((x_i^0,y_i^0)\) are arbitrary. We formalize the use of l(i, k) in the following Lemma from [5]:

Lemma 1

Suppose Assumption 2(1) holds. For all iterations \(k\ge M\) if Algorithm 1 has not already terminated, the updates can be written as

$$\begin{aligned} (\forall i\in \mathcal {I}_{{{\,\mathrm{B}\,}}})&\quad x^k_i+\rho _i^{l(i,k)}y^k_i = G_i z^{l(i,k)}+\rho ^{l(i,k)}_iw_i^{l(i,k)} \quad y^k_i \in T_i x^k_i \end{aligned}$$
(8)
$$\begin{aligned} (\forall i\in \mathcal {I}_{{{\,\mathrm{F}\,}}})&\quad x^k_{i} = G_{i} z^{l(i,k)} - \hat{\rho }^{l(i,k)}_{i}\big (T_{i} G_{i} z^{l(i,k)} - w^{l(i,k)}_{i}\big ) \quad y^k_{i} = T_i x^k_{i}. \end{aligned}$$
(9)

Proof

The proof follows from the definition of l(i, k) and s(i, k). After M iterations, all operators must have been in \(I_k\) at least once. Thus, after M iterations, every operator has been updated at least once using either the resolvent step on lines 5–7 or the backtracking forward step on lines 9–22 of Algorithm 1. Recall the variables defined to ease mathematical presentation, namely \(G_{n} = I\) and \(w_{n}^k\) defined in (4) and line 39. \(\square \)

Since Algorithm 1 is a projection method, it satisfies the following lemma, identical to [5, Lemmas 2 and 6]:

Lemma 2

Suppose Assumptions 1 and 2(1) hold. Then for Algorithm 1

  1. 1.

    The sequences \(\{p^k\}=\{z^k,w_1^k,\ldots ,w_{n-1}^k\}\) and \(w_n^k=-\sum _{i=1}^{n-1}G_i^* w_i^k\) generated by Algorithm 1 are bounded.

  2. 2.

    If Algorithm 1 runs indefinitely, then \(p^k - p^{k+1}\rightarrow 0\).

  3. 3.

    Lines 37 and 38 may be written as

    $$\begin{aligned} p^{k+1} = p^k - \frac{\beta _k\max \{\varphi _k(p^k),0\}}{\Vert \nabla \varphi _k\Vert _\gamma ^2}\nabla \varphi _k \end{aligned}$$

    where \(\varphi _k\) is defined in (6).

The stepsize assumptions differ from [5, 17] for \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\) in that we no longer assume Lipschitz continuity nor that the stepsizes are bounded by the inverse of the Lipschitz constant. However, the initial trial stepsize for the backtracking linesearch at each iteration is assumed to be bounded from above and below:

Assumption 3

In Algorithm 1,

$$\begin{aligned} \underline{\rho } \triangleq \min _{i=1,\ldots ,n} \left\{ \inf _{k\ge 1} \rho _i^k\right\} > 0 \quad \overline{\rho } \triangleq \max _{i=1,\ldots ,n} \left\{ \sup _{k\ge 1} \rho _i^k \right\} < \infty . \end{aligned}$$

3 Main analysis

3.1 Finite termination of backtracking

The following lemma establishes that the backtracking linesearch in Algorithm 1 always terminates in a finite number of iterations. This result does not follow from [5] as we no longer have a Lipschitz continuity assumption for \(T_i, i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\).

Lemma 3

Suppose Assumptions 1–3 hold. Then for all \(k\in \mathbb {N}\) and \(i\in I_k\) such that Algorithm 1 has not yet terminated, the backtracking linesearch on lines 9–22 terminates in a finite number of iterations.

Proof

For \(k\ge M\), consider any \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\cap I_k\) and assume that \(T_i G_i z^{l(i,k)}\ne w_i^{l(i,k)}\), since backtracking otherwise terminates immediately at line 13. Using the definitions of s(i, k) and l(i, k) and some algebraic manipulation, the condition for terminating the backtracking linesearch given on line 18 may be written as:

$$\begin{aligned} \frac{ \langle G_i z^{l(i,k)} - \tilde{x}_i^{(j,s(i,k))},\tilde{y}_i^{(j,s(i,k))} - w_i^{l(i,k)}\rangle }{\Vert G_i z^{l(i,k)} - \tilde{x}_i^{(j,s(i,k))}\Vert ^2} \ge \varDelta . \end{aligned}$$
(10)

For brevity, let \(\rho \triangleq \tilde{\rho }_i^{(j,s(i,k))} > 0\). Using lines 10, 11, 16 and 17, the left-hand side of (10) may be written

$$\begin{aligned} \frac{ \Big \langle T_iG_i z^{l(i,k)} - w_i^{l(i,k)}, T_i\big (G_i z^{l(i,k)} - \rho (T_iG_i z^{l(i,k)} - w_i^{l(i,k)})\big ) - w_i^{l(i,k)} \Big \rangle }{\rho \Vert T_iG_i z^{l(i,k)} - w_i^{l(i,k)}\Vert ^2}. \end{aligned}$$
(11)

The numerator of this fraction may be expressed as

$$\begin{aligned}&\Big \langle T_iG_i z^{l(i,k)} - w_i^{l(i,k)}, T_i\big (G_i z^{l(i,k)} - \rho (T_iG_i z^{l(i,k)} - w_i^{l(i,k)})\big ) - T_i G_i z^{l(i,k)} \Big \rangle \\&\quad +\,\Vert T_iG_i z^{l(i,k)} - w_i^{l(i,k)}\Vert ^2. \end{aligned}$$

Substituting this expression into (11) and applying the Cauchy–Schwarz inequality to the inner product yields that the left-hand size of (10) is lower bounded by

$$\begin{aligned} \frac{ \Vert T_iG_i z^{l(i,k)} - w_i^{l(i,k)}\Vert - \big \Vert T_i(G_i z^{l(i,k)} - \rho \big (T_iG_i z^{l(i,k)} - w_i^{l(i,k)})\big ) - T_iG_i z^{l(i,k)}\big \Vert }{\rho \Vert T_iG_i z^{l(i,k)}-w_i^{l(i,k)}\Vert .} \end{aligned}$$
(12)

The continuity of \(T_i\) implies that the second term in the numerator of the above expression converges to 0 as \(\rho \rightarrow 0\). Since the first term in the numerator is positive and independent of \(\rho \), the limit of the numerator is positive and bounded away from 0. On the other hand, the denominator is positive and converges to 0. Therefore the above expression tends to \(+\infty \) as \(\rho \rightarrow 0\). Since \(\tilde{\rho }_j^{(j,k)}\) decreases geometrically to 0 with j on line 21, it follows that (10) must eventually hold. \(\square \)

3.2 The key to weak convergence

The following Lemma is the key to establishing weak convergence to a solution.

Lemma 4

Suppose Assumptions 1–3 hold, Algorithm 1 produces an infinite sequence of iterates, and both

  1. 1.

    \(G_i z^{l(i,k)} - x_i^k\rightarrow 0\) for all \(i=1,\ldots ,n\)

  2. 2.

    \(y_i^k-w_i^{l(i,k)}\rightarrow 0\) for all \(i=1\ldots ,n\).

Then the sequence \(\{(z^k,\mathbf{w}^k)\}\) generated by Algorithm 1 converges weakly to some point \((\bar{z},\overline{\mathbf{w}})\) in the extended solution set \(\mathcal {S}\) of (3) defined in (5). Furthermore, \(x_i^k\rightharpoonup G_i \bar{z}\) and \(y_i^k\rightharpoonup \overline{w}_i\) for all \(i=1,\ldots ,n-1\), \(x_{n}^k\rightharpoonup \bar{z}\), and \(y_n^k\rightharpoonup -\sum _{i=1}^{n-1}G_i^* \overline{w}_i\).

Proof

First, note that \(w_i^{l(i,k)}-w_i^k\rightarrow 0\) for all \(i=1,\ldots ,n\) and \(z^{l(i,k)}-z^k \rightarrow 0\) [5, Lemma 9]. Combining \(z^k - z^{l(i,k)}\rightarrow 0\) with point (1) and the fact that \(G_i\) is bounded, we obtain that \( G_iz^k - x_i^k\rightarrow 0 \) for \(i=1,\ldots ,n\). Similarly, combining \(w_i^{l(i,k)}-w_i^k\rightarrow 0\) with point (2) we have \( y_i^k-w_i^{k}\rightarrow 0. \) The proof is now identical to part 3 of the proof of [5, Theorem 1]. \(\square \)

Lemma 4 can be understood intuitively as follows. For each \(k\ge 0\), define

$$\begin{aligned} \epsilon _k \triangleq \max _{i=1,\ldots ,n} \max \big \{\Vert y_i^k - w_i^k\Vert , \Vert G_i z^k - x_i^k\Vert \big \}. \end{aligned}$$

Using Assumption 2 it can be shown that \(k-l(i,k)< M+D\) (see [5, Lemma 8]). Then using Lemma 2(2) it follows that \(w_i^k - w_i^{l(i,k)}\rightarrow 0\) and \(z^k- z^{l(i,k)}\rightarrow 0\). Therefore Lemma 4 implies that \(\epsilon _k\rightarrow 0\). For all \(k\ge M\), \((x_i^k,y_i^k)\in \text {graph}(T_i)\). If \(\epsilon _k=0\) then \(w_i^k = y_i^k\in T_i x_i^k = T_i G_i z^k\) and since \(\sum _{i=1}^n G_i^* w_i^k = 0\), it follows that \((z^k,\mathbf{w}^k)\in \mathcal {S}\) and \(z^k\) solves (3). Thus \(\epsilon _k\) can be thought of as a “residual” measuring how far the algorithm is from finding a point in \(\mathcal {S}\) and a solution to (3). In finite dimensions, it is straightforward to show that if \(\epsilon _k\rightarrow 0\), \((z^k,\mathbf{w}^k)\) must converge to some element of \(\mathcal {S}\). This can be shown using Fejér monotonicity [15, Theorem 5.5] combined with the fact that the graph of a maximal-monotone operator in a finite-dimensional Hilbert space is closed [15, Proposition 20.38]. However, in the general Hilbert space setting the proof is more delicate, since the graph of a maximal-monotone operator is not in general closed in the weak-to-weak topology [15, Example 20.39]. Nevertheless, the overall result was established in the general Hilbert space setting in part 3 of Theorem 1 of [5], which is a special case of [3, Proposition 2.4] (see also [15, Proposition 26.5]).

3.3 Two technical lemmas

Next we include two technical Lemmas that are essentially the same as lemmas 12–13 and parts 1–2 of Theorem 1 of [5]. For completeness, we include somewhat condensed proofs. In these proofs we need the following definitions: \(\phi _k \triangleq \varphi _k(p^k)\) and

$$\begin{aligned} (\forall i=1,\ldots ,n) \quad \psi _{ik} \triangleq \langle G_i z^{l(i,k)} - x^k_i,y_i^k - w^{l(i,k)}_i\rangle , \quad \psi _k \triangleq {\sum _{i=1}^{n}\psi _{ik}}. \end{aligned}$$
(13)

Lemma 5

Suppose Assumptions 1–3 hold and that Algorithm 1 produces an infinite sequence of iterates with \(\{x_i^k\}\) and \(\{y_i^k\}\) being bounded. Then, for all \(i=1,\ldots ,n\), it holds that \(G_i z^{l(i,k)} - x_i^k\rightarrow 0\).

Proof

Using (7)

$$\begin{aligned} \Vert \nabla \varphi _k\Vert _\gamma ^2 = \gamma ^{-1}\left\| {\sum _{i=1}^{n-1} G_i^* y^k_i}+y_{n}^k\right\| ^2 + {\sum _{i=1}^{n-1} \Vert x^k_i - G_i x_{n}^k\Vert ^2} . \end{aligned}$$
(14)

By assumption, \(\{x_i^k\}\) and \(\{y_i^k\}\) are bounded sequences, therefore \(\{\Vert \nabla \varphi _k\Vert _\gamma \}\) is bounded; let \(\xi _1 > 0\) be some bound on this sequence. Next, we will establish that there exists some \(\xi _2>0\) such that

$$\begin{aligned} \psi _k \ge \xi _2 {\sum _{i=1}^n \Vert G_i z^{l(i,k)}-x^k_i\Vert ^2} . \end{aligned}$$
(15)

The proof resembles that of [5, Lemma 12]: since the backtracking linesearch terminates in a finite number of iterations, we must have

$$\begin{aligned} \langle G_i z^{l(i,k)} - x_i^k,y_i^k - w_i^{l(i,k)}\rangle \ge \varDelta \Vert G_i z^{l(i,k)} - x_i^k\Vert ^2 \end{aligned}$$
(16)

for every \(k\in \mathbb {N}\) and \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\). Terms in \(\mathcal {I}_{{{\,\mathrm{B}\,}}}\) are treated as before in [5, Lemma 12]: specifically, for all \(i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\),

$$\begin{aligned} \psi _{ik}&= \left\langle G_i z^{l(i,k)}-x^k_i,y_i^k-w^{l(i,k)}_i\right\rangle \nonumber \\&\overset{\text {(a)}}{=} \left\langle G_i z^{l(i,k)}-x^k_i, \big (\rho _i^{l(i,k)}\big )^{-1}\left( G_i z^{l(i,k)}-x^k_i\right) \right\rangle \nonumber \\&= \big (\rho ^{l(i,k)}_i\big )^{-1}\Vert G_i z^{l(i,k)}-x^k_i\Vert ^2. \end{aligned}$$
(17)

In the above derivation, (a) follows by substitution of (8). Combining (16) and (17) yields

$$\begin{aligned} \psi _k\ge \overline{\rho }^{-1} \sum _{i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}} \Vert G_i z^{l(i,k)}-x^k_i\Vert ^2 + \varDelta \sum _{i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}}\Vert G_i z^{l(i,k)}-x^k_i\Vert ^2, \end{aligned}$$
(18)

which yields (15) with \(\xi _2 = \min \{\overline{\rho }^{-1},\varDelta \}>0\).

We now proceed as in as in part 1 of the proof of [5, Theorem 1]: first, Lemma 2(3) states that the updates on lines 37–38 can be written as

$$\begin{aligned} p^{k+1} = p^k - \frac{\beta _k\max \{\phi _k,0\}}{\Vert \nabla \varphi _k\Vert _\gamma ^2}\nabla \varphi _k. \end{aligned}$$

Lemma 2(2) guarantees that \(p^k - p^{k+1} \rightarrow 0\), so it follows that

$$\begin{aligned} 0 = \lim _{k\rightarrow \infty }\Vert p^{k+1}-p^k\Vert _\gamma = \lim _{k\rightarrow \infty }\frac{\beta _k\max \{\phi _k,0\}}{\Vert \nabla \varphi _k\Vert _\gamma } \ge \frac{\underline{\beta }\limsup _{k\rightarrow \infty }\max \{\phi _k,0\}}{\sqrt{\xi _1}}. \end{aligned}$$

Therefore, \(\limsup _{k\rightarrow \infty } \phi _k\le 0\). Since [5, Lemma 10] states that \(\phi _k - \psi _k\rightarrow 0\), it follows that \(\limsup _{k\rightarrow \infty }\psi _k\le 0\). With (a) following from (15), we next obtain

$$\begin{aligned} 0 \ge \limsup _{k\rightarrow \infty } \psi _k&\overset{\text {(a)}}{\ge } \xi _2\limsup _k {\sum _{i=1}^{n}\Vert G_i z^{l(i,k)} - x^k_i\Vert ^2}\\&\ge \xi _2\liminf _k {\sum _{i=1}^{n}\Vert G_i z^{l(i,k)} - x^k_i\Vert ^2} \ge 0. \end{aligned}$$

Therefore, \( G_i z^{l(i,k)}-x_i^k\rightarrow 0 \) for \(i=1,\ldots ,n\). \(\square \)

Lemma 6

Suppose Assumptions 1–3 hold and that Algorithm 1 produces an infinite sequence of iterates with \(\{x_i^k\}\) and \(\{y_i^k\}\) being bounded. Then, for all \(i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\), one has \(y_i^k - w_i^{l(i,k)}\rightarrow 0\).

Proof

The argument to is similar to those of [5, Lemma 13] and [5, Theorem 1 (part 2)]: the crux of the proof is to establish for all \(k\ge M\) that

$$\begin{aligned} \psi _k + \sum _{i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}}\langle x^k_{i}-G_{i}z^{l(i,k)},T_i x^k_{i}-T_i G_{i}z^{l(i,k)}\rangle \ge \underline{\rho } \sum _{i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}} \Vert y_i^k - w_i^{l(i,k)}\Vert ^2. \end{aligned}$$
(19)

Since \(T_i\) is continuous and defined everywhere, \(x_i^k\) is bounded by assumption, and \(z^{l(i,k)}\) is bounded by Lemma 2, the extreme value theorem implies that \(T_i x^k_{i}-T_i G_{i}z^{l(i,k)}\) is bounded. Furthermore from Lemma 5, \( \lim \sup _{k\rightarrow \infty }\psi _k\le 0, \) and \(x_i^k - G_iz^{l(i,k)}\rightarrow 0\). Therefore the desired result follows from (19).

It remains to prove (19). For all \(k\ge M\), we have

$$\begin{aligned} \psi _k&= \sum _{i=1}^n\langle G_i z^{l(i,k)}-x^k_i,y^k_i-w^{l(i,k)}_i\rangle \nonumber \\&\overset{\text {(a)}}{=} \sum _{i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}} \langle \rho ^{l(i,k)}_i(y^k_i - w^{l(i,k)}_i),y^k_i - w^{l(i,k)}_i\rangle \nonumber \\&\quad +\, \sum _{i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}}\langle G_{i} z^{l(i,k)}-x^k_{i},T_i G_{i} z^{l(i,k)}-w_{i}^{l(i,k)}\rangle \nonumber \\&\quad +\, \sum _{i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}} \langle G_{i}z^{l(i,k)}-x^k_{i},y^k_{i}-T_i G_{i} z^{l(i,k)}\rangle \nonumber \\&\overset{\text {(b)}}{=} \sum _{i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}} \left( \rho ^{l(i,k)}_i\Vert y^k_i - w^{l(i,k)}_i\Vert ^2 \right) \nonumber \\&\quad +\, \sum _{i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}}\langle \rho ^{l(i,k)}_{i}(T_iG_{i} z^{l(i,k)}-w_{i}^{l(i,k)}),T_i G_{i} z^{l(i,k)}-w_{i}^{l(i,k)}\rangle \nonumber \\&\quad -\, \sum _{i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}}\langle x^k_{i}-G_{i}z^{l(i,k)},T_i x^k_{i}-T_i G_{i}z^{l(i,k)}\rangle \nonumber \\&\overset{\text {(c)}}{\ge } \underline{\rho }\sum _{i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}}\Vert y^k_i - w^{l(i,k)}_i\Vert ^2 - \sum _{i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}}\langle x^k_{i}-G_{i}z^{l(i,k)},T_i x^k_{i}-T_i G_{i}z^{l(i,k)}\rangle . \end{aligned}$$
(20)

In the above derivation, (a) follows by substition of (8) into the \(\mathcal {I}_{{{\,\mathrm{B}\,}}}\) terms and algebraic manipulation of the \(\mathcal {I}_{{{\,\mathrm{F}\,}}}\) terms. Next, (b) is obtained by algebraic simplification of the \(\mathcal {I}_{{{\,\mathrm{B}\,}}}\) terms and substitution of (9) into the two groups of \(\mathcal {I}_{{{\,\mathrm{F}\,}}}\) terms. Finally, (c) follows by dropping the terms from (20), which must be nonnegative. \(\square \)

3.4 Main result

We are now ready to prove the main result of this paper: weak convergence of the iterates of Algorithm 1 to a solution of (3). The main challenge is establishing \(y_i^k - w_i^{l(i,k)}\rightarrow 0\) for \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\). Since we no longer assume Lipschitz continuity, this requires significant innovation beyond our previous work [5] and constitutes the bulk of the following argument.

Theorem 1

Suppose Assumptions 1–3 hold. If Algorithm 1 terminates at line 34, then its final iterate \((z^{k+1},\mathbf{w}^{k+1})\) is a member of the extended solution set \(\mathcal {S}\) defined in (5). Otherwise, the sequence \(\{(z^k,\mathbf{w}^k)\}\) generated by Algorithm 1 converges weakly to some point \((\bar{z},\overline{\mathbf{w}})\) in \(\mathcal {S}\) and furthermore \(x_i^k\rightharpoonup G_i \bar{z}\) and \(y_i^k\rightharpoonup \overline{w}_i\) for all \(i=1,\ldots ,n-1\), \(x_{n}^k\rightharpoonup \bar{z}\), and \(y_n^k\rightharpoonup -\sum _{i=1}^{n-1}G_i^* \overline{w}_i\).

Proof

The argument when the algorithm terminates via line 34 is identical to [5, Theorem 1]. From now on we assume the algorithm produces an infinite sequence of iterates. The proof proceeds by showing that the two conditions of Lemma 4 are satisfied. To establish Lemma 4(1) for \(i=1,\ldots ,n\) and Lemma 4(2) for \(i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\), we will show that \(\{x_i^k\}\) and \(\{y_i^k\}\) are bounded, and then employ Lemmas 5 and 6. This argument is only a slight variation of what was given in [5]. The main departure from [5] is in establishing Lemma 4(2) for \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\), which requires significant innovation.

We begin by establishing that \(\{x_i^k\}\) and \(\{y_i^k\}\) are bounded. For \(i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\) the boundedness of \(\{x_i^k\}\) follows exactly the same argument as [16, Lemma 10]. For \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\) write using Lemma 1

$$\begin{aligned} \Vert x_i^k\Vert&\le \Vert G_i z^{l(i,k)} - \hat{\rho }_i^{l(i,k)}T_i G_i z^{l(i,k)}\Vert + \hat{\rho }_i^{l(i,k)}\Vert w_i^{l(i,k)}\Vert \end{aligned}$$
(21)
$$\begin{aligned}&\le \Vert G_i\Vert \Vert z^{l(i,k)}\Vert + \overline{\rho }\Vert T_i G_i z^{l(i,k)}\Vert + \overline{\rho }\Vert w_i^{l(i,k)}\Vert . \end{aligned}$$
(22)

Now \(z^{l(i,k)}\) and \(w_i^{l(i,k)}\) are bounded by Lemma 2. Furthermore, since \(T_i\) is continuous with full domain, \(G_i\) is bounded, and \(z^{l(i,k)}\) is bounded, \(\{T_iG_i z^{l(i,k)}\}\) is bounded by the extreme value theorem. Thus \(\{x_i^k\}\) is bounded for \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\).

Now we prove that \(\{y_i^k\}\) is bounded. For \(i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\), Lemma 1 implies that

$$\begin{aligned} y_i^k = \left( \rho _i^{l(i,k)}\right) ^{-1} \left( G_i z^{l(i,k)} - x_i^k + \rho _i^{l(i,k)} w_i^{l(i,k)} \right) . \end{aligned}$$

Since \(\rho _i^k\) is bounded from above and below, \(G_i\) is bounded, and \(z^{l(i,k)}\) and \(w_i^{l(i,k)}\) are bounded by Lemma 2, \(\{y_i^k\}\) is bounded for \(i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\). For \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\), since \(y_i^k = T_i x_i^k\) and \(T_i\) is continuous with full domain, it follows again from the extreme value theorem that \(\{y_i^k\}\) is bounded.

Therefore we can apply Lemma 5 to infer that \(G_i z^{l(i,k)} - x_i^k\rightarrow 0\) for \(i=1,\ldots ,n\), and Lemma 4(1) holds. Furthermore we can apply Lemma 6 to infer that \(y_i^k - w_i^{l(i,k)}\rightarrow 0\) for \(i\in \mathcal {I}_{{{\,\mathrm{B}\,}}}\).

It remains to establish that \(y_i^k - w_i^{l(i,k)}\rightarrow 0\) for \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\). The argument needs to be significantly expanded from that in [5], since it is not immediate that the stepsize \(\hat{\rho }_i^k\) is bounded away from 0.

From Lemma 2, we know that \(z^{l(i,k)}\) and \(w_i^{l(i,k)}\) are bounded, as is the operator \(G_i\) by assumption. Furthermore, since \(T_i\) is continuous with full domain, we know once again from the extreme value theorem that there exists \(B\ge 0\) such that

$$\begin{aligned} (\forall k\in \mathbb {N}) \quad \Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert \le B. \end{aligned}$$
(23)

We have already shown that \(x_i^k\) is bounded. Using the boundedness of \(z^k\) and \(w_i^k\) in conjunction with Assumption 3 and inspecting the steps in the backtracking search, there must exist a closed ball \(\mathcal {B}_x\subset \mathcal {H}_i\) such that \(\tilde{x}_i^{(j,s(i,k))}\in \mathcal {B}_x\) for all \(k,j\in \mathbb {N}\) such that \(i \in I_k\) and j is encountered during the backtracking linesearch at step k. In addition, let \(\mathcal {B}_{GZ}\subset \mathcal {H}_i\) be a closed ball containing \(G_iz^{l(i,k)}\) for all \(k\in \mathbb {N}\). Let \(\mathcal {B} \triangleq \mathcal {B}_x\cup \mathcal {B}_{GZ}\), which is another closed ball. Since \(\mathcal {H}_i\) is finite dimensional, \(\mathcal {B}\) is compact. Since \(T_i\) is continuous everywhere, by the Heine–Cantor theorem it is uniformly continuous on \(\mathcal {B}\) [18, Theorem 21.4].

Continuing, we write

$$\begin{aligned} y_i^k -w_i^{l(i,k)}= T_ix_i^k-w_i^{l(i,k)} = T_i G_i z^{l(i,k)}-w_i^{l(i,k)} + T_i x_i^k - T_i G_i z^{l(i,k)}. \end{aligned}$$
(24)

Since \(T_i\) is uniformly continuous on \(\mathcal {B}\) it must be Cauchy continuous, meaning that \(x_i^k - G_i z^{l(i,k)}\rightarrow 0\) implies \(T_i x_i^k - T_i G_i z^{l(i,k)}\rightarrow 0\). Thus, to prove that \(y_i^k - w_i^{l(i,k)}\rightarrow 0\) it is sufficient to show that \(T_i G_i z^{l(i,k)}-w_i^{l(i,k)}\rightarrow 0\).

We now show that indeed \(T_i G_i z^{l(i,k)}-w_i^{l(i,k)}\rightarrow 0\). Fix \(\epsilon >0\). Since \(T_i\) is uniformly continuous on \(\mathcal {B}\), there exists \(\delta >0\) such that whenever \(x,y \in \mathcal {B}\) and \(\Vert x-y\Vert \le \delta \), then \(\Vert T_ix-T_iy\Vert \le \epsilon /4\). Since \(G_i z^{l(i,k)} - x_i^k\rightarrow 0\), there exists \(K\ge 1\) such that for all \(k\ge K\),

$$\begin{aligned} \Vert G_i z^{l(i,k)} - x_i^k\Vert \le \epsilon \min \left( \frac{\nu \epsilon }{4B\varDelta },\frac{\nu \delta }{B},\underline{\rho } \right) \end{aligned}$$
(25)

with B as in (23), \(\varDelta \) from the linesearch termination criterion, and \(\underline{\rho }\) from Assumption 3. For any \(k\ge K\) we will show that

$$\begin{aligned} \Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert \le \epsilon . \end{aligned}$$
(26)

If \( \Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert \le \epsilon /2, \) then (26) clearly holds. So from now on it is sufficient to consider k for which \( \Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert > \epsilon /2. \) As in the proof of Lemma 3, let \(\rho \triangleq \tilde{\rho }_i^{(j,s(i,k))}\) for brevity. Reconsidering (12), we now have the following lower bound for the left-hand side of (10):

$$\begin{aligned}&\frac{ \Vert T_iG_i z^{l(i,k)} - w_i^{l(i,k)}\Vert - \Big \Vert T_i\big (G_i z^{l(i,k)} - \rho (T_iG_i z^{l(i,k)} - w_i^{l(i,k)})\big ) - T_iG_i z^{l(i,k)}\Big \Vert }{\rho \Vert T_iG_i z^{l(i,k)}-w_i^{l(i,k)}\Vert }\nonumber \\&\quad > \frac{ \epsilon /2 - \Big \Vert T_i\big (G_i z^{l(i,k)} - \rho (T_iG_i z^{l(i,k)} - w_i^{l(i,k)})\big ) - T_iG_i z^{l(i,k)}\Big \Vert }{\rho \Vert T_iG_i z^{l(i,k)}-w_i^{l(i,k)}\Vert }. \end{aligned}$$
(27)

Now, suppose it were true that

$$\begin{aligned} \Vert G_i z^{l(i,k)}-\tilde{x}_i^{(j,s(i,k))}\Vert = \rho \Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert \le \delta . \end{aligned}$$
(28)

Then the uniform continuity of \(T_i\) on \(\mathcal {B}\) would imply that

$$\begin{aligned}&\Vert T_i G_i z^{l(i,k)}-T_i \tilde{x}_i^{(j,s(i,k))}\Vert \\&\quad = \Big \Vert T_i\big (G_i z^{l(i,k)} - \rho (T_iG_i z^{l(i,k)} - w_i^{l(i,k)})\big ) - T_iG_i z^{l(i,k)}\Big \Vert \le \frac{\epsilon }{4}. \end{aligned}$$

We next observe that (28) is implied by \( \rho \le \frac{\delta }{B}, \) in which case (27) gives the following lower bound on the left-hand side of (10):

$$\begin{aligned} \frac{ \langle G_i z^{l(i,k)} - \tilde{x}_i^{(j,s(i,k))},\tilde{y}_i^{(j,s(i,k))} - w_i^{l(i,k)}\rangle }{\Vert G_i z^{l(i,k)} - \tilde{x}_i^{(j,s(i,k))}\Vert ^2} >\frac{\epsilon }{4\rho \Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert } \ge \frac{\epsilon }{4\rho B}. \end{aligned}$$

Therefore if \(\rho \) also satisfies \(\rho \le \frac{\epsilon }{4B\varDelta }\), then

$$\begin{aligned} \frac{ \langle G_i z^{l(i,k)} - \tilde{x}_i^{(j,s(i,k))},\tilde{y}_i^{(j,s(i,k))} - w_i^{l(i,k)}\rangle }{\Vert G_i z^{l(i,k)} - \tilde{x}_i^{(j,s(i,k))}\Vert ^2} >\varDelta . \end{aligned}$$
(29)

Thus, any stepsize satisfying \(\rho \le (1/B) \min \left\{ \epsilon /(4\varDelta ), \delta \right\} \) must cause the backtracking linesearch termination criterion at line 18 to hold. Therefore, since the backtracking linesearch proceeds by reducing the stepsize by a factor of \(\nu \) at each inner iteration, it must terminate with

$$\begin{aligned} \hat{\rho }_i^{l(i,k)}\ge \underline{\rho }^{bt} \triangleq \min \left\{ \frac{\nu \epsilon }{4 B\varDelta } , \frac{\nu \delta }{B}, \underline{\rho } \right\} . \end{aligned}$$
(30)

Now, using Lemma 1, we have

$$\begin{aligned} x_i^{k} - G_i z^{l(i,k)}&= -\hat{\rho }_i^{l(i,k)}(T_i G_i z^{l(i,k)} - w_i^{l(i,k)})\\ \implies \Vert x_i^{k} - G_i z^{l(i,k)}\Vert&= \hat{\rho }_i^{l(i,k)}\Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert . \end{aligned}$$

Thus,

$$\begin{aligned} \Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert&\le (\underline{\rho }^{bt})^{-1} \Vert x_i^{k} - G_i z^{l(i,k)}\Vert \\&\le \min \left\{ \frac{\nu \epsilon }{4 B\varDelta } , \frac{\nu \delta }{B}, \underline{\rho } \right\} ^{-1} \Vert x_i^{k} - G_i z^{l(i,k)}\Vert \le \epsilon \end{aligned}$$

and therefore (26) holds for all \(k\ge K\). Since \(\epsilon >0\) was chosen arbitrarily, it follows that \(\Vert T_i G_i z^{l(i,k)} - w_i^{l(i,k)}\Vert \rightarrow 0\) and thus \(\Vert y_i^k - w_i^{l(i,k)}\Vert \rightarrow 0\) by (24). The proof that Lemma 4(2) holds is now complete. The proof of the theorem now follows from Lemma 4. \(\square \)

If \(\mathcal {H}_i\) is not finite dimensional for \(i\in \mathcal {I}_{{{\,\mathrm{F}\,}}}\), Theorem 1 can still be proved if the assumption on \(T_i\) is strengthened to Cauchy continuity over all bounded sequences. This is slightly stronger than the assumption given in [7, Equation (1.1)] for proving weak convergence of Tseng’s forward–backward–forward method. That assumption is Cauchy continuity but only for all weakly convergent sequences.

4 Numerical example: fused \(L_p\) regression

Consider the following optimization problem:

$$\begin{aligned} F^* \triangleq \min _{x\in \mathbb {R}^d} F(x) \triangleq \frac{1}{p}\Vert Ax - b\Vert _p^p + \lambda _1\Vert Dx\Vert _1 + \lambda _2\Vert x\Vert _1 \end{aligned}$$
(31)

where \(1<p\le 2\), \(A:\mathbb {R}^d\rightarrow \mathbb {R}^m\) is linear, \(b\in \mathbb {R}^m\), \(\lambda _1,\lambda _2\ge 0\), and \(D:\mathbb {R}^d\rightarrow \mathbb {R}^{d-1}\) is the finite difference operator defined by \(\{Dx\}_i = x_{i+1}-x_i\). While increasing \(\lambda _2\) typically forces a sparser solution, increasing \(\lambda _1\) typically forces the nonzero coefficients of the solution to group together (i.e. “fuse” together) with the same value. Regression problems of this sort are common for \(p=2\) [19]. However, the loss function \(\Vert \cdot \Vert _2^2\) is highly sensitive to outliers in the noise distribution. If outliers are present, then choosing \(p<2\) has been shown to lead to more robust estimates [20, 21].

By [15, Thm. 27.2], (31) is equivalent to the following monotone inclusion: find \(z\in \mathbb {R}^d\) such that

$$\begin{aligned} 0\in D^* T_1 D z +T_2 z+ T_3 z, \end{aligned}$$
(32)

where \( T_1\triangleq \lambda _1\partial \{\Vert \cdot \Vert _1\}\), \(T_2\triangleq \lambda _2\partial \{\Vert \cdot \Vert _1\}\), and \(T_3 x\triangleq \nabla \big \{\frac{1}{p}\Vert Ax - b\Vert _p^p\big \} \) . Note that for \(1<p<2\), the operator \(T_3\) is continuous but not Lipschitz continuous (in fact, it is only \((p-1)\)-Hölder continuous). Thus, it is not possible to apply well-known first-order optimization methods such as the proximal gradient method and FISTA [22], as they require Lipschitz continuous gradients. Furthermore these methods can only handle one nonsmooth function via its proximal operator, but (31) has two. However, we can apply our method in Algorithm 1, since it only requires that the gradient be continuous in order to perform forward steps, and can handle sums of arbitrarily many nonsmooth functions through these functions’ corresponding proximal operators. Thus, we apply Algorithm 1 with \(\mathcal {I}_{{{\,\mathrm{F}\,}}}= \{3\}\), \(\mathcal {I}_{{{\,\mathrm{B}\,}}}= \{1,2\}\), \(G_1 = D\), and \(G_2=G_3=I\). We apply the algorithm with no delays and full synchronization, so that \(d(i,k)=k\) and \(I_k=\{1,2,3\}\) for all i and k. From now on we refer to this as ps, short for projective splitting.

One of the few proximal splitting methods that can be applied to (31) is the method of [11]. Note that the analysis of [11] requires Lipschitz continuity of \(T_3\). However, since the algorithm is an instance of Tseng’s method applied to the underlying primal–dual “monotone+skew” inclusion, one may modify it by applying the backtracking linesearch variant of Tseng’s method, which does not require Lipschitz continuity. We refer to this as tseng-pd. In order to achieve good performance with tseng-pd, we had to incorporate the following diagonal preconditioner:

$$\begin{aligned} U = \text {diag}(I_{d\times d},\gamma _{pd}I_{d\times d},\gamma _{pd}I_{d\times d}) \end{aligned}$$
(33)

where U is as in [23, Eq. (3.2)]. We also compare with the standard subgradient method sg as well as the proximal subgradient method prox-sg which takes proximal (resolvent) steps with respect to the term \(\lambda _2\Vert \cdot \Vert _1\) and (sub)gradient steps with respect to the other two terms [24].

We created a random instance of (31) as follows: we set \(m=1000\) and \(d=2000\). The entries of A are drawn i.i.d. from \(\mathcal {N}(0,1)\) and then the columns of A are normalized to have unit norm and 0 mean. A vector \(x_0\in \mathbb {R}^d\) was created with 500 nonzero entries which are grouped together into 10 blocks of size 50, all with the same value in each block. We then set \(b=Ax_0 + \epsilon \). For each entry of \(\epsilon \), with probability 0.9 it was drawn from \(\mathcal {N}(0,1)\), otherwise from \(\mathcal {N}(0,25)\). We tested three values of p: 1.7, 1.5,  and 1.3. For all p, we set \(\lambda _1=\lambda _2=1\).

For the two methods using backtracking linesearch (ps and tseng-pd), we set the initial trial stepsize to 1 at the first iteration, and afterwards set it to be the successful stepsize discovered in the previous iteration. For each failure of the backtracking exit condition the stepsize was reduced by a factor of 0.7. For the other parameters of ps, we used \(\rho _1^k=\rho _2^k=1\) for all k, and \(\gamma =\varDelta =1\). For tseng-pd, we used \(\theta =0.99\). The best-tuned value for \(\gamma _{pd}\) in the preconditioner in (33) was \(\gamma _{pd}=100\). Finally, the stepsizes for the subgradient methods were set to \(\alpha _k = \alpha _0 k^{-r}\), where for both sg and prox-sg we used \((\alpha _0,r)=(1,1)\), which performed best in practice. We implemented all the methods in Python using the numpy package. The Python code used in these experiments is publicly available at https://github.com/projective-splitting/just-continuity [25].

Fig. 1
figure 1

Left: \(p=1.3\), middle: \(p=1.5\), right: \(p=1.7\). The algorithms are: ps (our projective splitting method as in Algorithm 1), sg (the subgradient method), prox-sg (proximal subgradient method [24]), and tseng-pd (primal–dual version of Tseng’s method [11])

Full size image

In Fig. 1 we plot the performance of the methods in terms of the relative primal objective error \((F(x^k)-F^*)/F^*\), where the true minimum value \(F^*\) is estimated as the lowest value returned by any algorithm after 2000 iterations. The left, middle, and right plots correspond to \(p=1.3\), \(p=1.5\), and \(p=1.7\), respectively. The figure plots just one representative random instance but performance was very similar over 10 random instances. The x-axis counts the number of matrix multiplies by A, which is the dominant computation for all methods.

On all problems, sg and prox-sg are outperformed by ps and tseng-pd, and ps is that fastest method. For \(p=1.3\), the difference between ps and tseng-pd is fairly small, but for \(p=1.5\) and 1.7, the advantage of ps over tseng-pd is substantial. One advantage ps has over the other methods is that it allows for different stepsizes for each operator. So, even when backtracking results in a small stepsize for \(T_3\), the other stepsizes may be held constant. By contrast, tseng-pd only has one stepsize for all three operators, which may become small as the result of backtracking on one of them. This difference may explain tseng-pd’s slower convergence rate when \(p=1.5\). A possible explanation for the relatively poor performance of both sg and prox-sg is that their update directions are only subgradients rather than gradients.