1 Introduction

It has been confirmed through various well-known cosmological tests (Riess et al. 1998; Perlmutter et al. 1999; Miller et al. 1999; Astier et al. 2006) that our universe currently undergoes accelerated expansion. In order to understand the nature of this accelerated expansion phenomenon, various approaches have been adopted. The first approach consists of the presence of dark energy (DE) which contains the repulsive force to push the matter apart in the universe. In this respect, many reviews have been presented (Copeland et al. 2006; Sami 2009; Frieman et al. 2008; Bamba et al. 2012). The second approach is the modification of Einstein’s gravity into different theories. The basic idea behind this way is to present the gravitational description of DE (Brevik et al. 2005).

These modified gravities has some important features. One of them is that it has ability to explains both scenarios i.e., early inflation and late time accelerated expansion (Caramsa and de Mellob 2009). Different classes of modified gravity have been reviewed in the references (Nojiri and Odintsov 2005, 2011; Olmo 2011). Nojiri and Odintsov (2011) have given a detailed discussion on different well-known modified gravity models. Nojiri and Odintsov (2011) investigated the unified scenario of the universe through modified gravity background evolution for flat FRW universe. The popular modified gravity models include: f(R) gravity, \(f(\mathcal{G})\) gravity, f(T) gravity and Horava-Lifshitz gravity. A review on f(T) gravity is available in Myrzakulov (2011).

There is another well-known modified gravity introduced by Chaichian (2010) through a general approach which is invariant under foliation-preserving diffeomorphisms. Elizalde et al. (2005) investigated the early time inflation, late time acceleration phenomenon as well as finite time future singularities in detail and suggested a higher order term to cure these singularities in this gravity. It was also explored (Carloni et al. 2010) FRW cosmology for finite time singularities and explained reductions of this gravity by taking power-law MFRHL \(F(\tilde{R})\) model.

The correspondence scenario between dynamical DE models and modified theories of gravity has got much attraction nowadays. Various works has been done by choosing reconstruction scheme of many scenarios in modified theories of gravity (Nojiri and Odintsov 2006a, 2006b; Nojiri and Odintsov 2007a, 2007b, 2007c). Chattopadhyay has explored this phenomenon by using F(T) and F(G) gravities and QCD ghost DE and found interesting results (Chattopadhyay 2014a, 2014b). Chattopadhyay and Ghosh (2012) have analyzed the behavior of generalized second law of thermodynamics in this gravity and argued that it remains valid in quintessence phase. We have also explored different cosmological parameters through reconstruction scenario via different modified theories of gravity as well as dynamical DE models (Jawad et al. 2013a, 2013b, 2013c, 2013d, 2014; Jawad 2014a, 2014b).

In the present work, we re-investigate the correspondence phenomenon by choosing the scenario of modified Horava-Lifshitz F(R) gravity (MFRHL) gravity (Chaichian 2010) and pilgrim DE (PDE) (Wei 2012). We construct the \(F(\tilde{R})\) models by assuming the Hubble and event horizons as well as different values of PDE parameter. We also make the cosmological analysis of these models through EoS and squared speed of sound parameters, \(\omega_{\mathit{DE}}-\omega'_{\mathit{DE}}\) and r−s planes. Rest of the paper has been arranged as follows. In the next section, we provide basic scenario of MFRHL gravity in the flat FRW universe. Section 3 elaborates the cosmological discussion on reconstructed \(F(\tilde{R})\) models. We summarize these outcomes in the last section.

2 \(F(\tilde{R})\) gravity

The action of MFRHL gravity (\(F(\tilde{R})\) gravity) is defined as follows (Carloni et al. 2010; Chaichian 2010)

$$\begin{aligned} S_{F(\tilde{R})}=\int d^{4}\sqrt{g^{(3)}}N F( \tilde{R}) \end{aligned}$$

with

$$\begin{aligned} \tilde{R} =&K^{ij}K_{ij}-\lambda K^{2}\\ &{}+2\mu \nabla_{\mu} \bigl(n^{\mu}\nabla_{\nu}n^{\nu}-n^{\nu} \nabla_{\nu}n^{\mu}\bigr)- E^{ij}\mathcal{G}_{ijkl}E^{kl}, \end{aligned}$$

appears as modified Ricci scalar. In flat universe, it becomes

$$\begin{aligned} \tilde{R} =&\frac{(3-9\lambda)H^2}{N^2}+\frac{6\mu}{a^3 N}\frac{d}{dt} \biggl( \frac{Ha^3}{N} \biggr)\\ =&\frac{ (3-9\lambda+18\mu )H^2}{N^2}+ \frac{6\mu}{N}\frac{d}{dt} \biggl(\frac{H}{N} \biggr). \end{aligned}$$

The f(R) gravity can be recovered by setting λ=μ=1. For the action stated earlier, we get by variation over \(g_{ij}^{(3)}\) and by setting N=1:

$$\begin{aligned} 0 =&F(\tilde{R})-2(1-3\lambda+3\mu) \bigl(\dot{H}+3H^2 \bigr)F'(\tilde {R}) \\ &{}-2(1-3\lambda)H\frac{dF'(\tilde{R})}{dt}+2\mu \frac{d^2F'(\tilde{R})}{dt^2}+p. \end{aligned}$$
(1)

Here, prime shows the differentiation with respect to its argument and also the matter contribution is involved as pressure p. The conservation equation with respect to matter density becomes

$$ \dot{\rho}+3H(\rho+p)=0. $$
(2)

Using Eqs. (1) and (2), we get

$$\begin{aligned} 0 =&F(\tilde{R})-6 \bigl[(1-3\lambda+3\nu)H^{2}+\mu \dot{H} \bigr]F'(\tilde{R}) \\ &{}+6\mu H\frac{dF'(\tilde{R})}{dt}-\rho-Ca^{-3}, \end{aligned}$$
(3)

where C is an integration constant. Thus, the density corresponding to MFRHL gravity with C=0 turns out to be

$$\begin{aligned} \rho_{\tilde{R}} =&F(\tilde{R})-6 \bigl[(1-3\lambda+3 \mu)H^{2}+\mu \dot{H} \bigr]F'(\tilde{R}) \\ &{}+6\mu H \frac{dF'(\tilde{R})}{dt}. \end{aligned}$$
(4)

Here, we assume a power-law form of the scale factor for obtaining the analytical solutions of \(F(\tilde{R})\) as follows

$$ a(t)=a_0t^m $$
(5)

where the constant a 0 represents the present day value of the scale factor.

3 Reconstruction of pilgrim dark energy \(F(\tilde{R})\) models and their cosmological analysis

The PDE model is defined as (Wei 2012)

$$\begin{aligned} \rho_{\mathit{DE}}=3n^2 m_p^{4-u}L^{-u}, \end{aligned}$$
(6)

here L, u, n, m p indicate the IR cutoff and size of the system, PDE parameter, conventional constant and reduced Planck mass, respectively. Wei (2012) analyzed the PDE model through different possible theoretical and observational ways to make the BH free phantom universe with Hubble horizon through PDE parameter. Moreover, this model has been analyzed this proposal by choosing different IR cutoffs through well-known cosmological parameters in flat and non-flat universes (Sharif and Jawad 2013a, 2013b, 2014; Jawad 2014d). This model has also been in different modified gravities (Sharif and Rani 2014; Chattopadhyay et al. 2014).

Here, we make correspondence between PDE and \(F(\tilde{R})\) model by equating their energy densities, i.e. \(\rho_{\tilde{R}}=\rho_{\mathit{DE}}\), which gives

$$\begin{aligned}& 6\mu H\dot{\tilde{R}}F''(\tilde{R})-6 \bigl[(1-3\lambda+3\mu)H^{2}+\mu \dot{H} \bigr]F'( \tilde{R})+F(\tilde{R}) \\& \quad=3n^2 m_p^{4-u}L^{-u}. \end{aligned}$$
(7)

Further, we choose two IR cutoffs such Hubble and event horizons.

3.1 With Hubble horizon

The Hubble horizon is defined as follows

$$ L=\frac{1}{H} $$
(8)

By using Eqs. (5) and (8) in (7), we obtain

$$\begin{aligned}& \tilde{R}^2\frac{d^2F(\tilde{R})}{d\tilde{R}^2}+\frac{m(1-3\lambda +3\mu)-\mu}{2\mu} \tilde{R}\frac{dF(\tilde{R})}{d\tilde{R}} \\& \qquad{}-\frac{m(3-9\lambda+12\mu )}{12\mu}F(\tilde{R}) \\& \quad=\frac{n^2}{4\mu(3-9\lambda+12\mu)^{\frac{u-2}{2}}}\tilde{R}^{\frac{u}{2}}, \end{aligned}$$
(9)

which gives

$$\begin{aligned} F(\tilde{R}) =&A\tilde{R}^{\xi_-}+B\tilde{R}^{\xi_+}+ \frac{(3-9\lambda +12\mu)^{1-u/2} \tilde{R}^{u/2} n^2}{\mu(\xi_{+}-u)(\xi_{-}-u)}\tilde{R}^u. \end{aligned}$$
(10)

Here, A and B are integration constants while ξ ∓ is given by

$$\begin{aligned} \xi_{\mp} =&1-\frac{(-\mu+m-3\lambda m+3\mu m)}{(2\mu)}\\ &{}\mp \biggl(1- \frac{(-\mu+m-3\lambda m+3\mu m)}{\mu} \\ &{}+\frac{(-\mu+m-3\lambda m +3\mu m)^2}{4\mu^2}\\ &{}-\frac{(m-3\lambda m+4\mu m)}{\mu} \biggr)^{\frac{1}{2}}. \end{aligned}$$

The above reconstructed model (10) with u=2 characterizes as a realistic one because it satisfies the following sufficient condition

$$ \lim_{\tilde{R}\rightarrow0}F(\tilde{R})=0. $$
(11)

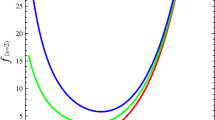
To analyze the behavior of constructed model \(F(\tilde{R})\), we plot it against its argument \(\tilde{R}\) as shown in Figs. 1 and 2. It shows decreasing behavior in both cases of u=±2.

Fig. 1
figure 1

Plot of \(f(\tilde{R})\) versus \(\tilde{R}\) for PDE parameter u=2 with m=2 (red), m=2.2 (green) and m=2.4 (blue) for Hubble horizon

Full size image
Fig. 2
figure 2

Plot of \(f(\tilde{R})\) versus \(\tilde{R}\) for PDE parameter u=−2 with m=2 (red), m=2.2 (green) and m=2.4 (blue) for Hubble horizon

Full size image

3.2 With event horizon

The event horizon is defined as follows

$$\begin{aligned} L=a(t)\int^{\infty}_{t}{ \frac{d\tilde{t}}{a(\tilde{t})}}, \end{aligned}$$
(12)

and the corresponding reconstructed model is given by

$$\begin{aligned} F(\tilde{R}) =&\frac{3^{1-\frac{u}{2}}(-1+m)^u m^{-\frac{u}{2}}(-2\mu+(1-3\lambda+6\mu)m)^{1-\frac{u}{2}} n^2}{\mu(\delta_{+}-u)(\delta_{-}-u)}\tilde{R}^{\frac{u}{2}} \\ &{}+C\tilde{R}^{\delta_-}+D\tilde{R}^{\delta_+}, \end{aligned}$$
(13)

where C and D are integrating constants while δ ∓ are

$$\begin{aligned} \delta_{\mp} =&1-\frac{(-\mu+m-3\lambda m+3\mu m)}{(2\mu)}\\ &{}\mp \biggl(1+ \frac{(-2\mu+m-3\lambda m+6\mu m)}{\mu} \\ &{}+\frac{(-\mu+m-3\lambda m +3\mu m)^2}{4\mu^2}\\ &{}-\frac{(-\mu m-3\lambda m+3\mu m)}{\mu} \biggr)^{\frac{1}{2}}. \end{aligned}$$

The model \(F(\tilde{R})\) against its arguments is shown in Figs. 3 and 4 for two values of u=±2, respectively. In first case (u=+2), the function decreases and approaches to minimum positive value. However, the function decreases and approaches to zero in all three cases of m in the second case (u=−2).

Fig. 3
figure 3

Plot of \(F(\tilde{R})\) versus \(\tilde{R}\) for PDE parameter u=2 with m=2 (red), m=2.2 (green) and m=2.4 (blue) for event horizon

Full size image
Fig. 4
figure 4

Plot of \(F(\tilde{R})\) versus \(\tilde{R}\) for PDE parameter u=−2 with m=2 (red), m=2.2 (green) and m=2.4 (blue) for event horizon

Full size image

4 Cosmological analysis for both horizons

4.1 Equation of state parameter

The EoS parameter is defined as follows

$$\begin{aligned} w_{\mathit{DE}}=\frac{p_{\mathit{DE}}}{\rho_{\mathit{DE}}}. \end{aligned}$$

Through reconstruction scenario, i.e., \(\rho_{\tilde{R}}=\rho_{\mathit{DE}}\) and \(p_{\tilde{R}}=p_{\mathit{DE}}\), we can get EoS parameter whose plots are shown in Figs. 5–8, with respect to Hubble and event horizons with u=±2, respectively. For Hubble horizon (with u=+2), the EoS parameter evolutes the universe in the quintessence region always for m=2.2. However, it shows transition from dust like matter to phantom region by crossing phantom divide line and then goes towards quintessence region in the latter epoch for other two cases of m as shown in Fig. 5. Figure 6 (u=−2 for Hubble horizon) shows quintom-like behavior for all cases of m. In case of event horizon (Figs. 7 and 8), we can attain quintom-like behavior (transition from matter dominated era towards phantom and then goes to quintessence era in the latter epoch) for u=−2. In case of u=+2, we only attain the quintessence and vacuum DE eras as shown in Fig. 7.

Fig. 5
figure 5

Plot of w DE versus t for PDE parameter u=2 with Hubble horizon

Full size image
Fig. 6
figure 6

Plot of w DE versus t for PDE parameter u=−2 with Hubble Horizon

Full size image
Fig. 7
figure 7

Plot of w DE versus t for PDE parameter u=2 with event horizon

Full size image
Fig. 8
figure 8

Plot of w DE versus t for PDE parameter u=−2 with event horizon

Full size image

4.2 Squared speed of sound

The squared speed of sound is used for analyzing the stability of a give model. The sign of \(v_{s}^{2}\) is very important to see the stability of background evolution of the model. A positive value indicates a stable model whereas instability of a given perturbation corresponds to the negative value of \(v^{2}_{s}\). The squared speed of sound takes the form in the present scenario

$$ \upsilon_{s}^2=\frac{\dot{p}_{\mathit{DE}}}{\dot{\rho}_{\mathit{DE}}}. $$
(14)

The plot of squared speed of sound with respect to time for two values of PDE parameter is shown in Figs. 9–12 for two horizons of PDE, respectively. For u=+2 in the Hubble horizon case (Fig. 9), the square speed of sound exhibits the instability of the model at the present as well as near present epochs (0≤t≤2.8), while it shows stability of the model in the later epoch. For u=−2, the squared speed of sound represents the stability of the present models forever (Fig. 10). The similar behavior has been observed in the event horizon case for u=± (Figs. 11 and 12).

Fig. 9
figure 9

Plot of \(v^{2}_{s}\) versus t for PDE parameter u=2 with m=2 (red), m=2.2 (green) and m=2.4 (blue)

Full size image
Fig. 10
figure 10

Plot of \(v^{2}_{s}\) versus t for PDE parameter u=−2 with m=2 (red), m=2.2 (green) and m=2.4 (blue)

Full size image
Fig. 11
figure 11

Plot of \(v^{2}_{s}\) versus t for PDE parameter u=2 with m=2 (red), m=2.2 (green) and m=2.4 (blue)

Full size image
Fig. 12
figure 12

Plot of \(v^{2}_{s}\) versus t for PDE parameter u=−2 with m=2 (red), m=2.2 (green) and m=2.4 (blue)

Full size image

4.3 \(w_{\mathit{DE}}-w'_{\mathit{DE}}\) plane

Caldwell and Linder (2005) tested the behavior of quintessence scalar field DE model through \(w_{\mathit{DE}}-w'_{\mathit{DE}}\) Plane. This plane is being divided into two regions such as thawing and freezing. The thawing region is described as (\(\omega'_{\varLambda}>0\), ω Λ <0) while freezing region as \((\omega'_{\varLambda}<0,\omega_{\varLambda}<0)\). Here, we develop the \(\omega_{\mathit{PDE}}-\omega'_{\mathit{PDE}}\) plane for reconstructed DE \(F(\tilde{R})\) models corresponding to u=±2 as shown in Figs. 13 and 16, respectively, for three different values of m=2,2.2,2.4. It can be observed that the plot corresponds to freezing as well as thawing regions for u=+2 only, in case of Hubble horizon (Fig. 13). However, we have obtained freezing region only for all other cases (Figs. 14 and 15).

Fig. 13
figure 13

Trajectories of \(w_{\mathit{PDE}}-w'_{\mathit{PDE}}\) for reconstructed PDE \(f(\tilde{R})\) model for u=2 with m=2 (red), m=2.2 (green), m=2.4 (blue)

Full size image
Fig. 14
figure 14

Trajectories of \(w_{\mathit{PDE}}-w'_{\mathit{PDE}}\) for reconstructed PDE \(f(\tilde{R})\) model for u=−2 with m=2 (red), m=2.2 (green), m=2.4 (blue)

Full size image
Fig. 15
figure 15

Trajectories of \(w_{\mathit{PDE}}-w'_{\mathit{PDE}}\) for reconstructed PDE \(f(\tilde{R})\) model for u=2 with m=2 (red), m=2.2 (green), m=2.4 (blue)

Full size image
Fig. 16
figure 16

Trajectories of \(w_{\mathit{PDE}}-w'_{\mathit{PDE}}\) for reconstructed PDE \(f(\tilde{R})\) model for u=−2 with m=2 (red), m=2.2 (green), m=2.4 (blue)

Full size image

4.4 r−s plane

Sahni et al. (2003) introduced the statefinder parameters as follows

$$\begin{aligned}& r=\frac{\dddot{a}}{aH^3},\qquad s=\frac{r-1}{3(q-\frac{1}{2})}, \\& q=- \frac{\ddot{a}}{aH^2}=- \biggl(1+\frac{\dot{H}}{H^2} \biggr). \end{aligned}$$
(15)

These parameters are useful which provide the distance of a given DE model from ΛCDM limit. These parameters can describe some useful regions as follows: (r,s)=(1,0) indicates ΛCDM limit, (r,s)=(1,1) shows CDM limit, while s>0 and r<1 represents the region of phantom and quintessence DE eras.

The r−s planes corresponding to Hubble and event horizons for reconstructed PDE \(F(\tilde{R})\) models with u=2,−2 for three different values of m=2,2.2,2.4 as shown in Figs. 17, 18, 19, 20. It can be observed that r−s planes correspond to ΛCDM for all possible cases. Moreover, the r−s planes (Hubble and event horizons) correspond to DE regions (quintessence and phantom) for u=2 and correspond to Chaplygin gas for u=−2, respectively.

Fig. 17
figure 17

Trajectories of r−s for reconstructed PDE \(f(\tilde{R})\) model for u=2 with m=2 (red), m=2.2 (green), m=2.4 (blue)

Full size image
Fig. 18
figure 18

Trajectories of r−s for reconstructed PDE \(f(\tilde{R})\) model for u=−2 with m=2 (red), m=2.2 (green), m=2.4 (blue)

Full size image
Fig. 19
figure 19

Trajectories of r−s for reconstructed PDE \(f(\tilde{R})\) model for u=2 with m=2 (red), m=2.2 (green), m=2.4 (blue)

Full size image
Fig. 20
figure 20

Trajectories of r−s for reconstructed PDE \(f(\tilde{R})\) model for u=−2 with m=2 (red), m=2.2 (green), m=2.4 (blue)

Full size image

5 Unifying the inflation with DE and Newton law corrections in \(f(\tilde{R})\) gravity

The unification scenario of inflation with DE was firstly discussed in Nojiri-Odintsov model (Nojiri and Odintsov 2003) in f(R) gravity and then it was generalized to more realistic versions (Nojiri and Odintsov 2007b; Cognola et al. 2008). The singularity has also remained an important problem in describing the early universe which is discussed by Nojiri and Odintsov (2008). Indeed, it has been shown that there exists a class of non-singular exponential gravity to unify the early and late-time accelerated expansion of the Universe (Elizalde et al. 2011). The detailed analysis is given in Nojiri and Odintsov (2011). The inflationary solution is given by

$$ H=\frac{H_1}{t} $$

The following two cases has been considered for this assumption.

5.1 Hubble horizon

In view of above assumption of H and at the inflationary (early) Universe, when t≪t 0, the dominant part of the \(f(\tilde{R})\) model turns out to be

$$ f(\tilde{R})\sim C_1\tilde{R}^{\xi_-}. $$
(16)

Hence, \(f(\tilde{R})\) produces also the inflationary (phantom) solution. Here, C 1 and C 2 are integration constants while ξ ∓ is given by

$$\begin{aligned} \xi_{-} =&1-\frac{(-\mu+H_1-3\lambda H_1+3\mu H_1)}{(2\mu)}\\ &{}- \biggl(1-\frac{(-\mu+H_1-3\lambda H_1+3\mu H_1)}{\mu} \\ &{}+\frac{(-\mu+H_1-3\lambda H_1 +3\mu H_1)^2}{4\mu^2}\\ &{}-\frac{(H_1-3\lambda H_1+4\mu H_1)}{\mu} \biggr)^{\frac{1}{2}}. \end{aligned}$$

It is well-known that modified gravity may cause violations of local tests. It was shown by Elizalde et al. (2011) that these violations could be avoided in \(F(\tilde{R})\) through Newton’s corrections. Also, it is well known that \(F(\tilde{R})\) theory include scalar particle which could give rise to a fifth force and to variations of the Newton law. This can be avoided with the help of chameleon mechanism (Khoury and Weltman 2004a, 2004b). Also, scalars with time-dependent mass were also considered in Mota and Barrow (2004). The corrections to the Newton law has come from the coupling appears between the scalar field and matter, which makes a test particle to deviate from its geodesic path, unless the mass of the scalar field is large enough (since then the effect could be very small). The detailed about this topic is given in the references (Nojiri and Odintsov 2003, 2007c; Elizalde et al. 2010). The precise value of scalar mass is given by

$$\begin{aligned} m^2_\phi =&\frac{1}{2}\frac{d^2V(\phi)}{d\phi^2} \\ =&\frac{1+f'(\tilde{A})}{f''(\tilde{A})}-\frac{\tilde{A}+f(\tilde {A})}{1+f'(\tilde{A})}, \end{aligned}$$
(17)

where, \(\tilde{A}=\tilde{R}\) and from this relation, one can analyze the models. Here, we are interested to analyze the behavior of the models at the local scales, as on earth, where the scalar curvature is around \(\tilde{A}=\tilde{R}\sim10^{-50}~\mbox{eV}^{2}\), or in the solar system, where \(\tilde{A}=\tilde{R}\sim10^{-61}~\mbox{eV}^{2}\). The function (36) and its derivatives can be approximated around these points as

$$\begin{aligned}& \begin{aligned} &f(\tilde{R})\sim C_1\tilde{R}^{\xi_-},\qquad f'(\tilde{R})\sim C_1\xi_-\tilde{R}^{\xi_-},\\ &f''(\tilde{R})\sim C_1\xi_- (\xi_--1) \tilde{R}^{\xi_-} \end{aligned} \end{aligned}$$
(18)

Inserting the above function and its derivatives in scaler mass and we may get

$$\begin{aligned} m^2_\phi\sim\frac{1}{C_1\xi_- (\xi_--1)} \tilde{R}^{2-\xi_-}. \end{aligned}$$

It can be seen that \(m^{2}_{\phi}\) is approximately equal to \(10^{50\xi_{-}-100}\) and \(10^{61\xi_{-}-122}\) on Earth and solar system, respectively. It can be observed from these relations that the scalar mass would be sufficiently large in order to avoid corrections to the Newton law for the case ξ −>2. Also, for limiting case ξ −=2, the constant C 1 can be chosen to be large enough so that any violation of the local tests is avoided.

5.2 Event horizon

For this horizon, the \(f(\tilde{R})\) model becomes

$$ f(\tilde{R})\sim C_3\tilde{R}^{\delta_-}, $$
(19)

at inflationary (early) Universe, when t≪t 0. Also,

$$\begin{aligned} \delta_{-} =&1-\frac{(-\mu+H_1-3\lambda H_1+3\mu H_1)}{(2\mu)}\\ &{}\mp \biggl(1+ \frac{(-2\mu+H_1-3\lambda H_1+6\mu H_1)}{\mu} \\ &{}+\frac{(-\mu+H_1-3\lambda H_1 +3\mu H_1)^2}{4\mu^2}\\ &{}-\frac{(-\mu H_1-3\lambda H_1+3\mu H_1)}{\mu} \biggr)^{\frac{1}{2}}. \end{aligned}$$

In the similar way, we can obtain

$$\begin{aligned} m^2_\phi\sim\frac{1}{C_3\delta_- (\delta_--1)} \tilde{R}^{2-\delta_-}. \end{aligned}$$

It can be seen that \(m^{2}_{\phi}\) is approximately equal to \(10^{50\delta_{-}-100}\) and \(10^{61\delta_{-}-122}\) on Earth and solar system, respectively. It can be observed from these relations that the scalar mass would be sufficiently large in order to avoid corrections to the Newton law for the case δ −>2. Also, for limiting case δ −=2, the constant C 3 can be chosen to be large enough so that any violation of the local tests is avoided.

6 Concluding remarks

In this paper, we have investigated the reconstruction scenario of MFRHL gravity with newly proposed PDE model in the presence of power law scale factor. We have constructed the \(F(\tilde{R})\) models with the help of Hubble and event horizons of PDE models and PDE parameter. The reconstructed models shows decreasing behavior in all cases and validated the realistic condition of modify gravity. In order to analyze its cosmological significance of these models, we have developed EoS and squared speed of sound parameters as well as cosmological planes.

The EoS parameter evolutes the universe in the quintessence region always for m=2.2 for Hubble horizon with u=+2 (Fig. 5). However, it shows transition from dust like matter to phantom region by crossing phantom divide line and then goes towards quintessence region in the latter epoch for other two cases of m as shown in Fig. 5. Figure 6 (u=−2 for Hubble horizon) shows quintom-like behavior for all cases of m. In case of event horizon (Figs. 7 and 8), we can attain quintom-like behavior (transition from matter dominated era towards phantom and then goes to quintessence era in the latter epoch) for u=−2. In case of u=+2, we only attain the quintessence and vacuum DE eras as shown in Fig. 7.

The square speed of sound exhibits the instability of the model at the present as well as near present epochs (0≤t≤2.8), while it shows stability of the model in the later epoch for u=+2 in the Hubble horizon case (Fig. 9). For u=−2, the squared speed of sound represents the stability of the present models forever (Fig. 10). The similar behavior has been observed in the event horizon case for u=± (Figs. 11 and 12). The plots of \(\omega_{\mathit{DE}}-\omega'_{\mathit{DE}}\) corresponds to freezing as well as thawing regions for u=+2 only, in case of Hubble horizon (Fig. 13). However, we have obtained freezing region only for all other cases. It can be observed that r−s planes correspond to ΛCDM for all possible cases. Moreover, the r−s planes (Hubble and event horizons) correspond to DE regions (quintessence and phantom) for u=2 and correspond to Chaplygin gas for u=−2, respectively.

Since, we have considered the DE universe model which possesses finite-time as well as future-like singularities. However, such singularities may behave in different ways depending on the content of the model. Hence, it would be useful to classify the future singularities in the following way (Nojiri and Odintsov 2005):

  • Type I: for t→t s , a→∞, ρ,|p|→∞, this singularity corresponds to Big Rip singularity.

  • Type II: for t→t s , a→a s , ρ→ρ s , |p|→∞, this singularity corresponds to sudden future singularity.

  • Type III: for t→t s , a→a s , ρ,|p|→∞.

  • Type IV: for t→t s , a→a s , ρ,|p|→0.

Our scenario correspond to Type I singularity because the EoS parameter attains phantom-like universe which describes the Big Rip singularity in future. It is strongly believed that universe undergoes the big rip singularity, where all the gravitationally bounded objects dispersed due to phantom DE.