1 Introduction

Cosmology is one of the most stimulating field in all physical sciences that deals with the study of origin and evolution of the universe. General relativity (GR) laid down the foundation of modern cosmology which leads to accelerating expansion phase of the universe. The force behind this phenomenon is an exotic type of energy called “dark energy” (DE) whose nature is unknown. The simplest model compatible with all cosmological observations is a \(\varLambda\)CDM model but it suffers issues like fine tuning and cosmic coincidence problems leading to some alternatives to investigate its description. There are two possible ways to describe the present status of the universe: dynamical DE models and the modification of gravity.

Dynamical models are obtained by modifying the matter part with unchanged gravitational part such as cosmological constant, quintessence, k-essence and perfect fluid models (Kamenshchik et al. 2001; Li 2004; Cai 2007; Wei 2009; Sheykhi and Jamil 2011). The modified theories of gravity are based on generalized models that came into being by modifying gravitational part of the Einstein-Hilbert action while matter part remains unchanged. The \(f(T)\) theory of gravity is the generalization of teleparallel gravity in which curvature free Weitzenböck connection is considered instead of torsionless Levi-Civita connection. By applying Born-Infeld strategy, Ferraro and Fiorini (2007, 2008) firstly introduced this theory and solved particle horizon problem as well as obtained singularity free solutions with positive cosmological constant. Many phenomena have extensively been studied in this gravity like static and dynamical wormhole solutions, reconstruction via dynamical models, instability ranges of collapsing stars, discussion of Birkhoff’s theorem, accelerated expansion of the universe, solar system constraints and many more.

Wu and Yu (2010, 2011) studied dynamical behavior of this theory for a concrete power-law model and analyzed that the crossing of phantom divide line is consistent with recent cosmological observational data by proposing two new \(f(T)\) models. Bamba et al. (2011) investigated the evolution of effective equation of state (EoS) for different \(f(T)\) models. Sharif and Rani (2011) considered Bianchi type I universe to discuss accelerated expansion of the universe. Daouda et al. (2012) constructed this model corresponding to holographic DE (HDE) model and found that the reconstructed model shows phantom behavior as well as unification of DE and dark matter.

Wei (2012) has introduced the idea of pilgrim dark energy (PDE) with a key point of phantom-like universe to prevent the black hole (BH) formation. He constructed PDE model as \(\rho_{\varLambda}=3\delta^{2}m_{p}^{4-u}L^{-u}\), where \(u\) and \(\delta\) are dimensionless constants, \(m_{p}\) is the reduced Planck constant. He investigated the behavior of interacting PDE models by using different cosmological parameters such as EoS, \(\omega_{\varLambda}-\omega'_{\varLambda}\) and statefinders. Sharif and Jawad (2013a, 2013b) studied the interacting PDE in flat as well as non-flat universe models with different IR cutoffs. Sharif and Rani (2014) developed PDE model in \(f(T)\) gravity to explain the behavior of BHs in the presence of phantom energy in the universe. Jawad and Debnath (2015) discussed the new agegraphic version of PDE in \(f(T,T_{G})\) gravity. Chattopadhyay et al. (2014) worked on the reconstruction scenario of PDE in \(f(T,T_{G})\) gravity. Fernandez (2012) proposed ghost scalar field models while Malekjani (2013) established different \(f(R)\) models in ghost and generalized ghost DE (GGDE) models. Zubair and Abbas (2015) discussed \(f(R,T)\) theory in the framework of quantum chromodynamics (QCD) ghost DE models. Jawad and Rani (2015) reconstructed generalized ghost PDE (GGPDE) model in \(f(R)\) gravity.

The thermodynamic behavior of accelerating universe is one of the major concerns in cosmology. The discovery of BH thermodynamics (Bardeen et al. 1973; Bekenstein 1973; Hawking 1975; Gibbons and Hawking 1977) suggests that there should be some relation between thermodynamics and gravitation. Jacobson (1995) was the first who discovered this connection and derived the Einstein equations by using the relation between entropy and horizon area in thermodynamics. Bousso (2005) explored thermodynamics in the quintessence dominated spacetime and showed that the first law of thermodynamics holds at the apparent horizon. Bamba and Geng (2011) studied both equilibrium and non-equilibrium descriptions of thermodynamics of the apparent horizon in this gravity. Sharif and Jawad (2013a, 2013b) investigated the validity of generalized second law of thermodynamics with corrected entropies for three different systems in the closed universe.

In this paper, we investigate the behavior of GGPDE model in \(f(T)\) gravity to explore the EoS parameter, \(\omega_{\varLambda}- \omega'_{\varLambda}\) phase plane and statefinder parameters. We also discuss thermodynamic laws for same temperature of the universe. The format of the paper is as follows. In the next section, we briefly review \(f(T)\) gravity and its field equations. Section 3 provides construction of GGPDE model in this gravity. In Sect. 4, we study the evolution trajectories through cosmological parameters. Section 5 explores the validity of first and second laws of thermodynamics. Finally, we conclude the results in Sect. 6.

2 \(f(T)\) gravity and its field equations

A teleparallel structure is induced by a non-trivial tetrad field on spacetime which is directly linked with the presence of gravitational field. For the tangent space, dynamical tetrad field \(h_{A}(x^{\mu})\) is an orthonormal basis at each point of the manifold. Dynamical tetrad field is analyzed by tetrad components \(h_{A}^{\mu}\) (\(\mu,A=0,1,2,3\)) in the coordinate basis \(h_{A}=h_{A}^{\mu}\partial_{\mu}\) related by \(h_{\mu}^{A}h_{B}^{\mu}=\delta_{B}^{A}\) and \(h_{\mu}^{A}h_{A}^{\nu}=\delta_{\mu}^{\nu}\). Greek indices \((\mu,\nu)\) are used to represent coordinates on manifold and Latin indices \((A,B)\) are used to represent coordinates on tangent space. The product of the tetrad field gives \(g_{\mu\nu}=\eta_{AB}h_{\mu}^{A}h_{\nu}^{B}\), where \(\eta_{AB}=\mathrm{diag}(1,-1, -1,-1)\) is the Minkowski metric for the tangent space. In teleparallelism, we use curvatureless Weitzenböck connection \((\tilde{\varGamma}^{\lambda}_{\mu\nu}=h_{A}^{\lambda}\partial_{\nu}h_{\mu}^{A})\) whose antisymmetric torsion tensor is given as

$$ T^{\rho}_{\mu\nu}=h_{A}^{\rho}\bigl( \partial_{\nu}h_{\mu}^{A}-\partial_{\mu }h_{\nu}^{A} \bigr), $$

and superpotential tensor is

$$ S^{\mu\nu}_{\rho}=\frac{1}{4}\bigl[-T^{\mu\nu}_{\rho}+T^{\nu\mu}_{\rho }+T_{\rho}^{\mu\nu}+ 2\delta^{\mu}_{\rho}T^{\theta\nu}_{\theta}-2 \delta^{\nu}_{\rho}T^{\theta \mu}_{\theta}\bigr]. $$

Using these tensors, we can define torsion scalar as \(T=S^{\mu\nu}_{\rho}T^{\rho}_{\mu\nu}\).

The action of \(f(T)\) gravity is given by Ferraro and Fiorini (2007)

$$ \mathcal{L}=\frac{m_{p}^{2}}{2} \int d^{4}xh \bigl(f(T)+\mathcal{L}_{m}\bigr), $$
(1)

where \(m_{p}^{2}=(8\pi\mathcal{G})^{-1}\) is the reduced Planck mass, \(\mathcal{L}_{m}\) is the matter Lagrangian density inside the universe, \(\mathcal{G}\) is the gravitational constant and \(h=\sqrt{-g}\). Varying the action with respect to tetrad yields the following field equations

$$\begin{aligned} &\bigl[h^{-1}\partial_{\mu}\bigl(hS^{\mu\nu}_{A} \bigr)+h^{\lambda}_{A}T^{\rho}_{\mu \lambda}S^{\nu\mu}_{\rho} \bigr] f_{T}+S^{\mu\nu}_{A}\partial_{\mu}(T)f_{TT}+ \frac{1}{4}h^{\nu}_{A}f \\ &\quad =\frac{1}{2}\kappa^{2}h^{\rho}_{A} \mathcal{T}^{\nu}_{\rho}, \end{aligned}$$

where \(\mathcal{T}^{\nu}_{\rho}\) is the matter energy-momentum tensor and a subscript \(T\) denotes differentiation with respect to \(T\). We take spatially flat FRW universe as

$$ ds^{2}=dt^{2}-a(t)^{2}\sum \bigl(dx^{i}\bigr)^{2}. $$

For this metric, \(h^{A}_{\mu}=\mathrm{diag}(1,a(t),a(t),a(t))\), \(H=\frac{\dot{a}}{a}\), \(T= -6H^{2}\), where \(H\) is the Hubble parameter and dot represents time derivative. The modified Friedmann equations are given by

$$\begin{aligned} &12H^{2}f_{T}+f=2m_{p}^{-2} \rho, \end{aligned}$$
(2)
$$\begin{aligned} &48H^{2}\dot{H}f_{TT}-\bigl(12H^{2}+4 \dot{H}\bigr)f_{T}-f=2m_{p}^{-2}p, \end{aligned}$$
(3)

and the conservation equation is

$$ \dot{\rho}+3H(\rho+p)=0. $$
(4)

The corresponding first equation of motion is

$$ H^{2}=\frac{1}{3m_{p}^{2}}(\rho_{m}+ \rho_{\varLambda}), $$
(5)

which in terms of fractional energy density can be written as

$$ 1=\varOmega_{m}+\varOmega_{\varLambda},\qquad \varOmega_{m}=\frac{\rho_{m}}{3m_{p}^{2}H^{2}},\qquad \varOmega_{\varLambda}= \frac{\rho_{\varLambda}}{3m_{p}^{2}H^{2}}, $$
(6)

where \(\rho_{m}\) and \(p_{m}\) represent energy density and pressure of matter inside the universe. Also, \(\rho_{\varLambda}\) and \(p_{\varLambda}\) are torsion contributions to the energy density and pressure as

$$\begin{aligned} &\rho_{\varLambda}=\frac{m_{p}^{2}}{2}(2Tf_{T}-f-T), \end{aligned}$$
(7)
$$\begin{aligned} &p_{\varLambda}=-\frac{m_{p}^{2}}{2}\bigl(-8\dot{H}Tf_{TT}+(2T-4 \dot {H})f_{T}-f-T+4\dot{H}\bigr). \end{aligned}$$
(8)

The energy conservation equations corresponding to standard matter and DE are

$$\begin{aligned} &\dot{\rho}_{m}+3H\rho_{m} = 0, \end{aligned}$$
(9)
$$\begin{aligned} &\dot{\rho}_{\varLambda}+3H\rho_{\varLambda}(1+ \omega_{\varLambda}) = 0. \end{aligned}$$
(10)

Here, \(\omega_{\varLambda}=\frac{p_{\varLambda}}{{\rho}_{\varLambda}}\) is the effective EoS parameter for \(f(T)\) gravity. The resulting EoS parameter is

$$\begin{aligned} \omega_{\varLambda} =&-1+\frac{\dot{H}}{H^{2}} \biggl[ \frac{T(2Tf_{TT} +f_{T}-1)}{2Tf_{T}-f-T} \biggr]. \end{aligned}$$
(11)

3 Generalized ghost PDE model

Here, we construct \(f(T)\) model for GGPDE model. The energy density of GGDE model is written as

$$ \rho_{T}=\alpha H+\beta H^{2}, $$

where \(H=\frac{\dot{a}}{a}\) is the Hubble parameter and \(\beta\) is a constant. Also, \(\alpha>0\) is roughly of order \(\varLambda^{3}_{\mathrm{QCD}}\) and \(\varLambda_{\mathrm{QCD}}\) is quantum chromodynamics (QCD) mass scale. For the present time, it is noted that \(\varLambda_{\mathrm{QCD}}\sim100~\mbox{MeV}\) and \(H\sim10^{-33}~\mbox{eV}\). Rozenzweig et al. (1980) investigated that the contribution of Veneziano QCD ghost field to the vacuum energy is not exactly of order \(H\). It is found that vacuum energy of the Veneziano ghost field can be written as \(H+O(H^{2})\), where the sub-leading term \(H^{2}\) could be helpful in describing the early evolution of the universe. We study cosmological parameters such as EoS parameter, \(\omega_{\varLambda}-\omega'_{\varLambda}\) and statefinders for this model. The GGDE density in terms of PDE is known as GGPDE and is of the form

$$ \rho_{T}=\bigl(\alpha H+\beta H^{2} \bigr)^{u}, $$
(12)

where \(u\) is the dimensionless constant. Equating Eqs. (7) and (13) as \(\rho_{\varLambda}=\rho_{T}\), we obtain \(f(T)\) model

$$\begin{aligned} f(T) =& T+c_{1}\sqrt{T}+\frac{1}{m_{p}^{2}} \biggl[ \frac{2\alpha^{u}}{(u-1)} \biggl(\frac{-1}{6} \biggr)^{\frac{u}{2}}T^{\frac{u}{2}} \\ &{}+\beta\alpha^{u-1}u \biggl(\frac{-1}{6} \biggr)^{\frac{u+1}{2}}T^{\frac{u+1}{2}} \biggr]. \end{aligned}$$
(13)

4 Cosmological parameters

In this section, we examine the evolution of EoS parameter, Hubble parameter, phase plane, statefinder parameter and check the stability criteria through GGPDE \(f(T)\) model by taking different values of pilgrim parameter.

4.1 Cosmological parameters

Here we study the behavior of Hubble parameter as well as EoS parameter for the GGPDE model. Differentiating Eq. (12), we get

$$\begin{aligned} \dot{\rho}_{T}=u \rho_{T} \biggl( \frac{\alpha+2\beta H}{\alpha+\beta H} \biggr)\frac{\dot{H}}{H}. \end{aligned}$$
(14)

Differentiating Eq. (5), then using \(\rho_{m}=\rho_{m_{0}}a^{-3}\) and Eq. (14) with \(a=a_{0}(1+z)^{-1}\), we obtain

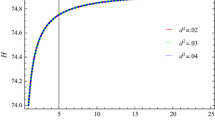
$$\begin{aligned} \frac{\dot{H}}{H^{2}}=\frac{3{H_{0}}^{2}\varOmega_{m_{0}}a^{-3}(\alpha +\beta H)}{u(\alpha+2\beta H)(\alpha H+\beta H^{2})^{u}-2H^{2}(\alpha+\beta H)}. \end{aligned}$$
(15)

We plot the above differential equation of \(H\) versus the redshift parameter \(z\) for three different values of PDE parameter \(u=1.5, 1.52, 1.502\) as shown in Fig. 1. The current values of other parameters are \(\varOmega_{\varLambda}=0.76\), \(\varOmega_{m}=0.24\), \(\alpha=1.55\), \(\beta=1.91\) and \(H_{0}=74\). Figure 1 shows that the value of Hubble parameter \(H\) versus \(z\), where \(-1\leq z\leq2\) lies in the range \((74.00,74.025)\) for all values of PDE parameter. Inserting Eq. (15) in (11), we have

$$\begin{aligned} \omega_{\varLambda} =&-1+\frac{{H_{0}}^{2}\varOmega_{m}a^{-3}u(\alpha+\beta H)}{2H^{2}(\alpha+\beta H)-u(\alpha H+\beta H^{2})^{u}(\alpha+2\beta H)} \\ &{}\times \biggl(\frac{2\alpha+u(u+1)\beta H}{2\alpha+u^{2}\beta H} \biggr). \end{aligned}$$
(16)

We discuss the EoS parameter \(\omega_{\varLambda}\) versus \(-1 \leqslant z \leqslant2\) with respect to three different choices of PDE parameter \(u= 1.5, 1.52, 1.502\) graphically. In Fig. 2, the EoS parameter shows a \(\varLambda\)CDM model for \(-1.0 \leqslant z \leqslant-0.4\). As \(z\) increases, it moves towards the phantom region for \(-0.4 \leqslant z \leqslant2\).

Fig. 1
figure 1

Plot of \(H\) for GGPDE with \(-1 \leqslant z \leqslant2\)

Full size image
Fig. 2
figure 2

Plot of \(\omega_{\varLambda}\) for GGPDE with \(-1 \leqslant z \leqslant2\)

Full size image

Now, we use the parameter squared speed of sound \({v_{s}}^{2}\) for the stability analysis of the present model. It is given by

$$ {v_{s}}^{2}=\frac{\dot{p}}{\dot{\rho}}= \omega_{\varLambda}+\dot{\omega}_{\varLambda}\frac{\rho}{\dot{\rho}}. $$

Using Eqs. (12), (14) and (16) in the above equation, it follows that

$$\begin{aligned} {v_{s}}^{2} =&\omega_{\varLambda}- \biggl( \frac{2(\alpha+\beta H)}{3u(\alpha+2\beta H)} \biggr) (1+\varOmega_{\varLambda}\omega_{\varLambda})^{-1} \\ &{}\times\biggl[\bigl(-3u^{2}\beta H(1+\varOmega_{\varLambda} \omega_{\varLambda}) (1-2\alpha\varOmega_{\varLambda}) \\ &{}-6\bigl(\varOmega_{\varLambda}\omega_{\varLambda}(\varOmega_{\varLambda}-1)- \xi(\varOmega_{\varLambda}-\varOmega_{m})\bigr) \\ &{}\times u\bigl(2\alpha+\beta u^{2}H\bigr) \bigl(2\alpha+ \bigl(u^{2}+u\bigr)\beta H\bigr)\bigr) \\ &{}\times \bigl(2\bigl(2\alpha+\beta u^{2}H\bigr)- \varOmega_{\varLambda}u\bigl(2\alpha+u(u+1)\beta H\bigr)\bigr)^{-2} \\ &{}-\xi \biggl(\frac{\varOmega_{\varLambda}-\varOmega_{m}}{\varOmega_{\varLambda}} \biggr) \bigl(-6\alpha \varOmega_{\varLambda} \beta u^{2}(1+\varOmega_{\varLambda}\omega_{\varLambda}) \\ &{}\times 6\bigl(\varOmega_{\varLambda}\omega_{\varLambda}( \varOmega_{\varLambda}-1)-\xi(\varOmega_{\varLambda}-\varOmega_{m})\bigr) \\ &{}\times u\bigl(2\alpha+\beta u^{2}H\bigr) \bigl(2\alpha + \bigl(u^{2}+u\bigr)\beta H\bigr)\bigr) \\ &{}\times\bigl(2\bigl(2\alpha+\beta u^{2}H\bigr)- \varOmega_{\varLambda}u\bigl(2\alpha+u(u+1)\beta H\bigr)\bigr)^{-2} \\ &{}+\bigl(2\bigl(2\alpha+\beta u^{2}H\bigr)\bigr) \biggl(3\xi \biggl( \frac{\varOmega_{m}^{2}}{\varOmega_{\varLambda}^{2}} -1 \biggr)-3\omega_{\varLambda}\frac{\varOmega_{m}}{\varOmega_{\varLambda}} \biggr) \\ &{}\times\bigl(2\bigl(2\alpha+\beta u^{2}H\bigr)- \varOmega_{\varLambda}u\bigl(2\alpha+u(u+1)\beta H\bigr)\bigr)^{-1} \biggr]. \end{aligned}$$

The graph of \({v_{s}}^{2}\) is plotted against the redshift parameter \(z\) in Fig. 3 for the same values of PDE parameter \(u \). This shows that \({v_{s}}^{2}<0\) for all values of \(u\) which indicates the instability of the model in the range \(-1\leq z\leq2\).

Fig. 3
figure 3

Plot of \({v_{s}}^{2}\) for GGPDE with \(-1\leqslant z \leqslant2\)

Full size image

4.2 \(\omega_{\varLambda}-\omega_{\varLambda'}\) analysis

The \(\omega_{\varLambda}-\omega_{\varLambda'}\) plane is considered as a useful tool to study the behavior of different models such as quintom (Guo et al. 2006), phantom (Chiba 2006), quintessence (Scherrer 2006), family of HDE (Setare et al. 2007), pilgrim DE (Sharif and Jawad 2013a, 2013b) etc. Caldwell and Linder (2005) introduced that the area covered by the quintessence DE model in phase plane can be divided into two regions, i.e., thawing region (\(\omega'>0\) when \(\omega<0\)) and freezing region (\(\omega'<0\) when \(\omega<0\)). Using Eqs. (9) and (10) in (6), it follows that

$$\begin{aligned} &\varOmega'_{m} = 3\varOmega_{\varLambda} \omega_{\varLambda}\varOmega_{m}, \end{aligned}$$
(17)
$$\begin{aligned} &\varOmega'_{\varLambda} = -3\varOmega_{\varLambda} \omega_{\varLambda}+3\varOmega_{\varLambda}^{2}\omega_{\varLambda}. \end{aligned}$$
(18)

Taking the derivative of Eq. (16) and using Eqs. (17) and (18), we obtain

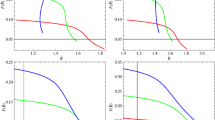
$$\begin{aligned} \omega'_{\varLambda} =& -6u^{2}\beta{H_{0}}^{2} \varOmega_{m}(1+z)^{3}(\alpha+\beta H)H(1-2\alpha \varOmega_{\varLambda}) \\ &{}-2\bigl(3{\varOmega_{\varLambda}}^{2}\omega_{\varLambda}-3 \omega_{\varLambda}\varOmega_{\varLambda}\bigr)u\bigl(2\alpha+\beta u^{2}H\bigr) \\ &{}\times\bigl(2\alpha+\bigl(u^{2}+u\bigr)\beta H\bigr) \bigl(2H^{2}(\alpha+\beta H) \\ &{} -u\bigl(\alpha H+\beta H^{2}\bigr)^{u}(\alpha+2\beta H)\bigr) \bigl(2H^{2}(\alpha+\beta H) \\ &{}-u\bigl(\alpha H+\beta H^{2}\bigr)^{u}(\alpha+2\beta H) \bigr)^{-1}\bigl(2\bigl(2\alpha+\beta u^{2}H\bigr) \\ &{}-\varOmega_{\varLambda}u\bigl(2\alpha+u(u+1)\beta H\bigr) \bigr)^{-2}. \end{aligned}$$
(19)

Figure 4 shows the plot of \(\omega'_{\varLambda}\) with respect to \(\omega_{\varLambda}\) for GGPDE model. We can easily observe that the curves for all values of \(u\) are in the thawing region when \(-1.030<\omega_{\varLambda}<-1\).

Fig. 4
figure 4

Plot of \(\omega_{\varLambda}-\omega_{\varLambda'}\) for GGPDE with \(-1\leqslant z \leqslant2\)

Full size image

4.3 Statefinder parameters

Sahni et al. (2003) introduced two parameters \(r=\frac{\dddot{a}}{aH^{3}}\) and \(s=\frac{r-1}{3(q-\frac{1}{2})}\), where \(q\) is the deceleration parameter. These parameters are called statefinder parameters. The plane of these parameters define different well-known regions of the universe like \((r,s)=(1,1)\) shows CDM limit and \((r,s)=(1,0)\) describes \(\varLambda\)CDM limit. The phantom and quintessence DE eras are represented by \(s>0\) and \(r<1\). The statefinder parameters for GGPDE \(f(T)\) model are expressed as

$$\begin{aligned} r =&1-\frac{3}{2}\varOmega_{\varLambda}\bigl(-6u^{2} \beta{H_{0}}^{2}\varOmega_{m}(1+z)^{3}( \alpha+\beta H) \\ &{}\times H(1-2\alpha\varOmega_{\varLambda})-2\bigl(3{\varOmega_{\varLambda}}^{2} \omega_{\varLambda}-3\omega_{\varLambda}\varOmega_{\varLambda}\bigr) \\ &{}\times u\bigl(2\alpha+\beta u^{2}H\bigr) \bigl(2\alpha+ \bigl(u^{2}+u\bigr)\beta H\bigr) \bigl(2H^{2}(\alpha+\beta H) \\ &{}-u\bigl(\alpha H+\beta H^{2}\bigr)^{u}(\alpha+2\beta H) \bigr) \bigl(2H^{2}(\alpha+\beta H) \\ &{}-u\bigl(\alpha H+\beta H^{2}\bigr)^{u}(\alpha+2\beta H) \bigr)^{-1}\bigl(2\bigl(2\alpha+\beta u^{2}H\bigr) \\ &{}-\varOmega_{\varLambda}u\bigl(2\alpha+u(u+1)\beta H\bigr) \bigr)^{-2}\bigr) +\frac{9}{2}\varOmega_{\varLambda} \biggl(-1 \\ &{}+\frac{{H_{0}}^{2}\varOmega_{m}a^{-3}u(\alpha+\beta H)}{2H^{2}(\alpha+\beta H)-u(\alpha H+\beta H^{2})^{u}(\alpha+2\beta H)} \\ &{}+\frac{2\alpha+u(u+1)\beta H}{2\alpha+u^{2}\beta H} \biggr) \\ &{}\times \biggl(\frac{{H_{0}}^{2}\varOmega_{m}a^{-3}u(\alpha+\beta H)}{2H^{2}(\alpha+\beta H)-u(\alpha H+\beta H^{2})^{u}(\alpha+\beta H)} \\ &{}+\frac{2\alpha+u(u+1)\beta H}{2\alpha+u^{2}\beta H} \biggr) \end{aligned}$$
(20)
$$\begin{aligned} s =& \biggl(\frac{{H_{0}}^{2}\varOmega_{m}a^{-3}u(\alpha+\beta H)}{2H^{2}(\alpha+\beta H)-u(\alpha H+\beta H^{2})^{u}(\alpha+2\beta H)} \biggr) \\ &{}\times \biggl(\frac{2\alpha+u(u+1)\beta H}{2\alpha+u^{2}\beta H} \biggr) \\ &{}+\bigl(6u^{2}\beta{H_{0}}^{2} \varOmega_{m}(1+z)^{3}(\alpha+\beta H)H(2\alpha \varOmega_{\varLambda}-1) \\ &{}-2\bigl(3{\varOmega_{\varLambda}}^{2}\omega_{\varLambda} -3 \omega_{\varLambda}\varOmega_{\varLambda}\bigr)u\bigl(2\alpha+\beta u^{2}H\bigr) \\ &{}\times\bigl(2\alpha+\bigl(u^{2}+u\bigr)\beta H\bigr) \bigl(2H^{2}(\alpha+\beta H) \\ &{}-u\bigl(\alpha H+\beta H^{2}\bigr)^{u}(\alpha+2\beta H) \bigr)\bigr) \bigl(2H^{2}(\alpha+\beta H) \\ &{}-u\bigl(\alpha H+\beta H^{2}\bigr)^{u}(\alpha+2\beta H) \bigr)^{-1}\bigl(2\bigl(2\alpha+\beta u^{2}H\bigr) \\ &{}-\varOmega_{\varLambda}u\bigl(2\alpha+u(u+1)\beta H\bigr) \bigr)^{-2}\biggl(-3\bigl(2\alpha+u^{2}\beta H \bigr)^{-1} \\ &{}+ \biggl(\frac{3{H_{0}}^{2}\varOmega_{m}a^{-3}u(\alpha+\beta H)(2\alpha+u(u+1)\beta H)}{2H^{2}(\alpha+\beta H)-u(\alpha H+\beta H^{2})^{u}(\alpha+2\beta H)} \biggr) \\ &{}\times\bigl(2\alpha+u^{2}\beta H\bigr)^{-1}\biggr). \end{aligned}$$
(21)

The plot of statefinder parameters is shown in Fig. 5. For the sake of better results, we consider \(-1 \leqslant z \leqslant8\). This indicates that GGPDE model provides the regions of quintessence and phantom DE eras as \(s>0\) and \(r<1\) when \(u=1.5, 1.52, 1.502\).

Fig. 5
figure 5

Plot of \(r-s\) for GGPDE with \(-1 \leqslant z \leqslant8\)

Full size image

5 Thermodynamics

In this section, we investigate thermodynamics (Bamba et al. 2012) in \(f(T)\) gravity. For this purpose, the equation of motion (5) can be redefined as

$$\begin{aligned} &H^{2}=\frac{1}{3m_{p}^{2}f_{T}}(\rho_{m}+\tilde{ \rho}_{\varLambda}), \end{aligned}$$
(22)
$$\begin{aligned} &\dot{H}=-\frac{1}{2m_{p}^{2}f_{T}}(\rho_{m}+\tilde{ \rho}_{\varLambda}+\tilde{p}_{\varLambda}), \end{aligned}$$
(23)

where

$$ \begin{aligned} &\tilde{\rho}_{\varLambda}=\frac{m_{p}^{2}}{2}(T f_{T}-f),\\ &\tilde{p}_{\varLambda}=\frac{m_{p}^{2}}{2}(4H f_{TT}-T f_{T}+f), \end{aligned} $$
(24)

are redefined torsion contributions. The corresponding continuity equation is given by

$$ \dot{\tilde{\rho}}_{\varLambda}+3H(\tilde{\rho}_{\varLambda}+ \tilde {p}_{\varLambda})=-\frac{m_{p}^{2}T}{2}f_{TT}. $$
(25)

In general relativity, the Bekenstein-Hawking horizon entropy is

$$ \tilde{S}=\frac{\tilde{A}f_{T}}{4\tilde{G}_{\mathrm{eff}}}, $$
(26)

where \(\tilde{G}_{\mathrm{eff}}=\frac{\tilde{G}}{f'}\) is the effective gravitational coupling and \(f'\) is the derivative of \(f\) with respect to the corresponding argument. Here, \(\tilde{A}=4\pi \tilde{R}_{A}^{2}\) is the area of horizon and \(\tilde{R}_{A}= \frac{1}{H}\) is the radius of apparent horizon. The time derivative of this relation (\(\dot{\tilde{R}}_{A}=-H\dot{H}\tilde{R}_{A}\)) yields

$$ \frac{f_{T}}{4\pi \tilde{G}}\frac{d\tilde{R}_{A}}{dt}=H(\rho_{m}+\tilde{ \rho}_{\varLambda }+\tilde{p}_{\varLambda})\tilde{R}_{A}^{3}. $$
(27)

Using Eqs. (26) and (27), it follows that

$$ \frac{1}{2\pi\tilde{R}_{A}}\frac{d\tilde{S}}{dt}=4\pi H(\rho_{m}+ \tilde{\rho}_{\varLambda}+\tilde{p}_{\varLambda}) \tilde{R}_{A}^{3}+ \frac{\tilde{R}_{A}}{2\tilde{G}}\frac{df_{T}}{dt}. $$
(28)

The dynamical apparent horizon is covered by the boundary of the universe for which Hawking temperature has the following form

$$ T_{H}=\frac{1}{2\pi \tilde{R}_{A}} \biggl(1-\frac{\dot{\tilde{R}}_{A}}{2H\tilde{R}_{A}} \biggr). $$
(29)

Introducing \(T_{H}\) in Eq. (28), we have

$$\begin{aligned} T_{H}d\tilde{S} =&4\pi H(\rho_{m}+\tilde{ \rho}_{\varLambda}+\tilde{p}_{\varLambda}) \tilde{R}_{A}^{3}dt \\ &{}-2\pi(\rho_{m}+\tilde{\rho}_{\varLambda}+\tilde{p}_{\varLambda})d \tilde{R}_{A}+\frac{\pi\tilde{R}_{A}^{2}}{\tilde {G}}T_{H}df_{T}. \end{aligned}$$
(30)

In \(f(T)\) gravity, the Misner-Sharp energy for Hubble horizon can be modified as

$$ \hat{E}=\frac{\tilde{R}_{A}f_{T}}{2\tilde{G}}=(\rho_{m}+\tilde{\rho }_{\varLambda})V, $$
(31)

where volume inside the horizon is denoted by \(V= (4/3)\pi\tilde{R}_{A}^{3}\). Its first derivative gives

$$\begin{aligned} d\hat{E} =&-4\pi H(\rho_{m}+\tilde{ \rho}_{\varLambda}+\tilde{p}_{\varLambda})\tilde{R}_{A}^{3}dt \\ &{}+4\pi(\rho_{m}+\tilde{\rho}_{\varLambda})\tilde{R}_{A}^{2}d \tilde {R}_{A}+\frac{\tilde{R}_{A}}{2\tilde{G}}df_{T}. \end{aligned}$$
(32)

Equations (30) and (32) yield

$$ T_{H}d\tilde{S}+T_{H}d\tilde{S}_{P}=-dE+WdV, $$
(33)

where the work density is

$$ W=-\frac{1}{2}\bigl(\textit{T}^{ ~\mu\nu}_{m}g_{\mu\nu}+ \tilde{\textit{T}}^{~\mu\nu}_{\varLambda}g_{\mu\nu}\bigr) = \frac{1}{2}(\rho_{m}+\tilde{\rho}_{\varLambda}- \tilde{p}_{\varLambda}), $$
(34)

\(\tilde{\textit{T}}^{~\mu\nu}_{\varLambda}\) is the energy-momentum tensor of the dark components. In the non-equilibrium thermodynamics, the additional term \(d\tilde{S}_{p}\) in Eq. (33) can be described as an entropy production term and has the general form

$$\begin{aligned} d\tilde{S}_{P} =&-\frac{\tilde{R}_{A}}{2T_{H}\tilde{G}}(1+2\pi\tilde {R}_{A}T_{A})df_{T} \\ =&\frac{6\pi}{\tilde{G}}\frac{8HT+\dot{T}}{T(4HT+\dot{T})}df_{T}. \end{aligned}$$
(35)

The behavior of entropy production term can be discussed by taking the second derivative of Eq. (14) and using it in Eq. (35), it follows that

$$\begin{aligned} \frac{d\tilde{S}_{P}}{dt} =&\frac{u\pi\dot{H}}{\tilde{G}m_{P}^{2}(u-1)} \biggl(\frac{4H^{2}+\dot{H}}{2H^{2}+\dot{H}} \biggr) \\ &{}\times \biggl[\frac{6\alpha^{u}}{38} \biggl(\frac{{H_{0}}^{u-1}}{H^{4}}+(u-2) H^{u-5} \biggr) \\ &{}+\frac{(u^{2}-1)\beta\alpha^{u-1}}{12} \biggl(\frac {H_{0}^{u}}{H^{4}}+(u-1)H^{u-4} \biggr) \biggr]. \end{aligned}$$
(36)

It is observed that \(H^{2}\pm\dot{H}>0\) due to the acceleration of the universe. Moreover, \(\dot{H}>0\) corresponds to an accelerating expanded phantom-like universe while \(\dot{H}<0\) corresponds to an accelerating expanded quintessence-like behavior. Thus, the behavior of \(\dot{\tilde{S}}_{P}\) depends on the signs of \(\dot{H}\) and \(u\). In this case, \(u\neq1\) whereas \(u=0\) leads to zero entropy production term which corresponds to teleparallel gravity.

In the phantom-like accelerating universe, we see that \(\dot{\tilde{S}}_{P}>0\) for \(u<0\) and \(u>2\), while the range \(0< u<1\) shows the decreasing entropy production term. Also, the range \(1< u<2\) represent the increasing entropy production term. A similar but opposite behavior is obtained for a quintessence-like accelerated expanding universe. The teleparallel gravity will be recovered in the case where one has a decreasing additive entropy term \((\dot{\tilde{S}}_{P}<0)\) and it goes to zero as the time evolves. With this type of behavior we can conclude that the production of entropy cannot always be viewed as permanent phenomenon. The Gibbs equation is given by

$$\begin{aligned} T_{H}d\tilde{S}_{\mathrm{in}}=d(V\tilde{ \rho}_{\varLambda})+\tilde{p}_{\varLambda}dV =Vdt+(\tilde{ \rho}_{\varLambda}+\tilde{p}_{\varLambda})dV. \end{aligned}$$
(37)

The second law of thermodynamics obeys the following condition

$$\begin{aligned} \dot{\tilde{S}}+\dot{\tilde{S}}_{p}+\dot{ \tilde{S}}_{\mathrm{in}}\geq0 \end{aligned}$$
(38)

Combining Eqs. (28), (35) and (36), we have

$$\begin{aligned} \dot{S}_{\mathrm{total}} =&\dot{\tilde{S}}+\dot{\tilde{S}}_{p}+\dot{ \tilde{S}}_{\mathrm{in}} \\ =&\frac{{\dot{H}}^{2}}{2\tilde{G}H^{4}}+ \frac{u\alpha^{u}{\dot{H}}^{2}}{12\tilde{G}m_{p}^{2}(u-1)} \biggl[\frac {H_{0}^{u-1}}{H^{5}} -H^{u-6} \biggr] \\ &{}+\frac{u(u+1)\alpha^{u-1}\beta\dot{H}^{2}}{24\tilde{G} m_{p}^{2}} \biggl[\frac{H_{0}^{u}}{H^{5}}-H^{u-5} \biggr]. \end{aligned}$$
(39)

Figure 6 shows that the generalized second law of thermodynamics is satisfied for the present day value of \(H\) with \(-1 \leqslant z \leqslant0.8\) and \(u\neq1\) regardless the sign of \(\dot{H}\).

Fig. 6
figure 6

Plot of \(\dot{S}_{\mathrm{total}}\) for GGPDE with \(-1 \leqslant z \leqslant2\)

Full size image

6 Concluding remarks

The GGPDE model has been discussed in different modified theories for different purposes such as describing evolution of the universe through different cosmological parameters, analysis of \(\omega_{\varLambda}-\omega'_{\varLambda}\), \(r-s\) planes and thermodynamics laws. Sharif and Jawad (2014) investigated the interacting and non-interacting GGPDE model in the flat universe. They analyzed the behavior of these parameters through two constant parameters such as interacting and PDE. For \(u\geq1.4\) and \(u\leq0\), the EOS parameter lies in the phantom region. They found that GGPDE model exhibited stability in the non-interacting scenario. The \(\omega_{\varLambda}-\omega'_{\varLambda}\) plane showed \(\varLambda\)CDM limit for non-interacting case. Finally, they pointed out that the \(r-s\) plane possessed the regions of Chaplygin gas, quintessence and phantom models.

In this paper, we have taken GGPDE model to discuss the non-interacting case by evaluating the EoS parameter as well as two cosmological planes (\(\omega_{\varLambda}-\omega'_{\varLambda}\) and \(r-s\)). We have analyzed GGPDE model through three different values of PDE parameter, i.e., \(u=1.5, 1.52\) and \(u=1.502\) and redshift parameter \(-1\leq z\leq2\). It is seen that the evolution of Hubble parameter lies in the range \((74.00,74.025)\) for all values of \(u\) as shown in Fig. 1.

It is found that EoS parameter satisfies PDE phenomenon for all three values of PDE parameter in the range \(-0.4\leq z\leq2\). We have found that the GGPDE exhibits instability in the range \(-1\leq z\leq2\). Also, the \(\omega_{\varLambda}-\omega'_{\varLambda}\) plane provides the thawing region for the same constant parameters. Finally, we have discussed first and second laws of thermodynamics by assuming the same temperature of the universe in non-equilibrium description. We have found that the first law of thermodynamics is violated for GGPDE model due to the existence of entropy production term. However, the generalized second law of thermodynamics holds for the present day value of \(H\) with \(-1 \leqslant z \leqslant 0.8\).