1 Introduction

The search for exact solutions of Einstein’s field equations with certain geometry that satisfy physical constraints has been remaining the subject of great interest to the researchers. Such findings are also important in relativistic astrophysics because they enable the distribution of matter in the interior of stellar object to be modeled in terms of simple algebraic relations. Due to the strong nonlinearity of Einstein’s field equations and the lack of a comprehensive algorithm to generate all solutions, it becomes difficult to obtain new exact solutions. A well number of exact solutions of Einstein’s field equations are known to date but not all of them are physically relevant in the description of relativistic structure of compact stellar objects. Now there exist a number of comprehensive collections (Delgaty and Lake 1998; Stephani et al. 2003) of static, spherically symmetric solutions which provide a useful guide to the literature.

Since the pioneering work of Oppenheimer and Volkoff (1939) the analysis and determination of maximum mass of very compact astrophysical objects has been a key issue in relativistic astrophysics. There are several astrophysical objects such as normal matter neutron star (bound by gravity) or self-bound strange quark star (bound by the strong interaction) where one needs to consider equation of state (EOS) of matter involving energy densities of the order of 1015 g cm−3 or higher, exceeding the normal nuclear matter density. The strange star with surface energy density greater than the normal nuclear matter density has maximum mass almost the same but the radius is less than as that of neutron stars, with higher compactness parameter (Weber et al. 2012). Compact objects like neutron stars or strange stars may be classified on the basis of mass-radius relation (Haensel et al. 1986). Recent observations show that the estimated mass and radius of several compact objects such as X-ray pulsar Her X-1 are not compatible with the standard neutron star models, a strange star model could be more consistent with these objects (Li et al. 1995, Dey et al. 1998, for a recent review see Table 5 of Weber 2005). This claim is reinforced by the refined mass measurement of 12 pulsars that obey the strange star equation of state developed in (Gangopadhyay et al. 2013) and revised radii for these stars have been predicted.

Due to the absence of reliable information about equation of state of matter content in the interior of such compact stars, insight into the structure can be obtained by reference to applicable analytic solutions to the equation of relativistic stellar structure (Lattimer and Prakash 2001; Lattimer 2004).

Two traditional approaches usually followed to obtain a realistic stellar model. In the first approach one can start with an explicit equation of state and the integration starts at the center of the star with a prescribed central pressure (Oppenheimer-Volkoff method). The integrations are iterated until the pressure decreases to zero, indicating the surface of the star has been reached. Such input equations of state do not normally allow for closed form solutions.

In the second approach one needs to solve Einstein’s gravitational field equations. It is almost impossible to obtain an exact solution of such an under-determined system of nonlinear ordinary differential equations of second order. For the special case of a static isotropic perfect fluid the field equations can be reduced to a set of three coupled ordinary differential equations in four unknowns. In arriving to exact solutions, one can solve the field equations by making an ad hoc assumption for one of the metric functions or for the energy density (Tolman 1939 method). Hence the equation of state can be computed from the resulting metric. As might be expected with Tolman’s method, unphysical pressure-density configurations are found more frequently than physical ones. Hence a new solution which should be regular, well behaved, and can reasonably model a compact astrophysical stellar object is always welcome.

A class of fluid spheres for whose surface density vanishes at where the pressure vanishes may be good approximation for normal matter neutron stars (this class include Tolman (1939) III, VII and Buchdahl 1967 solutions). And the class of solutions for which surface density is finite, about 2–3 times the normal nuclear matter saturation density, at the surface where pressure vanishes may be taken as an analytical model of self-bound strange quark star. Such models include Tolman IV solution and the solutions discussed in Wyman (1949), Buchdahl (1964), Mehra (1966), Leibovitz (1969), Heintzmann (1969), Adler (1974), Adams and Cohen (1975), Kuchowicz (1975), Vaidya and Tikekar (1982), Durgapal (1982), Durgapal and Bannerji (1983), Durgapal and Fuloria (1985), Tikekar (1990), Pant and Pant (1993), Pant (1994, 1996). This approach leads to physically viable and easily tractable models of compact stars in equilibrium. Tikekar and Jotania (2005) have shown that the ansatz suggested by Tikekar and Thomas (1998) has these features and the general three-parameter solution based on it also leads to physically plausible relativistic models of strange stars. Several aspects of physical relevance and the maximum mass of class of compact star models, based on Vaidya–Tikekar ansatz, have been investigated by Sharma et al. (2006) (also see Jotania and Tikekar 2006 for relevant references).

All the solutions mentioned so far are in curvature coordinates. Out of 127 static spherically symmetric solutions very few solutions (Nariai 1950; Goldman 1978) in isotropic coordinates are known to pass the elementary tests of physical relevance and hence relevant in modelling compact stellar objects in astrophysics (Delgaty and Lake 1998). Knutsen (1991) have investigated Goldman’s method for constructing physically valid fluid spheres. The main defect of the method, pointed out by Knutsen, was that it did not examine whether the pressure gradient is larger than the density gradient. However, taking this condition into account, the method is very valuable and yields new models with interesting physical properties. Kuchowicz presented some practical methods to solve Einstein’s equations in isotropic coordinates. The method outlined in his series of papers (Kuchowicz 1971a, 1971b, 1972a, 1972b, 1973) is able to yield all possible exact solutions for spheres of perfect fluid in isotropic coordinates. Such exact solutions provide simplified models of static relativistic objects. The generation technique used by Hajj-Boutros (1986) leads directly to several new solutions in isotropic coordinates. Rahman and Visser (2002) and Lake (2003) also discussed a simplified algorithm for constructing all possible spherically symmetric perfect fluid solutions of Einstein’s equations in isotropic coordinates. By means of a matrix transformation Mak and Harko (2005) have reduced Einstein’s equations to two independent Riccati differential equations for which three classes of solutions are obtained. John and Maharaj (2006) reduced the condition for pressure isotropy to a recurrence equation with variable, rational coefficients of order three. They found an exact solution to the field equations corresponding to a static spherically symmetric gravitational potential in terms of elementary functions. The metric functions, the energy density and the pressure are found continuous and well behaved which implies that this solution could be used to model the interior of a relativistic star.

In recent years the description of compact astrophysical objects in the framework Extended Theory of Gravity has drawn considerable attention (Capozziello et al. 2011). Among the modified gravity theories the f(R) theories are relatively simple to handle. However, even for these theories, the field equations are complicated and obtaining MTOV (modified Tolman-Oppenheimer-Volkoff) equations in a standard fashion is difficult. This difficulty is mainly due to field equations being fourth order unlike in the case of general relativity, which has second order field equations. However, the hydrostatic equilibrium for normal matter neutron stars and self-bound quark stars by solving MTOV equations and the stability of such compact relativistic stars in the context of perturbative gravity models with some particular f(R) models with realistic equations of states have been discussed in (Alavirad and Weller 2013). It has been shown that such models of f(R) gravity can give rise to neutron stars with smaller radii than in General Relativity and can describe the existence of peculiar neutron stars with mass ∼2M ⊙ (the measured mass of PSR J1614-2230) and compact stars (R∼9 km) with masses M∼1.6–1.7M ⊙ that evade explanation in the framework of standard General Relativity (Astashenok et al. 2013). Although the applicability of perturbative approach at high densities is doubtful, it indicates the possibility of a stabilization mechanism in f(R) gravity. This mechanism leads to the existence of stable neutron stars which are more compact objects than in General Relativity. Moreover, the observation of such compact stable objects could be an experimental probe for modified gravity at astrophysical level.

The discussion of compact astrophysical objects within the frame work of general relativity is relatively simple. Our principle motivation of this work is to present a simple particular class of exact relativistic compact stellar astrophysical objects by solving Einstein’s gravitational field equations in isotropic coordinates. In recent past one successful attempt in isotropic coordinates has been made by one of us (Pant et al. 2010). These solutions are not only well behaved but also simple in terms of expressions of field and physical variables. Our class comprises two particular well behaved solutions previously derived by one of us (Pant et al. 2012, 2013). Such solutions are expected to provide simplified but easy to mathematically analyzed compact stellar models of bare strange quark star, a star with nonzero ultra-high surface density.

2 Solutions of field equations in isotropic coordinates

The interior metric of a static spherically symmetric matter distribution in isotropic coordinates may be taken as,

$$ ds^{2} = e^{\alpha ( \rho )}c^{2}dt{}^{2} - e^{\beta ( \rho )} \bigl( d\rho^{2} + \rho^{2} \bigl( d \theta^{2} + \sin^{2}\theta d\varphi^{2} \bigr) \bigr) $$
(2.1)

where α and β are functions of ρ only.

For the metric (2.1) the Einstein’s field equations of gravitation for a nonempty space-time reduces to the following set of relevant equations

$$\begin{aligned} &\kappa P = e^{ - \beta} \biggl( \frac{\beta'^{2}}{4} + \frac{\beta '}{\rho} + \frac{\alpha'\beta'}{2} + \frac{\alpha'}{\rho} \biggr) \end{aligned}$$
(2.2)
$$\begin{aligned} & \kappa P = e^{ - \beta} \biggl( \frac{\beta''}{2} + \frac{\alpha ''}{2} + \frac{\alpha'^{2}}{4} + \frac{\beta'}{2\rho} + \frac{\alpha'}{2\rho} \biggr) \end{aligned}$$
(2.3)
$$\begin{aligned} & \kappa\mu c^{2} = - e^{ - \beta} \biggl( \beta'' + \frac{\beta'^{2}}{4} + \frac{2\beta'}{\rho} \biggr) \end{aligned}$$
(2.4)

where prime (′) denotes the differentiation with respect to ρ.

Eliminating the pressure, P, from (2.2) and (2.3) we obtain following differential equation in α and β, known as “pressure isotropy” equation,

$$ \alpha'' + \beta'' + \frac{\alpha'^{2}}{2} - \frac{\beta'^{2}}{2} - \alpha'\beta' - \biggl( \frac{\alpha'}{\rho} + \frac{\beta'}{\rho} \biggr) = 0 $$
(2.5)

By introducing the transformation, x=Cρ 2, Eqs. (2.2) and (2.4) can be expressed in terms of the new auxiliary variable x, as,

$$\begin{aligned} & \frac{\kappa}{C}P = e^{ - \beta} \biggl( x \biggl( \frac{d\beta}{dx} \biggr)^{2} + 2\frac{d\beta}{dx} + 2x\frac{d\alpha}{dx} \frac{d\beta}{dx} + 2\frac{d\alpha}{dx} \biggr) \end{aligned}$$
(2.6)
$$\begin{aligned} & \frac{\kappa}{C}\mu c^{2} = - e^{ - \beta} \biggl( 4x \frac{d^{2}\beta}{ dx^{2}} + x \biggl( \frac{d\beta}{dx} \biggr)^{2} + 6 \frac{d\beta}{dx}\biggr) \end{aligned}$$
(2.7)

And Eq. (2.5) becomes,

$$ \frac{d^{2}\alpha}{dx^{2}} + \frac{d^{2}\beta}{dx^{2}} + \frac{1}{2} \biggl( \frac{d\alpha}{dx} \biggr)^{2} - \frac{1}{2} \biggl( \frac{d\beta}{dx} \biggr)^{2} - \frac{d\alpha}{dx}\frac{d\beta}{dx} = 0 $$
(2.8)

Equation (2.8) is a Riccati type differential equation in dα/dx or dβ/dx. In the next subsection we explore its solution and obtain a physically meaningful matter distribution described by the fluid parameters P and μ from Eqs. (2.6) and (2.7).

2.1 Class of interior solutions

To solve the equation of pressure isotropy (2.8), by assuming an ad hoc relation of gravitational potential in x, analogous to Hajj-Boutros (1986) and Tewari (2013) and considering the parameters in such a manner so that the solution should be well behaved for perfect fluid. We may thus make a choice,

$$ e^{\frac{\beta}{2}} = B ( 1 + x )^{N} $$
(2.9)

Inserting Eq. (2.9) into Eq. (2.8) we obtain the following Riccati differential equation,

$$ \frac{dy}{dx} - \frac{2N}{ ( 1 + x )}y + \frac{1}{2}y^{2} = \frac{2N ( 1 + N )}{ ( 1 + x )^{2}} $$
(2.10)

where y=dα/dx.

The substitution y=2dz/zdx transforms Eq. (2.10) into a second order homogeneous linear Legendre differential equation (Riley et al. 2006)

$$( 1 + x )^{2}\frac{d^{2}z}{dx^{2}} - 2N ( 1 + x )\frac{dz}{dx} - \bigl( N + N^{2} \bigr)z = 0 $$

and this yields the following solution,

$$ z = e^{\frac{\alpha}{2}} = \frac{1}{B^{2}} \bigl[ ( 1 + x )^{n_{1}} + A ( 1 + x )^{n_{2}} \bigr] $$
(2.11)

where,

$$\begin{aligned} & n_{1} = \frac{1}{2} \Bigl[ ( 1 + 2N ) - \sqrt{8N^{2} + 8N + 1} \Bigr]\\ & n_{2} = \frac{1}{2} \Bigl[ ( 1 + 2N ) + \sqrt{8N^{2} + 8N + 1} \Bigr] \end{aligned}$$

In Eqs. (2.9) and (2.11) A, B, and Care constants. For n 1 and n 2 to be real number we must have,

$$- ( 2 - \sqrt{2} ) / 4 \le N < 0\quad\mbox{or},\quad - 1 \le N \le - ( 2 + \sqrt{2} ) / 4 $$

The expressions for pressure and density are obtained by inserting (2.9) and (2.11) into Eqs. (2.6) and (2.7) as,

$$\begin{aligned} & \frac{\kappa}{C}P = \frac{4}{ ( 1 + x )^{2 + 2N}B^{2}} \biggl[ ( N + n_{2} ) + \bigl( N + n_{2} + N^{2} \\ & \hphantom{\frac{\kappa}{C}P =}{}+ 2n_{2}N \bigr)x- \frac{ ( n_{2} - n_{1} ) ( 1 + ( 1 + 2N )x )}{1 + A ( 1 + x )^{n_{2} - n_{1}}} \biggr] \end{aligned}$$
(2.12)
$$\begin{aligned} & \frac{\kappa}{C}c^{2}\mu= - \frac{4N}{ ( 1 + x )^{2 + 2N}B^{2}} \bigl[ 3 + ( 1 + N )x \bigr] \end{aligned}$$
(2.13)

Hence, Eqs. (2.9), and (2.11)–(2.13) constitute the complete solution of Einstein’s field equation.

2.2 Some particular solutions

Solution I:

N=−3/23

$$\begin{aligned} & e^{\frac{\beta}{2}} = B ( 1 + x )^{ - \frac{3}{23}}\\ & e^{\frac{\alpha}{2}} = \frac{1}{B^{2}} \bigl[ ( 1 + x )^{\frac{5}{23}} + A ( 1 + x )^{\frac{12}{23}} \bigr]\\ & \frac{\kappa}{C}P = \frac{4}{23^{2} ( 1 + x )^{\frac{40}{23}}B^{2}} \biggl[ 207 + 144x - \frac{7 ( 23 + 17x )}{1 + A ( 1 + x )^{\frac{7}{23}}} \biggr]\\ & \frac{\kappa}{C}c^{2}\mu= \frac{12}{23^{2} ( 1 + x )^{\frac{40}{23}}B^{2}} ( 69 + 20x ) \end{aligned}$$

Solution II:

N=−6/41

$$\begin{aligned} & e^{\frac{\beta}{2}} = B ( 1 + x )^{ - \frac{6}{41}}\\ & e^{\frac{\alpha}{2}} = \frac{1}{B^{2}} \bigl[ ( 1 + x )^{\frac{14}{41}} + A ( 1 + x )^{\frac{15}{41}} \bigr]\\ & \frac{\kappa}{C}P = \frac{4}{41^{2} ( 1 + x )^{\frac{70}{41}}B^{2}} \biggl[ 369 + 225x - \frac{ ( 41 + 29x )}{1 + A ( 1 + x )^{\frac{1}{41}}} \biggr]\\ & \frac{\kappa}{C}c^{2}\mu= \frac{24}{41^{2} ( 1 + x )^{\frac{70}{41}}B^{2}} ( 123 + 35x ) \end{aligned}$$

Solution III:

\(N = - ( 2 - \sqrt{2} ) / 4\)

$$\begin{aligned} & e^{\frac{\beta}{2}} = B ( 1 + x )^{ - \frac{ ( 2 - \sqrt{2} )}{4}}\\ & e^{\frac{\alpha}{2}} = \frac{1}{B^{2}} \bigl[ ( 1 + x )^{\frac{\sqrt{2}}{4}} + A ( 1 + x )^{\frac{\sqrt{2}}{4}} \bigr]\\ & \frac{\kappa}{C}P = \frac{4}{ ( 1 + x )^{\frac{ ( 2 + \sqrt{2} )}{2}}B^{2}} \biggl[ \frac{ ( \sqrt{2} - 1 )}{2} + \biggl( \frac{ ( \sqrt{2} - 1 )}{2} + \frac{5}{8} \biggr)x \biggr]\\ & \frac{\kappa}{C}c^{2}\mu= \frac{ ( 2 - \sqrt{2} )}{ ( 1 + x )^{\frac{ ( 2 + \sqrt{2} )}{2}}B^{2}} \biggl( 3 + \frac{ ( 2 + \sqrt{2} )}{4}x \biggr) \end{aligned}$$

3 Elementary criteria for physical acceptability

From the physical point of view, the mathematical solutions must satisfy certain physical conditions to render them physically meaningful. The following requirements have been accepted in this paper which are available in the following papers (Kuchowicz 1971a, 1971b, 1972a, 1972b, 1973, Glass and Goldman 1978; Stewart 1982; Hajj-Boutros 1986; Knutsen 1991; Delgaty and Lake 1998),

  1. (i)

    The solution should be free from physical and geometrical singularities i.e. finite and positive values of central pressure, central density and non zero positive values of e α and e β. Mathematically,

    $$e^{\alpha} > 0,\quad e^{\beta} > 0,\quad P_{c} > 0,\quad \mu_{c} > 0 $$
  2. (ii)

    The solution should have positive values of pressure and density and monotonically decreasing functions for pressure and density (P,μ) with increasing radius. Mathematically,

    $$P ( r ) \ge0,\quad\mu ( r ) > 0,\quad\frac{dP}{dr} < 0,\quad \frac{d\mu}{dr} < 0 $$

    Or, in terms of auxiliary variable,

    $$P ( x ) \ge0,\quad\mu ( x ) > 0,\quad\frac{dP}{dx} < 0,\quad \frac{d\mu}{dx} < 0 $$

    (See theorem in Pant et al. 2011)

  3. (iii)

    To be isolated it is required that the pressure must be zero at some finite boundary radius. Mathematically,

    $$P ( r = R ) \ge0\quad\mbox{or},\quad P ( \rho= \rho_{\varSigma} ) \ge0 $$
  4. (iv)

    c 2 μ>P everywhere in the interior of the fluid sphere (dominant energy condition).

  5. (v)

    The trace condition, \(T_{i}^{i} = c^{2}\mu- 3P > 0\), must be satisfied in the interior of the star.

  6. (vi)

    The solution should have positive and monotonically decreasing expression for the pressure and density and the fluid parameter P/c 2 μ with increasing radius.

  7. (vii)

    The solution should have positive and monotonically decreasing expression for velocity of sound, \(\sqrt{dP / c^{2}d\mu}\), with increasing radius. Also the causality condition should be obeyed at the centre i.e., \(0 < \sqrt{ ( dP / c^{2}d\mu )_{c}} \le1\).

  8. (viii)

    The red shift z should be positive, finite and monotonically decreasing in nature with the increase of radius. The central red shift z c and surface redshift z s should be positive and finite.

    $$z_{c} = e^{ - \frac{1}{2}\alpha ( r = 0 )} - 1,\qquad z_{s} = \bigl( 1 - 2GM / c^{2}R \bigr)^{ - \frac{1}{2}} - 1 $$
  9. (ix)

    The interior solution must match continuously with the Schwarzschild exterior solution (Schwarzschild 1916), which requires the continuity of metric coefficients and their first derivatives across the boundary ρ=ρ Σ (Nariai 1965; Bonnor and Vickers 1981).

4 Physical boundary conditions

Schwarzschild exterior solution in canonical coordinates can be written as,

$$\begin{aligned} ds^{2} & = c^{2} \biggl( 1 - \frac{2GM}{c^{2}r} \biggr)dt{}^{2} - \biggl( 1 - \frac{2GM}{c^{2}r} \biggr)^{ - 1}dr^{2} \\ &\quad {}- r^{2} \bigl( d\theta^{2} + \sin^{2}\theta d \varphi^{2} \bigr) \end{aligned}$$
(4.1)

By the use of following transformation,

$$ r = \rho \biggl( 1 + \frac{GM}{2c^{2}\rho} \biggr)^{2} $$
(4.2)

Equation (4.1) can be transformed in the so called isotropic form (Adler et al. 1975),

$$\begin{aligned} ds^{2} & = c^{2}\frac{ ( 1 - \frac{GM}{2c^{2}\rho} )^{2}}{ ( 1 + \frac{GM}{2c^{2}\rho} )^{2}}dt{}^{2}- \biggl( 1 + \frac{GM}{2c^{2}\rho} \biggr)^{4} \\ &\quad {} \times \bigl( d\rho^{2} + \rho^{2} \bigl( d\theta^{2} + \sin^{2}\theta d \varphi^{2} \bigr) \bigr) \end{aligned}$$
(4.3)

In Eq. (4.1) M is the gravitational mass of the fluid sphere and R is the coordinate radius measured by the external observer. In order that the interior solution joins properly to the exterior Schwarzschild solution the usual boundary conditions are that the first and second fundamental forms are continuous over the boundary, ρ=ρ Σ (e.g. see Hajj-Boutros 1986), which read,

$$\begin{aligned} &(\mathrm{i})\ \ \ e^{\alpha ( \rho_{\varSigma} )} = \frac{ ( 1 - \frac{GM}{2c^{2}\rho_{\varSigma}} )^{2}}{ ( 1 + \frac{GM}{2c^{2}\rho_{\varSigma}} )^{2}},\quad\ \ \ (\mathrm{ii})\ \ \ \frac{d\alpha}{ d\rho} \bigg\vert _{\varSigma} = \frac{\frac{2GM}{c^{2}\rho_{\varSigma }^{2}}}{ ( 1 - \frac{G^{2}M^{2}}{4c^{4}\rho_{\varSigma}^{2}} )} \\ & (\mathrm{iii})\quad e^{\beta ( \rho_{\varSigma} )} = \biggl( 1 + \frac{GM}{2c^{2}\rho_{\varSigma}} \biggr)^{4},\\ & (\mathrm{iv})\quad \frac{d\beta}{ d\rho} \bigg\vert _{\varSigma} = - \frac{\frac{2GM}{c^{2}\rho_{\varSigma}^{2}}}{ ( 1 + \frac{GM}{2c^{2}\rho_{\varSigma}} )} \end{aligned}$$

By the use of condition (iv) \(X ( = C\rho_{\varSigma}^{2} )\) can expressed in terms of “compactness” parameter u(=GM/c 2 ρ Σ ) as following.

$$X \equiv C\rho_{\varSigma}^{2} = - \frac{u}{2N + ( 1 + N )u} $$

The condition X>0 also constrains u over the interval 0<u<−2N/(1+N).

4.1 Determination of A

Using the boundary condition P(ρ Σ )=0 the constant A can be calculated by the following equation,

$$A = - \frac{ ( N + n_{1} ) + ( 2Nn_{1} + N + n_{1} + N^{2} )X}{ ( N + n_{2} ) + ( 2Nn_{2} + N + n_{2} + N^{2} )X} ( 1 + X )^{ ( n_{1} - n_{2} )} $$

4.2 Determination of B

From the boundary condition iii) the constant B can be specified as follows,

$$B = \biggl( 1 + \frac{u}{2} \biggr)^{2} ( 1 + X )^{ - N} $$

5 Physical analysis of the models

In this section we derive the pressure and density gradients to investigate the behavior of the equation of state numerically.

5.1 Pressure and density gradients

Differentiating Eqs. (2.12) and (2.13), with respect to the auxiliary variable x, the pressure and density gradients become,

$$\begin{aligned} \frac{\kappa}{C}\frac{dP}{dx} = - \frac{4}{B^{2} ( 1 + x )^{3 + 2N}}\left ( \begin{array}{l} (n_{2} + N + N^{2} ) + ( N +n_{2} + 3N^{2} + 4n_{2}N + 2N^{3} + 4n_{2}N^{2} )x\\ \quad {}\times( 1 + 2N ) ( 1 + x ) [ 1 + A ( 1 + x )^{n_{2} - n_{1}} ]\\ - ( n_{2} - n_{1} )\frac{ - [ ( 2 + 2N ) [ 1 + A ( 1 + x )^{n_{2} - n_{1}} ] + ( n_{2} - n_{1} )A ( 1 + x )^{n_{2} - n_{1}} ] ( 1 + ( 1 + 2N )x )}{[ 1 + A ( 1 + x )^{n_{2} - n_{1}} ]} \end{array} \right ) \end{aligned}$$
$$\frac{\kappa}{C}c^{2}\frac{d\mu}{dx} = \frac{4N ( 1 + N ) ( 5 + ( 1 + 2N )x )}{B^{2} ( 1 + x )^{3 + 2N}} $$

The central values of pressure and density gradients are then given by

$$\begin{aligned} & \frac{\kappa}{C} \biggl( \frac{dP}{dx} \biggr)_{c}\\ & = - \frac{4}{B^{2}} \biggl( \bigl( n_{2} + N + N^{2} \bigr) + ( n_{2} - n_{1} ) \\ &\quad {}\times\frac { ( 1 + 2N ) ( 1 + A ) - [ ( 2 + 2N ) ( 1 + A ) + ( n_{2} - n_{1} )A ]}{ ( 1 + A )^{2}} \biggr)\\ & \frac{\kappa}{C}c^{2} \biggl( \frac{d\mu}{dx} \biggr)_{c} = \frac {20N ( 1 + N )}{B^{2}} \end{aligned}$$

The mass and other physical quantities of the fluid sphere may be determined for a given (i) radius, (ii) surface density, (iii) central density, or (iv) central pressure.

(i)

For a given radius

Boundary value of the coordinate, ρ=ρ Σ ,

$$ \rho_{\varSigma} = \frac{R}{B} ( 1 + X )^{ - N} $$
(5.1)

Then the central density, surface density and the total mass of the fluid sphere can be calculated by the use of following eqs.

$$\begin{aligned} & \mu_{c} = - \frac{12NX}{B^{2}\rho_{\varSigma}^{2}\kappa c^{2}} \end{aligned}$$
(5.2)
$$\begin{aligned} & \mu_{s} = - \frac{4NX [ 3 + ( 1 + N )X ]}{ ( 1 + X )^{2 + 2N}B^{2}\rho_{\varSigma}^{2}\kappa c^{2}} \end{aligned}$$
(5.3)
$$\begin{aligned} & M = \frac{uc^{2}\rho_{\varSigma}}{G} \end{aligned}$$
(5.4)

(ii)

For a given surface density

Boundary value of the coordinate ρ=ρ Σ

$$ \rho_{\varSigma} = \sqrt{ - \frac{4NX [ 3 + ( 1 + N )x ]}{ ( 1 + X )^{2 + 2N}B^{2}\kappa c^{2}\mu_{s}}} $$
(5.5)

From the Eq. (4.2) together with the boundary condition (iii), the radius of the fluid sphere can be calculated by

$$ R = \rho_{\varSigma} B ( 1 + X )^{N} $$
(5.6)

The central density and the total mass can be calculated by the Eqs. (5.2) and (5.4).

(iii)

For a given central density

Boundary value of the coordinate, ρ=ρ Σ ,

$$ \rho_{\varSigma} = \sqrt{ - \frac{12NX}{B^{2}\kappa c^{2}\mu_{c}}} $$
(5.7)

The total mass, radius and surface density can be calculated by Eqs. (5.4), (5.6), and (5.3) respectively.

(iv)

For a given central pressure

Boundary value of the coordinate, ρ=ρ Σ ,

$$ \rho_{\varSigma} = \sqrt{\frac{4X}{B^{2}\kappa P_{c}} \biggl[ ( N + n_{2} ) - \frac{ ( n_{2} - n_{1} )}{ ( 1 + A )} \biggr]} $$
(5.8)

The total mass, radius and surface density can be calculated by Eqs. (5.4), (5.6), and (5.3) respectively.

5.2 Construction of fluid spheres

For the particular set of values of (N,u) for which the fluid distribution satisfies the following inequalities (i)–(vii) of Sect. 3 are reported in Tables 1–2.Footnote 1 The mass, radius and other physical quantities of compact well-behaved fluid spheres obtained by specifying stellar surface density as parameter are reported in Table 3.

Table 1 Maximum value of u max(=GM/c 2 ρ Σ ) for which the inequalities (ii) and (vii) are satisfied
Full size table
Table 2 Central values of the various physical quantities for particular fluid spheres
Full size table
Table 3 Maximum mass and the various physical variables of fluid spheres with given surface density
Full size table

5.3 Discussions on numerical results

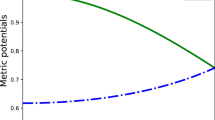
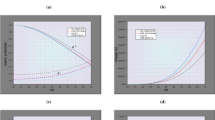
For \(N = - ( 2 - \sqrt{2} ) / 4\), the condition X>0 constrains u over the interval \(0 < u < ( 2 - \sqrt{2} )^{2}\). But the fluid distribution satisfies inequalities (i)–(vii) for the range of values 0<u≤0.247. The metric functions e α and e β are found regular and positive. The behaviors of isotropic pressure and energy density and the ratio of their respective gradients which are found positive and monotonically decreasing in the interior of the star are shown in Fig. 1. However, corresponding to any value of \(0.247 < u < ( 2 - \sqrt{2} )^{2}\), though the causality condition is obeyed throughout the sphere but the trend of adiabatic sound speed is erratic. Thus, the solution obtained in eqs. (2.9), and (2.11)–(2.13) is well behaved for all values of u satisfying the inequality 0<u≤0.247. Corresponding to maximum value u max=0.247, the model yield a physically acceptable perfect fluid sphere with maximum compactness which is obtained (GM/c 2 R)max=0.1956. Once the compactness of the compact fluid sphere is obtained the maximum mass can then be calculated by using one of the following quantity: (i) radius, (ii) central density, (iii) surface density, or, (iv) central pressure as parameter. For a particular choice of stellar surface densityFootnote 2 μ s =4.6×1014 g cm−3, the total mass and other physical quantities are calculated by the use of Eqs. (5.2), (5.4)–(5.6) M=1.1078M ⊙, R=8.41 km,P c =200.61 MeV fm−3, μ c =2.66×1015 g cm−3. The central and surface redshifts are obtained 0.666459 and 0.282473 respectively. The variation of the maximum mass M max, radius R, and the central density with respect to the parameter |N| are demonstrated in Figs. 2(a)–2(c). The mass-radius relation for a sequence of stars described by the input \(N = - ( 2 - \sqrt{2} ) / 4\) and 0<u≤0.247 with stellar surface density 4.6×1014 g cm−3 has been demonstrated in Fig. 3(a). In Fig. 3(b) the mass versus central density for the same configurations are plotted and this shows the necessary condition of stability is satisfied (dM/dμ c >0). However, no value of N belonging to the interval \(- 1 \le N < - ( 2 + \sqrt{2} ) / 4\) yields physically meaningful matter distribution as failed to satisfy necessary the physical conditions P≥0,μ≥0.

Fig. 1
figure 1

Behavior of (a) pressure, (b) energy density within fluid sphere described by the input \(N = - ( 2 - \sqrt{2} ) / 4\) and u max=0.247

Full size image
Fig. 2
figure 2

Variation of (a) maximum mass M max, (b) radius R, and (c) central density μ c,15 with respect to |N| with particular stellar surface density 4.6×1014 g cm−3

Full size image
Fig. 3
figure 3

(a) Mass-radius relationship, (b) Mass-central density for a sequence of strange stars described by the input \(N = - ( 2 - \sqrt{2} ) / 4\) and 0<u≤0.247 with stellar surface density 4.6×1014 g cm−3

Full size image

6 An application of the model for some possible strange star candidates

Based on the analytic model developed so far, to get an estimate of the range of various physical parameters, let us now consider some potential strange star candidates like Her X-1, 4U 1538–52, LMC X-4, SAX J1808.4−3658. Using the mass and radius reported in Gangopadhyay et al. (2013) for each of these pulsars we have calculated the values of the relevant physical quantities and reported in Table 4.

Table 4 Physical values of energy density and pressure for some strange stars candidates
Full size table

7 Concluding remarks

We thus have studied a particular simple class of exact relativistic compact astrophysical stellar objects with nonzero ultrahigh surface density in the framework of general relativity. In order to obtain a realistic stellar model Einstein’s gravitational field equations have been solved by making an ad hoc assumption on one of the metric functions e β/2=B(1+x)N and the equation of state has been computed from the resulting metric.

Due to the complicacy it is difficult to eliminate the auxiliary variable from Eqs. (2.12) and (2.13) and obtain an explicit relation for isotropic pressure in terms of energy density.

Numerical analysis reveals that the maximum compactness of the fluid sphere is obtained GM/c 2 R=0.1956 at \(N = - ( 2 - \sqrt{2} ) / 4\). To specify the mass and radius of the fluid sphere we have set the stellar surface density equal to the strange quark matter density at zero pressure which is much larger than the nuclear matter saturation density. A particular choice of stellar surface density \(\mu_{s} = 4.6 \times10^{14}~\mathrm{g\,cm}^{ - 3}\) could give rise a stable configuration of total mass M=1.1078M ⊙, radius R=8.41 km, and central density as high as μ c =2.66×1015 g cm−3. The mass-radius relation for a sequence of compact star demonstrates that the isotropic solution discussed in this work could reproduce strange stars.

To justify our results, for some suitable choices of input parameters N and u, we have generated compact fluid spheres similar to the mass and radius of some possible strange star candidates like Her X-1, 4U 1538−52, LMC X-4, SAX J1808.4−3658 (Gangopadhyay et al. 2013). The pressure-density profiles for these strange stars given by our analytical model, using Eqs. (2.12)–(2.13) are plotted in Fig. 4(a) and the behaviors of the quantity (dP/c 2 dμ≈constant) shown in Fig 4(b) demonstrates that the isotropic pressure varies almost linearly with respect to energy density. The values of various physical quantities for these pulsars have been calculated and the results endorse the astrophysical significance and viability of our model in the study of relativistic stellar structure of non-rotating compact objects like self-bound strange quark star.

Fig. 4
figure 4

(a) Pressure density profile P(μ) and (b) Adiabatic speed of sound \(\sqrt{ ( dP / c^{2}d\mu )}\) given by our model for \(N = - ( 2 - \sqrt{2} ) / 4\) for potential strange star candidates like Her X-1, 4U 1538−52, LMC X-4, SAX J1808.4−3658 with mass and radius reported in Gangopadhyay et al. (2013)

Full size image

As strange quark matter stars are not gravitationally bound, alternative gravity models do not produce different mass-radius relations for such objects (Arapoğlu et al. 2011). But, in principle, the formation, evolution, and observation of such objects could be an experimental probe to check the viability of for alternative theories of gravity such as f(R) gravity models.