1 Introduction

Compact objects [1,2,3] are the final fate of stars, and since these stars have ultra-high matter densities, the non-relativistic Newtonian description is not adequate. Dense, compact objects are relativistic, and as such, the framework of Einstein’s General Relativity (GR) [4] is the correct way to describe them. In particular, strange quark stars, as of today hypothetical objects, have been postulated to exist as a new branch of compact stars. Quark matter, by assumption, is absolutely stable, and it may be the real ground state of hadronic matter [5, 6]. Strange quark stars provide us with a plausible explanation of the puzzling observation of some super-luminous supernovae [7, 8], which occur in about one out of every 1000 supernovae explosions, and are more than 100 times brighter than ordinary supernovae. They are called “strange quark stars” [9,10,11,12,13,14], and since they are a much more stable configuration compared to neutron stars, they may explain the origin of the massive amount of energy released in super-luminous supernovae.

Modelling astrophysical objects, and obtaining exact analytical solutions to Einstein’s field equations which can describe realistic astrophysical configurations, is always challenging, and it has kept researchers occupied for decades now. Several techniques are employed to find solutions that describe non-rotating, spherically symmetric stars in the presence of a non-vanishing cosmological constant, electromagnetic fields, anisotropic matter etc. Since realistic astronomical objects are expected to be electrically neutral, or at least without a significant amount of electric charge, in studies of compact relativistic astrophysical objects the authors usually focus on electrically neutral stars made of isotropic matter, and the interior solution is matched to the exterior Schwarzschild solution [15] on the surface of the object. However, there is nowadays a considerable amount of articles in the literature investigating the properties of astrophysical objects with a net electric charge, see e.g. [16,17,18,19,20,21,22,23,24] and references therein. Almost 100 years ago Rosseland considered for the first time the possibility that stars could carry a non-vanishing electric charge [25]. Several decades after that, other works gave birth to the interest in studying electrically charged astrophysical objects, since it turns out that the presence of static electric fields may have certain interesting features, such as avoiding the point singularity or preventing total gravitational collapse of a spherically symmetric distribution of matter, see [26,27,28,29].

What is more, celestial bodies under certain conditions may become anisotropic. Such a possibility was mentioned for the first time in [30], where the author observed that relativistic particle interactions in a very dense nuclear matter medium could lead to the formation of anisotropies. Indeed, anisotropies arise in many scenarios of a dense matter medium, like phase transitions [31], pion condensation [32], or in the presence of type 3A super-fluid [33]. Anisotropic electrically neutral stars have been investigated in [34,35,36,37,38,39], while electrically charged objects with anisotropic matter were considered in [40,41,42,43,44,45], out of which only two correspond to strange quark stars ( [43, 45]), where a linear equation-of-state (EoS) “radiation plus constant” was adopted.

In the present work we obtain a new exact analytical solution to the Einstein–Maxwell field equations for anisotropic matter. The solution describes the interior of anisotropic electrically charged strange quark stars with a non-linear EoS assuming a finite mass for the s quark. To the best of our knowledge, this analysis is performed here for the first time. Our work differs from [43, 45] in two respects: First, the EoS considered here is non-linear, and in addition to that to obtain a tractable exact analytical solution we assume a specific form for the metric component \(g_{rr}\) instead of a particular form for the matter-energy density. Although both choices are equally good, in practice we find it slightly more convenient to start with a given metric potential, since in this case the mass function is known immediately, and then the energy density may be computed differentiating (in the temporal Einstein’s field equation) the mass function as well as the charge function with respect to the radial coordinate, see the discussion below. In contrary, if we start assuming a given density profile the mass function must be determined by integration.

We wish to emphasize at this point that in our work here we are only interested in the effect of the electric charge on properties of strange quark stars, and not in the precise mechanism that generates the net charge, although in the literature some mechanisms have been indeed proposed [46] (see also [47] for an indirect relevance to quark matter). Accretion is perhaps the most well-known astrophysical process that can induce a net electric charge into compact objects [48]. For accretion scenarios which may create black holes and stars with a non-vanishing electric charge big enough to have influence on the space-time geometry see e.g. [49,50,51].

The plan to present our work is the following: In the next section we discuss the model and the structure equations that describe the hydrostatic equilibrium for the interior of the stars. In Sect. 3 we obtain the exact analytical solution, and we discuss its properties. Finally, we conclude our work in the Sect. 4. We work in geometrical units where \(c=1=G\), and we adopt the mostly positive metric signature (–,+,+,+).

2 Structure equations

The model is described by the action

$$\begin{aligned} S = S_G + S_M + S_{EM} \end{aligned}$$
(1)

where the gravity part \(S_G\) is given by the usual Einstein-Hilbert term, the electromagnetic Lagrangian \(S_{EM}\) corresponds to Maxwell’s theory, while the matter contribution corresponds to an anisotropic fluid with energy density \(\rho \), radial pressure \(p_r\), transverse pressure \(p_t\), and an equation-of-state to be discussed later on. Varying with respect to the metric tensor we obtain Einstein’s field equations without a cosmological constant

$$\begin{aligned} G_{\mu \nu } \equiv R_{\mu \nu }-\frac{1}{2} R g_{\mu \nu } = 8 \pi T_{\mu \nu } \end{aligned}$$
(2)

where the Newton’s constant G is set equal to unity. The total stress-energy tensor has two contributions

$$\begin{aligned} T_{\mu \nu } = M_{\mu \nu } + E_{\mu \nu }, \end{aligned}$$
(3)

namely one from the fluid [34]

$$\begin{aligned} M_\nu ^\mu = Diag(-\rho , p_r, p_t, p_t) \end{aligned}$$
(4)

and one from the electromagnetic field [22]

$$\begin{aligned} E_{\nu \mu } = \frac{1}{4 \pi } \left[ -\frac{1}{4}F g_{\mu \nu } + F_{\nu \gamma } F_\mu ^ \gamma \right] \end{aligned}$$
(5)

where \(F=F_{\mu \nu } F^{\mu \nu }\) is the Maxwell invariant, and \(F_{\mu \nu }\) is the electromagnetic field strength. The electromagnetic energy-momentum tensor has the form

$$\begin{aligned} E_\mu ^\nu = Diag\left( -\frac{E^2}{8 \pi }, -\frac{E^2}{8 \pi }, \frac{E^2}{8 \pi }, \frac{E^2}{8 \pi } \right) \end{aligned}$$
(6)

where E(r) is the electric field. For later use we define the anisotropic factor \(\Delta \equiv p_t-p_r\).

Furthermore, varying with respect to the Maxwell potential one obtains Maxwell’s equations

$$\begin{aligned} \nabla _\nu F^{\mu \nu } = 4 \pi J^\mu \end{aligned}$$
(7)

where \(J_\mu \) is the current of the charged fluid.

For the exterior problem, \(r > R\), with R being the radius of the star, where \(M_{\mu \nu }\) vanishes, we seek static spherically symmetric solutions of the form

$$\begin{aligned} \mathrm {d}s^2 = -f(r) \mathrm {d}t^2 + g(r) \mathrm {d}r^2 + r^2 (\mathrm {d} \theta ^2 + \sin ^2{\theta } \mathrm {d} \phi ^2) \end{aligned}$$
(8)

for the metric tensor, while for the electromagnetic field the only non-vanishing component is the one that corresponds to the electric field, \(F_{tr}=E(r)=Q/r^2\). The solution to the exterior problem is of course the well-known Reissner-Nordström solution [52]

$$\begin{aligned} f(r) = g(r)^{-1} = 1 - \frac{2M}{r} + \frac{Q^2}{r^2} \end{aligned}$$
(9)

where M, Q are the mass and the electric charge, respectively, of the star. The electric charge takes values in the range \(0 \le Q \le M\), where in the limit \(Q \rightarrow 0\) we recover the Schwarzschild solution, while in the other limit the Reissner-Nordström solution becomes extremal.

For the interior solutions, \(r < R\), we have to solve the field equations in the presence of both the perfect fluid and the electromagnetic field. As usual we make the ansatz

$$\begin{aligned} \mathrm {d}s^2 = -e^{2 \nu (r)} \mathrm {d}t^2 + A(r) \mathrm {d}r^2 + r^2 (\mathrm {d} \theta ^2 + \sin ^2{\theta } \mathrm {d} \phi ^2) \end{aligned}$$
(10)

and we set for convenience

$$\begin{aligned} A(r)^{-1} = 1 - \frac{2m(r)}{r} + \frac{q(r)^2}{r^2} \end{aligned}$$
(11)

similar to the exterior solution, where m(r) is the mass function, and q(r) is the electric charge function.

The structure equations for the unknown quantities may be easily derived since the corresponding equations for anisotropic objects are known, see e.g. [34]. In the present work the components of the total energy-momentum tensor are found to be

$$\begin{aligned} \rho _{eff}\equiv & {} \rho + \frac{E^2}{8 \pi } \end{aligned}$$
(12)
$$\begin{aligned} P_r\equiv & {} p_r - \frac{E^2}{8 \pi } \end{aligned}$$
(13)
$$\begin{aligned} P_t\equiv & {} p_t + \frac{E^2}{8 \pi } \end{aligned}$$
(14)

Therefore, one finally obtains the following system of coupled differential equations [22, 27]

$$\begin{aligned} q'(r)&= 4 \pi \rho _e(r) r^2 \sqrt{A(r)} \end{aligned}$$
(15)
$$\begin{aligned} m'(r)&= 4 \pi \rho (r) r^2 + \frac{q(r) q'(r)}{r} \end{aligned}$$
(16)
$$\begin{aligned} p_r'(r) =&-(p_r(r)+\rho (r)) \, \nu '(r) + \frac{2}{r} \Delta \nonumber \\&+ \frac{q(r) q'(r)}{4 \pi r^4} \end{aligned}$$
(17)
$$\begin{aligned} \nu '(r) =&\frac{4 \pi r^3 p_r(r)+m(r)-\frac{q(r)^2}{r}}{r^2(1-\frac{2m(r)}{r} + \frac{q(r)^2}{r^2})} \end{aligned}$$
(18)

where \(\rho _e(r)\) is the electric density, and the prime denotes differentiation with respect to the radial coordinate r.Footnote 1 For neutral and isotropic stars, \(q=0=\Delta \), we recover the usual Tolman–Oppenheimer–Volkoff equations [53, 54].

Finally, the differential equations are to be integrated imposing the initial conditions at the center of the star

$$\begin{aligned} p(0)= & {} p_c \end{aligned}$$
(19)
$$\begin{aligned} m(0)= & {} 0 \end{aligned}$$
(20)
$$\begin{aligned} q(0)= & {} 0 \end{aligned}$$
(21)

with \(p_c\) being the central pressure, while upon matching the solutions on the surface of the star, the following conditions must be satisfied

$$\begin{aligned} p_r(R)= & {} 0 \end{aligned}$$
(22)
$$\begin{aligned} m(R)= & {} M \end{aligned}$$
(23)
$$\begin{aligned} q(R)= & {} Q \end{aligned}$$
(24)
$$\begin{aligned} e^{2 \nu (R)}= & {} 1- \frac{2M}{R} + \frac{Q^2}{R^2} \end{aligned}$$
(25)

The first condition allows us to determine the radius of the star, the second and the third allow us to compute both the mass and the charge of the object, while the last condition is needed to fix the constant of integration when computing \(\nu (r)\).

3 Interior solution of quark stars with a non-linear EoS

3.1 Exact analytical solution

Matter inside the star is modelled as a relativistic gas of de-confined quarks. Although in principle an EoS may relate all three quantities (namely, energy density as well as both radial and transverse pressure), in the following we shall assume that the underlying physics that governs the EoS in isotropic stars still holds in the case of anisotropic objects relating in the same way \(\rho \) to \(p_r\), while the anisotropic factor is generated via one of the mechanisms already mentioned in the introduction. Therefore, in the present work we shall consider an extension of the simplest MIT bag model [55, 56] assuming a finite mass for the s quark

$$\begin{aligned} p_r(\rho ) = \frac{1}{3} (\rho - 4B) + \frac{3 \alpha \mu ^2}{\pi ^2} \end{aligned}$$
(26)

where

$$\begin{aligned} \mu ^2 = -\alpha + \left( \alpha ^2 + \frac{4 \pi ^2}{9} (\rho -B) \right) ^{1/2} \end{aligned}$$
(27)

and \(\alpha =-m_s^2/6\), with B being the bag constant, and \(m_s\) being the mass of the s quark.

In total there are four field equations, and seven unknown quantities, namely the two metric potentials, the electric field, the pressures as well as the densities, both matter density \(\rho \) and electric density \(\rho _e\). In order to find a tractable reasonable solution, following previous works [38, 43] we shall assume certain functions for the electric charge function q(r) and the second metric potential \(A(r)=e^{2 \lambda (r)}\). In particular we shall assume power-laws of the form

$$\begin{aligned} 2 \lambda (r)= & {} a (r/r_0)^2 \end{aligned}$$
(28)
$$\begin{aligned} q(r)= & {} Q_0 \left( \frac{r}{r_0} \right) ^3 \end{aligned}$$
(29)

where we have introduced three parameters, namely a dimensionless parameter a, a length scale \(r_0\) and another parameter with dimensions of electric charge, \(Q_0\), not to be confused with the total electric charge of the star, \(Q=q(R)\).

Then using the structure equations we can compute the rest of the quantities one by one. So the mass function m(r), the electric field \(E(r)=q(r)/r^2\) and the densities \(\rho _e(r), \rho (r)\) are found to be

$$\begin{aligned} m(r)= & {} \frac{r}{2} \, \left( 1 + \frac{Q_0^2 r^4}{r_0^6} - e^{-a (r/r_0)^2} \right) \end{aligned}$$
(30)
$$\begin{aligned} \rho _e(r)= & {} \frac{3 Q_0}{4 \pi r_0^3} \, e^{-(a r^2)/(2 r_0^2)} \end{aligned}$$
(31)
$$\begin{aligned} \rho (r)= & {} \frac{r_0^6 - Q_0^2 r^4 + e^{-a (r/r_0)^2} (2 a r_0^4 r^2 - r_0^6)}{8 \pi r_0^6 r^2} \end{aligned}$$
(32)
$$\begin{aligned} E(r)= & {} \frac{Q_0 r}{r_0^3} \end{aligned}$$
(33)

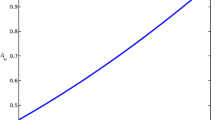
To be more precise, the electric density is computed using Maxwell’s equation, while the energy density is computed using the temporal Einstein’s field equation. Next \(p_r\) is computed using the EoS, while the anisotropic factor is computed using the continuity equation for the fluid, and finally \(p_t=\Delta + p_r\). Although it is a straightforward and elementary calculation, we shall omit here the expressions for the pressures as well as for the anisotropic factor since they are too long. In the next subsection, however, we show graphically the quantities versus normalized radial coordinate r/R for specific numerical values of the parameters involved.

The radial and transverse speed of sounds by definition are given by

$$\begin{aligned} c_r^2= & {} \frac{d p_r}{d \rho } \end{aligned}$$
(34)
$$\begin{aligned} c_t^2= & {} \frac{d p_t}{d \rho } \end{aligned}$$
(35)

Finally, the first metric component \(\nu \) may be computed using the rr Einstein’s field equation

$$\begin{aligned} \nu (r) = \nu (R) + {{\mathcal {I}}} \end{aligned}$$
(36)

performing the integral

$$\begin{aligned} {{\mathcal {I}}}= \int _R^r dx \frac{4 \pi x^3 p_r(x) + m(x)-\frac{q(x)^2}{x}}{x^2 (1-\frac{2m(x)}{x} + \frac{q(x)^2}{x^2})} \end{aligned}$$
(37)

and where \(\nu (R)\) is the value of \(\nu (r)\) evaluated at the surface of the star given by

$$\begin{aligned} \nu (R) = \frac{1}{2} \, ln\left( 1-\frac{2M}{R}+\frac{Q^2}{R^2} \right) \end{aligned}$$
(38)

Given the expressions for all quantities above, it is straightforward to verify that all field equations are satisfied.

3.2 Behavior and tests of the solution

The solution is fully determined once the numerical values of the parameters have been specified. In the figures below we show the interior solution for \(a=10, r_0=35.2~\mathrm{km}, Q_0=25 M_{\odot }, m_s=150~\mathrm{MeV}, B=80~\mathrm{MeV} \mathrm{fm}^{-3}=(0.157~\mathrm{GeV})^4\). This solution corresponds to a compact object with radius, mass, electric charge, and compactness \(C \equiv M/R\) as follows

$$\begin{aligned} R= & {} 10.40~\mathrm{km} \end{aligned}$$
(39)
$$\begin{aligned} M= & {} 2.06~M_{\odot } \end{aligned}$$
(40)
$$\begin{aligned} Q= & {} 0.31~M \end{aligned}$$
(41)
$$\begin{aligned} C= & {} 0.30 \end{aligned}$$
(42)

It is easy to verify that the compactness respects the upper bound for electrically charged objects [57]

$$\begin{aligned} \frac{M}{R} \le \frac{1}{9R^2} \, (3Q^2+2R^2+2R \sqrt{R^2+3Q^2}) \end{aligned}$$
(43)

which generalizes the Buchdahl bound [58] for neutral objects \(C \le 4/9 \simeq 0.44\).

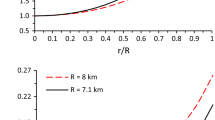
Figures 1 and 2 show the metric components \(A(r), e^{2 \nu (r)}\), the densities \(\rho , \rho _e\), the pressures \(p_r, p_t\), the anisotropic factor \(\Delta =p_r-p_t\), the mass function m(r) and the electric charge function q(r) versus the normalized radial coordinate r/R for the numerical values of the parameters mentioned before. The anisotropic factor starts from zero at the center and increases towards the surface of the star. Although the radial pressure vanishes at the surface, neither the transverse pressure nor the anisotropic factor has to vanish there. The behavior of the solution found here is qualitatively similar to the one of the solutions obtained elsewhere, see e.g. [36, 43].

Fig. 1
figure 1

Top: Metric components versus r/R. Bottom: Mass function m(r) and electric charge function q(r) (both in solar masses) versus r/R. The horizontal line represents the 2 solar mass constraint from observed massive pulsars

Full size image
Fig. 2
figure 2

Upper panel: Normalized radial and transverse pressures versus r/R, with B being the bag constant. Middle panel: Normalized anisotropic factor \(\Delta /B\) versus r/R. Lower panel: Normalized densities versus r/R

Full size image
Fig. 3
figure 3

Upper panel: Radial and transverse speed of sounds versus r/R. Middle panel: Adiabatic index versus r/R. The horizontal line corresponds to the Newtonian bound 4/3. Lower panel: E/B versus r/R, with \(E=\rho - p_r -2 p_t\) and B being the bag constant

Full size image
Fig. 4
figure 4

Mass-to-radius relationships for i) \(a=1.15\) and \(Q_0=10~M_{\odot }\) (red curve) and ii) \(a=2.1\) and \(Q_0=25~M_{\odot }\) (cyan curve). The horizontal straight lines represent the 2 solar mass constraint as well as the upper bound on the maximum mass of \(2.17~M_{\odot }\). The curve corresponding to the isotropic, electrically neutral object is shown as well (black curve) for comparison reasons

Full size image

Finally, the obtained solution should be able to describe realistic astrophysical configurations. Therefore, as a final check, we investigate if the energy conditions are fulfilled or not as well as the stability criterion [59]

$$\begin{aligned} \Gamma > \frac{4}{3} \end{aligned}$$
(44)

where the adiabatic index \(\Gamma \) is defined by

$$\begin{aligned} \Gamma \equiv c_r^2 \left[ 1 + \frac{\rho }{p_r} \right] \end{aligned}$$
(45)

Regarding the energy conditions first, we require that [35,36,37,38]

$$\begin{aligned}&\rho \ge 0 \end{aligned}$$
(46)
$$\begin{aligned}&\rho - p_{r,t} \ge 0 \end{aligned}$$
(47)
$$\begin{aligned}&E \equiv \rho - p_r -2 p_t \ge 0 \end{aligned}$$
(48)

It is sufficient to show that the last condition is fulfilled, since then the rest of the conditions will be fulfilled as well.

Figure 3 shows the radial and tangential speed of sounds, \(c_r^2, c_t^2\), the adiabatic index as well as E/B versus radial coordinate r/R for the same parameters mentioned before. First, both sound speeds take values between zero and unity throughout the star, and therefore causality is not violated. What is more, clearly E is positive throughout the star, and the condition \(\Gamma > 4/3\) is satisfied as well. We thus conclude that the solution obtained in the present work is a realistic solution within GR, and therefore it describes in a satisfactory way realistic astrophysical configurations.

Finally, the mass-to-radius relationships for two concrete sets of parameters \(a,Q_0,r_0\) are shown in Fig 4. The observed massive pulsars PSR J1614-2230 and PSR J0348-0432 with a mass at 2 solar masses [60,61,62] have put a stringent constrain on the EoS. In addition to that, the event GW170817 [63] has imposed a new constraint to the upper limit of the maximum mass, \(2.17~M_{\odot }\) [64]. For the two sets chosen here those requirements are met. Notice, however, that the limit \(R > 10.4~km\), set by the the event GW170817, is not fulfilled. Nevertheless, it is possible to meet that requirement as well for a different choice of the parameters, see for instance the particular solution discussed in the beginning of Sect. 3.

In Fig. 4 the curve corresponding to the isotropic, electrically neutral object is shown as well (in black) for comparison reasons. In this case clearly the highest mass is lower than the 2 solar mass bound, and therefore this EoS must be ruled out, at least for electrically neutral objects. Both the electric charge and the anisotropic factor lead to more massive stars. For a given electric charge, the right amount of anisotropy is required to increase the mass of the object, but not to make it too heavy. This is to be contrasted to the mass-to-radius relationship obtained in [43] and shown in Fig. 6 there, where the highest mass is too large.

4 Conclusions

In summary, in this work, we have obtained an exact analytical solution to Einstein–Maxwell field equations with anisotropic matter. The solution describes the interior of electrically charged, anisotropic strange quark stars with a non-linear equation-of-state corresponding to a finite mass of the s quark. The energy conditions are fulfilled, the speed of sounds (both radial and transverse) take values between zero and unity throughout the star, and the stability criterion for the adiabatic index, \(\Gamma > 4/3\), holds. Therefore the obtained solution describes realistic astrophysical configurations. Furthermore, constraints on the mass of the objects coming from observed massive pulsars and direct detection of gravitational waves are satisfied, and the upper bound on the compactness is respected.