Two-warehouse inventory model for non-instantaneous deteriorating items with stock-dependent demand and inflation using particle swarm optimization

Abstract

We investigate a two-warehouse inventory model for non-instantaneous deteriorating items with partial backlogging and stock-dependent demand under inflationary conditions. Shortages are allowed. The backlogging rate is variable and depends on the waiting time for the next replenishment. This paper seeks to determine an optimal replenishment policy that minimizes the present value of the total cost per unit time. The necessary and sufficient conditions for the existence and uniqueness of the optimal solution are found. The corresponding problems are formulated and solved with particle swarm optimization. Numerical experimentation and post-optimality analysis are conducted.

1 Introduction and literature review

It is common practice for sellers to lower the price of their products either to stimulate demand or to clear products that have begun to deteriorate. The intent of our paper is to look at the second phenomenon and gather analytic insights into how replenishments policies can be better designed to minimse lost sales. Deterioration can be viewed as damage, spoilage, decay, obsolescence, or evaporation that leads to a shorter than expected useful product life. Products such as steel, glassware, and furniture have a slow deterioration rate, so there is little need to consider deterioration when determining their economic lot size. However, items such as food, pharmaceuticals, and blood deteriorate rapidly over time. Thus, the loss from deterioration is significant. The inventory problem of deteriorating items has been widely studied under different assumptions. Ghare and Schrader (1963) first presented an EOQ model for deteriorating items under exponential decay. Covert and Philip (1973) extended this model by assuming a Weibull distribution for deterioration.

The extant literature has assumed that items deteriorate as soon as they enter the system. In reality, there are many items that do not deteriorate immediately. Jaggi et al. (2017a) term this phenomenon as non-instantaneous deterioration and the items of concern are labelled as non-instantaneous deteriorating items. Wu et al. (2006) first studied this phenomenon and established an optimal replenishment policy for non-instantaneous deteriorating items with stock dependent demand and partial backlogging. Subsequently, others such as Ouyang et al. (2006, 2008), Wu et al. (2009), Jaggi and Verma (2010), Jaggi and Tiwari (2014b), and Jaggi et al. (2015a, 2017b) studied inventory models for non-instantaneous deteriorating items under a variety of conditions. At the same time, most of the relevant studies have assumed an uncapacitated warehouse, which may not be practicable.

Further, the two-warehouse sub-problem has been studied under different assumptions. In this vein, Hartley (1976) first assumed that the holding cost for a rented warehouse (RW) is greater than that in a owned warehouse (OW). Therefore, items in the RW are first transferred to the OW to satisfy the demand until the stock in RW depletes to zero, and then the items in the OW are released. Sarma (1987) developed a model which assumes a capacitated OW and additional warehousing space can be obtained by renting RW. Yang (2004) studied an inventory system which has capacity constraints, constant demand rate, and shortages are completely backlogged. The item’s lifetime follows an exponential distribution. In a follow-up study, Yang (2006) then developed a similar model with partial backlogging. Wee et al. (2005) formed a model for partial backlogging in which the product lifetime is based on the two-parameter Weibull distribution. Pal et al. (2005) studied deteriorating items in a two-warehouse system under time-dependent demand and the demand is partially backlogged in the case of shortages. Lee (2006) developed a FIFO production inventory model with a finite production rate. The assumptions in our model are similar to Yang (2004). Similar work in this domain though not exhaustive can be found in Lo et al. (2007), Wee et al. (2008), Chung and Wee (2008), Taleizadeh et al. (2010), Gao et al. (2011), Sana (2015), Bhunia and Shaikh (2011a, b), Cárdenas-Barrón et al. (2014), Bhunia et al. (2013, 2015b, 2015c, 2016), Tiwari et al. (2016), Bhunia and Shaikh (2014b), Cárdenas-Barrón and Sana (2015), Sana and Goyal (2015), Sana (2010), Jaggi et al. (2014a, 2015b, 2017a, b), Das et al. (2015) and Saxena et al. (2016).

Taking stock of these research endeavours, our paper investigates a two warehouse inventory model for non-instantaneous deteriorating items with partial backlogging and stock-dependent demand under inflationary conditions. In our model, shortages are allowed and the backlogging rate is variable and depends on the waiting time for the next replenishment. We seek to find a replenishment policy that minimizes the Present value of the total cost per unit time. The necessary and sufficient conditions of the existence and uniqueness of the optimal solution are established. The corresponding problems are formulated and solved using particle swarm optimization (PSO). A numerical example is presented to demonstrate the developed model, followed by a post-optimality analysis on the key parameters of the inventory system to assess the robustness of the model.

This paper is structured as follows. Section 2 describes the problem assumptions and the notations used. Section 3 analyses the model formulation. Section 4 presents an algorithm to find the optimal solutions. In Sect. 5, a numerical experiment is performed to validate the model, and the robustness of our model is illustrated through a sensitivity analysis. Section 6 concludes the paper with some new research directions.

2 Assumption and notations

The model of the two-warehouse inventory problem assumes the following:

• 1. The own warehouse (OW) has a fixed capacity of W units; the rented warehouse (RW) has unlimited capacity.

• 2. The inventory costs (including holding cost and deterioration cost) in RW are higher than those in OW.

• 3. The replenishment rate is instantaneous.

• 4. The lead-time is negligible.

• 5 The demand rate $D\left( t \right)$ is a function of stock level I(t) at time t i.e.

  $$\begin{aligned} D\left( t \right) =\left\{ {\begin{array}{ll} a+bI\left( t \right) ;&{}\,I\left( t \right) >0 \\ a;&{}\,I\left( t \right) <0 \\ \end{array}} \right. ,\hbox { where }a,\, b\hbox { are positive constants.} \end{aligned}$$

• 6. The planning horizon of the inventory system is infinite.

• 7. Unsatisfied demand/shortages are allowed. Unsatisfied demand is partially backlogged and the fraction of shortages backlogged is a differentiable and decreasing function of time t, denoted by g(t), where t is the waiting time up to the next replenishment. We define the partial backlogging rate as $g(t)=e^{-\delta t}$, where $\delta$ is a positive constant.

In addition, the following notations are used throughout this paper.

A :

Replenishment cost per order

c :

Purchasing cost per unit

W :

Capacity of OW

Q :

Order quantity per cycle

Z :

Maximum inventory level per cycle.

H :

Holding cost per unit per unit time in OW.

F :

Holding cost per unit per unit time in RW, with $F>H$

s :

The backlogging cost per unit per unit time, if shortage is backlogged

$c_{1}$ :

Unit opportunity cost due to lost sale, if the shortage is lost

R :

Inflation rate

$\alpha$ :

Deterioration rate in OW, where $0\le \alpha < 1$

$\beta$ :

Deterioration rate in RW, where $0\le \beta< 1;\,\beta < \alpha .$

$t_{d}$ :

Period in which no deterioration occurs.

$t_{r}$ :

Time at which the inventory level reaches zero in RW.

$t_{w}$ :

Time at which the inventory level reaches zero in OW.

T :

Length of the replenishment cycle in a year.

$I_0 (t)$ :

Inventory level in the OW at any time $t, 0\le t\le T$

$I_r (t)$ :

Inventory level in the RW at any time $t, 0\le t\le T$

$TC_{i}$ :

Present value of total relevant cost per unit time for case i (i = I, II)

B(t):

Backlogged level at any time t where $t_w \le t\le T$

L(t):

Number of lost sales at any time t where $t_w \le t\le T$

p_size :

Population size

m_gen :

Maximum number of generations

$\chi$ :

Constriction factor or coefficient

$c_1$ (${>}$0):

Cognitive learning rate

$c_2$ (${>}$0):

Social learning rate

$r_{1}, r_{2}$ :

Uniformly-distributed random numbers in the interval [0, 1].

${v_i}^{(k)}$ :

Velocity of i-th particle at k-th generation/iteration

${x_i}^{(k)}$ :

Position of i-th particle of population at k-th generation

$p_i^{(k)}$ :

Best previous position of i-th particle at k-th generation

$p_g^{(k)}$ :

Position of the best particle among all particles

3 Model formulation

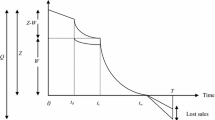
We formulate the replenishment problem of a two warehousing inventory model for a single non-instantaneous deteriorating item with complete backlogging. A lot size of Q units enters the system. After satisfying the backorders, Z units are left in stock. Of these Z units, W units are kept in the OW and the remaining ($Z-W)$ units are kept in the RW. As the deterioration of the items is non-instantaneous, the units do not deteriorate in period $t_d$. Thereafter, deterioration begins. We consider two cases: Case I - when the time during which no deterioration occurs is less than the time during which the inventory in RW becomes zero i.e. $t_{d} < t_{r}$ and Case II - when $t_{d} \ge t_{r.}$

3.1 Case I—when $t_d <t_r$

As there is no deterioration in the interval $\left[ {0,\,t_d } \right] ,$ the inventory in RW is depleted only due to demand while in OW the inventory level remains unchanged. In the interval $\left[ {t_d,\,t_r } \right]$ the inventory level in RW reduces to zero due to the combined effects of demand and deterioration, and in OW, the inventory is depleted through deterioration only. Further, in the interval $\left[ {t_r ,\,t_w } \right]$, the depletion of inventory occurs in OW due to the combined effects of demand and deterioration until it reaches zero at time $t_w$. Moreover, in the interval $\left[ {t_w,\,T} \right]$, the demand is backlogged. Figure 1 shows the behavior of the model behavior over the cycle $\left[ {0,\, T} \right]$.

Fig. 1

Two-warehouse inventory system when $t_d <t_r$

The differential equations that describe the inventory level in RW and OW at time t over period ($0,\, T)$ are given by:

$$\begin{aligned}&\frac{dI_r \left( t \right) }{dt}=-\left( {a+bI_r \left( t \right) } \right) , \qquad 0\le t\le t_d \end{aligned}$$

(1)

$$\begin{aligned}&\frac{dI_r \left( t \right) }{dt}+\beta I_r \left( t \right) =-\left( {a+bI_r \left( t \right) } \right) , \qquad t_d <t\le t_r \end{aligned}$$

(2)

$$\begin{aligned}&\frac{dI_0 \left( t \right) }{dt}+\alpha I_0 \left( t \right) =0, \qquad t_d <t\le t_r \end{aligned}$$

(3)

$$\begin{aligned}&\frac{dI_0 \left( t \right) }{dt}+\alpha I_0 \left( t \right) =-\left( {a+bI_0 \left( t \right) } \right) , \qquad t_r <t\le t_w \end{aligned}$$

(4)

$$\begin{aligned}&\frac{dB\left( t \right) }{dt}=ae^{-\delta (T-t)}, \qquad t_w <t\le T \end{aligned}$$

(5)

The solutions to Eqs. (1)–(5) with boundary conditions $I_r (0)=Z-W,I_r (t_r )=0,I_0 (t_d )=W,I_0 (t_w )=0 \& B(t_w )=0$ respectively are

$$\begin{aligned} I_r \left( t \right)= & {} \left( {Z-W} \right) e^{-bt}+\frac{a}{b}\left( {e^{-bt}-1} \right) , \qquad 0\le t\le t_d \end{aligned}$$

(6)

$$\begin{aligned} I_r \left( t \right)= & {} \frac{a}{\beta +b}\left( {e^{\left( {\beta +b} \right) \left( {t_r -t} \right) }-1} \right) , \qquad t_d <t\le t_r \end{aligned}$$

(7)

$$\begin{aligned} I_0 \left( t \right)= & {} We^{\alpha \left( {t_d -t} \right) }, \qquad t_d <t\le t_r \end{aligned}$$

(8)

$$\begin{aligned} I_0 \left( t \right)= & {} \frac{a}{\alpha +b}\left( {e^{\left( {\alpha +b} \right) \left( {t_w -t} \right) }-1} \right) , \qquad t_r <t\le t_w \end{aligned}$$

(9)

$$\begin{aligned} B\left( t \right)= & {} \frac{a}{\delta }\left\{ {e^{-\delta (T-t)}-e^{-\delta (T-t_w )}} \right\} , \qquad t_w <t\le T \end{aligned}$$

(10)

The number of lost sales at time t is

$$\begin{aligned} L(t)= & {} \int \limits _{t_w }^t {a\left\{ {1-e^{-\delta (T-t)}} \right\} dt} ; \qquad t_w <t\le T\nonumber \\= & {} a\left[ {\left( {t-t_w } \right) -\frac{1}{\delta }\left\{ {e^{-\delta (T-t)}-e^{-\delta (T-t_w )}} \right\} } \right] \end{aligned}$$

(11)

Considering the continuity of $I_r \left( t \right)$ at $t=t_d$, it follows from Eqs. (6) and (7) that

$$\begin{aligned} \left( {Z-W} \right) e^{-bt_d }+\frac{a}{b}\left( {e^{-bt_d }-1} \right) =\frac{a}{\beta +b}\left( {e^{\left( {\beta +b} \right) \left( {t_r -t_d } \right) }-1} \right) \end{aligned}$$

(12)

which leads us to the maximum inventory level per cycle as

$$\begin{aligned} Z=W+\frac{a}{\beta +b}\left( {e^{\left( {\beta +b} \right) \left( {t_r -t_d } \right) }-1} \right) e^{bt_d }-\frac{a}{b}\left( {1-e^{bt_d }} \right) \end{aligned}$$

(13)

Considering the continuity of $I_0 \left( t \right)$ at $t=t_r$ it follows from Eqs. (8) and (9) that

$$\begin{aligned} We^{\alpha \left( {t_d -t_r } \right) }= & {} \frac{a}{\alpha +b}\left( {e^{\left( {\alpha +b} \right) \left( {t_w -t_r } \right) }-1} \right) \nonumber \\ t_w= & {} t_r +\frac{1}{\alpha +b}\ln \left( {\frac{a+\left( {\alpha +b} \right) We^{\alpha (t_d -t_r )}}{a}} \right) \end{aligned}$$

(14)

Putting $t=T$ in Eq. (10), the maximum amount of demand backlogged per cycle is

$$\begin{aligned} B\left( T \right) =\frac{a}{\delta }\left( {1-e^{-\delta (T-t_w )}} \right) \end{aligned}$$

(15)

Therefore, the order quantity over the replenishment cycle can be expressed as

$$\begin{aligned} Q= & {} Z+B(T)\qquad (\hbox {from Eqs. }13\hbox { and }15)\nonumber \\= & {} W+\frac{a}{\beta +b}\left( {e^{\left( {\beta +b} \right) \left( {t_r -t_d } \right) }-1} \right) e^{bt_d }-\frac{a}{b}\left( {1-e^{bt_d }} \right) +\frac{a}{\delta }\left( {1-e^{-\delta (T-t_w )}} \right) \end{aligned}$$

(16)

The total cost per cycle consists of the following elements:

• 1. Present value of the replenishment cost = A

• 2. Present value of the inventory holding cost in RW

  $$\begin{aligned}= & {} F\left( {\int \limits _0^{t_d } {e^{-Rt}I_r \left( t \right) dt+\int \limits _{t_d }^{t_r } {e^{-Rt}I_r \left( t \right) dt} } } \right) \\= & {} F\left[ {\frac{1}{\left( {R+b} \right) }\left( {Z-W+\frac{a}{b}} \right) \left\{ {1-e^{-\left( {R+b} \right) t_d }} \right\} +\frac{a}{bR}\left\{ {e^{-Rt_d }-1} \right\} } \right. \\&\left. {\left. {+\frac{ae^{-Rt_r }}{\left( {\beta +b} \right) }\left\{ {\frac{1}{\left( {\beta +b+R} \right) }\left\{ {e^{(\beta +b+R)\left( {t_r -t_d } \right) }-1} \right\} } \right. -\frac{1}{R}\left\{ {e^{R\left( {t_r -t_d } \right) }-1} \right\} } \right\} } \right] \end{aligned}$$

• 3. Present value of the inventory holding cost in OW

  $$\begin{aligned}= & {} H\left( {\int \limits _0^{t_d } {We^{-Rt}dt+\int \limits _{t_d }^{t_r } {e^{-Rt}I_0 \left( t \right) dt+\int \limits _{t_r }^{t_W } {e^{-Rt}I_0 \left( t \right) dt} } } } \right) \\= & {} H\left[ \frac{W}{R}\left\{ {1-e^{-Rt_d }} \right\} +\frac{We^{-Rt_d }}{\alpha +R}\left\{ {1-e^{(\alpha +R)\left( {t_d -t_r } \right) }} \right\} \right. \\&\left. +\frac{ae^{-Rt_w }}{\alpha +b}\left\{ {\frac{1}{\alpha +b+R}\left\{ {e^{(\alpha +b+R)\left( {t_w -t_r } \right) }-1} \right\} } \right. \right. \\&\left. \left. -\frac{1}{R}\left\{ {e^{R\left( {t_w -t_r } \right) }-1} \right\} \right\} \right] \end{aligned}$$

• 4. Present value of the backlogging cost is $s\int \limits _{t_W }^T {B\left( t \right) e^{-Rt}dt}$

  $$\begin{aligned} =\frac{sa}{\delta }e^{-\delta T}\left[ {\frac{1}{\delta -R}\left\{ {e^{(\delta -R)T}-e^{(\delta -R)t_w }} \right\} +\frac{e^{\delta t_w }}{R}\left\{ {e^{-RT}-e^{-Rt_w }} \right\} } \right] \end{aligned}$$

• 5. Present value of the opportunity cost due to lost sales is

  $$\begin{aligned} =c_1 e^{-RT}\int \limits _{t_w }^T {\left\{ {1-e^{-\delta (T-t)}} \right\} adt} =c_1 ae^{-RT}\left[ {T-t_w -\frac{1}{\delta }\left\{ {1-e^{-\delta (T-t_w )}} \right\} } \right] \end{aligned}$$

• 6. Present value of the deterioration cost is

  $$\begin{aligned}= & {} c\left[ {\beta \int \limits _{t_d }^{t_r } {I_r (t)e^{-Rt}dt+\alpha \int \limits _{t_r }^{t_w } {e^{-Rt}I_0 (t)dt} } } \right] \\= & {} ca\left[ {\frac{e^{-Rt_r }}{\left( {\beta +b} \right) }\left\{ {\frac{1}{\left( {\beta +b+R} \right) }\left( {e^{(\beta +b+R)\left( {t_r -t_d } \right) }-1} \right) -\frac{1}{R}\left( {e^{R\left( {t_r -t_d } \right) }-1} \right) } \right\} } \right. \\&\left. {+\frac{e^{-Rt_w }}{\alpha +b}\left\{ {\frac{1}{\alpha +b+R}\left( {e^{(\alpha +b+R)\left( {t_w -t_r } \right) }-1} \right) -\frac{1}{R}\left( {e^{R\left( {t_w -t_r } \right) }-1} \right) } \right\} } \right] \end{aligned}$$

Hence, using the above elements, the present value of the total relevant cost per unit time is given by

$$\begin{aligned} TC_1 \left( {t_r ,T} \right)= & {} \frac{1}{T}\left[ A+F\left[ \frac{1}{\left( {R+b} \right) }\left( {Z-W+\frac{a}{b}} \right) \left\{ {1-e^{-\left( {R+b} \right) t_d }} \right\} +\frac{a}{bR}\left\{ {e^{-Rt_d }-1} \right\} \right. \right. \nonumber \\&\left. \left. \left. +\frac{ae^{-Rt_r }}{\left( {\beta +b} \right) }\left\{ {\frac{1}{\left( {\beta +b+R} \right) }\left\{ {e^{(\beta +b+R)\left( {t_r -t_d } \right) }-1} \right\} } \right. -\frac{1}{R}\left\{ {e^{R\left( {t_r -t_d } \right) }-1} \right\} \right\} \right] \right. \nonumber \\&\left. +H\left[ \frac{W}{R}\left\{ {1-e^{-Rt_d }} \right\} +\frac{We^{-Rt_d }}{\alpha +R}\left\{ {1-e^{(\alpha +R)\left( {t_d -t_r } \right) }} \right\} \right. \right. \nonumber \\&\left. \left. +\frac{ae^{-Rt_w }}{\alpha +b}\left\{ \frac{1}{\alpha +b+R}\left\{ {e^{(\alpha +b+R)\left( {t_w -t_r } \right) }-1} \right\} \right. \right. \left. \left. -\frac{1}{R}\left\{ {e^{R\left( {t_w -t_r } \right) }-1} \right\} \right\} \right] \right. \nonumber \\&\left. +\frac{sa}{\delta }e^{-\delta T}\left\{ {\frac{1}{\delta -R}\left( {e^{(\delta -R)T}-e^{(\delta -R)t_w }} \right) +\frac{e^{\delta t_w }}{R}\left( {e^{-RT}-e^{-Rt_w }} \right) } \right\} \right. \nonumber \\&\left. +c_1 ae^{-RT}\left\{ {T-t_w -\frac{1}{\delta }\left( {1-e^{-\delta (T-t_w )}} \right) } \right\} \right. \nonumber \\&\left. +ca\left[ {\frac{e^{-Rt_r }}{\left( {\beta +b} \right) }\left\{ {\frac{1}{\left( {\beta +b+R} \right) }\left( {e^{(\beta +b+R)\left( {t_r -t_d } \right) }-1} \right) -\frac{1}{R}\left( {e^{R\left( {t_r -t_d } \right) }-1} \right) } \right\} } \right. \right. \nonumber \\&\left. \left. +\frac{e^{-Rt_w }}{\alpha +b}\left\{ \frac{1}{\alpha +b+R}\left( {e^{(\alpha +b+R)\left( {t_w -t_r } \right) }-1} \right) -\frac{1}{R}\left( e^{R\left( {t_w -t_r } \right) }-1 \right) \right\} \right] \right] \end{aligned}$$

(17)

where

$$\begin{aligned} Z= & {} W+\frac{a}{\beta +b}\left( {e^{\left( {\beta +b} \right) \left( {t_r -t_d } \right) }-1} \right) e^{bt_d }-\frac{a}{b}\left( {1-e^{bt_d }} \right) ,t_w\\= & {} t_r +\frac{1}{\alpha +b}\ln \left( {\frac{a+\left( {\alpha +b} \right) We^{\alpha (t_d -t_r )}}{a}} \right) \end{aligned}$$

3.2 Case II—when $t_d \ge t_r$

Now, the time in which no deterioration occurs is longer than the time during which inventory in RW becomes zero and the behavior of the model over the cycle $\left[ {0,\,T} \right]$ is depicted in Fig. 2

Fig. 2

Two-warehouse inventory system when $t_d >t_r$

The differential equations that describe the inventory level in RW and OW at time t in period ($0,\,T)$ are given by:

$$\begin{aligned}&\frac{dI_r \left( t \right) }{dt}=-\left( {a+bI_r \left( t \right) } \right) , \qquad 0\le t\le t_r \end{aligned}$$

(18)

$$\begin{aligned}&\frac{dI_0 \left( t \right) }{dt}=-\left( {a+bI_0 \left( t \right) } \right) , \qquad t_r <t\le t_d \end{aligned}$$

(19)

$$\begin{aligned}&\frac{dI_0 \left( t \right) }{dt}+\alpha I_0 \left( t \right) =-\left( {a+bI_0 \left( t \right) } \right) , \qquad t_d <t\le t_w \end{aligned}$$

(20)

$$\begin{aligned}&\frac{dB\left( t \right) }{dt}=ae^{-\delta (T-t)}, \qquad t_w <t\le T \end{aligned}$$

(21)

The solutions of the above four differential Eqs. (18), (19), (20), and (21) with boundary conditions $I_r \left( {t_r } \right) =0,I_0 \left( {t_r } \right) =W,I_0 \left( {t_W } \right) =0,B\left( {t_W } \right) =0$ respectively are

$$\begin{aligned} I_r \left( t \right)= & {} \frac{a}{b}\left( {e^{b\left( {t_r -t} \right) }-1} \right) , \qquad 0\le t\le t_r \end{aligned}$$

(22)

$$\begin{aligned} I_0 \left( t \right)= & {} \left( {W+\frac{a}{b}} \right) e^{b\left( {t_r -t} \right) }-\frac{a}{b}, \qquad t_r <t\le t_d \end{aligned}$$

(23)

$$\begin{aligned} I_0 \left( t \right)= & {} \frac{a}{\alpha +b}\left( {e^{\left( {\alpha +b} \right) \left( {t_w -t} \right) }-1} \right) , \qquad t_d <t\le t_w \end{aligned}$$

(24)

$$\begin{aligned} B\left( t \right)= & {} \frac{a}{\delta }\left\{ {e^{-\delta (T-t)}-e^{-\delta (T-t_w )}} \right\} , \qquad t_w <t\le T \end{aligned}$$

(25)

The number of lost sales at time t is

$$\begin{aligned} L(t)= & {} \int \limits _{t_w }^t {a\left\{ {1-e^{-\delta (T-t)}} \right\} dt} ; \qquad t_w <t\le T\nonumber \\= & {} a\left[ {\left( {t-t_w } \right) -\frac{1}{\delta }\left\{ {e^{-\delta (T-t)}-e^{-\delta (T-t_w )}} \right\} } \right] \end{aligned}$$

(26)

Considering the continuity of $I_0 (t)$ at $t=t_{d}$, it follows from Eqs. (23) and (24) that

$$\begin{aligned}&\left( {W+\frac{a}{b}} \right) e^{b\left( {t_r -t_d } \right) }-\frac{a}{b}=\frac{a}{\alpha +b}\left( {e^{\left( {\alpha +b} \right) \left( {t_w -t_d } \right) }-1} \right) \end{aligned}$$

(27)

$$\begin{aligned}&t_w =t_d +\frac{1}{\alpha +b}\ln \left| {1+\frac{\alpha +b}{a}\left\{ {\left( {W+\frac{a}{b}} \right) e^{b\left( {t_r -t_d } \right) }-\frac{a}{b}} \right\} } \right| \end{aligned}$$

(28)

Now, at $t = 0$, when $I_{r}(t) = Z-W$ and solving Eq. (22) yields the maximum inventory as

$$\begin{aligned} Z=W+\frac{a}{b}\left( {e^{bt_r }-1} \right) \end{aligned}$$

(29)

Putting $t = T$ in Eq. (25), the maximum amount of demand backlogged per cycle is

$$\begin{aligned} B\left( T \right) =\frac{a}{\delta }\left( {1-e^{-\delta (T-t_w )}} \right) \end{aligned}$$

(30)

Therefore, the order quantity is $Q=Z+B(T)$

$$\begin{aligned} =W+\frac{a}{b}\left( {e^{bt_r }-1} \right) +\frac{a}{\delta }\left( {1-e^{-\delta (T-t_w )}} \right) \quad (\hbox {from Eqs. }29\hbox { and }30) \end{aligned}$$

(31)

Again, the total cost per cycle consists of the following elements:

• 1. Present value of the replenishment cost = A

• 2. Present value of the inventory holding cost in RW = $F\int \limits _0^{t_r } {e^{-Rt}I_r \left( t \right) dt}$

  $$\begin{aligned} =\frac{Fa}{b}\left\{ {\frac{1}{\left( {R+b} \right) }\left( {e^{bt_r }-e^{-Rt_r }} \right) +\frac{1}{R}\left( {e^{-Rt_r }-1} \right) } \right\} \end{aligned}$$

• 3. Present value of the inventory holding cost in OW

  $$\begin{aligned}= & {} H\left( {\int \limits _0^{t_r } {e^{-Rt}Wdt} +\int \limits _{t_r }^{t_d } {e^{-Rt}I_0 \left( t \right) dt+\int \limits _{t_d }^{t_w } {e^{-Rt}I_0 \left( t \right) dt} } } \right) \\= & {} H\left[ \frac{W}{R}\left( {1-e^{-Rt_r }} \right) +\frac{e^{-Rt_r }}{R+b}\left( {W+\frac{a}{b}} \right) \left( {1-e^{\left( {R+b} \right) \left( {t_r -t_d } \right) }} \right) \right. \\&\left. +\frac{ae^{-Rt_r }}{bR}\left( {e^{R\left( {t_r -t_d } \right) }-1} \right) \right. \\&\left. {\left. {+\frac{ae^{-Rt_w }}{\alpha +b}\left\{ {\frac{1}{\alpha +b+R}\left( {e^{\left( {\alpha +b+R} \right) \left( {t_w -t_d } \right) }-1} \right) } \right. +\frac{1}{R}\left( {1-e^{R\left( {t_w -t_d } \right) }} \right) } \right\} } \right] \end{aligned}$$

• 4. Present value of the backlogging cost = $s\int \limits _{t_W }^T {B\left( t \right) e^{-Rt}dt}$

  $$\begin{aligned} =\frac{sa}{\delta }e^{-\delta T}\left[ {\frac{1}{\delta -R}\left\{ {e^{(\delta -R)T}-e^{(\delta -R)t_w }} \right\} +\frac{e^{\delta t_w }}{R}\left\{ {e^{-RT}-e^{-Rt_w }} \right\} } \right] \end{aligned}$$

• 5. Present value of opportunity cost due to lost sales $=c_1 e^{-RT}\int \limits _{t_w }^T {\left\{ {1-e^{-\delta (T-t)}} \right\} Ddt}$

  $$\begin{aligned} =c_1 ae^{-RT}\left[ {T-t_w -\frac{1}{\delta }\left\{ {1-e^{-\delta (T-t_w )}} \right\} } \right] \end{aligned}$$

• 6. Present value of the cost of the deteriorated items $=c\alpha \int \limits _{t_d }^{t_w } {e^{-Rt}I_0 (t)dt}$

  $$\begin{aligned} =c\frac{ae^{-Rt_w }}{\alpha +b}\left\{ {\frac{1}{\alpha +b+R}\left( {e^{\left( {\alpha +b+R} \right) \left( {t_w -t_d } \right) }-1} \right) +\frac{1}{R}\left( {1-e^{R\left( {t_w -t_d } \right) }} \right) } \right\} \end{aligned}$$

Hence, the present value of the total relevant cost per unit time during the cycle ($0,\,T)$ is given by

$$\begin{aligned} TC_2 \left( {t_r ,T} \right)= & {} \frac{1}{T}\left[ {A+\frac{Fa}{b}\left\{ {\frac{1}{\left( {R+b} \right) }\left( {e^{bt_r }-e^{-Rt_r }} \right) +\frac{1}{R}\left( {e^{-Rt_r }-1} \right) } \right\} } \right. \nonumber \\&\left. +H\left\{ \frac{W}{R}\left( {1-e^{-Rt_r }} \right) +\frac{e^{-Rt_r }}{R+b}\left( {W+\frac{a}{b}} \right) \left( {1-e^{\left( {R+b} \right) \left( {t_r -t_d } \right) }} \right) \right. \right. \nonumber \\&\left. \left. +\frac{ae^{-Rt_r }}{bR}\left( {e^{R\left( {t_r -t_d } \right) }-1} \right) \right. \right. \nonumber \\&\left. \left. +\frac{ae^{-Rt_w }}{\alpha +b}\left\{ \frac{1}{\alpha +b+R}\left( {e^{\left( {\alpha +b+R} \right) \left( {t_w -t_d } \right) }-1} \right) +\frac{1}{R}\left( {1-e^{R\left( {t_w -t_d } \right) }} \right) \right\} \right\} \right. \nonumber \\&\left. +\frac{sa}{\delta }e^{-\delta T}\left\{ \frac{e^{(\delta -R)t_w }}{\delta -R}\left\{ {e^{(\delta -R)\left( {T-t_w } \right) }-1} \right\} +\frac{e^{\delta t_w }}{R}\left\{ {e^{-RT}-e^{-Rt_w }} \right\} \right\} \right. \nonumber \\&\left. +c_1 ae^{-RT}\left\{ {T-t_w -\frac{1}{\delta }\left\{ {1-e^{-\delta (T-t_w )}} \right\} } \right\} \right. \nonumber \\&\left. +c\frac{ae^{-Rt_w }}{\alpha +b}\left\{ {\frac{1}{\alpha +b+R}\left( {e^{\left( {\alpha +b+R} \right) \left( {t_w -t_d } \right) }-1} \right) +\frac{1}{R}\left( {1-e^{R\left( {t_w -t_d } \right) }} \right) } \right\} \right] \nonumber \\ \end{aligned}$$

(32)

where $Z=W+\frac{a}{b}\left( {e^{bt_r }-1} \right)$ and $t_w =t_d +\frac{1}{\alpha +b}\ln \left| {1+\frac{\alpha +b}{a}\left\{ {\left( {W+\frac{a}{b}} \right) e^{b\left( {t_r -t_d } \right) }-\frac{a}{b}} \right\} } \right|$.

Therefore, the present value of the total relevant cost per unit time during the cycle ($0,\,T)$ is given by

$$\begin{aligned} TC\left( {t_r ,T} \right) =\left\{ {\begin{array}{lll} TC_1 \left( {t_r ,T} \right) &{}\quad if&{} \quad t_d \le t_r \\ TC_2 \left( {t_r ,T} \right) &{} \quad if&{}\quad t_d \ge t_r \\ \end{array}} \right. \end{aligned}$$

(33)

which is a function of the continuous variables $t_{r}$ and T.

Optimality

We now determine the optimum values of $t_{r}$ and T which minimizes ${ TC}(t_{r,}\,T)$. The necessary conditions for minimizing the total cost function given by Eq. (33) are

$$\begin{aligned} \frac{\partial TC_i \left( {t_r ,T} \right) }{\partial t_r }=0,\hbox { and }\frac{\partial TC_i \left( {t_r ,T} \right) }{\partial T}=0\quad \hbox { for }i = 1,2 \end{aligned}$$

(34)

Eq. (34) can be solved simultaneously for the optimal values of $t_{ri}$ and $T_{i}$ (say ${t_{ri}}^{*}$ and ${T_{i}}^{*})$ for $i=\textit{1},\, \textit{2}$ provided it also satisfies the following sufficient conditions.

$$\begin{aligned}&\frac{\partial ^{2}TC_i \left( {t_r ,T} \right) }{\partial t_r^2 }>0,\frac{\partial ^{2}TC_i \left( {t_r ,T} \right) }{\partial T^{2}}>0~and~\\&\quad \left[ {\left( {\frac{\partial ^{2}TC_i }{\partial t_r ^{2}}\times \frac{\partial ^{2}TC_i }{\partial T^{2}}} \right) -\left( {\frac{\partial ^{2}TC_i }{\partial T\partial t_r }\times \frac{\partial ^{2}TC_i }{\partial t_r \partial T}} \right) } \right] >0 \hbox { for } i=1,2 \end{aligned}$$

4 Implementation of particle swarm optimization

Many studies have successfully used soft-computing methods to solve highly nonlinear optimization problems. Some of the algorithms used include simulated annealing, differential evolution, tabu search, genetic algorithm, ant colony optimization, and particle swarm optimization (PSO). We now turn our attention to PSO.

PSO is a population based meta-heuristic global search algorithm based on the social interaction and individual experience. It was first proposed by Eberhart and Kennedy (1995), and Kennedy and Eberhart (1995). It has widely been applied to find the optimal solutions to nonlinear optimization problems. This algorithm is inspired by the social behavior of bird flocking or fish schooling. In PSO, the potential solutions (called particles), fly through the search space of the problem by following the current optimum particles. PSO is initialized with a population of random particles positions (solutions) and PSO then searches for the optimum from generation to generation. At every iteration, each particle is updated with two best positions (solutions). The first one is the best position (solution) reached thus far by the particle and this best position is said to be the personal best position $p_i^{(k)}$. The other one is the current best position (solution), obtained thus far by any particle in the population. This best value is a global best position $p_g^{(k)}$.

In each generation, the velocity and position of particle $i\, \left( {i=1, 2,\ldots , p\_size} \right)$ are updated by the following rules:

$$\begin{aligned} v_i^{(k+1)} =wv_i^{(k)} +c_1 r_1 \left( {p_i^{(k)} -x_i^{(k)} } \right) +c_2 r_2 \left( {p_g^{(k)} -x_i^{(k)} } \right) \end{aligned}$$

(35)

and

$$\begin{aligned} x_i^{(k+1)} =x_i^{(k)} +v_i^{(k+1)} \end{aligned}$$

(36)

where w is the inertia weight, and $k\left( {=1, 2,\ldots , m\hbox {-}gen} \right)$ indicates the iterations (generations). The cognitive learning and social learning rates $c_1 \left( {>0} \right)$ and $c_2 \left( {>0} \right)$ are the acceleration constants responsible for varying the particle velocity towards $p_i^{(k)}$ and $p_g^{(k)}$ respectively.

From Eq. (35), the updated velocity of particle i is found by considering three components: (i) previous velocity of the particle, (ii) the distance between the particle’s best previous and current positions and (iii) the distance between swarm’s best experience (the position of the best particle in the swarm) and the current position of the particle. The velocity in Eq. (35) is also limited by the range $\left[ {-v_{\mathrm{max}},\, v_{\mathrm{max}}} \right]$ with $v_{\mathrm{max}}$ as the maximum velocity of the particle. Choosing too small a value for $v_{\mathrm{max}}$ can cause a minute update of the velocities and positions of the particles at each iteration. Hence, the algorithm may take long to converge, leading to a local optima. To avoid this case, Clerc (1999), and Clerc and Kennedy (2002) proposed an improved velocity update rule by employing a constriction factor $\chi$. Accordingly, the updated velocity is given by

$$\begin{aligned} v_i^{(k+1)} =\chi \left[ {v_i^{(k)} +c_1 r_1 \left( {p_i^{(k)} -x_i^{(k)} } \right) +c_2 r_2 \left( {p_g^{(k)} -x_i^{(k)} } \right) } \right] \end{aligned}$$

(37)

with the constriction factor $\chi$ expressed as

$$\begin{aligned} \chi =\frac{2}{\left| {2-\phi -\sqrt{\phi ^{2}-4\phi }} \right| } \end{aligned}$$

(38)

where $\phi =c_1 +c_2,\, \phi >4$ and $\chi$ is a function of $c_1$ and $c_2$. Typically, $c_1$ and $c_2$ are both set at 2.05. Thus, $\phi$ is set to 4.1 and $\chi$ is 0.729. This PSO is known as PSO-CO, i.e. the constriction coefficient based PSO.

The search procedure of PSO can be summarized as follows:

• Step 1 Initialize the PSO parameters and bounds of the decision variables of the optimization problem in the search space.

• Step 2 Initialize a population of particles with random positions and velocities.

• Step 3 Evaluate the fitness of all particles.

• Step 4 Keep track of the locations where each individual has its highest fitness so far.

• Step 5 Keep track of the position with the global best fitness.

• Step 6 Update the velocity of each particle.

• Step 7 Update the position of each particle.

• Step 8 If the stopping criterion is satisfied, goto Step 9, otherwise goto Step 3.

• Step 9 Print the position and fitness of global best particle.

• Step 10 Stop.

Generally, every particle is depicted by its position and velocity vectors which determine the trajectory of the particle. This means that a particle moves along a determined trajectory. However, in quantum mechanics, the term trajectory is meaningless, as the position and velocity of a particle cannot be determined simultaneously according to Heisenberg’s uncertainty principle. Hence, if a particle in a PSO system has quantum behavior, then the PSO algorithm works differently (Sun et al. 2004a, b). Considering quantum behavior, Sun et al. (2004a, b) first proposed the improved PSO algorithm leading to the quantum behaved PSO (QPSO). In the QPSO, the particles’ state equations are structured by a wave function and each particle’s state is described by the local attracter p and the characteristic length L of $\delta$-trap which is determined by the mean-optimal position (MP). As MP enhances the cooperation between the particles and the particles waiting with each other, QPSO can prevent particles from being trapped in a local minima (Pan et al. 2013). However the speed and accuracy of convergence are slow. From Sun et al. (2004a, b), the iterative equation for a particle’s position in QPSO is given by

$$\begin{aligned} x_{ij}^{(k)} =\tilde{p}_{ij}^{(k)} \pm {\beta }'\left| {m_j^{(k)} -x_{ij}^{(k)} } \right| \log \left( {\frac{1}{u_j }} \right) \end{aligned}$$

(39)

where $u_{j}$ is a random number uniformly distributed in (0,1). The parameter ${\beta }'$ is labelled as the contraction-expansion coefficient which can be tuned to control the convergence speed of the algorithm.

The global point, labelled as the Mainstream or Mean best $\left( {m^{(k)}} \right)$ of the population at kth iteration is defined as the mean of the pbest positions of all particles, i.e.

$$\begin{aligned} m^{(k)}=\left( {m_1^{(k)} ,m_2^{(k)} ,\ldots ,m_n^{(k)} } \right) =\left( {\frac{1}{p_{size} }\sum \limits _{i=1}^{p_{size} } {\tilde{p}_{i1}^{(k)} ,\frac{1}{p_{size} }\sum \limits _{i=1}^{p_{size} } {\tilde{p}_{i2}^{(k)} ,\ldots ,\frac{1}{p_{size} }\sum \limits _{i=1}^{p_{size} } {\tilde{p}_{in}^{(k)} } } } } \right) . \end{aligned}$$

(40)

The procedure for implementing the QPSO is given as follows:

• Step 1 Initialize the PSO parameters and bounds of the decision variables.

• Step 2 Initialize a population of particles with random positions.

• Step 3 Evaluate the fitness value of each particle.

• Step 4 Update the mean best position using Eq. (40).

• Step 5 Compare each particle’s fitness with the particle’s pbest. Store better one as pbest.

• Step 6 Compare current gbest position with earlier gbest position.

• Step 7 Update the position of each particle using Eq. (39).

• Step 8 If the stopping criterion is satisfied, goto Step 9, otherwise goto Step 3.

• Step 9 Print the position and fitness of global best particle.

• Step 10 Stop.

To improve the performance of the QPSO, many improved versions for the QPSO have been proposed, such as the Weighted QPSO i.e. WQPSO (Xi et al. 2008). AQPSO (Sun et al. 2005), RQPSO, RRQPSO, SRQPSO (Pan et al. 2013). Gaussian QPSO i.e. GQPSO (Coelho 2010).

Bhunia et al. (2015a) applied the PSO-CO technique to solve a two-warehouse inventory problem for deteriorating items considering partially backlogged shortages and inflation. Bhunia et al. (2014a) and Bhunia and Shaikh (2015) applied a variant of the PSO algorithm to solve the inventory problem.

In the WQPSO, the mean best position is replaced by the weighted mean best position. In that case, the particles are ranked in decreasing order according to their fitness values. A weighted coefficient $\alpha _i$ is then assigned, linearly decreasing, with the particle’s rank i.e. the nearer to the best solution, the larger is its weighted coefficient. The mean best position $m^{(k)}$, therefore, is calculated as follows:

$$\begin{aligned} m^{(k)}= & {} \left( {m_1^{(k)} ,m_2^{(k)} ,\ldots ,m_n^{(k)} } \right) \\= & {} \left( {\frac{1}{p_{size} }\sum \limits _{i=1}^{p_{size} } {\alpha _{i1} \tilde{p}_{i1}^{(k)} ,\frac{1}{p_{size} }\sum \limits _{i=1}^{p_{size} } {\alpha _{i2} \tilde{p}_{i2}^{(k)} ,\ldots ,\frac{1}{p_{size} }\sum \limits _{i=1}^{p_{size} } {\alpha _{in} \tilde{p}_{in}^{(k)} } } } } \right) \end{aligned}$$

where $\alpha _i$ is the weighted coefficient and $\alpha _{id}$ is the dimension coefficient of every particle respecitvely. In our paper, the weighted coefficient for each particle decreases linearly from 1.5 to 0.5.

5 Numerical and sensitivity analysis

5.1 Numerical example

Suppose an inventory system has the following data: A = $250/order, s = $10/unit/year, c = $20/unit, $c_{1} = { \$5/\mathrm{unit}}$, H = $0.5/unit/year, F = $0.7/unit/year, W = 200 units, a = 80, b =10, $\alpha = { 0.05/\mathrm{unit}}$, $\beta = { 0.03/\mathrm{unit}}$, ${ R = 0.06}$, $\delta = { 0.9, t}_{d} = { 0.1 \mathrm{year}}$. We now apply the PSO-CO. which has been coded in C and compiled on a PC with Intel Core-2-duo 2.5 GHz processor in a LINUX environment. For each case (I and II), 20 runs are performed by the proposed PSO for which the best value of the cost function is taken (Tables 1, 2).

Table 1 Best found solution of inventory models by PSO-CO

Table 2 Best found solution of inventory models by PSO-CO

For the entire computation, the values of the PSO parameters are as follows: ${ p\_size} = 100$, ${ m\_gen} = 100$, $C_{1} = 2.05$, $C_{2} = 2.05$. The initial velocity is assigned randomly between $-V_{\mathrm{max}}$ and $V_{\mathrm{max}}$ where $V_{\mathrm{max}}$ is set to be 20% of the range of each variable in the search domain. From the statistical analysis of the results obtained for the two cases (cf. Tables 3, 4), the proposed soft computing method PSO-CO and WQPSO are stable.

Table 3 Statistical analysis of the results for PSO-CO

Table 4 Statistical analysis of the results for WQPSO

5.2 Sensitivity analysis

Next, we perform a graphical sensitivity analyses to study the effect of under or over estimating the system parameters on the optimal solution corresponding to the best found value of the average cost of the system (i.e. the minimum value of the average cost, but the minimal property cannot be established theoretically). Here, the percentage changes are taken as measures of sensitivity. These analyses are carried out by altering the parameters individually by ±20% of their original values.

Table 5 Sensitivity analysis with different parameters of the inventory system of case-I

Table 6 Sensitivity analysis with different parameters of the inventory system of case-II

From Tables 5, 6, following insights are made:

• With the increase in the ordering cost (A) and holding cost of both OW and RW i.e. (H & F), the optimal cycle length (T), optimal maximum backorder (B), and optimal order quantity (Q) decrease but the present value of the total optimal cost (TC) increases.

• With the increase in the purchasing cost (c) and opportunity cost ($c_{1})$, the optimal cycle length (T), optimal maximum backorder (B) and optimal order quantity (Q) increases which results in an increase in the present value of total optimal cost (TC).

• Also, with an increase in the net rate of inflation (R), the order quantity (Q) and the Present value of the total optimal cost (TC) Increase. Further analysis on R shows that the influence of inflation should be considered even if it is small. To achieve higher sales during inflationary conditions, a customer should order more and for a longer period of time. It shows that as deterioration increases, one should order less while if the inflation increases, one should order more.

• There is a decrease in the present value of the total optimal cost (TC) and increases in the optimal cycle length (T) and order quantity (Q) with an decrease in backlogging parameter ($\delta$). As increasing the backlogging rate suggests accommodating more backlogged demand, this increases the order quantity. At the same time, the initial inventory for the cycle decreases, which decreases the holding cost, and in turn reduces the present value of the total optimal cost (TC). In short, when the backlogging rate is greater, a customer should order more to satisfy the backlogged demand.

• With an increase in the value of non-deteriorating period ($t_{d})$, it can be observed that the cycle length (T) and the order quantity (Q) increase but the Present value of the total optimal cost (TC) decreases. One explanation could be that as the period for non-deterioration ($t_{d})$ increases, the costs incurred due to deterioration decreases which accounts for less total cost to the system.

5.3 Graphical interactions of the decision variables

Graphical sensitivity analysis with respect to parameters a, b and W of case-I

Fig. 3

±20% change of parameter a on TC, Z, and B for Case I

Fig. 4

±20% change of parameter a on $\hbox {T}_{\mathrm{w}}$ and T for Case I

Fig. 5

±20% change of parameter b on TC, Z, and B for Case I

Fig. 6

±20% change of parameter b on $\hbox {T}_{\mathrm{w}}$ and T for Case I

Fig. 7

±20% change of parameter W on TC, Z, and B for Case I

Fig. 8

±20% change of parameter W on $\hbox {T}_{\mathrm{w}}$ and T for Case I

Graphical sensitivity analysis with respect to parameters a, b and W of case-II

Fig. 9

±20% change of parameter a on TC, Z, and B for Case II

Fig. 10

±20% change of parameter a on $\hbox {t}_{\mathrm{w}}$ and T for Case II

Fig. 11

±20% change of parameter b on TC, Z, and B for Case II

Fig. 12

±20% change of parameter b on $\hbox {t}_{\mathrm{w}}$ and T for Case II

Fig. 13

±20% change of parameter W on TC, Z, and B for Case II

Fig. 14

±20% change of parameter W on $\hbox {t}_{\mathrm{w}}$ and T for Case II

From Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14, the following observations are made:

• In both cases, the Present value of the total optimal cost (TC), maximum shortage (B) and cycle length (T) are highly sensitive to a, moderately sensitive to b and less so to W.

• In both cases, the highest stock level (Z) is moderately sensitive to a, b,  and insensitive to W.

• In both cases, the waiting time for the next replenishment $t_{w}$ is highly sensitive with respect to b and moderately sensitive to a and W.

6 Conclusion

Our paper has proposed a realistic model which is well practised in a retail setting that typically holds discounts at the end of a cycle, so as to sell off the current stock and to make space for the next replenishment period. We have discussed a two warehouse inventory model for non-instantaneous deteriorating items with stock-dependent demand under inflationary conditions. In the model, shortages are allowed and the backlogging rate is variable and depends on the waiting time for the next replenishment. We seek to obtain an optimal replenishment policy that minimizes the present value of the total cost per unit time. The necessary and sufficient conditions of the existence and uniqueness of the optimal solution for Cases I and II are found. Then for each case, the corresponding problems have been formulated and solved with the help of particle swarm optimization (PSO). A numerical example is presented to demonstrate the developed model, followed by a graphically sensitivity analysis of the optimal solution with respect to the key parameters of the inventory system.

Our inventory model can be extended further in several ways. The present model can be formulated under a single level and two-level trade credit policy. To inject more realism, the model can also be extended with different forms of demand such as the credit linked demand and advertisement dependent demand, which is of much interest in the cyberspace eCommerce domain currently.