An Application of PSO to Study Joint Policies of an Inventory Model with Demand Sensitive to Trade Credit and Selling Price While Deterioration of Item Being Controlled Using Preventive Technique

Abstract

This article contributes a joint inventory model for single deteriorating item with acceptable delay in payment. Effect of deterioration is considered and it is controlled by making an appropriate investment in preservation technology. The retailer gets credit period from the manufacturer with a deal to share portion of profit during this term and settle the accounts at the end of it. To boost the sales retailer permits credit period to a fraction of customers. To investigate the scenario mathematical model has been developed representing different cases. The corresponding problem is a nonlinear constrained optimization problem which is optimized by deploying Particle Swarm Optimization (PSO) algorithm. The objective is to cleverly decide unit selling price with suitable investment for preventive measures, cycle time and extended credit period; which maximizes the total profit. Lastly, to authenticate the model examples are presented and to examine the inventory parameters sensitivity analysis is carried out.

1 Introduction

The concept of paying the cost price of an item at its delivery time has now been outdated. In business transaction, offer of permissible credit period for stock purchased acts as a marketing tool for enhancing the sales, because it buys time for clearing accounts. Generally, in market, when the items are procured the account is not immediately settled by retailer; retailer gets some time from the supplier. Nowadays, permissible delay in payment is a common practice among players of supply chain. From supplier’s view, offering delay in payment attracts retailer and results increase in sales with reduced holding cost. For retailer, delay in payment reduces the opportunity cost of monetary fund to be invested, while retailer can also make surplus income by investing generated revenue in some interest bearing account during the permitted term. Hence, both supplier and retailer get benefited by implementing permissible delay period. The first Economic Order Quantity (EOQ) model permitting fixed delay period after the products are received is given by Goyal (1985). Afterwards, Aggarwal and Jaggi (1995) proposed inventory model with permissible delay for deteriorating items. For detailed review of permissible delay (trade credit) into inventory models refer Chang et al. (2008) and Soni et al. (2010). Sarkar (2012) discussed an inventory model that allows delay in payments in presence of imperfect production. For demand dependent on selling price and permissible delay period, Giri and Maiti (2013) proposed a model in which retailer takes bank loan to clear the debt. Mishra et al. (2019) determined the best payment option for the retailer along with finding the optimal cycle time.

It is not just that the supplier can avail the benefit by offering permissible credit period, even retailer can improve his sales by extending credit period to the end customers. To demonstrate that retailer also gets benefitted when permissible delay period availed from the supplier is extended to end customer, Huang (2003) proposed an EOQ model. In this model, delay period (N) offered to end customer by retailer was assumed to be less than the credit period (M) received. Later, by easing the assumption N < M, Teng and Chang (2009) studied an Economic Production Quantity (EPQ) model. This setup is also termed as two-level trade credit. Few articles using two-level trade credit policy are Min et al. (2010), Kaanodiya and Pachauri (2011), Shah et al. (2014), Shaikh and Mishra (2018). The mentioned articles emphases to reveal optimal strategies either from the supplier or retailer point of view.

There are a number of competitors in supply chain network and to survive in such situation is a difficult task. The motto of every competitor is to enhance the business by different means. In a non-integrated supply chain, members have different motives and this possibly can clash with supply chain’s objective. To enhance the productivity of supply chain network, members should unite and make decisions jointly, which can help in fulfilling customers need at lowest inventory cost. The first integrated model to study inventory policies was given by Goyal (1977). Afterwards, Abad and Jaggi (2003) combined the concept of permissible delay and integrated inventory model. Sarmah et al. (2007) gave the idea of sharing profit among the two members during the credit period. Assuming demand as a downstream credit period function, He and Huang (2013) studied a joint inventory model for items deteriorating non-instantaneously. In presence of two-level trade credit, Chung and Cárdenas-Barrón (2013) proposed an easy technique to get optimal solution for an inventory model with demand dependent on displayed units. In presence of permissible delay, Wu et al. (2014) studied replenishment policies for deteriorating items with demand reliant on price and stock. Aggarwal and Tyagi (2014) examined credit and inventory policies with demand related to date terms credit. Shah (2015) formulated an integrated model with an agreement of profit-sharing under two-level trade credit. Mishra and Shaikh (2017a) established an integrated model utilizing two warehouses with demand dependent on displayed units and trade credit liable on order size. Mishra and Shaikh (2017b) also studied ordering and pricing policies in an integrated environment for stock and price sensitive demand.

Another important concern for inventory items is deterioration, it is unavoidable. It plays a substantial role in inventory modelling as utility of item is affected. It occurs for items such as edibles, milk products, clothing, fashion accessories, and medical supplies. To overcome the effect of deterioration preventive steps should be taken. Several researchers have formulated models for controlling deterioration by investing in preservation technology. The first EOQ model including exponential decay was given by Ghare (1963). Hariga (1995) studied an EOQ model incorporating shortages for deteriorating items and demand varying with time. An EOQ model under inflationary conditions for deteriorating items with time-varying demand is given by Jaggi and Mittal (2003). Jaggi and Mittal (2011) also gave an EOQ model in presence of imperfect quality for deteriorating items. In presence of imperfect quality and demand dependent on displayed stock, Shah and Shah (2014) developed an inventory model incorporating the effect of inflation. For preservation of seasonal products, Sarkar et al. (2017) presented an inventory model with stock-dependent demand. Mishra et al. (2017) studied an EOQ model with demand dependent on displayed stock and selling price. An imperfect manufacturing system considering quadratic demand with inflation was given by Shah et al. (2017). Mishra and Shaikh (2017c) studied joint decision policies using preservation technology to control deterioration with quadratic demand sensitive to permissible credit period. Shaikh and Mishra (2019) formulated an inventory model for deteriorating items following price sensitive quadratic demand with suitable investment in preservation technology in an inflationary environment.

Generally, optimal solutions for most of the inventory models are obtained by traditional or gradient-based optimization methods. While employing these methods, one frequently faced limitation is that the traditional approach gets stuck to the local maxima or minima. In addition, these methods are unable to optimize nonlinear constrained complex problems. To overcome such limitations many evolutionary algorithms are used these days to solve real-world problems, Genetic Algorithm and particle swarm optimization (PSO) are two of them. Hence, the use of evolutionary algorithms would be advantageous as there will be less chances of getting stuck at local extrema while using them. For an inventory model with two warehouses and permissible delay, Bhunia and Shaikh (2015) utilized PSO to study optimal policies for deteriorating units. In an inventory model with items deteriorating in nature and demand dependent on marketing strategy and displayed stock, Bhunia et al. (2018) used Genetic Algorithm and PSO to frame optimal strategies. These search techniques are also used in optimizing the Multi-objective function. Garai and Garg (2019) studied multi-objective linear fractional inventory model with possibility and necessity constraints under intuitionistic fuzzy set environment. Shaikh et al. (2020) utilized Multi-objective Genetic Algorithm to allocate order in the list of available suppliers. Mishra et al. (2020) also used Multi-objective Genetic Algorithm to optimize the supply chain network through player selection. Waliv et al. (2020) presented a nonlinear programming approach to solve the stochastic multi-objective inventory model using the uncertain information. The use of heuristic search techniques for obtaining optimal solution has been rarely used by researchers working in the area of inventory management.

Reviewing the available literature, gap for an integrated inventory model under the following condition is observed; (i) the retailer’s demand increases with hike in permissible delay period offered to customer and decreases with hike in unit selling price, (ii) retailer gets a fix time slot from the manufacturer with a mutual agreement to share fraction of profit, (iii) items are deteriorating and precautionary measures are taken to control it, (iv) lastly, to determine the optimal value of decision variables the use of PSO algorithm is rarely done by researchers working in the area of inventory management. Hence, these are a few gaps as per our observation and proposed model is an attempt to fill it up.

This chapter is an effort to study the joint policies of manufacturer and retailer by means of an integrated inventory model. The retailer’s demand function is assumed as an elevating function of permissible delay period offered to customer, while declining function of unit selling price. Retailer avails fix credit period from the manufacturer with a mutual agreement to share fraction of profit during this period. Inventory items are deteriorating in nature and to control the deterioration process, appropriate amount is to be invested in preservation technology. The aim is to cleverly decide unit selling price with suitable investment for preventive measures, cycle time and credit period to be offered; which maximizes the total profit. The succeeding part of this chapter is arranged in the following manner. The notations used and assumptions made for proposed model is given in Sect. 2. In Sect. 3, the math modelling is done which leads to formulation of objective function. Along with this we present an overview of particle swarm optimization (PSO) algorithm. Then, to authenticate the model and to test the performance of the PSO algorithm, numerical examples are presented in Sect. 5. In Sect. 6, sensitivity analysis of inventory parameters is conducted. Lastly, in Sect. 7 conclusion is presented.

2 Notation and Assumptions

The notations used and assumptions made for proposed model are as follows:

2.1 Notation

Inventory Parameters for Retailer

$A_{{\text{r}}}$ :

Retailer’s ordering cost per order

$C_{{\text{r}}}$ :

Retailer’s unit purchase cost

$h_{{\text{r}}}$ :

Holding cost per annum

$\theta$ :

Constant deterioration rate, $0 \le \theta < 1$

$\delta$ :

Fraction of profit to be shared with manufacturer during the credit period $M$; $0 \le \delta < 1$

$I_{{\text{b}}}$ :

Interest rate on the loan taken from bank

$I_{{\text{e}}}$ :

Interest earned rate by the retailer

$\gamma$ :

Fraction of customer allowed by retailer to avail a trade credit period $N$

$I_{{\text{r}}} (t)$ :

Retailer inventory level at time $t$

$f(u) = 1 - \frac{1}{{1 + \mu u}}$ :

Proportion of reduced deterioration of item

$\pi _{{\text{r}}}$ :

Retailer total profit per unit time

Inventory Parameters for Manufacturer

$C_{{\text{m}}}$ :

Manufacturing cost of item per unit, $C_{{\text{m}}} < C_{{\text{r}}}$

$A_{{\text{m}}}$ :

Manufacturer setup cost per lot

$h_{{\text{m}}}$ :

Holding cost per annum

$M$ :

Credit period retailer gets from the manufacturer

$I_{{\text{m}}}$ :

Interest rate lost by manufacturer because to offering permissible delay period

$T_{{\text{m}}} = xT$ :

Manufacturer time delay to initiate the production, $(0 < x < 1)$

$I_{{\text{m}}} (t)$ :

Manufacturer inventory level at time $t$

$\pi _{{\text{m}}}$ :

Manufacturer total profit per unit time

Decision Variables

$T$ :

Cycle time

$N$ :

Credit period offered to end customer by retailer

$S$ :

Retailer unit selling price, $S > C_{{\text{r}}}$

$u$ :

Investment in preservation technology

For PSO

$r_{1} ,r_{2}$ :

Random variable which is uniformly lying between $\left[ {0,1} \right]$

p_size:

Size of the population

$c_{1} \left( { > 0} \right)$ :

Cognitive learning rate

$c_{2} \left( { > 0} \right)$ :

Social learning rate

m-gen:

Maximum iteration/generation

$x_{i}^{{\left( k \right)}}$ :

Velocity of ith particle at kth iteration/generation

$p_{i}^{{\left( k \right)}}$ :

Best previous position of ith particle at kth iteration

$p_{g}^{{\left( k \right)}}$ :

Position of best particle among all other particle in the population

$\chi$ :

Constriction factor

Inventory Parameters Relation

$N \le M$

$S > C_{{\text{r}}} > C_{{\text{m}}}$

$0 \le \theta < 1$

Functions

$D(N,S)$ :

Retailer’s demand rate; $D(N,S) = \alpha - \eta S + \beta N$, where $\alpha > 0$ represents scale demand, $\eta > 0$ signifies price elasticity and $\beta > 0$ is trade credit markup rate

$P(N,S)$ :

Manufacturer production rate proportionate to retailer’s demand rate, $P(N,S) = \lambda \cdot D(N,S),\,\,\lambda > 1$

$\pi (N,S,T,u)$ :

Joint total profit of manufacturer and retailer $(\pi _{{\text{m}}} + \pi _{{\text{r}}} )$

The aim of the integrated inventory model is stated as:

$${\text{Max}}\quad \quad \pi (N,S,T,u)$$

Subject to,

$$ N \le M, $$

$$ N,S,T,u \ge 0 $$

2.2 Assumptions

• 1. Inventory system consists of lone manufacturer, lone retailer dealing with single item.

• 2. The retailer’s demand function is assumed as an elevating function of permissible delay period offered to customer, while declining function of unit selling price. Therefore, demand rate is expressed as $D(N,S) = \alpha - \eta S + \beta N$. In this chapter, $D(N,S)$ and $D$ are used interchangeably for notational convenience.

• 3. Manufacturer’s production rate $P(N,S)$ is more than the retailer’s demand $D(N,S)$. This indicates manufacturer has adequate production ability to meet retailer’s demand.

• 4. Retailer avails fix credit period (M) from the manufacturer with a mutual agreement to share fraction of profit during this period.

• 5. When the cycle time exceeds the delay period permitted by manufacturer, retailer is bound to clear the accounts from the spare of his sales revenue. However, retailer does not have adequate fund to settle the accounts. So, to pay the rest of purchase cost at the end of the credit period $M$ retailer avails a bank loan at an interest rate $I_{{\text{b}}}$. Later, retailer pays the loan amount to the bank at the end of the cycle time.

• 6. During the permitted delay period, manufacturer incurs an interest loss at the rate of $I_{{\text{m}}}$. Further, retailer earns interest on generated income at the rate of $I_{{\text{e}}}$.

• 7. Only a fraction of customers is provided credit period $(N < M)$ by the retailer.

• 8. The quantity of reduced deterioration rate $f(u)$ is presumed to be continuously increasing and concave function of $u$ (i.e., preservation technology investment), i.e., $f^{\prime } (u) > 0$ and $f^{{\prime \prime }} (u) < 0$. Also $f(0) = 0$, in this model $f(u)$ and $f$ are used interchangeably for notational convenience.

• 9. Shortages are not allowed. Planning horizon is infinite and lead time is zero.

3 Mathematical Model

3.1 Retailer’s Total Profit Per Unit Time

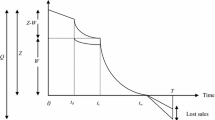
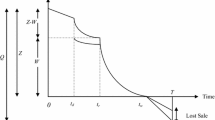
In the proposed model, the following differential equation indicates the status of retailer’s inventory level $I_{{\text{r}}} (t)$ at time $t$:

$$ \frac{{{\text{d}}I_{{\text{r}}} (t)}}{{{\text{d}}t}} + \theta (1 - f)I_{{\text{r}}} (t) = - (\alpha - \eta S + \beta N),\quad 0 \le t \le T $$

(1)

with $I_{{\text{r}}} (0) = Q\,\,{\text{and}}\,\,I_{{\text{r}}} (T) = 0$. The solution of (1) using $I_{{\text{r}}} (T) = 0$ is,

$$ I_{{\text{r}}} (t) = \frac{{(\alpha - \eta S + \beta N)}}{{\theta \left( {1 - f} \right)}}\left[ {1 - \exp \left( {\theta \left( {1 - f} \right)\left( {T - t} \right)} \right)} \right] $$

(2)

Employing the other condition $I_{{\text{r}}} (0) = Q$ and (2), optimal order quantity is

$$ Q = \frac{{(\alpha - \eta S + \beta N)}}{{\theta \left( {1 - f} \right)}}\left[ {1 - \exp \left( {\theta \left( {1 - f} \right)\left( T \right)} \right)} \right] $$

(3)

Further, costs associated with retailer’s total profit are

• Sales revenue generated, ${\text{SR}}_{{\text{r}}} = S\left[ {\int\nolimits_{0}^{T} {(\alpha - \eta S + \beta N){\text{d}}t} } \right]$

• Purchase cost, ${\text{PC}}_{{\text{r}}} = C_{{\text{r}}} Q$

• Ordering cost, ${\text{OC}}_{{\text{r}}} = A_{{\text{r}}}$

• Investment in preservation technology, ${\text{IPT}} = u$

• Holding cost, ${\text{HC}}_{{\text{r}}} = h_{{\text{r}}} \left[ {\int\nolimits_{0}^{T} {I_{{\text{r}}} (t){\text{d}}t} } \right]$.

Next, depending on the values of $M,N\,\,{\text{and}}\,\,T$, i.e., delay period availed and offered by the retailer and cycle time $T$. Either of the three situation may arise (i) $N \le M \le T$, (ii) $N \le T \le M$ and (iii) $T \le N \le M$. Further explanation of each scenario is as follows:

Case I: $N \le M \le T$

According to the contract, during the permitted delay period $\left[ {0,M} \right]$ retailer is bound to share $\delta \%$ of the profit with the manufacturer. Therefore, the profit shared with manufacturer is, ${\text{FP}}_{1} = \delta \left( {S - C_{{\text{r}}} } \right)\int_{0}^{M} {(\alpha - \eta S + \beta N){\text{d}}t}$ and the remaining of the sales revenue can be utilized to clear the accounts. At the end of the credit period $M$, retailer avails a bank loan at an interest rate $I_{{\text{b}}}$. When the cycle time ends retailer pays the loan amount to the bank. Therefore, interest charged by the bank is,

$$ {\text{ICB}}_{{\text{r}}} = I_{{\text{b}}} \left[ {C_{{\text{r}}} \int\limits_{0}^{T} {(\alpha - \eta S + \beta N){\text{d}}t} - S\int\limits_{0}^{M} {(\alpha - \eta S + \beta N){\text{d}}t} + {\text{FP}}_{1} } \right]\left( {T - M} \right) $$

(4)

Next, during the cycle time interest earned by the retailer is,

$$ {\text{IE}}_{{{\text{r}}1}} = I_{{\text{e}}} S\left[ {\int\limits_{0}^{M} {\left( {(\alpha - \eta S + \beta N) \cdot t} \right){\text{d}}t} + \int\limits_{0}^{{T - M}} {\left( {(\alpha - \eta S + \beta N) \cdot t} \right){\text{d}}t} } \right] $$

(5)

Also, opportunity cost bared by retailer for offering partial credit period $N$ is,

$$ {\text{OL}}_{{{\text{r}}1}} = \gamma I_{{\text{e}}} S\left[ {\int\limits_{0}^{N} {\left( {(\alpha - \eta S + \beta N) \cdot t} \right){\text{d}}t} } \right] $$

(6)

Hence, retailer’s profit per unit time is given by,

$$ \pi _{{{\text{r}}1}} = \frac{1}{T}\left( {{\text{SR}}_{{\text{r}}} - {\text{PC}}_{{\text{r}}} - {\text{OC}}_{{\text{r}}} - {\text{HC}}_{{\text{r}}} - {\text{FP}}_{1} - {\text{ICB}}_{{\text{r}}} - {\text{OL}}_{{{\text{r}}1}} + {\text{IE}}_{{{\text{r}}1}} } \right) - {\text{IPT}} $$

(7)

Case II: $N \le T \le M$

In this case, the profit shared with manufacturer during permissible delay period is, ${\text{FP}}_{2} = \delta \left( {S - {\text{C}}_{{\text{r}}} } \right)\int_{0}^{T} {(\alpha - \eta S + \beta N){\text{d}}t}$ and interest earned during the cycle time by the retailer is,

$$ {\text{IE}}_{{{\text{r}}2}} = I_{{\text{e}}} S\left[ {\int\limits_{0}^{T} {\left( {(\alpha - \eta S + \beta N) \cdot t} \right){\text{d}}t} + Q\left( {M - T} \right)} \right] $$

(8)

Also, retailer’s opportunity loss during $\left[ {0,N} \right]$ is,

$$ {\text{OL}}_{{{\text{r}}2}} = \gamma I_{{\text{e}}} S\left[ {\int\limits_{0}^{N} {\left( {(\alpha - \eta S + \beta N) \cdot t} \right){\text{d}}t} } \right] $$

(9)

Here, the retailer has sufficient fund to settle the accounts, so there is no need of taking loan from the bank. Therefore, retailer’s profit per unit time is given by,

$$ \pi _{{{\text{r}}2}} = \frac{1}{T}\left( {{\text{SR}}_{{\text{r}}} - {\text{PC}}_{{\text{r}}} - {\text{OC}}_{{\text{r}}} - {\text{HC}}_{{\text{r}}} - {\text{FP}}_{2} - {\text{OL}}_{{{\text{r}}2}} + {\text{IE}}_{{{\text{r}}2}} } \right) - {\text{IPT}} $$

(10)

Case III: $T \le N \le M$

Here, the profit shared with manufacturer during permissible delay period is same as in case II, ${\text{FP}}_{2} = \delta \left( {S - C_{{\text{r}}} } \right)\int_{0}^{T} {(\alpha - \eta S + \beta N){\text{d}}t}$ and interest earned during the cycle time by the retailer is,

$$ {\text{IE}}_{{{\text{r}}3}} = I_{{\text{e}}} S\left[ {\int\limits_{0}^{T} {\left( {(\alpha - \eta S + \beta N) \cdot t} \right){\text{d}}t} + Q\left( {M - T} \right)} \right] $$

(11)

Also offering credit period to end customer retailer incurs opportunity loss during $\left[ {0,N} \right]$ which is given by,

$$ {\text{OL}}_{{{\text{r}}3}} = \gamma I_{{\text{e}}} S\left[ {\int\limits_{0}^{T} {\left( {(\alpha - \eta S + \beta N) \cdot t} \right){\text{d}}t} + Q\left( {N - T} \right)} \right] $$

(12)

For this scenario, the retailer has adequate fund to settle the accounts, so there is no need of taking loan from the bank. Therefore, retailer’s profit per unit time is given by,

$$ \pi _{{{\text{r}}3}} = \frac{1}{T}\left( {{\text{SR}}_{{\text{r}}} - {\text{PC}}_{{\text{r}}} - {\text{OC}}_{{\text{r}}} - {\text{HC}}_{{\text{r}}} - {\text{FP}}_{2} - {\text{OL}}_{{{\text{r}}3}} + {\text{IE}}_{{{\text{r}}3}} } \right) - {\text{IPT}} $$

(13)

3.2 Manufacturer Total Profit Per Unit Time

In the proposed model, the following differential equation indicates the status of manufacturer inventory level $I_{{\text{m}}} (t)$ at time $t$:

$$ \frac{{{\text{d}}I_{{\text{m}}} (t)}}{{{\text{d}}t}} = P\left( {N,S} \right) - D\left( {N,S} \right),\quad T_{{\text{m}}} \le t \le T $$

(14)

with $I_{{\text{m}}} (T) = 0$. The solution of (14) using this condition is,

$$ I_{{\text{m}}} (t) = \left( {\lambda - 1} \right)\left( {\alpha - \eta S + \beta N} \right)\left( {t - T} \right) $$

(15)

The manufacturer total profit per unit time consists of setup cost, holding cost, opportunity loss sales revenue and production cost.

• Setup cost, ${\text{OC}}_{{\text{m}}} = A_{{\text{m}}}$

• Holding cost, ${\text{HC}}_{{\text{m}}} = h_{{\text{m}}} \left[ {\int_{{T_{{\text{m}}} }}^{T} {I_{{\text{m}}} (t)\text{d}t} } \right]$

• Interest loss happened for offering trade credit $M$ to retailer,

  $$ {\text{OL}}_{{\text{m}}} = I_{{\text{m}}} C_{{\text{r}}} M\left[ {\int\limits_{{T_{{\text{m}}} }}^{T} {\lambda \cdot (\alpha - \eta S + \beta N){\text{d}}t} } \right] $$

  (16)

Under the contract, $\delta \%$ of the profit made by the retailer is shared with the manufacturer during the permissible delay period. Thus, the portion of profit availed by manufacturer is given by,

$$ {\text{FP}}_{{\text{m}}} = \left\{ {\begin{array}{*{20}l} {{\text{FP}}_{{{\text{m}}1}} = \delta \left( {S - C_{{\text{r}}} } \right)\int\limits_{0}^{M} {(\alpha - \eta S + \beta N){\text{d}}t} ,\quad M \le T} \hfill \\ {{\text{FP}}_{{{\text{m}}2}} = \delta \left( {S - C_{{\text{r}}} } \right)\int\limits_{0}^{T} {(\alpha - \eta S + \beta N){\text{d}}t} ,\quad M > T} \hfill \\ \end{array} } \right. $$

(17)

Therefore, total profit of manufacturer per unit time is given by

$$ \pi _{{{\text{m}}1}} = \frac{1}{T}\left[ {\left( {C_{{\text{r}}} - C_{{\text{m}}} } \right)\int\limits_{0}^{T} {(\alpha - \eta S + \beta N){\text{d}}t} - {\text{OC}}_{{\text{m}}} - {\text{HC}}_{{\text{m}}} - {\text{OL}}_{{\text{m}}} + {\text{FP}}_{{{\text{m}}1}} } \right],\,\,\,M \le T $$

(18)

$$ \pi _{{{\text{m}}2}} = \frac{1}{T}\left[ {\left( {C_{{\text{r}}} - C_{{\text{m}}} } \right)\int\limits_{0}^{T} {(\alpha - \eta S + \beta N){\text{d}}t} - {\text{OC}}_{{\text{m}}} - {\text{HC}}_{{\text{m}}} - {\text{OL}}_{{\text{m}}} + {\text{FP}}_{{{\text{m}}2}} } \right],\,\,\,M > T $$

(19)

3.3 Joint Profit of Supply Chain

The joint total profit of integrated supply chain is given by sum of retailer and manufacturer profit, which is a multivariable function of partial trade credit, selling price, cycle time and preservation technology investment. Hence, depending on the cycle time and permissible delay period duration, joint total profit per unit time of supply chain is given by:

$$ \pi (N,S,T,u) = \left\{ {\begin{array}{*{20}l} {\pi _{1} (N,S,T,u) = \pi _{{\text{r}1}} + \pi _{{\text{m}1}} ,\quad N \le M \le T} \hfill \\ {\pi _{2} (N,S,T,u) = \pi _{{\text{r}2}} + \pi _{{\text{m}2}} ,\quad N \le T \le M} \hfill \\ {\pi _{3} (N,S,T,u) = \pi _{{\text{r}3}} + \pi _{{\text{m}2}} ,\quad T \le N \le M} \hfill \\ \end{array} } \right. $$

(20)

The aim is to maximize joint total profit of the supply chain with partial trade credit, unit selling price, cycle time and preservation technology investment as decision variables.

4 Solution Procedure

Several researchers have effectively employed heuristic search techniques to optimize their difficult problems in various streams of sciences. Few of the well-known techniques are simulated annealing, Genetic Algorithm, ant colony optimization and particle swarm optimization. For this study, we utilize the commonly used particle swarm optimization method for optimizing the objective function formed.

Based on the individual experience and social interaction of the population, Particle swarm optimization (PSO) is a heuristic global search technique. This technique was anticipated by Eberhart and Kennedy (1995a, 1995b). Getting inspiration from the social behaviour of bird gathering or fish schooling, this technique is generally used to optimize challenging problems. PSO algorithm initiates with random set of solutions (also known as particles) flying in the search space. These particles hunt for the optima in each iteration (also known as generation) by following the current optimal solutions. In each iteration, position of all the particles is updated by utilizing two best solutions. One of these best solutions is the personal best position so far attained by the particle and is denoted by $p_{i}^{{(k)}}$, while the second one is the present best position so far attained by any of the particle and is denoted by $p_{g}^{{(k)}}$.

In every iteration, the velocity and position of ith (i = 1, 2, …, p_size) particle is updated by using:

$$ v_{i}^{{\left( {k + 1} \right)}} = wv_{i}^{{\left( k \right)}} + c_{1} r_{1} \left( {p_{i}^{{\left( k \right)}} - x_{i}^{{\left( k \right)}} } \right) + c_{2} r_{2} \left( {p_{g}^{{\left( k \right)}} - x_{i}^{{\left( k \right)}} } \right) $$

(21)

and

$$ x_{i}^{{\left( {k + 1} \right)}} = x_{i}^{{\left( k \right)}} + v_{i}^{{\left( {k + 1} \right)}} $$

(22)

where k (= 1, 2, …, m-gen) represents the iterations (generations); w is the inertia weight. The cognitive learning rate $c_{1} \left( { > 0} \right)$ and social learning rate $c_{2} \left( { > 0} \right)$ are the responsible acceleration constants for varying the particle velocity in the direction of $p_{i}^{{(k)}}$ and $p_{g}^{{(k)}}$ respectively.

The updated velocity of ith particle is given by (21) which involves three components. The explanation of each of this component is as follow: (i) particles velocity in previous iteration, (ii) the distance between particle’s current and previous best position and (iii) the distance between particle’s current and swarm’s best position (the optimal position of particle in the swarm). The velocity given by (21) is also restricted by $v_{{\max }}$ called the maximum velocity of the particle; hence the range of velocity update is $\left[ { - v_{{\max }} ,v_{{\max }} } \right]$. Picking too small value for $v_{{\max }}$ can result to tiny change in velocity update and particles position at each iteration. As a result, algorithm can take longer time to converge and might face the problem of getting stuck at local extrema. To get rid of these circumstances, Clerc (1999), Clerc and Kennedy (2002) proposed a better rule to update velocity by using a constriction factor $\chi$. Using this factor, the velocity is updated using the following equation,

$$ v_{i}^{{\left( {k + 1} \right)}} = \chi \left[ {v_{i}^{{\left( k \right)}} + c_{1} r_{1} \left( {p_{i}^{{\left( k \right)}} - x_{i}^{{\left( k \right)}} } \right) + c_{2} r_{2} \left( {p_{g}^{{\left( k \right)}} - x_{i}^{{\left( k \right)}} } \right)} \right] $$

(23)

Here the constriction factor $\chi$ is expressed as

$$ \chi = \frac{2}{{\left| {2 - \phi - \sqrt {\phi ^{2} - 4\phi } } \right|}} $$

(24)

where $\phi = c_{1} + c_{2} ,\phi > 4$. The constriction factor is a function of $c_{1}$ and $c_{2}$. Generally, values of $c_{1}$ and $c_{2}$ is set to 2.05 which results $\phi$ as 4.1; hence, the constriction coefficient value is 0.729. This algorithm is recognized as constriction coefficient-based PSO.

The search technique of particle swarm optimization is summarized as below:

• 1. Define the PSO parameters and set bounds for the decision variables.

• 2. Initialize with a set of particles (solution) from search space with random positions and velocities.

• 3. Calculate the fitness value of every particle.

• 4. For each particle, keep track of the location where particle attains its best fitness value.

• 5. Keep track of the location with the global best fitness.

• 6. Update the velocity and position of each particle.

• 7. If the termination criterion is fulfilled, go to next step, else go to step 3.

• 8. Display the location and fitness score of global best particle.

• 9. End.

5 Numerical Examples

For PSO parameters we use the subsequent values

p_size = 100, $c_{1}$ = 2.05, $c_{2}$ = 2.05 and m-gen = 100.

Example 1: Consider $\alpha = 80$, $\beta = 0.5$, $\eta = 0.7$, $\lambda = 1.5$, $x = 0.1$, $C_{{\text{m}}} = \$ 8\,{\text{per}}\,{\text{unit}}$, $\delta = 10\%$, $C_{{\text{r}}} = \$ 15\,{\text{per}}\,{\text{unit}}$, $A_{\text{r}} = \$ 15{\text{ per order}}$, $h_{\text{r}} = \$ 5{\text{ per unit per year}}$, $I_{\text{b}} = 11\% {\text{ per annum}}$, $I_{{\text{e}}} = 10\% \,{\text{per}}\,{\text{annum}}$, $M = 0.6\,{\text{year}}$, $\theta = 30\%$, $\mu = 15\% ,$ $h_{{\text{m}}} = \$ 3\,{\text{per}}\,{\text{unit}}\,{\text{per}}\,{\text{year}}$, $\gamma = 0.5$, $I_{{\text{m}}} = 10\% \,{\text{per}}\,{\text{annum}}$ and $A_{{\text{m}}} = \$ 20\,{\text{per}}\,{\text{setup}}$.

Here, the maximum profit is $\pi _{1} = \$ 604.57$ for cycle time is $T = 0.8428\,{\text{years}}$ at unit selling price $41.59, offering credit period $N = 0.3008\,{\text{years}}$ to end customers and investing $\$ 10.93$ in preservation technology. It represents the scenario $N \le M \le T$ and Figs. 1, 2, 3, 4, 5 and 6 represents concavity of the profit function.

Fig. 1

Source Own

Concavity for T and N.

Fig. 2

Source Own

Concavity for S and N.

Fig. 3

Source Own

Concavity for u and N.

Fig. 4

Source Own

Concavity for S and T.

Fig. 5

Source Own

Concavity for u and T.

Fig. 6

Source Own

Concavity for u and S.

Example 2: Let $M = 0.8$ year and values of other inventory parameters as in Example 1. The maximum profit is $\pi _{2} = \$ 609.97$ which comes out for scenario $N \le T \le M$ at $T = 0.5622\,{\text{years}}$, $S = \$ 41.19$, $N = 0.2049\,{\text{years}}$ and $u = \$ 7.07$.

Example 3: Consider $\beta = 1.57,M = 1.2$ year and all other parameters same as in Example 1. The situation $T \le N \le M$ yields maximum profit as $\pi _{3} = \$ 623.53$ which comes out at $T = 1.1168\,{\text{year}}$, $S = \$ 43.56$, $N = 1.1849\,{\text{year}}$ and $u = \$ 13.98$.

Figure 7 shows the joint and individual profit for all the three examples, which represent all the possible cases. Next, to compare the integrated decision making policy with independent decision making policy we maximize retailer’s total profit with same values of inventory parameters as in Example 1 (i.e., retailer is the decision maker). Here the retailer’s total profit turns out to be $\pi _{{{\text{r}}1}} = \$ 463.46$ for cycle time $T = 0.9574\,{\text{year}}$ at unit selling price $44.94, offering credit period $N = 0.2990\,{\text{year}}$ to end customers and investing $\$ 11.18$ in preservation technology. It represents the scenario $N \le M \le T$ and for these values the manufacturer’s total profit is $133.16. Therefore, the joint profit from independent decision making is sum of retailer’s profit and manufacturer’s profit, which is $596.62. This represents that decision made in an integrated environment turns out to be more profitable for members of supply chain compared to independent one. The comparison of integrated and independent decision for Examples 2 and 3 is also shown in Table 1.

Fig. 7

Source Own

Joint and individual profit.

Table 1 Comparison of independent and integrated decision

6 Sensitivity Analysis

To study the impact of inventory parameters in decision making, we consider inventory parameter values same as taken in example 1. Next, by changing each parameter once at a time by −20%, −10%, +10% and +20% optimal solution is obtained. The solutions obtained are analysed cautiously and based on it managerial insights are provided as follows.

In Fig. 8, credit period (N) offered to end customer is plotted for variation in inventory parameters. It is being observed that increase in manufacturer’s holding cost, setup cost, manufacturing cost, credit period offered to retailer, retailer ordering cost, preservation rate and interest rate on amount borrowed increases the delay period (N) offered to end customer. Whereas it increases significantly for markup rate for trade credit and $\lambda$. Other inventory parameters show a negative impact on credit period (N) offered to end customer; among which scale demand, price elasticity, retailer’s holding cost and fraction of customer offered trade credit are highly sensitive.

Fig. 8

Source Own

Variation in credit period offered to end customer (N).

In Fig. 9, impact of inventory parameters on cycle time is observed. The major observations are; increase in markup for trade credit, manufacturer’s holding cost, interest loss rate, credit period offered to end customer, manufacturing cost, retailer ordering cost, preservation rate and interest rate on borrowed amount increases the cycle time. Whereas $\lambda$ and manufacturer setup cost increases cycle time rapidly. Other inventory parameters show negative impact on cycle time among which price elasticity, retailer’s unit purchase cost and holding cost are highly sensitive.

Fig. 9

Source Own

Variation in cycle time (T).

In Fig. 10, unit selling price is plotted for variation in inventory parameters. It is being observed that increase in fraction of profit shared with manufacturer, manufacturer’s holding cost, preservation rate and fraction of customer offered trade credit decreases the unit selling price. Whereas it decreases significantly for price elasticity. Other inventory parameters show a positive impact on unit selling price; among which scale demand and unit manufacturing cost are highly sensitive.

Fig. 10

Source Own

Variation in unit selling price (S).

In Fig. 11, effect of inventory parameters on preservation technology investment is observed. It shows that scale demand and deterioration rate has a high positive impact on preservation technology investment; while preservation technology investment decreases for increase in price elasticity and retailer holding cost. Effect of other inventory parameters can be seen in the figure.

Fig. 11

Source Own

Variation in preservation technology investment (u).

In Fig. 12, the effect of change in inventory parameters on joint total profit can be seen. The major observations made are; scale demand has a high impact on profit, while markup for trade credit, $\lambda ,x$, manufacturer holding cost, preservation rate, interest rate on borrowed amount and interest earned rate has a positive impact on profit. Whereas the other parameters show a negative impact on profit among which price elasticity, unit manufacturing cost, retailer’s unit purchase cost and holding cost are highly sensitive.

Fig. 12

Source Own

Variation in joint total profit.

On the basis of change in values of inventory parameters and their impact, the manufacturer and retailer can wisely interpret the cause that leads to increase and decrease in the values of decision variables. Hence, they can cleverly tune up the values of decision variables which will lead to favorable outcomes.

7 Conclusion

In this study, we optimize the formulated integrated inventory model using PSO algorithm. While performing the sensitivity analysis, major observations made are; (1) Increase in scale demand elevates the total profit with hiked up selling rate, preservation technology investment and reduces cycle time and credit period offered. (2) Higher deterioration rate leads to more investment in preservation technology resulting decrease in profit. (3) Retailer’s holding cost is very negatively sensitive to all decision variable except for selling price, which reduces the profit. For the numerical examples presented, integrated and independent decisions are studied and it has been found that an integrated decision is more fruitful for the supply chain. This model is applicable for variety of items like grains, vegetables, electronic devices, utility vehicle, etc. In addition, this model can be extended by allowing shortages, items possessing fixed lifetime, considering trade credit dependent on order size.