An Economic Order Quantity (EOQ) Inventory Model for a Deteriorating Item with Interval-Valued Inventory Costs, Price-Dependent Demand, Two-Level Credit Policy, and Shortages

Abstract

In today’s competitive environment, every leading organization wishes to improve the pricing strategies in order to increase revenue, credit policy is one of the best tools of it. This research work develops an economic order quantity (EOQ) inventory model for a deteriorating item that considers interval-valued inventory costs, price dependent demand, two-level credit policy, and shortages. Due to high and uncertainty in demand, sometimes organizations have to face the situation of stock out. So, keeping this scenario in mind, this work considers the situation of partially backlogging. Here, it is developed an EOQ inventory model by considering a non-linear interval-valued constrained optimization problem. Two types of particle swarm optimization (PSO) algorithm are used to resolve it, and then the results are compared. Sensitivity analysis is done in order to investigate the impact of key parameters on decision-making. Finally, conclusions along with some managerial insights are given.

2.1 Introduction

In the inventory management literature, very little research work has been done in relation to considering that the inventory costs are represented in an interval-valued. Many researchers assume that the inventory costs such that the ordering cost, inventory carrying cost, and purchasing cost are expressed as a fixed value known. Nevertheless, in reality, all of the mentioned costs are imprecise numbers in nature instead of a fixed value due to the fact that generally, the inventory costs fluctuate by reason of several factors such as changes in prices. In order to explain why it needs to use an interval number rather than the fixed value number, the following reason is mentioned. Normally, the inventory carrying cost is distinct during the seasons of the year. For example, the deterioration rate is different in summer and winter. During summer time, it is necessary to use preservation technology with the intention of decreasing the deterioration percentage of some perishable products and therefore the holding cost is different from holding cost in the winter time. Another cost that also varies is the labor charges, which change over the period of time.

To overcome the problem of imprecise numbers, the researchers and academicians use the following approaches: (i) stochastic, (ii) fuzzy, and (iii) fuzzy-stochastic. In the case of the stochastic approach, the inventory data are considered as random variables with a given and known probability distribution. In the case of the fuzzy approach, the data of the inventory system and the constraints are expressed with fuzzy sets with a given and known membership function. In the case of fuzzy-stochastic approach, some inventory data are supposed to be represented by fuzzy sets and the rest of the inventory parameters are assumed random variables. But it is not an easy task to select the most suitable membership function or probability distribution.

With the aim of avoiding the complexity in the selection of the right membership function or the right probability distribution, it is suggested to use interval numbers. With this, the imprecise problem is converted to an interval-valued problem, which can be solved, by any soft computing optimization technique, such as the different versions of particle swarm optimization (PSO) or genetic algorithm (GA). In this connection, the reader can see the related works, which apply interval number into the area of inventory control. Gupta et al. [1] applied the interval concept in the field of inventory theory. They resolved an inventory problem with interval-valued inventory costs using a genetic algorithm approach. After that, Dey et al. [2] formulated an inventory model considering interval-valued lead time. Again, Gupta et al. [3] developed an inventory model using interval-valued inventory costs. Bhunia et al. [4] solved a stock-dependent inventory model with interval-valued inventory costs using particle swarm optimization (PSO). Afterward, Bhunia and Shaikh [5] built a two-warehouse inventory model with inflation, and they solved it using particle swarm optimization.

In the current competitive markets, the permissible delay in payment has a vital role in promoting the business. Normally, the suppliers give different types of facilities to retailers, and the retailers give some facilities to their direct customers. This is done with the aim of attracting more customers to acquire products. Table 2.1 presents research works related to single-level or two-level credit policy.

Table 2.1 Research works related to single- and two-level permissible delay in payment

It is a well-known fact that inventory cost always is not a fixed value. This means that the inventory cost lies between certain interval numbers. Therefore, the major goal of this research work is to include the interval concept in an inventory model. In this direction, this research work derives an economic order quantity (EOQ) inventory model for a deteriorating item with price-dependent demand, and interval-valued inventory costs and shortages. The shortage is partially backordered according to a rate, which is reliant on the interval of waiting time till the occurrence of next lot. The inventory model is expressed as a nonlinear interval-valued continuous optimization problem. Then, different forms of particle swarm optimization (PSO) algorithm are applied to solve it. In continuous optimization, PSO gives better results than GA. For this reason, in this research work, the latest version of PSO is used.

The remnants sections of the research work are planned as follows. Section 2.2 defines the suppositions and the notations. Section 2.3 formulates the inventory model. Section 2.4 derives the mathematical solution for three different demand functions. Section 2.5 solves some instances. Section 2.6 does a sensitivity analysis. Section 2.7 provides conclusions and lines for research.

2.2 Suppositions and Notations

The suppositions and symbols that are used to build the inventory model are listed below.

2.2.1 Suppositions

• (i) The planning horizon is infinite.

• (ii) Inventory system handles a single item.

• (iii) Demand rate $D(.)$ is influenced by the selling price (p).

• (iv) Inventory costs are interval-valued.

• (v) The order is supplied in one delivery.

• (vi) Replenishment is instantaneous.

• (vii) Lead time is zero.

• (viii) Stockout is partially backlogged with a backlogging rate given by $\left[ {1 + \delta \left( {T - t} \right)} \right]^{ - 1}$.

• (ix) Two-level credit policy approach is assumed where the supplier gives a credit period (M) to his/her retailer, and the retailer also provides a credit facility (N) to his/her customer under certain terms and conditions. Here, it is established the following condition N < M.

2.2.2 Notations

Symbols	Description
Parameters
$I\left( t \right)$	Inventory level at time t (units)
$\alpha$	Deterioration rate ($0 < \alpha \ll 1$)
$[C_{oL} ,C_{oR} ]$	Interval-valued replenishment cost ($/order)
$\delta$	Backlogging parameter
$\left[ {C_{pL} ,C_{pR} } \right]$	Interval-valued purchasing cost ($/unit)
$D(.)$	Demand rate that is dependent on price (units/unit of time)
$[C_{hL} ,C_{hR} ]$	Interval-valued holding cost ($/unit/unit of time)
$[C_{bL} ,C_{bR} ]$	Interval-valued shortage cost ($/unit/unit of time)
$[C_{lsL} ,C_{lsR} ]$	Interval-valued opportunity cost due to a lost sale ($/unit/unit of time)
$t_{1}$	Time in which the stock level is zero (unit of time)
T	Cycle length (unit of time)
M	Credit period is given to the retailer by the supplier (unit of time)
N	Credit period provided to the customer by the retailer: N < M (unit of time)
$I_{e}$	Interest earned by the retailer (%/unit of time)
$I_{p}$	Interest charged by the supplier to the retailer (%/unit of time)
$\left[ {Z_{L}^{(.)} ,Z_{R}^{(.)} } \right]$	Interval-valued the total profit ($/unit of time)
Decision variables
S	Stock level (units)
R	Shortage level (units)
B	The time period after reaching the prescribed credit time M (unit of time)

2.3 Mathematical Derivation of the Inventory Model

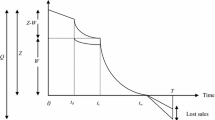
Initially, the retailer purchases a lot of (S + R) units. After fulfilling the backordered units of the preceding cycle, the stock level is S units at t = 0. Then, S units start to decrease due to both consumers’ demand and deterioration effect. Obviously, after a certain time period, the stock level reaches zero at the time $t = t_{1}$. After that, at time $t = t_{1}$, shortage occurs with a backlogging rate $\left[ {1 + \delta \left( {T - t} \right)} \right]^{ - 1}$ till the time $t = T.$ Then, a subsequent batch is received at T.

The behavior of the inventory $I\left( t \right)$ is modeled by the differential Eqs. (2.1) and (2.2):

$$ \frac{dI(t)}{dt} + \theta (t)I(t) = - D(.),\quad [0,t_{1} ] $$

(2.1)

$$ \frac{dI(t)}{dt} = \frac{ - D(.)}{1 + \delta (T - t)},\quad (t_{1} ,T] $$

(2.2)

with the initial and boundary conditions

$$ I\left( t \right) = S\,{\text{at}}\,t = 0,\,I(t) = 0\,{\text{at}}\,t = t_{1} $$

(2.3)

and

$$ I\left( t \right) = - R\,{\text{at}}\,t = T $$

(2.4)

It is significant to state that the inventory level $I(t)$ is continuous at $t = t_{1}$. Using the conditions (2.3) and (2.4), the solutions to the differential equations (2.1) and (2.2) are given below:

$$ \begin{aligned} I(t) & = - \frac{D(.)}{\theta } + \frac{D(.)}{\theta }e^{{\theta (t_{1} - t)}} ,\quad [0,t_{1} ] \\I(t) & = \frac{D(.)}{\delta }\log \left| {1 + \delta (T - t)} \right| - R,\quad (t_{1} ,T] \\ \end{aligned} $$

From condition (2.3), $I\left( t \right) = S$ at $t = 0.$ Thus, the maximum inventory level is computed with

$$ S = \frac{D\left( . \right)}{\theta }\left\{ {e^{{\theta t_{1} }} - 1} \right\} $$

(2.5)

Using the continuity condition, hence, the shortage quantity is determined with

$$ R = \frac{D(.)}{\delta }\log \left| {1 + \delta (T - t_{1} )} \right| $$

(2.6)

The total interval-valued inventory holding cost $C_{hol} = \left[ {C_{holL} ,C_{holR} } \right]$ of the system is expressed as follows:

$$ C_{holL} = C_{hL} \int\limits_{0}^{{t_{1} }} {I\left( t \right)} \,dt = C_{hL} \left[ {\frac{{(S + \frac{D(.)}{\theta })}}{\theta }\left( {1 - e^{{ - \theta t_{1} }} } \right) - \frac{{Dt_{1} }}{\theta }} \right] $$

(2.7)

and

$$ C_{holR} = C_{hR} \int\limits_{0}^{{t_{1} }} {I\left( t \right)} \,dt = C_{hR} \left[ {\frac{{(S + \frac{D(.)}{\theta })}}{\theta }\left( {1 - e^{{ - \theta t_{1} }} } \right) - \frac{{Dt_{1} }}{\theta }} \right] $$

(2.8)

The total interval-valued shortage cost $C_{sho} = \left[ {C_{shoL} ,C_{shoR} } \right]$ of the inventory system is given below:

$$ \begin{aligned} C_{shoL} & = C_{bL} \int\limits_{{t_{1} }}^{T} {[ - I(t)]\,dt} \\ & = C_{bL} \left[ {\left( {R + \frac{D(.)}{\delta }} \right)\left( {T - t_{1} } \right) - \frac{D(.)}{{\delta^{2} }}\left\{ {\left( {1 + \delta \left( {T - t_{1} } \right)} \right)\log \left( {1 + \delta \left( {T - t_{1} } \right)} \right)} \right\}} \right] \\ \end{aligned} $$

(2.9)

$$ \begin{aligned} C_{shoR} & = C_{bR} \int\limits_{{t_{1} }}^{T} {[ - I(t)]\,dt} \\ & = C_{bR} \left[ {\left( {R + \frac{D(.)}{\delta }} \right)\left( {T - t_{1} } \right) - \frac{D(.)}{{\delta^{2} }}\left\{ {\left( {1 + \delta \left( {T - t_{1} } \right)} \right)\log \left( {1 + \delta \left( {T - t_{1} } \right)} \right)} \right\}} \right] \\ \end{aligned} $$

(2.10)

The total interval-valued opportunity cost of lost sales $OC_{LS} = \left[ {OC_{LSL} ,OC_{LSR} } \right]$ during the entire cycle is determined by

$$ \begin{aligned} OC_{LSL} & = C_{lsL} \int\limits_{{t_{1} }}^{T} {\left\{ {1 - \frac{1}{{1 + \delta \left( {T - t} \right)}}} \right\}D(.)} \,dt \\ & = C_{lsL} D(.)\left[ {(T - t_{1} ) - \frac{{\log \left( {1 + \delta \left( {T - t_{1} } \right)} \right)}}{\delta }} \right] \\ \end{aligned} $$

(2.11)

and

$$ \begin{aligned} OC_{LSR} & = C_{lsR} \int\limits_{{t_{1} }}^{T} {\left\{ {1 - \frac{1}{{1 + \delta \left( {T - t} \right)}}} \right\}D(.)} \,dt \\ & = C_{lsR} D(.)\left[ {(T - t_{1} ) - \frac{{\log \left( {1 + \delta \left( {T - t_{1} } \right)} \right)}}{\delta }} \right] \\ \end{aligned} $$

(2.12)

As it was mentioned before, in two-level credit policy, the supplier provides a credit period to his/her retailer with a duration of M. Then, the retailer also gives a certain credit period to his/her client with a duration of N, where N is always less than M. Furthermore, here two cases occur: Case 1: $0 < N < M \le t_{1}$ and Case 2: $N < t_{1} < M \le T.$ Figures 2.1 and 2.2 show the behavior of the stock level over the period of time for Case 1 and Case 2, respectively. Below a discussion of these two cases is given.

Fig. 2.1

Inventory-level behavior for Case 1

Fig. 2.2

Inventory-level behavior for Case 2

Case 1: $0 < N < M \le t_{1}$

In this case, the total amount of purchase cost of the retailer is within the following interval $\left[ {C_{pL} \left( {S + R} \right),C_{pR} \left( {S + R} \right)} \right]$. This amount must be covered to the supplier at the time $t = M.$ In this credit time period, the retailer accumulates money due to sales during [0, M] as well as the interest gained during [N, M]. Hence, the total collected amount is calculated with

$$ U_{1} = p\int\limits_{0}^{M} {D(.)\,dt + pI_{e} \int\limits_{N}^{M} {\int\limits_{N}^{t} {D(.)\,dudt} + } } pR\left\{ {1 + I_{e} (M - N)} \right\}. $$

Thus,

$$ U_{1} = pD(.)\left\{ {M + I_{e} \frac{{\left( {M - N} \right)^{2} }}{2}} \right\}pR\left\{ {1 + I_{e} (M - N)} \right\} $$

(2.13)

The retailer collects $U_{1}$ and interval-valued for the purchase cost amount is $\left[ {C_{pL} \left( {S + R} \right),C_{pR} \left( {S + R} \right)} \right].$ Here, the following two subcases occur: Subcase 1: $U_{1} \ge \left[ {C_{pL} \left( {S + R} \right),C_{pR} \left( {S + R} \right)} \right]$ and Subcase 2: $U_{1} < \left[ {C_{pL} \left( {S + R} \right),C_{pR} \left( {S + R} \right)} \right].$ These subcases are developed below:

Subcase 1: $U_{1} \ge \left[ {C_{pL} \left( {S + R} \right),C_{pR} \left( {S + R} \right)} \right]$

In this Subcase 1, the total interval-valued profit of the inventory system is written as

$$ Z_{1L} \left( . \right) = \frac{{X_{L} (.)}}{T}\,{\text{and}}\,Z_{1R} \left( . \right) = \frac{{X_{R} (.)}}{T} $$

(2.14)

where

$\left[ {X_{L} ,X_{R} } \right]$ = <Excess amount on hand after paying the cost of purchased goods to the supplier> + <interest earned for excess amount in $\left[ {M,T} \right]$> + <sales revenue in $\left[ {M,t_{1} } \right]$> + <interest earned in $\left[ {M,t_{1} } \right]$> + <interest earned in $\left[ {t_{1} ,T} \right]$> − <ordering cost> − <holding cost> − <shortage cost> − <cost of lost sale>

$$ \begin{aligned} X_{L} (.) & = \left\{ {U_{1} - C_{pR} \left( {S + R} \right)} \right\}\left\{ {1 + I_{e} \left( {T - M} \right)} \right\} + D(.)p\left( {t_{1} - M} \right)\left\{ {1 + \frac{1}{2}I_{e} \left( {t_{1} - M} \right)} \right\} \\ & \quad \left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR} \\ \end{aligned} $$

(2.15)

and

$$ \begin{aligned} X_{R} (.) & = \left\{ {U_{1} - C_{pL} \left( {S + R} \right)} \right\}\left\{ {1 + I_{e} \left( {T - M} \right)} \right\} + D(.)p\left( {t_{1} - M} \right)\left\{ {1 + \frac{1}{2}I_{e} \left( {t_{1} - M} \right)} \right\} \\ & \quad \left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

(2.16)

Therefore, the corresponding interval-valued nonlinear optimization problem of the inventory system is written as follows.

Problem 1

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{1} \left( . \right) = \left[ {Z_{1L} \left( . \right),Z_{1R} \left( . \right)} \right] \\ & {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.17)

Subcase 2: $U_{1} < \left[ {C_{pL} \left( {S + R} \right),C_{pR} \left( {S + R} \right)} \right]$

In Subcase 2, the retailer collects an amount corresponding to sales and interest earned up to $t = M.$ This amount is less than the amount of the purchase cost. Taking into consideration this situation, the following two subcases happen: Subcase 2.1: Supplier takes a partial payment at $t = M$ of his/her retailer, and Subcase 2.2: Supplier does not take the partial payment at $t = M$ of his/her retailer. Now, these two subcases are discussed below.

Subcase 2.1: Supplier takes a partial payment at $t = M$ of his/her retailer.

In this subcase, it is considered that the supplier takes a partial payment and permits some time to the retailer regarding the payment of rest interval amount which is expressed as $\left[ {C_{pL} \left( {S + R} \right) - U_{1} ,C_{pR} \left( {S + R} \right) - U_{1} } \right]$. The interval relax time is $t = \left[ {B_{L} ,B_{R} } \right]\,{\text{where}}\,\left[ {B_{L} ,B_{R} } \right] > M$. In this situation, the supplier must charge the interest of unpaid amount $\left[ {C_{pL} \left( {S + R} \right) - U_{1} ,C_{pR} \left( {S + R} \right) - U_{1} } \right]$ during the interval $\left[ {M,\left[ {B_{L} ,B_{R} } \right]} \right]$ with interest paid rate $I_{p}$.

Thus, the total amount that must be paid to the supplier at a time $t = \left[ {B_{L} ,B_{R} } \right]$ is given by $\left[ {C_{pL} \left( {S + R} \right) - U_{1} ,C_{pR} \left( {S + R} \right) - U_{1} } \right]\left\{ {1 + I_{p} \left( {\left[ {B_{L} ,B_{R} } \right] - M} \right)} \right\}$.

On the other hand, the total available amount to the retailer is determined as < total sales revenue during the time interval $\left[ {M,\left[ {B_{L} ,B_{R} } \right]} \right]$> + <total interest earned during the time interval $\left[ {M,\left[ {B_{L} ,B_{R} } \right]} \right]$>. So, the total interest earned is

$$ = p\int\limits_{M}^{{B_{L} }} {D(.)\,dt + pI_{e} \int\limits_{M}^{{B_{L} }} {\int\limits_{M}^{t} {D(.)\,dudt} } } $$

and

$$ = p\int\limits_{M}^{{B_{R} }} {D(.)\,dt + pI_{e} \int\limits_{M}^{{B_{R} }} {\int\limits_{M}^{t} {D(.)\,dudt} } } $$

As a result, at the time $t = \left[ {B_{L} ,B_{R} } \right]$, the total payable amount available to the retailer is equal to the amount payable to the supplier, which is

$$ \begin{aligned} & \left[ {C_{pL} \left( {S + R} \right) - U_{1} ,C_{pR} \left( {S + R} \right) - U_{1} } \right]\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} \\ & \quad = pD(.)\left( {B_{L} - M} \right)\left\{ {1 + \frac{{I_{e} (B_{L} - M)}}{2}} \right\} \\ \end{aligned} $$

Thus,

$$ \left[ {C_{pL} \left( {S + R} \right) - U_{1} } \right]\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} = pD(.)\left( {B_{L} - M} \right)\left\{ {1 + \frac{{I_{e} (B_{L} - M)}}{2}} \right\} $$

and

$$ \left[ {C_{pR} \left( {S + R} \right) - U_{1} } \right]\left\{ {1 + I_{p} \left( {B_{R} - M} \right)} \right\} = pD(.)\left( {B_{R} - M} \right)\left\{ {1 + \frac{{I_{e} (B_{R} - M)}}{2}} \right\} $$

Consequently, the total interval-valued profit function of the inventory system is computed as

$$ Z_{2L} \left( . \right) = \frac{{X_{L} (.)}}{T}\quad {\text{and}}\quad Z_{2R} \left( . \right) = \frac{{X_{R} (.)}}{T} $$

where

$\left[ {X_{L} ,X_{R} } \right]$ = < sales revenue during the time interval $\left[ {\left[ {B_{L} ,B_{R} } \right],t_{1} } \right]$ > + < interest earned thru the time interval $\left[ {\left[ {B_{L} ,B_{R} } \right],t_{1} } \right]$ > + < interest earned through interval $\left[ {t_{1} ,T} \right]$ > − < ordering cost > − <holding cost > − <shortage cost > − <cost of lost sale>

$$ \begin{aligned} X_{L} (.) & = \left\{ {p\int\limits_{{B_{R} }}^{{t_{1} }} {D(.)dt} + pI_{e} \int\limits_{{B_{R} }}^{{t_{1} }} {\int\limits_{{B_{R} }}^{t} {D(.)dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR} \\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} (.) & = \left\{ {p\int\limits_{{B_{L} }}^{{t_{1} }} {D(.)dt} + pI_{e} \int\limits_{{B_{L} }}^{{t_{1} }} {\int\limits_{{B_{L} }}^{t} {D(.)dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL}\\ \end{aligned} $$

So, in this subcase, the interval-valued constrained optimization problem is formulated as follows.

Problem 2

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{2} \left( . \right) = \left[ {Z_{2L} (.),Z_{2R} (.)} \right] \\ & {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.18)

Subcase 2.2: Supplier does not take the partial payment at $t = M$ of his/her retailer.

In this situation, the supplier does not take a partial payment. In other words, the retailer needs to cover the credit amount to his/her supplier. This amount is calculated with $\left[ {C_{pL} \left( {S + R} \right) - U_{1} ,C_{pR} \left( {S + R} \right) - U_{1} } \right]$ after the time $t = M$. The interval time period $t = \left[ {B_{L} ,B_{R} } \right]$ when the supplier gets the full creditable amount within this time interval. Regarding this situation, supplier charges the interest for the period $\left[ {M,\left[ {B_{L} ,B_{R} } \right]} \right]$ with interest paid rate $I_{p}$.

Therefore, the total on-hand amount available to the retailer is equal to the amount payable to the supplier at the time $t = \left[ {B_{L} ,B_{R} } \right]$. Thus,

$$ \begin{aligned} & C_{pL} \left( {S + R} \right)\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} = U_{1} \left[ {1 + I_{e} (B_{L} - N)} \right] + pD(.)(B_{L} - M) \\ & \quad \left[ {1 + I_{e} \frac{{(B_{L} - M)}}{2}} \right] \\ \end{aligned} $$

and

$$ \begin{aligned} & C_{pR} \left( {S + R} \right)\left\{ {1 + I_{p} \left( {B_{R} - M} \right)} \right\} = U_{1} \left[ {1 + I_{e} (B_{R} - N)} \right] + pD(.)(B_{R} - M) \\ & \quad \left[ {1 + I_{e} \frac{{(B_{R} - M)}}{2}} \right] \\ \end{aligned} $$

Consequently, the total interval-valued profit of the inventory system is as follows:

$$ Z_{3L} \left( . \right) = \frac{{X_{L} (.)}}{T}\quad {\text{and}}\quad Z_{3R} \left( . \right) = \frac{{X_{R} (.)}}{T} $$

where

$\left[ {X_{L} ,X_{R} } \right]$ = < sales revenue during the time interval $\left[ {\left[ {B_{L} ,B_{R} } \right],t_{1} } \right]$ > + < interest earned for the duration of the time interval $\left[ {\left[ {B_{L} ,B_{R} } \right],t_{1} } \right]$ > + < interest earned within the interval $\left[ {t_{1} ,T} \right]$ > − < ordering cost > − <holding cost > − <shortage cost > − <cost of lost sale>

$$ \begin{aligned} X_{L} (.) & = \left\{ {p\int\limits_{{B_{R} }}^{{t_{1} }} {D(.)dt} + pI_{e} \int\limits_{{B_{R} }}^{{t_{1} }} {\int\limits_{{B_{R} }}^{t} {D(.)dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR}\\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} (.) & = \left\{ {p\int\limits_{{B_{L} }}^{{t_{1} }} {D(.)dt} + pI_{e} \int\limits_{{B_{L} }}^{{t_{1} }} {\int\limits_{{B_{L} }}^{t} {D(.)dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL}\\ \end{aligned} $$

(2.19)

Thus, the interval-valued constrained nonlinear optimization problem is expressed below:

Problem 3

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{3} \left( . \right) = \left[ {Z_{3L} (.),Z_{3R} (.)} \right] \\ & {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.20)

Case 2: $N < t_{1} < M \le T$

Owing to sales revenue and interest earned, the collected amount of the retailer is computed as

$$ U_{2} = \left[ {p\int\limits_{0}^{{t_{1} }} {D(.)dt + pI_{e} \int\limits_{N}^{M} {\int\limits_{N}^{t} {D(.)dudt} } } } \right]\left[ {1 + I_{e} (M - t_{1} )} \right] + pR\left\{ {1 + I_{e} (M - N)} \right\} $$

$$ U_{2} = pD\left( . \right)\left[ {t_{1} + I_{e} \frac{{\left( {M^{2} - N^{2} } \right)}}{2}} \right]\left[ {1 + I_{e} (M - t_{1} )} \right] + pR\left\{ {1 + I_{e} (M - N)} \right\} $$

Here, the interval-valued profit of the inventory system is formulated as

$$ Z_{4L} \left( . \right) = \frac{{X_{L} (.)}}{T}\quad {\text{and}}\quad \, Z_{4R} \left( . \right) = \frac{{X_{R} (.)}}{T} $$

where

$\left[ {X_{L} ,X_{R} } \right]$ = < Excess amount available of retailer after paying the supplier > + < total interest earned for that excess amount in $\left[ {M,T} \right]$ > − < ordering cost > − <holding cost > − <shortage cost > − <cost of lost sale>

$$ X_{L} (.) = U_{2} - \left( {C_{oR} + C_{holR} + C_{shoR} + OC_{LSR} } \right) $$

and

$$ X_{R} (.) = U_{2} - \left( {C_{oL} + C_{holL} + C_{shoL} + OC_{LSL} } \right) $$

For that reason, the corresponding interval-valued constrained nonlinear optimization problem is as follows.

Problem 4

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{4} \left( . \right) = \left[ {Z_{4L} (.),Z_{4R} (.)} \right] \\ & {\text{subject to}}\,\,N < t_{1} < M \le T \\ \end{aligned} $$

(2.21)

2.4 The Solution for Three Demand Functions

$D\left( \cdot \right) = a - bp,\,a,b > 0$, $D\left( \cdot \right) = ap^{ - \alpha } \quad a > 0,\alpha < 1$, and $D\left( \cdot \right) = ae^{( - p/k)} ,\; a,k > 0$.

This section derives the mathematical expressions for three price demand functions.

4.1: When $D\left( \cdot \right) = a - bp,\quad a,b > 0$

Here,

$$ U_{1} = p\int\limits_{0}^{M} {(a - bp)dt + pI_{e} \int\limits_{N}^{M} {\int\limits_{N}^{t} {(a - bp)dudt + } } } pR\left\{ {1 + I_{e} (M - N)} \right\} $$

• Case 4.1.1.

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{1}^{\left( 1 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & \quad {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.22)

where

$$ \begin{aligned} X_{L} & = \left\{ {U_{1} - C_{pR} \left( {S + R} \right)} \right\}\left\{ {1 + I_{e} \left( {T - M} \right)} \right\} + (a - bp)p\left( {t_{1} - M} \right)\left\{ {1 + \frac{1}{2}I_{e} \left( {t_{1} - M} \right)} \right\} \\ & \quad \left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR} \\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} & = \left\{ {U_{1} - C_{pL} \left( {S + R} \right)} \right\}\left\{ {1 + I_{e} \left( {T - M} \right)} \right\} + (a - bp)p\left( {t_{1} - M} \right)\left\{ {1 + \frac{1}{2}I_{e} \left( {t_{1} - M} \right)} \right\} \\ & \quad \left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

• Case 4.1.2.

  $$ \begin{aligned}& {\text{Maximize}}\,\,Z_{2}^{\left( 1 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & {\text{subject to}} \,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

  (2.23)
  $$ \left\{ {C_{pL} \left( {S + R} \right) - U_{1} } \right\}\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} = p\int\limits_{M}^{{B_{L} }} {(a - bp)dt + pI_{e} \int\limits_{M}^{{B_{L} }} {\int\limits_{M}^{t} {(a - bp)dudt} } } $$

and

$$ \left\{ {C_{pR} \left( {S + R} \right) - U_{1} } \right\}\left\{ {1 + I_{p} \left( {B_{R} - M} \right)} \right\} = p\int\limits_{M}^{{B_{R} }} {(a - bp)dt + pI_{e} \int\limits_{M}^{{B_{R} }} {\int\limits_{M}^{t} {(a - bp)dudt} } } $$

where

$$ \begin{aligned} X_{L} &= \left\{ {p\int\limits_{{B_{R} }}^{{t_{1} }} {(a - bp)dt} + pI_{e} \int\limits_{{B_{R} }}^{{t_{1} }} {\int\limits_{{B_{R} }}^{t} {(a - bp)dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR}\\ \end{aligned} $$

$$ \begin{aligned} X_{R} & = \left\{ {p\int\limits_{{B_{L} }}^{{t_{1} }} {(a - bp)dt} + pI_{e} \int\limits_{{B_{L} }}^{{t_{1} }} {\int\limits_{{B_{L} }}^{t} {(a - bp)dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

• Case 4.1.3.

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{3}^{\left( 1 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.24)

$$ \begin{aligned} & C_{pL} \left( {S + R} \right)\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} = U_{1} \left[ {1 + I_{e} (B_{L} - N)} \right] + p(a - bp)(B_{L} - M)\left[ {1 + I_{e} \frac{{(B_{L} - M)}}{2}} \right] \\ \end{aligned} $$

and

$$ \begin{aligned} & C_{pR} \left( {S + R} \right)\left\{ {1 + I_{p} \left( {B_{R} - M} \right)} \right\} = U_{1} \left[ {1 + I_{e} (B_{R} - N)} \right] + p(a - bp)(B_{R} - M) \\ & \quad \left[ {1 + I_{e} \frac{{(B_{R} - M)}}{2}} \right] \\ \end{aligned} $$

where

$$ \begin{aligned} X_{L} & = \left\{ {p\int\limits_{{B_{R} }}^{{t_{1} }} {(a - bp)dt} + pI_{e} \int\limits_{{B_{R} }}^{{t_{1} }} {\int\limits_{{B_{R} }}^{t} {(a - bp)dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR}\\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} & = \left\{ {p\int\limits_{{B_{L} }}^{{t_{1} }} {(a - bp)dt} + pI_{e} \int\limits_{{B_{L} }}^{{t_{1} }} {\int\limits_{{B_{L} }}^{t} {(a - bp)dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

• Case 4.1.4.

Here,

$$ \begin{aligned} U_{2} & = \left[ {p\int\limits_{0}^{{t_{1} }} {(a - bp)dt + pI_{e} \int\limits_{N}^{M} {\int\limits_{N}^{t} {(a - bp)dudt} } } } \right]\left[ {1 + I_{e} (M - t_{1} )} \right] \\ & \quad + pR\left\{ {1 + I_{e} (M - N)} \right\} \\ \end{aligned} $$

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{4}^{\left( 1 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & \quad {\text{subject to}}\,\,N < t_{1} < M \le T \\ \end{aligned} $$

(2.25)

where

$$ \, X_{L} = U_{2} - \left( {C_{oR} + C_{holR} + C_{shoR} + OC_{LSR} } \right) $$

and

$$ X_{R} = U_{2} - \left( {C_{oL} + C_{holL} + C_{shoL} + OC_{LSL} } \right) $$

4.2: When $D\left( \cdot \right) = ap^{ - \alpha } \quad a > 0,\alpha < 1$

Here,

$$ U_{1} = p\int\limits_{0}^{M} {ap^{ - \alpha } \,dt + pI_{e} \int\limits_{N}^{M} {\int\limits_{N}^{t} {ap^{ - \alpha } \,dudt + } } } pR\left\{ {1 + I_{e} (M - N)} \right\} $$

• Case 4.2.1.

  $$ \begin{aligned}& {\text{Maximize}}\,\,Z_{1}^{\left( 2 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & \quad {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

  (2.26)

where

$$ \begin{aligned} X_{L} & = \left\{ {U_{1} - C_{pR} \left( {S + R} \right)} \right\}\left\{ {1 + I_{e} \left( {T - M} \right)} \right\} + ap^{ - \alpha } p\left( {t_{1} - M} \right)\left\{ {1 + \frac{1}{2}I_{e} \left( {t_{1} - M} \right)} \right\} \\ & \quad \left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR} \\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} & = \left\{ {U_{1} - C_{pL} \left( {S + R} \right)} \right\}\left\{ {1 + I_{e} \left( {T - M} \right)} \right\} + ap^{ - \alpha } p\left( {t_{1} - M} \right)\left\{ {1 + \frac{1}{2}I_{e} \left( {t_{1} - M} \right)} \right\} \\ & \quad \left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

• Case 4.2.2.

  $$ \begin{aligned}& {\text{Maximize}}\,\,Z_{2}^{\left( 2 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & {\text{subject to}}\,\, 0 < N < M \le t_{1} < T \\ \end{aligned} $$

  (2.27)
  $$ \left\{ {C_{pL} \left( {S + R} \right) - U_{1} } \right\}\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} = p\int\limits_{M}^{{B_{L} }} {ap^{ - \alpha } \,dt + pI_{e} \int\limits_{M}^{{B_{L} }} {\int\limits_{M}^{t} {ap^{ - \alpha } \,dudt} } } $$

and

$$ \left\{ {C_{pR} \left( {S + R} \right) - U_{1} } \right\}\left\{ {1 + I_{p} \left( {B_{R} - M} \right)} \right\} = p\int\limits_{M}^{{B_{R} }} {ap^{ - \alpha } \,dt + pI_{e} \int\limits_{M}^{{B_{R} }} {\int\limits_{M}^{t} {ap^{ - \alpha } \,dudt} } } $$

where

$$ \begin{aligned} \, X_{L} & = \left\{ {p\int\limits_{{B_{R} }}^{{t_{1} }} {ap^{ - \alpha } \,dt} + pI_{e} \int\limits_{{B_{R} }}^{{t_{1} }} {\int\limits_{{B_{R} }}^{t} {ap^{ - \alpha } \,dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR} \\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} & = \left\{ {p\int\limits_{{B_{L} }}^{{t_{1} }} {ap^{ - \alpha } \,dt} + pI_{e} \int\limits_{{B_{L} }}^{{t_{1} }} {\int\limits_{{B_{L} }}^{t} {ap^{ - \alpha } \,dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL}\\ \end{aligned} $$

• Case 4.2.3.

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{3}^{\left( 2 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & \quad {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.28)

$$ \begin{aligned} & C_{pL} \left( {S + R} \right)\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} = U_{1} \left[ {1 + I_{e} (B_{L} - N)} \right] + pap^{ - \alpha } (B_{L} - M) \\ & \quad \left[ {1 + I_{e} \frac{{(B_{L} - M)}}{2}} \right] \\ \end{aligned} $$

and

$$ \begin{aligned} & C_{pR} \left( {S + R} \right)\left\{ {1 + I_{p} \left( {B_{R} - M} \right)} \right\} = U_{1} \left[ {1 + I_{e} (B_{R} - N)} \right] + pap^{ - \alpha } (B_{R} - M) \\ & \quad \left[ {1 + I_{e} \frac{{(B_{R} - M)}}{2}} \right] \\ \end{aligned} $$

where

$$ \begin{aligned} \,\, X_{L} & = \left\{ {p\int\limits_{{B_{R} }}^{{t_{1} }} {ap^{ - \alpha } \,dt} + pI_{e} \int\limits_{{B_{R} }}^{{t_{1} }} {\int\limits_{{B_{R} }}^{t} {ap^{ - \alpha } \,dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR} \\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} & = \left\{ {p\int\limits_{{B_{L} }}^{{t_{1} }} {ap^{ - \alpha } \,dt} + pI_{e} \int\limits_{{B_{L} }}^{{t_{1} }} {\int\limits_{{B_{L} }}^{t} {ap^{ - \alpha } \,dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

• Case 4.2.4.

Here,

$$ \begin{aligned} U_{2} & = \left[ {p\int\limits_{0}^{{t_{1} }} {ap^{ - \alpha } \,dt + pI_{e} \int\limits_{N}^{M} {\int\limits_{N}^{t} {ap^{ - \alpha } \,dudt} } } } \right]\left[ {1 + I_{e} (M - t_{1} )} \right] \\ & \quad + pR\left\{ {1 + I_{e} (M - N)} \right\} \\ \end{aligned} $$

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{4}^{\left( 2 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & \quad {\text{subject to}}\,\,N < t_{1} < M \le T \\ \end{aligned} $$

(2.29)

where

$$ X_{L} = U_{2} - \left( {C_{oR} + C_{holR} + C_{shoR} + OC_{LSR} } \right) $$

and

$$ X_{R} = U_{2} - \left( {C_{oL} + C_{holL} + C_{shoL} + OC_{LSL} } \right) $$

4.3: When $D\left( \cdot \right) = ae^{( - p/k)} ,\quad a,k > 0$

Here,

$$ U_{1} = p\int\limits_{0}^{M} {ae^{( - p/k)} \,dt + pI_{e} \int\limits_{N}^{M} {\int\limits_{N}^{t} {ae^{( - p/k)} \,dudt} } }+ pR\left\{ {1 + I_{e} (M - N)} \right\} $$

• Case 4.3.1.

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{1}^{\left( 3 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & \quad {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.30)

where

$$ \begin{aligned} X_{L} & = \left\{ {U_{1} - C_{pR} \left( {S + R} \right)} \right\}\left\{ {1 + I_{e} \left( {T - M} \right)} \right\} + ae^{( - p/k)} p\left( {t_{1} - M} \right)\left\{ {1 + \frac{1}{2}I_{e} \left( {t_{1} - M} \right)} \right\} \\ & \quad \left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR} \\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} & = \left\{ {U_{1} - C_{pL} \left( {S + R} \right)} \right\}\left\{ {1 + I_{e} \left( {T - M} \right)} \right\} + ae^{( - p/k)} p\left( {t_{1} - M} \right)\left\{ {1 + \frac{1}{2}I_{e} \left( {t_{1} - M} \right)} \right\} \\ & \quad \left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

• Case 4.3.2.

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{2}^{\left( 3 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.31)

$$ \begin{aligned} & \left\{ {C_{pL} \left( {S + R} \right) - U_{1} } \right\}\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} \\ & \quad = p\int\limits_{M}^{{B_{L} }} {ae^{( - p/k)} \,dt + pI_{e} \int\limits_{M}^{{B_{L} }} {\int\limits_{M}^{t} {ae^{( - p/k)} \,dudt} } } \\ \end{aligned} $$

and

$$ \begin{aligned} & \left\{ {C_{pR} \left( {S + R} \right) - U_{1} } \right\}\left\{ {1 + I_{p} \left( {B_{R} - M} \right)} \right\} \\ & \quad = p\int\limits_{M}^{{B_{R} }} {ae^{( - p/k)} \,dt + pI_{e} \int\limits_{M}^{{B_{R} }} {\int\limits_{M}^{t} {ae^{( - p/k)} \,dudt} } } \\ \end{aligned} $$

where

$$ \begin{aligned} X_{L} & = \left\{ {p\int\limits_{{B_{R} }}^{{t_{1} }} {ae^{( - p/k)} \,dt} + pI_{e} \int\limits_{{B_{R} }}^{{t_{1} }} {\int\limits_{{B_{R} }}^{t} {ae^{( - p/k)} \,dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR} \\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} & = \left\{ {p\int\limits_{{B_{L} }}^{{t_{1} }} {ae^{( - p/k)} \,dt} + pI_{e} \int\limits_{{B_{L} }}^{{t_{1} }} {\int\limits_{{B_{L} }}^{t} {ae^{( - p/k)} \,dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

• Case 4.3.3.

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{3}^{\left( 3 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & {\text{subject to}}\,\,0 < N < M \le t_{1} < T \\ \end{aligned} $$

(2.32)

$$ \begin{aligned} & C_{pL} \left( {S + R} \right)\left\{ {1 + I_{p} \left( {B_{L} - M} \right)} \right\} = U_{1} \left[ {1 + I_{e} (B_{L} - N)} \right] + pae^{( - p/k)} (B_{L} - M) \\ & \quad \left[ {1 + I_{e} \frac{{(B_{L} - M)}}{2}} \right] \\ \end{aligned} $$

and

$$ \begin{aligned} & C_{pR} \left( {S + R} \right)\left\{ {1 + I_{p} \left( {B_{R} - M} \right)} \right\} = U_{1} \left[ {1 + I_{e} (B_{R} - N)} \right] + pae^{( - p/k)} (B_{R} - M) \\ & \quad \left[ {1 + I_{e} \frac{{(B_{R} - M)}}{2}} \right] \\ \end{aligned} $$

where

$$ \begin{aligned} X_{L} &= \left\{ {p\int\limits_{{B_{R} }}^{{t_{1} }} {ae^{( - p/k)} \,dt} + pI_{e} \int\limits_{{B_{R} }}^{{t_{1} }} {\int\limits_{{B_{R} }}^{t} {ae^{( - p/k)} \,dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oR} - C_{holR} - C_{shoR} - OC_{LSR}\\ \end{aligned} $$

and

$$ \begin{aligned} X_{R} &= \left\{ {p\int\limits_{{B_{L} }}^{{t_{1} }} {ae^{( - p/k)} \,dt} + pI_{e} \int\limits_{{B_{L} }}^{{t_{1} }} {\int\limits_{{B_{L} }}^{t} {ae^{( - p/k)} dudt} } } \right\}\left\{ {1 + I_{e} \left( {T - t_{1} } \right)} \right\} \\ & \quad - C_{oL} - C_{holL} - C_{shoL} - OC_{LSL} \\ \end{aligned} $$

• Case 4.3.4.

Here,

$$ \begin{aligned} U_{2} & = \left[ {p\int\limits_{0}^{{t_{1} }} {ae^{( - p/k)} \,dt + pI_{e} \int\limits_{N}^{M} {\int\limits_{N}^{t} {ae^{( - p/k)} \,dudt} } } } \right]\left[ {1 + I_{e} (M - t_{1} )} \right] \\ & \quad + pR\left\{ {1 + I_{e} (M - N)} \right\} \\ \end{aligned} $$

$$ \begin{aligned}& {\text{Maximize}}\,\,Z_{4}^{\left( 3 \right)} \left( {S,R,t_{1} ,T} \right) = \left[ {\frac{{X_{L} }}{T},\frac{{X_{R} }}{T}} \right] \\ & \quad {\text{subject to}}\,\,N < t_{1} < M \le T \\ \end{aligned} $$

(2.33)

where

$$ X_{L} = U_{2} - \left( {C_{oR} + C_{holR} + C_{shoR} + OC_{LSR} } \right) $$

and

$$ X_{R} = U_{2} - \left( {C_{oL} + C_{holL} + C_{shoL} + OC_{LSL} } \right) $$

2.5 Numerical Examples

This section provides and solves three instances with the purpose of illustrating and validating the inventory model.

The solution procedure consists of applying the theory of interval numbers and two efficient and effective soft computing techniques: Particle swarm optimization constriction (PSO-CO) and weighted quantum particle swarm optimization (WQPSO). Both soft computing algorithms are programmed in C language. The computational experiments are done on a personal computer with the following technical characteristics: Intel Core-2-Duo, 2.5 GHz Processor, and LINUX environ. It is important to remark that Kennedy and Eberhart [27], Clerc and Kennedy [28], and Clerc [29] proposed the particle swarm optimization (PSO) and particle swarm optimization constriction (PSO-CO); and Sun et al. [30, 31] introduced weighted quantum particle swarm optimization (WQPSO). Sahoo et al. [32] introduced the definitions of interval order relations between two interval numbers with the aim of solving the maximization and minimization problems.

Example 1

Consider an inventory problem in which the demand function is given by $D = a - bp$ and the following parameters: $C_{oL} = \$ 195$, $C_{oR} = \$ 200$, $\theta = 0.1$, $a = 150$, $b = 0.7$, $\delta = 1.5$, $C_{hL} = \$ 1$, $C_{hR} = \$ 1.5$, $C_{bR} = \$ 10$, $C_{bL} = \$ 8$, $C_{pL} = \$ 22$, $C_{pR} = \$ 25$, $I_{e} = 0.12$, $I_{p} = 0.15$ $N = 0.16$, $M = 0.246$, $C_{lsL} = \$ 18$, $C_{lsR} = \$ 20$, $p = \$ 30$.

The solution is exhibited in Tables 2.2 and 2.3, where Table 2.2 shows the solution obtained by PSO-CO and Table 2.3 displays the solution determined by WQPSO.

Table 2.2 Optimal solution for Example 1 when demand function is modeled by $D = a - bp$ and PSO-CO is applied

Table 2.3 Optimal solution for Example 1 when demand function is expressed by $D = a - bp$ and WQPSO is used

Example 2

Consider an inventory system in which the demand function is as follows: $D = ap^{ - \alpha }$ and the following parameters: $C_{oL} = \$ 195$, $C_{oR} = \$ 200$, $\theta = 0.1$, $a = 150$, $\delta = 1.5$, $C_{hL} = \$ 1$, $C_{hR} = \$ 1.5$, $C_{bR} = \$ 10$, $C_{bL} = \$ 8$, $C_{pL} = \$ 22$, $C_{pR} = \$ 25$, $I_{e} = 0.12$, $I_{p} = 0.15$ $N = 0.16$, $M = 0.246$, $C_{lsL} = \$ 18$, $C_{lsR} = \$ 20$, $p = \$ 30$, $\alpha = 0.2$ (Tables 2.4 and 2.5).

Table 2.4 Optimal solution for Example 2 when demand function is given by $D = ap^{ - \alpha }$ and PSO-CO is utilized

Table 2.5 Optimal solution for Example 2 when demand function is given by $D = ap^{ - \alpha }$ and WQPSO is used

Example 3

Consider that the demand function is $D = ae^{{^{( - p/k)} }}$ and the following parameters: $C_{oL} = \$ 195$, $C_{oR} = \$ 200$, $\theta = 0.1$, $a = 150$, $\delta = 1.5$, $C_{hL} = \$ 1$, $C_{hR} = \$ 1.5$, $C_{bR} = \$ 10$, $C_{bL} = \$ 8$, $C_{pL} = \$ 22$, $C_{pR} = \$ 25$, $I_{e} = 0.12$, $I_{p} = 0.15$ $N = 0.16$, $M = 0.246$, $C_{lsL} = \$ 18$, $C_{lsR} = \$ 20$, $p = \$ 30$, $k = 40$ (Tables 2.6 and 2.7).

Table 2.6 Optimal solution for Example 3 when demand function is $D = ae^{( - p/k)}$, and PSO-CO is computed

Table 2.7 Optimal solution for Example 3 when demand function is $D = ae^{( - p/k)}$ and WQPSO is applied

2.6 Sensitivity Analysis

This section provides a sensitivity analysis, which is done, based on Example 1. The sensitivity analysis is made by varying the parameters by −20 to +20%. The results of the sensitivity analysis for Example 1 are shown in Table 2.8.

Table 2.8 Sensitivity analysis for Example 1 when $D\left( \cdot \right) = a - bp,\,a,\,b > 0$

From Table 2.8, the following interpretations are mentioned:

• With the increment in the value of replenishment cost $\left[ {C_{oL} ,C_{oR} } \right]$, the cycle length (T), the time at which the inventory level reaches zero ($t_{1}$), shortage level (R), and stock level (S) increase, but average profit decreases.

• When the holding cost $\left[ {C_{hL} ,C_{hR} } \right]$ increases, then the cycle length (T), the time at which the inventory level reaches zero ($t_{1}$), stock level (S), and average profit decrease, but shortage level (R) increases.

• With the increment in the value of shortage cost $\left[ {C_{bL} ,C_{bR} } \right]$, the time at which the inventory level reaches zero ($t_{1}$) and stock level (S) increase, but the shortage level (R), the cycle length (T), and the average profit decrease.

• When the value of purchasing cost $\left[ {C_{pL} ,C_{pR} } \right]$ increases, then the shortage level (R), the cycle length (T), the time at which the inventory level reaches zero ($t_{1}$), stock level (S) and the average profit decrease.

• When the scale parameter (a) of demand increases, then the cycle length (T) and the time at which the inventory level reaches zero ($t_{1}$) decrease, whereas the shortage level (R), the stock level (S), and the average profit increase.

• When the price elasticity parameters (b) of demand increases, then the shortage level (R), the stock level (S), and the average profit decrease, whereas the cycle length (T) and the time at which the inventory level reaches zero ($t_{1}$) increase.

• With the increment in the value of the deterioration rate $\left( \theta \right)$, the cycle length (T), stock level (S), the average profit, and the time at which the inventory level reaches zero ($t_{1}$) decrease, but the shortage level (R) increases.

• When the value of the backlogging parameter $\delta$ increases, then the shortage level (R), the cycle length (T) and the average profit decrease, but the time at which the inventory level reaches zero ($t_{1}$) and stock level (S) increase.

• With the increment in the value of opportunity cost $[C_{lsL} ,C_{lsR} ]$, then the shortage level (R), the cycle length (T), and the average profit decrease, but the time at which the inventory level reaches zero ($t_{1}$) and stock level (S) increase.

• With the increment in the value of selling price (p), then the shortage level (R), the cycle length (T), the time at which the inventory level reaches zero ($t_{1}$), stock level (S), and the average profit increase.

2.7 Conclusion

This paper develops an inventory model for deteriorating items with interval-valued inventory costs, partial backlogging, and price-dependent demand under two-level credit policy. In order to make a more realistic scenario, the shortages are permitted, and these are partially backlogged. The proposed inventory model is very helpful for retail and manufacturing industries in developing countries where credit policy plays a significant role in decision-making. This research work aims to find the retailer’s optimal replenishment policy that maximizes the total profit of the system. To solve the inventory model, two soft computing techniques are used: the PSO-CO and the WQPSO. The efficiency and effectiveness of the proposed inventory model are validated with numerical examples and a sensitivity analysis.

Finally, this research can be extended by considering: (1) stock-dependent demand, (2) inventory costs represented by a fuzzy number, (3) finite-time horizon, (4) inflation, and (5) an integrated supply chain model with two or more players with the coordination between the players, among others. These are some interesting and challenge research lines to explore by academicians and researchers.