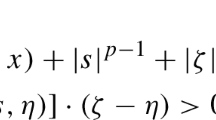Nonlinear Degenerate Parabolic Equations with a Singular Nonlinearity

Abstract

In this paper, we study the existence and regularity results for some parabolic equations with degenerate coercivity, and a singular right-hand side. The model problem is

$$ \left \{ \textstyle\begin{array}{l@{\quad }l} \frac{\partial u}{\partial t}-\text{div} \left ( \frac{\left (1+\vert \nabla u\vert ^{-\Lambda }\right )\vert \nabla u\vert ^{p-2}\nabla u}{(1+\vert u\vert )^{\theta }} \right )=\frac{f}{(e^{u}-1)^{\gamma }} & \text{in}\;\;Q_{T}, \\ u(x,0)=0 & \text{on}\;\; \Omega , \\ u =0 & \text{on}\;\; \partial Q_{T}, \end{array}\displaystyle \right . $$

(0.1)

where $\Omega$ is a bounded open subset of $\mathbb{R}^{N}$ $N\geq 2$, $T>0$, $\Lambda \in [0,p-1)$, $f$ is a non-negative function belonging to $L^{m}(Q_{T})$, $Q_{T}=\Omega \times (0,T)$, $\partial Q_{T}=\partial \Omega \times (0,T)$, $0\leq \theta < p-1+\frac{p}{N}+\gamma (1+\frac{p}{N})$ and $0\leq \gamma < p-1$.

1 Introduction

Let $\Omega$ is a bounded open subset of $\mathbb{R}^{N}$ ($N\geq 2$), $Q_{T}$ is the cylinder $\Omega \times (0,T)$ ($T>0$), $\partial Q_{T}$ is the lateral surface $\partial \Omega \times (0,T)$. We consider the following double nonlinear anisotropic singular parabolic problem

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{\partial u}{\partial t}+Bu =g(u)f & \text{in}\;\;Q_{T}, \\ u(x,0)=0 & \text{on}\;\; \Omega , \\ u =0 & \text{on}\;\; \partial Q_{T}, \end{array}\displaystyle \right . $$

(1.1)

where $Bu=-\text{div}(b(x,t,u,\nabla u))$, $f$ is a non-negative function belonging to a suitable Lebsgue space $L^{m}(Q_{T})$ ($m\geq 1$). Here, we suppose that $b : \Omega \times \mathbb{R}\times \mathbb{R}^{N}\rightarrow \mathbb{R}$ is a Carathéodory function, and satisfying for almost every $(x,t)$ in $Q_{T}$, for every $z\in \mathbb{R}$, for all $\xi ,\eta \in \mathbb{R}^{N}$ the following

$$\begin{aligned} & b(x,t,z,\xi )\cdot \xi \geq \frac{\alpha \vert \xi \vert ^{p}}{(1+\vert z\vert )^{\theta}}, \end{aligned}$$

(1.2)

$$\begin{aligned} &0\leq \theta < p-1+\frac{p}{N}+\gamma (1+\frac{p}{N}), \end{aligned}$$

(1.3)

$$\begin{aligned} & \vert b(x,t,z,\xi )\vert \leq a(x,t)+\vert z\vert ^{p-1}+\vert \xi \vert ^{p-1}, \end{aligned}$$

(1.4)

$$\begin{aligned} & (b(x,t,z,\xi )-b(x,t,z,\eta ))\cdot (\xi -\eta )>0,\quad \xi \neq \eta , \end{aligned}$$

(1.5)

where $\alpha$, $\beta$ are strictly positive real numbers and $a$ is a given positive function in $L^{p'}(Q_{T})$ with $\frac{1}{p}+\frac{1}{p'}=1$. Moreover, $g : [0,+\infty ) \rightarrow [0,+\infty )$ is a continuous and possibly singular function with $g(0)\neq 0$ which it is finite outside the origin and such that

$$ \exists \; c>0:\quad g(z)\leq \frac{c}{z^{\gamma}}\quad \text{for all}\; z>0, $$

(1.6)

where $0\leq \gamma < p-1$.

In the uniform ellipticity and non singular case (i.e. $\theta =0$ and $\gamma =0$, it is proved the existence results for the problems (1.1) in [1–5, 7, 8, 28–30] when $f\in L^{m}(Q_{T})$ or $f$ is a bounded Radon measure on $Q_{T}$. We cite the paper [16], and the references therein, when $p=2$, $\gamma =0$, $0\leq \theta <1+\frac{2}{N}$ and $f\in L^{m}(Q_{T})$, where $m\geq 1$. In the case $\theta =0$ and $p\geq 2$, the existence and regularity solution have been treated in [11]. Problem (1.1), in the coercive case, has been treated in [9], they have proved the existence and regularity of solutions to problem

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{\partial u}{\partial t}-\text{div}(\vert \nabla u\vert ^{p-2} \nabla u)=\frac{f}{u^{\gamma}} & \text{in}\;\;Q_{T}, \\ u(x,0)=u_{0}(x) & \text{on}\;\; \Omega , \\ u =0 & \text{on}\;\; \partial Q_{T}, \end{array}\displaystyle \right . $$

with $\gamma >0$, $p\geq 2$, $f>0$, $f\in L^{m}(Q_{T})$, $m\geq 1$ and $u_{0}\in L^{\infty}(\Omega )$. If $\gamma =0$, the problem (1.1) is studied in [12, 19, 25].

Finally, concerning the singular model case the authors in [14] studied existence and regularity of problem

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{\partial u}{\partial t}-\text{div}(b(x,t,u,\nabla u))+\vert u \vert ^{s-1}u=g(u) f& \text{in}\;\;Q_{T}, \\ u =0 & \text{on}\;\; \partial Q_{T}, \\ u(x,0) =0 & \text{in}\;\; \Omega , \end{array}\displaystyle \right . $$

where $f\in L^{m}(Q_{T})$ ($m\geq 1$), $a: Q_{T}\times \mathbb{R}\times \mathbb{R}^{N}\rightarrow \mathbb{R}$ is a carathéodory function satisfying for a.e $(x,t)\in Q_{T}$, $\forall z\in \mathbb{R}$, $\forall \xi \in \mathbb{R}^{N}$

$$ b(x,t,z,\xi ).\xi \geq \frac{\alpha \vert \xi \vert ^{p}}{(1+\vert z\vert )^{\theta (p-1)}} \quad \text{with} \quad 0\leq \theta < 1, $$

and the singular term $g$ satisfying (1.6) with $0<\gamma <1$. The corresponding results for parabolic equations with singularities have been developed in [13, 15, 17]. The existence and regularity results for weak solution of degenerate elliptic equation with singularities data have been proved in [18, 20, 21, 31–33].

Our main motive in this article is to investigate the results of [25] in the framework of the operator non-coercive $B(u)$. To reach this goal, we will face the following difficulties. First, let us note that (1.1) can be singular on the right-hand side in the following sense: the solution is required to be zero on the boundary of the domain but, simultaneously, the right- hand side of (1.1) could blow up. Another important feature is the lack of coercivity for positive $\theta$, the operator $B(u)$ is not coercive as $u$ becomes large. Due to the lack of coercivity, the classical methods can not be applied even if the data $g(u)f$ are sufficiently regular (see [27]). We will overcome these two difficulties by approximation, truncating the degenerate coercivity of the operator term and the singularity of the right-hand side (see problems (3.1)). We will prove by Schauder’s theorem that these problems admit a bounded finite energy solution $u_{n}$.

The following lemma is useful when proving the boundedness of the solution $u_{n}$ of problem (3.1).

Lemma 1.1

See [6]

Let $M_{1}$, $\nu$, $\rho$, $\vartheta$, $k_{0}$ be real positive numbers, where $\vartheta >1$ and $\rho \in [0,1)$. Let $\Lambda : \mathbb{R}_{+}\rightarrow \mathbb{R}_{+}$ be a decreasing function such that

$$ \Lambda (h)\leq \frac{M_{1}k^{\nu \rho}}{(h-k)^{\nu}}[\Lambda (k)]^{ \vartheta},\quad \forall h>k\geq k_{0}. $$

Then there exists $l>0$ such that $\Lambda (l)=0$.

Next, we will review the results of the renowned Gagliardo-Nirenberg embedding theorem.

Lemma 1.2

See [10]

Let $v\in L^{\kappa}(0,T;W_{0}^{1,\kappa}(\Omega ))\cap L^{\infty}(0,T;L^{ \varrho}(\Omega ))$, $\kappa ,\varrho \geq 1$. Then $v$ belongs to $L^{q}(Q_{T})$, where $q= \kappa \frac{N+\varrho}{N}$, and there exists a positive constant $M_{2}$ depending only on $N$, $\kappa$, $\varrho$ such that

$$\begin{aligned} &\int _{Q_{T}}\vert v(x,t)\vert ^{q}dxdt\leq M_{2} \Vert v\Vert _{L^{\infty}(0,T;L^{\varrho}(\Omega ))}^{ \frac{ \kappa}{N}}\int _{Q_{T}}\vert \nabla v(x,t) \vert ^{\kappa}dxdt. \end{aligned}$$

(1.7)

For any $q>1$, $q'=\frac{q}{q-1}$ is the Hölder conjugate of $q$. For fixed $k>0$ we will use of the truncation $T_{k}$ defined as $T_{k}(s)=\max (-k,\min (k,s))$ and $G_{k}(s)=s-T_{k}(s)$. We will also use the following function

$$ \Xi _{\lambda}(s)= \textstyle\begin{cases} 1 ,& \text{if}\;\; s\leq \lambda , \\ \frac{\lambda -s}{\lambda}, & \text{if}\;\; \lambda < s< 2\lambda , \\ 0, & \text{if}\;\; s\geq 2\lambda . \end{cases} $$

(1.8)

For the sake of completeness, we recall a well-known inequality that will be useful in what follows

$$\begin{aligned} &\forall a>0,\forall \mu >0, \, \exists C(\mu ,a)>0 \;:\quad (1+t)^{ \mu}\leq Ct^{\mu}, \quad \forall t\in [a,+\infty ). \end{aligned}$$

(1.9)

2 Statements of Results

We first define the notion of a weak solution to (1.1) as follows:

Definition 2.1

We say that $u\in L^{1}(0,T;W_{0}^{1,1}(\Omega ))$ is a weak solution of problem (1.1), if $b(x,t,u,\nabla u)\in (L^{1}(Q_{T}))^{N}$, $g(u)f\in L^{1}(Q_{T})$ and the equality

$$ \int _{Q_{T}} \frac{\partial u}{\partial t}\varphi dxdt+\int _{Q_{T}}b(x,t,u, \nabla u).\nabla \varphi dxdt=\int _{Q_{T}} g(u)f\varphi dxdt, $$

(2.1)

for every $\varphi \in C^{\infty}([0,T]\times \overline{\Omega})$ which is zero in a neighborhood of $\partial Q_{T}$ and $\Omega \times \{T\}$.

The first theorem we state concerns with the existence of $L^{\infty}$-solutions to problem (1.1), where $f\in L^{m}(Q_{T})$ with $m>\frac{N}{p}+1$.

Theorem 2.2

Assume that (1.2)-(1.6) hold true. Let $f\in L^{m}(Q_{T})$ with $m>\frac{N}{p}+1$. Then there exists $u\in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})$ a weak solution to problem (1.1).

Remark 1

We apply Lemma 1.1, which requires the assumption $p\geq 2$, to obtain the $L^{\infty}$-estimates for $u_{n}$ the solutions of (3.1). In the case $p=2$, $\gamma =0$ the result of Theorem 2.2 coincides with the classical boundedness results for degenerate parabolic equations ([16], Theorem 1.1), furthermore if $p> 2$ the results of Theorem 2.2 are similar than the regularity results of [14, 25]. To obtain the $L^{\infty}$-estimate, the conditions (1.4) and (1.5) are unnecessary. However, such conditions are needed to prove the existence of $u_{n}$ solution of problem (3.1).

In the following theorem we give the result of existence and regularity in the case of exact values of the summability exponent $m=\frac{N}{p}+1$.

Theorem 2.3

Suppose that assumptions (1.2)-(1.6) hold, $f\in L^{m}(Q_{T})$ with $m=\frac{N}{p}+1$. Then, for every $r\in [p,+\infty )$ there exists $u\in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{r}(Q_{T})$ a weak solution to problem (1.1).

Remark 2

Theorem 2.3 gives the result in the limit case $m=\frac{N}{p}+1$ for parabolic equations. As far as I know, the first time this case was addressed in the article [16] with $p=2$ and $\gamma =0$. The result of Theorem 2.3 has been obtained in [14, 25].

The next result deals with a given $m < \frac{N}{p} + 1$, which ensures the existence of solutions in $L^{p}(0,T;W_{0}^{1,p}(\Omega )) \cap L^{\delta}(Q_{T})$.

Theorem 2.4

Let us assume that (1.2)-(1.6) hold true, and that $f\in L^{m}(Q_{T})$, with

$$ m_{1}=\frac{p(N+\theta +2)}{(p-1)N+2p-(N-p)\theta +N\gamma}\leq m< \frac{N}{p}+1. $$

(2.2)

Then, there exists $u\in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\delta}(Q_{T})$ a weak solution to problem (1.1), such that

$$ \delta =\frac{m[p+N(p-1-\theta )+\gamma (N+p)]}{N+p-pm}. $$

(2.3)

Remark 3

The condition (1.3) implies that the assumption (2.2) is well defined. By (1.3) and (2.2), we have $\delta >p$, since

$$\begin{aligned} \text{(1.3)}&\Leftrightarrow \frac{p(N+\theta +2)}{(p-1)N+2p-(N-p)\theta +N\gamma}> \frac{p(N+p)}{p+N(p-1-\theta )+\gamma (N+p)+p^{2}} \\ &\Rightarrow m>\frac{p(N+p)}{p+N(p-1-\theta )+\gamma (N+p)+p^{2}} \\ &\Rightarrow \delta >p. \end{aligned}$$

If $0\leq \theta <\frac{2}{N-1}+\gamma \frac{N}{(N-1)}$, then $m_{1}< p'$, so $f\notin L^{p'}(0,T;W^{-1,p'}(\Omega ))$. If $\frac{2}{N-1}+\gamma \frac{N}{(N-1)}\leq \theta < p-1+\frac{p}{N}+ \gamma (1+\frac{p}{N})$, then $m_{1}\geq p'$, so $f\in L^{p'}(0,T;W^{-1,p'}(\Omega ))$.

The first result deals with the case when the summability of $f$ gives the existence of solution $u$ belong to $L^{q}(0,T;W_{0}^{1,q}(\Omega ))$, with $p-1< q< p$.

Theorem 2.5

If hypotheses (1.2)-(1.6) hold and $f\in L^{m}(Q_{T})$ with $m>1$, such that

$$ m_{2}=\frac{N+\theta +2}{(p-1)N+p+1-\theta (N-1)+\gamma (N+p-1)}< m< m_{1}, $$

(2.4)

then there exists $u\in L^{q}(0,T;W_{0}^{1,q}(\Omega ))\cap L^{\delta}(Q_{T})$ a weak solution to problem (1.1), such that

$$ q= \frac{m[N(p-\theta -1)+p+\gamma (N+p)]}{N+1-(\theta +1)(m-1)+m\gamma}, $$

(2.5)

where $\delta$ as defined in (2.3).

Remark 4

The hypothesis (2.5) is meaningful, because

$$ m_{2}< m_{1}\Leftrightarrow \theta < p-1+\frac{p}{N}+\gamma \left (1+ \frac{p}{N}\right ). $$

Notice that the inequality (2.4) guarantees that $p-1< q< p$. In Theorem 2.5, we also suppose $m>1$,

$$ m_{2}< 1 \Leftrightarrow 0\leq \theta < p-1+\frac{p}{N}+\gamma \left (1+ \frac{p}{N}\right )-\frac{N+\gamma +1}{N}. $$

If $\gamma =0$; the result of Theorem 2.5 is similar that of ([25], Theorem 2.5).

Remark 5

It will be noted to the reader that the choice of the test functions in the proof of the a priori estimates allowed us to widen the interval of variation of $\gamma$ and $\theta$ compared to that in [14], with the same regularity of the solution. If we compare the results of theorems 2.2-2.5 with those of theorems in [25], we can easily see that the singular term allowed us to widen the interval of variation of $\theta$ compared to that the assumption (3) in [25].

3 Approximating Problems

Let us first consider the following approximation problems

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{\partial u_{n}}{\partial t}-\text{div}(b(x,t,T_{n}(u_{n}), \nabla u_{n}))=g_{n}(u_{n})f_{n} & \text{in}\;\;Q_{T}, \\ u_{n}(x,0)=0 & \text{on}\;\; \Omega . \\ u_{n} =0 & \text{on}\;\; \partial Q_{T}, \end{array}\displaystyle \right . $$

(3.1)

where $f_{n}\in L^{\infty}(Q_{T})$ (for example, $f_{n}=T_{n}(f)$), such that

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \Vert f_{n}\Vert _{L^{m}(Q_{T})}\leq \Vert f\Vert _{L^{m}(Q_{T})} \leq C,& \\ f_{n}\rightarrow f\;\; \text{strongly in }\; L^{m}(Q_{T}), \quad m \geq 1 , \end{array}\displaystyle \right . $$

(3.2)

and, we define $g(0)=\lim _{z\rightarrow 0}g(z)$, we set

$$ g_{n}(z)= \textstyle\begin{cases} T_{n}(g(z))& \text{for}\;\; z> 0 , \\ \min \{n,g(0)\} & \text{otherwise}. \end{cases} $$

Using (1.6), we have for all $z>0$

$$\begin{aligned} \quad g_{n}(z)=T_{n}(g(z))\leq g(z)\leq \frac{c}{z^{\gamma}}. \end{aligned}$$

(3.3)

Lemma 3.1

Assume that (1.2), (1.5) and (1.6) hold true. Then, the approximating problem (3.1) has a non-negative solution $u_{n}$, such that

$$ u_{n}\in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap C([0,T];L^{2}(\Omega )), \quad \frac{\partial u_{n}}{\partial t}\in L^{p'}(0,T;W_{0}^{-1,p'}( \Omega )), $$

and satisfying the weak formulation

$$\begin{aligned} &\int _{0}^{T}\Big\langle \frac{\partial u_{n}}{\partial t},\varphi \Big\rangle dt+\int _{Q_{T}}b(x,t,T_{n}(u_{n}),\nabla u_{n}).\nabla \varphi dxdt \\ &\quad =\int _{Q_{T}}g_{n}(u_{n})f_{n}\varphi dxdt, \end{aligned}$$

(3.4)

for all $n\in \mathbb{N}$ fixed and for every $\varphi \in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})$, where

$$ \Big\langle \frac{\partial u_{n}}{\partial t},\varphi \Big\rangle = \int _{\Omega}\frac{\partial u_{n}}{\partial t}\varphi dx. $$

Proof

Let $n\in \mathbb{N}$ and $v\in L^{p}(Q_{T})$ be fixed. Consider the nonlinear parabolic problem

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{\partial w}{\partial t}-\text{div} (b(x,t,T_{n}(w),\nabla w))=g_{n}(v)f_{n} & \text{in}\;\;Q_{T}, \\ w(x,0)=0 & \text{on}\;\; \Omega , \\ w =0 & \text{on}\;\; \partial Q_{T}, \end{array}\displaystyle \right . $$

(3.5)

it is clear that the problem (3.5) has a unique solution $w$ with

$$ w\in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})\;\; \text{and}\;\; \frac{\partial w}{\partial t}\in L^{p'}(0,T;W_{0}^{-1,p'}( \Omega ))+L^{1}(Q_{T}). $$

Since the right-hand side on (3.5) belongs to $L^{\infty}(Q_{T})$ see for instance [23, 24]. In particular, it is well defined a map $P: L^{p}(Q_{T})\rightarrow L^{p}(Q_{T})$ where $P(v)=w$. By the boundedness of the sequence $\{g_{n}(v)f_{n}\}_{n}$ in $L^{\infty}(Q_{T})$, we have that $w\in L^{\infty}(Q_{T})$ (see for example [14]), then, there exists $C_{\infty}>0$, independents of $v$, $w$ (but possibly depending in $n$), such that

$$ \Vert w\Vert _{L^{\infty}(Q_{T})}\leq C_{\infty}. $$

(3.6)

Our aim is to prove the existence of fixed point of the map $P$. Using $w$ as test function in (3.5), one gets

$$\begin{aligned} &\frac{1}{2}\int _{\Omega}\vert w(T)\vert ^{2}dx+\int _{Q_{T}}b(x,t,T_{n}(w), \nabla w).\nabla w dxdt \\ &\quad =\int _{Q_{T}}g_{n}(v)f_{n}wdxdt. \end{aligned}$$

(3.7)

By (1.2), (1.6) and dropping a positive term on the left-hand side in (3.7)

$$\begin{aligned} &\alpha \int _{Q_{T}} \frac{\vert \nabla w\vert ^{p}}{(1+\vert T_{n}(w)\vert )^{\theta}}dxdt \leq n^{\gamma +1}\int _{Q_{T}}\vert w\vert dxdt. \end{aligned}$$

(3.8)

Using the Hölder’s inequality on the right-hand side in (3.8), we have

$$\begin{aligned} \int _{Q_{T}}\vert \nabla w\vert ^{p}dxdt&\leq \frac{C_{1}}{\alpha}n^{ \gamma +1}(1+n)^{\theta}\vert Q_{T}\vert ^{\frac{1}{p'}}\left (\int _{Q_{T}} \vert w\vert ^{p}dxdt\right )^{\frac{1}{p}} \end{aligned}$$

Poincaré inequality imply

$$\begin{aligned} &\Vert w\Vert _{L^{p}(Q_{T})}\leq C(n,\vert Q_{T}\vert ), \end{aligned}$$

(3.9)

for some constant $C(n,\vert Q_{T}\vert )$ independent of $v$ and $w$ (possible depending on $n$). Let $B$ is a ball of $L^{p}(Q_{T})$ of radius $C(n,\vert Q_{T}\vert )$ is invariant for the map $P$. Now, we prove that the map $P$ is continuous in $B$. Let $\{v_{h}\}_{n}$ be a bounded sequence in $B$. By (3.9) there exist a subsequence of $\{v_{h}\}_{n}$ still denoted by $\{v_{h}\}_{n}$, and a measurable function $v$ belonging to $L^{p}(Q_{T})$, such that

$$\begin{aligned} v_{h}\rightarrow v\quad \text{strongly in }\; L^{p}(Q_{T}). \end{aligned}$$

(3.10)

Let us choose $w_{h}$ as a test function in the weak formulation of the problem solved by $w_{h}$, (3.8) implies that

$$\begin{aligned} \int _{0}^{T}\Vert \nabla w_{h}\Vert _{L^{p}(\Omega )}^{p}dt\leq C_{4} \int _{0}^{T}\left (\int _{\Omega}\vert w_{h}\vert ^{p}dx\right )^{ \frac{1}{p}}dt. \end{aligned}$$

(3.11)

Since the ball of $L^{p}(Q_{T})$ is invariant for $P$, we have $w_{h}$ belong to $B$ and so, from the inequality (3.11), we obtain that $w_{h}$ is bounded in $L^{p}(0,T;W_{0}^{1,p}(\Omega ))$. The growth assumption (1.4), implies

$$\begin{aligned} \int _{Q_{T}}\vert b(x,t,w_{h},\nabla w_{h})\vert ^{p'}dxdt&\leq \int _{Q_{T}}\big[\vert a(x,t)\vert +\vert w_{h}\vert ^{p-1}+\vert \nabla w_{h}\vert ^{p-1}\big]^{\frac{p}{p-1}}dxdt \\ & \leq \Vert k\Vert _{L^{p'}(Q_{T})}^{p'}+\Vert w_{h}\Vert _{L^{p}(Q_{T})}^{p}+ \Vert w_{h}\Vert _{L^{p}(0,T;W_{0}^{1,p}(\Omega ))}^{p} \\ &< +\infty . \end{aligned}$$

Using the previous inequality with (3.5), and the fact that $g_{n}(v)f_{n}\in L^{1}(Q_{T})$ we have $\frac{\partial w_{h}}{\partial t}$ is bounded in $L^{p'}(0,T;W_{0}^{-1,p'}(\Omega ))+L^{1}(Q_{T})$. As a result of the Corollary 4 in [34], we can conclude that $w_{h}$ is relatively strongly compact in $L^{1}(Q_{T})$. Thus, there exists a subsequence of $w_{h}$ still denoted by $w_{h}$, and a measurable function $w$ belonging to $L^{1}(Q_{T})$ such that

$$\begin{aligned} & w_{h}\rightarrow w\quad \text{a.e in }\; L^{1}(Q_{T}). \end{aligned}$$

(3.12)

By (3.9), (3.12) and Lebesgue Theorem we have that $w_{h}$ converges strongly to $w$ in $L^{p}(Q_{T})$, and so $P$ is compact.

Now we prove that $P$ is continuous. Let $w_{h}=P(v_{h})$, (3.10) implies that $v_{h}\rightarrow v$ a.e in $Q_{T}$, hence $g_{n}(v_{h})f_{n}$ converges to $g_{n}(v)f_{n}$ a.e in $Q_{T}$ and by the dominated convergence theorem one has that $g_{n}(v_{h})f_{n}$ converge strongly to $g_{n}(v)f_{n}$ in $L^{p}(Q_{T})$. Hence, by uniqueness, one deduce that $w_{h}=P(v_{h})$ converges to $w=P(v)$ in $L^{p}(Q_{T})$. This gives the continuity of $S$. Using Schauder’s fixed point theorem for every fixed $n$, we have there exist $u_{n}$ in $L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap C([0,T];L^{2}(\Omega ))$ and $\frac{\partial u_{n}}{\partial t}\in L^{p'}(0,T;W_{0}^{-1,p'}( \Omega ))+L^{1}(Q_{T})$, such that $u_{n}=P(u_{n})$.

Choosing $\varphi =-u_{n}^{-}=-u_{n}\chi _{\{u_{n}\leq 0\}}$, where $\chi _{\{u_{n}\leq 0\}}$ denotes the characteristic function of $\{(x,t)\in Q_{T}: u_{n}(x,t)\leq 0\}$ as a test function in (3.1). Using (1.2), and recalling that $g_{n}(u_{n})f_{n}$ is nonnegative, we obtain

$$\begin{aligned} &-\frac{1}{2}\int _{\Omega}\vert u_{n}^{-}\vert ^{2}dx- \frac{\alpha}{(1+n)^{\theta}}\int _{Q_{T}}\vert \nabla u_{n}^{-} \vert ^{p}dxdt\geq - \int _{Q_{T}}g_{n}(u_{n})f_{n}u_{n}^{-}dxdt\geq 0, \end{aligned}$$

dropping the term $-\frac{1}{2}\int _{\Omega}\vert u_{n}^{-}\vert ^{2}dx$, we have

$$\begin{aligned} -\int _{Q_{T}}\vert \nabla u_{n}^{-}\vert ^{p}dxdt\geq 0, \end{aligned}$$

so that $\Vert u_{n}^{-}\Vert _{L^{p}(0,T;W_{0}^{1,p}(\Omega ))}=0$, thus $u_{n}\geq 0$ almost everywhere in $Q_{T}$. □

4 A Priori Estimates

We shall denote by $C_{i}, i=1,...,N$ various constants depending only on the structure of $p$, $\theta$, $\gamma$, $T$, $|\Omega |$. Let $u_{n}\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap C([0,T];L^{2}(\Omega ))$ be a solution to problem (3.1). In this section, we prove some uniform estimates for the sequence $\{u_{n}\}_{n}$ and $\big\{\frac{\partial u_{n}}{\partial t}\big\}_{n}$.

Lemma 4.1

Assume that (1.2)-(1.6), $p-2\leq \gamma <1$ hold true. Let $f\in L^{m}(Q_{T})$ with $m>\frac{N}{p}+1$. Then, the sequence $\{u_{n}\}_{n}$ is bounded in $L^{\infty}(Q_{T})\cap L^{p}(0,T;W_{0}^{1,p}(\Omega ))$ and $\big\{\frac{\partial u_{n}}{\partial t}\big\}_{n}$ is bounded in $L^{p'}(0,T;W^{-1,p'}(\Omega ))+L^{m}(Q_{T})$.

Proof

For every $\tau \in (0,T]$, we take $\varphi (u_{n})=[(1+u_{n})^{p-1}-1]G'_{k}(u_{n})\chi _{(0,\tau )}$ as a test function in (3.4), we use the assumption (1.2), and the fact that

$$\begin{aligned} &\Phi (u_{n})=\int _{0}^{u_{n}}\left ( (1+y)^{p-1}-1\right ) G'_{k}(y)dy \geq \frac{1}{p} G_{k}(u_{n})^{p}G'_{k}(u_{n}), \end{aligned}$$

we obtain

$$\begin{aligned} &\int _{\Omega} \Phi (u_{n}) dx+\alpha (p-1)\int _{0}^{\tau}\int _{ \Omega} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta}}(1+ u_{n})^{p-2}G'_{k}(u_{n}) dxdt \\ &\quad \leq \int _{0}^{\tau}\int _{\Omega} f_{n}g_{n}(u_{n})[(1+ u_{n}) ^{p-1}-1]G'_{k}(u_{n}) dxdt. \end{aligned}$$

By (3.3), (1.9), $(1+u_{n})^{p-1}-1\leq (1+u_{n})^{p-1}$ and the fact that

$$\begin{aligned} &\int _{Q_{T}\cap \{u_{n}=0\}}f_{n}g_{n}(u_{n})[(1+ u_{n}) ^{p-1}-1]G'_{k}(u_{n}) dxdt \\ &\quad \leq \int _{Q_{T}}f_{n}\lim _{z\rightarrow 0}g(z)[(1+ 0) ^{p-1}-1]G'_{k}(0)dxdt=0, \end{aligned}$$

we have

$$\begin{aligned} &\int _{\Omega} \Phi (u_{n}) dx+\alpha (p-1)\int _{0}^{\tau}\int _{ \Omega} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta}}(1+ u_{n})^{p-2}G'_{k}(u_{n}) dxdt \\ &\quad \leq \int _{Q_{T}\cap \{u_{n}>0\}} f_{n} \frac{(1+ u_{n}) ^{p-1}}{u_{n}^{\gamma}}G'_{k}(u_{n}) dxdt \\ &\qquad +\int _{Q_{T}\cap \{u_{n}=0\}}f_{n} g_{n}(u_{n})[(1+ u_{n}) ^{p-1}-1]G'_{k}(u_{n}) dxdt \\ &\quad \leq \int _{0}^{T}\int _{\Omega} f_{n}(1+ u_{n}) ^{p-1-\gamma}G'_{k}(u_{n}) dxdt. \end{aligned}$$

Using Hölder’s inequality on the right-hand side of the previous inequality, (3.2) and the fact that $1+ u_{n}\leq 2 (k+ G_{k}(u_{n}))$ as $k\geq 1$, one has

$$\begin{aligned} &\int _{E_{k,n}(\tau )} G_{k}(u_{n}(\tau ))^{p} dx+\int _{0}^{\tau} \int _{E_{k,n}(t)} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta -p+2}} dxdt \\ &\quad \leq C_{1}\Vert f\Vert _{L^{m}(Q_{T})} \left (\int _{0}^{T} \int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{(p-1-\gamma )m'} dxdt\right )^{ \frac{1}{m'}}, \end{aligned}$$

where $E_{k,n}(t)=\{x\in \Omega : u_{n}(x,t)> k\}$, $t\in (0,T)$. Hence

$$\begin{aligned} &\Vert G_{k}(u_{n})\Vert _{L^{\infty}(0,T;L^{p}(E_{k,n}))}^{p}+\int _{0}^{T} \int _{E_{k,n}(t)} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta -p+2}} dxdt \\ &\quad \leq C_{1}\Vert f\Vert _{L^{m}(Q_{T})} \left (\int _{0}^{T} \int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{(p-1-\gamma )m'} dxdt\right )^{ \frac{1}{m'}}. \end{aligned}$$

(4.1)

The proof is divided into two cases.

Case 1: Suppose that

$$ p-2< \theta < p-1+\frac{p}{N}+\gamma (1+\frac{p}{N}). $$

For all $1\leq p-1<\sigma <p$, Writing

$$ \int _{Q_{T}}\vert \nabla G_{k}(u_{n})\vert ^{\sigma}dxdt=\int _{Q_{T}} \frac{\vert \nabla u_{n}\vert ^{\sigma}}{(1+ u_{n})^{\frac{(\theta -p+2)\sigma}{p}}} (1+ u_{n})^{\frac{(\theta -p+2)\sigma}{p}}dxdt. $$

Using (3.2), (4.1) and Hölder’s inequality, we have

$$\begin{aligned} &\int _{Q_{T}}\vert \nabla G_{k}(u_{n})\vert ^{\sigma}dxdt \\ &\quad \leq \left (\int _{0}^{T}\int _{E_{k,n}(t)} \frac{\vert \nabla G_{k}(u_{n})\vert ^{p}}{(1+ u_{n})^{\theta -p+2}}dxdt \right )^{\frac{\sigma}{p}} \\ &\qquad \times \left (\int _{0}^{T}\int _{E_{k,n}(t)}(1+ u_{n})^{ \frac{(\theta -p+2)\sigma}{p-\sigma}}dxdt\right )^{\frac{p-\sigma}{p}} \\ &\quad \leq C_{2}\left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{m'(p-1- \gamma )}dxdt\right )^{\frac{\sigma}{pm'}} \\ &\qquad \times \left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{ \frac{(\theta -p+2)\sigma}{p-\sigma}}dxdt\right )^{\frac{p-\sigma}{p}}. \end{aligned}$$

(4.2)

Choosing $\sigma =\frac{2pN-2N+p^{2}-N\theta}{N+p}$, this choice of $\sigma$, implies that $p-1<\sigma <p$ and $0<\frac{(\theta -p+2)\sigma}{p-\sigma}=\frac{(N+p)\sigma}{N}$. By (4.2), we deduce that

$$\begin{aligned} &\int _{Q_{T}}\vert \nabla G_{k}(u_{n})\vert ^{\sigma} dxdt \\ &\quad \leq C_{2}\left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{m'(p-1- \gamma )}dxdt\right ) ^{\frac{\sigma}{pm'}} \\ &\qquad \times \left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{ \frac{(N+p)\sigma}{N}}dxdt\right )^{\frac{p-\sigma}{p}}. \end{aligned}$$

(4.3)

From Lemma 1.2 (here $v=G_{k}(u_{n})$, $\kappa =\sigma$, $\varrho =p$), (4.1) and (4.3), we obtain

$$\begin{aligned} &\int _{0}^{T}\int _{E_{k,n}(t)} G_{k}(u_{n})^{\frac{(N+p)\sigma}{N}}dxdt \\ &\quad \leq \left (\Vert G_{k}(u_{n})\Vert _{L^{\infty}(0,T;L^{p}(E_{k,n}))}^{p} \right )^{\frac{\sigma}{N}}\int _{0}^{T}\int _{E_{k,n}(t)}\vert \nabla G_{k}(u_{n})\vert ^{\sigma}dxdt \\ &\quad \leq C_{2}\left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{m'(p-1- \gamma )}dxdt\right ) ^{\frac{(N+p)\sigma}{pNm'}} \\ &\qquad \times \left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{ \frac{(N+p)\sigma}{N}}dxdt\right )^{\frac{p-\sigma}{p}}. \end{aligned}$$

(4.4)

Since

$$\begin{aligned} m>\frac{N}{p}+1,\quad \text{and}\quad \sigma >p-1>p-1-\gamma , \end{aligned}$$

(4.5)

then we have $\frac{\sigma (N+p)}{m'N(p-1-\gamma )}>1$. Thus, using Hölder’s inequality, we have

$$\begin{aligned} &\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{(p-1-\gamma )m'}dxdt \\ &\quad \leq \left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{ \frac{\sigma (N+p)}{N}} dxdt\right )^{ \frac{(p-1-\gamma )m'N}{(N+p)\sigma}} \\ &\qquad \times \left (\int _{0}^{T} \vert E_{k,n}(t)\vert \; dt \right )^{1-\frac{(p-1-\gamma )m'N}{(N+p)\sigma}}. \end{aligned}$$

(4.6)

We denote by

$$ \Lambda _{n}(k)=\int _{0}^{T} \vert E_{k,n}(t)\vert dt,\quad \mathbf{G}_{nk}=\int _{0}^{T}\int _{E_{k,n}(t)} G_{k}(u_{n})^{ \frac{(N+p)\sigma}{N}}dxdt. $$

From (4.6) and (4.4), we can write for all $k\geq 1$

$$\begin{aligned} \mathbf{G}_{nk}& \leq C_{3}\mathbf{G}_{nk}^{{ \frac{2p-1-\sigma -\gamma}{p}}}\Lambda _{n}(k) ^{{ \frac{(N+p)\sigma}{pNm'}-\frac{p-1-\gamma}{p}}} \\ &\quad + C_{3} k^{{\frac{(N+p)\sigma}{N}\left ( \frac{2p-1-\sigma -\gamma}{p}\right )}}\Lambda _{n}(k)^{{ \frac{(N+p)\sigma}{pNm'}+\frac{p-\sigma}{p}}}, \end{aligned}$$

(4.7)

(4.5) implies that $\frac{2p-1-\sigma -\gamma}{p}<1$, then, by Young’s inequality for all $\varepsilon >0$,

$$\begin{aligned} \mathbf{G}_{nk}^{{\frac{2p-1-\sigma -\gamma}{p}}}\Lambda _{n}(k) ^{{ \frac{(N+p)\sigma}{pNm'}-\frac{p-1-\gamma}{p}}}&\leq C(\varepsilon ) \Lambda _{n}(k) ^{{\left (\frac{(N+p)\sigma}{Nm'}-(p-1-\gamma ) \right )\frac{1}{\sigma +1-p+\gamma}}} \\ &\quad +\varepsilon \mathbf{G}_{nk}. \end{aligned}$$

(4.8)

Taking $\varepsilon =\frac{1}{2C_{3}}$ in (4.8) and applying (4.7) to (4.8), we get

$$\begin{aligned} \mathbf{G}_{nk}&\leq C_{4} \Lambda _{n}(k) ^{{ \frac{(N+p)\sigma -Nm'(p-1-\gamma )}{Nm'(\sigma +1-p+\gamma )}}} \\ &\quad + C_{4}k^{{\frac{(N+p)\sigma}{N}\left ( \frac{2p-1-\sigma -\gamma}{p}\right )}}\Lambda _{n}(k)^{{ \frac{(N+p)\sigma +Nm'(p-\sigma )}{pNm'}}}. \end{aligned}$$

(4.9)

The assumption $m>\frac{N}{p}+1$ implies

$$ \frac{(N+p)\sigma -Nm'(p-1-\gamma )}{Nm'(\sigma +1-p+\gamma )}> \frac{(N+p)\sigma +Nm'(p-\sigma )}{pNm'}>1. $$

We note that $|\Lambda _{n}(k)|\leq T|\Omega |$, $k\geq 1$, and so

$$\begin{aligned} \mathbf{G}_{nk}&\leq C_{5}k^{{\frac{\sigma (N+p)}{N}\left ( \frac{2p-1-\sigma -\gamma}{p}\right )}}\Lambda _{n}(k)^{{ \frac{(N+p)\sigma +Nm'(p-\sigma )}{pNm'}}}. \end{aligned}$$

(4.10)

Since $G_{k}(u_{n})>h-k$ on $E_{h,n}(t)$ if $h>k$ and $E_{h,n}(t)\subset E_{k,n}(t)$. By virtue of $\frac{2p-1-\sigma -\gamma}{p}<1$, (4.10) can be written as

$$ \Lambda _{n}(h)\leq \dfrac{C_{5}k^{{\frac{\sigma (N+p)}{N}\left (\frac{2p-1-\sigma -\gamma}{p}\right )}}\Lambda _{n}(k)^{{\frac{(N+p)\sigma}{pNm'}+\frac{p-\sigma}{p}}}}{(h-k)^{{\frac{\sigma (N+p)}{N}}}}, \quad \forall h>k\geq 1. $$

(4.11)

Lemma 1.1 applied to

$$ \rho =\frac{2p-1-\sigma -\gamma}{p},\quad \nu =\frac{(N+p)\sigma}{N}, \quad \text{and}\quad \vartheta =\frac{(N+p)\sigma}{pNm'}+ \frac{p-\sigma}{p}, $$

we have, there exists a positive constant $l$ such that $\Lambda _{n}(l)=0$. By the fact that $|\Lambda _{n}(k)|\leq T|\Omega |$ (see the proof of Lemma A.1 of [6]), there exists a positive constant $d_{0}$ independent of $n$ such that $l\leq d_{0}$, so that

$$ \Lambda _{n}(d_{0})=0. $$

(4.12)

Therefore, from (4.12), it follows that the sequence $\{u_{n}\}_{n}$ is bounded in $L^{\infty}(Q_{T})$.

Case 2: Suppose that $0\leq \theta \leq p-2$. By (4.1), we can write

$$\begin{aligned} \int _{Q_{T}}\vert \nabla G_{k}(u_{n}) \vert ^{p} dxdt &\leq \int _{0}^{T}\int _{E_{n,k}(t)}|\nabla u_{n}|^{p}(1+u_{n})^{p-2- \theta}dxdt \\ &\leq C_{6}\left ( \int _{0}^{T}\int _{E_{n,k}(t)}(k+G_{k}(u_{n}))^{(p-1- \gamma )m'}dxdt\right )^{\frac{1}{m'}}. \end{aligned}$$

From Lemma 1.2 (here $v=G_{k}(u_{n})$, $\kappa =\varrho =p$), the previous inequality and (4.1) gives

$$\begin{aligned} &\int _{0}^{T}\int _{E_{k,n}(t)} G_{k}(u_{n})^{\frac{(N+p)p}{N}}dxdt \\ &\quad \leq \left (\Vert G_{k}(u_{n})\Vert _{L^{\infty}(0,T;L^{p}(E_{k,n}))}^{p} \right )^{\frac{p}{N}}\int _{0}^{T}\int _{E_{k,n}(t)}\vert \nabla G_{k}(u_{n}) \vert ^{p}dxdt \\ &\quad \leq C_{7}\left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{m'(p-1- \gamma )}dxdt\right ) ^{\frac{(N+p)}{Nm'}}. \end{aligned}$$

By Hölder’s inequality with exponent $\frac{(N+p)p}{Nm'(p-1-\gamma )}>1$ (since $m>\frac{N}{p}+1$), we have

$$\begin{aligned} &\int _{0}^{T}\int _{E_{k,n}(t)} G_{k}(u_{n})^{\frac{(N+p)p}{N}}dxdt \\ &\quad \leq C_{8}\left (\int _{0}^{T}\int _{E_{k,n}(t)}(k+ G_{k}(u_{n}))^{ \frac{(N+p)p}{N}}dxdt\right )^{\frac{p-1-\gamma}{p}} \Lambda _{n}(k)^{ \frac{p+N}{Nm'}-\frac{p-1-\gamma}{p}}. \end{aligned}$$

Therefore, (4.11) holds true for $\sigma =p$

$$ \Lambda _{n}(h)\leq \dfrac{C_{9}k^{{\frac{(N+p)p}{N}\cdot \frac{p-1-\gamma}{p}}}\Lambda _{n}(k)^{{\frac{(N+p)}{Nm'}}}}{(h-k)^{{\frac{(N+p)p}{N}}}}, \quad \forall h>k\geq 1. $$

Using that $\frac{p-1-\gamma}{p}\in (0,1)$ (since $p-2\leq \gamma <1$) and that $\frac{(N+p)}{Nm'}>1$, thus $u_{n}$ is bounded in $L^{\infty}(Q_{T})$.

Now, choosing $u_{n}$ as a test function for problem (3.4). Using (1.2) and (1.6), we obtain

$$ \frac{1}{2}\int _{\Omega} u_{n}(T)^{2}dx+\alpha \int _{Q_{T}} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta}}dxdt\leq \int _{Q_{T}}f_{n}u_{n}^{1-\gamma}dxdt. $$

(4.13)

Dropping the non-negative term, by Hölder’s inequality on the right-hand side of the inequality (4.13), and the boundedness of the sequence $\{u_{n}\}_{n}$ in $L^{\infty}(Q_{T})$, we obtain

$$\begin{aligned} \int _{Q_{T}} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta}}dxdt &\leq \Vert f\Vert _{L^{m}(Q_{T})}\vert Q_{T}\vert ^{\frac{1}{m'}}\Vert u_{n}^{1- \gamma}\Vert _{L^{\infty}(Q_{T})} \\ &\leq C_{10}\Vert f\Vert _{L^{m}(Q_{T})}. \end{aligned}$$

(4.14)

Therefore, from (4.14) and since the sequence $\{u_{n}\}_{n}$ is bounded in $L^{\infty}(Q_{T})$, we get

$$\begin{aligned} \int _{Q_{T}}\vert \nabla u_{n}\vert ^{p}dxdt&= \int _{Q_{T}} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta}} (1+ u_{n})^{ \theta}dxdt \\ & \leq \left (1+\Vert u_{n}\Vert _{L^{\infty}(Q_{T})}\right )^{\theta} \int _{Q_{T}}\frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta}}dxdt \\ &\leq C_{11}. \end{aligned}$$

Consequently the sequence $\{u_{n}\}_{n}$ is bounded in $L^{p}(0,T;W_{0}^{1,p}(\Omega ))$. By (3.1), (3.2) and the boundedness of the sequence $\{u_{n}\}_{n}$ in $L^{p}(0,T;W_{0}^{1,p}(\Omega ))$, we obtain the sequence $\big\{\frac{\partial u_{n}}{\partial t}\big\}_{n}$ is bounded in $L^{p'}(0,T;W^{-1,p'}(\Omega ))+L^{m}(Q_{T})$. □

Lemma 4.2

Let $m=\frac{N}{p}+1$ and let (1.2)-(1.6) hold. Then, the sequence $\{u_{n}\}_{n}$ is bounded in $L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{r}(Q_{T})$ for every $r\in [p,+\infty )$.

Proof

For $\tau \in (0,T]$, if we take $\varphi (u_{n})=(1+ u_{n})^{(p-1)\mu}-1$ as a test function in (3.4), with

$$\begin{aligned} \mu \geq \frac{1+\theta}{p-1}. \end{aligned}$$

(4.15)

By assumptions (1.2), (1.6), we obtain

$$\begin{aligned} &\int _{\Omega}\Psi (u_{n}(x,\tau ))dx +(p-1)\mu \alpha \int _{0}^{ \tau}\int _{\Omega} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta}}(1+ u_{n})^{(p-1) \mu -1} dxdt \\ &\quad \leq \int _{0}^{\tau}\int _{\Omega} f_{n}u_{n}^{(p-1)\mu - \gamma}dx dt, \end{aligned}$$

(4.16)

where

$$ \Psi (s)=\int _{0}^{\zeta}\varphi (y)dy\geq \frac{\zeta ^{(p-1)\mu +1}}{(p-1)\mu +1}\quad \forall \zeta >0,\;\mu >1. $$

(4.17)

Thus, (4.16), (4.17), (3.2), and Hölder’s inequality on the last integral, we get

$$\begin{aligned} &\frac{1}{(p-1)\mu +1}\int _{\Omega} u_{n}(x,\tau )^{(p-1)\mu +1}dx \\ &\quad +(p-1)\mu \alpha \int _{0}^{\tau}\int _{\Omega} \vert \nabla u_{n} \vert ^{p}(1+ u_{n})^{(p-1)\mu -1-\theta} dxdt \\ &\quad \leq \Vert f\Vert _{L^{m}(Q_{T})}\left (\int _{Q_{T}} u_{n}^{((p-1) \mu -\gamma )m'} dx dt\right )^{\frac{1}{m'}}. \end{aligned}$$

(4.18)

The condition (4.15) implies that $(p-1)\mu +p-1-\theta \geq p$, so (4.18) and (3.2) yield

$$\begin{aligned} &ess\sup _{t\in [0,T]}\int _{\Omega} \left [ u_{n}(x,\tau )^{ \frac{(p-1)\mu +p-1-\theta}{p}}\right ] ^{ \frac{p((p-1)\mu +1)}{(p-1)\mu +p-1-\theta}} dx \\ &\quad +\int _{Q_{T}} \bigg\vert \nabla u_{n}^{ \frac{(p-1)\mu +p-1-\theta}{p}}\bigg\vert ^{p} dxdt \\ &\quad \leq C_{12}\left (\int _{Q_{T}} u_{n}^{((p-1)\mu -\gamma ) m'} dx dt\right )^{\frac{1}{m'}}+C_{12}. \end{aligned}$$

(4.19)

Thus, by the Gagliardo-Nirenberg inequality (1.7), where

$$ v(x,t)= u_{n}(x,t) ^{\frac{(p-1)\mu +p-1-\theta}{p}},\quad \varrho = \frac{p((p-1)\mu +1)}{(p-1)\mu +p-1-\theta}, \quad \kappa =p, $$

we have

$$\begin{aligned} &\int _{Q_{T}}\left [ u_{n}^{\frac{(p-1)\mu +p-1-\theta}{p}}\right ] ^{p \frac{N+\frac{p((p-1)\mu +1)}{(p-1)\mu +p-1-\theta}}{N}}dxdt \\ &\quad \leq M_{2}\left (ess\sup _{0\leq t\leq T}\int _{\Omega} \left [ u_{n}(x,t) ^{\frac{(p-1)\mu +p-1-\theta}{p}}\right ] ^{ \frac{p((p-1)\mu +1)}{(p-1)\mu +p-1-\theta}}dx\right )^{\frac{p}{N}} \\ &\qquad \times \int _{Q_{T}}\bigg\vert \nabla u_{n}^{ \frac{(p-1)\mu +p-1-\theta}{p}}\bigg\vert ^{p}dxdt. \end{aligned}$$

(4.20)

By (4.19)-(4.20) and taking

$$ s=\frac{p((p-1)\mu +1)+N((p-1)\mu +p-1-\theta )}{N}, $$

we obtain

$$ \int _{Q_{T}} u_{n}^{s}dxdt\leq C_{13}\left (\int _{Q_{T}} u_{n}^{((p-1) \mu -\gamma ) m'} dx dt\right )^{\frac{N+p}{Nm'}}+C_{13}. $$

(4.21)

Since $\frac{N+p}{Nm'}=1$ and by (1.3), we obtain

$$ ((p-1)\mu -\gamma ) m'=((p-1)\mu -\gamma )\frac{N+p}{N}< s. $$

(4.22)

From (4.22), Hölder’s inequality and Young’s inequality with $\varepsilon >0$, we deduce that

$$\begin{aligned} \int _{Q_{T}} u_{n}^{\frac{((p-1)\mu -\gamma )(N+p)}{N} } dx dt & \quad \leq C_{14}\left (\int _{Q_{T}} u_{n}^{s} dx dt\right )^{ \frac{((p-1)\mu -\gamma ) (N+p)}{sN}} \\ &\quad \leq \varepsilon \int _{Q_{T}} \vert u_{n}\vert ^{s} dx dt+ c( \varepsilon ). \end{aligned}$$

(4.23)

By (4.21), (4.23) and letting $\varepsilon =\frac{1}{2C_{13}}$, we get

$$ \int _{Q_{T}} \vert u_{n}\vert ^{s} dx dt\leq C_{15}. $$

(4.24)

On the other hand, since

$$ \mu \geq \frac{1+\theta}{p-1}\geq \frac{N(\theta +1)-p}{(p-1)(p+N)}, $$

and

$$ s\geq p\Leftrightarrow \mu \geq \frac{N(\theta +1)-p}{(p-1)(p+N)}, $$

therefore, from (4.24) with $r=s$, it follows that the sequence $\{u_{n}\}_{n}$ is bounded in $L^{r}(Q_{T})$. Inequalities (4.18), (4.23), and the boundedness of the sequence $\{u_{n}\}_{n}$ in $L^{r}(Q_{T})$, imply then

$$ \int _{Q_{T}}\vert \nabla u_{n}\vert ^{p}dxdt\leq \int _{Q_{T}} \vert \nabla u_{n}\vert ^{p}(1+ u_{n})^{(p-1)\mu -1-\theta} dxdt\leq C_{16}. $$

(4.25)

Thus from (4.25) immediately follows the boundedness of the sequence $\{u_{n}\}_{n}$ in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))$. □

Lemma 4.3

Let $f\in L^{m}(Q_{T})$, with $m$ satisfies (2.2), and (1.2)-(1.6) hold. Then, the sequence $\{u_{n}\}_{n}$ is bounded in $L^{\delta}(Q_{T})\cap L^{p}(0,T;W_{0}^{1,p}(\Omega ))$, where $\delta$ as in (2.3).

Proof

We put

$$ ((p-1)\mu -\gamma ) m'= \frac{p((p-1)\mu +1)+ N((p-1)\mu +p-1-\theta )}{N}, $$

(4.26)

in the proof of Lemma 4.2. By (2.2) and (4.26) we get

$$ \mu =\frac{(m-1)(p+N(p-1-\theta ))+\gamma mN}{(p-1)(N+p-pm)}\geq \frac{1+\theta}{p-1}. $$

Consequently

$$ \delta =((p-1)\mu -\gamma ) \frac{m}{m-1}= \frac{m(p+N(p-1-\theta )+\gamma (N+p))}{N+p-pm}. $$

(4.27)

Note that $\frac{N+p}{Nm'}<1$. The Young’s inequality gives

$$ \left (\int _{Q_{T}} u_{n}^{((p-1)\mu -\gamma ) m'}dxdt\right )^{ \frac{N+p}{Nm'}}\leq \varepsilon \int _{Q_{T}}u_{n}^{((p-1)\mu - \gamma ) m'}dxdt+c(\varepsilon ). $$

(4.28)

Taking (4.28) in (4.21) and letting $\varepsilon =\frac{1}{2C_{13}}$, by (4.26) and (4.27), we deduce that the sequence $\{u_{n}\}_{n}$ is bounded in $L^{\delta}(Q_{T})$. The rest of the proof is the same way in proof of Lemma 4.2. □

Lemma 4.4

Let $f$ belongs to $L^{m}(Q_{T})$, with $m$ satisfies (2.4), and (1.2)-(1.6) hold. Then, the sequence $\{u_{n}\}_{n}$ is bounded in $L^{\delta}(Q_{T})\cap L^{q}(0,T;W_{0}^{1,q}(\Omega ))$, where $\delta$ and $q$ are defined in Theorem 2.5.

Proof

Suppose that

$$ 0< \mu < \frac{1+\theta}{p-1}. $$

Let $\varphi$ and $\Psi$ as in (4.17). Choosing $\varphi (u_{n}(x,t))\chi _{(0,\tau )}(t)$ as a test function in (3.4). Using the fact that

$$ \Psi (\zeta )\geq c \zeta ^{\mu (p-1)+1}-c\quad \forall s\in \mathbb{R}_{+}, $$

we have

$$\begin{aligned} &ess\sup _{0\leq t\leq \tau}\int _{\Omega} u_{n}(x,\tau )^{(p-1) \mu +1}dx+ \int _{Q_{T}} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta +1-(p-1)\mu}} dxdt \\ &\quad \leq C_{17}\left (\int _{Q_{T}} u_{n}^{((p-1)\mu -\gamma ) m'} dx dt\right )^{\frac{1}{m'}}+C_{17}. \end{aligned}$$

(4.29)

Using Hölder’s inequality with the exponents $\frac{p}{q}$ and (4.29), we obtain

$$\begin{aligned} \int _{Q_{T}}\vert \nabla u_{n}\vert ^{q} dxdt&\leq \left (\int _{Q_{T}} \frac{\vert \nabla u_{n}\vert ^{p}}{(1+ u_{n})^{\theta +1-(p-1)\mu}} dxdt \right )^{\frac{q}{p}} \\ &\quad \times \left (\int _{Q_{T}}(1+ u_{n})^{ \frac{(\theta +1-(p-1)\mu )q}{p-q}}dxdt\right )^{\frac{p-q}{p}} \\ &\quad \leq C_{18}\left (\left (\int _{Q_{T}} u_{n}^{((p-1)\mu - \gamma ) m'}dxdt\right )^{\frac{1}{m'}}+1\right )^{\frac{q}{p}} \\ &\qquad \times \left (\int _{Q_{T}} u_{n}^{ \frac{(\theta +1-(p-1)\mu )q}{p-q}}dxdt+1\right )^{\frac{p-q}{p}}. \end{aligned}$$

(4.30)

Now we take $\mu$, such that

$$ \mu =\frac{(\theta +1)q+\gamma m'(p-q)}{(p-1)((p-q)m'+q)}< \frac{1+\theta}{p-1}, $$

hence

$$ ((p-1)\mu -\gamma ) m'=\frac{(\theta +1-(p-1)\mu )q}{p-q}. $$

(4.31)

Then, by the inequality (4.30), we get

$$ \int _{Q_{T}}\vert \nabla u_{n}\vert ^{q} dxdt\leq C_{19}\left (\int _{Q_{T}} u_{n}^{((p-1)\mu -\gamma ) m' dxdt}\right )^{\frac{q}{pm'}+ \frac{p-q}{p}}+C_{19}. $$

(4.32)

Applying Lemma 1.2 (here $v(x,t)=u_{n}(x,t)$, $\varrho =(p-1)\mu +1$, $\kappa =q$) and from (4.29), (4.32), we have

$$\begin{aligned} &\int _{Q_{T}} u_{n}^{\frac{(N+(p-1)\mu +1)q}{N}} dxdt \\ &\quad \leq \left (ess\sup _{0\leq t\leq T}\int _{\Omega} u_{n}(x,t)^{(p-1) \mu +1}dx\right )^{\frac{q}{N}}\int _{Q_{T}}\vert \nabla u_{n}\vert ^{q}dxdt \\ &\quad \leq C_{20}\left (\int _{Q_{T}} u_{n}^{((p-1)\mu -\gamma ) m'}dxdt \right )^{\frac{q(N+p)}{pNm'}+\frac{p-q}{p}}+C_{20}. \end{aligned}$$

(4.33)

Set

$$ ((p-1)\mu -\gamma ) \frac{m}{m-1}=\frac{(N+(p-1)\mu +1)q}{N}, $$

then, by (4.31) we obtain

$$\begin{aligned} &\mu =\frac{(m-1)(p+N(p-1-\theta ))+m\gamma N}{(p-1)(N+p-pm)}, \end{aligned}$$

(4.34)

and

$$\begin{aligned} &q= \frac{m[N(p-\theta -1)+p+\gamma (N+p)]}{N+1-(\theta +1)(m-1)+m\gamma}. \end{aligned}$$

(4.35)

By (4.34), (4.35) and (4.33), we have $(p-1)\mu m'=\delta$ and

$$ \int _{Q_{T}} u_{n}^{\delta} dxdt\leq C_{20}\left (\int _{Q_{T}} u_{n}^{ \delta}dxdt\right )^{\frac{q(N+p)}{pNm'}+\frac{p-q}{p}}+C_{20}. $$

(4.36)

Since $\frac{q(N+p)}{pNm'}+\frac{p-q}{p}<1$, then from (4.36), we deduce that the sequence $\{u_{n}\}_{n}$ is bounded in $L^{\delta}(Q_{T})$. Going back to (4.32) and (4.35), this in turn implies that the sequence $\{u_{n}\}_{n}$ is bounded in $L^{q}(0,T;W_{0}^{1,q}(\Omega ))$. □

5 Proof of Main Results

5.1 Proof of Theorem 2.2

In virtue of Lemma 4.1, we have the sequence $\{u_{n}\}_{n}$ is bounded in $L^{\infty}(Q_{T})\cap L^{p}(0,T; W_{0}^{1,p}(\Omega ))$. Then, there exists a function $u\in L^{\infty}(Q_{T})\cap L^{p}(0,T;W_{0}^{1,p}(\Omega ))$, such that, up to subsequence,

$$\begin{aligned} &u_{n}\rightharpoonup u\quad \text{weakly in }\; L^{p}(0,T;W_{0}^{1,p}( \Omega ), \\ &u_{n}\rightharpoonup u\quad \text{weakly}^{*} \text{in }\; L^{\infty}(Q_{T}) \;\; \text{for }\; \sigma ^{*}(L^{\infty}(Q_{T}),L^{1}(Q_{T})). \end{aligned}$$

In view of Lemma 4.1, we have that the sequence $\big\{\frac{\partial u_{n}}{\partial t}\big\}_{n}$ is bounded in $L^{1}(Q_{T})\cap L^{p'}(0,T;W_{0}^{-1,p'}(\Omega ))$. So, using compactness results (corollary 4 of [34]) we obtain $\{u_{n}\}_{n}$ is relatively compact in $L^{1}(Q_{T})$. This implies that

$$\begin{aligned} &u_{n}\rightarrow u\quad \text{strongly in }\; L^{1}(Q_{T}),\;\; \text{and a.e. in}\; Q_{T} . \end{aligned}$$

(5.1)

To carry on the proof, we need the following Lemma.

Lemma 5.1

[23] For all $k>0$, there exists a function $\theta _{k}$ such that for all $\varepsilon >0$, we have

$$ \limsup _{n}\int _{\{|u_{n}-u^{k}|\leq \varepsilon \}}a(x,t,T_{n}(u_{n}), \nabla u_{n})(\nabla u_{n}-\nabla u^{k})dxdt\leq \theta _{k}( \varepsilon ), $$

with $\lim \theta _{k}(\varepsilon )=0$, $u^{k}=\phi _{k}(u)$.

By Lemma 5.1, we can adopt the approach of [22, 26], we deduce that there exists a subsequence, still denoted by $\{u_{n}\}_{n}$, such that

$$ \nabla u_{n}\rightarrow \nabla u\quad \text{almost everywhere in}\; Q_{T}. $$

(5.2)

From (5.1), (5.2) and the fact that $b$ is Carathéodory function, we obtain

$$ b(x,t,u_{n},\nabla u_{n})\rightarrow b(x,t,u,\nabla u) \quad \text{almost everywhere in}\; Q_{T}. $$

(5.3)

By (5.3), and Vitali’s theorem, one has

$$ a(x,t,u_{n},\nabla u_{n})\rightarrow a(x,t,u,\nabla u) \quad \text{strongly in}\; L^{p'}(Q_{T}). $$

(5.4)

We begin by proving an important lemma useful to prove of Theorem 2.2-2.5.

Lemma 5.2

Let $u_{n}$ be a weak solution of (3.1). Then

$$ \lim _{n\rightarrow +\infty}\int _{Q_{T}}g_{n}(u_{n})f_{n} \psi dxdt=\int _{Q_{T}}g(u)f\psi dxdt, $$

(5.5)

for all $\psi \in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})$.

Proof

Let $\psi \in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})$ as a test function in (3.1), we obtain

$$\begin{aligned} &\int _{Q}\frac{\partial u_{n}}{\partial t}\psi dxdt+\int _{Q_{T}}b(x,t,T_{n}(u_{n}), \nabla u_{n}).\nabla \psi dxdt \\ &\quad =\int _{Q_{T}} g_{n}(u_{n})f_{n}\psi dxdt. \end{aligned}$$

(5.6)

If $g(0)<+\infty$, we obtain (5.5) hold true. Suppose that $g(0)=\lim _{z\rightarrow 0}g(z)$. Let $\psi$ be a non-negative function in $L^{\infty}(Q_{T})\cap L^{p}(0,T;W_{0}^{1,p}(\Omega ))$ as a test function in the weak formulation (5.6), using (1.4) and Young’s inequality, we obtain

$$\begin{aligned} \int _{Q_{T}} g_{n}(u_{n})f_{n}\psi dxdt&\leq \frac{1}{p}\int _{Q_{T}} \vert u_{n}\vert ^{p}dxdt+\frac{1}{p'}\int _{Q_{T}}\bigg\vert \frac{\partial \psi}{\partial t}\bigg\vert ^{p'}dxdt \\ &\quad +\frac{1}{p}\int _{Q_{T}}\vert \nabla \psi \vert ^{p}dxdt \\ &+ \frac{1}{p'}\int _{Q_{T}}\left (a(x,t)+\vert T_{n}(u_{n})\vert ^{p-1}+ \vert \nabla u_{n}\vert ^{p-1}\right )^{p'}dxdt \\ &\leq C\left (\Vert u_{n}\Vert _{L^{p}(Q_{T})}+\bigg\Vert \frac{\partial \psi}{\partial t}\bigg\Vert _{L^{p'}(Q_{T})}+\Vert k \Vert _{L^{p'}(Q_{T})}\right ) \\ &\quad + C\left (\Vert u_{n}\Vert _{L^{p}(0,T;W_{0}^{1,p}(\Omega )}+ \Vert \psi \Vert _{L^{p}(0,T;W_{0}^{1,p}(\Omega )}\right ) \\ &\leq C. \end{aligned}$$

(5.7)

Therefore (5.7) implies that $\{f_{n}g_{n}(u_{n})\}_{n}$ is bounded in $L^{1}(Q_{T})$. Passing to the limit as $n\rightarrow +\infty$ in (5.5), Fatou’s lemma implies

$$\begin{aligned} \int _{Q_{T}}fg(u)\psi dxdt\leq C\quad \forall n, \end{aligned}$$

(5.8)

then we have

$$ \int _{\{u=0\}}\lim _{z\rightarrow 0}g(z) f \varphi \ dxdt < + \infty , $$

so that, $f\varphi = 0 \ \text{a.e.}\ \text{on}\ \{u=0\}$ for all nonnegative $\varphi \in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})$. Yielding

$$\begin{aligned} f=0\ \text{a.e.}\ \text{on}\ \{u=0\}. \end{aligned}$$

(5.9)

For every fixed $\lambda >0$, we can write

$$\begin{aligned} \int _{Q_{T}}f_{n}g_{n}(u_{n})\psi dxdt&=\int _{Q_{T}\cap \{u_{n}> \lambda \}}f_{n}g_{n}(u_{n})\psi dxdt \\ &\quad +\int _{Q_{T}\cap \{u_{n}\leq \lambda \}}f_{n}g_{n}(u_{n}) \psi dxdt \\ &=\mathcal{I}_{n,\lambda}^{1}+ \mathcal{I}_{n,\lambda}^{2}. \end{aligned}$$

(5.10)

For $\mathcal{I}_{n,\lambda}^{1}$, we have

$$ 0\leq g_{n}(u_{n})f_{n}\chi _{\{u_{n}>\lambda \}}\varphi \leq \sup _{z\in [\lambda ,+\infty )}[g(z)]f\varphi \in L^{1}(Q_{T}). $$

(5.11)

Using Lebesgue’s dominated convergence theorem and that the sequence $\big\{\chi _{\{u_{n}>\lambda \}}\big\}_{n}$ converges to $\chi _{\{u\geq \lambda \}}$ a.e. in $Q_{T}$, we get

$$ \lim _{n\rightarrow \infty}\mathcal{I}_{n,\lambda}^{1}=\int _{Q_{T} \cap \{u\geq \lambda \}}g(u)f\psi dxdt. $$

Since $g(u)f \varphi \in L^{1}(Q_{T})$, Lebesgue’s theorem, with respect to $\lambda$, imply that

$$\begin{aligned} \lim _{\lambda \rightarrow 0^{+}}\lim _{n\rightarrow \infty}\mathcal{I}_{n,\lambda}^{1}=\int _{Q_{T}\cap \{u\geq 0\}}g(u)f \psi dxdt=\int _{Q_{T}}g(u)f\psi dxdt. \end{aligned}$$

By (5.9), it follows that

$$\begin{aligned} \lim _{\lambda \rightarrow 0^{+}}\lim _{n\rightarrow \infty}\mathcal{I}_{n,\lambda}^{1}=\int _{Q_{T}\cap \{u>0\}}g(u)f \psi dxdt=\int _{Q_{T}}g(u)f\psi dxdt. \end{aligned}$$

(5.12)

Now in order to get rid of $\mathcal{I}_{n,\lambda}^{2}$. We take $\Xi _{\lambda}(u_{n})\psi$ as test function in (3.1), where $\Xi _{\lambda}$ is defined in (1.8), we obtain

$$\begin{aligned} &\int _{Q_{T}}\frac{\partial u_{n}}{\partial t}\Xi _{\lambda}(u_{n}) \psi dxdt+\int _{Q_{T}}b(x,t,T_{n}(u_{n}),\nabla u_{n})\nabla (\Xi _{ \lambda}(u_{n})\psi )dxdt \\ &\quad =\int _{Q_{T}}f_{n}g_{n}(u_{n})\Xi _{\lambda}(u_{n})\psi dxdt. \end{aligned}$$

(5.13)

Using integration by parties and definition of $\Xi _{\lambda}$, we have

$$\begin{aligned} \int _{Q_{T}}\frac{\partial u_{n}}{\partial t}\Xi _{\lambda}(u_{n}) \psi dxdt=-\int _{Q_{T}}\Theta (u_{n}) \frac{\partial \psi}{\partial t} dxdt, \end{aligned}$$

(5.14)

where

$$ \Theta (\zeta )=\int _{0}^{\zeta}\Xi _{\lambda}(y)dy. $$

Using (1.2), $\Xi '_{\lambda}(u_{n})=-\frac{1}{\lambda}$ and the fact that

$$ \nabla (\Xi _{\lambda}(u_{n})\psi )=\Xi _{\lambda}(u_{n})\nabla \psi - \frac{1}{\lambda}(u_{n})\psi \nabla u_{n}, $$

we get

$$\begin{aligned} &\int _{Q_{T}}b(x,t,T_{n}(u_{n}),\nabla u_{n})\nabla (\Xi _{\lambda}(u_{n}) \psi )dxdt \\ &\quad \leq \int _{Q_{T}}b(x,t,T_{n}(u_{n}),\nabla u_{n})\Xi _{ \lambda}(u_{n}).\nabla \psi dxdt. \end{aligned}$$

(5.15)

On the other hand

$$\begin{aligned} \int _{Q_{T}}f_{n}g_{n}(u_{n})\Xi _{\lambda}(u_{n})\psi dxdt&=\int _{Q_{T} \cap \{u_{n}\leq \lambda \}}f_{n}g_{n}(u_{n})\Xi _{\lambda}(u_{n}) \psi dxdt \\ &\qquad +\int _{Q_{T}\cap \{\lambda < u_{n}< 2\lambda \}}f_{n}g_{n}(u_{n}) \Xi _{\lambda}(u_{n})\psi dxdt \\ &\quad \leq \int _{Q_{T}\cap \{u_{n}\leq \lambda \}}f_{n}g_{n}(u_{n}) \Xi _{\lambda}(u_{n})\psi dxdt. \end{aligned}$$

(5.16)

Combining (5.13)-(5.15) and (5.16), we obtain

$$\begin{aligned} \int _{Q_{T}\cap \{u_{n}\leq \lambda \}}f_{n}g_{n}(u_{n})\Xi _{ \lambda}(u_{n})\psi dxdt&\leq \int _{Q_{T}}b(x,t,T_{n}(u_{n}),\nabla u_{n}) \Xi _{\lambda}(u_{n}).\nabla \psi dxdt \\ &\quad -\int _{Q_{T}}\Theta (u_{n})\frac{\partial \psi}{\partial t} dxdt. \end{aligned}$$

Using that $\Xi _{\lambda}$ is bounded and $\Theta$ is continue we deduce that as $n$ tends to infinity

$$ \Theta (u_{n})\frac{\partial \psi}{\partial t}\rightarrow \Theta (u) \frac{\partial \psi}{\partial t}\quad \text{strongly in}\; L^{1}(Q_{T}), $$

and

$$ b(x,t,T_{n}(u_{n}),\nabla u_{n})\Xi _{\lambda}(u_{n})\rightharpoonup b(x,t,u, \nabla u)\Xi _{\lambda}(u)\quad \text{weakly in}\; L^{p'}(Q_{T}). $$

This implies that

$$\begin{aligned} &\limsup \limits _{n\rightarrow +\infty}\int _{Q_{T}\cap \{u_{n}\leq \lambda \}}f_{n}g_{n}(u_{n})\Xi _{\lambda}(u_{n})\psi dxdt \\ &\leq -\int _{\{u=0\}}\Theta (u)\frac{\partial \psi}{\partial t} dxdt+ \int _{\{u=0\}}b(x,t,u,\nabla u)\Xi _{\lambda}(u).\nabla \psi dxdt, \end{aligned}$$

then

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\lim _{n\rightarrow \infty}\mathcal{I}_{n,\lambda}^{2}=0. \end{aligned}$$

(5.17)

By (5.12) and (5.17) we deduce that, for all nonnegative $\psi \in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})$

$$ \lim _{n\rightarrow \infty}\int _{Q_{T}}f_{n}g_{n}(u_{n}) \psi dxdt=\int _{Q_{T}}fg(u)\psi dxdt. $$

(5.18)

Moreover, by decomposing any $\psi =\psi ^{+}-\psi ^{-}$ with $\psi ^{+}=\max \{\psi ,0\}$ and $\psi ^{-}= -\min \{\varphi ,0\}$, we deduce that (5.18) holds for every $\psi \in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})$. This concludes (5.5).

Let $n\rightarrow +\infty$ in (5.6), by (5.1), (5.4) and (5.5) we get

$$\begin{aligned} &\int _{Q_{T}}\frac{\partial u}{\partial t}\psi dxdt+\int _{Q_{T}}b(x,t,u, \nabla u).\nabla \psi dxdt=\int _{Q_{T}} g(u)f\psi dxdt, \end{aligned}$$

(5.19)

for every $\psi \in L^{p}(0,T;W_{0}^{1,p}(\Omega ))\cap L^{\infty}(Q_{T})$. □

5.2 Proof of the Theorem 2.5

From Lemma 4.4, we have the sequence $\{u_{n}\}_{n}$ is bounded in $L^{q}(0,T;W_{0}^{1,q}(\Omega ))\cap L^{\delta}(Q_{T})$ and $\big\{\frac{\partial u_{n}}{\partial t}\big\}_{n}$ is bounded in $L^{q'}(0,T;W^{-1,q'}(\Omega ))+L^{m}(Q_{T})$. Thus, the sequence $\big\{\frac{\partial u_{n}}{\partial t}\big\}_{n}$ is bounded in $L^{1}(0,T,W^{-1,\epsilon}(\Omega ))$ for every $\epsilon <\min \left \{\frac{N}{N-1},q'\right \}$. So, by corollary 4 of [34], we get the sequence $\{u_{n}\}_{n}$ is relatively compact in $L^{1}(Q_{T})$. This implies that we can extract a subsequence (denote again by $\{u_{n}\}_{n}$) such that the sequence $\{u_{n}\}_{n}$ converges to $u$ strongly in $L^{1}(Q_{T})$. From (5.1), (5.2), we obtain

$$ b(x,t,u_{n},\nabla u_{n})\rightarrow b(x,t,u,\nabla u) \quad \text{a.e. in}\;\; Q_{T}. $$

(5.20)

Using Lemma 4.4, (5.20), $\frac{q}{p-1}>1$ and Vitali’s theorem, one has

$$ b(x,t,u_{n},\nabla u_{n})\rightarrow b(x,t,u,\nabla u) \quad \text{strongly in}\;\; L^{\frac{q}{p-1}}(Q_{T}). $$

Thus, it is possible to pass to the limit in (5.6) as $n\rightarrow +\infty$, obtaining (5.19).