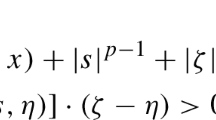Some Nonlinear Parabolic Problems with Singular Natural Growth Term

Abstract

In this paper, we study the existence and regularity results for nonlinear parabolic problems with singular natural growth gradient terms

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial u}{\partial t}-{\varDelta }_{p}u+b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }}=f &{} \text{ in } &{} Q,\\ u(x,t)=0 &{} \text{ on } &{} {\varGamma },\\ u(x,0)=0 &{} \text{ in } &{} {\varOmega }, \end{array} \right. \end{aligned}$$

where ${\varOmega }$ is a bounded open subset of ${\mathbb {R}}^{N},$ $N\ge 2,$ Q is the cylinder ${\varOmega }\times (0,T),$ $T>0,$ ${\varGamma }$ the lateral surface $\partial {\varOmega }\times (0,T),$ ${\varDelta }_{p}$ is the so-called $p-$Laplace operator, ${\varDelta }_{p}u=\text{ div }(|\nabla u|^{p-2}\nabla u)$ with $2\le p<N,$ b is a positive measurable bounded function, $0<\theta <1,$ and f belongs to Lebesgue space $L^{m}(Q),$ $m\ge 1$.

1 Introduction

This paper is devoted to the study of the following nonlinear singular parabolic problem:

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial u}{\partial t}-\text{ div }(|\nabla u|^{p-2}\nabla u)+b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }}=f &{} \text{ in } &{} Q,\\ u(x,t)=0 &{} \text{ on } &{} {\varGamma },\\ u(x,0)=0 &{} \text{ in } &{} {\varOmega }, \end{array} \right. \end{aligned}$$

(1)

where ${\varOmega }$ is a bounded open subset of ${\mathbb {R}}^{N},$ $N\ge 2,$ and Q is the cylinder ${\varOmega }\times (0,T),$ $T>0,$ ${\varGamma }$ the lateral surface $\partial {\varOmega }\times (0,T),$ $2\le p<N,$ $0<\theta <1,$ b(x, t) is a measurable function satisfying

$$\begin{aligned} 0<\alpha \le b(x,t)\le \beta , \end{aligned}$$

(2)

where $\alpha$ and $\beta$ are fixed real numbers, and f belongs to some Lebesgue space $L^{m}(Q),$ $m\ge 1,$ satisfying the condition

$$\begin{aligned} \text{ ess }\inf \{f(x,t):x\in \omega ,t\in (0,t)\}>0\,\,\,\,\, \forall \,\omega \subset \subset {\varOmega }. \end{aligned}$$

Singular problems of this type have been largely studied in the past for their connection with the theory of non-Newtonian fluids and heat conduction in electrically active materials (see for instance [15, 21] and references therein).

When the singular lower-order term does not appear (i.e. $b(x,t)=0$ in (1)), the existence and regularity results of solutions to problem (1) are proved in [14] under the hypothesis $f\in L^{r}(0,T;L^{q}({\varOmega })),$ $r\ge 1,\, q\ge 1.$ If $\theta =0,$ and $b(x,t)\equiv cst$ the authors in [13] studied the existence and uniqueness of solution to nonlinear parabolic problems with natural growth with respect to the gradient

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial u}{\partial t}-\text{ div }(a(x,t,u,\nabla u))=H(x,t,u,\nabla u)-\text{ div }(g(x,t)) &{} \text{ in } &{} D'(Q),\\ u(x,t)=0 &{} \text{ on } &{} {\varGamma },\\ u(x,0)=u_{0}(x) &{} \text{ in } &{} {\varOmega }, \end{array} \right. \end{aligned}$$

where $|H(x, t, s, \xi )|\le \nu |\xi |^{p}+f(x,t),$ $\nu$ is a positive constant, $f\ge 0$ belongs to $L^{r}(0,T; L^{q}({\varOmega }))$ with $q=r^{\prime }N/p$ and $1<r<\infty ,$ $|g|^{p^{\prime }}\in L^{r}(0,T; L^{q}({\varOmega })),$ and the initial datum $u_{0}\in L^{\infty }({\varOmega })$ satisfies

$$\begin{aligned} \int _{{\varOmega }}e^{pM|u_{0}(x)|}dx<+\infty , \end{aligned}$$

for $M>0$. In the same fashion, the authors shown in [6] the existence of solutions to problem parabolic

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial u}{\partial t}-{\varDelta }_{p}u=d|\nabla u|^{p}+f(x,t) &{} \text{ in } &{} Q,\\ u(x,t)=0 &{} \text{ on } &{} {\varGamma },\\ u(x,0)=u_{0}(x) &{} \text{ in } &{} {\varOmega }, \end{array} \right. \end{aligned}$$

where $1<p<N,$ $f\in L^{r}(0,T; L^{q}({\varOmega })),$ with $q, r>1$ are such that $q/r^{\prime }\ge N/p,$ and the initial datum $u_{0}\in L^{\infty }({\varOmega })$ satisfies

$$\begin{aligned} \int _{{\varOmega }}\left( e^{l|u_{0}|}-1\right) ^{2}dx<+\infty , \,\,\,\,\,\; \;\; \text{ for } \text{ every } \,\, l\in I\!\!{R}. \end{aligned}$$

See also [7, 12, 18]. When $b(x,t)=B,$ $\theta =1$ and $f\equiv 0$ the authors in [5] studied the existence of weak solutions to homogeneous nonlinear and singular parabolic problems as

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial u}{\partial t}-{\varDelta }_{p}u+B\frac{|\nabla u|^{p}}{u}=0 &{} \text{ in } &{} Q,\\ u(x,t)=0 &{} \text{ on } &{} {\varGamma },\\ u(x,0)=u_{0}(x) &{} \text{ in } &{} {\varOmega }, \end{array} \right. \end{aligned}$$

with $p>1, \,B>0,$ and $0\le u_{0}$ belonging to $L^{\infty }({\varOmega })$ such that $u_{0}\ge c>0$  a.e.  on ${\varOmega }$. In the case $p=2,$ several works studied the existence of solutions for singular parabolic problems. For example, the authors in [20] proved the existence of solutions to the following parabolic problem

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial u}{\partial t}-\text{ div }(M(x,t,u)\nabla u)+g(x,t,u)|\nabla u|^{2}=f(x,t) &{} \text{ in } &{} Q,\\ u(x,t)=0 &{} \text{ on } &{} {\varGamma },\\ u(x,0)=u_{0}(x) &{} \text{ in } &{} {\varOmega }, \end{array} \right. \end{aligned}$$

where $f\in L^{r}(0,T;L^{q}({\varOmega }))$ with $\frac{1}{r}+\frac{2}{Nq}<1,$ $q\ge 1,\, r>1,$ and $u_{0}\in L^{\infty }({\varOmega }),$ and the function $g(x,t,s):Q\times (0,+\infty )\rightarrow {\mathbb {R}}$ is a Caratheodory function which is singular at $s=0$, and it possibly negative (see also [8, 19]). In the elliptic case, several works studied existence and regularity results for the singular case. In [28] the authors proved existence and non existence of solutions to problem

$$\begin{aligned} \left\{ \begin{array}{lll} -{\varDelta }_{p}u+g(x,u)|\nabla u|^{p}=f &{} \text{ in } &{} {\varOmega },\\ u=0 &{} \text{ on } &{} \partial {\varOmega }, \end{array} \right. \end{aligned}$$

with $1<p<+\infty ,$ g(x, s) positive and singular at $s=0,$ $f\in L^{q}({\varOmega })$ $(q\ge 1)$ satisfying the condition

$$\begin{aligned} \exists f_{\omega }>0,\,\,\ \text{ such } \text{ that }\,\,\,\,\, f\ge f_{\omega }\,\,\, \text{ in }\,\, w,\,\,\,\, \forall \omega \subset \subset {\varOmega }. \end{aligned}$$

In the case $p=2,$ Souilah [26] proved existence and regularity results of solutions to the problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\text{ div }(M(x,u)\nabla u)+\frac{|\nabla u|^{2}}{u^{\theta }}=f+\lambda u^{r} \,\,\,&{}&{} x\in {\varOmega },\\ u=0 \,\, &{}&{} x\in \partial {\varOmega },\\ \end{array} \right. \end{aligned}$$

where $0<\theta <1,$   $0<r<2-\theta ,$   $\lambda >0,$  $f\in L^{m}({\varOmega })$ $(m\ge 1).$ The author in [4] proved existence of solution $u\in H_{0}^{1}({\varOmega })$ to the problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\text{ div }\left( \frac{b(x)}{(1+|u|)^{p}}\nabla u\right) +B\frac{|\nabla u|^{2}}{u^{\theta }}=f \,\,\,&{} \text{ in } &{} {\varOmega },\\ u=0 \,\, &{} \text{ on } &{} \partial {\varOmega },\\ \end{array} \right. \end{aligned}$$

where $B,p >0,$  $0<\theta <2;$  $f\in L^{m}({\varOmega })$ $(m\ge 1)$. Here, the non existence of solutions $u\in H_{0}^{1}({\varOmega })$ is proved for $\theta \ge 2$ (see also [3, 22] and references therein).

In the study of problem (1), the difficulty comes from the lower-order term: the natural growth dependence with respect to the gradient and the singular dependence with respect to u. To overcome this difficulty, we need to approximate the problem (1) by another non-singular one.

Notation: We will denote by meas(E) and |E| the Lebesgue measure of subsets E of ${\mathbb {R}}^{N}.$ For any $q>1,$ $q^{\prime }=q/(q-1)$ is the Hölder conjugate exponent of q,  while for any $1\le p<N,$ $p^{*}=Np/(N-p)$ is the Sobolev conjugate exponent of p. For fixed $k>0$ we will make use of the truncation functions $T_{k}$ and $G_{k}$ defined as

$$\begin{aligned} T_{k}(s)=\max (-k,\min (s,k)) \text{ and } G_{k}(s)=s-T_{k}(s)=(|s|-k)^{+}\text{ sign }(s). \end{aligned}$$

For the sake of simplicity we will often use the simplified notation

$$\begin{aligned} \int _{Q}f=\int _{Q}f(x,t)\,dx\,dt, \end{aligned}$$

when no ambiguity in the integration variables is possible. If not otherwise specified, we will denoted by C several constants whose value many change from line to line and, sometime, in the same line. These values will only depend on the parameters (for instance C can depend on $N, p, B, \theta , m, T, {\varOmega }, Q$) but they will never depend on the indexes of the sequences we will often introduce.

The plan of this article is the following. In Sect. 2 we give some preliminary results and we state our main ones. Section 3 is devoted to the proof of estimate on $u_{n}$ (the solution of the approximate problem), while the Sect. 4 contains the proofs of the main results

2 Some Preliminaries and Main Results

We need the Gagliardo-Nirenberg inequality that we used later in the proofs of our results.

Lemma 1

[9, Proposition 3.1] Let v be function in $W_{0}^{1,h}({\varOmega })\cap L^{\rho }({\varOmega })$, with $h\ge 1, \,\, \rho \ge 1$. Then there exist a positive constant C, depending on $N,\,h,\,\rho$ and $\sigma$ such that

$$\begin{aligned} ||v||_{L^{\sigma }({\varOmega })}\le C||\nabla u||_{(L^{h}({\varOmega }))^{N}}^{\eta }||v||_{L^{\rho }({\varOmega })}^{1-\eta }, \end{aligned}$$

for every $\eta$ and $\sigma$ satisfying

$$\begin{aligned} 0<\eta <1,\,\,\,\, \frac{1}{\sigma }=\eta \left( \frac{1}{h}-\frac{1}{N}\right) +\frac{1-\eta }{\rho }. \end{aligned}$$

An immediate consequence of the previous Lemma is the following embedding results

$$\begin{aligned} \int _{Q}|v|^{\sigma }dxdt\le C||v||_{L^{\infty }(0,T;L^{\rho }({\varOmega }))}^{\frac{\rho h}{N}}\int _{Q}|\nabla u|^{h}dxdt, \end{aligned}$$

which holds for every function $v\in L^{h}(0,T;W_{0}^{1,h}({\varOmega }))\cap L^{\infty }(0,T;L^{\rho }({\varOmega }))$, with $h\ge 1,\, \rho \ge 1$ and $\sigma =\frac{h(N+\rho )}{N}$.

Lemma 2

Let $C,\,\lambda ,\,k_{0},\,\mu$ be real positive numbers, where $\mu >1$. Let $\varrho :{\mathbb {R}}_{+}\longrightarrow {\mathbb {R}}_{+}$ be a decreasing function such that

$$\begin{aligned} \varrho (h)\le \frac{C}{(h-k)^{\lambda }}[\varrho (k)]^{\mu },\,\,\, \forall h>k\ge k_{0}. \end{aligned}$$

Then $\varrho (k_{0}+d)=0$, where $d^{\lambda }=C[\varrho (k_{0})]^{\mu -1}2^{\frac{\mu \lambda }{\mu -1}}$.

Now we give the definition of weak solution of problem (1).

Definition 1

A weak solution to problem (1) is a function u in $L^{1}(0,T;W_{0}^{1,1}({\varOmega }))$ such that, for every $\omega \subset \subset {\varOmega },$ there exists $c_{\omega }$ such that $u\ge c_{\omega }>0$ in $\omega \times (0,T)$, $\frac{|\nabla u|^{p}}{u^{\theta }}\in L^{1}(Q)$. Furthermore, we have that

$$\begin{aligned}&-\int _{Q}u\phi _{t}\,dx\,dt+\int _{Q}|\nabla u|^{p-2}\nabla u \cdot \nabla \phi \,dx\,dt+\int _{Q}b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }}\phi \,dx\,dt\nonumber \\&\quad =\int _{Q}f\phi \,dx\,dt, \end{aligned}$$

(3)

for every $\phi \in L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\infty }(Q).$

Now we give our main results.

Theorem 1

Let $0<\theta <1.$ Assume that f is a positive function belonging to $L^{m}(Q),$ with $m>\frac{N}{p}+1.$ Then there exists a function

$$\begin{aligned} u\in L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\infty }(Q) \end{aligned}$$

solution of problem (1) in the sense of Definition 1.

Theorem 2

Let $0<\theta <1.$ Assume that f is a positive function belonging to $L^{m}(Q),$ with $m=\frac{N}{p}+1.$ Then there exists a function

$$\begin{aligned} u\in L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\frac{N(p-\theta )}{N-p}}(Q) \end{aligned}$$

solution of problem (1) in the sense of Definition 1.

Theorem 3

Let $0<\theta <1.$ Assume that f is a positive function belonging to $L^{m}(Q),$ with

$$\begin{aligned} \frac{p(N+2+\theta )}{p(N+2+\theta )-N(1+\theta )}\le m<\frac{N}{p}+1. \end{aligned}$$

Then there exists a function

$$\begin{aligned} u\in L^{p}(0,T;W_{0}^{1,p}({\varOmega })) \end{aligned}$$

solution of problem (1) in the sense of Definition 1. Moreover $u\in L^{\sigma }(Q),$ where

$$\begin{aligned} \sigma =\frac{m(N(p-1-\theta )+p)}{N-pm+p}. \end{aligned}$$

Theorem 4

Let $0<\theta <1.$ Assume that f is a positive function belonging to $L^{m}(Q),$ with

$$\begin{aligned} \max \left( 1,\, \frac{(p-1)(N+2+\theta )}{(p-1)(N+2+\theta )-(N\theta -1)}\right)<m<\frac{p(N+2+\theta )}{p(N+2+\theta )-N(1+\theta )}. \end{aligned}$$

Then there exists a function

$$\begin{aligned} u\in L^{q}(0,T;W_{0}^{1,q}({\varOmega }))\cap L^{\sigma }(Q) \end{aligned}$$

solution of problem (1) in the sense of Definition 1, where

$$\begin{aligned} q=\frac{m(N(p-1-\theta )+p)}{N+1-(1+\theta )(m-1)} \text{ and } \sigma =\frac{m(N(p-1-\theta )+p)}{N-pm+p}. \end{aligned}$$

Remark 1

The condition $m>\max \left( 1,\, \frac{(p-1)(N+2+\theta )}{(p-1)(N+2+\theta )-(N\theta -1)}\right)$ is due to the fact that q must not be smaller than $p-1$ and the choice of $m>1$ in the above Theorem. Note that if $0<\theta <\frac{1}{N},$ then $\frac{(p-1)(N+2+\theta )}{(p-1)(N+2+\theta )-(N\theta -1)}<1.$

Theorem 5

Let $0<\theta <1.$ Assume that f is a positive function belonging to $L^{1}(Q).$ Then there exists a function

$$\begin{aligned} u\in L^{\delta }(0,T;W_{0}^{1,\delta }({\varOmega })) \end{aligned}$$

solution of problem (1) in the sense of Definition 1, where $\delta =\frac{N(p-\theta )}{N-\theta }.$

Remark 2

If $p=2,$ the results we obtain are similar to the regularity ones concerning the elliptic case. More precisely, we refer to [26, Theorem 2.2] for Theorem 1, [4, Theorem 1.1] for Theorem 3, [26, Theorem 2.3] for Theorem 4 and [26, Theorem 2.4] for Theorem 5.

3 A Priori Estimate and Preliminary Facts

Let $n\in {\mathbb {N}}$. We approximate the problem (1) by the following nonlinear and non-singular problem

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial u_{n}}{\partial t}-\text{ div }(|\nabla u_{n}|^{p-2}\nabla u_{n})+b(x,t)\frac{u_{n}|\nabla u|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}=f_{n} &{} \text{ in } &{} Q,\\ u_{n}(x,t)=0 &{} \text{ on } &{} {\varGamma },\\ u_{n}(x,0)=0 &{} \text{ in } &{} {\varOmega }, \end{array} \right. \end{aligned}$$

(4)

where $f_{n}=\frac{f}{1+\frac{1}{n}f}$ and $f_{n}\in L^{\infty }(Q),$ such that

$$\begin{aligned} ||f_{n}||_{L^{m}(Q)}\le ||f||_{L^{m}(Q)} \,\,\;\text{ and } \,\;\; f_{n}\rightarrow f\;\; \text{ strongly } \text{ in }\;\; L^{m}(Q), \; m\ge 1. \end{aligned}$$

(5)

The problem (4) admits weak solutions $u_{n}$ belonging to $L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\infty }(Q),$ see [1, 5, 17]. Since the right hand side of (4) is non-negative, this implies that $u_{n}$ is non-negative.

We are now going to prove some a priori estimates. The next Lemma gives a control of the natural growth term.

Lemma 3

Let $u_{n}$ be solutions to problem (4).Then it results

$$\begin{aligned} \int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\le \int _{Q}f. \end{aligned}$$

(6)

Proof

For any fixed $h>0,$ let us consider $\frac{T_{h}(u_{n})}{h}$ as a test function in the approximated problem (4). Then, we have

$$\begin{aligned}&\int _{0}^{T}\int _{{\varOmega }}\frac{\partial u_{n}}{\partial t}\frac{T_{h}(u_{n})}{h}+\frac{1}{h}\int _{Q}|\nabla u_{n}| ^{p-2}\nabla u_{n}\nabla T_{h}(u_{n})\\&\quad +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\frac{T_{h}(u_{n})}{h}=\int _{Q}f_{n}\frac{T_{h}(u_{n})}{h}. \end{aligned}$$

Therefore

$$\begin{aligned}&\int _{{\varOmega }}S_{k}(u_{n}(x,T))+\frac{1}{h}\int _{\{u_{n}\le h\}}|\nabla T_{h}(u_{n})|^{p}\\&\quad +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\frac{T_{h}(u_{n})}{h}=\int _{Q}f_{n}\frac{T_{h}(u_{n})}{h}, \end{aligned}$$

where $S_{k}(y)=\int _{0}^{y}T_{k}(\ell )\,d\ell .$ Observe that $S_{k}(y)\ge \frac{T_{k}(y)^{2}}{2}$ for every $y\ge 0.$

Now, dropping the first and second non-negative terms in the last equality and using (2), we obtain

$$\begin{aligned} 0\le \int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\frac{T_{h}(u_{n})}{h}\le \int _{Q}f_{n}\frac{T_{h}(u_{n})}{h}. \end{aligned}$$

Using the fact that $f_{n}\le f$ and $\frac{T_{h}(u_{n})}{h}\le 1,$ then

$$\begin{aligned} \int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\frac{T_{h}(u_{n})}{h}\le \int _{Q}f. \end{aligned}$$

Letting h tend to 0,  we deduce (6) by Fatou’s Lemma. $\square$

Remark 3

In view of Lemma 3, from (2) and the fact $u_{n}\ge 0,$ we have $\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\ge 0,$ $f\in L^{1}(Q)$ one has that

$$\begin{aligned} \int _{Q} \bigg | b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}-f\bigg |\le \int _{Q} b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}+\int _{Q}f\le 2\int _{Q}f<C, \end{aligned}$$

where C not depending on n. Hence

$$\begin{aligned} b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}-f\in L^{1}(Q). \end{aligned}$$

We now prove five a priori estimates on $u_{n},$ which are true for every $\theta \in (0,1).$

Lemma 4

Let the assumptions of Theorem 1 be in force. Then the solution $u_{n}$ of (4) is uniformly bounded in $L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\infty }(Q).$

Proof

For $k>0,$ choose $G_{k}(u_{n})$ as test function in the approximate problem (4). We have

$$\begin{aligned}&\int _{0}^{t}\int _{{\varOmega }}\frac{\partial u_{n}}{\partial t }G_{k}(u_{n})+\int _{0}^{t}\int _{{\varOmega }}|\nabla u_{n}|^{p-2}\nabla u_{n}\nabla G_{k}(u_{n})\\&\quad +\int _{0}^{t}\int _{{\varOmega }}b(x,\tau )\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}G_{k}(u_{n})=\int _{0}^{t}\int _{{\varOmega }}f_{n}G_{k}(u_{n}), \end{aligned}$$

for $t\in (0,T].$ Let as denoted by $A_{k,n}(t)$ the following set

$$\begin{aligned} A_{k,n}(t)=\{x\in {\varOmega }: |u_{n}(x,t)|>k\}. \end{aligned}$$

Dropping the third non-negative term, using integration by part and by Hölder’s inequality in last equality, we get

$$\begin{aligned}&\int _{A_{k,n}(t)}|G_{k}(u_{n}(t))|^{2}+2\int _{0}^{t}\int _{A_{k,n}(\tau )}|\nabla G_{k}(u_{n})|^{p}\\&\quad \le C\left( \int _{0}^{t}\int _{A_{k,n}(\tau )}|G_{k}(u_{n})|^{m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned}&||G_{k}(u_{n})||^{2}_{L^{\infty }(0,T;L^{2}(A_{k,n}(t))}+2\int _{0}^{T}\int _{A_{k,n}(t)}|\nabla G_{k}(u_{n})|^{p}\\&\quad \le C\left( \int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}. \end{aligned} \end{aligned}$$

(7)

Applying Lemma 1 (here $\rho =2,\, h=p$ and $v=G_{k}(u_{n})$)

$$\begin{aligned}&\int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{\frac{p(N+2)}{N}}\\&\quad \le ||G_{k}(u_{n})||^{\frac{2p}{N}}_{L^{\infty }(0,T;L^{2}(A_{k,n}(t))}\int _{0}^{T}\int _{A_{k,n}(t)}|\nabla G_{k}(u_{n})|^{p}. \end{aligned}$$

Using (7) in last inequality, we deduce that

$$\begin{aligned} \int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{\frac{p(N+2)}{N}}\le C\left( \int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{m^{\prime }}\right) ^{\frac{1}{m^{\prime }}(\frac{p}{N}+1)}. \end{aligned}$$

(8)

By virtue of $m>\frac{N}{p}+1,$ then $\frac{p(N+2)}{Nm^{_\prime }}>1$. Applying Hölder’s inequality with indices $\left( \frac{p(N+2)}{Nm^{\prime }},\, \frac{p(N+2)}{p(N+2)-Nm^{\prime }}\right)$ in (8), we get

$$\begin{aligned}&\int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{\frac{p(N+2)}{N}}\le C\left( \int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{\frac{p(N+2)}{N}}\right) ^{\frac{p+N}{p(N+2)}}\\&\quad \times \left( \int _{0}^{T}|A_{k,n}(t)|\right) ^{\frac{1}{m^{\prime }}(\frac{p}{N}+1)(1-\frac{Nm^{\prime }}{p(N+2)})}. \end{aligned}$$

Thanks to Young’s inequality with parameter $\epsilon ,$ we obtain

$$\begin{aligned}&\int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{\frac{p(N+2)}{N}}\le \epsilon {\bar{C}} \int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{\frac{p(N+2)}{N}}\\&\quad +C_{\epsilon }\left( \int _{0}^{T}|A_{k,n}(t)|\right) ^{\frac{1}{m^{\prime }}(\frac{p}{N}+1)(1-\frac{Nm^{\prime }}{p(N+2)})\frac{p(N+2)}{N(p-1)+p}}, \end{aligned}$$

where ${\bar{C}}$ is a positive constant independent on n. Taking $\epsilon =\frac{1}{2{\bar{C}}},$ we obtain that

$$\begin{aligned} \int _{0}^{T}\int _{A_{k,n}(t)}|G_{k}(u_{n})|^{\frac{p(N+2)}{N}}\le C\left( \int _{0}^{T}|A_{k,n}(t)|\right) ^{\frac{1}{m^{\prime }}(\frac{p}{N}+1)(1-\frac{Nm^{\prime }}{p(N+2)})\frac{p(N+2)}{N(p-1)+p}}. \end{aligned}$$

We not that, if $h>k,$ we have $|G_{k}(u_{n})|>h-k$ on $A_{k,n}(t)$ and $A_{h,n}(t)\subset A_{k,n}(t).$ Hence

$$\begin{aligned} \int _{0}^{T}A_{h,n}(t)\le \frac{C}{(h-k)^{\frac{p(N+2)}{N}}}\left( \int _{0}^{T}|A_{k,n}(t)|\right) ^{\frac{1}{m^{\prime }}(\frac{p}{N}+1)(1-\frac{Nm^{\prime }}{p(N+2)})\frac{p(N+2)}{N(p-1)+p}}. \end{aligned}$$

Let $\varrho (k)=\displaystyle \int _{0}^{T}|A_{k,n}(t)|,$ then

$$\begin{aligned} \varrho (h)\le \frac{C}{(h-k)^{\lambda }}\left[ \varrho (k)\right] ^{\mu }, \end{aligned}$$

(9)

where $\lambda =\frac{p(N+2)}{N}>0$   and   $\mu = \frac{1}{m^{\prime }}\left( \frac{p}{N}+1\right) \left( 1-\frac{Nm^{\prime }}{p(N+2)}\right) \frac{p(N+2)}{N(p-1)+p}.$ By the fact that $m>\frac{N}{p}+1,$ then we have $\mu >1$ and by Lemma 2, there exists $\gamma _{1}>1$ such that

$$\begin{aligned} \varrho (\gamma _{1})=0. \end{aligned}$$

Hence there exists a constant $C>0,$ independent of n such that

$$\begin{aligned} \Vert u_{n}\Vert _{L^{\infty }(Q)}\le C\;\; in\;\; Q. \end{aligned}$$

(10)

Let us $u_{n}$ test function in problem (4), obtaining

$$\begin{aligned} \frac{1}{2}\int _{{\varOmega }}u_{n}(x,T)^{2}+\int _{Q}|\nabla u_{n}|^{p}+\int _{Q}b(x,t)\frac{u_{n}^{2}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}=\int _{Q}f_{n}u_{n}. \end{aligned}$$

Since $0<\alpha \le b(x,t),$ then we can drop the first and third non-negative terms, we get

$$\begin{aligned} \int _{Q}|\nabla u_{n}|^{p}\le \int _{Q}f_{n}u_{n}. \end{aligned}$$

Applying Hölder’s inequality twice and from (5), (10), it follows that

$$\begin{aligned} \int _{Q}|\nabla u_{n}|^{p}\le \int _{Q} f_{n}u_{n}\le \Vert u_{n}\Vert _{L^{\infty }(Q)}\Vert f\Vert _{L^{m}(Q)}|Q|^{\frac{1}{m^{\prime }}}\le C. \end{aligned}$$

(11)

As consequence of estimate (10) and (11), $u_{n}$ is uniformly bounded in $L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\infty }(Q).$ $\square$

Lemma 5

Let the assumptions of Theorem 2 be in force. Then the solution $u_{n}$ of (4) is uniformly bounded in $L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\frac{N(p+\theta )}{N-p}}(Q).$

Proof

We test (4) by $\varphi (u_{n})=((u_{n}+1)^{\theta +1}-1)$, obtaining

$$\begin{aligned}&\int _{{\varOmega }}{\varPsi }(u_{n}(x,T))+(\theta +1)\int _{Q}|\nabla u_{n}|^{p}(u_{n}+1)^{\theta }\\&\qquad +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}(u_{n}+1)^{\theta +1} \\&\quad =\int _{Q}f_{n}\left( (u_{n}+1)^{\theta +1}-1\right) +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}, \end{aligned}$$

where ${\varPsi }(y)=\int _{0}^{y}\varphi (\ell )\,d\ell .$ Observe that $\varphi$ is increasing and positive on $[0, +\infty ),$ we deduce that $\int _{{\varOmega }}{\varPsi }(u_{n}(x,T))\ge 0,$ and from (6), we have

$$\begin{aligned} \int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\le \int _{Q}f. \end{aligned}$$

Dropping the first non-negative term, recalling (2), and by the fact that $\frac{1}{(u_{n}+1)^{\theta +1}}\le \frac{1}{(u_{n}+\frac{1}{n})^{\theta +1}},$ we deduce

$$\begin{aligned} (\theta +1)\int _{Q}|\nabla u_{n}|^{p}(u_{n}+1)^{\theta }+\alpha \int _{Q}u_{n}|\nabla u_{n}|^{p}\le \int _{Q} f_{n}(u_{n}+1)^{\theta +1}+ C.\qquad \end{aligned}$$

(12)

Applying Hölder’s inequality with indices $(m,\, m^{\prime })=\left( \frac{N+p}{p},\, \frac{N+p}{N}\right) ,$ we get

$$\begin{aligned} \begin{aligned}&\frac{(\theta +1)p^{p}}{(\theta +p)^{p}}\int _{Q}|\nabla (u_{n}+1)^{\frac{\theta +p}{p}}|^{p}+\alpha \int _{Q}u_{n}|\nabla u_{n}|^{p}\\&\quad \le C \left( \int _{Q} (u_{n}+1)^{\frac{(\theta +1)(N+p)}{N}}\right) ^{\frac{N}{N+p}}+ C. \end{aligned} \end{aligned}$$

(13)

Thanks to the Sobolev inequality applied in (13), we have

$$\begin{aligned} \left( \int _{Q}(u_{n}+1)^{\frac{N(p+\theta )}{N-p}}\right) ^{\frac{N-p}{p}}&=\left( \int _{Q}(u_{n}+1)^{\frac{p^{*}(\theta +p)}{p}}\right) ^{\frac{N-p}{N}}\nonumber \\&\le C \left( \int _{Q} (u_{n}+1)^{\frac{(\theta +1)(N+p)}{N}}\right) ^{\frac{N}{N+p}}+ C. \end{aligned}$$

(14)

Being $\frac{(\theta +1)(N+p)}{N}<\frac{N(p+\theta )}{N-p},$ we apply Hölder’s inequality with indices $\left( \frac{N^{2}(p+\theta )}{(N^{2}-p^{2})(\theta +1)},\, \frac{N^{2}(\theta +p)}{N^{2}(p+\theta )-(N^{2}-p^{2})(\theta +1)} \right)$, we deduce

$$\begin{aligned} \left( \int _{Q}(u_{n}+1)^{\frac{N(p+\theta )}{N-p}}\right) ^{\frac{N-p}{N}}\le C\left( \int _{Q}(u_{n}+1)^{\frac{N(p+\theta )}{N-p}}\right) ^{\frac{(N-p)(\theta +1)}{N(p+\theta )}}+C. \end{aligned}$$

(15)

Note that $\frac{(N-p)(\theta +1)}{N(p+\theta )}<\frac{N-p}{N}.$ Using Young’s inequality in the above estimate, we get

$$\begin{aligned} \int _{Q}(1+u_{n})^{\frac{N(p+\theta )}{N-p}}\le C. \end{aligned}$$

(16)

Therefore

$$\begin{aligned} \int _{Q}u_{n}^{\frac{N(p+\theta )}{N-p}}\le C. \end{aligned}$$

(17)

Let us suppose that $u_{n}\ge 1.$ Then, we come back to (13), so we obtain that

$$\begin{aligned} \alpha \int _{\{u_{n}\ge 1\}}|\nabla u_{n}|^{p} \le C \left( \int _{Q} (u_{n}+1)^{\frac{(\theta +1)(N+p)}{N}}\right) ^{\frac{N}{N+p}}+ C. \end{aligned}$$

Being $\frac{(\theta +1)(N+p)}{N}<\frac{N(p+\theta )}{N-p}.$ We apply again the Hölder inequality with the same indices used in (15), so we get

$$\begin{aligned} \alpha \int _{\{u_{n}\ge 1\}}|\nabla u_{n}|^{p}\le C\left( \int _{Q}(u_{n}+1)^{\frac{N(p+\theta )}{N-p}} \right) ^{\frac{(N-p)(\theta +1)}{N(p+\theta )}}+C. \end{aligned}$$

Then, from (16), it follows that

$$\begin{aligned} \int _{\{u_{n}\ge 1\}}|\nabla u_{n}|^{p}\le C. \end{aligned}$$

(18)

It remains to analyse the behaviour of $\nabla u_{n}$ in $\{u_{n}< 1\}.$ Taking $T_{1}(u_{n})$ as a test function in (4), we get

$$\begin{aligned}&\int _{0}^{T}\int _{{\varOmega }}\frac{\partial u_{n}}{\partial t}T_{1}(u_{n})+\int _{Q}|\nabla u_{n}|^{p-2}\nabla u_{n}\nabla T_{1}(u_{n})\\&\quad +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n})=\int _{Q}f_{n}T_{1}(u_{n}). \end{aligned}$$

Therefore, we get from (2), that

$$\begin{aligned} \int _{{\varOmega }}S_{1}(u_{n}(x, T))+\int _{\{u_{n}< 1\}}|\nabla T_{1}(u_{n})|^{p}+\alpha \int _{Q}\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\le \int _{Q}f_{n}T_{1}(u_{n}), \end{aligned}$$

where $S_{1}(y)=\int _{0}^{y}T_{1}(\ell )\,d\ell .$ Observe that $S_{1}(y)\ge \frac{T_{1}(y)^{2}}{2}\,$ for every $y\ge 0.$

Dropping the first and third non-negative terms and using (5), we obtain

$$\begin{aligned} \int _{\{u_{n}< 1\}}|\nabla u_{n}|^{p}=\int _{Q}|\nabla T_{1}(u_{n})|^{p}\le \int _{Q}f_{n}T_{1}(u_{n})\le \int _{Q}f\le C. \end{aligned}$$

(19)

The inequality (18) combined with (19), implies that

$$\begin{aligned} \int _{Q}|\nabla u_{n}|^{p}=\int _{\{u_{n}\ge 1\}}|\nabla u_{n}|^{p}+\int _{\{u_{n}< 1\}}|\nabla u_{n}|^{p}\le C. \end{aligned}$$

(20)

Then (17) and (20) imply that $u_{n}$ is uniformly bounded in $L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\frac{N(p+\theta )}{N-p}}(Q)$ This completes the proof of Lemma 5. $\square$

Lemma 6

Let the assumptions of Theorem 3 be in force. Then the solution $u_{n}$ of (4) is uniformly bounded in $L^{p}(0,T;W_{0}^{1,p}({\varOmega }))\cap L^{\sigma }(Q),$ where

$$\begin{aligned} \sigma =\frac{m(N(p-1-\theta )+p)}{N-pm+p}. \end{aligned}$$

Proof

Taking $\psi (u_{n})=((1+u_{n})^{\lambda }-1)\chi _{(0,t)},$ (with $\lambda \ge 1+\theta$ ) as a test function in problem (4), we have

$$\begin{aligned} \begin{aligned}&\displaystyle \int _{{\varOmega }}{\varPsi }(u_{n}(x,t))+\lambda \displaystyle \int _{0}^{t}\int _{{\varOmega }}|\nabla u_{n}|^{p}(1+u_{n})^{\lambda -1}\\&\qquad +\displaystyle \int _{0}^{t}\int _{{\varOmega }}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}(u_{n}+1)^{\lambda }\\&\qquad \le \displaystyle \int _{Q}f((u_{n}+1)^{\lambda }-1)+\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}, \end{aligned} \end{aligned}$$

(21)

where

$$\begin{aligned} {\varPsi }(s)=\int _{0}^{s}\psi (z)dz. \end{aligned}$$

(22)

By using (6) in the right hand side and (2) in the left hand side in (21), we get

$$\begin{aligned} \begin{aligned}&\int _{{\varOmega }}{\varPsi }(u_{n}(x,t))+\lambda \int _{0}^{t}\int _{{\varOmega }}|\nabla u_{n}|^{p}(1+u_{n})^{\lambda -1}\\&\qquad +\alpha \int _{0}^{t}\int _{{\varOmega }}\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}(1+u_{n})^{\lambda }\\&\qquad \le \int _{Q}f((1+u_{n})^{\lambda }-1)+C. \end{aligned} \end{aligned}$$

(23)

By the definitions of ${\varPsi }(s)$ and $\psi (s)$, we can get whenever $\lambda >1$

$$\begin{aligned} {\varPsi }(s)\ge \frac{s^{\lambda +1}}{\lambda +1},\qquad \forall s\in {\mathbb {R}}^{+}. \end{aligned}$$

(24)

Combining (23) and (24) and applying Hölder’s inequality with indices $(m,m^{\prime })$, we have

$$\begin{aligned} \begin{aligned}&\frac{1}{\lambda +1}\int _{{\varOmega }}u_{n}^{\lambda +1}+\lambda \int _{Q}|\nabla u_{n}|^{p}(1+u_{n})^{\lambda -1}\\&\qquad +\alpha \int _{0}^{t}\int _{{\varOmega }}\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}(1+u_{n})^{\lambda }\\&\quad \le C\left( \int _{Q}((1+ u_{n})^{\lambda }-1)^{m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned} \end{aligned}$$

(25)

By easy simplifications we can write (25) as follows

$$\begin{aligned} \begin{aligned}&\frac{1}{\lambda +1}\int _{{\varOmega }}u_{n}^{\lambda +1}+\int _{0}^{t}\int _{{\varOmega }}|\nabla u_{n}|^{p}(1+u_{n})^{\lambda -\theta -1}\left[ \lambda (1+u_{n})^{\theta }+\alpha u_{n}\right] \\&\quad \le C\left( \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned} \end{aligned}$$

Since $\lambda ,\,\alpha ,\,u_{n}\ge 0,$ we have $\lambda (1+u_{n})^{\theta }+\alpha u_{n}\ge \lambda .$ Furthermore, recalling that $\lambda \ge 1+\theta ,$ we can estimate the last inequality as follows

$$\begin{aligned} \begin{aligned}&\frac{1}{\lambda +1}\int _{{\varOmega }}[u_{n}^{\frac{\lambda -1-\theta +p}{p}}]^{\frac{p(\lambda +1)}{\lambda -1-\theta +p}}+\frac{p^{p}\lambda }{(\lambda -1-\theta +p)^{p}}\int _{0}^{t}\int _{{\varOmega }}|\nabla u_{n}^{\frac{\lambda -1-\theta +p}{p}}|^{p} \\&\quad \le C\left( \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned} \end{aligned}$$

Now passing to the supremum in time for $t\in (0,T)$ in the last inequality, we deduce

$$\begin{aligned}&\frac{1}{\lambda +1}\Vert u_{n}^{\frac{\lambda -1-\theta +p}{p}}\Vert ^{\frac{p(\lambda +1)}{\lambda -1-\theta +p}}_{L^{\infty }(0,T;L^{\frac{p(\lambda +1)}{\lambda -1-\theta +1}}({\varOmega }))}+\frac{p^{p}\lambda }{(\lambda -1-\theta +p)^{p}}\int _{Q}|\nabla u_{n}^{\frac{\lambda -1-\theta +p}{p}}|^{p} \nonumber \\&\quad \le C\left( \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(26)

Applying Lemma 1 (here $v=u_{n}^{\frac{\lambda -1-\theta +p}{p}},\, \rho =\frac{p(\lambda +1)}{\lambda -1-\theta },\, h=p$ ) and from (26), we have

$$\begin{aligned}&\int _{Q}[u_{n}^{\frac{\lambda -1-\theta +p}{p}}]^{p\frac{N+\frac{p(\lambda +1)}{\lambda -1-\theta +p}}{N}}\le C\left( \Vert u_{n}^{\frac{\lambda -1-\theta +p}{p}}\Vert ^{\frac{p(\lambda +1)}{\lambda -1-\theta +p}}_{L^{\infty }(0,T;L^{\frac{p(\lambda +1)}{\lambda -1-\theta +1}}({\varOmega }))}\right) ^{\frac{p}{N}}\\&\quad \times \displaystyle \int _{Q}|\nabla u_{n}^{\frac{\lambda -1-\theta +p}{p}}|^{p} \le C\left( \displaystyle \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C. \end{aligned}$$

Then, we can write the last inequality as follows

$$\begin{aligned} \int _{Q}u_{n}^{\frac{N(\lambda -1-\theta +p)+p(\lambda +1)}{N}}\le C\left( \displaystyle \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(27)

Choose now $\lambda$ such that

$$\begin{aligned} \sigma =\frac{N(\lambda -1-\theta +p)+p(\lambda +1)}{N}=\lambda m^{\prime }, \end{aligned}$$

(28)

that is

$$\begin{aligned} \lambda =\frac{(m-1)(N(p-1-\theta )+p)}{N-pm+p},\;\;\; \sigma =\frac{m(N(p-1-\theta )+p)}{N-pm+p}. \end{aligned}$$

Combining (27) and (28), we get

$$\begin{aligned} \int _{Q}u_{n}^{\sigma }\le C\left( \int _{Q}(1+u_{n})^{\sigma } \right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(29)

By virtue of $m<\frac{N}{p}+1,$ we have $\left( \frac{p}{N}+1\right) \frac{1}{m^{\prime }}<1$ and applying Young’s inequality with indices $\left( \frac{Nm^{\prime }}{N+p},\, \frac{Nm^{\prime }}{Nm^{\prime }-(N+p)}\right)$ in (29), we deduce that

$$\begin{aligned} \int _{Q}u_{n}^{\sigma }\le C. \end{aligned}$$

(30)

The condition $m\ge \frac{p(N+2+\theta )}{p(N+2+\theta )-N(1+\theta )}$ ensures that $\lambda \ge 1+\theta$. By the fact that $(1+u_{n})^{\lambda -1-\theta }\ge 1$ and combining (26), (30), we get

$$\begin{aligned}&\int _{Q}|\nabla u_{n}|^{p}\le \int _{Q}|\nabla u_{n}|^{p}(1+u_{n})^{\lambda -1-\theta }\le C\left( \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C \\&\quad \le C\left( \int _{Q}u_{n}^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C= C\left( \int _{Q}u_{n}^{\sigma }\right) ^{\frac{1}{m^{\prime }}}+C\le C. \end{aligned}$$

This implies

$$\begin{aligned} \int _{Q}|\nabla u_{n}|^{p}\le C. \end{aligned}$$

(31)

$\square$

Lemma 7

Let the assumptions of Theorem 4 be in force. Then the solution $u_{n}$ of (4) is uniformly bounded in $L^{q}(0,T;W_{0}^{1,q}({\varOmega }))\cap L^{\sigma }(Q),$ where

$$\begin{aligned} q=\frac{m(N(p-1-\theta )+p)}{N+1-(1+\theta )(m-1)} \text{ and } \sigma =\frac{m(N(p-1-\theta )+p)}{N-pm+p}. \end{aligned}$$

Proof

By the definitions of ${\varPsi }(s)$ and $\psi (s)$ in the proof of Lemma 6, we also have

$$\begin{aligned} {\varPsi }(s)\ge Cs^{\lambda +1}-C,\quad \forall s\in {\mathbb {R}}^{+}, \end{aligned}$$

(32)

assuming $0< \lambda < 1 + \theta$. Going back to (23) and from (32), we get

$$\begin{aligned}&C\displaystyle \int _{{\varOmega }}u_{n}(x,t)^{\lambda +1}+\lambda \displaystyle \int _{0}^{t}\int _{{\varOmega }}|\nabla u_{n}|^{p}(1+u_{n})^{\lambda -1}\\&\qquad +\alpha \displaystyle \int _{0}^{t}\int _{{\varOmega }}u_{n}|\nabla u_{n}|^{p}(1+u_{n})^{\lambda -1-\theta }\\&\quad \le \displaystyle \int _{Q}f(1+u_{n})^{\lambda }+Cmeas({\varOmega })+C. \end{aligned}$$

By the fact that $\lambda (1+u_{n})^{\theta }+\alpha u_{n}\ge \lambda$, and applying Hölder’s inequality with indices $(m,\, m^{\prime }),$ the last inequality can be estimate as follows

$$\begin{aligned}&C\displaystyle \int _{{\varOmega }}u_{n}(x,t)^{\lambda +1}+\lambda \displaystyle \int _{0}^{t}\int _{{\varOmega }}\frac{|\nabla u_{n}|^{p}}{(1+u_{n})^{1+\theta -\lambda }}\\&\quad \le C \displaystyle \left( \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

Passing to the supremum in time for $t\in (0,T),$ we have

$$\begin{aligned} \begin{aligned}&C\Vert u_{n}\Vert ^{\lambda +1}_{L^{\infty }(0,T;L^{\lambda +1}({\varOmega }))}+\lambda \displaystyle \int _{Q}\frac{|\nabla u_{n}|^{p}}{(1+u_{n})^{1+\theta -\lambda }}\\&\quad \le C \displaystyle \left( \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned} \end{aligned}$$

(33)

Let $1<q<p$. Applying Hölder’s inequality with indices $\left( \frac{p}{q},\frac{p}{p-q}\right) ,$ we get

$$\begin{aligned}&\displaystyle \int _{Q}|\nabla u_{n}|^{q}=\int _{Q}\frac{|\nabla u_{n}|^{q}}{(1+u_{n})^{\frac{(1+\theta -\lambda )q}{p}}}(1+u_{n})^{\frac{(1+\theta -\lambda )q}{p}} \nonumber \\&\quad \le \left( \displaystyle \int _{Q}\frac{|\nabla u_{n}|^{p}}{(1+u_{n})^{1+\theta -\lambda }}\right) ^{\frac{q}{p}}\left( \displaystyle \int _{Q}(1+u_{n})^{\frac{(1+\theta -\lambda )q}{p-q}}\right) ^{\frac{p-q}{p}}. \end{aligned}$$

(34)

The inequality (33), combined with (34), implies that

$$\begin{aligned} \begin{aligned} \int _{Q}|\nabla u_{n}|^{q}\le C\left( \left( \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+1\right) ^{\frac{q}{p}} \left( \int _{Q}(1+u_{n})^{\frac{(1+\theta -\lambda )q}{p-q}}\right) ^{\frac{p-q}{p}}. \end{aligned} \end{aligned}$$

(35)

Applying Lemma 1 (here $v=u_{n},\, \rho =\lambda +1,\, h=q$ ), we have

$$\begin{aligned} \int _{Q}u_{n}^{\frac{q(N+\lambda +1)}{N}}\le ||u_{n}||_{L^{\infty }(0,T;L^{\lambda +1}({\varOmega }))}^{\frac{q(\lambda +1)}{N}}\int _{Q}|\nabla u_{n}|^{q}. \end{aligned}$$

We improve the above estimate using (33) and (35), obtaining

$$\begin{aligned} \begin{aligned} \int _{Q}u_{n}^{\frac{q(N+\lambda +1)}{N}}&\le C\left( \left( \int _{Q}(1+u_{n})^{\lambda m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+1\right) ^{\frac{q}{p}+\frac{q}{N}}\\&\quad \times \left( \int _{Q}(1+u_{n})^{\frac{(1+\theta -\lambda )q}{p-q}}\right) ^{\frac{p-q}{p}}. \end{aligned} \end{aligned}$$

(36)

Choose now $\lambda$ such that

$$\begin{aligned} \sigma =\frac{q(N+\lambda +1)}{N}=\lambda m^{\prime }=\frac{(1+\theta -\lambda )q}{p-q}, \end{aligned}$$

(37)

that is equivalent to

$$\begin{aligned} \begin{aligned}&\lambda =\frac{(m-1)(N(p-1-\theta )+p)}{N-pm+p},\,\,\; q=\frac{m(N(p-1-\theta )+p)}{N+1-(1+\theta )(m-1)}\\&\quad \text{ and } \sigma =\frac{m(N(p-1-\theta )+p)}{N-pm+p}. \end{aligned} \end{aligned}$$

(38)

By using (37) in (36), we deduce

$$\begin{aligned} \int _{Q}u_{n}^{\sigma }\le C\left( \int _{Q}(1+u_{n})^{\sigma }\right) ^{\frac{1}{m^{\prime }}(\frac{q}{p}+\frac{q}{N})+\frac{p-q}{p}}+C. \end{aligned}$$

(39)

By virtue of $m<\frac{N}{p}+1,$ then $\frac{1}{m^{\prime }}\left( \frac{q}{p}+\frac{q}{N}\right) +\frac{p-q}{p} <1$. Applying Young’s inequality, we deduce

$$\begin{aligned} \int _{Q}u_{n}^{\sigma }\le C. \end{aligned}$$

(40)

Since $\lambda <1+\theta$ (i.e $m<\frac{p(N+2+\theta )}{p(N+2+\theta )-N(1+\theta )}$ ), and using (37) in (35), we get

$$\begin{aligned} \int _{Q}|\nabla u_{n}|^{q}\le \left( C\left( \int _{Q}(1+u_{n})^{\sigma }\right) ^{\frac{1}{m^{\prime }}}+C\right) ^{\frac{q}{p}}\left( \int _{Q}(1+u_{n})^{\sigma }\right) ^{\frac{p-q}{p}}. \end{aligned}$$

The above estimate and (40) allow to conclude

$$\begin{aligned} \int _{Q}|\nabla u_{n}|^{q}\le C. \end{aligned}$$

(41)

The estimates (40) and (41) completed the proof of Lemma 7. $\square$

Lemma 8

Let the assumptions of Theorem 5 be in force. Then the solution $u_{n}$ of (4) is bounded in $L^{\delta }(0,T;W_{0}^{1,\delta }({\varOmega })),$ where $\delta =\frac{N(p-\theta )}{N-\theta }.$ Moreover, the sequence $T_{k}(u_{n})$ is bounded in $L^{p}(0,T;W_{0}^{1,p}({\varOmega }))$   for every $k>0.$

Proof

By (6) and using (2), we have

$$\begin{aligned} \frac{\alpha }{2^{\theta +1}}\int _{\{u_{n}\ge 1\}}\frac{|\nabla u_{n}|^{p}}{u_{n}^{\theta }}\le \int _{\{u_{n}\ge 1\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\le \int _{Q}f. \end{aligned}$$

(42)

Let $\delta$ any positive real number such that $1<\delta <p.$ Using Hölder’s inequality with indices $\left( \frac{p}{\delta },\, \frac{p}{p-\delta }\right)$, we obtain

$$\begin{aligned}&\int _{Q}|\nabla G_{1}(u_{n})|^{\delta }= \int _{\{u_{n}\ge 1 \}}\frac{|\nabla u_{n} |^{\delta }}{u_{n}^{\frac{\theta \delta }{p}}}u_{n}^{\frac{\theta \delta }{p}} \\&\quad \le C\left[ \int _{\{u_{n}\ge 1\}}\frac{|\nabla u_{n}|^{p}}{u_{n}^{\theta }}\right] ^{\frac{\delta }{p}}\left[ \int _{\{u_{n}\ge 1\}}u_{n}^{\frac{\theta \delta }{p-\delta }}\right] ^{\frac{p-\delta }{p}}. \end{aligned}$$

Using (42) in the last inequality, we get

$$\begin{aligned} \int _{Q}|\nabla G_{1}(u_{n})|^{\delta }\le C \left[ \int _{\{u_{n}\ge 1\}}u_{n}^{\frac{\theta \delta }{p-\delta }}\right] ^{\frac{p-\delta }{p}}. \end{aligned}$$

(43)

The choice of $\delta =\frac{N(p-\theta )}{N-\theta }$ implies that $\delta ^{*}=\frac{\delta \theta }{p-\delta }.$ By Sobolev’s inequality on the first term of (43), we have

$$\begin{aligned} \begin{aligned}&\left( \int _{Q}G_{1}(u_{n})^{\delta ^{*}}\right) ^{\frac{\delta }{\delta ^{*}}}\le C_{0}\int _{Q}|\nabla G_{1}(u_{n})|^{\delta }\le C \left[ \int _{\{u_{n}\ge 1\}}u_{n}^{\frac{\theta \delta }{p-\delta }}\right] ^{\frac{p-\delta }{p}}\\&\quad =C \left[ \int _{\{u_{n}\ge 1\}}u_{n}^{\delta ^{*}}\right] ^{\frac{\theta }{\delta ^{*}}}\le C \left[ \int _{\{u_{n}\ge 1\}}G_{1}(u_{n})^{\delta ^{*}}\right] ^{\frac{\theta }{\delta ^{*}}}+C, \end{aligned} \end{aligned}$$

(44)

where $C_{0}$ is the Sobolev constant. Since $\theta <1,$ the inequality (44) implies that $G_{1}(u_{n}),$ hence $u_{n},$ is bounded in $L^{\delta ^{*}}(Q).$ From (43), it follows the boundedness of $G_{1}(u_{n})$ in $L^{\delta }(0,T;W_{0}^{1,\delta }({\varOmega })).$ Using $T_{1}(u_{n})$ as test function in (4), we have

$$\begin{aligned}&\int _{0}^{T}\int _{{\varOmega }}\frac{\partial u_{n}}{\partial t}T_{1}(u_{n})+\int _{Q}|\nabla u_{n}|^{p-2}\nabla u_{n}\nabla T_{1}(u_{n})\\&\qquad +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}) \\&\quad =\int _{Q}f_{n}T_{1}(u_{n})\le \int _{Q}f_{n}\le \int _{Q}f. \end{aligned}$$

Therfore

$$\begin{aligned} \int _{{\varOmega }}S_{1}(u_{n}(T))+\int _{Q}|\nabla T_{1}(u_{n})|^{p}+\alpha \int _{Q}\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}) \le \int _{Q}f_{n}T_{1}(u_{n}), \end{aligned}$$

where $S_{1}(u_{n}(T))=\int _{0}^{u_{n}(T)}T_{1}(s)\, ds.$ Since $u_{n}\ge 0,$ it easy to se that $S_{1}(u_{n}(T))\ge 0\,$ a.e. in ${\varOmega }.$ After dropping the first and third non-negative terms and using (5), the last inequality becomes

$$\begin{aligned} \int _{Q}|\nabla T_{1}( u_{n})|^{p}\le \int _{Q}f\le C. \end{aligned}$$

We deduce that $T_{1}(u_{n})$ is bounded in $L^{p}(0,T;W_{0}^{1,p}({\varOmega })),$ hence in $L^{\delta }(0,T;W_{0}^{1,\delta }({\varOmega })).$ Since $u_{n}=G_{1}(u_{n})+T_{1}(u_{n}),$ then we deduce that $u_{n}$ is bounded in $L^{\delta }(0,T;W_{0}^{1,\delta }({\varOmega })).$ Moreover, testing (4) by $T_{k}(u_{n}),$ it is follows that $T_{k}(u_{n})$ is bounded in $L^{p}(0,T;W_{0}^{1,p}({\varOmega }))$ for every $k>0.$ $\square$

Lemma 9

Let $u_{n}$ be a solution of (4). Then for every $\omega \subset \subset {\varOmega },$ there exists a positive constant $c_{\omega }$ such that

$$\begin{aligned} u_{n}\ge c_{\omega }>0,\,\,\, \, in\,\, \omega \times (0,T), \, \text{ for } \text{ every } \,\, n\in {\mathbb {N}}. \end{aligned}$$

Proof

For $s>0,$ we define the non decreasing function

$$\begin{aligned} H(s)=\int _{s}^{1}{\tilde{h}}(\sigma )d\sigma =\int _{s}^{1}h(\sigma )d\sigma -(p-1)\log s, \end{aligned}$$

where ${\tilde{h}}(s)=h(s)+\frac{p-1}{s},$   $h(s)=\frac{1}{s^{\theta }},$  and we then consider the non increasing function

$$\begin{aligned} \psi (s)=\int _{s}^{1}e^{-\beta H(\ell )}d\ell . \end{aligned}$$

Observe that    $\lim _{s\rightarrow 0^{+}}\psi (s)=+\infty$    and    $\lim _{s\rightarrow +\infty }\psi (s)=\psi _{\infty }\in [-\infty ,0).$

Let $0<\phi \in C^{\infty }_{c}({\varOmega }),$ and take $e^{-\beta H(u_{n})}\phi \in L^{p}(0,T;W_{0}^{1,p}({\varOmega }))$ as a test function in (4). Then, we have

$$\begin{aligned}&\int _{0}^{T}\int _{{\varOmega }}\frac{\partial u_{n}}{\partial t}\phi e^{-\beta H(u_{n})}+\int _{Q}|\nabla u_{n}|^{p-2}\nabla u_{n}\cdot \nabla \phi e^{-\beta H(u_{n})} \\&\qquad -\beta \int _{Q}|\nabla u_{n}|^{p}{\tilde{h}}(u_{n})\phi e^{-\beta H(u_{n})} +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{2}}{(u_{n}+\frac{1}{n})^{\theta +1}}\phi e^{-\beta H(u_{n})}\\&\quad =\int _{Q}f_{n}\phi e^{-\beta H(u_{n})}. \end{aligned}$$

Thanks to easy simplification in the last equality, we can write as follows

$$\begin{aligned}&\int _{0}^{T}\int _{{\varOmega }}\frac{\partial u_{n}}{\partial t}\phi e^{-\beta H(u_{n})}+\int _{Q}|\nabla u_{n}|^{p-2}\nabla u_{n}\cdot \nabla \phi e^{-\beta H(u_{n})}\\&\quad +\int _{Q}|\nabla u_{n}|^{p}\phi e^{-\beta H(u_{n})}\left[ \frac{b(x,t)u_{n}}{(u_{n}+\frac{1}{n})^{\theta +1}}-\beta {\tilde{h}}(u_{n})\right] =\int _{Q}f_{n}\phi e^{-\beta H(u_{n})}. \end{aligned}$$

By the fact that $\frac{s}{(s+\epsilon )^{\theta +1}}\le h(s)\le {\tilde{h}}(s),$ with $0<\epsilon <1$ and using (2), we get

$$\begin{aligned}&\int _{0}^{T}\int _{{\varOmega }}\frac{\partial u_{n}}{\partial t}\phi e^{-\beta H(u_{n})}+\int _{Q}|\nabla u_{n}|^{p-2}\nabla u_{n}\cdot \nabla \phi e^{-\beta H(u_{n})}\\&\quad \ge \int _{Q}f_{n}e^{-\beta H(u_{n})}\phi \ge \int _{Q}f_{n}(e^{-\beta H(u_{n})}-1)\phi . \end{aligned}$$

Let $v_{n}:=\psi (u_{n}),$ then $\nabla v_{n}=-e^{\beta H(u_{n})}\nabla u_{n},$ and so we can write the last inequality as follows

$$\begin{aligned} -\int _{0}^{T}\int _{{\varOmega }}\frac{\partial v_{n}}{\partial t}\phi -\int _{Q}|\nabla v_{n}|^{p-2}\nabla v_{n}\cdot \nabla \phi \ge \int _{Q}f_{n}(e^{-\beta H(\psi ^{-1}(v_{n}))}-1)\phi . \end{aligned}$$

Thus, we deduce that $v_{n}$ is subsolution of

$$\begin{aligned} \frac{\partial z}{\partial t}-{\varDelta }_{p}z+f(x,t)g(z)=0,\,\, \text{ in } \, Q, \end{aligned}$$

with $g(s)=e^{-\beta H(\psi ^{-1}(s))}-1$   for every $s\in (\psi _{\infty },+\infty ).$ The function g(s) satisfies:

• (1) $\frac{g(s)}{s^{p-1}}$ is increasing   for $s>0$   large.

• (2) The Keller-Osserman condition, i.e.,

  $$\begin{aligned} \int _{\sigma _{0}}^{+\infty }\left( \int _{0}^{\sigma }g(s)\,ds\right) ^{\frac{-1}{p}}d\sigma <+\infty \,\,\, \text {for some}\,\, \,\, \sigma _{0}>0. \end{aligned}$$

For the proof of (1) and (2) see [28]. Since f satisfies

$$\begin{aligned} \text {ess}\inf \{f(x,t):x\in \omega ,t\in (0,t)\}>0\,\,\,\,\, \forall \,\omega \subset \subset {\varOmega }, \end{aligned}$$

we can apply Lemma 3.12 in [16] to the previous equation to obtain the existence of $C_{\omega ,T}>0$ such that

$$\begin{aligned} v_{n}\le C_{\omega ,T}\,\,\,\,\, \forall x\in \omega \,\,\, and\,\, t\in (0,T). \end{aligned}$$

Therefore, there exists $c_{\omega }>0$ (independent of n) such that

$$\begin{aligned} u_{n}\ge \psi (C_{0})=c_{\omega }, \,\,\, in\,\,\, \omega \times (0,T). \end{aligned}$$

$\square$

4 Proof of Main Results

Because the proofs of Theorem 1 and Theorem 2 are similar too that of Theorem 3, and the proof of Theorem 4 is also similar to that of Theorem 5, here we only detail the proofs of Theorem 3 and Theorem 4.

Proof of Theorem 3

By Lemma 6, there exist a subsequence of $\{u_{n}\}$ (still denoted by $\{u_{n}\}$) and a measurable function u such that

$$\begin{aligned}&u_{n}\rightharpoonup u\, \, \text {weakly in }\, \, L^{p}(0,T;W_{0}^{1,p}({\varOmega })), \end{aligned}$$

(45)

$$\begin{aligned}&u_{n}\rightharpoonup u\, \, \text {weakly in }\, \, L^{\sigma }(Q). \end{aligned}$$

(46)

In view of Lemma 6 and Remark 3, we have that $\{\frac{\partial u_{n}}{\partial t}\}$ is bounded in the space $L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}({\varOmega }))+L^{1}(Q)$. Then, using compactness results (see [25]), we obtain

$$\begin{aligned} u_{n}\longrightarrow u\,\,\, \text {strongly in }\, L^{1}(Q)\, \text{ and } \text{ a.e. } \text{ in }\, Q. \end{aligned}$$

(47)

Let $z_{n}=f_{n}-b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}.$ From (5) and (47), we have $z_{n}$ converges to $f-b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }}$ a.e. in Q. By (6), we get

$$\begin{aligned} \int _{Q}|z_{n}|\le \int _{Q}f_{n}+\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\le 2\int _{Q}f. \end{aligned}$$

Then by (5) and (47), and the Dominated Convergence Theorem, we obtain $z_{n}$ strongly converges in $L^{1}(Q).$ Since $u_{n}$ is solution of

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial u_{n}}{\partial t}-{\varDelta }_{p}u_{n}=z_{n} &{} \text{ in } &{} Q,\\ u_{n}(x,t)=0 &{} \text{ on } &{} {\varGamma },\\ u_{n}(x,0)=0 &{} \text{ in } &{} {\varOmega }, \end{array} \right. \end{aligned}$$

then we can be adopting the approach of [2, Theorem 3.1], we deduce that there exist a subsequence, still denoted $u_{n},$ such that

$$\begin{aligned} \nabla u_{n}\longrightarrow \nabla u\,\, \text {a.e. in }\, Q. \end{aligned}$$

(48)

From (45) we obtain

$$\begin{aligned} |\nabla u_{n}|^{p-2}\nabla u_{n}\rightharpoonup |\nabla u|^{p-2}\nabla u\,\, \text{ weakly } \text{ in }\, \left( L^{p^{\prime }}(Q)\right) ^{N}. \end{aligned}$$

(49)

$\square$

Now we prove that

$$\begin{aligned} b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\longrightarrow b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }}\,\,\, \text {strongly in}\,\, L^{1}(Q). \end{aligned}$$

Let $E\subset \omega$ be a compact subset in Q,  we have

$$\begin{aligned} \int _{E}\frac{b(x,t)u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}= & {} \displaystyle \int _{E\cap \{u_{n}\le k\}}\frac{b(x,t)u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}+\int _{E\cap \{u_{n}> k\}}\frac{b(x,t)u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\\\le & {} \displaystyle \int _{E\cap \{u_{n}\le k\}}b(x,t)\frac{|\nabla u_{n}|^{p}}{u_{n}^{\theta }}+\int _{E\cap \{u_{n}> k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}. \end{aligned}$$

By Lemma 9, we get

$$\begin{aligned} \int _{E}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\le & {} \frac{1}{c_{w}^{\theta }}\int _{E}b(x,t)|\nabla T_{k}(u_{n})|^{p}\\&+\int _{E\cap \{u_{n}> k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}. \end{aligned}$$

Let $\epsilon >0$ be fixed. For $k>1,$ we use  $T_{1}(u_{n}-T_{k-1}(u_{n}))$ as test function in (4), obtaining

$$\begin{aligned}&\int _{0}^{T}\int _{{\varOmega }}\frac{\partial u_{n}}{\partial t}T_{1}(u_{n}-T_{k-1}(u_{n}))+\int _{Q}|\nabla u_{n}|^{p-2}\nabla u_{n}\nabla T_{1}(u_{n}-T_{k-1}(u_{n}))\\&\quad +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}-T_{k-1}(u_{n}))=\int _{Q}f_{n}T_{1}(u_{n}-T_{k-1}(u_{n})). \end{aligned}$$

Therefore

$$\begin{aligned}&\int _{{\varOmega }}S_{1}(u_{n}(T))+\int _{\{k-1\le u_{n}\le k\}}|\nabla u_{n}|^{p}\\&\quad +\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}-T_{k-1}(u_{n}))=\int _{Q}f_{n}T_{1}(u_{n}-T_{k-1}(u_{n})), \end{aligned}$$

where $S_{1}(u_{n}(T))=\int _{0}^{u_{n}(T)}T_{1}(s-T_{k-1}(s))\,ds.$

It easy to see that $S_{1}(u_{n}(T))\ge 0$ a.e. in ${\varOmega }.$ Dropping the first and second non-negative terms, the last equality becomes

$$\begin{aligned} \int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}-T_{k-1}(u_{n}))\le \int _{Q}f_{n}T_{1}(u_{n}-T_{k-1}(u_{n})). \end{aligned}$$

(50)

Since $T_{1}(u_{n}-T_{k-1}(u_{n}))\ge 0,$   $T_{1}(u_{n}-T_{k-1}(u_{n}))=0$   if  $u_{n}\le k-1,$ and   $T_{1}(u_{n}-T_{k-1}(u_{n}))=1$    if    $u_{n}>k,$ we have

$$\begin{aligned} \begin{aligned}&\int _{Q}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}-T_{k-1}(u_{n}))\\&\quad =\int _{Q\cap \{u_{n}>k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}-T_{k-1}(u_{n}))\\&\qquad +\int _{Q\cap \{u_{n}\le k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}-T_{k-1}(u_{n}))\\&\quad =\int _{Q\cap \{u_{n}>k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\\&\qquad +\int _{Q\cap \{u_{n}\le k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}T_{1}(u_{n}-T_{k-1}(u_{n}))\\&\qquad \ge \int _{E\cap \{u_{n}>k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\int _{Q}f_{n}T_{1}(u_{n}-T_{k-1}(u_{n}))=\int _{Q\cap \{u_{n}\le k-1\}}f_{n}T_{1}(u_{n}-T_{k-1}(u_{n}))\\&\qquad +\int _{Q\cap \{k-1<u_{n}\le k\}}f_{n}T_{1}(u_{n}-T_{k-1}(u_{n}))+\int _{Q\cap \{u_{n}> k\}}f_{n}T_{1}(u_{n}-T_{k-1}(u_{n}))\\&\quad =\int _{Q\cap \{k-1<u_{n}\le k\}}f_{n}T_{1}(u_{n}-(k-1))+\int _{Q\cap \{u_{n}> k\}}f_{n}\\&\qquad \le \int _{Q\cap \{k-1<u_{n}\le k\}}f_+\int _{Q\cap \{u_{n}> k\}}f=\int _{Q\cap \{u_{n}\ge k-1\}}f. \end{aligned} \end{aligned}$$

Therefore, from (1) and the two later inequalities we obtain

$$\begin{aligned} \int _{E\cap \{u_{n}> k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\le \int _{Q\cap \{u_{n}\ge k-1\}}f. \end{aligned}$$

It follows from $f\in L^{1}(Q)$ that

$$\begin{aligned} \int _{E\cap \{u_{n}> k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\longrightarrow 0 \,\,\,\, \text {as}\,\, \, k\longrightarrow \infty . \end{aligned}$$

Then, there exist $k_{0}>1$ such that

$$\begin{aligned} \int _{E\cap \{u_{n}> k\}}b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\le \frac{\epsilon }{2},\,\, \, \forall k\ge k_{0},\, \, \forall n\in {\mathbb {N}}. \end{aligned}$$

(51)

Moreover, similar to the proof of [5, Proposition 3.4] we obtain  $T_{k}(u_{n})\longrightarrow T_{k}(u)$   strongly in $L^{p}(0,T;W_{loc}^{1,p}({\varOmega })).$ Then, there exits $n_{\epsilon }, \delta _{\epsilon }$ such that $meas(E)\le \delta _{\epsilon }$ we have

$$\begin{aligned} \frac{1}{c_{w}^{\theta }}\int _{E}b(x,t)|\nabla T_{k}(u_{n})|^{p}\le \frac{\epsilon }{2} \;\; \, \, \forall n\ge n_{\epsilon }. \end{aligned}$$

(52)

The estimates (51) and (52), implies that $b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}$ is equi-integrable. This fact, together with a.e. convergence of this term to $b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }},$ implies by Vitali’s Theorem that

$$\begin{aligned} b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\longrightarrow b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }},\,\,\, \text {strongly in}\,\, L^{1}(Q). \end{aligned}$$

(53)

Let $\varphi \in C^{\infty }({\overline{Q}})$ which is zero in a neighborhood of ${\varGamma }\cup ({\varOmega }\times \{T\}).$ Taking $\varphi$ as a test function in problem (4), by (5), (47), (49) and (53), we can let $n\rightarrow +\infty$ obtaining

$$\begin{aligned} -\int _{Q}u\frac{\partial \varphi }{\partial t}+\int _{Q}|\nabla u|^{p-2}\nabla u\cdot \nabla \varphi +\int _{Q}b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }}\varphi =\int _{Q}f\varphi . \end{aligned}$$

Thus Theorem 3 is proved.

Proof of Theorem 4

By Lemma 7, there exists a subsequence of $\{u_{n}\}$ (still denoted by $\{u_{n}\}$) and a measurable function u such that

$$\begin{aligned}&u_{n}\rightharpoonup u\, \, \text {weakly in }\, \, L^{q}(0,T;W_{0}^{1,q}({\varOmega })), \end{aligned}$$

(54)

$$\begin{aligned}&u_{n}\rightharpoonup u\, \, \text {weakly in }\, \, L^{\sigma }(Q). \end{aligned}$$

(55)

In view of Lemma 7 and Remark 3, we have that $\{\frac{\partial u_{n}}{\partial t}\}$ is bounded in the space $L^{s}(0,T; W^{-1,s}({\varOmega }))+L^{1}(Q)$ with $s=\frac{q}{p-1},$ which is sufficient to apply [25, Corollary 4] in order to deduce that

$$\begin{aligned} u_{n}\longrightarrow u\,\,\, \text {strongly in }\, L^{1}(Q)\, \text{ and } \text{ a.e. } \text{ in }\, Q. \end{aligned}$$

(56)

We repeat the same proof as in Theorem 3, obtaining

$$\begin{aligned} \nabla u_{n}\longrightarrow \nabla u\,\, \text {a.e. in }\, Q. \end{aligned}$$

(57)

Using the same proof as in Theorem 3, we obtain

$$\begin{aligned} b(x,t)\frac{u_{n}|\nabla u_{n}|^{p}}{(u_{n}+\frac{1}{n})^{\theta +1}}\longrightarrow b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }}\,\,\, \text {strongly in}\,\, L^{1}(Q). \end{aligned}$$

(58)

Since $m>\max \left( 1,\, \frac{(p-1)(N+2+\theta )}{(p-1)(N+2+\theta )-(N\theta -1)}\right) ,$ then $q>p-1.$ By Lemma 7, (57) and using Vitali’s Theorem, we can show

$$\begin{aligned} |\nabla u_{n}|^{p-1}\longrightarrow |\nabla u|^{p-1}\, \text{ strongly } \text{ in }\, L^{1}(Q). \end{aligned}$$

(59)

Let $\varphi \in C^{\infty }({\overline{Q}})$ which is zero in a neighborhood of ${\varGamma }\cup ({\varOmega }\times \{T\})$. Taking $\varphi$ as a test function in problem (4), by (5), (56), (58) and (59), we can let $n\rightarrow +\infty$ obtaining

$$\begin{aligned} -\int _{Q}u\frac{\partial \varphi }{\partial t}+\int _{Q}|\nabla u|^{p-2}\nabla u\cdot \nabla \varphi +\int _{Q}b(x,t)\frac{|\nabla u|^{p}}{u^{\theta }}\varphi =\int _{Q}f\varphi . \end{aligned}$$

$\square$