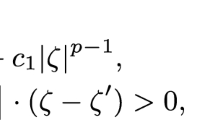Existence of positive solutions to nonlinear singular parabolic equations with Hardy potential

Abstract

In this paper, we study existence and regularity results for the solution to a nonlinear singular parabolic problems involving Hardy potential

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial u}{\partial t}-{\text {div}}a(x,t,\nabla u)-\mu \frac{u^{p-1}}{|x|^{p}}=\frac{f(x,t)}{u^{\gamma }} &{}\text{ in }&{}\,\, \Omega \times (0,T),\\ u=0 &{}\text{ on } &{}\,\, \partial \Omega \times (0,T),\\ u(x,0)=u_{0}(x) &{}\text{ in } &{}\,\, \Omega , \end{array} \right. \end{aligned}$$

where $\Omega$ is a bounded open subset on ${\mathbb {R}}^{N}, N\ge 3, 0\in \Omega$ and $\gamma >0,\; 2\le p<N,$ $0<T<+\infty ,\; \mu >0,$ $0\le f\in L^{m}(Q),\; m\ge 1$ and $u_{0}\in L^{\infty }(\Omega )$ satisfies

$$\begin{aligned} \forall w\subset \subset \Omega , \exists \, M_{w}>0:\;\; u_{0}\ge M_{w}\;\; \text{ in }\;\omega . \end{aligned}$$

1 Introduction

In this paper, we are interested to prove existence and regularity results for a class of nonlinear singular parabolic equations involving Hardy potential, as following model

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial u}{\partial t}-{\text {div}}(a(x,t,\nabla u))-\mu \frac{u^{p-1}}{|x|^{p}}=\frac{f}{u^{\gamma }} &{}{\text{ in }}&{}\,\, Q,\\ u=0 &{}\text{ on } &{}\,\, \Gamma ,\\ u(x,0)=u_{0}(x) &{}\text{ in } &{}\,\, \Omega , \end{array} \right. \end{aligned}$$

(1.1)

where $\Omega$ is a bounded open subset of ${\mathbb {R}}^{N},$ $(N\ge 3),$ $2\le p<N,$ $\gamma ,\mu >0,$ $Q=\Omega \times (0,T),$ $\Gamma =\partial \Omega \times (0,T),$ with $T>0,$ f is a nonnegative function belonging a suitable Lebesgue space, the initial datum $u_{0}\in L^{\infty }(\Omega )$ and satisfies the following bound

$$\begin{aligned} \forall \, \omega \subset \subset \Omega ,\,\,\,\, \exists \, M_{\omega }>0\,\, :\,\,\, u_{0}\ge M_{\omega }\,\, \text{ in }\,\,\,\, \omega . \end{aligned}$$

(1.2)

Moreover, the function $a: \Omega \times (0,T)\times {\mathbb {R}}^{N}\longrightarrow {\mathbb {R}}^{N}$ is a Caratheodory function satisfying the following conditions: there exist positive constants $\alpha , \beta$ such that

$$\begin{aligned}&a(x,t,\xi )\cdot \xi \ge \alpha |\xi |^{p}, \end{aligned}$$

(1.3)

$$\begin{aligned}&|a(x,t,\xi )|\le \beta |\xi |^{p-1}, \end{aligned}$$

(1.4)

$$\begin{aligned}&[a(x,t,\xi )-a(x,t,\xi ^{\prime })]\cdot [\xi -\xi ^{\prime }]>0, \end{aligned}$$

(1.5)

for almost every $x\in \Omega , t\in (0,T),$ for every $\xi ,\xi ^{\prime }\in {\mathbb {R}}^{N},$ with $\xi \ne \xi ^{\prime }.$

Under assumptions (1.3), (1.4) and (1.5), the differential operator defined by

$$\begin{aligned} A(u)=-{\text {div}}(a(x,t,\nabla u)),\;\;\; u\in L^{p}(0,T; W_{0}^{1,p}(\Omega )) \end{aligned}$$

is coercive and monotone operator acting from the space $L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ into its dual $L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}(\Omega )).$ The simplest example is the one in which the operator A is the p-Laplacian: $A(u)=-{\text {div}}(|\nabla u|^{p-2}\nabla u).$

The interest in problem (1.1) (with $p=2,\; \mu =0$ and smooth data) started in [18] in connection with the study of thermo-conductivity ($u^{\gamma }$ represented the resistivity of the material), and later in the study of signal transmissions and in the theory of non-Newtonian pseudoplastic fluid [20, 23, 24].

From a purely mathematical point of view the literature is wide. In the case $\mu =0$ and $\gamma =0,$ the existence and regularity of problem (1.1) has been studied in [9, 10, 13, 21, 22, 29] under the different assumptions on the data. If $\gamma =0, f=0$ and $\mu >0$ the existence and nonexistence of solution of problem (1.1) depending the value of $\mu$ has been studied by the authors in [19, 27]. When $\gamma =0, f\ne 0$ and $\mu >0,$ the authors in [5] has been studied the existence and summability of elliptic problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\text {div(M(x)}\nabla \text {u)}+b|u|^{r-2}u=\mu \displaystyle \frac{u}{|x|^{2}}+f &{}\text{ in }&{}\,\, \Omega ,\\ u=0 &{}\text{ on } &{}\,\, \partial \Omega , \end{array} \right. \end{aligned}$$

where $b>0, \mu>0, r>2^{*}$ and $f\in L^{m}(\Omega ),\, m>1,$ M(x) is a matrix satisfies $M(x)\xi \cdot \xi \ge \alpha |\xi |^{2}; |M(x)|\le \beta$ with $\alpha ,\beta \ge 0$ for all $\xi \in {\mathbb {R}}^{N}$ and almost every $x\in \Omega .$ Baras in [8] studied the existence and nonexistence of problem

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial u}{\partial t}-\Delta u=v(x)u+f(x,t) &{}\text{ in }&{}\,\, Q,\\ u=0 &{}\text{ on } &{}\,\, \Gamma , \\ u(x,0)=u_{0}(x) &{}\text{ in } &{} \Omega , \end{array} \right. \end{aligned}$$

where $v(x)=c/|x|^{2}, c>0, v\in L^{\infty }(\Omega \backslash B_{\epsilon })$ (where $B_{\epsilon }=\{x: |x|<\epsilon \}),$ the function v is singular at the origin and $u_{0},f\ge 0$ satisfies some conditions. In the same contexts Porzio [28] showed that the problem

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial u}{\partial t}-\text {div(a(x,t,u,}\nabla \text {u))}=\mu \frac{u}{|x|^{2}}+f &{}\text{ in }&{}\,\, Q,\\ u=0 &{}\text{ on } &{}\,\, \Gamma ,\\ u(x,0)=u_{0}(x) &{}\text{ in }&{}\,\, \Omega , \end{array} \right. \end{aligned}$$

admits a solution for $0<\mu <\varrho _{1}\left( \frac{N-2}{2} \right) ^{2},$ where $\varrho _{1}$ is the coercivity constant of $a(x,t,u,\nabla u),$ $f\in L^{r}(0,T; L^{q}(\Omega )),$ with $r>1, q>1,$ and the summability of solution also obtained (See also [17, 26]). When $\mu =0$ and $\gamma >0,$ the problem of existence, regularity and uniqueness (sometimes partial uniqueness) results of (1.1) have been investigated in different contexts by several authors (see [11, 14,15,16, 25, 30, 31] and references therein). The authors in [11] proved the existence, regularity and uniqueness of solution to singular parabolic problem

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial u}{\partial t}-\text {div}(a(x,t,\nabla u))=\frac{f}{u^{\gamma }} &{}\text{ in }&{}\,\, Q,\\ u=0 &{}\text{ on } &{}\,\, \Gamma ,\\ u(x,0)=u_{0}(x) &{}\text{ in }&{}\,\, \Omega , \end{array} \right. \end{aligned}$$

where $\gamma >0$ and $0\le f\in L^{m}(Q),\, m\ge 1$ and $u_{0}\in L^{\infty }(\Omega )$ satisfies

$$\begin{aligned} \forall \omega \subset \subset \Omega , \exists \, d_{\omega }>0: \; u_{0}\ge d_{\omega }. \end{aligned}$$

Finally in the elliptic framework when $\mu>0, \gamma >0$ the author in [33] proved the existence of one positive solution to singular problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\text {div}(M(x)\nabla u)-\mu \frac{u}{|x|^{2}}=\frac{f}{u^{\gamma }} &{}\text{ in }&{}\,\, \Omega ,\\ u> &{}\text{ in }&{}\,\, \Omega ,\\ u=0 &{}\text{ on } &{}\,\, \partial \Omega , \end{array} \right. \end{aligned}$$

where $0\in \Omega , \gamma >0, 0\le f\in L^{m}(\Omega ),\, 1<m<\frac{N}{2}$ and $0<\mu <\left( \frac{N-2}{2} \right) ^{2}.$ The stationary problem associated to problem (1.1) has been studied in [3]; the authors proved the existence and regularity (and partial uniqueness ) results of solution to singular problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\Delta _{\text {p}}\text {u}=\mu \frac{u^{p-1}}{|x|^{p}}+\frac{f}{u^{\gamma }} &{}\text{ in }&{}\,\, \Omega ,\\ u=0 &{}\text{ on } &{}\,\, \partial \Omega , \end{array} \right. \end{aligned}$$

where $0\in \Omega , \gamma >0, 0<\mu \le \left( \frac{N-p}{p} \right) ^{p}$ and $0\le f\in L^{m}(\Omega ), m\ge 1.$ If $\mu >\left( \frac{N-p}{p} \right) ^{p},$ then the problem has non solution (see [4]), and also the authors proved that if f is a singular measure with respect to the p-Capacity associated to $W_{0}^{1,p}(\Omega )$ the problem has a non-negative solution in suitable sense.

The aim of this work is to analyze the interaction between the Hardy potential and the singular term $u^{-\gamma }$ in order to get a solution for largest possible class of the datum f.

1.1 Preliminary and notations

The problem (1.1) is related to the following classical Hardy inequality (see [19])

$$\begin{aligned} C_{N,p}\int _{{\mathbb {R}}^{N}}\frac{|\psi |^{p}}{|x|^{p}}dx\le \int _{{\mathbb {R}}^{N}}|\nabla \psi |^{p}dx, \quad \text{ for } \text{ all }\; \psi \in W^{1,p}({\mathbb {R}}^{N}), \end{aligned}$$

where $C_{N,p}=\left( \frac{N-p}{p} \right) ^{p}$ is optimal and is not attained.

Also we need to the Gagliardo–Nirenberg inequality that we used later in the proof of our results.

Lemma 1.1

[12, Proposition 3.1] Let v be a function in $W_{0}^{1,h}(\Omega )\cap L^{\rho }(\Omega ),$ with $h\ge 1, \rho \ge 1.$ Then there exist a positive constant $C_{G}$ depending on $N, h, \rho$ and $\sigma$ such that

$$\begin{aligned} ||v||_{L^{\sigma }(\Omega )}\le C_{G}||\nabla v||_{(L^{h}(\Omega ))^{N}}^{\eta }||v||_{L^{\rho }(\Omega )}^{1-\eta }, \end{aligned}$$

for every $\eta$ and $\sigma$ satisfying

$$\begin{aligned} 0<\eta <1,\;\;\; \frac{1}{\sigma }=\eta \left( \frac{1}{h}-\frac{1}{N} \right) +\frac{1-\eta }{\rho }. \end{aligned}$$

An immediate consequence of the previous Lemma is the following embedding results

$$\begin{aligned} \iint _{Q}| v|^{\sigma }dxdt\le C_{G}||v||_{L^{\infty }(0,T; L^{\rho }(\Omega ))}^{\frac{\rho h}{N}}\iint _{Q}|\nabla v|^{h}dxdt, \end{aligned}$$

which holds for every function $v\in L^{h}(0,T; W_{0}^{1,h}(\Omega ))\cap L^{\infty }(0,T; L^{\rho }(\Omega )),$ with $h\ge 1, \rho \ge 1$ and $\sigma =\frac{h(N+\rho )}{N}.$

We denote by |E| measure of Lebesgue measurable subset E of ${\mathbb {R}}^{N}.$ For any $q>1,$ $q^{\prime }=\frac{q}{q-1}$ is the Hölder conjugate exponent of q,  while for any $1\le p<N,$ $p^{*}=\frac{Np}{N-p}$ is the Sobolev conjugate exponent of p. For fixed $k>0$ we will make use of the truncation functions $T_{k}$ and $G_{k}$ defined as

$$\begin{aligned} T_{k}(s)=\max (-k,\min (s,k)), \end{aligned}$$

and

$$\begin{aligned} G_{k}(s)=s-T_{k}(s)=(|s|-k)^{+}sign(s), \end{aligned}$$

for every $s\in {\mathbb {R}}.$ For the sake of simplicity we will often use the simplified notation

$$\begin{aligned} \iint _{Q}f(x,t)dxdt=\iint _{Q}f, \end{aligned}$$

when referring to integrals when no ambiguity to the variable of integration is possible. If not otherwise specified, we will denote by C several constants whose value many change from line to line and, some times in the same line. These values will only depend on the data ( for instance C can depend on $N, p, C_{N,p},C_{G}, \alpha , \gamma , m, T, \Omega , Q)$ but they will never depend on the indexes of the sequences we will often introduce.

Definition 1.2

We will say that a function $u\in L^{1}(0,T; W_{loc}^{1,1}(\Omega ))$ is a distributional solution of (1.1) if

$$\begin{aligned}&|\nabla u|^{p-1}\in L^{1}(0,T; L_{loc}^{1}(\Omega )),\;\;\; \frac{|u|^{p-1}}{|x|^{p}}\in L^{1}(0,T; L_{loc}^{1}(\Omega )) \end{aligned}$$

(1.6)

$$\begin{aligned}&u=0 \; \; \text{ on }\; \partial \Omega \times (0,T)\;\; \text{ in } \text{ weak } \text{ sense, } \end{aligned}$$

(1.7)

i.e., some positive power of u belongs to a Sobolev space $L^{r}(0,T; W_{0}^{1,r}(\Omega )),$ $r>1.$ Moreover, we require that

$$\begin{aligned} \forall \omega \subset \subset \Omega \;\; \exists c_{\omega }>0: \;\; u\ge c_{\omega }\;\; \text{ in }\;\; \omega \times (0,T), \end{aligned}$$

(1.8)

and that

$$\begin{aligned} \begin{aligned}&-\int _{\Omega }u_{0}(x)\varphi (x,0)-\iint _{Q}u\frac{\partial \varphi }{\partial t}+\iint _{Q}a(x,t,\nabla u)\nabla \varphi \\&\quad =\iint _{Q}\frac{u^{p-1}}{|x|^{p}}\varphi +\iint _{Q}\frac{f}{u^{\gamma }}\varphi , \end{aligned} \end{aligned}$$

(1.9)

for all $\varphi \in C^{1}_{c}(\Omega \times [0,T)).$

2 The approximation scheme

Let $n\in {\mathbb {N}}$ and $f_{n}(x,t)$ be defined by $f_{n}(x,t)=\min (f(x,t), n);$ we will consider the following approximation of (1.1)

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial u_{n}}{\partial t}-{\text {div}}(a(x,t,\nabla u_{n}))-\mu \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}=\frac{f_{n}}{(|u_{n}|+\frac{1}{n})^{\gamma }} &{}{\text{ in }}&{}\,\, Q,\\ u_{n}=0 &{}\text{ on } &{}\,\, \Gamma ,\\ u_{n}(x,0)=u_{0}(x) &{}\text{ in } &{} \Omega . \end{array} \right. \end{aligned}$$

(2.1)

Lemma 2.1

The problem (2.1) has a nonnegative solution belonging to $L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(Q)$ for all $\mu <\alpha C_{N,p}$ and $2\le p<N.$

Proof

Let $v\in L^{p}(Q)$ and we define $S: L^{p}(Q)\longrightarrow L^{p}(Q)$ such that $S(v)=w,$ with $w\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap C([0,T]; L^{2}(\Omega ))$ the unique solution of problem

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial w}{\partial t}-{\text {div}}(a(x,t,\nabla w))-\mu \frac{w^{p-1}}{|x|^{p}+\frac{1}{n}}=\frac{f_{n}}{(|v|+\frac{1}{n})^{\gamma }} &{}{\text{ in }}&{}\,\, Q,\\ w=0 &{}\text{ on } &{}\,\, \Gamma ,\\ w(x,0)=u_{0}(x) &{}\text{ in } &{} \Omega . \end{array} \right. \end{aligned}$$

The existence of solution of above problem assured by [22]. Let us take w as a test function in the above problem, from (1.3), we have

$$\begin{aligned} \frac{1}{2}\int _{\Omega }w^{2}(x,t)+\alpha \iint _{Q}|\nabla w|^{p}-\mu \iint _{Q}\frac{w^{p}}{|x|^{p}}\le \iint _{Q}\frac{f_{n}w}{(|v|+\frac{1}{n})^{\gamma }}+\frac{1}{2}\int _{\Omega }u_{0}^{2}, \end{aligned}$$

since $u_{0}\in L^{\infty }(\Omega )$ and by Hardy inequality implies

$$\begin{aligned} \frac{1}{2}\int _{\Omega }w^{2}(x,t)+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \iint _{Q}|\nabla w|^{p}\le \iint _{Q}\frac{f_{n}w}{(|v|+\frac{1}{n})^{\gamma }}+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}.\nonumber \\ \end{aligned}$$

(2.2)

Dropping the first non-negative term and thanks to Hölder’s inequality, we have

$$\begin{aligned} \left( \alpha -\frac{\mu }{C_{N,p}}\right) \iint _{Q}|\nabla w|^{p}\le |Q|^{\frac{1}{p^{\prime }}}n^{\gamma +1}\left( \iint _{Q}|w|^{p}\right) ^{\frac{1}{p}}+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}. \end{aligned}$$

By application of Poincaré inequality in the right hand side, it hold that

$$\begin{aligned} ||\nabla w||_{L^{p}(Q)}^{p}\le \frac{|Q|^{p^{\prime }}n^{\gamma +1}C_{p}}{(\alpha -\frac{\mu }{C_{N,p}})}||\nabla w||_{L^{p}(Q)}+\frac{1}{2(\alpha -\frac{\mu }{C_{N,p}})}||u_{0}||_{L^{2}(\Omega )}^{2}, \end{aligned}$$

(2.3)

where $C_{p}$ is the Poincaré constant. This implies that

$$\begin{aligned} ||w||_{L^{p}(Q)}\le R, \end{aligned}$$

(2.4)

for some constant R independent of v. So that the ball of radius R is invariant under S. Using Sobolev embedding Theorem, it is easy to prove that S is both continuous and compact on $L^{p}(Q),$ so that by Shauder’s fixed point Theorem there exist $u_{n}\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(Q)$ such that $S(u_{n})=u_{n},$ for all $n\in {\mathbb {N}}, \, 2\le p<N,$ i.e. $u_{n}$ solves

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial u_{n}}{\partial t}-{\text {div}}(a(x,t,\nabla u_{n}))-\mu \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}=\frac{f_{n}}{(|u_{n}|+\frac{1}{n})^{\gamma }} &{}{\text{ in }}&{}\,\, Q,\\ u_{n}=0 &{}\text{ on } &{}\,\, \Gamma ,\\ u_{n}(x,0)=u_{0}(x) &{}\text{ in } &{} \Omega . \end{array} \right. \end{aligned}$$

Moreover, since $\frac{f_{n}}{(|u_{n}|+\frac{1}{n})^{\gamma }}\ge 0,$ taking $u_{n}^{-}=\min (u_{n},0)$ test function in (2.1) and using (1.3), then we have

$$\begin{aligned} \frac{1}{2}\int _{\Omega }|u_{n}^{-}|^{2}+\alpha \iint _{Q}|\nabla u_{n}^{-}|^{p}-\mu \iint _{Q}\frac{{u_{n}^{-}}^{p}}{|x|^{p}}\le 0, \end{aligned}$$

dropping the first nonnegative term and by Hardy inequality, we can get

$$\begin{aligned} (\alpha -\frac{\mu }{C_{N,p}})\iint _{Q}|\nabla u_{n}^{-}|^{p}\le 0, \end{aligned}$$

as $\alpha -\frac{\mu }{C_{N,p}}>0,$ then we deduce that

$$\begin{aligned} \iint _{Q}|\nabla u_{n}^{-}|^{p}\le 0, \end{aligned}$$

that implies that $u_{n}^{-}=0$ a.e and hence $u_{n}\ge 0.$ a.e.. $\square$

Lemma 2.2

Let $u_{n}$ be a solution of (2.1). Then

$$\begin{aligned} \forall \omega \subset \subset \Omega ,\; \exists \; c_{\omega }>0\;\; \text{(independent } \text{ of } \text{ n) }:\;\; u_{n}\ge c_{\omega } \;\text{ in }\;\; \omega \times [0,T],\, \forall n\in {\mathbb {N}}. \end{aligned}$$

Proof

Since $u_{n}$ solution of (2.1), then

$$\begin{aligned} \frac{\partial u_{n}}{\partial t}-{\text {div}}(a(x,t, \nabla u_{n}))-\mu \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}=\frac{f_{n}}{(|u_{n}|+\frac{1}{n})^{\gamma }}, \end{aligned}$$

as $\mu >0,$ then we obtain

$$\begin{aligned} \frac{\partial u_{n}}{\partial t}-{\text {div}}(a(x,t, \nabla u_{n}))\ge \frac{f_{n}}{(|u_{n}|+\frac{1}{n})^{\gamma }}, \end{aligned}$$

this implies that the sequence $u_{n}$ is a sub-solution to problem

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial v}{\partial t}-{\text {div}}(a(x,t,\nabla v))=\frac{f_{n}}{(|v|+\frac{1}{n})^{\gamma }} &{}{\text{ in }}&{}\,\, Q,\\ v=0 &{}\text{ on } &{}\,\, \Gamma ,\\ v(x,0)=u_{0}(x) &{}\text{ in } &{} \Omega . \end{array} \right. \end{aligned}$$

Thanks to Proposition 2.2 in [11], $\exists \; c_{\omega }>0$ (independent of n) such that

$$\begin{aligned} v\ge c_{w}\;\; \text{ in }\;\; \omega \times (0,T),\; \forall n\in {\mathbb {N}},\; \forall \, \omega \subset \subset \Omega , \end{aligned}$$

since $u_{n}\ge v,$ so

$$\begin{aligned} u_{n}\ge c_{\omega }\;\; \text{ in }\;\; \omega \times (0,T),\; \forall n\in {\mathbb {N}},\; \forall \, \omega \subset \subset \Omega . \end{aligned}$$

$\square$

3 A priori estimate and main results

Now, we prove some a priori estimates on the sequence of approximated solutions $u_{n}.$

Lemma 3.1

Assume that (1.3)–(1.5) hold true, $f\in L^{\frac{p(N+2)}{p(N+2)-N(1-\gamma )}}(Q).$ If $\gamma <1$ and $\mu <\alpha C_{N,p},$ then the sequence $u_{n}$ is uniformly bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(0,T; L^{2}(\Omega )).$

Proof

Take $u_{n}\chi _{(0,t)}$ as a test function in (2.1) (with $0< t\le T$), from (1.3) and $f_{n}\le f$ we have

$$\begin{aligned}&\frac{1}{2}\int _{\Omega }u_{n}^{2}(x,t)+\alpha \int _{0}^{t}\int _{\Omega }|\nabla u_{n}|^{p}-\mu \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{p}}{|x|^{p}}\\&\quad \le \int _{0}^{t}\int _{\Omega }f_{n}u_{n}^{1-\gamma }+\frac{1}{2}\int _{\Omega }u_{0}^{2}\le \iint _{Q}fu_{n}^{1-\gamma }+\frac{1}{2}\int _{\Omega }u_{0}^{2}, \end{aligned}$$

since $u_{0}\in L^{\infty }(\Omega ),$ thanks to Hölder’s and Hardy inequalities imply that

$$\begin{aligned}&\displaystyle \frac{1}{2}\int _{\Omega }u_{n}^{2}(x,t)+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \displaystyle \int _{0}^{t}\int _{\Omega }|\nabla u_{n}|^{p}\\&\quad \displaystyle \le ||f||_{L^{\frac{p(N+2)}{p(N+2)-N(1-\gamma )}}(Q)}\left( \iint _{Q}u_{n}^{\frac{p(N+2)}{N}}\right) ^{\frac{N(1-\gamma )}{p(N+2)}}+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}. \end{aligned}$$

Passing to the supremum for $t\in [0,T]$

$$\begin{aligned}&\displaystyle \frac{1}{2}||u_{n}||_{L^{\infty }(0,T; L^{2}(\Omega ))}^{2}+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \iint _{Q}|\nabla u_{n}|^{p}\\&\quad \displaystyle \le ||f||_{L^{\frac{p(N+2)}{p(N+2)-N(1-\gamma )}}(Q)}\left( \iint _{Q}u_{n}^{\frac{p(N+2)}{N}}\right) ^{\frac{N(1-\gamma )}{p(N+2)}}+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}. \end{aligned}$$

By Lemma 1.1, we can write

$$\begin{aligned} \displaystyle \iint _{Q}|u_{n}|^{\frac{p(N+2)}{N}}\le & {} C_{G} ||u_{n}||_{L^{\infty }(0,T; L^{2}(\Omega ))}^{\frac{2p}{N}} \displaystyle \iint _{Q}|\nabla u_{n}|^{p}\\\le & {} C\left( \displaystyle \iint _{Q}|u_{n}|^{\frac{p(N+2)}{N}}\right) ^{\frac{(p+N)(1-\gamma )}{p(N+2)}}+C(u_{0}), \end{aligned}$$

since $0<\gamma <1$ then $\frac{(p+N)(1-\gamma )}{p(N+2)}<1,$ this implies the sequence $u_{n}$ is bounded in $L^{\frac{p(N+2)}{N}}(Q),$ hence $u_{n}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(0,T; L^{2}(\Omega ))$ with respect to n. $\square$

Lemma 3.2

Assume that (1.3)–(1.5) hold true, $\gamma \ge 1,$ $\mu <\alpha C_{N,p}$ and $f\in L^{1}(Q),$ then

i):

If $\gamma =1,$ then $u_{n}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(0,T; L^{2}(\Omega )).$

ii):

If $\gamma >1,$ then $u_{n}$ is bounded in $L^{p}(0,T; W_{loc}^{1,p}(\Omega ))$ and $T_{k}(u_{n})^{\frac{\gamma +p-1}{p}}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega )).$ Moreover if $\alpha \left( \frac{p}{\gamma +p-1}\right) ^{p}-\frac{\mu }{C_{N,p}} >0,$ then $u_{n}^{\frac{\gamma +p-1}{p}}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and $u_{n}$ is bounded in $L^{\infty }(0,T; L^{\gamma +1}(\Omega )).$

Proof

First case: $\gamma =1$

Choosing $u_{n}\chi _{(0,t)}$ as a test function in (2.1) (with $0< t\le T$ ), by (1.3) and the fact that $0\le \frac{u_{n}}{u_{n}+\frac{1}{n}}\le 1,\, f_{n}\le f,$ we have

$$\begin{aligned} \begin{aligned}&\displaystyle \frac{1}{2}\int _{\Omega }u_{n}^{2}(x,t)+\alpha \displaystyle \int _{0}^{t}\int _{\Omega }|\nabla u_{n}|^{p}-\mu \displaystyle \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{p}}{|x|^{p}}\\&\quad \le \displaystyle \int _{0}^{t}\int _{\Omega }f_{n}\frac{u_{n}}{u_{n}+\frac{1}{n}}+\frac{1}{2}\displaystyle \int _{\Omega }u_{0}^{2}\\&\quad \le \displaystyle \int _{0}^{t}\int _{\Omega }f+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}, \end{aligned} \end{aligned}$$

thanks to Hardy inequality, there result that

$$\begin{aligned} \frac{1}{2}\int _{\Omega }u_{n}^{2}(x,t)+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \int _{0}^{t}\int _{\Omega }|\nabla u_{n}|^{p}\le \int _{0}^{t}\int _{\Omega }f+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}. \end{aligned}$$

Passing to the supremum for $t\in [0,T]$ and the fact that $u_{0}\in L^{\infty }(\Omega ),$ we get

$$\begin{aligned} \frac{1}{2}||u_{n}||^{2}_{L^{\infty }(0,T; L^{2}(\Omega ))}+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \iint _{Q}|\nabla u_{n}|^{p}\le \iint _{Q}f+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}\le C, \end{aligned}$$

since $\alpha -\frac{\mu }{C_{N,p}}>0,$ then the sequence $u_{n}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and in $L^{\infty }(0,T; L^{2}(\Omega ))$ with respect to n. Hence the proof of item i) is achieved.

Second case: $\gamma >1$

Now taking $G_{k}(u_{n})$ as test function in (2.1), from (1.3) we arrive to

$$\begin{aligned}&\frac{1}{2}\int _{\Omega }|G_{k}(u_{n}(x,T))|^{2}+\alpha \iint _{Q}|\nabla G_{k}( u_{n})|^{p}-\mu \iint _{Q}\frac{u_{n}^{p-1}G_{k}(u_{n})}{|x|^{p}}\nonumber \\&\quad \le \iint _{Q}\frac{f_{n}G_{k}(u_{n})}{(u_{n}+\frac{1}{n})^{\gamma }}+\frac{1}{2}\int _{\Omega }|G_{k}(u_{0}(x))|^{2}, \end{aligned}$$

(3.1)

dropping the first nonnegative term and as $G_{k}(u_{n})=0$ if $u_{n}\le k$ and the fact that $G_{k}(u_{0}(x))\le u_{0}(x),$ then

$$\begin{aligned}&\alpha \iint _{Q}|\nabla G_{k}(u_{n})|^{p}-\mu \iint _{Q}\frac{u_{n}^{p-1}G_{k}(u_{n})}{|x|^{p}}\nonumber \\&\quad \le \iint _{Q\cap \{u_{n}>k\}}\frac{f_{n}G_{k}(u_{n})}{(u_{n}+\frac{1}{n})^{\gamma }}+\frac{1}{2}\int _{\Omega }|u_{0}(x)|^{2} \nonumber \\&\quad \le \frac{1}{k^{\gamma -1}}\iint _{Q}f+\frac{1}{2}\int _{\Omega }|u_{0}(x)|^{2}\le \frac{1}{k^{\gamma -1}}\iint _{Q}f+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}. \end{aligned}$$

(3.2)

Notice that for all $a,b\ge 0$ and for all $\epsilon >0,$ we have

$$\begin{aligned} (a+b)^{r}\le (1+\epsilon )^{r-1}a^{r}+(1+\frac{1}{\epsilon })^{r-1}b^{r},\;\;\;\text{ if }\,\ r>1. \end{aligned}$$

For $u_{n}>k,$ we have $u_{n}^{p-1}G_{k}(u_{n})=(G_{k}(u_{n})+k)^{p-1}G_{k}(u_{n})$ and $p\ge 2,$ then from the previous estimate we reach that

$$\begin{aligned} u_{n}^{p-1}G_{k}(u_{n})\le (1+\epsilon )^{p-2}(G_{k}(u_{n}))^{p}+(1+\frac{1}{\epsilon })^{p-2}k^{p-1}G_{k}(u_{n}). \end{aligned}$$

(3.3)

In view of (3.2) and (3.3), it follows that

$$\begin{aligned}&\alpha \iint _{Q}|\nabla G_{k}(u_{n})|^{p}-\mu (1+\epsilon )^{p-2}\iint _{Q}\frac{(G_{k}(u_{n}))^{p}}{|x|^{p}} \nonumber \\&\quad \le \mu (1+\frac{1}{\epsilon })^{p-2}k^{p-1}\iint _{Q}\frac{G_{k}(u_{n})}{|x|^{p}}+\frac{1}{k^{\gamma -1}}\iint _{Q}f+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}, \end{aligned}$$

(3.4)

as $\mu <\alpha C_{N,p},$ choosing $\epsilon$ small enough and by Hardy inequality, we get

$$\begin{aligned} C(\alpha , \epsilon , \mu , C_{N,p})\iint _{Q}|\nabla G_{k}(u_{n})|^{p}\le \mu k^{p-1}\iint _{Q}\frac{G_{k}(u_{n})}{|x|^{p}}+ C(k, f, ||u_{0}||_{L^{2}(\Omega )}).\nonumber \\ \end{aligned}$$

(3.5)

Applying Hölder, Young and Hardy inequalities we conclude that

$$\begin{aligned} \iint _{Q}|\nabla G_{k}(u_{n})|^{p}\le C(\alpha , \epsilon , \mu , k^{p-1}, C_{N,p,}, f,||u_{0}||_{L^{2}(\Omega )}). \end{aligned}$$

(3.6)

Testing now (2.1) by $(T_{k}(u_{n}))^{\gamma },$ so that, from (1.3) and (3.6)

$$\begin{aligned} \iint _{Q}T_{k}(u_{n})^{\gamma -1}|\nabla T_{k}(u_{n})|^{p}\le C(\alpha , k, \mu , f, ||u_{0}||_{L^{2}(\Omega )}). \end{aligned}$$

(3.7)

There hold

$$\begin{aligned} \frac{p^{p}}{(\gamma +p-1)^{p}}\iint _{Q}|\nabla T_{k}(u_{n})^{\frac{\gamma +p-1}{p}}|^{p}\le C(\alpha , k, \mu , f, ||u_{0}||_{L^{2}(\Omega )}), \end{aligned}$$

this implies that the sequence $T_{k}(u_{n})^{\frac{\gamma +p-1}{p}}$ is bounden in $L^{p}(0,T; W_{0}^{1,p}(\Omega )).$ By Lemma 2.2 and (3.6), yields that $T_{k}(u_{n})$ is bounded in $L^{p}(0,T; W_{loc}^{1,p}(\Omega )).$ Collecting the last affirmation with (3.6), assume that the sequence $u_{n}$ is bounded in $L^{p}(0,T; W_{loc}^{1,p}(\Omega )).$ Using $u_{n}^{\gamma }\chi _{(0,t)}$ as test function in (2.1) (with $0< t\le T$), from (1.3), $u_{0}\in L^{\infty }(\Omega )$ and applying Hardy inequality, we get

$$\begin{aligned}&\frac{1}{\gamma +1}\int _{\Omega }u_{n}^{\gamma +1}(x,t)+\left( \alpha \left( \frac{p}{\gamma +p-1}\right) ^{p}-\frac{\mu }{C_{N,p}}\right) \int _{0}^{t}\int _{\Omega }|\nabla u_{n}^{\frac{\gamma +p-1}{p}}|^{p}\\&\quad \le \iint _{Q}f_{n}+\frac{1}{\gamma +1}\int _{\Omega }|u_{0}(x)|^{\gamma +1}\le \iint _{Q}f+\frac{1}{\gamma +1}||u_{0}||_{L^{\infty }(\Omega )}^{\gamma +1}\le C, \end{aligned}$$

since $\alpha \left( \frac{p}{\gamma +p-1}\right) ^{p}-\frac{\mu }{C_{N,p}}>0,$ passing to the supremum for $t\in [0,T],$ we deduce that

$$\begin{aligned} \frac{1}{\gamma +1}||u_{n}||^{\gamma +1}_{L^{\infty }(0,T; L^{\gamma +1}(\Omega ))}+\left( \alpha \left( \frac{p}{\gamma +p-1}\right) ^{p}-\frac{\mu }{C_{N,p}}\right) \iint _{Q}|\nabla u_{n}^{\frac{\gamma +p-1}{p}}|^{p}\le C, \end{aligned}$$

this implies that $u_{n}^{\frac{\gamma +p-1}{p}}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and $u_{n}$ is bounded in $L^{\infty }(0,T; L^{\gamma +1}(\Omega ))$ with respect to n. Since the proof of item ii) is achieved. $\square$

Theorem 3.3

Assume that (1.3)–(1.5) holds true. If $\gamma<1, \mu <\alpha C_{N,p}$ and $f\in L^{\frac{p(N+2)}{p(N+2)-N(1-\gamma )}}(Q).$ Then, there exists a solution u to problem (1.1) in the sense of Definition 1.2. Moreover $u\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(0,T; L^{2}(\Omega ))$ and $\frac{\partial u}{\partial t}\in L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}(\Omega ))+ L^{1}(0,T; L_{loc}^{1}(\Omega )).$

Remark 3.4

If $\mu =0,$ then the result of Theorem 3.3 coincide with result of Theorem 1.3 in [11].

Theorem 3.5

Suppose that (1.3)–(1.5) holds true. If $\gamma \ge 1, \, \mu <\alpha C_{N,p}$ and $f\in L^{1}(Q).$ Then, there exists a solution u to problem (1.1) in the sense of Definition 1.2 with the following regularity:

• a) If $\gamma =1,$ then $u\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(0,T; L^{2}(\Omega ))$ and $\frac{\partial u}{\partial t}\in L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}(\Omega ))+ L^{1}(0,T; L_{loc}^{1}(\Omega )).$

• b) If $\gamma >1,$ then $u\in L^{p}(0,T; W_{loc}^{1,p}(\Omega ))$ and $T_{k}(u)^{\frac{p+\gamma -1}{p}}\in L^{p}(0,T; W_{0}^{1,p}(\Omega )).$ If $\alpha \left( \frac{p}{p+\gamma -1}\right) ^{p}-\frac{\mu }{C_{N,p}} >0,$ then $u^{\frac{p+\gamma -1}{p}}\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and $u\in L^{\infty }(0,T; L^{\gamma +1}(\Omega ))$ and $\frac{\partial u}{\partial t}\in L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}(\omega ))+ L^{1}(0,T; L^{1}(\omega ))$ for all $\omega \subset \subset \Omega .$

Remark 3.6

If $\mu =0,$ then the result of Theorem 3.5 coincide with result of Theorem 1.3 in [11].

Before giving the proof of Theorems 3.3 and 3.5 , we need the following results:

Proposition 3.7

Under the assumptions of Lemmas 3.1 and 3.2 there exists $u\in L^{p}(0,T; W_{loc}^{1,p}(\Omega ))$ such that, up to a subsequence, $u_{n}$ converges to u a.e. on Q,  weakly in $L^{p}(0,T; W_{loc}^{1,p}(\Omega ))$ and strongly in $L^{1}(0,T; L^{1}_{loc}(\Omega )).$

Proof

From Lemmas 3.1 and 3.2 we know that $u_{n}$ is bounded in the space $L^{p}(0,T; W_{loc}^{1,p}(\Omega )).$ The last affirmation and Lemma 2.2 imply the sequence $\bigg \{\mu \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}+\frac{f_{n}}{(u_{n}+\frac{1}{n})^{ \gamma }}\bigg \}$ is bounded in $L^{1}(0,T; L_{loc}^{1}(\Omega )).$ Hence, let $\varphi \in C_{c}^{1}(\Omega )$ then one has that $\{\frac{\partial (u_{n}\varphi )}{\partial t}\}$ is bounded in $L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}(\Omega ))+L^{1}(Q),$ which is sufficient to apply [32, Corollary 4] in order to deduce that $u_{n}$ converges to a function $u\in L^{1}(0,T; L_{loc}^{1}(\Omega ))$ and $u_{n}$ converges to u a.e. in Q. $\square$

In the following proposition, we are going to prove the almost everywhere convergence of the gradient of $u_{n}.$

Proposition 3.8

Let $u_{n}$ be a solution of problem (2.1) and assume that $f\in L^{\frac{p(N+2)}{p(N+2)-N(1-\gamma )}}(Q)$ if $\gamma <1$ and $f\in L^{1}(Q)$ if $\gamma \ge 1$ respectively. Then the sequence $T_{k}(u_{n})$ strongly converges to $T_{k}(u)$ in $L^{p}(0,T; W_{loc}^{1,p}(\Omega ))$ and so, in particular, $\nabla u_{n}$ converges to $\nabla u$ almost everywhere in Q.

Proof

Let $n,m\in {\mathbb {N}}$ denote two value of the parameter describing the approximation. Since (2.1) is non-singular problem, we can take $T_{2k}(u_{n}-u_{m})\varphi \in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(Q)$ as a test function in the difference of the approximating equations solved by $u_{n}$ and $u_{m},$ with $\varphi \in C_{c}^{1}(\Omega )$ independent of $t\in [0,T]$ and such that $0\le \varphi \le 1$, obtaining

$$\begin{aligned} \begin{aligned}&\int _{0}^{T}\int _{\Omega }\frac{\partial (u_{n}-u_{m})}{\partial t}T_{2k}(u_{n}-u_{m})\varphi (x)\\&\qquad +\int _{0}^{T}\int _{\Omega }(a(x,t, \nabla u_{n})-a(x,t, \nabla u_{m}))\nabla (T_{2k}(u_{n}-u_{m})\varphi (x))\\&\quad =\int _{0}^{T}\int _{\Omega }\left( \frac{f_{n}}{(u_{n}+\frac{1}{n})^{\gamma }}-\frac{f_{m}}{(u_{m}+\frac{1}{m})^{m}}\right) T_{2k}(u_{n}-u_{m})\varphi (x)\\&\qquad +\int _{0}^{T}\int _{\Omega }\mu \left[ \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}-\frac{u_{m}^{p-1}}{|x|^{p}+\frac{1}{m}}\right] T_{2k}(u_{n}-u_{m})\varphi (x). \end{aligned} \end{aligned}$$

Observe that

$$\begin{aligned} \int _{0}^{T}\int _{\Omega }\frac{\partial (u_{n}-u_{m})}{\partial t}T_{2k}(u_{n}-u_{m})\varphi (x)= & {} \int _{\Omega }\int _{0}^{T}\frac{d}{dt}(\theta _{2k}(u_{n}-u_{m}))\varphi (x) \nonumber \\= & {} \int _{\Omega }\theta _{2k}(u_{n}-u_{m})(T)\varphi (x), \end{aligned}$$

(3.8)

where $\theta _{2k}(t)$ is the primitive of $T_{2k}(t)$ which vanishes for $t=0,$ and so we can drop the parabolic term (3.8) (since it is nonnegative) obtaining

$$\begin{aligned}&\int _{0}^{T}\int _{\Omega }(a(x,t, \nabla u_{n})-a(x,t, \nabla u_{m}))\nabla (T_{2k}(u_{n}-u_{m}))\varphi (x) \nonumber \\&\qquad +\int _{0}^{T}\int _{\Omega }(a(x,t, \nabla u_{n})-a(x,t, \nabla u_{m}))\nabla \varphi T_{2k}(u_{n}-u_{m}) \nonumber \\&\quad \le 2k\int _{Q\cap supp(\varphi )}\bigg | \frac{f_{n}}{(u_{n}+\frac{1}{n})^{\gamma }}-\frac{f_{m}}{(u_{m}+\frac{1}{m})^{\gamma }}\bigg | \nonumber \\&\qquad +\int _{0}^{T}\int _{\Omega }\mu \left[ \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}-\frac{u_{m}^{p-1}}{|x|^{p}+\frac{1}{m}}\right] T_{2k}(u_{n}-u_{m})\varphi (x). \end{aligned}$$

We denote by

$$\begin{aligned} A_{k,n}=\{(x,t)\in Q: u_{n}\le k\}\,\,\,\, \text{ and }\,\,\,\, A_{k,n, m}=\{(x,t)\in Q: u_{n}\le k,\, u_{m}\le k\}, \end{aligned}$$

since $A_{k,n, m}\subset \{(x,t)\in Q: |u_{n}-u_{m}|\le 2k \},$ we have

$$\begin{aligned}&\iint _{Q}(a(x,t,\nabla u_{n})-a(x,t,\nabla u_{m})\nabla (T_{2k}(u_{n}-u_{m}))\varphi \\&\quad =\iint _{\{(x,t)\in Q: |u_{n}-u_{m}|\le 2k\}}(a(x,t, \nabla u_{n})-a(x,t, \nabla u_{m}))\nabla (u_{n}- u_{m})\varphi \\&\quad \ge \iint _{A_{k,n,m}}(a(x,t,\nabla T_{k}(u_{n}))-a(x,t,\nabla T_{k}(u_{m})))(\nabla T_{k}(u_{n})-\nabla T_{k}(u_{m}))\varphi \\&\quad =\iint _{A_{k,n}}a(x,t,\nabla T_{k}(u_{n}))\nabla T_{k}(u_{n})\varphi -\iint _{A_{k,n,m}}a(x,t,\nabla T_{k}(u_{n}))\nabla T_{k}(u_{m})\varphi \\&\qquad -\iint _{A_{k,n,m}}a(x,t,\nabla T_{k}(u_{m}))\nabla T_{k}(u_{n})\varphi +\iint _{A_{k,m}}a(x,t,\nabla T_{k}(u_{m}))\nabla T_{k}(u_{m})\varphi . \end{aligned}$$

In conclusion, we found that

$$\begin{aligned}&\iint _{A_{k,n}}a(x,t,\nabla T_{k}(u_{n}))\nabla T_{k}(u_{n})\varphi -\iint _{A_{k,n,m}}a(x,t,\nabla T_{k}(u_{n}))\nabla T_{k}(u_{m})\varphi \nonumber \\&\qquad -\iint _{A_{k,n,m}}a(x,t,\nabla T_{k}(u_{m}))\nabla T_{k}(u_{n})\varphi +\iint _{A_{k,m}}a(x,t,\nabla T_{k}(u_{m}))\nabla T_{k}(u_{m})\varphi \nonumber \\&\quad \le 2k\int _{Q\cap supp(\varphi )}\bigg | \frac{f_{n}}{(u_{n}+\frac{1}{n})^{\gamma }}-\frac{f_{m}}{(u_{m}+\frac{1}{m})^{\gamma }}\bigg | \nonumber \\&\qquad +\int _{0}^{T}\int _{\Omega }\mu \left[ \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}-\frac{u_{m}^{p-1}}{|x|^{p}+\frac{1}{m}}\right] T_{2k}(u_{n}-u_{m})\varphi (x) \nonumber \\&\qquad -\iint _{Q}(a(x,t,\nabla u_{n})-a(x,t,\nabla u_{m}))\nabla \varphi (x)T_{2k}(u_{n}-u_{m}). \end{aligned}$$

(3.9)

The right-hand side of the previous inequality is infinitesimal for $n,m\rightarrow +\infty$ and we denote by r(n, m) a quantity that goes to zero from $n,m\rightarrow +\infty .$

By using the same proof as Proposition 3.2 in [11], we have

$$\begin{aligned} \int _{Q\cap supp(\varphi )}\bigg | \frac{f_{n}}{(u_{n}+\frac{1}{n})^{\gamma }}-\frac{f_{m}}{(u_{m}+\frac{1}{m})^{m}}\bigg |=r(n,m), \end{aligned}$$

and

$$\begin{aligned} \iint _{Q\cap supp(\varphi )}(a(x,t,\nabla u_{n})-a(x,t,\nabla u_{m}))\nabla \varphi (x)T_{2k}(u_{n}-u_{m})=r(n,m). \end{aligned}$$

Now, we prove

$$\begin{aligned} \int _{0}^{T}\int _{\Omega }\mu \left[ \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}-\frac{u_{m}^{p-1}}{|x|^{p}+\frac{1}{m}}\right] T_{2k}(u_{n}-u_{m})\varphi (x)=r(n,m). \end{aligned}$$

(3.10)

First of all we prove that

$$\begin{aligned} \frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}\, \text{ is } \text{ bounded } \text{ in }\, L^{{\bar{h}}}(0,T; L_{loc}^{{\bar{h}}}{\Omega }),\, \text{ for } \text{ every }\, 1<{\bar{h}}<\frac{pN}{p+(p-1)N}.\nonumber \\ \end{aligned}$$

(3.11)

Notice that it results $1<\frac{pN}{p+(p-1)N}<p^{\prime }.$ As matter of fact, for every compact $\omega \subset \Omega$ it results (thanks to Hardy inequality and Lemmas 3.1 and 3.2 )

$$\begin{aligned} \begin{aligned}&\int _{0}^{T}\int _{\omega }\bigg |\frac{u_{n}^{(p-1)}}{|x|^{p}+\frac{1}{n}}\bigg |^{{\bar{h}}}\le \int _{0}^{T}\int _{\omega }\frac{|u_{n}|^{{\bar{h}}(p-1)}}{|x|^{p{\bar{h}}}}=\int _{0}^{T}\int _{\omega }\frac{|u_{n}|^{{\bar{h}}(p-1)}}{|x|^{{\bar{h}}(p-1)}}\frac{1}{|x|^{{\bar{h}}}}\\&\quad \le \left( \int _{0}^{T}\int _{\omega } \frac{|u_{n}|^{p}}{|x|^{p}} \right) ^{\frac{{\bar{h}}(p-1)}{p}} \left( \int _{0}^{T}\int _{\omega }\frac{1}{|x|^{{\bar{h}}\left( \frac{p}{{\bar{h}}(p-1)} \right) ^{\prime }}} \right) ^{1-\frac{{\bar{h}}(p-1)}{p}} \le C, \end{aligned} \end{aligned}$$

where the last integral in the right-hand side is finite since it results

$$\begin{aligned} {\bar{h}}\left( \frac{p}{{\bar{h}}(p-1)}\right) ^{\prime }<N\Leftrightarrow {\bar{h}}<\frac{pN}{p+(p-1)N}. \end{aligned}$$

Hence, by (3.11) and the convergence a.e. of $u_{n}$ to u in Q we deduce that

$$\begin{aligned} \bigg [\frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}-\frac{u_{m}^{p-1}}{|x|^{p}+\frac{1}{m}}\bigg ]\varphi (x)\rightharpoonup 0\,\, \text{ weakly } \text{ in }\, L^{{\bar{h}}}(Q). \end{aligned}$$

Notice that, thanks to the Lebesgue Theorem, it results

$$\begin{aligned} T_{2k}(u_{n}-u_{m})\rightarrow 0\,\, \text{ strongly } \text{ in }\,\, L^{s}(Q),\,\, \text{ for } \text{ every }\,\, 1<s<+\infty , \end{aligned}$$

and thus it convergences also in $L^{{\bar{h}}^{\prime }}(Q)$ and (3.10) follows.

Then, the rest of the proof, we proceed as Proposition 3.2 in [11], we obtain up to subsequences, $T_{k}(u_{n})\rightarrow T_{k}(u)$ in $L^{p}(0,T; W_{loc}^{1,p}(\Omega )),$ and so $\nabla u_{n}\rightarrow \nabla u$ a.e. in Q. $\square$

Proof of Theorems 3.3 and 3.5

If $\gamma <1,$ by Lemma 3.1, we have $u_{n}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and in $L^{\infty }(0,T; L^{2}(\Omega )).$ Then, by Lemma 2.2, Proposition 3.7 and Fatou’s Lemma $u\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(0,T; L^{2}(\Omega )),$ and moreover $\frac{u^{p-1}}{|x|^{p}}, \frac{f}{u^{\gamma }}\in L^{1}(0,T; L^{1}_{loc}(\Omega ))$ since u satisfies (1.8), in particular

$$\begin{aligned} \displaystyle \frac{\partial u}{\partial t}\in L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}(\Omega ))+ L^{1}(0,T; L^{1}_{loc}(\Omega )). \end{aligned}$$

If $\gamma =1,$ thanks to Lemma 3.2, we have $u_{n}$ is bounded in

$$\begin{aligned} L^{p}(0,T; W_{0}^{1,p}(\Omega )) \text{ and } \text{ in } L^{\infty }(0,T; L^{2}(\Omega )), \end{aligned}$$

as before, we get $u\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(0,T; L^{2}(\Omega ))$ and u satisfies (1.8); Moreover $\frac{\partial u}{\partial t}\in L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}(\Omega ))+ L^{1}(0,T; L^{1}_{loc}(\Omega )).$

In the case $\gamma >1,$ in view of Lemma 3.2, we have that $u_{n}^{\frac{p+\gamma -1}{p}}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega )),$ while $u_{n}$ is bounded in

$$\begin{aligned} L^{p}(0,T; W_{loc}^{1,p}(\Omega )) \text{ and } \text{ in } L^{\infty }(0,T; L^{\gamma +1}(\Omega )). \end{aligned}$$

Then

$$\begin{aligned} u\in L^{p}(0,T; W_{loc}^{1,p}(\Omega )) \text{ and } u^{\frac{p+\gamma -1}{p}} \in L^{p}(0,T; W_{0}^{1,p}(\Omega )), \end{aligned}$$

in particular, $u=0$ on $\partial \Omega \times (0,T)$ in weak-sense and

$$\begin{aligned} \frac{\partial u}{\partial t}\in L^{p^{\prime }}(0,T; W^{-1,p^{\prime }}(w))+ L^{1}(0,T; L^{1}_{loc}(\Omega )), \text{ for } \text{ all } w\subset \subset \Omega . \end{aligned}$$

Using Lemma 2.2, Proposition 3.7 and Fatou’s Lemma deduce that u satisfies the condition (1.8). Now we fix $\varphi \in C_{c}^{1}(\Omega \times [0,T)),$ by Lemma 3.1 and Lemma 3.2, we have the boundedness of the sequence $u_{n}$ in the space $L^{p}(0,T; W_{loc}^{1,p}(\Omega ))$ and from (1.4), implies that the sequence $a(x,t,\nabla u_{n})$ is bounded in $L^{p^{\prime }}(\omega \times (0,T))$ for all $\omega \subset \subset \Omega .$ As $supp(\varphi )$ is a compact subset of $\Omega \times [0,T),$ then $a(x,t,\nabla u_{n})$ is bounded in $L^{p^{\prime }}(supp(\varphi ))$ and $\frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}$ is bounded in $L^{1}(supp(\varphi )).$ From Propositions 3.7 and 3.8 , we have $u_{n}\rightarrow u$ a.e. in Q and $\nabla u_{n}\rightarrow \nabla u$ a.e. in Q and by Vitali’s Theorem we obtain

$$\begin{aligned} \lim _{n\rightarrow +\infty }\iint _{Q}a(x,t, \nabla u_{n})\nabla \varphi =\iint _{Q}a(x,t, \nabla u)\nabla \varphi \,\,\,\,\;\; \forall \varphi \in C_{c}^{1}(\Omega \times [0,T)),\nonumber \\ \end{aligned}$$

(3.12)

and

$$\begin{aligned} \lim _{n\rightarrow +\infty }\iint _{Q}\frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}\varphi =\iint _{Q}\frac{u^{p-1}}{|x|^{p}}\varphi \,\,\,\,\;\; \forall \varphi \in C_{c}^{1}(\Omega \times [0,T)). \end{aligned}$$

(3.13)

Concerning the passage of limit of term in the right of the approximating problem (2.1), since $supp(\varphi )$ is a compact subset of $\Omega \times [0,T),$ thanks to Lemma 2.2, there exists a constant $c_{supp(\varphi )}>0$ such that $u_{n}\ge c_{supp(\varphi )},$ then

$$\begin{aligned} \left| \frac{f_{n}}{(u_{n}+\frac{1}{n})^{\gamma }}\varphi \right| \le \frac{f}{c_{supp(\varphi )}^{\gamma }}||\varphi ||_{L^{\infty }(Q)}, \end{aligned}$$

for every $(x,t)\in supp(\varphi ),$ since it is a.e. convergent to $\frac{f}{u^{\gamma }}\varphi$ for $n\longrightarrow +\infty ,$ by Lebesgue Theorem, implies that

$$\begin{aligned} \lim _{n\rightarrow +\infty }\iint _{Q}\frac{f_{n}}{(u_{n}+\frac{1}{n})^{\gamma }}\varphi =\iint _{Q}\frac{f}{u^{\gamma }}\varphi \,\,\,\,\;\; \forall \varphi \in C_{c}^{1}(\Omega \times [0,T)). \end{aligned}$$

(3.14)

By Proposition 3.7, we have

$$\begin{aligned} \lim _{n\rightarrow +\infty }\iint _{Q}u_{n}\frac{\partial \varphi }{\partial t}=\iint _{Q}u\frac{\partial \varphi }{\partial t}, \,\,\,\,\;\; \forall \varphi \in C_{c}^{1}(\Omega \times [0,T)). \end{aligned}$$

(3.15)

Take now $\varphi \in C_{c}^{1}(\Omega \times [0,T))$ as a test function in problem (2.1), by the convergences results (3.12), (3.13), (3.14), (3.15) and letting $n\longrightarrow +\infty ,$ we get

$$\begin{aligned} -\int _{\Omega }u_{0}(x)\varphi (x,0)-\iint _{Q}u\frac{\partial \varphi }{\partial t}+\iint _{Q}a(x,t, \nabla u)\nabla \varphi -\mu \iint _{Q}\frac{u^{p-1}}{|x|^{p}}\varphi =\iint _{Q}\frac{f}{u^{\gamma }}\varphi . \end{aligned}$$

$\square$

4 Regularity results

In this section we study the regularity of solutions of problem (1.1) depending on $\mu , \gamma >0$ and the summability of f.

4.1 The case $\gamma \ge 1$

Theorem 4.1

Let $\gamma \ge 1$ and suppose that f belongs to $L^{m}(Q)$ with $1<m<\frac{N}{p}+1.$ If

$$\begin{aligned}&0< \mu <\alpha C_{N,p}\frac{(Np-N+p)(m-1)+N\gamma m}{N-pm+p}\times \\&\left( \frac{p(N-pm+p)}{N(p+\gamma -1)m-p(p-2)(m-1)}\right) ^{p}, \end{aligned}$$

then the solution u of (1.1) found in Theorem 3.5 satisfies the following summability $u\in L^{\sigma }(Q),$ where $\sigma =m\displaystyle \frac{N(p+\gamma -1)+p(\gamma +1)}{N-pm+p}.$

Proof

Let now choosing $u_{n}^{p\delta -p+1}\chi _{(0,t)}$ as test function in (2.1), $\delta >\frac{p+\gamma -1}{p}$ and $0<t<T,$ then we get

$$\begin{aligned}&\displaystyle \int _{0}^{t}\int _{\Omega }\frac{\partial u_{n}}{\partial t}u_{n}^{p\delta -p+1}+(p\delta -p+1)\displaystyle \int _{0}^{t}\int _{\Omega }u_{n}^{p\delta -p}a(x,t, \nabla u_{n}).\nabla u_{n}\\&\quad \le \mu \displaystyle \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{p\delta }}{|x|^{p}}+\displaystyle \int _{0}^{t}\int _{\Omega }\frac{f_{n}}{(u_{n}+\frac{1}{n})^{\gamma }}u_{n}^{p\delta -p+1}, \end{aligned}$$

from (1.3), it follows that

$$\begin{aligned}&\frac{1}{p\delta -p+2}\int _{\Omega }u_{n}^{p\delta -p+2}(x,t)+\alpha (p\delta -p+1)\int _{0}^{t}\int _{\Omega }u_{n}^{p\delta -p}|\nabla u_{n}|^{p}\\&\quad \le \mu \displaystyle \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{p\delta }}{|x|^{p}}+\int _{0}^{t}\int _{\Omega }f_{n}u_{n}^{p\delta -p+1-\gamma }+\frac{1}{p\delta -p+2}\int _{\Omega }u_{0}^{p\delta -p+2}. \end{aligned}$$

Thanks to $u_{0}\in L^{\infty }(\Omega )$ and $u_{n}^{p\delta -p}|\nabla u_{n}|^{p}=\frac{1}{\delta ^{p}}|\nabla u_{n}^{\delta }|^{p},$ the last inequality becomes

$$\begin{aligned}&\frac{1}{p\delta -p+2}\int _{\Omega }[u_{n}^{\delta }]^{\frac{p\delta -p+2}{\delta }}+\frac{\alpha (p\delta -p+1)}{\delta ^{p}}\int _{0}^{t}\int _{\Omega }|\nabla u_{n}^{\delta }|^{p}\\&\quad \le \mu \displaystyle \int _{0}^{t}\int _{\Omega }\frac{(u_{n}^{\delta })^{p}}{|x|^{p}}+\int _{0}^{t}\int _{\Omega }f_{n}u_{n}^{p\delta -p+1-\gamma }+\frac{1}{p\delta -p+2}||u_{0}||_{L^{\infty }(\Omega )}^{p\delta -p+2}, \end{aligned}$$

applying Hardy and Hölder’s inequalities, yields

$$\begin{aligned}&\frac{1}{p\delta -p+2}\displaystyle \int _{\Omega }[u_{n}^{\delta }]^{\frac{p\delta -p+2}{\delta }}+\left( \frac{\alpha (p\delta -p+1)}{\delta ^{p}}-\frac{\mu }{C_{N,p}}\right) \displaystyle \int _{0}^{t}\int _{\Omega }|\nabla u_{n}^{\delta }|^{p}\\&\quad \le ||f||_{L^{m}(Q)}\left( \displaystyle \iint _{Q}u_{n}^{(p\delta -p+1-\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

Passing to supremum for $t\in (0,T)$ we have

$$\begin{aligned}&\frac{1}{p\delta -p+2}||u_{n}^{\delta }||_{L^{\infty }(0,T; L^{\frac{p\delta -p+2}{\delta }}(\Omega ))}^{\frac{p\delta -p+2}{\delta }}+ \left( \frac{\alpha (p\delta -p+1)}{\delta ^{p}}-\frac{\mu }{C_{N,p}}\right) \displaystyle \iint _{Q}|\nabla u_{n}^{\delta }|^{p} \nonumber \\&\quad \le ||f||_{L^{m}(Q)}\left( \displaystyle \iint _{Q}u_{n}^{(p\delta -p+1-\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(4.1)

Since $u_{n}\in L^{\infty }(Q)\cap L^{p}(0,T; W_{0}^{1,p}(\Omega )),$ then in view to Lemma 1.1 and by (4.1), we get

$$\begin{aligned}&\iint _{Q}(u_{n}^{\delta })^{p\frac{N+\frac{p\delta -p+2}{\delta }}{N}}\le C_{G} ||u_{n}^{\delta }||_{L^{\infty }(0,T; L^{\frac{p\delta -p+2}{\delta }}(\Omega ))}^{\frac{p(p\delta -p+2)}{N\delta }}\iint _{Q}|\nabla u_{n}^{\delta }|^{p}\\&\quad \le C\left( \iint _{Q}u_{n}^{(p\delta -p+1-\gamma )m^{\prime }}\right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C, \end{aligned}$$

hence

$$\begin{aligned} \iint _{Q}u_{n}^{\frac{p(N\delta +p\delta -p+2)}{N}} \le C\left( \iint _{Q}u_{n}^{(p\delta -p+1-\gamma )m^{\prime }}\right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(4.2)

Choosing now $\delta$ such that

$$\begin{aligned} \sigma =\frac{p(N\delta +p\delta -p+2)}{N}=(p\delta -p+1-\gamma )m^{\prime }, \end{aligned}$$

(4.3)

this equivalent to

$$\begin{aligned} \delta =\frac{ Nm(p+\gamma -1)-p(p-2)(m-1)}{p(N-pm+p)},\;\; \sigma =m\frac{N(p+\gamma -1)+p(\gamma +1)}{N-pm+p}. \end{aligned}$$

Collecting (4.2) with (4.3), we conclude that

$$\begin{aligned} \iint _{Q}u_{n}^{\sigma }\le C\left( \iint _{Q}u_{n}^{\sigma }\right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(4.4)

By virtue of $m<\frac{N}{p}+1,$ then $(\frac{p}{N}+1)\frac{1}{m^{\prime }}<1,$ since $\delta >\frac{p+\gamma -1}{p}$ gives $m>1$ and applying Young’s inequality implies that

$$\begin{aligned} \iint _{Q}u_{n}^{\sigma }\le C, \end{aligned}$$

(4.5)

this last estimate yields that the sequence $u_{n}$ is bounded in $L^{\sigma }(Q),$ and so $u\in L^{\sigma }(Q).$

$\square$

Theorem 4.2

Let $\gamma \ge 1$ and $f\in L^{m}(Q)$ with $m\ge \frac{N}{p}+1.$ Then the solution of problem (1.1) found in Theorem (3.5) satisfies the following regularity:

If $\lambda \ge \gamma$ and $\frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}>0,$ then $u^{\frac{\lambda +p-1}{p}}\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and $u\in L^{\infty }(0,T; L^{\lambda +1}(\Omega )).$

Proof

Choosing $u_{n}^{\lambda }\chi _{(0,t)}$ with $\lambda >0$ as test function in (2.1)

$$\begin{aligned}&\displaystyle \frac{1}{\lambda +1}\int _{\Omega }u_{n}^{\lambda +1}(x,t)+\lambda \displaystyle \int _{0}^{t}\int _{\Omega } u_{n}^{\lambda -1}a(x,t,\nabla u_{n})\cdot \nabla u_{n}\\&\quad =\mu \displaystyle \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{\lambda +p-1}}{|x|^{p}}+\displaystyle \int _{0}^{t}\int _{\Omega }\frac{f_{n}u_{n}^{\lambda }}{(u_{n}+1)^{\gamma }}+\frac{1}{\lambda +1}\int _{\Omega }|u_{0}(x)|^{\lambda +1}. \end{aligned}$$

From (1.3) and the fact that $\frac{1}{(u_{n}+1)^{\gamma }}\le \frac{1}{u_{n}^{\gamma }}, u_{0}\in L^{\infty }(\Omega )$ we have

$$\begin{aligned}&\frac{1}{\lambda +1}\displaystyle \int _{\Omega }u_{n}^{\lambda +1}(x,t)+\lambda \alpha \int _{0}^{t}\int _{\Omega }|\nabla u_{n}|^{p}u_{n}^{\lambda -1}\\&\quad \le \mu \displaystyle \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{\lambda +p-1}}{|x|^{p}}+\int _{0}^{t}\int _{\Omega }f_{n}u_{n}^{\lambda -\gamma }+\frac{|\Omega |}{\lambda +1}||u_{0}||_{L^{\infty }(\Omega )}^{\lambda +1}. \end{aligned}$$

By Hardy inequality the later inequality implies

$$\begin{aligned}&\displaystyle \frac{1}{\lambda +1}\int _{\Omega }u_{n}^{\lambda +1}(x,t)+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}} \right) \int _{0}^{t}\int _{\Omega }|\nabla u_{n}^{\frac{\lambda +p-1}{p}}|^{p}\\&\quad \displaystyle \le \int _{0}^{t}\int _{\Omega }f_{n}u_{n}^{\lambda -\gamma }+C. \end{aligned}$$

Passing to supremum for $t\in [0,T]$ we get

$$\begin{aligned}&\displaystyle \frac{1}{\lambda +1}||u_{n}||_{L^{\infty }(0,T; L^{\lambda +1}(\Omega ))}^{\lambda +1}+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}} \right) \iint _{Q}|\nabla u_{n}^{\frac{\lambda +p-1}{p}}|^{p}\\&\quad \displaystyle \le \iint _{Q}f_{n}u_{n}^{\lambda -\gamma }+C, \end{aligned}$$

applying Hölder inequality we conclude that

$$\begin{aligned}&\frac{1}{\lambda +1}||u_{n}||_{L^{\infty }(0,T; L^{\lambda +1}(\Omega ))}^{\lambda +1}+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}} \right) \iint _{Q}|\nabla u_{n}^{\frac{\lambda +p-1}{p}}|^{p} \nonumber \\&\quad \le C\left( \iint _{Q}u_{n}^{(\lambda -\gamma )m^{\prime }} \right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(4.6)

Using Sobolev inequality and by the above estimate, we get

$$\begin{aligned} \left( \iint _{Q}u_{n}^{\frac{N(\lambda +p-1)}{N-p}} \right) ^{\frac{p}{p^{*}}}\le C\iint _{Q}|\nabla u_{n}^{\frac{\lambda +p-1}{p}}|^{p}\le C\left( \iint _{Q}u_{n}^{(\lambda -\gamma )m^{\prime }} \right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

By $m\ge \frac{N}{p}+1$ we have $m^{\prime }\le \frac{N+p}{N}$, then for all $\lambda \ge \gamma ,$ we get $(\lambda -\gamma )m^{\prime }\le \frac{(\lambda -\gamma )(N+p)}{N} \le \frac{N(\lambda +p-1)}{N-p}$. Thus choosing $\lambda$ such that $\frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}>0.$ Using Hölder’s inequality in the later estimate, we have

$$\begin{aligned} \left( \iint _{Q}u_{n}^{\frac{N(\lambda +p-1)}{N-p}} \right) ^{\frac{p}{p^{*}}}\le C\left( \iint _{Q}u_{n}^{\frac{N(\lambda +p-1)}{N-p}}\right) ^{\frac{(N-p)(\lambda -\gamma )}{N(\lambda +p-1)}}+C. \end{aligned}$$

(4.7)

Since $\frac{p}{p^{*}}=\frac{N-p}{N}> \frac{(N-p)(\lambda -\gamma )}{N(\lambda +p-1)},$ then by Young inequality we deduce that

$$\begin{aligned} \iint _{Q}u_{n}^{\frac{N(\lambda +p-1)}{N-p}}\le C. \end{aligned}$$

(4.8)

By the fact that $(\lambda -\gamma )m^{\prime }<\frac{N(\lambda +p-1)}{N-p},$ (4.8) and using Hölder inequality in (4.6), we obtain

$$\begin{aligned}&\displaystyle \frac{1}{\lambda +1}||u_{n}||^{\lambda +1}_{L^{\infty }(0,T; L^{\lambda +1}(\Omega ))}+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}} \right) \displaystyle \iint _{Q}|\nabla u_{n}^{\frac{\lambda +p-1}{p}}|^{p} \\&\quad \le C\left( \displaystyle \iint _{Q}u_{n}^{\frac{N(\lambda +p-1)}{N-p}}\right) ^{\frac{(N-p)(\lambda -\gamma )}{N(\lambda +p-1)}}+C\le C. \end{aligned}$$

Since $\lambda \ge \gamma ,$ $\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}} \right) >0$ and the later estimate we deduce that the sequence $u_{n}^{\frac{\lambda +p-1}{p}}$ is uniformly bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and $u_{n}$ is bounded $L^{\infty }(0,T; L^{\lambda +1}(\Omega ))$ with respect to n for all $\lambda \ge \gamma ,$ so $u^{\frac{\lambda +p-1}{p}}\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and $u\in L^{\infty }(0,T; L^{\lambda +1}(\Omega ))$ for all $\lambda \ge \gamma .$ This completed the proof of Theorem 4.2. $\square$

4.2 The case $\gamma <1$

Theorem 4.3

Let $\gamma <1,$ and suppose that $f\in L^{m}(Q), m\ge 1$ and

$$\begin{aligned} 0\le & {} \mu <\alpha C_{N,p}\frac{(m-1)[N(p-1)+p]+Nm\gamma }{N-pm+p} \nonumber \\&\times \left( \frac{p(N-pm+p)}{(m-1)[(N-p)(p-1)+p]+N(m\gamma +p-1)}\right) ^{p}. \end{aligned}$$

(4.9)

Then

(i):

If $\frac{p(N+2)}{p(N+2)-N(1-\gamma )}\le m<\frac{N}{p}+1,$ then the solution u of (1.1) found in Theorem 3.3, satisfies the following regularity $u\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\sigma }(Q),$ with $\sigma =m\frac{N(p+\gamma -1)+p(\gamma +1)}{N-pm+p}.$

(ii):

If $1\le m<\frac{p(N+2)}{p(N+2)-N(1-\gamma )},$ then there exists a weak solution u of problem (1.1) such that $u\in L^{q}(0,T; W_{0}^{1,q}(\Omega ))\cap L^{\sigma }(Q),$ with

$$\begin{aligned} q=m\frac{N(p+\gamma -1)+p(\gamma +1)}{N+2-m(1-\gamma )}\; \text{ and } \; \sigma =m\frac{N(p+\gamma -1)+p(\gamma +1)}{N-pm+p}. \end{aligned}$$

(iii):

If $m\ge \frac{N}{p}+1$ and $0< \mu <\alpha C_{N,p},$ then the solution u of (1.1) found in Theorem 3.3 satisfies the following regularity $u\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\infty }(Q).$

Proof

Taking $\varphi (u_{n})=((u_{n}+a)^{\lambda }-a^{\lambda })\chi _{(0,t)}$ as a test function in (2.1), $0<a< \frac{1}{n}, \; \lambda >0$ and using the ellipticity condition (1.3) we have

$$\begin{aligned}&\int _{0}^{t}\int _{\Omega }\frac{\partial u_{n}}{\partial t}\varphi (u_{n})+\lambda \alpha \int _{0}^{t}\int _{\Omega }(u_{n}+a)^{\lambda -1}|\nabla u_{n}|^{p}\\&\quad \le \mu \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{p-1}(u_{n}+a)^{\lambda }}{|x|^{p}}+\int _{0}^{t}\int _{\Omega }\frac{f_{n}|(u_{n}+a)^{\lambda }-a^{\lambda }|}{(u_{n}+\frac{1}{n})^{\gamma }}. \end{aligned}$$

By the fact that $\frac{1}{(u_{n}+\frac{1}{n})^{\gamma }}\le \frac{1}{(u_{n}+a)^{\gamma }}$ and $u_{n}^{p-1}(u_{n}+a)^{\lambda }\le (u_{n}+a)^{\lambda +p-1},$ we obtain

$$\begin{aligned}&\displaystyle \int _{\Omega }\Psi (u_{n}(x,t))+\lambda \alpha \displaystyle \int _{0}^{t}\int _{\Omega }(u_{n}+a)^{\lambda -1}|\nabla u_{n}|^{p}\\&\quad \le \mu \displaystyle \int _{0}^{t}\int _{\Omega }\frac{(u_{n}+a)^{\lambda +p-1}}{|x|^{p}}+\displaystyle \int _{0}^{t}\int _{\Omega }f_{n}(u_{n}+a)^{\lambda -\gamma }+\displaystyle \int _{\Omega }\Psi (u_{0}), \end{aligned}$$

where $\Psi (s)=\displaystyle \int _{0}^{s}\varphi (\ell )d\ell .$ Since $(u_{n}+a)^{\lambda -1}|\nabla u_{n}|^{p}=\frac{p^{p}}{(\lambda +p-1)^{p}}|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p},$ then the last estimate becomes

$$\begin{aligned}&\int _{\Omega }\Psi (u_{n}(x,t))+\frac{\lambda \alpha p^{p}}{(\lambda +p-1)^{p}}\int _{0}^{t}\int _{\Omega }|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p} \nonumber \\&\quad \le \mu \int _{0}^{t}\int _{\Omega }\frac{((u_{n}+a)^{\frac{\lambda +p-1}{p}})^{p}}{|x|^{p}}+\int _{0}^{t}\int _{\Omega }f(u_{n}+a)^{\lambda -\gamma }+\int _{\Omega }\Psi (u_{0}). \end{aligned}$$

(4.10)

Since $u_{0}\in L^{\infty }(\Omega ),$ applying Hölder and Hardy inequalities, we find that

$$\begin{aligned}&\displaystyle \int _{\Omega }\Psi (u_{n}(x,t))+\left( \frac{\lambda \alpha p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) \displaystyle \int _{0}^{t}\int _{\Omega }|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p}\\&\quad \le ||f||_{L^{m}(Q)}\left( \displaystyle \iint _{Q}(u_{n}+a)^{(\lambda -\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

If $\lambda \ge 1,$ by definition of $\varphi (u_{n})$ and $\Psi (u_{n}),$ we reach that

$$\begin{aligned} \Psi (s)\ge \frac{|s|^{\lambda +1}}{\lambda +1}, \quad \;\; \forall s\in {\mathbb {R}}. \end{aligned}$$

(4.11)

Therefore we obtain that

$$\begin{aligned}&\displaystyle \frac{1}{\lambda +1}\int _{\Omega }u_{n}^{\lambda +1}(x,t)+\left( \frac{\lambda \alpha p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) \displaystyle \int _{0}^{t}\int _{\Omega }|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p}\\&\quad \le ||f||_{L^{m}(Q)}\left( \displaystyle \iint _{Q}(u_{n}+a)^{(\lambda -\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

Observing that $u_{n}^{\lambda +1}(x,t)=\left( u_{n}^{\frac{\lambda +p-1}{p}}(x,t)\right) ^{\frac{p(\lambda +1)}{\lambda +p-1}},$ then the last inequality becomes

$$\begin{aligned}&\displaystyle \frac{1}{\lambda +1}\int _{\Omega }[u_{n}^{\frac{\lambda +p-1}{p}}]^{\frac{p(\lambda +1)}{\lambda +p-1}}+\left( \frac{\lambda \alpha p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) \displaystyle \int _{0}^{t}\int _{\Omega }|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p}\\\nonumber&\quad \le ||f||_{L^{m}(Q)}\left( \displaystyle \iint _{Q}(u_{n}+a)^{(\lambda -\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

Now passing to the supremum for $t\in (0,T),$ we obtain

$$\begin{aligned}&||u_{n}^{\frac{\lambda +p-1}{p}}||^{\frac{p(\lambda +1)}{\lambda +p+1}}_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p+1}}(\Omega ))}+ \displaystyle \iint _{Q}|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p}\nonumber \\&\quad \le C\left( \displaystyle \iint _{Q}(u_{n}+a)^{(\lambda -\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(4.12)

From (4.12) and applying Lemma 1.1, we have

$$\begin{aligned}&\displaystyle \iint _{Q}[u_{n}^{\frac{\lambda +p-1}{p}}]^{p\frac{N+\frac{p(\lambda +1)}{\lambda +p-1}}{N}}\le C_{G}||u_{n}^{\frac{\lambda +p-1}{p}}||_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega )}^{\frac{p}{N}\times \frac{p(\lambda +1)}{\lambda +p-1}}\displaystyle \iint _{Q}|\nabla u_{n}^{\frac{\lambda +p-1}{p}}|^{p}\\&\quad \le C\left( \displaystyle \iint _{Q}(u_{n}+a)^{(\lambda -\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C, \end{aligned}$$

where $C=C(\alpha , \lambda , m, p, \mu , C_{N,p}, C_{G}, ||u_{0}||_{L^{\infty }(\Omega )}).$ Thus we get

$$\begin{aligned} \iint _{Q}u_{n}^{\frac{N(\lambda +p-1)+p(\lambda +1)}{N}}\le C\left( \iint _{Q}(u_{n}+a)^{(\lambda -\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

Letting $a\rightarrow 0,$ we reach that

$$\begin{aligned} \iint _{Q}u_{n}^{\frac{N(\lambda +p-1)+p(\lambda +1)}{N}}\le C\left( \iint _{Q}u_{n}^{(\lambda -\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C, \end{aligned}$$

(4.13)

choosing $\lambda$ such that

$$\begin{aligned} \sigma =\frac{N(\lambda +p-1)+p(\lambda +1)}{N}=(\lambda -\gamma )m^{\prime }, \end{aligned}$$

(4.14)

this equivalent to

$$\begin{aligned} \lambda =\frac{(m-1)(N(p-1)+p)+Nm\gamma }{N-pm+p}\;\;\; \text{ and }\;\; \sigma =m\frac{N(p+\gamma -1)+p(\gamma +1)}{N-pm+p}. \end{aligned}$$

From (4.14), the estimate (4.13) becomes

$$\begin{aligned} \iint _{Q}u_{n}^{\sigma }\le C\left( \iint _{Q}u_{n}^{\sigma }\right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C. \end{aligned}$$

The condition $\frac{p(N+2)}{p(N+2)-N(1-\gamma )}\le m<\frac{N}{p}+1,$ ensure that $\lambda \ge 1$ and $(\frac{p}{N}+1)\frac{1}{m^{\prime }}<1,$ and thanks to Young inequality we deduce that

$$\begin{aligned} \iint _{Q}u_{n}^{\sigma }\le C. \end{aligned}$$

(4.15)

From (4.9) and, by the fact that and $|\nabla u_{n}|^{p}\le (u_{n}+a)^{\lambda -1}|\nabla u_{n}|^{p}$ $(a>0, \; \lambda \ge 1)$ going back to (4.12) and using (4.14), (4.15) yield that

$$\begin{aligned} \iint _{Q}|\nabla u_{n}|^{p}\le \iint _{Q}(u_{n}+a)^{\lambda -1}|\nabla u_{n}|^{p}\le C\left( \iint _{Q}u_{n}^{\sigma }\right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C\le C.\nonumber \\ \end{aligned}$$

(4.16)

Then by estimates (4.15) and (4.16) we deduce that the sequence $u_{n}$ is bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega ))$ and in $L^{\sigma }(Q)$ with respect to n,  and so $u\in L^{p}(0,T; W_{0}^{1,p}(\Omega )\cap L^{\sigma }(Q).$ Hence the proof of item (i) is achieved.

Now we prove item (ii). Let now taking $\gamma<\lambda <1$ and by definition of $\varphi (u_{n})$ and $\Psi (u_{n}),$ we can get

$$\begin{aligned} \Psi (s)\ge C|s|^{\lambda +1}-C \quad \;\;\; \forall s\in {\mathbb {R}}. \end{aligned}$$

(4.17)

From (4.17) and going back to (4.10), we have

$$\begin{aligned}&C\displaystyle \int _{\Omega }\Psi (u_{n}(x,t))+\alpha \lambda \displaystyle \int _{0}^{t}\int _{\Omega }(u_{n}+a)^{\lambda -1}|\nabla u_{n}|^{p}\\&\quad \le \mu \displaystyle \int _{0}^{t}\int _{\Omega }\frac{(u_{n}+a)^{\lambda +p-1}}{|x|^{p}}+\displaystyle \int _{0}^{t}\int _{\Omega }f_{n}(u_{n}+a)^{\lambda -\gamma }+\int _{\Omega }\Psi (u_{0})+C|\Omega |. \end{aligned}$$

We proceed as before, we obtain that

$$\begin{aligned}&C||u_{n}^{\frac{\lambda +p-1}{p}}||_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}^{\frac{p(\lambda +1)}{\lambda +p-1}} \nonumber \\&\qquad +\left( \frac{\lambda \alpha p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}} \right) \iint _{Q}|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p} \nonumber \\&\quad \le C\left( \iint _{Q}(u_{n}+a)^{(\lambda -\gamma )m^{\prime }} \right) ^{\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(4.18)

Thanks to Lemma 1.1 and repeat the above process, it hold that

$$\begin{aligned} \iint _{Q}u_{n}^{\frac{N(\lambda +p-1)+p(\lambda +1)}{N}}\le C\left( \iint _{Q}u_{n}^{(\lambda -\gamma )m^{\prime }} \right) ^{(\frac{p}{N}+1)\frac{1}{m^{\prime }}}+C. \end{aligned}$$

(4.19)

Let now choosing $\lambda$ such that

$$\begin{aligned} \sigma =\frac{N(\lambda +p-1)+p(\lambda +1)}{N}=(\lambda -\gamma )m^{\prime }, \end{aligned}$$

(4.20)

this yields that

$$\begin{aligned} \sigma =m\frac{N(p+\gamma -1)+p(\gamma +1)}{N-pm+p} \;\; \text{ and }\;\; \lambda =\frac{(m-1)(N(p-1)+p)+Nm\gamma }{N-pm+p}. \end{aligned}$$

Since $\lambda <1,$ then $m<\frac{p(N+2)}{p(N+2)-N(1-\gamma )}<\frac{N}{p}+1,$ and $(\frac{p}{N}+1)\frac{1}{m^{\prime }}<1,$ from (4.19), (4.20) and thanks to Young inequality it hold that

$$\begin{aligned} \iint _{Q}u_{n}^{\sigma }\le C. \end{aligned}$$

(4.21)

By (4.9), then we have $\frac{\lambda \alpha p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}>0.$ Let $1<q<p,$ applying Hölder’s inequality and from (4.18), we get

$$\begin{aligned} \iint _{Q}|\nabla u_{n}|^{q}= & {} \iint _{Q}\frac{|\nabla u_{n}|^{q}}{(u_{n}+a)^{\frac{q(1-\lambda )}{p}}}(u_{n}+a)^{\frac{q(1-\lambda )}{p}} \nonumber \\\le & {} \left( \iint _{Q}\frac{|\nabla u_{n}|^{p}}{(u_{n}+a)^{1-\lambda }}\right) ^{\frac{q}{p}}\left( \iint _{Q}(u_{n}+a)^{\frac{q(1-\lambda )}{p-q}} \right) ^{\frac{p-q}{p}} \nonumber \\\le & {} \left[ C\left( \iint _{Q}(u_{n}+a)^{(\lambda -\gamma )m^{\prime }}\right) ^{\frac{1}{m^{\prime }}}+C\right] ^{\frac{q}{p}}\left( \iint _{Q}(u_{n}+a)^{\frac{q(1-\lambda )}{p-q}} \right) ^{\frac{p-q}{p}},\nonumber \\ \end{aligned}$$

(4.22)

we take q such that

$$\begin{aligned} \frac{q(1-\lambda )}{p-q}=(\lambda -\gamma )m^{\prime }, \end{aligned}$$

(4.23)

this equivalent to $q=m\frac{N(p+\gamma -1)+p(\gamma +1)}{N+2- m(1-\gamma )}.$ Using (4.23) in (4.22) and letting $a\rightarrow 0,$ we hold that

$$\begin{aligned} \iint _{Q}|\nabla u_{n}|^{q}\le \left( C\left( \iint _{Q}u_{n}^{\sigma }\right) ^{\frac{1}{m^{\prime }}}+C\right) ^{\frac{q}{p}}\left( \iint _{Q}u_{n}^{\sigma }\right) ^{\frac{p-q}{p}}. \end{aligned}$$

From (4.21) it follows that

$$\begin{aligned} \iint _{Q}|\nabla u_{n}|^{q}\le C. \end{aligned}$$

(4.24)

Therefore estimates (4.21) and (4.24) imply that the sequence $u_{n}$ is bounded in $L^{q}(0,T; W_{0}^{1,q}(\Omega ))$ and in $L^{\sigma }(Q)$ with respect to n,  and so $u\in L^{q}(0,T; W_{0}^{1,q}$ $(\Omega ))\cap L^{\sigma }(Q).$

Now we give the proof of item (iii). Taking $G_{k}(u_{n})\chi _{(0,t)}$ as a test function in (2.1) for $t\in (0,T),$ we have

$$\begin{aligned}&\int _{0}^{t}\int _{\Omega }\frac{\partial u_{n}}{\partial t}G_{k}(u_{n})+\int _{0}^{t}\int _{\Omega }a(x,t,\nabla u_{n})\nabla G_{k}(u_{n}) \nonumber \\&\quad -\mu \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{p-1}}{|x|^{p}+\frac{1}{n}}G_{k}(u_{n}) \le \int _{0}^{t}\int _{\Omega }\frac{f_{n}G_{k}(u_{n})}{(u_{n}+\frac{1}{n})^{\gamma }}. \end{aligned}$$

(4.25)

We observe that the function $G_{k}(u_{n})$ is different from zero only on the set $A_{k,n}=\{(x,t)\in Q: u_{n}(x,t)>k\},$ and that, on this set, we have $u_{n}+\frac{1}{n}\ge k\ge 1.$ Note that

$$\begin{aligned}&\int _{0}^{t}\int _{\Omega }a(x,t,\nabla u_{n})\nabla G_{k}(u_{n})=\iint _{A_{k,n}}a(x,t,\nabla u_{n})\nabla u_{n}\\&\quad \ge \alpha \iint _{A_{k,n}}|\nabla u_{n}|^{p}=\alpha \int _{0}^{t}\int _{\Omega }|\nabla G_{k}(u_{n})|^{p} \end{aligned}$$

and

$$\begin{aligned} \displaystyle \int _{0}^{t}\int _{\Omega }\frac{\partial u_{n}}{\partial t}G_{k}(u_{n})= & {} \frac{1}{2}\iint _{A_{k,n}}\frac{\partial }{\partial t}(u_{n}-k)^{2}=\frac{1}{2}\iint _{A_{k,n}}\frac{\partial }{\partial t}\left( (u_{n}-k)^{+}\right) ^{2}\\= & {} \displaystyle \frac{1}{2}\int _{\Omega }G_{k}(u_{n}(x,t))^{2} -\frac{1}{2}\int _{\Omega }G_{k}^{2}(u_{0}), \end{aligned}$$

applying Hardy inequality and using the fact that $G_{k}(u_{n})\le u_{n}$ in the set $A_{k,n},$ we can write

$$\begin{aligned}&\displaystyle \int _{0}^{t}\int _{\Omega }\frac{u_{n}^{p-1}G_{k}(u_{n})}{|x|^{p}+\frac{1}{n}} =\iint _{A_{k,n}}\frac{u_{n}^{p-1}G_{k}(u_{n})}{|x|^{p}+\frac{1}{n}}\le \displaystyle \iint _{A_{k,n}}\frac{u_{n}^{p}}{|x|^{p}}\\&\quad \le \frac{1}{C_{N,p}}\iint _{A_{k,n}}|\nabla u_{n}|^{p}\displaystyle =\frac{1}{C_{N,p}}\iint _{A_{k,n}}|\nabla G_{k}(u_{n})|^{p}\le \frac{1}{C_{N,p}}\int _{0}^{t}\int _{\Omega }|\nabla G_{k}(u_{n})|^{p}. \end{aligned}$$

Inequality (4.25) becomes

$$\begin{aligned}&\displaystyle \frac{1}{2}\int _{\Omega }G_{k}^{2}(u_{n})+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \int _{0}^{t}\int _{\Omega }|\nabla G_{k}(u_{n})|^{p}\\&\quad \le \displaystyle \int _{0}^{t}\int _{\Omega }fG_{k}(u_{n})+\frac{1}{2}\int _{\Omega }G_{k}^{2}(u_{0}). \end{aligned}$$

Passing to the supremum in $t\in (0,T),$ we get

$$\begin{aligned}&\displaystyle \frac{1}{2}||G_{k}(u_{n})||_{L^{\infty }(0,T; L^{2}(\Omega ))}^{2}+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \iint _{Q}|\nabla G_{k}(u_{n})|^{p}\\&\quad \le \displaystyle \iint _{Q}fG_{k}(u_{n})+\frac{1}{2}\int _{\Omega }G_{k}^{2}(u_{0}). \end{aligned}$$

From now on, we can follow the standard technique used for the non-singular case in [7], we deduce there exist a constant $C_{\infty }$ independent of n such that

$$\begin{aligned} ||u_{n}||_{L^{\infty }(Q)}\le C_{\infty }. \end{aligned}$$

(4.26)

Now taking $u_{n}$ as a test function in (2.1), by (1.3) and Hardy inequality, we have

$$\begin{aligned} \displaystyle \frac{1}{2}\int _{\Omega }u_{n}^{2}(x,T)+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \iint _{Q}|\nabla u_{n}|^{p}\le \displaystyle \iint _{Q}fu_{n}^{1-\gamma }+\frac{1}{2}\int _{\Omega }u_{0}^{2}. \end{aligned}$$

Since $u_{0}\in L^{\infty }(\Omega )$ and by (4.26) and Hölder’s inequality,we have

$$\begin{aligned} \begin{aligned}&\displaystyle \frac{1}{2}\int _{\Omega }u_{n}^{2}(x,T)+\left( \alpha -\frac{\mu }{C_{N,p}}\right) \iint _{Q}|\nabla u_{n}|^{p}\\&\quad \le \displaystyle ||u_{n}||_{L^{\infty }(Q)}^{1-\gamma }\iint _{Q}f+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}\\&\quad \displaystyle \le ||u_{n}||_{L^{\infty }(Q)}^{1-\gamma }||f||_{L^{m}(Q)}|Q|^{1-\frac{1}{m}}+\frac{1}{2}||u_{0}||_{L^{2}(\Omega )}^{2}\le C. \end{aligned} \end{aligned}$$

As $0\le \mu <\alpha C_{N,p},$ and by the last estimate, we obtain

$$\begin{aligned} \iint _{Q}|\nabla u_{n}|^{p}\le C, \end{aligned}$$

(4.27)

where C is a positive constant independent of n. Hence the proof of Theorem  4.3 is completed. $\square$

In the following Theorem we are interesting to prove regularity of u solution of (1.1) when the datum f belong to $L^{r}(0,T; L^{q}(\Omega )),$ with $r,q>1.$

Theorem 4.4

Under the hypothesis (1.3)–(1.5), if $0<\gamma <1$ and $0\le \mu <\alpha M C_{N,p},$ with

$$\begin{aligned}&M=\frac{Nq(r(p+\gamma -1)-(p-2))-Nr+pq(r-1)}{Nr-pq(r-1)}\\&\quad \times \left( \frac{p[Nr-pq(r-1)]}{Nqr(p+\gamma -1)+(p-2)[N(r-q)-pq(r-1)]}\right) ^{p}, \end{aligned}$$

$f\in L^{r}(0,T; L^{q}(\Omega ))$ with q and r be real numbers such that

$$\begin{aligned} r>1,\; q>1;\;\;\; p\le \frac{N}{q}+\frac{p}{r}\le \min \{\theta _{1}, \theta _{2}\}, \end{aligned}$$

where

$$\begin{aligned} \theta _{1}=\frac{N}{r}+p \,\;\; \text{ and }\;\;\; \theta _{2}=\frac{N}{r}\left( 1-\frac{p}{2}\right) +\frac{Np+2p+N(\gamma -1)}{2}. \end{aligned}$$

Then there exists a weak solution $u\in L^{p}(0,T; W_{0}^{1,p}(\Omega ))\cap L^{\delta }(Q)$ to problem (1.1) with

$$\begin{aligned} \delta = \frac{qr(N+p)(\gamma +1)+N(p-2)(pr-q+r)}{Nr-pq(r-1)}. \end{aligned}$$

Remark 4.5

If $\gamma , \mu \rightarrow 0,$ then the result of Theorem 4.4 coincides with classical regularity results for parabolic problems with coercivity (see [10, Theorem 1.1]).

Proof

Let now testing (1.3) by $\varphi (u_{n})=((u_{n}+a)^{\lambda }-a^{\lambda })\chi _{(0,t)},$ $0<a<\frac{1}{n},\;\; \lambda >0$ and repeating the same passage of proof of item (i) of Theorem 4.3 in order to arrive to the following inequality

$$\begin{aligned}&\displaystyle \frac{1}{\lambda +1}\int _{\Omega }u_{n}^{\lambda +1}(x,t)+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) \displaystyle \int _{0}^{t}\int _{\Omega }|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p}\\&\quad \le \displaystyle \int _{0}^{t}\int _{\Omega }f(u_{n}+a)^{\lambda -\gamma }+C. \end{aligned}$$

Passing to supremum for $t\in [0,T],$ we obtain

$$\begin{aligned}&c_{0}||u_{n}||^{\lambda +1}_{L^{\infty }(0,T; L^{\lambda +1}(\Omega ))}+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) \displaystyle \iint _{Q}|\nabla (u_{n}+a)^{\frac{\lambda +p-1}{p}}|^{p} \nonumber \\&\quad \quad \quad \quad \quad \quad \le \displaystyle \iint _{Q}f(u_{n}+a)^{\lambda -\gamma }+C. \end{aligned}$$

(4.28)

Setting $v_{n}=u_{n}^{\frac{\lambda +p-1}{p}}$ and $I= \displaystyle \iint _{Q}f(u_{n}+a)^{\lambda -\gamma }$, formula (4.28) can be rewritten as

$$\begin{aligned} c_{0}||v_{n}||^{\frac{p(\lambda +1)}{\lambda +p-1}}_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) \displaystyle \iint _{Q}|\nabla v_{n}|^{p}\le I+C.\nonumber \\ \end{aligned}$$

(4.29)

Using Hölder’s inequality twice, for all $q>1$ and $r>1$ we get

$$\begin{aligned} I\le & {} \displaystyle \int _{0}^{T}\left( \int _{\Omega }f^{q} \right) ^{\frac{1}{q}} \left( \int _{\Omega }v_{n}^{\frac{p(\lambda -\gamma )}{\lambda +p-1}\frac{q}{q-1}} \right) ^{\frac{q-1}{q}}\nonumber \\\le & {} ||f||_{L^{r}(0,T; L^{q}(\Omega ))}\left[ \int _{0}^{T}\left( \int _{\Omega }v_{n}^{\frac{p(\lambda -\gamma )}{\lambda +p-1}\frac{q}{q-1}} \right) ^{\frac{q-1}{q}\frac{r}{r-1}}\right] ^{\frac{r-1}{r}}\nonumber \\= & {} C_{f}\left[ \int _{0}^{T}||v_{n}||_{L^{\frac{p(\lambda -\gamma )q}{(\lambda +p-1)(q-1)}}(\Omega )} ^{\frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}}\right] ^{\frac{r-1}{r}}. \end{aligned}$$

(4.30)

Let us define $\eta \in (0,1)$ such that

$$\begin{aligned} \frac{(\lambda +p-1)(q-1)}{p(\lambda -\gamma )q}=\eta \left( \frac{1}{p}-\frac{1}{N}\right) +(1-\eta )\frac{\lambda +p-1}{p(\lambda +1)}. \end{aligned}$$

(4.31)

Thus, by the Lemma 1.1, applied to

$$\begin{aligned} \sigma =\frac{p(\lambda -\gamma )q}{(\lambda +p-1)(q-1)}\;\; \text{ and }\;\;\; \rho =\frac{p(\lambda +1)}{\lambda +p-1}, \end{aligned}$$

(4.32)

we have

$$\begin{aligned} ||v_{n}||_{L^{\frac{p(\lambda -\gamma )q}{(\lambda +p-1)(q-1)}}(\Omega )}^{\frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}}\le C_{G}||v_{n}||_{L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega )}^{(1-\eta )\frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}}||\nabla v_{n}||_{L^{p}(\Omega )}^{\eta \frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}}. \end{aligned}$$

(4.33)

Integrating on time we obtain

$$\begin{aligned}&\left[ \int _{0}^{T} ||v_{n}||_{L^{\frac{p(\lambda -\gamma )q}{(\lambda +p-1)(q-1)}}(\Omega )}^{\frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}} \right] ^{\frac{r-1}{r}} \nonumber \\&\quad \le ||v_{n}||^{(1-\eta )\frac{p(\lambda -\gamma )}{(\lambda +p-1)}}_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}\left[ \int _{0}^{T}||\nabla v_{n}||_{L^{p}(\Omega )}^{\eta \frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}}\right] ^{\frac{r-1}{r}}. \end{aligned}$$

(4.34)

If $\eta <1,$ applying the Young inequality with exponents

$$\begin{aligned} \frac{\lambda +1}{(1-\eta )(\lambda -\gamma )}\;\;\; \text{ and }\;\;\;\; \frac{\lambda +1}{1+\gamma +\eta (\lambda -\gamma )}, \end{aligned}$$

we deduce

$$\begin{aligned}&\left[ \int _{0}^{T}||v_{n}||_{L^{\frac{p(\lambda -\gamma )q}{(\lambda +p-1)(q-1)}}(\Omega )}^{\frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}}\right] ^{\frac{r-1}{r}} \nonumber \\&\quad \le \epsilon ||v_{n}||_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}^{\frac{p(\lambda +1)}{\lambda +p-1}}+C_{\epsilon }\left[ \int _{0}^{T}||\nabla v_{n}||_{L^{p}(\Omega )}^{\eta \frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}}\right] ^{\frac{r-1}{r}\frac{\lambda +1}{1+\gamma +\eta (\lambda -\gamma )}}. \end{aligned}$$

(4.35)

Letting $\epsilon =\frac{c_{0}}{2C_{f}}$ and collecting (4.29), (4.30) and (4.35), we have

$$\begin{aligned}&c_{0}||v_{n}||_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}^{\frac{p(\lambda +1)}{\lambda +p-1}}+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) ||\nabla v_{n}||_{L^{p}(Q)}^{p} \nonumber \\&\quad \le \frac{c_{0}}{2}||v_{n}||_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}^{\frac{p(\lambda +1)}{\lambda +p-1}} \nonumber \\&\qquad +C_{f}C_{\epsilon }\left[ \int _{0}^{T}||\nabla v_{n}||_{L^{p}(\Omega )}^{\eta \frac{p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}}\right] ^{\frac{r-1}{r}\frac{\lambda +1}{1+\gamma +\eta (\lambda -\gamma )}}+c_{1}. \end{aligned}$$

(4.36)

Now we choose $\lambda$ satisfying

$$\begin{aligned} \frac{\eta p(\lambda -\gamma )r}{(\lambda +p-1)(r-1)}=p, \end{aligned}$$

(4.37)

such that $\lambda>\gamma>0,\; r>1$ and $0\le \mu <\frac{\alpha \lambda p^{p}C_{N,p}}{(\lambda +p-1)^{p}}.$ From (4.37), it hold that

$$\begin{aligned} \begin{aligned}&\frac{c_{0}}{2}||v_{n}||_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}^{\frac{p(\lambda +1)}{\lambda +p-1}}+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) ||\nabla v_{n}||_{L^{p}(Q)}^{p}\\&\quad \le C_{f}C_{\epsilon }||\nabla v_{n}||_{L^{p}(Q)}^{\frac{p(r-1)}{r}\frac{\lambda +1}{1+\gamma +\eta (\lambda -\gamma )}}+c_{1}. \end{aligned} \end{aligned}$$

(4.38)

Since, from (4.37)

$$\begin{aligned} r\eta (\lambda -\gamma )=(\lambda +p-1)(r-1) \end{aligned}$$

we have

$$\begin{aligned}&\beta =\frac{r-1}{r}\times \frac{\lambda +1}{1+\gamma +\eta (\lambda -\gamma )}\\&\quad =\frac{(r-1)(\lambda +1)}{r(1+\gamma )+r\eta (\lambda -\gamma )}=\frac{(r-1)(\lambda +1)}{r(1+\gamma )+(\lambda +p-1)(r-1)}\\&\quad =\frac{(r-1)(\lambda +1)}{(r-1)(\lambda +1)+r(1+\gamma )+(r-1)(p-2)}<1, \end{aligned}$$

and so

$$\begin{aligned}&\frac{c_{0}}{2}||v_{n}||_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}^{\frac{p(\lambda +1)}{\lambda +p-1}}+\left( \frac{\alpha \lambda p^{p}}{(\lambda +p-1)^{p}}-\frac{\mu }{C_{N,p}}\right) ||\nabla v_{n}||_{L^{p}(Q)}^{p} \nonumber \\&\qquad \le C_{f}C_{\epsilon }||\nabla v_{n}||_{L^{p}(Q)}^{p\beta }+c_{1}, \end{aligned}$$

(4.39)

with $\beta <1.$ If $\eta =1,$ choosing $\lambda$ as in (4.37), (4.35) becomes (4.39) with $\beta =\frac{r-1}{r}<1.$ Thus from (4.39) immediately follows

$$\begin{aligned} ||v_{n}||_{L^{\infty }(0,T; L^{\frac{p(\lambda +1)}{\lambda +p-1}}(\Omega ))}^{\frac{p(\lambda +1)}{\lambda +p-1}}+||\nabla v_{n}||_{L^{p}(Q)}^{p}\le c_{2}. \end{aligned}$$

(4.40)

Thanks to Lemma 1.1, we obtain

$$\begin{aligned} \Vert v_{n}\Vert _{L^{\sigma }(Q)}\le c_{3}, \end{aligned}$$

where $\sigma = p\frac{N+\frac{p(\lambda +1)}{\lambda +p-1}}{N}.$ Recalling the definition of $v_{n}$ we thus have proved that

$$\begin{aligned} ||u_{n}||_{L^{\delta }(Q)}\le c_{3}, \end{aligned}$$

(4.41)

where $c_{3}$ is a positive constant independent of n,  and

$$\begin{aligned} \delta =\sigma \frac{\lambda +p-1}{p}=\frac{N(\lambda +p-1)+p(\lambda +1)}{N}. \end{aligned}$$

(4.42)

From (4.31) and (4.37), we deduce that

$$\begin{aligned} \lambda +1=\frac{Nq[r(p+\gamma -1)-(p-2)]}{Nr-pq(r-1)}, \end{aligned}$$

(4.43)

which implies, by (4.43)

$$\begin{aligned} \delta =\frac{qr(N+p)(\gamma +1)+N(p-2)(qr-q+r)}{Nr-pq(r-1)}. \end{aligned}$$

we now have to check that $\lambda \ge 1$ and that $\eta ,$ defined in (4.31), belong to (0, 1). After easy calculations, we obtain that $\lambda \ge 1$ if and only if

$$\begin{aligned} p<\frac{N}{q}+\frac{p}{r}\le \frac{N}{r}\left( 1-\frac{p}{2}\right) +\frac{Np+2p+N(\gamma -1)}{2} \end{aligned}$$

while the condition $\eta \le 1$ hold is satisfied and only if

$$\begin{aligned} \frac{N}{q}+\frac{p}{r}< \frac{N}{r}+p. \end{aligned}$$

The condition $\eta \ge 0$ is automatically satisfied if $\lambda \ge 1.$

It remains to prove the estimate in $L^{p}(0,T; W_{0}^{1,p}(\Omega )).$ By (4.28), (4.30), (4.40) and $\lambda \ge 1,$ we obtain

$$\begin{aligned} \iint _{Q}|\nabla u_{n}|^{p}\le \iint _{Q}|\nabla u_{n}|^{p}(u_{n}+a)^{\lambda -1}\le c_{2}, \end{aligned}$$

(4.44)

then the sequence $u_{n}$ bounded in $L^{p}(0,T; W_{0}^{1,p}(\Omega )),$ and so $u\in L^{p}(0,T; W_{0}^{1,p}$

$(\Omega )).$ The estimates (4.41) and (4.44) completed the proof of Theorem 4.4. $\square$