1 Introduction

The fluid-conveying pipes are indispensable for many industrial applications, including biological engineering, aerospace industry, heat exchangers, and so on. Due to the complexity of the interaction between the pipe and the internal fluid, the vibration and dynamics of the fluid-conveying pipe has been attracting the attention of numerous researchers since about 50 years ago (Paidoussis and Denise 1972; Paidoussis and Issid 1974). After decades of research and development, the study on pipes conveying fluid has become a typical paradigm in fluid–structure dynamics (Paidoussis 1998, Mohammad Hosseini 2017, Wang et al. 2017) and the literature on this topic is constantly increasing (Zhi Hang Li 2019; Jiayin Dai 2020; Xiaofei Lyu 2020; Jiang et al. 2021; Mao et al. 2021; Zheng et al. 2021).

In recent years, micro/nano electromechanical systems has developed rapidly, and micro/nano-structures have attracted enormous attentions due to the outstanding and superior properties. Micro/nano-tube based devices have high frequencies and quality factors in the liquid environment and can be used for high-precision measurement of micro and nano-particles such as cells, viruses and proteins in fluid (Burg et al. 2007; Lee et al. 2010; Bryan et al. 2014; Kim et al. 2016). Reducing the size of the tube can dramatically improve the detection accuracy, but the small effects of both the structure and fluid pose challenges to the dynamic modelling of nanotubes conveying fluid. It is well known that the classical elastic theory, which describes the dynamic characteristics of structures and the Navier–Stokes equation, which characterizes the hydrodynamic behavior of fluid, are both based on the continuity assumption. However, for the nanostructure and nanoflow, the continuity assumption no longer holds. In addition, surface roughness is an inherent byproduct of almost all fabrication techniques (Parfenyev et al. 2019). The roughness height is usually between tens of nanometers and several microns, which can be neglected for macro-tubes but should be taken into account for nanotubes.

To account for the small size of nano-structures, nonlocal elastic theories were presented (Wang et al. 2007). Lee and Chang (2008) first introduced the nonlocal theory to analyzing the dynamics of fluid-conveying nanotubes. It was shown that the nonlocal parameter dramatically affected both the frequency and mode shape. And increasing the nonlocal effect decreased the frequency. Yun et al. (2012) presented a nonlocal Timoshenko beam model for studying the vibration and instability characteristics of single- and multi-walled carbon nanotubes conveying fluid. The results demonstrated that by increasing the strain gradient length scale and decreasing the small length scale, the critical flutter velocity and stability region increased. Bağdatli and Togun (2017) developed a nonlinear model for fluid-conveying nanotubes using the Hamilton’s principle by considering the nonlocal effect. The effects of the nonlocal parameters, mean speed value and ratios of fluid mass to the total mass on the linear and nonlinear frequencies, stability, frequency–response curves and bifurcation point were analyzed and discussed in detail. Jin et al. (2021) developed a higher-order size-dependent beam model for the functionally graded nanotubes carrying fluid. The nonlocal stress, strain gradient effects, surface energy effects were considered and the small size effects on post buckling, natural frequency and nonlinear vibration of were studied.

To characterize the discontinuity of fluid, the Knudsen number (Kn), which is defined as the ratio of the mean free path of the fluid molecules to the characteristic length of the fluid flow, was introduced. Generally, the flow can be divided into four regimes according to the Knudsen number (Zhang et al. 2012): the continuum regime (Kn < 0.001), the slip flow regime (0.001 < Kn < 0.1), the transition regime (0.1 < Kn < 10), and the free molecular regime (Kn > 10). The flow characteristics are quite different for various Knudsen numbers. For the continuum regime, the continuum and thermodynamic equilibrium assumptions are appropriate, and the flow can be described by the N–S equations with conventional no-slip boundary conditions. For the slip flow regime, the non-equilibrium effects dominate near the walls and the no-slip boundary condition fails. However, the rarefied flow can still be analyzed by solving the N–S equations with slip velocity boundary. For the transition regime, the rarefaction effects dominate and the continuum and thermodynamic equilibrium assumptions of the N–S equations begin to break down. The flow can be studied using N–S equations with more complex slip boundaries or other method, such as direct simulation Monte Carlo method. For the free molecular regime, the inter-molecular collisions are negligible as compared with the collisions between the gas molecules and wall surfaces. The molecular dynamics should be utilized. Consequently, the dynamic behaviors of fluid-conveying nanotubes, which are typical fluid–structure systems, are certainly affected by the Knudsen number. Rashidi et al. (2012) first introduced the Knudsen number into the analysis of fluid-conveying nanotubes. The equivalent bulk viscosity and slip boundary condition of nanoflow were considered and the velocity correction factor was used to describe the effects of Knudsen number on the governing equation for nanotubes conveying nanoflow. The results demonstrated that as the Knudsen number increased, the critical velocity for divergence decreased. After this work, researchers usually taken account the effect of Knudsen number into the analysis of fluid-conveying nanotubes. Liu et al. (2018) presented an improved model of fluid-conveying carbon nanotube by considering comprehensive effects of Knudsen number. The effective viscosity, slip boundary condition and non-uniform flow profile were all taken into account. Ghayesh et al. (2019) studied the global dynamic characteristics of the nanotube containing nanoflow by considering the geometric nonlinearity, the nanostructure and the nanoflow. Ghane et al. (2020) investigated the flutter vibrations of fluid-conveying thin-walled nanotubes subjected to magnetic field. The Knudsen number was considered to describe the slip between the nanoflow and the wall of nanotube. Hosseini and Ghadiri (2021) analyzed the influence of the residual surface stress on the instability and nonlinear dynamic behaviors of fluid-conveying double-walled nanotubes.

In general, the surface roughness is inevitable because of the limitation of fabrication technologies. The roughness height usually ranges from tens of nanometers to several micrometers (Jaeger et al. 2012; Zhou et al. 2017), which can be neglected for macrotubes but is comparable to the characteristic length of microtubes and nanotubes. About 20 years ago, Mala and Li (1999) investigated the fluid flow through microtubes with diameters ranging from 50 to 254 μm. The experimental results showed that the friction factor for rough microtubes was obviously higher than that for smooth microtubes. Afterwards numerous scholars studied the surface roughness effect on the flow characteristics in micro and nano tubes using analytical, numerical and experimental methods (Mala and Li 1999; Tang et al. 2007; Akyildiz and Siginer 2017; Song et al. 2018; Dey and Saha 2021). Ou et al. (2004) presented a series of experiments on water flow through microchannels using hydrophobic surfaces with well-defined surface roughness. The results demonstrated significant drag reduction for the laminar flow. Duan and Muzychka (2008) developed an analytical model to predict velocity distributions and friction factors for rough microtubes based on the Navier–Stokes equations with a velocity slip boundary. Yan et al. (2015) numerically analyzed the flow characteristics in rough microtubes by solving the 3D Navier–Stokes equation with an extended slip model. The effect of rarefication, compressibility, roughness height and fractal dimension were investigated and discussed. Eduard et al. (Marusic-Paloka and Pazanin 2020) studied the influences of both surface roughness and inertia on the flow in a corrugated pipe and proposed a higher-order correction of the Hagen–Poiseuille velocity. And a new formula for the Darcy friction coefficient was developed. Yao et al. (2021) analyzed the influences of rough morphology and wall-fluid interaction on the flow and thermal characteristics in nanotubes by the molecular dynamics method. They found that the surface roughness and the interaction between the fluid and wall lead to different variations in temperature jump and velocity slip.

By reviewing the literature, it can be found that the surface roughness has an important effect on the flow in nanotubes. As a classical fluid–structure coupling system, the fluid-conveying nanotube is influenced by the surface roughness. However, few researchers have paid attention to the instability and dynamics of rough nanotubes carrying nanoflow. Jiang et al. (2021) analyzed and discussed the effects of surface roughness on the stability of both fixed–fixed and cantilevered microtubes. Because the research object is the microtube, for which the discontinuity effect of the structure and fluid is not obvious, the nonlocal effect and Knudsen number were not considered in the model. To the best knowledge of authors, the stability and dynamic characteristics of fluid-conveying nanotubes has not been studied by comprehensively considered the nonlocal effect of nanostructure, the rarefication effect of nanoflow and the surface roughness effect of interface between nanostructure and nanoflow. In this article, this topic is addressed.

The article is outlined as follows. In Sect. 2, a theoretical model is developed by comprehensively considering the surface roughness, rarefication effect and nonlocal effect of nanotubes conveying nanoflow to characterize the dynamic behaviors of the fluid–structure coupling system. The influences of surface roughness, Knudsen number and nonlocal effect on the instability and natural frequencies of nanotubes with different boundary conditions are analyzed and discussed in Sect. 3. Some conclusions are drawn in Sect. 4.

2 Model development

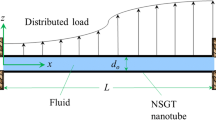
Figure 1 illustrates the schematic for fixed–fixed and cantilevered nanotubes conveying fluid with surface roughness (Kim et al. 2016). In the axial direction of the nanotube, the inner radius almost keeps constant. And in the circumferential direction, the distribution of radius is approximately periodic. Hence, the nanotube with sinusoidally wavy surface roughness is taken into account, as shown in Fig. 1b. Two coordinate systems are adopted for modelling. One is for modelling the vibration of nanotube, as illustrated in Fig. 1a. The x-axis is the direction of fluid flow and the y-axis is the direction of vibration. The other is a cylindrical coordinate system (r, θ, x), which is for modelling the fluid flow in the rough nanotube, as shown in Fig. 1b. The inner radius of nanotube by considering the surface roughness is described by

$$R_{i} = R_{m} \left[ {1 + \varepsilon \sin \left( {\lambda \theta } \right)} \right],$$
(1)

where \(R_{i}\) is the real radius of the inner wall, \(R_{m}\) is the mean radius, \(\varepsilon\) is the relative roughness which is defined as \(\varepsilon = {\Delta \mathord{\left/ {\vphantom {\Delta {R_{m} }}} \right. \kern-\nulldelimiterspace} {R_{m} }}\), \(\lambda\) is the wave number that can be expressed as \(\lambda = {{2\pi R_{m} } \mathord{\left/ {\vphantom {{2\pi R_{m} } b}} \right. \kern-\nulldelimiterspace} b}\). The parameters \(\Delta\) and b are the amplitude and wavelength of the surface roughness, respectively.

Fig. 1
figure 1

a Schematic for fixed–fixed and cantilevered nanotubes conveying fluid (Kim et al. 2016). b Rough surface of nanotubes (Kim et al. 2016)

Full size image

According to the authors’ previous work, the governing equation for a rough microtube without nonlocal effect can be given as:

$$EI^{(r)} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {\rho_{t} A_{t}^{\left( r \right)} + \rho_{f} A_{f}^{\left( r \right)} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\rho_{f} \left( {\int_{{S_{f} }} {u_{x} dS} } \right)\frac{{\partial^{2} w}}{\partial x\partial t} + \rho_{f} \left( {\int_{{S_{f} }} {u_{x}^{2} dS} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0,$$
(2)

where E is the Young’s modulus, \(I\) is the second moment of cross-sectional area, w is the lateral displacement of microtube, \(\rho\) is the density, A is the area, \(u_{x}\) is the fluid velocity in the x direction and \(S_{f}\) is cross-section of the fluid. The superscript (r) means “rough”, and (s) represents “smooth”. The subscript t means parameters for tube, and the subscript f means for fluid. For nanotube, the nonlocal effect should be considered because of the size effect. In this paper, the modified couple stress theory is adopted. Hence, the governing equation for nanotube conveying fluid can be written as:

$$\left( {EI^{\left( r \right)} + GA_{t}^{\left( r \right)} l^{2} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {\rho_{t} A_{t}^{\left( r \right)} + \rho_{f} A_{f}^{\left( r \right)} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\rho_{f} \left( {\int_{{S_{f} }} {u_{x} dS} } \right)\frac{{\partial^{2} w}}{\partial x\partial t} + \rho_{f} \left( {\int_{{S_{f} }} {u_{x}^{2} dS} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0,$$
(3)

where \(G = {E \mathord{\left/ {\vphantom {E {2\left( {1 + \nu } \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {1 + \nu } \right)}}\), \(\nu\) is the Poisson’s ratio and l is the value of the material length scale parameter, which describes the nonlocal effect of structure.

For fixed–fixed nanotubes, the boundary conditions are subjected to,

$$\begin{gathered} w\left( {0,t} \right) = 0,\quad \frac{{\partial w\left( {0,t} \right)}}{\partial x} = 0, \hfill \\ w\left( {L,t} \right) = 0,\quad \frac{{\partial w\left( {L,t} \right)}}{\partial x} = 0. \hfill \\ \end{gathered}$$
(4)

For cantilevered nanotubes, the boundary conditions are subjected to,

$$\begin{gathered} w\left( {0,t} \right) = 0,\quad \frac{{\partial w\left( {0,t} \right)}}{\partial x} = 0 \hfill \\ \frac{{\partial^{2} w\left( {L,t} \right)}}{{\partial x^{2} }} = 0,\quad \frac{{\partial^{3} w\left( {L,t} \right)}}{{\partial x^{3} }} = 0 \hfill \\ \end{gathered}$$
(5)

To obtain the flow velocity \(u_{x}\), the flow characteristics in the nanotube should be analyzed by considering the surface roughness and the rarefication effect. In order to study the effect of rarefaction, it is necessary to determine the flow regime of gas in nanotubes. The mean free path of gas can be given as \(\lambda_{m} = k_{\lambda } \left( {{\mu \mathord{\left/ {\vphantom {\mu p}} \right. \kern-\nulldelimiterspace} p}} \right)\sqrt {2R_{s} T}\), where \(k_{\lambda } = {{\sqrt \pi } \mathord{\left/ {\vphantom {{\sqrt \pi } 2}} \right. \kern-\nulldelimiterspace} 2}\) according to the hard sphere model, \(R_{s}\) is specific gas constant, \(\mu\), p and T are the dynamic viscosity, pressure and temperature, respectively (Ewart et al. 2006). Therefore, the mean free path of common gases is about 10 nm to 100 nm under normal temperature and pressure (e.g., ~ 40 nm for carbon dioxide, ~ 60 nm for nitrogen, ~ 120 nm for hydrogen, etc.). And the diameter of nanotubes is usually in the order of 10 nm to 100 nm. Consequently, the gas flow in the nanotube is generally in the slip regime and the transition regime. Using the Navier–Stokes equations with an appropriate velocity slip boundary (Beskok and Karniadakis 1999), the nanoflow in the slip regime and the transition regime can be well characterized (Rashidi et al. 2012; Sadeghi-Goughari and Hosseini 2015). By referring to the published work (Mirramezani and Mirdamadi 2012; Rashidi et al. 2012), the fluid flow with Knudsen number ranging from 0.001 to 2 is focused on in this paper.

The considered nanotube is axisymmetric, and the cross-section keeps constant in the axial direction. Hence, the velocity components in the radial and circumferential directions are zero. And for fully developed fluid, \({{du_{x} } \mathord{\left/ {\vphantom {{du_{x} } {dx}}} \right. \kern-\nulldelimiterspace} {dx}}\) is zero. The momentum equation for fluid in the rough nanotube is written as,

$$- \frac{dp}{{dx}} + \mu \left( {\frac{{\partial^{2} u_{x} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{x} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u_{x} }}{{\partial \theta^{2} }}} \right) = 0,$$
(6)

where p is the pressure and \(\mu\) is the dynamic viscosity. Because of the rarefication effect, the fluid velocity at the solid surface is not equal to the corresponding value of the wall. The difference between the fluid velocity and the wall velocity is known as the slip velocity. Consequently, the boundary condition at the solid surface is given by (Beskok and Karniadakis 1999),

$$u_{x} \left( {r,\theta } \right) = \left( {\frac{{2 - \sigma_{v} }}{{\sigma_{v} }}} \right)\left( {\frac{Kn}{{1 - bKn}}} \right)\left( {\frac{{\partial u_{x} }}{\partial n}} \right)\;\;{\text{at}}\;\,r = R_{m} \left[ {1 + \varepsilon \sin \left( {\lambda \theta } \right)} \right],$$
(7)

where \(\sigma_{v}\) is the tangential moment accommodation coefficient, Kn is the Knudsen number, and n is the normal vector. Choosing an appropriate b, the effect of slip condition can be as accurate as a second-order term. For fully developed flows in channels, \(b = - \;1\) (Beskok and Karniadakis 1999). \(\sigma_{v}\) is related to the tangential momentum of incoming, reflected and reemitted molecules, and for most practical purposes, \(\sigma_{v}\) can be considered to be 0.7. Using the velocity slip boundary condition in Eq. (7), the fluid characteristics of flow in the slip regime and the transition regime can be accurately predicted.

Using the perturbation method, the velocity ux is expanded in terms of \(\varepsilon\)

$$u_{x} \left( {r,\theta } \right) = u_{x}^{\left( 0 \right)} \left( {r,\theta } \right) + \varepsilon u_{x}^{\left( 1 \right)} \left( {r,\theta } \right) + \varepsilon^{2} u_{x}^{\left( 2 \right)} \left( {r,\theta } \right) + \cdots .$$
(8)

By substituting Eq. (8) into Eqs. (6) and (7), the expressions of \(u_{x}^{\left( 0 \right)}\), \(u_{x}^{\left( 1 \right)}\) and \(u_{x}^{\left( 2 \right)}\) can be given as (Sadeghi et al. 2011),

$$u_{x}^{\left( 0 \right)} = a_{0} + b_{0} \left( {\frac{r}{{R_{m} }}} \right)^{2} ,$$
(9)
$$u_{x}^{\left( 1 \right)} = a_{1} \left( {\frac{r}{{R_{m} }}} \right)^{\lambda } \sin \left( {\lambda \theta } \right),$$
(10)
$$u_{x}^{\left( 2 \right)} = a_{2} + b_{2} \left( {\frac{r}{{R_{m} }}} \right)^{2\lambda } \cos \left( {2\lambda \theta } \right),$$
(11)

with the coefficients,

$$\begin{gathered} a_{0} = - \frac{{R_{m}^{2} }}{4\mu }\frac{dp}{{dx}}\left( {1 + 2\beta_{m} Kn} \right),b_{0} = \frac{{R_{m}^{2} }}{4\mu }\frac{dp}{{dx}}, \hfill \\ a_{1} = - \frac{{R_{m}^{2} }}{2\mu }\frac{dp}{{dx}}\frac{{1 + \beta_{m} Kn}}{{1 + \lambda \beta_{m} Kn}}, \hfill \\ a_{2} = \frac{{R_{m}^{2} }}{\mu }\frac{dp}{{dx}}\left[ {\lambda \beta_{m} Kn\left( {\frac{\lambda }{8} - \frac{1}{4}\frac{{1 + \beta_{m} Kn}}{{1 + \lambda \beta_{m} Kn}}} \right) + \frac{\lambda }{4}\frac{{1 + \beta_{m} Kn}}{{1 + \lambda \beta_{m} Kn}} - \frac{1}{8}} \right], \hfill \\ b_{2} = \frac{{R_{m}^{2} }}{\mu }\frac{dp}{{dx}}\frac{1}{{1 + 2\lambda \beta_{m} Kn}}\left[ {\lambda \beta_{m} Kn\left( {\frac{\lambda }{8} + \frac{1 - 2\lambda }{4}\frac{{1 + \beta_{m} Kn}}{{1 + \lambda \beta_{m} Kn}}} \right) - \frac{\lambda }{4}\frac{{1 + \beta_{m} Kn}}{{1 + \lambda \beta_{m} Kn}} + \frac{1}{8}} \right], \hfill \\ \end{gathered}$$
(12)

where \(\beta_{m} = \left( {\frac{{2 - \sigma_{v} }}{{\sigma_{v} }}} \right)\left( {\frac{Kn}{{1 - bKn}}} \right)\).

According to Eqs. (9)–(12), the parameters in the governing Eq. (3) associated with \(u_{x}\) are written as:

$$\begin{gathered} \int_{{S_{f} }} {u_{x} } dS = \pi R_{m}^{4} \left( { - \frac{1}{\mu }\frac{dp}{{dx}}} \right)\left[ {a_{0}^{*} + \frac{{b_{0}^{*} }}{2} + \left( {\frac{{a_{0}^{*} }}{2} + \frac{{3b_{0}^{*} }}{2} + a_{1}^{*} + a_{2}^{*} } \right)\varepsilon^{2} } \right], \hfill \\ \int_{{S_{f} }} {u_{x}^{2} dS} = \pi R_{m}^{6} \left( { - \frac{1}{\mu }\frac{dp}{{dx}}} \right)^{2} \left[ \begin{gathered} \left( {a_{0}^{*2} + a_{0}^{*} b_{0}^{*} + \frac{1}{3}b_{0}^{*2} } \right) + \varepsilon^{2} \hfill \\ \left( {\frac{1}{2}a_{0}^{*2} + 3a_{0}^{*} b_{0}^{*} + 2a_{1}^{*} b_{0}^{*} + 2a_{0}^{*} a_{1}^{*} + 2a_{0}^{*} a_{2}^{*} + a_{2}^{*} b_{0}^{*} + \frac{5}{2}b_{0}^{*2} + \frac{1}{2\lambda + 2}a_{1}^{*2} } \right) \hfill \\ \end{gathered} \right], \hfill \\ \end{gathered}$$
(13)

where \(\varsigma = - \frac{1}{\mu }\frac{dp}{{dz}}\frac{{R^{2} }}{U}\varsigma^{*}\) and \(\varsigma\) represents \(a_{0}\), \(b_{0}\), \(a_{1}\), \(a_{2}\) and \(b_{2}\).

Substituting Eq. (13) into Eq. (12), the fluid–structure interaction equation for nanotube conveying fluid by considering the surface roughness and rarefication effect of fluid is given as,

$$\begin{gathered} \left( {EI^{\left( r \right)} + GA_{t}^{\left( r \right)} l^{2} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {\rho_{t} A_{t}^{\left( r \right)} + \rho_{f} A_{f}^{\left( r \right)} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + \hfill \\ 2\rho_{f} A_{f}^{\left( s \right)} \left( {{\text{CFF}}_{1} } \right)U_{s} \frac{{\partial^{2} w}}{\partial x\partial t} + \frac{4}{3}\left( {{\text{CFF}}_{2} } \right)\rho_{f} A_{f}^{\left( s \right)} \left( {{\text{CFF}}_{{1}} } \right)U_{s}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} = 0, \hfill \\ \end{gathered}$$
(14)

where \(A_{t}^{(r)}\) and \(A_{f}^{(r)}\) are the cross-sectional areas of the rough nanotube and the internal fluid, respectively, \(A_{f}^{(s)} = \pi R_{m}^{2}\) is the fluid cross-sectional area of the smooth microtube, CFF1 and CFF2 are Correction Factors for Fluid due to the surface roughness and rarefication effect, and \(U_{s} = \left( { - \frac{1}{\mu }\frac{dp}{{dz}}} \right)\frac{{R_{m}^{2} }}{8}\) is the averaged fluid velocity of smooth microtube without considering the rarefication effect. The coefficients in Eq. (14) are written as

$$\begin{gathered} I^{\left( r \right)} = \frac{1}{4}\pi R_{m}^{4} \left( {\alpha^{4} - 1 - 3\varepsilon^{2} } \right), \hfill \\ A_{t}^{\left( r \right)} = \pi R_{m}^{2} \left( {\alpha^{2} - 1 - \frac{1}{2}\varepsilon^{2} } \right), \hfill \\ A_{f}^{\left( r \right)} = \pi R_{m}^{2} \left( {1 + \frac{1}{2}\varepsilon^{2} } \right), \hfill \\ {\text{CFF}}_{1} = 8\left[ {a_{0}^{*} + \frac{{b_{0}^{*} }}{2} + \left( {\frac{{a_{0}^{*} }}{2} + \frac{{3b_{0}^{*} }}{2} + a_{1}^{*} + a_{2}^{*} } \right)\varepsilon^{2} } \right], \hfill \\ {\text{CFF}}_{2} = 64\left[ \begin{gathered} \left( {a_{0}^{*2} + a_{0}^{*} b_{0}^{*} + \frac{1}{3}b_{0}^{*2} } \right) + \varepsilon^{2} \hfill \\ \left( {\frac{1}{2}a_{0}^{*2} + 3a_{0}^{*} b_{0}^{*} + 2a_{1}^{*} b_{0}^{*} + 2a_{0}^{*} a_{1}^{*} + 2a_{0}^{*} a_{2}^{*} + a_{2}^{*} b_{0}^{*} + \frac{5}{2}b_{0}^{*2} + \frac{1}{2\lambda + 2}a_{1}^{*2} } \right) \hfill \\ \end{gathered} \right], \hfill \\ \end{gathered}$$
(15)

where \(\alpha = {{R{}_{o}} \mathord{\left/ {\vphantom {{R{}_{o}} {R_{m} }}} \right. \kern-\nulldelimiterspace} {R_{m} }}\) is the ratio of the outer radius to the mean inner radius.

Equation (14) is developed by taking the nonlocal effect of structure, the surface roughness at the inner wall and the rarefication effect of fluid into account. If the nonlocal effect and the rarefication effect are neglected, the equation is equivalent to the model presented for rough microtubes conveying fluid (Jiang et al. 2021). If the surface roughness is ignored, the equation is equivalent to the model for smooth nanotubes conveying nanoflow developed by Rashidi et al. (2012) If both the surface roughness and rarefication effect are neglected, the equation is equivalent to the model for size-dependent analysis presented by Wang (2010).

The governing Eq. (14) can be nondimensionalized as:

$$\left( {{\text{CFS}}_{1} + {\text{CFS}}_{2} \cdot \kappa } \right)\eta \prime \prime \prime \prime + \left( {{\text{CFS}}_{3} } \right)\ddot{\eta } + \left( {{\text{CFF}}_{1} } \right)2\sqrt \beta \hat{U}\dot{\eta} \prime + \left( {{\text{CFF}}_{2} } \right)\frac{4}{3}\hat{U}^{2} \eta \prime \prime = 0$$
(16)

with parameters

$$\begin{gathered} \eta = \frac{w}{L},\quad \xi = \frac{x}{L},\quad {\text{CFS}}_{1} = \frac{{I^{(r)} }}{{I^{(s)} }},\quad {\text{CFS}}_{2} = \frac{{A_{t}^{\left( r \right)} }}{{A_{t}^{\left( s \right)} }},\quad \kappa = \frac{2}{{\chi^{2} \left( {1 + \nu } \right)(1 + \alpha^{2} )}}, \hfill \\ {\text{CFS}}_{3} = \frac{{\rho_{t} A_{t}^{\left( r \right)} + \rho_{f} A_{f}^{\left( r \right)} }}{{\rho_{t} A_{t}^{\left( s \right)} + \rho_{f} A_{f}^{\left( s \right)} }},\quad \tau = \sqrt {\frac{{EI^{(s)} }}{{\rho_{t} A_{t}^{\left( s \right)} + \rho_{f} A_{f}^{\left( s \right)} }}} \frac{t}{{L^{2} }}, \hfill \\ \hat{U} = \sqrt {\frac{{\rho_{f} A_{f}^{(s)} }}{{EI^{(s)} }}} U_{s} L,\quad \beta = \frac{{\rho_{f} A_{f}^{(s)} }}{{\rho_{t} A_{t}^{\left( s \right)} + \rho_{f} A_{f}^{\left( s \right)} }}, \hfill \\ \end{gathered}$$
(17)

where \(\chi = {{R_{m} } \mathord{\left/ {\vphantom {{R_{m} } l}} \right. \kern-\nulldelimiterspace} l}\), \(\eta^{\prime} = \left( {{{\partial \eta } \mathord{\left/ {\vphantom {{\partial \eta } {\partial \varepsilon }}} \right. \kern-\nulldelimiterspace} {\partial \varepsilon }}} \right)\) and \(\dot{\eta } = \left( {{{\partial \eta } \mathord{\left/ {\vphantom {{\partial \eta } {\partial \tau }}} \right. \kern-\nulldelimiterspace} {\partial \tau }}} \right)\). The parameters CFS1, CFS2 and CFS3 are Correction Factors for Structures induced by the surface roughness. The boundary conditions in non-dimensional form are expressed as:

$$\eta \left( {0,t} \right) = 0,\quad \eta^{\prime}\left( {0,t} \right) = 0,\quad \eta \left( {1,t} \right) = 0,\quad \eta^{\prime}\left( {1,t} \right) = 0$$
(18)

for fixed–fixed nanotubes and

$$\eta \left( {0,t} \right) = 0,\quad \eta^{\prime}\left( {0,t} \right) = 0,\quad \eta \prime \prime \left( {1,t} \right) = 0,\quad \eta \prime \prime \prime \left( {1,t} \right) = 0$$
(19)

for cantilevered nanotubes. In the next, by solving the governing equation through the Galerkin method, the stability and dynamic behaviors of nanotubes conveying fluid by considering the surface roughness, rarefication effect and nonlocal effect are analyzed and discussed.

3 Results and discussions

3.1 Correction factors

The correction factors in Eq. (16), CFS1, CFS2, CFS3, CFF1 and CFF2, relate the surface roughness of inner wall and rarefication effect of fluid to the stability and dynamic behaviors of nanotubes conveying nanoflow. Moreover, these factors are important characteristics that distinguish the present model from other models. If the surface roughness and rarefication effect are not considered, \({\text{CFS}}_{1} = {\text{CFS}}_{2} = {\text{CFS}}_{{3}} = 1\) and \({\text{CFF}}_{1} = {\text{CFF}}_{2} = 0\). Then Eq. (16) is equivalent to the classical model for size-dependent analysis of fluid-conveying microtubes developed by Wang (2010). Because of the significance of correction factors, it is necessary to study and discuss the variation of correction factors with the surface roughness and Knudsen number.

Parameters CFS1, CFS2 and CFS3 are correction factors for the structure. The previous work has discussed the effects of surface roughness on these factors in detail (Jiang et al. 2021). For the completeness, Fig. 2 illustrated the variation of correction factors for structures with the roughness height. Because CFS1, CFS2 and CFS3 are only related to \(\varepsilon^{2}\), which is high order small quantity, the three factors are almost unchanged with the increase of relative roughness height. As Fig. 2 is shown, when \(\varepsilon\) increases from 0 to 0.05, the variation of CFS1, CFS2 and CFS3 is less than 1%. It can be concluded that the surface roughness has no obvious effect on correction factors for structures. Consequently, the influences of CFS1, CFS2 and CFS3 on dynamics of fluid-conveying nanotube can be neglected.

Fig. 2
figure 2

Variation of correction factors for structures with surface roughness for different geometrical parameters a CFS1 b CFS2 c CFS3, \({{\rho_{t} } \mathord{\left/ {\vphantom {{\rho_{t} } {\rho_{f} }}} \right. \kern-\nulldelimiterspace} {\rho_{f} }} = 10\) and d CFS4, \({{\rho_{t} } \mathord{\left/ {\vphantom {{\rho_{t} } {\rho_{f} }}} \right. \kern-\nulldelimiterspace} {\rho_{f} }} = 0.1\)

Full size image

Parameters CFF1 and CFF2 are correction factors for fluid, which are affected by not only the surface roughness, but also the slip velocity on the boundary. From the literature (Duan and Muzychka 2008), it is known that the surface roughness can reduce the flow velocity while the rarefication effect can increase the fluid velocity. When the fluid velocity varies, the Coriolis force and centripetal force related to the fluid flow also change. The physical meaning of CFF1 is the ratio of Coriolis force caused by nanoflow in rough nanotube to the one in smooth tubes without considering the rarefication effect. The CFF1 is affected by three parameters, the relative roughnes height \(\varepsilon\), the wave number \(\lambda\) and the Knudsen number Kn. The first two parameters characterize the surface roughness, and the latter parameter represents the rarefication effect of fluid. The increasing of \(\varepsilon\) or \(\lambda\) means that the surface is more rough. And the increasing of Kn indicates that the rarefication effect is more significant. Figure 3 shows the variation of CFF1 with the relative roughness height and Knudsen number for different wave numbers. It can be found that with the increasing of roughness height, CFF1 decreases while with the increasing of Knudsen number, CFF1 increases. This is because the surface roughness reduces the flow velocity, thereby reducing the Coriolis force, while the boundary slip increases the flow velocity, thereby increasing the Coriolis force.

Fig. 3
figure 3

Variation of CFF1 with the relative roughness height and Knudsen number for different wave numbers a \(\lambda = 10\) and b \(\lambda = 25\)

Full size image

To more clearly show the effects of roughness height, wave number and Knudsen number on CFF1, Fig. 4a and b shows the variation of CFF1 with \(\varepsilon\) for different \(\lambda\) and Kn. Comparing the two figures, it can be found that the change of Kn does not vary the trend of the CFF1-\(\varepsilon\) curve, while the increasing of \(\lambda\) makes CFF1 decrease faster as the roughness height increases. In addition, the relationship between CFF1 and \(\varepsilon\) is nonlinear. Actually, from Eq. (15) it is known that when \(\lambda\) and Kn keep constant, CFF1 is proportional to \(\varepsilon^{2}\). Figure 4c and d show the variation of CFF1 with \(\lambda\) for different \(\varepsilon\) and Kn. Similar to \(\varepsilon\), the increase of \(\lambda\) also reduces CFF1. Figure 4e and f illustrate the variation of CFF1 with Kn for different \(\varepsilon\) and \(\lambda\). It is obvious that as Kn increases, the CFF1 dramatically increases.

Fig. 4
figure 4

Effects of roughness height, wave number and Knudsen number on CFF1

Full size image

The physical meaning of CFF2 is the ratio of centripetal force caused by nanoflow in rough nanotube to the one in smooth tubes without considering the rarefication effect. As shown in Figs. 5 and 6, the effects of roughness height, wave number and Knudsen number on CFF2 are very similar to the ones on CFF1. The difference is that the variation of CFF2 with \(\varepsilon\), \(\lambda\) and Kn is more sharp. This is because the centrifugal force caused by fluid is directly proportional to the square of fluid velocity, which is more significantly affected by the uneven distribution of fluid velocity. Moreover, it is found that as the Knudsen number increases, the effect of surface roughness on CFF2 is more significant. As shown in Fig. 6a, when the relative roughness height increases from 0 to 0.05, CFF2 decreases from about 1.1 to about 0.93 (by 15%) for \(\lambda = 25\). On the other hand, for Kn = 1, CFF2 decreases from about 16.5 to about 6.8 (by 59%) as illustrated in Fig. 6b. This is because the velocity at the boundary gradually dominates with the increasing of Knudsen number. Moreover, the surface roughness hinders the fluid flow at the boundary. As a result, when the gas rarefaction effect increases, the influence of surface roughness on flow characteristics is more significant (Yan et al. 2015).

Fig. 5
figure 5

Variation of CFF2 with the relative roughness height and Knudsen number for different wave numbers a \(\lambda = 10\) and b \(\lambda = 25\)

Full size image
Fig. 6
figure 6

Effects of roughness height, wave number and Knudsen number on CFF2

Full size image

To study the stability and dynamic behaviors of nanotubes conveying nanoflow, Sects. 3.2 and 3.3 are allocated to demonstrate the influences of several parameters, including the material length scale parameter, relative roughness height, wave numbers, Knudsen number, mass ratio, etc., on the frequencies and critical velocities of system subjected to fixed–fixed and cantilevered boundary conditions.

3.2 Fixed–fixed nanotubes

By referring to (Wang 2011), the mean inner radius of the nanotube is chosen as \(R_{m} = 10\,{\text{nm}}\) and the Poisson ratio is specified as 0.19. The material length scale parameter l is very different for various materials. For example, for most metals, the characteristic length scale is about 0.25 nm (Zhang and Sharma 2005); for the gallium arsenide, l is about 0.82 nm; for the graphite, l is about 3.3 nm; and for the rubber, l is about 4.6 nm (Zhang and Sharma 2005; Nikolov et al. 2007). As a result, the characteristic length scale in the range from 0.25 to 4.6 nm is considered.

Solving the governing equations subjected to the fixed–fixed boundary condition through the Galerkin method, the complex eigenfrequencies \(\hat{\omega }\) can be obtained. The real part of \(\hat{\omega }\) is the dimensionless oscillation frequency, and the ratio of the imaginary to the real parts is the damping ratio of the system. Figure 7 illustrates the Argand diagrams for smooth and rough nanotubes. The surface roughness, rarefication effect and nonlocal effect do not influence the instability mode of fixed–fixed nanotubes conveying fluid. As the flow velocity increases, the frequency decreases and the damping ratio keeps constant as zero. And once the flow velocity exceeds the critical value, the instability of divergence occurs. However, the surface roughness, rarefication effect and nonlocal effect have significant effect on the critical flow velocity for divergence. Figure 7a demonstrates the variation of complex frequency with flow velocity for a smooth nanotube without considering the rarefication effect. Figure 7b is for a rough nanotube with Kn = 0. By comparing Fig. 7b with Fig. 7a, it is found that the critical flow velocity increases by about 7% due to the surface roughness. Figure 7c shows the Argand diagram for a smooth nanotube by taking the rarefication effect into account. As the Knudsen number increases from 0 to 1, the nondimensional critical velocity decreases from 5.51 to 1.33. The influence of surface roughness and rarefaction effect on the critical velocity is opposite. The former increases the critical velocity, while the latter decreases the one. Figure 7d illustrates the combined effect of both surface roughness and velocity slip at the boundary. It can be found that due to the opposite influence of surface roughness and rarefaction effect, the critical velocity obtained by comprehensively considering the rough wall and boundary velocity slip is between the ones obtained by only taking one single effect into account.

Fig. 7
figure 7

The variation of dimensionless complex frequencies with the increasing of the dimensionless flow velocity for smooth and rough nanotubes with \(\kappa = 0.007\) a Smooth, \(Kn = 0\) b \(\varepsilon = 0.05,\;\lambda = 20,\;{\text{Kn}} = 0\) c Smooth, \(Kn = 1\) d \(\varepsilon = 0.05,\;\lambda = 20,\;Kn = 1\)

Full size image

The variation of natural frequencies is shown in Fig. 8 for different parameters. It is found that for different conditions, the nondimensional natural frequency decreases with the increasing of flow velocity. As illustrated in Fig. 8a, with the enhancement of nonlocal effect, the curve describing the relationship between the natural frequency and flow velocity moves along the positive direction of Y axis, which means that the natural frequency and critical velocity of the system increase. This is because nonlocal effects enhance the stiffness of nanotubes (Wang 2010). Figure 8b–d demonstrates the influences of surface roughness and rarefication effect on the natural frequency, which are absolutely opposite. As the roughness height increases or Knudsen number decreases, both the natural frequency and the critical velocity increase. This is due to the fact that the centripetal force induced by the internal flow can be equivalent to an axial compressive force which makes the nanotube softer. And the impacts of surface roughness and rarefication effect on fluid flow are opposite. The former reduces the velocity while the latter increases the velocity. Consequently, the increase of surface roughness or the decrease of Knudsen number can reduce the stiffness softening effect caused by the centripetal force, thus making the frequency and critical velocity increase.

Fig. 8
figure 8

Influences of nonlocal effect, surface roughness and rarefication effect on the variation of frequency with flow velocity: a nonlocal effect, b surface roughness, c rarefication effect, d combined effect of surface roughness and rarefication

Full size image

Figure 9 demonstrates the variation of nondimensional critical velocities \(\hat{U}_{cr}\) with the roughness height and Knudsen number. On one hand, as the roughness height increases, the critical flow velocity increases. On the other hand, as the Knudsen number increases, which indicates the rarefication effect dominates, the nondimensional critical velocity decreases. In addition, the increasing of \(\kappa\) only makes \(\hat{U}_{cr}\) increase and it has no effect on the variation trend of \(\hat{U}_{cr}\) with \(\varepsilon\) and Kn. Figure 10 more clearly illustrates the opposite influence of surface roughness and rarefaction effect on the critical velocity. This opposite effect can cause a phenomenon that the critical velocity may be the same for different surface roughness and Kn numbers, as shown in Fig. 11. This indicates that even if there are dramatic differences in roughness and fluid rarefication between fluid-conveying nanotubes, their stability behavior may be consistent.

Fig. 9
figure 9

Variation of nondimensional critical velocity with roughness height and Knudsen number for a \(\kappa = 0\) and b \(\kappa = 0.1\)

Full size image
Fig. 10
figure 10

a Variation of \(\hat{U}_{cr}\) with relative roughness height for different Knudsen numbers b variation of \(\hat{U}_{cr}\) with Knudsen number for different roughness height

Full size image
Fig. 11
figure 11

Contours of nondimensional critical velocities for different roughness height and Knudsen numbers a \(\kappa = 0\) and b \(\kappa = 0.1\)

Full size image

In the above analysis, the critical flow velocities are presented in the dimensionless form. According to Eq. (17), the corresponding dimensional values can be directly given as,

$$U_{cr} = \hat{U}_{cr} \sqrt {\frac{{EI^{(s)} }}{{\rho_{f} A_{f}^{(s)} }}} \frac{1}{L} = \hat{U}_{cr} \sqrt {\frac{E}{{\rho_{f} }}} \frac{{\sqrt {\alpha^{4} - 1} }}{{4\alpha \alpha_{1} }},$$
(20)

where \(U_{cr}\) is the dimensional critical velocity, \(\alpha = {{R_{o} } \mathord{\left/ {\vphantom {{R_{o} } {R_{m} }}} \right. \kern-\nulldelimiterspace} {R_{m} }}\) is the cross-sectional aspect ratio, and \(\alpha_{1} = {L \mathord{\left/ {\vphantom {L {2R_{o} }}} \right. \kern-\nulldelimiterspace} {2R_{o} }}\) is the slenderness ratio. The materials for nanotubes are various, including silicon (about 160 GPa, by referring to (Hopcroft et al. 2010)), carbon, and so on. To obtain the dimensional critical velocity, the carbon nanotube is analyzed. The cross-sectional aspect ratio, slenderness ratio and the Young’s module are set to be 1.2, 500 and 1 GPa by referring to Rashidi et al. (Rashidi et al. 2012). The internal fluid is considered as gas, whose density is 1.169 kg/m3. From Fig. 7, it is known that the nondimensional critical velocity for four different cases are 5.51, 5.91, 1.33 and 1.70, respectively. According to Eq. (20), it is easy to obtain the dimensional critical velocities 69.58 m/s, 74.63 m/s, 16.79 m/s and 21.47 m/s.

3.3 Cantilevered nanotubes

The dynamic behaviors of cantilevered nanotubes conveying fluid are very different from the fixed–fixed ones. Figure 12 illustrates the Argand diagram of smooth and rough cantilevered nanotubes with rarefication effect for \(\beta = 0.2\). The parameters used for calculation are the same to the fixed–fixed nanotubes in Sect. 3.2. It can be found that with the increasing of the flow velocity, the imaginary part of \(\hat{\omega }\) for the second mode first increases and then decreases. And once the flow velocity exceeds the critical value, the damping becomes negative and the system loses stability, which is known as fluttering. For the smooth nanotube, the nondimensional critical velocity is about 4.46 without considering the rarefication effect, while the value is about 4.78 for the rough nanotube with \(\varepsilon = 0.05\) and \(\lambda = 20\). Once the rarefication effect is taken into account, the critical velocity for the smooth nanotube decreases from 4.46 to about 1.18, as shown in Fig. 12c. When both the surface roughness and rarefication are considered, the critical velocity is about 1.54. Similar to fixed–fixed nanotubes conveying fluid, surface roughness and fluid rarefaction have opposite effects on the critical velocity of cantilevered nanotubes for \(\beta = 0.2\). The former increases the critical velocity, while the latter decreases the one. The opposite influences are clearly demonstrated by Fig. 13, which illustrates the variation of critical velocities with the roughness height and Knudsen numbers.

Fig. 12
figure 12

The variation of dimensionless complex frequencies with the increasing of the dimensionless flow velocity for \(\beta = 0.2\)

Full size image
Fig. 13
figure 13

Variation of nondimensional critical velocity with roughness height and Knudsen number for cantilevered nanotubes

Full size image

It is known that the mass ratio \(\beta\) has significant effect on the instability of fluid-conveying cantilevered tubes. Figure 14 illustrates the Argand diagram for \(\beta = 0.4\), which indicates that the dynamic behavior is so different from the one for \(\beta = 0.2\). As the flow velocity increases, the imaginary part of \(\hat{\omega }\), i.e. \({\text{Im}} \left( {\hat{\omega }} \right)\), first increases, then decreases, then increases and finally decreases. For the smooth nanotubes without considering the rarefication effect, \({\text{Im}} \left( {\hat{\omega }} \right)\) firstly drops to about 0.08 and then increases. And for the second decreasing, \({\text{Im}} \left( {\hat{\omega }} \right)\) reduces below 0 and the nanotube flutters. As illustrated in Fig. 12b, \({\text{Im}} \left( {\hat{\omega }} \right)\) of the rough nanotube without considering the rarefication effect drops to below 0 for the first decreasing. Consequently, the surface roughness makes the critical velocity decrease from about 7.20 to about 6.58, which is opposite to the case for \(\beta = 0.2\). Figure 12c shows the influence of rarefication effect. It can be found that \({\text{Im}} \left( {\hat{\omega }} \right)\) reduces to below 0 for the second decreasing, which is similar to the case for Kn = 0. And the critical velocity decreases from about 7.20 to about 6.92. Hence, the effect of fluid rarefication on the critical velocity for \(\beta = 0.4\) is the same with the one for \(\beta = 0.2\). When the surface roughness and rarefication effect are both taken into account, \({\text{Im}} \left( {\hat{\omega }} \right)\) also drops to below 0 for the second decreasing. And the critical velocity increases to about 7.34.

Fig. 14
figure 14

The variation of dimensionless complex frequencies with the increasing of the dimensionless flow velocity for \(\beta = 0.4\)

Full size image

Figure 15 demonstrates the variation of \(\hat{U}_{cr}\) with \(\beta\) for different parameters. Every curve describing the relationship between the critical velocity and mass ratio includes a S-shaped segment, which is associated with the instability–restabilization–instability sequence (I–R–I sequence) (Paidoussis 1998). Inside the I–R–I sequence region, each \(\beta\) corresponds to three critical velocities, and the critical speed changes sharply as \(\beta\) varies. Outside the region, every \(\beta\) corresponds to a unique critical velocity, and the critical velocity increases slowly with the increasing of \(\beta\). The nonlocal effect, surface roughness and Knudsen number have different influences on the relationship between \(\hat{U}_{cr}\) and \(\beta\). As shown in Fig. 15a, the increasing of \(\kappa\) makes the \(\hat{U}_{cr}\)-\(\beta\) curve move up to the top of coordinate system, which indicates that the nonlocal effect can increase the critical velocity. In addition, the nonlocal effect does not change the position of the I–R–I sequence region. When \(\beta\) is about in the range (0.38, 0.40), the nanotube may go through the instability-restabilization-instability sequence. The roughness height and Knudsen number have opposite effects on the \(\hat{U}_{cr}\)-\(\beta\) curve. The former makes the curve move to the top right of the \(\hat{U}_{cr}\)-\(\beta\) plane as shown in Fig. 15b, while the latter induces the curve shifting to the bottom left, which is illustrated in Fig. 15c. Outside the I–R–I sequence region, the surface roughness increases the critical velocity, while the rarefication effect reduces the critical velocity, which is similar to the fixed–fixed nanotube. On the other hand, the surface roughness makes the I–R–I sequence region move right along the \(\beta\) axis, while the rarefication effect makes the region move left. Figure 15d shows the coupled effect of surface roughness and fluid rarefication on the \(\hat{U}_{cr}\)-\(\beta\) curve. In order to detailed show the influence of roughness height and Knudsen number on the instability-restabilization-instability sequence, Fig. 16 illustrates the variation of \({\text{Im}} \left( {\hat{\omega }} \right)\) for the second mode with the increasing of nondimensional flow velocity for \(\beta = 0.395\). For the nanotube with Kn = 0, \({\text{Im}} \left( {\hat{\omega }} \right)\) of the second mode passes through the zero point three times with the increasing of the fluid velocity, which corresponds to three critical velocities. The surface roughness and rarefication effect change the variation trend of \({\text{Im}} \left( {\hat{\omega }} \right)\) with \(\beta\), so that \({\text{Im}} \left( {\hat{\omega }} \right)\) only passes through the zero point once, which corresponds to a unique critical velocity.

Fig. 15
figure 15

Variation of the nondimensional critical velocity with mass ratio \(\beta\) for different conditions

Full size image
Fig. 16
figure 16

The variation of \({\text{Im}} \left( {\hat{\omega }} \right)\) for the second mode with the nondimensional flow velocity for \(\beta = 0.395\)

Full size image

Figure 17 demonstrates the effects of surface roughness and Knudsen number on the frequencies of the first and second mode. As the flow velocity increases, the frequency of the first order first increases and when the velocity reaches a certain value, the frequency decreases. On the other hand, the frequency of the second order decreases. The surface roughness and Knudsen number have opposite effects on the frequency. With the increasing of the roughness height or the decreasing of the Knudsen number, the frequency of the first order decreases while the frequency of the second order increases. The difference can be attributed to the different mode shapes of the two modes (Yan et al. 2017; Jiang et al. 2021).

Fig. 17
figure 17

The variation of the first and second order frequencies with the nondimensional flow velocity

Full size image

4 Conclusions

A theoretical model is developed to describe influences of surface roughness, fluid rarefication and nonlocal effect on the instability and dynamic behaviors of rough nanotubes conveying nanoflow. Correction factors for fluid are utilized to characterize the effects of the surface roughness and Knudsen number on the internal fluid and dynamic behaviors of the system. The results demonstrated that the surface roughness of nanotube and rarefication effect of nanoflow have opposite influences on the correction factors for fluid, CFF1 and CFF2. The increasing of roughness parameters makes CFF1 and CFF2 decrease, while the increasing of Knudsen number induces CFF1 and CFF2 increasing. Because the physical meaning of CFF1/CFF2 is the ratio of Coriolis/centripetal force caused by nanoflow in rough nanotube to the one in smooth tubes without considering the rarefication effect, the influences of surface roughness and rarefication effect on the stability and natural frequencies are also opposite. For fixed–fixed nanotubes, as the roughness height increases, the critical flow velocity increases. On the other hand, as the Knudsen number increases, which indicates the rarefication effect dominates, the nondimensional critical velocity decreases. In addition, with the increasing of roughness height or the decreasing of Knudsen number, the natural frequency of the first mode increases. For cantilevered nanotubes, the surface roughness makes the curve, which describes the relationship between the critical velocity \(\hat{U}_{cr}\) and the mass ratio \(\beta\), move to the top right of the \(\hat{U}_{cr}\)-\(\beta\) plane while the rarefication effect induces the curve shifting to the bottom left. In addition, the influences of nonlocal effect are also analyzed and discussed. The material length scale parameter can enhance the stiffness of nanotube and increase the critical velocity.