1 Introduction

The dynamics of fluid-conveying pipes, in both macroscale and nanoscale, have been extensively investigated by many researchers in the past decades. Due to the wide range of engineering background, dynamic problems such as wave propagation [1] and vibration behavior [2] of pipes conveying fluid have been investigated in recent years. Nanotubes have grabbed growing attention since being discovered, due to their great potentials in nano-electromechanical systems [3], hydrogen storage [4] and drug delivery [5]. The flow-induced vibration of nanotube is a critical problem amid the implementation of these applications.

Therefore, many researchers have conducted investigations on dynamic problems of nanotubes (especially carbon nanotubes) conveying fluid. Yoon et al. made the first attempt to analyze the vibration and instability of fluid-conveying carbon nanotube (CNT) with the same method used for studying macro pipes [6]. Lee and Chang considered the size effect based on nonlocal elastic theory and analyzed the free transverse vibration of single-walled CNT conveying fluid [7]. Wang investigated the wave propagation characteristics of single-walled CNT utilizing gradient elasticity theory [8].Yang et al. considered the size effect based on nonlocal strain gradient theory into the wave propagation analysis [9]. Wang et al. took geometry imperfection into consideration and modeled the fluid-conveying CNT with wavy Timoshenko beam theory to conduct the vibration analysis [10]. Zhang et al. focused on the quantum effects on the thermal vibration of single-walled CNT [11].

The boron nitride nanotube (BNNT), which was first synthesized by Chopra et al. [12] after theoretical prediction [13], is a structural analog of the carbon nanotube with carbon atoms replaced by boron and nitride atoms. It displays far better thermal and chemical stability especially at high temperature, superb elasticity and excellent flexibility [14] than the CNT. There was also a large amount of research on the fluid-conveying dynamics of BNNT. Abdollahian et al. employed the differential quadrature method to analyze the wave propagation behavior of a fluid-conveying armchair triple-walled BNNT embedded in Winkler and Pasternak foundation [15]. Ansari et al. developed a size-dependent nonlinear Timoshenko beam model to simulate the nonlinear vibration and predicted the instability modes of fluid-conveying single-walled BNNT [16]. Arani and Roudbari investigated the wave propagation of fluid-conveying single-walled BNNTs via nonlocal piezoelasticity with comprehensively considering the influences of surface stress, initial stress and Knudsen number [17]. Arani et al. applied stress and strain–inertia gradient elasticity theories and carried out the wave propagation analysis of a double-walled BNNT conveying ferrofluid in the presence of magnetic field [18].

The performance of uniform material with single structure could not satisfy the rapidly increasing requirement for engineering practice. Many CNT-based structures have been noticed by researchers, giving the material a new life. For instance, Kiani modeled an aligned forest of single-walled CNT based on nonlocal discrete and continuous theories, and simulated the wave characteristics [19]. Zhang et al. studied the acoustic nanowave absorption through clustered CNT conveying fluid [20].

Research on synthesizing boron/carbon/nitride (B/C/N) material by replacing C atoms in graphite network by B and N atoms has been conducted due to the similar structure but quite different physical properties between B–N bonds and C–C bonds [21]. The stability and properties of the \(\hbox {B}_{{x}} \hbox {N}_{{y}} \hbox {C}_{{z}}\) nanotube heterojunctions have been investigated both theoretically and experimentally [22,23,24,25,26], which has been reviewed by Ayala [27]. These heterostructure nanotubes have potentials in nano-electromechanical systems and could compensate the limitations of uniform material and simple structure.

Mechanical and dynamic problems of these hybrid nanotubes have been noticed by researchers recently. Shen simulated the melting and axial compression of one BNNT embedded in a CNT by molecular dynamics to study the thermal-stability and compressive properties [28]. Cheng et al. constructed a fluid-conveying nanotube with BNNT and CNT, and analyzed the influences of length ratio and supporting condition on the stability [29].

Periodic structure is a basic pattern to construct materials, and the dynamics of macro pipes with periodic structure have been studied by researchers. Yu et al. focused on the stability of periodic cantilevered pipes conveying fluid and studied the influences of periodicity on geometry and material properties [30].

However, to the best of the authors’ knowledge, no studies have been conducted on the vibration behaviors of periodic heteronanotubes, or focused on the effects of periodic distributions of different nanotube components. Therefore, in this study, we hope to fill the gap and investigate the fluid-conveying stability of a fluid-conveying heterogeneous nanotube system with periodic structures. And we take CNT and BNNT as the constituent materials of the nanotube system with periodic heterostructure for instance.

In the following section, the model of the periodic nanotube constructed by CNNT and BNT is established and the governing equations are obtained via the nonlocal Euler–Bernoulli beam theory. In Sect. 3, the dynamic stiffness method is employed to solve the equations. In Sect. 4, we reveal the calculation results of the periodic nanotube in three aspects: (1) with different period numbers; (2) with different length ratios; and (3) with different boundary conditions. Finally, the influences of the mentioned three factors are concluded in Sect. 5 accordingly.

Fig. 1
figure 1

The schematic diagram of the periodic nanotube constructed by CNT and BNNT

Full size image

2 Governing Equations of Periodic Heteronanotube Conveying Fluid

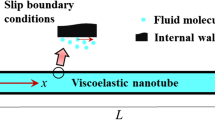
As shown in Fig. 1, the periodic unit (noted as cell) of a fluid-conveying nanotube system is modeled. In this study, the CNT and BNNT as constituent materials are taken as examples. The length of a nanotube cell is \(L_{1} +L_{2} \), in which \(L_{1}\) and \(L_{2}\) represent the lengths of CNT and BNNT, respectively. The inner and outer radii of the nanotube are \(R_{i}\) and \(R_{o}\), respectively. Though the Timoshenko beam theory has advantages in considering shear deformation and rotary inertia, the use of Euler–Bernoulli beam theory can simplify the equations and put more emphasis on the influence on axially varying periodic hetero-structures. Compared with the Timoshenko beam theory, employing the Euler–Bernoulli beam theory can cause increment in frequencies and critical velocities [31, 32], while the influences of the hetero-structures being studied tend to maintain the same, especially with pretty large aspect ratio (which is 100) chosen in our research. From the work of Wang in 2009 [33] and Cheng et al. in 2019 [29], the governing equations based on the nonlocal Euler–Bernoulli beam theory in the n-th period can be written as

$$\begin{aligned}&E_{c} I\frac{\partial ^{4}w}{\partial x{ }^{4}}+m_{f} U^{2}\frac{\partial ^{2}w}{\partial x^{2}}+2m_{f} U\frac{\partial ^{2}w}{\partial x\partial t}+\left( {m_{f} +m_{c} } \right) \frac{\partial ^{2}w}{\partial x^{2}} \nonumber \\&\quad -\left( {e_{0} a} \right) ^{2}\left[ {m_{f} U^{2}\frac{\partial ^{4}w}{\partial x^{4}}+2m_{f} U\frac{\partial ^{4}w}{\partial x^{3}\partial t}+\left( {m_{f} +m_{c} } \right) \frac{\partial ^{4}w}{\partial x^{2}\partial t^{2}}} \right] =0 \nonumber \\&\qquad \left( {n-1} \right) \left( {L_{1} +L_{2} } \right) \le x<\left( {n-1} \right) \left( {L_{1} +L_{2} } \right) +L_{1} \end{aligned}$$
(1)
$$\begin{aligned}&E_{bn} I\frac{\partial ^{4}w}{\partial x{ }^{4}}+m_{f} U^{2}\frac{\partial ^{2}w}{\partial x^{2}}+2m_{f} U\frac{\partial ^{2}w}{\partial x\partial t}+\left( {m_{f} +m_{bn} } \right) \frac{\partial ^{2}w}{\partial x^{2}} \nonumber \\&\quad -\left( {e_{0} a} \right) ^{2}\left[ {m_{f} U^{2}\frac{\partial ^{4}w}{\partial x^{4}}+2m_{f} U\frac{\partial ^{4}w}{\partial x^{3}\partial t}+\left( {m_{f} +m_{bn} } \right) \frac{\partial ^{4}w}{\partial x^{2}\partial t^{2}}} \right] =0 \nonumber \\&\qquad \left( {n-1} \right) \left( {L_{1} +L_{2} } \right) +L_{1} \le x<n\, \left( {L_{1} +L_{2} } \right) \end{aligned}$$
(2)

where \(E_{c}\) and \(E_{bn}\) denote the Young’s moduli of CNT and BNNT, respectively; \(m_{f}\), \(m_{c}\) and \(m_{bn}\) represent the masses within unit length of the flow, CNT and BNNT, respectively; and I,U and \(e_{0}a \) represent moment of inertia for the cross section of the nanotube, flow velocity of the fluid and nonlocal parameter relevant to the small size effect, respectively. We take the displacement w along the lateral direction (the z-direction in Fig. 1), which is a function of coordinate x and time t.

The dimensionless form of the equation writes,

$$\begin{aligned}&{\begin{array}{*{20}c} {\begin{array}{l} \frac{\partial ^{4}Y}{\partial X^{4}}+u^{2}\frac{\partial ^{2}Y}{\partial X^{2}}+2\sqrt{\beta }u\frac{\partial ^{2}Y}{\partial X\partial \tau }+\frac{\partial ^{2}Y}{\partial \tau ^{2}} \\ -e_{n}^{2}\left( {u^{2}\frac{\partial ^{4}Y}{\partial X^{4}}+2\sqrt{\beta }u\frac{\partial ^{2}Y}{\partial X^{3}\partial \tau }+\frac{\partial ^{4}Y}{\partial X^{2}\partial \tau ^{2}}} \right) =0 \\ \end{array}} &{} {\left( {\frac{n-1}{N}\le X<\frac{n-1}{N}+\frac{\xi _{c} }{N}} \right) } \\ \end{array} } \end{aligned}$$
(3)
$$\begin{aligned}&{\begin{array}{*{20}c} {\begin{array}{l} \alpha _{1} \frac{\partial ^{4}Y}{\partial X^{4}}+u^{2}\frac{\partial ^{2}Y}{\partial X^{2}}+2\sqrt{\beta }u\frac{\partial ^{2}Y}{\partial X\partial \tau }+\alpha _{2} \frac{\partial ^{2}Y}{\partial \tau ^{2}} \\ -e_{n}^{2}\left( {u^{2}\frac{\partial ^{4}Y}{\partial X^{4}}+2\sqrt{\beta }u\frac{\partial ^{2}Y}{\partial X^{3}\partial \tau }+\alpha _{2} \frac{\partial ^{4}Y}{\partial X^{2}\partial \tau ^{2}}} \right) =0 \\ \end{array}} &{} {\left( {\frac{n-1}{N}+\frac{\xi _{c} }{N}\le X<\frac{n}{N}} \right) } \\ \end{array} } \end{aligned}$$
(4)

in which N denotes the total period number, by substituting the following dimensionless quantities

$$\begin{aligned} Y= & {} \frac{w}{L}, \quad {X=\frac{x}{L},} \quad {u=\sqrt{\frac{m_{f} }{E_{c} I}} UL,} \quad {\tau =\sqrt{\frac{E_{c} I}{m_{f} +m_{c} }} \frac{t}{L^{2}},} \quad {e_{n} =\frac{e_{0} a}{L}} \nonumber \\ \beta= & {} \frac{m_{f} }{m_{f} +m_{c} }, \quad {\alpha _{1} =\frac{E_{bn} }{E_{c} },} \quad {\alpha _{2} =\frac{m_{f} +m_{bn} }{m_{f} +m_{c} },} \quad {L=N(L_{1} +L_{2} ),} \quad {\xi _{c} =\frac{L_{1} }{L_{1} +L_{2}}} \end{aligned}$$
(5)

into Eqs. (1) and (2).

3 Dynamic Stiffness Method for Periodical Nanotubes

In this paper, the governing equations are numerically solved by the dynamic stiffness method (DSM). We set the form of the solutions to the dimensionless governing equations [Eqs. (3) and (4)] as

$$\begin{aligned} Y_{nc} \left( {X,\tau } \right)= & {} \overline{Y}_{nc} \left( X \right) \text{ e}^{\mathrm{{i}}\omega \tau } \quad \left( \frac{n-1}{N}\le X<\frac{n-1}{N}+\frac{\xi _{c} }{N}\right) \end{aligned}$$
(6)
$$\begin{aligned} Y_{nb} \left( {X,\tau } \right)= & {} {\overline{Y}}_{nb} \left( X \right) \text{ e}^{\mathrm{{i}}\omega \tau } \quad \left( \frac{n-1}{N}+\frac{\xi _{c} }{N}\le X<\frac{n}{N}\right) \end{aligned}$$
(7)

where the subscript n denotes the n-th period, and subscripts c and b represent CNT and BNNT, respectively. \(\omega \) is the circular frequency, \(\text{ i }=\sqrt{-1}\), and \({\overline{Y}} \) indicates the amplitude of Y. We take

$$\begin{aligned} {\overline{Y}}_{nc} \left( X \right)= & {} A_{nc} \text{ e}^{\mathrm{{i}}k_{nc} X} \quad {\left( \frac{n-1}{N}\le X<\frac{n-1}{N}+\frac{\xi _{c} }{N}\right) } \end{aligned}$$
(8)
$$\begin{aligned} {\overline{Y}}_{nb} \left( X \right)= & {} A_{nb} \text{ e}^{\mathrm{{i}}k_{nb} X} \quad \left( \frac{n-1}{N}+\frac{\xi _{c} }{N}\le X<\frac{n}{N} \right) \end{aligned}$$
(9)

in which k is the wave number and A is constant.

By substituting Eqs. (6) and (7) into Eqs. (3) and (4), we can get

$$\begin{aligned}&\left( {1-e_{n}^{2}u^{2}} \right) k_{nc}^{4}-2\sqrt{\beta }e_{n}^{2}u\omega k_{nc}^{3}-\left( {u^{2}+e_{n}^{2}\omega ^{2}} \right) k_{nc}^{2}-2\sqrt{\beta }u\omega k_{nc} -\omega ^{2}=0 \end{aligned}$$
(10)
$$\begin{aligned}&\left( {\alpha _{1} -e_{n}^{2}u^{2}} \right) k_{nb}^{4}-2\sqrt{\beta }e_{n} ^{2}u\omega k_{nb}^{3}-\left( {u^{2}+\alpha _{2} e_{n}^{2}\omega ^{2}} \right) k_{nb}^{2}-2\sqrt{\beta }u\omega k_{nb} -\alpha _{2} \omega ^{2}=0 \end{aligned}$$
(11)

Equations (10) and (11) are quartic equations of wave number, that is to say, each \(k_{nc}\) or \(k_{nb}\) has four roots. Then we can transform Eqs. (8) and (9) into

$$\begin{aligned} {\overline{Y}}_{nc} \left( X \right)= & {} \sum \limits _{j=1}^4 {{{A}_{ncj}} \text{ e}^{{\mathrm{{i}}k_{nc}}_{j} X}} \quad {\left( \frac{n-1}{N}\le X<\frac{n-1}{N}+\frac{\xi _{c} }{N}\right) } \end{aligned}$$
(12)
$$\begin{aligned} {\overline{Y}}_{nb} \left( X \right)= & {} \sum \limits _{j=1}^4 {{{A}_{nbj}} \text{ e}^{{\mathrm{{i}}k_{nb}}_{j} X}} \quad \left( \frac{n-1}{N}+\frac{\xi _{c} }{N}\le X<\frac{n}{N}\right) \end{aligned}$$
(13)

The rotation \({\overline{\theta }}\) can be written as

$$\begin{aligned} {\overline{\theta }}_{nc} \left( X \right)= & {} {\sum \limits _{j=1}^4 {{\text{ i }k_{nc}}_{j} {{A}_{ncj}} \text{ e}^{{\mathrm{{i}}k_{nc}}_{j} X}}} \quad \left( \frac{n-1}{N}\le X<\frac{n-1}{N}+\frac{\xi _{c} }{N} \right) \end{aligned}$$
(14)
$$\begin{aligned} {\overline{\theta }}_{nb} \left( X \right)= & {} {\sum \limits _{j=1}^4 {{\text{ i }k_{nb}}_{j} A_{nbj} \text{ e}^{{\mathrm{{i}}k_{nb}}_{j} X}}} \quad \left( \frac{n-1}{N}+\frac{\xi _{c} }{N}\le X<\frac{n}{N}\right) \end{aligned}$$
(15)

The bending moment \({\overline{M}}\) can be expressed as

$$\begin{aligned} {\overline{M}}_{nc} \left( X \right)&= \sum \limits _{j=1}^4 \left[ {\left( {{1-e_{n}}^{2}u^{2}} \right) {k_{nc}}_{j}^{2}-2\sqrt{\beta }e_{n}^{2}u\omega {k_{nc}}_{j} -{e_{n}}^{2}\omega ^{2}} \right] {A_{ncj}} \text{ e}^{{\mathrm{{i}}k_{nc}}_{j} X} \quad \left( \frac{n-1}{N}\le X<\frac{n-1}{N}+\frac{\xi _{c} }{N}\right) \end{aligned}$$
(16)
$$\begin{aligned} {\overline{M}}_{nb} \left( X \right)&= {\sum \limits _{j=1}^4 {\left[ {\left( {\alpha _{1} -{e_{n}}^{2}u^{2}} \right) {k_{nb}}_{j}^{2}-2\sqrt{\beta }{e_{n}}^{2}u\omega {k_{nb}}_{j} -\alpha _{2} {e_{n}}^{2}\omega ^{2}} \right] {A_{nbj}} \text{ e}^{{\mathrm{{i}}k_{nb}}_{j} X}} } \quad \left( \frac{n-1}{N}+\frac{\xi _{c} }{N}\le X<\frac{n}{N}\right) \end{aligned}$$
(17)

The shear force \({\overline{Q}}\) in the frequency domain can be shown as

$$\begin{aligned} {\overline{Q}}_{nc} \left( X \right)&= \sum \limits _{j=1}^4 {\left[ {\text{ i }\left( {1-e_{n}^{2}u^{2}} \right) {{k_{nc}}_{j}}^{3}-2\text{ i }\sqrt{\beta }e_{n}^{2}u\omega {k_{nc}}_{j} ^{2}-\text{ i }{e_{n}}^{2}\omega ^{2}{k_{nc}}_{j}} \right] {A_{ncj}} \text{ e}^{{\mathrm{{i}}k_{nc}}_{j} X}} \quad \left( \frac{n-1}{N}\le X<\frac{n-1}{N}+\frac{\xi _{c} }{N}\right) \end{aligned}$$
(18)
$$\begin{aligned} {\overline{Q}}_{nb} \left( X \right)&= {\sum \limits _{j=1}^4 {\left[ {\text{ i }\left( {\alpha _{1} -e_{n}^{2}u^{2}} \right) {k_{nb}}_{j}^{3}-2\text{ i }\sqrt{\beta }e_{n}^{2}u\omega {k_{nb}}_{j} ^{2}-\text{ i }\alpha _{2} e_{n}^{2}\omega ^{2}{k_{nb}}_{j} } \right] {A_{nbj}} \text{ e}^{{\mathrm{{i}}k_{nb}}_{j} X}} } \quad {\left( \frac{n-1}{N}+\frac{\xi _{c} }{N}\le X<\frac{n}{N}\right) } \end{aligned}$$
(19)

For apiece of the periodic nanotube, we can use nodal displacements and nodal forces to describe its mechanical behavior. We take the CNT part in the n-th period (which can be seen in Fig. 2) to conduct the analysis. Let the left end be the origin of the local coordinate, and let the axis pointing to the right end be the x-axis.

Fig. 2
figure 2

Schematic of local coordinates, nodal displacements and forces in the CNT section

Full size image

The linear displacements along the z-axis at the left node and the right node are denoted with \({\overline{Y}}_{n1}\) and \({\overline{Y}}_{n2}\), respectively. The angular displacements in the xz-plane at the left node and the right node are expressed with \({\overline{\theta }}_{n1}\) and \({\overline{\theta }}_{n2}\), respectively. And we can get the expression of the nodal displacements according to Eqs. (12) and (14) as

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {{\overline{Y}}_{n1} } \\ {{\overline{\theta }}_{n1} } \\ {{\overline{Y}}_{n2} } \\ {{\overline{\theta }}_{n2} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} 1 &{} 1 &{} 1 &{} 1 \\ {\text{ i }k_{nc1} } &{} {\text{ i }k_{nc2} } &{} {\text{ i }k_{nc3} } &{} {\text{ i }k_{nc4} } \\ {\text{ e}^{\mathrm{{i}}k_{nc1} \xi _{c} }} &{} {\text{ e}^{\mathrm{{i}}k_{nc2} \xi _{c} }} &{} {\text{ e}^{\mathrm{{i}}k_{nc3} \xi _{c} }} &{} {\text{ e}^{\mathrm{{i}}k_{nc4} \xi _{c} }} \\ {\text{ i }k_{nc1} \text{ e}^{\mathrm{{i}}k_{nc1} \xi _{c} }} &{} {\text{ i }k_{nc2} \text{ e}^{\mathrm{{i}}k_{nc2} \xi _{c} }} &{} {\text{ i }k_{nc3} \text{ e}^{\mathrm{{i}}k_{nc3} \xi _{c} }} &{} {\text{ i }k_{nc4} \text{ e}^{\mathrm{i}k_{nc4} \xi _{c} }} \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {{\overline{A}}_{nc1} } \\ {{\overline{A}}_{nc2} } \\ {{\overline{A}}_{nc3} } \\ {{\overline{A}}_{nc4} } \\ \end{array} }} \right\} \end{aligned}$$
(20)

where \({\begin{array}{*{20}c} {{\overline{A}}_{ncj} =\hbox {e}^{\frac{n-1}{N}}A_{ncj} }&{\left( {j=1,2,3,4} \right) } \end{array}}\). Equation (20) can be simply denoted as \(\left\{ {W_{nc} } \right\} =\left[ {P_{nc} } \right] \left\{ A \right\} \).

The shear forces along the z-axis at the left node and the right node are denoted with \({\overline{Q}}_{n1}\) and \({\overline{Q}}_{n2} \), respectively. The bending moments in the xz-plane at the left node and the right node are expressed with \({\overline{M}}_{n1} \) and \({\overline{M}}_{n2}\), respectively. And we can obtain the expression of the nodal forces according to Eq. (18) and Eq. (16) as

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {{\overline{Q}}_{n1} } \\ {{\overline{M}}_{n1} } \\ {{\overline{Q}}_{n2} } \\ {{\overline{M}}_{n2} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {-\text{ i }k_{nc1} \varepsilon _{nc1} } &{} {-\text{ i }k_{nc2} \varepsilon _{nc2} } &{} {-\text{ i }k_{nc3} \varepsilon _{nc3} } &{} {-\text{ i }k_{nc4} \varepsilon _{nc4} } \\ {-\varepsilon _{nc1} } &{} {-\varepsilon _{nc2} } &{} {-\varepsilon _{nc3} } &{} {-\varepsilon _{nc4} } \\ {\text{ i }k_{nc1} \varepsilon _{nc1} \text{ e}^{\mathrm{{i}}k_{nc1} \xi _{c} }} &{} {\text{ i }k_{nc2} \varepsilon _{nc2} \text{ e}^{\mathrm{{i}}k_{nc2} \xi _{c} }} &{} {\text{ i }k_{nc3} \varepsilon _{nc3} \text{ e}^{\mathrm{{i}}k_{nc3} \xi _{c} }} &{} {\text{ i }k_{nc4} \varepsilon _{nc4} \text{ e}^{\mathrm{{i}}k_{nc4} \xi _{c} }} \\ {\varepsilon _{nc1} \text{ e}^{\mathrm{{i}}k_{nc1} \xi _{c} }} &{} {\varepsilon _{nc2} \text{ e}^{\mathrm{{i}}k_{nc2} \xi _{c} }} &{} {\varepsilon _{nc3} \text{ e}^{\mathrm{{i}}k_{nc3} \xi _{c} }} &{} {\varepsilon _{nc4} \text{ e}^{\mathrm{{i}}k_{nc4} \xi _{c} }} \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {{\overline{A}}_{nc1} } \\ {{\overline{A}}_{nc2} } \\ {{\overline{A}}_{nc3} } \\ {{\overline{A}}_{nc4} } \\ \end{array} }} \right\} \end{aligned}$$
(21)

where \({\begin{array}{*{20}c} {\varepsilon _{ncj} =\left( {{1-e_{n}}^{2}u^{2}} \right) {k_{nc}}_{j} ^{2}-2\sqrt{\beta }e_{n}^{2}u\omega {k_{nc}}_{j} -{e_{n}}^{2}\omega ^{2}}&{\left( {j=1,2,3,4} \right) } \end{array} }\). Equation (21) can be simply noted as \(\left\{ {F_{nc} } \right\} =\left[ {G_{nc} } \right] \left\{ A \right\} \).

Then, we can get the relationship between nodal forces and nodal displacements

$$\begin{aligned} \left\{ {F_{nc} } \right\} =\left[ {K_{nc} } \right] \left\{ {W_{nc} } \right\} \end{aligned}$$
(22)

and the called local stiffness matrix

$$\begin{aligned} \left[ {K_{nc} } \right] =\left[ {G_{nc} } \right] \left[ {P_{nc} } \right] ^{-1} \end{aligned}$$
(23)

Similarly, for the BNNT part of the n-th period, we have

$$\begin{aligned} \left\{ {F_{nb} } \right\} =\left[ {K_{nb} } \right] \left\{ {W_{nb} } \right\} \end{aligned}$$
(24)

and

$$\begin{aligned} \left[ {K_{nb} } \right] =\left[ {G_{nb} } \right] \left[ {P_{nb} } \right] ^{-1} \end{aligned}$$
(25)

where

$$\begin{aligned} \left\{ {W_{nb} } \right\}= & {} \left\{ {{\begin{array}{*{20}c} {{\overline{Y}}_{n2} } &{} {{\overline{\theta }}_{n2} } &{} {\overline{Y}_{n3} } &{} {{\overline{\theta }}_{n3} } \\ \end{array} }} \right\} ^\mathrm{{T}} \end{aligned}$$
(26)
$$\begin{aligned} \left\{ {F_{nb} } \right\}= & {} \left\{ {{\begin{array}{*{20}c} {{\overline{Q}}_{n2} } &{} {{\overline{M}}_{n2} } &{} {{\overline{Q}} _{n3} } &{} {{\overline{M}}_{n3} } \\ \end{array} }} \right\} ^\mathrm{{T}} \end{aligned}$$
(27)
$$\begin{aligned} \left[ {P_{nb} } \right]= & {} \left[ {{\begin{array}{*{20}c} 1 &{} 1 &{} 1 &{} 1 \\ {\text{ i }k_{nb1} } &{} {\text{ i }k_{nb2} } &{} {\text{ i }k_{nb3} } &{} {\text{ i }k_{nb4} } \\ {\text{ e}^{\mathrm{{i}}k_{nb1} \xi _{b} }} &{} {\text{ e}^{\mathrm{{i}}k_{nb2} \xi _{b} }} &{} {\text{ e}^{\mathrm{{i}}k_{nb3} \xi _{b} }} &{} {\text{ e}^{\mathrm{{i}}k_{nb4} \xi _{b} }} \\ {\text{ i }k_{nb1} \text{ e}^{\mathrm{{i}}k_{nb1} \xi _{b} }} &{} {\text{ i }k_{nb2} \text{ e}^{\mathrm{{i}}k_{nb2} \xi _{b} }} &{} {\text{ i }k_{nb3} \text{ e}^{\mathrm{{i}}k_{nb3} \xi _{b} }} &{} {\text{ i }k_{nb4} \text{ e}^{\mathrm{{i}}k_{nb4} \xi _{b} }} \\ \end{array} }} \right] \end{aligned}$$
(28)
$$\begin{aligned} \left[ {G_{nb} } \right]= & {} \left[ {{\begin{array}{*{20}c} {-\text{ i }k_{nb1} \varepsilon _{nb1} } &{} {-\text{ i }k_{nb2} \varepsilon _{nb2} } &{} {-\text{ i }k_{nb3} \varepsilon _{nb3} } &{} {-\text{ i }k_{nb4} \varepsilon _{nb4} } \\ {-\varepsilon _{nb1} } &{} {-\varepsilon _{nb2} } &{} {-\varepsilon _{nb3} } &{} {-\varepsilon _{nb4} } \\ {\text{ i }k_{nb1} \varepsilon _{nb1} \text{ e}^{\mathrm{{i}}k_{nb1} \xi _{b} }} &{} {\text{ i }k_{nb2} \varepsilon _{nb2} \text{ e}^{\mathrm{{i}}k_{nb2} \xi _{b} }} &{} {\text{ i }k_{nb3} \varepsilon _{nb3} \text{ e}^{\mathrm{{i}}k_{nb3} \xi _{b} }} &{} {\text{ i }k_{nb4} \varepsilon _{nb4} \text{ e}^{\mathrm{{i}}k_{nb4} \xi _{b} }} \\ {\varepsilon _{nb1} \text{ e}^{\mathrm{{i}}k_{nb1} \xi _{b} }} &{} {\varepsilon _{nb2} \text{ e}^{\mathrm{{i}}k_{nb2} \xi _{b} }} &{} {\varepsilon _{nb3} \text{ e}^{\mathrm{{i}}k_{nb3} \xi _{b} }} &{} {\varepsilon _{nb4} \text{ e}^{\mathrm{{i}}k_{nb4} \xi _{b} }} \\ \end{array} }} \right] \end{aligned}$$
(29)
$$\begin{aligned} \varepsilon _{nbj}= & {} \left( {{{1-e_{n}}^{2}}u^{2}} \right) {k_{nb}}_{j} ^{2}-2\sqrt{\beta }{e_{n}}^{2}u\omega {k_{nb}}_{j} -{e_{n}}^{2}\omega ^{2} \quad {\left( {j=1,2,3,4} \right) } \end{aligned}$$
(30)

We can obtain the local stiffness matrix of the n-th period section constructed by CNT and BNNT parts by assembling their local stiffness matrices, which can be expressed as

$$\begin{aligned} \left[ {K{ }_{n}} \right] =\left[ {{\begin{array}{*{20}c} {\left[ {K_{nc} } \right] } &{} {\left\{ 0 \right\} _{4\times 2} } \\ {\left\{ 0 \right\} _{2\times 4} } &{} {\left[ 0 \right] _{2\times 2} } \\ \end{array} }} \right] +\left[ {{\begin{array}{*{20}c} {\left[ 0 \right] _{2\times 2} } &{} {\left\{ 0 \right\} _{2\times 4} } \\ {\left\{ 0 \right\} _{4\times 2} } &{} {\left[ {K_{nb} } \right] } \\ \end{array} }} \right] \end{aligned}$$
(31)

And the corresponding relationship between nodal forces and nodal displacements in the whole n-th period is

$$\begin{aligned} \left\{ {F_{n} } \right\} =\left[ {K_{n} } \right] \left\{ {W_{n} } \right\} \end{aligned}$$
(32)

with \(\left\{ {W_{n} } \right\} =\left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\overline{Y}}_{n1} } &{} {{\overline{\theta }}_{n1} } \\ \end{array} }} &{} {{\overline{Y}}_{n2} } \\ \end{array} }} &{} {{\overline{\theta }}_{n2} } &{} {{\overline{Y}} _{n3} } &{} {{\overline{\theta }}_{n3} } \\ \end{array} }} \right\} ^\mathrm{{T}}\) and \(\left\{ {F_{n} } \right\} =\left\{ {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{\overline{Q}}_{n1} } &{} {{\overline{M}}_{n1} } \\ \end{array} }} &{} {{\overline{Q}}_{n2} } \\ \end{array} }} &{} {{\overline{M}}_{n2} } &{} {{\overline{Q}}_{n3} } &{} {{\overline{M}}_{n3} } \\ \end{array} }} \right\} ^\mathrm{{T}}\).

Similarly, we can get the global dynamic stiffness matrix \(\left[ K \right] \) of the periodic nanotube which indicates the relationship \(\left\{ F \right\} =\left[ K \right] \left\{ W \right\} \). We can also apply the displacement boundary conditions in the stiffness matrix \(\left[ K \right] \) and the nodal forces can be set as \(\left\{ F \right\} =\left\{ 0 \right\} \) in the free vibration case. Therefore, we have a new relation \(\left[ {\overline{K} } \right] \left\{ {{\overline{W}} } \right\} =\left\{ 0 \right\} \). To obtain the nontrivial solution of \(\left\{ {{\overline{W}} } \right\} \), we set \(\det \left( {\left[ {{\overline{K}} } \right] } \right) =0\), from which we can obtain the natural frequencies of the structure.

4 Numerical Results and Discussions

DSM is employed in this section and the influence of periodic heterostructure on the stability of the fluid-conveying nanotube is discussed. We study the natural frequencies and critical flow velocities of nanotubes with different period numbers, length ratios of the material and boundary conditions, which correspond to the three subsections below, respectively. We also add the homogeneous cases with the same integrals of material properties (as those of the corresponding heterogeneous ones) along the whole length to isolate the influence of periodic structure in the three situations. The mass density and Young’s modulus of CNT are 2300  kg/m\(^{\mathrm {3}}\) and 1 TPa, while those of BNNT are 2180  kg/m\(^{\mathrm {3}}\) and 1 TPa, respectively.

For validation, we calculate the natural frequencies of a uniform CNT in Fig. 3a and a constructed nanotube with only one period in Fig. 3b, and the results agree well with those in references [29, 34], respectively.

Fig. 3
figure 3

Variation of the first and second dimensionless natural frequencies with dimensionless flow velocity with different period numbers

Full size image

4.1 Different Period Numbers

We first calculate the dimensionless natural frequencies of the systems varying with inner flow velocity, as shown in Fig. 3.The real part of each natural frequency represents the vibration frequency, and the imaginary part denotes the damping ratio of that mode. For simplicity, we use \(\hbox {Re}(\omega )\) and \(\hbox {Im}(\omega )\) to denote the real part and the imaginary part of natural frequency, respectively. We take the length ratio \(\xi _{c} =0.5\), and both ends of the nanotubes are simply supported (SS). And we take the dimensionless nonlocal parameter \(e_{n} =0.1\). From Fig. 3, we can see that with the increase in flow velocity, \(\hbox {Re}(\omega _{1} )\) falls to zero, then appears again and couples with the second natural frequency. Meanwhile, the imaginary part maintains zero with small flow velocity, then appears in pairs and also couples with the second natural frequency. In the first stage, when \(\hbox {Re}(\omega _{1} )>0\) and \(\hbox {Im}(\omega _{1} )=0\), according to Eqs. (6) and (7), we can find that in the first mode, the nanotube vibrates and the amplitude of the nanotube would not become larger or smaller, which indicates that the system can maintain stable. In the second stage, when \(\hbox {Re}(\omega _{1} )=0\) and \(\hbox {Im}(\omega _{1} )\ne 0\), the nanotube does not have a vibration frequency of the first mode and the displacement of that mode keeps increasing with time, which can be called the static instability. In the third stage of the increasing flow, when \(\hbox {Re}(\omega _{1} )>0\) and \(\hbox {Im}(\omega _{1} )\ne 0\), the first mode of the nanotube vibrates again and the amplitude increases as time goes on. And the system is of dynamic instability. To simply describe these three stage, we use \(u_{\mathrm{cr}1}\) and \(u_{\mathrm{cr}2}\) to denote the critical flow velocities of the disappearance and reappearance of \(\hbox {Re}(\omega _{1} )\). In the second mode, the three stages also happen but with different critical flow velocities.

Comparing Fig. 3a with b, we find larger \(u_{\mathrm{cr}1} \) and \(u_{\mathrm{cr}2}\) in Fig. 3b than in Fig. 3a, which indicates that both static instability and dynamic instability occur later after we construct BNNT with CNT. The higher stability is due to the higher strength of BNNT. In order to further reveal the effect of the constructed structure and eliminate the influence from the difference in material properties, we choose a homogeneous nanotube in Fig. 3c, and the material properties are determined by the weighted averages of the material properties of CNT and BNNT, respectively. The two weighting coefficients are the same as the two length ratios, respectively, to make sure the compared homogeneous nanotube has the same integrals of material properties along the length direction with those of the constructed nanotube (with one period or more). This method to eliminate the influence of material properties has been introduced in our previous work [35].

Comparing Fig. 3b with Fig. 3c, we can find that the \(u_{\mathrm{cr}1}\) of the homogeneous nanotube (at \(u=3.64)\) is slightly larger than that of the constructed nanotube with \(N=1\) (at \(u=3.39)\). The \(u_{\mathrm{cr}2}\) of the homogeneous nanotube (at \(u=6.44)\) is also slightly larger than that of the case with \(N=1\)(at \(u=6.32)\). Larger 1st order and 2nd order of \(\hbox {Re}(\omega )\) are also found in the homogeneous nanotube before they decline to zero. Therefore, we can see that the homogeneity itself can slightly enhance the stability.

From Fig. 3b, d and e, we cannot see much difference in the first order of \(\hbox {Re}(\omega )\), while the 2nd order of \(\hbox {Im}(\omega )\) in Fig. 3d (with \(N=3\)) or Fig. 3e (with \(N=5\)) is quite larger than that in Fig. 3b. As to velocities, \(u_{\mathrm{cr}1}\) changes little with N. And as N increases from 1 to 5, \(u_{\mathrm{cr}2}\) decreases.

The influences of period number on higher-order frequencies are further studied, and the results are shown in Table 1. We find that all the first five frequencies fluctuate and reach certain values as we increase the value of N. In particular, there is a relatively large gap when N passes the order number of the frequency we observe. For example, when N increases from 3 to 4, the 4\(^{\mathrm {th}}\)-order frequency changes from 115.5 to 112.4 with a gap of 3.1, while 0.8 is found between \(N=1\) and \(N=2\).

Table 1 First five natural frequencies with different N
Full size table

4.2 Different Length Ratios

Fig. 4
figure 4

Variation of the first-two dimensionless natural frequencies with dimensionless flow velocity with different length ratios

Full size image

In Fig. 4, we calculate the real parts and imaginary parts of natural frequencies with varying flow velocity with the length ratio of CNT \(\xi _{c}\) equaling 0.2, 0.4 and 0.8. The period number N is 3 in this subsection. Both ends of the nanotube are simply supported. For each value of \(\xi _{c} \), we also give the frequency results of homogeneous nanotube whose integrals of material properties along the length direction are the same with those of the heteronanotube with corresponding value of \(\xi _{c} \) for comparison. Similar to the previous subsection, we hope to isolate the influence of periodic constructing structure from the effect of divergence in material properties between CNT and BNNT.

The heterogeneity seems to make system less stable in all the three values of \(\xi _{c}\), especially when \(\xi _{c} =0.4\) in Fig. 4b. Both static and dynamic instability flow velocity points of the nanotube decrease. We also find that the longer the BNNT part is, the higher the real part of the natural frequencies are. These results indicate that if we increase the integrals of the material properties more smoothly, the strengthening effect tends to become more significant.

Fig. 5
figure 5

Variation of dimensionless critical flow velocity with length ratio \(\xi _c\)

Full size image

In Fig. 5, we present the results of \(u_{\mathrm{cr}1}\) and \(u_{\mathrm{cr}2} \) varying with length ratio \(\xi _{c}\). Here, the period number N is also taken as 3. In previous literature [29] working on the CNT and BNNT constructed nanotube with single period, similar trends were observed: stability decreased as length ratio increased.

Fig. 6
figure 6

Variation of the first and second dimensionless natural frequencies with dimensionless flow velocity with different boundary conditions

Full size image

4.3 Different Boundary Conditions

In Fig. 6, we calculate the relationship between dimensionless natural frequencies and flow velocity with different boundary conditions. Since the boundary condition being simply supported at both ends (denoted as SS) has been shown in the first subsection of this section, we here exhibit the frequency results of the five-period (\(N=5\)) constructed nanotube with the boundary conditions being CC (clamped at both ends), CS (clamped at the left end and simply supported at the right end) and SC (simply supported at the left end and clamped at the right end). The black curves represent the results of homogeneous nanotubes, and the blue curves denote those of the five-period constructed ones. From the black curves in Fig. 6b and c, we can observe that the frequencies of nanotubes with SC and CS conditions are equal. For the homogeneous nanotube, the two boundary conditions do not change the structure we analyze due to geometric symmetry. As to the blue curves, we can see that the stability of the CC nanotube is the strongest, followed by the nanotubes with SC and CS boundary conditions. Considering the nanotube whose left end is CNT and right end is BNNT, we can say that stronger conditions (clamped conditions) at stronger ends (BNNT) may lead to higher stability of the first mode and second mode.

We also compare the first five frequencies of periodically constructed nanotube at \(u=0\) with \(N=3\) and \(N=5\) in Table 2. It can be seen that SS nanotubes have the smallest frequencies, whereas CC nanotubes have the largest frequencies. The difference in frequencies between nanotubes with SC and CS boundary conditions becomes smaller when we increase period number N from 3 to 5. What’s more, lower frequencies (1\(^{\mathrm {st}}\) order, 2\(^{\mathrm {nd}}\) order and 3\(^{\mathrm {rd}}\) order) are more easily influenced than higher frequencies (4\(^{\mathrm {th}}\) order and 5\(^{\mathrm {th}}\) order) if the boundary condition is changed from SC to CS.

5 Conclusions

In this paper, we focus on the influence of periodic structure on fluid-conveying stability of heteronanotube. We study the effects of period number N, the length ratio \(\xi _{c}\) and boundary conditions on natural frequencies and critical flow velocities. According to the numerical results, we can draw the following conclusions:

Table 2 Higher frequencies of the three-period constructed nanotube with different boundary conditions with three periods (\(N=3\)) and five periods (\(N=5\))
Full size table
  1. 1.

    The period number has an effect on the natural frequencies of the systems, especially on high-order frequencies. When the order number of frequency surpasses the period number, the influence of order number becomes fairly slight.

  2. 2.

    The stability of the periodically constructed nanotube decreases with the increase in length ratio \(\xi _{c}\). Different length ratios can also change the decrement in natural frequencies between homogeneous nanotube and periodic heteronanotube.

  3. 3.

    The boundary conditions have influences on both lower frequencies and higher frequencies, and the stability relationship of the nanotubes is CC>CS/SC>SS. The difference in frequencies of CS and SC nanotubes is smaller with higher orders and larger period numbers.