1 Introduction

In recent years, various nanotubes have been synthesised and used in nanoscale electromechanical systems. The widespread application of nanotubes is due to their excellent mechanical, thermal and electrical properties. For instance, carbon nanotubes have an exceptional strength and a high thermal conductivity, leading to the extensive applications of them in different nanosystems such as nanoresonators, nanogenerators, thermal conductors and scaffolds for bone growth (De Volder et al. 2013). Strong nonlinear dynamics has been found in the fundamental structures of many microelectromechanical and nanoelectromechanical systems (MEMS and NEMS) (Farokhi and Ghayesh 2016, 2018; Ghayesh and Farokhi 2018; Sassi and Najar 2018), making the investigation of this phenomenon extremely important in analysing MEMS and NEMS devices.

The vibration response of macroscale structures has widely been explored via the classical elasticity (Ghayesh et al. 2013a; Ghayesh and Moradian 2011; Malekzadeh 2007; Malekzadeh and Vosoughi 2009). However, since classical continuum-based models lead to size-independent results for small-scale structures, they are modified to include size effects (Babaei and Yang 2019; Ebrahimi and Barati 2019; Farajpour et al. 2018b; Farajpour et al. 2018c; Ghayesh and Farajpour 2018b; Lin et al. 2018; Sahmani and Aghdam 2018), and accurately estimate the mechanical behaviour at small-scales (Farokhi et al. 2018a, 2018b; Ghayesh 2018a, 2019; Kamali et al. 2018; Pradiptya and Ouakad 2018; Yayli 2018). Various modified continuum-based models involving the nonlocal (Farajpour et al. 2017; Reddy 2010), couple stress (Ghayesh et al. 2016a; Nejad et al. 2017) and a theory incorporating the gradient of strain (Akgöz and Civalek 2011; Ghayesh et al. 2013b) have been developed and utilised for small-scale structures (Farokhi and Ghayesh 2015; Ghayesh et al. 2016b; Farajpour et al. 2018d; Gholipour et al. 2015; Farajpour et al. 2019b). Recently, an advanced version of the nonlocal theory, which includes strain gradient effects, has attracted much attention in the continuum modelling of nanostructures (Lim et al. 2015; Zhu and Li 2017). This size-dependent theory is technically termed as “nonlocal strain gradient”. In this work, using this theory, size effects on the mechanical response are captured.

Modified continuum-based models have widely been presented for the vibration, bending and instability analyses of nanotubes. In one pioneering study, Zhang et al. (2005) presented a nonlocal model to analyse the free vibration of a system of two nanotubes. In another work, Reddy and Pang (2008) presented different scale-dependent beam models for the mechanical behaviours of nanotubes involving the static deformation, oscillation and stability responses; they utilised the nonlocal constitutive relation for developing the scale-dependent formulation. Malekzadeh and Shojaee (2013b) developed a nonlinear beam model with incorporation of both nonlocal and surface influences for analysing the large-amplitude oscillations of nanobeams; they presented numerical results based on both Euler–Bernoulli and Timoshenko theories of beams. Moreover, Malekzadeh and Shojaee (2013a) analysed the static stability of quadrilateral laminated sheets made of several layers reinforced with carbon nanotubes; they used a first-order theory of shear deformations to model the quadrilateral laminated sheet. Khaniki et al. (2018) also developed a two-phase scale-dependent model for dynamics of nanoscale beams; the nanosystem was embedded in a varying elastic medium. Aydogdu and Filiz ( 2011) proposed a scale-dependent model for mass nanosensors using nanotubes; the axial vibration of carbon nanotubes was exploited for mass detection at nanoscales. In addition, Aydogdu (2014) employed the nonlocal elasticity for analysing axial wave propagations in multi-walled nanotubes; the effects of van der Waals forces between various walls on the wave propagation were captured via an analytical model. In another study, Malekzadeh et al. (2014) investigated the free vibration of a skew small-scale plate with large displacements capturing size effects; surface effects were also taken into consideration in the model. Setoodeh and Afrahim (2014) utilised the strain gradient theory to explore the large-amplitude dynamics of microscale pipes conveying fluid; in the formulation, it was assumed that the pipe was made of functionally graded materials. More recently, Li et al. (2016) analysed the wave dispersion in nanotubes with viscoelastic properties via a nonlocal strain gradient theory (NSGT).

In addition to pure nanotube systems, the mechanics of fluid-conveying nanotubes has attracted noticeable attention in the literature (Dai et al. 2015; Wang et al. 2010). Understanding the mechanical behaviour of these systems is important in applications such as drug delivery systems and microfluidics-based devices. Although some valuable research works have been performed on the fluid-conveying nanotubes (Ansari et al. 2016; Maraghi et al. 2013; Soltani et al. 2010; Zeighampour and Beni 2014), further investigation is required to understand the large-amplitude dynamics of nanotubes conveying nanofluid since the majority of previously published works are restricted to small deformations. In addition, for the sake of simplification, only transverse motion has been analysed. Furthermore, to the best of our knowledge, modal interactions and energy transfer between different modes of fluid-conveying nanotubes have not been examined yet. In the present paper, an advanced scale-dependent model is presented for the frequency response of a nanotube with large amplitudes of vibrations. The elastic nanotube is used to convey fluid flow. The Beskok–Karniadakis approach is implemented to consider slip boundary conditions on the nonlinear behaviour. The NSGT, Galerkin’s approach and continuation scheme are, respectively, utilised to derive, discretise and solve the motion equations. The frequency–amplitude plots are constructed for studying the possibility of energy transfer between modes together with modal interaction in both supercritical and subcritical regimes.

2 A NSGT-based model

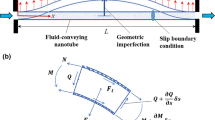
To develop a continuum model, a single nanotube of a high length-to-thickness ratio is taken into account as shown in Fig. 1. The nanotube is used to convey fluid flow at nanoscales. It is assumed that the tube is perfectly straight. In addition, there is no internal friction in both the fluid and solid parts. The length, mass per length and diameter of the nanotube are, respectively, indicated by L, m and do. Furthermore, M is utilised to indicate the mass per length of the nanofluid. For the displacement components of the tube, we assume that (u, w) = (axial displacement, transverse displacement). It is assumed that the effects of shear deformation are negligible. In addition, the tube cross-section is constant in this analysis. Only geometrical nonlinearity caused by the stretching influence of the tube centreline is captured. Using Euler–Bernoulli theory and incorporating the geometrical nonlinearity, the strain is

$$\varepsilon_{xx} = \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} - z\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right).$$
(1)
Fig. 1
figure 1

A NSGT nanotube conveying fluid subject to a distributed load

Full size image

In reality, taking into account the effects of nonlinearity is important to develop precise modelling (Ghayesh and Farokhi 2015a; Gholipour et al. 2018a, b; Farajpour et al. 2018e; Ghayesh et al. 2019).

The force and couple resultants related to the total stress \((\sigma_{xx}^{(tot)} )\) are as

$$N_{xx} = \int\limits_{A} {\sigma_{xx}^{(tot)} dA} , \, M_{xx} = \int\limits_{A} {z\sigma_{xx}^{(tot)} dA} .$$
(2)

Using the NSGT, one can express the total stress in terms of the strain as.

$$\sigma_{xx}^{(tot)} - \left( {e_{0} a} \right)^{2} \nabla^{2} \sigma_{xx}^{(tot)} = E\left( {1 - l_{sg}^{2} \nabla^{2} } \right)\left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right] - zE\left( {1 - l_{sg}^{2} \nabla^{2} } \right)\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right),$$
(3)

in which \(\nabla^{2}\), \(l_{sg}^{{}}\), E, e0 and a are the Laplacian operator, strain gradient parameter, elasticity constant, calibration coefficient and internal characteristic size, respectively (Farajpour et al. 2018a; Ghayesh and Farajpour 2018a, 2019). In view of the above constitutive equation (i.e. Eq. (3)), the following relations are obtained from Eq. (2)

$$N_{xx} = EA\left[ {\frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial u}{{\partial x}}} \right] - EAl_{sg}^{2} \nabla^{2} \left[ {\frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial u}{{\partial x}}} \right] + \left( {e_{0} a} \right)^{2} \nabla^{2} N_{xx} ,$$
(4)
$$M_{xx} = - EI\frac{{\partial^{2} w}}{{\partial x^{2} }} + EIl_{sg}^{2} \nabla^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {e_{0} a} \right)^{2} \nabla^{2} M_{xx} ,$$
(5)

where I denotes the second moment area. Let us indicate the classical and higher-order stresses by \(\sigma_{xx}\) and \(\sigma_{xx}^{(1)}\), respectively (Farajpour et al. 2019a; Lim et al. 2015). For the strain energy (\(\Pi_{s}\)), one can write

$$\begin{aligned} \delta \Pi_{s} & = \int\limits_{0}^{L} {\int\limits_{A} {\left( {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{xx}^{(1)} \frac{\partial }{\partial x}\delta \varepsilon_{xx} } \right)dAdx} } \\ & = \left[ {\int\limits_{A} {\sigma_{xx}^{(1)} \delta \varepsilon_{xx} dA} } \right]_{0}^{L} + \int\limits_{0}^{L} {\int\limits_{A} {\sigma_{xx}^{(tot)} \delta \varepsilon_{xx} dAdx} } , \\ \end{aligned}$$
(6)

where

$$\sigma_{xx}^{(tot)} = \sigma_{xx} - \frac{{\partial \sigma_{xx}^{(1)} }}{\partial x},$$
(7)

Assuming U is the fluid velocity, the kinetic energy of the nanosystem (Tk) is (Ghayesh et al. 2018; Paidoussis 1998)

$$\begin{aligned} T_{k} & = \frac{1}{2}\int\limits_{0}^{L} {m\left( {\frac{\partial w}{{\partial t}}} \right)^{2} dx} + \frac{1}{2}\int\limits_{0}^{L} {m\left( {\frac{\partial u}{{\partial t}}} \right)^{2} dx} \\ & \quad + \frac{1}{2}\int\limits_{0}^{L} {M\left[ {\frac{\partial u}{{\partial t}} + \kappa_{v} U\left( {1 + \frac{\partial u}{{\partial x}}} \right)} \right]^{2} dx} + \frac{1}{2}\int\limits_{0}^{L} {M\left( {\frac{\partial w}{{\partial t}} + \kappa_{v} U\frac{\partial w}{{\partial x}}} \right)^{2} dx} . \\ \end{aligned}$$
(8)

Here a correction factor for the fluid velocity (\(\kappa_{v}\)) is utilised for capturing slip conditions at the wall. Using the Beskok–Karniadakis approach (Beskok and Karniadakis 1999), one obtains

$$\kappa_{v} = \left( {\lambda Kn + 1} \right)\left[ {\left( {\frac{4Kn}{{Kn + 1}}} \right)\left( {\frac{{2 - \sigma_{v} }}{{\sigma_{v} }}} \right) + 1} \right],$$
(9)

where

$$\lambda = \frac{{2\lambda_{0} }}{\pi }\tan^{ - 1} \left[ {\alpha_{0} \left( {Kn} \right)^{{\alpha_{1} }} } \right],$$
(10)

in which Kn is the Knudsen number. For nanotubes, it is commonly assumed that \(\sigma_{v} = 0.7\), \(\alpha_{0} = 4\), \(\alpha_{1} = 0.4\) and \(\lambda_{0} = {{64} \mathord{\left/ {\vphantom {{64} {15\pi }}} \right. \kern-\nulldelimiterspace} {15\pi }}\). Assuming the amplitude F(x) and frequency \(\omega\) for the applied load, the external work is given by

$$\delta W_{q} = \int_{0}^{L} {q\delta w\,\,\text{d} x} .$$
(11)

where

$$q = F\left( x \right)\,\cos \left( {\omega \,t} \right).$$
(12)

For deriving the motion equations, Hamilton’s principle is employed as follows

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta W_{q} + \delta T_{k} - \delta \Pi_{s} } \right)\text{d} t} = 0.$$
(13)

Substituting Eqs. (6), (8) and (11) into the above principle, one can obtain

$$\frac{{\partial N_{xx} }}{\partial x} - \left( {\left( {m + M} \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{2} u}}{\partial t\partial x} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }}} \right) = 0,$$
(14)
$$\frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left( {N_{xx} \frac{\partial w}{{\partial x}}} \right) + F\left( x \right)\cos \left( {\omega t} \right) - \left( {\left( {m + M} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{2} w}}{\partial t\partial x} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) = 0.$$
(15)

Using the above equations (i.e. Eqs. (14) and (15)) together with Eqs. (4) and (5), the motion equations are derived as

$$\begin{aligned} & EA\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) - EAl_{sg}^{2} \nabla^{2} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ & = \left( {m + M} \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{2} u}}{\partial t\partial x} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} \\ & \quad - \left( {e_{0} a} \right)^{2} \nabla^{2} \left[ {\left( {m + M} \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{2} u}}{\partial t\partial x} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }}} \right], \\ \end{aligned}$$
(16)
$$\begin{aligned} & - EI\frac{{\partial^{4} w}}{{\partial x^{4} }} + EIl_{sg}^{2} \nabla^{2} \frac{{\partial^{4} w}}{{\partial x^{4} }} + F\left( x \right)\cos \left( {\omega t} \right) - \left( {e_{0} a} \right)^{2} \cos \left( {\omega t} \right)\nabla^{2} F\left( x \right) \\ & + EA\frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right] + EA\frac{\partial w}{{\partial x}}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ & - l_{sg}^{2} EA\frac{{\partial^{2} w}}{{\partial x^{2} }}\nabla^{2} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right] - l_{sg}^{2} EA\frac{\partial w}{{\partial x}}\nabla^{2} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ & + \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {\left( {m + M} \right)\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{3} u}}{{\partial t\partial x^{2} }} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right] \\ & + \left( {e_{0} a} \right)^{2} \frac{\partial w}{{\partial x}}\left[ {\left( {m + M} \right)\frac{{\partial^{4} u}}{{\partial x^{2} \partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{4} u}}{{\partial t\partial x^{3} }} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }}} \right] \\ & - \left( {e_{0} a} \right)^{2} \nabla^{2} \left\{ {EA\frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right] + EA\frac{\partial w}{{\partial x}}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right. \\ & - l_{sg}^{2} EA\frac{{\partial^{2} w}}{{\partial x^{2} }}\nabla^{2} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right] - l_{sg}^{2} EA\frac{\partial w}{{\partial x}}\nabla^{2} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ & + \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {\left( {m + M} \right)\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{3} u}}{{\partial t\partial x^{2} }} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right] \\ & \left. { + \left( {e_{0} a} \right)^{2} \frac{\partial w}{{\partial x}}\left[ {\left( {m + M} \right)\frac{{\partial^{4} u}}{{\partial x^{2} \partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{4} u}}{{\partial t\partial x^{3} }} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }}} \right]} \right\} \\ & = \left( {m + M} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{2} w}}{\partial t\partial x} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad - \left( {e_{0} a} \right)^{2} \nabla^{2} \left[ {\left( {m + M} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2M\kappa_{v} U\frac{{\partial^{2} w}}{\partial t\partial x} + M\kappa_{v}^{2} U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right]. \\ \end{aligned}$$
(17)

Now without losing the generality, a set of dimensionless parameters is utilised as follows

$$\begin{aligned} & u^{ * } = \frac{u}{{d_{o} }},{\text{ }}w^{ * } = \frac{w}{{d_{o} }},{\text{ }}x^{ * } = \frac{x}{L},{\text{ }}\chi _{{sg}} = \frac{{l_{{sg}} }}{L}, \\ & \Xi = \frac{{AL^{2} }}{I},{\text{ }}\chi _{{nl}} = \frac{{e_{0} a}}{L},{\text{ }}s = \frac{L}{{d_{o} }},{\text{ }}\bar{M} = \frac{M}{{M + m}}, \\ & \omega ^{ * } = \sqrt {\frac{{L^{4} \left( {m + M} \right)}}{{EI}}} \omega ,{\text{ }}t^{ * } = \frac{t}{{L^{2} }}\sqrt {\frac{{EI}}{{m + M}}} , \\ & U^{ * } = \sqrt {\frac{M}{{EI}}} UL,{\text{ }}F^{ * } = \frac{{FL^{4} }}{{EId_{o} }},{\text{ }}\bar{\nabla }^{2} = \frac{{\partial ^{2} }}{{\partial x^{{ * 2}} }}, \\ \end{aligned}$$
(18)

Here \(\bar{\nabla }^{2}\) denotes the dimensionless Laplacian operator. Employing Eq. (18) together with Eqs. (16) and (17), the dimensionless motion equations are derived as

$$\begin{aligned} & \frac{{\partial^{2} u}}{{\partial t^{2} }} + 2\kappa_{v} \sqrt {\bar{M}} U\frac{{\partial^{2} u}}{\partial t\partial x} + \kappa_{v}^{2} U^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} \\ & - \chi_{nl}^{2} \left( {\frac{{\partial^{4} u}}{{\partial x^{2} \partial t^{2} }} + 2\kappa_{v} \sqrt {\bar{M}} U\frac{{\partial^{4} u}}{{\partial t\partial x^{3} }} + \kappa_{v}^{2} U^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }}} \right) \\ & - \Xi \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{1}{s}\frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \Xi \chi_{sg}^{2} \left( {\frac{{\partial^{4} u}}{{\partial x^{4} }} + \frac{3}{s}\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{1}{s}\frac{\partial w}{{\partial x}}\frac{{\partial^{4} w}}{{\partial x^{4} }}} \right) = 0, \\ \end{aligned}$$
(19)
$$\begin{aligned} & \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\kappa_{v} \sqrt {\bar{M}} U\frac{{\partial^{2} w}}{\partial t\partial x} + \kappa_{v}^{2} U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & - \chi_{nl}^{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} + 2\kappa_{v} \sqrt {\bar{M}} U\frac{{\partial^{4} w}}{{\partial t\partial x^{3} }} + \kappa_{v}^{2} U^{2} \frac{{\partial^{4} w}}{{\partial x^{4} }}} \right) \\ & + \frac{{\partial^{4} w}}{{\partial x^{4} }} - \chi_{sg}^{2} \frac{{\partial^{6} w}}{{\partial x^{6} }} - F_{1} \cos \left( {\omega t} \right) - \frac{\Xi }{{s^{2} }}\left\{ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {s\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right]} \right. \\ & + \frac{\partial w}{{\partial x}}\left( {s\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) - \chi_{sg}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {s\frac{{\partial^{3} u}}{{\partial x^{3} }} + \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right] \\ & - \chi_{sg}^{2} \frac{\partial w}{{\partial x}}\left[ {s\frac{{\partial^{4} u}}{{\partial x^{4} }} + 3\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{4} w}}{{\partial x^{4} }}} \right] \\ & + \frac{s}{\Xi }\chi_{nl}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} + 2\kappa_{v} \sqrt {\bar{M}} U\frac{{\partial^{3} u}}{{\partial t\partial x^{2} }} + \kappa_{v}^{2} U^{2} \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right] \\ &\left. { + \frac{s}{\Xi }\chi_{nl}^{2} \frac{\partial w}{{\partial x}}\left[ {\frac{{\partial^{4} u}}{{\partial x^{2} \partial t^{2} }} + 2\kappa_{v} \sqrt {\bar{M}} U\frac{{\partial^{4} u}}{{\partial t\partial x^{3} }} + \kappa_{v}^{2} U^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }}} \right]} \right\} \\ & + \frac{\Xi }{{s^{2} }}\chi_{nl}^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}\left\{ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {s\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right] + \frac{\partial w}{{\partial x}}\left( {s\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right. \\ & - \chi_{sg}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {s\frac{{\partial^{3} u}}{{\partial x^{3} }} + \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right] \\ & - \chi_{sg}^{2} \frac{\partial w}{{\partial x}}\left( {s\frac{{\partial^{4} u}}{{\partial x^{4} }} + 3\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{4} w}}{{\partial x^{4} }}} \right) \\ & + \frac{s}{\Xi }\chi_{nl}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} + 2\kappa_{v} \sqrt {\bar{M}} U\frac{{\partial^{3} u}}{{\partial t\partial x^{2} }} + \kappa_{v}^{2} U^{2} \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right] \\ &\left. { + \frac{s}{\Xi }\chi_{nl}^{2} \frac{\partial w}{{\partial x}}\left[ {\frac{{\partial^{4} u}}{{\partial x^{2} \partial t^{2} }} + 2\kappa_{v} \sqrt {\bar{M}} U\frac{{\partial^{4} u}}{{\partial t\partial x^{3} }} + \kappa_{v}^{2} U^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }}} \right]} \right\} = 0, \\ \end{aligned}$$
(20)

in which “*” is dropped in Eqs. (19) and (20) for the sake of convenience.

3 Galerkin-based discretisation and solution technique

A Galerkin-based discretisation is performed in this section using the following expressions for the displacement components

$$\left\{ {\begin{array}{*{20}c} u \\ w \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\sum\nolimits_{k = 1}^{{N_{\zeta } }} {r_{k} (t)\zeta_{k} (x)\,} } \\ {\sum\nolimits_{k = 1}^{{N_{\eta } }} {q_{k} (t)\eta_{k} (x)} } \\ \end{array} } \right\},$$
(21)

where rk and qk are generalised coordinates whereas \(\zeta_{k}\) and \(\eta_{k}\) are trial functions (Ghayesh 2018b, c; Farokhi et al. 2017; Farajpour et al. 2018f; Ghayesh and Farokhi 2015b). Assuming clamped–clamped boundary conditions and using Eq. (21), one can obtain

$$\begin{aligned} & \sum\limits_{k = 1}^{{N_\zeta }} {{{\ddot r}_k}\left( {\int\limits_0^1 {{\zeta _i}{\zeta _k}dx} } \right)} + 2{\kappa _v}\sqrt {\bar M} U\sum\limits_{k = 1}^{{N_\zeta }} {{{\dot r}_k}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\zeta _k}} \right)}^\prime }dx} } \right)} \\ &\quad + \kappa _v^2{U^2}\sum\limits_{k = 1}^{{N_\zeta }} {{r_k}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\zeta _k}} \right)}^{\prime \prime }}dx} } \right)} - \chi _{nl}^2\left[ {\sum\limits_{k = 1}^{{N_\zeta }} {{{\ddot r}_k}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\zeta _k}} \right)}^{\prime \prime }}dx} } \right)} } \right. \\ & \left. { + 2{\kappa _v}\sqrt {\bar M} U\sum\limits_{k = 1}^{{N_\zeta }} {{{\dot r}_k}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\zeta _k}} \right)}^{\prime\prime\prime} }dx} } \right)} + \kappa _v^2{U^2}\sum\limits_{k = 1}^{{N_\zeta }} {{r_k}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\zeta _k}} \right)}^{\prime\prime\prime\prime} } dx} } \right)} } \right] \\ & - \Xi \left[ {\sum\limits_{k = 1}^{{N_\zeta }} {{r_k}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\zeta _k}} \right)}^{\prime \prime }}dx} } \right)} + \frac{1}{s}\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\eta _j}} \right)}^{\prime \prime }}{{\left( {{\eta _k}} \right)}^\prime }dx} } \right)} } } \right] \\ & + \Xi \chi _{sg}^2\left[ {\sum\limits_{k = 1}^{{N_\zeta }} {{r_k}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\zeta _k}} \right)}^{\prime\prime\prime\prime} } dx} } \right)} + \frac{3}{s}\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\eta _j}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _k}} \right)}^{\prime \prime }}dx} } \right)} } } \right. \\ & \left. { + \frac{1}{s}\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}\left( {\int\limits_0^1 {{\zeta _i}{{\left( {{\eta _j}} \right)}^{\prime\prime\prime\prime} } {{\left( {{\eta _k}} \right)}^\prime }dx} } \right)} } } \right] = 0,\end{aligned} $$
(22)
$$\begin{aligned} & \sum\limits_{k = 1}^{{N_\eta }} {{{\ddot q}_k}\left( {\int\limits_0^1 {{\eta _i}{\eta _k}dx} } \right)} + 2{\kappa _v}\sqrt {\bar M} U\sum\limits_{k = 1}^{{N_\eta }} {{{\dot q}_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _k}} \right)}^\prime }dx} } \right)} \\ & + \kappa _v^2{U^2}\sum\limits_{k = 1}^{{N_\eta }} {{q_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _k}} \right)}^{\prime \prime }}dx} } \right)} - \chi _{nl}^2\left[ {\sum\limits_{k = 1}^{{N_\eta }} {{{\ddot q}_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _k}} \right)}^{\prime \prime }}dx} } \right)} } \right. \\ & \left. { + 2{\kappa _v}\sqrt {\bar M} U\sum\limits_{k = 1}^{{N_\eta }} {{{\dot q}_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _k}} \right)}^{\prime \prime \prime }}dx} } \right)} + \kappa _v^2{U^2}\sum\limits_{k = 1}^{{N_\eta }} {{q_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _k}} \right)}^{\prime\prime\prime\prime} } dx} } \right)} } \right] \\ & + \sum\limits_{k = 1}^{{N_\eta }} {{q_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _k}} \right)}^{\prime\prime\prime\prime} } dx} } \right)} - \chi _{sg}^2\sum\limits_{k = 1}^{{N_\eta }} {{q_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _k}} \right)}^{(6)}}dx} } \right)} - \left( {\int\limits_0^1 {{\eta _i}dx} } \right){F_1}\cos \left( {\omega t} \right) \\ & - \frac{\Xi }{{{s^2}}}\left\{ {s\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\zeta _k}} \right)}^\prime }{{\left( {{\eta _l}} \right)}^{\prime \prime }}dx} } \right)} } + \frac{1}{2}\sum\limits_{j = 1}^{{N_\zeta }} {\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}{r_j}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _j}} \right)}^\prime }{{\left( {{\eta _k}} \right)}^\prime }{{\left( {{\eta _l}} \right)}^{\prime \prime }}dx} } \right)} } } } \right. \\ & + s\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\zeta _k}} \right)}^{\prime \prime }}{{\left( {{\eta _l}} \right)}^\prime }dx} } \right)} } + \sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{q_k}{q_j}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _j}} \right)}^{\prime \prime }}{{\left( {{\eta _k}} \right)}^\prime }{{\left( {{\eta _l}} \right)}^\prime }dx} } \right)} } } \\ & - \chi _{sg}^2\left[ {s\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\zeta _k}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _l}} \right)}^{\prime \prime }}dx} } \right) + \sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}{q_l}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _l}} \right)}^{\prime \prime }}{{\left( {{\eta _j}} \right)}^{\prime \prime }}{{\left( {{\eta _k}} \right)}^{\prime \prime }}dx} } \right)} } } } } } \right. \\ & \left. { + \sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}{q_l}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _l}} \right)}^{\prime \prime }}{{\left( {{\eta _j}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _k}} \right)}^\prime }dx} } \right)} } } } \right] - \chi _{sg}^2\left[ {s\sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\zeta }} {{r_k} \times {q_l}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _l}} \right)}^\prime }{{\left( {{\zeta _k}} \right)}^{\prime\prime\prime\prime} } dx} } \right)} } } \right. \\ & \left. { + 3\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{q_k}{q_j}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _j}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _k}} \right)}^{\prime \prime }}{{\left( {{\eta _l}} \right)}^\prime }dx} } \right)} } } + \sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}{q_l}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _l}} \right)}^\prime }{{\left( {{\eta _j}} \right)}^{\prime\prime\prime\prime} } {{\left( {{\eta _k}} \right)}^\prime }dx} } \right)} } } } \right] \\ & + \frac{{s\chi _{nl}^2}}{\Xi }\left[ {\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{{\ddot r}_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\zeta _k}} \right)}^\prime }{{\left( {{\eta _l}} \right)}^{\prime \prime }}dx} } \right)} } + \kappa _v^2{U^2}\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\zeta _k}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _l}} \right)}^{\prime \prime }}dx} } \right)} } } \right. \\ & \left. { + 2{\kappa _v}\sqrt {\bar M} U\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{{\dot r}_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\zeta _k}} \right)}^{\prime \prime }}{{\left( {{\eta _l}} \right)}^{\prime \prime }}dx} } \right)} } } \right] + \frac{{s\chi _{nl}^2}}{\Xi }\left[ {\sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\zeta }} {{{\ddot r}_k}{q_l}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _l}} \right)}^\prime }{{\left( {{\zeta _k}} \right)}^{\prime \prime }}dx} } \right)} } } \right. \\ & \left. {\left. { + \kappa _v^2{U^2}\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\zeta _k}} \right)}^{\prime\prime\prime\prime} } {{\left( {{\eta _l}} \right)}^\prime }dx} } \right)} } + 2{\kappa _v}\sqrt {\bar M} U\sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\zeta }} {{{\dot r}_k}{q_l}\left( {\int\limits_0^1 {{\eta _i}{{\left( {{\eta _l}} \right)}^\prime }{{\left( {{\zeta _k}} \right)}^{\prime \prime \prime }}dx} } \right)} } } \right]} \right\} \\ & + \frac{{\Xi \chi _{nl}^2}}{{{s^2}}}\int\limits_0^1 {\left\{ {{\eta _i}\left[ {s\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}{{\left( {{\zeta _k}} \right)}^{\prime \prime }}{{\left( {{\eta _l}} \right)}^\prime }} } + \sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{q_k}{q_j}{{\left( {{\eta _j}} \right)}^{\prime \prime }}{{\left( {{\eta _k}} \right)}^\prime }{{\left( {{\eta _l}} \right)}^\prime }} } } } \right.} \right.} \\ & + s\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}{{\left( {{\zeta _k}} \right)}^\prime }{{\left( {{\eta _l}} \right)}^{\prime \prime }}} } + \frac{1}{2}\sum\limits_{j = 1}^{{N_\zeta }} {\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}{r_j}{{\left( {{\eta _j}} \right)}^\prime }{{\left( {{\eta _k}} \right)}^\prime }{{\left( {{\eta _l}} \right)}^{\prime \prime }}} } } \\ & - \chi _{sg}^2\left( {s\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}{{\left( {{\zeta _k}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _l}} \right)}^{\prime \prime }} + \sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}{q_l}{{\left( {{\eta _l}} \right)}^{\prime \prime }}{{\left( {{\eta _j}} \right)}^{\prime \prime }}{{\left( {{\eta _k}} \right)}^{\prime \prime }}} } } } } } \right. \\ & \left. { + \sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}{q_l}{{\left( {{\eta _l}} \right)}^{\prime \prime }}{{\left( {{\eta _j}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _k}} \right)}^\prime }} } } } \right) - \chi _{sg}^2\left( {s\sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\zeta }} {{r_k}{q_l}{{\left( {{\eta _l}} \right)}^\prime }{{\left( {{\zeta _k}} \right)}^{\prime\prime\prime\prime} } } } } \right. \\ & \left. { + 3\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{q_k}{q_j}{{\left( {{\eta _j}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _k}} \right)}^{\prime \prime }}{{\left( {{\eta _l}} \right)}^\prime }} } } + \sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{j = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\eta }} {{q_k}{q_j}{q_l}{{\left( {{\eta _l}} \right)}^\prime }{{\left( {{\eta _j}} \right)}^{\prime\prime\prime\prime} } {{\left( {{\eta _k}} \right)}^\prime }} } } } \right) \\ & + \frac{{s\chi _{nl}^2}}{\Xi }\left( {\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{{\ddot r}_k}{{\left( {{\zeta _k}} \right)}^\prime }{{\left( {{\eta _l}} \right)}^{\prime \prime }} + 2{\kappa _v}\sqrt {\bar M} U\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{{\dot r}_k}{{\left( {{\zeta _k}} \right)}^{\prime \prime }}{{\left( {{\eta _l}} \right)}^{\prime \prime }}} } } } } \right. \\ & \left. { + \kappa _v^2{U^2}\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}{{\left( {{\zeta _k}} \right)}^{\prime \prime \prime }}{{\left( {{\eta _l}} \right)}^{\prime \prime }}} } } \right) + \frac{{s\chi _{nl}^2}}{\Xi }\left( {\sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\zeta }} {{{\ddot r}_k}{q_l}{{\left( {{\eta _l}} \right)}^\prime }{{\left( {{\zeta _k}} \right)}^{\prime \prime }}} } } \right. \\ & \left. {{{\left. {\left. { + 2{\kappa _v}\sqrt {\bar M} U \times \sum\limits_{l = 1}^{{N_\eta }} {\sum\limits_{k = 1}^{{N_\zeta }} {{{\dot r}_k}{q_l}{{\left( {{\eta _l}} \right)}^\prime }{{\left( {{\zeta _k}} \right)}^{\prime \prime \prime }}} } + \kappa _v^2{U^2}\sum\limits_{k = 1}^{{N_\zeta }} {\sum\limits_{l = 1}^{{N_\eta }} {{q_l}{r_k}{{\left( {{\zeta _k}} \right)}^{\prime\prime\prime\prime} } {{\left( {{\eta _l}} \right)}^\prime }} } } \right)} \right]}^{\prime \prime }}} \right\}dx = 0. \end{aligned}$$
(23)

Equations (22) and (23) indicate a set of time-dependent ordinary differential equations, which can be solved via a continuation approach. It is worth mentioning that for developing a numerical solution, ten trial functions are assumed.

4 Results and discussion

For constructing the frequency-response curves of the fluid-conveying nanosystem incorporating both stress nonlocality and strain gradients, the tube material and geometrical parameters are assumed as \(\rho\) = 1024 kg/m3, v = 0.3, E = 610 MPa, h = 66.0 nm and Ro = 290.5 nm where h, \(\rho\) and Ro are respectively the nanotube thickness, density and outer radius. In the numerical solution, a dimensionless damping coefficient of 0.25 is added for both u and w motions. The focus of this paper is not on the influence of viscoelastic medium. The system dimensionless parameters are \(\kappa_{v}\) = 1.0788, \(\bar{M}\) = 0.5915, \(\chi_{sg} = 0.04\), \(\chi_{nl} = 0.09\), \(\Xi\) = 4006.9411 and s = 20.0, unless otherwise specifically mentioned.

The change of maximum transverse and axial displacements versus the frequency ratio (the ratio of excitation frequency to fundamental natural one) is plotted in Fig. 2 for F1 = 2.0 and U = 3.25. The flow regime is subcritical since the flow speed is less than the critical one associated with buckling (Ucr = 5.1862). Both unstable and stable branches are indicated in the figure. Two bifurcation points at ω/ω1 = 1.1608 and 1.0378 are seen for the fluid-conveying nanosystem. Moreover, it is found that the nonlinearity of the nanosystem is of hardening type. In addition, modal interactions are found in the nonlinear response.

Fig. 2
figure 2

Change of maximum transverse and axial displacements versus the frequency ratio in the subcritical flow regime for F1 = 2.0 and U = 3.25; awmax at x = 0.5; bumax at x = 0.657; ω1 = 15.5031

Full size image

In order to study the modal interaction in the nonlinear dynamics of the fluid-conveying nanosystem, the change of first four generalised coordinates of the transverse motion versus the frequency ratio is plotted in Fig. 3. Strong modal interactions as well as energy transfer between modes are observed in the nonlinear response of the nanosystem, especially for higher generalised coordinates.

Fig. 3
figure 3

Change of aq1, bq2, cq3 and dq4 versus the ratio of the excitation frequency to the natural one in the subcritical flow regime

Full size image

The detailed motion characteristics of the nanotube of Fig. 2 are shown in Figs. 4 and 5 for ω/ω1 = 1.0522 and ω/ω1 = 1.1608, respectively; the former case is the one when the modal interactions are strongest. Time histories and phase-plane plots for both types of motions are plotted. It should be noticed that tn denotes normalised time with respect to the period of oscillation. It can be concluded that in the presence of strong modal interactions, the motion characteristics of the nanotube are different, especially for the axial motion.

Fig. 4
figure 4

Detailed motion characteristics of the system of Fig. 2 at ω/ω1 = 1.0522 (i.e. when the modal interactions are strongest). a, bw versus tn for x = 0.5 and u versus tn for x = 0.657, respectively; c, ddw/dt versus w for x = 0.5 and du/dt versus u for x = 0.657, respectively

Full size image
Fig. 5
figure 5

Detailed motion characteristics of the system of Fig. 2 at ω/ω1 = 1.1608 (i.e. at peak oscillation amplitude). a, bw versus tn for x = 0.5 and u versus tn for x = 0.657, respectively; c, ddw/dt versus w for x = 0.5 and du/dt versus u for x = 0.657, respectively

Full size image

The change of maximum transverse and axial displacements versus the excitation frequency is plotted in Fig. 6 for various fluid speeds in the subcritical regime. The forcing amplitude, speed correction factor, nonlocal coefficient and strain gradient coefficient are set to F1 = 1.5, κs = 1.0788, χnl = 0.09, and χsg = 0.04, respectively. It is found that higher fluid speeds yield higher peak amplitudes but lower resonance frequencies for both motion types of the fluid-conveying nanosystem.

Fig. 6
figure 6

Change of maximum transverse and axial displacements versus the excitation frequency for different fluid speeds in subcritical flow regime; awmax at x = 0.5; bumax at x = 0.657

Full size image

Figure 7 is plotted for comparing the nanosystem frequency response for slip conditions with that calculated using no-slip boundary conditions. The forcing amplitude, speed correction factor, fluid speed, nonlocal coefficient and strain gradient coefficient are set to F1 = 2, κs = 1.0788, U = 3.5, χnl = 0.09, and χsg = 0.04, respectively. The no-slip condition yields overestimated results for both resonance frequency and peak amplitude of the nanotube. Figure 8 also compares the slip and no-slip boundary conditions for a higher fluid speed (U = 4.5) in the subcritical regime. The amplitude of the external distributed loading is F1 = 1.2. Comparing Figs. 7 and 8 indicates that the effect of slip conditions on the subcritical frequency response increases as the flow speed increases.

Fig. 7
figure 7

Effects of slip boundary conditions on the forced oscillation when U = 3.5 (subcritical flow regime); awmax at x = 0.5; bumax at x = 0.657

Full size image
Fig. 8
figure 8

Effects of slip boundary conditions on the forced oscillation when U = 4.5 (subcritical flow regime); awmax at x = 0.5; bumax at x = 0.657

Full size image

The change of maximum transverse and axial displacements versus the excitation frequency is plotted in Fig. 9 for both the classical theory of beams and the NSGT-based model. For the classical theory of beams, both scale coefficients are zero (i.e. χnl = χsg = 0) whereas the scale coefficients are as χnl = 0.09, χsg = 0.04 for the NSGT-based model. The speed correction factor and forcing amplitude are κs = 1.0788 and F1 = 2.5, respectively. The NSGT yields a relatively high peak amplitude but a low resonance frequency, compared to the classical theory. This is due to the high value of nonlocal coefficient compared to the strain gradient coefficient. In fact, since nonlocal effects are dominant for this case, the total structural stiffness of NSGT nanotubes is less than that calculated via the classical theory. This results in a lower resonance frequency as well as a higher peak amplitude for the nanosystem.

Fig. 9
figure 9

Change of maximum transverse and axial displacements versus the excitation frequency obtained via the nonlocal strain gradient theory and classical theory for U = 3.0 (subcritical flow regime); awmax at x = 0.5; bumax at x = 0.657

Full size image

Figure 10 illustrates the change of maximum transverse and axial displacements versus the frequency ratio for F1 = 1.0, U = 6.15, κs = 1.0788, χnl = 0.09, and χsg = 0.04; the fundamental frequency is ω1 = 12.9072. It should be noticed that this time, the fluid speed is higher than the critical one (i.e. supercritical regime). The frequency response is of softening type containing two bifurcation points at ω/ω1 = 0.9706 and 0.6705. This is in contrast to the subcritical frequency response in which a hardening nonlinearity is observed. Moreover, modal interactions are found in the nonlinear response for both motion types. Figure 11 gives the frequency response of the tube for the first four generalised coordinates. Strong modal interactions as well as energy transfer between modes are observed in the nonlinear response, especially for higher generalised coordinates. Furthermore, the detailed motion characteristics of the nanosystem of Fig. 10 at ω/ω1 = 0.6705 (i.e. at peak oscillation amplitude) are indicated in Fig. 12; phase-plane plots and time histories for both motion types are shown.

Fig. 10
figure 10

Change of maximum transverse and axial displacements versus the excitation frequency in the supercritical flow regime; awmax at x = 0.5; bumax at x = 0.657

Full size image
Fig. 11
figure 11

Change of aq1, bq2, cq3 and dq4 versus the ratio of the excitation frequency to the natural one in the supercritical flow regime

Full size image
Fig. 12
figure 12

Detailed motion characteristics of the nanosystem of Fig. 10 at ω/ω1 = 0.6705. a, bw versus tn for x = 0.5 and u versus tn for x = 0.657, respectively; c, ddw/dt versus w for x = 0.5 and du/dt versus u for x = 0.657, respectively

Full size image

Figure 13 depicts the change of maximum transverse and axial displacements versus the frequency ratio for F1 = 1.0, κs = 1.0788, χnl = 0.09, and χsg = 0.04. In contrast to the subcritical regime in which increasing U decreases natural frequency, in supercritical regime increasing U increases natural frequency (shifts frequency response to the right). Figure 14 compares the frequency responses using no-slip and slip conditions in the supercritical regimes for χnl = 0.09, χsg = 0.04, and F1 = 0.8. The no-slip condition underestimates both peak amplitude and resonance frequency in the supercritical regime. This is in contrast to the subcritical frequency response in which the no-slip condition yields overestimated results for both the resonance frequency and peak amplitude.

Fig. 13
figure 13

Change of maximum transverse and axial displacements versus the excitation frequency for different fluid speeds in supercritical flow regime; awmax at x = 0.5; bumax at x = 0.657

Full size image
Fig. 14
figure 14

Effects of slip boundary conditions on the forced oscillation when U = 6.4 (supercritical flow regime); awmax at x = 0.5; bumax at x = 0.657

Full size image

5 Conclusions

The large-amplitude forced oscillations of nanotubes conveying fluid were analysed via a size-dependent coupled nonlinear model of beams. The proposed model contained two different size parameters, leading to a better simulation of size effects on the nonlinear oscillations. Both axial and transverse inertial terms were taken into consideration. To incorporate the mean free path of molecules at the tube/fluid interface, the Beskok–Karniadakis approach was implemented. The coupled nonlinear equations were finally obtained, discretised and solved via application of the NSGT, Galerkin’s technique and continuation method, respectively.

In the supercritical flow regime, the frequency response is of softening type containing two saddle-node bifurcations while the subcritical frequency response is of a hardening nonlinearity. When nonlocal influences are dominant, the total stiffness of NSGT nanotubes is less, and this leads to a lower resonance frequency and a higher peak amplitude for the nanosystem conveying fluid. Strong modal interactions as well as energy transfer between modes are observed in both flow regimes. In contrast to the subcritical regime in which higher fluid speeds yield a decrease in the natural frequency, in supercritical regime, the natural frequency increases with increasing fluid speed. Furthermore, no-slip boundary conditions lead to underestimated supercritical peak amplitudes and resonance frequencies for the NSGT nanotube whereas no-slip boundary conditions yield overestimated subcritical resonance frequencies and peak amplitudes.