1 Introduction

Thanks to the combination of reduced dimension, unique geometry and special lattice structure (Iijima 1991; Wong and Akinwande 2011), carbon nanotube (CNT) displays extraordinary mechanical and physical properties (Treacy et al. 1996; Hone 2001; Saito and Kataura 2001; Yakobson and Avouris 2001; Zhang et al. 2017) and promises an exciting potential for drug delivery (Bianco et al. 2005; Liu et al. 2009), nanosensory (Mubeen et al. 2007) and energy harvesting (Zhang et al. 2016). Underlying most of the applications, the behavior of conveying flow is fundamental. And when fluid flows through CNT, fascinating phenomena, such as vibration and pitchfork instability occur.

It is quite an attraction to study CNT conveying flow (CNTCF) and its theoretical model evolves as time elapses. The work of Yoon et al. (Yoon et al. 2005) directly introduced classical continuum theory into this field. They employed Euler–Bernoulli beam theory and plug flow to model CNT and the flow inside it, respectively, and investigated the vibrations with various flow velocities and the critical flow velocity. By considering viscosity and slip boundary condition, Khosravian et al. (Khosravian and Rafii-Tabar 2007) re-derived the force applied by the flow from Navier–Stokes (NS) equation. Compared with Yoon’s equation, Khosravian’s contained two more extra terms which were directly related to viscosity. To give CNT a more precise description, Khosravian et al. (Khosravian and Rafii-Tabar 2008) then took the shear effect and rotational inertia into account and employed Timoshenko beam theory to model CNTs. Although the critical flow velocity of Timoshenko’s model was smaller than that of Euler’s, the variance decreased with an increasing aspect ratio, which meant that Euler’s model was accurate enough if the aspect ratio of CNT was sufficiently big. At this stage, the theories which were usually used to study pipe conveying fluid were introduced into the research of CNTCF without modification.

It cannot be denied that classical continuum theory was accurate enough to be applied to studying pipe conveying flow in macroscale. However, it lacks descriptions of microstructure and long-range interaction, and thus is not good enough in the scale of CNT(s) (Askes and Aifantis 2011). Nonlocal continuum theory (Eringen 1983; Wang 2010; Li et al. 2015; Zhu and Li 2017c, d), which strengthened the classical one by taking small-scale effects into account, was widely accepted in study of nano-carbon materials (Lu et al. 2006; Wang et al. 2007; Wang and Varadan 2007; Wang and Liew 2007; Yang et al. 2014; Li et al. 2016; Zhu and Li 2017a, b). Inspired by this, Lee et al. (Lee and Chang 2008) added a term which represented the small-scale effects of CNT just like the one in the governing equations of CNT into the equation of fluid-conveying CNT. Based on Lee’s work, Soltani et al. (Soltani et al. 2010) and Hashemnia et al. (Hashemnia et al. 2011) added other terms on account of fluid viscosity and matrixes that CNT was embedded in. It was an inspiring step to introduce nonlocal continuum theory into this area. Unfortunately, the equation derived by Lee et al. however, was not justified (Tounsi et al. 2009). It seemed that Lee et al. used the equation of CNT without fluid rather than that with fluid to cancel out the second derivative of moment in the equation of motion. Tounsi et al. noticed this defect and obtained a new equation, which was widely recognized (Wang 2009; Liang and Su 2013).

So far, the work mentioned above only involved small-scale effects of CNT. It should not be neglected that the fluid inside CNT was confined in small scale, too. Considering this, Rashidi et al. (Rashidi et al. 2012) suggested employing Knudsen number (\(Kn\)) to model small-scale effects of the inside flow. Indeed, \(Kn\), which was often used to determine the flow regime (Karniadakis et al. 2005), was a non-dimensional parameter defined as the ratio of mean free path of fluid molecules to the diameter of CNT and could be considered an excellent index of scale. It could reach even beyond 0.3 in the case of CNT conveying water flow (Holt et al. 2006), where it fell into the slip flow regime and transition flow regime. Clearly, no-slip boundary condition was unjustified in such scale. Furthermore, both dynamic viscosity of fluid and slip velocity on the interface (Ali Beskok 1999) depended on \(Kn\). Rashidi et al. defined a factor named velocity correction factor (VCF), which is the ratio of the average velocity with and without considering \(Kn\), to correct the average velocity in the equation of motion obtained by Khosravian and Rafii-Tabar (2007). Then, they studied its first eigenfrequency and found an appreciable influence of \(Kn\). Inspired by the definition of VFC, Mirramezani and Mirdamadi (2012a) corrected the most basic equation of pipe conveying fluid (Paidoussis 2014) and found that an increasing \(Kn\) resulted in a decreasing critical flow velocity. Besides, they detected a coupled-mode flutter under clamped–pinned condition, if \(Kn\) was nonzero. Based on this, Kaviani and Mirdamadi (2012) studied the effects of \(Kn\) on viscosity employing Polard model and Roohi model, respectively. They reported that as \(Kn\) increased, representing a decreasing scale, the viscosity of fluid went down and VFC went up. As a result, the critical velocity decreased. On the other hand, we had learnt from the study of fluid-conveying pipe in macroscale (Guo et al. 2010; Hellum et al. 2010; Kutin and Bajsić 2014) that a parameter named momentum correction factor was needed when fluid with non-uniform velocity profiles flows inside the pipe, because there was a quadratic term of fluid velocity in the equation. This parameter in small scale was investigated by Sadeghi-goughari and Hosseini (Sadeghi-goughari and Hosseini 2015).

Hereafter, most of the work combining small-scale effects of both CNT and inside flow concerned complex beam model (Kiani 2017) or shell model (Zeighampour et al. 2017; Mahinzare et al. 2017), complicated geometry (such as multi-wall, bifurcation or multi-span) (Arani et al. 2015, 2016; Deng et al. 2017) and coupling with surroundings (such as matrixes, temperature and magnetic field) (Hosseini and Sadeghi-Goughari 2016; Askari and Esmailzadeh 2017; Sadeghi-Goughari et al. 2017). The fundamental effects of small scale of both CNT and fluid, nevertheless, received scant attention. It either neglected the effects of nonlocal parameter, or considered the effects of \(Kn\) not in a thorough way. The effects of effective viscosity and non-uniform flow, for example, were missing (and the resultant model, herein, is referred to as the ‘original model’). In the present work, we built an improved model of CNTCF by comprehensively considering small-scale effects of both CNT and inside flow, respectively, quantified by nonlocal parameter \(\xi\) and Knudsen number \(Kn\). The compatibility condition is extended from the interface of CNT and inside flow to the whole cross section of inside flow. Then by systematically considering all the factors related to \(Kn\), including effective viscosity, slip boundary condition and non-uniform flow profile, the governing equation is derived from nonlocal elastic theory and Navier–Stokes equation, which shows that the correction of flow velocity in viscosity terms should be taken into account as well. Besides the numerical results of eigenvalues and critical flow velocity, a formula of critical flow velocity is also obtained analytically.

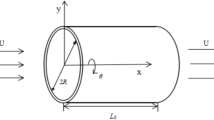
2 Equation of motion

2.1 Equation on lateral motions of nonlocal beams

For Euler–Bernoulli beam model with only distributed loads which herein indicate those applied by the inside flow, the equilibrium equation for lateral vibration can be expressed as

$${m_{\text{p}}}\frac{{{\partial ^2}w}}{{\partial {t^2}}}={F_{\text{f}}} - \frac{{{\partial ^2}M}}{{\partial {x^2}}},$$
(1)

where \({m_{\text{p}}}\) is linear density of CNT, \(w\) is lateral displacement, \({F_{\text{f}}}\) is fluid load, \(M\) is flexural moment, \(t\) is coordinate of time and \(x\) is axial coordinate.

Although nonlocal differential elastic models were reported to be approximate ones (Zhu and Li 2017c, d), considering their simplicity, a large amount of recent work, such as Tang and Yang (2018a), Bahaadini and Hosseini (2018), Zhang et al. (2018) and Oveissi and Ghassemi (2018), have been still based on them, which suggests that such models can still provide valuable references. Therefore, the Eringen nonlocal model (Eringen 1983) is employed in the present work to simplify the depiction, according to which stress is expressed as

$$\sigma ={\left( {{e_0}a} \right)^2}\frac{{{\partial ^2}\sigma }}{{\partial {x^2}}}+E\varepsilon ,$$
(2)

where \({e_0}\) is a constant depending on material, \(a\) is an internal characteristic length, \(E\) is Young’s modulus, and \(\varepsilon\) is strain. Combining (1) with (2), one can obtain

$${\text{EI}}\frac{{{\partial ^4}w}}{{\partial {x^4}}}+{m_{\text{p}}}\frac{{{\partial ^2}w}}{{\partial {t^2}}} - {F_{\text{f}}} - {\left( {{e_0}a} \right)^2}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left( {{m_{\text{p}}}\frac{{{\partial ^2}w}}{{\partial {t^2}}} - {F_{\text{f}}}} \right)=0,$$
(3)

where \(I\) is flexural inertia.

2.2 Small-scale effects of fluid

Under the continuum flow regime, the boundary condition of a domain is usually assumed approximately to be no-slip (Baudry et al. 2001; Lauga et al. 2007). To extend the validation of NS equation to transitional flow, the partial-slip boundary condition should be introduced. Based on the tangential momentum flux analysis near an isothermal surface (Thompson and Owens 1975; Ali Beskok 1997), a relation is obtained (Ali Beskok 1999)

$${v_{\text{s}}}=\frac{1}{2}\left( {{v_\lambda }+\left( {1 - {\sigma _{\text{v}}}} \right){v_\lambda }+{\sigma _{\text{v}}}{v_{\text{w}}}} \right),$$
(4)

where \({v_{\text{s}}}\) is the slip velocity near the wall, \({v_\lambda }\) is the tangential velocity one mean free path \(\lambda\) away from the wall, \({v_{\text{w}}}\) is the tangential velocity of the wall and \({\sigma _{\text{v}}}\) is tangential momentum accommodation coefficient which characterizes the exchange of momentum between fluid particles and wall. After expanding \({v_\lambda }\) at \({v_{\text{s}}}\) in Eq. (4), one obtains

$${v_s} - {v_w}=\frac{{2 - {\sigma _v}}}{{{\sigma _v}}}\left( {\lambda {{\left( {\frac{{\partial v}}{{\partial {\varvec{n}}}}} \right)}_s}+\frac{{{\lambda ^2}}}{2}{{\left( {\frac{{{\partial ^2}v}}{{\partial {{\varvec{n}}^2}}}} \right)}_s}+ \ldots } \right),$$
(5)

where \({\varvec{n}}\) is the normal vector of the well. In order to get a second-order slip boundary condition, the higher-order terms are cut off. Besides, a slip coefficient \(b\) is introduced to avoid the computational difficulties brought by the second-order derivative of \(v\). It is an empirical parameter and can be determined either by experiments or by data of linearized Boltzmann (Ohwada et al. 1989; Loyalka and Hamoodi 1990) or direct-simulation Monte Carlo method (Bird 1994). For fully developed flow in channels, \(b= - 1\). Considering that the wall does not move along the axial direction of CNT, i.e., \({v_{\text{w}}}=0\), the expression of slip velocity at boundary is (Ali Beskok 1999; Mirramezani and Mirdamadi 2012a)

$${v_{{\text{sl}}}}\left( {r=R} \right)=R\left( {\frac{{{\sigma _{\text{v}}} - 2}}{{{\sigma _{\text{v}}}}}} \right)\left( {\frac{{{K_{\text{n}}}}}{{1 - bKn}}} \right){\left( {\frac{{\partial {v_{{\text{sl}}}}}}{{\partial r}}} \right)_{r=R}},$$
(6)

where \({v_{{\text{sl}}}}\) is the velocity profile of the slip flow, \(R\) is the radius of CNT, \(Kn\) is Knudsen number and \({\sigma _{\text{v}}}\) is assumed \(0.7\) (Shokouhmand et al. 2010).

Furthermore, in small scale, when the scale of channel goes down, the interaction among fluid particles is influenced, and therefore, the viscosity changes. To describe the relation of viscosity and scale parameter, a formula is adopted as (Pollard and Present 1948; Ali Beskok 1999; Karniadakis et al. 2005; Kaviani and Mirdamadi 2012)

$${\mu _{\text{e}}}={\mu _0} \cdot Cr,$$
(7)

where

$$Cr=\frac{1}{{1+\bar {\alpha }Kn}},$$
(8)

\({\mu _e}\) is the effective viscosity in nanoscale, while \({\mu _0}\) is the bulk one. According to both theoretical and experimental data (Karniadakis et al. 2005), \(\bar {\alpha }\) is a function of \(Kn\), i.e.,

\(\bar {\alpha }={\alpha _0}\left( {{{\tan }^{ - 1}}\left( {{\alpha _1}K{n^B}} \right)} \right)\) and \({\alpha _1}=4,{\text{~}}B=0.4\) are two empirical parameters. \({\alpha _0}\) can be determined by

$${\alpha _0}=\mathop {\lim }\limits_{{{K_{\text{n}}} \to \infty }} \bar {\alpha }=\frac{{64}}{{3\pi \left( {1 - \frac{4}{b}} \right)}}=\frac{{64}}{{15\pi }}.$$

2.3 Extended compatibility condition and derivation of fluid load

For deriving fluid load from NS equation, the compatibility condition is critical. In the previous work (Khosravian and Rafii-Tabar 2007; Mirramezani et al. 2013) which narrates the derivation of fluid load from NS equation, the compatibility condition is described as that on the interface of pipe and internal flow, the corresponding velocities and accelerations along the lateral displacement direction were equal, i.e.,

$${v_{\text{r}}}=\frac{{{\text{d}}w}}{{{\text{d}}t}},$$
(9)
$$\frac{{{\text{d}}{v_{\text{r}}}}}{{{\text{d}}t}}=\frac{{{{\text{d}}^2}w}}{{{\text{d}}{t^2}}},$$
(10)

and

$$\frac{{\text{d}}}{{{\text{d}}t}}=\frac{\partial }{{\partial t}}+{v_{\text{x}}}\left( r \right)\frac{\partial }{{\partial x}},$$
(11)

where \({v_{\text{x}}}(r)\) represents the axial velocity distribution of internal flow along radial direction, and thus, \(r\) herein should equal \(R\), because it is on the interface. Going down this road without modification, one will end up gaining a governing equation depending on \({v_{\text{x}}}(R)\) rather than \({v_{\text{x}}}(r)\). This is a disaster for non-slip flow regime, where \({v_{\text{x}}}(R)\) is zero, and in other words, the governing equation has nothing to do with the velocity of internal flow.

To keep consistency with the governing equations in previous work, we propose an extended compatibility condition that the corresponding lateral velocities and accelerations of internal flow on the entire cross section equal those of CNT on the very same cross section. Hence the \(r\) in Eq. (11) can take the value all over the cross section. Since the fluid–solid interaction is usually considered to be a sort of “weak coupling” in the case of pipe conveying flow, i.e., the state of flow can influence the motion of CNT but not vice versa, our proposal is reasonable.

Substituting Eq. (11) into linear NS equation,

$${\rho _{\text{f}}}\frac{{{\text{d}}{\varvec{v}}}}{{{\text{d}}t}}= - \nabla p+{\mu _{\text{e}}}{\nabla ^2}{\varvec{v}},$$
(12)

where \({\rho _{\text{f}}},\;~{\varvec{v}}\) and \(p\) represent density of internal flow, flow velocity and pressure of internal flow, and project the resultant equation in lateral direction, one can gain the expression of fluid load at specific position \(r\),

$$\frac{{\partial p}}{{\partial r}}= - {\rho _{\text{f}}}\left( {\frac{{{\partial ^2}w}}{{\partial {t^2}}}+2{v_{\text{x}}}\left( r \right)\frac{{{\partial ^2}w}}{{\partial t\partial x}}+v_{{\text{x}}}^{{\text{2}}}\left( r \right)\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right)+{\mu _{\text{e}}}\left( {\frac{{{\partial ^3}w}}{{\partial t\partial {x^2}}}+{v_{\text{x}}}\left( r \right)\frac{{{\partial ^3}w}}{{\partial {x^3}}}} \right),$$
(13)

where the first three terms on the right-hand side represent the inertial force, Coriolis force and centrifugal force and the last two terms are related to the viscous effects. Then, the fluid load can be derived by integrating Eq. (13) over the cross section, i.e.,

$${F_{\text{f}}}=\mathop \int \limits_{0}^{R} \left( { - {\rho _{\text{f}}}\left( {\frac{{{\partial ^2}w}}{{\partial {t^2}}}+2{v_{\text{x}}}\left( r \right)\frac{{{\partial ^2}w}}{{\partial t\partial x}}+v_{{\text{x}}}^{{\text{2}}}\left( r \right)\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right)+{\mu _{\text{e}}}\left( {\frac{{{\partial ^3}w}}{{\partial t\partial {x^2}}}+{v_{\text{x}}}\left( r \right)\frac{{{\partial ^3}w}}{{\partial {x^3}}}} \right)} \right) \cdot 2\pi r{\text{d}}r.$$
(14)

In the light of small-scale effects, the velocity profile of internal flow is derived from NS equation as

$${v_{{\text{sl}}}}\left( r \right)=\frac{1}{{4{\mu _{\text{e}}}}} \cdot \frac{{\partial p}}{{\partial x}}\left( {{r^2} - {R^2} - 2{R^2}\frac{{2 - {\sigma _{\text{v}}}}}{{{\sigma _{\text{v}}}}}\frac{{Kn}}{{1 - bKn}}} \right)$$
(15)

whose average over the cross section is

$${U_{sl}}=\frac{1}{{{A_f}}}\mathop \int \limits_{0}^{R} {v_{sl}}\left( r \right) \cdot 2\pi r{\text{d}}r,$$
(16)

where the cross-sectional area of CNT chamber is referred to as \({A_{\text{f}}}\). On the other hand, the average velocity without small-scale effects is also calculated,

$$U=\frac{1}{{{A_{\text{f}}}}}\mathop \int \limits_{0}^{R} {v_{{\text{ns}}}}\left( r \right) \cdot 2\pi r{\text{d}}r.$$
(17)

Thus, VCF can be expressed as

$${\text{VCF}}=\frac{{{U_{{\text{sl}}}}}}{U}=\left( {1+\tilde {a}Kn} \right)\left( {1+\frac{{2 - {\sigma _{\text{v}}}}}{{{\sigma _{\text{v}}}}} \cdot \frac{{4Kn}}{{1 - bKn}}} \right).$$
(18)

Since the inertial force of an infinitesimal element is proportional to the square of its axial velocity, if \({F_{\text{f}}}\) is expressed as the function of average flow velocity, the coefficient in inertial term should be

$$\alpha =\frac{{\mathop \int \nolimits_{0}^{R} {v_{\text{x}}}{{\left( r \right)}^2} \cdot 2\pi r{\text{d}}r}}{{{{\left( {\mathop \int \nolimits_{0}^{R} {v_{\text{x}}}\left( r \right) \cdot 2\pi r{\text{d}}r} \right)}^2}}}=1+\frac{1}{{3{{\left( {\frac{{2 - {\sigma _{\text{v}}}}}{{{\sigma _{\text{v}}}}}\frac{{4{K_{\text{n}}}}}{{1 - bKn}}+1} \right)}^2}}}.$$
(19)

Therefore, fluid load is derived as

$${F_{\text{f}}}= - {\rho _{\text{f}}}{A_{\text{f}}}\left( {\frac{{{\partial ^2}w}}{{\partial {t^2}}}+2{\text{VCF}} \cdot U\frac{{{\partial ^2}w}}{{\partial t\partial x}}+\alpha {{\left( {{\text{VCF}}} \right)}^2}{U^2}\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right)+{\mu _0}{A_{\text{f}}} \cdot Cr\left( {\frac{{{\partial ^3}w}}{{\partial t\partial {x^2}}}+\;{\text{VCF}} \cdot U\frac{{{\partial ^3}w}}{{\partial {x^3}}}} \right).$$
(20)

Substitute Eq. (20) into Eq. (3), and non-dimensionalize the resultant expression to gain a general knowledge on CNTCF without the distraction of specific physical situation. Then one can obtain the dimensionless equation of motion

$$\frac{{{\partial ^4}\eta }}{{\partial {\zeta ^4}}}+\frac{{{\partial ^2}\eta }}{{\partial {\tau ^2}}}+2{\beta ^{\frac{1}{2}}} \cdot {\text{VCF}} \cdot u\frac{{{\partial ^2}\eta }}{{\partial \tau \partial \zeta }}+\alpha \cdot {\left( {{\text{VCF}}} \right)^2}{u^2}\frac{{{\partial ^2}\eta }}{{\partial {\zeta ^2}}} - \nu \cdot Cr \cdot s\left( {\frac{{{\partial ^3}\eta }}{{\partial \tau \partial {\zeta ^2}}}+{\text{VCF}} \cdot {\beta ^{ - \frac{1}{2}}}u\frac{{{\partial ^3}\eta }}{{\partial {\zeta ^3}}}} \right) - {\xi ^2}\frac{{{\partial ^2}}}{{\partial {\zeta ^2}}}\left( {\frac{{{\partial ^2}\eta }}{{\partial {\tau ^2}}}+2{\beta ^{\frac{1}{2}}} \cdot {\text{VCF}} \cdot u\frac{{{\partial ^2}\eta }}{{\partial \tau \partial \zeta }}+\alpha \cdot {{\left( {{\text{VCF}}} \right)}^2}{u^2}\frac{{{\partial ^2}\eta }}{{\partial {\zeta ^2}}} - \nu \cdot Cr \cdot s\left( {\frac{{{\partial ^3}\eta }}{{\partial \tau \partial {\zeta ^2}}}+{\text{VCF}} \cdot {\beta ^{ - \frac{1}{2}}}u\frac{{{\partial ^3}\eta }}{{\partial {\zeta ^3}}}} \right)} \right)=0,$$
(21)

with dimensionless parameters

$$\begin{array}{*{20}{c}} {\eta =\frac{w}{L},}&{\zeta =\frac{x}{L},}&{\tau ={{\left( {\frac{{EI}}{{{m_{\text{p}}}+{m_{\text{f}}}}}} \right)}^{\frac{1}{2}}}\frac{t}{{{L^2}}},}&{s=\frac{{{A_{\text{f}}}}}{{{L^2}}},} \\ {\beta =\frac{{{m_{\text{f}}}}}{{{m_{\text{p}}}+{m_{\text{f}}}}},}&{\xi =\frac{{{e_0}a}}{L},}&{\nu =\frac{{{L^2}{\mu _0}}}{{{{\left( {\left( {{m_{\text{f}}}+{m_{\text{p}}}} \right)EI} \right)}^{\frac{1}{2}}}}},}&{u={{\left( {\frac{{{m_{\text{f}}}}}{{EI}}} \right)}^{\frac{1}{2}}}{\text{LU}},} \end{array}$$

where \(\eta ,~\zeta ,~\tau ,~s,~\beta ,~\xi ,~\nu\) and \(u\) are dimensionless lateral displacement, axial coordinate, time coordinate, cross-sectional area of CNT chamber, mass parameter, nonlocal parameter, bulk viscosity parameter and axial flow velocity, respectively. \(L\) is the length of CNT and \({m_{\text{f}}}\) represents the linear density of internal flow, i.e., \({m_{\text{f}}}={\rho _{\text{f}}} \cdot {A_{\text{f}}}\).

It should be noted that the viscosity is taken into account and it naturally needs to be corrected in the nonlocal terms in our derivation, unlike that in previous work (Mirramezani and Mirdamadi 2012b; Kaviani and Mirdamadi 2013).

3 Solving method

3.1 Parameters of the system

The fluid flowing inside CNT is assumed as water with density of 103 kg/m3 and bulk viscosity of 1.12 × 10−3 Pa s. CNT is assumed as continuum with linear density of 4.26 × 10−15 kg/m and flexural rigidity of 2.74 × 10−23 N m2. \(Kn\) is defined as

$$Kn=\frac{\Lambda }{D}.$$
(22)

\(\Lambda\) is the mean free path of water molecules, which is around 0.3 nm (Holt et al. 2006), and \(D\) is the diameter of fluid-conveying CNT. It is reported that the diameter of CNT is between 0.4–50 nm (Ma et al. 2010), but water molecules can flow through CNT(6,6) only in single file (Andreev et al. 2005; Chopra and Choudhury 2013), which suggests that \(D\) is between 0.81–50 nm. Therefore, \(Kn\) is 0.006–0.369. In the practical calculation, six samples of \(Kn\) are sampled by equal path from this range, and together with the case where small-scale effects are neglected, they compose the value set of \(Kn\), i.e., \(\left\{ {0,~0.0060,~0.0786,~0.1512,~0.2238,~0.2964,~~0.369} \right\}\).

The value of nonlocal parameter is determined according to prior work. It should be pointed out that there is a dispute over the value of nonlocal parameter and the literature (Soltani et al. 2010; Narendar et al. 2011; Arash and Wang 2012; Liang and Han 2014) shows quite a distribution of the value. (It should be noted that, in the present paper, we do not intend to give our own preferential value of nonlocal parameter. Instead, we choose a set of values according to the prior literature and try to give a big picture of the influence of \(Kn\), no matter what value nonlocal parameter is assigned to.) As one can see in Fig. 1, the selections of nonlocal parameter gather around the points of \(0.0024,~0.0525\) and \(0.2\). And the maximum and minimum are \(9.7830 \times {10^{ - 5}}\) and \(0.2\). Including the case where nonlocal effect of CNT is not taken into account, \(\xi\) is taken from the set \(\left\{ {0,~9.783 \times {{10}^{ - 5}},~0.0024,~~0.0525,~0.2} \right\}\).

Fig. 1
figure 1

Distribution of nonlocal parameter \(\xi\)

Full size image

3.2 Basis functions and the corresponding discrete system

In order to gain the eigenvalues and critical flow velocity, Eq. (21) is discretized by Galerkin method. By taking the vibration mode shapes, \(\phi =\left\{ {{\phi _j}\left( \zeta \right)} \right\}~(j=1,2,3, \ldots ,N)\), of corresponding beam as basic functions and referring to corresponding coordinates as \({\varvec{q}}={\left\{ {{q_j}\left( \tau \right)} \right\}^T}\), the system described by Eq. (21) can be discretized into

$$\left[ {\varvec{M}} \right]\frac{{{{\text{d}}^2}{\varvec{q}}}}{{{\text{d}}{\tau ^2}}}+\left[ {\varvec{C}} \right]\frac{{{\text{d}}{\varvec{q}}}}{{{\text{d}}\tau }}+\left[ {\varvec{K}} \right]{\varvec{q}}=0,$$
(23)

where

$${\left[ {{b_0}} \right]_{kj}}=\mathop \int \limits_{0}^{1} {\phi _k}{\phi _j}{\text{d}}\zeta ,$$
$${\left[ {{b_1}} \right]_{kj}}=\mathop \int \limits_{0}^{1} {\phi _k}\frac{{d{\phi _j}}}{{d\zeta }}{\text{d}}\zeta ,$$
$${\left[ {{b_2}} \right]_{kj}}=\mathop \int \limits_{0}^{1} {\phi _k}\frac{{{d^2}{\phi _j}}}{{d{\zeta ^2}}}{\text{d}}\zeta ,$$
$${\left[ {{b_3}} \right]_{kj}}=\mathop \int \limits_{0}^{1} {\phi _k}\frac{{{d^3}{\phi _j}}}{{d{\zeta ^3}}}{\text{d}}\zeta ,$$
$${\left[ {{b_4}} \right]_{kj}}=\mathop \int \limits_{0}^{1} {\phi _k}\frac{{{d^4}{\phi _j}}}{{d{\zeta ^4}}}{\text{d}}\zeta ,$$
$${\left[ {{b_5}} \right]_{kj}}=\mathop \int \limits_{0}^{1} {\phi _k}\frac{{{d^5}{\phi _j}}}{{d{\zeta ^5}}}{\text{d}}\zeta .$$

In the practical calculation, \(N\) is taken as \(12\) and the system is solved under pinned–pinned boundary condition.

4 Results and discussion

4.1 Validation of model and results

It should be pointed out that any conception related to instability in the following parts, such as instability and critical velocity, exclusively refers to that of the first order, since that of higher order occurs after the finite deformation of the first order and makes no sense under the framework of linear theories (Yoshizawa et al. 1985; Tang and Yang 2018b).

To validate the model, the imaginary parts of eigenvalues are compared with those of reference, when a specific set of values are assigned to the parameters. Taking \(\alpha =1\) and \(\nu =0\) in Eq. (21), one can gain the original model. When \(\xi =0.2\) and \(Kn=0.001\), the imaginary parts of eigenvalues of the first two modes, which indicate the vibrational frequencies of corresponding modes, were calculated. Figure 2 shows how they change with various flow velocities. When flow velocity increases from \(0\) to a critical point, the vibrational frequencies decrease. For the first mode, it reaches its critical point at \(u=2.64\), when the vibrational frequency reaches zero, which means the vibration stops. For the second mode, it gets there at \(u=3.882\), when the vibrational frequency shows a sharp turn. The results shown in Fig. 2 contain no appreciable difference compared with the previous work (Mirramezani and Mirdamadi 2012b).

Fig. 2
figure 2

Imaginary part of eigenvalue versus flow velocity \(u\), when \(\xi =0.2\) and \(Kn=0.001\)

Full size image

To validate the numerical results, the expression of critical velocity when \(\xi =0\) under pinned–pinned boundary condition is derived as follows. When pitchfork instability which is static occurs, all the terms related to the derivative of time \(\tau\) equal \(0\) in Eq. (21), i.e.,

$$\frac{{{\partial ^4}\eta }}{{\partial {\zeta ^4}}} - \nu s \cdot Cr \cdot {\text{VCF}} \cdot u\frac{{{\partial ^3}\eta }}{{\partial {\zeta ^3}}}+\alpha \cdot \beta \cdot {\left( {{\text{VCF}}} \right)^2}{u^2}\frac{{{\partial ^2}\eta }}{{\partial {\zeta ^2}}}=0$$
(24)

of which the eigen-equation is

$${\lambda ^2}\left( {{\lambda ^2} - \nu s \cdot Cr \cdot {\text{VCF}} \cdot u\lambda +\alpha \cdot \beta \cdot {{\left( {{\text{VCF}}} \right)}^2}{u^2}} \right)=0~.$$
(25)

Then, Eq. (24) has two eigenvalues \({\lambda _{1,2}}=0\) and another two nonzero eigenvalues, \({\lambda _{3,4}}\), meet

$${\lambda ^2} - \nu s \cdot Cr \cdot {\text{VCF}} \cdot u\lambda +\alpha \cdot \beta \cdot {\left( {VCF} \right)^2}{u^2}=0.$$
(26)

To find out if \({\lambda _{3,4}}\) are multiple roots, the discriminant of Eq. (26) is derived

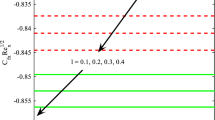
$${\Delta _\lambda }={u^2}{\left( {{\text{VCF}}} \right)^2}\left( {\frac{{C{r^2}{s^2}{\nu ^2}}}{\beta } - 4\alpha } \right).$$
(27)

It is easy to show that \({\text{VCF}}>0\) and \(C{r^2}{s^2}{\nu ^2}/\beta \ll 4\alpha\), if their profiles depending on \(Kn\) are drawn (see the dotted line of Figs. 3, 4). Therefore, \({\Delta _\lambda }<0\) with \(u>0\), which indicates that the two nonzero eigenvalues of Eq. (24) compose a conjugate complex pair. As a result, the general solution of Eq. (24) can be expressed as.

Fig. 3
figure 3

The evolvement of VCF, \(\alpha\) and \(Cr\) versus \(Kn\)

Full size image
Fig. 4
figure 4

Comparison between \(4\alpha\) and \(C{r^2}{s^2}{\nu ^2}/\beta\) versus \(Kn\)

Full size image
$$\eta ={c_1}+{c_2}\zeta +{c_3}{e^{{\lambda _3}\zeta }}+{c_4}{e^{{\lambda _4}\zeta }}.$$
(28)

Because the pitchfork instability of CNTCF with both ends supported is a kind of buckling like that of beams, Eq. (24) should have nonzero solution, which requires that not all of the coefficients on the right-hand side of Eq. (28) equal \(0\). Considering pinned–pinned boundary condition, one can obtain the expression of critical flow velocity

$${u_{Cr}}=\frac{{2\pi }}{{{\text{VCF}} \cdot \gamma }},$$
(29)

where

$$\gamma =\sqrt {4\alpha - C{r^2}{s^2}{\nu ^2}\beta } .$$
(30)

Draw the profiles of both theoretical and numerical critical flow velocity as Fig. 5, where the two profiles are almost indistinguishable with the relative error no more than \(0.18\%\). It should be noted that the relative error is always positive which means that theoretical values are always a bit smaller than the numerical ones. This can be understood by looking into the process of recognizing the critical flow velocity. The real parts of the first eigenvalue pair of the system are equal until the flow velocity reaches its critical point. To gain the critical flow velocity, the differences of the real parts are calculated and sequenced in the order of increasing flow velocity. And the velocity corresponding to the first nonzero difference is recognized as the critical flow velocity. This process by itself should statistically make the numerical value lag behind the theoretical one by the exact step value of velocity, herein \(0.001\). The red dashed line in the inset of Fig. 5 shows the relative errors caused by this bias. If this bias is canceled out, the overall relative errors will fluctuate around \(0\), which are mainly caused by round-off errors. Hence, the theoretical and numerical critical values agree with each other perfectly well.

Fig. 5
figure 5

Comparison between theoretical and numerical values of critical velocity and their relative error

Full size image

Besides, a comparison between the tendency of the real parts of eigenvalues in the present work and that in the previous work is made for validation. The real parts of eigenvalues are responsible for the decay of corresponding modal vibration of the system. It is expected to be negative once the viscosity of the fluid is taken into account, for the system itself contains damping. As shown in Fig. 6, the real parts of eigenvalues increase with an increasing \(Kn\). This is reasonable because the effective viscosity diminishes as \(Kn\) goes up (see the solid line of Fig. 3) and an increasing real parts of eigenvalues suggests a decreasing damping effect, which agrees well with previous work (Wang and Ni 2009; Rashidi et al. 2012).

Fig. 6
figure 6

The real parts of eigenvalues versus \(Kn\) (\(u=0.3\))

Full size image

4.2 Comparison between improved model and original model

Critical flow velocity is predicted through both improved model and original model. Their differences are calculated (see Fig. 7). The decrease of critical flow velocity given by the improved model can reach as much as \(13.4\%\), and it almost remains unchanged, when \(\xi\) increase. However, as \(Kn\) increase, the difference between the two shrinks. Only around \(1.8{\text{\% }}\) of reduction is left, once \(Kn=0.369\). This change can be explained by the evolvement of \(Cr\) and \({{\varvec{\upalpha}}}\) versus \(Kn\). As is shown in Fig. 3, when \(Kn\) increases, \(Cr\) goes down and \(\alpha\) tends to approach \(1\). In other words, when the scale of the system is relatively big but still far below the threshold of nanoscale, the effects of effective viscosity and non-uniform flow profile are considerable. As the scale consistently goes down, the effective viscosity decreases and slip velocity on the interface increases. This means a decreasing drag of both neighboring fluid and CNT, which encourages the flow profile to be uniform. As a result, the improved model evolves towards the original model. All in all, the improved model can considerably decrease the critical flow velocity, though these effects are weakened by an increased \(Kn\).

Fig. 7
figure 7

Decrease of \({u_{Cr}}\) obtained by the improved model relative to that by the original model

Full size image

4.3 Effects of \({\varvec{K}}{\varvec{n}}\)

To exclusively look into the effects of \(Kn\), the nonlocal parameter \(\xi\) is temporarily assumed \(0\). Under the pinned–pinned boundary condition, as one can see in Fig. 5, when \(Kn\) is limited to \(0.001\), the drift of critical flow velocity is unquestionably insignificant, merely around \(0.8\%\) of reduction, to be precise, according to Mirramezani et al. (Mirramezani and Mirdamadi 2012b). With \(Kn\) going from \(0\) to as high as \(0.369\), however, the drop of critical flow velocity is dramatic, \(76.5{\text{\% }}\), and cannot be neglected. This phenomenon can be predicted by Eq. (29), which shows that the critical flow velocity \({u_{Cr}}\) is inversely proportional to the product of VCF and \(\gamma\). Figure 4 illustrates that \(4\alpha\) is far bigger than \(C{r^2}{s^2}{\nu ^2}/\beta\) by at least three orders of magnitude. \(C{r^2}{s^2}{\nu ^2}\beta\) should be even smaller which can then be neglected compared to \(4\alpha\), since \(\beta\) is the ratio of linear density of internal flow to that of CNTCF and less than 1. Therefore, \(\gamma\) is dominated by \(4\alpha\) or \(\gamma \approx 2\sqrt \alpha\), more specifically. It is seemingly confusing where \({u_{Cr}}\) goes, with VCF going up and \(\alpha\) going down as shown by dotted line and dashed line in Fig. 3 when \(Kn\) increases. But after comparing VCF marked by the dotted line in Fig. 3 with \(4\alpha\) marked by the dotted line in Fig. 4, one can reasonably infer that VCF dominates the product of the two, which suggests that it is the slip boundary condition arising out of the small-scale effect of fluid that makes a main contribution to the dramatic decrease of critical flow velocity.

As mentioned in the validation subsection, a drop of damping effect caused by increasing \(Kn\) is also observed. Indeed, as shown in Fig. 6, the real parts of eigenvalues increase with \(Kn\), the extent to which varies with different \(\xi\), though. Taking \(u=0.3\) for example, the growth can reach as much as \(33.3{\text{\% }}\) relative to that where small-scale effects of fluid are missing. Clearly, this is caused by the reduction of effective viscosity due to the increase of \(Kn\) (see the solid line of Fig. 3). Hence, in the light of \(Kn\), the predictive energy efficiency of CNTCF may see a significant improvement.

4.4 Effects of \(\varvec{\xi}\)

When \(\xi\) varies, the trends shown by profiles of \({u_{Cr}}\) versus \(Kn\) are similar (see Fig. 8), though the quantity of the line does decline with an increased \(\xi\). Obviously, the effects of \(\xi\) on critical flow velocity are not as significant as those of \(Kn\), provided that \(Kn\) is limited to \(0.369\) and \(\xi\) to \(0.2\). Especially when \(\xi\) takes values in the vicinity of \(0\), the lines are so close that their differences are unappreciable no matter how \(Kn\) varies, which suggests that the effects of \(\xi\) on critical flow velocity is negligible. If \(\xi\) is taken as high as \(0.2\), however, things are different. \({u_{Cr}}\) drops at least \(14.24\%\), compared with the case where \(\xi =0\). Thus taking a proper \(\xi\) is important to give a reasonable prediction of \({u_{Cr}}\), and undoubtedly, the dispute over \(\xi\) impairs the reliability of the theoretical prediction.

Fig. 8
figure 8

The profiles of \({u_{Cr}}\) versus \(Kn\) with various \(\xi\). The inset is a zoomed-in picture around \(Kn=0\)

Full size image

4.5 Effects of \({\varvec{K}}{\varvec{n}}\) and \(\varvec{\xi}\)

It is noteworthy that if one looks into Fig. 8, one may find the gaps between different lines become smaller, when \(Kn\) goes up, i.e., the quantities of the lines drops. Indeed, \({u_{Cr,\xi }}/{u_{Cr,0}}\), the ratios of \({u_{Cr}}\) corresponding with various \(\xi\) to that with \(\xi =0\), are extremely close with each other, despite various \(Kn\) (see Fig. 9). Even if \(\xi =0.525\), where the biggest difference is detected, the variance is still no more than \(0.001\). It seems that \(\xi\) determines a factor that scales down the line of \({u_{Cr}}\) versus \(Kn\). Similar phenomenon can be observed if \({u_{Cr,Kn}}/{u_{Cr,0}}\) (herein, the subscript \(0\) means \(Kn=0\)) is computed. To describe these in mathematics, fix other parameters and exclusively assume \({u_{Cr}}\) is a function of \(Kn\) and \(\xi\),

Fig. 9
figure 9

The ratio of \({u_{Cr,\xi }}\) to \({u_{Cr,0}}\). The inset is a zoomed-in picture around \(\xi =0.0525\)

Full size image
$${u_{Cr}}=f(Kn,\xi )$$
(31)

According to the above observations, it can be rewritten as

$${u_{Cr}}={f_1}\left( \xi \right) \cdot f\left( {Kn,0} \right)={f_2}\left( {Kn} \right) \cdot f(0,\xi )$$
(32)

where \({f_1}(\xi )\) is a function of \(\xi\) and independent of \(Kn\), while \({f_2}\left( {Kn} \right)\) is exclusively dependent on \(Kn\) and can be taken as Eq. (29). Then,

$${u_{Cr}}={f_1}\left( \xi \right) \cdot {f_2}(Kn)$$
(33)

which suggests that the effects of \(Kn\) and \(\xi\) on \({u_{Cr}}\) are probably uncoupled.

5 Conclusions

In this paper, we proposed an improved model by comprehensively taking small-scale effects of both CNT and inside flow, respectively, marked by nonlocal parameter (\(\xi\)) and Knudsen number (\(Kn\)) into account. By extending the compatibility condition from the interface of CNT and inside flow into the whole cross section, and systematically considering nonlocal elastic theory and all the factors related to \(Kn\), viz. effective viscosity, slip boundary condition and non-uniform flow profile, the governing equation of CNTCF was derived. Based on this new governing equation, a formula of critical flow velocity was derived in addition to numerical results of eigenvalues and critical flow velocity. Comparing with the original model, we demonstrated that the improved model could foresee a considerable decrease of critical velocity, especially when \(Kn\) was relatively small.

According to the results, an increased \(Kn\) resulted in a drop of critical flow velocity. After cautiously comparing the three factors related to \(Kn\), we found VCF was the dominant factor in the formula of critical flow velocity. Therefore, it was the slip boundary condition arising out of the small-scale effect of fluid that mainly caused this reduction, though the contribution of effective viscosity and non-uniform profile was also considerable and should not be neglected. Besides, when \(Kn\) went up, a considerable rise of the real parts of eigenvalues which were responsible for the decay of corresponding modal vibration, was also observed, due to the fall of effective viscosity. Consequently, a bigger \(Kn\) might witness a significantly improved predictive energy efficiency of this system. On the other hand, limited to \(0.2\), \(\xi\) could shrink the critical flow velocity by as big as \(14.24\%\). In the light of dispute over \(\xi\), the reliability of theoretical prediction was undoubtedly impaired. Moreover, the ratios of critical flow velocity corresponding with various \(\xi\) to that with \(\xi =0\) were tremendously close. A similar pattern was observed as well when it was \(Kn\) that was under consideration, which indicated that the small-scale effects of CNT and inside fluid on critical flow velocity were probably uncoupled.