1 Introduction

The problem of clustering around linear structures is particularly appealing and has received growing interest in the literature. Latent class regression has applications in many fields, including engineering, genetics, biology, econometrics, marketing, computer vision, pattern recognition, tomography, fault detection, among others. The reader is pointed to García-Escudero et al. (2009) for a large collection of references. This paper is motivated by the fact that noisy data frequently appear in every field of application. When the sample data is contaminated by the occurrence of outliers, it is well known that maximum likelihood estimation (MLE) is likely to lead to unreliable results. In a mixture setting, the bias of at least one of the component parameters estimate can be arbitrarily large and the true underlying clustering structure might be hidden. Therefore, there is the need for a suitably robust procedure providing protection against outliers. The reader is pointed to the book by Farcomeni and Greco (2015a) for a gentle introduction to robustness issues.

The problem of robust fitting of a mixture of linear regressions has been already tackled in the literature. In general, the robust solutions are driven by a suitable modification of the EM algorithm for mixtures or the classification EM algorithm (CEM), concerning the M step, which is enhanced by some robust estimation approach in place of maximum likelihood. Some existing proposals are based on the idea of (hard) trimming: estimation is performed over a subset of the original data obtained after discarding those units with the lowest contributions to the likelihood function. According to such trimming strategies, potential outliers are discarded in the estimation process, that is observations are given crispy weights in \(\left\{ 0, 1\right\}\). Neykov et al. (2007) introduced a mixture fitting approach based on the trimmed likelihood, García-Escudero et al. (2010) extended the TCLUST methodology, developed in García-Escudero et al. (2008) for mixtures of multivariate Gaussian distributions, exploiting the idea of impartial trimming in TCLUST-REG, a related proposal has been presented in García-Escudero et al. (2009) and an adaptive hard trimming procedure has been described in Riani et al. (2008) based on the Forward Search methodology. In particular, TCLUST-REG is characterized by group scatter constraints aimed at making the mixture fitting a well-posed problem and the addition of a second trimming step to mitigate the effect of outliers in the space of explanatory variables acting as leverage points. A very recent adaptive version of TCLUST-REG has been discussed in Torti et al. (2019). An alternative approach meant to automatically take into account leverage points has been considered by García-Escudero et al. (2017) where trimming and restrictions have been introduced to get a robust version of the cluster weighted model, named Trimmed Clustered Weighted Restricted Model (TCWRM). In this approach restrictions concern both the set of eigenvalues of the covariance matrix evaluated on the X-space and the variances of the regression error term. The reader is pointed to Torti et al. (2019) for a comparative analysis of TCLUST-REG and TCWRM under general settings. The benefits of trimming for robust regression clustering have been also investigated in Dotto et al. (2017) where a fuzzy approach has been developed.

In a different but complementary fashion, Bashir and Carter (2012) and Bai et al. (2012) modified the M step by resorting to soft rather than hard trimming procedures. Actually, they replaced the single component MLE problems by M- (and S-) estimation problems for linear regression (see also Campbell (1984) and Maronna et al. (2019)). In particular, in both papers the authors developed an EM-type algorithm featured by componentwise weights but this approach can be extend to obtain robust versions of the CEM algorithm based on M- and S-estimation, as well. According to a soft trimming strategy, observations are attached a weight lying in [0, 1] according to some measure of outlyingness. Potential outliers are expected to be heavily downweighted, whereas genuine observations receive a weight close to one.

It is worth to mention that there are different proposals aimed at robust latent class linear regression estimation that are not based on soft or hard trimming procedures in which the assumed model is embedded in a larger one to account for outliers. Yao et al. (2014) considered a mixtures of linear regression models with Student t error distributions; Punzo and McNicholas (2017) developed an approach based on the Contaminated Gaussian Cluster Weighted Model in which each mixture component has some parameters controlling the proportion of (different type of) outliers; Yu et al. (2017) proposed a case-specific and scale-dependent mean-shift mixture model and a penalized likelihood approach to induce sparsity among the mean-shift parameters.

Here, we propose the use of the weighted likelihood methodology (Markatou et al. 1998) as a valid alternative to the existing methods. Weighted likelihood is an appealing robust techniques for estimation and testing (Agostinelli and Markatou 2001). In particular, reliable statistical tools have been developed for linear regression (Agostinelli and Markatou 1998; Agostinelli 2002), generalized linear models (Alqallaf and Agostinelli 2016) and multivariate analysis (Agostinelli and Greco 2019). Recently, Greco and Agostinelli (2020) also introduced weighted likelihood estimation of mixtures of multivariate normal distributions. The authors explored the behavior of both EM and CEM type algorithms and found that weighted likelihood gives powerful devices for robust estimation, classification and outliers detection. Then, the same ideas can be extended to the context of mixtures of linear regressions.

Weighted likelihood belongs to the group of soft trimming techniques and the weighted likelihood estimator (WLE) can be thought as an M-estimator. The main differences are in the genesis of the weights and in their asymptotic behavior at the assumed model. Actually, weighted likelihood estimation can correspond to a minimum disparity estimation problem (Basu and Lindsay 1994). Then, the WLE is expected to be highly robust under contamination but, conversely to M-estimators, also asymptotically efficient at the assumed model. Some necessary preliminaries on weighted likelihood estimation are given in Sect. 2. The weighted EM and penalized CEM algorithms for robust fitting of mixtures of regressions are introduced in Sect. 3. Section 4 highlights some computational details, Sect. 5 is devoted to a very general result about consistency and aymptotic normality of the proposed estimator. Then, the outlier detection rule is described in Sect. 6 and some illustrative examples based on simulated data are presented in Sect. 7. In Sect. 8 some strategies to select the number of latent classes are presented. Section 9 gives some numerical studies whereas a real data example is discussed in Sect. 10. Concluding remarks end the paper.

2 Background

Let \(y = (y_1, \cdots , y_n)^{^\mathrm T}\) be a random sample of size n drawn from a r.v. Y with distribution function \(M(y; \theta )\) and probability (density) function \(m(y; \theta )\), which is an element of the parametric family of distributions \(\mathcal {M} = \{ M(y; \theta ), \theta \in \Theta \subseteq \mathbb {R}^d, d\ge 1, y\in \mathcal {Y} \}\). Let \(\hat{F}\) be the empirical distribution function. The WLE \(\hat{\theta }^{w}\) is defined as the root of the Weighted Likelihood Estimating Equations (WLEE)

$$\begin{aligned} \sum _{i=1}^n w(y_i; \theta , \hat{F}) s(y_i; \theta ) = 0, \end{aligned}$$
(1)

where \(s(y;\theta )=\sum _{i=1}^n s(y_i;\theta )\) is the score function. The WLEE in (1) is a modified version of the (system of) likelihood equations, since a data dependent weight, \(w_i=w(y_i; \theta , \hat{F}) \in [0,1]\), is attached to each individual score component. The weights are meant to be small for those data points that are in disagreement with the assumed sampling model. The degree of agreement between the data and the assumed model is measured by the Pearson residual function. Let

$$\begin{aligned} f^*(y)=\int _\mathcal {Y}k(y;t,h)d\hat{F}(t) \end{aligned}$$

be a non parametric kernel density estimate and

$$\begin{aligned} m^*(y; \theta )=\int _\mathcal {Y}k(y;t,h)m(t;\theta ) \ dt \end{aligned}$$

a smoothed version of the model density obtained by using the same kernel function k(y; t, h). Then, the Pearson residual is

$$\begin{aligned} \delta (y) = \frac{f^*(y) - m^{*}(y; \theta )}{m^*(y; \theta )}, \end{aligned}$$

with \(\delta (y)\in [-1,+\infty )\). By smoothing the model, the Pearson residuals converge to zero with probability one for every y under the assumed model; the reader is pointed to Basu and Lindsay (1994), Markatou et al. (1998) and references therein. When the model is discrete, \(f^*(y)\) is the empirical probability function and \(m^{*}(y; \theta )\) simply reduces to \(m(y;\theta )\). In this paper, we will make use of the Pearson residuals established in Agostinelli and Greco (2019). Actually, a valid WLEE can be also obtained by using Pearson residuals that are defined as

$$\begin{aligned} \delta (y) = \frac{f^{*}(\tilde{y}) - m^*(\tilde{y})}{m^{*}(\tilde{y})}, \end{aligned}$$

where \(\tilde{y}=g(y;\theta )\) is a pivot at the assumed model whose (smoothed) distribution does not depend on the parameter value.

Large values of the Pearson residual function correspond to regions of the support of Y where the model fits the data poorly. According to this approach, outliers can be defined as observations that are highly unlikely to occur under the assumed model (Markatou et al. 1998), rather than from a geometric point of view as observation that are far from the model fitted to the bulk of the data, as in the classical theory of M-estimators.

The weight function is defined as

$$\begin{aligned} w(\delta (y)) = \frac{\left[ A(\delta (y)) + 1\right] ^+}{\delta (y) + 1}, \end{aligned}$$
(2)

where \([\cdot ]^+\) denotes the positive part and \(A(\delta )\) is the Residual Adjustment Function (RAF, Basu and Lindsay (1994)). The RAF plays the role to bound the effect of large Pearson residuals on the fitting procedure. By using a RAF such that \(|A(\delta )| \le |\delta |\) both outliers and inliers (whose nature will be described in the following) will be downweighted. The RAF function is connected to minimum disparity estimation problems. Actually, it is defined as \(A(\delta )=(\delta +1)G'(\delta )-G(0)\), with prime denoting differentiation, where \(G(\cdot )\) is a strictly convex function over \([-1,+\infty )\) and thrice differentiable, which determines a disparity measure, that, in the continuous case, is defined as

$$\begin{aligned} \rho (f^{*}(y), m^{*}(y;\theta )=\int _\mathcal {Y} G(y)m^{*}(y;\theta ) \ dy. \end{aligned}$$

In principle, by following the approach developed in Markatou et al. (1998), it is possible to build a WLEE matching a minimum disparity objective function. One can consider the families of RAF stemming from the Symmetric Chi-Squared divergence, the family of Power divergence or Generalized Kullback–Leibler divergence measures. The resulting weight function is unimodal and decline smoothly to zero as \(\delta (y)\rightarrow -1\) or \(\delta (y)\rightarrow +\infty\). The weighting function corresponding to a Symmetric Chi-Squared divergence, which is driven by \(G(\delta )=\frac{2\delta^{2}}{\delta +2}\), is given in Fig. 1.

Fig. 1
figure 1

Weighting function corresponding to a Symmetric Chi-Squared divergence

Full size image

Under the assumptions given in Markatou et al. (1998) and Agostinelli and Markatou (2001), that establish some regularity conditions on the model, the kernel and the weight function, at the assumed model, we have that:

  1. 1.

    \(\hat{\theta }^{w}\) is a consistent and first order efficient estimator of \(\theta\), that is

    $$\begin{aligned} \sqrt{n}(\hat{\theta }^w-\theta ){\mathop {\rightarrow }\limits^{d}} N(0, I_1^{-1}(\theta )) \end{aligned}$$

    where \(I_1(\theta )=E[u(Y; \theta )^2]\) is the expected Fisher information;

  2. 2.

    \(\text {sup}|w(y, \hat{\theta }^{w}, \hat{F})-1|{\mathop {\rightarrow }\limits ^{a.s.}}0\) (Agostinelli and Greco 2013);

  3. 3.

    the weighted versions of the likelihood ratio, Wald and score test all share the usual asymptotic behavior (Agostinelli and Markatou 2001).

For what concerns the robustness properties of the WLE, the reader is pointed to Lindsay (1994); Markatou et al. (1998). In particular, the the robust behaviour of the WLE in finite samples is characterized by the curvature parameter \(A''(0)\) being negative, despite an unbounded influence function that is just that of the MLE. Furthermore, the WLE has a strong breakdown point equal to 0.5.

It is worth to claim that the shape of the kernel function has a very limited effect on weighted likelihood estimation. On the contrary, the smoothing parameter h allows to control the robustness/efficiency trade-off of the methodology in finite samples. Actually, large values of h lead to Pearson residuals all close to zero and weights all close to one and, hence, large efficiency, since the kernel density estimate is stochastically close to the postulated model. On the other hand, small values of h make the kernel density estimate more sensitive to the occurrence of outliers and the Pearson residuals become large for those data points that are in disagreement with the model.

2.1 Weighted likelihood for linear regression

Let us consider a linear regression model with normally distributed errors, i.e. \(y=X\beta +\sigma \epsilon\), where y is the response, \(X=[x_1,\ldots ,x_p]\) is the \(n\times p\) design matrix, \(\beta =(\beta _1,\ldots ,\beta _p)^{^\mathrm T}\) is the vector of regression coefficients, \(\sigma\) is a scale parameter and \(\epsilon \sim N(0,1)\). In this setting, Pearson residuals and the weights can be evaluated over the scaled residuals \(e=g(y; \beta , \sigma )=(y-X\beta )/\sigma\). An appealing strategy to compute Pearson residuals consists in using a normal kernel with bandwidth equal to h. In such a way, the smoothed model density is still normal with variance \((1+h^2)\), that is

$$\begin{aligned} \delta (y) = \frac{f^{*}(e)}{\frac{1}{\sqrt{1+h^2}}\phi \left( \frac{e}{\sqrt{1+h^2}}\right) }-1 \ , \end{aligned}$$
(3)

where \(\phi (\cdot )\) denotes the standard normal density function. Then, the WLE of \((\beta , \sigma )\) is obtained as the result of weighted least squares. Clearly, the computation of the WLE of \((\beta , \sigma )\) yields an iterative procedure. At each iteration, based on the current parameter estimates, scaled residuals are obtained. Then, their non parametric density estimate is fitted based on the chosen kernel and Pearson residuals and weights are updated according to (3) and (2).

3 Robust fitting of a latent class linear regression model

Let us assume a latent class regression model featured by K components, where K is fixed in advance, with density function denoted by

$$\begin{aligned} m(y;x,\tau )=\sum _{k=1}^K\pi _k\phi (y;\mu _k, \sigma _k), \end{aligned}$$
(4)

where \(\mu _k=X\beta _k\), \(\pi _k\) is the prior probability of component k, \((\beta _k, \sigma _k)\) are the component specific parameters and \(\tau =(\pi _1,\ldots ,\pi _K, \beta _1,\ldots ,\beta _K, \sigma _1,\ldots ,\sigma _K)^{^\mathrm T}\) is the vector of all parameters.

The mixture loglikelihood function based on a sample of size n is

$$\begin{aligned} \ell (\tau )=\sum _{i=1}^n\log \sum _{k=1}^K \pi _k\phi (y_i;\mu _{ik}, \sigma _k). \end{aligned}$$
(5)

Maximum likelihood estimation is commonly performed by the EM algorithm, that works with the classification loglikelihood

$$\begin{aligned} \ell _c(\tau )=\sum _{i=1}^n\sum _{k=1}^K\log ( \pi _k\phi (y_i;\mu _{ik}, \sigma _k))u_{ik}, \end{aligned}$$
(6)

where \(u_{ij}\) is an indicator of the ith unit belonging to the jth cluster. The EM algorithm iterates, over the index s, between the E step, in which posterior membership probabilities are evaluated as

$$\begin{aligned} u_{ik}^{(s)}=\frac{\pi _k^{(s-1)}\phi \left( y_i; \mu _{ik}^{(s-1)},\sigma _k^{(s-1)}\right) }{\sum _{k=1}^K \pi _k^{(s-1)}\phi \left( y_i; \mu _{ik}^{(s-1)},\sigma _k^{(s-1)}\right) } \end{aligned}$$

and the M step, where parameters’ estimates are updated as

$$\begin{aligned} \pi _k^{(s)}& = \frac{\sum _{i=1}^n u_{ik}^{(s)}}{n} \\ \beta _k^{(s)}& = (X^{^\mathrm T}U_k^{(s)}X)^{-1}X^{^\mathrm T}U_k^{(s)}y \\ \sigma _k^{2(s)}& = \frac{\left( y-\mu _k^{(s)}\right) ^{^\mathrm T}U_k^{(s)}\left( y-\mu _k^{(s)}\right) }{n} \end{aligned}$$

where \(U_k^{(s)}\) is a diagonal matrix with elements \(u_{ik}\).

At convergence, cluster assignments can be pursued according to a Maximum a Posteriori (MAP) rule: units are assigned to the most likely component. In the CEM algorithm, after the E step, a classification step is performed (together they form the CE step). Let \(k_i=\mathrm {argmax}_k u_{ik}^{(s)}\), then \(u_{ik_i}^{(s)}=1\) and \(u_{ik}^{(s)}=0\) for \(k\ne k_i\) and \(U^{(s)}\) becomes a dummy matrix. Conversely to the EM algorithm, the CEM directly provides a classification of the units at convergence. Actually, the classification approach is aimed at maximizing the classification loglikelihood over both the mixture parameters and the individual components’ labels.

Weighted versions of the above algorithms can be designed by introducing the computation of the weights defined in (2) before the M step at the current parameter value. In particular, the weighted EM (WEM) will require componentwise sets of weights, wheres in the weighted CEM (WCEM) weights will be computed conditionally on the current cluster assignments driven by the CE step. More in details, the WEM algorithm iterates between the classical E step and an M step in which the single components MLE problems are replaced by K one-step WLE problems. The single iteration is summarized in Algorithm 1. On the contrary, the WCEM algorithm iterates between the standard CE step and K one-step weighted likelihood based M-step in which weights are evaluated conditionally to the current cluster assignment and not for each component anymore, that is \(u_{ik}=1\) for \(k= k_i\) and zero otherwise. Furthermore, the proposed algorithm can be successfully augmented by introducing scatter similarity restrictions as described by García-Escudero et al. (2010). These constraints are posed by fixing a constant \(c_{\sigma }\) such that

$$\begin{aligned} \frac{\max \sigma _k}{\min \sigma _k} \le c_\sigma , \quad k=1,2,\ldots , K \end{aligned}$$
(7)

and are needed to avoid spurious solutions and make the mixture fitting and classification well defined problems (see also Fritz et al. (2013); Garcia-Escudero et al. (2015); Greco and Agostinelli (2020)).

figure a

Here, as one referee pointed out, the interest focuses on a general mixture model in which all parameters are class-dependent. However, in some applications a more parsimonious model may be needed, that is characterized by homogeneous slopes and is nested into the more general one. Maximum likelihood estimation can be performed by using a different set of estimating equations in the M-step and its weighted counterpart can be obtained as well. For instance, let us consider a mixture model whose components only differ in the intercept term, i.e \(\beta =(\beta _{01}, \ldots , \beta _{0K}, \beta _{-0})\), where \(\beta _{-0}\) is the \(p_{-0}\) dimensional vector of common slopes with \(p_{-0}\ge 1\). Then, the M-step in Algorithm 1 changes as follows:

$$\begin{aligned} \beta _{-0}^{(s+1)}& = \sum _{k=1}^{K}\left( X^T\tilde{W}^{(s)} X\right) ^{-1}X^T\tilde{W}^{(s)}\left( y-\beta _{0k}^{(s)} \right) \\ \nonumber \beta _{0k}^{(s+1)}& = \frac{\sum _{i=1}^n\left( y_i-x_{i}\beta _{-0}^{(s)}\right) \tilde{w}_{ik}}{\sum _{i=1}^n \tilde{w}_{ik}}, \quad k=1,2,\ldots , K. \\ \nonumber \end{aligned}$$
(8)

4 Computational details

One of the first issues to deal with the estimation of a mixture model by the EM or CEM algorithm and their robust counterparts is the choice of a suitable starting point. A solution is represented by subsampling (Markatou et al. 1998; Neykov and Müller 2003; Neykov et al. 2007; Torti et al. 2019). A subsample of size \(n^{*}\) is selected randomly from the data sample, then the model is fitted to these \(n^{*}\) observations by the classical EM (or CEM) algorithm to get a trial estimate. This approach shows some limitations since from the one hand \(n^{*}\) should be as small as possible in order to increase the chance of drawing at least one outlier free subsample, but from the other hand a larger trial sample size will avoid the algorithm to fail in finding a solution.

Here, in a different fashion, a deterministic initialization will be considered: first units are assigned to the different components by running TCLUST to the multivariate data (y, X), then cluster specific parameters’ estimates are initialized by running a robust regression conditionally on clusters’ assignments. In particular, weighted likelihood regression has been used but M-type regression could be used as well. This strategy is well justified since in García-Escudero et al. (2010) it is stated that TCLUST could serve as starting point for others approaches. The initial clustering depends on a couple of tuning constants that allow control of TCLUST: the level of trimming \(\alpha\) and the eigen-ratio constraint factor (García-Escudero et al. 2008; Fritz et al. 2013), that will be denoted by c to avoid confusion with the scatter constraint factor \(c_\sigma\) in (7) characterizing the proposed WEM and WCEM algorithms.

An alternative deterministic initial solution may be obtained by computing the trimmed likelihood estimator of Neykov et al. (2007); other candidate initial solutions can be evaluated according to the approach discussed in Coretto and Hennig (2017) that is based on a combination of nearest neighbor denoising and agglomerative hierarchical clustering. Further starting points can be obtained by randomly perturbing the deterministic starting solution and/or the final one obtained from it (Farcomeni and Greco 2015b).

When using TCLUST, in order to avoid the algorithm to be dependent on the initial partition of the data and trapped in (spurious) local optima, a general advise is to run it (several times) for different values of \((\alpha , c)\) and then select the final fitted model according to one criterion. For instance, when the initial TCLUST is not properly robust with respect to the actual amount of contamination in the data, then the fitted model could exhibit lack of robustness as well. On the contrary, a large level of trimming can lead to solutions that are characterized by an excess of downweighting. As well, the choice of the eigen restriction factor could be crucial.

Formal solutions to the problem of root selection in weighted likelihood estimation have been provided in Markatou et al. (1998), Agostinelli (2006), Agostinelli and Greco (2019). Here, we decided to select the root leading to the minimum fitted approximate disparity as defined in Agostinelli and Greco (2019), that is

$$\begin{aligned} \tilde{\rho }(f^{*}, m^{*}) =\frac{1}{n}\sum _{i=1}^n\frac{G(\delta _i)+\delta _i}{\delta _i+1} \end{aligned}$$
(9)

where the Pearson residuals \(\delta _i\) are evaluated conditionally on the final cluster assignments, that is \(\delta _i= \delta _{ik_i}\), at convergence.

Another remarkable aspect is represented by the selection of the bandwidth parameter h. The tuning of the smoothing parameter h could be based on several quantities of interest stemming from the fitted mixture model: a safe selection can be achieved by monitoring the unit specific weights, residuals or the empirical downweighting level \((1-\hat{\bar{\omega }})\) as h varies (Markatou et al. 1998; Greco 2017; Agostinelli and Greco 2018), with \(\hat{\bar{\omega }}=n^{-1}\sum _{i=1}^n \hat{w}_i\) and the weights are evaluated conditionally on the final cluster assignments, that is \(\hat{w}_i=\hat{w}_{ik_i}\).

An abrupt change in the monitored empirical downweighting level or in the residuals may indicate, for instance, the transition from a robust to a non robust fit (Agostinelli and Greco 2018) or to an extremely robust fit leading to the detection of an even intolerable number of false outliers, as shown in the bottom right panel of Fig. 10. Hence, monitoring can aid in the selection of a value of h that gives an appropriate compromise between efficiency and robustness at finite samples. A monitoring approach is commonly applied to select the trimming level in TCLUST, TCLUST-REG and TCWRM, for instance. The reader is pointed to Cerioli et al. (2018b) for a recent general account on the benefits and potentials of monitoring.

5 WEM and WCEM as special cases

The WEM and WCEM are obtained by replacing maximum likelihood by a different set of estimating equations, characterized by the introduction of weights aimed at bounding the effect of outliers on the fit. In a fashion similar to what stated in Bai et al. (2012), the proposed algorithms represent a special case of the algorithm first introduced by Elashoff and Ryan (2004), where an EM algorithm has been established for very general estimating equations. Here, in the M-step, it is suggested to solve a complete data estimating equation of the form

$$\begin{aligned} \varPsi (y; X, \tau )=(\varPsi _\pi (y;X, \tau ), \varPsi _\beta (y;X, \tau ), \varPsi _\sigma (y;X, \tau ) )^{^\mathrm T}=0 \end{aligned}$$
(10)

with

$$\begin{aligned} \varPsi _\pi (y;X, \tau ) & = (\varPsi _{\pi _1}(y;X, \tau ), \ldots , \varPsi _{\pi _K}(y;X, \tau ))^{^\mathrm T},\\ \varPsi _\beta (y;X, \tau )& = (\varPsi _{\beta _1}(y;X, \tau ), \ldots , \varPsi _{\beta _K}(y;X, \tau ))^{^\mathrm T},\\ \varPsi _\sigma (y;X, \tau )& = (\varPsi _{\sigma _1}(y;X, \tau ), \ldots , \varPsi _{\sigma _K}(y;X, \tau ))^{^\mathrm T} \end{aligned}$$

and

$$\begin{aligned} \varPsi _\pi (y;X, \tau )& = \sum _{i=1}^n \psi _{\pi _j}(y_i; \tau )u_{ij}=\sum _{i=1}^n w(y_i; \tau , \hat{F}) s_{\pi _j}(y_i;\tau )u_{ij}, \\ \varPsi _\beta (y;X, \tau )& = \sum _{i=1}^n \psi _{\beta _j}(y_i; \tau )u_{ij}=\sum _{i=1}^n w(y_i; \tau , \hat{F}) s_{\beta _j}(y_i;\tau )u_{ij}, \\ \varPsi _\sigma (y;X, \tau )& = \sum _{i=1}^n \psi _{\sigma _j}(y_i; \tau )u_{ij}=\sum _{i=1}^n w(y_i; \tau , \hat{F}) s_{\sigma _j}(y_i;\tau )u_{ij}. \\ \end{aligned}$$

Very general conditions for consistency and asymptotic normality of the solution to (10) are given in Elashoff and Ryan (2004), whereas Bai et al. (2012) gives conditions in the case of M-estimators. The main requirements are that

  1. 1.

    \(\psi\) defines an unbiased estimating function, i.e. \(E_\tau [\psi (Y; X,\tau )]=0\);

  2. 2.

    \(E_\tau [\varPsi (Y;X, \tau )\varPsi (Y;X, \tau )^{^\mathrm T}]\) exists and is positive definite;

  3. 3.

    \(E_\tau [\partial \varPsi (Y;X, \tau )/\partial \tau ]\) exists and is negative definite, \(\forall \tau\).

This conditions are satisfied by the proposed WLEE, that are characterized by weighted score functions as in (10) (see also the Supplementary material in Agostinelli and Greco (2019)). Since the WLEE can be considered as M-type estimating equations and all the above requirements are fulfilled, one can state the following result, along the lines of Bai et al. (2012). Under the regularity conditions of Sect. 2, under the further identifiability conditions of the model (4) given in Hennig (2000), existence, consistency and asymptotic normality of the WLE \(\hat{\tau }^{w}\) implicitly defined by equation (10) hold. In particular, the asymptotic covariance matrix of \(\hat{\tau }^{w}\) can be obtained in the usual sandwich fashion. Consistency is defined conditionally on the true labels and concerns the case in which the WLEE admits a unique solution. In the presence of multiple solutions, the selection of the consistent root can be effectively pursued according to the strategies described in Sect. 4.

6 Outlier detection

The WEM and WCEM algorithms lead to classify all the sample units, both genuine and contaminated observations, meaning that also outliers are assigned to a cluster. Actually, we are not interested in classifying outliers and for purely clustering purposes outliers have to be discarded. Outlier detection should be based on the robust fitted model and performed separately by using formal rules. The key ingredients in outlier detection are the (scaled) residuals. For a fixed significance level \(\alpha\), an observation is flagged as an outlier when the corresponding residual in absolute value exceeds a fixed threshold, corresponding to the \((1-\alpha /2)\)-level quantile of the reference standard normal distribution. In the case of finite mixtures, the main idea is that the outlyingness of each data point should be measured conditionally on the final assignment (Greco and Agostinelli 2020), i.e. an observation is flagged as outlying when

$$\begin{aligned} \frac{|y_i-\hat{\mu }_{ik_i}|}{\hat{\sigma }_{k_i}} > z_{1-\frac{\alpha }{2}} \end{aligned}$$
(11)

with \(\hat{\mu }_{ik_i}=x_i\hat{\beta }_{k_i}\). Popular choices are \(\alpha =0.05\) and \(\alpha =0.01\). The process of outlier detection may result in type-I and type-II errors. In the former case, a genuine observation is wrongly flagged as outlier (swamping), in the latter case, a true outlier is not identified (masking). Swamped genuine observations are false positives, whereas masked outliers are false negatives. A measure of the level of the test is provided by the rate of false positives, whereas the power of the testing procedure is given by the rate of true positives. A large number of flagged outliers is expected to lead to high power but, then, genuine observations are likely to be misclassified, that is swamping also increases. On the other side, with a low rate of correctly flagged true outliers, the power and the level are expected to both decrease. The outliers detection process could also be designed to take into account multiplicity arguments in the simultaneous testing of all the n data points. For instance, one could base the outlier detection rule on the False Discovery Rate (FDR, Cerioli and Farcomeni (2011)).

7 Illustrative examples with synthetic data

The overall behavior of WEM and WCEM is illustrated in the following examples based on simulated data. The proposed methodology has been tested on some data configurations that have been already used in the literature concerning robust fitting of mixtures of regression lines. The interest lies on both fitting and classification accuracy and in the outlier detection testing rule. The WLEE are based on a symmetric Chi-squared RAF. For each example, we display the data with their original clustering and the true regression lines superimposed and, in separated panels, the results stemming from WEM and WCEM. The outlier detection rule relies on the FDR at a \(5\%\) level. We use different symbols and colors for the clusters with a black \(+\) standing for the detected outliers (and the true outliers in the panel with the true assignments). In every situation the classical EM and CEM algorithms give unreliable results because of contamination in the sample at hand.

Example 1

Let us consider a mixture of three simple normal linear regressions. The regression lines were generated according to the models

$$\begin{aligned} \left\{ \begin{array}{l} y_1=3+1.4x+0.1\epsilon \\ y_2=3-1.1x+0.1\epsilon \\ y_3=0.2x+0.1\epsilon \\ \end{array} \right. \end{aligned}$$

with \(\epsilon \sim N(0,1)\) (Neykov et al. 2007). The clusters’ sizes are 70, 70, 60, respectively. Then 50 outliers were added that are uniformly distributed in the rectangle that contains the genuine data points. Outliers are such that their distance from the true regression lines, as measured by the scaled residual in absolute value, is above the 0.95-level quantile of the standard normal distribution. The data, the fitted models and the final classification are displayed in Fig. 2: the left panel gives the true assignments and the true lines, the middle panel and the right panel display the results stemming from WEM and WCEM, respectively, with \(c_\sigma =2\). The weighted likelihood methodology provides quite satisfactory outcomes both in terms of fitting and classification accuracy.

Fig. 2
figure 2

Example 1. True assignments (left), WEM (middle), WCEM (right)

Full size image

To illustrate the problem concerning the initialization of the WEM and WCEM algorithms combined with the choice of \(c_\sigma\) and the selection of the best root, we consider different starting points obtained by varying the tuning parameters of TCLUST \((\alpha , c)\), for a fixed \(h=0.015\) and \(c_\sigma =2,20\). The top row panels of Fig. 3 display the empirical downweighting level at convergence stemming from WEM. In each monotoring plot, three groups of solutions are apparent: in the central part we find the majority of solutions leading to a correct downweighting level (root 1), in the bottom left corner there are some solutions characterized by insufficient downweighting (root 2), whereas in the top right corner there are those solutions characterized by an excess of downweighting (root 3). Examples of root 2 and root 3 are given in the bottom row panels of Fig. 3, respectively. The root selection criterion based on the minimum fitted approximate disparity (9) leads to choose the right solution: we have \(\tilde{\rho }(f^*, m^*)=0.96\) for root 1, \(\tilde{\rho }(f^*, m^*)=1.31\) for root 2 and \(\tilde{\rho }(f^*, m^*)=1.58\) for root 3.

Fig. 3
figure 3

Example 1. Top row: monitoring of \(1-\bar{w}\) by varying \((\alpha , c)\) of the intial TCLUST for \(c_\sigma =2\) (left) and \(c_\sigma =20\). Bottom row: WEM root 2 (middle) and WEM root 3 (right)

Full size image

Example 2

Let us consider a mixture of two regression lines. Genuine data are drawn according to the model

$$\begin{aligned} \left\{ \begin{array}{l} y_1=1+x+\epsilon \\ y_2=3+5x+\epsilon \\ \end{array} \right. \end{aligned}$$

with \(\epsilon \sim N(0,1)\) (Bai et al. 2012). Each group is composed by 100 points. By looking at the plots in Fig. 4, we notice that the two clusters are overlapped and the regression lines share the same sign of the slope. Then, 20 clustered bad leverage points are added in the top left corner that violate the patterns exhibited by the genuine points. In this scenario, both the classical EM and CEM lead to a fitted mixture in which one fitted component is wrongly rotated and attracted by the outliers, whereas the other is not able to fit neither of the two true linear structures. On the contrary, the behavior of the robust techniques is satisfactory. Here we set \((\alpha , c ,c_\sigma )=(0.25,2,2)\).

Fig. 4
figure 4

Example 2. True assignments (left), WEM (middle), WCEM (right)

Full size image

Example 3

Let us consider a data constellation inspired by García-Escudero et al. (2009). We have a mixture of three linear models disposed according to a slanted \(\pi\) configuration. The sample size is 300, data are simulated according to equal membership probabilities. There are 50 outliers that are of two types: 25 are scattered in the rectangle that contains the genuine observations, 25 are inliers, since they lie between the linear patterns. Figure 5 displays the data and the results. The weighted likelihood methodology still provides accurate and satisfactory results. Here we set \((\alpha , c ,c_\sigma )=(0.25,50,2)\).

Fig. 5
figure 5

Example 3. True assignments (left), WEM (middle), WCEM (right)

Full size image

Example 4

Here, we consider a data constellation similar to that analyzed in García-Escudero et al. (2017) (see their Fig. 6). The solutions displayed in the middle and right panel of Fig. 6 have been obtained for \(c_\sigma =5\). The initial TCLUST settings are \((\alpha , c)=(0.25,10)\). The results are in strong agreement with those stemming from TCWRM, that, nevertheless, needs the specification of a further constraint on the eigenvalues in the covariates’ space.

Fig. 6
figure 6

Example 4. True assignments (left), WEM (middle), WEM (right)

Full size image

Example 5

This example has been taken from García-Escudero et al. (2010). In that paper, tha authors proposed TCLUST-REG allowing for a second trimming step to handle those data points acting as bad leverage points for the linear regressions. On the contrary, weighted likelihood regression is able to deal with outliers in the x-space and, according to our experience, there is not the need to introduce a second trimming. The data includes two linear regression clusters made up of 225 observations each from the model

$$\begin{aligned} \left\{ \begin{array}{l} y_1=1+x+0.5\epsilon \\ y_2=10-0.5x+0.5\epsilon \\ \end{array} \right. \end{aligned}$$

with \(\epsilon \sim N(0,1)\). Then, 30 points are generated as a background noise and, finally, 20 more data points are concentrated around the point (10, 8.5), acting as bad leverage points in the estimation of one linear structure. This data configuration will be also considered in the numerical studies in Sect. 9 as a part of larger numerical study following the lines of García-Escudero et al. (2010). Figure 7 displays the true assignments with the true lines and the fitted models by WEM and WCEM, with \((\alpha , c, c_\sigma )=(0.25, 10, 2)\). In the middle and right panel, we superimposed both the true lines and the regression lines fitted by the trimmed likelihood, to better appreciate the nice behavior of WEM and WCEM in this scenario, since the trimmed likelihood approach of Neykov et al. (2007) is not able to take into account bad leverages. Actually, trimmed likelihood estimation suffers from the presence of the group of bad leverages, since one regression line is rotated towards their direction. On the contrary, the weighted likelihood technique still gives robust estimates, in a fashion similar to TCLUST-REG, but without any second trimming. It is worth noting that both WEM and WCEM wrongly classify some data points, even if characterized by large uncertainties. Actually, the misclassified points by WEM and WCEM are about those trimmed in the second step of TCLUST-REG.

Fig. 7
figure 7

Example 5. True assignments (left), WEM (middle), WCEM (right)

Full size image

8 Selecting the number of latent classes

The choice of the number of latent classes K is more than an open issue in latent class modeling. In the classical likelihood-based framework, a very general approach is to minimize over K some complexity-penalized version of the (negative) loglikelihood function, such as the well known BIC, AIC and ICL. Agostinelli (2002) and Greco and Agostinelli (2020) tackled the problem of model selection by introducing a weighted version of the AIC and BIC respectively, in which the genuine loglikelihood is replaced by its weighted counterpart evaluated at the WLE. Then, the proposed strategy is based on minimizing

$$\begin{aligned} Q^w(K)=-2q^{w}(y; \hat{\tau })+m(K) \end{aligned}$$
(12)

where \(q^w(y; \hat{\tau })=\sum _{i=1}^{n} \hat{w}_{ik_i}\ell (y_i;\hat{\tau })\) and the weights are those stemming from the largest fitted model (Agostinelli 2002). An alternative criterion can be built on the idea of minimum disparity by minimizing a penalized approximate disparity

$$\begin{aligned} D^w(K)= 2n\tilde{\rho }_k(f^*, m^*)+m(K), \end{aligned}$$
(13)

where the subscript now is meant to stress the dependency on the number of latent classes. The penalty term m(K) reflects model complexity depending on the number of free parameters. Since the larger the scatter similarity constraint the higher model complexity, Cerioli et al. (2018a) suggested a modified version of the penalty term \(m(K, c_\sigma )\) that is also aimed at taking into account model complexity entailed by scatter similarity constraints.

For illustration purposes, let us consider the synthetic data used in Example 1. We tackle the problem of choosing between \(K=2\), \(K=3\) and \(K=4\) components. The results are shown in Table 1: both criteria (12) and (13) lead to choose the right number of latent classes (in bold).

Table 1 Example 1: selection of the number of latent classes
Full size table

It is worth to point out that criteria such those defined in (12) and (13) should be better used in conjunction with appropriate monitoring strategies, for instance by investigating their behavior as the smoothing parameter h varies (Agostinelli and Greco 2018; Farcomeni and Dotto 2018). In particular, at least in this example, the choice \(K=2\) always leads to a remarkable larger empirical downweighting level for every value of h.

9 Numerical studies

In this section the finite sample behavior of the proposed WEM and WCEM methodologies has been investigated by some numerical studies. We consider a mixture of two regression lines, i.e. with \(p=2\), according to the model described in Example 5. Here, by following the lines of García-Escudero et al. (2010), the covariates in the second groups are drawn from a uniform distribution \(U(D,D+7)\), where the tuning parameter D controls the degree of overlapping by setting 3, 6, 12. Two different degrees of complexity have been taken into account: in the first we set equal clusters’ proportions \(\pi _1=\pi _2\) and scales \(\sigma _1=\sigma _2=0.5\), whereas in the second we assumed unequal proportions and variances, with \(\pi _1=0.4\), \(\pi _2=0.6\), and \(\sigma _1=0.4, \ \sigma _2=0.6\). The behavior of WEM and WCEM has been investigated both when any contamination does not occur (\(\epsilon =0\)) and when outliers are present. For what concerns the contamination rates, we set \(\epsilon =10\%, 25\%\). Two types of outliers configurations have been considered. In the first scenario, outliers are generated as background noise (Cont.1), whereas in the second scenario we have both background noisy points and bad leverage points concentrated around a point mass (Cont.2). The considered sample size is \(n=500\). Table 2 summarizes the structure of the data for each combination of complexity, scenario and outliers’ rate. Furthermore, we also considered the case with \(p=4\) by adding uninformative explanatory variables, that is the corresponding coefficients are set to zero. In summary, the numerical studies are composed by \(2\times 5 \times 3\times 2=60\) separate simulations. The numerical studies are based on 500 Monte Carlo trials.

Table 2 Data configurations used in the numerical studies with \(n=500\), \(p=2, 4\)
Full size table

The weighted likelihood algorithms are based on a symmetric Chi-square RAF. The smoothing parameter h has been selected in such a way that the empirical downweighting level lies in the range (0.15, 0.20) for \(\epsilon =0.10\) and (0.35, 0.45) for \(\epsilon =0.25\), whereas it is about 0.10 when no outliers occur. We set \((\alpha , c, c_\sigma )=(0.25, 10, 2)\). The algorithm is assumed to reach convergence when \(\max |\hat{\beta }^{(s+1)}-\hat{\beta }^{(s)}| < tol\), with a tolerance tol set to \(10^{-4}\), where \(\hat{\beta }^{(s)}\) is the matrix of centroids estimates at the sth iteration and the differences are elementwise. The algorithms run on non-optimized R code.

Fitting accuracy has been evaluated according to the Mean Squared Error (MSE) for the mixture parameters, whereas classification accuracy has been measured by the Adjusted Rand Index (ARI) evaluated over true negatives, i.e. genuine observations that are not wrongly declared outliers. In order to detect outliers, we considered a testing rule with \(\alpha =0.01\), according to (11). In addition, we also adopted a strategy based on the FDR for the same overall level, in order to take into account multiplicity effects. Then, we reported the empirical level and power of the test, measured as the swamping rate and the rate of true positives respectively, as explained in Sect. 6. Of course, when \(\epsilon =0\), swamping only is taken into account. The performance of the proposed WEM and WCEM has been compared with the classical EM and CEM (fitted by using the functions available from the R package flexmix), their M-type counterparts, MEM and MCEM, based on M-estimation at the M-step and TCLUST-REG. Here, we considered M-estimation based on the Tukey biweight function for an \(85\%\) efficiency level, whereas TCLUST-REG runs with the first trimming level set equal to 0.10 for \(\epsilon =0\) and the actual contamination rate under contamination and the second trimming level set to 0.15, as in García-Escudero et al. (2010). It is worth to point out that TCLUST-REG is built on a CEM-type algorithm. We implemented our own non optimized R code according to the details given in García-Escudero et al. (2010). In particular, we use the same starting values used for WEM and WCEM. In order to make a fair comparison across the different methodologies, we stress that, according to existing literature about it, we do not consider any testing strategy after TCLUST-REG but trimmed observations coincide with detected outliers.

As an overall result, we do appreciate the satisfactory behaviour of WEM and WCEM in terms of both classification and fitting accuracy. In particular, the superiority of WEM and WCEM with respect to the oracle TCLUST-REG make them quite valuable and promising. WEM and WCEM exhibit a satisfactory efficiency loss at the true model when contamination does not occur, whereas they provide stable results under contamination by dealing with outliers successfully. All Tables showing the detailed results of the numerical studies are given in the Appendix. The entries in Table 4 give the ARI evaluated over true negatives after that outliers have been discarded according to a testing rule based on a fixed \(1\%\) level or by controlling the overall level of the multiple testing procedure by using the FDR, when \(p=2\). The results are quite satisfactory both for the genuine and contaminated data. The classification accuracy clearly improves for increasing values of the tuning parameter D and there are no relevant differences when using a fixed level or multiplicity issues are taken into account. Table 8 give the results for the case \(p=4\). Table 5 gives the MSE corresponding to the fitted mixture parameters \((\beta , \sigma , \pi )\) stemming from all the considered techniques, for \(p=2\), the entries in Table 9 give the results for the case \(p=4\). The overall behavior of WEM and WCEM is quite accurate.

Here, in order to present the results, the simulation setting has been divided in 9 macro scenarios by collapsing them with respect to \(\epsilon =0, 0.10, 0.25\) and \(D=3,6,12\). The empirical distribution of the ARI is displayed in Fig. 8. The results corresponding to the overlapping level \(D=12\) have not been reported since classification accuracy is almost always perfect for all macro-scenarios and procedures. Furthermore, the ARI for maximum likelihood under contamination is not given since it is well below those stemming from the robust techniques. The reader is pointed to the Tables given in the Appendix section. Classification accuracy provided by WEM and WCEM is quite satisfactory. We notice that WEM and WCEM improves over TCLUST-REG, in particular in the challenging case \(D=3\). Figure 9 gives the empirical distribution of the Sum of Squares for the regression coefficients. The overall behavior of WEM and WCEM is quite accurate in all macro scenarios. The loss of efficiency with respect to maximum likelihood is negligible when no outliers occurs. The performance with respect to M-based techniques is often quite similar. On the other hand, WEM and WCEM improve over the oracle TCLUST-REG, in particular for \(D=6, 12\).

Fig. 8
figure 8

ARI for WEM, WCEM, MEM, MCEM, TCLUST-REG, EM for \(\epsilon =0\) (top), \(\epsilon =0.10\) (middle) \(\epsilon =0.25\) (right) and \(D=3\) (left), \(D=6\) (right)

Full size image
Fig. 9
figure 9

MSE for WEM, WCEM, MEM, MCEM, TCLUST-REG, EM for \(\epsilon =0\) (top), \(\epsilon =0.10\) (middle) \(\epsilon =0.25\) (right) and \(D=3\) (left), \(D=6\) (middle), \(D=12\) (right)

Full size image

Swamping and power of the outliers tests are given in Tables 6 and 7, respectively, for \(p=2\), whereas Table 10 and Table 10 give the results for \(p=4\). It is worth to stress that the behavior of the tests depends on the actual robustness-efficiency trade-off of the procedure, that is on the value of the selected bandwidth parameter h for weighted likelihood estimation. In summary, the chosen values of h lead to an appreciable compromise between swamping and power. WEM and WCEM well compares with the results stemming from the other methods, in particular with TCLUST-REG. It is worth to notice that FDR leads to improved swamping but lower power than those resulting from the use of a fixed threshold (Cerioli et al. 2018a).

10 Pinus nigra data set

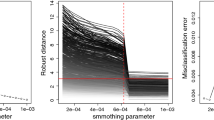
The data gives the height (in meters) and diameter (in millimeters) of \(n=362\) Pinus nigra trees located in the north of Palencia (Spain). The Diameter is considered as an explicative variables wheres Height is the response. The data are displayed in the left panel of Fig. 11. They exhibit the presence of three linear groups apart from a small group of trees forming its own cluster on the top right corner and one isolated point on the bottom right corner. The example has been taken from García-Escudero et al. (2010). We ran WEM and WCEM by setting \(h=0.01\), with \(c_\sigma =2\) and employing a symmetric chi square RAF. The starting solution stems from an unconstrained TCLUST (actually \(c=500\)) wth \(\alpha =0.1\). The same solution has been obtained by using the denoising approach suggested by Coretto and Hennig (2017). The smoothing parameter has been selected according to a monitoring strategy. The left panel of Fig. 10 shows the empirical downweighting level as h varies on a fixed grid. We selected the value where the empirical downweighting level stabilizes. By monitoring the change in individual residuals (in absolute value) as h varies, we observe that the clustered outliers and the isolated outlier are clearly spotted during all the monitoring process and that the other data points have residuals below the threshold line for most of the monitoring. Here, the cut-off has been set equal to the square root of the qth quantile of the \(\chi ^2_1\) distribution with \(q=1-0.99^{1/n}\), by using a Bonferroni adjustment to take into account multiplicity. The fitted models and detected outliers are shown in Fig. 11. The outlier detection rule is based on the FDR at \(1\%\) level. The results are in strong agreement with those stemming from TCLUST-REG. Evidence for the choice \(K=3\) has been confirmed by using the criteria (12) and (13), as given in Table 3.

Fig. 10
figure 10

Pinus nigra. Monitoring of the empirical downweighting level (left) and clusterwise residuals (right) from WEM

Full size image
Fig. 11
figure 11

Pinus nigra. Fitted mixtures by WEM (left) and WCEM (right). Clusters are denoted by different colors and symbols. Outliers are denoted by +

Full size image
Table 3 Pinus nigra
Full size table

The fitted model suggests that a more parsimonious mixture model characterized by homogeneous slopes may be fitted to the data at hand. To this end, we ran the WEM algorithm by assuming homogeneous slopes, that is using the estimating equations given in (8) for what concerns the estimation of the three class-dependent intercepts and the common slope. The fitted slope is \(\hat{\beta }_{-0}=0.015\), whereas the fitted intercepts are \((\hat{\beta }_1, \hat{\beta }_2, \hat{\beta }_3)=(3.75, 7.41, 10.44)\). The outlier detection rule (6) leads to identify the same data points. In order to test if there is evidence supporting the reduced model with homogeneous slopes, one could resort to the weighted likelihood ratio test (WLRT) developed in Agostinelli and Markatou (2001). The WLRT is obtained as

$$\begin{aligned} \Lambda ^{oss}=2\sum _{i=1}^n\hat{w}_{i}\left[ \ell (y_i; \hat{\tau })-\ell (y_i; \hat{\tau }_R)\right] \end{aligned}$$

where \(\hat{\tau }_R\) denotes the WLE under the reduced model. In this example we have \(\Lambda ^{oss}=2.45\) with a p-value \(Prob\left( \chi ^2_2>2.45\right) =0.29\), confirming evidence for the reduced model against the full model with class dependent slopes.

11 Concluding remarks

In this paper we developed weighted likelihood estimation for mixtures of linear structures in the presence of contamination in the data at hand. The proposed techniques behave satisfactory in all the considered scenario providing both fitting and classification accuracy. Furthermore, the suggested outliers detection rule exhibits reasonable level and power. The method inherits the main properties characterizing weighted likelihood estimation both in terms of efficiency at the assumed model and robustness in the presence of outliers. Both the WEM and WCEM compare satisfactory with existing methods. One of the main aspects concerns the selection of the smoothing parameter tuning the efficiency/robustness trade-off in finite samples. However, the same problem arises for the other robust techniques that all need some constant to be tuned. The researcher is advised to resort to a monitoring strategy for an effective tuning. Then, one clear advantage of the method is the availability of weighted counterparts of the likelihood ratio test and the information criteria with the standard asymptotic behavior.

Some possible further directions of research could concern initialization issues in order to reduce the number of initial partitions but also more challenging model selection problems that were out of the scope of the present paper, indeed. Moreover, the extension of the proposed methodology to mixtures of linear regressions with concomitant variables or to mixtures of generalized linear models seems feasible.