Weighted likelihood mixture modeling and model-based clustering

Abstract

A weighted likelihood approach for robust fitting of a mixture of multivariate Gaussian components is developed in this work. Two approaches have been proposed that are driven by a suitable modification of the standard EM and CEM algorithms, respectively. In both techniques, the M-step is enhanced by the computation of weights aimed at downweighting outliers. The weights are based on Pearson residuals stemming from robust Mahalanobis-type distances. Formal rules for robust clustering and outlier detection can be also defined based on the fitted mixture model. The behavior of the proposed methodologies has been investigated by numerical studies and real data examples in terms of both fitting and classification accuracy and outlier detection.

1 Introduction

Multivariate normal mixture models represent a very popular tool for both density estimation and clustering (McLachlan and Peel 2004). The parameters of a mixture model are commonly estimated by maximum likelihood by resorting to the EM algorithm (Dempster et al. 1977). Let $y=(y_1,y_2,\ldots ,y_n)^{^\top }$ be a random sample of size n. The mixture likelihood can be expressed as

$$\begin{aligned} L(y; \tau )=\prod _{i=1}^n\sum _{k=1}^K \pi _k\phi _p(y_i; \mu _k,\varSigma _k) \ , \end{aligned}$$

(1)

where $\tau =(\pi , \mu _1, \ldots , \mu _K, \varSigma _1, \ldots , \varSigma _K)$, $\phi _p(\cdot ;\cdot )$ is the p-dimensional multivariate normal density, $\pi =(\pi _1,\ldots ,\pi _K)$ denotes the vector of prior membership probabilities and $(\mu _k,\varSigma _k)$ are the mean vector and variance-covariance matrix of the $k\mathrm{th}$ component, respectively. Rather than using the likelihood in (1), the EM algorithm works with the complete likelihood function

$$\begin{aligned} L^c(y;\tau )=\prod _{i=1}^n\prod _{k=1}^K \left[ \pi _k\phi _p(y_i; \mu _k,\varSigma _k) \right] ^{u_{ik}}\ , \end{aligned}$$

(2)

where $u_{ik}$ is an indicator of the $i\mathrm{th}$ unit belonging to the $k\mathrm{th}$ component. The EM algorithm iteratively alternates between two steps: expectation (E) and maximization (M). In the E-step, the posterior expectation of (2) is evaluated by setting $u_{ik}$ equal to the posterior probability that $y_i$ belongs to the $k\mathrm{th}$ component, i.e.

$$\begin{aligned} u_{ik}\propto \pi _k\phi _p(y_i; \mu _k,\varSigma _k) \ , \end{aligned}$$

whereas at the M-step $\pi$, $\mu _k$ and $\varSigma _k$ are estimated conditionally on $u_{ik}$.

An alternative strategy is given by the penalized classification EM (CEM) algorithm (Symon 1977; Bryant 1991; Celeux and Govaert 1993): the substantial difference is that the E-step is followed by a C-step (where C stands for classification) in which $u_{ik}$ is estimated as either 0 or 1, meaning that each unit is assigned to the most likely component, conditionally on the current parameters’ values, i.e. $k_i=\mathrm {argmax}_k u_{ik}$, $u_{ik_i}=1$ and $u_{ik}=0$ for $k\ne k_i$. The classification approach is aimed at maximizing the corresponding classification likelihood (2) over both the mixture parameters and the individual components’ labels. In the case $\pi _k=1/K$, then the standard CEM algorithm is recovered. A detailed comparison of the EM and CEM algorithms can be found in Celeux and Govaert (1993).

When the sample data are prone to contamination and several unexpected outliers occur with respect to (w.r.t.) the assumed mixture model, maximum likelihood is likely to lead to unrealistic estimates and to fail in recovering the underlying clustering structure of the data (see Farcomeni and Greco 2015a, for a recent account). In the presence of noisy data that depart from the underlying mixture model, there is the need to replace maximum likelihood with a suitable robust procedure, leading to estimates and clustering rules that are not badly affected by contamination.

The need for robust tools in the estimation of mixture models has been first addressed in Campbell (1984), who suggested to replace standard maximum likelihood with M-estimation. In a more general fashion, Farcomeni and Greco (2015b) proposed to resort to multivariate S-estimation of location and scatter in the M-step. Actually, the authors focused their attention on hidden Markov models, but their approach can be adapted from dynamic to static finite mixtures. According to such strategies, each data point is attached a weight lying in [0, 1] (a strategy commonly addressed as soft trimming). An alternative approach to robust fitting and clustering is based on hard trimming procedures, i.e. a crispy weight $\left\{ 0, 1\right\}$ is attached to each observation: atypical observations are expected to be trimmed, and the model is fitted by using a subset of the original data. The tclust methodology (Garcia-Escudero et al. 2008; Fritz et al. 2013) is particularly appealing: model parameters are estimated by developing a penalized CEM algorithm augmented with an impartial trimming step. Very recent extensions have been discussed in Dotto et al. (2016), who proposed a reweighted trimming procedure (rtclust) and Dotto and Farcomeni (2019), in which trimming has been introduced in parsimonious model-based clustering (mtclust). A related proposal has been presented in Neykov et al. (2007) based on the so-called trimmed likelihood methodology. Furthermore, it is worth to mention that mixture model estimation and clustering can be also implemented by using the adaptive hard trimming strategy characterizing the Forward Search (Atkinson et al. 2013).

There are also different proposals aimed at being robust that are not based on soft or hard trimming procedures. Some of them are characterized by the use of flexible components in the mixture. The idea is that of embedding the Gaussian mixture in a supermodel: McLachlan and Peel (2004) introduced a mixture of Student’s t distributions, a mixture of skewed Student’s t distributions has been proposed in Lin (2010) and Lee and McLachlan (2014), whereas Fraley and Raftery (1998, 2002) considered an additional component modeled as a Poisson process to handle noisy data (the method is available from package mclust (Fraley et al. 2012) in R (R Core Team 2019). A robust approach, named otrimle, has been proposed recently by Coretto and Hennig (2016, 2017), who considered the addition of an improper uniform mixture component to accommodate outliers.

We propose a robust version of both the EM and the penalized CEM algorithms to fit a mixture of multivariate Gaussian components based on soft trimming, in which weights are evaluated according to the weighted likelihood methodology (Markatou et al. 1998). A first attempt in this direction has been pursued by Markatou (2000). Here, that approach has been developed further and made more general leading to a newly established technique, in which weights are based on the recent results stated in Agostinelli and Greco (2018). The methodology leads to a robust fit and is aimed at providing both cluster assignment of genuine data points and outlier detection rules. Data points flagged as anomalous are not meant to be classified into any of the clusters. Furthermore, a relevant aspect of our proposal is represented by the introduction of constraints, not considered in Markatou (2000), aimed at avoiding local or spurious solutions (Fritz et al. 2013).

Some necessary preliminaries on weighted likelihood estimation are given in Sect. 2. The weighted EM and penalized CEM algorithms are introduced in Sect. 3: some computational details are discussed concerning constraints, initialization issues, the tuning of the methods and classification and outlier detection rules are outlined. Section 4 states asymptotic results, whereas Sect. 5 is devoted to model selection. Numerical studies are presented in Sect. 6, and real data examples are discussed in Sect. 7.

2 Background

Let us assume a mixture model composed by K heterogeneous multivariate Gaussian components, where K is fixed in advance, with density function denoted by $m(y;\tau )=\sum _{j=1}^K\pi _j\phi _p(y_i;\mu _j, \varSigma _j)$. Markatou (2000) suggested to work with the following weighted likelihood estimating equation (WLEE) in the M-step of the EM algorithm:

$$\begin{aligned} \sum _{i=1}^n w_i \sum _{j=1}^k u_{ij}\frac{\partial }{\partial \nu }\left[ \log \pi _j +\log \phi _p(y_i;\mu _j, \varSigma _j)\right] =0 \ . \end{aligned}$$

(3)

We notice that maximum likelihood equations are replaced by weighted equations. The weights are defined as

$$\begin{aligned} w_i=w(\delta (y_i)) = \frac{\left[ A(\delta (y_i)) + 1\right] ^+}{\delta (y_i) + 1} \ , \end{aligned}$$

(4)

where $[\cdot ]^+$ denotes the positive part, $\delta (y)$ is the Pearson residual function and $A(\delta )$ is the residual adjustment function (RAF, Basu and Lindsay 1994). The Pearson residual gives a measure of the agreement between the assumed model $m(y; \tau )$ and the data that are summarized by a nonparametric density estimate ${\hat{m}}_n(y)=n^{-1}\sum _{i=1}^n k(y; y_i, h)$, based on a kernel k(y; t, h) indexed by a bandwidth h, that is

$$\begin{aligned} \delta (y) = \frac{{\hat{m}}_n(y) }{m(y; \tau )}-1 \ , \end{aligned}$$

(5)

with $\delta \in [-1, \infty )$. In the construction of Pearson residuals, Markatou (2000) suggested to use a smoothed model density in the continuous case, by using the same kernel involved in nonparametric density estimation (see Basu and Lindsay 1994; Markatou et al. 1998, for general results), i.e.

$$\begin{aligned} m^*(y; \tau )=\int k(y;t,h) m(t;\tau ) \mathrm{d}t. \end{aligned}$$

When the model is correctly specified, the Pearson residual function (5) evaluated at the true parameter value converges almost surely to zero, whereas, otherwise, for each value of the parameters, large Pearson residuals detect regions where the observation is unlikely to occur under the assumed model. The weight function (4) can be chosen to be unimodal so that it declines smoothly as the residual $\delta (y)$ departs from zero. Hence, those observations lying in such regions are attached a weight that decreases with increasing Pearson residual. Large Pearson residuals and small weights will correspond to data points that are likely to be outliers. The RAF plays the role to bound the effect of large residuals on the fitting procedure, as well as the Huber and Tukey bisquare function bound large distances in M-estimation and we assume is such that $|A(\delta )|<|\delta |$. Here, we consider the families of RAF based on the Power Divergence Measure

$$\begin{aligned} A_{pdm}(\delta ) = \left\{ \begin{array}{lc} \nu \left( (\delta + 1)^{1/\nu } - 1 \right) &{}\quad \nu < \infty \\ \log (\delta + 1) &{}\quad \nu \rightarrow \infty \end{array} \right. \end{aligned}$$

Special cases are maximum likelihood ($\nu = 1$, as the weights become all equal to one), Hellinger distance ($\nu = 2$), Kullback–Leibler divergence ($\nu \rightarrow \infty$) and Neyman’s Chi-square ($\nu =-1$). Another example is given by the generalized Kullback–Leibler divergence (GKL) defined as

$$\begin{aligned} A_{gkl}(\delta )=\log (\nu \delta +1)/\nu , \ 0\le \nu \le 1. \end{aligned}$$

Maximum likelihood is a special case when $\nu \rightarrow 0$ and Kullback–Leibler divergence is obtained for $\nu =1$.

The shape of the kernel function has a very limited effect on weighted likelihood estimation. On the contrary, the smoothing parameter h directly affects the robustness/efficiency trade-off of the methodology in finite samples. Actually, large values of h lead to Pearson residuals all close to zero and weights all close to one and, hence, large efficiency, since the kernel density estimate is stochastically close to the postulated (smoothed) model. On the other hand, small values of h make the kernel density estimate more sensitive to the occurrence of outliers and the Pearson residuals become large for those data points that are in disagreement with the model. In other words, in finite samples more smoothing will lead to higher efficiency but larger bias under contamination.

2.1 Multivariate estimation

The computation of weights based on the Pearson residuals given in (5) becomes troublesome with growing dimensions since the data are more sparse and multivariate kernel density estimation may become unfeasible. In order to circumvent this curse of dimensionality, Agostinelli and Greco (2018) proposed a novel technique which is based on the Mahalanobis distances

$$\begin{aligned} d=d(y;\mu ,\varSigma )=[(y-\mu )^{^\top }\varSigma ^{-1}(y-\mu )]^{1/2} \ . \end{aligned}$$

Then, Pearson residuals can be evaluated by comparing a univariate kernel density estimate based on squared distances and their underlying $\chi ^2_p$ distribution at the assumed multivariate normal model, rather than working with multivariate data and multivariate kernel density estimates, that is

$$\begin{aligned} \delta (y)=\frac{{\hat{m}}_n\left( d^2\right) }{m_{\chi ^2_p}\left( d^2\right) }-1 \ , \end{aligned}$$

(6)

where

$$\begin{aligned} {\hat{m}}_n(t)=n^{-1}\sum _{i=1}^n k(t; d^2, h) \end{aligned}$$

is an unbiased at the boundary univariate kernel density estimate over $(0, \infty )$ and $m_{\chi ^2_p}(t)$ denotes the $\chi ^2_p$ density function. It is worth noting that Pearson residuals can be evaluated w.r.t. the original $\chi ^2_p$ density, so avoiding model smoothing (see also Kuchibhotla and Basu 2015, 2018). Assumptions and proofs concerning existence, convergence and asymptotic normality of the WLE of multivariate location and scatter have been also established (see the Supplementary material of Agostinelli and Greco 2018).

3 Weighted likelihood mixture modeling

The technique for weighted likelihood mixture modeling proposed by Markatou (2000) exhibits the same limitations that have been highlighted in Agostinelli and Greco (2018) in the case of weighted likelihood estimation of multivariate location and scatter. The main drawbacks are driven by the employ of multivariate kernels.

The availability of consistent estimators of multivariate location and scatter based on the Pearson residuals (6) is the starting point to build a weighted likelihood methodology to fit robustly the mixture model (5) that is also capable to handle situations in which the number of features is large enough. Therefore, by exploiting the approach developed in Agostinelli and Greco (2018), we propose both a weighted EM algorithm and a weighted penalized CEM algorithm whose M-steps are characterized by a WLEE based on the Pearson residuals (6).

It is worth to notice that the method is expected to work in large dimensions, even if it is still over-parameterized in high-dimensional spaces. The technique is meant for and confined to the $n>p$ case and to dimensions that still allow evaluation of Mahalanobis distances. The development of weighted likelihood methodologies for model-based clustering in very large dimensions and in the $n<p$ situation is beyond the scope of the present work.

The weighted EM algorithm (WEM) is structured as follows:

• 1. Initialization

  $$\begin{aligned} \tau ^{(0)}=(\pi ^{(0)}, \mu _1^{(0)}, \ldots , \mu _K^{(0)}, \varSigma _1^{(0)}, \ldots , \varSigma _1^{(K)}) \ . \end{aligned}$$

  Details on the sensitivity of the results to different initializations and the selection of the best solution will be given in Sect. 3.5.

• 2. E-step the standard E-step is left unchanged, with

  $$\begin{aligned} u_{ik}^{(s)}=\frac{\pi _k^{(s-1)}\phi _p\left( y_i; \mu _k^{(s-1)},\varSigma _k^{(s-1)}\right) }{\sum _{k=1}^K \pi _k^{(s-1)}\phi _p\left( y_i; \mu _k^{(s-1)},\varSigma _k^{(s-1)}\right) } \end{aligned}$$

• 3. Weighted M-step based on current parameter estimates,

  • (a) Soft trimming let us evaluate component-wise Mahalanobis-type distances

    $$\begin{aligned} d_{ik}^{(s)}=d\left( y_i; \mu _k^{(s-1)}, \varSigma _k^{(s-1)}\right) \ . \end{aligned}$$

    Then, for each group, compute Pearson residuals and weights as

    $$\begin{aligned} \delta _{ik}^{(s)}=\frac{{\hat{m}}_n\left( d_{ik}^{(s)^2}\right) }{m_{\chi ^2_p}\left( d_{ik}^{(s)^2}\right) }-1 \end{aligned}$$

    and

    $$\begin{aligned} w_{ik}^{(s)}=\frac{\left[ A\left( \delta _{ik}^{(s)}\right) +1\right] ^+}{\delta _{ik}^{(s)}+1} \end{aligned}$$

    respectively.

  • (b) Update membership probabilities and component-specific parameter estimates

    $$\begin{aligned} \pi _k^{(s+1)}= & {} \frac{\sum \nolimits _{i=1}^n u_{ik}^{(s)}w_{ik}^{(s)}}{\sum _{i=1}^n \sum _{k=1}^Ku_{ik}^{(s)}w_{ik}^{(s)}}\\ \mu _k^{(s+1)}= & {} \frac{\sum \nolimits _{i=1}^n y_i w_{ik}^{(s)}u_{ik}^{(s)}}{\sum _{i=1}^n w_{ik}^{(s)}u_{ik}^{(s)}}\\ \varSigma _k^{(s+1)}= & {} \frac{\sum \nolimits _{i=1}^n \left( y_i-\mu _k^{(s+1)}\right) \left( y_i-\mu _k^{(s+1)}\right) ^{^\top } w_{ik}^{(s)}u_{ik}^{(s)}}{\sum _{i=1}^n w_{ik}^{(s)}u_{ik}^{(s)}} \end{aligned}$$

  • (c) Set$\tau ^{(s+1)}=\left( \pi ^{(s+1)}, \mu _1^{(s+1)}, \ldots , \mu _K^{(s+1)}, \varSigma _1^{(s+1)}, \ldots , \varSigma _K^{(s+1)}\right)$.

It is worth noting that at the M-step it is proposed to solve the following WLEE

$$\begin{aligned} \sum _{i=1}^n \sum _{j=1}^k u_{ij}\frac{\partial }{\partial \tau }\left[ \log \pi _j +\log \phi _p(y_i;\mu _j, \varSigma _j)\right] w_{ij} =0, \end{aligned}$$

(7)

that is characterized by the evaluation of K component-wise sets of weights, rather than one weight for each observation, as in equation (3).

The weighted penalized CEM algorithm (WCEM) is obtained by introducing a standard C-step between the E-step and the weighted M-step. The main feature of the WCEM algorithm is that one single weight is attached to each unit, based on its current assignment after the C-step, rather than component-wise weights. Then, the resulting WLEE shows the same structure as in (3) but with the difference that $u_{ij}=1$ or $u_{ij}=0$. The WCEM is described as follows:

• 1. Initialization

  $$\begin{aligned} \tau ^{(0)}=(\pi ^{(0)}, \mu _1^{(0)}, \ldots , \mu _K^{(0)}, \varSigma _1^{(0)}, \ldots , \varSigma _K^{(0)}) \ . \end{aligned}$$

• 2. E-step

  $$\begin{aligned} u_{ik}^{(s)}=\frac{\pi _k^{(s-1)}\phi _p\left( y_i; \mu _k^{(s-1)},\varSigma _k^{(s-1)}\right) }{\sum _{k=1}^K \pi _k^{(s-1)}\phi _p\left( y_i; \mu _k^{(s-1)},\varSigma _k^{(s-1)}\right) } \end{aligned}$$

• 3. C-step let $k_i^{(s)}=\mathrm {argmax}_k u_{ik}^{(s)}$ identify the cluster assignment for the $i\mathrm{th}$ unit at the $s\mathrm{th}$ iteration. Then

  $$\begin{aligned} {\tilde{u}}_{ik}^{(s)}=\left\{ \begin{array}{cc} 1 &{}\quad \text {if} \ k=k_i,\\ 0 &{}\quad \text {if} \ k\ne k_i.\\ \end{array} \right. \end{aligned}$$

• 4. Weighted M-step based on current parameter estimates $\tau ^{(s)}$ and cluster assignments $k_i$,

  • (a) Soft trimming evaluate the Mahalanobis-type distances of each point w.r.t. the component it belongs in

    $$\begin{aligned} d_{ik_i}^{(s)}=d\left( y_i; \mu _{k_i}^{(s-1)}, \varSigma _{k_i}^{(s-1)}\right) . \end{aligned}$$

    Then, compute the corresponding Pearson residuals and weights as

    $$\begin{aligned} \delta _{ik_i}^{(s)}=\frac{{\hat{m}}_n\left( d_{ik_i}^{(s)^2}\right) }{m_{\chi ^2_p}\left( d^{(s)^2}_{ik_i}\right) }-1 \end{aligned}$$

    and

    $$\begin{aligned} w_i^{(s)}=w_{ik_i}^{(s)}=\frac{\left[ A\left( \delta _{ik_i}^{(s)}\right) +1\right] ^+}{\delta _{ik_i}^{(s)}+1} \end{aligned}$$

    respectively, where

    $$\begin{aligned} {\hat{m}}_n(d^2)&= \frac{1}{\sum _{i=1}^n{\tilde{u}}_{ik_i}} \sum _{i=1}^n k(d^2; d^2_{ik_i}, h) \ , \\&= \frac{1}{\sum _{i=1}^n{\tilde{u}}_{ik}} \sum _{i=1}^n k(d^2; d^2_{ik}, h){\tilde{u}}_{ik} \ . \end{aligned}$$

    Hence, component-wise kernel density estimates only involve distances conditionally on cluster assignment.

  • (b) Update membership probabilities and component-specific parameter estimates

    $$\begin{aligned} \pi _k^{(s+1)}&= \frac{\sum \nolimits _{i=1}^n {\tilde{u}}_{ik}^{(s)}w_{ik_i}^{(s)}}{\sum _{i=1}^n w_{ik_i}^{(s)}} \ , \\ \mu _k^{(s+1)}&= \frac{\sum \nolimits _{i=1}^n y_i w_{ik_i}^{(s)}{\tilde{u}}_{ik}^{(s)}}{\sum _{i=1}^n w_{ik_i}^{(s)}{\tilde{u}}_{ik}^{(s)}}, \\ \varSigma _k^{(s+1)}&= \frac{\sum \nolimits _{i=1}^n \left( y_i{-}\mu _k^{(s+1)}\right) \left( y_i{-}\mu _k^{(s+1)}\right) ^{^\top } w_{ik_i}^{(s)}{\tilde{u}}_{ik}^{(s)}}{\sum _{i=1}^n w_{ik_i}^{(s)}{\tilde{u}}_{ik}^{(s)}} . \end{aligned}$$

  • (c) Set$\tau ^{(s+1)}=\left( \pi ^{(s+1)}, \mu _1^{(s+1)}, \ldots , \mu _K^{(s+1)}, \varSigma _1^{(s+1)}, \ldots , \varSigma _K^{(s+1)}\right)$

It is worth noting that both weighted algorithms return weighted estimates of covariance. The final output can be suitably modified in order to provide unbiased weighted estimates.

3.1 Eigen-ratio constraint

It is well known that maximization of the mixture likelihood (1) or the classification likelihood (2) is an ill-posed problem since the objective function may be unbounded (Day 1969; Maronna and Jacovkis 1974). Therefore, in order to avoid such problems, the optimization is performed under suitable constraints. In particular, we employed the eigen-ratio constraint defined as

$$\begin{aligned}&\frac{\max _j\max _k \lambda _j(\varSigma _k)}{\min _j\min _k \lambda _j(\varSigma _k)} \le c, \qquad j=1,2 \ldots ,p, \quad \nonumber \\&\quad k=1,2,\ldots ,K \end{aligned}$$

(8)

where $\lambda _j(\varSigma _k)$ denoted the $j\mathrm{th}$ eigenvalue of the covariance matrix $\varSigma _k$ and c is a fixed constant not smaller than one aimed at tuning the strength of the constraint. For $c=1$ spherical clusters are imposed, while as c increases varying shaped clusters are allowed. The eigen-ratio constraint (8) can be satisfied at each iteration by adjusting the eigenvalues of each $\varSigma _k^{(s)}$. This is achieved by replacing them with a truncated version

$$\begin{aligned} \lambda _j^*(\varSigma _k)=\left\{ \begin{array}{ll} c &{}\quad \text {if} \ \lambda _j(\varSigma _k) < c \\ \lambda _j(\varSigma _k) &{}\quad \text {if} \ c\le \lambda _j(\varSigma _k) \le c\theta _c \\ c\theta _c &{}\quad \text {if} \ \lambda _j(\varSigma _k) > c\theta _c \\ \end{array} \right. \end{aligned}$$

where $\theta _c$ is an unknown bound depending on c. The reader is pointed to Fritz et al. (2013); Garcia-Escudero et al. (2015) for a feasible solution to the problem of finding $\theta _c$.

3.2 Classification and outlier detection

The WCEM automatically provides a classification of the sample units, since the value of ${\tilde{u}}_{ik}$ at convergence is either zero or one. With the WEM, by paralleling a common approach, a maximum a posteriori criterion can be used for cluster assignment, that is, a C-step is applied after the last E-step. Such criteria lead to classify all the observations, both genuine and contaminated data, meaning that also outliers are assigned to a cluster. Actually, we are not interested in classifying outliers and for purely clustering purposes outliers have to be discarded.

We distinguish two main approaches to outlier detection. According to the first, outlier detection should be based on the robust fitted model and performed separately by using formal rules. The key ingredients in multivariate outlier detection are the robust distances (Rousseeuw and Van Zomeren 1990; Cerioli 2010). The reader is pointed to Cerioli and Farcomeni (2011) for a recent account on outlier detection. An observation is flagged as an outlier when its squared robust distance exceeds a fixed threshold, corresponding to the $(1-\alpha )$-level quantile of the reference (asymptotic) distribution of the squared robust distances. A common solution is represented by the use of the $\chi ^2_p$, and popular choices are $\alpha =0.025$ and $\alpha =0.01$. In the case of finite mixtures, the main idea is that the outlyingness of each data point should be measured conditionally on the final assignment. Hence, according to a proper testing strategy, an observation is declared as outlying when

$$\begin{aligned} d_{ik_i}^2 > \chi ^2_{p;1-\alpha } \ , \ d_{ik_i}^2=(y_i-{\hat{\mu }}_{k_i})^{^\top } {\hat{\varSigma }}_{k_i}(y_i-{\hat{\mu }}_{k_i}) \ . \end{aligned}$$

(9)

The second approach stems from hard trimming procedures, such as tclust, rtclust and otrimle. These techniques are not meant to provide simultaneous robust fit and outlier detection based on formal testing rules, but outliers are identified with those data points falling in the trimmed set or assigned to the improper density component, respectively. Therefore, by paralleling what happens with hard trimming, one could flag as outliers those data points whose weight, conditionally on the final cluster assignment, is below a fixed (small) threshold. Values as 0.10 or 0.20 seem reasonable choices. Furthermore, the empirical downweighting level represents a natural upper bound for the cutoff value that would give an indication of the largest tolerable swamping and of the minimum feasible masking for the given level of smoothing. This approach is motivated by the fact that the multivariate WLE shares important features with hard trimming procedures, even if it is based on soft trimming, as claimed in Agostinelli and Greco (2017).

The process of outlier detection may result in type I and type II errors. In the former case, a genuine observation is wrongly flagged as outlier (swamping); in the latter case, a true outlier is not identified (masking). Swamped genuine observations are false positives, whereas masked outliers are false negatives. According to the first strategy, the larger $\alpha$ the more swamping and the less masking. In a similar fashion, the higher the threshold the more swamping and the less masking will characterize the second approach to outlier detection.

In the following, both approaches to outlier detection will be taken into account and critically compared.

3.3 The selection of h

The selection of h is a crucial task. According to authors’ experience (see Agostinelli and Greco 2018, 2017; Greco 2017, for instance), but also as already suggested by Markatou et al. (1998), a safe selection of h can be achieved by monitoring the empirical downweighting level $(1-\hat{{\bar{\omega }}})$ as h varies, with $\hat{{\bar{\omega }}}=n^{-1}\sum _{i=1}^n {\hat{w}}_i$, where the weights at convergence ${\hat{w}}_i={\hat{w}}_{ik_i}$ are evaluated at the fitted parameter value and conditionally on the final cluster assignment, both for WEM and WCEM, along the lines outlined in Sect. 3.2. The monitoring of WLE analyses has been applied successfully in Agostinelli and Greco (2017) to the case of robust estimation of multivariate location and scatter. The reader is pointed to Cerioli et al. (2017) for an account on the benefits of monitoring. A good strategy in the tuning of the smoothing parameter would be to monitor several quantities of interest stemming from the fitted mixture model in addition to the empirical downweighting level. One could monitor the weighted log-likelihood at convergence, unit-specific robust distances conditionally on the final cluster assignment, unit-specific weights, a misclassification error if a training set with known labels is available. For instance, an abrupt change in the monitored empirical downweighting level or in the robust distances may indicate the transition from a robust to a non-robust fit and aid in the selection of a value of h that gives an appropriate compromise between efficiency and robustness. Values beyond this threshold would lead to at least one arbitrarily biased fitted component that can compromise the accuracy of clustering. It is worth to note that, the trimming level in tclust or the improper density constant in otrimle is selected in a monitoring fashion, as well.

3.4 Synthetic data

Let us consider a three component mixture model with $\pi =(0.2,0.3,0.5)$, $\mu _1=(-5,0)^{^\top }$, $\mu _2=(0,-5)^{^\top }$, $\mu _3=(5,0)^{^\top }$ and

$$\begin{aligned} \varSigma _1= & {} \left( \begin{array}{ll} 1&{}\quad -0.5\\ -0.5 &{}\quad 1\\ \end{array} \right) , \quad \varSigma _2=\left( \begin{array}{ll} 2&{}\quad 1.25\\ 1.25 &{}\quad 2\\ \end{array} \right) , \quad \\ \varSigma _3= & {} \left( \begin{array}{ll} 3&{}\quad -1.75\\ -1.75 &{}\quad 3\\ \end{array} \right) . \end{aligned}$$

Fig. 1

Simulated data. Monitoring the empirical downweighting level (left), robust distances (middle), misclassification error (right) based on WEM. The vertical lines give the selected h. The horizontal line in the middle panel gives the $\chi ^2_{2;0.99}$ quantile

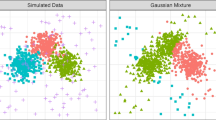
and a simulated sample of size $n=1000$, with $40\%$ of background noise. Outliers have been generated uniformly within an hypercube whose dimensions include the range of the data and are such that the distance to the closest component is larger than the 0.99-level quantile of a $\chi ^2_2$ distribution. WEM and WCEM have been run by setting the eigen-ratio restriction constant to $c=15$. (The true value is 9.5.) The weights are based on the generalized Kullback–Leibler divergence and a folded normal kernel. Initialization has been provided by running tclust with a $50\%$ level of trimming. The smoothing parameter h has been selected by monitoring the empirical downweighting level and unit-specific clustering-conditioned distances over a grid of h values (Agostinelli and Greco 2017). Figure 1 displays the monitoring analyses of the empirical downweighting level, the robust distances and the misclassification error for the WEM. In all panels an abrupt change is detected, meaning that for h values on the right side of the vertical line the procedure is no more able to identify the outliers, hence being not robust w.r.t. the presence of contamination. Similar trajectories are observed for the WCEM and not reported here. In the monitoring of robust distances, a color map has been used that goes from light gray to dark gray in order to highlight those trajectories corresponding to observations that are flagged as outlying for most of the monitoring. Figure 2 displays the result of applying both the WEM and WCEM algorithm to the sample at hand with an outlier detection rule based on the 0.99-level quantile of the $\chi ^2_2$ distribution and on a threshold for weights set at 0.2. Component-specific tolerance ellipses are based on the 0.95-level quantile of the $\chi ^2_2$ distribution. We notice that both methods succeed in recovering the underlying structure of the clean data despite the challenging contamination rate and that the outliers detection rules provide quite similar and satisfactory outcomes. The entries in Table 1 give the rate of detected outliers $\epsilon$, swamping and masking stemming from the alternative strategies.

Table 1 Simulated data

Fig. 2

Simulated data. Fitted components, cluster assignments and outlier detection by WEM (left) and WCEM (right). Top row: outlier detection based on $d^2_{k_i}<\chi ^2_{p;0.99}$. Bottom row: outlier detection based on $w_{k_i}<0.2$, $95\%$ tolerance ellipses overimposed

3.5 Sensitivity to initialization and root selection

In order to initialize WEM and WCEM, tclust based on a large rate of trimming is an appealing solution. Other candidate solutions can be used to initialize the algorithm. For instance, one approach has been discussed in Coretto and Hennig (2017) that is based on a combination of nearest neighbor denoising and agglomerative hierarchical clustering. Given the initial partition, starting values for component-specific parameters are obtained by the sample mean and covariance matrix of the points belonging to each cluster. Here, we also consider a safer strategy that is based on the evaluation of clusterwise robust estimates (for instance, by using the OGK estimator), since the initial denoising may still include dangerous outliers, especially with a large rate of contamination.

In order to check the extent to which results change by varying the initialization, we ran a numerical study based on 500 Monte Carlo trials according to the data configuration of the example in Sect. 3.4. In each trial, for a fixed h, the WEM starts iterating from tclust (with $50\%$ trimming, tclust50), the initial values from Coretto and Hennig (2017) (InitClust) and its robust counterpart described above (InitClustOGK). The same numerical study has been also performed when the level of contamination is set to null, $10\%$ and $20\%$. In the former scenario, with $40\%$ of noisy points, InitClust leads to one inflated estimate of covariance and a smaller empirical downweighting level. On the contrary, the other two starting values give solutions with negligible differences in parameters estimates, depending on the chosen stopping rule and tolerance (here the stopping rule is based on the absolute value of the maximum difference between consecutive estimates of the centroids matrix and the tolerance is $10^{-4}$) and the same final classification and detected outliers. In the latter cases, the algorithm was less dependent on the initial values in the sense that the all three alternatives led to practically indistinguishable fitted models.

When, for several initial values and a fixed value of the bandwidth h, the algorithm ends with different estimates, but still characterized by close empirical downweighting levels, by paralleling the classical approach, one could select the solution leading to the largest value of the weighted likelihood. The likelihood evaluated at the WLE, in general, could be misleading, as also discussed in Sect. 5. In the numerical studies, the solutions characterized by a smaller empirical downweighting level for $\epsilon =40\%$ showed lower weighted likelihood values at convergence but larger likelihoods. At least in this example, tclust50 provides the largest value of the weighted likelihood on average but the three initializations leads to the largest weighted likelihood value with almost equal frequencies, but for $\epsilon =40\%$, where tclust50 gives the selected root slightly more often than InitClustOGK. Figure 3 gives the distributions of the weighted likelihood values at convergence for the case $\epsilon =20\%$. We do not observe significant differences. These findings give evidence supporting the convergence of the proposed algorithm. Similar results are also valid for the WCEM.

Fig. 3

Distribution of weighted likelihood values at convergence when the WEM algorithm is initialized by tclust50, InitClustOGK and InitClust, with $\epsilon =20\%$ and the data configuration of example in Sect. 3.4

A simple and common strategy to check the stability of the results is to run the algorithm for a number (say, 20 to 50) of starting values. For instance, different initial solutions can be obtained by randomly perturbing the deterministic starting solution and/or the final one obtained from it (Farcomeni and Greco 2015b).

The empirical downweighting level provides one guidance to assess the reliability of the fitted model. Actually, if the sum of the estimated weights is approximately 1 then the WLE is close to the MLE, whereas if it is too small, then the corresponding WLE is a degenerate solution, indicating that it only represents a small subset of the data. In the case of excess of downweighting, the criterion based on the weighted likelihood can fail.

A strategy to root selection in the WLE framework has been introduced by Agostinelli (2006) and extended to the multivariate framework in Agostinelli and Greco (2018). The main idea is that the probability of observing a very small value of the Pearson residual is expected to be as small as the fitted model is close to the model underlying the majority of the data. Then, the selected root is that with the lowest fitted probability

$$\begin{aligned} \Pr _{{\hat{\tau }}}\left[ \delta ({\hat{d}}^2; {\hat{\tau }}, {\hat{M}}_n)<-q\right] \ , \end{aligned}$$

(10)

with $q=0.9, 0.95$. The probability in (10) is obtained by drawing a large number of instances (say $N=10,000$) from the fitted model. In the example of Sect. 3.4, the criterion in (10) correctly discards the biased root with the lowest weighted likelihood value, whereas it is not able to discriminate between the other two set of estimates, since they are very close and essentially lead to the same results.

4 Properties

The WEM and WCEM algorithms have been obtained by introducing a different set of estimating equations that defines a WLEE as in (7) or (3), in place of the likelihood equations. In particular, in the M-step K separate WLE of multivariate location and scatter are obtained. The proposed algorithms are a special case of the algorithm first introduced by Elashoff and Ryan (2004), where an EM-type algorithm has been established for very general estimating equations. Here, solving the WLEE, for each separate problem, corresponds to solve a complete data estimating equation of the form

$$\begin{aligned} \varPsi (y; \tau )=(\varPsi _\pi (y; \tau ), \varPsi _\mu (y; \tau ), \varPsi _\varSigma (y; \tau ) )^{^\top }=0 \end{aligned}$$

(11)

Very general conditions for consistency and asymptotic normality of the solution to (11) are given in Elashoff and Ryan (2004). The main requirements are that

• 1. $\varPsi (y; \tau )$ defines an unbiased estimating equation at the assumed model, i.e. $E_\tau [\varPsi (Y; x,\tau )]=0$;

• 2. $E_\tau [\varPsi (Y;x, \tau )\varPsi (Y;x, \tau )^{^\top }]$ exists and is positive definite;

• 3. $E_\tau [\partial \varPsi (Y;x, \tau )/\partial \tau ]$ exists and is negative definite, $\forall \tau$.

This conditions are satisfied by the proposed WLEE that are characterized by weighted score functions stemming from (2). The reader is pointed to the Supplementary material in Agostinelli and Greco (2018) for detailed assumptions and proofs.

5 Model selection

In model-based clustering, formal approaches to choose the number of components are based on the value of the log-likelihood function at convergence. Criteria such as the BIC or the AIC are commonly used to select K when running the classical EM algorithm. In a robust setting, in tclust the number of clusters is chosen by monitoring the changes in the trimmed classification likelihood over different values of K and contamination levels. A formal approach has not been investigated yet in the case of the otrimle, even if the authors conjecture that a monitoring approach or the development of information criteria can be pursued as well.

Fig. 4

Example 1. Monitoring the weighted BIC (left) and the classical BIC evaluated at the WLE (right). The vertical line in the left panel gives the selected h

Here, when the robust fit is achieved by the WEM algorithm, we suggest to resort to a weighted counterparts of the classical AIC or BIC criteria. Then, the proposed strategy is based on minimizing

$$\begin{aligned} Q^w(K)=-2\ell ^w(y; {\hat{\tau }})+m(K) \end{aligned}$$

(12)

where $\ell ^w(y; {\hat{\tau }})=\sum _{i=1}^n {\hat{w}}_{ik_i}\ell (y_i;\tau )$ and m(K) is a penalty term reflecting model complexity. The rationale behind the use of a weighted criterion is that we want to implement a model selection device leading to results close to those one would obtain by using the standard criteria on the genuine part of the data only. Actually, if one uses the standard criteria based on the log-likelihood function evaluated at the WLE, outliers still contribute to its value and, even if these individual contributions are the smallest, the overall behavior of the corresponding BIC and AIC may be badly affected. Let us consider the set of simulated data of Sect. 3.4. The two panels in Figure 4 display, respectively, the behavior of the weighted BIC and the classical BIC evaluated at the WLE for different choices of K over a grid of values for the smoothing parameter h. The unpleasant behavior of the BIC is evident from the inspection of the right panel of Figure 4. On the contrary, the weighted BIC, shown in the left panel of Figure 4, allows selection of the correct clustering complexity. We notice that a similar trajectory is observed for both $K=2$ and $K=3$. The abrupt change is detected at the same value of h but the choice $K=3$ is preferred since it leads to a smaller weighted BIC before the robust fit turns into a non-robust one.

It is well known that the BIC approximate the twice log-Bayes factor for model comparison. One could extend the same relationship to the weighted BIC (12) and the weighted Bayes factor defined in Agostinelli and Greco (2013). Furthermore, for what concerns the WCEM algorithm, one could mimic the approach used in tclust and monitor the weighted conditional likelihood at convergence for varying K and h. Then, the number of clusters should be set equal to the minimum K for which there is no substantial improvement in the objective function when adding one group more.

It can be proved that the robust criterion in (12) is asymptotically equivalent to its classical counterparts at the assumed model, i.e. when the data are not prone to contamination. The proof is based on some regularity conditions about the kernel and the model that are required to assess the asymptotic behavior of the WLE (Agostinelli 2002; Agostinelli and Greco 2013, 2018). In the case of finite mixture models, it is assumed further that an ideal clustering setting holds under the postulated mixture model, that is, data are assumed to be well clustered. The following result holds.

Proposition

Let ${\mathcal {Y}}_j$ be the set of points belonging to the $j\mathrm{th}$ component, whose cardinality is $n_j$. The full data is defined as $\cup _{j=1}^K{\mathcal {Y}}_j$ with $\sum \nolimits _{j=1}^K n_j=n$ and $\lim \nolimits _{n_j\rightarrow \infty }\frac{n_j}{n}=0$. Assume that (i) the model is correctly specified, (ii) the WLE ${\hat{\tau }}$ is a consistent estimator of $\tau$, (iii) $\sup \nolimits _{y\in {\mathcal {Y}}_j} \left| w(\delta (y)) - 1 \right| {\mathop {\longrightarrow }\limits ^{p}} 0$. Then, $|Q^w(k)-Q(k)|{\mathop {\rightarrow }\limits ^{p}}0$.

Proof

Let ${\tilde{\tau }}$ denote the maximum likelihood estimate.

$$\begin{aligned} \frac{1}{2}|Q^w(k)-Q(k)|= & {} \left| \sum _iw_i\ell (y_i;{\hat{\tau }})-\sum _i\ell (y_i;{\tilde{\tau }})\right| \\\le & {} \left\{ \left| \sum _i (w_i-1)\ell (y_i;{\hat{\tau }})\right| \right\} \\&+\left\{ \left| \sum _i\left[ \ell (y_i;{\hat{\tau }})-\ell (y_i;{\tilde{\tau }})\right] \right| \right\} \\\le & {} \sum _i|(w_i-1)\ell (y_i;{\hat{\tau }})|\\\le & {} \sup _y|w_i-1|\sum _i\ell (y_i;{\hat{\tau }})\\&{\mathop {\rightarrow }\limits ^{p}}0 \text {as} \ n_j\rightarrow \infty \end{aligned}$$

$\square$

Table 2 Average measures of fitting accuracy for WEM, WCEM, EM, CEM and otrimle with $p=2,5,10,25$, $\epsilon =0$, $\beta =10,8,6$

6 Numerical studies

We investigate the finite sample behavior of the proposed WEM and WCEM algorithms. Both algorithms are still based on non-optimized R code. Nevertheless, the results that follow are satisfactory and computational time always lays in a feasible range. We set $n=1000$, $K=3$ and simulate data according to the M5 scheme as introduced in Garcia-Escudero et al. (2008). Clusters have been generated by p-variate Gaussian distributions with parameters

$$\begin{aligned} \mu _1= & {} (-\beta ,-\beta ,0,\ldots ,0), \\ \mu _2= & {} (0,\beta ,0,\ldots ,0),\\ \mu _3= & {} (\beta ,0,0,\ldots ,0) \end{aligned}$$

and

$$\begin{aligned} \varSigma _1= & {} \left( \begin{array}{rrr} 15&{}\quad -10&{}\quad 0_{p-2}\\ -10 &{}\quad 15&{}\quad 0_{p-2}\\ 0_{p-2}^{^\top }&{}\quad 0_{p-2}^{^\top }&{}\quad {\mathrm {I}}_{p-2}\\ \end{array} \right) , \\ \varSigma _2= & {} {\mathrm {I}}_p, \ \varSigma _3=\left( \begin{array}{rrr} 45&{}\quad 0&{}\quad 0_{p-2}\\ 0 &{}\quad 30&{}\quad 0_{p-2}\\ 0_{p-2}^{^\top }&{}\quad 0_{p-2}^{^\top }&{}\quad {\mathrm {I}}_{p-2}\\ \end{array} \right) , \end{aligned}$$

where $0_d$ is a null row vector of dimension d and ${\mathrm {I}}_d$ is the $d\times d$ identity matrix. Dimensions $p=2,5,10, 25$ have been taken into account. The parameter $\beta$ regulates the degree of overlapping among clusters: smaller values yield severe overlapping whereas larger values give a better separation. Here, we set $\beta =6,8,10$. Theoretical cluster weights are fixed as $\pi =(0.2,0.4,0.4)$. Outliers have been generated uniformly within an hypercube whose dimensions include the range of the data and are such that the distance to the closest component is larger than the 0.99-level quantile of a $\chi ^2_p$ distribution. When $p=25$, outliers only occur in the first ten dimensions. This setting is more challenging and allows to assess the quality of the proposed model-based clustering techniques in larger-dimensional problems. The rate of contamination has been set to $\epsilon =0.10,0.20$. The case $\epsilon =0$ has been used to evaluate the efficiency of the proposed techniques when applied to clean data. The numerical studies are based on 500 Monte Carlo trials. The weighted likelihood algorithms are both based on a folded normal kernel and a GKL RAF (with $\tau =0.9$), whereas we set $c=50$ as eigen-ratio constraint. The smoothing parameter h has been selected in such a way that the empirical downweighting level lies in the range (0.2, 0.35) under contamination, whereas it is about $10\%$ when no outliers occur. The algorithm is assumed to reach convergence when $\max |{\hat{\mu }}^{(s+1)}-{\hat{\mu }}^{(s)}| < tol$, with a tolerance tol set to $10^{-4}$, where ${\hat{\mu }}^{(s)}$ is the matrix of centroids estimates at the $s\mathrm{th}$ iteration and the differences are elementwise.

Table 3 Swamping rate for WEM, WCEM and otrimle with $p=2,5,10,25$, $\epsilon =0$, $\beta =10,8,6$

Table 4 Average measures of classification accuracy for WEM, WCEM, EM, CEM and otrimle with $p=2,5,10,25$, $\epsilon =0$, $\beta =10,8,6$

Fitting accuracy has been evaluated according to the following measures:

• 1. $||{\hat{\mu }}-\mu ||$, where ${\hat{\mu }}$ and $\mu$ are $3\times p$ matrices with ${\hat{\mu }}_j$ and $\mu _j$ in each row, respectively, for $j=1,2,3$;

• 2. ${\mathrm {ave}}_{\mathrm {j}}\log {\mathrm {cond}}\left( {\hat{\varSigma }}_j\varSigma _j^{-1} \right)$, where ${\mathrm {cond}}(A)$ denotes the condition number of the matrix A;

• 3. $||{\hat{\pi }}-\pi ||$.

For what concerns the task of outlier detection, several strategies have been compared: we considered a detection rule based on the 0.99-level quantile of the $\chi ^2_p$ distribution, according to (9), but also based on the fitted weights, with thresholds set at 0.1, 0.2 and $1- \hat{{\bar{\omega }}}$. For each decision rule, for the contaminated scenario, we report (a) the rate of detected outliers $\epsilon$; (b) the swamping rate; (c) the masking rate. The first is a measure of the fitted contamination level, whereas the others give insights on the level and power of the outlier detection procedure. The comparisons across the different methods should be considered for close values of $\epsilon$. Actually, the more outliers are detected the more likely a genuine observation can be misclassified, whereas, on the contrary, the more true outliers are correctly flagged. For $\epsilon =0$, swamping only is taken into account.

Table 5 Average measures of fitting accuracy for WEM, WCEM, tclust and otrimle with $p=2, 5, 10, 25$, $\epsilon =0.10,0.20$, $\beta =10$ (well-separated clusters)

Table 6 Average measures of fitting accuracy for WEM, WCEM, tclust and otrimle with $p=2,5,10,25$, $\epsilon =0.10,0.20$, $\beta =8$ (moderate overlapping)

Classification accuracy has been measured by (i) the adjusted Rand index and (ii) the misclassification error rate (MCE), both evaluated over true negatives for the robust techniques. The results are based on the testing decision rule (9). In order to avoid problems due to label switching issues, cluster labels have been sorted according to the first entry of the fitted location vectors.

Under the assumed model, WEM and WCEM have been initialized by tclust with $20\%$ of trimming and their behavior have been compared with the EM and CEM algorithms and the otrimle, for the same eigen-ratio constraint and the same initial values. In the presence of contamination, we do not report the results concerning the non-robust EM and CEM but only those regarding the WEM, WCEM, otrimle and oracletclust, i.e. with trimming level equal to the actual contamination level (tclust10 and tclust20, respectively). Under this scenario, starting values have been driven by tclust with $50\%$ of trimming.

It is worth to stress, here, that the comparison in terms of outlier detection reliability between weighted likelihood estimation, tclust and otrimle can be considered fair only by looking at the rate of weights below the fixed threshold for the former methodology and trimmed observation or those assigned to the improper density group for the latter techniques, since formal testing rules have not been considered neither for tclust or otrimle.

First, let us consider the behavior of WEM and WCEM at the assumed model. The entries in Table 2 give the considered average measures of fitting accuracy; Table 3 gives the level of swamping according to the different strategies for WEM and WCEM that are based on the $\chi ^2_p$ distribution and the inspection of weights; Table 4 reports classification accuracy. The overall behavior of WEM and WCEM is appreciable: we observe a tolerable efficiency loss, a negligible swamping effect and a reliable classification accuracy, indeed, as compared with the non-robust procedures. Furthermore, the results are quite similar to those stemming from otrimle and quite often the inspection of the weights from WEM and WCEM leads to a smaller number of false positives, on average.

Table 7 Average measures of fitting accuracy for WEM, WCEM, tclust and otrimle with $p=2,5,10$, $\epsilon =0.10,0.20$, $\beta =6$ (severe overlapping)

Table 8 Outlier detection for WEM, WCEM, tclust and otrimle with $p=2,5,10$, $\epsilon =0.10,0.20$, $\beta =10$ (well-separated clusters)

The performance of WEM and WCEM under contamination is explored next. The fitting accuracy provided by the proposed weighted likelihood based strategies is illustrated in Tables 5, 6, 7. In all considered scenarios, the behavior of WEM and WCEM is satisfactory and they both compare well with the oracle tclust and otrimle. In particular, the good performance of WEM and WCEM has to be remarked in the challenging situation of severe overlapping. Furthermore, for all data configurations, we notice the ability of WEM to combine accurate estimates of component-specific parameters with those of the cluster weights. The entries in Tables 8, 9, 10 show the behavior of the testing procedure based on the $\chi ^2_p$ distribution and the inspection of weights for all considered scenarios. The empirical level of contamination is always larger than the nominal one, but it is acceptable and stable as p and $\beta$ change. Masking is always negligible, hence highlighting the appreciable power of the testing procedure. We remark that one could also consider multiple testing adjustments in outlier detection as outlined in Cerioli and Farcomeni (2011). To conclude the analysis, Tables 11, 12, 13 give the considered measures of classification accuracy as $\beta$ varies. The results are quite stable across the four methods and all dimensions. As well as before, WEM and WCEM lead to a satisfactory classification, even in the challenging case of severe overlapping. The results obtained for $p=25$ deserve some special remarks. Actually, fitting and classification accuracies deteriorate, particularly in the presence of moderate-to-severe overlapping. Nevertheless, the proposed WEM and WCEM still behave in a fashion not dissimilar from the other well-established techniques.

6.1 Computational burden

The numerical studies are enriched by evaluating the computational demand of the proposed methodology for increasing sample size and dimension. Time needed for convergence with non-optimized R code on a 3.4 GHz Intel Core i5 processor is given in Table 14. We report the sample times needed for convergence of the algorithm on a single dataset with $K=3$, $\epsilon =20\%$, $b=10$, $c=50$. The smoothing parameter has been chosen in order to achieve an empirical downweighting level about equal to 0.25. Initialization has been included in time evaluation. It can be seen that computing time increases both with the sample size and the dimension but always at a reasonable slow rate. We underline that the speed of convergence also depends on the choice of h: values of the smoothing parameter leading to an excess of downweighting can make it slow down.

Table 9 Outlier detection for WEM, WCEM, tclust and otrimle with $p=2,5,10$, $\epsilon =0.10,0.20$, $\beta =8$ (moderate overlapping)

Table 10 Outlier detection for WEM, WCEM, tclust and otrimle with $p=2,5,10$, $\epsilon =0.10,0.20$, $\beta =6$ (severe overlapping)

Table 11 Average measures of classification accuracy for WEM, WCEM, tclust and otrimle with $p=2,5,10$, $\epsilon =0.10,0.20$, $\beta =10$ (well-separated clusters)

Table 12 Average measures of classification accuracy for WEM, WCEM, tclust and otrimle with $p=2,5,10$, $\epsilon =0.10,0.20$, $\beta =8$ (moderate overlapping)

Table 13 Average measures of classification accuracy for WEM, WCEM, tclust and otrimle with $p=2,5,10\hbox {x}$, $\epsilon =0.10,0.20$, $\beta =6$ (severe overlapping)

7 Real data examples

7.1 Swiss bank note data

Let us consider the well-known Swiss banknote dataset concerning $p=6$ measurements of $n=200$ old Swiss 1000-franc banknotes, half of which are counterfeit. The weighted likelihood strategy is based on a gamma kernel and a symmetric Chi-square RAF. Our first task is to choose the number of clusters. To this end, we look at the weighted BIC (12) on a fixed grid of h values for $K=1,2,3,4$ and a restriction factor $c=12$. The inspection of Figure 5 clearly suggests a two-group structure for all considered values of the smoothing parameter h. The empirical downweighting level is fairly stable for a wide range of h values. We decided to set $h=0.05$ leading to an empirical downweighting level equal to 0.10. The WEM algorithm based on the testing rule (9) with $\alpha =0.01$ leads to identify 21 outliers that include 15 forged and 6 genuine bills.

On the contrary, there are 19 data points whose weight is lower than $1-\hat{{\bar{w}}}$ that include 14 forged and 5 genuine bills. The cluster assignments stemming from the latter approach are displayed in Figure 6. It is worth to note that the outlying forged bills coincide with the group that has been recognized to follow a different forgery pattern and characterized by a peculiar length of the diagonal (see García-Escudero et al. 2011; Dotto et al. 2016, and references therein). On the other hand, the outlying genuine bills all exhibit some extreme measures. For the same value of the eigen-ratio constraint, the otrimle assigns 19 bills to the improper component density, leading to the same classification of the WEM, whereas rtclust includes in the trimming set one counterfeit bill more.

A visual comparison between the three results is possible from Figure 7, whose panels show a scatterplot of the fourth against the sixth variable with the classification resulting from WEM (with both outlier detection rules), rtclust and otrimle, respectively. The WCEM has been tuned to achieve the same empirical downweighting level and leads to the same results.

7.2 2018 world happiness report data

In this section the weighted likelihood methodology is applied to a dataset from the 2018 World Happiness Report by the United Nations Sustainable Development Solutions Network (Helliwell et al. 2018) (hereafter denoted by WHR18). The data give measures about six key variables used to explain the variation of subjective well-being across countries: per capita Gross Domestic Product (on log scale), Social Support, i.e. the national average of the binary responses to the Gallup World Poll (GWP) question If you were in trouble, do you have relatives or friends you can count on to help you whenever you need them, or not?, Health Life Expectancy at birth, Freedom to make life choices, i.e. the national average of binary responses to the GWP question Are you satisfied or not with your freedom to choose what you do with your life?, Generosity, measured by the residual of regressing the national average of GWP responses to the question Have you donated money to a charity in the past month? on GDP per capita, perception of Corruption, i.e. the national average of binary responses to the GWP questions Is corruption widespread throughout the government or not? and Is corruption widespread within businesses or not?. The dataset is made of 142 rows, after the removal of some countries characterized by missing values. The objective is to obtain groups of countries with a similar behavior, to identify possible countries with anomalous and unexpected traits and to highlight those features that are the main source of separation among clusters.

In this example, a GKL RAF has been chosen, the unbiased at the boundary kernel density estimate has been obtain by first evaluating a kernel density estimate on the log-transformed squared distance over the whole real line and then back-transforming the fitted density to $(0, \infty )$ (Agostinelli and Greco 2018), and we set $c=50$.

In order to select the number of clusters, we monitored the weighted BIC stemming from WEM and the classification log-likelihood at convergence from WCEM for different values of K and h. The corresponding monitoring plots are given in Figure 8, respectively. Based on the WEM algorithm, $K=3$ is to be preferred, even if the gap with the case $K=4$ is very small for all considered values of the smoothing parameter. On the other hand, the inspection of the weighted classification log-likelihood driven by the WCEM suggests $K=4$. Therefore, we have applied our WEM and WCEM algorithms both based on $K=3$ and $K=4$. As with $K=4$ two groups are not very separated, we preferred $K=3$ and reported only those results for reasons of space. Moreover, the results stemming from WEM and WCEM were very similar both in terms of fitted parameters, cluster assignments and detected outliers. Then, in the following we only give the results driven by WEM. The empirical downweighting level was found not to depend in a remarkable fashion on the number of groups. In particular, for $K=3$, in the monitoring process of $1-\hat{{\bar{w}}}$ we did not observe any abrupt change but a smooth decline until a stabilization of the level of contamination occurred. Then, we decided to use a h value leading to $(1-\hat{{\bar{w}}})\approx 0.10$. Figure 9 displays the distance plot stemming from WEM. According to (9) for a level $\alpha =0.01$, 12 outliers are detected. A closer inspection of the plot unveils that some of such points are close to the cutoff value. Therefore, they are not considered as outliers but correctly assigned to the corresponding cluster. Furthermore, we notice that all the points leading to the largest distances are attached a very small weight ($<0.01$). The weight corresponding to Myanmar is about 0.40. The other countries near the threshold line all show weights about equal to 0.80.

Table 14 Time (in s) for convergence of WEM on simulated data sets of increasing size $n=1000, 2000, 5000, 10,000$ and dimensions $p=2, 5, 10, 25$, with $\epsilon =0.20$, $\beta =10$, $c=50$

Fig. 5

Swiss banknote data. Monitoring the weighted BIC for WEM, $K=1, 2, 3, 4$

Fig. 6

Swiss banknote data. Cluster assignments by WEM. Observation whose weight is lower than $1-{\bar{w}}$ are considered outliers. Genuine bills are denoted by a green $+$, forged bills by a red $\triangle$. Outliers are denoted by a black filled circle. (Color figure online)

Fig. 7

Swiss banknote data. Fourth against the sixth variable with cluster assignments by WEM ($\alpha =0.01)$, WEM ($w_{k_i}<1-{\bar{w}})$, rtclust and otrimle in clockwise fashion. Genuine bills are denoted by a green $+$, forged bills by a red $\triangle$. Outliers are denoted by a black filled circle. (Color figure online)

Fig. 8

WHR18 data. Monitoring the weighted BIC for WEM (left) and the weighted classification log-likelihood for WCEM, $K=2, 3, 4, 5, 6$

The cluster profiles and raw measurements for the detected outlying countries are reported in Table 15. The three clusters are well separated in terms of all of the items considered, even if small differences are seen in terms of perception of Corruption between clusters 1 and 2. Cluster 3 includes all the countries characterized by the highest level of subjective well-being. The differences with the other two clusters concerning GDP, HLE and Corruption are outstanding. On the opposite, in cluster 1 we find all the countries with the hardest economic and social conditions. For what concerns the explanation of the outliers, we notice that the subgroup of African countries composed by Central African Republic, Chad, Ivory Coast, Lesotho, Nigeria and Sierra Leone might belong to group 1 but is characterized by the six lowest HLE values. For what concerns Myanmar, it exhibits extremely large Freedom and Generosity indexes and a surprising small value for Corruption. It should belong to cluster 1 but it is closer to cluster 3 according to the last three measurements, indeed. For instance, it may be supposed that such measurements are not completely reliable because of problems with the questionnaires and the sampling or they may revel a surprising positive attitude despite the difficult economic and life conditions.

A spatial map of cluster assignments is given in Figure 10 that confirms the goodness and coherence of the results and the ability of the considered six features to find reasonable clusters. Cluster 1 is mainly localized in Africa, cluster 2 is composed by developing countries, whereas cluster 3 includes the world leading countries, among which there are USA, Canada, Australia and the countries in the European Union.

7.3 Anuran calls

This example concerns the problem of recognition and classification of anuran (frogs and tods) families through their calls. The classification task is a very complex problem due to the large anuran diversity (Colonna et al. 2016). The data gives $p=22$ normalized Mel-frequency cepstral coefficients (MFCCs), measures that are commonly used as features in sound processing and speech recognition, for each of $n=7195$ syllables, extracted after the segmentation of 60 audio records belonging to $k=4$ different families. The data are publicly available at the UCI Machine Learning Repository. Despite the challenging nature of the problem, in particular for model-based clustering techniques, we want to assess the reliability of the proposed methodology on such high-dimensional example and its behavior as an unsupervised learning device. To this end, we decided to split half the data in a training and test set.

The entries in Table 16 give the adjusted Rand index evaluated on both sets, averaged over 100 replicated splits, in order to honestly estimate the accuracy of classification. We compare the results from mclust, tclust10, tclust20, WEM and WCEM. WEM and WCEM are characterized by a GKL RAF and a gamma kernel. On the training set, the adjusted Rand index is evaluated only on those observations not flagged as outliers. By looking at the results, one can state that the robust methods are feasible also in this challenging settings and lead to improved classification accuracy w.r.t. the non-robust mclust, indeed.

On the other hand, the robust techniques only succeed to a limited extent in recovering the actual classification on the test set, because of the problem complexity, which comes from the large dimensionality and sample size but also from the severe overlapping of the groups corresponding to the anuran families. Nevertheless, the behavior of the weighted likelihood methodologies is satisfactory when compared with the other competing techniques. The behavior of tclust10 on the training set is a consequence of the smaller number of detected outliers.

8 Conclusions

We have proposed a robust technique for fitting a finite mixture of multivariate Gaussian components based on recent developments in weighted likelihood estimation. Actually, the proposed methodology is meant to provide a step further with respect to the original proposal in Markatou (2000). The method is based on the idea of using a univariate kernel density estimate based on robust distances rather than a multivariate one based on the data in order to compute weights. Furthermore, the proposed technique is characterized by the introduction of an eigen constraint aimed at avoiding problems connected with an unbounded likelihood or spurious solutions.

Fig. 9

WHR18 data. Distance plot for WEM with $K=3$. The horizontal line gives the $\chi ^2_{6;0.99}$ quantile

Table 15 WHR18 data: cluster profiles and raw measurements for the detected outlying countries

Fig. 10

WHR18 data. Spatial classification from WEM with $K=3$

Based on the robustly fitted mixture model, a model-based clustering strategy can be built in a standard fashion by looking at the value of posterior membership probabilities. At the same time, formal rules for outlier detection can be derived, as well. Then, one could assign units to clusters provided that the corresponding outlyingness test is not significant that means that detected outliers have to be discarded and not assigned to any group. The numerical studies and the real data examples showed the satisfactory reliability of the proposed methodology.

Table 16 Anuran calls

There is still room for further work, along a path shared with tclust, rtclust, mtclust and otrimle. Actually the proposed method works for a given smoothing parameter h and a fixed number of clusters K. In addition, outlier detection depends upon a fixed threshold. At the moment, the selection of h stemming from the monitoring of several quantities, such as the empirical downweighting level, the unit-specific robust distances or even the fitted parameters, provides an acceptable adaptive solution. Such a procedure is not different from the implementation of a sequence of refinement steps of an initial robust partition stemming from a sequence of decreasing values of h. The selection of K remains a difficult problem to deal with too, despite the satisfactory behavior of the proposed criteria, i.e. the weighted BIC and the weighted classification log-likelihood. Outlier detection is a novel aspect in the framework of robust mixture modeling and model-based clustering. In the specific context, the outlyingness of each unit is tested conditionally on the final cluster assignment. The number of outliers clearly depends on the chosen level $\alpha$ or the selected threshold for the final weights. A fair choice of the level of the test is still an open problem in outlier detection. However, the suggested testing strategies work satisfactory, at least in those considered scenarios, and provide a good compromise between swamping and masking that could be improved further by using multiplicity adjustments (Cerioli and Farcomeni 2011). The extent to which the proposed methodology allows to deal with very large-dimensional problems remains limited, as well as for the other robust model-based clustering techniques we also considered in this paper. Nevertheless, the weighted likelihood methodology looks promising if one is willing to develop robust procedures specifically suited for high-dimensional problems. For instance, multivariate weighted likelihood estimation could be considered in model-based subspace clustering methods and in particular in the framework of mixtures of factor analyzers (McLachlan et al. 2003). The reader is pointed to Bouveyron and Brunet-Saumard (2014) for a recent account on high-dimensional clustering.