A polyhedral study on chance constrained program with random right-hand side

Abstract

The essential structure of the mixed-integer programming formulation for chance-constrained program (CCP) is the intersection of multiple mixing sets with a 0–1 knapsack. To improve our computational capacity on CCP, an underlying substructure, the (single) mixing set with a 0–1 knapsack, has received substantial attentions recently. In this study, we consider a CCP problem with stochastic right-hand side under a finite discrete distribution. We first present a family of strong inequalities that subsumes known facet-defining ones for that single mixing set. Due to the flexibility of our generalized inequalities, we develop a new separation heuristic that has a complexity much less than existing one and guarantees generated cutting planes are facet-defining for the polyhedron of CCP. Then, we study lifting and superadditive lifting on knapsack cover inequalities, and provide an implementable procedure on deriving another family of strong inequalities for the single mixing set. Finally, different from the traditional approach that aggregates original constraints to investigate polyhedral implications due to their interactions, we propose a novel blending procedure that produces strong valid inequalities for CCP by integrating those derived from individual mixing sets. We show that, under certain conditions, they are the first type of facet-defining inequalities describing intersection of multiple mixing sets, and design an efficient separation heuristic for implementation. In the computational experiments, we perform a systematic study and illustrate the efficiency of the proposed inequalities on solving chance constrained static probabilistic lot-sizing problems.

1 Introduction

Chance constraints appear in optimization formulations of many important applications that model service levels, risk measures, or reliability requirements. When the randomness occurs only at the right-hand side vector, the chance-constrained program with joint probabilistic constraints (CCP) can be formulated as follows

$$\begin{aligned} \min&\quad \mathbf {c}^T \mathbf {x}&\\ s.t.&\quad \mathbf {y}= \mathbf {A} \mathbf {x}&\\&\quad \mathbb {P}\left\{ \mathbf {y} \ge \mathbf {h}(\omega ) \right\} \ge 1 - \tau&\\&\quad \mathbf {x} \in \mathbf {X} \subseteq \mathbb {R}^{m_1} \times \mathbb {Z}^{m_2}, \mathbf {y} \in \mathbb {R}^d_+ \end{aligned}$$

where $\mathbf {X}$ is a polyhedron, d and $\mathsf {m}$ are positive integers with $\mathsf {m}=m_1 + m_2$ for other two positive integers $m_1$ and $m_2, \omega$ is an element of an underlying probability space $\varOmega , \mathbf {x}$ is an $\mathsf {m}$-dimensional decision variable, $\mathbf {A}$ is a $d \times \mathsf {m}$ matrix, $\mathbf {h}(\omega )$ is a d-dimensional column random vector, $\mathbf {c}$ is an $\mathsf {m}$-dimensional cost vector, and $\tau$ is a threshold probability with $0 \le \tau \le 1$. The major challenge in solving the CCP is that the feasible region may not be represented by a convex (or quasiconvex) function and is typically difficult to evaluate. For continuously distributed random variables, many researches focus on the identification of conditions under which the feasible set defined by the chance constraint is convex. Prékopa [33] shows that the feasible region can be represented by quasiconvex functions if $\mathbf {h}$ is quasiconvex and $\omega$ has a logconcave probability distribution. Henrion [16] and Henrion and Strugarek [18] show that a joint chance constraint in certain forms defines a convex set. Hanasusanto et al. [15] study the ambiguous joint chance constrained program and provide tight conditions when it is conic representable. Efficient methods for computing the gradients and the value of multivariate continuous distributions are proposed, see [17, 41, 42] for Gaussian, Student’s and lognormal distributions. A widely applied approach is approximating the chance constraint with a more tractable function if the convexity of the feasible region is not verifiable. Many approximations have been proposed, e.g., the quadratic approximation [4], the conditional value-at-risk approximation [35], the Bernstein approximation [31] and Monte Carlo simulations [8, 20]. Luedtke et al. [29] propose a sample approximation approach to substitute the underlying continuous distribution by a finite sample and reformulate it as a mixed-integer programming problem. Thus, algorithms based on cutting planes for mixed-integer reformulations are available in [22, 28, 29]. Recently, the cutting plan approach is extended to multi-stage chance-constrained programs and multivariate risk constraints, e.g., valid inequalities for the deterministic equivalent formulation in [48], strong feasibility and optimality cuts for decomposition algorithms in [27, 28, 45, 47], and cuts generation for multivariate conditional value-at-risk or second-order stochastic dominance in [23]. For joint chance constraints with discrete distribution, a disjunctive programming reformulation for CCP is studied in [38] by using the concept of p-level efficient points (pLEPs) [32]. A bundle method for energy problem is proposed by [44] and combined with pLEPs for better performance [40]. Dentcheva et al. [9] use pLEPs to obtain various reformulations and derive valid bounds for the objective value. Beraldi and Ruszczyński [6] propose a branch-and-bound algorithm based on the enumeration of pLEPs, see also [36]. Lejeune and Noyan [25] generate pLEPs by solving a series of increasingly tighter outer approximations with several other algorithmic techniques. Lejeune [24] introduces Boolean reformulation framework, which is extended recently for nonlinear chance constraints [26]. Another study on nonlinear chance constraints is in [2] where optimality conditions are studied and approximation algorithms have been developed. Kogan and Lejeune [21] propose a Boolean method to solve CCP where the elements of the multirow random technology matrix follow a joint probability distribution. Many applications on the chance-constrained program are also studied in literature, such as probabilistic lot-sizing [6, 48], health care [5, 39], probabilistic set covering [7, 37], hydro reservoir management [43] and logistic [10].

In this paper, we consider a mixed-integer programming (MIP) reformulation of chance-constrained program. Suppose $\varOmega$ has finitely many realizations, i.e., $\varOmega = \{\omega _1,\omega _2,\ldots , \omega _n\}$ and $\pi _i$ is the probability associated with $\omega _i, \forall i \in \{1,\ldots ,n\}$. Let $h_{r i}$ be the r-th component of $\mathbf {h}(\omega _i)$. As described in [22, 29], we can assume $h_{r i} \ge 0$ without loss of generality. Throughout, we denote $[i,j] \equiv \{r \in \mathbb {Z}: i\le r \le j\}$. A deterministic equivalent formulation of the chance–constrained program is (see also [1, 22, 29])

$$\begin{aligned} \min&\quad \mathbf {c}^T \mathbf {x}&\nonumber \\ s.t.&\quad \mathbf {y} = \mathbf {A} \mathbf {x}&\nonumber \\&\quad y_{r} \ge h_{r i}(1-z_i) \qquad \forall r \in [1,d], i \in [1,n]&\end{aligned}$$

(1)

$$\begin{aligned}&\quad \sum _{i=1}^{n} \pi _i z_i \le \tau&\nonumber \\&\quad \mathbf {x} \in \mathbf {X} \subseteq \mathbb {R}^{m_1} \times \mathbb {Z}^{m_2} \nonumber \\&\quad \mathbf {z} \in \{0,1\}^n, \mathbf {y} \in \mathbb {R}^d_+ \end{aligned}$$

(2)

where $z_i=0$ indicates that $\mathbf {y} \ge h(\omega )$ is satisfied when $\omega =\omega _i$ and $z_i=1$ otherwise. The constraints (1) and (2) define the key substructure of this MIP reformulation, i.e., the polyhedron of CCP

$$\begin{aligned} \mathcal {Q} \!= \!\left\{ (\mathbf {y}, \mathbf {z}) \in \mathbb {R}_+^d \times \{0,1\}^n: \sum _{i=1}^{n} \pi _i z_i \!\le \!\tau , \text { } y_{r} \ge h_{r i}(1- z_i), \text { } r \!\in \![1,d], i \in [1,n] \right\} . \end{aligned}$$

For $r \in [1,d]$, we have a mixing set with 0–1 knapsack

$$\begin{aligned} \mathcal {Q}_{r} = \left\{ (y_r, \mathbf {z}) \in \mathbb {R}_+ \times \{0,1\}^n: \sum _{i=1}^{n} \pi _i z_i \le \tau , y_{r} \ge h_{r i} (1-z_i), \text { } i \in [1,n]\right\} . \end{aligned}$$

By dropping the index r, we redefine the mixing set with 0–1 knapsack as

$$\begin{aligned} \mathcal {K} = \left\{ (y,\mathbf {z}) \in \mathbb {R}_+ \times \{0,1\}^n : \sum _{i=1}^{n} \pi _i z_i \le \tau , \text { } y \ge h_i(1- z_i), \text { } i \in [1,n] \right\} . \end{aligned}$$

Importantly, the study of the polyhedron of CCP is fundamental for solving chance-constrained programs efficiently. Most literature focuses on its substructure the set $\mathcal {K}$. Since our contributions include studies on the set $\mathcal {Q}$ and $\mathcal {K}$, we give literature review on both sets in following subsections.

1.1 Mixing set with 0–1 knapsack

Observe that the set $\mathcal {K}$ consists of a mixing set, introduced by Günlük and Pochet [14] on general integer variables. The mixing set was extensively studied in varying degrees of generality by many authors in [3, 13, 30, 34, 49, 50] and its convex hull can be described by the so-called star inequalities in [3].

Without loss of generality, we can assume $h_1 \ge h_2 \ge \cdots \ge h_n \ge 0$ in the set $\mathcal {K}$. As in [1, 22, 29], we introduce two parameters $\nu$ and p. The parameter $\nu$ is defined such that

$$\begin{aligned} \sum _{i=1}^{\nu } \pi _i \le \tau \quad \text {and} \quad \sum _{i=1}^{\nu +1} \pi _i > \tau . \end{aligned}$$

As noted by [29], we have $y \ge h_{\nu +1}$ and the set $\mathcal {K}$ can be strengthened as follows

$$\begin{aligned} \left\{ (y,\mathbf {z}) \in \mathbb {R}_+ \times \{0,1\}^\nu : \sum _{i=1}^{n} \pi _i z_i \le \tau , \text { } y + (h_i-h_{\nu +1})z_i\ge h_i, \text { } i \in [1,\nu ] \right\} . \end{aligned}$$

(3)

Indeed, by using $y + (h_i-h_{\nu +1})z_i\ge h_i$ in (3) to replace (1), we obtain a new formulation of CCP with a tighter LP relaxation and less constraints. Let $\{\langle 1 \rangle ,\langle 2 \rangle ,\ldots ,\langle n \rangle \}$ be a permutation of set [1, n] with

$$\begin{aligned} \pi _{\langle 1 \rangle } \le \pi _{\langle 2 \rangle } \le \cdots \le \pi _{\langle n \rangle }. \end{aligned}$$

The parameter p is defined such that

$$\begin{aligned} \sum _{i=1}^{p} \pi _{\langle i \rangle } \le \tau \ \text { and} \ \sum _{i=1}^{p+1} \pi _{\langle i \rangle } > \tau . \end{aligned}$$

Note that in the case of equal probabilities, i.e., $\pi _i = 1/n\,\forall i \in [1,n]$, the knapsack constraint reduces to the following cardinality constraint

$$\begin{aligned} \sum _{i=1}^{n} z_i \le p \end{aligned}$$

and $p = \nu$. Luedtke et al. [29] applied the star inequality proposed in [3] to the strengthened star inequality (which is stated as Theorem 1 in [22])

$$\begin{aligned} y + \sum _{j=1}^{a} (h_{t_j} - h_{t_{j+1}}) z_{t_j} \ge h_{t_1} \quad \forall T=\{t_1,\ldots ,t_a\} \subseteq [1,\nu ] \end{aligned}$$

(4)

where $t_1< \cdots < t_a$ and $h_{t_{a+1}}=h_{\nu +1}$, and showed that it is facet-defining for $\mathcal {K}$ when $t_1=1$. This result was generalized in [1] and [22] where more facet-defining inequalities were introduced for mixing set with either cardinality constraint or general knapsack. Luedtke et al. [29] and Küçükyavuz [22] also performed numerical studies for their proposed inequalities to evaluate the computational impact on solving lot-sizing based CCP instances.

1.2 Polyhedron of CCP

The polyhedron of CCP, i.e., $\mathcal {Q}$, was initially studied in [22]. When the 0–1 knapsack in the set $\mathcal {Q}$ is just a cardinality constraint, the author in [22] developed so-called TL inequalities and showed that they are facet-defining for both $\mathcal {K}$ and $\mathcal {Q}$. We actually find that this result could be significantly generalized to any facet-defining inequalities as follows.

Proposition 1

(i) If an inequality is valid and facet-defining for $\mathcal {Q}_r$ for some $r\in [1,d]$, then the inequality is valid and facet-defining for $\mathcal {Q}$; moreover, (ii) if an inequality is valid and facet-defining for $\displaystyle {\cap _{r \in \mathcal {D}}} \mathcal {Q}_r$ for a set $\mathcal {D} \subseteq [1,d]$, then the inequality is valid and facet-defining for $\mathcal {Q}$.

Proof

We omit the proof since it is the same as the last paragraph of the proof for Theorem 4 in [22]. $\square$

Clearly, this proposition implies that the study of the single set $\mathcal {K}$ (i.e., a single $\mathcal {Q}_r$) provides a crucial polyhedral description to the set $\mathcal {Q}$. However, it can only bring us inequalities with at most one nonzero coefficient of $y_r$ for some $r \in [1,d]$. As illustrated by a numerical example in [22], non-trivial inequalities for the polyhedron of CCP with $d=2$, which are not obtainable from its single mixing subset $\mathcal {Q}_1$ or $\mathcal {Q}_2$, can be obtained by studying an aggregation of $\mathcal {Q}_1$ and $\mathcal {Q}_2$. Specifically, it involves selecting two scalars $\beta _1, \beta _2$, setting $y=\beta _1y_1+\beta _2y_2$, and obtaining a new set

$$\begin{aligned} \mathcal {Q}^\prime= & {} \left\{ (y, \mathbf {z}) \in \mathbb {R}_+ \times \{0,1\}^n: \sum _{i=1}^{n} \pi _i z_i \le \tau , y \right. \\&\quad \left. \ge (\beta _1h_{1i}+\beta _2h_{2i}) (1-z_i) \text { } \forall i \in [1,n] \right\} . \end{aligned}$$

Then, all the results on the set $\mathcal {K}$ can be readily applied to $\mathcal {Q}^\prime$. Nevertheless, no analytical study has been done and the effectiveness of this combining approach is either theoretically or computationally unknown. For example, we do not know if this approach will derive any facet-defining inequalities of $\mathcal {Q}$.

1.3 Main contributions and outline

Our main contributions are in both theory and computation, and presented in each of the following sections in details. Here we summarize our contributions as follows,

• In Sect. 2, we derive a new family of inequalities for the mixing set with general 0–1 knapsack, which subsumes all known facet-defining inequalities proposed in [1, 22, 29] as special cases. Due to the flexibility of our generalized inequalities, we are able to develop a new separation heuristic different from those in [1, 22], which has a much less complexity and is guaranteed to identify the strongest (i.e., facet-defining) cutting planes for the polyhedron of CCP.

• In Sect. 3, we present another large family of inequalities by performing lifting and superadditive lifting procedures on cover inequalities of 0–1 knapsack. Noting that all existing valid inequalities (including our results in Sect. 2) are based on star inequalities for the basic mixing set, our results are the first type of valid inequalities with a different structure. Unlike a characterization on parameters of valid inequalities derived in [1] for $\mathcal {K}$, our inequalities are explicit and constructive, which provide an implementable procedure to identify strong inequalities to strengthen the polyhedral description and to improve our solution capacity of CCP.

• In Sect. 4, we introduce a novel blending approach to study $\mathcal {Q}$ such that, instead of combining original formulation, we are blending facet-defining inequalities of $\mathcal {Q}_r$ for $r \in [1,d]$. Especially, we are able to show when the resulting inequalities are facet-defining for $\mathcal {Q}$. To the best of our knowledge, they are the first group of facet-defining inequalities capturing interactions among multiple mixing sets. We also develop a very effective separation heuristic that can find violated facet-defining blending inequalities.

• In Sect. 5, we fully test the strengthened star inequality, TL inequalities (as described in [22]) and our three families of inequalities. We show that our inequalities outperform other known inequalities in the literature and substantially improve a commercial solver’s ability to solve large static probabilistic lot-sizing problems.

The last section concludes the paper.

2 Strong inequalities derived from mixing set

On the top of the classical mixing inequality, a family of strong inequalities was developed in [29] for the set $\mathcal {K}$ when the knapsack constraint was replaced by a cardinality constraint. Then, Küçükyavuz [22] generalized that result for the cardinality constrained mixing set and extended those inequalities as valid ones for $\mathcal {K}$. Recently, Abdi et al. [1] provided a characterization of valid inequalities for $\mathcal {K}$, and explicitly developed a set of facet-defining inequalities for $\mathcal {K}$ under some special conditions. In the following, we present a large family of strong inequalities for $\mathcal {K}$, and derive sufficient conditions under which our proposed inequalities are facet-defining. In order to understand the connections to existing research on $\mathcal {K}$, we provide a detailed analysis and numerical examples to show that explicit strong inequalities or facet-defining inequalities developed in [1, 22] are either dominated or subsumed by ours. Due to the flexibility of our inequalities, we can further present a separation heuristic which can identify potential facet-defining inequalities with a computational complexity less than those of [1, 22].

Theorem 1

For $m \in [1,\nu ]$ and $q \in [0,p-m]$, we define

• a set $T = \{t_1,\ldots ,t_a\} \subseteq [1,m]$ with $t_1<\cdots <t_a$;

• a set L with a permutation $\varPi _L = \{l_1,\ldots ,l_{q}\}$;

• a sequence of integers $s_j \in [0,\nu -m+1]$ such that $0 \le s_1 \le \cdots \le s_{q} \le s_{q+1}=\nu -m+1$.

If $L \subseteq [m+s_1+1,n]$ with $l_j \ge m+\min \{1+s_j,s_{j+1}\}$ and

$$\begin{aligned} \sum _{i=1}^{m+s_j} \pi _i + \sum _{i=j}^{q} \pi _{k_i} > \tau \quad \forall j \in [1,q] \end{aligned}$$

where $\{k_1,\ldots ,k_{q}\}$ is a permutation of L with $\pi _{k_1} \ge \cdots \ge \pi _{k_{q}}$, we have the following inequality

$$\begin{aligned} y + \sum _{j=1}^{a} (h_{t_j} - h_{t_{j+1}}) z_{t_j} + \sum _{j=1}^{q} \delta _j(1-z_{l_j}) \ge h_{t_1} \end{aligned}$$

(5)

that is valid for $\mathcal {K}$, where $t_{a+1} = m + s_1$ and

$$\begin{aligned} \delta _j = \left\{ \begin{aligned}&h_{m+s_1} - h_{m+s_2}&j=1 \\&\max \left\{ \delta _{j-1}, h_{m+s_1} - h_{m+s_{j+1}} - \sum _{i \in [1,j-1] \text { and } l_i \ge m+\min \{1+s_j,s_{j+1}\} } \delta _i \right\}&j \in [2,q]. \end{aligned} \right. \end{aligned}$$

(6)

Proof

It is clear that if $y \ge h_{t_1}$, the inequality (5) is trivially satisfied. If $y \ge h_{t_i}$ for some $i=2,\ldots ,a+1$ and $y < h_{t_j}$ for all $j \in [1,i-1]$, then we must have $z_{t_j}=1$ for all $j \in [1,i-1]$. Thus,

$$\begin{aligned} y + \sum _{j=1}^{a} (h_{t_j}-h_{t_{j+1}}) z_{t_j}\ge & {} h_{t_i} + \sum _{j=1}^{i-1} (h_{t_j}-h_{t_{j+1}}) \\= & {} h_{t_1} \ge h_{t_1} - \sum _{j=1}^{q} \delta _j(1-z_{l_j}) \end{aligned}$$

and inequality (5) is satisfied when $y \ge h_{t_{a+1}} = h_{m+s_1}$. Therefore, we assume that $y < h_{m+s_1}$, which implies $z_{t_j}=1\,\forall j=1, \ldots , a$ and

$$\begin{aligned} \sum _{j=1}^{a} (h_{t_j}-h_{t_{j+1}}) z_{t_j} = h_{t_1} - h_{m+s_1} \end{aligned}$$

in the rest of proof.

If $q=0$, we have $m+s_1=m+\nu -m+1 = \nu +1$. Such case is trivial because $y \ge h_{\nu +1}$ and the resulting inequality is the strengthened star inequality. It is sufficient to consider $q \ge 1$. Because $y \ge h_{\nu +1}$ and $s_{q+1} = \nu -m+1$, we must have $h_{m+s_{i^\prime }} > y \ge h_{m+s_{i^\prime +1}}$ for some $i^\prime =1,\ldots ,q$. Without loss of generality, we assume that $s_{i^\prime +1} \ge s_{i^\prime }+1$, i.e., $m+\min \{1+s_{i^\prime }, s_{i^\prime +1}\} = m+1+s_{i^\prime }$. Thus, $z_j=1$ for all $j=1,\ldots ,m+s_{i^\prime }$, which implies

$$\begin{aligned} \sum _{i=1}^{m+s_{i^\prime }} \pi _i + \sum _{i=m+s_{i^\prime }+1}^{n} \pi _i z_i \le \tau \end{aligned}$$

(7)

from the knapsack inequality, and we have

$$\begin{aligned}&\sum _{j=1}^{q} \delta _j(1-z_{l_j}) = \sum _{j \in [1,q] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _j(1-z_{l_j}) \nonumber \\&\quad = \sum _{j =i^\prime +1}^{q} \delta _j(1-z_{l_j}) + \sum _{j \in [1,i^\prime ] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _j(1-z_{l_j}) \nonumber \\&\quad = \sum _{j =i^\prime +1}^{q} \delta _j + \sum _{j \in [1,i^\prime ] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _j - \sum _{j =i^\prime +1}^{q} \delta _j z_{l_j} - \sum _{j \in [1,i^\prime ] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _i z_{l_j}. \nonumber \\ \end{aligned}$$

(8)

The first equality holds because $z_j=1\,\forall j \in [1,m+s_{i^\prime }]$. The second equality holds because

$$\begin{aligned} l_j \ge {\left\{ \begin{array}{ll} m+s_{j}+1 \ge m+s_{i^\prime }+1 , \\ m+s_{j+1} \ge m+s_{i^\prime +1} \ge m+s_{i^\prime }+1 \end{array}\right. } \text { } \forall j \in [i^\prime +1,q]. \end{aligned}$$

Next, we show that

$$\begin{aligned} \sum _{j=1}^{q} z_{l_j} \le q-i^\prime \end{aligned}$$

(9)

by introducing a contradiction. Suppose $\sum _{j=1}^{q} z_{l_j} \ge q-i^\prime +1$. We have

$$\begin{aligned} \tau\ge & {} \sum _{i=1}^{m+s_{i^\prime }} \pi _i + \sum _{i=m+s_{i^\prime }+1}^{n} \pi _i z_i \end{aligned}$$

(10)

$$\begin{aligned}\ge & {} \sum _{i=1}^{m+s_{i^\prime }} \pi _i + \sum _{j \in [1,q] \text { and } l_j \ge m+s_{i^\prime }+1} \pi _{l_j} z_{l_j} \nonumber \\\ge & {} \sum _{i=1}^{m+s_{i^\prime }} \pi _i + \sum _{j=i^\prime }^{q} \pi _{l_j} z_{l_j} + \sum _{j \in [1,i^\prime ] \text { and } l_j \ge m+s_{i^\prime }+1} \pi _{l_j} z_{l_j} \end{aligned}$$

(11)

$$\begin{aligned}\ge & {} \sum _{i=1}^{m+s_{i^\prime }} \pi _i + \sum _{j=i^\prime }^{q} \pi _{k_j} > \tau \end{aligned}$$

(12)

where inequality (10) is just (7). Inequality (11) holds because

$$\begin{aligned} l_j \ge {\left\{ \begin{array}{ll} m+s_{j}+1 \ge m+s_{i^\prime }+1 , \\ m+s_{j+1} \ge m+s_{i^\prime +1} \ge m+s_{i^\prime }+1 \end{array}\right. } \text { } \forall j \in [i^\prime ,q]. \end{aligned}$$

Inequality (12) holds because $\sum _{j=1}^{q} z_{l_j} \ge q-i^\prime +1$ and $\pi _{k_1} \ge \cdots \ge \pi _{k_q}$.

Given the contradiction introduced by (10)–(12), we have that (9) holds. Note that $\delta _1 \le \cdots \le \delta _{q+1}$ is monotonic. With (9), we get

$$\begin{aligned} \sum _{j =i^\prime +1}^{q} \delta _j \ge \sum _{j =i^\prime +1}^{q} \delta _j z_{l_j} + \sum _{j \in [1,i^\prime ] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _j z_{l_j}. \end{aligned}$$

Then from (8), we have

$$\begin{aligned} \sum _{j=1}^{q} \delta _j(1-z_{l_j})= & {} \sum _{j =i^\prime +1}^{q} \delta _j + \sum _{j \in [1,i^\prime ] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _j - \sum _{j =i^\prime +1}^{q} \delta _j z_{l_j}\\&- \sum _{j \in [1,i^\prime ] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _j z_{l_j} \\\ge & {} \sum _{j \in [1,i^\prime ] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _j \\\ge & {} \delta _{i^\prime } + \sum _{j \in [1,i^\prime -1] \text { and } l_j \ge m+s_{i^\prime }+1} \delta _j \ge h_{m+s_1} - h_{m+s_{i^\prime +1}}. \end{aligned}$$

The last inequality holds because of the definition of $\delta _{i^\prime }$. Therefore, we have

$$\begin{aligned}&y + \sum _{j=1}^{a} (h_{t_j} - h_{t_{j+1}}) z_{t_j} + \sum _{j=1}^{q} \delta _j(1-z_{l_j})\\&\quad \ge h_{m+s_{i^\prime +1}} + h_{t_1} - h_{m+s_1} + h_{m+s_1}-h_{m+s_{i^\prime +1}} \ge h_{t_1}. \end{aligned}$$

$\square$

Next, we give necessary condition that (5) is facet-defining for $\mathcal {K}$.

Proposition 2

If (5) is facet-defining for $\mathcal {K}$, then we have $t_1=1$ and

$$\begin{aligned} \sum _{i=1}^{m+s_j-1} \pi _i + \sum _{i=j}^{q} \pi _{k_i} \le \tau \quad \forall j \in [1,q] \text { with } s_j \ge 1. \end{aligned}$$

(13)

Proof

Note that the inequality (5) is uniquely determined by a triple $(T,\varPi _L,\mathbf {s})$. We will denote (5) as the triple $(T,\varPi _L,\mathbf {s})$ in the proof. First, we will prove the necessary condition that $t_1=1$. Given a $(T,\varPi _L,\mathbf {s})$ with $t_1>1$. We can have $(T^\prime ,\varPi _L,\mathbf {s})$ with $T^\prime =T \cup \{1\}$, i.e.,

$$\begin{aligned} y + (h_1-h_{t_1})z_1 + \sum _{j=1}^{a} (h_{t_j} - h_{t_{j+1}}) z_{t_j} + \sum _{j=1}^{q} \delta _j(1-z_{l_j}) \ge h_{1} \end{aligned}$$

which implies

$$\begin{aligned} (h_1-h_{t_1})(z_1-1) + y + \sum _{j=1}^{a} (h_{t_j} - h_{t_{j+1}}) z_{t_j} + \sum _{j=1}^{q} \delta _j(1-z_{l_j}) \ge h_{t_1}. \end{aligned}$$

As $(h_1-h_{t_1})(z_1-1) \le 0$, The $(T^\prime ,\varPi _L,\mathbf {s})$ is at least as strong as the $(T,\varPi _L,\mathbf {s})$ inequality.

Suppose the condition (13) does not hold for a $(T,\varPi _L,\mathbf {s})$ with coefficient $\delta _j\,\forall j \in [1,q]$ and $i^\prime \in [1,q]$ is the first index that the condition (13) does not hold. Thus, we have

$$\begin{aligned} \sum _{i=1}^{m+s_{i^\prime }-1} \pi _i + \sum _{i=i^\prime }^{q} \pi _{k_i} > \tau \quad \text { but } \sum _{i=1}^{m+s_{i^\prime -1}-1} \pi _i + \sum _{i=i^\prime }^{q} \pi _{k_i} \le \tau \end{aligned}$$

which implies that $s_{i^\prime -1} < s_{i^\prime }$. We can define a triple $(T,\varPi _L,\mathbf {s}^\prime )$ such that $s^\prime _j = s_j\,\forall j \in [1,q]-\{i\}$ and $s^\prime _{i^\prime } = s_{i^\prime }-1$. Note that $s^\prime$ is still a monotonic sequence as s. It is clear that we have $\delta ^\prime _j \le \delta _j\,\forall j \in [1,q]$ where $\delta ^\prime _j$ is the coefficient for $(T,\varPi _L,\mathbf {s}^\prime )$. So $(T,\varPi _L,\mathbf {s}^\prime )$ inequality is at least as strong as the $(T,\varPi _L,\mathbf {s})$ inequality. $\square$

In Theorem 1, we have parameter $q \in [0,p-m]$. It is obvious that inequality (5) becomes the strengthened star inequality when $q=0$. Next, when $q=p-m$, we show that Theorem 1 improves Theorem 6 in [22].

Corollary 1

Let $q = p-m$ and $s_j = \min \{j,\nu -m+1\}\,\forall j \in [1,q]$, we have valid inequalities

$$\begin{aligned} y + \sum _{j=1}^{a} (h_{t_j} - h_{t_{j+1}}) z_{t_j} + \sum _{j=1}^{p-m} \delta _j(1-z_{l_j}) \ge h_{t_1} \end{aligned}$$

(14)

where

$$\begin{aligned} \delta _j = \left\{ \begin{aligned}&h_{m+1} - h_{m+\min \{\nu -m+1,2\}}&j=1 \\&\max \left\{ \delta _{j-1}, h_{m+1} - h_{m+\min \{\nu -m+1,j+1\}} - \sum _{i \in [1,j-1] \text { and } l_i \ge m+1+\min \{\nu -m+1,j\}} \delta _i \right\}&j \in [2,q]. \end{aligned} \right. \end{aligned}$$

Proof

Because the definition of p in Sect. 1 implies that the summation of any $p+1$ many $\pi _i$’s for $i \in [1,n]$ is strictly greater than $\tau$, we have the following result for any permutation $\{k_1,\ldots ,k_{q}\}$ of L

$$\begin{aligned} \sum _{i=1}^{m+s_j} \pi _i + \sum _{i=j}^{q} \pi _{k_i} \ge \left\{ \begin{aligned} \sum _{i=1}^{m+j} \pi _i + \sum _{i=j}^{p-m} \pi _{k_i} \\ \sum _{i=1}^{m+(\nu -m+1)} \pi _i + \sum _{i=j}^{p-m} \pi _{k_i} \end{aligned} \right. > \tau \quad \forall j \in [1,q]. \end{aligned}$$

Apparently $s_1 = \min \{1,\nu -m+1\} = 1$ since $m \in [1,\nu ]$. Therefore, the expected result follows. $\square$

Remark 1

• (i) Corollary 1 is equivalent to Theorem 3 in [22] when the knapsack constraint is reduced to a cardinality constraint. In such case, we have $p=\nu$ and $s_j = \min \{j,p-m+1\} = j\,\forall j \in [1,p-m]$.

• (ii) Corollary 1 improves Theorem 6 in [22], which is the main result in [22] for general $\mathcal {K}$. Note that

  $$\begin{aligned}&\large \{i \in [1,j-1] : l_i \ge m+1+\min \{\nu -m+1,j\}\large \}\\&\quad \supseteq \{i \in [1,j-1] : l_i \ge m+1+j\} \end{aligned}$$

  and $\delta _j$s are all positive. Hence, inequality (14) is at least as strong as the one in [22].

• (iii) We note that the choice of $s_j$ in Corollary 1 does not need to satisfy (13). If it is the case, (14) could be dominated by (5), which is demonstrated in an example adopted from [22].

Example 1

(Example 1 in [22]) Let $h=(40,38,34,31,26,16,8,4,2,1)$ for $n=10$, and $\pi _1 = \cdots = \pi _4 = \tau /4$ and $\pi _5 = \cdots = \pi _{10} = \tau /6$ with $\tau =0.5$. It is easy to check that $\nu =4$ and $p=6$. As showed in [22], inequality (14) with $m=1, t_1=1$ and $\varPi _L=\{4,6,7,8,9\}$ gives

$$\begin{aligned} y + (h_1-h_2) z_1+ & {} (h_2-h_3)(1-z_4) + (h_2-h_3)(1-z_6) + (h_2-h_5-\delta _2)(1-z_7) \\+ & {} (h_2-h_5-\delta _2)(1-z_8) + (h_2-h_5-\delta _2)(1-z_9) \ge h_1 \end{aligned}$$

or specifically,

$$\begin{aligned} y + 2 z_1 + 4(1-z_4) + 4(1-z_6) + 8(1-z_7) + 8(1-z_8) + 8(1-z_9) \ge 40\qquad \end{aligned}$$

(15)

where $\delta _2 = h_2 - h_3$ is the coefficient for term $(1-z_6)$. This inequality, nevertheless, is not facet-defining as it is dominated by

$$\begin{aligned}&y + (h_1-h_2) z_1 + (h_2-h_3)(1-z_4) + (h_2-h_3)(1-z_7)\nonumber \\&\quad +(h_2-h_5 - \delta _2)(1-z_8) \ge h_1 \end{aligned}$$

(16)

or specifically,

$$\begin{aligned} y + 2 z_1 + 4(1-z_4) + 4(1-z_7) + 8(1-z_8)\ge 40 \end{aligned}$$

which is valid and facet-defining. According to Theorem 1, inequality (16) can be generated by letting $m=1, \varPi _L=\{4,7,8\}$ with $q=3$. So $\{k_1,k_2,k_3\} = \{4,7,8\}$ as well since $\pi _4 \ge \pi _{7} \ge \pi _8$. It is easy to see that we can choose $(s_1,s_2,s_3) = (1,2,3)$ because, for $j \in [1,q] = [1,3]$, we have

$$\begin{aligned} \sum _{i=1}^{m+s_j} \pi _i + \sum _{i=j}^q \pi _{k_i} ={\left\{ \begin{array}{ll} \frac{2}{4}\tau + \frac{1}{4}\tau + \frac{2}{6}\tau = \frac{13}{12}\tau &{} \text { when } j=1 \\ \frac{3}{4}\tau + \frac{2}{6}\tau = \frac{13}{12}\tau &{} \text { when } j=2 \\ \tau + \frac{1}{6}\tau = \frac{7}{6}\tau &{} \text { when } j=3 \end{array}\right. } \quad > \tau . \end{aligned}$$

Because of Proposition 2, we make the following assumption to have stronger inequalities (5).

Assumption 1

In Theorem 1, we always choose $s_j\,\forall j \in [1,q+1]$ such that

$$\begin{aligned} \sum _{i=1}^{m+s_j-1} \pi _i + \sum _{i=j}^{q} \pi _{k_i} \le \tau \quad \forall j \in [1,q]. \end{aligned}$$

Next, we provide sufficient conditions that guarantee (5) to be facet-defining for $\mathcal {K}$.

Theorem 2

The inequality (5) is facet-defining for $\mathcal {K}$ if $t_1=1, \pi _{l_1} \ge \cdots \ge \pi _{l_{q}}$, and

$$\begin{aligned} \sum _{i=1}^{q} \pi _{l_i} + \pi _j \le \tau \quad \forall j \notin T \cup L. \end{aligned}$$

(17)

Proof

The proof is similar to that of Theorem 4 in [22]. However, since our inequality (5) is more general, we give a self-contained proof. First, let $y^0 = h_1$, vector $\mathbf {z}^0$ with $\mathbf {z}_j^0 = 1$ if $j \in L$ and $\mathbf {z}^0_j=0$ otherwise. Next, for each $j \notin (T \cup L)$, we have point $(y^j,\mathbf {z}^j)=(y^0,\mathbf {z}^0+e_j)$, where $e_j$ is an n dimensional unit vector with jth component equal to 1. The point is feasible because of (17).

For each $j \in [1,a]$, let $y^{t_j} = h_{t_{j+1}}, \mathbf {z}^{t_j}_i=1$ if $i \in [1,t_{j+1}-1] \cup L$ and $\mathbf {z}^{t_j}_i=0$ otherwise. The point is feasible because of the condition

$$\begin{aligned} \sum _{i=1}^{t_{j+1}-1} \pi _i + \sum _{i=1}^{q} \pi _{l_i} \le \sum _{i=1}^{m+s_1-1} \pi _i + \sum _{i=1}^{q} \pi _{l_i} \le \tau . \end{aligned}$$

For $j \in [1,q]$, first we let $y^{l_1}=h_{m+s_2}$ and

$$\begin{aligned} \mathbf {z}^{l_j}_i = 1 \text { } \forall i \in [1,m+s_2-1] \cup \{l_{2},\ldots ,l_{q+1}\} \text { and } \mathbf {z}^{l_j}_i = 0 \text { otherwise}. \end{aligned}$$

The point is feasible because of Assumption 1. Then, for $j \in [2,q+1]$, if

$$\begin{aligned} \delta _j = h_{m+s_1} - h_{m+s_j} - \sum _{i \in [1,j-1] \text { and } l_i \ge m+1+s_j} \delta _i, \end{aligned}$$

let $y^{l_j}=h_{m+s_{j+1}}$ and

$$\begin{aligned} \mathbf {z}^{l_j}_i = 1 \text { } \forall i \in [1,m+s_{j+1}-1] \cup \{l_{j+1},\ldots ,l_{q+1}\} \text { and } \mathbf {z}^{l_j}_i = 0 \text { otherwise} . \end{aligned}$$

If $\delta _j = \delta _{j-1}$, we let

$$\begin{aligned} (y^{l_j},\mathbf {z}^{l_j}) = (y^{l_{j-1}},\mathbf {z}^{l_{j-1}} + e_{l_{j-1}} - e_{l_j}). \end{aligned}$$

Note that $\pi _{l_{j}} \ge \pi _{l_{j-1}}$. In either case, the point is feasible because of Assumption 1. These $n+1$ points on the face defined by inequality (5) are affinely independent. $\square$

In the following, we consider an implementation strategy of this type of strong inequalities in our numerical study.

Corollary 2

When $|L|=1$, the inequality (5) in Theorem 1 is facet-defining if $t_1=1$, and

$$\begin{aligned} \pi _{l_1} + \pi _j \le \tau \quad \forall j \in [1,n] {\setminus } \{l_1\}. \end{aligned}$$

Next we will provide a separation algorithm for implementing Corollary 2.

Separation Heuristic

We always set $t_1=1$. Let $z^*$ be a fraction solution and we keep an ordered list of the elements in $\{i \in [\nu +1,n]: z_i^* = 1, \pi _{i} + \pi _j \le \tau , \text { } \forall j \in [1,n]{\setminus }\{i\}\}$, denoted as $\varOmega$, in decreasing order of $\pi _i$. We choose the first element in the list to be in the set L, i.e., $L = \{l_1\}$ where $l_1 = {{\mathrm{\arg \max }}}_i \{\pi _i : i \in \varOmega \}$. We let

$$\begin{aligned} m+s_1 = \min \left\{ j : \sum _{i=1}^{j} \pi _i + \pi _{l_1} > \tau , j \in [1,\nu ] \right\} \end{aligned}$$

which can be found in $O(\nu )$. Then, the best choice of the set T in the inequality (5) can be found by solving a shortest path problem from the source 1 to the sink $m+s_1$ on a directed acyclic graph with vertices $\{1,\ldots ,m+s_1\}$, edges $(i,j), 1 \le i < j \le m+s_1$, and associated cost of $(h_i - h_j)z^*_i$ (see also Sect. 3.1 in [22]) and the complexity is $O(\nu ^2)$. The coefficient $\delta _1 = h_{m+s_1} - h_{\nu +1}$. Note that $z^*_{l_1} = 1$ and shortest path algorithm is used to find the best choice of the set T. Therefore, our separation algorithm can find the most violated inequality in the form of Corollary 2, which is facet-defining for $\mathcal {Q}$, in $O(\nu ^2)$.

Note that the separation algorithm in [22] is $O(p^4)$ without guarantee of finding facet-defining inequalities of $\mathcal {Q}$. Abdi et al. [1] mentioned that the same separation algorithm can be applied in their case without providing computational evaluation.

As mentioned, a set of facet-defining inequalities for $\mathcal {K}$ was developed in Theorem 14 of [1]. In the following, we analyze the connection between those facet-defining inequalities and results in Theorems 1 and 2. In particular, we show that they are subsumed as special cases of (5).

Corollary 3

Let M be a positive integer, $a_i = M\pi _i\,\forall i \in [1,n]$ and $\mu =M\tau$. The inequality (5) in Theorem 1 is valid for $\mathcal {K}$ if

• $a_i = 1\,\forall i \in L$ and $q = \mu - \sum _{i=1}^m a_i$ is an integer;

• $s_1=1$ and $m+s_j = \mathfrak {m}(j-1)+1\,\forall j \in [2,q]$;

• $l_j > \mathfrak {m}(j)\,\forall j \in [1,q]$

where $\mathfrak {m}(j) = max\left\{ k : j \ge \sum _{i=1}^{k} a_i - \sum _{i=1}^{m} a_i \right\}$. The inequality is facet-defining if $t_1=1$ and $a_j \le \sum _{i=1}^{m} a_i\,\forall j \in [1,n] {\setminus } L$.

It is not difficult to verify that Corollary 3 is equivalent to Theorem 14 in [1]. So, before providing a proof to this result, we make a few remarks on the applicability of Corollary 3 (equivalently, Theorem 14 of [1]).

Remark 2

• (i) The condition that $a_i = 1\,\forall i \in L$ requires that $\pi _i\,\forall i \in L$ are equal, which is a very special case of the knapsack constraint of $\mathcal {K}$. For example, Corollary 3 cannot explain (15) (derived in [22]) or (16) because $\pi _4 \ne \pi _6$. Note however that Corollary 1 or Theorem 6 in [22] is able to generate explicit valid inequalities for a general $\mathcal {K}$. Hence, different from the understanding made in [1], we cannot conclude that Corollary 3 subsumes Corollary 1 or Theorem 6 in [22].

• (ii) The condition that $q = \mu - \sum _{i=1}^m a_i$ is an integer is very restrictive. Actually, Corollary 3 cannot describe any inequalities in Example 1 with $m=1$. Since we need to have $a_i = 1\,\forall i \in L$, we have either $L \subseteq \{1,\ldots ,4\}$ with $M=8$ or $L \subseteq \{5,\ldots ,10\}$ with $M=12$. If $L \subseteq \{1,\ldots ,4\}, q = M (\tau - \pi _1) = 3$. So, we must have $L=\{2,3,4\}$. However, $l_j > \mathfrak {m}(j) = j+1$ implies that the choice of L is not viable. If $L \subseteq \{5,\ldots ,10\}, q = M (\tau - \pi _1) = 4.5$, which is not an integer. So, there is no valid L satisfying those conditions.

• (iii) Corollary 3 could fail to provide any inequalities other than strengthened star inequalities. Consider an example with $n=8, \pi _1=\cdots =\pi _3=\tau /3$, and $\pi _4=\cdots =\pi _8=\tau /5$ where $\tau =0.5$. Since we need to have $a_i = 1\,\forall i \in L$, we have either $L \subseteq \{1,\ldots ,3\}$ with $M=6$ or $L \subseteq \{4,\ldots ,8\}$ with $M=10$. Suppose $m < \nu = 3$. To have that $q = \mu - \sum _{i=1}^m a_i$ is an integer, we can only set $L \subseteq \{1,\ldots ,3\}$ with $M=6$. If $m=1$ or 2, it is easy to check that $\mathfrak {m}(j) = j+m$, which implies that a viable choice of L with $l_j > \mathfrak {m}(j)$ does not exist. So, $m=\nu$, i.e., the only set of inequalities Corollary 3 implies is the strengthened star inequalities.

• (iv) Comparing to Corollary 3, we mention that Theorem 1 has no such limitations but includes it as a special case. Therefore, Theorem 1 generalizes one of the main theorems in [1]. Note also that Corollary 3 does not imply Corollary 2 because $q = \frac{1}{\pi _{l_1}}(\tau - \sum _{i=1}^m \pi _i)$ might not be an integer.

Proof

Note that $\forall j \in [1,q], l_j > \mathfrak {m}(j)$ implies $l_j \ge m+s_{j+1}$, and

$$\begin{aligned} s_j= & {} \mathfrak {m}(j-1)-m+1 = \mathop {{{\mathrm{\arg \max }}}}\limits _s \left\{ \sum _{i=1}^{m+s} a_i - \sum _{i=1}^{m} a_i \le j-1 \right\} + 1 \\= & {} \mathop {{{\mathrm{\arg \min }}}}\limits _s \left\{ \sum _{i=1}^{m+s} a_i - \sum _{i=1}^{m} a_i > j-1 \right\} . \end{aligned}$$

For any $j \in [1,q]$, we have

$$\begin{aligned} \sum _{i=1}^{m+s_j} \pi _i + \sum _{i=j}^{q} \pi _{k_i}= & {} \frac{1}{M} \left( \sum _{i=1}^{m+s_j} a_i + \sum _{i=j}^{q} a_{k_i}\right) \nonumber \\= & {} \frac{1}{M} \left( \sum _{i=1}^{m+s_j} a_i + q-j+1\right) \nonumber \\= & {} \frac{1}{M} \left( \sum _{i=1}^{m+s_j} a_i - \sum _{i=1}^{m} a_i + \mu -j+1\right) \nonumber \\> & {} \frac{1}{M} \left( M \tau \right) > \tau \end{aligned}$$

(18)

where (18) holds because $a_i = 1\,\forall i \in L$. By Theorem 1, the inequality (1) is valid for $\mathcal {K}$. We have

$$\begin{aligned} \mu&= q + \sum _{i=1}^m a_i = \sum _{i \in L} a_i + \sum _{i=1}^m a_i \ge \sum _{i \in L} a_i + a_j \text { } \forall j \in [1,n]/L, \end{aligned}$$

(19)

$$\begin{aligned}&\Rightarrow \quad \tau \ge \sum _{i \in L} \pi _i + \pi _j \text { } \forall j \in [1,n] {\setminus } L , \end{aligned}$$

(20)

$$\begin{aligned}&\Rightarrow \quad \tau \ge \sum _{i \in L} \pi _i + \pi _j \text { } \forall j \in [1,n] {\setminus } (T \cup L), \end{aligned}$$

(21)

where (20) is obtained from dividing (19) by M. Note that Corollary 3 follows Theorem 1 by imposing more restricted requirements on parameters other than T. Actually, according to Theorem 1, set T is an arbitrary subset of [1, m]. Since $j \in [1,n]{\setminus }(T \cup L)$ implies $j \in [1,n]{\setminus }L$ obviously, we have (21), i.e., (17), holds. Thus, Theorem 2 implies that (5) is facet-defining. $\square$

3 Strong inequalities derived from lifting

In Sect. 2, although a large number facet-defining inequalities subsuming those identified in [1, 22, 29] are proposed for $\mathcal {K}$, they are not sufficient to define its convex hull. For instance, we observe that the following inequalities are facet-defining for the set in Example 1, which, nevertheless, cannot be derived based on Theorem 1.

$$\begin{aligned} \frac{1}{3} z_1 - \frac{1}{3} z_2 + z_3 + z_4 + z_5 + z_7 + z_8 + z_9\le & {} 4 + \frac{1}{3} (y - 40) + \frac{8}{3}(1-z_{10}) \nonumber \\ \frac{1}{3} z_1 - \frac{1}{3} z_2 + z_3 + z_4 + z_5 + z_6 + z_7 + z_9\le & {} 4 + \frac{1}{3} (y - 40) + \frac{8}{3}(1-z_{10})\nonumber \\ \frac{1}{3} z_1 - \frac{1}{3} z_2 + z_3 + z_4 + z_6 + z_7 + z_8 + z_9\le & {} 4 + \frac{1}{3} (y - 40) + \frac{8}{3}(1-z_{5}).\nonumber \\ \end{aligned}$$

(22)

Indeed, as pointed out by Abdi and Fukasawa [1], set $\mathcal {K}$ has abundant polyhedral structure and many of its valid inequalities are related to 0–1 knapsack polyhedron. They further presented a characterization of all valid inequalities of $\mathcal {K}$. Yet, from our understanding, such result does not have explicit representation for implementation, unless a general purpose solver is called for separation. To advance our understanding on $\mathcal {K}$ as well as our solution capacity for chance-constrained problem, we directly make use of the cover inequality of 0–1 knapsack polyhedron and develop lifting techniques with consideration of mixing inequalities to derive valid inequalities. As demonstrated at the end of this section, inequalities in (22) can be simply obtained using this approach. We mention that, the family of inequalities obtained through this approach is, to the best of our knowledge, the first type that has a different structure from those of all star inequality based ones, including those in [1, 22, 29], as well as ours presented in Sect. 2.

For $m \in [1,\nu ]$, let $N_0 = [1,m-1]$ and $N_1 = \{l_1,\ldots ,l_q\} \subseteq [\nu +2,n]$ with cardinality q such that

$$\begin{aligned} \sum _{i=1}^{m} \pi _i + \sum _{i \in N_1} \pi _i \le \tau \text { and }\sum _{i=1}^{m+1} \pi _i + \sum _{i \in N_1} \pi _i > \tau . \end{aligned}$$

(23)

We consider a restricted 0–1 knapsack polytope $\mathcal {S}(N_0,N_1)$, where

$$\begin{aligned} \mathcal {S}(N_0,N_1) = \left\{ \mathbf {z} \in \{0,1\}^n: \sum _{i=1}^{n} \pi _i z_i \le \tau , z_i = 0 \text { } \forall i \in N_0 \text { and } z_i=1 \text { } \forall i \in N_1 \right\} . \end{aligned}$$

Let $\tau ^\prime = \tau - \sum _{i \in N_1} \pi _i$. Then, for set $\hat{N} = [1,n]{\setminus }(N_0 \cup N_1)$, we assume that a cover $\mathbb {C}$ is available with respect to $\tau ^\prime$ and a lifted cover inequality (LCI) is derived as the following

$$\begin{aligned} \sum _{i \in E} \alpha _i z_i \le |\mathbb {C}|-1 \end{aligned}$$

(24)

with $\alpha _i > 0\,\forall i \in E\subseteq \hat{N}$ and $\alpha _i = 0\,\forall i \in \hat{N} \setminus E$.

We then define the following function with set $W \subseteq E$ and scalar $\beta \le \sum _{i=1}^{m} \pi _i$.

$$\begin{aligned} G(W,\beta ) =&\max \quad \sum _{i \in W} \alpha _i z_i \\&\text { s.t. } \quad \sum _{i \in W} \pi _i z_i \le \tau ^\prime - \beta , \text { } z_i \in \{0,1\} \text { } \forall i \in W. \end{aligned}$$

The function G is well defined because of (23). Note that the lifting function of (24) can be defined as $|\mathbb {C}|-1 - G(E, \beta )$. Let $\bar{\rho } = G\left( E,\sum _{i=1}^{m-1} \pi _i \right) - G\left( E{\setminus }\{m\}, \sum _{i=1}^{m} \pi _i \right) - \alpha _m$, which is nonnegative noting that an optimal solution of $G\left( E{\setminus }\{m\}, \sum _{i=1}^{m} \pi _i \right)$, together with $z_m=1$, is just feasible to $G\left( E,\sum _{i=1}^{m-1} \pi _i \right)$.

Theorem 3

Let $m \in [1,\nu ]$ and $N_1 \subseteq [\nu +2,n]$. Suppose a superadditive function $\varPhi (\beta )$ exists and $0\le \varPhi (\beta )\le |\mathbb {C}|-1 - G(E, \beta )$. If $h_{m} > h_{m+1}$ and $0\le \rho \le \bar{\rho }$, then the inequality

$$\begin{aligned} \sum _{i=1}^{m-1} \phi _i z_i + \sum _{i \in E} \alpha _i z_i \le |\mathbb {C}|-1 + \frac{\rho }{h_{m}-h_{m+1}} (y - h_1) \end{aligned}$$

(25)

is valid for the set $\mathcal {K}(N_1) = \mathcal {K} \cap \left\{ \mathbf {z} \in \{0,1\}^n: z_i=1 \text { } \forall i \in N_1 \right\}$, where

$$\begin{aligned} \phi _i=\varPhi (\pi _i) + \frac{\rho }{h_{m}-h_{m+1}} (h_{i+1}-h_{i}) \quad \forall i = 1,\ldots ,m-1. \end{aligned}$$

(26)

Proof

By the definition of $\mathcal {K}(N_1)$, we can fix $z_i=1 \text { } \forall i \in N_1$ for the rest of proof. Note that $y \ge h_{m+1}$ in the set $\mathcal {K}(N_1)$, because of condition (23). Next, we consider all three situations based on the value of y.

First, if $y \ge h_1$, we assume that $z_i=1\,\forall i \in Q \subseteq [1,m-1]$ and $z_i=0\,\forall i \in [1,m-1]{\setminus }Q$ for a set Q. Then the knapsack constraint in $\mathcal {K}(N_1)$ becomes

$$\begin{aligned} \sum _{i \in E} \pi _i z_i \le \tau ^\prime - \sum _{i \in Q} \pi _i \end{aligned}$$

and we have

$$\begin{aligned}&\sum _{i=1}^{m-1} \phi _i z_i + \sum _{i \in E} \alpha _i z_i \le \sum _{i \in Q} \varPhi (\pi _i) + \sum _{i \in E} \alpha _i z_i \\&\quad \le \varPhi \left( \sum _{i \in Q} \pi _i\right) + \sum _{i \in E} \alpha _i z_i \le \varPhi \left( \sum _{i \in Q} \pi _i\right) + G\left( E, \sum _{i \in Q} \pi _i\right) \le |\mathbb {C}|-1 \\&\quad \le |\mathbb {C}|-1 + \frac{\rho }{h_{m}-h_{m+1}} (y - h_1) \end{aligned}$$

where the first inequality holds because $\phi _i \le \varPhi (\pi _i)$.

Second, if $h_{t-1} > y \ge h_{t}$ for some $t=2,\ldots ,m$. We must have $z_i=1\,\forall i \in [1,t-1]$, and also assume that $z_i=1\,\forall i \in Q \subseteq [t,m-1]$ and $z_i=0\,\forall i \in [1,m-1]{\setminus }Q$ for a set Q. Then the knapsack constraint in $\mathcal {K}(N_1)$ becomes

$$\begin{aligned} \sum _{i \in E} \pi _i z_i \le \tau ^\prime - \sum _{i=1}^{t-1} \pi _i - \sum _{i \in Q} \pi _i \end{aligned}$$

and we get

$$\begin{aligned}&\sum _{i=1}^{m-1} \phi _i z_i + \sum _{i \in E} \alpha _i z_i = \sum _{i=1}^{t-1} \phi _i + \sum _{i=t}^{m-1} \phi _i z_i + \sum _{i \in E} \alpha _i z_i \\&\quad \le \sum _{i=1}^{t-1} \varPhi (\pi _i) + \frac{\rho }{h_{m}-h_{m+1}}(h_{t}-h_{1}) + \sum _{i \in Q} \varPhi (\pi _i) + \sum _{i \in E} \alpha _i z_i \\&\quad \le \varPhi \left( \sum _{i=1}^{t-1} \pi _i + \sum _{i \in Q} \pi _i\right) + \frac{ \rho }{h_{m}-h_{m+1}}(h_{t}-h_{1}) + \sum _{i \in E} \alpha _i z_i \\&\quad \le \varPhi \left( \sum _{i=1}^{t-1} \pi _i + \sum _{i \in Q} \pi _i\right) + \frac{ \rho }{h_{m}-h_{m+1}}(h_t-h_{1}) + G\left( E, \sum _{i=1}^{t-1} \pi _i + \sum _{i \in Q} \pi _i\right) \\&\quad \le |\mathbb {C}|-1 + \frac{\rho }{h_{m}-h_{m+1}} (y - h_1). \end{aligned}$$

Otherwise, $h_{m} > y \ge h_{m+1}$ and $z_i=1\,\forall i \in [1,m]$. So, we get

$$\begin{aligned}&\sum _{i=1}^{m-1} \phi _i z_i + \sum _{i \in E} \alpha _i z_i = \sum _{i=1}^{m-1} \phi _i + \alpha _m + \sum _{i \in E {\setminus } \{m\}} \alpha _i z_i \nonumber \\&\quad \le \sum _{i=1}^{m-1} \varPhi (\pi _i) + \frac{\rho }{h_{m}-h_{m+1}}(h_{m}-h_{1}) + \alpha _m + \sum _{i \in E {\setminus } \{m\}} \alpha _i z_i \nonumber \\&\quad = \varPhi \left( \sum _{i=1}^{m-1} \pi _i\right) + \frac{\rho }{h_{m}-h_{m+1}}(h_{m+1}-h_{1}) + \rho + \alpha _m + \sum _{i \in E {\setminus } \{m\}} \alpha _i z_i \nonumber \\&\quad \le \varPhi \left( \sum _{i=1}^{m-1} \pi _i\right) + \frac{\rho }{h_{m}-h_{m+1}}(h_{m+1}-h_{1}) + G\left( E, \sum _{i=1}^{m-1} \pi _i\right) \nonumber \\&\quad \le |\mathbb {C}|-1 + \frac{\rho }{h_{m}-h_{m+1}}(h_{m+1}-h_{1}) \nonumber \\&\quad \le |\mathbb {C}|-1 + \frac{\rho }{h_{m}-h_{m+1}}(y-h_{1}) \end{aligned}$$

(27)

where the inequality (27) holds because of the definition of G.

With analysis on all three cases, it can be seen that the inequality (25) is valid for the set $\mathcal {K}(N_1)$. $\square$

Remark 3

• (i) LCI in (24) can be easily obtained through the sequential lifting algorithm in [46]. Note that $\alpha _i$ are positive integers for $i \in E$, and $G(E,\beta )$ (also the lifting function $|\mathbb {C}|-1-G(E,\beta )$) will be a staircase function [11]. Then, a dynamic program algorithm can be used to analytically describe the lifting function, whose superadditive approximation $\varPhi (\beta )$ can be constructed using the approximation method developed in [12].

• (ii) To support our example at the end of this section and to make this paper self-contained, we next provide a valid superadditive approximation for the lifting function $|\mathbb {C}|-1-G(E,\beta )$. Our intention here is for demonstration, rather than deriving the strongest but complicated ones, i.e., maximal and non-dominated approximations, which certainly is a future research direction. Assume step lengths of lifting function are $p_0, \dots , p_{|\mathbb {C}|-1}$. We sort them from large to small to obtain a permutation $(p_{a_0},\dots , p_{a_{|\mathbb {C}|-1}})$. Then, by [12], the following function is a valid superadditive approximation.

  $$\begin{aligned} \varPhi (\beta ) = {\left\{ \begin{array}{ll} 0 &{} \text {if } 0\le \beta< p_{a_0}\\ \mathfrak {h} &{} \text { if } \sum \limits _{k=0}^{\mathfrak {h}-1} p_{a_k} \le \beta < \sum \limits _{k=0}^{\mathfrak {h}} p_{a_k}, \ \mathfrak {h}=1,\dots , |\mathbb {C}|-1. \end{array}\right. } \end{aligned}$$

Note that when $\bar{\rho }=\rho =0$, (25) reduces to an LCI of 0–1 knapsack set $\mathcal {S}(\emptyset ,N_1)$. Then performing exact lifting with respect to variables fixed at 1 provides us a valid inequality for both $\mathcal {S}(\emptyset ,\emptyset )$ and $\mathcal {K}$. It actually corresponds the observation made in [1] that facet-defining inequalities of $\mathcal {S}(\emptyset ,\emptyset )$ are also facet-defining for $\mathcal {K}$. To study more interesting interactions between mixing set and 0–1 knapsack set, we next limit ourselves to the case that $\rho >0$ in Theorem 3 and investigate lifting (25) sequentially with respect to variables $z_i\,\forall i \in N_1$ in the order of $\{l_1,\ldots ,l_q\}$. Suppose we already have lifting coefficients for $z_{l_1},\ldots ,z_{l_{r-1}}$ such that

$$\begin{aligned} \sum _{i=1}^{m-1}\alpha _i z_i + \sum _{i \in E} \alpha _i z_i \le |\mathbb {C}|-1 + \frac{\rho }{h_{m}-h_{m+1}} (y - h_1) + \sum _{j=1}^{r-1} \delta _{l_j} (1-z_{l_j}) \end{aligned}$$

(28)

is valid for the set $\mathcal {K} \cap \left\{ \mathbf {z} \in \{0,1\}^n: z_i=1 \text { } \forall i \in \{l_r,\ldots ,l_q\}\right\}$, and we are lifting inequality (28) with respect to variable $z_{l_r}$. By denoting the lifting coefficient as $\delta _{l_r}$, we have

Proposition 3

The lifting coefficient $\delta _{l_r}$ can be defined as

$$\begin{aligned} \delta _{l_r} = \frac{\rho }{h_{m}-h_{m+1}} h_1 -\sum _{j=1}^{r-1} \delta _{l_j} - (|\mathbb {C}|-1) + \max _{t \in [1,\eta _r+1]} \Big \{\varDelta _{t,r}- \frac{\rho }{h_{m}-h_{m+1}} h_t\Big \}\nonumber \\ \end{aligned}$$

(29)

where

$$\begin{aligned} \eta _r = \max \Big \{j : \sum _{i=1}^{j} \pi _i \le \tau ^\prime + \sum _{i=1}^{r} \pi _{l_i} \Big \} \end{aligned}$$

and $\varDelta _{t,r}$ for $t \in [1,\eta _r+1]$ are arbitrary scalars satisfying

$$\begin{aligned}&\varDelta _{t,r} \ge \sum _{i=1}^{t-1} \alpha _i + \max \sum _{i \in E \cup [t,m-1]} \alpha _i z_i + \sum _{j=1}^{r-1} \delta _{l_j} z_{l_j} \nonumber \\&\qquad \text {s.t.} \sum _{i \in [t,n]-N_1} \pi _i z_i + \sum _{j=1}^{r-1} \pi _{l_j} z_{l_j}\le \tau ^\prime + \sum _{j=1}^{r} \pi _{l_j} - \sum _{i=1}^{t-1} \pi _i \nonumber \\&\qquad \quad \quad z_i \in \{0,1\} \quad \forall i \in [t,n] {\setminus } \{l_r,\ldots ,l_{q}\}. \end{aligned}$$

(30)

Proof

To prove that $\delta _{l_r}$ is a valid coefficient by lifting from (28), it is sufficient to show that

$$\begin{aligned} \sum _{i=1}^{m-1}\alpha _i z_i + \sum _{i \in E} \alpha _i z_i \le |\mathbb {C}|-1 + \frac{\rho }{h_{m}-h_{m+1}} (y - h_1) + \sum _{j=1}^{r} \delta _{l_j} (1-z_{l_j}) \end{aligned}$$

(31)

is valid for the set $\mathcal {K} \cap \left\{ \mathbf {z} \in \{0,1\}^n: z_i=1 \text { } \forall i \in \{l_{r+1},\ldots ,l_q\} \text { and } z_{l_r}=0 \right\} \triangleq \mathcal {K}^\prime$. Distinct from most literature, our lifting procedure involves a continuous variable y, which requires special treatments. Based on the definition of $\eta _r$, we know that $y \ge h_{\eta _r}$. Since $z_{l_r}=0$ in $\mathcal {K}^\prime$, from (31), we must have

$$\begin{aligned} \delta _{l_r} \ge&\max _{\mathbf {z} \in \mathcal {K}^\prime , y \ge h_{\eta _r}} \sum _{i=1}^{m-1}\alpha _i z_i + \sum _{i \in E} \alpha _i z_i - (|\mathbb {C}|-1) \nonumber \\&- \frac{\rho }{h_{m}-h_{m+1}} (y - h_1) - \sum _{j=1}^{r-1} \delta _{l_j} (1-z_{l_j}) \nonumber \\ =&\max _{t \in [1,\eta _r]} \max _{\begin{array}{c} \mathbf {z} \in \mathcal {K}^\prime \nonumber \\ h_{t-1}> y \ge h_t \end{array}} \sum _{i=1}^{m-1}\alpha _i z_i + \sum _{i \in E} \alpha _i z_i - (|\mathbb {C}|-1)\nonumber \\&- \frac{\rho }{h_{m}-h_{m+1}} (y - h_1) - \sum _{j=1}^{r-1} \delta _{l_j} (1-z_{l_j}) \nonumber \\ =&\max _{t \in [1,\eta _r]} \max _{\begin{array}{c} \mathbf {z} \in \mathcal {K}^\prime \nonumber \\ h_{t-1} > y \ge h_t \end{array}} \sum _{i=1}^{t-1} \alpha _i + \sum _{i \in E \cup [t,m-1]} \alpha _i z_i - (|\mathbb {C}|-1) \nonumber \\&- \frac{\rho }{h_{m}-h_{m+1}} (y - h_1) - \sum _{j=1}^{r-1} \delta _{l_j} (1-z_{l_j}) \end{aligned}$$

(32)

where we denote $h_0$ as $+\infty$ for simplicity and (32) holds because $h_{t-1} > y \ge h_{t}$ implies $z_j=1\,\forall j \in [1,t-1]$ ($[1,t-1]=\emptyset$ when $t=1$). Recall that we set $\alpha _i=0\,\forall i \in \hat{N} - E$.

Apparently, (32) holds if we can show

$$\begin{aligned} \delta _{l_r} \ge&\max _{t \in [1,\eta _r]} \max _{\begin{array}{c} \mathbf {z} \in \mathcal {K}^\prime \\ h_{t-1} > y \ge h_t \end{array}} \sum _{i=1}^{t-1} \alpha _i + \sum _{i \in E \cup [t,m-1]} \alpha _i z_i - (|\mathbb {C}|-1) \nonumber \\&- \frac{\rho }{h_{m}-h_{m+1}} (h_t - h_1) - \sum _{j=1}^{r-1} \delta _{l_j} (1-z_{l_j}) \end{aligned}$$

(33)

$$\begin{aligned} =&\max _{t \in [1,\eta _r]} \left[ \left( \max _{\mathbf {z} \in \mathcal {K}^\prime } \sum _{i=1}^{t-1} \alpha _i + \sum _{i \in E \cup [t,m-1]} \alpha _i z_i + \sum _{j=1}^{r-1} \delta _{l_j} z_{l_j} \right) - \frac{\rho }{h_{m}-h_{m+1}} h_t\right] \nonumber \\&\quad + \frac{\rho }{h_{m}-h_{m+1}} h_1 -\sum _{j=1}^{r-1} \delta _{l_j} - (|\mathbb {C}|-1) \end{aligned}$$

(34)

where (33) implies (32) because of $y \ge h_t$. Thus the continuous variable y is dropped from the lifting procedure in (34).

To show that the definition of $\delta _{l_r}$ in (29) satisfies (34), we only need to demonstrate that

$$\begin{aligned} \varDelta _{t,r} \ge \max _{\mathbf {z} \in \mathcal {K}^\prime } \sum _{i=1}^{t-1} \alpha _i + \sum _{i \in E \cup [t,m-1]} \alpha _i z_i + \sum _{j=1}^{r-1} \delta _{l_j} z_{l_j} \end{aligned}$$

(35)

Note that $\mathcal {K}^\prime$ (similar to $\mathcal {K}$) includes only a knapsack inequality, which becomes

$$\begin{aligned} \sum _{i \in [t,n]-N_1} \pi _i z_i + \sum _{j=1}^{r-1} \pi _{l_j} z_{l_j}\le \tau ^\prime + \sum _{j=1}^{r} \pi _{l_j} - \sum _{i=1}^{t-1} \pi _i \end{aligned}$$

with $z_i \in \{0,1\} \text { } \forall i \in [t,n] {\setminus } \{l_r,\ldots ,l_{q}\}$ in $\mathcal {K}^\prime$ since $z_i \text { } \forall i \in \{l_{r+1},\ldots ,l_q\}$ are fixed to 1 and recall that $z_j=1\,\forall j \in [1,t-1]$. Thus, (35) is equivalent to (30) and the definition of $\delta _{l_r}$ in (29) is valid. $\square$

Therefore, by summarizing Theorem 3 together with Proposition 3, we get

Theorem 4

If $h_{m}>h_{m+1}$, then, for any $\rho \le \overline{\rho }$, the inequality

$$\begin{aligned} \sum _{i=1}^{m-1}\phi _i z_i + \sum _{i \in E} \alpha _i z_i \le |\mathbb {C}|-1 + \frac{\rho }{h_{m}-h_{m+1}} (y - h_1) + \sum _{j=1}^{q} \delta _{l_j} (1-z_{l_j}) \end{aligned}$$

(36)

is valid for $\mathcal {K}$, where $\phi _i\,\forall i \in N_0$ are defined in (26) and $\delta _i\,\forall i \in N_1$ are given by lifting procedure in (29).

Remark 4

Given that knapsack cover inequalities have been intensively implemented in commercial solvers, we point it out that they can be readily strengthened by Theorem 4. Although the computation of (29) is a little bit involved, we can address this issue by computing LP relaxations of (30) with a simple greedy algorithm.

Example 1 (cont.) We suppose general probabilities as shown previously, where $\nu =4$. Let $m=3, N_0=\{1,2\}$ and $N_1 = \{10\}$. Note that the condition (23) holds. So, we have set $\mathcal {S}(N_0,N_1)$ that includes a knapsack as follows,

$$\begin{aligned} \frac{\tau }{4} z_3 + \frac{\tau }{4} z_4 + \frac{\tau }{6} z_{5} + \frac{\tau }{6} z_6 + \frac{\tau }{6} z_7 + \frac{\tau }{6} z_8 + \frac{\tau }{6} z_9 \le \tau - \frac{\tau }{6}. \end{aligned}$$

The set $\{3,4,5,6,8\}$ gives a minimal cover for this 0–1 knapsack and we have the minimal cover inequality

$$\begin{aligned} z_3 + z_4 + z_5 + z_6 + z_8 \le 4. \end{aligned}$$

By lifting the cover inequality with respect to variable $z_9$, we have

$$\begin{aligned} z_3 + z_4 + z_5 + z_6 + z_8 + z_9 \le 4. \end{aligned}$$

For its lifting function, we note that all step lengths are $\frac{\tau }{6}$. According to the superadditive function presented in Remark 3, that lifting function is naturally superadditive. Therefore, Theorem 3 gives the following inequality

$$\begin{aligned}&\left( 1 + \frac{1}{h_{3}-h_{4}} (h_2-h_1)\right) z_1 + \left( 1-\frac{1}{h_{3}-h_{4}} (h_3-h_2)\right) z_2 + z_3 \\&\qquad \qquad +\,z_4 + z_5 + z_6 + z_8 + z_9 \le 4 + \frac{1}{h_{3}-h_{4}} (y - h_1), \end{aligned}$$

or specifically

$$\begin{aligned} \frac{1}{3} z_1 - \frac{1}{3} z_2 + z_3 + z_4 + z_5 + z_6 + z_8 + z_9 \le 4 + \frac{1}{3} (y - h_1), \end{aligned}$$

(37)

which is valid for the set $\mathcal {K} \cap \left\{ \mathbf {z} \in \{0,1\}^{10}: z_{10}=1 \right\}$. Then, by lifting inequality (37) with respect to $z_{10}$, we get

$$\begin{aligned} \varDelta _{t1} = {\left\{ \begin{array}{ll} 1 &{} \text { when }t=1 \\ 1 &{} \text { when }t=2 \\ 1 &{} \text { when }t=3 \\ 1 &{} \text { when }t=4 \\ \frac{8}{3}&{}\text { when }t=5. \\ \end{array}\right. } \end{aligned}$$

So $\delta _1=8/3$ and we have the valid inequality

$$\begin{aligned} \frac{1}{3} z_1 - \frac{1}{3} z_2 + z_3 + z_4 + z_5 + z_6 + z_8 + z_9 \le 4 + \frac{1}{3} (y - 40) + \frac{8}{3}(1-z_{10}) \end{aligned}$$

for $\mathcal {K}$, which is the first inequality in the list (22). Similar procedures can produce other inequalities in the list.

Implementation

Because we cannot access the cover inequality generating procedure in commercial solvers, we added (36) into the initial formulation in our numerical study. Specifically, we let $N_1 = \emptyset$, i.e., $m=\nu$, cover $\mathbb {C}$ be obtained by Algorithm 1 in the following and E be an extended cover of $\mathbb {C}$. Since $\alpha _i=1\,\forall i \in E$, the value of $\bar{\rho }$ can be obtained easily and we set $\rho = \bar{\rho }$. Then the inequalities (36) can be derived from Theorem 3 for $\mathcal {Q}_r\,\forall r \in [1,d]$. Overall, we could include up to d lifting inequalities into the initial formulation.

4 Intersection of multiple mixing sets with knapsack

Up to now, we focus on deriving strong valid inequalities for a single mixing set with a 0–1 knapsack constraint, i.e., $\mathcal {K}$, which, according to Proposition 1, are crucial to understand the polyhedron $\mathcal {Q}$ of CCP. It is clear that such types of inequalities are not sufficient to describe $\mathcal {Q}$. Hence, in this section, we investigate the intersection of multiple mixing sets with knapsack constraint by developing valid inequalities that explicitly capture their interactions, i.e., valid inequalities with nonzero coefficients of multiple $y_r$s, where $r \in [1,d]$.

Given existing algebraic derivations of valid inequalities for $\mathcal {K}$, one direct approach to study $\mathcal {Q}$ is to aggregate multiple mixing sets (with assigned weights) into a single mixing set and derive valid inequalities from that aggregation, which definitely are valid for $\mathcal {Q}$. Using a numerical example, [22] illustrated that such strategy could lead to a new valid inequality that cannot be obtained from each individual mixing set. Nevertheless, observing that there is no systematical study on this approach, it remains unknown that: (1) how to select appropriate weights to generate a significant aggregation carrying rich interactive information among mixing sets; and (2) what is the strength of inequalities obtained from that aggregation with respect to $\mathcal {Q}$. In this section, instead of aggregating original constraints, we propose a novel blending procedure that allows us to aggregate derived strong inequalities from individual mixing sets into a strong one for the polyhedron $\mathcal {Q}$. Moreover, a set of sufficient conditions is derived, which ensures the resulting blending inequality is facet-defining. It is worth mentioning that it is the first type of facet-defining inequalities for the intersection of multiple mixing sets.

Apparently, in the study of $\mathcal {Q}$, it is not valid to assume $h_{r1} \ge \cdots \ge h_{rn}$ for all $r \in [1,d]$ without loss of generality. So, we keep subscript r and for each $r \in [1,d]$, we define a $1-1$ mapping $\langle \cdot \rangle _r$ on [1, n] such that

$$\begin{aligned} h_{r\langle 1\rangle _r} \ge h_{r\langle 2\rangle _r} \ge \cdots \ge h_{r\langle n\rangle _r}. \end{aligned}$$

We also use the notation that $\langle X \rangle _r = \{\langle i\rangle _r: \forall i \in X\}$ for any set $X \subseteq [1,n]$. For each $\mathcal {Q}_r$, we define $\nu _r$ such that

$$\begin{aligned} \sum _{i=1}^{\nu _r} \pi _{\langle i \rangle _r} \le \tau \text { but } \sum _{i=1}^{\nu _r+1} \pi _{\langle i \rangle _r} > \tau . \end{aligned}$$

Note that the value p is independent of index r, since it is based on the monotonic order of all $\pi _i$’s.

Definition 1

Given $\theta \in [1,n]$, for each $r \in [1,d]$, let $m_r \in [1,\nu _r]$ and $q_r \in [0,p-m_r]$, we define

• a set $T_r = \{t_{r1},t_{r2},\ldots ,t_{ra_r}\} \subseteq \{1,\ldots ,m_r\}$ with $t_{r1}<t_{r2}<\cdots <t_{ra_r}$;

• a set $L_r$ with a permutation $\varPi _{L_r} = \left\{ l_{r1}, l_{r2}, \ldots , l_{r,q_r}\right\}$ and $l_{r1} = \theta$;

• a sequence of integers $s_{rj} \in [0,\nu _r-m_r+1]\,\forall j \in [1,q+1]$ such that

  • $L_r \subseteq \{m_{r}+s_{r1} + 1,\ldots ,n\}$ with $l_{rj} \ge m_r+ \min \{s_{rj}+1, s_{r,j+1}\}$;

  • $0 \le s_{r1} \le \cdots \le s_{q_r+1} = \nu _r-m_r+1$; and

  • $$\begin{aligned} \sum _{i=1}^{m_r+s_{rj}} \pi _{\langle i \rangle _r} + \sum _{i=j}^{q_r} \pi _{\langle k_{ri} \rangle _r} > \tau \ \forall j \end{aligned}$$

    (38)

  where $\{k_{r1},\ldots ,k_{rq_r}\}$ is a permutation of set $L_r$ with $\pi _{\langle k_{r1} \rangle _r} \ge \cdots \ge \pi _{\langle k_{rq_r} \rangle _r}$;

• an expression

  $$\begin{aligned} \mathcal {I}_r = y_r + \sum _{j=1}^{a_r} (h_{r \langle t_{rj} \rangle _r} - h_{r\langle t_{r,j+1}\rangle _r}) z_{\langle t_{rj} \rangle _r} + \sum _{j=1}^{q_r} \delta _{rj} (1-z_{\langle l_{rj} \rangle _r}) \end{aligned}$$

  where

  $$\begin{aligned} \delta _{rj}= & {} \left\{ \begin{aligned}&h_{r,\langle m_r+s_{r1} \rangle _r} - h_{r,\langle m_r + s_{r2} \rangle _r}&j=1 \\&\max \left\{ \delta _{r,j-1}, h_{r,\langle m_r+s_{r1} \rangle _r} - h_{r,\langle m_r+s_{r,j+1} \rangle _r} - \sum _{i: i<j \text { and } l_{ri} \ge m_r+ \min \{1+s_{rj},s_{r,j+1} \}} \delta _{ri} \right\}&j \in [2,q_r]. \end{aligned} \right. \end{aligned}$$

When the sets $\langle L_r \rangle _r {\setminus } \{\theta \}\,\forall r \in [1,d]$ are mutually disjoint, we define the blending inequality as

$$\begin{aligned} \sum _{r \in [1,d]} \frac{1}{\delta _{r1}} \mathcal {I}_r - (1-z_{\theta })\ge \sum _{r \in [1,d]} \frac{1}{\delta _{r1}} h_{r \langle t_{r1} \rangle _r}. \end{aligned}$$

(39)

Next, we give a necessary condition that the blending inequality is valid for $\mathcal {Q}$.

Theorem 5

The blending inequality is valid for $\mathcal {Q}$ if

$$\begin{aligned} \sum _{i \in \bigcup _{r \in [1,d]} \langle [1,m_r + s_{r1}]\rangle _r} \pi _i > \tau . \end{aligned}$$

(40)

Proof

Consider a single mixing set $\mathcal {Q}_r$ for a given $r \in [1,d]$. We can assume $\langle i \rangle _r = i\,\forall i \in [1,n]$ without loss of generality. Thus, the next inequality is exactly the inequality (5) for $\mathcal {Q}_r$

$$\begin{aligned} \mathcal {I}_r \ge h_{r \langle t_{r1} \rangle _r }. \end{aligned}$$

(41)

Since $\mathcal {Q}_r \supseteq \mathcal {Q}$, the inequality (41) is valid for $\mathcal {Q}$. Next, we show that for some $u \in [1,d], \mathcal {I}_u - \delta _{u1}(1-z_{\theta }) \ge h_{u\langle t_{u1} \rangle _u}$ is valid for $\mathcal {Q}_u$.

Because of the condition (40), we claim that there exists some $u \in [1,d]$ such that $y_{u} \ge h_{u,m_{u}+s_{u 1}}$. Suppose the claim is not true. Then we have $y_r < h_{r,m_r+s_{r1}}$ for all $r \in [1,d]$. It implies that $z_i=1\,\forall i \in \langle [1,m_r + s_{r1}]\rangle _r, r \in [1,d]$, which violates the knapsack constraint because of (40).

Then, for that particular u, we assume $y_u \ge h_{u,m_u+s_{u1}}$. Because we are considering single mixing set, without loss of generality, we can assume $\langle i \rangle _u = i\,\forall i \in [1,n]$ and write the inequality $\mathcal {I}_u - \delta _{u1}(1-z_{\theta }) \ge h_{u\langle t_{u1} \rangle _u}$ explicitly as follows,

$$\begin{aligned} y_u + \sum _{j=1}^{a_u} (h_{u t_{uj} } - h_{u t_{u,j+1}}) z_{ t_{uj} } + \sum _{j=2}^{q_u} \delta _{uj} (1-z_{ l_{uj}}) \ge h_{ut_{u1}}. \end{aligned}$$

To simplify the notation, we can drop subscript u and have inequality

$$\begin{aligned} y + \sum _{j=1}^{a} (h_{ t_{j} } - h_{ t_{j+1}}) z_{ t_{j} } + \sum _{j=2}^{q} \delta _{j} (1-z_{ l_{j}}) \ge h_{t_1}. \end{aligned}$$

Because of the assumption that $y_u \ge h_{u,m_u+s_{u1}}$, we need to show that the above inequality is valid when $y \ge h_{m+s_1}$, which is already proved in the first paragraph of the proof for Theorem 1. Now, we have $\mathcal {I}_u - \delta _{u1}(1-z_{\theta }) \ge h_{u\langle t_{u1} \rangle _u}$ is valid for $\mathcal {Q}_u$, i.e., valid for $\mathcal {Q}$.

Together with (41) for any $r \in [1,d]{\setminus }\{u\}$, we get

$$\begin{aligned}\sum _{r \in [1,d]} \frac{1}{\delta _{r1}} \mathcal {I}_r - (1-z_{\theta })= & {} \sum _{r \in [1,d]-\{u\}} \frac{1}{\delta _{r1}} \mathcal {I}_r + \frac{1}{\delta _{u1}} \mathcal {I}_u- (1-z_{\theta })\\\ge & {} \sum _{r \in [1,d]-\{u\}} \frac{1}{\delta _{r1}} h_{r t_{r1}} + \frac{1}{\delta _{u1}} h_{u t_{u1}} = \sum _{r \in [1,d]} \frac{1}{\delta _{r1}} h_{r t_{r1}}. \end{aligned}$$

Therefore, the blending inequality is valid for $\mathcal {Q}$. $\square$

When all the scenarios have equal probabilities, the condition that the blending inequality is valid follows immediately after Theorem 5.

Corollary 4

Suppose all the scenarios have equal probabilities, then the blending inequality is valid for $\mathcal {Q}$ if

$$\begin{aligned} \left| \bigcup _{r \in [1,d]} \langle [1,m_r + 1]\rangle _r \right| > p. \end{aligned}$$

(42)

In the next theorem, we show that the blending inequality is facet-defining under certain conditions.

Theorem 6

Suppose all scenarios have equal probabilities, $d=2$ and (42) is satisfied. The blending inequality is facet-defining for $\mathcal {Q}$ if, $\forall r \in \{1,2\}$, the sets $\langle T_{r} \rangle _{r}, \langle L_{r} \rangle _{r}{\setminus }\{\theta \}$ are mutually disjoint, $t_{r1} = 1$ and we have

• 1. $\langle 1 \rangle _1 \notin \langle [1,m_{2}] \rangle _{2} \bigcup \langle L_{2} \rangle _{2}, \langle 1 \rangle _2 \notin \langle [1,m_{1}] \rangle _{1} \bigcup \langle L_{1} \rangle _{1}$;

• 2. $\langle L_{1} \rangle _{1}{\setminus }\{\theta \} \subsetneq \langle [1,m_{2}] \rangle _{2}, \langle L_{2} \rangle _{2}{\setminus }\{\theta \} \subsetneq \langle [1,m_{1}] \rangle _{1}$.

Proof

To show that the blending inequality is facet-defining for $conv(\mathcal {Q})$, we give $n+2$ affinely independent points. The idea is that we can always set $y_{r}=h_{r\langle 1 \rangle _r}$ and enumerate extreme points as in the proof of Theorem 2 for $y_{\bar{r}}$ because of condition 1.

First, we let $y^0_{1}=h_{1\langle 1 \rangle _1}, y^0_{2}=h_{2\langle 1 \rangle _2}$, and $\mathbf {z}^0_j = 1$ if $j \in \langle L_1 \rangle _1 \bigcup \langle L_2 \rangle _2$. Note that

$$\begin{aligned} \langle L_1 \rangle _1 \cup \langle L_2 \rangle _2 \subsetneq \langle L_1 \rangle _1 \cup \langle [1,m_1] \rangle _1 \cup \{\theta \} = \langle L_1 \rangle _1 \cup \langle [1,m_1] \rangle _1. \end{aligned}$$

(43)

So, $|\langle L_1 \rangle _1 \bigcup \langle L_2 \rangle _2 | \le |\langle L_1 \rangle _1 \cup \langle [1,m_1] \rangle _1| = p$ and the point is feasible.

Next, for each $j \notin \langle T_1 \cup L_1 \rangle _1 \bigcup \langle T_2 \cup L_2 \rangle _2$, we consider the point $(\mathbf {y}^j, \mathbf {z}^j) = (\mathbf {y}^0, \mathbf {z}^0 + e_j)$. For each $t_{1j} \in \{t_{11},\ldots ,t_{1a_1}\}$, we let $y^{t_{2j}}_2 = h_{2\langle 1 \rangle _2}, y^{t_{1j}}_1 = h_{1t_{1,j+1}}, \mathbf {z}^{t_{1j}}_i = 1$ if $i \in \langle [1,t_{1,j+1}-1] \rangle _1 \cup \langle L_1 \rangle _1 \cup \langle L_2 \rangle _2$ and 0 otherwise. The point is feasible because (43) implies

$$\begin{aligned} \left| \langle [1,t_{1,j+1}-1] \rangle _1 \cup \langle L_1 \rangle _1 \cup \langle L_2 \rangle _2 \right| \le \left| \langle L_1 \rangle _1 \cup \langle [1,m_1] \rangle _1\right| = p. \end{aligned}$$

Due to the symmetry, we have similar way to get points for each $t_{2j} \in \{t_{21},\ldots ,t_{2a_2}\}$ by letting $y^{t_{1j}}_1 = h_{1\langle 1 \rangle _1}$.

Let $y^{l_{11}}_1 = h_{1\langle 1 \rangle _1}, y^{l_{21}}_2 = h_{m_2+2}, \mathbf {z}_i^{l_{21}} = 1$ if $i \in \langle [1,m_2+1]\rangle _2$ and $\mathbf {z}_{l_{2i}}^{l_{21}} = 1$ for $i > 1$, and 0 otherwise. The point is feasible because of condition 2. For each $j \in [2,p-m_2]$ if $\delta _{2j} = \delta _{2,j-1}$, we have

$$\begin{aligned} (\mathbf {y}^{l_{2j}}, \mathbf {z}^{l_{2j}}) = (\mathbf {y}^{l_{2,j-1}}, \mathbf {z}^{l_{2,j-1}}+ e_{l_{2,j-1}} - e_{l_{2j}}), \end{aligned}$$

otherwise we have that $y^{l_{1j}}_1 = h_{1\langle 1 \rangle _1}, y^{l_{2j}}_2 = h_{m_2+1+j}, \mathbf {z}_i^{l_{2j}} = 1$ if $i \in \langle [1,m+j]\rangle _2$ and $\mathbf {z}_{l_{2i}}^{l_{2j}} = 1$ for $i > j$, and 0 otherwise. Thus, we get points for each $l_{2j} \in \{l_{21},\ldots ,l_{2,p-m_2}\}$. Due to the symmetry, we can also get points for each $l_{1j} \in \{l_{11},\ldots ,l_{1,p-m_1}\}$.

Note that $\langle T_1 \rangle _1, \langle T_2 \rangle _1, \langle L_1 \rangle _1, \langle L_2 \rangle _2$ are mutually disjoint except $\langle L_1 \rangle _1 \cap \langle L_2 \rangle _2 = \{\theta \}$. So, we get totally $n+2$ points on the face defined by blending inequality and they are affinely independent. $\square$

We next give a numerical example to illustrate Theorem 6.

Example 2

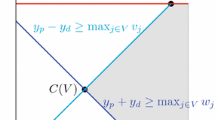
Let $n=6$ and $p=3$. Suppose we have equal probabilities for all scenarios and

$$\begin{aligned} (h_{11},\ldots ,h_{16}) = (28,25,15,8,5,3) \text { and } (h_{21},\ldots ,h_{26}) = (2,5,6,8,17,10) \end{aligned}$$

The inequality (5) implies that

$$\begin{aligned} y_1 + 3z_1 + 10 (1-z_3) + 17(1-z_6) \ge 28&\text { is valid for } \mathcal {Q}_1 \text { with } m_1=1&\\ y_2 + 9z_5 + 2(1-z_3) \ge 17&\text { is valid for } \mathcal {Q}_2 \text { with } m_2=2&\end{aligned}$$

Let $\theta =3$. We have

• $\langle 1 \rangle _1 = 1 \notin \{5,6\} \bigcup \{3\} = \langle [1,m_2] \rangle _2 \bigcup \langle L_{2} \rangle _{2}$;

• $\langle 1 \rangle _2 = 5 \notin \{1\} \bigcup \{3,6\} = \langle [1,m_{1}] \rangle _{1} \bigcup \langle L_{1} \rangle _{1}$;

• $\langle L_1 \rangle _1{\setminus }\{\theta \} = \{3,6\}{\setminus }\{3\} \subseteq \{5,6\} = \langle [1,m_2] \rangle _2$;

• $\langle L_2 \rangle _2{\setminus }\{\theta \} = \{3\}{\setminus } \{3\} \subseteq \{1\} = \langle [1,m_1] \rangle _1$.

Thus, the conditions in Theorem 6 are satisfied and we have a blending inequality

$$\begin{aligned} y_1 + 5y_2 + 3z_1 + 45z_5 + 10 (1-z_3) + 17(1-z_6) \ge 113 \end{aligned}$$

which is valid and facet-defining for $\mathcal {Q}$.

Next, we give a special case of Theorem 6 and show how to use it as our separation algorithm.

Corollary 5

Suppose all scenarios have equal probabilities and $d=2$. If $L_1 = L_2 = \{\theta \}$ for some $\theta \in [1,n]$, then the blending inequality is valid and facet-defining for $\mathcal {Q}$ if following conditions hold

• $\theta \in \langle [p+1,n] \rangle _{1} \bigcap \langle [p+1,n] \rangle _{2}$;

• $\langle T_{1} \rangle _{1} \cap \langle T_{2} \rangle _{2} = \emptyset$;

• $\langle 1 \rangle _1 \notin \langle [1,p] \rangle _{2} \bigcup \{\theta \}$; and

• $\langle 1 \rangle _2 \notin \langle [1,p] \rangle _{1} \bigcup \{\theta \}$.

Proof

Because $\langle 1 \rangle _1 \notin \langle [1,p] \rangle _{2} \bigcup \{\theta \}$, condition (42) holds, which implies that the blending inequality is valid. It is easy to check that all conditions in Theorem 6 are satisfied. Therefore, the blending inequality is valid and facet-defining for $\mathcal {Q}$. $\square$

Separation Heuristic

First, we collect a set R consisting of pairs $(r_1,r_2)$ where $r_1 \ne r_2 \in [1,d], \langle 1 \rangle _{r_1} \notin \langle [1,p] \rangle _{r_2}$ and $\langle 1 \rangle _{r_2} \notin \langle [1,p] \rangle _{r_1}$. Suppose $z^*$ is a fraction solution. For each pair $(r_1,r_2) \in R$, let $\theta = {{\mathrm{\arg \max }}}_i \{\pi _i : z^*_i = 1, i \in \langle [p+1,n] \rangle _{r_1} \bigcap \langle [p+1,n] \rangle _{r_2} \}$. Next, we find the set $T_1$ by solving a shortest path problem from the source $\langle 1 \rangle _{r_1}$ to the sink $\langle p-1 \rangle _{r_1}$ on a directed acyclic graph with vertices $\langle \{1, \ldots , p-1\} \rangle _{r_1}$, edges $(\langle i \rangle _{r_1}, \langle j \rangle _{r_1}), 1 \le i < j \le p-1$ and associated cost of $(h_{\langle i \rangle _{r_1}} - h_{\langle j \rangle _{r_1}}) z^*_{\langle i \rangle _{r_1}}$. Finally, the set $T_2$ is obtained by solving another shortest path problem from the source $\langle 1 \rangle _{r_2}$ to the sink $\langle p-1 \rangle _{r_2}$ on a directed acyclic graph with vertices $\langle \{1, \ldots , p-1\} \rangle _{r_2} {\setminus } \langle T_1 \rangle _{r_1}$, edges $(\langle i \rangle _{r_2}, \langle j \rangle _{r_2}), 1 \le i < j \le p-1$ but $\langle i \rangle _{r_2}, \langle j \rangle _{r_2} \notin \langle T \rangle _{r_1}$, and associated cost of $(h_{\langle i \rangle _{r_2}} - h_{\langle j \rangle _{r_2}}) z^*_{\langle i \rangle _{r_2}}$. Following Corollary 5, all violated inequalities found by this separation algorithm are facet-defining for $\mathcal {Q}$.

At the end of this section, we adopt an example from [22] to show that our blending inequalities are stronger than those generated from a single mixing set, which is obtained by combining original formulation.

Example 3

(Example 2 in [22]) We have the chance-constrained program

$$\begin{aligned} \min&\quad \quad \quad x_1 + x_2 \\ \text {s.t.}&\quad P \left\{ \begin{aligned} 2x_1 - x_2 \ge \omega _1 \\ x_1 + 2x_2 \ge \omega _2 \end{aligned} \right\} \ge 0.6 = 1 - \tau \\&\quad \quad \quad x_1, x_2 \ge 0 \end{aligned}$$

where $\omega _1$ and $\omega _2$ are dependent random variables with joint probability density function given in Table 1. The optimal solution is $(x,y) = (0.55,0.35,0.75,1.25)$ with objective value 0.9.

Table 1 Joint probability mass function of $\omega = (\omega _1,\omega _2)$

For this example, we have $\tau =0.4, d=2$, $p=6, \nu _1=3$ and $\nu _2=5$. Let $y_1=2x_1-x_2$ and $y_2=x_1 + 2x_2$. Then the mixing set reformulation is

$$\begin{aligned} y_1 + 0.75z_1 \ge 0.75&y_2 + 2.00z_7 \ge 2.00 \\ y_1 + 0.50z_2 \ge 0.50&y_2 + 1.75z_4 \ge 1.75 \\ y_1 + 0.50z_3 \ge 0.50&y_2 + 1.50z_2 \ge 1.50 \\ y_1 + 0.25z_4 \ge 0.25&y_2 + 1.50z_5 \ge 1.50 \\ y_1 + 0.25z_5 \ge 0.25&y_2 + 1.50z_8 \ge 1.50 \\ y_1 + 0.25z_6 \ge 0.25&y_2 + 1.25z_1 \ge 1.25 \\ \vdots \quad \qquad&\qquad \quad \vdots \\ \sum _{i=1}^{9} \pi _{i}z_i\le & {} 0.4 = \tau \end{aligned}$$

and the tighter formulation (3) in [29] is

$$\begin{aligned} y_1 + 0.50z_1 \ge 0.75&y_2 + 0.75z_7 \ge 2.00 \\ y_1 + 0.25z_2 \ge 0.50&y_2 + 0.50z_4 \ge 1.75 \\ y_1 + 0.25z_3 \ge 0.50&y_2 + 0.25z_2 \ge 1.50 \\ y_1 \ge 0.25&y_2 + 0.25z_5 \ge 1.50 \\&y_2 + 0.25z_8 \ge 1.50 \\ \vdots \quad \qquad&y_2 \ge 1.25 \\&\qquad \quad \vdots \\ \sum _{i=1}^{9} \pi _{i}z_i\le & {} 0.4 = \tau . \end{aligned}$$

The initial linear programming (LP) relaxation solution by using tight formulation (3) is

$$\begin{aligned} (x,y) = (0.49,0.38,0.60,1.25). \end{aligned}$$

In [22], the author proposed 3 inequalities in the form of (14), which were generated for $y_1$ and $y_2$, respectively. Then the author combined two mixing sets with $y_1$ and $y_2$ (with equal weights), and derived a valid inequality $y_1 + y_2 \ge 2$ from that aggregation. Augmented with those inequalities, the updated LP relaxation has a solution with optimal (x, y).

For this example, based on our previously presented theorems, we are able to develop several new facet-defining inequalities. First, we have facet-defining inequality

$$\begin{aligned} y_2 + 0.25z_2 + 0.25z_4 + 0.25z_7 \ge 2 \end{aligned}$$

(44)

which is a strengthened star inequality in [29] and also a special case of inequality (5). Then, we have another facet-defining inequality

$$\begin{aligned} z_2 + z_4 + z_6 \le 2 + 4 (y_1 - 0.75) + (1-z_7) \end{aligned}$$

(45)

which is derived from lifting by fixing $z_7=1$ and letting $m=2$. Note that, with these choices, we have a minimal cover inequality

$$\begin{aligned} z_2 + z_4 + z_6 \le 2. \end{aligned}$$

From Theorem 3, we can easily calculate $\rho =1$ and $\varPhi (\pi _1) = \varPhi (0.2) = 1$. So we have

$$\begin{aligned} z_2 + z_4 + z_6 \le 2 + 4 (y_1 - 0.75) \end{aligned}$$

which is valid when $z_7=1$. By performing lifting procedure on variable $z_7$, we can derive inequality (45). Indeed, by summing (44) and $0.25\times$(45), we have a valid inequality $y_1 + y_2 \ge 2+ 0.25z_6$. Because it dominates the inequality $y_1 + y_2 \ge 2$, the latter one clearly is not facet-defining. Instead, the blending inequality proposed in this section gives a facet-defining inequality

$$\begin{aligned} y_1 + y_2 + 0.25z_1 + 0.5z_7 + 0.25(1-z_9) \ge 2.75 \end{aligned}$$

(46)

by blending following two inequalities as in (39)

$$\begin{aligned} y_1 + 0.25z_1 + 0.25(1-z_9) \ge 0.75 \end{aligned}$$

(47)

$$\begin{aligned} y_2 + 0.5z_7 + 0.25(1-z_9) \ge 2 \end{aligned}$$

(48)

where (47) and (48) are facet-defining inequalities for two individual mixing sets respectively, and can be derived by (5).

5 Computational study

In order to investigate the computational advantages of the proposed strong inequalities, we implement them as cutting planes within professional solver CPLEX’s branch-and-bound process, i.e., an implementation of of branch-and-cut (B&C) algorithm. In particular, the CALLABLE libraries of CPLEX 12.6.1 are called for adding user defined cuts and a single thread with traditional branch-and-bound search method is adopted. All tests are subject to 3600 CPU seconds time limit. If no optimal solution is obtained within the time limit, then the optimality gap will be reported. Because it is often the case that a very large number of user defined cuts will be generated, we activate the purging option (which is the default option as well) in CPLEX to allow ineffective ones to be removed by CPLEX. The complete computational study is carried out on the Texas Tech High Performance Computing Center’s node based system, where each node contains two Westmere 2.8 GHz 6-core processors with 24 GB main memory [19].

Our numerical study data sets (available at [51]) consist of a set of difficult and large instances of the static probabilistic lot-sizing (SPLS) model as described in [48] with d periods, n scenarios and service level $1-\tau$. Let $x_t$ be the decision variable of ordering quantity in period $t, I_{it}$ be the inventory level at the end of period t under scenario i, and $w_t$ be binary variables to indicate order setup. The natural deterministic equivalent of SPLS model is

$$\begin{aligned} \max&\quad \sum _{t=1}^{d} \sum _{i=1}^{n} \pi _i (c_{t}x_t + h_{it}I_{it} + g_{t}w_{t}) \\ \text {s.t.}&\quad y_t = \sum _{j=1}^{t} x_j&t \in \{1,\ldots ,d\} \\&\quad y_t \ge D_{it}(1-z_i)&t \in \{1,\ldots ,d\}, i \in \{1,\ldots ,n\} \\&\quad I_{it} \ge y_t - D_{it}&t \in \{1,\ldots ,d\}, i \in \{1,\ldots ,n\} \\&\quad 0 \le x_t \le M_t w_t&t \in \{1,\ldots ,d\} \\&\quad \sum _{i=1}^{n} \pi _i z_i \le \tau \\&\quad I_{i,t} \ge 0, z_i, w_t \in \{0,1\}&t \in \{1,\ldots ,d\}, i \in \{1,\ldots ,n\} \end{aligned}$$

where $D_{it}$ is the cumulative demand until period t under scenario $i, c_t$ and $g_t$ are the variable and fixed costs of ordering, $h_{it}$ is the variable holding cost in period t under scenario i, and $M_t$ is the order capacity in period t. As mentioned in Sect. 1, this natural formulation can be easily strengthened by using (3), which has a tighter LP relaxation and less constraints. Hence, the reformulation (3) is applied on those instances to build our testing platform for both CPLEX and B&C algorithms.

We assume that the demands are i.i.d. across periods. In any time period, the demand follows a normal distribution with mean 100 and standard deviation 40, i.e., Normal(100, 40), and we set demand to 0 if a negative number is generated (denoted as Normal$^+$(100,40)). Then, the cumulative demand $D_{i1}$ is generated from Normal$^+$(100,40), and $D_{it}$ is generated by adding an i.i.d. random number from Normal$^+$(100,40) to $D_{i,t-1}\,\forall t \in [2,d]$. The variable production costs are generated from a uniform distribution between 1 and 5 and inventory holding costs are generated from an uniform distribution between 1 and 2. The fixed costs follow a discrete uniform distribution between 900 and 1000. We set the order capacity $M_t=500$.

5.1 Computational results of instances with general probabilities

To generate instances with scenarios of general probabilities, we first assign every scenario a random number from a discrete uniform distribution between 1 and 99, and then normalize those numbers by dividing their total summation to obtain probabilities for all scenarios. By varying values of d, n and $\tau , 45$ instances with different sizes are produced. Those random instances are tested by our implementations of the following computing methods. Observing that adding cuts at every node of branch-and-bound tree is rather ineffective, our implementations mainly focus on cut generation at the root node.

• CPX indicates the default CPLEX with traditional B&C in single thread mode;

• Mix indicates a B&C algorithm by adding strengthened star inequalities [3, 29] at every node of branch-and-bound tree;

• MixR indicates a B&C algorithm by adding strengthened star inequalities [3, 29] at the root node only;

• TL indicates a B&C algorithm by adding TL inequalities (using the separation algorithm described in [22]) at every node of the B&C tree;

• TLR indicates a B&C algorithm by adding TL inequalities (using the separation algorithm described in [22]) at the root node only;

• LF indicates applying the algorithm MixR on an updated formulation with lifting cover inequalities (see Sect.  3 for implementation details);

• GMixR indicates a B&C algorithm by adding new inequalities (5) (using the separation algorithm presented in Sect. 2) at the root node only.

The detailed computational results of each algorithm are presented in two tables, i.e., Tables 5 and 6, due to space limitation. To evaluate the overall performance of those algorithms and gain a general understanding, a summary is presented in Table 2, where we report the number of instances solved to the optimality (column Solved), the number of unsolved instances (column Unsolved), the average gap before termination among unsolved instances (column Avg. Gap (Unsolved)), and the average number of user defined cuts added before termination but after CPLEX purging (column Avg. Cuts). Given that B&C algorithms have different behaviors and almost all of them (excluding TL) are actually able to solve instances that are solved by CPLEX, we benchmark their performances against CPLEX on those instances to have a fair comparison basis. Hence, in Table 2, we also report algorithms’ data on those instances, specifically, the average CPU seconds (column Avg. Time (CPX Solved)), the ratio of the average CPU seconds between CPLEX and a B&C algorithm (column $\frac{\text {CPX Time}}{\text {B} \& \text {C Time}}$), the average number of nodes explored (column Avg. Nodes (CPX Solved)), and the ratio of the average number of nodes explored between CPLEX and a B&C algorithm (column $\frac{\text {CPX Nodes}}{\text {B} \& \text {C Nodes}}$).

Table 2 Summarized results of computing lot-sizing instances with general probabilities

Based on Table 2, a few non-trivial observations can be made. First, as mentioned, adding cuts at every node of the whole branch-and-bound tree is not an effective strategy. As demonstrated in Mix and TL, an extremely large number of cuts are generated, which drastically increase the complexity of SPLS formulation. Such situation is especially severe in TL. Note that SPLS only has $d+1$ non-sparse constraints, i.e., the first set of constraints and the 0–1 knapsack. Nevertheless, the average number of generated TL inequalities, which are non-sparse, is almost twenty-seven thousands. Comparing to the performances of their two corresponding variants, i.e., MixR and TLR, we can clearly see the benefits of adding cuts in a less frequent fashion.

Second, among all implemented computing methods, our GMixR and LF provide the most significant computational improvements and perform much better than CPLEX. Note that only 22 of 45 instances can be solved to optimality by CPLEX, while LF and GMixR can solve 39 and 40 instances, respectively. In addition, GMixR and LF, on instances solved by CPLEX, have the best computation speed (are faster by 2.5 and 3.3 times, respectively) with the smaller numbers of branch-and-bound nodes (roughly 28  and 24 % of CPLEX nodes, respectively). Also, for those that cannot be solved to optimality, the average gaps before termination in GMixR and LF are the least ones. For the efficacy of GMixR, we believe that it is mainly due to the fact that the separation algorithm based on Corollary 2 leads to facet-defining cuts for the polyhedron of CCP. As the strengthened star inequalities are also facet-defining cuts for the polyhedron of CCP, results of GMixR and MixR show that they are all practically useful and the former has more computationally advantages. For LF, we think the lifted inequalities largely capture the non-trivial interactions between mixing set and the 0–1 knapsack. Their strong performance suggests that a more sophisticated separation algorithm is worth further exploring.

Third, although TL inequalities are theoretically valid and strong, they are less effective than the strengthened star inequalities in computation. One explanation is that, as shown in Corollary 1 and Example 1, TL inequalities are usually weak for CCP instances with general probabilities. Another interesting observation is that TL has much more user defined cuts than Mix, while the root node implementation variant TLR has much less cuts than the corresponding MixR. One possibility is that we allow CPLEX to purge user defined cuts if they are deemed weak, CPLEX may decide to purge a high proportion of TL cuts and start branching very soon.

5.2 Computational results of instances with equal probabilities

In Sect. 4, we develop a new technique to blend strong inequalities (5) derived from individual mixing sets into a strong one for CCP. In particular, we show that blending inequality could be facet-defining when scenarios have equal probabilities. In order to computationally evaluate this new type of inequalities, we generate 45 instances with equal probabilities (by simply setting scenario probabilities as $\frac{1}{n}$) and compute them by the following computing methods.

• CPX indicates the default CPLEX with transitional branch-and-bound in single thread mode;

• Mix indicates a branch-and-cut algorithm by adding strengthened star inequalities at every node of branch-and-bound tree;

• Mix100 indicates a branch-and-cut algorithm by adding strengthened star inequalities at every 100 nodes of branch-and-bound tree;

• BL indicates a branch-and-cut algorithm by adding blending inequalities at the root node and strengthened star inequalities at every 100 nodes of the branch-and-bound tree.

The Mix100 is implemented due to the observation made from Table 2 that adding cuts at every node of the whole branch-and-bound tree is not effective. With some preliminary tests, we find that adding strengthened star inequalities at every 100 nodes of branch-and-bound tree gives the best result in general. Then, on top of the Mix100, we develop BL algorithm by adding blending inequalities at the root node. Similar to the organization of Sect. 5.1, the detailed computational results are presented in Table 7 and a summary is presented in Table 3.

Table 3 Summarized results of computing lot-sizing instances with equal probabilities

Based on the performances of CPLEX and Mix in Tables 2 and 3, we first note that the instances with equal probabilities are not necessarily easier than the instances with general probabilities. It is different from the observation made in [29], but reasonable since $p \ge \nu$ (or $p \ge \nu _r\,\forall r \in [1,d]$) and hence the instances with equal probabilities usually have much larger problem size in the reformulation (3).

Regarding the effectiveness of B&C methods, we observe that BL completely dominates other algorithms by optimally computing almost all instances (44 out of 45 instances) and demonstrating much fast computational speed (as 4.5 $\times$ CPLEX). We believe that such strong performance shows that the generated blending cuts, which capture the interactive information among mixing sets and are facet-defining for CCP, have a great computational advantage over existing strong inequalities derived from single mixing sets. The ratio of the average number of nodes between CPLEX and BL supports our understanding. Note that BL generally has 13 % less user defined cuts than Mix100 while it explores 23 % less nodes in the branch-and-bound trees than Mix100.

6 Conclusion and future research

In this paper, we study the polyhedral structure of chance-constrained program with stochastic right-hand side, which is computationally very challenging. We develop three families of strong inequalities from different perspectives. Following the tradition that considers a single mixing set with a 0–1 knapsack, our first family of inequalities of that set dominates or subsumes all explicit inequalities described in [1, 22, 29]. Our second family of inequalities builds a direct link between a single mixing set and 0–1 knapsack through lifting and superadditive lifting with respect to cover inequality. In order to analyzing the interactions among multiple mixing sets, we design a novel technique to integrate facet-defining inequalities derived from individual mixing sets, which leads to our third family of inequalities, i.e., blending inequalities. Finally, we implement all three families of strong inequalities and test them on random instances of static probabilistic lot-sizing problem. Through benchmarking with a professional MIP solver and existing cutting plane methods, we observe significant computational improvements can be achieved by all those proposed inequalities, especially by the newly developed blending inequalities.

There are three directions, we believe, that deserve further studies. The first one is to develop more general and effective separation algorithms. Note that cutting planes generated in our current numerical study is just a small proportion of our first family of strong inequalities. So, more powerful separation algorithms will allow us to make good use of that large family of strong inequalities. Another one is to develop stronger superadditive lifting functions and better lifting techniques. For example, our current superadditive approximation scheme is adopted from existing research, which probably is not the best one. A deeper study on the lifting function should help us develop tighter valid approximations for stronger cutting planes. Finally, given the outstanding computational performance of blending inequalities, this technique should be fully investigated and we will extend it for other similar models.

Appendices

Appendix 1: Notations

Table 4 presents our key notations, their definitions and the first usage place. Note that many notations are reused in Sect. 4 (especially in Definition 1) with an additional subscript r because we extend our results in Sect. 2 to multiple mixing sets.

Table 4 Key notations used in this paper

Appendix 2: Computational tables for instances with general probabilities

The column $d \times n \times \tau$ indicates that the instance has d periods and n scenarios with service level $1-\tau$. For a given combination of $d,n,\tau$, we solve 5 instances. In all tables, we compare the percentage of root node gap (column %RootGap), the number of branch-and-cut tree nodes explored (column Nodes), and CPU time in second on solving the instance to the optimality (column Time (%Endgap)). We indicate the instance that could not be solved within one hour with T(gap), where gap, in parenthesis, is the percentage gap between the best lower bound and the best integer solution found in the search tree when the time limit is reached. We also report the number of user cuts added (column Cuts) after purging. Due to the page size restriction, we partition the results into two tables as in Tables 5 and 6.

Table 5 Static probabilistic lot-sizing problem with general probabilities (cuts on every node)

Table 6 Static probabilistic lot-sizing problem with general probabilities (cuts on root node)

Table 7 Static probabilistic lot-sizing problem with equal probabilities

Appendix 3: Computational tables for instances with equal probabilities

We keep the same table format as in “Appendix 1”. For a given combination of $d,n,\tau$, we solve 5 instances. Results are presented in Table 7.