A branch-and-cut decomposition algorithm for solving chance-constrained mathematical programs with finite support

Abstract

We present a new approach for exactly solving chance-constrained mathematical programs having discrete distributions with finite support and random polyhedral constraints. Such problems have been notoriously difficult to solve due to nonconvexity of the feasible region, and most available methods are only able to find provably good solutions in certain very special cases. Our approach uses both decomposition, to enable processing subproblems corresponding to one possible outcome at a time, and integer programming techniques, to combine the results of these subproblems to yield strong valid inequalities. Computational results on a chance-constrained formulation of a resource planning problem inspired by a call center staffing application indicate the approach works significantly better than both an existing mixed-integer programming formulation and a simple decomposition approach that does not use strong valid inequalities. We also demonstrate how the approach can be used to efficiently solve for a sequence of risk levels, as would be done when solving for the efficient frontier of risk and cost.

1 Introduction

We introduce a new approach for exactly solving chance-constrained mathematical programs (CCMPs) having discrete distributions with finite support. A chance constraint (also known as a probabilistic constraint) states that the chosen decision vector should, with high probability, lie within a region that depends on a set of random variables. A generic CCMP can be stated as

$$\begin{aligned} \min \left\{ f(x) \mid \mathbb P \{ x \in P(\omega ) \} \ge 1 - \epsilon , \ x \in X \right\} , \end{aligned}$$

(1)

where $x \in \mathbb R ^n$ is the vector of decision variables to be chosen to minimize $f:\mathbb R ^n \rightarrow \mathbb R$, $\omega$ is a random vector, $P(\omega ) \subseteq \mathbb R ^n$ is a region parameterized by $\omega$, and $X \subseteq \mathbb R ^n$ represents a set of deterministic constraints on $x$. The interpretation is that the region $P(\omega )$ is defined such that the event $x \notin P(\omega )$ is an undesirable outcome. The likelihood of such an outcome is restricted to be less than the given risk tolerance $\epsilon \in (0,1)$, which is typically small. We don’t make explicit assumptions on the form of the objective function $f(\cdot )$, or the deterministic constraint set $X$, but our algorithm will require solving subproblems at least as hard as minimizing $f(x)$ over $x \in X$, so $f$ and $X$ should be sufficiently “nice” so that these subproblems can be solved (e.g., one could assume $f$ and $X$ are convex).

Our algorithm solves CCMPs of the form (1) satisfying the following assumptions:

• (A1) The random vector $\omega$ has discrete and finite support: specifically $\mathbb P \{\omega = \omega ^k \} = 1/N$ for $k \in \mathcal N := \{1,\ldots , N\}$.¹

• (A2) Each $P(\omega ^k)$, $k \in \mathcal N$ is a non-empty polyhedron.

• (A3) $P(\omega ^k)$ have the same recession cone for all $k \in \mathcal N$, i.e., there exists $C \subseteq \mathbb R ^n$ such that $C = \{ r \in \mathbb R ^n \mid x + \lambda r \in P(\omega _k) \ \forall x \in P(\omega _k), \lambda \ge 0\}$ for all $k \in \mathcal N$.

We refer to the possible outcomes of $\omega$, $\omega ^k$ for $k \in \mathcal N$, as scenarios. Also, to simplify notation, we let $P_k = P(\omega ^k)$ for $k \in \mathcal N$. While assumption A1 is certainly a restriction, recent results on using sample-average approximation on CCMPs with general distributions [1] demonstrate that such finite support approximations, when obtained from a Monte Carlo sample of the original distribution, can be used to find good feasible solutions to the original problem and statistical bounds on solution quality. See also [2–5] for related results on sampling approaches to CCMPs. Assumption A2 includes the case where $P_k$, $k \in \mathcal N$ are defined by the set of vectors for which a feasible recourse action exists, i.e.,

$$\begin{aligned} P_k = \left\{ x \in \mathbb R _+^n \mid \exists y \in \mathbb R _+^d \text{ with } T^k x + W^k y \ge b^k \right\} , \end{aligned}$$

(2)

where $b^k \in \mathbb R ^m$ and $T^k$ and $W^k$ are appropriately sized matrices. The special case with $d=0$ yields a mathematical program with chance-constrained linear constraints having random coefficients: $\mathbb P \{ T(\omega )x \ge b(\omega )\} \ge 1- \epsilon$. The assumption that the polyhedra $P_k$ are non-empty is without loss of generality, since we can discard any scenario with $P_k = \emptyset$ and consider a problem with risk tolerance $\epsilon ^{\prime } = \epsilon - 1/N$. Assumption A3 can be motivated by the result of Jeroslow [6] that, a general set $S \subseteq \mathbb R ^n$ is representable using a binary mixed-integer program if and only if $S$ is the union of finitely many polyhedra having the same recession cone. A simple case in which assumption A3 holds is if each $P_k$ is bounded, so that $C = \{0\}$ for all $k \in \mathcal N$. The problem we use for our computational study in Sect. 3 provides an example where assumption A3 holds with $C = \mathbb R _+^n$.

Although the CCMP (1) can implicitly model recourse actions, e.g., when the polyhedra $P_k$ are described as in (2), this model doesn’t consider costs associated with these recourse actions, making this essentially a static model. Of course, a limit on the cost of the recourse actions can be included in the definition of $P_k$, thus requiring that a recourse action with cost not exceeding a (possibly random) threshold exist with probability at least $1 - \epsilon$. On the other hand, many CCMPs fit exactly the structure of (1). In Sect. 3.1 we describe a flexible resource planning application that fits this model. In this application, one wishes to determine the quantity of different resources to have available, while requiring that the resources available are sufficient to meet the random demands with high probability. In this context, the costs are incurred when resources are acquired, but the allocation of resources to demands incurs no additional cost. A small list of example applications of CCMPs that fit the structure of (1) includes multicommodity flow [7], optimal vaccination planning [8], air quality management [9], aquifer remediation [10], and reliable network design [11, 12].

CCMPs have a long history dating back to Charnes, Cooper and Symonds [13]. The version considered here, which requires a system of constraints to be enforced with high probability, was introduced by Prékopa [14]. However, CCMPs have remained computationally challenging for two reasons: the feasible region is generally not convex, and evaluating solution feasibility requires multi-dimensional integration. Because of these difficulties, methods for obtaining provably good solutions for CCMPs have been successful in only a few very special cases. If the chance constraint consists of a single row and all random coefficients are normally distributed [15, 16], then a deterministic (nonlinear and convex) reformulation is possible if $\epsilon < 1/2$. If the randomness appears only in the right-hand side (i.e., $P(\omega ) = \{x \ | \ Tx \ge b(\omega ) \}$) and the distribution of $b(\omega )$ is discrete, then approaches based on certain “efficient points” of the random vector [17, 18] or on strong integer programming formulations [19–21] have been successful.

While the algorithm proposed in this paper cannot be directly applied to a CCMP that violates assumption A1, it can be used to solve a sample-average approximation (SAA) of such a problem. We believe that this approach is complementary to approaches that attempt to directly solve a CCMP without using SAA (e.g., [14, 22–26]). The advantage of the SAA approach is that it requires relatively few assumptions on the structure of the CCMP or the distribution of $\omega$. On the other hand, the SAA will only yield statistical bounds on solution feasibility and optimality, and requires replication to do so. In addition, the SAA problem with $\epsilon >0$ is always non-convex, whereas, in some special cases the original chance constraint defines a convex feasible region. For example, if the randomness appears only in the right-hand side of the chance constraints and the random vector $b(\omega )$ has a log-concave distribution, then the resulting feasible region is convex and so nonlinear programming techniques can be used [14].

Very few methods are available for finding provably good solutions for CCMPs with the structure we consider here, i.e., for problems having linear constraints with random coefficients or recourse actions as in (2). In [7], an approach based on an integer programming formulation (which we give in Sect. 2.1), strengthened with precedence constraints is presented. In more recent work, [27] presents a specialized branch-and-cut algorithm based on identification of irreducible infeasible sets of certain linear inequality systems, and a specialized branch-and-bound algorithm applicable for CCMPs with random constraint matrix is given in [28]. While these are important contributions, the size of instances that are demonstrated to be solvable with these approaches is very limited, in particular, because these approaches do not enable decomposition. In another recent important stream of research, a number of conservative approximations [2, 4, 29–33] have been studied that solve tractable (convex) approximations to yield feasible solutions to many classes of CCMPs. However, these approaches do not say anything about the cost of the resulting solutions relative to the optimal, and tend to yield highly conservative solutions.

The key contribution of this paper is to present an exact approach for solving CCMPs that requires relatively few assumptions about the problem structure, and, as we show in Sect. 3, has the potential to solve problems with high-dimensional random parameters and a large number of scenarios. Our algorithm builds on the ideas of [20, 34] that were successful for solving chance-constrained problems with random right-hand side by developing a method to apply the same types of valid inequalities used there to the more general case considered here. The other important aspect of our algorithm is that it enables decomposition of the problem into single-scenario optimization and separation subproblems. This is important for solving CCMPs with discrete distributions because the problem size grows as the size of the support increases. Another advantage is that the decomposed single-scenario optimization and separation subproblems can be solved using specialized algorithms for the deterministic counterpart, if available. The decomposition approach also enables a straightforward parallel implementation.

When using a chance-constrained formulation, the risk tolerance $\epsilon$ is an important user input, as it controls the balance between solution cost and risk of violating the uncertain constraints. Consequently, it is important in practice to perform a sensitivity analysis on this parameter. For example, this can done by solving the CCMP with varying values of risk level $\epsilon$, and then constructing an efficient frontier displaying the non-dominated solutions in terms of the two objectives of cost and risk. While any algorithm that can solve a CCMP for a given risk level $\epsilon$ can be used to construct such an efficient frontier by simply applying the algorithm at each risk level, we show that our algorithm can effectively take advantage of information obtained in the solution at one risk level to more efficiently solve problems at other risk levels.

Decomposition has long been used for solving traditional two-stage stochastic programming problems, where the objective is to minimize the sum of costs of the first stage decisions and the expected costs of second-stage recourse decisions (see, e.g., [35–37]). For CCMPs, the only existing paper we are aware of that considers a decomposition approach is [38]. The decomposition idea is similar to what we present here, but the mechanism for generating cuts is significantly different: they use a convex hull reformulation (based on the Reformulation-Linearization Technique [39]) which involves “big-$M$” constants, likely leading to weak inequalities. In contrast, we combine the valid inequalities we obtain from different subproblems in a way that avoids the need for “big-$M$” constants and hence yields strong valid inequalities. As we see in the computational results in Sect. 3, the use of these stronger inequalities makes a very significant difference beyond the benefits obtained from decomposition.

An extended abstract of this paper appeared in [40]. This full version includes a convergence proof of the algorithm, more details on how to effectively implement the algorithm, and the approach for solving for multiple risk levels to obtain an efficient frontier of risk and cost. This paper also introduces and conducts extensive computational tests on the chance-constrained resource planning application, which generalizes the model used in [40] because it allows the recourse constraints to include random coefficients.

The remainder of this paper is organized as follows. The algorithm is described in Sect. 2. In Sect. 3, we describe the chance-constrained resource planning application, show how the algorithm can be specialized for this application, and present computational results demonstrating the effectiveness of the algorithm for this application. In Sect. 4, we describe how the algorithm can be used to solve for multiple risk levels in sequence and present a numerical illustration. We close in Sect. 5 with some comments on possible modifications of the algorithm that may help when solving mixed-integer CCMPs, in which some of the decision variables have integer restrictions, and nonlinear CCMPs.

2 The branch-and-cut decomposition algorithm

We begin this section with an overview of the approach in Sect. 2.1. We describe the primary subproblems our algorithm is required to solve in Sect. 2.2. In Sect. 2.3 we describe how we obtain strong valid inequalities. Section 2.4 describes the algorithm details and proves its correctness, and computational enhancements are discussed in Sect. 2.5.

2.1 Overview

We first state a mixed-integer programming formulation for (1) that uses logical constraints. Introduce a binary variable $z_k$ for each $k \in \mathcal N$, where $z_k = 0$ implies $x \in P_k$. Then (1) is formulated as:

$$\begin{aligned}&\min \ f(x) \end{aligned}$$

(3a)

$$\begin{aligned}&\text{ s.t. } z_k = 0 \ \Rightarrow \ x \in P_k , \quad k \in \mathcal N \; ,\end{aligned}$$

(3b)

$$\begin{aligned}&\sum _{k=1}^N z_k \le p \; , \end{aligned}$$

(3c)

$$\begin{aligned}&x \in X, \ \ z \in \{0,1\}^N , \end{aligned}$$

(3d)

where $p := \lfloor \epsilon N \rfloor$. Inequality (3c) is a rewritten and strengthened version of the constraint $\frac{1}{N} \sum _{k=1}^N (1 - z_k) \ge 1 - \epsilon ,$ and so models the constraint $\mathbb P \{ x \in P(\omega ) \} \ge 1 - \epsilon$. Let $F = \{ (x,z) \mid$(3b)–(3d)$\}$ be the feasible region of (3).

A natural approach to solve (3) is to use “big-$M$” constraints to reformulate the conditions (3b). For example, if $P_k, k \in \mathcal N$ are explicitly given by (2) and are compact, (3b) can be formulated using additional variables as

$$\begin{aligned}&T^k x + W^k y^k + z_k M_k \ge b^k , \quad k \in \mathcal N \; \end{aligned}$$

(4a)

$$\begin{aligned}&y^k \in \mathbb R ^{d}_+, \quad k \in \mathcal N . \end{aligned}$$

(4b)

Here $M_k \in \mathbb R _+^m, k \in \mathcal N$ are sufficiently large to ensure that when $z_k = 1$, constraints (4a) are not active. On the other hand, when $z_k = 0$, constraints (4a) enforce $x \in P_k$. Our goal is to avoid the use of big-$M$ constants as in (4a), which are likely to lead to weak lower bounds when solving a continuous relaxation, and to use decomposition to avoid explicit introduction of the constraints (4a) and recourse variables $y^k$ that make a formulation based on (4) a very large mixed-integer program when $N$ is large.

The goal of our approach is similar in spirit to the goal of combinatorial Benders cuts introduced by Codato and Fischetti [41]. However, we are able to take advantage of the structural properties of the CCMP to obtain stronger valid inequalities. In particular, the valid inequalities we use include both the “logical” $z$ variables and the variables $x$, in contrast to the combinatorial Benders cuts that are based only on the logical variables. The approach in [27] has a closer connection to combinatorial Benders cuts.

Our decomposition algorithm is based on a master problem that includes the original variables $x$, and the binary variables $z$. The constraints (3b) are enforced implicitly with cutting planes, as in a Benders decomposition approach. The key difference, however, is that given the mixed-integer nature of our master problem, we seek to add cutting planes that are strong. Specifically, we are interested in strong valid inequalities for the feasible region $F$, of (3).

2.2 Required subproblems

Our algorithm assumes we have available algorithms (i.e., oracles) to solve three primary subproblems. Specialized algorithms that take advantage of the structure of the problem (e.g., the constraint set of a shortest path problem) may be used to solve any of these, if available.

The first subproblem is optimization of a linear function over $P_{k} \cap \, \bar{X}$, where $\bar{X}\, \subseteq \, \mathbb R ^n$ is a fixed closed set containing $X$, i.e., $\bar{X}\supseteq X$, chosen such that $P_k \cap \bar{X}\ne \emptyset$. Any $\bar{X}\supseteq X$ can be used for the algorithm to be correct (e.g., one can take $\bar{X}= \mathbb R ^n$). In Sect. 2.3, we discuss the trade-offs involved in choosing $\bar{X}$. The single scenario optimization subproblem for scenario $k \in \mathcal N$ is then:

$$\begin{aligned} h_k(\alpha ) := \min \bigl \{ \alpha x \mid x \in P_k \cap \bar{X}\bigr \} \end{aligned}$$

(5)

where $\alpha \in \mathbb R ^n$. Problem (5) is always feasible because we require $\bar{X}\cap P_k \ne \emptyset$. In addition, if $\alpha$ is chosen to be a vector in the dual cone of $C$, $C^* := \{ \alpha \in \mathbb R ^N \mid \alpha r \ge 0, \quad \forall r \in C \}$, then (5) is bounded, and hence the optimal value $h_k(\alpha )$ exists and is finite.

The second subproblem is the single scenario separation problem over the sets $P_k$, $k \in \mathcal N$:

Because each $P_k$ is defined by finitely many linear inequalities, the assumption that the separation problem returns a separating hyperplane from a finite set $\Pi$ is not restrictive. For example, if $P_k$ is given explicitly as $\{ x \mid T^k x \ge b^k\}$, then this separation routine can be implemented by returning $\mathrm {viol}= \mathrm {FALSE}$ if $T^k \hat{x} \ge b^k$, and otherwise returning $\mathrm {viol}= \mathrm {TRUE}$ and $(T^k_i,b^k_i)$ for some $i$ such that $T^k_i \hat{x} < b_i$, where $T^k_i$ denotes the $i$th row of $T^k$. As a less trivial example, if $P_k$ is defined as in (2), the oracle $\mathrm{{Sep}}(k,\hat{x})$ can be implemented by obtaining an extreme point optimal solution to the following linear program:

$$\begin{aligned} v(\hat{x}) =&\max _{\pi } \ \pi ^T(b^k - T^k \hat{x}) \nonumber \\&\text{ s.t. }\quad \pi ^T W^k \le 0, \pi ^T e = 1, \pi \in \mathbb R _+^m. \end{aligned}$$

(6)

If $v(\hat{x}) > 0$ and $\hat{\pi }$ is an optimal extreme point solution, then the oracle returns $\mathrm {TRUE}$ with $\alpha = \hat{\pi }^T T^k$ and $\beta = \hat{\pi }^T b^k$, otherwise the oracle returns $\mathrm {FALSE}$.

Finally, the algorithm requires solving a master problem of the form:

$$\begin{aligned} \text{ RP }(N_0,N_1,R) := \min&f(x)\end{aligned}$$

(7a)

$$\begin{aligned} \text{ s.t. }&\sum _{k=1}^N z_k \le p, \ \ (x,z) \in R, \ \ x \in X, \ \ z \in [0,1]^N \; , \end{aligned}$$

(7b)

$$\begin{aligned}&z_k = 0, k \in N_0, z_k = 1, \ k \in N_1 \; , \end{aligned}$$

(7c)

where $R\subseteq \mathbb R ^{n+N}$ is a polyhedron that contains $F$, and $N_0,N_1 \subseteq N$ are such that $N_0 \cap N_1 = \emptyset$. To ensure (7) is well-defined, we make the following assumption:

• (A4) For any polyhedron $R\subseteq \mathbb R ^{n+N}$ such that $F \subseteq R$, and any $N_0,N_1 \subseteq N$ such that $N_0 \cap N_1 = \emptyset$ with $|N_1| \le p$, problem (7) is either infeasible, or has an optimal solution.

This assumption is satisfied, for example, if $f$ is continuous and $X$ is compact, or if $f$ is linear and $X$ is a polyhedron. We adopt the convention that if (7) is infeasible, then $\mathrm {RP}(N_0,N_1,R) = +\infty$. In our algorithm, the restrictions on the binary variables $z$ given by $N_0$ and $N_1$ are obtained by branching, and the set $R$ is defined by cuts, valid for $F$, that are added in the algorithm to enforce (3b). If $f$ is linear and $X$ is a polyhedron, (7) is a linear program. If $f$ is convex, and $X$ is a convex set, then (7) is a convex program. If $f$ is linear, and $X$ is a set defined by linear inequalities and integer restrictions on some of the variables, then (7) is a mixed-integer program, so this subproblem will not be efficiently solvable in general. In Sect. 2.5, we discuss a modification to the algorithm that avoids solving mixed-integer programs for this case. Finally, if we don’t assume $f$ is convex, or that $X$ is a convex set, then again (7) is not efficiently solvable in general, so the requirement to solve this problem would be a severe limitation of our algorithm. Of course, in this case the problem (1) is generally intractable even without the chance constraint.

2.3 Generating strong valid inequalities

We now describe our procedure for generating valid inequalities of the form

$$\begin{aligned} \alpha x + \pi z \ge \beta \end{aligned}$$

(8)

for the set $F$, where $\alpha \in \mathbb R ^n$, $\pi \in \mathbb R ^N$, and $\beta \in \mathbb R$. We assume here that the coefficients $\alpha \in C^*$ are given, so our task is find $\pi$ and $\beta$ that make (8) valid for $F$. In addition, given a point $(\hat{x},\hat{z})$ our separation task is to find, if possible, $\pi$ and $\beta$ such that $(\hat{x},\hat{z})$ violate the resulting inequality.

The approach is very similar to that used in [20, 34], which applies only to chance-constrained problems with random right-hand side. However, by exploiting the fact that we have assumed $\alpha$ to be fixed, we are able to reduce our more general problem to the structure studied in [20, 34] and ultimately apply the same types of valid inequalities.

The first step is to solve the single scenario optimization problems (5):

$$\begin{aligned} h_k(\alpha ) := \min \bigl \{ \alpha x \ | \ x \in P_k \cap \bar{X}\bigr \}, \quad k \in \mathcal N \;. \end{aligned}$$

We have assumed that $\bar{X}$ is chosen so that $P_k \cap \bar{X}\ne \emptyset$, and hence these problems are feasible. In addition, $\alpha \in C^*$ and so $\alpha r \ge 0$ for all $r \in C$, the common recession cone of each $P_k$. Thus, each of these problems is bounded and so the values $h_k(\alpha ), k \in \mathcal N$ are well-defined. The choice of $\bar{X}$ represents a trade-off in time to compute the values $h_k(\alpha )$ and strength of the resulting valid inequalities. Choosing $\bar{X}= \mathbb R ^n$ leads to a problem for calculating $h_k(\alpha )$ that has the fewest number of constraints (and presumably the shortest computation time), but choosing $\bar{X}= X$ yields larger values for $h_k(\alpha )$ and consequently stronger inequalities. For example, if $X$ is described as a polyhedron with additional integer restrictions on some of the variables, problem (5) would become a mixed-integer program and hence could be computationally demanding to solve, although doing so may yield significantly better valid inequalities.

Having obtained the values $h_k(\alpha )$ for $k \in \mathcal N$, we then sort them to obtain a permutation $\sigma$ of $\mathcal N$ such that:

$$\begin{aligned} h_{\sigma _1}(\alpha ) \ge h_{\sigma _2}(\alpha ) \ge \cdots \ge h_{\sigma _N}(\alpha ) \;. \end{aligned}$$

Although the permutation depends on $\alpha$, we suppress this dependence to simplify notation. Our first lemma uses these values to establish a set of “base” inequalities that are valid for $F$, which we ultimately combine to obtain stronger valid inequalities.

Lemma 1

The following inequalities are valid for $F$:

$$\begin{aligned} \alpha x + (h_{\sigma _i}(\alpha ) - h_{\sigma _{p+1}}(\alpha )) z_{\sigma _i} \ge h_{\sigma _i}(\alpha ), \quad i = 1,\ldots , p \;. \end{aligned}$$

(9)

The proof of this result is almost identical to an argument in [34] and follows from the observation that $z_k = 0$ implies $\alpha x \ge h_k(\alpha )$, whereas (3c) implies that $z_k = 0$ for at least one of the $p+1$ largest values of $h_k(\alpha )$, and hence $\alpha x \ge h_{\sigma _{p+1}}(\alpha )$ is always valid.

Now, as was done in [20, 34], we can apply the star inequalities of [42], or equivalently in this case, the mixing inequalities of [43] to “mix” the inequalities (9) to obtain additional strong valid inequalities.

Theorem 1

([42, 43]) Let $T = \{t_1,t_2,\ldots , t_\ell \} \subseteq \{\sigma _1,\ldots ,\sigma _p\}$ be such that $h_{t_i}(\alpha ) \ge h_{t_{i+1}}(\alpha )$ for $i=1,\ldots ,\ell$, where $h_{t_{\ell +1}}(\alpha ) := h_{\sigma _{p+1}}(\alpha )$. Then the inequality

$$\begin{aligned} \alpha x + \sum _{i=1}^\ell (h_{t_i}(\alpha ) - h_{t_{i+1}}(\alpha )) z_{t_i} \ge h_{t_1}(\alpha ) \end{aligned}$$

(10)

is valid for $F$.

These inequalities are strong in the sense that, if we consider the set

$$\begin{aligned} Y = \bigl \{(y,z) \in \mathbb R \times \{0,1\}^p \ | \ y \!+\! (h_{\sigma _i}(\alpha ) \!-\! h_{\sigma _{p+1}}(\alpha )) z_{\sigma _i} \!\ge \! h_{\sigma _i}(\alpha ), \quad i \!=\! 1,\ldots , p \bigr \} \; , \end{aligned}$$

then the inequalities (10), with $\alpha x$ replaced by $y$, define the convex hull of $Y$ [42]. Furthermore, the inequalities of Theorem 1 are facet-defining for the convex hull of $Y$ (again with $y = \alpha x$) if and only if $h_{t_1}(\alpha ) = h_{\sigma _1}(\alpha )$, which suggests that when searching for a valid inequality of the form (10), one should always include $\sigma _1 \in T$. In particular, for any fixed $i \in \{2,\ldots ,p\}$, using $T = \{\sigma _1,\sigma _p\}$ in (10) yields the inequality

$$\begin{aligned} \alpha x + (h_{\sigma _1}(\alpha ) - h_{\sigma _i}(\alpha ))z_{\sigma _1} + (h_{\sigma _i}(\alpha ) - h_{\sigma _{p+1}}(\alpha )) z_{\sigma _i} \ge h_{\sigma _1}(\alpha ) \; , \end{aligned}$$

(11)

which dominates the inequality (9) for this $i$.

Theorem 1 presents an exponential family of valid inequalities, but given a point $(\hat{x},\hat{z})$ separation of these inequalities can be accomplished very efficiently. In [42] an algorithm based on finding a longest path in an acyclic graph is presented that has complexity $O(p^2)$, and [43] gives an $O(p \log p)$ algorithm. We use the algorithm of [43].

Additional classes of inequalities have been derived in [20] and [19] for the set defined by (9) and $\sum _{k} z_k \le p$, and these could be applied in this algorithm. However, as the results in [20] indicate that the mixing inequalities (10) provide a substantial portion of the strength of this relaxation, we do not pursue this option in the current work.

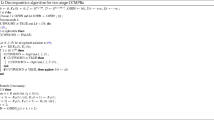
2.4 Algorithm details

A basic version of our proposed algorithm is given in Algorithm 1. The algorithm is a basic branch-and-bound algorithm, with branching being done on the binary variables $z_k$. A node $\ell$ in the search tree is defined by the sets $N_0(\ell )$ and $N_1(\ell )$, representing the sets of variables $z_k$ fixed to zero and to one, respectively. The algorithm also uses a polyhedral set $R$, defined by the cuts added throughout the algorithm. The algorithm is initialized with $R= \mathbb R ^{n\times N}$ and a root node $0$ having $N_0(0) = N_1(0) = \emptyset$. The only important difference between this algorithm and a standard branch-and-bound algorithm is how nodes are processed (Step $2$ in the algorithm). In this step, the current node relaxation (7) is solved repeatedly until no cuts have been added to the description of $R$ or the lower bound exceeds the incumbent objective value $U$. Whenever an integer feasible solution $\hat{z}$ is found, and optionally otherwise, the cut separation routine $\mathrm{{SepCuts}}$ is called. The $\mathrm{{SepCuts}}$ routine must be called when $\hat{z}$ is integer feasible to check whether the solution $(\hat{x},\hat{z})$ is in the set $F$ (i.e., is truly a feasible solution). The routine is optionally called otherwise to possibly improve the lower bound.

The $\mathrm{{SepCuts}}$ routine, described in Algorithm 2, attempts to find strong violated inequalities using the approach described in Sect. 2.3. The key here is the method for selecting the coefficients $\alpha$ that are taken as given in Sect. 2.3. The idea is to test whether the conditions that define $F$,

$$\begin{aligned} z_k = 0 \ \Rightarrow \ x \in P_k, \quad \forall k \in \mathcal N , \end{aligned}$$

(12)

are satisfied. If so, the solution is feasible, otherwise, we identify a scenario $k$ such that $\hat{z}_k = 0$ and $x \notin P_k$. We then find an inequality, say $\alpha x \ge \beta$, that is valid for $P_k$ and that separates $\hat{x}$ from $P_k$.

In line 2 of Algorithm 2, we test whether $\hat{x} \in P_k$ for any $k$ such that $\hat{z}_k < 1$. To obtain a convergent algorithm, it is sufficient to check only those $k$ such that $\hat{z}_k = 0$; we also optionally check $k$ such that $\hat{z}_k \in (0,1)$ in order to possibly generate additional violated inequalities. We now establish that Algorithm 1 solves (3).

Theorem 2

Assume A1–A4, and that we have algorithms available to solve subproblems (5), $\mathrm{{Sep}}(k,\hat{x})$ for any $\hat{x} \in X$ and $k \in \mathcal N$, and (7). Then, algorithm 1 terminates finitely, and at termination if $U = +\infty$, problem (3) is infeasible, otherwise $U$ is the optimal value of (3).

Proof

First, we verify that the values $h_k(\alpha )$, $k \in \mathcal N$, obtained in solving (5) are well defined (these are used in line 5 of the $\mathrm{{SepCuts}}$ subroutine, when separating inequalities of the form (10)). The coefficient vector $\alpha \in \mathbb R ^n$, obtained from the procedure $\mathrm{{Sep}}(k,\hat{x})$, defines a valid inequality of the form $\alpha x \ge \beta$ for $P_k$. Thus, $\alpha r \ge 0$ for any $r \in C$, since otherwise there would not exist a $\beta$ such that $\alpha x \ge \beta$ for all $x \in P_k$. Thus, $\alpha \in C^*$, and so $h_k(\alpha ), k \in \mathcal N$ are well-defined by the arguments in Sect. 2.3.

We next argue that the algorithm terminates finitely. Indeed, the algorithm trivially processes a finite number of nodes as it is based on branching on a finite number of binary variables. In addition, the set of possible inequalities that can be produced by the procedure $\mathrm{{SepCuts}}$ procedure is finite because for any coefficient vector $\alpha$ there are finitely many mixing inequalities of the form (10), and furthermore there are finitely many coefficient vectors $\alpha$ since the $\mathrm{{SepCuts}}$ procedure is assumed to return inequalities from a finite set. Thus, the terminating condition for processing a node (line 21) must be satisfied after finitely many iterations.

Next, the algorithm never cuts off an optimal solution because the branching never excludes part of the feasible region and only valid inequalities for the set $F$ are added. This proves that, at termination, if $U = +\infty$, then (3) is infeasible, and otherwise that $U$ is an upper bound on the optimal value of (3). The final point we must argue is that $U$ is only updated (in line 14) if the solution $(\hat{x},\hat{z}) \in F$ (i.e., it is feasible), and hence $U$ is also a lower bound on the optimal value of (3). $U$ is updated only if $\hat{z} \in \{0,1\}^N$ and $\mathrm{{SepCuts}}(\hat{x},\hat{z},R)$ returns $\mathrm {FALSE}$. We therefore must argue that if $\hat{z} \in \{0,1\}^N$ but $\hat{z} \notin F$, then $\mathrm{{SepCuts}}(\hat{x},\hat{z},R)$ must return $\mathrm {TRUE}$. If $\hat{z} \notin F$, then there must exist a scenario $k^{\prime }$ such that $\hat{z}_{k^{\prime }} = 0$ but $\hat{x} \notin P_{k^{\prime }}$. For the first such scenario $k^{\prime }$, the separation procedure $\mathrm{{Sep}}(k^{\prime },\hat{x})$ returns $\mathrm {viol}= \mathrm {TRUE}$ and $(\alpha ,\beta )$ such that $\alpha x \ge \beta$ is valid for $P_{k^{\prime }}$ and $\alpha \hat{x} < \beta$. The vector $\alpha$ is then used to calculate $h_k(\alpha )$ for all $k \in \mathcal N$. Because $\alpha x \ge \beta$ holds for any $x \in P_{k^{\prime }}$,

$$\begin{aligned} h_{k^{\prime }}(\alpha ) = \min \left\{ \alpha x \mid x \in P_{k^{\prime }} \cap \bar{X} \right\} \ge \beta . \end{aligned}$$

We then consider two cases. First, if $h_{\sigma _{p+1}}(\alpha ) \ge h_{k^{\prime }}(\alpha )$ then any inequality of the form (10) is violated by $(\hat{x},\hat{z})$ because

$$\begin{aligned} h_{t_1}(\alpha ) - \sum _{i=1}^{\ell } (h_{t_{i}}(\alpha ) - h_{t_{i+1}}(\alpha )) \hat{z}_{t_i} \ge h_{\sigma _{p+1}}(\alpha ) \ge h_{k^{\prime }}(\alpha ) \ge \beta > \alpha \hat{x}. \end{aligned}$$

Otherwise, if $h_{\sigma _{p+1}}(\alpha ) < h_{k^{\prime }}(\alpha )$ then $k^{\prime } = \sigma _{i}$ for some $i=1,\ldots ,p$. Then, the inequality (10) defined by taking $T = \{k^{\prime }\}$ reduces to:

$$\begin{aligned} \alpha x + (h_{k^{\prime }}(\alpha ) - h_{\sigma _{p+1}}(\alpha )) z_{k^{\prime }} \ge h_{k^{\prime }}(\alpha ) \end{aligned}$$

which cuts off $(\hat{x},\hat{z})$ since $\hat{z}_{k^{\prime }} = 0$. Because separation of the inequalities (10) is done exactly, this implies that in either case a violated inequality is added to $R$ and $\mathrm{{SepCuts}}(\hat{x},\hat{z},R)$ returns $\mathrm {TRUE}$. $\square$

An advantage of this algorithm is that most of the subproblems are decomposed and so can be solved one scenario at a time and can be implemented in parallel. In particular, the subproblems $\mathrm{{Sep}}(k,\hat{x})$ for any $k$ such that $\hat{z}_k < 1$ can be solved in parallel. The subsequent work of generating a strong valid inequality is dominated by calculation of the values $h_k(\alpha )$ as in (5), which can also be done in parallel.

2.5 Computational enhancements

We have stated our approach in relatively simple form in Algorithm 1. However, as this approach is a variant of branch-and-cut for solving a particularly structured mixed-integer programming problem, we can and should also use all the computational enhancements commonly used in such algorithms. In particular, it is important to use heuristics to find good feasible solutions early and use some sort of pseudocost branching [44], strong branching [45], or reliability branching [46] approach for choosing which variable to branch. These enhancements are easily achieved if the algorithm is implemented within a commercial integer programming solver such as IBM Ilog CPLEX, which already has these and many other useful techniques implemented.

In our experience, we found that a potential bottleneck in the algorithm is solving the separation subproblem $\mathrm{{Sep}}(k,\hat{x})$, which we implemented using the linear program (6), within the $\mathrm{{SepCuts}}$ routine. In the worst case, this problem may be solved for all scenarios $k$ with $\hat{z}_k < 1$. If the solution $(\hat{x},\hat{z})$ is feasible, this effort is necessary to verify that it is feasible. However, it is often the case that it is eventually found that $(\hat{x},\hat{z})$ is not feasible, and hence the time spent solving $\mathrm{{Sep}}(k,\hat{x})$ for scenarios in which $\hat{x} \in P_k$ is unproductive as these separations problems fail to yield an inequality that cuts off $(\hat{x},\hat{z})$. Stated another way, if a violated inequality exists, we would prefer to find it at one of the first scenarios we check. This potential for significant unproductive calls to $\mathrm{{Sep}}(k,\hat{x})$ is the reason we terminate the $\mathrm{{SepCuts}}$ routine after finding the first scenario that yields one or more violated inequalities, as opposed to continuing through all scenarios. In addition, two other strategies helped to minimize unproductive calls to $\mathrm{{Sep}}(k,\hat{x})$.

The first and most beneficial strategy is to save a list of all the $\alpha$ vectors generated in the $\mathrm{{SepCuts}}$ routine, along with the corresponding calculated values $h_k(\alpha )$, throughout the algorithm in a coefficient pool. The coefficient pool is similar to the standard strategy in mixed-integer programming solvers of maintaining a “cut pool” that stores valid inequalities that may be later added to the linear programming relaxation; the difference is that the coefficient pool does not store valid inequalities, but instead stores information useful for generating valid inequalities. When the $\mathrm{{SepCuts}}$ routine is called we first solve the separation problem to search for violated mixing inequalities (10) for each of the coefficient vectors in the coefficient pool. If we find any violated inequalities by searching through the coefficient pool, we add these and avoid solving $\mathrm{{Sep}}(k,\hat{x})$ altogether. While there is some computational expense in solving the separation problem for the inequalities (10) for all the vectors in the coefficient pool, the separation of (10) is very efficient and hence this time was significantly outweighed by the time saved by avoiding solving $\mathrm{{Sep}}(k,\hat{x})$. Although we did not pursue this option, if the coefficient pool becomes too large, a strategy could be implemented to “prune” the list, e.g., based on the frequency in which each vector in the pool yielded a violated inequality.

The second strategy for limiting unproductive calls to $\mathrm{{Sep}}(k,\hat{x})$ is to heuristically choose the sequence of scenarios in a way that finds a scenario that yields a violated inequality, if there is one, earlier. First, observe that when $\hat{z}_k > 0$, it is possible to find $\hat{x} \notin P_k$, and yet not find a violated mixing inequality (10). This motivates first checking scenarios with $\hat{z}_k = 0$, and more generally, checking scenarios in increasing order of $\hat{z}_k$. In addition, it seems intuitive that scenarios that have yielded inequalities previously are the ones that are more likely to yield inequalities in future calls to $\mathrm{{SepCuts}}$. Thus, for each scenario $k$, we also keep a count $s_k$, of the total number of times that scenario $k$ has yielded a violated inequality (10). We heuristically combine these observations by searching scenarios in decreasing order of the value $(1 -\hat{z}_k) s_k$.

3 Application and computational results

3.1 A probabilistic resource planning problem

We tested our approach on a probabilistic resource planning problem. This problem consists of a set of resources (e.g., server types), denoted by $i \in I := \{1,\ldots ,n\}$, which can be used to meet demands for a set of customer types, denoted by $j \in J := \{1,\ldots ,m\}$. The objective is to choose the quantity of each resource to have on hand to meet customer demands.

A deterministic version of this problem can be stated as:

$$\begin{aligned} \min _{x \in \mathbb R _+^n, y \in \mathbb R _+^{nm}} \left\{ cx \mid \sum _{j \in J} y_{ij} \le \rho _i x_i, \ \forall i \in I, \ \ \sum _{i \in I} \mu _{ij} y_{ij} \ge \lambda _j, \ \forall j \in J \right\} . \end{aligned}$$

Here $c_i$ represents the unit cost of resource $i$, $\rho _i \in (0,1]$ represents the yield of resource $i$, i.e., the fraction of what is planned to be available that actually can be used, $\lambda _j \ge 0$ represents the demand of customer type $j$, and $\mu _{ij} \ge 0$ represents the service rate of resource $i$ for customer type $j$, i.e., how many units of demand of customer type $j$ can be met with a unit of resource $i$. The variables $x_i$ determine the quantity of resource $i$ to have on hand, and the variables $y_{ij}$ represent the amount of resource $i$ to allocate to customer type $j$. Thus, the problem is to choose resource levels and allocations of these resources to customer types to minimize the total cost of resources, while requiring that the allocation does not exceed the available resource levels and is sufficient to meet customer demands.

In the probabilistic resource planning problem, the customer demands, resource yields, and service rates are nonnegative random vectors of appropriate size denoted by $\tilde{\lambda }$, $\tilde{\rho }$, and $\tilde{\mu }$. The resource decisions $x_i$ must be made before these random quantities are observed, but the allocation decisions can adapt to these realizations. We require that all customer demands should be met with high probability, leading to the chance-constrained model

$$\begin{aligned} \min _{x \in \mathbb R _+^n} \Bigl \{ cx \ \big | \ \mathbb P \bigl \{ x \in P(\tilde{\lambda },\tilde{\rho },\tilde{\mu }) \bigr \} \ge 1 - \epsilon \Bigr \} \; , \end{aligned}$$

where

$$\begin{aligned} P(\lambda ,\rho ,\mu )&= \left\{ x \in \mathbb R _+^n \ | \ \exists y \in \mathbb R _+^{n m} \text{ s.t. } \sum _{j=1}^m y_{ij} \le \rho _i x_i,\ \forall i \in I,\right. \nonumber \\& \left. \sum _{i=1}^n \mu _{ij} y_{ij} \ge \lambda _j, \ \forall j \in J \ \right\} . \end{aligned}$$

(13)

We test our algorithm on three versions of this problem, varying which components are random. In the first version, only the arrival rates $\tilde{\lambda }$ are random; this is the model that was used in the call center staffing problem studied in [47] and was used as the test case in [40]. In the second version, both the arrival rates and the yields are random, and all are random in the final version.

When we use a finite scenario approximation of the random vectors $\tilde{\lambda }$, $\tilde{\rho }$, and $\tilde{\mu }$, assumption A1 of Sect. 2.1 is satisfied. Assumption A2 is satisfied because $P(\lambda ,\rho ,\mu )$ is a non-empty polyhedron for any nonnegative vectors $\lambda ,\rho$, and $\mu$. It is easy to see that the recession cone of $P(\lambda ,\rho ,\mu )$ is $C = \mathbb R _+^n$ for any nonnegative $\lambda ,\rho ,\mu$ and hence Assumption A3 is satisfied. Assumption A4 is satisfied because the master problem (7) is always a feasible linear program.

3.2 Implementation details

A key advantage of the proposed algorithm is the ability to use problem-specific structure to efficiently solve the separation and optimization problems over $P_k$ for all scenarios $k$. As an illustration, we describe here how the optimization problems can be solved efficiently for this application.

Given a coefficient vector $\alpha \in \mathbb R _+^n$, the following optimization problem is to be solved for each scenario $k$:

$$\begin{aligned} h_k(\alpha ) = \min _{x,y}&\ \sum _{i \in I} \alpha _i x_i \nonumber \\ \text{ s.t. }&\sum _{j \in J} y_{ij} - \rho ^k_i x_i \le 0, \quad \forall i \in I, \end{aligned}$$

(14a)

$$\begin{aligned}&\sum _{i \in I} \mu ^k_{ij} y_{ij} \ge \lambda ^k_j, \quad \;\;\;\; \forall j \in J,\nonumber \\&x \in \mathbb R _+^n, y \in \mathbb R _+^{nm}. \end{aligned}$$

(14b)

Because $\alpha \ge 0$ and $\rho ^k_i > 0$ for all $i$, there exists an optimal solution in which inequalities (14a) are tight, and hence $x$ can be eliminated from the problem.

After doing so, the problem can be decomposed by customer type yielding

$$\begin{aligned} h_k(\alpha )&= \sum _{j \in J} \min _{y_{\cdot j}} \left\{ \sum _{i \in I} \Bigl (\frac{\alpha _i}{\rho _i^k} \Bigr ) y_{ij} \ \Big | \ \sum _{i \in I} \mu _{ij}^k y_{ij} \ge \lambda _j^k, \ y_{\cdot j} \in \mathbb R _+^m \right\} \\&= \sum _{j \in J} \min _{i \in I} \left\{ \frac{\alpha _i \lambda _j^k}{\rho _i^k \mu _{ij}^k } \right\} . \end{aligned}$$

Thus, given a coefficient vector $\alpha$, optimization over all scenario sets $P_k$ can be accomplished with $O(Nnm)$ calculations using the above closed-form expression.

When the yields and service rates are not random, optimization over all scenario sets can be done even more efficiently. Specifically, in this case the expression for $h_k(\alpha )$ reduces to:

$$\begin{aligned} h_k(\alpha ) =\sum _{j \in J} \min _{i \in I} \left\{ \frac{\alpha _i \lambda _j^k}{\rho _i \mu _{ij}} \right\} =\sum _{j \in J} \lambda _j^k \min _{i \in I} \left\{ \frac{\alpha _i}{\rho _i \mu _{ij}} \right\} . \end{aligned}$$

Thus, the minimization over $i \in I$ is independent of scenario, and hence can be done just once for each customer type $j$, allowing optimization over all scenarios to be accomplished in $O(Nn + mn)$.

In this application, the set of deterministic constraints is simply $X = \mathbb R _+^n$. Thus, the only choice for $\bar{X}$ is to use $\bar{X}= X = \mathbb R _+^n$.

We implemented our approach within the commercial integer programming solver CPLEX 12.2. The main component of the approach, separation of valid inequalities of the form (10), was implemented within a cut callback that CPLEX calls whenever it has finished solving a node (whether the solution is integer feasible or not) and also after it has found a heuristic solution. In the feasibility checking phase of the $\mathrm{{SepCuts}}$ routine (line 2) we searched for $k$ with $\hat{z}_k < 1$ and $x \notin P_k$ in decreasing order of $(1-\hat{z}_k)s_k$. The separation problem $\mathrm{{Sep}}(k,\hat{x})$ was implemented by solving the linear program (6), also using CPLEX. For the first $k$ we find in which $\hat{z}_k < 1$ and $x \notin P_k$ (and only the first) we add all the violated valid inequalities of the form (11) as well as the single most violated inequality of the form (10). Our motivation for adding the inequalities (11) is that they are sparse and this is a simple way to add additional valid inequalities in one round; we found that doing this yielded somewhat faster convergence. As required in the algorithm, the separation of valid inequalities is always attempted if the relaxation solution $\hat{z}$ is integer feasible. When $\hat{z}$ is not integer feasible, at the root node we continued generating valid inequalities until no more were found, or until the relative improvement in relaxation objective value from one round of cuts to the next was less than 0.01 %. Throughout the branch-and-bound tree, we attempt to generate cuts if $\hat{z}$ is fractional only every 20 nodes, and for such nodes we add only one round of cuts. This strategy appeared to offer a reasonable balance between time spent generating valid inequalities and the corresponding improvement in relaxation objective values, but it is certainly possible that an improved strategy could be found.

All computational tests were conducted on a Mac Mini, running OSX 10.6.6, with a two-core 2.66 GHz (only a single core was used) having 8GB memory. A time limit of 1 h was enforced.

3.3 Test instances

We randomly generated test instances. For a given problem size (number of resources and customer types) we first generated a single “base instance” consisting of the unit costs of the resources and a set of base service rates. A significant fraction of the service rates $\mu _{ij}$ were randomly set to zero, signifying that resource $i$ cannot be used to meet customer type $j$. The costs were generated in such a way that “more efficient” resources were generally more expensive, in order to make the solutions nontrivial. Customer demands $\tilde{\lambda }$ are assumed to be multivariate normally distributed. When the yields $\tilde{\rho }$ are random, they are assumed to take the form $\tilde{\rho } = \max \{\hat{\rho },e\}$ where $e$ is a vector of all ones and $\hat{\rho }$ is a vector of independent normal random variables. For the test instances in which $\tilde{\mu }$ is random, it is modeled as $\tilde{\mu }_{ij} = e^{-Z_{ij}} \mu _{ij}$ where $\mu _{ij}$ are the base service rates and $Z_{ij}$ are independent normal random variables with mean zero and standard deviation $0.05$. For each base instance, we generated five different base distributions of the arrival rate and yield random vectors and for each of these we generated a sample of 3,000 realizations for instances in which only $\tilde{\lambda }$ is random, and 1,500 realizations for instances in which $\tilde{\rho }$ and/or $\tilde{\mu }$ are random. For each base instance we also generated $5$ independent samples of 1,500 realizations of $\tilde{\mu }_{ij}$ from the same base distribution (i.e., in contrast to $\tilde{\lambda }$ and $\tilde{\rho }$, the base distribution of $\tilde{\mu }$ is the same in all instances; only the random sample varies). Instances with $N <3{,}000$ (or $N <1{,}500$ when $\tilde{\rho }$ or $\tilde{\mu }$ are random) are obtained by using only the first $N$ scenarios in the sample. For the version of the problem in which only the arrival rates are random, we used $\rho _i = 1$ for all resources $i$, and used the base service rates without modification. In addition to varying the sample size $N$, we also considered two risk levels, $\epsilon = 0.05$ and $\epsilon = 0.1$. Complete details of the instance generation, and the actual instances used, are available from the author [48].

3.4 Results

We compared our algorithm against the Big-$M$ formulation that uses (4) and also against a basic decomposition algorithm that does not use the strong valid inequalities of Sect. 2.3 or the computational enhancements discussed in Sect. 2.5. We compare against this simple decomposition approach to understand whether the success of our algorithm is due solely to decomposition, or whether the strong inequalities are also important. The difference between the basic decomposition algorithm and the strengthened version is in the type of cuts that are added in the $\mathrm{{SepCuts}}$ routine. Specifically, given a solution $(\hat{x},\hat{z})$ such that there exists scenario $k$ with $\hat{z}_k = 0$ and $\hat{x} \notin P_k$, and a valid inequality $\alpha x \ge \beta$ for the set $P_k$ that is violated by $\hat{x}$, the basic decomposition algorithm simply adds the inequality

$$\begin{aligned} \alpha x \ge \beta (1-z_k) \;. \end{aligned}$$

When the sets $P_k$ have the form (13), this inequality is valid for $F$ because $x \ge 0$ and any valid inequality for $P_k$ has $\alpha \ge 0$. Furthermore, this inequality successfully cuts off the infeasible solution $(\hat{x},\hat{z})$.

The main results are presented in Tables 1, 2 and 3. These tables compare the results for solving these instances with three methods: directly solving the big-$M$ formulation based on (4), the simple Benders decomposition algorithm (labeled Basic Decomp), and the algorithm proposed in this paper (labeled Strong Decomp). Each row in these tables presents summary results for $5$ instances with the same characteristics: a base instance with size $(n,m)$, risk level $\epsilon$, and $N$ scenarios. In most cases, three entries are reported for each method: the # column reports how many of the five instances were solved to optimality within the time limit, the Time column reports the average solution time of the instances that were solved to optimality, in seconds rounded to the nearest integer, and the Gap column reports the average optimality gap at the time limit for the instances that were not solved to optimality. Optimality gap is calculated as $(UB - LB)/UB$ where $UB$ and $LB$ are the values of the best feasible solution and best lower bound, respectively, found by that method. A ‘–’ in a Time or Gap entry indicates there were no instances on which to calculate this average (because either none or all of them were solved to optimality, respectively). A ‘*’ in the Gap column indicates that for at least one of the instances no feasible solution was found within the time limit, and hence such instances were not included in the average gap calculation. If a ‘*’ appears with no number, no feasible solution was found for any of the instances.

Table 1 Results for instances with random demands only

Table 2 Results with random demands and yields

Table 3 Results with random demands, yields, and service rates

Table 1 gives the results for instances in which only the demands ($\tilde{\lambda })$ are random. The big-$M$ formulation based on (4) is not able to solve any of these instances within the time limit (and hence, only a “Gap” column is reported). This formulation only successfully solves the LP relaxation and finds a feasible solution for the smallest instance sizes (and not even for all of these). The basic decomposition approach significantly improves over the big-$M$ formulation in that it is able to find feasible solutions for most of the instances. However, only some of the smallest of the instances could be solved to optimality, and the larger instances had very large optimality gaps after the limit. The branch-and-cut decomposition algorithm is able to solve all these instances to optimality in an average of less than two minutes. Table 1 also shows that the total number of nodes required to solve these instances with this method is very small on average (0 nodes indicates the instances were solved at the root node), which occurs because for this problem class the lower bounds produced by the strong valid inequalities are almost identical to the true optimal values.

Table 2 gives the results for instances with random demands and yields and Table 3 gives the results for the case where demands, yields, and service rates are random. These instances are significantly more challenging than those with only random demands, and hence we report results for smaller instances. However, these instances are still large enough to prevent solution using the big-$M$ formulation based on (4), as the linear programming relaxation again is often not solved within the time limit, and when it does the optimality gap is very large. We see that again the basic decomposition algorithm has more success solving the smallest instances, but leaves large optimality gaps for the larger instances. While the branch-and-cut decomposition algorithm solves many more of the instances to optimality, a significant portion of the larger instances are not solved to optimality within the time limit, in contrast to the random demands only case. However, the optimality gap achieved within the time limit is still quite small, usually less than 1 %, and almost always less than 2 %.

Table 4 presents results comparing the optimality gap and solution times of the two decomposition approaches at the root node for some of the instances with random yields and service rates. Specifically, for the largest instances in this test set, we report the average quality of the lower bound obtained at the root node (compared against the optimal solution, or best solution found by any method if optimal is unknown) and the average time to process the root node. These results indicate that the strong valid inequalities close substantially more of the optimality gap at the root node than the basic Benders inequalities, and do so in a comparable amount of time. In addition, the computation times suggest that although many of these instances are not solved to optimality in the 1 h time limit, it is possible to obtain strong bounds on solution quality relatively quickly. Finally, these gaps also suggest that, in addition to obtaining additional classes of strong valid inequalities to close the gap further, investigating problem-specific branching strategies may also be beneficial in helping to finish solving these instances to optimality.

Table 4 Root gaps and times for decomposition approaches for instances with $n=20$, $m = 30$

4 Solving for the efficient frontier

We now describe how the proposed algorithm can be used to efficiently solve for multiple risk levels in sequence, as would be done when constructing an efficient frontier between cost and risk of constraint violation. We assume we have a fixed set of $N$ scenarios, and we wish to solve the CCMP for a set of risk levels $\epsilon _1 < \epsilon _2 < \cdots < \epsilon _r$. Of course, one option is simply to solve these $r$ instances independently. Alternatively, we demonstrate how, by solving the instances in a particular sequence, the branch-and-cut decomposition algorithm can use information obtained from solving one instance to “warm-start” the solution of later instances. This is not straightforward because these are mixed-integer programming instances with different feasible regions.

First, observe that if $x^*_{t}$ is an optimal solution to the instance with risk level $\epsilon _t$, then $x^*_{t}$ is a feasible solution to the instance with risk level $\epsilon _{t+1}$, since $\epsilon _t < \epsilon _{t+1}$. This motivates solving the instances in order of increasing risk level, so that the optimal solution of one instance can be used as a starting incumbent solution for the next.

Another strategy for using information from one solution of a mixed-integer program to the next is to use valid inequalities derived from one for the next. Unfortunately, if the instances are being solved in increasing order of risk level, a valid inequality for the instance with risk level $\epsilon _t$ may not be valid for the instance with risk level $\epsilon _{t+1} > \epsilon _t$, since this instance has a larger feasible region. However, the information used to generate the mixing inequalities (10)—the coefficient vectors $\alpha$ and the corresponding scenario objective values $h_k(\alpha )$—is independent of the risk level. Thus, we can save all the information in the coefficient pool (described in Sect. 2.5) from one instance to the next, and continue to use this information to generate the mixing inequalities (10). As the primary work in generating these inequalities is the derivation of the coefficient vector $\alpha$ by solving a separation problem and the calculation of the scenario objective values $h_k(\alpha )$, this can save a significant amount of time.

When saving the coefficient pool from one instance to the next, its size can grow very significantly. To prevent the time spent checking the coefficient pool from becoming a bottleneck of the algorithm we keep only a subset of the coefficient vectors in the pool from one instance to the next. To choose which to keep, we maintain a count of how many times a violated inequality was found using each coefficient vector throughout the solution of an instance, and keep 20 % of the coefficient vectors that have the highest counts (we also keep any that are tied with the smallest count in the top 20 %, so the number kept may exceed 20 %). In addition to limiting the size of the coefficient pool, this strategy has the potential benefit of identifying and focusing attention on the coefficient vectors that are most effective at generating valid inequalities.

We conducted a computational experiment to test this approach for computation of an efficient frontier. For this test we chose three base instances; one with only demands ($\tilde{\lambda }$) random, one with random demands and yields ($\tilde{\lambda },\tilde{\rho }$), and one with random demands, yields and service rates ($\tilde{\lambda },\tilde{\rho },\tilde{\mu }$). We also chose a single sample size $N$ for each. These instances were chosen to be the largest in our test set that our algorithm can solve to optimality within the time limit at the largest risk level we solve for. For each of these base instances, we solved for 16 risk levels $\epsilon$ ranging from 0.0 to 0.15 in increments of 0.01, with and without using warm-start information. We repeated this exercise for the five different random instances of each base instance.

Table 5 presents the average total solution time and average total number of nodes to solve all 16 risk levels using the two approaches. The results indicate that these warm-start strategies can indeed effectively reduce the total solution time for computing an efficient frontier. The ideas were particularly effective for the instances in which only the demands are random, reducing the total solution time by about 75 % on average. When the yields and/or service rates are random the warm-start strategies were relatively less helpful, but still reduced total solution time by about 50 % on average. The reduced impact can be explained by the total number of nodes processed. When only demands are random, very few branch-and-bound nodes are processed, so a significant portion of the total time is spent finding a good feasible solution and generating valid inequalities to solve the initial LP relaxation, and this work is aided significantly by the warm-start techniques. In contrast, when the yields and/or service rates are random, relatively more branch-and-bound nodes are processed, and the number processed is not significantly affected by the warm-start techniques. As a result, in these instances, the proportion of the time spent solving the node linear programming relaxations is higher, and this time is not helped by the warm-start techniques.

Table 5 Impact of warm-start strategies for computing an efficient frontier

5 Discussion

We close by discussing adaptations and extensions of the algorithm. In our definition of the master relaxation (7), we have enforced the constraints $x \in X$. If $X$ is a polyhedron and $f(x)$ is linear, (7) is a linear program. However, if $X$ is not a polyhedron, suitable modifications to the algorithm could be made to ensure that the relaxations solved remain linear programming problems. For example, if $X$ is defined by a polyhedron $Q$ with integrality constraints on some of the variables, then we could instead define the master relaxation to enforce $x \in Q$, and then perform branching both on the integer-constrained $x$ variables and on the $z$ variables. Such a modification is straightforward to implement within existing integer programming solvers. In this case, $Q$ would be a natural choice for the relaxation $\bar{X}$ of $X$ used in Sect. 2.3 when obtaining the $h_k(\alpha )$ values as in (5). In addition, $Q$ could be augmented with inequalities that are valid for $X \cap P_k$ to obtain a linear relaxation that is a closer approximation to $\mathrm{conv }(X \cap P_k)$.

Although these modifications are likely to help our algorithm when $X$ contains integrality restrictions, we should also point out that the algorithm may face some difficulties with such problems due to these integrality restrictions. For example, suppose that $X = Q \cap \mathbb Z ^n$ where $Q$ is a polyhedron, and consider the (trivial) case with $\epsilon = 0$, so that the feasible set becomes $Q \cap \bar{P} \cap \mathbb Z ^n$ where $\bar{P} = \cap _{k=1}^N P_k$. Because our approach does not make use of integrality of the $x$ variables, except possibly when solving single scenario problems to obtain the $h_k(\alpha )$ values, the absolute best relaxation our valid inequalities could produce would be $\bigcap _{k=1}^N \mathrm{conv }(Q \cap P_k \cap \mathbb Z ^n)$, which could certainly be a poor approximation to $\mathrm{conv }\Bigl (Q \cap \bar{P} \cap \mathbb Z ^n\Bigr )$. As a result, for chance-constrained mixed-integer programs, we expect that further research will be needed to find strong valid inequalities that yield tighter relaxations of the latter set.

If $X$ is defined by convex nonlinear inequalities of the form $g(x) \le 0$, then the master relaxation problem (7) could be made a linear program by using an outer approximation of $X$, as in the LP/NLP branch-and-bound algorithm for solving mixed-integer nonlinear programs (MINLPs) [49]. In this case, when a solution $(\hat{x},\hat{z})$ is found in which $\hat{z}$ is integer feasible, in addition to being required to check feasibility of the logical conditions (3b), a nonlinear programming problem $\min \{ f(x) \mid g(x) \le 0, x \in R\}$ would also be solved, and the gradient inequalities at the optimal solution $\hat{x}$,

$$\begin{aligned} g(\hat{x}) + \nabla g(\hat{x})^T (x - \hat{x}) \le 0, \end{aligned}$$

would be added to the current outer approximation linear programming relaxation for each nonlinear constraint. (A similar inequality, with an auxiliary variable, would be added if the objective is a convex nonlinear function.) The details are beyond the scope of this paper, but we conjecture that this algorithm could be shown to converge finitely provided that a constraint qualification holds at every nonlinear programming problem solved in the algorithm, an assumption that is standard for convergence of the LP/NLP algorithm.

Many special cases of (1) are known to be $\mathcal NP$-hard [12, 20, 50]. Therefore, we cannot expect a polynomial-time algorithm for (1), which is why we propose a branch-and-cut algorithm. On the other hand, in our tests, the proposed algorithm performed remarkably well on the instances in which randomness appeared only in the right-hand side of the constraints, most notably requiring a very small number of branch-and-bound nodes to be explored. We therefore think it would be an interesting direction for future research to investigate whether a polynomial-time algorithm, or approximation algorithm with a priori guarantee on optimality or feasibility violation, may exist for this special case, possibly with additional assumptions on the data (e.g., that it was a obtained as a sample approximation from a log-concave distribution).