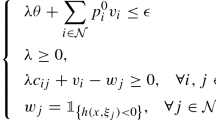Distributionally robust chance-constrained programs with right-hand side uncertainty under Wasserstein ambiguity

Abstract

We consider exact deterministic mixed-integer programming (MIP) reformulations of distributionally robust chance-constrained programs (DR-CCP) with random right-hand sides over Wasserstein ambiguity sets. The existing MIP formulations are known to have weak continuous relaxation bounds, and, consequently, for hard instances with small radius, or with large problem sizes, the branch-and-bound based solution processes suffer from large optimality gaps even after hours of computation time. This significantly hinders the practical application of the DR-CCP paradigm. Motivated by these challenges, we conduct a polyhedral study to strengthen these formulations. We reveal several hidden connections between DR-CCP and its nominal counterpart (the sample average approximation), mixing sets, and robust 0–1 programming. By exploiting these connections in combination, we provide an improved formulation and two classes of valid inequalities for DR-CCP. We test the impact of our results on a stochastic transportation problem numerically. Our experiments demonstrate the effectiveness of our approach; in particular our improved formulation and proposed valid inequalities reduce the overall solution times remarkably. Moreover, this allows us to significantly scale up the problem sizes that can be handled in such DR-CCP formulations by reducing the solution times from hours to seconds.

1 Introduction

We consider the following chance-constrained program (CCP)

where $\mathbf {c}\in \mathbb {R}^L$ is a cost vector, $\mathcal {X}\subset \mathbb {R}^L$ is a compact domain for the decision variables $\mathbf {x}$, $\mathcal {S}(\mathbf {x}) \subseteq \mathbb {R}^K$ is a decision-dependent safety set, $\varvec{\xi }\in \mathbb {R}^K$ is a random variable with distribution $\mathbb {P}^*$, and $\epsilon \in (0,1)$ is the risk tolerance for the random variable $\varvec{\xi }$ falling outside the safety set $\mathcal {S}(\mathbf {x})$.

CCP is one of the most common models to handle uncertainty in optimization. Nevertheless, in practice, the distribution $\mathbb {P}^*$ in the chance constraint in (CCP) is often unavailable to the optimizer. Instead, independent and identically distributed (i.i.d.) samples $\{ \varvec{\xi }_i \}_{i \in [N]}$, where $[N]:=\{1,\ldots ,N\}$, are drawn from $\mathbb {P}^*$, and $\mathbb {P}^*$ is approximated using the empirical distribution $\mathbb {P}_N$ on these samples. Such an approach is known as the sample average approximation (SAA) of (CCP). Note that evaluating $\mathbb {P}^*[\varvec{\xi }\not \in \mathcal {S}(\mathbf {x})]$ exactly is often difficult even when $\mathbb {P}^*$ is available. Consequently, the SAA approach is often employed whenever the computation of $\mathbb {P}^*[\varvec{\xi }\not \in \mathcal {S}(\mathbf {x})]$ is expensive, even if $\mathbb {P}^*$ is available. The SAA formulation of (CCP) is

where $\varvec{1}(\cdot )$ is the indicator function. For certain forms of safety sets $\mathcal {S}(\cdot )$, (SAA) can be reformulated as a mixed-integer program (MIP) and thus off-the-shelf optimization solvers can be used to solve it.

While there are statistical guarantees for using (SAA) to approximate (CCP) [5, 7, 24], the out-of-sample performance of the solution from (SAA) is quite sensitive to the specific sample $\{ \varvec{\xi }_i \}_{i \in [N]}$, and can result in high variance, particularly for small N. In order to remedy this and regularize the out-of-sample performance of (SAA), one can solve a distributionally robust chance-constrained program:

where $\mathcal {F}_N(\theta )$ is an ambiguity set of distributions on $\mathbb {R}^K$ that contains the empirical distribution $\mathbb {P}_N$, and $\theta$ is a parameter that governs the size of the ambiguity set, and thereby the conservatism of (DR-CCP). For a recent comprehensive survey on distributionally robust optimization problems, their properties, and exact and approximate methods to solve them, we refer the reader to Rahimian and Mehrotra [30] and references therein.

Several types of ambiguity sets of probability distributions, such as those based on moments, $\phi$-divergences, unimodality, or support have been studied in the literature; see e.g., [6, 9, 12, 15, 19, 33]. More recently, the Wasserstein ambiguity set, that is, the Wasserstein distance ball of radius $\theta$ around the empirical distribution $\mathbb {P}_N$, is shown to possess particularly attractive statistical properties. The dual representation for the worst-case probability $\mathbb {P}[\varvec{\xi }\not \in \mathcal {S}(\mathbf {x})]$ under the Wasserstein ambiguity set $\mathbb {P}\in \mathcal {F}_N(\theta )$ is given in [4, 10, 27]. Various studies [8, 13, 32] exploit this dual representation to give a deterministic non-convex reformulation of (DR-CCP). See also Hota et al. [13] for reformulations based on the conditional value-at-risk (CVaR) inner approximation of (DR-CCP) for several different types of safety sets.

For common linear forms of safety sets $\mathcal {S}(\cdot )$, Chen et al. [8] and Xie [32] show that (DR-CCP) under Wasserstein ambiguity sets admits a MIP reformulation. Ji and Lejeune [14] also explore MIP formulations of (DR-CCP) under Wasserstein ambiguity. However, they impose additional structure on the support of $\varvec{\xi }$, thus their formulations are different from Chen et al. [8] and Xie [32]. Such MIP reformulations pave the path of using standard optimization solvers to formulate and solve these problems, however, according to [8, 32] these MIP reformulations are difficult to solve in certain cases. Even for relatively small size problems with only a few hundred samples and small radii, the resulting formulations still have a large optimality gap even after an hour of computation time with a commercial solver.

1.1 Contributions

Motivated by these computational challenges, our focus in this paper is on developing effective methods to solve the exact reformulation of (DR-CCP) for such hard cases. In particular, we closely examine the MIP reformulations of (DR-CCP) with random right-hand side uncertainty under Wasserstein ambiguity sets from Chen et al. [8] and Xie [32]. We present theoretical results that have strong computational impact in solving (DR-CCP).

We first exploit the close relationship between (DR-CCP) over Wasserstein ambiguity sets and its nominal counterpart (SAA) to identify an implied mixing set with a cardinality constraint over the existing binary variables in the (DR-CCP) reformulation, which enables the use of existing inequalities for such a set. We use the established technique of quantile strengthening [23, 25] to significantly reduce the big-M constants of this mixing set, and then show how to adapt these to (DR-CCP). Our result also shows that existing mixing inequalities for (SAA) can be readily applied to (DR-CCP).

We further analyze the formulation with reduced coefficients obtained from the quantile strengthening. We exploit the conditional value-at-risk (CVaR) interpretation for (DR-CCP) described by Xie [32] to bound key variables in the formulation. Using these, we show that we can further improve our new formulation for (DR-CCP) by eliminating a significant portion of constraints. Furthermore, the improved bounds we establish on variables allow us to identify a specific substructure in our improved formulation which arises in robust 0–1 programming [2]. Consequently, we show that we can directly use results from Atamtürk [2] to describe a class of valid inequalities for our improved formulation.

We then assess the computational impact of the improved formulation and the new valid inequalities on solving (DR-CCP) on a class of stochastic transportation problems. We observe that the improved formulation uniformly reduces solution times by at least an order of magnitude for any radius, number of original decision variables and number of scenarios. In the difficult small radius regime for $N=100$ scenarios, the original formulation cannot verify optimality within 1 h, whereas our formulation solves within seconds. For the most difficult instances with small Wasserstein radius and $N=3000$ scenarios, the improved formulation results in less than $0.8\%$ average optimality gap, whereas the original formulation cannot even find a feasible solution for any of the tested instances.

To the best of our knowledge, our work is the first that examines these connections between traditional SAA, mixing sets, and robust 0–1 programming in the context of distributionally robust chance constraints, and demonstrates the huge computational effectiveness of these approaches for the difficult instances. It is interesting to note that distributionally robust optimization is a paradigm of modeling uncertainty that does not require a complete knowledge of the distribution as in (SAA), but is also less conservative than robust optimization that considers the worst-case realizations of uncertain parameters, without any knowledge of their joint distribution. Nevertheless, our analysis and computational results show that the formulations for distributionally robust optimization can be significantly improved by employing its connections to both SAA and robust optimization.

1.2 Outline

In Sect. 2, we provide a formal problem description and elaborate on the connections between the existing MIP models for (DR-CCP) and the safety set. In Sect. 3, we explore the connection between (SAA) and (DR-CCP). We describe the mixing structure in (SAA) and demonstrate its application to (DR-CCP). In Sect. 4, we employ the CVaR representation of (DR-CCP) to reveal the substructure from robust 0–1 programming that is hidden in MIP reformulations of (DR-CCP). Using results from Atamtürk [2], we provide valid inequalities resulting from this substructure. In Sect. 5, we report our computational experience with the improved formulation and the proposed inequalities on a class of stochastic transportation problems.

2 Problem formulation

We consider Wasserstein ambiguity sets $\mathcal {F}_N(\theta )$ defined as the $\theta$-radius Wasserstein ball of distributions on $\mathbb {R}^K$ around the empirical distribution $\mathbb {P}_N$. We will use the 1-Wasserstein distance, based on a norm $\Vert \cdot \Vert$, between two distributions $\mathbb {P}$ and $\mathbb {P}'$. This is defined as follows:

$$\begin{aligned} d_W(\mathbb {P},\mathbb {P}') := \inf _{\Pi } \left\{ \mathbb {E}_{(\varvec{\xi },\varvec{\xi }') \sim \Pi }[\Vert \varvec{\xi }- \varvec{\xi }'\Vert ] : \Pi \text { has marginal distributions } \mathbb {P}, \mathbb {P}' \right\} . \end{aligned}$$

Then, the Wasserstein ambiguity set is

$$\begin{aligned} \mathcal {F}_N(\theta ) := \left\{ \mathbb {P}: d_W(\mathbb {P}_N,\mathbb {P}) \le \theta \right\} . \end{aligned}$$

Given a decision $\mathbf {x}\in \mathcal {X}$ and random realization $\varvec{\xi }\in \mathbb {R}^K$, the distance from $\varvec{\xi }$ to the unsafe set is

$$\begin{aligned} {{\,\mathrm{dist}\,}}(\varvec{\xi },\mathcal {S}(\mathbf {x})) := \inf _{\varvec{\xi }' \in \mathbb {R}^K} \left\{ \Vert \varvec{\xi }- \varvec{\xi }'\Vert : \varvec{\xi }' \not \in \mathcal {S}(\mathbf {x}) \right\} . \end{aligned}$$

(1)

Throughout Sects. 2, 3 and 4, we assume that the sample $\{\varvec{\xi }_i\}_{i \in [N]}$, the risk tolerance $\epsilon \in (0,1)$ and the radius $\theta > 0$ are fixed. As short-hand notation, we denote the feasible regions of (SAA) and (DR-CCP) as follows:

$$\begin{aligned} \mathcal {X}_{{{\,\mathrm{SAA}\,}}}(\mathcal {S})&:= \left\{ \mathbf {x}\in \mathcal {X}:~ \frac{1}{N} \sum _{i \in [N]} \varvec{1}(\varvec{\xi }_i \not \in \mathcal {S}(\mathbf {x})) \le \epsilon \right\} , \end{aligned}$$

(2a)

$$\begin{aligned} \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S})&:= \left\{ \mathbf {x}\in \mathcal {X}:~ \sup _{\mathbb {P}\in \mathcal {F}_N(\theta )} \mathbb {P}[\varvec{\xi }\not \in \mathcal {S}(\mathbf {x})] \le \epsilon \right\} . \end{aligned}$$

(2b)

Note that here the dependence on the safety set function $\mathcal {S}$ is made explicit, since the relationship between existing formulations and our new valid inequalities depends on the safety set.

Using tools from duality theory for Wasserstein distributional robustness [4, 10], Chen et al. [8] and Xie [32] give an extended formulation for the distributionally robust chance constraint in (DR-CCP). Specifically, it was shown in [8, Theorem 3] (see also [32, Proposition 1]) that when $\mathcal {S}(\mathbf {x})$ is open for each $\mathbf {x}\in \mathcal {X}$ and $\theta > 0$, we have

$$\begin{aligned} \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S}) = \left\{ \mathbf {x}\in \mathcal {X}: \begin{aligned}&\quad \exists \ t \ge 0, \ \mathbf {r}\ge \varvec{0},\\&\quad {{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i, \ i \in [N],\\&\quad \epsilon \, t \ge \theta + \frac{1}{N} \sum _{i \in [N]} r_i \end{aligned} \right\} . \end{aligned}$$

(3)

(Note that a similar formulation holds when $\theta = 0$, but we need to make the restriction $t > 0$.) Therefore, the ability to model (DR-CCP) depends on the ability to model the constraints ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i$. For a given set $\mathcal {S}(\mathbf {x})$, let ${{\,\mathrm{int}\,}}\mathcal {S}(\mathbf {x})$ denote its interior and ${{\,\mathrm{cl}\,}}\mathcal {S}(\mathbf {x})$ denote its closure. Also, note that Gao and Kleywegt [10, Proposition 3] show

$$\begin{aligned} \sup _{\mathbb {P}\in \mathcal {F}(\theta )} \mathbb {P}[\varvec{\xi }\not \in {{\,\mathrm{int}\,}}\mathcal {S}(\mathbf {x})] = \sup _{\mathbb {P}\in \mathcal {F}(\theta )} \mathbb {P}[\varvec{\xi }\not \in \mathcal {S}(\mathbf {x})] = \sup _{\mathbb {P}\in \mathcal {F}(\theta )} \mathbb {P}[\varvec{\xi }\not \in {{\,\mathrm{cl}\,}}\mathcal {S}(\mathbf {x})], \end{aligned}$$

and ${{\,\mathrm{dist}\,}}(\varvec{\xi }, {{\,\mathrm{int}\,}}\mathcal {S}(\mathbf {x})) = {{\,\mathrm{dist}\,}}(\varvec{\xi }, \mathcal {S}(\mathbf {x})) = {{\,\mathrm{dist}\,}}(\varvec{\xi }, {{\,\mathrm{cl}\,}}\mathcal {S}(\mathbf {x}))$. Therefore, (3) holds regardless of whether $\mathcal {S}(\mathbf {x})$ is open or closed. With this in mind, in what follows, we express $\mathcal {S}(\mathbf {x})$ as an open set, for convenience.

The classical literature on CCP typically considers two types of safety sets which are defined by linear inequalities and are known to admit exact MIP reformulations: individual chance constraints with left-hand side (LHS) uncertainty and joint chance constraints with right-hand side (RHS) uncertainty. In this paper, we consider only joint chance constraints with RHS uncertainty, which have safety set and distance function given by

$$\begin{aligned} \mathcal {S}(\mathbf {x})&:= \left\{ \varvec{\xi }:~ \mathbf {b}_p^\top \varvec{\xi }+ d_p - \mathbf {a}_p^\top \mathbf {x}> 0, \ p \in [P] \right\} , \end{aligned}$$

(4a)

$$\begin{aligned} {{\,\mathrm{dist}\,}}(\varvec{\xi },\mathcal {S}(\mathbf {x}))&= \max \left\{ 0,\ \min _{p \in [P]} \frac{\mathbf {b}_p^\top \varvec{\xi }+ d_p - \mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*} \right\} , \end{aligned}$$

(4b)

for given $\mathbf {a}_p\in \mathbb {R}^K, \mathbf {b}_p\in \mathbb {R}^L$ and $d_p\in \mathbb {R}$ for all $p \in [P]$ where $\Vert \cdot \Vert _*$ is the dual norm. Chen et al. [8, Proposition 2] show that, in this case, (DR-CCP) can be reformulated as

$$\begin{aligned} \min \limits _{\mathbf {z}, \mathbf {r}, t, \mathbf {x}} \quad&\mathbf {c}^\top \mathbf {x} \end{aligned}$$

(5a)

$$\begin{aligned} \text {s.t.}\quad&\mathbf {z}\in \{0,1\}^N,\ t \ge 0, \ \mathbf {r}\ge \varvec{0},\ \mathbf {x}\in \mathcal {X}, \end{aligned}$$

(5b)

$$\begin{aligned}&\epsilon \, t \ge \theta + \frac{1}{N} \sum _{i \in [N]} r_i, \end{aligned}$$

(5c)

$$\begin{aligned}&M (1-z_i) \ge t-r_i, \quad i \in [N], \end{aligned}$$

(5d)

$$\begin{aligned}&\frac{\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*}+ M z_i\ge t-r_i, \quad i \in [N],\ p \in [P], \end{aligned}$$

(5e)

where M is a sufficiently large positive constant. In particular, for joint chance constraints with RHS uncertainty, we have

$$\begin{aligned} \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S}) = \left\{ \mathbf {x}\in \mathcal {X}: \text {(5b)--(5e)} \right\} . \end{aligned}$$

(6)

3 Connection with the nominal chance constraint and mixing sets

Our first idea to strengthen the MIP reformulations of distributionally robust CCPs originates from the following simple observation between the relation of the empirical probability distribution and the Wasserstein ambiguity set.

When the radius $\theta$ of the Wasserstein ambiguity set $\mathcal {F}_N(\theta )$ is 0, (DR-CCP) coincides with (SAA) since $\mathcal {F}_N(0)=\left\{ \mathbb {P}_N\right\}$. In general, as $\mathcal {F}_N(0)\subseteq \mathcal {F}_N(\theta )$ for any $\theta \ge 0$, (SAA) is a relaxation of (DR-CCP), i.e., we have

$$\begin{aligned} \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S}) \subseteq \mathcal {X}_{{{\,\mathrm{SAA}\,}}}(\mathcal {S}). \end{aligned}$$

When the safety set is defined as $\mathcal {S}(\mathbf {x}) = \left\{ \varvec{\xi }:~ s(\mathbf {x},\varvec{\xi }) \ge 0\right\}$ for a continuous function $s(\cdot )$, Ruszczyński [31] shows that (SAA) can be reformulated as the following MIP:

$$\begin{aligned} \min \limits _{\mathbf {z}, \mathbf {r}, t, \mathbf {x}} \quad&\mathbf {c}^\top \mathbf {x} \end{aligned}$$

(7a)

$$\begin{aligned} \text {s.t.}\quad&\mathbf {z}\in \{0,1\}^N,\ \mathbf {x}\in \mathcal {X}, \end{aligned}$$

(7b)

$$\begin{aligned}&\sum _{i\in [N]} z_i \le \lfloor \epsilon N\rfloor , \end{aligned}$$

(7c)

$$\begin{aligned}&s(\mathbf {x},\varvec{\xi }_i) + M z_i \ge 0, \quad i \in [N], \end{aligned}$$

(7d)

where M is a sufficiently large positive constant. Inequalities (7c) and (7d) are often referred to as the knapsack (or cardinality) constraint and the big-M constraints, respectively. Then, when the safety set $\mathcal {S}(\mathbf {x})$ is given by $\mathcal {S}(\mathbf {x}) = \left\{ \varvec{\xi }:~ s(\mathbf {x},\varvec{\xi }) > 0\right\}$, (7) provides a relaxation of (DR-CCP). Therefore, by solving (7), one can provide a lower bound on the optimum value of (DR-CCP). Note that the safety set (4) can be written in this form by defining $s(\cdot )$ appropriately.

The formulation (7) for (SAA) is well-studied in the literature, and many classes of valid inequalities for the formulation have been developed; see e.g., [1, 16, 17, 20, 22, 23, 25, 34, 35]. In fact, we develop a more direct connection between formulation (7) and (DR-CCP) so that we can apply techniques for solving (7) directly to (DR-CCP). It is clear that inequalities of the form (7c)–(7d) can be added to the MIP formulation (5) of (DR-CCP) to obtain a stronger formulation. In turn, this implies that the reformulation can be further strengthened by the inequalities developed for strengthening (7). If we do this naïvely, we would add (7c)–(7d) to (5) with new binary variables $\mathbf {z}' \in \{0,1\}^N$. Our first key result is that the same binary variables $\mathbf {z}$ from the MIP formulation (5) can be used to define (7c)–(7d). This then means that we can strengthen these formulations without adding any additional binary variables.

3.1 Strengthening the formulation by the nominal chance constraint

We now verify that the SAA inequalities for the joint chance constraint of (2b) can be used to strengthen the formulation (5). Given $\mathcal {S}(\mathbf {x})$ defined by (4), consider the following MIP formulation

$$\begin{aligned} \min \limits _{\mathbf {x},\mathbf {z}, \mathbf {r}, t} \quad&\mathbf {c}^\top \mathbf {x} \end{aligned}$$

(8a)

$$\begin{aligned} \text {s.t.}\quad&(\mathbf {z},\mathbf {r},t,\mathbf {x})\ \text {satisfies} \ (5b)\text {--}(5e), \end{aligned}$$

(8b)

$$\begin{aligned}&\sum _{i\in [N]} z_i \le \lfloor \epsilon N \rfloor , \end{aligned}$$

(8c)

$$\begin{aligned}&\frac{\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*}+ M z_i\ge 0, \quad i \in [N],\ p \in [P], \end{aligned}$$

(8d)

where M is a sufficiently large positive constant. (Note that in this formulation, the inequality (8c) is equivalent to (7c).) We can write constraints (8d) in the form (7d): individually $s_p(\mathbf {x},\varvec{\xi }_i) := \frac{\mathbf {b}_p^\top \varvec{\xi }_i + d_p -\mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*}$ or jointly $s(\mathbf {x},\varvec{\xi }) := \min \nolimits _{p\in [P]}\left\{ \frac{\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*}\right\}$. More importantly, (8c) and (8d) share the same set of binary variables as the other constraints in (5). We next argue that this MIP formulation (8) is an exact reformulation of (DR-CCP) with a safety set $\mathcal {S}(\mathbf {x})$ from (4).

Theorem 1

When the safety set $\mathcal {S}$ is defined as in (4), formulation (8) is an exact reformulation of (DR-CCP), i.e.,

$$\begin{aligned} \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S}) = \left\{ \mathbf {x}\in \mathcal {X}: \text {(8b)--(8d)} \right\} . \end{aligned}$$

(9)

Proof

By (6), it is sufficient to show that

$$\begin{aligned} \left\{ \mathbf {x}\in \mathcal {X}: \text {(5b)--(5e)} \right\} =\left\{ \mathbf {x}\in \mathcal {X}: \text {(8b)--(8d)} \right\} . \end{aligned}$$

By (8b), we know that the set on the right-hand side is contained in the set on the left-hand side. Let us show that the reverse direction also holds. To this end, take a vector $\mathbf {x}\in \mathcal {X}$ satisfying (5b)–(5e) with some $\mathbf {z},\mathbf {r},t$. For ease of notation, we define $s(\mathbf {x},\varvec{\xi }_i):=\min \nolimits _{p\in [P]}\left\{ \frac{\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*}\right\}$. We claim that $(\mathbf {x},{\bar{\mathbf {z}}},\mathbf {r},t)$ satisfies (8b)–(8d) where ${\bar{\mathbf {z}}}\in \{0,1\}^N$ is a vector such that ${\bar{z}}_i=1$ if and only if $s(\mathbf {x},\varvec{\xi }_i)<0$ for all $i\in [N]$. Since M is sufficiently large so that $s(\mathbf {x},\varvec{\xi }_i)+M\ge 0$, it is clear that $\mathbf {x},{\bar{\mathbf {z}}}$ satisfy (8d). Next, we observe that $(\mathbf {x},{\bar{\mathbf {z}}},\mathbf {r},t)$ satisfies (5d) and (5e), which can be equivalently rewritten as

$$\begin{aligned} \min \left\{ s(\mathbf {x},\varvec{\xi }_i)+Mz_i,\, M(1-z_i)\right\} \ge t-r_i, \quad i \in [N]. \end{aligned}$$

By the choice of ${\bar{\mathbf {z}}}$ and M, we have $\min \left\{ s(\mathbf {x},\varvec{\xi }_i)+M{\bar{z}}_i,\, M(1-{\bar{z}}_i)\right\}$ is equal to 0 if $s(\mathbf {x},\varvec{\xi }_i)<0$, and it is equal to $s(\mathbf {x},\varvec{\xi }_i)$ otherwise. Hence,

$$\begin{aligned} \min \left\{ s(\mathbf {x},\varvec{\xi }_i)+M{\bar{z}}_i,\, M(1-{\bar{z}}_i)\right\} \ge \min \left\{ s(\mathbf {x},\varvec{\xi }_i)+Mz_i,\, M(1-z_i)\right\} \end{aligned}$$

for any $z_i\in \{0,1\}$. This implies that $(\mathbf {x},{\bar{\mathbf {z}}},\mathbf {r},t)$ satisfies (5d) and (5e) as they are satisfied already by $(\mathbf {x},\mathbf {z},\mathbf {r},t)$. To finish the proof, it remains to show that ${\bar{\mathbf {z}}}$ satisfies (8c). Since $\theta >0$, we obtain from (5c) that $t>0$. This implies that $\frac{r_i}{t}\ge 0$. We claim that $\frac{r_i}{t}\ge {\bar{z}}_i$ for all $i\in [N]$. As $\frac{r_i}{t}\ge 0$, we have $\frac{r_i}{t}\ge {\bar{z}}_i$ holds when ${\bar{z}}_i=0$. When ${\bar{z}}_i=1$, by rearranging (5d) we get $\frac{r_i}{t}\ge 1={\bar{z}}_i$. Since $\frac{r_i}{t}\ge {\bar{z}}_i$ for all $i\in [N]$, it follows from (5c) that $\epsilon N\ge \sum _{i\in [N]}\frac{r_i}{t}\ge \sum _{i\in [N]}{\bar{z}}_i$, implying in turn that $\sum _{i\in [N]}{\bar{z}}_i\le \lfloor \epsilon N\rfloor$, as required. $\square$

Remark 1

Chen et al. [8] argue that there is a finite value of M for the validity of (5). Essentially, we need to choose an appropriate value of M so that (5d)–(5e) correctly represent the constraint ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i$. When $\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}<0$ for some $p\in [P]$, we have ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))=0$ by (4) and thus ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i$ becomes $0\ge t-r_i$. As long as $\frac{\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*} + M\ge 0$ holds for all $\mathbf {x}\in \mathcal {X}$, (5d)–(5e) can capture this situation by setting $z_i=1$. Similarly, (5d)–(5e) can represent the case when $\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}\ge 0$ for all $p\in [P]$ if $M\ge \mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}$ for all $\mathbf {x}\in \mathcal {X}$, $p\in [P]$. So, setting

$$\begin{aligned} M:=\max _{\mathbf {x}\in \mathcal {X},\ p\in [P]}\left\{ \frac{\left| \mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}\right| }{\Vert \mathbf {b}_p \Vert _*}\right\} \end{aligned}$$

(10)

ensures that the constraints (8d) are indeed valid. $\square$

3.2 Mixing substructure

Although (8) is already stronger than (5) due to the additional constraints (8d)–(8c), we can further strengthen this formulation by adding more valid inequalities originating from these constraints. To this end, for any fixed p, the constraints (8d)–(8c) give rise to the following substructure:

$$\begin{aligned} Q_p:=\left\{ (\mathbf {x},\mathbf {z})\in \mathcal {X}\times \{0,1\}^N : \begin{aligned} \&s_p(\mathbf {x},\varvec{\xi }_i) + M z_i \ge 0, \quad i \in [N],\\&\sum _{i\in [N]} z_i \le \lfloor \epsilon N\rfloor \end{aligned} \right\} . \end{aligned}$$

(11)

So, one can generate valid inequalities for the formulation (8) by finding inequalities of the form $\varvec{\mu }^\top \mathbf {x}+ \varvec{\pi }^\top \mathbf {z}\ge \beta$ that are valid for the mixed-integer set $Q_p$ in (11). Luedtke et al. [25] and Luedtke [23] introduce a procedure of generating inequalities that are valid for $Q_p$. In order to make our paper self-contained, we next explain this procedure.

Given a fixed linear function $\varvec{\mu }^\top \mathbf {x}$, we solve the following single scenario subproblem for each scenario $i\in [N]$

$$\begin{aligned} {\bar{h}}_i(\varvec{\mu }):=\min \left\{ \varvec{\mu }^\top \mathbf {x}:\ s_p(\mathbf {x},\varvec{\xi }_i)\ge 0, \ \mathbf {x}\in {\bar{\mathcal {X}}}\right\} , \end{aligned}$$

(12)

where $\mathcal {X}\subseteq {\bar{\mathcal {X}}} \subseteq \mathbb {R}^L$. Then $\varvec{\mu }^\top \mathbf {x}\ge {\bar{h}}_i(\varvec{\mu })$ holds for $(\mathbf {x},\mathbf {z})\in Q_p$ with $z_i=0$. Having computed the values ${\bar{h}}_i(\varvec{\mu })$ for $i\in [N]$, we sort them in non-decreasing order. Without loss of generality, we may assume that

$$\begin{aligned} {\bar{h}}_N(\varvec{\mu })\ge {\bar{h}}_{N-1}(\varvec{\mu })\ge \cdots \ge \bar{h}_1(\varvec{\mu }). \end{aligned}$$

For ease of notation, let

$$\begin{aligned} k:=\lfloor \epsilon N\rfloor . \end{aligned}$$

Notice that because $\sum _{i\in [N]} z_i \le k$ is also enforced in $Q_{p}$, by the pigeonhole principle there must exist $i \in \{N-k,N-k+1,\ldots ,N\}$ with $z_i=0$. In turn, this implies that $\varvec{\mu }^\top \mathbf {x}\ge {\bar{h}}_{N-k}(\varvec{\mu })$ because ${\bar{h}}_i(\varvec{\mu })\ge {\bar{h}}_{N-k}(\varvec{\mu })$ for all $i\ge N-k$. In summary, we have just argued that $\varvec{\mu }^\top \mathbf {x}\ge {\bar{h}}_i(\varvec{\mu })$ holds if $z_i=0$ and that $\varvec{\mu }^\top \mathbf {x}\ge {\bar{h}}_{N-k}(\varvec{\mu })$ is satisfied always, in particular, when $z_i=1$ for $i\in [N]$. Equivalently,

$$\begin{aligned} \varvec{\mu }^\top \mathbf {x}+ \left( {\bar{h}}_i(\varvec{\mu })-\bar{h}_{N-k}(\varvec{\mu })\right) z_i\ge {\bar{h}}_i(\varvec{\mu }) \end{aligned}$$

(13)

is valid. In fact, inequalities (13) for $i\le N-k$ are redundant because $\varvec{\mu }^\top \mathbf {x}\ge {\bar{h}}_i(\varvec{\mu })$ is implied by $\varvec{\mu }^\top \mathbf {x}\ge {\bar{h}}_{N-k}(\varvec{\mu })$ if $i\le N-k$. Because inequalities (13) share a common linear function $\varvec{\mu }^\top \mathbf {x}$ but each one has a distinct integer variable, the mixing procedure of  Günlük and Pochet [11], can be applied to obtain stronger inequalities. For any $J=\{j_1,\ldots ,j_\ell \}$ with $N\ge j_1\ge \cdots \ge j_\ell \ge N-k+1$, the mixing inequality derived from J and (13) is

$$\begin{aligned} \varvec{\mu }^\top \mathbf {x}+ \sum _{i\in [\ell ]}\left( {\bar{h}}_{j_i}(\varvec{\mu })-\bar{h}_{j_{i+1}}(\varvec{\mu })\right) z_{j_i}\ge \bar{h}_{j_1}(\varvec{\mu }), \end{aligned}$$

(14)

where $j_{\ell +1}:=N-k$. The mixing inequalities of the form (14) are equivalent to the star inequalities by Atamtürk et al. [3]. The inequalities (14) are the strongest possible ones that can be generated from (13) in that the convex hull of solutions $(\mathbf {x},\mathbf {z})\in \mathbb {R}^L\times \{0,1\}^N$ satisfying (13) is described by (14) [3, 11, 16].

Consider any $p\in [P]$. For $s_p(\mathbf {x},\varvec{\xi }_i) := \frac{1}{\Vert \mathbf {b}_p \Vert _*}\left( \mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}\right)$ as in (8), we can take $-\frac{1}{\Vert \mathbf {b}_p \Vert _*}\mathbf {a}_p$ for $\varvec{\mu }$. For this choice of $\varvec{\mu }$, the value of ${\bar{h}}_i(\varvec{\mu })$ from the single scenario subproblem (12) with ${\bar{\mathcal {X}}}=\mathbb {R}^L$ is precisely

$$\begin{aligned} \min _x\left\{ -\frac{\mathbf {a}^\top _p}{\Vert \mathbf {b}_p \Vert _*}\mathbf {x}:\ \frac{1}{\Vert \mathbf {b}_p \Vert _*}\left( \mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}\right) \ge 0\right\} =-\frac{\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p}{\Vert \mathbf {b}_p \Vert _*}. \end{aligned}$$

So, assuming $-\mathbf {b}^\top _p {\varvec{\xi }}_N\ge \cdots \ge -\mathbf {b}^\top _p {\varvec{\xi }}_1$ and letting

$$\begin{aligned} q_p:=-\mathbf {b}_p^\top \varvec{\xi }_{N-k} \end{aligned}$$

($q_p$ is the $(k+1)$-th largest value), the inequalities $\varvec{\mu }^\top \mathbf {x}\ge \bar{h}_{N-k}(\varvec{\mu })$ and (13) for $\varvec{\mu }=-\frac{1}{\Vert \mathbf {b}_p \Vert _*}\mathbf {a}_p$ correspond to

$$\begin{aligned}&\displaystyle \frac{-q_p + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*} \ge 0,&\end{aligned}$$

(15a)

$$\begin{aligned}&\displaystyle \frac{\mathbf {b}^\top _p \varvec{\xi }_i + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*} + \frac{-\mathbf {b}^\top _p {\varvec{\xi }}_i-q_p}{\Vert \mathbf {b}_p \Vert _*}z_i \ge 0,&i\in [N]. \end{aligned}$$

(15b)

Moreover, the mixing inequalities (14) obtained from (13) have the following form:

$$\begin{aligned} \frac{\mathbf {b}^\top _p {\varvec{\xi }}_{j_1} + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*} + \sum _{i\in [\ell ]}\frac{-\mathbf {b}^\top _p {\varvec{\xi }}_{j_i} + \mathbf {b}^\top _p {\varvec{\xi }}_{j_{i+1}}}{\Vert \mathbf {b}_p \Vert _*} z_{j_i} \ge 0 \end{aligned}$$

(16)

where $N\ge j_1\ge \cdots \ge j_\ell \ge N-k+1$ and $j_{\ell +1}:=N-k$.

The number of mixing inequalities (16) is exponential, but they can be separated in $O(N\log N)$ time [11, 16].

Notice that the inequalities (13)–(16) are big-M-free; the coefficients of the binary variables and the right-hand sides depend only on $s_p(\mathbf {x},\varvec{\xi }_i)$. This is important for practical purposes. In particular, when M is larger than $\frac{-\mathbf {b}^\top _p {\varvec{\xi }}_i -q_p}{\Vert \mathbf {b}_p \Vert _*}$, the constraints (8d) are dominated by the inequalities (15b), and thus, by (16).

3.3 Reducing big-M values

In Sect. 3.2, we argued that letting $q_p$ be the $(k+1)$-th largest value amongst $\{-\mathbf {b}_p^\top \varvec{\xi }_i\}_{i \in [N]}$, the inequalities (15) are valid for (8), and based on this we generate the mixing inequalities (16). In fact, we can replace the big-M in (5e) with its strengthened version from (15b) to obtain a new formulation:

$$\begin{aligned} \min \limits _{\mathbf {z}, \mathbf {r}, t, \mathbf {x}} \quad&\mathbf {c}^\top \mathbf {x}\end{aligned}$$

(17a)

$$\begin{aligned} \text {s.t.}\quad&(\mathbf {z},\mathbf {r},t,\mathbf {x})\ \text {satisfies} \ (5b)\text {--}(5d)\ \text {and} \ (5c),\end{aligned}$$

(17b)

$$\begin{aligned}&\frac{\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*}+ \frac{-\mathbf {b}^\top _p {\varvec{\xi }}_i - q_p}{\Vert \mathbf {b}_p \Vert _*} z_i\ge t-r_i, \quad i \in [N],\ p \in [P]. \end{aligned}$$

(17c)

Theorem 2

Formulation (17) is an exact reformulation of (DR-CCP) where the safety set is given by (4).

Proof

By Theorem 1, (5) with (8c) is an exact reformulation. Hence, we need to argue that reducing the big-M value in (5e) to obtain (17c) keeps the formulation valid. To this end, it suffices to argue that constraints (5d) and (17c) correctly represent ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i$ for $i\in [N]$. Let $i\in [N]$. If $\min \nolimits _{p \in [P]} \left\{ \frac{\mathbf {b}_p^\top \varvec{\xi }_i + d_p - \mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*}\right\} \ge 0$, we can set $z_i=0$ and we obtain ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))=\min \nolimits _{p \in [P]} \left\{ \frac{\mathbf {b}_p^\top \varvec{\xi }_i + d_p - \mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*}\right\}$. In this case, (5d) becomes redundant and (17c) represents ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i$. On the other hand, if we set $z_i = 1$, then (5d) is $0 \ge t - r_i$ and (17c) becomes redundant. However, ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i$ is less restrictive on $(\mathbf {x},\mathbf {r},t)$ than $0 \ge t-r_i$, so at optimality, there is at least one solution such that $z_i = 0$ whenever $\min \nolimits _{p \in [P]} \left\{ \frac{\mathbf {b}_p^\top \varvec{\xi }_i + d_p - \mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*}\right\} \ge 0$, hence ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i$ is correctly represented.

If $\min \nolimits _{p \in [P]} \left\{ \frac{\mathbf {b}_p^\top \varvec{\xi }_i + d_p - \mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*}\right\} <0$, then ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))=0$ and we must have $z_i=1$ by (15b). Since $z_i=1$, (17c) and (5d) respectively become

$$\begin{aligned} t - r_i&\le \frac{\mathbf {b}_p^\top \varvec{\xi }_i + d_p - \mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*}+ \frac{-\mathbf {b}^\top _p {\varvec{\xi }}_i -q_p}{\Vert \mathbf {b}_p \Vert _*}=\frac{-q_p + d_p - \mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*} \\ t - r_i&\le 0. \end{aligned}$$

By (15a) we know that $\frac{-q_p + d_p - \mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*} \ge 0$ so the first inequality is weaker than the second, hence we have ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))=0 \ge t-r_i$ as required. $\square$

In contrast to (5e), the inequality (17c) is big-M-free. During our computational study summarized in Sect. 5, we observed that the coefficients of the variables $\mathbf {z}$ in (17c) are significantly smaller than the big-M value computed from Remark 1.

4 Improved formulation and valid inequalities from robust 0–1 programming

In this section, we study, in closer detail, the set of constraints from (17c). By appealing to the conditional value-at-risk interpretation for (DR-CCP), we prove a bound on t. Consequently, we uncover another hidden structure related to robust 0–1 programming with a budget uncertainty set. This allows us to derive a new class of valid inequalities.

For a given $p\in [P]$, recall the definition of $q_p$ being the $(k+1)$-th largest value amongst $\left\{ -\mathbf {b}_p^\top \varvec{\xi }_i\right\} _{i \in [N]}$ where $k:= \lfloor \epsilon N \rfloor$. We also define $h_{i,p} := \frac{-\mathbf {b}_p^\top \varvec{\xi }_i -q_p}{\Vert \mathbf {b}_p\Vert _*}$ and $u_p := \frac{-q_p+d_p-\mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*} - t$. The constraints (17c) can be cast as the mixed-integer set

$$\begin{aligned} R_p :=\left\{ (u_p,\mathbf {r},\mathbf {z}) \in \mathbb {R}\times \mathbb {R}_+^N \times \{0,1\}^N: \ u_p + r_i \ge h_{i,p} (1-z_i),\ i \in [N]\right\} . \end{aligned}$$

In fact, a similar mixed-integer set has been studied in the context of robust 0–1 programming by Atamtürk [2]:

$$\begin{aligned} R^+ := \left\{ (u,\mathbf {r},\mathbf {z})\in \mathbb {R}_+\times \mathbb {R}_+^N \times \{0,1\}^N: \ u + r_i \ge h_i (1-z_i),\ i \in [N] \right\} , \end{aligned}$$

where $h_1,\ldots , h_N$ are assumed to all be positive. The main difference between $R_p$ and $R^+$ is that $u_p$ is unrestricted in $R_p$ but is non-negative in $R^+$, and some $h_{i,p}$ may be negative or zero in $R_p$, but all $h_i$ are positive in $R^+$. We refer to the set $R^+$ as the robust 0–1 set, since it originates from the robust counterpart of a 0–1 program whose objective vector belongs to a “budget uncertainty set”. In Atamtürk [2], the binary variables in $R^+$ correspond to the original decision variables of the 0–1 program.

The fact that $R_p$ is so similar to $R^+$ may seem surprising at first, yet is less so if we consider the conditional value-at-risk (CVaR) interpretation for the Wasserstein robust chance constraint. More precisely, Xie [32, Corollary 1] gives the following alternate version of (3):

$$\begin{aligned} \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S})&= \left\{ \mathbf {x}\in \mathcal {X}:~ \frac{\theta }{\epsilon } + {{\,\mathrm{CVaR}\,}}_{1-\epsilon }\left( -{{\,\mathrm{dist}\,}}(\varvec{\xi },\mathcal {S}(\mathbf {x}));\mathbb {P}_N \right) \le 0 \right\} \end{aligned}$$

(18a)

$$\begin{aligned}&= \left\{ \mathbf {x}\in \mathcal {X}:~ \frac{\theta }{\epsilon } + \max _{y \in B} \frac{1}{\epsilon N} \sum _{i \in [N]} (-{{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))) y_i \le 0 \right\} \end{aligned}$$

(18b)

$$\begin{aligned} \text {where }&{{\,\mathrm{CVaR}\,}}_{1-\epsilon }(v(\varvec{\xi });\mathbb {P}_N) := \min _t \left\{ t + \frac{1}{\epsilon N} \sum _{i \in [N]} \max \{0,v(\varvec{\xi }_i) - t\} \right\} , \end{aligned}$$

(18c)

$$\begin{aligned}&B := \left\{ \mathbf {y}:~ \frac{1}{N} \sum _{i \in [N]} y_i = \epsilon , \ \varvec{0} \le \mathbf {y}\le \varvec{1} \right\} . \end{aligned}$$

(18d)

Note that (18b) comes from the dual interpretation of the CVaR, see e.g., [28, (3)]. In particular, B has exactly the same structure as the budget uncertainty set studied in Atamtürk [2].

We now further exploit the CVaR interpretation (18a) of (3) so that we can cast $R_p$ exactly in the same form as $R^+$. Specifically, we show that $u_p \ge 0$ is a valid inequality for (17), which will then allow us to eliminate constraints with negative $h_{i,p}$. Consequently, this allows us to directly apply the valid inequalities derived for $R^+$ from Atamtürk [2] to $R_p$. We first provide a bound on the value of the t-variable in (3) (which then translates to a bound on the t-variables for all subsequent formulations).

Lemma 1

Let $k:=\lfloor \epsilon N \rfloor$ and fix any $\mathbf {x}\in \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S})$. Then there exists $(\mathbf {r},t)$ such that t is equal to the $(k+1)$-th smallest value amongst $\{{{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))\}_{i \in [N]}$ and the constraints of (3) are satisfied.

Proof

Recall that the CVaR of a random variable $v(\varvec{\xi })$ from (18c), where $\varvec{\xi }\sim \mathbb {P}_N$, has two equivalent primal and dual optimization representations:

$$\begin{aligned} {{\,\mathrm{CVaR}\,}}_{1-\epsilon }(v(\varvec{\xi });\mathbb {P}_N)&= \max _{y \in B} \frac{1}{\epsilon N} \sum _{i \in [N]} v(\varvec{\xi }_i) y_i \end{aligned}$$

(19a)

$$\begin{aligned}&= \min _{\mathbf {r},t'} \left\{ t' + \frac{1}{\epsilon N} \sum _{i \in [N]} r_i : r_i \ge v(\varvec{\xi }_i) - t', i \in [N], \mathbf {r}\ge {\mathbf {0}} \right\} , \end{aligned}$$

(19b)

where B is defined in (18d). Without loss of generality, assume that we have an ordering $v(\varvec{\xi }_1) \ge \dots \ge v(\varvec{\xi }_N)$. It is easy to check that a primal-dual optimal pair for (19) is given by

$$\begin{aligned} y_i&= {\left\{ \begin{array}{ll} 1, &{}i=1,\ldots ,k\\ \epsilon N - k, &{}i=k+1\\ 0, &{}i > k+1 \end{array}\right. }\\ t'&= v(\varvec{\xi }_{k+1})\\ r_i&= \max \left\{ 0, v(\varvec{\xi }_i) - t'\right\} , \end{aligned}$$

as $\mathbf {y}\in B$ and $\mathbf {r}\ge \varvec{0}$, and

$$\begin{aligned} \frac{1}{\epsilon N} \sum _{i \in [N]} v(\varvec{\xi }_i) y_i = t' + \frac{1}{\epsilon N} \sum _{i \in [N]} r_i. \end{aligned}$$

Now take $v(\varvec{\xi }_i) = -{{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))$ for each $i \in [N]$, and recall that we assume $v(\varvec{\xi }_1)=-{{\,\mathrm{dist}\,}}(\varvec{\xi }_1,\mathcal {S}(\mathbf {x})) \ge \cdots \ge v(\varvec{\xi }_N)=-{{\,\mathrm{dist}\,}}(\varvec{\xi }_N,\mathcal {S}(\mathbf {x}))$. Let $(\mathbf {r},t')$ be the optimal solution to the CVaR formulation (19b) specified above with $t' = v(\varvec{\xi }_{k+1}) = -{{\,\mathrm{dist}\,}}(\varvec{\xi }_{k+1},\mathcal {S}(\mathbf {x}))$, $r_i=\max \{0, v(\varvec{\xi }_i) - t'\}$ for all $i \in [N]$. Since $\mathbf {x}\in \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S})$, we know from (18a) that

$$\begin{aligned} \frac{\theta }{\epsilon } + {{\,\mathrm{CVaR}\,}}_{1-\epsilon }\left( -{{\,\mathrm{dist}\,}}(\varvec{\xi },\mathcal {S}(\mathbf {x}));\mathbb {P}_N \right) \le 0 \implies \theta + \frac{1}{N} \sum _{i \in [N]} r_i \le -\epsilon t'. \end{aligned}$$

Now take $t = -t' = {{\,\mathrm{dist}\,}}(\varvec{\xi }_{k+1},\mathcal {S}(\mathbf {x})) \ge 0$, and notice that $r_i = \max \left\{ 0, v(\varvec{\xi }_i) - t'\right\} = \max \left\{ 0, t - {{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))\right\}$ for all $i \in [N]$, so the constraints in (3) are satisfied. $\square$

The main result for this section is to show that $u_p \ge 0$ is valid for (17) for each $p \in [P]$.

Proposition 1

Suppose that $\theta > 0$. Consider an arbitrary $\mathbf {x}\in \mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S})$. There exists $(\mathbf {r},t,\mathbf {z})$ such that $(\mathbf {x},\mathbf {r},t,\mathbf {z})$ satisfies (17b)–(17c) and that for every $p \in [P]$,

$$\begin{aligned} u_p= \frac{-q_p+d_p-\mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*} - t \ge 0. \end{aligned}$$

Proof

For convenience, for each $p \in [P]$, denote $g_{i,p}(\mathbf {x}) := \frac{\mathbf {b}_p^\top \varvec{\xi }_i+d_p-\mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*}$ and $g_p^*(\mathbf {x}) := \frac{-q_p+d_p-\mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*}$. With these definitions, the distance function from (4) is

$$\begin{aligned} {{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) = \max \left\{ 0, \min _{p \in [P]} g_{i,p}(\mathbf {x}) \right\} . \end{aligned}$$

Without loss of generality, assume that ${{\,\mathrm{dist}\,}}(\varvec{\xi }_1,\mathcal {S}(\mathbf {x})) \le \cdots \le {{\,\mathrm{dist}\,}}(\varvec{\xi }_N,\mathcal {S}(\mathbf {x}))$, and denote $d^*(\mathbf {x}) := {{\,\mathrm{dist}\,}}(\varvec{\xi }_{k+1},\mathcal {S}(\mathbf {x}))$ to be the $(k+1)$-smallest distance value.

By Lemma 1, take $(\mathbf {r},t)$ to be a solution that satisfies $t = d^*(\mathbf {x})$, $r_i = \max \left\{ 0, t - {{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \right\}$, and set $z_i = 1$ when $\min _{p \in [P]} g_{i,p}(\mathbf {x}) < 0$, otherwise $z_i = 0$ for each $i \in [N]$. It is straightforward to check that $(\mathbf {x},\mathbf {r},t,\mathbf {z})$ satisfies (17b), so we focus on (17c). If $z_i = 0$, then since ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) \ge t - r_i$ and ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))=\min _{p \in [P]} g_{i,p}(\mathbf {x})$, (17c) holds. If $z_i=1$, then ${{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))=0$, and $r_i=t$, so $t-r_i=0$, hence (17c) reduces to (15a).

It remains to show that for every $p \in [P]$, $0\le u_p=g_p^*(x)-t=g_p^*(x)-d^*(x)$, i.e., $d^*(\mathbf {x}) \le g_p^*(\mathbf {x})$ holds. Note that by definition of $-q_p$, $g_p^*$ is the $(k+1)$-th smallest value amongst $\{g_{i,p}(\mathbf {x})\}_{i \in [N]}$. Focusing on the definition of $d^*(\mathbf {x}) := {{\,\mathrm{dist}\,}}(\varvec{\xi }_{k+1},\mathcal {S}(\mathbf {x}))$, we consider two cases.

If $\min _{p \in [P]} g_{k+1,p}(\mathbf {x}) \le 0$, then $d^*(\mathbf {x}) = t = 0$. But, then we cannot have $\epsilon t \ge \theta + \frac{1}{N} \sum _{i \in [N]} r_i$, since $\theta > 0$ and $\mathbf {r}\ge {\mathbf {0}}$. Thus, we cannot have $\min _{p \in [P]} g_{k+1,p}(\mathbf {x}) \le 0$.

Now consider $\min _{p \in [P]} g_{k+1,p}(\mathbf {x}) > 0$. Then, for any $i \ge k+1$ and $p \in [P]$, we have

$$\begin{aligned} 0 < \min _{p \in [P]} g_{k+1,p}(\mathbf {x}) =d^*(\mathbf {x}) \le {{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x})) = \min _{p' \in [P]} g_{i,p'}(\mathbf {x}) \le g_{i,p}(\mathbf {x}), \end{aligned}$$

where the second inequality follows from the fact that $i\ge k+1$ and the assumption that ${{\,\mathrm{dist}\,}}(\varvec{\xi }_1,\mathcal {S}(\mathbf {x})) \le \cdots \le {{\,\mathrm{dist}\,}}(\varvec{\xi }_N,\mathcal {S}(\mathbf {x}))$, and the last equation follows from the fact that $0 < {{\,\mathrm{dist}\,}}(\varvec{\xi }_i,\mathcal {S}(\mathbf {x}))$. Based on this relation, then there are at least $N-k$ indices i such that $g_{i,p}(\mathbf {x}) \ge d^*(\mathbf {x})$, and thus we must have $g_p^*(\mathbf {x}) \ge d^*(\mathbf {x})$. This completes the proof. $\square$

We can now explicitly impose the constraint $u_p \ge 0$ into the formulation for (DR-CCP). When we do this, the constraint $u_p + r_i \ge h_{i,p} (1-z_i)$ corresponding to any indices i, p such that $h_{i,p} \le 0$ becomes redundant since the left-hand side of this constraint is non-negative, and its right-hand side is non-positive. Based on this, in our improved formulation, we define the following index sets:

$$\begin{aligned} {[}N]_p := \left\{ i \in [N] : -\mathbf {b}_p^\top \varvec{\xi }_i > q_p \right\} , \quad p \in [P]. \end{aligned}$$

Then, $h_{i,p} > 0$ if and only if $i \in [N]_p$. Our proposed formulation is as follows:

$$\begin{aligned} \min \limits _{\mathbf {z}, \mathbf {r}, t, \mathbf {x}} \quad&\mathbf {c}^\top \mathbf {x}\end{aligned}$$

(20a)

$$\begin{aligned} \text {s.t.}\quad&(\mathbf {z},\mathbf {r},t,\mathbf {x})\ \text {satisfies} \ (5b)\text {--}(5d)\ \text {and} \ (8c), \end{aligned}$$

(20b)

$$\begin{aligned}&\frac{\mathbf {b}^\top _p {\varvec{\xi }}_i + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*}+ \frac{-\mathbf {b}^\top _p {\varvec{\xi }}_i - q_p}{\Vert \mathbf {b}_p \Vert _*} z_i\ge t-r_i, \quad i \in [N]_p,\ p \in [P], \end{aligned}$$

(20c)

$$\begin{aligned}&\frac{-q_p + d_p -\mathbf {a}^\top _p \mathbf {x}}{\Vert \mathbf {b}_p \Vert _*} \ge t, \quad p \in [P]. \end{aligned}$$

(20d)

Theorem 3

Formulation (20) is an exact reformulation of (DR-CCP) where the safety set is given by (4).

Proof

The correctness of (20) follows from the above discussion. $\square$

Remark 2

The size of each index set $[N]_p$ is at most $k = \lfloor \epsilon N \rfloor$, so (20) reduces the number of constraints of (17) by at least $((1-\epsilon ) N - 1) P$. This is particularly significant when $\epsilon$ is small (e.g., 0.1) and N, P are large. $\square$

Note that similar bounding and scenario elimination strategies using the VaR interpretation are shown to be effective in multivariate CVaR-constrained optimization and risk-averse Markov decision processes [18, 21, 26, 29].

Importantly, via the constraints (20c) and (20d), we can re-define the mixed-integer set $R_p$ to have the exact same structure as $R^+$:

$$\begin{aligned} R_p :=\left\{ (u_p,\mathbf {r},\mathbf {z})\in \mathbb {R}_+ \times \mathbb {R}_+^N \times \{0,1\}^N:\ u_p + r_i \ge h_{i,p} (1-z_i),\ i \in [N]_p\right\} , \end{aligned}$$

where it is understood that $u_p = \frac{-q_p+d_p-\mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*} - t$. Atamtürk [2, Theorem 1] proposes a class of valid inequalities for $R^+$, which we adapt to obtain valid inequalities for $R_p$. To do this, we let $N_p$ be the size of each $[N]_p$ and define an ordering $[N]_p = \left\{ (j,p) \in \mathbb {N}: j \in [N_p] \right\}$ as follows:

$$\begin{aligned} h_{(N_p,p),p} \ge \cdots \ge h_{(1,p),p}. \end{aligned}$$

Proposition 2

For any $p \in [P]$ and $J=\{j_1,\ldots , j_m\}$ satisfying $m \ge 1$, $N_p \ge j_1\ge \cdots \ge j_m\ge 1$, the following inequality is valid for (20):

$$\begin{aligned} \frac{-q_p+d_p-\mathbf {a}_p^\top \mathbf {x}}{\Vert \mathbf {b}_p\Vert _*} - t + \sum _{i\in [m]}r_{(j_i,p)} \ge \sum _{i\in [m]} (h_{(j_i,p),p}-h_{(j_{i+1},p),p})(1-z_{(j_i,p)}) \end{aligned}$$

(21)

where $h_{(j_{m+1},p),p}:=0$.

Proof

This follows immediately from Atamtürk [2, Theorem 1]. $\square$

We refer to the inequalities (21) as the path inequalities.

Remark 3

Atamtürk [2] gives an $O(N_p^2) = O(\lfloor \epsilon N\rfloor ^2)$-time separation algorithm for (21), which is based on finding a shortest path in an acyclic graph. Atamtürk [2, Theorems 1 and 2] also proves that inequalities (21) are sufficient to describe the convex hull of $R^+$ and are facet-defining. $\square$

5 Computational study

In this section, we assess the numerical performance of our improved formulation (20) of (DR-CCP) and valid inequalities from Sects. 3 and 4.

All experiments are conducted on an Intel Core i5 3GHz processor with 6 cores and 32GB memory. Each experiment was in single-core mode, and five experiments were run in parallel. For each model, we set the CPLEX time limit to be 3600 s.

CPLEX 12.9 is used as the MIP solver. Valid inequalities from Sects. 3 and 4 are separated and added via the CPLEX user-cut callback feature. Since using a user-cut callback function is known to affect various internal CPLEX dynamics (such as dynamic search, aggressiveness of CPLEX presolve and cut generation procedures, etc.), in order to do a fair comparison, we include an empty user-cut callback function (that does not separate any user cuts) whenever we test a formulation which does not employ cuts, e.g., basic formulation from the literature, i.e., from  Chen et al. [8]. We have also conducted tests under the default CPLEX settings without the empty user cut callback to confirm that our overall conclusions do not change under the default settings. Our preliminary tests indicated that separating a large number of inequalities throughout the branch-and-cut tree slows down the search process, so we separate our inequalities only at the root node.

The maximum value of $\theta$ at which (DR-CCP) is feasible can be computed by solving a variant of (5), that is, with the same set of constraints (5b)–(5e) but treating $\theta$ as a variable to be maximized. We first describe our test instances in Sect. 5.1 and then discuss the performance of our proposed approaches in Sect. 5.2.

5.1 Test instances

We consider the distributionally robust chance-constrained formulation of a transportation problem from Chen et al. [8]. This is the problem of transshipping a single good from a set of factories [F] to a set of distribution centers [D] to meet their demands while minimizing the transportation cost. Each factory $f\in [F]$ has an individual production capacity $m_f$, each distribution center $d\in [D]$ faces a random demand $\xi _d$ from the end customers, and transshipping one unit of the good from factory f to distribution center incurs a cost $c_{fd}$. Given N samples $\left\{ \varvec{\xi }_i=(\xi _{id})_{d\in [D]}: i\in [N] \right\}$ of $\varvec{\xi }$, this problem is given by

$$\begin{aligned} \min \quad&\mathbf {c}^\top \mathbf {x} \end{aligned}$$

(22a)

$$\begin{aligned} \text {s.t.} \quad&\mathbb {P}\left[ \sum \limits _{f\in [F]} x_{fd} \ge {\xi }_d,\quad \forall d \in [D] \right] \ge 1-\epsilon , \quad \mathbb {P}\in \mathcal {F}(\theta ), \end{aligned}$$

(22b)

$$\begin{aligned}&\sum \limits _{d\in [D]} x_{fd} \le m_f, \quad f \in [F], \end{aligned}$$

(22c)

$$\begin{aligned}&x_{fd} \ge 0, \quad f \in [F],\ d\in [D]. \end{aligned}$$

(22d)

Here, (22b) is a joint chance constraint with right-hand side uncertainty, so (22) can be reformulated as in (5).

We use the same random instance generation scheme from Chen et al [8]. We generate instances with $F\in \{5,10\}$ factories and $D\in \{50,100\}$ distribution centers whose locations are chosen uniformly at random from the Euclidean plane $[0,10]^2$. We set the transportation cost $c_{fd}$ to the Euclidean distance between factory $f\in [F]$ and distribution center $d\in [D]$. We obtain the scenarios by sampling for the demand vector $\varvec{\xi }$ from a uniform distribution supported on $\left[ 0.8\varvec{\mu }, 1.2\varvec{\mu }\right]$, where the expected demand $\mu _d$ of any distribution center $d\in [D]$ is chosen uniformly at random from [0, 10]. The capacity $m_f$ of each factory $f\in [F]$ is drawn uniformly from [0, 1] at first, but the capacities are scaled later so that the total capacity $\sum _{f\in [F]}m_f$ equals $\frac{3}{2}\max _{i\in [N]}\left\{ \sum _{d\in [D]}\xi _{id}\right\}$. For each instance, we test ten different values $\theta _1<\cdots <\theta _{10}$ for the Wasserstein radius. As in Chen et al.[8], we set $\theta _1=0.001$. For the other values, we compute the maximum value $\theta _{\max }$ of $\theta$ such that (5) is feasible and set $\theta _j=\frac{j-1}{10}\theta _{\max }$ for $j=2,\ldots , 10$. We have empirically found that the value $\theta _{\max }$ is between 0.1 and 0.35 for our instances, so $\theta _2$ is between 0.01 and 0.035 and thus greater than $\theta _1=0.001$. We fix the risk tolerance $\epsilon$ to be 0.1. Lastly, we select M to be

$$\begin{aligned} M:=\max \left\{ \sum _{f\in [F]}m_f-\min _{i\in [N],d\in [D]}\left\{ \xi _{id}\right\} ,\ \max _{i\in [N],d\in [D]}\left\{ \xi _{id}\right\} \right\} , \end{aligned}$$

(23)

which is sufficiently large (see Remark 1). For each problem parameter combination, we generate 10 random instances and report the average statistics.

As noted in Chen et al. [8], there is no need to specify which norm $\Vert \cdot \Vert$ to use in (5) and (8) when reformulating (22) because the random right-hand side inside (22b) contains a single random variable with coefficient 1 so that all $\Vert \mathbf {b}_p\Vert _*$ in (5) and (8) equal 1 in the instances generated.

5.2 Performance analysis

In this section, we summarize our experiments with radius $\theta = \theta _1,\dots ,\theta _{10}$ and the number of samples $N=100, {1000}, 3000$. We compare the following five formulations:

Basic::

the basic formulation (5) given by Chen et al. [8] with the big-M value computed as in Remark 1,

Improved::

the improved formulation (20),

Mixing::

the improved formulation (20) with the mixing inequalities (16),

Path::

the improved formulation (20) with the path inequalities (21), and

Mixing+Path::

the improved formulation (20) with both mixing (16) and path inequalities (21).

In Tables 1 and 3, the following statistics are reported:

Time(Gap)::

the average solution time (in seconds measured externally from CPLEX by C++) of the instances that were solved to optimality, and, in parentheses, the average of the final optimality gap of the instances that were not solved to optimality within the CPLEX time limit. The optimality gap is computed as $(UB-LB)/LB*100$ where UB and LB respectively are the objective values of the best feasible solution and the best lower bound value at the corresponding time of the solution process. A ‘*’ in a Time or Gap entry indicates that either no instance was solved to optimality or all instances were solved to optimality within the CPLEX time limit so that there were no instances for measuring the corresponding statistic.

We also report in this column the number of instances solved to optimality within the CPLEX time limit, s, and the number of instances for which a feasible solution was found f. Since for most cases, we observed that $s=f=10$, we add [s/f] in front of the Time(Gap) statistic only when $s<10$ or $f < 10$.

A ‘n/a’ entry for the Time(Gap) statistic denotes when no feasible solution was found in any of the 10 instances.

Cuts::

the average number of cuts added for Mixing, Path, and Mixing+Path. For Mixing+Path, the ‘Cuts’ are broken down into the number of mixing inequalities and the number of path inequalities added respectively.

In Tables 2 and 4, the following statistics are reported:

R.time::

the average time spent (in seconds measured externally from CPLEX by C++) at the root node of the branch-and-bound tree over all instances. A ‘n/a’ entry indicates that no feasible solution was found in any of the 10 instances within the CPLEX time limit.

R.gap::

the final optimality gap at the root node of the branch-and-bound tree. A ‘n/a’ entry indicates that no solution was found in any of the 10 instances within the CPLEX time limit.

The results in all tables highlight that when the radius $\theta$ is small, the resulting problems are much harder to solve. This was also reported in Chen et al. [8].

When $N=100$, $F=5, D=50$, and $\theta =\theta _1$, Table 1 shows that Basic does not finish within the CPLEX time limit of 3600 s for any of the 10 randomly generated instances and terminates with a 1.16% optimality gap, on average. In contrast, Improved solves all instances to optimality in under 5 s on average. In fact, Improved is so effective that it does not leave much room for improvement for the additional valid inequalities in Mixing, Path and Mixing+Path, and the separation of the valid inequalities results in a slight increase in the solution time in most cases. Nevertheless, the latter three formulations solve all instances to optimality in under 9 s on average. When $\theta \ge \theta _2$, Basic solves all instances to optimality in under 27 s on average, but all other formulations solve in under 0.06 s on average. In “Appendix 1”, we provide supplementary results that show that the mixing and path inequalities are very effective when added to Basic, but Improved without any valid inequalities performs better than Basic with these inequalities.

To test the scalability of our proposed approaches with respect to the number of scenarios, in Table 1, we also report the performance of the five formulations on instances with $N=1000$ and $N=3000$, respectively for $F=5, D=50$. In the out-of-sample tests for these instances reported in [8], for $N=1000$, the authors state the difficulty of solving the problem to proven optimality and report their results with a not necessarily optimal solution obtained after a couple of minutes of computing. Our results in Table 1 show that our proposed formulation provides provably optimal solutions within less than a minute in all instances but those with $\theta _1$. Furthermore, as indicated in Table 1, we can scale up the number of scenarios even further. In the experiments with $N=3000$, we observe that even for the largest value of $\theta _{10}$, Basic was unable to solve any of the ten instances within the CPLEX time limit, while all of the new formulations Improved, Mixing, Path and Mixing+Path solved all instances to optimality for $\theta \ge \theta _3$ with an average time of at most 20 s. For $\theta \le \theta _2$, our new formulations did not manage to solve any instances to optimality, but did reduce the average optimality gap to at most 0.8%. In contrast, Basic failed to solve all instances for $\theta \le \theta _2$, and in fact did not even find a feasible solution within the time limit for many instances. For the instances where a feasible solution was found, the gap remained quite large at $\approx 70\%$ at termination.

Table 1 Results for $F=5$, $D=50$, $\epsilon =0.1$

Table 2 Results at root node for $F=5$, $D=50$, $\epsilon =0.1$

Table 3 Results for $F=10$, $D=100$, $\epsilon =0.1$

Table 4 Results at root node for $F=10$, $D=100$, $\epsilon =0.1$

We also test the scalability of various methods with respect to the number of original decision variables in the original problem. To this end, we let $F=10, D=100$ and report our results in Table 3 for $N=100,1000,3000$. (Note that an increase in D implies an increase in the dimension of the random data, which may in turn require an increase in sample size to ensure the same out-of-sample performance.) Comparing Tables 1 and 3, we see that not surprisingly, the problems with a larger number of original decision variables are harder to solve. Fewer instances can be solved to optimality with Basic. In fact, Basic cannot even obtain a feasible solution after an hour of computing for instances with $F=10, D=100, N=3000.$ In contrast, Improved solves all instances to optimality in less than a minute except for the ones with $\theta _1$ when $N=100,1000$ and with $\theta \le \theta _5$ in the case of $N=3000$. Indeed, we observe a very slight increase in solution times for our proposed formulations in the case of $F=10, D=100$ in contrast to $F=5, D=50$, and all trends reported for $F=5, D=50$ remain the same in the case of $F=10, D=100.$

Tables 1 and 3 also give us insight into the marginal effect of each class of inequalities. We observe that mixing inequalities are only generated for $\theta =\theta _1$ (plus a total of 3 inequalities across all instances when $\theta =\theta _2$ and $N=100$). When the radius of the Wasserstein ball is small, the nominal region $\mathcal {X}_{{{\,\mathrm{SAA}\,}}}(\mathcal {S})$ is a better approximation for the distributionally robust region $\mathcal {X}_{{{\,\mathrm{DR}\,}}}(\mathcal {S})$. Since mixing inequalities are valid for $\mathcal {X}_{{{\,\mathrm{SAA}\,}}}(\mathcal {S})$, it is expected that they have stronger effects as for smaller radius $\theta$, thus the observed behavior is not surprising. As mentioned above, when $N=100$, the Improved formulation is already so effective that separating inequalities slightly increases solution times. However, when $N=3000$, $F=5$ and $D=50$, from Table 1, we see that while Improved is still quite effective, and manages to reduce the gap to $0.78\%$ for $\theta =\theta _1$, separating the valid inequalities reduces this further ($0.52\%$ for Mixing, $0.62\%$ for Path, and $0.48\%$ for Mixing+Path). We see a similar phenomenon for $\theta = \theta _2$, but only path inequalities are separated. Similar observations can be made for $N=3000$, $F=10$, $D=100$.

Tables 2 and 4 provide further information on the performance of the formulations at the root node of the branch-and-bound tree. From Table 2, we see that the root gap of the new formulations Improved, Mixing, Path and Mixing+Path are at most $0.8\%$ on average for the most difficult regime $\theta =\theta _1,\theta _2$ and $N=3000$. This is significantly better than the root gap of Basic. In fact, in our experiments, we have observed that for these types of distributionally robust CCPs, the branch-and-bound process is very ineffective in terms of reducing the remaining gap, with only a small difference between root gap and final gap. This also highlights the importance of starting off with very strong formulations. In fact, we observed that for $\theta \ge \theta _2$, the gap threshold of $0.01\%$ is achieved at the root node for our improved formulations.

6 Conclusion

This paper studies in detail the formulation for distributionally robust chance-constrained programs under Wasserstein ambiguity, focusing on the case of linear safety sets with right-hand side uncertainty. We reveal a hidden connection with nominal chance-constraints, and provide a class of valid inequalities which are exactly the mixing inequalities for the nominal chance constraint. We also adapt the quantile strengthening technique to the distributionally robust setting, making one set of constraints (5e) in the original MIP formulation (5) big-M-free. We then exploit the CVaR interpretation of the distributionally robust constraint (18a) to provide an improved formulation (20) with significantly fewer constraints. Finally, we uncover a mixed-integer substructure which has been studied in the context of robust 0–1 programming Atamtürk [2], and provide second class of valid inequalities based on this connection.

Our computational results demonstrate the benefit of our improved formulation and valid inequalities. Solution times are drastically reduced and larger problems can now be solved in seconds, e.g., problems with thousands of scenarios (rather than hundreds).

Supplementary Numerical Results

In Table 5 we report the performance of the basic formulation (5) when combined with mixing (16) and path inequalities (21) for $F=5$, $D=50$, $\epsilon =0.1$. These results highlight that mixing and path inequalities are indeed useful when applied to the basic formulation, without all the other enhancements we propose.

Table 5 Supplementary results for $F=5$, $D=50$, $\epsilon =0.1$

We see that for $N=100$, Basic+Mixing+Path solves all instances (and with slightly quicker times on average) whereas Basic in Table 1 does not manage to solve any instances for $\theta _1$. For $N=1000$, we again see an improvement in the number of instances solved when using the inequalities, but for larger $\theta _8,\theta _9,\theta _{10}$, times are slightly slower. We believe this is due to the extra time required to solve the larger LP relaxations as a result of adding cuts. For $N=3000$, we now see that Basic+Mixing+Path is unable to find a feasible integer solution within 1 h for a larger number of instances than Basic (we again believe this is due to larger LP relaxations), but whenever it does, it often solves to optimality, which Basic never does.

In contrast to Improved, there are more cuts generated for Basic for all $\theta$ values. Nevertheless, as expected, the performance achieved by Basic+Mixing+Path is still worse than the performance of our improved formulation (20), with or without inequalities.