Numerical solution of the space-time fractional diffusion equation based on fractional reproducing kernel collocation method

Abstract

This paper present an effective numerical approach for solving a class of space-time fractional diffusion equations. By discretizing the time-fractional derivative, the original problem is transformed to a semi-discrete problem, which was solved by using the fractional reproducing kernel collocation method (FRKCM). Additionally, the stability and convergence analysis are given and some numerical examples demonstrate the feasibility and reliability of the method.

1 Introduction

This paper focus on the numerical solution of the space-time fractional diffusion equation

$$\begin{aligned} {^{C}_{0}D_{t}^{\alpha }}u(x,t)=a(x,t){^{C}_{0}D_{x}^{\beta }}u(x,t)+f(x,t),\qquad x\in (0,1),\ t\in (0,T] \end{aligned}$$

(1.1)

with the initial condition

$$\begin{aligned} u(x,0)=g(x),\qquad x\in (0,1) \end{aligned}$$

(1.2)

and the boundary conditions

$$\begin{aligned} u(0,t)=0,u(1,t)=l(t),\qquad t\in (0,T] \end{aligned}$$

(1.3)

where $0<\alpha <1$ and $1<\beta <2$, a(x, t) is a nonngeative function, f(x, t) is the source term, u(x, t) is the unknown function. ${^C_0D_t^\alpha }u(x,t)$ is the left Caputo time-fractional derivative of order $\alpha$ defined as

$$\begin{aligned} {^C_0D_t^\alpha }u(x,t)= \dfrac{1}{\Gamma (1-\alpha )}\int _{0}^{t}(t-\xi )^{-\alpha }\dfrac{\partial u(x,\xi )}{\partial \xi }\textrm{d}\xi ,\quad 0<\alpha <1. \end{aligned}$$

And ${^{C}_{0}D_{x}^{\beta }}u(x,t)$ is the left Caputo space-fractional derivatives of order $\beta$ defined as

$$\begin{aligned} {^{C}_{0}D_{x}^{\beta }}u(x,t)= \dfrac{1}{\Gamma (2-\beta )}\int _{0}^{x}(x-\eta )^{1-\beta }\dfrac{\partial ^2 u(\eta ,t)}{\partial \eta ^2}\textrm{d}\eta ,\quad 1<\beta <2. \end{aligned}$$

Fractional diffusion equations were introduced to describe anomalous diffusion phenomena in the transport process of a complex or disordered system [1,2,3,4,5,6,7]. For flow in porous media, fractional space derivative models large motions through highly conductive layers or fractures, while fractional time derivative describes particles that remain motionless for extended periods of time [4].

Recently the reaction-diffusion equation, also called the parabolic equation as a standard and classical partial differential equation attracted much attention with the research interests in the well-posedness of solution [8,9,10,11,12,13,14], especially for the model with Caputo time-fractional derivative [9]. The authors [15] introduced a new hybrid scheme based on a finite difference method and Chebyshev collocation method for solving the space-time fractional advection–diffusion equation and the corresponding convergence and stability are investigated. Baseri et al. [16] employed the shifted Chebyshev and rational Chebyshev polynomials to obtain the approximate solution of (1.1). In [17], the authors discussed such equation based on normalized Bernstein polynomials. Feng et al. [18] applied the finite element method to obtain a numerical solution of the space-time fractional diffusion equation.

Over the past 30 years, the numerical analysis theory of reproducing kernel has been widely used in solving various differential equations [19,20,21,22,23,24,25,26,27]. The reproducing kernel particle methods was proposed in 1995 by Liu et al. [28] as an extension to the method Smooth Particle Hydrodynamics. Mahdavi et al. applied the gradient reproducing kernel in conjunction with the collocation method to solve 2nd- and 4th-order equations [29]. In solving fractional differential equations, the approximate solution given by fractional reproducing kernel method is more accurate than the traditional integer-order reproducing kernel method [30]. Therefore, it is crucial to seek efficient numerical algorithms for solving fractional-order problems. Chen et al. [31] firstly constructed a new fractional weighted reproducing kernel space and presented the exact representation of the reproducing kernel function. In 2021, the authors presented a new numerical method to solve a class of fractional differential equations using the fractional reproducing kernel method [32] which can lessen computation costs and provide highly precise approximate solutions.

In this paper, a new numerical algorithm is proposed to solve the space-time fractional diffusion equation. First, the time-fractional derivative is discretized by L1 scheme, which is a classical time-fractional derivative discretization method and widely used in many literatures [33,34,35,36]. When the time-fractional derivative is approximately discretized by difference, the information of the solution at all past time points is considered, which ensures the stability of the discretization. After the above treatment, the space-time fractional problem (1.1)–(1.3) is transformed into a semi-discrete problem that only contains the spatial fractional derivative. Then the fractional reproducing kernel collocation method is proposed to solve the semi-discrete problem. According to the order of the space-fractional derivatives, a fractional reproducing kernel function space is selected. We calculate the reproducing kernel function and its fractional derivative. To obtain the approximate solution of the semi-discrete problem, a set of fractional basis is constructed by using reproducing kernel and polynomial functions. Compared with the traditional practice of using integer-order polynomials as the basis, the use of fractional-order polynomial basis is more effective for fractional partial differential equation. Next, under three different types of collocation points, the undetermined coefficients in the approximate solution are solved by the collocation method. Compared with the traditional reproducing kernel method, FRCKM avoids the Schmidt orthogonalization processing. Finally, the uniform convergence, stability and error estimation of the approximate solution are analyzed. In addition, global error estimation and stability analysis are carried out for the semi-discrete iterative scheme which is obtained after the difference approximation of the time-fractional derivative. Some numerical examples indicate the universality and flexibility of the method by selecting multiple types of collocation points.

The remaining sections are organized as follows. Section 2 investigated a new numerical method to solve (1.1)–(1.3). In Sect. 3, stability and convergence analysis are surveyed. Numerical examples are shown in Sect. 4 to demonstrate the efficiency and accuracy. Section 5 ends the paper with a brief conclusion.

2 Numerical method

In this section, we will study the construction process of numerical method to solve the problem (1.1)–(1.3).

2.1 Construction of the basis

First, we adopted the L1 scheme that is described in [36] to approximate the time-fractional derivative.

Let $t_{n}=n\Delta t,\ n=0,1,...,N,\$ and$\ \Delta t=\frac{T}{N}$ is the time step, then

$$\begin{aligned} {^C_0D_t^\alpha }u\left( x,t_{n}\right)= & {} \frac{1}{\Gamma (1-\alpha )}\displaystyle \int _{0}^{t_n}\left( t_n-\xi \right) ^{-\alpha }\dfrac{\partial u(x,\xi )}{\partial \xi }\textrm{d}\xi \nonumber \\= & {} \frac{1}{\Gamma (1-\alpha )}\sum _{j=0}^{n-1}\int _{t_j}^{t_{j+1}}\left( t_n-\xi \right) ^{-\alpha }\dfrac{\partial u(x,\xi )}{\partial \xi }\textrm{d}\xi , \end{aligned}$$

(2.1)

And using $\dfrac{u(x,t_{j+1})-u(x,t_j)}{\Delta t}$ approximation for $\dfrac{\partial u(x,\xi )}{\partial \xi }$ in (2.1). Explicitly, the L1 approximation for the time fractional derivative of order $\alpha$ with respect to time at $t=t_n$ is given by

$$\begin{aligned} \begin{aligned}&{^C_0D_t^\alpha }u\left( x,t_{n}\right) \\&\quad =\frac{1}{\Gamma (1-\alpha )}\sum _{j=0}^{n-1}\displaystyle \int _{t_j}^{t_{j+1}}\left( t_n-\xi \right) ^{-\alpha }\frac{u\left( x,t_{j+1}\right) -u\left( x,t_j\right) }{\Delta t}\textrm{d}\xi +R_{n,u}\\&\quad =\frac{1}{\Gamma (2-\alpha )\Delta t^{\alpha }}\sum _{j=0}^{n-1}\left[ u\left( x,t_{j+1}\right) -u\left( x,t_j\right) \right] \left[ (n-j)^{1-\alpha }-(n-j-1)^{1-\alpha }\right] +R_{n,u}\\&\quad =\frac{1}{\Gamma (2-\alpha )\Delta t^{\alpha }}\sum _{j=0}^{n-1}b_{n-j-1} \left[ u\left( x,t_{j+1}\right) -u\left( x,t_j\right) \right] +R_{n,u}\\&\quad =\frac{1}{\alpha _0}\left[ b_{0}u\left( x,t_{n}\right) -b_{n-1}u(x,0)-\sum _{j=1}^{n-1}\left( b_{j-1}-b_j\right) u\left( x,t_{n-j}\right) \right] +R_{n,u}, \end{aligned} \end{aligned}$$

(2.2)

where $\alpha _{0}=\Gamma (2-\alpha )\Delta t^{\alpha }$, $b_{j}=(j+1)^{1-\alpha }-j^{1-\alpha }$ and $R_{n,u}$ is the truncation error.

It is easy to verify the following properties for the coefficients $b_{j}$

$$\begin{aligned} \left\{ \begin{aligned}&b_{j}>0, j=0,1,...,n,\\&1=b_{0}>b_{1}>\cdots >b_{n},\quad b_{n}\longrightarrow 0, n\longrightarrow \infty ,\\&\sum _{j=1}^{n-1}\left( b_{j-1}-b_{j}\right) +b_{n-1}=1. \end{aligned} \right. \end{aligned}$$

(2.3)

Denote $u^n(x)$ is approximate solution of $u(x,t_n)$, the semi-discrete form of (1.1) at points $\left\{ {t_{n}}\right\} _{n=0}^{N}$ is given by

$$\begin{aligned}{} & {} u^n(x)-\alpha _{0}a\left( x,t_n\right) {_0^CD_{x}^\beta }u^n(x)=b_{n-1}u^0(x)\nonumber \\{} & {} \quad +\sum _{j=1}^{n-1}\left( b_{j-1}-b_{j}\right) u^{n-j}(x)+\alpha _{0}f\left( x,t_n\right) . \end{aligned}$$

(2.4)

The boundary conditions (1.3) can be discretized as follows

$$\begin{aligned} u^n(0)=0,\ u^n(1)=l\left( t_n\right) . \end{aligned}$$

(2.5)

Here, we introduce briefly some necessary knowledges of reproducing kernel which will be used throughout the later work.

Definition 2.1

([31]) The reproducing kernel space $W_2^1[0,1]$ is defined by

$$\begin{aligned} W_{2}^{1}[0,1]=\left\{ u(x)\arrowvert u(x)\ is\ absolute\ continuous\ function\ on\ [0,1],\ u'(x)\in L^{2}[0,1]\right\} , \end{aligned}$$

and endowed with the inner product and norm respectively

$$\begin{aligned} \langle u,v\rangle _{W_2^1}= & {} u(0)v(0)+\int _{0}^{1}u'(x)v'(x)\textrm{d}x,\ u,v\in W_{2}^{1}[0,1],\\{} & {} \quad \Vert u\Vert _{W_2^1}=\sqrt{\langle u,u \rangle _{W_2^1} }. \end{aligned}$$

Definition 2.2

([31]) The fractional reproducing kernel space $W_2^\beta [0,1]$ is defined by

$$\begin{aligned} W_{2}^{\beta }[0,1]=\left\{ u(x)\arrowvert {_0^CD_x^\beta } u(x)\in W_{2}^{1}[0,1],u^{(i)}(0)=0,i=0,1\right\} , \end{aligned}$$

(2.6)

and endowed with the inner product and norm respectively

$$\begin{aligned} \langle u,v\rangle _{\beta }= & {} \left<{_0^CD_x^\beta }u,{_0^CD_x^\beta }v\right>_{W_2^1} ={_0^CD_x^\beta }u(0){_0^CD_x^\beta }v(0)\\{} & {} +\int _{0}^{1}\left( {_0^CD_x^\beta }u\right) '(s)\left( {_0^CD_x^\beta }v\right) '(s)\textrm{d}s,\ u,v\in W_{2}^{\beta }[0,1], \\ \Vert u\Vert _{\beta }= & {} \sqrt{\langle u,u \rangle _{\beta } }=\sqrt{\left<{_0^CD_x^\beta }u,{_0^CD_x^\beta }u\right>_{W_2^1}}. \end{aligned}$$

Lemma 2.1

([31]) The expression of the reproducing kernel function of $W_{2}^{\beta }[0,1]$ is

$$\begin{aligned} K(x,y)=\frac{x^{\beta }y^{\beta }}{\Gamma ^{2}(\beta +1)}+\frac{1}{\Gamma ^{2}(\beta +1)}\left\{ \begin{aligned} \int _{0}^{x}(x-s)^{\beta }(y-s)^{\beta }\textrm{d}s,\ x\le y,\\ \int _{0}^{y}(x-s)^{\beta }(y-s)^{\beta }\textrm{d}s,\ x> y. \end{aligned} \right. \end{aligned}$$

(2.7)

with the corresponding left Caputo fractional derivative

$$\begin{aligned} {_0^CD_x^\beta }K(x,y)=\frac{y^{\beta }}{\Gamma (\beta +1)}+\frac{y^{\beta +1}}{\Gamma (\beta +2)}-\left\{ \begin{array}{ll} \frac{(y-x)^{\beta +1}}{\Gamma (\beta +2)},&{}\quad x\le y,\\ 0,&{}\quad x> y. \end{array} \right. \end{aligned}$$

(2.8)

Now, based on the reproducing kernel K(x, y) in fractional reproducing kernel space $W_{2}^{\beta }[0,1]$, the approximate solution of (2.4)–(2.5) can be constructed.

Theorem 2.1

Suppose $\left\{ x_{i}\right\} _{i=1}^{M}$ is a dense subset in [0, 1], then $\left\{ 1,x^{2},K(x,x_{i}) \right\} _{i=1}^{M}$ are linearly independent on $W_2^\beta [0,1]$.

Proof

Assume that there exits constants $\left\{ \mu _i\right\} _{i=1}^{M+2}$ such that

$$\begin{aligned} \mu _1+\mu _2x^2+\sum _{i=1}^{M}\mu _{i+2}K(x,x_i)=0. \end{aligned}$$

(2.9)

Taking $h_k(x)\in W_2^\beta [0,1]$ such that

$$\begin{aligned} h_k^{(3)}(x_j)=\left\{ \begin{aligned}&0,\quad k\ne j,\\&1,\quad k= j. \end{aligned} \right. \end{aligned}$$

Then we have the third order derivative of (2.9) with respect to x

$$\begin{aligned} \sum _{i=1}^{M}\mu _{i+2}K^{(3)}(x,x_i)=0, \end{aligned}$$

and

$$\begin{aligned} \sum _{i=1}^{M}\mu _{i+2}\left\langle K^{(3)}(x,x_i),h_k{(x)}\right\rangle _\beta =\langle 0,h_k(x)\rangle _\beta =0. \end{aligned}$$

Since $\left\langle K^{(3)}(x,x_i),h_k{(x)}\right\rangle _\beta =h_k^{(3)}(x_i)$, we see

$$\begin{aligned} \mu _{i+2}=0,i=1,2,\ldots ,M, \end{aligned}$$

then

$$\begin{aligned} \mu _1+\mu _2x^2=0, \end{aligned}$$

which means that $\mu _1=\mu _2=0$, and completes the proof. $\square$

Define the approximate solution space

$$\begin{aligned} S_{M+2}=\textrm{span}\left\{ 1,x^{2},K(x,x_{1}),K(x,x_{2}),\ldots ,K(x,x_{M}) \right\} . \end{aligned}$$

Apparently, the number of basis functions in the space $S_{M+2}$ is $M+2$, and $S_{M+2}$ is a subspace of $W_2^\beta [0,1].$

2.2 Approximate method

Define a linear operator $L:W_{2}^{\beta }[0,1]\longrightarrow W_{2}^{1}[0,1]$ as follows

$$\begin{aligned} \begin{aligned}&Lu^n(x):=\frac{1}{\alpha _{0}}\left( b_{0}u^n(x)-b_{n-1}u^0(x)-\sum _{j=1}^{n-1}(b_{j-1}-b_{j})u^{n-j}(x)\right) \\&-a(x,t_n){_0^CD_x^\beta }u^n(x)=f(x,t_n). \end{aligned} \end{aligned}$$

(2.10)

Lemma 2.2

$L:W_{2}^{\beta }[0,1]\longrightarrow W_{2}^{1}[0,1]$ is a bounded linear operator.

Proof

In view of the definition of L, it is obvious that L is a linear operator.

According to reproducing property of K(x, y), we have

$$\begin{aligned} \begin{aligned} u^n(x)&=\left\langle u^n(\cdot ),K(x,\cdot )\right\rangle _{\beta },\\ \partial _{x}Lu^n(x)&=\left\langle u^n(\cdot ),\partial _{x}LK(x,\cdot )\right\rangle _{\beta }. \end{aligned} \end{aligned}$$

By virtue of the Cauchy-Schwarz inequality, we obtain

$$\begin{aligned} \left| \partial _{x}Lu^n(x)\right| =\left| \left\langle u^n(\cdot ),\partial _{x}LK(x,\cdot )\right\rangle _{\beta }\ \right| \le \left\| u^n(x)\right\| _{\beta }\cdot \left\| \partial _{x}LK\right\| _{\beta }\le M_{1}\left\| u^n(x)\right\| _{\beta }, \end{aligned}$$

where $\partial _{x}LK$ is continuous on [0, 1], and its norm is bounded.

Then

$$\begin{aligned} \begin{aligned} \left\| Lu^n(x)\right\| _{W_2^1}^{2}&=\left\langle Lu^n(x),Lu^n(x)\right\rangle _{W_2^1}\\&=\left( Lu^n(0)\right) ^2+\int _{0}^{1}\left( \partial _{x}Lu^n(x)\right) ^{2}\textrm{d}x\\&\le \int _{0}^{1}M_{1}^{2}\left\| u^n(x)\right\| _{\beta }^{2}\textrm{d}x\\&=M\left\| u^n(x)\right\| _{\beta }^{2}. \end{aligned} \end{aligned}$$

The proof is completed. $\square$

Next, we set the process of solving the semi-discrete problem (2.4)–(2.5) by using the presented FRKCM. We find the approximate solution of problem (2.4)–(2.5)

$$\begin{aligned} \begin{aligned}&u^n_{m}(x)=a_{1}+a_{2}x^{2}+\sum _{i=1}^{M}a_{i+2}K(x,x_{i})=a_{1}+a_{2}x^{2}+\sum _{i=1}^{M}a_{i+2}\\&\quad \left\{ \begin{aligned}&\frac{x^{\beta }x_i^{\beta }}{\Gamma ^{2}(\beta +1)}+\frac{1}{\Gamma ^{2}(\beta +1)}\int _{0}^{x}(x-s)^{\beta }(x_i-s)^{\beta }\textrm{d}s,\ x\le x_i,\\&\frac{x^{\beta }x_i^{\beta }}{\Gamma ^{2}(\beta +1)}+\frac{1}{\Gamma ^{2}(\beta +1)}\int _{0}^{x_i}(x-s)^{\beta }(x_i-s)^{\beta }\textrm{d}s,\ x> x_i. \end{aligned} \right. \end{aligned} \end{aligned}$$

(2.11)

such that the collocation equations

$$\begin{aligned}&Lu^n_{m}(x_k)=a_{1}L1+a_{2}Lx_{k}^{2}+\sum _{i=1}^{M}a_{i+2}LK\left( x_{k},x_{i}\right) =f\left( x_{k},t_n\right) ,\ k=1,\ldots ,M,\end{aligned}$$

(2.12)

$$\begin{aligned}&u^n_{m}(0)=a_{1}+\sum _{i=1}^{M}a_{i+2}K\left( 0,x_{i}\right) =0,\end{aligned}$$

(2.13)

$$\begin{aligned}&u^n_{m}(1)=a_{1}+a_{2}+\sum _{i=1}^{M}a_{i+2}K\left( 1,x_{i}\right) =l(t_n), \end{aligned}$$

(2.14)

where $\left\{ x_{k}\right\} _{k=1}^{M}\in [0,1]$ are collocation points as following.

In the numerical process later, we will choose three different collocation points

(2.15)

(2.16)

(2.17)

As the undetermined coefficients $\left\{ a_{i}\right\} _{i=1}^{M+2}$ can be obtained by solving (2.12)–(2.14), the approximate solution $u^n_{m}(x)$ is determined. Therefore, the algorithm for solving the space-time fractional diffusion problem (1.1)–(1.3) can be divided into the following two steps. First, we discretized the time-fractional derivative to obtain the semi-discrete problem (2.4)–(2.5), and then we use FRKCM to solve this semi-discrete problem. The above process is summarized as Algorithm 1.

3 Stability and convergence analysis

3.1 The stability and convergence of the approximate solution

We first investigate the stability analysis of the approximate solution given by FRKCM.

Theorem 3.1

Suppose ${\widetilde{f}}(x,t_n)=f(x,t_n)+\delta$, where $\delta$ is a perturbation and $L{\widetilde{u}}^n_m(x)={\widetilde{f}}(x,t_n)$, then

$$\begin{aligned} \left\| u^n_{m}(x)-{\widetilde{u}}^n_m(x)\right\| _{\beta }\le H\Vert \delta \Vert _{\beta }, \end{aligned}$$

where H is a nonnegative constant.

Proof

$$\begin{aligned} \begin{aligned} \left\| u^n_{m}(x)-{\widetilde{u}}^n_m(x)\right\| _{\beta }&=\left\| L^{-1}f(x,t_n)-L^{-1}{\widetilde{f}}(x,t_n)\right\| _{\beta }\\&=\left\| L^{-1}f(x,t_n)-L^{-1}(f(x,t_n)+\delta )\right\| _{\beta }\\&=\left\| L^{-1}\delta \right\| _{\beta }\\&\le \left\| L^{-1}\right\| _{\beta }\Vert \delta \Vert _{\beta }\\ {}&\le H\Vert \delta \Vert _{\beta }, \end{aligned} \end{aligned}$$

where H is a nonnegative constant. The proof is completed. $\square$

Next, we present three lemmas for analysing the convergence of the approximate solution.

Lemma 3.1

Suppose $u^n(x)$ is the solution of the semi-discrete problem (2.4)–(2.5), $u^n_m(x)$ is the approximate solution of $u^n(x)$, $\left\{ x_i\right\} _{i=1}^{\infty }$ is a dense set in [0, 1], then

$$\begin{aligned} Lu^n_m(x_{i})=Lu^n(x_{i}),\ i=1,2,\ldots ,\infty . \end{aligned}$$

Proof

Let R(x, y) be the reproducing kernel function of the reproducing kernel space $W_2^1[0,1]$. From (2.10), there holds

$$\begin{aligned} Lu^n(x)=f\left( x,t_n\right) . \end{aligned}$$

(3.1)

Taking the inner product of (3.1) with $R(x,x_i)$, we obtain

$$\begin{aligned} \left\langle Lu^n(x),R(x,x_i)\right\rangle _{W_2^1}=\left\langle f(x,t_n),R(x,x_i)\right\rangle _{W_2^1}. \end{aligned}$$

(3.2)

Due to the reproducing property of reproducing kernel, (3.2) becomes

$$\begin{aligned} Lu^n(x_i)=f(x_i,t_n),\ i=1,2,\ldots ,\infty . \end{aligned}$$

(3.3)

It follows from (2.12) to (2.14) that

$$\begin{aligned} Lu^n_m(x_k)=f(x_k,t_n),\ k=1,2,\ldots ,M. \end{aligned}$$

(3.4)

Taking the inner product of (3.4) with $R(x_k,x_i)$, then we have

$$\begin{aligned} \left\langle Lu^n_m(x_k),R(x_k,x_i)\right\rangle _{W_2^1}=\left\langle f(x_k,t_n),R(x_k,x_i)\right\rangle _{W_2^1}, \end{aligned}$$

also

$$\begin{aligned} Lu^n_m\left( x_i\right) =f\left( x_i,t_n\right) ,\ i=1,2,\ldots ,\infty . \end{aligned}$$

(3.5)

Combining (3.3) and (3.5), it can be concluded

$$\begin{aligned} Lu^n_m\left( x_i\right) =Lu^n\left( x_i\right) ,\ i=1,2,\ldots ,\infty . \end{aligned}$$

The proof is completed. $\square$

Lemma 3.2

([37]) $X=\left\{ u^n_{m}(x)|\ \Vert u^n_{m}(x)\Vert _{\beta }\le \gamma \right\}$ is a compact set of C[0, 1], where $\gamma$ is a constant.

Lemma 3.3

Suppose that $u^n(x)$ is the solution of the semi-discrete problem (2.4)–(2.5), $u^n_m(x,t_n)$ is the approximate solution of $u^n(x)$, $\left\{ x_{i}\right\} _{i=1}^{\infty }$ is dense set in [0, 1], then $\Vert u^n_m(x)-u^n(x)\Vert _\beta \rightarrow 0.$

Proof

Since $u^n_{m}(x)=a_{1}+a_{2}x^{2}+\sum _{i=1}^{M}a_{i+2}K(x,x_{i})$ is continuous on [0, 1], we know $\Vert u^n_{m}(x)\Vert _{\beta }\le \gamma$, where $\gamma$ is a constant. From Lemma 3.2, it is known that X is a compact set, hence there exists a convergent subsequence $\left\{ u^n_{m_{l}}(x)\right\} _{l=1}^{\infty } \subset \left\{ u^n_{m}(x)\right\} _{m=1}^{\infty }\subset X$.

Assume subsequence $\lbrace u^n_{m_{l}}(x)\rbrace _{l=1}^{\infty }$ converges to $u(x,t_n)\in X$, i.e.

$$\begin{aligned} u^n_{m_{l}}(x)\longrightarrow u^n(x),\ l\longrightarrow \infty . \end{aligned}$$

According to Lemma 3.1, we have

$$\begin{aligned} Lu^n_{m}\left( x_i\right) =Lu^n\left( x_i\right) =f\left( x_i,t_n\right) ,\ i=1,2,\ldots ,\infty . \end{aligned}$$

Hence,

$$\begin{aligned} Lu^n_{m_l}\left( x_i\right) =f\left( x_i,t_n\right) . \end{aligned}$$

(3.6)

As $l\rightarrow \infty$, take the limit of (3.6) to get

$$\begin{aligned} Lu^n\left( x_i\right) -f\left( x_i,t_n\right) =0. \end{aligned}$$

Due to the fact that $Lu^n(x)-f(x,t_n)$ is a continuous function and $\left\{ x_{i}\right\} _{i=1}^{\infty }$ is a dense set, we have

$$\begin{aligned} Lu^n\left( x\right) -f\left( x,t_n\right) =0. \end{aligned}$$

Thus, $u^n(x)$ is the solution of the semi-discrete problem (2.4)–(2.5).

Since L is a bounded linear operator,

$$\begin{aligned} Lu^n_{m_l}(x)\longrightarrow Lu^n(x). \end{aligned}$$

(3.7)

As $l\rightarrow \infty$, take the limit of (3.7) to get

$$\begin{aligned} Lu^n_{m}(x)\longrightarrow f(x,t_n). \end{aligned}$$

Since $L^{-1}:W_2^1[0,1]\rightarrow W_2^\beta [0,1]$ exists, we have

$$\begin{aligned} \left\| u^n_{m}(x)-u^n(x)\right\| _{\beta }=\left\| L^{-1}(Lu^n_{m}(x)-Lu^n(x))\right\| _{\beta }=\left\| L^{-1}\left( Lu^n_{m}(x)-f(x,t_n)\right) \right\| _{\beta }\longrightarrow 0. \end{aligned}$$

$\square$

Now, we prove that the approximate solution uniformly converges to the solution of the semi-discrete problem (2.4)–(2.5).

Theorem 3.2

Suppose that $u^n(x)$ is the solution of the semi-discrete problem (2.4)–(2.5), $u^n_m(x)$ is the approximate solution of $u^n(x)$, then $u^n_{m}(x)$ is uniformly convergent to $u^n(x)$.

Proof

From the reproducing properties and Lemma 3.3 we have,

$$\begin{aligned} \begin{aligned} \left| u^n_{m}(x)-u^n(x)\right|&=\left| \ \left\langle u^n_{m}(\cdot )-u^n(\cdot ),K_{x}(\cdot )\right\rangle _{\beta }\ \right| \\&\le \left\| u^n_{m}(\cdot )-u^n(\cdot )\right\| _{\beta }\cdot \left\| K_{x}(\cdot )\right\| _{\beta }\\&\le \eta \left\| u^n_{m}(x)-u^n(x)\right\| _{\beta }\longrightarrow 0,\ m\rightarrow \infty \end{aligned} \end{aligned}$$

where $\Vert K_x(\cdot )\Vert _\beta =\sqrt{\langle K_x(\cdot ),K_x(\cdot ) \rangle _\beta }=\sqrt{K_x(x)}<\eta$. Namely, $u^n_{m}(x)$ uniformly converges to $u^n(x)$. $\square$

Here, we establish error estimation for the approximate solution given by FRKCM.

Theorem 3.3

Let $\Delta x=\frac{1}{M}$, where M is a nonnegative integer, $u^n(x)$ is the solution of the semi-discrete problem (2.4)–(2.5) and $u^n_m(x)$ is the approximate solution of $u^n(x)$, then $|u^n_m(x)-u^n(x)|\le o\left( \Delta x\right)$.

Proof

There exists $x_i\in [0,1]$, such that $|x-x_i|\le \Delta x$. From Lemma 3.1, we obtain

$$\begin{aligned} Lu^n_m(x_{i})=Lu^n(x_{i}), \end{aligned}$$

thus,

$$\begin{aligned} \begin{aligned} Lu^n_{m}(x)-Lu^n(x)&=Lu^n_{m}(x)-Lu^n_{m}(x_{i})-\left( Lu^n(x)-Lu^n_m(x_{i})\right) \\&=Lu^n_{m}(x)-Lu^n_{m}(x_{i})-\left( Lu^n(x)-Lu^n(x_{i})\right) \\&=\left\langle u^n_{m}(\cdot ),LK(x,\cdot )\right\rangle _\beta -\left\langle u^n_{m}(\cdot ),LK(x_i,\cdot )\right\rangle _\beta -\left\langle u^n(\cdot ),\right. \\&\left. LK(x,\cdot )\right\rangle _\beta +\left\langle u^n(\cdot ),LK(x_i,\cdot )\right\rangle _\beta \\&=\left\langle u^n_{m}(\cdot ),LK(x,\cdot )-LK(x_i,\cdot )\right\rangle _\beta -\left\langle u^n(\cdot ), \right. \\&\left. LK(x,\cdot )-LK(x_i,\cdot )\right\rangle _{\beta }\\&=\left\langle u^n_{m}(\cdot )-u^n(\cdot ),LK(x,\cdot )-LK(x_{i},\cdot )\right\rangle _{\beta }. \end{aligned} \end{aligned}$$

As $L^{-1}$ exists,

$$\begin{aligned} \begin{aligned} \left| u^n_m(x)-u^n(x)\right|&=\left| \left\langle u^n_{m}(\cdot )-u^n(\cdot ),L^{-1}\left( LK(x,\cdot )-LK(x_{i},\cdot )\right) \right\rangle _{\beta }\right| \\&\le \Vert L^{-1}\Vert _{\beta }\cdot \Vert u^n(x)-u^n_{m}(x)\Vert _{\beta }\cdot \left\| LK(x,\cdot )-LK(x_{i},\cdot )\right\| _{\beta }. \end{aligned} \end{aligned}$$

From Lagrange mean value theorem, we have

$$\begin{aligned} LK(x,\cdot )-LK(x_{i},\cdot )=\dfrac{\partial LK(\xi ,\cdot )}{\partial \xi }(x-x_{i}),\quad \xi \in (x,x_i). \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} \left| u^n(x)-u^n_{m}(x)\right|&\le \left\| L^{-1}\right\| _{\beta }\cdot \left\| u^n(x)-u^n_{m}(x)\right\| _{\beta }\cdot \left\| \dfrac{\partial LK(\xi ,\cdot )}{\partial {\xi }}\right\| _{\beta }\cdot \left\| x-x_{i}\right\| _{\beta }\\&\le \Delta x\cdot \left\| L^{-1}\right\| _{\beta }\cdot \left\| u^n(x)-u^n_{m}(x)\right\| _{\beta }\cdot \left\| \dfrac{\partial LK(\xi ,\cdot )}{\partial _{\xi }}\right\| _{\beta }. \end{aligned} \end{aligned}$$

Making use of Lemma 3.3 and the bounded properties of $\Vert L^{-1}\Vert$ and $\left\| \dfrac{\partial }{\partial _{\xi }}LK(\xi ,\cdot )\right\|$, it is easy to verify that

$$\begin{aligned} \left| u^n(x)-u^n_{m}(x)\right| =o\left( \Delta x\right) . \end{aligned}$$

The proof is completed. $\square$

3.2 The stability and convergence of the semi-discrete scheme

Now, we introduce the following lemmas for the stability of the semi-discrete scheme (2.4).

Lemma 3.4

Suppose $u(x)\in W_2^\beta [0,1]$, then $u(x)\in W_2^{\frac{\beta }{2}}[0,1]$.

Proof

It is enough to show that $\dfrac{\partial }{\partial x}\left( {_0^CD_x^{\frac{\beta }{2}}}u(x)\right) \in L^{2}[0,1]$. In fact

$$\begin{aligned} \begin{aligned} \dfrac{\partial }{\partial x}\left( {_0^CD_x^{\frac{\beta }{2}}}u(x)\right)&=\dfrac{\partial }{\partial x}\dfrac{1}{\Gamma \left( {1-\frac{\beta }{2}}\right) }\int ^{x}_{0}(x-t)^{-\frac{\beta }{2}}u'(t)\textrm{d}t\\&=\dfrac{\partial }{\partial x}\dfrac{1}{\Gamma \left( {1-\frac{\beta }{2}}\right) }\int ^{x}_{0}s^{-\frac{\beta }{2}}u'(x-s)\textrm{d}s\\&=\dfrac{1}{\Gamma \left( {1-\frac{\beta }{2}}\right) }u'(0)x^{-\frac{\beta }{2}}+\dfrac{1}{\Gamma ({1-\frac{\beta }{2}})}\int _{0}^{x}s^{-\frac{\beta }{2}}u''(x-s)\textrm{d}s\\&=\dfrac{1}{\Gamma \left( {1-\frac{\beta }{2}}\right) }u'(0)x^{-\frac{\beta }{2}}+\dfrac{1}{\Gamma \left( {1-\frac{\beta }{2}}\right) }\int _{0}^{x}(x-t)^{-\frac{\beta }{2}}u''(t)\textrm{d}t. \end{aligned} \end{aligned}$$

Obviously, $\dfrac{1}{\Gamma ({1-\frac{\beta }{2}})}u'(0)x^{-\frac{\beta }{2}}\in L^2[0,1]$, and

$$\begin{aligned} \begin{aligned}&\int _{0}^{1}\left( \dfrac{1}{\Gamma \left( {1-\frac{\beta }{2}}\right) }\int _{0}^{x}(x-t)^{-\frac{\beta }{2}}u''(t)\textrm{d}t\right) \textrm{d}x\\&=\dfrac{1}{\Gamma \left( {1-\frac{\beta }{2}}\right) }\int _{0}^{1}\int _{t}^{1}(x-t)^{-\frac{\beta }{2}}u''(t)\textrm{d}x\textrm{d}t\\&=\dfrac{1}{\Gamma \left( {2-\frac{\beta }{2}}\right) }\int _{0}^{1}(1-t)^{1-\frac{\beta }{2}}u''(t)\textrm{d}t\\&\le \dfrac{1}{\Gamma \left( {2-\frac{\beta }{2}}\right) }(u'(1)-u'(0))\\&<\infty , \end{aligned} \end{aligned}$$

thereby $\dfrac{1}{\Gamma ({1-\frac{\beta }{2}})}\int _{0}^{x}(x-t)^{-\frac{\beta }{2}}u''(t)\textrm{d}t \in L^1[0,1]$.

According to the fact, $\dfrac{1}{\Gamma ({1-\frac{\beta }{2}})}\int _{0}^{x}(x-t)^{-\frac{\beta }{2}}u''(t)\textrm{d}t \in L^2[0,1]$, we have $\dfrac{\partial }{\partial x}\left( {_0^CD_x^{\frac{\beta }{2}}}u(x)\right) \in L^{2}[0,1]$. From the definition of $W_2^{\frac{\beta }{2}}[0,1]$ given by (2.6), we know that $u(x)\in W_2^{\frac{\beta }{2}}[0,1]$. $\square$

Lemma 3.5

([38, 39]) For $u,v \in W_{2}^{\frac{\beta }{2}}[0,1]$, we have

$$\begin{aligned} \begin{aligned} \left\langle {_0^CD_x^\beta }u,{_x^CD_1^\beta }u\right\rangle _{L^2}=\cos (\beta \pi )\left\| {_0^CD_x^\beta }u\right\| _{L^{2}}^{2}=\cos (\beta \pi )\left\| {_x^CD_1^\beta }u\right\| _{L^{2}}^{2},\quad \beta >0&\\ \left\langle {_0^CD_x^\beta }u,v\right\rangle _{L^2}=\left\langle {_0^CD_x^{\frac{\beta }{2}}}u,{_x^CD_{1}^{\frac{\beta }{2}}}v\right\rangle _{L^2},\left\langle {_x^CD_1^\beta }u,v\right\rangle _{L^2}=\left\langle {_x^CD_1^{\frac{\beta }{2}}}u,{_0^CD_x^{\frac{\beta }{2}}}v \right\rangle _{L^2},\ \ \ \ \beta \in (1,2)&\end{aligned} \end{aligned}$$

Lemma 3.6

Let $u^n(x)\in W_{2}^{\beta }[0,1](n=1,2,\ldots ,N)$ be the solution of the semi-discrete problem (2.4)–(2.5), then

(3.8)

where $C>0$.

Proof

Here we use induction to prove (3.8). First (2.4) can be transformed into the following equivalent form in case of $n=1$.

$$\begin{aligned} u^1(x)-\alpha _{0}a(x,t_1){_0^CD_x^\beta }u^1(x)=u^0(x)+\alpha _{0}f(x,t_1). \end{aligned}$$

(3.9)

Multiplying (3.9) by $u^1(x)$ and integrating on [0, 1] gives

$$\begin{aligned} \begin{aligned}&\left\langle u^1(x),u^1(x)\right\rangle _{L^2}-\alpha _{0}a\left( x,t_1\right) \left\langle {_0^CD_x^\beta }u^1(x),u^1(x)\right\rangle _{L^2}\\&=\left\langle u^0(x),u^1(x)\right\rangle _{L^2}+\alpha _{0}\left\langle f(x,t_1),u^1(x)\right\rangle _{L^2}. \end{aligned} \end{aligned}$$

(3.10)

According to Lemma 3.5, we see

$$\begin{aligned} \begin{aligned}&\left\langle {_0^CD_x^\beta }u^1(x),u^1(x)\right\rangle _{L^2}=\left\langle {_0^CD_x^\frac{\beta }{2}}u^1(x),{_x^CD_1^\frac{\beta }{2}}u^1(x)\right\rangle _{L^2}\\&=\cos \left( \frac{\beta }{2}\pi \right) \left\| {_0^CD_x^\beta }u^1(x)\right\| _{L^{2}}^{2}<0,\quad \forall \ 1<\beta <2. \end{aligned} \end{aligned}$$

(3.11)

By using the properties of $b_{j}$ given by (2.3) and (3.11), (3.10) can be rewritten as follows

$$\begin{aligned} \left\| u^1(x)\right\| _{L^{2}}\le \left\| u^0(x)\right\| _{L^{2}}+\alpha _{0}\mathop {\max }_{0\le x\le 1}\left\| f(x,t_1)\right\| _{L^{2}}\le \left\| u^0(x)\right\| _{L^{2}}+C\mathop {\max }_{0\le x\le 1}\left\| f(x,t_1)\right\| _{L^{2}}, \end{aligned}$$

where $C>0$, which demonstrates that (3.8) is valid for the case $n=1$.

Now, assuming that the inequality (3.8) is true for $n=1,2,\ldots ,N-1$. Taking $n=N$ for (2.4), we obtain

$$\begin{aligned}{} & {} u^N(x)-\alpha _{0}a\left( x,t_N\right) {_0^CD_x^\beta }u^N(x)\nonumber \\{} & {} =\sum _{j=1}^{N-1}\left( b_{j-1}-b_{j}\right) u^{N-j}(x)+b_{N-1}u^0(x)+\alpha _{0}f\left( x,t_N\right) . \end{aligned}$$

(3.12)

Multiplying (3.12) by $u^N(x)$ and integrating on [0, 1] gives

$$\begin{aligned} \begin{aligned}&\left\langle u^N(x),u^N(x)\right\rangle _{L^2}-\alpha _{0}a(x,t_N)\left\langle {_0^CD_x^\beta }u^N(x),u^N(x)\right\rangle _{L^2}\\=&\sum _{j=1}^{N-1}(b_{j-1}-b_{j})\left\langle u^{N-j}(x),u^N(x)\right\rangle _{L^2}+b_{N-1}\left\langle u^0(x),u^N(x)\right\rangle _{L^2}\\&+\alpha _{0}\left\langle f(x,t_N),u^N(x)\right\rangle _{L^2}. \end{aligned} \end{aligned}$$

(3.13)

By Lemma 3.5, the properties of $b_{j}$ given by (2.3) and the Cauchy-Schwarz inequality, we arrive at

(3.14)

where $C>0$. $\square$

Here, we prove that the semi-discrete scheme (2.4) is unconditionally stable.

Theorem 3.4

Suppose that $u^n(x)\in W_{2}^{\beta }[0,1]$ is the solution of the semi-discrete problem (2.4)–(2.5) at $t=t_n$. Then, the semi-discrete scheme (2.4) is unconditionally stable.

Proof

Suppose that $v^n(x)$ is the solution of (2.4) with corresponding initial condition v(x, 0), therefore $v(x,t_n),n=1,2,\ldots ,N$ is also the solution of the semi-distcrete problem (2.4)–(2.5). Similar to (2.4), there exists

$$\begin{aligned}{} & {} v^n(x)-\alpha _{0}a(x,t_n){_0^CD_{x}^\beta }v^n(x)\nonumber \\{} & {} \quad =b_{n-1}v(x,0)+\sum _{j=1}^{n-1}\left( b_{j-1}-b_{j}\right) v^{n-j}(x)+\alpha _{0}f(x,t_n). \end{aligned}$$

(3.15)

Let $\varepsilon ^{n}=u^n(x)-v^n(x)$ be the error, then subtracting (2.4) from (3.15) gives

$$\begin{aligned} \varepsilon ^{n}-\alpha _0a(x,t_n){_0^CD_x^\beta }\varepsilon ^{n}=b_{n-1}\varepsilon ^{0}+\sum _{j=1}^{n-1}\left( b_{j-1}-b_{j}\right) \varepsilon ^{n-j}. \end{aligned}$$

(3.16)

Further, with the help of Lemma 3.6 and (3.16), we obtain

$$\begin{aligned} \left\| \varepsilon ^{n}\right\| _{L^2}\le \Vert \varepsilon ^{0}\Vert _{L^2},n=1,2,\ldots ,N, \end{aligned}$$

which means that the semi-distrete problem (2.4)–(2.5) is unconditionally stable. $\square$

Next, we introduce a lemma to prove the convergence order of the semi-discrete scheme (2.4).

Lemma 3.7

([40]) Suppose $\theta$ be a nonnegative constant, $s_{m}$ and $r_{k}$ are nonnegative sequences that the sequence $v_{m}$ satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} v_{m}\le \theta ,&{}\quad m=0,\\ v_{m}\le \theta +\sum _{k=0}^{m-1}r_{k}+\sum _{k=0}^{m-1} s_{k}v_{m},&{}\quad m\ge 1, \end{array} \right. \end{aligned}$$

then $v_{m}$ satisfies

$$\begin{aligned} v_{m}\le \left( \theta +\sum _{k=0}^{m-1}r_{k}\right) \textrm{exp}\left( \sum _{k=0}^{m-1}s_{k}\right) . \end{aligned}$$

Finally, we obtain the convergence order of the semi-discrete scheme (2.4) is $O(\Delta t)$.

Theorem 3.5

Suppose u(x, t) is the exact solutions of (1.1)–(1.3), and $\eta ^{n}=u(x,t_n)-u^n(x),\ (n=1,2,\ldots ,N)$ is the error function, then the semi-discrete scheme (2.4) has convergence order $O(\Delta t)$.

Proof

First (1.1) can be rewritten as

$$\begin{aligned}{} & {} u\left( x,t_{n}\right) -\alpha _{0}a\left( x,t_n\right) {_0^CD_x^\beta }u\left( x,t_{n}\right) =b_{n-1}u(x,0)\nonumber \\{} & {} \quad +\sum _{j=1}^{n-1}\left( b_{j-1}-b_{j}\right) u\left( x,t_{n-j}\right) +\alpha _{0}f\left( x,t_{n}\right) +\alpha _{0}R_{n,u}, \end{aligned}$$

(3.17)

where $R_{n,u}$ is the truncation error satisfying $R_{n,u}\le C_{u}O(\Delta t^{2-\alpha })$(see pages 1535–1538, [35]), and $C_{u}$ is a constant depending only on u.

Subtracting (2.4) from (3.17), we obtain

$$\begin{aligned} \eta ^{n}-\alpha _0a(x,t_n){_0^CD_x^\beta }\eta ^{n}=\sum _{j=1}^{n-1}\left( b_{j-1}-b_{j}\right) \eta ^{n-j}+\alpha _{0}R_{n,u}. \end{aligned}$$

(3.18)

The following formulation can be obtained by multiplying (3.18) by $\varepsilon ^{n}$ and integrating on [0, 1],

$$\begin{aligned} \begin{aligned} \left\langle \eta ^{n},\eta ^{n}\right\rangle _{L^2}-\alpha _{0}a(x,t_n)\left\langle {_0^CD_x^\beta }\eta ^{n},\eta ^{n}\right\rangle _{L^2}=&\sum _{j=1}^{n-1}(b_{j-1}-b_{j})\langle \eta ^{n-j},\eta ^{n}\rangle _{L^2}+\alpha _{0}\left\langle R_{n,u},\eta ^{n}\right\rangle _{L^2}. \end{aligned} \end{aligned}$$

By virtue of the Cauchy–Schwarz inequality, Lemma 3.5 and the properties of $b_{j}$ given by (2.3), we obtain

$$\begin{aligned} \begin{aligned} \left\| \eta ^{n}\right\| _{L^2}&\le \sum _{j=1}^{n-1}\left( b_{j-1}-b_{j}\right) \left\| \eta ^{n-j}\right\| _{L^2}+\alpha _{0}\Vert R_{n,u}\Vert _{L^2}\\&=\left( 1-b_{1}\right) \left\| \eta ^{n-1}\right\| _{L^2}+\sum _{j=2}^{n-1}\left( b_{j-1}-b_{j}\right) \left\| \eta ^{n-j}\right\| _{L^2}+\alpha _{0}\Vert R_{n,u}\Vert _{L^2}\\&\le \left\| \eta ^{n-1}\right\| _{L^2}+\sum _{j=2}^{n-1}\left( b_{j-1}-b_{j}\right) \left\| \eta ^{n-j}\right\| _{L^2}+\alpha _{0}\Vert R_{n,u}\Vert _{L^2}, \end{aligned} \end{aligned}$$

which leads to

$$\begin{aligned} \left\| \eta ^{n}\right\| _{L^2}-\left\| \eta ^{n-1}\right\| _{L^2}\le \sum _{j=2}^{n-1}\left( b_{j-1}-b_{j}\right) \left\| \eta ^{n-j}\right\| _{L^2}+\alpha _{0}\Vert R_{n,u}\Vert _{L^2}. \end{aligned}$$

Summing up for n from 1 to M, and due to $\Vert \eta ^{0}\Vert _{L^2}=0$, we have

$$\begin{aligned} \begin{aligned} \left\| \eta ^{N}\right\| _{L^2}&\le \sum _{n=1}^{N}\sum _{j=2}^{n-1}\left( b_{j-1}-b_{j}\right) \left\| \eta ^{n-j}\right\| _{L^2}\\&\quad +\alpha _{0}\sum _{n=1}^{N}\Vert R_{n,u}\Vert _{L^2} =\sum _{n=2}^{N-1}\left( b_{n-1}-b_{n}\right) \left\| \eta ^{N-n}\right\| _{L^2}+\alpha _{0}\sum _{n=1}^{N}\Vert R_{n,u}\Vert _{L^2}. \end{aligned}\qquad \quad \end{aligned}$$

(3.19)

and also, the inequality (3.19) can be rewritten as

$$\begin{aligned} \begin{aligned} \left\| \eta ^{N}\right\| _{L^2}&\le \left\| \eta ^{N}\right\| _{L^2}+\left( 1-b_{1}\right) \left\| \eta ^{N-1}\right\| _{L^2}\\&\le \sum _{n=1}^{N-1}\left( b_{n-1}-b_{n}\right) \left\| \eta ^{N-n}\right\| _{L^2}+\alpha _{0}\sum _{n=1}^{N-1}\Vert R_{n,u}\Vert _{L^2}\\&=\sum _{n=0}^{N-1}\left( b_{n}-b_{n+1}\right) \left\| \eta ^{N-n-1}\right\| _{L^2}+\alpha _{0}\sum _{n=0}^{N-1}\Vert R_{n+1,u}\Vert _{L^2}. \end{aligned} \end{aligned}$$

Employing Lemma 3.7 and the properties of $b_{j}$ given by (2.3), we have

$$\begin{aligned} \begin{aligned} \Vert \eta ^{N}\Vert&\le \left( \alpha _{0}\sum _{n=0}^{N-1}\Vert R_{n+1,u}\Vert _{L^2}\right) \textrm{exp}\left( \sum _{n=0}^{N-1}(b_{n}-b_{n+1})\right) \\&\le \left( \Gamma (2-\alpha )\Delta t^{\alpha }\sum _{n=0}^{N-1}\Vert R_{n+1,u}\Vert _{L^2}\right) \textrm{exp}\left( 1\right) \\&\le \left( \Gamma (2-\alpha )\Delta t^{\alpha }N\mathop {\max }_{1\le n\le N}\Vert R_{n,u}\Vert _{L^2}\right) \textrm{exp}(1)\\&= \left( \Gamma (2-\alpha )\Delta t^{\alpha -1}T\mathop {\max }_{1\le n\le N}\Vert R_{n,u}\Vert _{L^2}\right) \textrm{exp}(1)\\&\le CO(\Delta t), \end{aligned} \end{aligned}$$

where $C>0$. The proof is completed. $\square$

4 Numerical results

In this section, three examples are solved to verify our theoretical findings. Write $u^N_m(x)$ as the approximate solutions determined by the method provided in the paper. Example 4.1 is taken from [15, 16], and Example 4.2–4.3 are taken from [17, 18] respectively and we construct numerical results with them. All computations were performed by using Mathematica 9.0. The accuracy of the proposed method is measured using the $\Vert e\Vert _{abs}$, $\Vert e\Vert _{L_2}$ and $\Vert e\Vert _{L_{\infty }}$ error norms for the test problems. The error norms, convergence rates in both time and space direction are respectively defined as

$$\begin{aligned}&\Vert e\Vert _{abs}=\left| u^N_m(x)-u(x,T)\right| ,\ \ \Vert e\Vert _{L_\infty }=\max \limits _{1\le k\le M}|u^N_m(x_k)-u(x_k,T)|,\ \ \Vert e\Vert _{L_2}\\&=\left( \sum _{k=1}^{M}|u^N_m(x_k)-u(x_k,T)|^2\right) ^{\frac{1}{2}}.\\&CR_t=log_{\frac{n_2}{n_1}}\frac{\max \limits _{1\le k\le M}|u^{n_1}_{m}(x_k)-u(x_k,T)|}{\max \limits _{1\le k\le M}\left| u^{n_2}_{m}(x_k)-u(x_k,T)\right| },\\&CR_s=log_{\frac{m_2}{m_1}}\frac{\max \limits _{1\le k\le M}\left| u^{n}_{m_1}(x_k)-u(x_k,T)\right| }{\max \limits _{1\le k\le M}\left| u^{n}_{m_2}(x_k)-u(x_k,T)\right| }. \end{aligned}$$

Table 1 Comparison of $\Vert e\Vert _{abs}$ with $N=M=3$ for different $\alpha =0.2, 0.6$ at $T=1$ for Example 4.1

Table 2 The maximum absolute error of $Lu^n_m(x)$ with $N=2,\ M=2$ for different $\alpha$ at $T=1$ for Example 4.1

Example 4.1

Consider the following space-time fractional diffusion problem

$$\begin{aligned}\left\{ \begin{aligned}&{^{C}_{0}D_{t}^{\alpha }}u(x,t)=\Gamma (1.2)x^{1.8}{^{C}_{0}D_{x}^{1.8}}u(x,t)+3x^2(2x-1)e^{-t},\\&u(x,0)=x^2(1-x),\\&u(0,t)=u(1,t)=0. \end{aligned} \right. \end{aligned}$$

The exact solution is $u(x,t)=x^2(1-x)e^{-t}$. $\Vert e\Vert _{abs}$ is compared with [15, 16] when $N=M=3$ and for different values of $\alpha$ at $T=1$. Numerical results are presented in Table 1 indicates that when the error order is the same, the calculation speed of the present method is fast and only a few nodes are needed. Table 2 shows the maximum absolute error $|Lu^n_m(x)-Lu(x,T)|$ for $N=2,\ M=2$ with collocation points for three cases at $T=1$. Note that in these tables, we provide CPU time consumed in the algorithms for obtaining the numerical solution, our method acting in a short time.

Table 3 Comparison of $\Vert e\Vert _{L_\infty }$ with $N =30,\ M=4$ for different $\alpha$ at $T=2,10,50,100$ for Example 4.2

Example 4.2

Consider the following space-time fractional diffusion problem

$$\begin{aligned}\left\{ \begin{aligned}&{^{C}_{0}D_{t}^{\alpha }}u(x,t)=\dfrac{\Gamma (2.2)}{6}x^{2.8}{^{C}_{0}D_{x}^{1.8}}u(x,t)+f(x,t),\\&u(x,0)=x^3,\\&u(0,t)=0,\ u(1,t)=e^{-t}. \end{aligned} \right. \end{aligned}$$

The exact solution is $u(x,t)=x^3e^{-t}$ for suitable source term. Table 3 compares $\Vert e\Vert _{L_\infty }$ with the Galerkin method in [17] for $N=30,\ M=4$ and different values of $\alpha \in (0,1)$. Table 4 shows the maximum absolute errors $|Lu^n_m(x)-Lu(x,T)|$ with $N=2,\ M=4$ for different values of $\alpha$ with collocation points for three cases at $T=1$, and we calculated CPU time for a number of different $\alpha$ which is a very short time. The numerical results of this example demonstrate that our methods are more accurate and faster.

Table 4 The maximum absolute error of $Lu^n_m(x)$ with $N=2,\ M=4$ for different $\alpha$ at $T=1$ for Example 4.2

Table 5 Comparison of $\Vert e\Vert _{L_2}$ with $M=4$ for different $\alpha$ and N at $T = 1$ for Example 4.3

Fig. 1

$\Vert e\Vert _{abs}$ of Example 4.3 for $N=10$ (left side) and $N=20$ (right side)

Fig. 2

$\Vert e\Vert _{abs}$ of Example 4.3 for $\alpha =0.3$

Example 4.3

Consider the following space-time fractional diffusion problem

$$\begin{aligned}\left\{ \begin{aligned}&{^{C}_{0}D_{t}^{\alpha }}u(x,t)={^{C}_{0}D_{x}^{1.6}}u(x,t)+f(x,t),\\&u(x,0)=0,\\&u(0,t)=0,\ u(1,t)=t^2. \end{aligned} \right. \end{aligned}$$

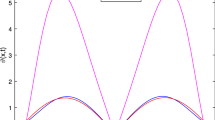
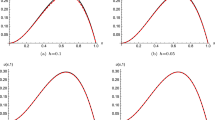
The exact solution is $u(x,t)=t^2x^2$. $\Vert e\Vert _{L_2}$ of our method and the existing approach in [18] which is used finite element method for solving this problem are compared in Table 5. We can see from this table that the maximum error absolute order obtained by the present method is one order higher than the method [18]. $\Vert e\Vert _{abs}$ for $\alpha =0.3,0.6,0.9$ based on $M=4$ and $N=10,20$ at $T=1$, which are shown in Fig. 1. Figure 2 depicts $\Vert e\Vert _{abs}$ for $M=4$ and $N=10,20,50,100$, $\alpha =0.3$ at $T=1$. This illustrates that the accuracy of the approximate solution will be getting best as N increases, it implies that the method proposed in this paper is stable. Table 6 reports the convergence order with $\alpha =0.9$ at $T=1,\ M=3,\ 4$ and different values of N. From this table, one can observe that the obtained convergence orders are in close agreement with the theoretical order $O(\Delta t)$ in time direction.

Table 6 $\Vert e\Vert _{L_\infty }$ and $CR_t$ with $\alpha =0.9$ at $T=1$ for Example 4.3

Example 4.4

Consider the following space-time fractional diffusion problem

$$\begin{aligned}\left\{ \begin{aligned}&{^{C}_{0}D_{t}^{\alpha }}u(x,t)={^{C}_{0}D_{x}^{\beta }}u(x,t)+f(x,t),\\&u(x,0)=0,\\&u(0,t)=0,\ u(1,t)=0. \end{aligned} \right. \end{aligned}$$

The exact solution is $u(x,t)=txsin(\pi x)$. Tables 7, 8 display the results of the FRKCM. Table 7 lists the $\Vert e\Vert _{abs}$ of the present method for $N=2,\ M=4$ and $\beta =1.4,\ 1.6,\ 1.8$ at $T=1$. The convergence orders and $\Vert e\Vert _{L_\infty }$ are shown in Table 8 at $T=1$ with $\alpha =0.9$, $N=2$ for different values $\alpha$ and M. It is clear that the space order of convergence supports the theoretical result $o(\Delta x)$.

Table 7 $\Vert e\Vert _{abs}$ with $N=2,\ M=4$ for different $\beta$ at $T = 1$ for Example 4.4

Table 8 $\Vert e\Vert _{L_\infty }$ and $CR_s$ with $N=2$ for different $\alpha$ and M at $T = 1$ for Example 4.4

5 Conclusion

In this paper, the semi-discrete process and FRKCM have been used for approximating the solution of the space-time fractional diffusion equations. We established stability and convergence analysis of the approximate solution. The unconditional stability of the semi-discrete scheme is rigorously discussed, and we have proved that the semi-discrete scheme is of $O(\Delta t)$ convergence. Numerical examples demonstrate the feasibility and reliability of our algorithm.