Abstract
The High order Gradient Reproducing Kernel in conjunction with the Collocation Method (HGRKCM) is introduced for solutions of 2nd- and 4th-order PDEs. All the derivative approximations appearing in PDEs are constructed using the gradient reproducing kernels. Consequently, the computational cost for construction of derivative approximations reduces tremendously, basis functions for derivative approximations are smooth, and the accumulated error arising from calculating derivative approximations are controlled in comparison to the direct derivative counterparts. Furthermore, it is theoretically estimated and numerically tested that the same number of collocation points as the source points can be used to obtain the optimal solution in the HGRKCM. Overall, the HGRKCM is roughly 10–25 times faster than the conventional reproducing kernel collocation method. The convergence of the present method is estimated using the least squares functional equivalence. Numerical results are verified and compared with other strong-form-based and Galerkin-based methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Beside FEM, with a solid mathematical basis and a considerably wide range of applications, other methods have been proposed and developed for solving the partial differential equations based on the Galerkin weak formulation. Meshfree methods using approximation functions with compact support such as diffuse approximation (DA) [1], moving least-squares (MLS) [2,3,4], and reproducing kernel (RK) [5,6,7], have been widely used for solving problems in a Galerkin-form scheme. Partition of unity method (PUM) [8], H-P clouds [9], meshless local Petrov-Galerkin method (MLPG) [10], generalized finite element method (GFEM) [11], and reproducing kernel element method RKEM [12] are other examples of weak form based methods implemented for solving various problems. Among all of the mentioned methods, MLS and RK approximation methods have been considerably more adopted and applied to engineering problems comparing to others [3,4,5,6]. Inheriting all advantages of FEM, meshfree methods generally address the issues regarding mesh construction and mesh distortion difficulties in the finite element method. However, despite of all the advantages, the domain integration arising from the Galerkin procedures require special attention to gain desirable accuracy since meshfree shape functions are typically rational and of overlapping support. In addition, essential boundary condition imposition in Galerkin-based meshfree methods is not as straightforward as in FEM. This is due to the lack of Kronecker delta property in general meshfree shape functions. Many efforts have been introduced to overcome the complexities of Galerkin-based formulation due to domain integration and boundary condition imposition [13,14,15,16,17]. Radial Basis Functions (RBF) are used to construct meshfree shape functions in the Galerkin form scheme for stress analysis of three-dimensional solids [18]. Despite the fact that RBFs posses Kronecker delta property and address the essential boundary conditions imposition issues, choosing proper parameters to guarantee the moment matrix invertibility becomes challenging.
On the other hand, strong form collocation methods [19, 20], seeking the approximation solutions directly based on the strong form, has gained a considerable amount of interest recently. Mainly, two different type of approximation functions can be considered in strong collocation meshfree methods. Firstly, using an infinite differentiable radial basis functions [21, 22] was proposed. The method was shown to posses exponential convergence properties [19, 23]. However, the discrete linear system using the radial basis functions becomes fully dense and ill-conditioned due to the non-local nature of RBFs [24, 25]. As a remedy, instead of RBFs, a smooth approximation using compact support such as the RK or MLS were introduced in the strong colocation method [26,27,28,29,30]. Addressing the ill-conditioned discrete system issue, reproducing kernel collocation method (RKCM) avoids the domain integration and the difficulties regarding the Dirichlet boundary conditions imposition. Nevertheless, the convergence rate obtained from RKCM is algebraic [29, 30]. In spite of all the advantages offered by RKCM, calculation of higher order derivatives remains as a concern. The calculation of higher order derivatives of RK is computationally costly and often inaccurate owing to accumulated errors from inversion of the moment matrix and excessive amount of matrix multiplication [29, 30]. Moreover, for optimal convergence, a considerably larger number of collocation points comparing to the source points must be used, which makes the method computationally intense [29, 31]. A superconvergant gradient smoothing meshfree collocation method [32] is recently introduced, which improves the numerical implementation within the collocation scheme based on constructing the smoothed gradient derivatives of meshfree shape functions by interpolation of the standard derivatives of those functions. Super-convergent solutions are shown to be obtained for odd-order basis functions within this scheme. Moreover, to address the mentioned issues regarding RKCM, a gradient reproducing kernel collocation method (GRKCM) was proposed [33]. The basic idea of this method is to construct the derivative approximation independently using gradient RK shape functions [34,35,36,37]. In GRKCM, the first derivative approximation is formulated based on the gradient reproducing condition. The higher order derivatives are then derived by calculating the explicit derivatives of the first derivative approximation, which was derived implicitly. Resolving the issue with need of larger number of collocation points comparing to the source points, GRKCM yields the algebraic convergence similar to RKCM [33]. Nonetheless, besides all the benefits from GRKCM, calculation of higher derivatives of RK shape functions remains computationally challenging. For solving higher order PDEs, computation effort for derivative approximations may become more crucial since calculating the moment matrix inversion adds more complexities to the problem. Another issue which will be discussed in detail in the following sections is related to the fact that higher order derivatives of RK shape functions derived by direct differentiation exhibit oscillating behavior which results in a method of nodal distribution pattern dependency. It is also observed that derivatives of higher orders do not pass the reproducing conditions test which lead to inaccurate results. In this paper, a higher order gradient reproducing kernel collocation method (HGRKCM) is introduced. This method is implemented for solving second-order PDEs as well as higher order fourth order PDEs such as Bernoulli beam and Kirchhoff plate. The method is based on calculating all RK shape function derivatives implicitly by directly satisfying derivatives reproducing conditions. The proposed method is compared with other collocation methods such as RKCM and GRKCM in term of error analysis and convergence rate. To show the robustness and computational efficiency of the method, CPU-time comparison between HGRKCM, RKCM, Galerkin-based methods such as FEM, and RKPM with Stabilized Conforming Nodal Integration (SCNI) [38] is performed.
The structure of this paper is as follows. In Sect. 2, the construction of RK approximation procedure is reviewed and the basic motivation of this work is defined. Section 3 reviews the strong-form collocation methods including RKCM and gradient RKCM and the new Higher order gradient RKCM is presented. HGRKCM implementation process is shown and the error estimation is presented in Sect. 4. In Sect. 5, several numerical examples are presented and results are discussed to show the effectiveness and robustness of the proposed method. Finally, in Sect. 6, CPU-time comparisons between the present method and some other existing strong collocation and Galerkin weak form methods are provided. Conclusions and remarks are provided in Sect. 7.
2 Reproducing kernel (RK) approximation and its derivatives approximations
In contrast to mesh-based methods, such as FEM and IGA, where the shape functions of the approximations are constructed in the parent domain and transformed to the physical domain through mapping, in meshfree methods, the approximation function is constructed directly based on the nodal positions in the physical domain. Many meshfree approximations have been proposed, see [39]. Commonly used approximations with basis (shape) functions that possess compact support are the Moving Least-Squares (MLS) [7] and Reproducing Kernel (RK) approximation [6]. Despite derived from different perspectives, the two approximations yield the same mesh-free approximation structure in the discrete form. The RK approximation is employed in the work and is reviewed in this section.
2.1 Review of reproducing kernel approximation
Consider an open domain \(\Omega \) and its boundary \(\partial \Omega \) to construct the closed domain \({\overline{\Omega }}\), such that \({\overline{\Omega }}=\Omega \bigcup \partial \Omega \). If this domain is discretized by a set of nodes \(\varvec{x}_I\) where \(I=1, 2, \cdots , NP\) and \(\varvec{x}_I\in {\overline{\Omega }}\), the RK approximation of an arbitrary function u, denoted by \(\varvec{u}^{h}\), is expressed as,
where \(\Psi _I(\varvec{x})\) is the RK shape function and \(d_I\) is the corresponding nodal coefficient, also called generalized nodal value. RK shape function is comprised of a kernel function \(\phi _a\) and a correction function \(\varvec{C}\).
the kernel function is defined on a bounded space centered at \(\varvec{x}_I\) and a is the support measure of the kernel function. It determines the smoothness (order of continuity) and locality of shape functions. Usually, B-splines of different orders are used as the kernel functions. The most common kernel used for constructing RK shape functions is cubic B-spline which provides \(C^2\) continuity. For higher order PDEs, higher order kernel B-splines are required to achieve optimal convergence.
On the other hand, the correction function \(\varvec{C}(\varvec{x};\varvec{x} - \varvec{x}_I)\) is introduced for obtaining monomial reproductivity [5] as below,
The multi-index notation is adopted in the paper and defined as follows. In Eq. (3), \(\alpha =(\alpha _1,\alpha _2, \cdots , \alpha _d)\) and \(|\alpha |=\sum ^{d}_{i=1} \alpha _i\) is the length of \(\alpha \), where d is the number of dimensions, and n is the highest order of monomial reproductivity imposed. \(\alpha != \alpha _1 ! \cdots \alpha _d !\) and \(\varvec{x}^{\alpha }=x_1^{\alpha _1} \cdots x_d^{\alpha _d}\). When \(\varvec{x}^{\alpha }\) is complete, by applying the binomial theorem, Eq. (3) can be shown to be equivalent to,
where \(\delta \) is the Kronecker delta. The correction function can be expressed in the form below,
where \(\varvec{H}^T(\varvec{x}-\varvec{x}_I)\) is the basis vector which consists of a set of linearly independent basis functions and \(\varvec{b}(\varvec{x})\) is the coefficient vector to be determined. When the set of complete monomials is selected, \(\varvec{H}^T(\varvec{x}-\varvec{x}_I)\) is given as,
Introducing (5) and (6) into (4), \(\varvec{b}(\varvec{x})\) can be obtained as,
and consequently,
above \(\varvec{H}(\varvec{0})\) is the vector form of \(\delta _{\alpha 0}\) and \(\varvec{M}(\varvec{x})\) is called the moment matrix. Finally, substituting (7) into (5) and then into (2), The RK shape function is obtained as,
For any sufficiently smooth \(\varvec{u}\), the RK approximation satisfies the following error bound [29, 40]:
where c is a generic constant, \(\kappa \) is the overlapping factor, and a is the maximum support size.
The invertibility and conditioning of \(\varvec{M}(\varvec{x})\) controls the quality of the RK approximation. To ensure that the moment matrix \(\varvec{M}(\varvec{x})\) is non-singular, the kernel support size must be chosen large enough such that at least \((n+d)!/(n!d!)\) kernels, with non-colinear (\(d=2\)) or non-co-planar (\(d=3\)) centers, cover each evaluation point \(\varvec{x}\). Moreover, the kernel function \(\phi _a(\varvec{x}-\varvec{x}_I)\) must be positive to ensure that the moment matrix is positive definite. B-spline functions are commonly used as the kernel function in mesh-free methods, such as cubic B-spline, with a \(C^2\) continuity, in weak-form-based methods. Higher order B-spline functions are required for the strong-form-based methods and for high order PDEs. In this study, three different of cubic, quintic, and sextic B-spline kernel functions are used:
-
Cubic B-spline:
$$\begin{aligned} \phi _a(z)= {\left\{ \begin{array}{ll} \frac{2}{3} - 4z^2 + 4z^3, &{} 0\le z<\frac{1}{2} \\ \frac{4}{3} - 4z + 4z^2 - \frac{4z^3}{3}, &{} \frac{1}{2}\le z <1 \\ 0, &{} z \ge 1, \end{array}\right. } \end{aligned}$$(11) -
Quintic B-spline:
$$\begin{aligned} \phi _a(z)= {\left\{ \begin{array}{ll} \frac{11}{20}-\frac{9z^2}{2} + \frac{81 z^4}{4} - \frac{81 z^5}{4}, &{} 0\le z<\frac{1}{3} \\ \frac{17}{40} + \frac{15z}{8} - \frac{63z^2}{4} + \frac{135z^3}{4} - \frac{243z^4}{8} +\frac{81z^5}{8}, &{} \frac{1}{3}\le z<\frac{2}{3}\\ \frac{81}{40}-\frac{81z}{8}+\frac{81z^2}{4}-\frac{81z^3}{4}+\frac{81z^4}{8}-\frac{81z^5}{40}, &{} \frac{2}{3}\le z <1 \\ 0 &{} z \ge 1, \end{array}\right. }\nonumber \\ \end{aligned}$$(12) -
Sextic B-spline:
$$\begin{aligned} \phi _a(z)= {\left\{ \begin{array}{ll} \frac{5887}{1920} - \frac{3773z^2}{128} + \frac{16807z^4}{128} - \frac{117649z^6}{384}, &{} 0\le z<\frac{1}{7} \\ \frac{7861}{2560} - \frac{49z}{256} - \frac{13377z^2}{512} - \frac{12005z^3}{384}\\ ~~~+ \frac{151263z^4}{512} - \frac{117649z^5}{256} + \frac{117649z^6}{512}, &{} \frac{1}{7}\le z<\frac{3}{7} \\ \frac{1379}{1280} + \frac{8869z}{320} - \frac{48363z^2}{256} + \frac{45619z^3}{96} \\ ~~~- \frac{151263z^4}{256} + \frac{117649z^5}{320} - \frac{117649z^6}{1280}, &{} \frac{3}{7}\le z<\frac{5}{7} \\ \frac{117649}{7680} - \frac{117649z}{1280} + \frac{117649z^2}{512} - \frac{117649z^3}{384} \\ ~~~+ \frac{117649z^4}{512} - \frac{117649z^5}{1280} + \frac{117649z^6}{7680}, &{} \frac{5}{7}\le z <1 \\ 0, &{} z \ge 1 \end{array}\right. }\nonumber \\ \end{aligned}$$(13)
where z is the normalized nodal distance shown as \(z=\Vert \varvec{x}-\varvec{x}_I\Vert /a\), which offers a circular support with a nodal support domain radius of a. The kernel function in the d-dimension can be also expressed by the tensor product of the one-dimensional one as:
where \(\phi _{a_i}\) and \(a_i\) denote the kernel function’s value at node \(\varvec{x}\) and the nodal domain support size in the i direction, respectively, where \(i=1,\ldots ,d\). The kernel function’s value \(\phi _a\) at point \(\varvec{x}\) is obtained by multiplying of kernel values of all directions shown by \(\phi _{a_i}\).
2.2 Direct derivative
The derivatives of the RK approximation of a function u can be obtained by directly taking the derivations of RK shape function in Eq. (9), which hereafter are referred to as “direct derivatives”.
where \(\partial ^{\alpha }=\partial ^{|\alpha |}(\varvec{.})/\partial x_1^{\alpha _1} \cdots \partial x_d^{\alpha _d}\). The general form of direct derivatives of RK shape function can be expressed using the general Leibniz rule as:
where the derivatives of \(\varvec{M}^{-1}\) can be obtained from
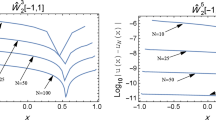
The calculation of direct derivatives involves matrix products and the derivatives of inverse of M matrix, making it computationally costly for high order derivatives. Moreover, when the order of differentiation increases, the direct derivatives of the RK shape function become highly oscillatory which affects the numerical stability and reliability (see Fig. 1).
2.3 Implicit gradient
The derivations of a function u can be approximated, in a similar manner, in Eq. (1), by
above \({}^{\beta }\Psi _I\) is called the implicit gradient of RK [33] or, since it can be viewed as the approximation of \(\partial ^{\beta }\Psi _I\), therefore, is called the diffuse derivative [1]. In this paper, the implicit gradient term is adopted. The implicit gradient of the RK is expressed in a similar manner as in Eq. (2):
Comparison of one-dimensional RK shape function. a First. b Second. c Third. d Fourth direct derivatives and implicit gradients
In the case that the same set of monomials as in (6) are chosen for \(\varvec{C}^{\beta }(\varvec{x};\varvec{x}-\varvec{x}_I)\), it can be expressed as,
the coefficients \(\varvec{b}^{\beta }(\varvec{x})\) is determined by enforcing the gradient reproducing conditions:
or equivalently,
where \(\partial ^{\beta }\varvec{H}(\varvec{0})\) is the direct derivative of the basis vector up to desired order of \(\beta \) when \(\varvec{x}=\varvec{x}_I\). To clear the implementation, as an example, Eq. (A.10) shows the equivalence in (22) for a specific case. Now, by the similar procedures described in Sect. 2.1, the coefficient vector can be derived as
and the implicit gradients of the RK follows straightaway:
The implicit gradient RK approximation satisfies the following error bound [33, 41]:
2.4 Direct and implicit gradient comparison
By comparing (24) and the equation for constructing the RK shape function (9), it can easily be noticed that the difference of \({}^{\beta }\Psi _I\) from \(\Psi _I\) is merely replacing term \(\varvec{H}(\varvec{0})\) in (9) by the term \((-1)^{|\beta |}\partial ^{\beta }\varvec{H}(\varvec{0})\) in (24). Therefore, the computational cost of computing \({}^{\beta }\Psi _I\) is essentially the same as that of computing \(\Psi _I\) regardless the order of differentiation (see “Appendix A”). In contrast, the computation of direct derivative \(\partial ^{\beta }\Psi _I\) increases with the increase of order of differentiation. As an example of one-dimensional RK, the operation count of computing the second order implicit gradient is approximately ten times less than that of computing the direct derivative counterpart. The details of complexity analysis can be found in [33]. Moreover, as can be seen in (24), the order of continuity of implicit gradients does not decrease with the increase of differentiation. Thus, higher order kernel functions is not required when the implicit gradients are used for derivative approximations. Additionally, since no direct derivatives involved in the calculation, the implicit gradients remain much smoother comparing to the direct derivative counterparts as shown in Fig. 1 for one-dimensional RK.
Condition number of moment (\(\varvec{M}\)) matrix increasing rate comparison with increase of the basis order
2.5 Scaling for high order RK approximation
The RK approximation has the flexibility to increase the order of completeness by introducing desired order of complete monomials as basis functions, see the vector in Eq. (6). The total number of monomials for n-th order completeness in the d-dimensional space is \((n+d)!/(n!d!)\). Consequently, the size of \(\varvec{M}\) matrix in Eq. (8), which is the Gram matrix comprised of monomials, increases exponentially with the increase of n. Moreover, when the order elevates, monomials become more difficult to distinguish from each other and their values increases exponentially when input variables get away from the origin. The \(\varvec{M}\) matrix, therefore, suffers ill-conditioning by increase of n. To control the conditioning of the \(\varvec{M}\) matrix, scaling factors are introduced for monomial bases, such that the monomials are equal to unity when evaluated at \(h_v\), the nominal nodal spacing. The scaled basis vector is given as follows [41]:
For a non-uniform nodal distribution, \(h_v\) is chosen to be equal to the averaged nodal distance as \(h_v=\sum _{I=1}^{NP} (\underset{1\le J\le NP,~J\ne I}{min}\Vert x_I-x_J\Vert )/NP\) in this work. To demonstrate, RK approximations with different basis orders of p are constructed based on a set of equally spaced \(10\times 10\) nodes over the domain \([0,10] \times [0,10]\), and the support size \(a=(n+0.5)h\) is chosen for different basis order with h the average nodal distance. The comparison of the condition number of M matrix with and without scaling is shown in Fig. 2. It can be noted that with scaling, the condition number of \(\varvec{M}\) matrix reduces at least 2 order and, more importantly, the rate of increase of condition number with respect to basis order decreases. The theoretical estimation of the condition number of \(\varvec{M}\) matrix is referred to [41].
3 RK based strong collocation methods review
In this section, the strong collocation formulation is presented and RKCM [26], weighted RKCM [30, 31], and the gradient RKCM [33] are discussed. This lays the foundation for the present method in this paper, where issues regarding the higher order derivatives of the RK shape functions for solving higher order PDEs are depicted and addressed.
3.1 RKCM and weighted RKCM
Consider a general linear second-order boundary value problem shown as follows:
where \(\varvec{u}\) is the primary field variable, \(\Omega \) is an open domain enclosed by the boundary \(\partial \Omega =\Gamma _g\cup \Gamma _h\) , \(\Gamma _g\) and \(\Gamma _h\) are the Dirichlet and Neumann boundaries, respectively. \(\varvec{L}\), \(\varvec{B}_g\), and \(\varvec{B}_h\) are the algebraic operators associated with the domain and the Dirichlet and Neumann boundaries, respectively. The notation \(\partial ^j(\varvec{.})\equiv \partial ^{\beta }(\varvec{.})\), \(|\beta |=j\) is adopted.
In the RKCM framework a set of \(N_s\) distinct points, \(\varvec{x}_I \in \Omega \cup \partial \Omega \) , referred to as “source point”, is used to construct the RK approximation and its direct derivatives as in (1) and (15), respectively:
and,
Introducing \(\varvec{u}^h\) and \(\partial ^{\beta }\varvec{u}^h\) into (27) and enforcing the set of equations at collocation points leads to,
where \(\varvec{x}_d\), \(\varvec{x}_g\) , and \(\varvec{x}_h\) represent the collocation points in the domain, on the Dirichlet and Neumann boundaries, respectively, and the total number of collocation points is denoted by \(N_c\). \(\varvec{\Psi }=\{\Psi _I\}^{N_s}_{I=1}\) , \(\partial ^{\beta }\varvec{\Psi }=\{\partial ^{\beta }\Psi _I\}_{I=1}^{N_s}\) , and \(\varvec{D}=\{\varvec{d}_I\}_{I=1}^{N_s}\) are the vector forms of shape functions and shape function direct derivatives and nodal coefficients, respectively. Equation (30) could be shown a system of linear equations and can be expressed in a matrix form as:
where \(\varvec{K}=\Big [\varvec{L}(\partial ^2\varvec{\Psi })|_{\varvec{x}_d},~ \varvec{B}_g(\varvec{\Psi })|_{\varvec{x}_g},~\varvec{B}_h(\partial ^1\varvec{\Psi })|_{\varvec{x}_h}\Big ]^T \) and \(\varvec{F}=\Big [(\varvec{f})_{\varvec{x}_d},~(\varvec{g})_{\varvec{x}_g},~(\varvec{h})_{\varvec{x}_h} \Big ]^T\) with dimensions of \(mN_c \times mN_s\) and \(mN_c \times 1\), respectively, where m is the number of unknowns per node. The unknown coefficient \(\varvec{D}\) can be obtained from solving Eq. (31) in the case where the number of source points \(N_s\) is equal to the number of collocation points \(N_c\). It has been observed that more collocation points than source points are needed (\(N_c>N_s\)) [29,30,31] for an optimal convergence in the RKCM, which leads to an over-determined system. The over-determined system typically can be solved by the least-squares method. The least-squares solution of (31) is equivalent to the minimization of the least-square functional [31]. The problem states finding the solutions \(\varvec{u}^a\in V\) such that,
where \(E(\varvec{u}^h)\) in (32) is defined as follows,
Above, \({\hat{\int }} \) denotes the integration with quadrature, in which the collocation points are viewed as quadrature points. \(w_g\) and \(w_h\) are weights introduced to balance the errors from the domain and boundary terms [31]. For optimal convergence, \(\sqrt{w_g}\approx O(\rho N_s)\) and \(\sqrt{w_h}\approx O(1)\) are estimated, where \(\rho =1\) for the Poisson equation and \(\rho =max\{\lambda ,\mu \}\) for the elasticity problem [31]. Introducing the weights into the discrete equations, the unknown coefficients are obtained by solving the following weighted equations by the least square method:
The error from RKCM solution is bounded by Hu et al. [31],
where,
3.2 Gradient reproducing kernel collocation method (GRKCM)
GRKCM was proposed based on [34, 35] to address the issues regarding constructing higher order derivatives of RK shape functions for solving second-order partial differential equations. These issues are mostly related to calculating derivatives of inverse of moment matrix (\(\varvec{M}^{-1}\)) at the collocation points.
In the GRKCM, the first derivatives of RK approximation are obtained by using the implicit gradient derivatives of RK shape functions and thereafter the second derivatives are calculated using the direct derivatives of the first-order implicit gradients. The approximation of \(\varvec{u}\) and its first and second derivative approximations in the GRKCM are given:
here, \({\overline{\Psi }}_I\) denotes a different set of RK basis functions from \(\Psi _I\) and \(\Delta ^1\) represents the implicit gradient of first order. It is noted that different orders of RK basis functions can be introduced for \(\varvec{u}(\varvec{x})\) and its first derivative approximation. Let the orders of \(\{\Psi _I\}_{I=1}^{N_s}\) and \(\{\Delta ^1{\overline{\Psi }}_I\}_{I=1}^{N_s}\) to be p and q, respectively. Following the similar analysis in the weighted RKCM method in Sect. 3.1, the solution of the GRKCM is obtained from solving the following system of weighted equations:
where for optimal convergence \(\sqrt{{\overline{w}}_g}\approx O(1)\) and \(\sqrt{{\overline{w}}_h}\approx O(\rho a^{q-p-1})\) are estimated in [31], with the use of error estimate of gradient RK provided by Li and Liu [35],
where \(C_1\) and \(C_2\) are genetic constants independent of support size and,
It is noted that the convergence of GRKCM is dependent only on the order q in the first derivative approximation of \(\varvec{u}\) using the implicit gradients of RK and \(q \ge 2\) is required for convergence. More importantly, it has been shown that since the order of direct derivatives employed in the GRKCM is reduced, the use of \(N_c=N_s\) achieves sufficient solution accuracy for second-order PDEs [35]. This observation essentially motivates the proposed HGRKCM to further enhance the computation speed while maintaining solution accuracy.
4 HGRKCM model problem, implementation, and error analysis
As reviewed in the previous section, weighted RKCM was shown to resolve the issues regarding unbalanced domain-boundary errors which yields promising convergence rates. This method, however, is computationally expensive since the number of collocation points needed for obtaining an optimal convergence rate must be more than the number of source points. On the other hand, calculating the moment matrix inversion and its derivatives, even for a second order PDE, remain as a concern. GRKCM addressed this issue partially by reducing the order of differentiation to first order for a second-order PDE with the same convergence rate as RKCM but considerably faster approach comparing to RKCM. Nonetheless, for constructing the second derivatives of shape functions, a direct differentiation is employed in the GRKCM framework where complexities issues related to moment matrix mentioned above emerges again. This problem becomes bolder in higher order PDE cases. In the following chapters it is shown and numerically tested that HGRKCM can address the complexity issues regarding higher order derivatives calculation since all derivatives of desired orders are calculated implicitly without the need of direct differentiation of the moment matrix. For clarifying the implementation procedure, two model problems are discussed. First, a general two-dimensional boundary value problem is considered to show the implementation for Poisson equation and elasticity problems. Using the second model problem, HGRKCM implementation for fourth order equation is discussed.
4.1 General HGRKCM model problem description
Consider a general high-order boundary value problem shown as follows:
similarly, L, \(B_g\), and \(B_h\) are the algebraic operators with the domain and the Dirichlet and Neumann boundaries, respectively. In HGRKCM, the RK approximation and its implicit gradients are introduced in the collocation method. The implementation for specific problems are detailed in the following sections.
4.2 HGRKCM for Poisson equation and elasticity problem
For demonstration purposes, the Poisson and elasticity problems in 2-D are considered, which can be expressed as:
where \({\varvec{L}}^{1}\) and \({\varvec{L}}^{2}\) are coefficient matrices for domain equation in \(\Omega \), \(\varvec{B}_g\) and \(\varvec{B}_h\) are the coefficient matrices for the Dirichlet boundary \(\Gamma _g\) and the Neumann boundary \(\Gamma _h\), respectively. The explicit form of these operators for the Poisson and elasticity problems are shown in Table 1. The coefficient matrices are the same for RKCM, GRKCM, and HGRKCM. The difference between each method is merely the choice of derivative approximations. In HGRKCM, the implicit gradient approximation is employed. Specifically,
and,
Following the same argument discussed in Sect. 3.1, the weighted discrete equations for obtaining the unknown coefficients in HGRKCM is:
where sub-matrices \(\varvec{A}^i\) (\(i=1,\ldots ,6\)) in (45) are defined as the following,
and sub-matrices \(\varvec{b}^i\) (\(i=1, 2, 3\)) can are expressed as,
Error \(L_2\) norm convergence rate of RK approximations of sinusoidal function by basis orders of \(p=1,2,\ldots ,6\). Estimated convergence rate according to theory is \(p+1\)
Remark 4.1
If \(N_c > N_s\), the weighted discrete equations can be solved by the least square method. The weights are the same as the ones estimated in the RKCM, \(\sqrt{(}w_g)\approx O(\rho N_s)\) and \(\sqrt{(}w_h)\approx O(1)\) since the direct derivatives and implicit gradients have the same derivative approximation properties (25). Moreover, as shown in GRKCM [33], since no direct derivatives are used in HGRKCM, \(N_c=N_s\) maintains sufficient solution accuracy and provides computational efficiency while the implementation and domain nodal distribution becomes straightforward.
Error \(L_2\) norm convergence rate of RK approximations of sinusoidal function’s first derivative by basis orders of \(p=1,2,\ldots ,6\). Estimated convergence rate according to theory is p
Error \(L_2\) norm convergence rate of RK approximations of sinusoidal function’s second derivative by basis orders of \(p=2,\ldots ,6\). Estimated convergence rate according to theory is \(p-1\)
Error \(L_2\) norm convergence rate of RK approximations of sinusoidal function’s third derivative by basis orders of \(p=3,4,5\), and 6. Estimated convergence rate according to theory is \(p-2\)
Error \(L_2\) norm convergence rate of RK approximations of sinusoidal function’s fourth derivative by basis orders of \(p=4,5\), and 6. Estimated convergence rate according to theory is \(p-3\)
Error \(L_2\) norm convergence rate of one-dimensional 2nd-order PDE (with Dirichlet boundary conditions) using basis orders of \(p=2,5\), and 6 within RKCM, GRKCM, and HGRKCM schemes
Error \(L_2\) norm convergence rate of one-dimensional 2nd-order PDE (with mixed boundary conditions) using basis orders of \(p=2,5\), and 6 within RKCM, GRKCM, and HGRKCM schemes
Error \(L_2\) norm convergence rate of one-dimensional 2nd-order PDE using basis orders of \(p=4,5\), and 6 within RKCM and HGRKCM schemes (non-uniform nodal distribution)
Error \(L_2\) norm convergence rate of one-dimensional 4th-order PDE using basis orders of \(p=4,5\), and 6 within RKCM and HGRKCM schemes
Error \(L_2\) norm convergence rate of one-dimensional 4th-order PDE using basis orders of \(p=4,5\), and 6 within RKCM and HGRKCM schemes
Error \(L_2\) norm convergence rate of two-dimensional Poisson equation using basis orders of \(p=2,3,\ldots ,6\) within RKCM and HGRKCM schemes
RKCM error convergence comparison between determined and weighted over-determined systems using a second (\(p=2\)) and b fourth (\(p=4\)) order basis
Error convergence comparison for a weighted over-determined RKCM and b HGRKCM using fourh-order basis and different RK shape function support domain sizes
Sample non-uniform nodal distribution patterns for a RKCM over determined system and b HGRKCM determined system with source-points located at similar locations for both cases
4.3 HGRKCM for fourth order PDEs (Kirchhoff plate)
As the model problem for 4th order PDE, Consider a homogeneous isotropic rectangular plate of constant rigidity G shown in (48) ,
where \(G=Et^3/[12(1-\nu ^2)]\), t is the plate’s thickness, and g(x, y) is the load per unit area of the plate in z-direction. \(u_g\), \({\bar{h}}\), M, and Q are prescribed displacement, rotation, moment, and effective shear, respectively on the corresponding boundaries. Boundary conditions must be satisfied on the boundary collocation points \(\varvec{x}^g\in \Gamma _g\), \(\varvec{x}^h\in \Gamma _h\), \(\varvec{x}^m\in \Gamma _m\), \(\varvec{x}^q\in \Gamma _q\), where \(\Gamma _g\), \(\Gamma _h\), \(\Gamma _m\), and \(\Gamma _q\) are the displacement (deflection), rotation, moment, and shear boundaries, respectively. It is noted that when the edge of the plate is composed of piece-wise smooth curves that are joined at corners, a twisting moment condition is required at the free corner. The details are referred to plate and shell textbooks, e.g. [42].
With the same approach for Poisson and elasticity problems in (42), the Kirchhoff plate and its boundary conditions equations could be written in the following form,
where \(L^1\), \(L^2\), and \(L^3\) are the coefficients matrices on the domain equation. \(B_g\), \(B_h^1\), and \(B_h^2\) are the same as defined in (42). \(B_m^1\), \(B_m^2\), and \(B_m^3\) represent the coefficient matrices on the moment boundary equation whereas \(B_q^1\), \(B_q^2\), \(B_q^3\), and \(B_q^4\) on the shear boundary equation. These operators are given in Table 2. The implicit gradient approximations of RK shape functions in (49) are defined as follows,
Taking the same approach as for the 2nd order PDE, the weighted least-squares functional E(D) of the HGRKCM for the 4th order PDE after substituting (50) into (49) can be written as:
where \(w_q,w_m,w_h,\) and \(w_g\) are boundary weights, and,
then, the stationary condition for the minimization of \(E(\varvec{D})\) leads to the following variational equation:
Applying a proper quadrature rule to \(\delta E(\varvec{D})\) at different sets of collocation points in the domain and on the boundaries, it is equivalent to solving the following linear system of equations by the least-squares method:
Sub-matrices \(\varvec{A}^i\) (\(i=1,\ldots ,13\)) and \(\varvec{b}^i\) (\(i=1,\ldots ,5\)) in Eq. (54) for the 4th-order Kirchhoff plate discrete equation are shown in “Appendix B”.
Error \(L_2\) norm convergence rate of two-dimensional Poisson equation using basis orders of \(p=2,3,\ldots ,6\) within RKCM and HGRKCM schemes
Internally pressurized elastic tube. a Configuration and properties. b Dirichlet and Neumann boundaries
Nodal distribution for over-determined RKCM (left) and determined HGRKCM (right) cases
Error \(L_2\) norm convergence rate of elasticity problem using basis orders of \(p=2,3,\ldots ,6\) within RKCM and HGRKCM schemes
Rectangular Kirchhoff plate. a Source and collocation points pattern configuration. b Error \(L_2\) norm convergence rate using basis orders of \(p=4,5\), and 6 using HGRKCM
CPU-time comparison versus source points number comparison between RKCM and HGRKCM for a two-dimensional Poisson. b Elasticity and c Rectangular Kirchhoff plate problems
4.4 Convergence analysis of 4th-order problem
Consider the problem given in Eq. (48). Based on the least-squares functional in Eq. (51), E-norm is defined as follows:
where \(R^i\) , \(i=1,\ldots ,5\), are the associated differential operators in Eq. (48), and \(v^{(i)}\) denotes the i-th-order complete derivatives of v. Let w and \(w^{(i)}\) be the approximations of u and \(u^{(i)}\) by the RK and gradient RKs described in Eqs. (1) and (15). HGRKCM error measured in the E-norm is:
where,
Above, \(C_i\) denotes the generic constant independent of support size, a. The approximation properties of RK and implicit gradient RK, Eqs. (10) and (25), is further introduced in Eqs. (57)–(61). In order to balance errors from the domain and boundary terms in Eq. (56), the following weights are selected:
with weights in Eq. (62) and the properties in Eqs. (10) and (25), the E-norm is bounded as follows,
Considering the balance of errors in the E-norm and the properties in Eqs. (57)–(61), the convergence is therefore estimated as:
5 Numerical examples
In this section, several numerical problems are presented to show how the HGRKCM performs for solving one and two-dimensional second and fourth-order differential equations. The list of solved problems and their purpose of study are summarized:
-
Function and derivatives approximation: examining the convergence of derivatives approximations using implicit gradient, particularly for higher order derivatives.
-
One-dimensional 2nd-order PDE: convergence from three methods are compared with different sets of boundary conditions to show HGRKCM performance, especially when using higher basis orders.
-
One-dimensional 4th-order PDE: demonstrating the performance of HGRKCM and compare with other collocation methods.
-
Two-dimensional Poisson problem: demonstrating the performance of HGRKCM for two-dimensional Poisson problem.
-
Two-dimensional elasticity problem: an internally pressurized tube problem is selected to show HGRKCM performance in solving elasticity problems with non-regular geometry.
-
Rectangular Kirchhoff plate problem: HGRKCM is applied for Kirchhoff plate problem. This is where regular RKCM fails to show acceptable convergence. Different basis orders are used and results are compared with results from other studies.
Finally, CPU run-time for constructing the shape functions and stiffness matrices versus accuracy of the method is compared with regular RKCM and two Galerkin-based methods, FEM and RKPM with SCNI.
5.1 Function and derivatives approximations
A simple one-dimensional sinusoidal function is considered as in (65),
For this problem, the number of collocation points is considered to be equal to the number of source points (determined system). Quintic B-splines are used as the kernel function and basis orders of \(p=1, \ldots , 6\) are used to solve the problem. For all the numerical examples solved and discussed in this paper, the normalized support size for RK shape functions are considered as \(a=(p+0.5) \times h\), unless otherwise stated. Here h is the average source points nodal distance. In cases which for nonuniform nodal distribution is used, a search algorithm is developed such that each arbitrary evaluation node is covered by the mimum number of source points to assure the moment matric invertibility. The minimum number of neighbor nodes depends on the basis order used for approximation. The derivative approximations are performed up to 4th-order and the error \(L_2\) norms are presented. Error norms for function approximation are shown in Fig. 3 which are in agreement with the theory [29], equal to \(p+1\).
For first-order derivative approximating, all three methods show promising results in term of error convergence rate, almost for all basis orders (shown in Fig. 4). However, in case of RKCM, when \(p=6\) is selected, even by using sextic B-splines, convergence rate decreases when nodal spaces are considerably refined. This happens because of ill-conditioning in derivatives of the moment matrix. Although according to [27] using higher order basis function should yield more accurate results, obtaining acceptable convergence rate and accurate results become more critical for regular RKCM and GRKCM when approximating higher order derivatives by higher order basis functions, as observed in Figs. 5, 6 and 7.
As observed in Fig. 7c, in the most critical case for the fourth-order approximation, when using \(p=6\), RKCM and GRKCM fail in yielding acceptable convergence rate. This also happens for second and third derivatives approximation when using higher-order polynomials as basis terms. On the other hand, HGRKCM, for which all the shape function’s derivatives are constructed based on implicit gradient of RK, yield convergence rates in agreement with theoretical estimations [29, 30].
5.2 2nd-order one-dimensional equation
To study HGRKCM performance in solving PDEs, as the first step, a one-dimensional 2nd-order differential Eq. (66) with two cases of boundary conditions is considered,
In the first case, two Dirichlet boundary conditions are applied at both ends (\(u(0)=0, u(10)=0\)). In the second case, a Neumann boundary condition is applied on the right end (\(u_{,x}(10)=\frac{\pi }{5}\)). Basis orders of \(p=2,3, \ldots , 6\) are implemented for error convergence study. While the same amount of source and collocation points are used in HGRKCM case, for RKCM and GRKCM, an over-determined system (\(N_c = 4~N_s\)) is employed to get the optimal convergence rate and a more accurate set of results. The problem is manufactured such that it contains function u and all its derivatives to assure all the effects of shape function derivatives are considered in the study. The convergence rates for both cases are shown in Figs. 8 and 9.
This is obvious from the obtained convergence rates that all three methods perform almost the same in solving the second-order problem. However, for obtaining a reliable error convergence rate using RKCM, over-determined weighted systems are required. Beside the fact that over-determined systems need more computational effort to solve, proper boundary weight need to be derived for different PDEs. On the other hand, HGRKCM is shown to yield the same, if not better, error convergence rates under a determined system without any weights used on the boundaries.
Beside the advantages mentioned above, HGRKCM is shown to be less sensitive to changes in the support domain size. Error convergence from RKCM is observed to change considerably if different support sizes are used or a non-uniform nodal distribution is of interest or complicated geometry is considered. In the case of non-uniform nodal distribution, the error \(L_2\) norm shows oscillations and usually convergence rate is observed to be sub-optimal, specially when higher order shape functions are utilized to solve the problem.
To compare the performance of RKCM and the higher order gradient RKCM, the differential equation shown in (66) is solved by the same number of source points (with \(30\%\) perturbation from the uniform nodal locations), support domain size, and kernel orders. Again, for RKCM, a weighted over-determined system is used to guarantee the optimal error convergence rate. Results shown in Fig. 10 state that HGRKCM yields the same rate as error estimation, where the results from RKCM show a sub-optimal convergence rate.
Remark 5.1
As shown in [29], analytically, error \(L_2\) norm convergence rate for second-order differential problems is \(p-1\), where p is the basis order used for constructing the shape functions and derivatives. However, numerical results indicate the convergence error as \(p-1\) and p when odd and even values for p are selected. These results are confirmed numerically for one-dimensional case in Figs. 8 and 9. Similar convergence behavior has been reported in isogeometric collocation method in [43, 44]. Similar results are also reported in studying the second- and fourth-order structural vibration problems for the frequency accuracy orders [45].
5.3 4th-order one-dimensional equation
Consider the 4th-order differential equation as below,
where \(g(x)=\frac{1}{625} [5\pi (25+\pi ^2)]\cos (\frac{\pi x}{5}) + (625+25\pi ^2+\pi ^4)\sin (\frac{\pi x}{5})\) and the the analytical solution is \(u(x)=\sin (\frac{\pi x}{5})\). The equation is designed such that all u derivative terms be included in the problem. Basis orders \(p=4,~5,~6\) are used for approximation and both quintic and sextic kernel functions are employed for obtaining the best convergence rates. For the case of fourth-order differential equations, two cases of boundary conditions must be satisfied on each of the boundary collocation points. Two sets of boundary conditions are considered for this problem. In both cases, predefined values of \(u(0)=0\) and \(u(10)=0\) are applied on two end points. Then, in the first case, predefined values of the first derivative values are considered as \(u_{,x}(0)=\frac{\pi }{5}, u_{,x}(10)=\frac{\pi }{5}\). For the second case, predefined values of second derivatives at end points are considered; \(u_{,xx}(0)=0, u_{,xx}(10)=0\). Same as the 2nd-order problem, number of collocation points for RKCM and GRKCM are 4 times the source points, where for HGRKCM are set to be equal (\(N_s=N_c\)). Note that since two extra collocation points are needed on the boundary points for this problem, the number of domain collocation points are selected to be less than the number of source points accordingly to keep the linear system of equations determined. The error \(L_2\) norm convergence rates are presented in Figs. 11 and 12.
This is obvious from the results that regular RKCM starts losing accuracy when moving to higher order differential equation, and also the obtained convergence rate is not as reliable as HGRKCM. On the other hand, HGRKCM yields the optimal convergence rate in all cases. Moreover, the method still forms a determined system which keeps the computational costs much lower compared to the other two methods. This is important to mention that results by GRKCM looks promising, but still a weighted over-determined system is required for obtaining an optimal convergence rate in this problem. Nevertheless, from Figs. 11c and 12c, it is noted that GRKCM convergence rate decreases, specially when nodal distance becomes smaller, due to accumulated error rising from direct derivatives calculation. Error convergence rate for 2nd order differential case is extendable to the 4th-order problems. The numerical results confirm that for RK approximation of order p, error \(L_2\) norm convergence rate will be \(p-3\) and \(p-2\) for odd and even orders of p, respectively. This is similar to what is reported in isogeometric collocation method in [44].
5.4 Two-dimensional Poisson’s equation
As the first two-dimensional example, the Poisson’s equation in (68) is considered.
The analytical solution is \(u(x,y)=e^{\frac{xy}{4}}\). In this problem, all the boundary conditions are applied as predefined values of u as essential boundary conditions. For convergence study, different number of source points of \(\{12\times 12 , 20\times 20, 28 \times 28 , 36\times 36 , 44\times 44 \}\) are used. For HGRKCM, the same number of collocation points is used as the number of source points, whereas for regular RKCM, collocation points are approximately four times the number of source points, \(\{ 23\times 23 , 39\times 39, 55\times 55 , 71\times 71 , 87\times 87 \}\). The numerical results are provided in Fig. 13.
Error \(L_2\) norm versus CPU-time comparison between RKCM and HGRKCM for elasticity problem
a CPU-time comparison versus source points number and b Error \(L_2\) norm versus CPU-time comparison between HGRKCM, FEM, and SCNI
Error \(L_2\) norm convergence rate for two-dimensional Poisson problem is approximately p and \(p-1\) for even and odd basis orders, respectively, which is consistent with the observation in one-dimensional problems. However, when using higher order basis orders, regular RKCM is unable to yield the expected optimal convergence rate. As mentioned in the previous sections, for obtaining optimal convergence rate by regular RK collocation methods, a weighted over-determined system is required. Although RKCM convergence and error estimation is comprehensively studied in [29, 31], to highlight the need of using an over-determined system, the Poisson’s equation is solved by using the same number of collocation and source points with second- and fourth-order basis and error convergence rates are compared with the ones from over-determined systems in Fig. 14a, b, respectively. As it is obvious from the plots in Fig. 14, error convergence rate decreases significantly in the case of determined system. Besides, even by using more collocation points than the source points, RKCM shows considerable sensitivity to the selected support size for constructing the RK shape functions. To show this sensitivity, the Poisson’s equation is solved with two other choices for support sizes of \(a=(p+0.1)h\) and \(a=(p+1.5)h\) using the fourth-order basis. Results are provided in Fig. 15a which imply the sensitivity of RKCM convergence rate to the shape function support size. In this specific example, for RKCM, \(p=4.5h\) yields the optimal convergence rate for the fourth-order basis. On the other hand, HGRKCM shows considerably lower sensitivity to the support domain size where for different choices of support radius, the convergence rate remains the same and solution accuracy changes insignificantly compared to RKCM (Fig. 15b).
Same as the second-order one-dimensional case, this problem is also solved using a non-uniform nodal distribution by RKCM and HGRKCM methods to examine the sensitivity of both methods to the nodal distribution. HGRKCM yields convergence rate consistent with the error estimation discussed in the previous section, while RKCM shows less accurate results and in some cases severe fluctuations in the convergence rate. Similar to 1D case, for RKCM, a weighted over-determined system with collocation points about four times the source points is used, while HGRKCM is implemented with a determined system with no weights. The nodal distribution for both cases are demonstrated in Fig. 16. The error convergence rates are also shown in Fig. 17, indicating that HGRKCM results are reliable and error convergence rates are stable compared to the RKCM.
5.5 Elasticity problem (internally pressurized elastic tube)
For testing HGRKCM in solving vector-field problems, an infinite internally pressurized elastic tube, as shown in Fig. 18a, is considered. Due to symmetry, a quarter of the actual configuration is modeled and solved (Fig. 18b). The boundary value problem and the boundary conditions are defined as:
The problem is solved by regular RKCM and HGRKCM. Since GRKCM performs closely to RKCM in most cases, it is not applied for solving the remaining problems in the paper. For both cases, numbers of source points used for constructing the shape functions are \(N_s=\{54, 187, 693, 2665\}\). While HGRKCM shows promising error convergence rate using a determined system (\(N_s=N_c\)), RKCM needs roughly four times more collocation points to converge. Corresponding collocation points are as \(N_c=\{187, 693, 2665, 10449\}\). Nodal distribution for both methods are depicted in Fig. 19. In this problem, nodal distances are not equal, which shows the behavior of both methods in a more general case of nodal distribution and domain geometry. Error \(L_2\) norm convergence rates are presented and compared in Fig. 20. This is where RKCM shows a high sensitivity to the nodal distribution pattern, including cases with the irregular domain geometry. It is observed that changing the nodal support size affects the convergence rate considerably. For RKCM, results shown in Fig. 20 are the best convergence rates obtained by trying different nodal support sizes and kernel orders. Notable point about HGRKCM is that optimal convergence rates are obtained with less sensitivity to support domain size and kernel order choices. The error decrease in numerical results on the corners and areas close to the boundaries is another observation from this example when using HGRKCM.
This is considered as a notable advantage of to obtain optional convergence rate and more accurate results for general problems, with less nodal pattern sensitivity and domain’s geometry dependency.
5.6 Rectangular Kirchhoff plate
A rectangular plate with clamped boundaries on four sides and material properties such that \(G=1\) in the domain \(\Omega \in [0,10] \times [0,10]\) is considered. For results comparison, the problem is selected similar to the one in [44]. The distributed load equation g(x, y) and the analytical solution \(u_z (x,y)\) are respectively:
In the case of 4th-order differential equations, two boundary conditions must be satisfied on each boundary. Consequently, the number of boundary collocation points must be at least twice the second-order PDEs. For this reason and for keeping the node construction simple, another set of collocation points are added on the primarily located points on the boundary. Therefore, the number of rows in \(\varvec{A}\) and \(\varvec{b}\) in (54) increases by the number of boundary collocation points. This is noteworthy to mention that the linear system for the 4th-order problem could be kept determined by adding extra source points to the domain or on the boundary. However, for the sake of simplicity in node construction process, it is easier to just add needed number of collocation points on the boundary. Both cases of determined and over-determined systems are observed yielding the same convergence rate in HGRKCM scheme. Since the extra boundary collocation points are added on exactly the same coordinate as the displacement collocation nodes, the shape functions values are the same as the essential boundary collocation points.
Explicit derivatives of RK shape functions need considerable computational effort, which besides being time-consuming may result in a high amount of accumulative numerical errors in the nodal values of the derivatives. The error is observed to considerably increase for higher order derivatives. Although for 4th-order one-dimensional equations RKCM yields solution (but not with an acceptable convergence rate in most cases), in two-dimensional case obtaining accurate results becomes almost impossible. Therefore, for all the following two-dimensional fourth-order cases, only HGRKCM is implemented and results for RKCM are not presented.
The error convergence rates using basis orders of \(p=4, 5, 6\) are presented in Fig. 21b. Similar to the 1D case, for odd and even basis orders the error convergence rates are \(p-3\) and \(p-2\), respectively. Numerical results are in agreement with those reported in [44] using IGA and [45] using RK collocation analysis. This is noted that for the simply supported rectangular plate, the same set of results are obtained.
6 CPU and running time comparison
CPU-time for constructing the shape functions, force and stiffness matrices are calculated for the purpose of performance comparison between conventional RKCM and the HGRKCM method. CPU-time comparison is performed for three different problems solved in the paper; two-dimensional Poisson’s and elasticity problems in Sects. 5.4 and 5.5. and the rectangular Kirchhoff plate. For the first two problems, as second-order PDEs, HGRKCM is shown to be ten times faster than RKCM in average. The CPU-time versus source points number plots in logarithmic scale are shown in Fig. 22 . Also, as an example, the error \(L_2\) norm is plotted versus CPU-time for the pressurized tube elasticity problem in Fig. 23. The plot indicates HGRKCM performs computationally more efficient than RKCM while keeping the numerical error considerably smaller.
As a more general comparison, HGRKCM is compared with FEM (4-node linear element with full integration) and RKPM with stabilized conforming nodal integration (SCNI) [38]. SCNI was introduced to address the inaccuracy of solution procedure caused by domain integration using Gauss quadrature in Galerkin mesh-free methods [38, 39, 46]. However, since it is required to construct smoothed shape functions over the nodal representative domains [39, 47], computational effort regarding constructing Voronoi cells must be considered. Therefore, for this comparison, beside the force and stiffness matrices construction, mesh and/or Voronoi-cells CPU-time is taken into account. Fig. 24a compares the error \(L_2\) norm versus CPU-time between FEM, RKPM-SCNI, and HGRKCM for solving Poisson equitation. Results show both FEM and HGRKCM running CPU-time are close, however HGRKCM shows a higher accuracy in solution. This should be mentioned that for keeping the comparison fair, second-order basis vector is used for HGRKCM. Obviously, with a negligible add-up to CPU-time, higher accuracy is obtainable by using higher order basis for HGRKCM. This is also shown that SCNI yields less accuracy and considerably higher CPU-time since constructing Voronoi cells and integrating over the boundaries of each cell is considerable. Figure 24b shows CPU-time versus number of nodes for all three cases. It is obvious from the results that HGRKCM remains the fastest method comparing to the other methods used for this comparison.
7 Conclusion
In this paper, the implicit gradient reproducing kernels are introduced in the collocation framework for solutions of 2nd and 4th order PDEs. All the derivatives approximations appearing in PDEs in the present method are constructed using the gradient reproducing conditions, instead of taking the direct derivatives of the RK approximation. Immediate advantages of doing so are threefold: in comparison to the direct derivative counterpart, (1) the computational cost for construction of derivative approximations reduces tremendously, (2) basis functions for derivative approximations are smooth and thus solutions are less sensitive to collocation point distribution and the support size, and (3) the accumulated error arising from calculating derivative approximations are greatly reduced and subsequently solutions become more accurate and stable in terms of error convergence rate, nodal perturbation, and support size in comparison to the direct derivative counterpart. Furthermore, since the direct derivatives are not used in the formulation, it is theoretically estimated and numerically tested that the same number of collocation points as the source points can be used to obtain the optimal solution in the least-squares sense, which enhances further the computational efficiency. Overall, the present method is around 10 to 25 times faster than its RKCM counterparts, dependent on the problem and discretization. The convergence property of the present method is estimated through a least-squares error analysis. The convergence rate of the least-squares error norm, measuring errors from the domain equation and boundary conditions, is estimated to be \(p-1\) and \(p-3\) for 2nd and 4th-order PDEs, respectively. It is interesting to note that although the further analysis is ongoing and has not yet been established, numerical results consistently show that the convergence rate elevates one order, p and \(p-2\) for 2nd and 4th-order PDEs, respectively, when even-order basis functions are used. The overall performance of the present method is compared with Galerkin based methods for solving 2nd-order PDEs. The present method shows better efficiency than RKPM with SCNI and comparable performance as FEM in terms of accuracy versus CPU time. The present method is also applied to solutions of one- and two-dimensional fourth-order PDEs such as Kirchhoff plate problem. The implementation is straightforward, solutions are accurate, and the convergence rates are shown to be stable in comparison to RKCM.
References
Nayroles B, Touzot G, Villon P (1992) Generalizing the finite element method: diffuse approximation and diffuse elements. Comput Mech 10(5):307–318
Belytschko T, Krongauz Y, Organ D, Fleming M, Krysl P (1996) Meshless methods: an overview and recent developments. Comput Methods Appl Mech Eng 139(1–4):3–47
Belytschko T, Lu YY, Gu L (1994) Element-free Galerkin methods. Int J Numer Methods Eng 37(2):229–256
Lancaster P, Salkauskas K (1981) Surfaces generated by moving least squares methods. Math Comput 37(155):141–158
Chen J-S, Pan C, Wu C-T, Liu WK (1996) Reproducing kernel particle methods for large deformation analysis of non-linear structures. Comput Methods Appl Mech Eng 139(1–4):195–227
Liu WK, Jun S, Zhang YF (1995) Reproducing kernel particle methods. Int J Numer Methods Fluids 20(8–9):1081–1106
Liu W-K, Li S, Belytschko T (1997) Moving least-square reproducing kernel methods (i) methodology and convergence. Comput Methods Appl Mech Eng 143(1–2):113–154
Babuska I, Melenk JM (1995) The partition of unity finite element method. tech. rep., DTIC Document
Sukumar N (1998) The natural element method in solid mechanics. Ph.D. thesis, Northwestern University
Atluri S, Cho J, Kim H-G (1999) Analysis of thin beams, using the meshless local Petrov–Galerkin method, with generalized moving least squares interpolations. Comput Mech 24(5):334–347
Strouboulis T, Babuška I, Copps K (2000) The design and analysis of the generalized finite element method. Comput Methods Appl Mech Eng 181(1):43–69
Liu WK, Han W, Lu H, Li S, Cao J (2004) Reproducing kernel element method. Part I: theoretical formulation. Comput Methods Appl Mech Eng 193(12):933–951
Chen J-S, Wang H-P (2000) New boundary condition treatments in meshfree computation of contact problems. Comput Methods Appl Mech Eng 187(3–4):441–468
Fernández-Méndez S, Huerta A (2004) Imposing essential boundary conditions in mesh-free methods. Comput Methods Appl Mech Eng 193(12–14):1257–1275
Moës N, Bechet E, Tourbier M (2005) Imposing essential boundary conditions in the extended finite element method, In: VIII international conference on computational plasticity. Citeseer, Barcelona
Fonseca A, Viana S, Silva E, Mesquita R (2008) Imposing boundary conditions in the meshless local Petrov–Galerkin method. IET Sci Meas Technol 2(6):387–394
Boyce B, Kramer S, Bosiljevac T, Corona E, Moore J, Elkhodary K, Simha C, Williams B, Cerrone A, Nonn A et al (2016) The second sandia fracture challenge: predictions of ductile failure under quasi-static and moderate-rate dynamic loading. Int J Fract 198(1–2):5–100
Liu G-R, Zhang G, Gu Y, Wang Y (2005) A meshfree radial point interpolation method (RPIM) for three-dimensional solids. Comput Mech 36(6):421–430
Hu H-Y, Li Z-C (2006) Collocation methods for Poisson’s equation. Comput Methods Appl Mech Eng 195(33):4139–4160
Li Z-C, Lu T-T, Hu H-Y, Cheng AH (2008) Trefftz and collocation methods. WIT Press, Ashurst
Hardy RL (1971) Multiquadric equations of topography and other irregular surfaces. J Geophys Res 76(8):1905–1915
Hardy RL (1990) Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968–1988. Comput Math Appl 19(8–9):163–208
Kansa EJ (1990) Multiquadrics—a scattered data approximation scheme with applications to computational fluid-dynamics—II solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput Math Appl 19(8):147–161
Hon Y, Schaback R (2001) On unsymmetric collocation by radial basis functions. Appl Math Comput 119(2):177–186
Kansa E, Hon Y (2000) Circumventing the ill-conditioning problem with multiquadric radial basis functions: applications to elliptic partial differential equations. Comput Math Appl 39(7–8):123–137
Aluru N (2000) A point collocation method based on reproducing kernel approximations. Int J Numer Methods Eng 47(6):1083–1121
Kim DW, Kim Y (2003) Point collocation methods using the fast moving least-square reproducing kernel approximation. Int J Numer Methods Eng 56(10):1445–1464
Onate E, Idelsohn S, Zienkiewicz O, Taylor R (1996) A finite point method in computational mechanics. Applications to convective transport and fluid flow. Int J Numer Methods Eng 39(22):3839–3866
Hu H-Y, Chen J-S, Hu W (2011) Error analysis of collocation method based on reproducing kernel approximation. Numer Methods Partial Differ Equ 27(3):554–580
Hu H-Y, Lai C-K, Chen J-S (2009) A study on convergence and complexity of reproducing kernel collocation method. National Science Council Tunghai University Endowment Fund for Academic Advancement Mathematics Research Promotion Center, Taichung City
Hu H, Chen J, Hu W (2007) Weighted radial basis collocation method for boundary value problems. Int J Numer Methods Eng 69(13):2736–2757
Wang D, Wang J, Wu J (2018) Superconvergent gradient smoothing meshfree collocation method. Comput Methods Appl Mech Eng 340:728–766
Chi S-W, Chen J-S, Hu H-Y, Yang JP (2013) A gradient reproducing kernel collocation method for boundary value problems. Int J Numer Methods Eng 93(13):1381–1402
Li S, Liu WK (1999) Reproducing kernel hierarchical partition of unity, part I—formulation and theory. Int J Numer Methods Eng 45(3):251–288
Li S, Liu WK (1999) Reproducing kernel hierarchical partition of unity, part II—applications. Int J Numer Methods Eng 45(3):289–317
Chen J-S, Zhang X, Belytschko T (2004) An implicit gradient model by a reproducing kernel strain regularization in strain localization problems. Comput Methods Appl Mech Eng 193(27):2827–2844
Li S, Liu WK (1998) Synchronized reproducing kernel interpolant via multiple wavelet expansion. Comput Mech 21(1):28–47
Chen J-S, Wu C-T, Yoon S, You Y (2001) A stabilized conforming nodal integration for Galerkin mesh-free methods. Int J Numer Methods Eng 50(2):435–466
Chen J-S, Hillman M, Chi S-W (2017) Meshfree methods: progress made after 20 years. J Eng Mech 143(4):04017001
Han W, Meng X (2001) Error analysis of the reproducing kernel particle method. Comput Methods Appl Mech Eng 190(46–47):6157–6181
Mirzaei D, Schaback R, Dehghan M (2012) On generalized moving least squares and diffuse derivatives. IMA J Numer Anal 32(3):983–1000
Timoshenko SP, Woinowsky-Krieger S (1959) Theory of plates and shells. McGraw-hill, New York
Auricchio F, Da Veiga LB, Hughes T, Reali A, Sangalli G (2010) Isogeometric collocation methods. Math Models Methods Appl Sci 20(11):2075–2107
Reali A, Gomez H (2015) An isogeometric collocation approach for Bernoulli–Euler beams and Kirchhoff plates. Comput Methods Appl Mech Eng 284:623–636 (Isogeometric Analysis Special Issue)
Qi D, Wang D, Deng L, Xu X, Wu C-T (2019) Reproducing kernel mesh-free collocation analysis of structural vibrations. Eng Comput 36(3):734–764
Guan P, Chi S, Chen J, Slawson T, Roth M (2011) Semi-Lagrangian reproducing kernel particle method for fragment-impact problems. Int J Impact Eng 38(12):1033–1047
Siriaksorn T, Chi S-W, Foster C, Mahdavi A (2018) u-p semi-Lagrangian reproducing kernel formulation for landslide modeling. Int J Numer Anal Methods Geomech 42(2):231–255
Acknowledgements
Research reported in this paper was partially supported by DoD SERDP under contract number W912HQ18C0099.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
To demonstrate how exactly the procedure shown in Sect. 2.4 works for constructing gradient reproducing kernel shape function’s derivative of a desired order, second derivative approximation of the two-dimensional vector field \(\varvec{u}\) is considered:
where \(\varvec{w}_{xx}\), \(\varvec{w}_{xx}\), and \(\varvec{w}_{xy}\) are the gradient second order derivatives approximation of vector field \(\varvec{u}\). Recalling (19),
where \(\varvec{C}^i\), \(i=1, 2, 3\), are the corresponding correction functions for each case constructed by the related coefficients vector and quadratic basis vector,
where \(\varvec{b}^i\) in each case is obtained by satisfying the partition of nullity and derivative reproducing conditions, in this case second order derivatives reproducing conditions.
For the second derivative with respect to x the reproducing condition are,
By multiplying (A.4a) by x and subtracting (A.4b):
Multiplying (A.4a) by y and subtracting (A.4c) results in:
For quadratic terms, By multiplying (A.4a) by \(x^2\), adding (A.4d), and then subtracting two times of (A.4f),
By following the same procedure and multiplying (A.4a) by \(y^2\) and adding (A.4e) and abstracting two time of (A.4f),
and finally, for the last term, by multiplying (A.4a) by xy, \(-y\) by (A.4b), \(-x\) by (A.4c), and summing up all these expressions with (A.4f),
Writing all Eqs. (A.5)–(A.9) and including the partition of nullity in (A.4a),
The right-hand side in (A.10) is the second-order explicit derivative of quadratic basis vector where \(\varvec{x}-\varvec{x}_I=0\). By taking the same steps for satisfying \(\Psi ^{yy}\) and \(\Psi ^{xy}\) all the second-order derivative reproducing conditions become,
By using the definitions of gradient derivatives of RK function in (A.2) and correction function in (A.3) and substituting those into Eq. (A.11),
where \(\varvec{M}\) is the moment matrix defined in (8). Eventually, by having coefficients vector in (A.12), the second-order gradient derivatives are derived as,
Obviously, equations in (A.13) are just different by their first terms, which indicates that the method is straightforward and computationally efficient. More importantly, the inversion of moment matrix derivatives, which suffer from ill-conditioning and large condition numbers are no longer needed to be calculated. Following the same rule, higher order gradient derivatives could be obtained.
Appendix B
Sub-matrices shown in Eq. (54) are shown in the following. \(\varvec{A}^i\) (\(i=1,\ldots ,13\)) in the case of 4th-order Kirchhoff plate discrete equation is defined as,
and for sub-matrices \(\varvec{b}^i\) (\(i=1,\ldots ,5\)),
where \(N_d\) denotes the domain collocation points. \(N_g\), \(N_h\), \(N_m\), and \(N_q\) are the numbers of displacement, rotation, moment and shear boundary collocation points, respectively.
Rights and permissions
About this article
Cite this article
Mahdavi, A., Chi, SW. & Zhu, H. A gradient reproducing kernel collocation method for high order differential equations. Comput Mech 64, 1421–1454 (2019). https://doi.org/10.1007/s00466-019-01724-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-019-01724-0