1 Introduction

Fractional calculus attracts much interest due to its ability to describe hereditary properties and memory phenomena in science and engineering fields such as in the areas of engineering vibrations [1], viscoelastic mechanics and rheology [2,3,4], control theory [5], anomalous diffusion [2, 6, 7], etc. Initial and boundary value problems for the fractional diffusion equation are an important research subject. The stability and existence of a solution of fractional differential equation were shown in [6, 8, 9].

It is well known that it is difficult to obtain an exact analytical solution within the scope of elementary functions for such a fractional differential equation. The finite difference method was used in [10,11,12,13] because it is easy to be understood and put into practice. In [12], Meerschaert and Tadjeran studied the approximate solution of fractional partial differential equation by the finite difference method and discussed the convergence under given conditions. Rawashdeh [14] used collocation method in polynomial spline space to study the numerical solution of a fractional integro-differential equation. Jafari and Daftardar-Gejji [15] used Adomian’s decomposition to solve fractional diffusion and wave equations. In [16], the boundedness theorem of general fractional integrals was proved. In [17], the discrete scheme was used to solve the time fractional diffusion equation in the sense of Caputo. Garrappa [18] gave a survey for numerical methods of the fractional differential equations including the multi-step methods, and designed a set of Matlab programs for problems of fractional order. Deng and Hesthaven [19] used local discontinuous Galerkin method to solve the spatial fractional diffusion equation. Chen and Li [20] used the compact difference scheme to solve the time fractional diffusion-wave equation.

The Chebyshev polynomials, applied in approximation theory and spectral methods of differential equation, play an increasingly important role in analytical and numerical analyses. Khader [21] proposed the shifted Chebyshev collocation method to solve the space fractional diffusion equation. Sweilam et al. [22, 23] used the second and third kind shifted Chebyshev polynomials to solve the space fractional diffusion equation.

In the present paper, we consider using the shifted Chebyshev polynomials of the first kind and the Picard iterative process to approximate the solution for the initial and boundary value problem of the time-space fractional diffusion equation. In the next section, we introduce some basic concepts used in this article. In Section 3, we describe the presented method by using the shifted Chebyshev polynomials and collocation method for the space variable combined with the Picard iterative process and matrix Mittag-Leffler function for the time variable. The method is verified by a numerical example. Conclusions are presented in Section 4.

2 Basic concepts

Definition 1

The Riemann-Liouville fractional integral of order \(\alpha \) is defined as the convolution,

$$\begin{aligned} J_{x}^\alpha f(x) =\frac{{{x^{\alpha - 1}}}}{{\Gamma ( \alpha )}} * f(x)= \int _0^x {\frac{{{{(x - \xi )}^{\alpha - 1}}}}{{\Gamma (\alpha )}}f(\xi )} d\xi ,\ x>0, \end{aligned}$$
(1)

if \(\alpha >0\), and \(J_{x}^0 f(x) = f(x)\) if \(\alpha =0\), where \(\Gamma (\cdot )\) is Euler’s Gamma function. The fractional integral has the properties

$$\begin{aligned} J_x^\alpha J_x^\lambda f(x)= & {} J_x^{\alpha + \lambda }f(x),\alpha ,\lambda \ge 0, \end{aligned}$$
(2)
$$\begin{aligned} J_x^\alpha {x^\eta }= & {} \frac{{\Gamma (\eta + 1)}}{{\Gamma (\eta + \alpha + 1)}}{x^{\alpha + \eta }},\alpha \ge 0,\eta > - 1. \end{aligned}$$
(3)

Definition 2

Let \(m-1<\alpha \le m\) and \(m \in \textbf{N}^+\). Then the \(\alpha \)-order Caputo fractional derivative is defined as the composition of the fractional integral and integer-order derivative

$$\begin{aligned} D_x^\alpha f(x) = {J_x^{m - \alpha }}{f^{(m)}}(x), \ x>0. \end{aligned}$$
(4)

The fractional integral and the Caputo fractional derivative satisfy linear law, e.g.

$$\begin{aligned} {D_x^\alpha }(\lambda f(x) + \mu g(x)) = \lambda {D_x^\alpha }f(x) + \mu {D_x^\alpha }g(x), \end{aligned}$$
(5)

where \(\lambda \) and \(\mu \) are constants. The Caputo fractional derivative of a monomial is [7]

$$\begin{aligned} {D_x^\alpha }{x^n}=\left\{ { \begin{array}{*{20}{l}} {0,}&{}{n < \lceil \alpha \rceil }\\ {\frac{{\Gamma (n + 1)}}{{\Gamma (n + 1 - \alpha )}}{x^{n - \alpha }},}&{}{n \ge \lceil \alpha \rceil } \end{array}} \right. , \end{aligned}$$
(6)

where n is a nonnegative integer and \(\lceil \alpha \rceil \) is the smallest integer not less than \(\alpha \). The \(\alpha \)-order integral of \(\alpha \)-order Caputo fractional derivative of function f(x) has the following relation with the initial values [24],

$$\begin{aligned} {J_x^{\alpha }}{D_x^\alpha }f(x) = f(x) - \sum \limits _{k = 0}^{m - 1} {{f^{(k)}}(0)} \frac{{{{x }^k}}}{{k!}},\ m - 1 < \alpha \le m. \end{aligned}$$
(7)

More definitions and properties of fractional derivative were introduced in [7].

Definition 3

The Mittag-Leffler function with two parameters is defined as [25]:

$$\begin{aligned} {E_{\alpha ,\beta }}(z) = \sum \limits _{k = 0}^\infty {\frac{{{z^k}}}{{\Gamma (\alpha k + \beta )}}} ,\alpha> 0,\beta > 0,z \in \textbf{C}. \end{aligned}$$
(8)

The definition can be generalized to the case of matrix variable, i.e. the matrix Mittag-Leffler function

$$\begin{aligned} {E_{\alpha ,\beta }}(A) = \sum \limits _{k = 0}^\infty {\frac{{{A^k}}}{{\Gamma (\alpha k + \beta )}}} ,\ \alpha> 0,\ \beta > 0, \end{aligned}$$
(9)

where A is an nth-order matrix and \({A^0} = I\), the nth-order unit matrix.

Definition 4

The Chebyshev polynomials of the first kind are defined by the formulae [26]

$$\begin{aligned} {T_n}(z) = \cos \left( {n\arccos z} \right) , \ - 1 \le z \le 1,\ n = 0,1,\ldots . \end{aligned}$$
(10)

The zeros of \({T_n}(z)\) have the exact expression \({z_i} = \cos \left( {\frac{{2i + 1}}{{2n}}\pi } \right) ,\ i = 0,1,\ldots ,n - 1,\) and the explicit expressions of \({T_n}(z)\) have the forms

$$\begin{aligned} {T_0}(z)=1,\ {T_n}(z) = n\sum \limits _{i = 0}^{\left[ {\frac{n}{2}} \right] } {{{( - 1)}^i}{2^{n - 2i - 1}}} \frac{{(n - i - 1)!}}{{(i)!(n - 2i)!}}{z^{n - 2i}},\ n=1,2,\dots , \end{aligned}$$
(11)

where \(\left[ {\frac{n}{2}} \right] \) is the integral part of \(\frac{n}{2}\).

The shifted Chebyshev polynomials are defined by

$$\begin{aligned} T_n^*(x)=T_n(2x - 1), \ 0\le x \le 1, \end{aligned}$$

which have the zeros \({x_i} = \frac{1}{2} + \frac{1}{2}\cos \left( {\frac{{2i + 1}}{{2n}}\pi } \right) ,i = 0,1,\ldots ,n - 1,\) and the explicit expressions

$$\begin{aligned} T_0^*(x) =1,\ T_n^*(x) = n \sum \limits _{i = 0}^n {{{( - 1)}^i}{2^{2n - 2i}}} \frac{{(2n - i - 1)!}}{{(i)!(2n - 2i)!}}{x^{n - i}},\ n=1,2,\dots . \end{aligned}$$
(12)

Suppose y(x) is \(L_2\) integrable on the interval [0, 1] with respect to the weight function \(\rho (x)=\frac{1}{\sqrt{x - x^2 }}\), then it has series expansion in the shifted Chebyshev polynomials

$$\begin{aligned} y(x) = \sum \limits _{i = 0}^\infty {{c_i}T_i^*} (x), \end{aligned}$$
(13)

where the coefficient \(c_i\) are given as the follows:

$$\begin{aligned} {c_0} = \frac{1}{\pi }\int _0^1 {\frac{1}{{\sqrt{x - {x^2}} }}y(x)T_0^*(x)} dx,\ {c_i} = \frac{2}{\pi }\int _0^1 {\frac{1}{{\sqrt{x - {x^2}} }}y(x)T_i^*(x)} dx,\ i\ge 1. \end{aligned}$$
(14)

When the series in (13) is approximated by its truncation

$$\begin{aligned} {y_m}(x) = \sum \limits _{i = 0}^m {{c_i}T_i^*} (x), \end{aligned}$$
(15)

the error is no more than the sum of the absolute values of the coefficients after the first \((m+1)\)-terms in (13) [21]. For more results on convergence, see [26].

3 The solution of the time-space fractional diffusion equation

We consider the time-space fractional diffusion equation

$$\begin{aligned} D_t^\beta u(x,t) = c D_x^\alpha u(x,t) + s(x,t),\ 0<x<1,\ t >0, \end{aligned}$$
(16)

where \(0 < \beta \le 1\), \(1 < \alpha \le 2\), c is a constant and s(x, t) is a source term, subject to the following initial and the Dirichlet boundary conditions:

$$\begin{aligned} u(x,0)= & {} {u_0}(x),\ 0< x < 1, \end{aligned}$$
(17)
$$\begin{aligned} u(0,t)= & {} {b_0},\ u(1,t) = {b_1},\ t>0. \end{aligned}$$
(18)

The solving process is divided into the following three steps.

3.1 The integration with respect to the space variable merging the boundary conditions

We use \(J_{x,\eta }^{\alpha } f(x)\) to represent the value of the fractional integral \(J_{x}^{\alpha } f(x)\) at \(x=\eta \),

$$\begin{aligned} J_{x,\eta }^\alpha f(x) = \int _0^\eta {\frac{{{{(\eta - \xi )}^{\alpha - 1}}}}{{\Gamma (\alpha )}}f(\xi )} d\xi . \end{aligned}$$
(19)

Applying the integral operator \(J_x^\alpha ( \cdot )\) to both sides of equation (16) leads to

$$\begin{aligned} cJ_x^\alpha D_x^\alpha u(x,t) = J_x^\alpha D_t^\beta u(x,t) - J_x^\alpha s(x,t). \end{aligned}$$
(20)

According to equation (7), the composition of the left hand side of (20) involves the boundary values at \(x=0\)

$$\begin{aligned} J_x^\alpha D_x^\alpha u(x,t) = u(x,t) - {b_0} - {u_x^\prime } (0,t)x, \end{aligned}$$
(21)

where \({u_x^\prime } (0,t)\) is to be determined.

Substituting (21) into (20) yields

$$\begin{aligned} cu(x,t) - c{b_0} - c{u_x^\prime } (0,t)x = J_x^\alpha D_t^\beta u(x,t) - J_x^\alpha s(x,t). \end{aligned}$$
(22)

Collocating equation (22) at \(x=1\) and using the boundary value at \(x=1\) we have

$$\begin{aligned} c{u_x^\prime } (0,t) = c{b_1} - c{b_0} -J_{x,1}^\alpha D_t^\beta u(x,t) + J_{x,1}^\alpha s(x,t). \end{aligned}$$
(23)

Substituting (23) into (22) we obtain

$$\begin{aligned} cu(x,t) \!=\! c{b_0}(1 - x) + c{b_1}x - x J_{x,1}^\alpha D_t^\beta u(x,t) + xJ_{x,1}^\alpha s(x,t) + J_x^\alpha D_t^\beta u(x,t) - J_x^\alpha s(x,t). \end{aligned}$$
(24)

So the initial and boundary value problem, (16)–(18), is converted to the initial value problem of equation (24) with the initial value (17).

3.2 The shifted Chebyshev polynomial expansion and collocation method

We use the truncation of the shifted Chebyshev polynomial expansion with respect to the space variable x to approximate the solution u(x, t) as

$$\begin{aligned} u(x,t) \doteq \sum \limits _{i = 0}^m {{a_i}(t)T_i^*(x)}. \end{aligned}$$
(25)

So equation (24) can be written in the following form

$$\begin{aligned} \begin{array}{*{20}{l}} {c\sum \limits _{i = 0}^m {{a_i}(t)T_i^*(x) = } }&{}{c{b_0}(1 - x) + c{b_1}x - xJ_{x,1}^\alpha D_t^\beta \sum \limits _{i = 0}^m {{a_i}(t)T_i^*(x)} }\\ {}&{}{ + J_x^\alpha {D_t^\beta \sum \limits _{i = 0}^m {{a_i}(t)T_i^*(x)} } + xJ_{x,1}^\alpha s(x,t) - J_x^\alpha s(x,t)}, \end{array} \end{aligned}$$
(26)

Rearranging equation (26) leads to

$$\begin{aligned} \begin{array}{l} \sum \limits _{i = 0}^m {D_t^\beta {a_i}(t)\left[ {xJ_{x,1}^\alpha T_i^*(x) - J_x^\alpha T_i^*(x)} \right] } \\ \qquad = - c\sum \limits _{i = 0}^m {{a_i}(t)T_i^*(x)} + c{b_0}(1 - x) + c{b_1}x + xJ_{x,1}^\alpha s(x,t) - J_x^\alpha s(x,t). \end{array} \end{aligned}$$
(27)

In order to solve the \(m+1\) functions \(a_i(t)\), \(i=0,1,\dots , m\), we collocate equation (27) at the \(m+1\) zeros \({x_p}\) of the shifted Chebyshev polynomial \(T_{m+1}^*(x)\) to get \(m+1\) fractional differential equations as follows,

$$\begin{aligned}{} & {} \sum \limits _{i = 0}^m {D_t^\beta {a_i}(t)\left[ {{x_p}J_{x,1}^\alpha T_i^*(x) - J_{x,{x_p}}^\alpha T_i^*(x)} \right] } \nonumber \\{} & {} \quad = - c\sum \limits _{i = 0}^m {{a_i}(t)T_i^*({x_p})} + c{b_0}(1 - {x_p}) + c{b_1}{x_p} + {x_p}J_{x,1}^\alpha s(x,t) - J_{x,{x_p}}^\alpha s(x,t),\nonumber \\{} & {} p=0,1,\ldots ,m, \end{aligned}$$
(28)

where the zeros have the precise expressions \({x_p} = \frac{1}{2} + \frac{1}{2}\cos \left( {\frac{{2p + 1}}{{2m + 2}}\pi } \right) \), \(p=0,1,\ldots ,m\).

In matrix notation, the equation system has the form

$$\begin{aligned} AD_t^\beta {\textbf{a}}(t) = B{\textbf{a}}(t) + {\textbf{c}}(t), \end{aligned}$$
(29)

where \({\textbf{a}}(t) = {({a_0}(t),{a_1}(t),\ldots ,{a_m}(t))^T}\),

$$\begin{aligned} {\textbf{c}}(t)= & {} \left( { \begin{array}{*{20}{c}} {c{b_0}(1 - {x_0}) + c{b_1}{x_0} + {x_0}J_{x,1}^\alpha s(x,t) - J_{x,{x_0}}^\alpha s(x,t)}\\ \vdots \\ {c{b_0}(1 - {x_m}) + c{b_1}{x_m} + {x_m}J_{x,1}^\alpha s(x,t) - J_{x,{x_m}}^\alpha s(x,t)} \end{array}} \right) ,\\ A= & {} \left( \begin{array}{*{20}{c}} {{x_0}J_{x,1}^\alpha T_0^*(x) - J_{x,{x_0}}^\alpha T_0^*(x)}&{} \cdots &{}{{x_0}J_{x,1}^\alpha T_m^*(x) - J_{x,{x_0}}^\alpha T_m^*(x)}\\ \vdots &{} \ddots &{} \vdots \\ {{x_m}J_{x,1}^\alpha T_0^*(x) - J_{x,{x_m}}^\alpha T_0^*(x)}&{} \cdots &{}{{x_m}J_{x,1}^\alpha T_m^*(x) - J_{x,{x_m}}^\alpha T_m^*(x)} \end{array}\right) , \\ B= & {} \left( { \begin{array}{*{20}{c}} { - cT_0^*({x_0})}&{} \cdots &{}{ - cT_m^*({x_0})}\\ \vdots &{} \ddots &{} \vdots \\ { - cT_0^*({x_m})}&{} \cdots &{}{ - cT_m^*({x_m})} \end{array}} \right) . \end{aligned}$$

Premultiplication by \(A^{-1}\) on both sides of equation (29) leads to

$$\begin{aligned} D_t^\beta {\textbf{a}}(t) = {A^{ - 1}}B{\textbf{a}}(t) + {A^{ - 1}}{\textbf{c}}(t). \end{aligned}$$
(30)

The initial values \({{a}_i}(0)\) are the coefficients of the shifted Chebyshev polynomial expansion of u(x, 0), 

$$\begin{aligned} u(x,0) = {u_0}(x) = \sum \limits _{i = 0}^m {{a_i}(0)T_i^*(x)} , \end{aligned}$$
(31)

where

$$\begin{aligned} \begin{array}{l} {a_0}(0) = \frac{1}{\pi }\int _0^1 {\frac{1}{{\sqrt{x - {x^2}} }}{u_0}(x)T_0^*(x)} dx,\\ {a_i}(0) = \frac{2}{\pi }\int _0^1 {\frac{1}{{\sqrt{x - {x^2}} }}{u_0}(x)T_i^*(x)} dx, \ i=1,2,\ldots ,m. \end{array} \end{aligned}$$
(32)

3.3 Solution for \({\textbf{a}}(t)\) by the Picard iterative process

Now we derive the series solution of the initial value problem, (30) and (32), by using the Picard iterative process. Operating the fractional integral \(J_t^\beta (\cdot )\) on both sides of equation (30) yields

$$\begin{aligned} {\textbf{a}}(t) ={\textbf{a}}(0) + {A^{ - 1}}BJ_t^\beta {\textbf{a}}(t) + J_t^\beta {A^{ - 1}}{\textbf{c}}(t). \end{aligned}$$
(33)

Denote the kth approximate solution of the Picard iteration by \({{\varvec{\varphi }} _k}(t)\), then the iterative scheme starting from the 0th approximate solution is

$$\begin{aligned} {{\varvec{\varphi }} _0}(t)= & {} {\textbf{a}}(0),\end{aligned}$$
(34)
$$\begin{aligned} {{\varvec{\varphi }} _k}(t)= & {} {\textbf{a}}(0) + {A^{ - 1}}BJ_t^\beta {{\varvec{\varphi }} _{k - 1}}(t) + J_t^\beta {A^{ - 1}}{\textbf{c}}(t),\ k \ge 1. \end{aligned}$$
(35)

The expression of the kth approximate solution is derived as follows,

$$\begin{aligned} {{\varvec{\varphi }} _1}(t)= & {} {\textbf{a}}(0) + \frac{{{A^{ - 1}}B{t^\beta }}}{{\Gamma (\beta + 1)}}{\textbf{a}}(0) + J_t^\beta {A^{ - 1}}{\textbf{c}}(t),\nonumber \\ {{\varvec{\varphi }} _2}(t)= & {} {\textbf{a}}(0) + \frac{{{A^{ - 1}}B{t^\beta }}}{{\Gamma (\beta + 1)}}{\textbf{a}}(0) + \frac{{{{\left( {{A^{ - 1}}B} \right) }^2}{t^{2\beta }}}}{{\Gamma (2\beta + 1)}}{\textbf{a}}(0) + J_t^\beta {A^{ - 1}}{\textbf{c}}(t) + {A^{ - 1}}BJ_t^{2\beta }{A^{ - 1}}{\textbf{c}}(t),\nonumber \\{} & {} \cdots \nonumber \\ {{\varvec{\varphi }} _k}(t)= & {} \sum \limits _{j = 0}^k {\frac{{{{\left( {{A^{ - 1}}B} \right) }^j}{t^{j\beta }}}}{{\Gamma (j\beta + 1)}}{\textbf{a}}(0)} + \sum \limits _{j = 0}^{k - 1} {{{\left( {{A^{ - 1}}B} \right) }^j}J_t^{(j + 1)\beta }{A^{ - 1}}{\textbf{c}}(t)} . \end{aligned}$$
(36)

Denoting the fractional integrals as convolutions and taking the limit \(k \rightarrow \infty \) for \({{\varvec{\varphi }} _k}(t)\) we get the series form of the solution,

$$\begin{aligned} {\textbf{a}}(t) = \sum \limits _{j = 0}^\infty {\frac{{{{\left( {{A^{ - 1}}B} \right) }^j}{t^{j\beta }}}}{{\Gamma (j\beta + 1)}}{\textbf{a}}(0) + } \sum \limits _{j = 0}^\infty {\frac{{{{\left( {{A^{ - 1}}B} \right) }^j}{t^{j\beta + \beta - 1}}}}{{\Gamma (j\beta + \beta )}}} *{A^{ - 1}}{\textbf{c}}(t). \end{aligned}$$
(37)

In matrix Mittag-Leffler functions, equation (37) can be written as follows,

$$\begin{aligned} {\textbf{a}}(t) = {{\mathbf{a_t}}}(t) + {{\mathbf{a_s}}}(t) = {E_{\beta ,1}}({A^{ - 1}}B{t^\beta }){\textbf{a}}(0) + {t^{\beta - 1}}{E_{\beta ,\beta }}({A^{ - 1}}B{t^\beta }) * {A^{ - 1}}{\textbf{c}}(t), \end{aligned}$$
(38)

where

$$\begin{aligned} {{\textbf{a}}_{\textbf{t}}}(t)= & {} {E_{\beta ,1}}({A^{ - 1}}B{t^\beta }){\textbf{a}}(0), \end{aligned}$$
(39)
$$\begin{aligned} {{\textbf{a}}_{\textbf{s}}}(t)= & {} {t^{\beta - 1}}{E_{\beta ,\beta }}({A^{ - 1}}B{t^\beta })*{A^{ - 1}}{\textbf{c}}(t)= \int _0^t {{\tau ^{\beta - 1}}{E_{\beta ,\beta }}({A^{ - 1}}B{\tau ^\beta }){A^{ - 1}}{\textbf{c}}(t - \tau )d\tau },\ \ \end{aligned}$$
(40)

are the transient component caused by the initial condition u(x, 0) and the steady-state component caused by the boundary condition and the source term, respectively. After finding out \({\textbf{a}}(t)\), we can write out the approximate solution of the original initial and boundary problem by equation (25).

We note that the convolution in equation (40) is an improper integral. By using the relation

$$\begin{aligned} \frac{d}{{dt}}\left( {{t^\beta }{E_{\beta ,\beta + 1}}({A^{ - 1}}B{t^\beta })} \right) = {t^{\beta - 1}}{E_{\beta ,\beta }}({A^{ - 1}}B{t^\beta }), \end{aligned}$$
(41)

which can be verified by termwise derivation, the singularity in the convolution in equation (40) can be removed through integration by parts

$$\begin{aligned} {{\textbf{a}}_{\textbf{s}}}(t)= & {} \int _0^t {{\tau ^{\beta - 1}}{E_{\beta ,\beta }}({A^{ - 1}}B{\tau ^\beta }){A^{ - 1}}{\textbf{c}}(t - \tau )d\tau }\nonumber \\= & {} {t^\beta }{E_{\beta ,\beta + 1}}({A^{ - 1}}B{t^\beta }){A^{ - 1}}{\textbf{c}}(0) + \int _0^t {{\tau ^\beta }{E_{\beta ,\beta + 1}}({A^{ - 1}}B{\tau ^\beta }){A^{ - 1}}{\mathbf{c'}}(t - \tau )d\tau } \nonumber \\= & {} {t^\beta }{E_{\beta ,\beta + 1}}({A^{ - 1}}B{t^\beta }){A^{ - 1}}{\textbf{c}}(0) + {t^\beta }{E_{\beta ,\beta + 1}}({A^{ - 1}}B{t^\beta })*{A^{ - 1}}{\mathbf{c'}}(t). \end{aligned}$$
(42)

Here we suppose that \({\textbf{c}}'(t)\) is continuous on the interested interval [0, T].

If it is difficult to compute analytically the convolution integrals in (40) or (42), we can use a numerical integral method to cope with the definite integral in (42). For example, by introducing \(t_n = n h\), \(n=0,1,\ldots ,N\), then for \(1 \le n \le N\) we have from the composite trapezoidal integration,

$$\begin{aligned} \begin{array}{rcl} {{\textbf{a}}_{\textbf{s}}}({t_n}) &{}=&{} t_n^\beta {E_{\beta ,\beta + 1}}({A^{ - 1}}Bt_n^\beta ){A^{ - 1}}{\textbf{c}}(0) + \int _0^{{t_n}} {{\tau ^\beta }{E_{\beta ,\beta + 1}}({A^{ - 1}}B{\tau ^\beta }){A^{ - 1}}{\mathbf{c'}}({t_n} - \tau )d\tau } \\ &{}\doteq &{} t_n^\beta {E_{\beta ,\beta + 1}}({A^{ - 1}}Bt_n^\beta ){A^{ - 1}}{\textbf{c}}(0) + \sum \limits _{j = 0}^n {{\omega _{n,j}}t_j^\beta {E_{\beta ,\beta + 1}}({A^{ - 1}}Bt_j^\beta ){A^{ - 1}}{\mathbf{c'}}({t_n} - {t_j})}\\ &{}=&{} t_n^\beta {E_{\beta ,\beta + 1}}({A^{ - 1}}Bt_n^\beta ){A^{ - 1}}{\textbf{c}}(0) + \sum \limits _{j = 0}^n {{\omega _{n,j}}(jh)^\beta {E_{\beta ,\beta + 1}}({A^{ - 1}}B(jh)^\beta ){A^{ - 1}}{\mathbf{c'}}((n-j)h)} , \end{array} \ \ \end{aligned}$$
(43)

where \({\omega _{n,0}} = {\omega _{n,n}} = \frac{h}{2},\ {\omega _{n,j}} = h,\ j = 1,2,\ldots ,n - 1.\) We note that for a second-order continuously differentiable function, the truncation error of the composite trapezoidal integration is proportional to \(t_n h^2\).

Example

Consider the initial and boundary value problem of the fractional diffusion equation

$$\begin{aligned}{} & {} D_t^{\frac{1}{2}}u(x,t) = D_x^{\frac{3}{2}}u(x,t) + s(x,t),0< x < 1,t > 0,\end{aligned}$$
(44)
$$\begin{aligned}{} & {} u(x,0) = {x^2}(1 - x),\end{aligned}$$
(45)
$$\begin{aligned}{} & {} u(0,t) = u(1,t) = 0, \end{aligned}$$
(46)

where the source function is \(s(x,t) = \frac{4}{3}\sqrt{\frac{x}{\pi }} \left( { 2\left( {1-x } \right) {{\left( {tx} \right) }^{\frac{3}{2}}} + 3\left( {1 + {t^2}} \right) \left( {2x - 1} \right) } \right) \). The problem has the exact solution \({u_{\textrm{exa}}}(x,t) = {x^2}(1 - x)(1 + {t^2})\).

The problem is solved by applying the suggested method with \(m=3\), i.e.

$$\begin{aligned} {u}(x,t) = \sum \limits _{i = 0}^3 {{a_i}(t)T_i^*(x)}. \end{aligned}$$
(47)

The coefficients are derived as in equation (38),

$$\begin{aligned} {\textbf{a}}(t) = {E_{\frac{1}{2},1}}({A^{ - 1}}B{t^{\frac{1}{2}}}){\textbf{a}}(0) + {t^{-\frac{1}{2}}}{E_{\frac{1}{2},\frac{1}{2}}}({A^{ - 1}}B{t^{\frac{1}{2}}})*{A^{ - 1}}{\textbf{c}}(t), \end{aligned}$$
(48)

where

$$\begin{aligned} A= & {} \left( { \begin{array}{*{20}{r}} {0.0139042}&{}{0.0188288}&{}{0.00530401}&{}{ - 0.00519951}\\ {0.0876465}&{}{0.0892460}&{}{ - 0.0468704}&{}{ - 0.0947289}\\ {0.103192}&{}{0.0507067}&{}{ - 0.110300}&{}{ - 0.0170167}\\ {0.0230453}&{}{ - 0.000310640}&{}{ - 0.0155545}&{}{0.00714167} \end{array}} \right) ,\\ B= & {} \left( { \begin{array}{*{20}{r}} { - 1.00000}&{}{ - 0.923880}&{}{ - 0.707107}&{}{ - 0.382683}\\ { - 1.00000}&{}{ - 0.382683}&{}{0.707107}&{}{0.923880}\\ { - 1.00000}&{}{0.382683}&{}{0.707107}&{}{ - 0.923880}\\ { - 1.00000}&{}{0.923880}&{}{ - 0.707107}&{}{0.382683} \end{array}} \right) ,\\ \textbf{c}(t)= & {} \left( { \begin{array}{*{20}{c}} {0.0352182 + 0.00193840{t^{\frac{3}{2}}} + 0.0352182{t^2}}\\ {0.147524 + 0.0212986{t^{\frac{3}{2}}} + 0.147524{t^2}}\\ {0.0658641 + 0.0232590{t^{\frac{3}{2}}} + 0.0658641{t^2}}\\ {0.00139345 + 0.00327922{t^{\frac{3}{2}}} + 0.00139345{t^2}} \end{array}} \right) ,\\ {\textbf{a}}(0)= & {} {\left( {0.0625,0.03125,-0.0625,-0.03125} \right) ^T}. \end{aligned}$$

Approximating the convolution integral in equation (48) by using the composite trapezoidal integration rule as in equation (43), we have at \(t_n=nh,\) \(n\ge 1\),

$$\begin{aligned} {\textbf{a}}({t_n}) \doteq {\hat{\textbf{a}}}({t_n})= & {} {E_{\frac{1}{2},1}}({A^{ - 1}}B{t_n^{\frac{1}{2}}}){\textbf{a}}(0) + {t_n^{\frac{1}{2}}}{E_{\frac{1}{2},\frac{3}{2}}}({A^{ - 1}}B{t_n^{\frac{1}{2}}}){A^{ - 1}}{\textbf{c}}(0)\nonumber \\{} & {} + \sum \limits _{j = 0}^n {{\omega _{n,j}}(jh)^{\frac{1}{2}} {E_{\frac{1}{2},\frac{3}{2}}}({A^{ - 1}}B(jh)^{\frac{1}{2}} ){A^{ - 1}}{\mathbf{c'}}((n-j)h)} , \end{aligned}$$
(49)

where \({\omega _{n,0}} = {\omega _{n,n}} = \frac{h}{2},\ {\omega _{n,j}} = h,\ j = 1,2,\ldots ,n - 1. \) Using this result of numerical integration, the approximate solution of the original problem at \(t=t_n\) is denoted by \(u_{\textrm{Che}}(x, t_n) = \sum \limits _{i = 0}^3 {{{\hat{a}}_i}(t_n)T_i^*(x)}\).

Fig. 1
figure 1

At \(t=1\), the exact solution \({u_{\textrm{exa}}}(x,1)\) (solid line) and the approximate solutions \(u_{\textrm{Che}}(x,1)\) (dash line) computed by using the different time step-sizes h

Full size image
Fig. 2
figure 2

The absolute errors of the approximate solutions \(u_{\textrm{Che}}(x,1)\) computed by using the different time step-sizes \(h=0.1\) (solid line), \(h=0.05\) (dash line), \(h=0.025\) (dot line) and \(h=0.0125\) (dot-dash line)

Full size image

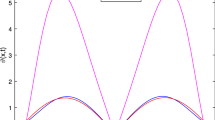
In Figure 1, the approximate solutions \(u_{\textrm{Che}}(x, 1)\) at \(t=1\) are plotted together with the exact solution \({u_{\textrm{exa}}}(x,1)\), where the convolution integration was computed by using the different time step-sizes \(h=0.1\), 0.05, 0.025 and 0.0125. The corresponding absolute errors \(|{u}_{\textrm{exa}}(x,1) - u_{\textrm{Che}}(x,1)|\) for the four approximations are plotted in Figure 2. Corresponding to the four decreasing values of the step-size h, the maxima of the absolute errors are calculated to be 0.0105972, 0.00448355, 0.00182718 and 0.000718710. An obvious convergence is displayed.

4 Conclusions

We considered the solution of the initial and boundary value problem for the time-space fractional diffusion equation in the sense of Caputo based on the Chebyshev collocation method. First we converted the problem to an initial value problem of fractional integral-differential equation merging the boundary conditions. Then the solution was expanded by using the shifted Chebyshev polynomials with respect to the space variable and the collocation method led to a fractional ordinary differential equation system about the coefficient functions of the time variable. Further, the coefficient functions of the time variable were obtained in terms of the matrix Mittag-Leffler functions by using the Picard iterative process. We also presented a numerical method to cope with the improper convolution integral on the time variable in the steady-state component of the coefficient functions.

We verified the proposed method with a numerical example with exact solution. For the approximate solutions obtained by using the proposed method, the absolute errors become smaller with the decreasing of the step-size h of the time variable. This conclusion demonstrates the effectiveness and great potential of the Chebyshev collocation method for the solution of the fractional differential equation. All plots were generated by using Wolfram Mathematica 12.