1 Introduction

In the field of statistical mechanics, people can deduce the time-fractional diffusion equation (tFDE) by assuming the jump length and the waiting time between two successive jumps are independent and respectively follow Gaussian distribution and power law distribution as time large, see, e.g., Metzler and Klafter [30]. Because tFDEs were well performed in catching the behavior of the diffusion processes with memory effect, it attracted more and more attention from many fields, such as rheology [1], transport theory [8], viscoelasticity [28], non-Markovian stochastic processes [31], etc.

However, on the attempting to describe some complex dynamical systems, several researches confronted with the situation that the fractal dimension of the heterogeneous media determined by the Hurst index [29] that changes as the geometrical structure or property of the media changes. Mathematically, it reflects that the fractional orders in tFDEs are temporally or spatially varying.

The fractional models involving variable-order derivatives have more feasibility to catch some behavior of complex dynamical system than the constant fractional order case in a large class of physical, biological and physiological diffusion phenomena. For example, shape memory polymer due to the change of its microstructure [23], the shale gas production due to the hydraulic fracturing [37], the tritium transport through a highly heterogeneous medium at the macrodispersion experimental site [39], polymer gels [34] and magnetorheological elastomers [5] in imposed electric and magnetic fields. We also refer to [9] for the relaxation processes and reaction kinetics of proteins under changing temperature field. These work indicated that the behavior of the above diffusion processes in response to temperature, electrostatic field strength or magnetic field strength changes may be better described using variable order elements rather than the constant order.

Variable-order tFDEs have appeared in more and more applications, but mathematical researches on analyzing the variable-order tFDEs is relatively new and is still at an early stage. For the variable-order tFDEs with the time independent principle elliptic part, Umarov and Steinberg [42] proved the existence and uniqueness theorem of a solution of the Cauchy problem for variable order tFDEs via the explicit representation formula (see, e.g., [21, 33]) of the solution for constant-order fractional PDEs. Wang and Zheng [44] studied the wellposedness of the initial-boundary value problems of variable order tFDE, in which the principle elliptic part is time independent, so the Mittag-Leffler function and the eigenfunction expansion argument, which is a widely used technique in analyzing tFDEs, can be used to derive the desired results. Kian, Soccorsi and Yamamoto [16] studied tFDEs with space depending variable order, in which the t-analyticity of the solution is proved and so the Laplace transform technique is utilized to derive the wellposedness. For the numerical methods for solving the variable order tFDEs, we refer to some work given by W. Chen and his group [11, 37, 38], F. Liu and his group [2, 3, 53], Wu, Baleanu, Xie and Zeng [46] , Zaky, Doha, Taha and Baleanu [49] and the references therein.

In this paper, assuming \(T\in (0,\infty )\) and \(\Omega\) is an open bounded domain in \({\mathbb {R}}^d\) with a sufficiently smooth boundary \(\partial \Omega\), we will consider the following initial-boundary value problem of variable-order tFDE:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u + q(x)\partial _t^{\alpha (\cdot )} u + L(t)u + p(t)u = f(x,t), &{} (x,t) \in \Omega _T:=\Omega \times (0,T),\\ u(x,0)=0, &{} x\in \Omega , \\ \sum _{i=1}^d a_{ij}(x,t) \partial _{x_i} u(x,t) \nu _j=0, &{} (x,t) \in \Sigma :=\partial \Omega \times (0,T), \end{array}\right. } \end{aligned}$$
(1.1)

where \((\nu _1,\nu _2,\ldots ,\nu _d)\) is the unit out normal vector at the boundary \(\partial \Omega\), and L(t) is a symmetric uniformly elliptic operator defined by

$$\begin{aligned} L(t) u(x):= -\sum _{i,j=1}^d \partial _{x_i} \left( a_{ij}(x,t) \partial _{x_j} u(x)\right) , \quad u\in H^2(\Omega ) \end{aligned}$$

with \(a_{ij}(x,t) = a_{ji}(x,t)\) \((1\le i,j \le d),\ x\in {\overline{\Omega }}\) and \(a_{ij}\in C^1(\overline{\Omega _T})\) such that

$$\begin{aligned} \sum _{i,j=1}^d a_{ij}(x,t)\xi _i \xi _j \ge a_0\sum _{i=1}^d\xi _j^2 ,\quad \forall (x,t)\in \overline{\Omega _T},\ \forall (\xi _1,\ldots ,\xi _d )\in {\mathbb {R}}^d \end{aligned}$$

for some positive constant \(a_0\). In the system (1.1), by \(\partial ^{\alpha (\cdot )}_t\) we denote the Caputo fractional derivative of temporal variable order \(\alpha (t)\in (0,1)\):

$$\begin{aligned} \partial ^{\alpha (\cdot )}_t g(t) := \frac{1}{\Gamma (1-\alpha (t))} \int _0^t (t-\tau )^{-\alpha (t)}\, \frac{d}{d\tau } g(\tau )\, d\tau . \end{aligned}$$

The coefficient q depends only on x, the potential function p is only t-dependent, and they are assumed to be in function spaces \(L^\infty (\Omega )\), \(L^\infty (0,T)\) respectively. We assume the source term \(f\in L^2(\Omega _T)\). In the above variable-order tFDE (1.1), the variable order, diffusion coefficient and potential are all time dependent, hence the previous analytical techniques, such as the Fourier expansion and Laplace transform argument used in [16, 42, 44], do not work in the current context, which increases the difficulty in the study of the wellposedness for the forward problem.

In addition, the parameters e.g., fractional order, source, potential and initial value, are usually unknown and cannot be obtained directly in most practical applications. It should be inferred as an inverse problem from suitable additional data which can be easily obtained based on the forward problems. This is a more practical issue and has been widely concerned in theoretical and numerical researches for tFDEs in recent years. We do not intend to give a full list of the works. We refer to Huang, Li and Yamamoto [12], Jiang, Li, Liu and Yamamoto [13], Liu, Rundell and Yamamoto [26] for inverse source problems. We refer to Chen, Liu, Jiang, Turner and Burrage [4], Li, Zhang, Jia and Yamamoto [20], Li, Imanuvilov and Yamamoto [22] for recovering the fractional orders. Kian, Li, Liu and Yamamoto [18], Kian, Oksanen, Soccorsi and Yamamoto [17], Jin and Rundell [14] are concerned with the inverse problem in determining the spatially varying potential. For recovering t-dependent potential, we refer to Zhang and Zhou [50], Sun, Zhang and Wei [40]. For backward problems, we refer to Liu and Yamamoto [25] , Florida, Li and Yamamoto [7] and Wang and Liu [43]. We also refer to Jin and Rundell [15] for a survey of the inverse problems for fractional differential equations. It seems that the most existing works are concerned with inverse problems for (constant-order) tFDEs. Up to now, the available study on inverse problems associated with variable-order case are meager. Wang, Wang, Li and Wang [45] investigated a tFDE involving space and time depending variable fractional order derivative in which the homotopy regularization algorithm was applied to solve the inverse problem in simultaneously determining the fractional order and the diffusion coefficient. Zheng, Cheng and Wang [51] proved the uniqueness of determining the variable fractional order of the initial-boundary value problems of variable-order tFDEs in one space dimension with some available observed values of the unknown solutions inside the spatial domain.

As far as we know, there is no theoretical analysis and numerical algorithm for inverse coefficient problems in the variable-order tFDEs with time dependent principle elliptic part, since the useful analytic techniques, e.g., Mittag-Leffler function expression and Laplace transform argument cannot work here. Regarding the importance of inverse coefficient problems, we here consider the theoretical analysis and numerical reconstruction of the time dependent potential from energy type measured data. The reasons why we choose the integral type observation conclude two aspects. One is that the energy method could help us investigate the mathematical theories, and the other one is that it can average the error of point measurements, which will make the inversion algorithm more stable.

Inverse Problem 1.1

We assume \(u\in H^1(0,T;L^2(\Omega ))\cap L^2(0,T;H^2(\Omega ))\) is the solution to the system (1.1). We intend to determine the temporally varying potential \(p\in L^\infty (0,T)\) by measuring the energy data

$$\begin{aligned} E(t):=\left( \int _\Omega u^2(x,t) dx\right) ^{\frac{1}{2}},\quad t\in (0,T]. \end{aligned}$$
(1.2)

As this is the first paper to study the uniqueness and numerical algorithms for the reconstruction of the time dependent potential in a variable-order tFDE with time dependent principle elliptic part. We would like to point out the main difficulties for the reconstruction and the novelties of this paper. The essential difficulties are

  1. 1.

    the fractional order, diffusion coefficient and potential are time varying, which makes the usual analytical techniques, like Mittag-Leffler function expression and Laplace transform argument, cannot work;

  2. 2.

    the inverse problem of identifying the potential is nonlinear, which makes that there are quite a few mathematical tools can work. Indeed, it is difficult to give an exact formula for the solution operator of our inverse problem. Moreover, the techniques based on linearity, such as compact operator theory and Fredholm alternative principle, are no longer applicable to our inverse problem.

The main novelties of this paper include

  1. 1.

    we prove the wellposedness for the forward problem (1.1) by regarding the fractional order term as a perturbation of the first order time derivative and using the theoretical results for the parabolic equations;

  2. 2.

    we obtain the uniqueness for the inverse potential problem by the use of the energy methods on basis of a newly established coercivity of the variable order time fractional derivative in Lemma 4.1;

  3. 3.

    numerically, we construct a newly wellposed adjoint system and propose an iterative thresholding algorithm, which makes the numerical implementation easy and computationally cheap.

2 Main results and outline

For the initial-boundary value problem (1.1), we will first prove the well-posedness of the solution. Before stating the main theorem, we list several restrictions on the coefficients.

Assumption 2.1

  1. (a)

    \(\alpha (\cdot )\in C[0,T]\) such that \(0<\alpha (\cdot )<1\) in [0, T].

  2. (b)

    \(p(\cdot )\in L^\infty (0,T)\), \(q(\cdot )\in L^\infty (\Omega )\) and \(f\in L^2(\Omega _T)\).

Under Assumption 2.1, by regarding the fractional order term as a perturbation of the first order time-derivative, the unique existence of the solution as well as regularity of the solution can be proved by Fredholm principle for compact operators. We now state the first main theorem.

Theorem 2.1

Under Assumption 2.1, the initial-boundary value problem (1.1) admits a unique weak solution \(u\in H^1(0,T;L^2(\Omega ))\cap L^2(0,T;H^2(\Omega ))\) such that

$$\begin{aligned} \Vert \partial _tu\Vert _{L^2(0,T;L^2(\Omega ))} + \Vert u\Vert _{L^2(0,T;H^2(\Omega ))} \le C\Vert f\Vert _{L^2(0,T;L^2(\Omega ))}. \end{aligned}$$

The above theorem indicates that the solution has the full regularity as the parabolic analogues do. Most importantly, based on the above regularity of the solution, one can show the coercivity of the variable order time-fractional derivative (see Lemma 4.1 ), from which we can further derive the uniqueness of the inverse problem.

Theorem 2.2

Under Assumption 2.1, and we further suppose that ess \(\inf _{\Omega } q(x) > 0\) and \(\alpha (\cdot )\in C^1[0,T]\). Let \(u_1, u_2\in H^1(0,T;L^2(\Omega )) \cap L^2(0,T;H^2(\Omega ))\) be the solutions to (1.1) with respect to \(p_1,p_2\in L_+^\infty (0,T):=\{p\in L^\infty (0,T); p\ge 0, \text{ a.e. } t\in (0,T) \}\), then the observation data

$$\begin{aligned} \left( \int _\Omega u_1^2(x,t) dx\right) ^{\frac{1}{2}} = \left( \int _\Omega u_{2}^{2}(x,t)dx\right) ^{\frac{1}{2}} >0 \end{aligned}$$

for any \(t\in (0,T)\) implies

$$\begin{aligned} p_1 = p_2 \text{ and } u_1 = u_2. \end{aligned}$$

The remaining parts of this manuscript are structured as follows. Section 3 is concerned with the well-posedness of the initial-boundary value problem (1.1). In Sect. 4, we address a coercivity of the variable order time-fractional derivatives, based on which we prove a uniqueness result for an inverse problem of the determination of the potential from the energy type observed value of the unknown solution. In Sect. 5, we transform the inverse problem into an optimization problem with Tikhonov regularization, which will be solved by an iterative thresholding algorithm. Several examples are also given to show the accuracy and efficiency of our algorithm. Finally, the concluding remarks are given in Sect. 6.

3 Well-posedness of the forward problem

In this part, we are concerned with the unique existence of the solution to the initial-boundary value problem (1.1) as well as the regularity estimates for the solution under suitable topology. Recalling that the coefficients in (1.1) are t and/or x dependent, the Fourier expansion argument in Sakamoto and Yamamoto [33] cannot be directly used any more. Here we will introduce a novel method to avoid the expansion argument. The key idea is regarding the fractional order term as a source term and using the theoretical results for the parabolic equations to construct a compact operator, and then the well-posedness of the problem (1.1) can be shown from the Fredholm alternative principle.

For the purpose, we introduce the Riemann-Liouville integral operator \(J^{\alpha }\): for any \(v(t)\in L^2(0,T)\),

$$\begin{aligned} J^{\alpha }v(t) = \frac{1}{\Gamma (\alpha )}\int ^t_0 (t-s)^{\alpha -1} v(s) ds. \end{aligned}$$
(3.1)

Then we first establish the following useful lemma for later use.

Lemma 3.1

Let \(\alpha (\cdot )\in C[0,T]\) such that \(0< \alpha (t)<1\) for any \(t\in [0,T]\), and we choose \(\varepsilon >0\) being small enough such that \(1-\varepsilon -\alpha (t)>0\) for any \(t\in [0,T]\). Then the following estimate

$$\begin{aligned} \Vert \partial _t^{\alpha (\cdot )} g\Vert _{L^{2}(0,T)} \le C\Vert g\Vert _{H^{1-\varepsilon }(0,T)} \end{aligned}$$

is valid for any \(g\in H^{1}(0,T)\) satisfying \(g(0)=0\).

Proof

Firstly, from Wang and Zheng [44, Lemma 2.2], it follows that

$$\begin{aligned} \partial _t^{\alpha (\cdot )} g(t) =\left[ \frac{1}{\Gamma (1-\alpha (t))} \frac{d}{ds} \int _0^s ( s - \tau )^{-\alpha (t)} g(\tau )d\tau \right] _{s=t}. \end{aligned}$$
(3.2)

From the assumptions on g, it follows that \(g\in H^{1-\varepsilon }(0,T)\), and then we can find an element \(h\in L^2(0,T)\) such that \(g=J^{1-\varepsilon } h\) in view of Gorenflo, Luchko and Yamamoto [10, Theorem 2.1]. Then from the definition of \(J^{1-\varepsilon }\) and the Fubini lemma, we see that

$$\begin{aligned} \partial _t^{\alpha (\cdot )} g(t)&=\frac{1}{\Gamma (1-\varepsilon )} \frac{1}{\Gamma (1-\alpha (t))} \left[ \frac{d}{ds} \int _0^s ( s - \tau )^{-\alpha (t)} \int _0^\tau (\tau -\eta )^{-\varepsilon } h(\eta ) d\eta d\tau \right] _{s=t}\\&=\frac{1}{\Gamma (1-\varepsilon )} \frac{1}{\Gamma (1-\alpha (t))} \left[ \frac{d}{ds} \int _0^s \int _\eta ^s ( s - \tau )^{-\alpha (t)} (\tau -\eta )^{-\varepsilon } d\tau h(\eta ) d\eta \right] _{s=t}\\&=\frac{1}{\Gamma (2-\varepsilon -\alpha (t))} \left[ \frac{d}{ds} \int _0^s (s-\eta )^{1-\varepsilon -\alpha (t)} h(\eta ) d\eta \right] _{s=t}. \end{aligned}$$

Since \(1-\varepsilon -\alpha (t)>0\) for any \(t\in [0,T]\), we further see that

$$\begin{aligned} \partial _t^{\alpha (\cdot )} g(t)&=\frac{1}{\Gamma (1-\varepsilon -\alpha (t))} \int _0^t (t-\eta )^{-\varepsilon -\alpha (t)} h(\eta ) d\eta . \end{aligned}$$

Noting the fact that

$$\begin{aligned} t^{-\varepsilon -\alpha (t)} \le t^{-\varepsilon -\overline{\alpha }} T^{{\overline{\alpha }} - \alpha (t)} \le t^{-\varepsilon -\overline{\alpha }} \max \{1, T^{{\overline{\alpha }}}\},\quad t\in (0,T], \end{aligned}$$
(3.3)

where \({\overline{\alpha }}:=\sup _{t\in [0,T]} \alpha (t)\), we see that \(\partial _t^{\alpha (\cdot )} g\) can be estimated as follows

$$\begin{aligned} |\partial _t^{\alpha (\cdot )} g| \le \max \{1,T^{{\overline{\alpha }}}\}\sup _{t\in [0,T]} \left| \frac{1}{\Gamma (1-\varepsilon -\alpha (t))} \right| \int _0^t (t-\eta )^{-\varepsilon -{\overline{\alpha }}} |h(\eta )| d\eta . \end{aligned}$$

Further, we employ the Young inequality for the convolution to derive

$$\begin{aligned} \Vert \partial _t^{\alpha (\cdot )} g\Vert _{L^2(0,T)}&\le \max \{1,T^{{\overline{\alpha }}}\}\sup _{t\in [0,T]} \left| \frac{1}{\Gamma (1-\varepsilon -\alpha (t))} \right| \int _0^T t^{-\varepsilon -{\overline{\alpha }}} dt \Vert h\Vert _{L^2(0,T)}\\&\le \frac{T^{1-\varepsilon -{\overline{\alpha }}}}{1-\varepsilon -{\overline{\alpha }}} \max \{1, T^{{\overline{\alpha }}}\}\sup _{t\in [0,T]} \left| \frac{1}{\Gamma (1-\varepsilon -\alpha (t))} \right| \Vert h\Vert _{L^2(0,T)} \le C\Vert h\Vert _{L^2(0,T)}. \end{aligned}$$

Finally, noting that \(\Vert h\Vert _{L^2(0,T)} \sim \Vert g\Vert _{H^{1-\varepsilon }(0,T)}\), see e.g., Gorenflo, Luchko and Yamamoto [10, Theorem 2.1], Kubica and Yamamoto [19], we finish the proof of the lemma. \(\square\)

The above lemma indicates that the definition of the variable order Captuo derivative \(\partial _t^{\alpha (\cdot )}\) can be extended to the fractional Sobolev space \(H^{1-\varepsilon }(0,T)\) by following the argument used in Gorenflo, Luchko and Yamamoto [10]. Actually, in the case of \(1-\varepsilon -\alpha (t)>0\), \(\forall t\in [0,T]\), by noting the relation (3.2), for \(g\in H^{1-\varepsilon }(0,T)\) satisfying \(g(0)=0\), we define

$$\begin{aligned} \partial _t^{\alpha (\cdot )} g(t)&:= \lim _{n\rightarrow \infty } \partial _t^{\alpha (\cdot )} g_n(t)\\&=\lim _{n\rightarrow \infty } \left[ \frac{1}{\Gamma (1-\alpha (t))} \frac{d}{ds} \int _0^s ( s - \tau )^{-\alpha (t)} g_n(\tau )d\tau \right] _{s=t}. \end{aligned}$$

Here \(g_n\in H^{1-\varepsilon }(0,T)\) such that \(g_n(0)=0\). We still denote the extended operator by \(\partial _t^{\alpha (\cdot )}\) if there is no conflict. Then Lemma 3.1 immediately implies the following corollary.

Corollary 3.1

Let \(\alpha (\cdot )\in C[0,T]\) such that \(0< \alpha (t)<1\) for any \(t\in [0,T]\), and we choose \(\varepsilon >0\) being small enough such that \(1-\varepsilon -\alpha (t)>0\) for any \(t\in [0,T]\). Then the following estimate

$$\begin{aligned} \Vert \partial _t^{\alpha (\cdot )} g\Vert _{L^2(0,T)} \le C\Vert g\Vert _{H^{1-\varepsilon }(0,T)} \end{aligned}$$

is valid for any \(g\in H^{1-\varepsilon }(0,T)\) satisfying \(g(0)=0\).

We also need a unique result for the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t v + L(t)v + p(t)v = - q\partial _t^{\alpha (\cdot )} v, &{} x\in \Omega _T,\\ v(x,0) = 0, &{} x\in \Omega ,\\ \sum _{i,j=1}^d a_{ij}(x,t) \partial _{x_i}v(x,t) \nu _j= 0, &{} x\in \Sigma . \end{array}\right. } \end{aligned}$$
(3.4)

Lemma 3.2

Suppose \(v\in H^1(0,T;L^2(\Omega )) \cap L^2(0,T; H^2(\Omega ))\) is a solution to the system (3.4), then \(v\equiv 0\) in \(\Omega _T\).

Proof

By regarding the term \(-q\partial _t^{\alpha (\cdot )}v\) as a new source term, we multiply equation in (3.4) by v and \(\partial _t v\) separately, and follow the argument used in the proof of [6, Theorem 5, p.360] to discover

$$\begin{aligned} \begin{aligned}&\Vert v(\cdot ,t)\Vert _{H^1(\Omega )} + \int _0^t \Vert \partial _\tau v(\cdot ,\tau )\Vert _{L^2(\Omega )}^2 d\tau \\&\quad \le C\int _0^t \left| \int _\Omega \partial _\tau v(x,\tau )\partial _\tau ^{\alpha (\cdot )}v(x,\tau )dx \right| d\tau + C\int _0^t \left| \int _\Omega v(x,\tau )\partial _\tau ^{\alpha (\cdot )}v(x,\tau )dx \right| d\tau , \end{aligned} \end{aligned}$$
(3.5)

where C is a constant which is independent of t. Moreover, from the definition of the Caputo derivative of variable order, in view of the Hölder inequality, it follows that

$$\begin{aligned} \begin{aligned}&\left| \int _\Omega v(x,t)\partial _t^{\alpha (\cdot )}v(x,t) dx \right| \\&\quad \le \frac{1}{\Gamma (1-\alpha (t))} \int _0^t (t-\tau )^{-\alpha (t)} \left| \langle \partial _\tau v(\cdot ,\tau ),v(\cdot ,t) \rangle _{L^2(\Omega )} \right| d\tau \\&\quad \le \frac{\Gamma _0}{4\varepsilon } \int _0^t (t-\tau )^{-\alpha (t)} \Vert \partial _\tau v(\cdot ,\tau )\Vert _{L^2(\Omega )}^2 d\tau + \varepsilon \Gamma _0 \int _0^t (t-\tau )^{-\alpha (t)} \Vert v(\cdot ,t)\Vert _{L^2(\Omega )}^2 d\tau . \end{aligned} \end{aligned}$$
(3.6)

Here \(\varepsilon >0\) is sufficiently small and \(\Gamma _0:=\sup _{t\in [0,T]} \frac{1}{\Gamma (1-\alpha (t))}\). Now using the inequality (3.3), we conclude that \((t-\tau )^{-\alpha (t)} \le \max \{1,T^{{\overline{\alpha }}}\}(t-\tau )^{-{\overline{\alpha }}}\). Therefore, the above estimate (3.6) can be further treated as follows

$$\begin{aligned}&\left| \int _\Omega v(x,t)\partial _t^{\alpha (\cdot )}v(x,t) dx \right| \\&\quad \le \frac{\Gamma _0\max \{1,T^{-{\overline{\alpha }}}\}}{4\varepsilon } \int _0^t (t-\tau )^{-{\overline{\alpha }}} \Vert \partial _\tau v(\cdot ,\tau )\Vert _{L^2(\Omega )}^2 d\tau \\&\qquad + \varepsilon \Gamma _0\max \{1, T^{1-{\overline{\alpha }}}\} \frac{T^{1-{\overline{\alpha }}}}{1-{\overline{\alpha }}} \Vert v(\cdot ,t)\Vert _{L^2(\Omega )}^2. \end{aligned}$$

Similarly, we can obtain

$$\begin{aligned}&\left| \int _\Omega \partial _\tau v(x,\tau )\partial _\tau ^{\alpha (\cdot )}v(x,\tau ) dx \right| \\&\quad \le \frac{\Gamma _0\max \{1,T^{-{\overline{\alpha }}}\}}{4\varepsilon } \int _0^t (t-\tau )^{-{\overline{\alpha }}} \Vert \partial _\tau v(\cdot ,\tau )\Vert _{L^2(\Omega )}^2 d\tau \\&\qquad + \varepsilon \Gamma _0\max \{1, T^{1-{\overline{\alpha }}}\} \frac{T^{1-{\overline{\alpha }}}}{1-{\overline{\alpha }}} \Vert \partial _tv(\cdot ,t)\Vert _{L^2(\Omega )}^2. \end{aligned}$$

Substituting the above two estimates into (3.5), and choosing \(\varepsilon >0\) sufficiently small, we see that (3.5) can be rephrased as follows

$$\begin{aligned} \Vert \partial _t v(\cdot ,t)\Vert _{L^2(\Omega )}^2 \le C \int _0^t \left[ \int _0^\tau (\tau -\eta )^{-{\overline{\alpha }}} \Vert \partial _\eta v(\cdot ,\eta )\Vert _{L^2(\Omega )}^2 d\eta \right] d\tau ,\quad t\in (0,T). \end{aligned}$$

We conclude from the Fubini lemma that

$$\begin{aligned} \Vert \partial _t v(\cdot ,t)\Vert _{L^2(\Omega )}^2&\le C \int _0^t \left[ \int _\eta ^t (\tau -\eta )^{-{\overline{\alpha }}} d\tau \right] \Vert \partial _\eta v(\cdot ,\eta )\Vert _{L^2(\Omega )}^2d\eta ,\\&\le C \int _0^t (t-\eta )^{1-{\overline{\alpha }}} \Vert \partial _\eta v(\cdot ,\eta )\Vert _{L^2(\Omega )}^2 d\eta ,\quad t\in (0,T). \end{aligned}$$

Finally, from the Gronwall inequality, we derive \(\partial _t v=0\) in \(\Omega _T\), which combined with \(v(x,0)=0\) in \(\Omega\) implies \(v=0\) in \(\Omega _T\).

The proof of the lemma is finished. \(\square\)

Now we are ready to show the well-posedness of the problem (1.1).

Lemma 3.3

Let \(T>0\) and \(\alpha (\cdot )\in C[0,T]\) such that \(\alpha (t)\in (0,1)\) for \(t\in [0,T]\), and we suppose \(f\in L^2(\Omega _T)\). Then the initial-boundary value problem (1.1) admits a unique weak solution \(u\in H^1(0,T;L^2(\Omega ))\cap L^2(0,T;H^2(\Omega ))\) satisfying

$$\begin{aligned} \Vert \partial _tu\Vert _{L^2(0,T;L^2(\Omega ))} + \Vert u\Vert _{L^2(0,T;H^2(\Omega ))} \le C\Vert f\Vert _{L^2(0,T;L^2(\Omega ))}. \end{aligned}$$

Proof

From the superposition of the problem (1.1), we consider the following two subproblems separately:

$$\begin{aligned} \partial _t v + L(t)v + p(t)v = f(x,t) \end{aligned}$$
(3.7)

and

$$\begin{aligned} \partial _t w + L(t)w + p(t)w = - q\partial _t^{\alpha (\cdot )} u \end{aligned}$$
(3.8)

with the same initial and boundary conditions as in (1.1). Here in the above equation (3.8), we assume \(u\in H^{1-\varepsilon }(0,T;L^2(\Omega ))\). In view of Lemma 3.1, we see from the theoretical results of parabolic equations that there exist unique solutions to the above two problems (3.7) and (3.8). We denote them as \(u_f\) and \(K_\alpha u\) separately. It remains to show that there exists a unique solution \(u\in H^1(0,T;L^2(\Omega ))\cap L^2(0,T;H^2(\Omega ))\) for the operator equation \(u=K_\alpha u + u_f\).

From Lemma 3.1 and the well-known regularity for parabolic equations (e.g., [24, Section 4.7.1, p.243]), we have \(u_f, K_\alpha u\in H^1(0,T; L^2(\Omega ))\cap L^2(0,T; H^2(\Omega ))\) such that

$$\begin{aligned} \Vert \partial _t u_f\Vert _{L^2(0,T; L^2(\Omega ))} + \Vert u_f\Vert _{L^2(0,T; H^2(\Omega ))} \le C\Vert f\Vert _{L^2(0,T;L^2(\Omega ))}, \end{aligned}$$
(3.9)

and

$$\begin{aligned} \Vert \partial _t K_\alpha u\Vert _{L^2(0,T; L^2(\Omega ))} + \Vert K_\alpha u\Vert _{L^2(0,T; H^2(\Omega ))} \le C\Vert q\partial _t^{\alpha (\cdot )} u\Vert _{L^2(0,T;L^2(\Omega ))}\le C\Vert u\Vert _{H^{1-\varepsilon }(0,T;L^2(\Omega ))}. \end{aligned}$$
(3.10)

By [41, Theorem 2.1] and [24, Theorem 16.2, Chapter 1], we see that \(H^1(0,T; L^2(\Omega ))\cap L^2(0,T; H^2(\Omega ))\) is compact in \(H^{1-\varepsilon }(0,T; L^2(\Omega ))\), which further implies \(K_\alpha\): \(H^{1-\varepsilon }(0,T; L^2(\Omega )) \rightarrow H^{1-\varepsilon }(0,T; L^2(\Omega ))\) is a compact operator. By the Fredholm alternative for compact operators, \(u=K_\alpha u + u_f\) admits a unique solution in \(H^{1-\varepsilon }(0,T; L^2(\Omega ))\) as long as

$$\begin{aligned} I-K_\alpha \text{ is } \text{ one-to-one } \text{ on } H^{1-\varepsilon }(0,T; L^2(\Omega )). \end{aligned}$$

Here I denotes the identity operator.

Therefore, we need to show that \((I-K_\alpha )v = 0\) implies \(v=0\). Indeed, noting that \(v=K_\alpha v\) is just the solution to (3.4), then we obtain from Lemma 3.2 that \(I-K_\alpha\) is one-to-one on \(H^{1-\varepsilon }(0,T; H^{-1}(\Omega ))\). Hence, by Fredholm alternative, there exists a unique solution of \(u=K_\alpha u + u_f\) and the solution admits the following regularity estimates

$$\begin{aligned} \Vert u\Vert _{H^{1-\varepsilon }(0,T;L^2(\Omega ))} \le \Vert (I-K_\alpha )^{-1}\Vert \Vert u_f\Vert _{L^2(0,T;L^2(\Omega ))} \le C\Vert f\Vert _{L^2(0,T;L^2(\Omega ))}. \end{aligned}$$

We further derive from (3.9) and (3.10) that

$$\begin{aligned} \Vert u\Vert _{L^2(0,T;H^2(\Omega ))} = \Vert K_\alpha u +u_f\Vert _{L^2(0,T;H^2(\Omega ))} \le C\Vert f\Vert _{L^2(0,T;L^2(\Omega ))} \end{aligned}$$

and

$$\begin{aligned} \Vert \partial _t u\Vert _{L^2(0,T;L^2(\Omega ))} = \Vert \partial _t(K_\alpha u +u_f)\Vert _{L^2(0,T;L^2(\Omega ))} \le C\Vert f\Vert _{L^2(0,T;L^2(\Omega ))}. \end{aligned}$$

Combining all the above estimates, we finish the proof of the lemma. \(\square\)

4 Uniqueness of the inverse potential problem

In this section, we shall prove the uniqueness theorem proposed in Sect. 2. For the sake of convenience in fractional calculus, we will first establish several estimates related to the Caputo derivatives of variable order which will be useful for the proof of Theorem 2.2.

The first lemma indicates the coercivity of the Caputo derivative.

Lemma 4.1

(Coercivity) Let \(\alpha (\cdot )\in C[0,T]\) such that \(\alpha (t)\in (0,1)\), \(t\in [0,T]\). Then the following coercivity inequality

$$\begin{aligned} g(t)\partial _t^{\alpha (\cdot )}g(t) \ge \frac{1}{2}\partial _t^{\alpha (\cdot )} |g(t)|^2,\quad \text{ a.e. } t\in (0,T) \end{aligned}$$

holds true for any function \(g\in H^1(0,T)\).

Proof

For simplicity, we denote

$$\begin{aligned} I(t) := g(t)\partial _t^{\alpha (\cdot )}g(t) - \frac{1}{2}\partial _t^{\alpha (\cdot )} |g(t)|^2. \end{aligned}$$

Then it is sufficient to prove \(I \ge 0\). The proof is done by direct calculations. By the definition of Caputo fractional derivative, we find

$$\begin{aligned} I(t)&= \frac{1}{\Gamma (1-\alpha (t))} \left( \int _0^t (t-\tau )^{-\alpha (t)} g(t) g'(\tau ) d\tau - \int _0^t (t-\tau )^{-\alpha (t)} g(\tau ) g'(\tau ) d\tau \right) \\&= \frac{1}{\Gamma (1-\alpha (t))} \int _0^t (t-\tau )^{-\alpha (t)} (g(t)-g(\tau )) g'(\tau ) d\tau \\&= -\frac{1}{2\Gamma (1-\alpha (t))} \int _0^t (t-\tau )^{-\alpha (t)} \frac{d}{d\tau } |g(t)-g(\tau )|^2 d\tau . \end{aligned}$$

By a direct calculation, we further claim that

$$\begin{aligned} \lim _{\tau \rightarrow t}(t-\tau )^{-\alpha (t)} |g(t)-g(\tau )|^2 =0. \end{aligned}$$
(4.1)

Indeed, by noting that

$$\begin{aligned} (t-\tau )^{-\alpha (t)} |g(t)-g(\tau )|^2&\le (t-\tau )^{-\alpha (t)} \left( \int _\tau ^t |g'(s)| ds \right) ^2\\&\le (t-\tau )^{-\alpha (t)} \int _\tau ^t |g'(s)|^2 ds \int _\tau ^t 1^2 ds\\&\le (t-\tau )^{1-\alpha (t)} \Vert g\Vert _{H^1(0,T)}^2, \end{aligned}$$

where in the second inequality we used the Hölder inequality. Thus the claim (4.1) is true. Finally, by integration by parts, we see that

$$\begin{aligned} I(t)&= -\frac{1}{2\Gamma (1-\alpha (t))} (t-\tau )^{-\alpha (t)} |g(t)-g(\tau )|^2 \Big |_{\tau =0}^{\tau =t} \\&\quad + \frac{\alpha (t)}{2\Gamma (1-\alpha (t))} \int _0^t (t-\tau )^{-\alpha (t)-1} |g(t)-g(\tau )|^2 d\tau \\&= \frac{1}{2\Gamma (1-\alpha (t))} t^{-\alpha (t)} |g(t)-g(0)|^2 \\&\quad + \frac{\alpha (t)}{2\Gamma (1-\alpha (t))} \int _0^t (t-\tau )^{-\alpha (t)-1} |g(t)-g(\tau )|^2 d\tau \ge 0. \end{aligned}$$

This completes the proof of the lemma. \(\square\)

Lemma 4.2

Let \(\alpha (\cdot )\in C[0,T]\) satisfy \(\alpha (t)\in (0,1)\), \(t\in [0,T]\). Then there exists a positive constant \(C=C(T,\alpha )\) such that the following inequality

$$\begin{aligned} \left| \int _0^t \partial _\tau ^{\alpha (\cdot )} g(\tau ) d\tau \right| \le C\int _0^t (1+|\ln (t-\eta )|)(t-\eta )^{-{\overline{\alpha }}} |g(\eta )| d\eta ,\quad t\in (0,T) \end{aligned}$$

is valid for any \(g\in H^1(0,T)\) with \(g(0)=0\), where \({\overline{\alpha }}:=\sup _{t\in [0,T]} \alpha (t)\).

Proof

From the notation of \(\partial _t^{\alpha (\cdot )}\), and using the Fubini lemma, we see that

$$\begin{aligned}&\int _0^t \partial _\tau ^{\alpha (\cdot )} g(\tau ) d\tau =\int _0^t \left[ \frac{1}{\Gamma (1-\alpha (\tau ))} \int _0^\tau (\tau -\eta )^{-\alpha (\tau )} g'(\eta ) d\eta \right] d\tau \nonumber \\&\quad =\int _0^t \left( \int _\eta ^t \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -\eta )^{-\alpha (\tau )} d\tau \right) g'(\eta )d\eta \nonumber \\&\quad =\int _\eta ^t \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -\eta )^{-\alpha (\tau )} d\tau g(\eta )\Big |_{\eta =0}^{\eta =t}\nonumber \\&\qquad - \int _0^t \frac{\partial }{\partial \eta } \left( \int _\eta ^t \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -\eta )^{-\alpha (\tau )} d\tau \right) g(\eta )d\eta \nonumber \\&\quad =- \int _0^t \frac{\partial }{\partial \eta } \left( \int _\eta ^t \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -\eta )^{-\alpha (\tau )} d\tau \right) g(\eta )d\eta . \end{aligned}$$
(4.2)

Here in the last equality we used the fact \(g(0)=0\) and the estimate

$$\begin{aligned}&\left| \int _\eta ^t \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -\eta )^{-\alpha (\tau )} d\tau \right| \le \sup _{t\in [0,T]} \frac{1}{\Gamma (1-\alpha (t))} \left| \int _\eta ^t (\tau -\eta )^{-\alpha (\tau )} d\tau \right| \\&\quad \le \sup _{t\in [0,T]} \frac{1}{\Gamma (1-\alpha (t))} \max \{1,T^{{\overline{\alpha }}}\} \left| \int _\eta ^t (\tau -\eta )^{-{\overline{\alpha }}} d\tau \right| \\&\quad \le \sup _{t\in [0,T]} \frac{1}{\Gamma (1-\alpha (t))} \max \{1,T^{{\overline{\alpha }}}\} \frac{(t-\eta )^{1-{\overline{\alpha }}}}{1-{\overline{\alpha }}} \rightarrow 0\quad \text{ as } \quad \eta \rightarrow t. \end{aligned}$$

Moreover, by letting \({\tilde{\tau }}=\frac{\tau -\eta }{t-\eta }\) and a direct calculation, we obtain

$$\begin{aligned}&\int _\eta ^t \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -\eta )^{-\alpha (\tau )} d\tau \\&\quad =\int _0^1 \frac{(t-\eta )^{1 - \alpha ( {\tilde{\tau }} t + (1-{\tilde{\tau }}) \eta )}}{\Gamma (1-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} {{\tilde{\tau }}}^{-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} d{\tilde{\tau }}. \end{aligned}$$

Now noting the facts that \(\frac{1}{\Gamma (1-\alpha (\cdot ))} \in C^1[0,T]\) and \(\alpha (\cdot )\in C^1[0,T]\) satisfying \(0<\alpha (t)<1\) for \(t\in [0,T]\), we derive

$$\begin{aligned}&\left| \frac{\partial }{\partial \eta } \left( \frac{{{\tilde{\tau }}}^{-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))}}{\Gamma (1-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} \right) \right| \\&\quad \le {{\tilde{\tau }}}^{-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} \left| \frac{\partial }{\partial \eta } \left( \frac{1}{\Gamma (1-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} \right) \right| \\&\qquad + \left| \frac{\partial }{\partial \eta } {{\tilde{\tau }}}^{-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))}\right| \frac{1}{\Gamma (1-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))}\\&\quad \le \max \{1,T^{{\overline{\alpha }}}\} {{\tilde{\tau }}}^{-{\overline{\alpha }}} \left\| \frac{1}{\Gamma (1-\alpha (\cdot ))} \right\| _{C^1[0,T]} \Vert \alpha (\cdot ) \Vert _{C^1[0,T]}\\&\qquad + \left\| \frac{1}{\Gamma (1-\alpha (\cdot ))} \right\| _{C^1[0,T]} \left| {{\tilde{\tau }}}^{-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} \alpha '({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ) \ln {\tilde{\tau }} \right| \\&\quad \le \max \{1,T^{{\overline{\alpha }}}\} {{\tilde{\tau }}}^{-{\overline{\alpha }}} \left\| \frac{1}{\Gamma (1-\alpha (\cdot ))} \right\| _{C^1[0,T]} \Vert \alpha (\cdot ) \Vert _{C^1[0,T]}\\&\qquad + \max \{1,T^{{\overline{\alpha }}}\} {{\tilde{\tau }}}^{-{\overline{\alpha }}}\left\| \frac{1}{\Gamma (1-\alpha (\cdot ))} \right\| _{C^1[0,T]} \Vert \alpha (\cdot )\Vert _{C^1[0,T]} |\ln {\tilde{\tau }} |\\&\quad \le \max \{1,T^{{\overline{\alpha }}}\} \left\| \frac{1}{\Gamma (1-\alpha (\cdot ))} \right\| _{C^1[0,T]} \Vert \alpha (\cdot )\Vert _{C^1[0,T]} {{\tilde{\tau }}}^{-{\overline{\alpha }}} (1+ |\ln {\tilde{\tau }}|) \end{aligned}$$

and

$$\begin{aligned}&\left| \frac{\partial }{\partial \eta } (t-\eta )^{1 - \alpha ( {\tilde{\tau }} t + (1-{\tilde{\tau }}) \eta )} \right| \\&\quad \le (t-\eta )^{ - \alpha ( {\tilde{\tau }} t + (1-{\tilde{\tau }}) \eta )} + (t-\eta )^{1 - \alpha ( {\tilde{\tau }} t + (1-{\tilde{\tau }}) \eta )} |\alpha '({\tilde{\tau }} t + (1-{\tilde{\tau }}) \eta ) \ln (t-\eta )|\\&\quad \le \max \{1,T^{{\overline{\alpha }}}\} (t-\eta )^{ - {\overline{\alpha }}} + \max \{1,T^{{\overline{\alpha }}}\} (t-\eta )^{ - {\overline{\alpha }}} \Vert \alpha \Vert _{C^1[0,T]} |\ln (t-\eta )|. \end{aligned}$$

Consequently, collecting all the above estimates, we arrive at

$$\begin{aligned}&\left| \frac{\partial }{\partial \eta }\left( \int _\eta ^t \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -\eta )^{-\alpha (\tau )} d\tau \right) \right| \\&\quad \le \left| \int _0^1 \frac{\partial }{\partial \eta } \left( \frac{{{\tilde{\eta }}}^{- \alpha ( {\tilde{\tau }} t + (1-{\tilde{\tau }}) \eta )}}{\Gamma (1-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))}\right) (t-\eta )^{1-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} d{\tilde{\tau }} \right| \\&\qquad + \left| \int _0^1 \frac{{{\tilde{\eta }}}^{- \alpha ( {\tilde{\tau }} t + (1-{\tilde{\tau }}) \eta )}}{\Gamma (1-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} \frac{\partial }{\partial \eta } (t-\eta )^{1-\alpha ({\tilde{\tau }} t + (1-{\tilde{\tau }})\eta ))} d{\tilde{\tau }} \right| \\&\quad \le C\int _0^1{{\tilde{\tau }}}^{-{\overline{\alpha }}} (1+|\ln {\tilde{\tau }}|) d{\tilde{\tau }} (t-\eta )^{1-{\overline{\alpha }}} + C\int _0^1 {{\tilde{\tau }}}^{ - {\overline{\alpha }}} d{\tilde{\tau }}(1+|\ln (t-\eta )|) (t-\eta )^{-{\overline{\alpha }}}. \end{aligned}$$

Since \(0<{\overline{\alpha }}<1\), we see that the two functions \({{\tilde{\tau }}}^{-{\overline{\alpha }}} (1+|\ln {\tilde{\tau }}|)\) and \({{\tilde{\tau }}}^{ - {\overline{\alpha }}}\) are integrable on [0, 1], hence

$$\begin{aligned}&\left| \frac{\partial }{\partial \eta }\left( \int _\eta ^t \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -\eta )^{-\alpha (\tau )} d\tau \right) \right| \\&\quad \le C(t-\eta )^{1-{\overline{\alpha }}} + C(1+|\ln (t-\eta )|) (t-\eta )^{-{\overline{\alpha }}}\\&\quad \le CT(t-\eta )^{-{\overline{\alpha }}} + C(1+|\ln (t-\eta )|) (t-\eta )^{-{\overline{\alpha }}} ,\quad 0<t<T. \end{aligned}$$

Taking the above inequality into (4.2), we conclude that

$$\begin{aligned}&\left| \int _0^t \partial _\tau ^{\alpha (\cdot )} g(\tau ) d\tau \right| \le C\int _0^t (1+|\ln (t-\eta )|) (t-\eta )^{-{\overline{\alpha }}} |g(\eta )| d\eta ,\quad t\in (0,T), \end{aligned}$$

which completes the proof of the lemma. \(\square\)

Now we are ready to give the proof of Theorem 2.2.

Proof of Theorem 2.2

Let \(u_1\) and \(u_2\) be the solutions to the fractional diffusion equations (1.1) with respect to \(p_1\) and \(p_2\). Then we see that \(w:=u_1-u_2\) admits the following initial-boundary value problem

$$\begin{aligned} \partial _t w +q\partial _t^{\alpha (\cdot )} w + L(t)w + p_1w + (p_1-p_2)u_2=0, \end{aligned}$$
(4.3)

with the homogeneous initial and boundary conditions. An equivalent form of (4.3) read as

$$\begin{aligned} \partial _t w +q\partial _t^{\alpha (\cdot )} w + L(t)w + p_2w + (p_1-p_2)u_1=0. \end{aligned}$$
(4.4)

Summing the above two equations implies

$$\begin{aligned} 2\partial _t w+ 2q\partial _t^{\alpha (\cdot )} w + 2L(t)w + (p_1+p_2)w + (p_1-p_2)(u_1+u_2)=0. \end{aligned}$$
(4.5)

Now multiplying the above equation with w and integrating the resulted equation over \(\Omega\), we have

$$\begin{aligned} \langle 2\partial _tw, w\rangle +2\langle q\partial _t^{\alpha (\cdot )} w, w\rangle + 2\langle L(t)w,w\rangle + (p_1+p_2)\langle w,w\rangle = - (p_1-p_2)\langle u_1+u_2,w\rangle , \end{aligned}$$
(4.6)

where \(\langle \cdot ,\cdot \rangle\) denotes the inner product in \(L^2(\Omega )\). Further, in view of the observation

$$\begin{aligned} \left( \int _\Omega u_1^2(x,t) dx\right) ^{\frac{1}{2}} = \left( \int _\Omega u_2^2(x,t) dx\right) ^{\frac{1}{2}}, \end{aligned}$$

we see that \(\langle u_1+u_2,w\rangle = \langle u_1,u_1\rangle - \langle u_2,u_2\rangle =0\), which implies

$$\begin{aligned} \langle 2\partial _tw, w\rangle +2\langle q\partial _t^{\alpha (\cdot )} w, w\rangle + 2\langle L(t)w,w\rangle + (p_1+p_2)\langle w,w\rangle = 0. \end{aligned}$$
(4.7)

By integration by parts and the ellipticity of the operator L(t), we see that

$$\begin{aligned} \langle L(t)w,w\rangle \ge a_0 \Vert \nabla w\Vert _{L^2(\Omega )}^2. \end{aligned}$$

Moreover, we conclude from Lemma 4.1 that

$$\begin{aligned} 2\langle q\partial _t^{\alpha (\cdot )} w, w\rangle \ge \partial _t^{\alpha (\cdot )} \int _\Omega q(x) |w(x,t)|^2 dx = \partial _t^{\alpha (\cdot )} \Vert q^{\frac{1}{2}} w\Vert _{L^2(\Omega )}^2. \end{aligned}$$

Now taking the above two estimates into (4.7) and noting \(p_1,p_2\ge 0\), we derive

$$\begin{aligned} \partial _t \Vert w\Vert _{L^2(\Omega )}^2 + \partial _t^{\alpha (\cdot )} \Vert q^{\frac{1}{2}}w\Vert _{L^2(\Omega )}^2 + a_0\Vert \nabla w\Vert _{L^2(\Omega )}^2\le 0. \end{aligned}$$

Integrating with respect to t over (0,t) on both sides of the above inequality and using the fact \(\Vert w(0)\Vert _{L^2(\Omega )}=0\) and the estimate in Lemma 4.2, we obtain

$$\begin{aligned} \Vert w\Vert _{L^2(\Omega )}^2 + a_0\int _0^t \Vert \nabla w\Vert _{L^2(\Omega )}^2d\tau \le C \int _0^t (1+|\ln (t-\tau )|)(t-\tau )^{-{\overline{\alpha }}} \Vert w\Vert _{L^2(\Omega )}^2 d\tau . \end{aligned}$$

Moreover, since \({\overline{\alpha }}\in (0,1)\), we see that there exists a sufficiently small \(\varepsilon >0\) such that \({\overline{\alpha }}+\varepsilon <1\) and \(1+|\ln t| \le Ct^{-\varepsilon }\) are valid for any \(t\in (0,T)\), therefore we have

$$\begin{aligned} \Vert w\Vert _{L^2(\Omega )}^2 + a_0\int _0^t \Vert \nabla w\Vert _{L^2(\Omega )}^2d\tau \le C \int _0^t (t-\tau )^{-\varepsilon -{\overline{\alpha }}} \Vert w\Vert _{L^2(\Omega )}^2 d\tau . \end{aligned}$$

We further use the Gronwall inequality to derive that \(w=0\) in \(\Omega _T\), that is, \(u_1=u_2\). We thus have \(p_1=p_2\) from (4.4) and the positivity of the observation data, which completes the proof of the theorem. \(\square\)

Remark 4.1

We point out here that the assumption on the observation data \(\left( \int _\Omega u^2(x,t)dx\right) ^{\frac{1}{2}} >0\) for \(t\in (0,T)\) is essential for our proof and it may be achieved by choosing the source being positive. Indeed, one may prove \(u(x,t)>0\) for any \((x,t)\in \Omega _T\) in view of the maximum principle for the fractional diffusion equation. We postpone the proof of the positivity of the solution to the appendix..

5 Numerical inversion

In this section, we are devoted to developing an effective numerical method and presenting several numerical experiments for the reconstruction of the unknown potential p(t) in the domain (0, T) from the addition data \(\left( \int _\Omega u^2(x,t) dx\right) ^{\frac{1}{2}}\) in (0, T).

5.1 Tikhonov regularization

We write the solution of system (1.1) as u(p) in order to emphasize its dependence on the unknown function p. Here and henceforth, we set \(p^*\in L_+^\infty (0,T):=\{p\in L^\infty (0,T); p\ge 0, \text{ a.e. } t\in (0,T) \}\) as the true solution to the proposed Inverse Problem 1.1 and investigate the numerical reconstruction by noise contaminated observation data \(E^{\delta }(t)\) in (0, T). Here \(E^{\delta }\) satisfies \(\left\| \Vert u(p^*)\Vert _{L^2(\Omega )} - E^\delta (t)\right\| _{L^2(0,T)}\le \delta\) with the noise level \(\delta\).

In the framework of the Tikhonov regularization technique, we propose the following output least squares functional related to our inverse potential problem:

$$\begin{aligned} \min \limits _{p\in L_+^\infty (0,T)} \Phi (p),\quad \Phi (p):=\frac{1}{2}\left\| \Vert u(p)\Vert _{L^2(\Omega )} - E^{\delta }(t)\right\| _{L^2(0,T)}^2 +\frac{1}{2}\beta \Vert p\Vert _{L^{2}(0,T)}^{2}, \end{aligned}$$
(5.1)

where \(\beta >0\) is the regularization parameter.

As the majority of the efficient iterative methods do, we need the information about the G\({\hat{a}}\)teaux derivative \(\Phi '(p)\) of the objective functional \(\Phi (p)\). For an arbitrarily fixed direction \(\xi \in L^{2}(0,T)\), a direct calculation implies

$$\begin{aligned} \Phi '(p)\xi= & {} \int _0^T \left[ 1- \frac{E^{\delta }(t)}{\Vert u(p)(\cdot ,t)\Vert _{L^2(\Omega )}}\right] \left[ \int _\Omega (u'(p)\xi )u(p) dx \right] dt \nonumber \\&+ \beta \int _0^T p(t) \xi (t) dt, \end{aligned}$$
(5.2)

where \(u'(p)\xi\) denotes the G\({\hat{a}}\)teaux derivative of u(p) in the direction \(\xi\) and it is the solution to the following variable order time-fractional differential equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t w + q\partial _t^{\alpha (t)} w + L(t)w + p(t)w =-\xi (t)u(p), &{} (x,t) \in \Omega _T,\\ w(x,0)=0, &{} x\in \Omega , \\ \sum _{i=1}^d a_{ij}(x,t) \partial _{x_i} w(x,t) \nu _j=0, &{} (x,t) \in \Sigma . \end{array}\right. } \end{aligned}$$
(5.3)

In view of the fact that \(u(p)\in L^2(0,T;L^2(\Omega ))\cap H^1(0,T;H^2(\Omega ))\), by a similar argument used in the proof for Lemma 3.3, we can show that the above problem (5.3) admits a unique solution \(u'(p)\xi \in H^1(0,T;L^2(\Omega )) \cap L^2(0,T;H^2(\Omega ))\).

Remark 5.1

It is not applicable to find the minimizer of the functional \(\Phi\) directly in terms of the above formula (5.2) of the G\({\hat{a}}\)teaux derivative. Indeed, in the computation for \(\Phi '(p)\) in (5.2), one should solve system (5.3) for \(u'(p)\xi\) with \(\xi\) varying in \(L^2(0,T)\), which is undoubtedly quite hard and computationally expensive.

5.2 Adjoint system and its well-posedness

In order to reduce the computational costs for the G\({\hat{a}}\)teaux derivative \(\Phi '(p)\), we first define the backward Riemann-Liouville integral operator \(J_T^{1-\alpha (t)}\) and the backward Riemann-Liouville fractional derivative \(D_T^{\alpha (t)}\): for any \(g(t)\in L^2(0,T)\),

$$\begin{aligned} J_T^{1-\alpha (t)}g(t)= & {} \int _t^T \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -t)^{-\alpha (\tau )} g(\tau ) d\tau ,\\ D_T^{\alpha (t)} g(t)= & {} \partial _tJ_T^{1-\alpha (t)}g(t)=\partial _t \left[ \int _t^T \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -t)^{-\alpha (\tau )} g(\tau ) d\tau \right] . \end{aligned}$$

By the Fubini Lemma and the integration by parts, for any \(g_1,g_2\in L^2(0,T)\) with \(g_1(0)=0\) and \(\lim _{t\rightarrow T}J_T^{1-\alpha (t)}g_2(t)=0\), we have

$$\begin{aligned}&\int _0^T (\partial _t^{\alpha (t)}g_1(t))\,g_2(t)dt=\int _0^T\frac{1}{\Gamma (1-\alpha (t))} \int _0^t (t-\tau )^{-\alpha (t)}\, g'_1(\tau )\, d\tau g_2(t)dt\nonumber \\&\quad =\int _0^T \int _\tau ^T \frac{1}{\Gamma (1-\alpha (t))} (t-\tau )^{-\alpha (t)}\, g_2(t)dt\,g'_1(\tau ) d\tau =\int _0^T (J_T^{1-\alpha (\tau )}g_2(\tau ))\,g'_1(\tau ) d\tau \nonumber \\&\quad =-\int _0^T g_1(\tau )\partial _\tau (J_T^{1-\alpha (\tau )}g_2(\tau )) d\tau =-\int _0^T g_1(t)\,(D_T^{\alpha (t)} g_2(t)) dt. \end{aligned}$$
(5.4)

Then we shall introduce the following backward variable order time-fractional differential equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\partial _t z - qD_T^{\alpha (t)} z + L(t)z + p(t)z = \left[ \frac{E^{\delta }(t)}{\Vert u(p)(\cdot ,t)\Vert _{L^2(\Omega )}} - 1\right] u(p), &{} (x,t) \in \Omega _T,\\ z(x,T)=0, &{} x\in \Omega , \\ \sum _{i,j=1}^d a_{ij}(x,t)\partial _{x_i}z(x,t) \nu _j=0, &{} (x,t) \in \Sigma . \end{array}\right. } \end{aligned}$$
(5.5)

Now we are ready to propose the following lemma for getting the adjoint relation.

Lemma 5.1

For any fixed direction \(\xi \in L^{2}(0,T)\), the following equality holds:

$$\begin{aligned} \int _0^T \left[ 1- \frac{E^{\delta }(t)}{\Vert u(p)(\cdot ,t)\Vert _{L^2(\Omega )}}\right] \left[ \int _\Omega (u'(p)\xi )u(p) dx \right] dt =\int _0^T\xi (t)\int _\Omega u(p)\,z dx\,dt. \end{aligned}$$
(5.6)

Proof

By the variational forms of the systems (5.3) and (5.5), for any \(\varphi ,\psi \in L^2(0,T;H^1(\Omega ))\), we have

$$\begin{aligned}&\int _{\Omega _T} \left\{ \partial _t (u'(p)\xi )\varphi +q\partial _t^{\alpha (t)} (u'(p)\xi )\varphi + \sum _{i,j=1}^d a_{ij} \frac{\partial u'(p)\xi }{\partial x_i} \frac{\partial \varphi }{\partial x_j}+ p(t)(u'(p)\xi )\varphi \right\} dxdt\nonumber \\&\quad =-\int _{\Omega _T}\xi (t) u(p)\varphi dxdt, \end{aligned}$$
(5.7)
$$\begin{aligned}&\int _{\Omega _T}\{-\partial _t z \psi -qD_T^{\alpha (t)} z \psi + \sum _{i,j=1}^d a_{ij} \frac{\partial z}{\partial x_i} \frac{\partial \psi }{\partial x_j}+ p(t)z \psi \} dxdt\nonumber \\&\quad =\int _{\Omega _T}\left[ \frac{E^{\delta }(t)}{\Vert u(p)(\cdot ,t)\Vert _{L^2(\Omega )}} - 1\right] u(p) \psi dxdt. \end{aligned}$$
(5.8)

As \((u'(p)\xi )(x,0)=0=z(x,T)\), we obtain by the integration by parts with respect to t and (5.4) that

$$\begin{aligned} \int _{\Omega _T} \partial _t (u'(p)\xi )\,z dxdt= & {} -\int _{\Omega _T} \partial _t z\, (u'(p)\xi ) dxdt,\\ \int _{\Omega _T} \partial _t^{\alpha (t)} (u'(p)\xi )\,z dxdt= & {} -\int _{\Omega _T} D_T^{\alpha (t)}z\, (u'(p)\xi ) dxdt. \end{aligned}$$

Hence, taking \(\varphi =z\) and \(\psi =u'(p)\xi\) in (5.7) and (5.8) respectively, we derive

$$\begin{aligned} \int _0^T \left[ 1- \frac{E^{\delta }(t)}{\Vert u(p)(\cdot ,t)\Vert _{L^2(\Omega )}}\right] \left[ \int _\Omega (u'(p)\xi )u(p) dx \right] dt =\int _0^T\xi \int _\Omega u(p)\,zdx\,dt. \end{aligned}$$

We finish the proof of the lemma. \(\square\)

Next, we shall show that the new system (5.5) is well-posed. Correspondingly, in a similar manner as the proof of Lemma 3.3, one can show the following well-posedness result for the backward boundary value problem (5.5). Indeed, by the change of the variable \({\tilde{t}}=T-t\) and setting \({\tilde{v}}({\tilde{t}}):=z(t)=z(T-{\tilde{t}})\), we first see that \(\partial _t z(t) = -\partial _{{\tilde{t}}} {\tilde{v}}({\tilde{t}})\) and

$$\begin{aligned} D_T^{\alpha (t)} z(t):&= \frac{\partial }{\partial t} \left[ \int _t^T \frac{1}{\Gamma (1-\alpha (\tau ))} (\tau -t)^{-\alpha (\tau )} z(\tau ) d\tau \right] \\&=-\frac{\partial }{\partial {\tilde{t}}} \left[ \int _0^{{\tilde{t}}} \frac{1}{\Gamma (1-\alpha (T-\tau ))} ({\tilde{t}}- \tau )^{-\alpha (T-\tau )} {\tilde{v}}(\tau ) d\tau \right] =:-d_{{\tilde{t}}}^{\alpha (t)} {\tilde{v}}({\tilde{t}}). \end{aligned}$$

Then we can equivalently change the problem (5.5) to the following initial-boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{{\tilde{t}}} {\tilde{v}} + qd_{{\tilde{t}}}^{\alpha (t)} {\tilde{v}} + L(T-{\tilde{t}}){\tilde{v}} + p(T-{\tilde{t}}){\tilde{v}} = \left[ \frac{E^{\delta }(T-{\tilde{t}})}{\Vert u[p](\cdot ,T-{\tilde{t}})\Vert _{L^2(\Omega )}}-1\right] u(p), &{} (x,{\tilde{t}}) \in \Omega _T,\\ {\tilde{v}}(x,0)=0, &{} x\in \Omega , \\ \sum _{i,j=1}^d a_{ij}(x,T-{\tilde{t}})\partial _{x_i} {\tilde{v}}(x,{\tilde{t}}) \nu _j=0, &{} (x,{\tilde{t}}) \in \Sigma . \end{array}\right. } \end{aligned}$$

We notice that

$$\begin{aligned} \left[ \frac{E^{\delta }}{\Vert u[p]\Vert _{L^2(\Omega )}}-1\right] u(p) \in L^2(0,T;L^2(\Omega )). \end{aligned}$$

Then in order to prove the well-posedness of the problem (), it is sufficient to show that \(d_{{\tilde{t}}}^{\alpha (t)} {\tilde{v}} \in L^2(0,T;L^2(\Omega ))\) for any \({\tilde{v}}\in {_0}H^{1-\varepsilon }(0,T;L^2(\Omega ))\) with small enough \(\varepsilon >0\).

Lemma 5.2

Let \(\alpha (\cdot )\in C^1[0,T]\) such that \(0< \alpha (t)<1\) for any \(t\in [0,T]\), and we choose \(\varepsilon >0\) being small enough such that \(1-\varepsilon -\alpha (t)>0\) for any \(t\in [0,T]\). Then the following estimate

$$\begin{aligned} \Vert d_t^{\alpha (t)} g\Vert _{L^2(0,T)} \le C\Vert g\Vert _{H^{1-\varepsilon }(0,T)} \end{aligned}$$

is valid for any \(g\in H^{1-\varepsilon }(0,T)\) satisfying \(v(0)=0\).

Proof

From the assumptions on g, we can find \(h\in L^2(0,T)\) such that \(z=J^{1-\varepsilon } h\), then from the notations of \(d_t^{\alpha (t)}\) and \(J^{1-\varepsilon }\) and the Fubini lemma, we see that

$$\begin{aligned} d_t^{\alpha (t)} g(t)&=\frac{1}{\Gamma (1-\varepsilon )}\frac{d}{d t} \left[ \int _0^t \frac{1}{\Gamma (1-\alpha (T-\tau ))} (t- \tau )^{-\alpha (T-\tau )} \int _0^\tau (\tau -\eta )^{-\varepsilon }h(\eta ) d\eta d\tau \right] \\&=\frac{1}{\Gamma (1-\varepsilon )}\frac{d}{d t} \left[ \int _0^t \left( \int _\eta ^t \frac{1}{\Gamma (1-\alpha (T-\tau ))} (t- \tau )^{-\alpha (T-\tau )} (\tau -\eta )^{-\varepsilon } d\tau \right) h(\eta )d\eta \right] \\&=\frac{1}{\Gamma (1-\varepsilon )}\left[ \int _0^t \frac{\partial }{\partial t} \left( \int _\eta ^t \frac{1}{\Gamma (1-\alpha (T-\tau ))} (t- \tau )^{-\alpha (T-\tau )} (\tau -\eta )^{-\varepsilon } d\tau \right) h(\eta )d\eta \right] . \end{aligned}$$

Here in the last inequality we used

$$\begin{aligned} \left| \int _\eta ^t \frac{1}{\Gamma (1-\alpha (T-\tau ))} (t- \tau )^{-\alpha (T-\tau )} (\tau -\eta )^{-\varepsilon } d\tau \right| \le C(t-\eta )^{1-\varepsilon - {\bar{\alpha }}} \rightarrow 0 \end{aligned}$$

as \(\eta \rightarrow t\). Moreover, we can show the following assertion

$$\begin{aligned} \frac{\partial }{\partial t}\left( \int _\eta ^t \frac{1}{\Gamma (1-\alpha (T-\tau ))} (t- \tau )^{-\alpha (T-\tau )} (\tau -\eta )^{-\varepsilon } d\tau \right) \in L^1(0,T). \end{aligned}$$
(5.9)

This can be done by the change of variables. In fact, by letting \({\tilde{\tau }}=\frac{\tau -\eta }{t-\eta }\), we have

$$\begin{aligned}&\int _\eta ^t \frac{1}{\Gamma (1-\alpha (T-\tau ))} (t- \tau )^{-\alpha (T-\tau )} (\tau -\eta )^{-\varepsilon } d\tau \\&\quad =\int _0^1 \frac{(t-\eta )^{1-\varepsilon - \alpha (T-{\tilde{\tau }}(t-\eta ) -\eta )}}{\Gamma (1-\alpha (T-{\tilde{\tau }}(t-\eta ) - \eta ))} (1-{\tilde{\tau }})^{-\alpha (T-{\tilde{\tau }}(t-\eta )-\eta )} {\tilde{\tau }}^{-\varepsilon } d{\tilde{\tau }}. \end{aligned}$$

Now by noting the facts that \(\frac{1}{\Gamma (1-\alpha (\cdot ))} \in C^1[0,T]\), \(1-\varepsilon -\alpha (t)>0\) and \(\alpha (\cdot )\in C^1[0,T]\), we can show that the assertion (5.9) is true. Collecting all the above estimates, from the Young inequality for the convolution, it follows that

$$\begin{aligned}&\Vert d_t^{\alpha (t)} g\Vert _{L^2(0,T)} \le C\Vert h\Vert _{L^2(0,T)}. \end{aligned}$$

Then the proof of the lemma can be finished by noting that \(\Vert h\Vert _{L^2(0,T)} \sim \Vert g\Vert _{H^{1-\varepsilon }(0,T)}\), see Gorenflo, Luchko and Yamamoto [10, Theorem 2.1]. \(\square\)

Now, by an argument similar to the proof of Lemma 3.3, we have the well-posedness of the problem (5.5).

Lemma 5.3

Let \(T>0\) and \(\alpha (\cdot )\in C^1[0,T]\) such that \(\alpha (t)\in (0,1)\) for any \(t\in [0,T]\). We suppose \(\Vert u(p)(\cdot ,t)\Vert _{L^2(\Omega )} >0\) for any \(t\in [0,T]\) and \(p\in L^2(0,T)\). Then the problem (5.5) admits a unique weak solution \(z\in H^1(0,T;L^2(\Omega ))\cap L^2(0,T;H^2(\Omega ))\) such that

$$\begin{aligned} \Vert \partial _tz\Vert _{L^2(0,T;L^2(\Omega ))} + \Vert z\Vert _{L^2(0,T;H^2(\Omega ))} \le C\left[ \Vert E^\delta (t)\Vert _{L^2(0,T)} + \Vert u(p)\Vert _{L^2(0,T;L^2(\Omega ))} \right] . \end{aligned}$$

On the basis of the above regularity result of the solution to the adjoint system (5.5), we now aim to give a weak form of the solution to the problem (5.5). Let \(z\in H^1(0,T;L^2(\Omega ))\cap L^2(0,T; H^2(\Omega ))\) be the solution to the problem (5.5). The use of integration by parts implies that the solution z to the problem (5.5) admits the following weak form

$$\begin{aligned}&\sum _{i,j=1}^d \int _{\Omega _T} a_{ij} \frac{\partial \psi }{\partial x_i} \frac{\partial z}{\partial x_j} dxdt + \int _0^T p(t) \langle \psi ,z\rangle dt- \int _0^T \langle \psi , \partial _t z + q D_T^{\alpha (\cdot )}z\rangle dt \nonumber \\&\quad = \int _0^T \langle {\tilde{f}},\psi \rangle dt, \end{aligned}$$
(5.10)

where \({\tilde{f}}:=\left[ \frac{E^{\delta }(t)}{\Vert u(p)(\cdot ,t)\Vert _{L^2(\Omega )}} - 1\right] u(p)\), and \(\psi \in H^1(0,T;L^2(\Omega ))\cap L^2(0,T;H^2(\Omega ))\) satisfying \(\psi (\cdot ,0)=0\).

5.3 Iterative thresholding algorithm

Due to the adjoint relation (5.6), we find that for any \(\xi \in L^2(0,T)\),

$$\begin{aligned} \Phi '(p)\xi= & {} \int _0^T \left[ 1- \frac{E^{\delta }(t)}{\Vert u(p)(\cdot ,t)\Vert _{L^2(\Omega )}}\right] \left[ \int _\Omega (u'(p)\xi )u(p) dx \right] dt + \beta \int _0^T p(t) \xi (t) dt\\= & {} \int _0^T\xi \int _\Omega u(p)\,z(p)dx\,dt+ \beta \int _0^T p(t) \xi (t)dt. \end{aligned}$$

Here we write the solution z to system (5.5) as z(p) to emphasize its dependence on p(t). This suggests a characterization of the solution to the minimization problem (5.1), i.e., the function \(p^*(t)\in L^2(0,T)\) is a minimizer of the functional \(\Phi (p)\) in (5.1) only if it satisfies the variational equation

$$\begin{aligned} \int _\Omega u(p^*)\,z(p^*)dx+ \beta p^*=0. \end{aligned}$$

Now we are ready to propose the iterative thresholding algorithm (see e.g. [32] [48]) for the reconstruction.

Algorithm 5.1

Choose a tolerance parameter \(\epsilon >0\) and an initial value \(p^{0}\), and set \(k:=0\).

  1. 1.

    Compute

    $$\begin{aligned} p^{k+1} =\frac{1}{A+\beta }\Big (Ap^k-\int _\Omega u(p^k)\,z(p^k)dx\Big ). \end{aligned}$$
    (5.11)
  2. 2.

    If \(\frac{\Vert p^{k+1}-p^{k}\Vert _{L^2(0,T)}}{\Vert p^{k}\Vert _{L^2(0,T)}}\le \epsilon\), stop the iteration; otherwise set \(k:=k+1\), go to Step 1.

Remark 5.2

Here \(A>0\) is a tuning parameter and it should satisfy that \(A\Vert p-q\Vert _{L^2(0,T)}^2\ge \int _0^T|\Vert u(p)\Vert _{L^2(\Omega )}-\Vert u(q)\Vert _{L^2(\Omega )}|^2dt\) for any \(p,\,q\in L^\infty _+(0,T)\) for the convergence of the Algorithm 5.1 (please refer to [48] for more details). We can see from (5.11) that at each iteration step, we only need to solve the forward problem (1.1) once for \(u(p^k)\) and the backward problem (5.5) once for \(z(p^k)\) subsequently. As a result, the numerical implementation of algorithm 5.1 is easy and computationally cheap.

5.4 Numerical experiments

In this subsection, we shall present several numerical examples in one and two dimensional spaces to show the accuracy and efficiency of the proposed iterative thresholding Algorithms 5.1. To begin with, we assign the general settings of the reconstructions as follows. Without loss of generality, in (1.1) we set

$$\begin{aligned} q=1, \quad T=1, \quad L(t)u=-\nabla \cdot (a(x,t)\nabla u). \end{aligned}$$

The noisy data \(u^\delta\) is obtained by adding some uniform random noise to the exact data \(\Vert u(p^*)\Vert _{L^2(\Omega )}\), which means

$$\begin{aligned} u^\delta =(1+ \delta R(-1,1))\, \Vert u(p^*)\Vert _{L^2(\Omega )}, \end{aligned}$$

where \(R(-1,1)\) is a uniform random function varying in the range [-1,1].

Let \(p^{k}\) be the numerical reconstruction by Algorithms 5.1 at the kth iteration, other than the illustrative figures, we mainly evaluate the numerical performance by the relative \(L^2\)-norm error

$$\begin{aligned} e_k=\frac{\Vert p^{k}-p^*\Vert _{L^2(0,T)}}{\Vert p^*\Vert _{L^2(0,T)}}. \end{aligned}$$

We divide the space-time region \(\Omega \times [0,1]\) as equidistant meshes. All the variable-order time-fractional differential equations in Algorithm 5.1 are solved by the continuous linear finite element method in space. And for the time discretization, we use the forward difference scheme to approximate the first order time derivative, while apply the similar finite difference scheme proposed in [52] to approximate the variable-order time-fractional derivative, i.e.,

$$\begin{aligned} \partial _t^{\alpha (t)} u(x,t_{m+1})= & {} \frac{1}{\Gamma (1-\alpha _{m+1})}\sum _{j=0}^m\int _{t_j}^{t_{j+1}}\frac{\partial _su(x,s)}{(t_{m+1}-s)^{\alpha (t)}}\,d s\nonumber \\\approx & {} \frac{1}{\Gamma (1-\alpha _{m+1}))}\sum _{j=0}^m\frac{u(x,t_{j+1})-u(x,t_j)}{\tau }\int _{t_j}^{t_{j+1}}(t_{m+1}-s)^{-\alpha _{m+1}}\,d s\nonumber \\= & {} \frac{1}{\Gamma (2-\alpha _{m+1})}\sum _{j=0}^m\frac{u(x,t_{m+1-j})-u(x,t_{m-j})}{\tau ^{\alpha _{m+1}}}\{(m+1-j)^{1-\alpha _{m+1}}-(m-j)^{1-\alpha _{m+1}}\}\\= & {} \frac{1}{\Gamma (2-\alpha _{m+1})\tau ^{\alpha _{m+1}}}( u(x,t_{m+1})+\sum _{j=0}^{m-1} (d_{j+1}^m-d_j^m)u(x,t_{m-j})-d_m^m u(x,t_0)), \end{aligned}$$

where \(d_j^m:=(j+1)^{1-\alpha _{m+1}}-j^{1-\alpha _{m+1}}\) for \(j=0,1,\ldots ,m\).

We first start two numerical experiments for the reconstructions of the time-dependent potential in system (1.1) with \(d=1\). We set \(\Omega =(0,1)\) and divide the space-time region \([0,1]\times [0,1]\) into \(40\times 40\) equidistant meshes. We fix \(f(x,t)=5+2\pi x t\), \(a(x,t)=1+x+t\) and set the tuning parameter \(A=2\), the tolerance parameter \(\epsilon =7\times 10^{-3}\) and the regularization parameter \(\beta =0.02\).

Example 5.1

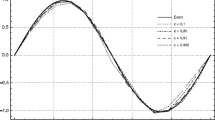
In this example, we take the exact time-dependent component \(p^*(t)=\sin (\pi t)\) in [0, 1] and set the initial guess \(p^0(t)=\frac{3}{2}-6(t-\frac{1}{2})^2\) in [0, 1].

Figure 1 (left) presents the reconstructed solutions and the exact ones, the iteration number k and the relative error \(e_k\) by fixing the noise level \(\delta =3\%\). We can see that the numerical reconstructed solutions appear to be quite satisfactory in the presence of a 3% noise in the data.

Fig. 1
figure 1

Exact and reconstructed solutions for Examples 5.1 (left) and 5.2 (right) with \(\delta =3\%\): (left) \(k=44\), \(e_k=4.38\%\); (right) \(k=34\), \(e_k =2.53\%\)

Full size image

Example 5.2

In this example, we take the exact time-dependent component \(p^*(t)=1-t\) in [0, 1] and set the initial guess \(p^0(t)=5(\ln 4-\ln (3+t))\) in [0, 1].

Figure 1 (right) presents the exact and reconstructed solutions, the iteration number k and the relative error \(e_k\) by fixing the noise level \(\delta =3\%\). It appears that the numerical reconstructed solutions is also quite satisfactory in the presence of a 3% noise in the data.

Then we start two numerical experiments for the reconstructions of the time-dependent potential in system (1.1) with \(d=2\). We set \(\Omega =(0,1)^2\) and divide the space-time region \([0,1]^2\times [0,1]\) into \(40^2\times 40\) equidistant meshes. We fix \(f(x_1,x_2,t)=5+2\pi (x_1+x_2) t\), \(a(x_1,x_2,t)=1+x_1+x_2+t\) and set the tuning parameter \(A=2\), the tolerance parameter \(\epsilon =8\times 10^{-3}\) and the regularization parameter \(\beta =0.02\).

Example 5.3

In this example, we take the exact time-dependent component \(p^*(t)=\sin (\pi t)\) in [0, 1] and set the initial guess \(p^0(t)=\frac{3}{2}-6(t-\frac{1}{2})^2\) in [0, 1].

Fig. 2
figure 2

Exact and reconstructed solutions for Examples 5.3 (left) and 5.4 (right) with \(\delta =3\%\): (left) \(k=42\), \(e_k=4.52\%\); (right) \(k=33\), \(e_k =2.90\%\)

Full size image

Example 5.4

In this example, we take the exact time-dependent component \(p^*(t)=1-t\) in [0, 1] and set the initial guess \(p^0(t)=5(\ln 4-\ln (3+t))\) in [0, 1].

Figure 2 (left) and (right) present the reconstructed solutions and the exact ones, the iteration number k and the relative error \(e_k\) by fixing the noise level \(\delta =3\%\) for Example 5.3 and Example 5.4 respectively. We can see that the numerical reconstructed solutions also appear to be quite satisfactory in the presence of a 3% noise in the data for two dimensional cases.

6 Concluding remarks

In this paper, we have discussed the inverse problem of recovering a temporally varying potential in the variable order time-fractional diffusion equation from a nonlinear and nonlocal type additional data. We have shown the well-posedness of the forward problem by using the Fredholm alternative principle for compact operators and also proved the uniqueness of the inverse problem by assuming the measurement is strictly positive. Numerically, in order to reduce the computational cost of the Frechét derivative of the minimizing functional, a newly backward adjoint system has been constructed, whose well-posedness has also been verified. The iterative thresholding algorithm has been proposed and several numerical experiments have been presented to show its feasibility and efficiency.

Finally, it would be interesting to investigate what happens with the inverse problem if the additional data can touch zero. Moreover, it is known that the conditional stability results hold for the inverse problems for recovering the spatially varying potential in parabolic or hyperbolic equations based on Carleman estimates. Unfortunately, such techniques do not work in our case. It will be a challenging and interesting direction of research to investigate the stability of the inverse problem.