1 Introduction

The development of microfluidic devices has advanced significantly due to progress in micro manufacturing (Wilkinson et al. 2019; Dharmadhikari et al. 2023; Huang et al. 2023). These devices are highly sensitive to electrolytic solutions because charged groups at the interface allow for ionic interaction and the formation of electrically charged double layers (Sarma et al. 2017, 2018). Electroosmotic flow, whereby an external electric field moves the liquid, offers superior controllability and manipulation compared to pressure-driven flows in microfluidic devices (Kaushik et al. 2017; Gaikwad et al. 2018; Mondal and Wongwises 2020).

DC electroosmotic pumps are extensively designed for cooling electronic components and chips, leveraging electroosmotic flow strength (Berrouche et al. 2009; Al-Rjoub et al. 2011; Han et al. 2013; Pramod and Sen 2014). Joule heating generated in electrolytic solutions with electrical resistance significantly impacts heat flow within microfluidic systems (Xuan et al. 2004; Eng et al. 2010). Recent studies have investigated electroosmotic heat flow in various microchannel configurations, including those with vibrating walls, hybrid nanofluids, non-uniform divergent walls, porous geometrical topology, grafted walls with non-uniform surface charge, and combinations of pressure-driven and electroosmotic flow (Aslam et al. 2023; Barnoon 2023; Irfan et al. 2024; Noreen et al.; Wang and Li 2023; Merdasi et al. 2023; Mehta et al. 2023).

The second law of thermodynamics dictates that heat-transporting devices/system should minimize entropy production for maximum efficiency (Mallick et al. 2019; Ramesh et al. 2019; Selimefendigil and Oztop 2019; Sheikholeslami et al. 2019; Banerjee et al. 2020; Rothan 2022; Mehta and Mondal 2023). Several studies have investigated irreversibility analysis for electroosmotic flow systems, considering biomimetic flows, two-layered flows, non-Newtonian fluid flows, closed-end microchannels, peristaltically induced microchannels, nanofluids in micro-tubes, flows in porous media, conjugate heat transfer effects, slip effects, and finite size effects (Narla et al. 2020; Xie and Jian 2017; Escandón et al. 2013; Zhao and Liu 2010; Ranjit et al. 2019; Deng et al. 2021; Noreen and Ain 2019; Goswami et al. 2016; Liu and Jian 2019). Recent investigations have also considered hydrodynamic slip, finite ionic size, and imposing magnetic fields (Munawar et al. 2023; Oni and Jha 2023; Sharma et al. 2023; Sujith et al. 2023).

Wavy walls facilitate vortex development and undulating flow patterns, promoting mixing within microchannels. Various studies have explored mixing, and flow properties inside corrugated or wavy microchannels based on electroosmotic action (Mondal et al. 2021; Mehta et al. 2021, 2022; Mehta and Pati 2022).

Notably, fluids used in microfluidic devices often exhibit non-Newtonian behavior, particularly significant for higher zeta potential magnitudes, and employing wavy walls in heat-exchanging systems is advised to minimize entropy generation. However, investigation into entropy production for non-Newtonian fluid flow inside wavy microchannels with finite ionic size has not been addressed in the scientific community. Hence, the primary objective of this work is to fill this gap in understanding.

2 Mathematical formulation

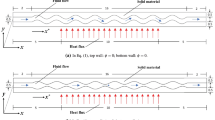
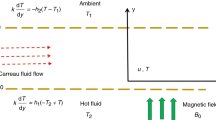
Figure 1 illustrates a schematic representation of the wavy microchannel through which electroosmotic flow of the non-Newtonian ionic liquid occurs. We consider the walls of the microchannel are experiencing a uniform heat flux. The wavy microchannel's average height is taken as 2H. For a steady, incompressible, and laminar flow, and assuming that the ionic distribution is static owing to the very low ionic Peclet number in the chosen fluidic pathway, the transport equations for the EDL potential field, external potential field, flow field, and temperature field can be expressed mathematically as discussed next.

Fig. 1
figure 1

The asymmetric wavy channel is schematically illustrated, showing electroosmotic flow and heat transport, with a uniform heat flux provided at the intermediate wavy walls

Full size image

The dimensionless EDL potential field (\(\psi\)) may be governed by the modified Poisson–Boltzmann equation, which takes into consideration the effect of finite ionic size by incorporating a steric factor, v, which has the following mathematical definition (Mehta et al. 2023):

$${\nabla }^{2}\psi ={\kappa }^{2}\frac{\mathit{sin}h\left(\psi \right)}{1+4\upsilon {\mathit{sin}h}^{2}\left(\frac{\psi }{2}\right)}$$
(1)

In Eq. (1), the term \(\kappa \left(=\frac{H}{{\lambda }_{D}}\right)\) is called as dimensionless Debye parameter, and the Debye parameter mathematically represented as \({\lambda }_{D}={\left(\frac{2{n}_{o}{z}^{2}{e}^{2}}{\varepsilon {k}_{B}T}\right)}^{-0.5}\). In this expression, \(T\), \(\varepsilon\), \({k}_{B}\), \(z\), \(e\) and \({n}_{o}\) termed as absolute temperature (= 298 K), electrical permittivity of the non-Newtonian ionic liquid, Boltzmann constant, valance of the ionic component (= 1), charge on a single electron and bulk ionic concentration, respectively. The scale used to normalize the EDL potential field is taken as \({\psi }_{ref}^{*}=\frac{{k}_{B}T}{ze}\).

Mathematically, the Laplace equation can be described as follows for resolving the dimensionless external potential field (\(\varphi\)):

$${\nabla }^{2}\varphi =0,$$
(2)

The scale chosen to normalize the external potential field is taken as \({\varphi }_{ref}^{*}\left(=\frac{\Delta V\times H}{30H}\right)\). Where \(\Delta V\) symbolizes the potential difference across a wavy microchannel.

By employing the continuity and momentum equations, as written below, the associated flow field governed by the electroosmotic actuation in a wavy microchannel can be computed. The following are the continuity and momentum equations:

$$\nabla \cdot {\varvec{u}}=0$$
(3)
$$Re\left({\varvec{u}}\cdot \nabla \right){\varvec{u}}=-\nabla P+\left(\nabla \cdot{\varvec{\tau}}\right)+\left[{\kappa }^{2}\frac{\mathit{sin}h\left(\psi \right)}{1+4\upsilon {\mathit{sin}h}^{2}\left(\frac{\psi }{2}\right)}\right]\nabla \left(\frac{\psi }{\Lambda }+\varphi \right)$$
(4)

Here, the dimensionless velocity vector, pressure, Reynolds number are denoted by \({\varvec{u}}\equiv \left(u,v\right)\), P and \(\mathit{Re}=\frac{\rho {u}_{HS}^{*}H}{{\mu }_{o}}\). The scale taken for the velocity field is mathematically expressed in terms of zero shear rate viscosity (\({\mu }_{o}\)) and reference electric field (\({E}_{ref}^{*}=\frac{\Delta V}{30H}\)) as \({u}_{HS}^{*}=\frac{{\psi }_{ref}^{*}{E}_{ref}^{*}\varepsilon }{{\mu }_{o}}\). The ratio of \({\varphi }_{ref}^{*}\) to that of \({\psi }_{ref}^{*}\) is expressed by the symbol \(\Lambda\). Now, the dimensionless form of deviatoric stress tensor is mathematically illustrated as \({\varvec{\tau}}={{\varvec{\tau}}}^{*}{\left(\frac{{\mu }_{o}{u}_{HS}^{*}}{H}\right)}^{-1}\). Moreover, considering the strain rate as \({\varvec{S}}=\left[\left(\nabla {{\varvec{u}}}^{*}\right)+{\left(\nabla {{\varvec{u}}}^{*}\right)}^{T}\right]\) and the second invariant of the rate of deformation tensor as \({\dot{\gamma }}^{*}=\sqrt{\left(\frac{1}{2}\right)\left({\varvec{S}}:{\varvec{S}}\right)}\), we can express the deviatoric stress tensor as \({{\varvec{\tau}}}^{*}=\mu \left({\dot{\gamma }}^{*}\right)\left[\left(\nabla {{\varvec{u}}}^{*}\right)+{\left(\nabla {{\varvec{u}}}^{*}\right)}^{T}\right]\). Under such conditions, the Carreau model could govern the apparent viscosity of the ionic non-Newtonian liquid, which has the following mathematical expression (Mehta et al. 2021):

$$\mu \left({\dot{\gamma }}^{*}\right)={\mu }_{\infty }+\left({\mu }_{o}-{\mu }_{\infty }\right){\left(1+{\left(\lambda {\dot{\gamma }}^{*}\right)}^{2}\right)}^{\left(\frac{\left(n-1\right)}{2}\right)}$$
(5)

In Eq. (5), the infinite share rate viscosity, time parameter and flow behavior index are presented by the terms \({\mu }_{\infty }\), \(\lambda\) and n, respectively. Now, normalizing the Eq. (5) using the zero shear-rate viscosity (\({\mu }_{o}\)), we obtain the scaled expression of apparent viscosity as \(\overline{\mu }\left( {\dot{\gamma }} \right) = \overline{\mu }_{\infty } + \left( {1 - \overline{\mu }_{\infty } } \right)\left( {1 + \left( {Cu\dot{\gamma }} \right)^{2} } \right)^{{\left( {\frac{{\left( {n - 1} \right)}}{2}} \right)}},\) where, Carreau number is expressed as \(Cu = \frac{{\lambda u_{HS}^{*} }}{H}\) and \(\dot{\gamma }\) represents the dimensionless the second invariant of the rate of deformation tensor. It may be mentioned in this context, the value of \({\overline{\mu }}_{\infty }\) is taken as 0.0616 (Mehta et al. 2021).

The dimensionless form of the energy equation can be represented as follows when taking into account the impact of viscous dissipation and the Joule heating effect:

$$Pe\left({\varvec{u}}\cdot \nabla \theta \right)={\nabla }^{2}\theta +Br\phi +G$$
(6)

In Eq. (6), the definition of dimensionless temperature is expressed in terms of inlet temperature difference and heat flux, q and defined as: \(\theta =\frac{\left(T-{T}_{in}\right)}{\left(\frac{qH}{k}\right)}\). The Brinkman number, thermal Peclet number and Joule heating parameter are expressed as \(Br\left(=\frac{{\mu }_{o}{\left(\frac{{u}_{HS}^{*}}{H}\right)}^{2}H}{q}\right)\) \(Pe\left(=\frac{\rho {c}_{p}H{u}_{HS}^{*}}{k}\right)\) and \(G\left(=\frac{\sigma {\left({E}_{ref}^{*}\right)}^{2}H}{q}\right)\), respectively. The specific heat capacity at constant pressure and thermal conductivity of liquid are presented by letter \({c}_{p}\) and k, respectively. Now, the term relevant to the viscous dissipation in Eq. (6) can be expressed by these mathematical expressions (Mehta et al. 2023): \(\phi = \left[ {\frac{\partial u}{{\partial x}}\left( {\tau_{xx} - \tau_{yy} } \right) + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)\tau_{xy} } \right]\); where, \(\tau_{xx} = 2\left( {\overline{\mu }_{\infty } + \left( {1 - \overline{\mu }_{\infty } } \right)\left( {1 + \left( {Cu\dot{\gamma }} \right)} \right)^{{\left( {\frac{{\left( {n - 1} \right)}}{2}} \right)}} } \right)\frac{\partial u}{{\partial x}}\); \(\tau_{xy} = \left( {\overline{\mu }_{\infty } + \left( {1 - \overline{\mu }_{\infty } } \right)\left( {1 + \left( {Cu\dot{\gamma }} \right)} \right)^{{\left( {\frac{{\left( {n - 1} \right)}}{2}} \right)}} } \right)\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)\) and \(\tau_{yy} = 2\left( {\overline{\mu }_{\infty } + \left( {1 - \overline{\mu }_{\infty } } \right)\left( {1 + \left( {Cu\dot{\gamma }} \right)} \right)^{{\left( {\frac{{\left( {n - 1} \right)}}{2}} \right)}} } \right)\left( {\frac{\partial v}{{\partial y}}} \right)\) are generally referred as components of stresses. In those expressions, we have \(\dot{\gamma } = \sqrt {2\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} + 2\left( {\frac{\partial v}{{\partial y}}} \right)^{2} }\) (Noreen et al. 2019).

The domain is subjected to the following boundary conditions, which are used to solve the aforementioned transport equations. For the inlet of the microchannel, we imposed \({\varvec{n}}\cdot \left(\nabla \psi \right)=0\), \(\varphi =30\), \(P={P}_{atm}\), \(\theta =0\); while, at the outlet, we have taken as \({\varvec{n}}\cdot \left(\nabla \psi \right)=0\), \(\varphi =0\), \(P={P}_{atm}\), \(\frac{\partial \theta }{\partial x}=0\). For the wavy walls, we imposed as \(\psi =\zeta =4\), \({\varvec{n}}\cdot \left(\nabla \varphi \right)=0\), \({\varvec{u}}=0\), \(\frac{\partial \theta }{\partial n}=1\) and for the planner walls, we imposed \(\psi =4\), \({\varvec{n}}\cdot \left(\nabla \varphi \right)=0\), \({\varvec{u}}=0\), \(\frac{\partial \theta }{\partial n}=0\). In these equations, \({\varvec{n}}\) represents the outward unit normal to the wavy surface.

The dimensionless form of the local total entropy generation can be expressed mathematically, providing that the thermal transport of heat, viscous dissipation, and Joule heating effect contribute to the entropy generation in the present endeavor (Sujith et al. 2023):

$$N^{\prime\prime\prime}_{total} = \frac{1}{{\left( {\Theta + \theta } \right)^{2} }}\left( {\left( {\frac{\partial \theta }{{\partial x}}} \right)^{2} + \left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} } \right) + \frac{Br}{{\left( {\Theta + \theta } \right)}}\overline{\mu }\left( {\begin{array}{*{20}c} {2\left( {\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial v}{{\partial y}}} \right)^{2} } \right)} \\ { + \left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^{2} } \\ \end{array} } \right) + \frac{G}{{\left( {\Theta + \theta } \right)}}.$$
(7)

Here, the scale taken to normalize the entropy generation is \(k/{H}^{2}\).

The following is a mathematical expression for the domain average of the overall dimensionless average entropy generation:

$$N_{total} = \frac{{\iint_{\Omega } {N^{\prime\prime\prime}_{total} d\Omega }}}{{\iint_{\Omega } {d\Omega }}}$$
(8)

Here, \(d\Omega\) is the dimensionless elemental area of the domain, and \(\Theta =\frac{{T}_{in}k}{qH}\).

3 Numerical simulation and model verification

Using the previously established boundary conditions, we solve the aforementioned equations using the finite element method-based solver COMSOL Multiphysics® v. 5.2 (http://www.comsol.com), a commercial software program. Irregular triangular mesh elements are employed to divide the physical space into smaller subdomains. The mesh along the walls is taken narrower to accurately estimate a sudden change in transport variables pertaining to EDL. The following shape functions have been used to convert the controlling differential equations into an ensemble of linear equations: quadratic for the external potential field and EDL, linear for the velocity component and pressure, and quadratic for the temperature field. The local matrices are produced soon after all transport variables have been tentatively computed using those shape functions and inserted in the integral form of the differential equation.

The global matrix is formed by combining these local matrices and applying all boundary conditions. The multifrontal massively parallel shape direct solver (MUMPS) is now used to solve these global matrices for the external potential and EDL. The flow field, however, is calculated using the parallel direct sparse solver for clusters (PARDISO). Lastly, the dimensionless temperature field is iteratively computed using the generalized minimum residual solver (GMRES) until the residual condition is met, which is 10–6. Additionally, the average generation of entropy for various mesh sets has been computed for the grid independence test and is shown in Table 1. The mesh system M4, which has a lower percentage error (less than 0.1%) than a more precise M5 mesh size, serves as the basis in the current endeavor for the numerical simulations. For this reason, mesh type 5 is employed in every numerical simulation.

Table 1 Grid independency test conducted by calculating average entropy generation when Br = 0.1, Pe = 10, \(\zeta =4\), \(\upsilon =0.3\), \(Cu=1\) and \(n=0.4\)
Full size table

We have verified our current numerical results with the established theoretical findings in Fig. 2. When the Brinkman number is 0, the Joule heating parameter is 1, the thermal Peclet number is 1, and the flow behaviour index is 1, Fig. 2 compares the average Nusselt number with the variation in the inverse of the dimensionless Debye parameter using the reported results of Sadeghi et al. (2011). The average Nusselt number is defined as \(\overline{Nu}=0.5\left[{\left(\frac{{\int }_{5}^{25}Nud\Omega }{{\int }_{5}^{25}d\Omega }\right)}_{Top}+{\left(\frac{{\int }_{5}^{25}Nud\Omega }{{\int }_{5}^{25}d\Omega }\right)}_{Bottom}\right]\), here, local Nusselt number is \(Nu=\frac{1}{\left({\theta }_{w}-{\theta }_{m}\right)}\), dimensionless bulk mean temperature is expresses as \({\theta }_{m}\left(=\frac{{\int }_{y}u\theta dy}{{\int }_{y}udy}\right)\) and \(d\Omega\) is the dimensionless arc length of the undulated wall. For the benchmarking analysis, we consider the analytical expression of average Nusselt number as proposed by Sadeghi et al. (2011) for limiting case (n = 1, Br = 0) and represented as:

$$\overline{Nu} = {4 \mathord{\left/ {\vphantom {4 {\left( {A_{1} E_{1} + B_{1} E_{2} + C_{1} E_{3} + A_{2} E_{4} + B_{2} E_{5} + C_{2} E_{6} + D_{2} E_{7} } \right)}}} \right. \kern-0pt} {\left( {A_{1} E_{1} + B_{1} E_{2} + C_{1} E_{3} + A_{2} E_{4} + B_{2} E_{5} + C_{2} E_{6} + D_{2} E_{7} } \right)}}$$
(9)
Fig. 2
figure 2

Using the theoretical findings of Sadeghi et al. (2011), comparisons averaged values of Nusselt number along the variation in the inverse of the dimensionless Debye parameter at the limiting case when the Brinkman number is 0, the parameter for Joule heating contribution is 1, while the thermal Peclet number is 1, and the flow behaviour index is 1

Full size image

Here, \(A_{1} = \frac{ - 1}{{12}}\left[ {(1 + G)b_{1} \kappa^{2} } \right]\), \(A_{2} = \frac{{a_{2} }}{2}(1 + G) - \frac{G}{2}\), \(B_{1} = \frac{{a_{1} }}{2}(1 + G) - \frac{G}{2}\), \(B_{2} = - (1 + G)b_{2} \left( {\frac{1}{\kappa }} \right)^{2}\).

\(C_{1} = \left[ {4\kappa^{ - 4} - 4\kappa^{ - 3} - \kappa^{ - 4} } \right]A_{1} + \left( {\frac{1}{{\kappa^{2} }} - \frac{2}{\kappa }} \right)B_{1} + \left( {\frac{2}{\kappa } - \frac{1}{{\kappa^{2} }} - 1} \right)A_{2} + \left( {\kappa e - e^{\kappa } } \right)B_{2}\), \(C_{2} = 4\kappa^{ - 3} A_{1} + \frac{2}{\kappa }(B_{1} - A_{2} )\), \(D_{2} = \left( { - 4\kappa^{ - 3} A_{1} } \right) - \frac{2}{\kappa }B_{1} + \left( {\frac{2}{\kappa } - 1} \right)A_{2}\), \(a_{1} = \frac{{1 + e^{\kappa } - e}}{\omega }\),\(a_{2} = \frac{{e^{\kappa } }}{\omega }\), \(b_{1} = b_{1} = \frac{1}{\omega }\) and \(\omega = \left( {1 - \frac{1}{\kappa }} \right)e^{\kappa } + \frac{2}{3\kappa }\).

In the considered range of dimensionless Debye parameter, the percentage variance between the current numerical results and the approximated analytical solutions of Sadeghi et al. (2011) has been estimated to be in the range of 1.17—2.8%. Note that the reported results of Sadeghi et al. (2011) are consistent with the approximated analytical method, while the results of current study are obtained from full-scale numerical simulations. A small deviation between the present and reported results, as seen in Fig. 2, is attributed to the solution methodologies mentioned above. Thus, as compared to the analytical/approximate analytical solutions, a more accurate solution can be obtained using the modeling framework developed in this endeavour.

4 Results and discussion

In this work, we explored the entropy generation associated with the electroosmotically actuated flow in the uniformly heated wavy microchannel. We systematically analyze the average thermal, viscous, Joule, and total entropy generation inside the wavy microchannel as well as the local entropy generation by varying the Brinkmann number (Br), thermal Peclet number (Pe), steric factor for finite ionic size (ν), Carreau number (Cu) and dimensionless amplitude (α) in the physically realistic ranges, which are as follows: \(1{0}^{-5}\le Br\le 1{0}^{-1}\), \(1{0}^{-3}\le Pe\le 1{0}^{1}\), \(0\le \upsilon \le 0.3\), \(0.01\le Cu\le 1\) and \(0\le \alpha \le 0.7\) (Sarma et al. 2017, 2018, 2022; Gaikwad et al. 2018; Kumar Mondal and Wongwises 2020; Mehta et al. 2023). Furthermore, Λ is set to 20 for the reference EDL potential of 25 mV, H to be 5 μm, and the reference electric field of 104 V/m.

Figure 3 displays the changes in the local entropy generation contours for the steric factor, v = 0 and 0.3. In contrast to the situation of v = 0.3, it appears that the intensity for local entropy production is greater for the case of v = 0 (see zones in Fig. 3 marked by the elliptical boxes). The reason behind this observation is attributed as follows. When v = 0, the flow velocity is predicted to be stronger (Mehta et al. 2023), leading to a stronger velocity gradient along the wall, particularly at the wavy wall's throat, which in turn, results in a substantial generation of local viscous entropy therein. Therefore, a possibility of less entropy generation is predicted by taking into account the finite ionic size, or the non-zero v (= 0.3).

Fig. 3
figure 3

Dimensionless local total entropy generation contours at different ν when n = 0.4, Cu = 1, Br = 0.1, α = 0.3 and Pe = 1

Full size image

Figure 4 illustrates the variation of the pertinent factors, which are thermal, viscous, and Joule heating effect, contributing to the entropy generation in the configuration considered in this study with change in Brinkman number. The following parameters are used for this plot as n = 0.4, Cu = 1, α = 0.3 and Pe = 1. Equation (7) can be utilized to explain the dominating role played by any of the pertinent factors described above contributing to the thermodynamic irreversibility in the system. It is evident that at smaller Brinkman number values, the contribution of Joule heating predominates. We attribute this observation as follows: a lower Brinkman number signifies a weaker formation of viscous dissipation modulated entropy production, which eventually results in lower domain temperature. Because of this lower domain temperature or \(\theta\) (see last term of Eq. (7)), the contribution of Joule heating effect becomes more prominent to the overall entropy generation for smaller Brinkman numbers. On the other hand, the higher dissipation for relatively larger values of Brinkman number leads to the amplification of viscous entropy generation in the system.

Fig. 4
figure 4

Plot of dimensionless averaged thermal (\({N}_{Thermal}\)), viscous (\({N}_{Viscous}\)), Joule (\({N}_{Joule}\)), and total (\({N}_{Total}\)) entropy generation with change in Brinkman number when n = 0.4, Cu = 1, α = 0.3 and Pe = 1

Full size image

Figure 5 demonstrates how the averaged total entropy generation varies as the thermal Peclet number changes for different values of steric factors. We consider other parameters for plotting Fig. 5 are as follows: Br = 0.1, when n = 0.4, Cu = 1 and α = 0.3. Our findings indicate that an increase in the lower values of thermal Peclet number can lead to a reduction in the generation of total entropy up to a critical limit. It is explained by the conduction-dominated flow of heat at the lower thermal Peclet number forming a vertical sort of isotherm region in the domain. Also, lower thermal Peclet number permits a region with a greater temperature differential close to the inlet only due to the colder inlet and warmer heated domain. Therefore, when the convection effect intensifies with an increase in lower values of thermal Peclet number, it eventual impact leads to decrease in domain temperature. Hence, the intensity of the temperature gradient by vertical isotherms decreases. Conversely, the mean total entropy generation increases with increasing thermal Peclet number beyond the critical limit. It results from increased strength of convective transport of heat at higher thermal Peclet number, which lowers the temperature in the core region and simultaneously, improves the temperature gradient near to the wall. Therefore, a greater temperature gradient near the wall with a higher thermal Peclet number enhances the contribution of thermal transport of heat to the entropy generation and total entropy production. Furthermore, as the magnitude of steric factor increases, the averaged overall entropy decreases owing to the reduction in intensity of local entropy generation, as illustrated in Fig. 3.

Fig. 5
figure 5

Plot of dimensionless total entropy generation with change in thermal Peclet number at different steric factor for Br = 0.1, when n = 0.4, Cu = 1 and α = 0.3

Full size image

Figure 6 depicts the contours of the production of local total entropy for different Carreau numbers (Cu). The other parameters being ν = 0.15, n = 0.4, Br = 0.1, α = 0.3 and Pe = 1. We observe from Fig. 6 that the intensity of local entropy production increases with increasing the value of Cu. As the magnitude of Cu increases, the apparent viscosity declines as the share-thinning characteristic grows, which in turn, enhances the velocity gradient toward the wall. The increase in viscous dissipation modulated entropy generation with an increase in Cu, hence, improves the overall entropy (average) generation in the process. It is because of this augmentation in overall entropy generation, the amount of total entropy (average) production increases with the Cu as witnessed in Fig. 7. Note that Fig. 7 plots production of dimensionless total entropy at various Carreau numbers (Cu). The other parameters used for this plot are n = 0.4, v = 0.15, α = 0.3, and Pe = 1. Additionally, at the higher values of Cu in Fig. 7, a substantial change in the order of magnitude of averaged total entropy production with an increase in Brinkmann number is anticipated. It is caused by the combined impact of a greater contribution of viscous entropy formation at higher values of Brinkman number and a higher intensity of velocity gradient for larger Cu.

Fig. 6
figure 6

Dimensionless local total entropy generation contours at different Cu when ν = 0.15, n = 0.4, Br = 0.1, α = 0.3, \(\kappa =10\). and Pe = 1

Full size image
Fig. 7
figure 7

Plot showing the production of dimensionless total entropy at various Carreau numbers when n = 0.4, v = 0.15, α = 0.3, \(\kappa =10\).and Pe = 1

Full size image

We present the entropy generation contours in Fig. 8a contributed by the thermal transport of heat, viscous dissipation, and Joule heating effect. As such, by depicting Fig. 8a, we compare the role of different entropy generation contributors in the context of electrically actuated transport both in planar and wavy microchannel. The following explanations attempt to provide the underlying physical aspects of several types of entropy generation factors in planar and wavy microchannels. Compared to wavy microchannels, it is noted that the planar microchannel exhibits much higher thermal transport of heat modulated entropy generation intensity (see Fig. 8a). This is because the corrugation wall profile of way microchannel provides resistance to the underlying flow, which in turn, reduces the temperature difference between the wall and core fluid at the entrance. Therefore, in the wavy microchannel (see Fig. 8b), the weaker temperature gradient permits a smaller thermal entropy generation intensity at the entrance, allowing for comparatively cooler fluid at the entrance region. In the case of a planar channel, a higher temperature gradient yields a larger thermal entropy generation (entropy generation associated with thermal transport of heat) intensity. Furthermore, compared to planar microchannels, wavy microchannels provide a greater temperature homogeneity due to the accelerated-deaccelerated flow pattern in the convex-concave wavy sections respectively, that facilitates fluid mixing. Due to heat transfer being dominated by conduction, the temperature field remained uniform. Consequently, the concave portion's almost negligible temperature differential permits for the creation of zero thermal entropy. Additionally, quicker flow in the convex section (see Fig. 8b) allows for a smaller thermal boundary layer. Therefore, higher thermal entropy production (local) over smaller regions is made possible by the convex region's sharper temperature gradient. Remarkably, due to the lack of convexity and concavity, the planar microchannel exhibits a thicker thermal entropy generating zone than the wavy microchannel.

Fig. 8
figure 8

(a) Dimensionless local thermal, viscous and Joule heating entropy generation contours (b) dimensionless field contours showing streamlines for plane and wavy microchannel when ν = 0.15, n = 0.4, Br = 0.1, Cu = 1, Pe = 1, G = 1, \(\alpha =0.5\) and \(\kappa =10\)

Full size image

Because of the increased shear rate (see Fig. 8b), the intensity of the viscous dissipation modulated entropy generation becomes consistently larger along the planar microchannel wall. On the other hand, due to the higher flow velocity gradient, the viscous dissipation modulated entropy formation becomes maximum in the region closer to the convex wavy wall (see from core). It is interesting to note that the decelerating flow in the diverging region allows for a relatively weaker flow field, which results in a minimal viscous entropy formation inside the concave wavy region. Thus, the intensity of viscous heating driven entropy generation becomes almost negligible in the concave sections of wavy wall.

In addition, it is found that the contribution of Joule heating to the entropy generation is two orders of magnitude lower than that of thermal transport of heat and viscous dissipation modulated entropy generation (see Fig. 8a). A comparatively lower order of external electric field intensity (104 V/m) is the reason behind it. Additionally, it is found that, in the entry region, the Joule heating modulated entropy generation is less in the wavy microchannel than the planar microchannel. The reason for this observation is discussed as follows. The higher flow resistance owing to the wall corrugation, which significantly enhances the temperature (\(\theta\)) in the wavy microchannel's entrance region. Hence, using the expression of Joule heating entropy generation as \(\frac{G}{\left(\Theta +\theta \right)}\), we can say that the enhanced temperature at the entrance of wavy microchannel enables lower Joule heating entropy generation intensity.

From the aforesaid discussion, it can be inferred here that the geometric modulation of the fluidic configuration, introducing waviness in this case, substantially changes all kinds of local entropy production. The unique pattern of total entropy generation (local) is thus assisted by the combined contribution of all the entropy generation components. Hence, the contours of the local total entropy generation for the flat and wavy microchannel are illustrated in Fig. 9 for more discussion. The wall region, especially the area next to the inlet side, is seen to have a higher intensity of entropy production. This phenomenon results from the colder incoming fluids, which in turn, causes the higher temperature gradient in the fluid mass to be attained in the zone closer to the channel inlet (see Fig. 8). Moreover, the existence of a wavy trough and the lowered flow velocity within it permit the formation of less (or nearly zero) thermal transport of heat driven entropy due to a more uniform temperature field. In addition, the reduced flow velocity in that area permits a lower velocity gradient and a generation of less viscous dissipation modulated entropy (see Fig. 8). Thus, the area of the “zero-entropy generation region” within the wavy trough or concave section increases together with the amplitude on the wavy wall (see Fig. 9). Consequently, as illustrated in Fig. 10 illustrates, an increase in amplitude leads to a decrease in the total entropy generation (average). Having a look at the entropy generation contours depicted in Fig. 8, one can delve deep into the underlying physics behind the reduction in total averaged entropy generation in wavy microchannel as compared to the planar channel.

Fig. 9
figure 9

Dimensionless local total entropy generation contours at different amplitude when ν = 0.15, n = 0.4, Br = 0.1, Cu = 1 and Pe = 1

Full size image
Fig. 10
figure 10

Plot shows dimensionless overall entropy production for various dimensionless amplitudes with n = 0.4, v = 0.15, and Pe = 1 shows the change in the Brinkman number

Full size image

Additionally, Fig. 11 shows the percentage drop in total value of averaged entropy production in the wavy microchannel compared to that in a planar microchannel. The variations are depicted with the Brinkman number for three different values of dimensionless amplitude (α). Figure 10 demonstrates that average entropy generation decreases with an increase in amplitude. The percentage reduction of the production of entropy in the wavy microchannel increases for lower values of Brinkman number, as the corresponding averaged entropy generation of the wavy case increases with Brinkman number (see Fig. 10). The dominance of the increasing magnitude of averaged entropy generation in planar microchannel reduces the percentage reduction of averaged entropy generation at higher Brinkman number values. The greatest decline of the overall entropy generation in a wavy microchannel is found to be about 46% for dimensionless amplitude 0.7. Thus, it can be argued that it makes sense to use wavy microchannels/microdevices in heat-exchanging applications and in thermal management of heat.

Fig. 11
figure 11

Plot of the percentage decrease in averaged dimensionless total entropy generation in wavy channel relative to plane channel with change in Brinkman number at different dimensionless amplitude when n = 0.4, ν = 0.15, Cu = 1 and Pe = 1

Full size image

In accordance with the second law of thermodynamics, the performance of a thermal heat exchanging device is maximized when the entropy generation associated with the underlying thermohydrodynamics becomes minimal. Since electroosmotic effect has been established as a more beneficial flow actuation mechanism for micro/nano fluidic systems than pressure-driven flow, this work focuses on the entropy production rate, originating from the thermal transport of heat, viscous heating and Joule heating effect, associated with electrically actuated thermofluidic transport at microfluidic scale. In this work, we demonstrate that the wavy microchannel has a lesser entropy generation as compared to the plane microchannel, especially at the lower Brinkman number. The inferences of the current work seem to provide valuable insights into optimizing the micro-electro-mechanical heat exchanging systems/devices to run at optimal thermal performance essentially by reducing the entropy generation for the specified flow and geometric parameters.

5 Conclusion

The present investigation focuses on analyzing entropy generation in wavy microchannels induced by electroosmotic action. Through varying parameters within physically acceptable ranges, including the Brinkman number (Br), thermal Peclet number (Pe), steric factor for finite ionic size (v), Carreau number (Cu), and dimensionless amplitude (α), we examined thermal, Joule, and total entropy generation, along with local entropy generation. The study yielded several significant findings:

  • At lower Brinkman numbers, Joule heating dominates entropy generation, while at higher values, viscous dissipation becomes predominant.

  • Increasing the Carreau number enhances total entropy production, whereas increasing ionic size reduces it. However, total entropy generation may vary non-monotonically within the considered range of thermal Peclet numbers.

  • Total entropy generation decreases with higher amplitudes of the wavy wall. Moreover, total entropy generation in wavy microchannels is consistently lower than in planar microchannels. For a dimensionless amplitude of 0.7, the highest reduction in total entropy generation in a wavy microchannel is approximately 46%.

These findings suggest that use of wavy microchannels in applications pertaining to thermal management of heat under electroosmotic flow is justified. The insights gained from this study hold relevance for the development of cost-effective heat-exchanging equipment for electronic cooling.