Rotational electrohydrodynamics of a non-Newtonian fluid under electrical double-layer phenomenon: the role of lateral confinement

Abstract

We investigate the transient analysis of the transport features of a non-Newtonian fluid in a rotating microfluidic channel as modulated by the electrical double-layer effect. We use the power-law model to describe rheology of the non-Newtonian fluid in this study. We bring out the rotational force-induced development of the secondary flows inside the channel, taking the effects of the lateral confinement into account. We show that the consideration of lateral confinement into the analysis gives rise to a complex flow dynamics, allowing the formation of double-vortex structures as well as the sister vortexes in the flow field. In particular, we show that the sister vortexes formed in the flow field exhibit different senses of rotations under the influence of the electrical forcing, leading to a potential enhancement in mixing in microfluidic channel. Also, we show the variation of the volume flow rate through the channel for different cases and unveil the secondary flow-induced alteration in the device throughput. We believe that the inferences obtained from this analysis may improve the design of miniaturized systems/devices, typically used for the transportation of bio-fluids, which are largely non-Newtonian in nature, in a rotating platform.

1 Introduction

Emerging applications and implications of rotationally actuated microfluidic systems/devices, which include biochemical processing and medical diagnostics in one side as well as the systematic interrogation of the complex flow physics on the other, have motivated humongous research interests to both the theoretical and experimental research communities (Stone et al. 2004; Madou et al. 2006; Chakraborty et al. 2009, 2011; Ng and Qi 2015). The application of electrical forcing in realizing transport through microfluidic pathways, which is an experimentally proven phenomenon (Ramos et al. 1998, 2003; Green et al. 2000), has also received considerable attention owing to a few distinctive transport features such as on-chip integrability, removal of moving components, finer controllability, to name a few (Ajdari 1995; Squires and Bazant 2004; Bazant et al. 2004; Mondal et al. 2013; Goswami et al. 2015). As a consequence (Ng and Qi 2015; Abhimanyu et al. 2016; Kaushik et al. 2017a), microflow manipulations by exploiting the rotation-induced forces in conjunction with electrokinetic influences are likely to enhance the functionality as well as the device performance. It may be mentioned here that the instabilities in electrokinetic flows have also been extensively studied in the literature for both the internal and free surface flows (Ray et al. 2011, 2012, 2013; Reddy et al. 2011; Bandyopadhyay et al. 2012). Introduction of non-Newtonian fluids, which mimics practical bio-microfluidic applications, adds further complexity to the analysis of the physical problem (Xie and Jian 2014; Li et al. 2015; Abhimanyu et al. 2016).

A survey of the literature reveals that research in the context of the rotationally actuated microflows under the influence of the electrical forcing has been initiated by a number of groups in recent times (Ruo et al. 2010; Chang and Wang 2011; Li et al. 2015; Ng and Qi 2015). It is important to mention here that the Coriolis force arising due to the rotational effect induces secondary flow in the channel, while the secondary flow, in the presence of electrical forcing, may lead to an enhancement in mixing in the fluidic pathways essentially by distracting the axial momentum developed due to the applied electrical field. Also, it should be highlighted in this context here that rotationally actuated microfluidic devices are commonly used for the transportation and analysis of DNA solutions, blood and bio-fluids, which are, in general, non-Newtonian in nature. In particular, the miniaturized devices involved with the application of these kinds require a proper mixing and augmented flow rate, which, in turn, necessitates an apposite design of these devices (Chang and Wang 2011; Ng and Qi 2015). We would like to mention in this context here that these augmented functionalities (an enhancement in mixing to be precise) of rotational force-induced transport in narrow fluidic pathways can be realized only in the presence of lateral confinements, since the consideration of the side wall effect of the channel will alter the flow dynamics, following the development of the induced flow across the channel.

Here, we attempt to address the underlying dynamical behavior of a power-law fluid in a rotation-induced flow environment, under the influence of the electrical double-layer (EDL) effect. We bring out the development of secondary flow inside the microchannel, realized through the formation of vortexes in the field, arising due to complex coupling among the electrical forcing and the rotation-induced forces as modulated by the rheological effect of the fluid. We demonstrate the formation of sister vortexes in the flow field and pinpoint its effects on the alteration in the overall rotational sense of the main vortexes. This effect leads to the possibility of significant enhancement in mixing in a rotating microfluidic channel. We further depict two distinct regimes showing the rotation-induced alteration in flow rate for different rheological parameters. We believe that the inferences obtained from our investigations will be capable of providing fundamental physical basis, which may effectively be used to improve the design of the rotationally actuated microfluidic devices/systems, which are commonly used in medical diagnostics.

2 Problem description and governing equations

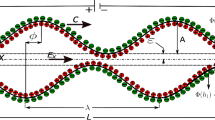
We schematically represent, in Fig. 1, the problem considered in this study. The flow of a non-Newtonian fluid is initiating along the x-direction of the channel under the combined influences of applied electrical field ${\mathbf{E}} = \left( {E_{x} ,0,0} \right)$ and rotation-induced forces. We here consider Ostwald–de Waele power-law model to describe the constitutive behavior of the non-Newtonian fluid (Mondal et al. 2015). We assume that the fluid is initially at rest in the channel, while the channel is rotating about z-axis at a constant angular velocity ${\varvec{\Omega}} = \left( {0,\;0,\;\varOmega } \right)$. We further assume that the coordinates are rotating with the channel itself (as depicted in Fig. 1), while the coordinate axes $x,\;y\;\text{and} \;z$ are taken along the along the length (L), width (B) and height (2H) of the channel, respectively. We assume that the length of the channel is much larger than its width and height, i.e., $L \gg B\sim2H$. Also, an incompressible flow is considered in the present analysis with no external pressure gradient acting to drive the flow except the pressure arising due to the centrifugal force. Note that the pressure due to centrifugal force is maintaining the secondary flow in the $y - z$ plane of the channel.

Fig. 1

(Color online) Schematic diagram showing the problem under consideration in the present study. The channel is considered of rectangular cross section. There is an applied electric field ${\mathbf{E}} = \left( {E_{x} ,0,0} \right)$ in the x-direction. The channel is rotating in the z-direction at a constant angular velocity ${\varvec{\Omega}} = \left( {0,\;0,\;\varOmega } \right)$. Here the coordinate system is also considered to rotate along with the channel

2.1 The velocity distribution in the flow field

The governing equations in the frame of reference rotating along with the channel may be written as (Chang and Wang 2011; Xie and Jian 2014; Mondal et al. 2015; Ng and Qi 2015):

$$ \nabla \cdot {\mathbf{u}} = 0 $$

(1)

$$ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + \left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} + 2\left( {{\varvec{\Omega}} \times {\mathbf{u}}} \right) + {\varvec{\Omega}} \times \left( {{\varvec{\Omega}} \times {\mathbf{r}}} \right)} \right) = - \nabla p + \nabla \cdot {\varvec{\uptau}} + \rho_{e} {\mathbf{E}} $$

(2)

where τ is the stress tensor and $\rho_{e} {\mathbf{E}}$ is the electroosmotic body force per unit volume, ${\mathbf{u}}$ is the velocity vector, ${\mathbf{r}}$ is the radial coordinate and ${\varvec{\Omega}}$ is the angular velocity vector. The stress tensor ${\varvec{\uptau}}$ for a fluid described by the power-law constitutive model equation is written as (Das and Chakraborty 2006; Chakraborty 2007; Deng et al. 2012; Mondal et al. 2015; Kaushik et al. 2017b):

$$ {\mathbf{T}} = \kappa \left( {\sqrt {\frac{1}{2}{\mathbf{D}}:{\mathbf{D}}} } \right)^{n - 1} {\mathbf{D}}, $$

(3)

where $\kappa$ is the consistency parameter, $n$ is the power-law index and the rate of deformation ${\mathbf{D}}$ is defined as:

$$ {\mathbf{D}} = \frac{1}{2}\left( {\nabla {\mathbf{u}} + \nabla {\mathbf{u}}^{T} } \right) $$

(4)

In order to represent the stress tensor in a bit simplified form, we further consider the following expression in this analysis as:

$$ \eta = \kappa \left( {\sqrt {\frac{1}{2}{\mathbf{D}}:{\mathbf{D}}} } \right)^{n - 1} $$

(5)

Also, we define the modified pressure, which includes the term containing centrifugal force (Chandrasekhar 1961) and can be written as:

$$ P = p - \left( {\frac{{\rho \left| {{\varvec{\Omega}} \times {\mathbf{r}}} \right|^{2} }}{2}} \right) $$

(6)

In that case, the momentum transport equation [Eq. (2)] further reduces to:

$$ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + \left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} + 2\left( {{\varvec{\Omega}} \times {\mathbf{u}}} \right)} \right) = - \nabla P + \nabla \cdot \left( {\eta {\mathbf{D}}} \right) + \rho_{e} {\mathbf{E}} $$

(7)

It is important to mention here that the assumption of $L \gg B\sim2H$ as employed in this study following the lead by Ng and Qi (Ng and Qi 2015) reduces to the following conditions in our analysis which can be given as: $\partial_{x} \left( {} \right) \ll \partial_{y} \left( {} \right) \sim \partial_{z} \left( {} \right)$. Therefore, considering these implemented features of this analysis, we drop out the terms containing $\partial_{x} \left( {} \right)$ and $\partial_{xx} \left( {} \right)$ from the equations governing the flow dynamics in our subsequent discussions.

2.2 Electrostatic potential distribution in the channel

For a further simplification of the electroosmotic body force term $\rho_{e} {\mathbf{E}}$ appearing in Eq. (7), we need to know the spatial distribution of the potential in the electrical double layer (EDL). In order to obtain the spatial distribution of the electrical potential distribution $\psi$ within the EDL, we invoke the Poisson equation, which for the problem considered in this study can be written as (Huter 1981; Masliyah and Bhattacharjee 2006):

$$ \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }} = - \frac{{\rho_{e} }}{\varepsilon } $$

(8)

where $\rho_{e}$ is the total charge density of the ions present in the EDL and is given for a $\zeta :\zeta$ symmetric electrolyte as: $\rho_{e} = e\zeta \left( {n^{ + } - n^{ - } } \right)$, where $e$ is the protonic charge, $\zeta$ corresponds to the valence of the ions. We here mention that the number densities of the co-ion $\left( {n^{ + } } \right)$ and counter-ion $\left( {n^{ - } } \right)$ in the EDL are obtained by appealing to the Boltzmann distribution and can be written as: $n^{ \pm } = n_{\infty } Exp\left[ { \mp e\tilde{z}\psi /k_{B} T} \right]$, where $n_{\infty }$ is the bulk ionic concentration, $k_{B}$ is the Boltzmann constant and $T$ is the absolute temperature. Also, we here consider the surface potential $\left( {\psi_{w} } \right)$ to be low $\left( {\psi_{w} < 25\,\text{mV} } \right)$, leading to a validity of the Debye–Hückel approximation in the present study (Huter 1981; Masliyah and Bhattacharjee 2006; Mondal et al. 2014; Goswami et al. 2015). However, considering this assumption, we may further write Eq. (8) as given below (Huter 1981; Masliyah and Bhattacharjee 2006):

$$ \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }} = \psi_{ref} \kappa^{2} \text{Sinh} \left( {\frac{e\zeta \psi }{{k_{B} T}}} \right) $$

(9)

In Eq. (9), $\kappa^{2}$ is the Debye–Hückel parameter and is given by $\kappa^{2} = {{\left( {2n_{\infty } e^{2} \zeta^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {2n_{\infty } e^{2} \zeta^{2} } \right)} {\left( {\varepsilon k_{B} T} \right)}}} \right. \kern-0pt} {\left( {\varepsilon k_{B} T} \right)}}$. Note that the inverse of the Debye–Hückel parameter $\lambda \left( { = \kappa^{ - 1} } \right)$ is a representative measure of the EDL thickness. In order to obtain the solution of Eq. (9), we employ the following boundary conditions:

$$ \left. \psi \right|_{y = \pm B} = \psi_{1} \quad{\text{and}}\quad\left. \psi \right|_{y = \pm H} = \psi_{2} $$

(10)

We next describe the transport equations coupled with electrical forcing for the problem under present consideration. However, a further progress to this end leads to the following set of equations, which can be given as:

$$ \nabla \cdot {\mathbf{u}} = 0 $$

(11)

$$ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + \left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} + 2\left( {{\varvec{\Omega}} \times {\mathbf{u}}} \right)} \right) = - \nabla P + \nabla \cdot \left( {\eta {\mathbf{D}}} \right) + \varepsilon \psi_{\text{ref}} \kappa^{2} \text{Sinh} \left( {\frac{e\zeta \psi }{{k_{B} T}}} \right){\mathbf{E}} $$

(12)

It should be mentioned here that, based on the assumption $L \gg B\sim2H$ as taken in the present analysis, we may ignore the terms containing $\partial_{x} \left( {} \right)$ in comparison with the terms containing $\partial_{y} \left( {} \right)$ and $\partial_{z} \left( {} \right)$ without sacrificing the essential physics of interest. Also, we consider that the fluid is initially at rest in the channel. Employing these considerations into the present analysis, we can simplify the transport equation [Eqs. (11) and (12)] one step further. Below we write the reduced equations as:

$$ \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 $$

(13a)

$$ \rho \left( {\frac{\partial u}{\partial t} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} + 2\varOmega v} \right) = \frac{\partial }{\partial y}\left( {\eta \frac{\partial u}{\partial y}} \right) + \frac{\partial }{\partial z}\left( {\eta \frac{\partial u}{\partial z}} \right) + \varepsilon \psi_{ref} \kappa^{2} \text{Sinh} \left( {\frac{e\zeta \psi }{{k_{B} T}}} \right)E_{x} $$

(13b)

$$ \rho \left( {\frac{\partial v}{\partial t} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} - 2\varOmega u} \right) = - \frac{\partial P}{\partial y} + \frac{\partial }{\partial y}\left( {\eta \frac{\partial v}{\partial y}} \right) + \frac{\partial }{\partial z}\left( {\eta \frac{\partial v}{\partial z}} \right) + \frac{\partial \eta }{\partial y}\frac{\partial v}{\partial y} + \frac{\partial \eta }{\partial z}\frac{\partial w}{\partial y} $$

(13c)

$$ \rho \left( {\frac{\partial w}{\partial t} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{\partial z}} \right) = - \frac{\partial P}{\partial z} + \frac{\partial }{\partial y}\left( {\eta \frac{\partial w}{\partial y}} \right) + \frac{\partial }{\partial z}\left( {\eta \frac{\partial w}{\partial z}} \right) + \frac{\partial \eta }{\partial y}\frac{\partial v}{\partial z} + \frac{\partial \eta }{\partial z}\frac{\partial w}{\partial z} $$

(13d)

Also, we use the following set of the initial and boundary conditions for Eqs. (13a)–(13d), which can be given as:

$$ {\text{Initial}}\,{\text{condition}}:\,t \le 0,u = 0,v = 0,w = 0 \quad \forall \, y,z $$

(14a)

$$ {\text{Boundary}}\,{\text{conditions}}:\left\{ {\begin{array}{*{20}l} {t > 0,\left. u \right|_{z = \pm H} = 0,\left. v \right|_{z = \pm H} = 0,\left. w \right|_{z = \pm H} = 0 \, \forall \, y} \hfill \\ {t > 0,\left. u \right|_{z = \pm B} = 0,\left. v \right|_{z = \pm B} = 0,\left. w \right|_{z = \pm B} = 0 \, \forall \, z} \hfill \\ \end{array} } \right. $$

(14b)

2.3 Non-dimensionalization of the transport equations

We here take an effort to cast the transport equations and the associated boundary conditions into their dimensionless counterparts. In an effort to do so, we use the channel half-height $H$, the Helmholtz–Smoluchowski (HS) velocity, $u_{\text{HS}} = - \varepsilon E_{x} \psi_{\text{ref}} /\eta_{\text{eff,ref}}$ and $\varOmega^{ - 1}$ as the characteristic length, velocity and time scales, respectively. Note that the effective viscosity of the non-Newtonian fluid $\eta_{\text{eff}}$ may be defined as: $\eta_{\text{eff}} = - k_{p} \left( {{{u_{\text{HS}} } \mathord{\left/ {\vphantom {{u_{\text{HS}} } H}} \right. \kern-0pt} H}} \right)^{n - 1}$. Therefore, the remaining dimensionless parameters are as follows: $u^{*} = u\left( {\varepsilon E_{x} \psi_{\text{ref}} /\eta_{\text{eff,ref}} } \right)^{ - 1}$, $v^{*} = v\left( {\varepsilon E_{x} \psi_{\text{ref}} /\eta_{\text{eff,ref}} } \right)^{ - 1}$, $z^{*} = zH^{ - 1}$, $y^{*} = yH^{ - 1}$, $t^{*} = tu_{\text{HS}} \left( H \right)^{ - 1}$, $Re_{\varOmega } = {{2\rho \varOmega H^{2} } \mathord{\left/ {\vphantom {{2\rho \varOmega H^{2} } {\eta_{\text{eff,ref}} }}} \right. \kern-0pt} {\eta_{\text{eff,ref}} }}$, $Re = {{\rho u_{\text{HS}} H} \mathord{\left/ {\vphantom {{\rho u_{\text{HS}} H} {\eta_{\text{pl,ref}} }}} \right. \kern-0pt} {\eta_{\text{pl,ref}} }}$, $k^{*} = kH$, $\varPsi^{*} = \varPsi \left( {\psi_{\text{ref}} } \right)^{ - 1}$, $\eta_{\text{eff}}^{*} = \eta \left( {\eta_{\text{eff,ref}} } \right)^{ - 1}$. We also define the aspect ratio of the rectangular channel as $B^{*} = {B \mathord{\left/ {\vphantom {B H}} \right. \kern-0pt} H}$. Using these parameters, we get the set of dimensionless transport equations, which are then read as:

2.3.1 Potential distribution equation in dimensionless form

$$ \frac{{\partial^{2} \psi^{*} }}{{\partial y^{*2} }} + \frac{{\partial^{2} \psi^{*} }}{{\partial z^{*2} }} = \kappa^{*2} \text{Sinh} \left( {\psi^{*} } \right) $$

(15)

Note that the dimensionless boundary conditions for above equation [Eq. (15)] are written as:

$$ \left. {\psi^{*} } \right|_{{\bar{y} = \pm w}} = \xi_{1} \quad{\text{and}}\quad\left. {\psi^{*} } \right|_{{\bar{z} = \pm 1}} = \xi_{2} $$

(16)

2.3.2 Continuity and momentum transport equation in dimensionless form

$$ \frac{{\partial v^{*} }}{{\partial y^{*} }} + \frac{{\partial w^{*} }}{{\partial z^{*} }} = 0 $$

(17a)

$$ Re\left( {\frac{{\partial u^{*} }}{{\partial t^{*} }} + v^{*} \frac{{\partial u^{*} }}{{\partial y^{*} }} + w^{*} \frac{{\partial u^{*} }}{{\partial z^{*} }}} \right) + Re_{\varOmega } v^{*} = \frac{\partial }{{\partial y^{*} }}\left( {\eta^{*} \frac{{\partial u^{*} }}{{\partial y^{*} }}} \right) + \frac{{\partial^{*} }}{{\partial z^{*} }}\left( {\eta^{*} \frac{{\partial u^{*} }}{{\partial z^{*} }}} \right) + \kappa^{*2} \text{Sinh} \left( {\psi^{*} } \right) $$

(17b)

$$ \text{Re} \left( {\frac{{\partial v^{*} }}{{\partial t^{*} }} + v^{*} \frac{{\partial v^{*} }}{{\partial y^{*} }} + w^{*} \frac{{\partial v^{*} }}{{\partial z^{*} }}} \right) - Re_{\varOmega } u^{*} = - \frac{{\partial P^{*} }}{{\partial y^{*} }} + \frac{\partial }{{\partial y^{*} }}\left( {\eta^{*} \frac{{\partial v^{*} }}{{\partial y^{*} }}} \right) + \frac{\partial }{{\partial z^{*} }}\left( {\eta^{*} \frac{{\partial v^{*} }}{{\partial z^{*} }}} \right) + \frac{{\partial \eta^{*} }}{{\partial y^{*} }}\frac{{\partial v^{*} }}{{\partial y^{*} }} + \frac{{\partial \eta^{*} }}{{\partial z^{*} }}\frac{{\partial w^{*} }}{{\partial y^{*} }} $$

(17c)

$$ Re\left( {\frac{{\partial w^{*} }}{{\partial t^{*} }} + v^{*} \frac{{\partial w^{*} }}{{\partial y^{*} }} + w^{*} \frac{{\partial w^{*} }}{{\partial z^{*} }}} \right) = - \frac{{\partial P^{*} }}{{\partial z^{*} }} + \frac{{\partial^{*} }}{{\partial y^{*} }}\left( {\eta^{*} \frac{{\partial w^{*} }}{{\partial y^{*} }}} \right) + \frac{\partial }{{\partial z^{*} }}\left( {\eta^{*} \frac{{\partial w^{*} }}{{\partial z^{*} }}} \right) + \frac{{\partial \eta^{*} }}{{\partial y^{*} }}\frac{{\partial v^{*} }}{{\partial z^{*} }} + \frac{{\partial \eta^{*} }}{{\partial z^{*} }}\frac{{\partial w^{*} }}{{\partial z^{*} }} $$

(17d)

where $\eta^{*} = \left[ {\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{2} + \left( {\frac{{\partial u^{*} }}{{\partial z^{*} }}} \right)^{2} + 2\left( {\frac{{\partial v^{*} }}{{\partial y^{*} }}} \right)^{2} + 2\left( {\frac{{\partial w^{*} }}{{\partial z^{*} }}} \right)^{2} + \left( {\frac{{\partial v^{*} }}{{\partial z^{*} }} + \frac{{\partial w^{*} }}{{\partial y^{*} }}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} .$

It is important to note that, with the above method of non-dimensionalization, we can get a full electroosmotic flow equations if we set $Re_{\varOmega } = 0$. The corresponding boundary conditions in their dimensionless take the following form, which can be given as:

$$ {\text{Initial}}\,{\text{condition:}}\,t^{*} \le 0, \, u^{*} = 0, \, v^{*} = 0 \, ,w^{*} = 0\quad\forall \, y^{*} ,z^{*} $$

(18a)

$$ {\text{Boundary}}\,{\text{conditions:}}\left\{ {\begin{array}{*{20}l} {t^{*} > 0,\left. {u^{*} } \right|_{z = \pm 1} = 0,\left. {v^{*} } \right|_{z = \pm 1} = 0,\left. {w^{*} } \right|_{z = \pm 1} = 0\,\forall \, y^{*} } \hfill \\ {t^{*} > 0,\left. {u^{*} } \right|_{{z = \pm b^{*} }} = 0,\left. {v^{*} } \right|_{{z = \pm b^{*} }} = 0,\left. {w^{*} } \right|_{{z = \pm b^{*} }} = 0\,\forall \, z^{*} } \hfill \\ \end{array} } \right. $$

(18b)

3 Numerical approach and model benchmarking

We solve the transport equations as mentioned above using the finite-volume framework of our in-house code. We here give a brief description of the code as employed in this analysis. The code employs first-order scheme for the temporal discretization, while the spatial terms are discretized using second-order central difference scheme. We use a fully explicit scheme to track the temporal advancement of the flow (Bell et al. 1989; Fernandez-Feria and Sanmiguel-Rojas 2004). The pressure equation is solved by the two-step projection method (Brown et al. 2001). Furthermore, we obtain the solutions until the steady state is attained. We would like to mention here that, from here onward, the ‘*’ symbol is removed from the dimensionless variables only for the sake of ease in the presentation.

Before we proceed to discuss the results obtained from the present study, we here take an effort to show the grid independence and convergence test results pertinent to the present analysis. In the present study, we use the same number of uniform grids in both the $y$ and $z$-directions, i.e., $\Delta y = \Delta z = \delta$. We show, in Fig. 2a, b, the grid independence study for different values of $\delta$, while Fig. 2a, b depicts the variation of $v$ and $w$ velocities, respectively, along $y$-direction. It is observed from the present figures that the change in velocities becomes insignificant as $\delta$ is changed from $1/80$ to $1/96$. We, therefore, consider $\delta = 1/80$ for all the simulations in the present study. Also, we show the variation of velocity, in Fig. 2c, for different time step sizes as mentioned in the figure. One may note from the figure under present focus is that the variation becomes negligibly small as $\Delta t$ changes from $5 \times 10^{ - 8}$ to $1 \times 10^{ - 8}$, and hence, we have considered $\Delta t = 5 \times 10^{ - 8}$ throughout this study. In an effort to establish the efficacy of the present numerical model, we also take an attempt in Fig. 2d to reproduce the results reported by Ng and Qi (Ng and Qi 2015), using our in-house code. A close match between the results obtained from the present numerical framework and the reported results in the literature (Ng and Qi 2015), indeed, vouches for the accurateness of the present modeling framework.

Fig. 2

(Color online) Grid independence and convergence test: a Variation of v-velocity $v\left( {t,y,0} \right)$ versus $y$ for different grid sizes $\delta$ and b variation of $w$-velocity $w\left( {t,y,0} \right)$ versus $y$ for different grid sizes $\delta$ and c variation of $u$-velocity versus $z$ for different time step values and obtained for $n = 1.2$, $t = 0.0001$ and $Re_{\varOmega } = 40$. The change in variation of both the velocities becomes insignificant as $\delta$ changes from 1/80 to 1/96, while a change in $\Delta t$ from $5e^{ - 8}$ to $1e^{ - 8}$ does not bring a substantial change in the velocity. Model Benchmarking: Plot showing the variation of $u$-velocity for different $Re_{\varOmega }$. The other parameters used are $B = 1$, $Re = 0.01$, $n = 1$, $\kappa = 10$. The variations obtained from the present study match well with the results reported by Ng and Qi (2015), for a Newtonian fluid at steady state

4 Results and discussion

We here discuss different issues, originating from the rotation-induced forcing factors, which are likely to influence the underlying transport as considered in this analysis non-trivially. In fact, we will be discussing the augmented functionalities involved with the microscale transport over rotationally actuated platform as modulated by the combined consequences of the fluid rheology and EDL phenomena. Typical values of the fluid properties are $\eta \sim 8 \times 10^{ - 4} \,{\text{N}}\,{\text{sm}}^{ - 2}$, $\rho \sim 1000\,{\text{kg}}\,{\text{m}}^{ - 3}$ and $n \sim 0.6 - 1.3$. Typical height of the microchannel is $H \sim 300\,\upmu{\text{m}}$ (Lee et al. 2011), while the rotational speeds of rotating microfluidic platforms typically become $\varOmega \sim 5000\,{\text{rpm}}$ (Andersson et al. 2007; Richard et al. 2009). Considering these values, we get a rotational Reynolds number of $Re_{\varOmega } \sim 20$. In an effort to do so, we mainly look at the development of flow velocities and their consequential effect on the volume transport rate through the channel as discussed in the subsequent sections. We first discuss the underlying dynamical behavior during initial transience, and then, we proceed to elaborate several issues of the flow dynamics as the steady state is attained. Unless specified otherwise, we consider the following set of parameters in this study as: $Re_{\varOmega } = 40$, $Re = 0.01$ and $\kappa = 10$. We also consider unit aspect ratio $B = 1$ through this study.

4.1 Transient analysis of axial flow velocity: interplay among electrokinetics, fluid rheology and rotation-induced forcing

4.1.1 Variation of axial $\left( u \right)$ velocity

We begin our discussion with Fig. 3, which shows the variation of $u$-velocity in $y - z$ plane at different temporal instants and obtained for different values of power-law index $n = 0.8$, 1 and 1.2, respectively. The other parameters considered in plotting the figure are as follows:$B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$, $\kappa = 10$. Having a closer look at Fig. 3, one may find the appearance of the depression in the interior to the flow field. The appearance of the depression is a consequential effect of the Coriolis force on the flow dynamics that stems from the effect of channel rotation. Although the flow velocity (precisely, the $u$-velocity) in the middle of the channel reduces and becomes negative due to the Coriolis effect, the velocity at the exterior to the flow field, i.e., in the region close to the walls of the channel, remains still positive, largely attributed to the electrical forcing.

Fig. 3

(Color online) Plot depicting the temporal evolution of $u$-velocity in $y - z$ plane. We have used the following parameters to obtain the variation such as $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$, $\kappa = 10$

Since the electrical forcing is mainly acting over the EDL (a region close to the walls of the channel), the velocity becomes positive over there even for the rotating Reynolds number as high as $Re_{\varOmega } = 40$. In fact, the electrical double-layer phenomena together with the mass conservation effect lead to a rise in $u$-velocity (precisely, a positive value) at the exterior as shown in Fig. 3. Also, we see from the present figure that, with increasing temporal instant $t = 0.001$, the $u$-velocity starts becoming positive at the middle and only a mild depression is seen over that region at steady-state condition. We attribute this weak depression appearing on the $u$-velocity contour even at steady-state condition to the effect of Coriolis force on the underlying transport originating from the channel rotation. Even though the flow dynamics exhibits a qualitative similar behavior for all the values of power-law index $\left( n \right)$ considered, a quantitative dissimilarity on the underlying dynamical behavior for a change in the rheological behavior of the fluid is witnessed in Fig. 3. Since the effective viscosity and the viscous drag increase with the increasing non-Newtonian behavior of the fluid $\left( {n > 1} \right)$, the flow velocity for, a given strength of applied forcing, both at the exterior and at the interior regions gets altered with a change in $n$ as reflected in Fig. 3. We further observe from Fig. 3 that, for shear-thickening fluid $\left( {n = 1.2} \right)$, the $u$-velocity in the region closer to the walls of the channel becomes relatively lesser, while the reduction in $u$-velocity at the middle also gets weakened. This observation can be attributed to a relative stronger influence of viscous drag in the flow field, mainly arising due to shear-thickening behavior of the fluid. Note that the rheology-modulated change in the flow dynamics is observed for all the temporal instants considered, which one can find from the figure presented above (Fig. 3). These observations are well supported by the fact that the depression appearing in the middle becomes weaker with increasing value of $n$.

4.1.2 Secondary flow development: streamlines and contour in $y - z$ plane

In an effort to bring out more insights into the flow dynamics, we depict in Fig. 4 the velocity vectors and streamlines at different temporal instants. Note that to describe the streamlines and the velocity vectors, we consider three different values of $n$, while the other parameters considered for this plot are $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$, $\kappa = 10$. We have shown the streamlines over the entire section of $y - z$ plane essentially to obtain a much clearer picture of the flow pattern inside the channel. One may see from Fig. 4 that, although the streamlines are parallel in the middle of the channel, double-vortex structures formed one at the upper part of the channel $\left( {z > 0} \right)$ and another at the lower part of the channel $\left( {z < 0} \right)$, indeed, are in compliance with the development of secondary flow inside the channel. At the earlier instant of time $\left( {t < 0.0001} \right)$, while the vortex at the upper part of the channel shows counterclockwise rotation, the lower vortex exhibits an clockwise sense of rotation (see the velocity vectors). It is worth mentioning here that the formation of double-vortex structures inside the flow domain along with their rotational sense largely corroborates with the similar structures from the perspective of experimental as well as numerical evidence as reported in the literature (Hart 1971; Speziale 1982; Kheshgi and Scriven 1985), albeit the flow configuration in this analysis differs from those reported studies.

Fig. 4

(Color online) Plot showing the temporal evolution of velocity vectors and streamlines in the $y - z$ plane. Three different values of $n = 0.8$, $1$ and $1.2$ have been considered to obtain the variations depicted in the present figure. We have considered the following other parameters as: $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$, $\kappa = 10$. a $n = 0.8$, $t = 0.0001$, b $n = 0.8$, $t = 0.001$, c $n = 0.8$, steady state, d $n = 1$, $t = 0.0001$, e $n = 1$, $t = 0.001$, f $n = 1$, steady state, g $n = 1.2$, $t = 0.0001$, h $n = 1.2$, $t = 0.001$, i $n = 1.2$, steady state

One may further note from Fig. 4 that, with increasing time, the shape of the vortexes formed inside the channel changes. Importantly, we observe the formation of sister vortexes at the corner of the channel at $t = 0.001$, which, however, disappears at a higher temporal instant, precisely at steady state. In fact, this observation holds true for all the values of $n$ considered in the present analysis. Having a closer scrutiny at Fig. 4, we further observe that the sister vortexes formed at both halves of the channel demonstrate an opposite sense of rotation. Notably, out of these two sister vortexes, one sister vortex at each half resembles the rotational sense of the main vortex, while the other sister vortex, in stark contrast to the main vortex, shows an opposite sense of rotation.

Quite remarkably, the formation of sister vortexes in the flow field is, indeed, an interesting phenomena in the purview of microscale transport, since the appearance of these sister vortexes leads to an enhancement in mixing by altering the overall rotational sense of the main vortexes as aptly confirmed in Fig. 4 (see the streamlines and velocity vectors at steady state). We would like to attribute this phenomenon to the strong interplay between the rotation-induced forces and the electrical forcing as modulated by the confinement effect. It is worth mentioning here that the rotational sense of the main vortexes at steady-state condition becomes completely different from those demonstrated during transience. Albeit, in Fig. 4, we have speculated different facets of the vortex formation dynamics in the channel qualitatively, we also take an effort to figure out the underlying physical issues that give rise to such an interesting flow behavior from different perspectives. We attempt to look at this phenomenon of vortex formation dynamics in the flow field from the variation of development in vorticity in the channel as modulated by the confinement effect and discussed in the next section.

4.1.3 Vorticity vector

We show, in Fig. 5, the vorticity vectors in the flow field at different temporal instants, which includes the initial transience as well as steady-state condition for different values of the power-law index. In Fig. 5, we show only the one-fourth of the channel cross section essentially for the clarity in the presentation as the other three-fourths are symmetric. The other parameters are: $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$, $\kappa = 10$. The electrical forcing due to the double-layer phenomena at all the walls of the channel leads to a development of flow in the $x$-direction of the channel, while the Coriolis force originating from the rotational effect induces the secondary flow in the $y$-direction as well. As constrained by the confinement effects, we observe recirculation vortices in the $y - z$ plane. At early times, it is observed that the variation in the magnitude of vorticity from the center of the channel to near the walls is much less at larger times. This is true for all values of $n$. We also observe that the vorticity vector forms a clockwise chain in all the cases with the largest of the magnitude being closer to the walls. This is due to the larger gradients of velocity close the walls, which is inherent with electroosmotically driven flows. It is also observed that the influence of vorticity closer to the center of the channel is more for higher values of $n$ as shown in Fig. 5g–i. During the middle stages of flow development $\left( {t = 0.001} \right)$, the gradients of the velocity are higher over the cross section, and hence, we see a comparable vorticity magnitude between the center of the channel and near the walls.

Fig. 5

(Color online) Plot showing the vectors of vorticity in the $y - z$ plane for different values $n$, while obtained at different temporal instants. The other parameters used are $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$, $\kappa = 10$. a $n = 0.8$, $t = 0.0001$, b $n = 0.8$, $t = 0.001$, c $n = 0.8$, steady state, d $n = 1$, $t = 0.0001$, e $n = 1$, $t = 0.001$, f $n = 1$, steady state, g $n = 1.2$, $t = 0.0001$, h $n = 1.2$, $t = 0.001$, i $n = 1.2$, steady state

4.2 General dynamics

4.2.1 Effect of $Re_{\varOmega }$ and n on the axial flow velocity

We discuss, in Fig. 6, the spatial evolution of the axial velocity in the channel during steady condition as obtained for different values of $\text{Re}_{\varOmega }$. In an effort to have an understanding about the rheological effect on the underlying transport, we consider three different values of power-law index $n = 0.8,1\;\text{and} \;1.2$ in Fig. 6 as well.

Fig. 6

(Color online) Plot showing the variation of $u$-velocity in $y - z$ plane during steady state. The above variations are obtained for different values of $n$ and $Re_{\varOmega }$. The other parameters used are $B = 1$, $Re = 0.01$ and $\kappa = 10$

The other parameters taken into consideration for plotting the present figure have been mentioned in the caption. Since all the walls are considered to be charged in this case, we see the development of EDLs on four walls, leading to a plug-like flow dynamics at the channel core. We would like to discuss a few distinctive transport features as evident from Fig. 6. First, for $Re_{\varOmega } \ne 0$, a depression is appearing on the velocity profile at the core region of the channel, which, however, becomes stronger with an increasing value of rotational Reynolds number $\left( {Re_{\varOmega } } \right)$. This observation holds true for all the values of power-law index considered here. Albeit an equal electroosmotic effect, arising from the double-layer phenomena on four walls, tries to pump the fluid in an uniform manner in $z$-direction, the Coriolis acceleration resulting from the channel rotation together with the no-slip condition at $z = \pm 1$ becomes strong enough to induce secondary flow in the channel as well, thereby disturbing the axial velocity profile at the channel interior. Note that the constraint of no-slip condition at $z = \pm 1$ leads to a reduction in axial velocity at the channel core essentially to maintain a uniform profile in the $z$-direction. The reduction in axial velocity at the core of the channel gets further accelerated by the stronger effect of Coriolis force at a higher $Re_{\varOmega }$, leading to an appearance of depression at the middle as reflected in Fig. 6 (see the variation for $Re_{\varOmega } \ge 20$). We may mention here that the ultimate consequence of a reduction in axial velocity as shown in Fig. 6 is the development of secondary flow inside the channel. We will discuss the formation of secondary flow during steady-state condition in the next subsection. An increase in $n$ increases the effective viscosity of the fluid, which, in turn, increases the viscous resistance to the flow field as well. Our results reveals that, experiencing a relatively higher viscous resistance for a higher value of $n$, the drop downing tendency of the axial flow velocity at the channel center becomes stringent for a higher value of $n$, since the net driving force remains unaltered.

4.2.2 Secondary flow in the development in the channel

In order to obtain further insights into the development of secondary flows, we depict, in Fig. 7, the streamlines and velocity vectors in $y - z$ plane as influenced by the $Re_{\varOmega }$ for three different values of power-law index. The following parameters are considered for plotting Fig. 7 as: $B = 1$, $Re = 0.01$, $\kappa = 10$. The formation of secondary flow in the channel is largely supported by the appearance of the double-vortex structures, which are having different senses of rotation, in the flow field. Figure 7 shows that the top vortex $\left( {z > 0} \right)$ shows a clockwise rotation, while the vortex formed at the bottom $\left( {z < 0} \right)$ exhibits an anticlockwise sense of rotation. We have discussed the underlying physical issues of the formation of vortex structures in the context of the discussion of vorticity vector (see detail discussions in Fig. 5). During steady-state condition, a favorable pressure gradient in the transverse direction of the channel $\left( {{{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial y}}} \right. \kern-0pt} {\partial y}} < 0} \right)$ allows the fluid to move in the positive $y$-direction of the channel.

Fig. 7

(Color online) Variation of velocity vectors and streamlines in the $y - z$ plane with $n$ and $Re_{\varOmega }$. The variations depicted in the present figure correspond to steady-state condition. The other parameters considered to obtain the variations are $B = 1$, $Re = 0.01$, $\kappa = 10$. a $n = 0.8$, $Re_{\varOmega } = 20$, b $n = 0.8$, $Re_{\varOmega } = 20$, c $n = 0.8$, $Re_{\varOmega } = 20$, (d) $n = 0.8$, $Re_{\varOmega } = 40$, e $n = 0.8$, $Re_{\varOmega } = 40$, f $n = 0.8$, $Re_{\varOmega } = 40$

Contrarily, the stronger effect of the Coriolis force at the core of the channel pushes the fluid back toward the opposite direction (i.e., in the negative $y$-direction). The gross effect of these two opposing forcing factors leads to the formation of vortex structures in the flow field as shown in Figs. 4 and 7. For a given $Re_{\varOmega }$, a quantitative change in the vortex dynamics with a change in flow behavior index $n$ as shown in Fig. 7 is attributed to the rheology-driven alteration in the effective viscosity of the fluid. On the contrary, we attribute a qualitative difference in the shape of the vortex structures with a change in $Re_{\varOmega }$, which is shown in Fig. 7 as well, to the effect of the Coriolis force.

4.2.3 Effect of Debye parameter and power-law index on the flow dynamics

As mentioned, the volume transport is an important quantity of interest in microfluidic systems/devices, which, in turn, strongly depends upon the development of axial velocity in the systems/devices under concern. Considering this aspect, we here discuss the variation of axial velocity in the channel for different values of $\kappa$ as shown in Fig. 8a, b. The flow velocities depicted in Fig. 8a, b correspond to the shear-thinning $\left( {n = 0.8} \right)$ and shear-thickening $\left( {n = 1.2} \right)$ fluids, respectively. We have considered the following other parameters for the present figures as: $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$.

Fig. 8

(Color online) Variation of $u$-velocity versus $z$ for different values $\kappa$: a for shear-thinning fluid $\left( {n = 0.8} \right)$ and b for shear-thickening fluid $\left( {n = 1.2} \right)$. The variations are obtained during steady-state condition at $y = 1$. The other parameters used for this plotting are $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$

Although the rotation-induced forces remain unaltered for the variation depicted in the present figures, we observe from Fig. 8a, b that, with increasing value of $\kappa$, the axial velocity responds non-trivially with a change in the rheological behavior of the fluid. Note that the parameter $\kappa$ is a representative measure of the EDL thickness. One may find from Fig. 8a that an increase in $\kappa$ leads to an enhancement in $u$-velocity for the flow of a shear-thinning fluid $\left( {n = 0.8} \right)$, which is as expected. Since with increasing value of $\kappa$, for which the charge density in the EDL becomes relatively higher (EDL becomes thinner), the net electrical body force acting over the fluid mass in the EDL increases and results in an enhancement in flow velocity. On the contrary, we observe a reverse phenomenon for the flow of a shear-thickening $\left( {n = 1.2} \right)$ fluid, where u-velocity decreases both in the EDL and in the bulk with the increasing magnitude of $\kappa$. Even though this reverse flow dynamics can be apparently attributed to the effect of the change in the fluid rheology, we would like to describe this alteration in flow velocity from the perspective of the electrical force-modulated alteration in the viscous drag in the fluid continua. As $\kappa$ increases, the net electrical body force increases, which, in turn, brings an increment in velocity gradient near the walls of the channel. The higher velocity gradient stimulates the viscous drag to the flow field following an increment in effective viscosity of the fluid and leads to a reduction in $u$-velocity as aptly confirmed in Fig. 8b. Also, having a closer look at above two figures (Fig. 8a, b), one may perceive the effect of rotation-induced forces on the underlying transport as witnessed by the appearance of depression at the central part of the velocity profiles.

We have seen in the previous section that the depression appearing in the middle of the u-velocity profile, which results from the effect of the Coriolis force, culminates in the development of secondary flow inside the channel. We have also verified from Figs. 4, 5, 6 and 7 that the induction of secondary flow inside the channel leads to an enhancement in mixing accounting the formation of vortex structures in the flow domain. Albeit the effective viscosity and so is the viscous drag to the flow becomes lesser for the transport of shear-thinning fluids, we still observe a weak depression at the central part of the $u$-velocity profile for a relatively smaller $\kappa \left( { {=} 10} \right)$. Note that the $u$-velocity profile for a higher $\kappa \left( { {=} 30} \right)$ becomes almost flat irrespective of the rheological behavior of the fluid, largely attributed to the stronger effect of electrical forcing on the underlying transport. It may be mentioned here that the reduction of $u$-velocity owing to the depression appearing at the central part of the channel gives rise to the development of secondary flow ($v$-velocity) in the channel, since the continuity in the field is needed to be satisfied. We have depicted the development in $v$-velocity in Fig. 9a, b as well.

Fig. 9

(Color online) Plot showing the variation of $v$-velocity versus $z$, obtained for different values of $\kappa$: a for shear-thinning fluid $\left( {n = 0.8} \right)$ and b for shear-thickening fluid $\left( {n = 1.2} \right)$. The above variations are obtained at $y = 1$ and during steady-state condition. We have considered the other parameters as follows: $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$

4.3 Variation of flow rate in the channel

4.3.1 Effect of fluid rheology

In the purview of microscale/nanoscale transport, an important quantity of interest is the rate of volumetric transport through the channel. Considering this aspect, in this section, we take an effort to demonstrate the variation of flow rate for different cases. Since our major focus in this analysis lies on the understanding of the transport of rheological fluids, as a first case, we show, in Fig. 10, the temporal variation of the flow rate in the $x$-direction of the channel for different values of power-law index $n$. Note that the other parameters are being $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$, $\kappa = 10$, while they have been mentioned in the caption as well. One may observe from the present figure that, at the earlier of instants of time, the flow rate increases for all the values of power-law index considered. On the other hand, a steady behavior of the flow rate is observed as time grows further. We would like to mention here that the steady behavior of the flow rate as shown in Fig. 10 is the consequence of the attainment of a steady flow velocity as described in the preceding sections.

Fig. 10

(Color online) Plot showing the variation of flow rate $Q$ versus $t$ obtained for different values of $n$. The other parameters used are $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$, $\kappa = 10$

Having a look at Fig. 10, one may find an escalation in volume transport for the flow of a shear-thinning fluid $\left( {n = 0.8} \right)$, albeit the other parameters considered remain same. During initial transience as well as at steady-state condition, a relatively higher and lower volume transport of a shear-thinning $\left( {n = 0.8} \right)$ and shear-thickening $\left( {n = 1.2} \right)$ fluids, respectively, as witnessed in Fig. 10, is attributed to the rheological effect on the underlying flow dynamics as modulated by the combined consequences of the electrical forcing and rotational effect. We would like to discuss here that, in a rotational platform, the induced flow velocity develops in the transverse direction of the channel distracts the axial momentum ($x$-momentum) originating from the applied electrical field, thereby attenuating the velocity gradient in the axial direction. Furthermore, in an electrically actuated transport the main driving force remains confined over a small region near the walls of the channel, and thus, the velocity gradient ceases to exist in the bulk region of the flow field. Accounting for these two factors, the velocity gradient in the bulk reduces, which, in turn, drops down the effective viscosity of the shear-thinning fluid $\left( {n = 0.8} \right)$ as compared to that of the shear-thickening fluid $\left( {n = 1.2} \right)$ in the present scenario. Since the effective viscosity becomes lesser, the viscous resistance to the underlying transport of a shear-thinning fluid $\left( {n = 0.8} \right)$ gets reduced, leading to an augmentation in flow velocity and the volume flow rate in the channel as confirmed in Fig. 10.

4.3.2 Effect of EDL parameter

In Fig. 11a, b, we show the transient variation of the flow rate for different values of $\kappa$, while obtained for different other values as mentioned in the caption. Let us first look at Fig. 11a, which describes the flow rate variation of a shear-thinning fluid $\left( {n = 0.8} \right)$. We get a relatively higher flow rate of a shear-thinning fluid $\left( {n = 0.8} \right)$ with an increasing value of $\kappa$ as supported by Fig. 11a. This can be explained as follows: a higher value of $\kappa$ (inverse of which is a measure of EDL thickness) thins the EDL and thus squeezes more number of ions inside the EDL. With increasing value of $\kappa$, the ionic change density in the EDL increases, which, in turn, leads to a higher body force on the fluid mass inside the layer. The higher electrical body force imparts a higher flow velocity and results in a higher flow rate as confirmed in Fig. 11a. Contrarily, we observe, in Fig. 11b, a different trend of the flow rate variation of a shear-thickening fluid $\left( {n = 1.2} \right)$ with $\kappa$. What we observe from Fig. 11b is that the flow rate of a shear-thickening fluid $\left( {n = 1.2} \right)$ increases as $\kappa$ increases from 10 to 20, while a further increases in $\kappa \left( { = 30} \right)$ leads to a reduction in flow rate. Albeit an enhancement in flow rate with an increment in $\kappa$ from 10 to 20 can be explained from the perspective of the fortification of electrical body force being applied on the fluid mass (we have discussed the same effect in the context of the shear-thinning fluid), a reduction of flow rate beyond $\kappa = 20$ can be attributed to the rheological effect of the fluid as modulated by the electrical double-layer phenomena. Since the flow velocity and the velocity gradient increase with an increment in $\kappa$, the rise in velocity gradient for $\kappa = 30$ in conjunction with the stronger non-Newtonian behavior of the fluid $\left( {n = 1.2} \right)$ leads to an enhancement in effective viscosity of the fluid. This effect, in turn, offers a relatively higher viscous resistance to the flow field and diminishes the flow rate essentially by attenuating the flow velocity as shown in Fig. 11b. Also, having a closer look at Fig. 11a, b, one may find a lesser flow rate of a shear-thickening fluid $\left( {n = 1.2} \right)$ in the channel albeit the set of other parameters considered to obtain the present figures remains unaltered. This observation once more underlines the rheology-driven alteration in the flow dynamics under the combined influences of electrical forcing and rotational effect. Interplay between the effective viscosity of the fluid and viscous resistance in the field as modulated by the electrical forcing gives rise to a complex variation of the flow rate of a shear-thickening fluid $\left( {n = 1.2} \right)$ as evident in Fig. 11b.

Fig. 11

(Color online) Variation of flow rate $Q$ with $t$ for different values of $\kappa$: a for shear-thinning fluid $\left( {n = 0.8} \right)$ and b for shear-thickening fluid $\left( {n = 1.2} \right)$. The other parameters considered are $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$

4.3.3 Effect of rotation Reynolds number

We show, in Fig. 12a, b, the flow rate variation in the channel as influenced by the rotation Reynolds number $\text{Re}_{\varOmega }$ for two different values of $n\left( {{=} 0.8,1.2} \right)$, respectively. Note that the variations depicted in Fig. 12a, b correspond to a unit aspect ratio of the channel. The following other parameters are considered for plotting the above figures as $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$. From the figures depicted above (Fig. 12), we observe two distinct regimes, viz. regime-I and regime-II, on the variation of flow rate. In regime-I, during initial transience, the flow rate increases with increasing $Re_{\varOmega }$. On the other hand, the dependence of $Q$ on $Re_{\varOmega }$ is seen to be completely contrary in regime-II. We mention here that these observations hold true for both the cases of power-law indices considered. A relative increment in flow rate with increasing value of $Re_{\varOmega }$ as seen in regime-I is mainly attributed to the combined effects of electroosmotic (EO) pumping and centrifugal force. At the earlier instants of time, higher the value of $Re_{\varOmega }$, the higher the initial acceleration of the fluid mass inside the channel, leading to an augmented flow velocity and so is the flow rate in the channel. The contrasting behavior of a reduction in flow rate at a higher value of $Re_{\varOmega }$ as seen in regime-II can be explained as follows: When the flow time overshadows the initial transience, the formation of the secondary flow inside the channel weakens the electroosmotic (EO) pumping essentially by distracting the axial momentum developed due to electroosmotic effect.

Fig. 12

(Color online) Variation of flow rate $Q$ with $t$ for different values of $Re_{\varOmega }$: a for shear-thinning fluid $\left( {n = 0.8} \right)$ and b for shear-thickening fluid $\left( {n = 1.2} \right)$. The following other parameters are considered for plotting the figures as: $B = 1$, $Re = 0.01$, $Re_{\varOmega } = 40$

Also, we would like to mention here that the higher value of $\text{Re}_{\varOmega }$ accelerates the development of secondary flow at a larger instant of time, since the Coriolis acceleration becomes stronger at a higher $Re_{\varOmega }$. In fact, it may be mentioned in this conjecture that the contribution of the Coriolis forcing plays a big role on the underlying transport as the flow time crosses the initial transience. Thus, the development of the secondary flows inside the channel at a larger time as aggravated by the Coriolis force due to a relatively larger $Re_{\varOmega }$ reduces the axial flow rate, which is verified in our results depicted in Fig. 12a, b. Albeit other parameters remain unaltered, having a closer look at Fig. 12a, b, one may find a quantitative difference in the volume flow rate. We attribute this observation to the rheological effect of the fluid on the underlying electrohydrodynamics. It is worth mentioning here that the results depicted in Fig. 12a, b are in compliance with what is expected to be and support the variations of flow velocities those demonstrated in previous figures.

5 Conclusions

We have executed transient analysis of the rotational flow of a non-Newtonian fluid in a microfluidic channel under the influence of the electrical double-layer effect. While investigating the underlying electrohydrodynamics, we have taken the effect of the lateral confinement of the channel into account in the present analysis. We have described the rotational force-induced complex flow dynamics, realized though the development of the secondary flows, in the channel as modulated by the correlative-cooperative effects of the electrical forcing and the fluid rheology on the underlying transport. Also, we have shown the formation of double-vortex structures in the flow field mainly originating from the interactive effects of the rotation-induced Coriolis acceleration and the electrical force-driven uniform velocity profile in the channel. Furthermore, we have investigated that the combined consequences of the no-slip condition at the wall along with the effect of favorable pressure gradient developed in the adverse direction of the channel lead to the formation of sister vortexes in the flow domain following a complex competition among the electrical forcing and the fluid rheology. In particular, we have been able to show that the formation of sister vortexes enforces to alter the overall rotational sense of the main vortexes, thus enabling to get an augmentation in mixing in rotational microflows. Finally, we have demonstrated the rate of volumetric transport though the channel under different conditions. In particular, we have depicted two distinct regimes showing the rotation-induced alteration in flow rate for different values of power-law index, where we have shown that, in regime-I, the flow rate during initial transience increases with increasing magnitude of rotational effect, while the flow rate, in regime-II, is seen to decrease with increasing rotational effect at steady-state condition. We believe that the results obtained from this analysis may bear a significant impact in designing the lab-on-chip-based diagnostic microsystems/devices, which are typically used for the transportation of bio-fluids.