1 Introduction

Several scientist selected phase change materials for saving energy in heat storage units. Also, they added metallic Nano sized particles to overcome the low thermal conductivity. Selimefendigil and Oztop (2019) scrutinized CNT nanoparticles transportation due to MHD inside a corrugated cavity. Sheikholeslami et al. (2018) illustrated the unsteady solidification of NEPCM. They employed Galerkin approach to show the phase change process. Nanofluid mass transfer over step with elastic wall was scrutinized by Selimefendigil and Oztop (2018). Khan et al. (2017) demonstrated nanomaterial treatment due to radiative heating. They utilized non-Newtonian model in presence of MHD. Sheikholeslami et al. (2019) employed nanoparticles and V shaped fins to reach higher rate of solidification. They presented FEM simulation for solving unsteady problem. Heatline approach has been applied by Bondareva et al. (2016) for natural convection of nanoparticles inside a wavy enclosure with local heater. Sheremet et al. (2015) presented second law behavior of nanomaterial thorough a cavity with hot obstacle. They utilized hemogenious model (Tiwari model) for thermal conductivity. Mahian et al. (2013) scrutinized irreversibility analysis of nnaoparticles in existence of MHD impact. Tahir et al. (2017) studied the Maxwell nanofluid radiation along a sheet. They supposed uniform magnetic field to control the flow. Copper oxide migration due to MHD impact in a duct was scrutinized by Selimefendigil and Oztop (2018). They examined optimization procedure via ANFIS. Nguyen et al. (2016) demonstrated the transient nanofluid flow in an enclosure with various heaters. Moatimid et al. (2017) scrutinized nanofluid transient double diffusion flow. Characteristics of nanofluid inside a heat exchanger were examined by Qi et al. (2018). They reported stability behavior of nanofluid and its characteristics. Finding better working fluid in view of heat transfer is hot topic in recent decade (Rehman et al. 2018; Sun et al. 2017; Sheikholeslami et al. 2019; Sheikholeslami and Oztop 2016, 2017; Sheikholeslami 2018, 2019a, b; Khan et al. 2018a, b; Eldabe et al. 2018; Hayat et al. 2018; Darzi et al. 2016; Ahmed et al. 2017).

In present report, V shaped fins and NEPCM are considered as two effective methods to improve the melting rate. Simulation is done via FEM. Entropy and exergy contours at various stages are demonstrated.

2 Geometry and formulations

2.1 Enclosure with fins

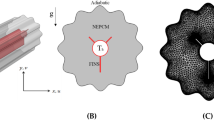
The aim of current article is to carry out numerical investigation of transient, two-dimensional melting process inside the cavity with V shaped fins. The cavity is filled with PCM based copper oxide nanoparticle. This geometry can be fins in Fig. 1. In this paper, we consider L = 0.04 m, D = 0.02 m, l = 0.01 m, t = 0.5 mm. The concentration of copper oxide is 0.05.

Fig. 1
figure 1

Enclosure with V shaped fins

Full size image

2.2 Problem formulations

Let us consider transient laminar 2D melting process considering Boussinesq estimation as follows:

$$ \nabla \cdot \vec{V} = 0, $$
(1)
$$ C\frac{{\left( {1 - \lambda } \right)^{2} }}{{\lambda^{3} + \varepsilon }}u + \frac{1}{{\rho_{nf} }}\left( {\mu_{nf} \nabla^{2} u - \nabla P} \right) = \frac{\partial u}{\partial t} + \vec{V} \cdot \nabla u, $$
(2)
$$ \begin{aligned} & v\frac{{\left( {1 - \lambda } \right)^{2} }}{{\lambda^{3} + \varepsilon }}C + \frac{1}{{\rho_{nf} }}\left( {\mu_{nf} \nabla^{2} v - \nabla P + g\left( {\rho \beta } \right)_{nf} \left( {T - T_{ref} } \right)} \right) = \frac{\partial v}{\partial t} + \vec{V} \cdot \nabla v \\ & \left( {\rho C_{p} } \right)_{nf} = \phi \left( {\rho C_{p} } \right)_{s} + \left( { 1 - \phi } \right)\left( {\rho C_{p} } \right)_{f} , \\ \end{aligned} $$
(3)
$$ - \frac{{\partial \left( {\rho L\lambda } \right)_{nf} }}{\partial t} + \frac{{k_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }}\nabla^{2} T = \frac{\partial T}{\partial t} + \vec{V} \cdot \nabla T. $$
(4)

Here we considered ɛ = 10−3, C = 105.

(ρβ)nf, ρnf, (ρL)nf and (ρCp)nf are:

$$ {\raise0.7ex\hbox{${\left( {\rho \beta } \right)_{nf} }$} \!\mathord{\left/ {\vphantom {{\left( {\rho \beta } \right)_{nf} } {\left( {\rho \beta } \right)_{f} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {\rho \beta } \right)_{f} }$}} = (1 - \phi ) + \phi \frac{{\left( {\rho \beta } \right)_{s} }}{{\left( {\rho \beta } \right)_{f} }}, $$
(5)
$$ \rho_{nf} = \rho_{f} (1 - \phi ) + \rho_{s} \phi , $$
(6)
$$ \frac{{\left( {\rho L} \right)_{nf} }}{(1 - \phi )} = \left( {\rho L} \right)_{f} , $$
(7)
$$ \left( {\rho C_{p} } \right)_{f} (1 - \phi ) + \left( {\rho C_{p} } \right)_{s} \phi = \left( {\rho C_{p} } \right)_{nf} , $$
(8)

knf, μnf are obtained as:

$$ k_{nf} = \frac{{2k_{f} + k_{p} + 2\phi \left( {k_{s} - k_{f} } \right)}}{{k_{p} - \phi \left( {k_{s} - k_{f} } \right) + 2k_{f} }}k_{f} , $$
(9)
$$ \mu_{nf} = \left( {1 - \phi } \right)^{ - 2.5} \mu_{f} . $$
(10)

To see the properties, Table 1 has been presented.

Table 1 Characteristics of CuO and (n-octadecane paraffin)
Full size table

Equation (11) and (12) can be employed to find the enthalpy:

$$ H_{e} = h + \lambda L, $$
(11)
$$ h = h_{ref} + \int_{{T_{ret} }}^{T} {\left( {C_{p} } \right)_{nf} } dT, $$
(12)
$$ \lambda = \left\{ {\begin{array}{*{20}l} 0 \hfill & {T < T_{s} } \hfill \\ {\frac{{T - T_{s} }}{{T_{l} - T_{s} }}} \hfill & {T_{s} \, < T < T_{l} } \hfill \\ 1 \hfill & {T < T_{l} } \hfill \\ \end{array} } \right.. $$
(13)

In above equation, we considered href as enthalpy at 273 K.

In the present work, the definitions of Sgen,total, Sgen,th, Sgen,f are:

$$ \begin{aligned} S_{gen,total} & = S_{gen,th} + S_{gen,f} \\ & = \frac{{k_{nf} }}{{T^{2} }}\left[ {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] \\ & \quad + \frac{{\mu_{nf} }}{T}\left\{ \begin{aligned} 2\left[ {\left( {\frac{{\partial u_{x} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial u_{y} }}{\partial y}} \right)^{2} } \right] \\ + \left( {\frac{{\partial u_{x} }}{\partial y} + \frac{{\partial u_{y} }}{\partial x}} \right)^{2} \hfill \\ \end{aligned} \right\} \\ \end{aligned} $$
(14)

2.3 Detail of modeling

Governing equations with the boundary conditions have solution which is obtained via FVM utilizing ANSYS Fluent 18.1. The space domain is modeled using Enthalpy-porosity method (Brent et al. 1988). PRESTO model is selected for pressure correction. Velocity under-relaxation is considered 0.2 and SIMPLE algorithm has been utilized. Figures 2 and 3 demonstrate sample grid and verification (Tan et al. 2009).

Fig. 2
figure 2

Example for Grid

Full size image
Fig. 3
figure 3

Validation of code with Tan et al. (2009)

Full size image

3 Results and discussion

Current section has been devoted to the analysis of melting process in an enclosure with V shaped fins. Not only melt fraction and temperature but also entropy generation and exergy have been analyzed. The system is filled with n-octadecane paraffin in which CuO has been dispersed. The solution of equations was calculated using Finite Volume Method.

Both first and second law analysis during process was illustrated in Figs. 4, 5, 6 and 7. In lower time, the buoyancy is not enough strong to affect the melting. In greater time, convective mechanism affects the melting front and its shape become more complex. Vortex becomes stronger as the melting front reach to outer surface. The middle up of the enclosure converts to liquid phase sooner than the middle down. The region near the down wall is the final space in which the remained solid convert to liquid. This phenomena is due to absence of rotating eddies in that region. As temperature enhances, thermal entropy generation detracts as depicted in contours. Exergy loss has same treatment, too. Liquid fraction, Sgen,f and Sgen,th are shown in Fig. 8. As time progress, average temperature enhances and melts fraction increases until it reaches to its maximum value. Thermal entropy generation detracts with rise of melt fraction. Frictional component has on maximum point in beginning times.

Fig. 4
figure 4

Contours plots of t = 60 s

Full size image
Fig. 5
figure 5

Contours plots of t = 180 s

Full size image
Fig. 6
figure 6

Contours plots of t = 300 s

Full size image
Fig. 7
figure 7

Contours plots of t = 540 s

Full size image
Fig. 8
figure 8

Variation of temperature, entropy generation during melting process

Full size image

4 Conclusion

The NEPCM melting heat transfer inside a cylinder with V shaped fins are demonstrated. The unsteady problem has been modeled as governing PDEs which were solved via Finite Volume Method. Contours for melt fraction, entropy, isotherm and exergy are reported in various times. Melt fraction enhances as time progress which means greater convection mode and higher temperature. So, Sgen,th reduces with augment of time. At start of process, conduction has main role, thus Sgen,f has one maximum point in its profile.