1 Introduction

Due to the current situation of world water resources and the increasing problem of surface and groundwater pollution, water quality management is prioritized by many managers and researchers in this field. A source of contamination released into the water is rapidly diffused into it and transported downstream along with the water flow due to molecular motion, turbulence and uneven velocity at the cross-sectional area of the flow [1].

The governing equation for pollutant transmission is the advection–diffusion equation, expressed as Eq. (1) [2].

$$\left( {\frac{\partial C}{{\partial t}}} \right) + U\left( {\frac{\partial C}{{\partial x}}} \right) = K\left( {\frac{{\partial^{2} C}}{{\partial x^{2} }}} \right)$$
(1)

where C is the cross-sectional average concentration \(\left( {\frac{kg}{{m^{3} }}} \right)\), U is the cross-sectional average velocity \(\left( \frac{m}{s} \right)\), x is direction of the mean flow, t is time (s) and K is representing the longitudinal dispersion coefficient in rivers \(\left( {\frac{{m^{2} }}{s}} \right)\).

It is a partial differential equation that can be solved using numerical methods and defining the appropriate boundary and initial conditions [3, 4]. According to this equation, the longitudinal dispersion coefficient is considered the most important parameter that the accurate estimation of which is critical in hydraulic engineering [5]. This coefficient can be measured directly by sampling the upstream and downstream sections of the river. This is difficult due to the complex geometry of the natural channel bed and the various hydraulic prevailing conditions. Thus, it is usually calculated using empirical and theoretical relations [6].

The longitudinal dispersion coefficient was firstly introduced by Taylor as a measure of the longitudinal dispersion process by the advection–diffusion equation [7]. Then, Elder began to extend the Taylor method. Assuming that the velocity profile in the vertical direction is logarithmic, he proposed Eq. (2) to estimate the longitudinal dispersion coefficient for wide channels [8].

$$\frac{K}{{HU_{*} }} = 5.93$$
(2)

where H and \(U_{*}\) are the depth of flow and the bed shear velocity, respectively.

Although the Elder's equation was considered a great success in predicting the longitudinal dispersion coefficient, ignoring changes in cross-sectional velocity profiles showed a large difference between the observed values and the predicted values [1, 9]. According to Fisher, the transverse velocity profile was more important than the vertical velocity profile for predicting the longitudinal dispersion coefficient in the wide channel. Accordingly, he proposed a triangular integral [Eq. (3)] to estimate the longitudinal dispersion coefficient in wide channels [10].

$$K = - \frac{1}{A}\mathop \int \limits_{0}^{W} h u^{\prime} \mathop \int \limits_{0}^{y} \frac{1}{{\varepsilon_{y} h}} \mathop \int \limits_{0}^{y} h u^{\prime} {\text{d}}y\;{\text{d}}y\;{\text{d}}y$$
(3)

in which A and W represent the cross-sectional area and the channel width, respectively. h is the local flow depth, u′ is the difference between the local depth-averaged velocity and the cross-sectional average velocity and \(\varepsilon_{y}\) is the transverse turbulent diffusion coefficient.

Many attempts have been made so far, such as tracking measurements, empirical models and theoretical relationships, to estimate the longitudinal dispersion coefficient [5].

Kashefipour and Falconer proposed a new equation for predicting the longitudinal dispersion coefficient for natural channels using dimensional analysis and regression of hydraulic flow parameters. A comparison of statistical parameters showed that the method was more accurate than other equations for calculating the longitudinal dispersion coefficient. By linearly combining of their proposed equation with the equation proposed by Soe and Cheong, they also proposed another equation to estimate the longitudinal dispersion coefficient. The efficiency of this equation was proved by analyzing it using statistical methods [11].

Continuing efforts to find a more accurate way to calculate the dispersion coefficient, optimization algorithms have become more popular in recent decades due to the high speed of soft computing methods. Sahay and Dutta used the genetic algorithm (GA) and Etemad-Shahidi and Taghipour used the M5 tree model, a flexible computational method, to estimate the longitudinal dispersion coefficient of natural rivers [9, 12]. Li et al. used the differential evolution (DE) algorithm to estimate the longitudinal dispersion coefficient of rivers by minimizing the sum-square error. This study used observational data from 29 rivers in the USA to evaluate the performance of the proposed algorithm [13]. Sattar and Gharabaghi used the gene expression programming (GEP) model to develop an empirical relationship between longitudinal dispersion coefficient and control variables including Froude number, dimensional ratio and bed roughness. For this purpose, they used 150 series of natural flow data including geometric and hydraulic parameters of the flow. Comparing the proposed model with other methods in terms of uncertainty indicated the higher accuracy of the GEP model [14]. Alizadeh et al. used the Bayesian network method to provide a model for predicting the longitudinal dispersion coefficient of natural rivers. To increase the accuracy of the proposed model, they used cluster analysis for data processing couples with Bayesian network [6]. Kargar et al. used the M5 model tree (M5P) model to predict longitudinal dispersion coefficient as a function of flow depth, channel width, average velocity and shear velocity [15].

Consequently, many different kinds of techniques have been developed for estimating the longitudinal dispersion coefficient in rivers. They consist of soft computing techniques (e.g., GA, DE, PSO, etc.), artificial intelligence methods (e.g., ANN, GEP, Model Tree, etc.) and empirical (e.g., mathematical, statistical, etc.). A brief description of previous models/equations is presented in Table 1.

Table 1 Empirical and artificial intelligence-based equations for prediction of longitudinal dispersion coefficient
Full size table

According to the investigations, there are various experimental studies on empirical equations for estimating the longitudinal dispersion coefficient in rivers; however, they are limited with the laboratory conditions (e.g., bed configuration, channel width and flow properties) and they have not reliable results for all types of channels [1, 16, 17]. In addition, the used AI-based models, in previous studies, shown some limitations like slow convergence, needs to find the best tuning parameters of method and other drawbacks that need user interaction. Therefore, it is necessary to develop a model with higher accuracy to estimate the longitudinal dispersion coefficient [11]. Among AI-based predictive models, ANN has high teaching and learning power. It has been used in recent years, especially to predict complex issues [18,19,20,21,22,23,24]. However, it is challenging for users to choose the suitable ANN parameters, such as size of input layers, learning curve and the number of hidden layers. These parameters are generally determined based on the user experience using the MATLAB toolbox with a limited number of learning algorithms, leading to non-optimized ANN.

Nowadays, well-known metaheuristic algorithms such as PSO, GA and ABC are exploited as tools to find optimal ANN parameters in many cases, such as predicting the axial compression capacity of columns [25,26,27]; modeling evaporation [28,29,30]; and prediction of river flow [31,32,33].

Metaheuristic optimization techniques are considered for their simplicity, flexibility, derivation-free mechanism and overcoming local optimization problem. But according to the NFLFootnote 1 theory, none of the metaheuristic methods are appropriate for solving all optimization problems [34, 35]. In other words, a particular metaheuristic may show incredible results to solve a series of specific problems, but this algorithm may have poor performance for a number of other issues [36]. Therefore, the original contribution of this work is investigating the capability of a new hybrid expert system (MLP combined with a recent metaheuristic algorithm, namely HHO) to predict the longitudinal dispersion coefficient in rivers so as to provide a robust model for solving such a complex environmental engineering problem. In order to evaluate the feasibility of the proposed HHO-based training algorithm in improving prediction performance of MLP, this training tool was compared with the other two powerful known metaheuristic optimizers, ICA and PSO by integrating into MLP as an efficient training tool for estimating the longitudinal dispersion coefficient in rivers. A review of studies on the methods of determining the longitudinal dispersion coefficient of rivers indicates that hybrid HHO-MLP has not been used for this purpose up to now. Current study proposes three hybrid models: HHO-MLP, PSO-MLP and GA-MLP, for streamflow forecasting problems. For this purpose, 164 observed data set was gathered. In the first stage, the longitudinal dispersion coefficient under influence hydraulic parameters including depth, width, velocity and shear velocity was predicted by each of these developed models with the aim of minimizing the mean square error. Then, the observed data are compared with the results of the above models and the most powerful algorithm for optimizing MLP has been identified using the statistical indexes.

The rest of the paper is organized as follows: in Sect. 2 describes the proposed hybrid models. The details of databases and the employed statistical indicators are presented in Sects. 3 and 4, respectively. The results of the numerical experiment and their discussions are presented in Sect. 5 while some conclusion remarks are given in Sect. 6.

2 Materials and methods

2.1 Concept and theory background

According to previous studies, some of the important parameters affecting the longitudinal dispersion coefficient of rivers are:

  1. (1)

    The geometric properties of the flow, including the width of the flow path (\(W\)), the bed shape factor (\(S_{f}\)), the slope of the channel floor (\(S\)), the sinuosity (σ), the coefficient of the roughness of the channel (\(k_{s}\)) and the depth of flow (\(H\));

  2. (2)

    Hydraulic properties of flow, including the average flow velocity (\(U\)) and shear velocity (\(U_{*}\)); and

  3. (3)

    The properties of the fluid, including the density of the fluid (\(\rho\)) and the kinematic viscosity of the flow (\(\mu\)).

which can be expressed as Eq. (4) using dimensional analysis [37]:

$$\frac{{\text{K}}}{{U_{*} H}} = f^{\prime}\left( {\rho \frac{HU}{\mu },\frac{W}{H},\frac{U}{{U_{*} }},\sigma ,\frac{U}{{\sqrt {gH} }},\frac{{k_{s} }}{H},S_{f} ,S} \right)$$
(4)

where \(\frac{{\text{K}}}{{U_{*} H}}\) is the dimensionless dispersion coefficient parameter, \(\rho \frac{HU}{\mu }\) is the Reynolds number, \(\frac{W}{H}\) is the width-to-depth ratio and \(\frac{U}{{U_{*} }}\) is the flow resistance term. Here, the direct influence of parameters such as the slope of the channel, the shape of the bed and the sinusoidal value of the river path, which are not easily measurable and their effect can be seen in the term of resistance, is omitted. The effect of the Reynolds number can be also ignored due to the usually turbulent flow of rivers. Equation (4) can finally be written as Eq. (5) [6]:

$$\frac{K}{{U_{*} H}} = f^{\prime\prime}\left( {\frac{W}{H},\frac{U}{{U_{*} }}} \right)$$
(5)

where the longitudinal dispersion coefficient (K) depends on the following four parameters: U average flow velocity, H flow depth, W width of flow and \(U_{*}\) bed shear velocity.

2.2 Artificial neural network (ANN)

ANN is an idea for processing information like the brain, inspired by the biological nervous system. This system comprises many processing elements called neurons, which work in unison to solve a problem [38]. ANN is considered a tool for estimating the approximate performance, applicable in places where there is a nonlinear and complex relationship between input(s) or predictor(s) and output(s) [39, 40].

ANNs need to be trained with certain learning algorithms to approximate the goal and achieve the desired results [38, 41]. Numerous network learning algorithms have been developed by examining simple, nonlinear mathematical solutions based on human biological neurons. Learning algorithms are a series of processes, which help to adjust the weights of the network. During the training process, a network can learn tasks and similarities without a predefined program. The learning system usually lacks any prior information about the problem such as various input parameters set in the input data layers [42, 43]. The most common learning algorithm is the backpropagation (BP) algorithm. It is developed based on the downward slope optimization method, which can minimize the network error between the desired values and the estimated values [41, 44].

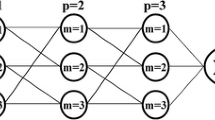
One of the most common neural networks is the multilayer perceptron. It is also known as backpropagation because its training algorithm is usually backpropagation. The perceptron neural network method was introduced by Rosenblatt [45]. The input layer only acts as an intermediary with the outside world. Each node sends an unchanged input to the next layer of neurons. Therefore, the number of input layer nodes is equal to the number of independent variables. The number of neurons in the output layer indicates the number of dependent variables. Also, the number of nodes in each layer will depend on the complexity of the problem.

2.3 Metaheuristic algorithm

Metaheuristic algorithms are a flexible method for solving complex optimization problems based on swarm intelligence, inspired by biological and physical systems in nature. These methods use a special mechanism that many particles are scattered in the problem space and simultaneously search for optimal solutions. These methods are called nature-inspired, population-based or metaheuristic algorithms. Considering various constraints, metaheuristic algorithms also achieve a set of non-dominant solutions as the best solution of the solution set, or hopefully have a short distance from the original solution set [46, 47].

2.3.1 Particle swarm optimization algorithm (PSO)

The particle swarm optimization (PSO) algorithm was first introduced by Eberhart, inspired by the social behavior of birds [48]. This algorithm considers each solution as a bird in a bird group, called a particle. In such a structure, birds have individual intelligence and group behavior, which leads them to the goal.

First, the process begins with a bunch of randomly selected particles, each as a solution to the problem. Then, a bunch of particles move and the search space is searched to find the best solution.

In this algorithm, each particle has an adaptive velocity, representing the vector of the particle's move in the search space and memory, which means it remembers its best position up to that point. Particles are measured in terms of value based on the criterion function of the optimization problem [49]. For each particle, the best solution and position are stored in the variables \(P_{best}\) and \(g_{best}\), respectively [48]. Then, in each iteration, the particles accelerate toward their \(P_{best}\) and \(g_{best}\) based on the velocity vector \(v_{i}\). As a result, in each iteration, a new position is found in the search space for each particle by adding their displacement vector. Finally, \(g_{best}\) is considered the optimal solution to the problem. The velocity (\(v_{i}^{k + 1}\)) and new position (\(x_{i}^{k + 1}\)) of the particles are updated in each iteration by the following equations [50]:

$$v_{i}^{k + 1} = w \times v_{i}^{k} + c_{1} \times r_{1} \times \left( {P_{{best_{i} }} - x_{i}^{k} } \right) + c_{2} \times r_{2} \times \left( {g_{{best_{i} }} - x_{i}^{k} } \right)$$
(6)
$$x_{i}^{k + 1} = x_{i}^{k} + v_{i}^{k + 1}$$
(7)

where \(v_{i}^{k}\) and \(x_{i}^{k}\) are the velocities and positions of the particle i in the kth iteration, respectively. \(c_{1}\) and \(c_{2}\) are acceleration constants, \(r_{1}\) and \(r_{2}\) are also random numbers obtained from a uniform distribution between 0 and 1. \(w\) is the inertia weight factor. Algorithm 1 presents the PSO pseudocode.

figure a

2.3.2 Imperialist competitive algorithm (ICA)

The imperialist competitive algorithm (ICA) is inspired from a human social phenomenon. Like other evolutionary algorithms, this algorithm starts with an initial population. Each member of this population is referred to as a "country." Each country has a set of characteristics, which determine its location in the search space. Among these points, the points with the lowest cost, according to the optimization function, are considered imperialist and the rest as colonies [51]. The normalized cost for each colonizer is initially calculated as follows:

$$C_{n} = c_{n} - {\text{max}}_{i} \left\{ {c_{i} } \right\}$$
(8)

where cn is the cost of the nth imperialist and Cn is the normalized cost for this imperialist. The normalized power for each imperialist (\(P_{n}\)) is calculated by Eq. (9). On this basis, the colonial countries are divided among these imperialists:

$$P_{n} = \left| {\frac{{C_{n} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{imp} }} C_{i} }}} \right|$$
(9)

The initial number of colonies of an imperialist will be equal to:

$$N \cdot C_{ \cdot n} = round\left\{ {P_{n} ,N_{col} } \right\}$$
(10)

where \(N \cdot C_{ \cdot n}\) is the initial number of colonies of nth empire and \(N_{col}\) is the total number of colonies in the population of the primary countries.

Following the division of all the colonies between the emperors and the formation of the first empires, the colonies began to move toward the emperors. This movement models the policy of absorption. Figure 1 shows the movement of a colony toward the emperor.

Fig. 1
figure 1

Moving colonies toward their relevant imperialist

Full size image

As shown in Fig. 1, d is the direct distance between the imperialist and the colonies. A colony moves toward the imperialist, not directly and linearly, but at an angle \(\theta\) to the size of x. Then the amount of deflection angle and the size of move are determined uniformly in randomly determined intervals.

$$X\sim U\left( {0 \cdot \beta \times d} \right)$$
(11)
$$\theta \sim U\left( { - \gamma \cdot \gamma } \right)$$
(12)

where \(\beta\) and \(\gamma\) are arbitrary numbers, which determine the clone search space around the empire.

As colonial countries move toward imperialist countries, some of them may achieve better colonial status. In this case, the colonial country and the imperialist country change their place together. This is followed by colonial competition. At this stage, the weakest colony is selected from the weakest empire and given to a stronger empire. The stronger an empire, the more likely it is to be chosen. Finally, when an empire loses all its colonies, it is excluded from the list of empires and granted to other empires as a colony during a colonial rivalry. The evolutionary process takes place in a loop and continues until a stop criterion is met.

2.3.3 Harris hawk optimization (HHO)

Harris hawk optimization (HHO) is a population-based optimization algorithm proposed by Heidari et al. [52]. Inspired by Harris hawks' behavior in nature, this algorithm is based on cooperation between falcons to hunt prey [53, 54]. It uses a solid strategy: a group of Harris hawks launches a joint attack from different directions to catch the prey by surprise. These hawks cooperate in the process of the attack. Meanwhile, the Harris hawks’ leader attacks the target prey, chases it and suddenly disappears. The next Harris hawk continues the pursuit action. At this point, the Harris hawk utilizes different attack strategies for different prey escape modes. In this way, the prey is exhausted and eventually hunted. In the HHO algorithm, these steps are mathematically modeled in three basic steps: exploration, transition and exploitation (Fig. 2) [52,53,54,55].

Fig. 2
figure 2

Different phases of HHO [52]

Full size image

The exploration phase involves waiting, searching and discovering the proposed prey. In other words, this step determines the position of the hawk before finding the prey [55].

$$X\left( {t + 1} \right) = \left\{ {\begin{array}{ll} X_{rand} \left( t \right) - r_{1} \left| {X_{rand} \left( t \right) - 2r_{2} X\left( t \right)} \right| &q \ge 0.5 \\ \left( {X_{rabbit} \left( t \right) - X_{m} \left( t \right)} \right) - r_{3} \left( {LB + r_{4} \left( {UB - LB} \right)} \right) &q < 0.5 \\ \end{array} } \right.$$
(13)

where \(X\left( t \right)\) and \(X\left( {t + 1} \right)\) represent the position of the hawks in the t and t + 1 iteration, respectively. \(X_{rabbit} \left( t \right)\) indicates the position of the prey. \(r_{1}\), \(r_{2}\), \(r_{3}\), \(r_{4}\) and \(q\) are random numbers inside (0, 1), which are updated during each iteration. LB and UB represent the lower and upper bound of the decision variables, respectively. \(X_{rand}\) is the position of a randomly selected hawk. Concerning \(X_{i} \left( t \right)\) as the position of each hawk in the iteration of t and N as the total number of hawks, \(X_{m}\), representing the average position of the hawks, can be calculated using the following equation [52]:

$$X_{m} \left( t \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} X_{i} \left( t \right)$$
(14)

The intermediate phase is defined as transition from exploration to exploitation which expressing the function of wasting energy prey during the escape. Due to the reduced energy of the prey during the escape, the prey energy is modeled using the following equation:

$$E = 2E_{0} \left( {1 - \frac{t}{T}} \right)$$
(15)

where E represents the energy of escape of the prey and T represents the maximum number of iterations. \(E_{0}\), varying randomly in the range (−1, 1) per repetition, indicates the initial state of prey energy. If \(\left| E \right| \ge 1\), the HHO algorithm executes the exploration phase; However, if \(\left| E \right| < 1\), exploitation occurs.

In the third phase of the HHO algorithm, entitled exploitation, four surprise attack models are proposed based on prey escape behavior and hawk pursuit strategies. In this phase, \(r\) is considered the prey chance parameter. \(r < 0.5{ }\) means a successful escape of prey and contrariwise. In this phase, based on the escape energy E, soft besiege \(\left( {\left| E \right| \ge 0.5} \right)\)) or hard besiege (\((\left| E \right| < 0.5)\)) is performed by Harris hawk (Fig. 1) [52, 56]. Algorithm 2 presents the HHO pseudocode.

figure b

As explained, the three metaheuristic algorithms, PSO, ICA and HHO are used in this work to improve the prediction performance of the MLP. The metaheuristic optimizers need to be integrated with an MLP to optimize its weights and biases. In brief, the solution of the metaheuristic learning tools is a matrix of optimized computational parameters to redesign a robust MLP using them. The algorithm of the proposed hybrid MLP model described by the following steps:

  • Step 1: Initialize the problem of training MLP as an optimization approach.

  • Step 2: Initialize the main parameters of metaheuristic algorithms (e.g., the maximum iteration, upper and lower bounds of variables and the number of search agents).

  • Step 3: Generate the random solutions (e.g., decision variables) and calculate the value of objective function for each solution.

  • Step 4: Use the metaheuristic algorithms to find the optimal values of decision variables.

  • Step 5: Repeat Step 4 until the finish criteria of algorithms is satisfied. The best values of weights and biases are obtained.

Figure 3 shows the flowchart of the proposed hybrid MLP methods.

Fig. 3
figure 3

Flowchart of the proposed hybrid models based on the MLP and metaheuristic algorithms

Full size image

3 Data and statistical analysis

Hydraulic and geometric flow data are essential for accurate estimation of the longitudinal dispersion coefficient. Thus, in this study a range of data that gathered from the previous studies where the required parameter values were provided are exploited to investigate the abilities of the proposed hybrid AI models for robust and efficient prediction of the longitudinal dispersion coefficient. This information includes 164 series of data related to the flow characteristics, such as the width (W), depth (H), velocity (U), shear velocity (\(U_{*}\)) and the measured longitudinal dispersion coefficient (K) [6].

Table 2 report the statistical properties of the utilized database in terms of the minimum, maximum, mean and standard deviation values. Moreover, the coefficient of correlation between the input variables and the longitudinal dispersion coefficient is reported in Table 2. Besides, Fig. 4 shows the frequency histogram of the input and output variables. Based on the table and figures illustrated results, the utilized data have different type and range, which complicates the problem of estimating the longitudinal dispersion coefficient of rivers.

Table 2 Summary of the geometric, hydraulic and dispersion coefficient data sets employed in this study
Full size table
Fig. 4
figure 4

Frequency histograms of the input/output variables for the longitudinal dispersion coefficient prediction, a channel width, W (m), b flow depth, H (m), c cross-sectional average velocity, U (m/s), d shear velocity, U* (m/s) and f experimental results of dispersion coefficient, K (m2/s)

Full size image

The statistical analysis results showed a significant correlation between the longitudinal dispersion coefficient and the width-to-depth ratio (W/H) [57]. This ratio is used in most developed experimental relationships of estimating the longitudinal dispersion coefficient to improve the accuracy of the predictive models. Therefore, this paper also exploited this ratio for categorizing different flows to increase the accuracy of the proposed predictive AI model [6]. Accordingly, the 164 data sets were divided into two groups as \(\frac{W}{H} \le 28\) and \(\frac{W}{H} > 28\).

4 Statistical evaluation indicators

To compare the results efficiency of the proposed predictive neural network model integrated with the indicated metaheuristic algorithms above as a novel framework for accurate modeling of the longitudinal dispersion coefficient, several statistical criteria and parameters are employed. The utilized statistical indicators include the mean bias error (MBE), the root mean square error (RMSE), the normalized root mean square error (NRMSE), the mean absolute error (MAE), coefficient of determination (R2), t-statistics and uncertainty at 95% (U95), which the equation of each index is presented as follows [58, 59]:

$$MBE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {K_{{\left( {observed} \right)}}^{i} - K_{{\left( {predicted} \right)}}^{i} } \right)$$
(16)
$$RMSE = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {K_{{\left( {observed} \right)}}^{i} - K_{{\left( {predicted} \right)}}^{i} } \right)^{2} }$$
(17)
$$NRMSE = \frac{{\sqrt {\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} \left( {K_{{\left( {observed} \right)}}^{i} - K_{{\left( {predicted} \right)}}^{i} } \right)^{2} } }}{{\overline{{K_{{\left( {observed} \right)}} }} }}$$
(18)
$$MAE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {K_{{\left( {observed} \right)}}^{i} - K_{{\left( {predicted} \right)}}^{i} } \right|$$
(19)
$$t{ - }statistics = \frac{1}{n}\sqrt {\frac{{\left( {n - 1} \right)MBE^{2} }}{{RMSE^{2} - MBE^{2} }}}$$
(20)
$$U_{95} = 1.96\left( {SD^{2} + RMSE} \right)^{1/2}$$
(21)
$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {K_{{\left( {observed} \right)}}^{i} - K_{{\left( {predicted} \right)}}^{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\overline{{K_{{\left( {observed} \right)}} }} - K_{{\left( {predicted} \right)}}^{i} } \right)^{2} }}$$
(22)

In the above-mentioned formulas, \(K_{{\left( {observed} \right)}}^{i}\), \(K_{{\left( {predicted} \right)}}^{i}\) and \(\overline{{K_{{\left( {observed} \right)}} }}\) are the observed value, the predicted and the observed mean values of the longitudinal dispersion coefficient (K), respectively. It should be mentioned that the model with the lowest values of the statistical indicators as MBE, RMSE, NRMSE, MAE, t-statistics and U95 is considered to be the best performing model for the prediction of the longitudinal dispersion coefficient among the others.

5 Results and discussion

5.1 Statistical evaluation of the models' performance

In order to achieve the best performance of the metaheuristic algorithms in each optimization problem, it is necessary to determine a set of setting parameters using the trial and error method to minimize or maximize the desired objective function. The optimal setting parameters values of PSO algorithm and MLP are tabulated in Table 3. It is noticeable that only PSO has setting parameters among the used algorithms.

Table 3 Sitting parameters of the models
Full size table

As mentioned before, the 164 data sets presented in Sect. 3 were divided into two groups as \(\frac{W}{H} \le 28\) and \(\frac{W}{H} > 28\). Then the developed MLP models based on the metaheuristic algorithms were implemented separately for two groups of data, training data (80%) and test data (20%).

Tables 4 and 5 show the performance of the developed predictive AI models, including MLP, MLP-ICA, MLP-PSO and MLP-HHO, using the statistical parameters of MBE, RMSE, NRMSE, R2, MAE, t-statistic and U95.

Table 4 Average values of statistical indicators for the proposed hybrid models based on the MLP approach for the longitudinal dispersion coefficient prediction in train, test and overall phases \(\left( {\frac{W}{H} \le 28} \right)\)
Full size table
Table 5 Average values of statistical indicators for the hybrid proposed models based on the MLP approach for the longitudinal dispersion coefficient prediction in train, test and overall phases \((\frac{W}{H} > 28)\)
Full size table

Investigating the obtained results using the statistical parameters presented in Tables 4 and 5, it is noticeable that the closer the value of a statistical parameter to 0, the more the predicted results of the longitudinal dispersion coefficient is accurate. As a result, the algorithm has shown better performance in predicting data.

Therefore, according to Tables 4 and 5, it can be said that all the three MLP models optimized using ICA, HHO and PSO have better performance than the MLP standalone model and predict the dispersion coefficient more accurately. The values of the statistical parameters for the proposed models are lower than those given by the MLP.

All the proposed models showed an acceptable performance in calculating the longitudinal dispersion coefficient. However, the new MLP-HHO hybrid AI model yield the best results based on most of the statistical indicators used in the prediction process, including the training, testing and overall phases. Such that, the yielded RMSE was 28.5178, 1.5809 and 23.3026, in the training, testing and overall stages, respectively, for the first group of data (\(\frac{W}{H} \le 28\)). In addition, the RMSE was 66.4141, 48.6601 and 61.0201, in the training, testing and overall phases, respectively, for the second group data of (\(\frac{W}{H} > 28\)). In the other side, the lowest performance among the proposed models according to the indicators metrics was found to be obtained by the MLP in which the recorded values of RMSE were 85.3782, 4.4405 and 69.7582 in the training, testing and overall phases for data of \(\frac{W}{H} \le 28\), respectively. Also, RMSE values of the MLP for the group data of \(\frac{W}{H} > 28\) were 104.2541, 143.9363 and 119.0904 in the training, testing and overall phases, respectively. Thus, the correlation of MLP Showed low abilities for accurate modeling of the longitudinal dispersion coefficient among the proposed models.

In addition to the investigated statistical parameters, the correlation coefficient (R2) was used to evaluate the accuracy of the longitudinal dispersion coefficient predicted using the mentioned AI models, according to Eq. (22). Figures 5 and 6 show the scatter plots of all three developed hybrid and the MLP models for both groups, \(\frac{W}{H} \le 28\) and \(\frac{W}{H} > 28\). It is noted that the R2 indicates the uncertainty of the proposed model. The closer it is to 1, the greater the correlation between the predicted data and the observational data.

Fig. 5
figure 5

Scatterplots of the proposed hybrid MLP models in the train and test phases \(\left( {\frac{W}{H} \le 28} \right)\)

Full size image
Fig. 6
figure 6

Scatterplots of the proposed hybrid MLP models in the train and test phases \(\left( {\frac{W}{H} > 28} \right)\)

Full size image

In each figure, the linear equation between the predicted and the measured values is shown as Eq. (23).

$$y = aX + b$$
(23)

where y and X represent the predicted and the actual longitudinal dispersion coefficient values, respectively; a and b also represent the linear ratios and bias, respectively. As shown from the figures, the MLP-HHO hybrid model obtained the highest correlation coefficient for both data groups with value equal to R2 = 0.9587 for data of \(\frac{W}{H} \le 28\) and R2 = 0.9761 for data of \(\frac{W}{H} > 28\) in testing phase. It is worth noting that the R2 of all optimized MLP hybrid models is higher than the MLP model, that indicating the superiority of the proposed models than the MLP. So that, R2 value of MLP-HHO, MLP-PSO and MLP-ICA shows 36, 18 and 12% increase than MLP for data group of \(\frac{W}{H} \le 28\), respectively. Also, for data of \(\frac{W}{H} > 28\), this value for MLP-HHO, MLP-PSO and MLP-ICA is 41, 26 and 14% higher than MLP, respectively.

Moreover, the \(K_{{\left( {predicted} \right)}} /K_{{\left( {observed} \right)}}\) ratio in Figs. 7 and 8 has been used to illustrate the uncertainty of the proposed hybrid MLP models results using the train and test phases. According to the figures, the ratio results for both train and test phases are in lower rang in the case of MLP-HHO. The \(K_{{\left( {predicted} \right)}} /K_{{\left( {observed} \right)}}\) for overall data of MLP-HHO included in the range of [0.246, 138.284] and [0.024, 6.879] for \(\frac{W}{H} \le 28\) and \(\frac{W}{H} > 28\) respectively, that have the lowest prediction uncertainties compared to the other investigated models.

Fig. 7
figure 7

Comparison of the experimental to predicted longitudinal dispersion coefficient using the proposed hybrid MLP models in the train and test phases \(\left( {\frac{W}{H} \le 28} \right)\)

Full size image
Fig. 8
figure 8

Comparison of the experimental to predicted longitudinal dispersion coefficient using the proposed hybrid MLP models in the train and test phases \(\left( {\frac{W}{H} > 28} \right)\)

Full size image

5.2 Taylor diagram

In the following, the Taylor diagram (TD) is plotted to show the accuracy of the developed models. In fact, the TD express the performance of models in summarized form. Thus, the relationship between predicted and observed values is displayed by correlation coefficient, standard deviations and the root mean square difference (RMSD) [60, 61].

In the TD, which is plotted as a semicircle or quadrilateral, the values of the correlation coefficient in the radius, the values of standard deviations in the form of concentric circles with the circle center [0, 0] and the RMSD values in the form of concentric circles with the reference point as the center are shown [60]. In this diagram, the evaluation is done in a way in which the values of the standard deviations, correlation coefficient and RMSD deviation from the models are specified on the diagram as points [62]. Then the point that has a closer distance to the reference point (observed data) represented by the black dot has more accurate prediction credibility [61].

As shown in Figs. 9 and 10, the developed MLP-HHO model is more accurate than the MLP-ICA, MLP-PSO and MLP in predicting the longitudinal dispersion coefficient for both group of data including \(\frac{W}{H} \le 28\) and \(\frac{W}{H} > 28\). The MLP-HHO has the closest distance to the reference point that refers to observed data, followed by the MLP-PSO model that indicated average results with a close correlation coefficient value to the observed data by 0.9. However, both MLP-ICA and MLP models show low results compared to the other models, which indicate that these models have the weak abilities for modeling the longitudinal dispersion coefficient in rivers.

Fig. 9
figure 9

Plot of results in Taylor diagram for \(\left( {\frac{W}{H} \le 28} \right)\)

Full size image
Fig. 10
figure 10

Plot of results in Taylor diagram for \(\left( {\frac{W}{H} > 28} \right)\)

Full size image

5.3 Prediction performance validation

To confirm the superiority of the proposed hybrid models, the results of MLP-based models were also compared with the artificial intelligence-based models and empirical equations from previous works. In this regard, the statistical metrics (MBA, RMSE, NRMSE, MAE, t-statistics and U95) were applied for modeling the longitudinal dispersion coefficient for all data sets (see Table 6). According to the results, it is clear that the MLP-HHO is superior to the other existing equations with respect to all performance indicators. Afterward, the proposed MLP-ICA model (RMSE = 77.750, MAE = 41.99 and R2 = 0.80) and the proposed soft computing-based model by Alizadeh et al. [6] (RMSE = 89.825, MAE = 45.159 and R2 = 0.73) ranked second and third, respectively. Moreover, the empirical-based equation by Seo and Cheong [63] (RMSE = 85.390, MAE = 40.804 and R2 = 0.76) was able to provide a good prediction of the longitudinal dispersion coefficient.

Table 6 Comparison between the existing and proposed models
Full size table

Regarding Fig. 11, it is clear that the MLP-HHO model has highest accuracy in comparison with other models (selected empirical and soft computing-based equations), which indicates a good correlation between simulated and measured values.

Fig. 11
figure 11

R2 of different models for the all data set; a empirical-based models; b AI-based models; c MLP-based models

Full size image

Figure 12 compares the observed and predicted values of the longitudinal dispersion coefficient using the three MLP models based on HHO, ICA and PSO, as well as MLP and the other existing equations. Each model's performance can be understood conceptually by displaying the measured values of the data versus the predicted values for each model. As shown in Fig. 12, the developed hybrid MLP models based on the three metaheuristic algorithms have higher accuracy than the MLP model. Also, among the three MLP models based on metaheuristic algorithms, the MLP-HHO hybrid model can accurately identify the prediction pattern and provide accurate longitudinal dispersion coefficients.

Fig. 12
figure 12figure 12

Time series plots for the all data set; a empirical-based models; b AI-based models; c MLP-based models

Full size image

Another statistical indicator used to illustrate the performance of the developed MPL models is the discrepancy ratio (DR), which can be calculated as Eq. (24):

$$DR = log\frac{{K_{pred i} }}{{K_{obs i} }}$$
(24)

where \(K_{pred i} \;{\text{and}}\; K_{obs i}\) are ith value of the predicted and observed longitudinal dispersion coefficient obtained from the considered models respectively.

DR indicates the correlation between the longitudinal dispersion coefficients measured and the estimated values by each model, in such a way that the predicted values are the same as the measured values DR = 0. If the predicted values are higher than the measured values, DR > 0, also DR < 0 when the predicted models were underestimate than the measured values. The closer the DR is to 0, the closer the predicted dispersion coefficients are to the measured values. In other words, the model has shown better performance in estimating this parameter.

According to Table 7, DRs are closer to 0 using the MLP-HHO model than the other MLP-based models, empirical equations and AI models, indicating a more successful performance of the MLP-HHO despite the acceptable solution provided by all the hybrid MLP models in estimating the longitudinal dispersion coefficient.

Table 7 DR values of the hybrid models developed to predict the longitudinal dispersion coefficient
Full size table

5.4 Boosting the proposed MLP-HHO model

Training and testing data are typically determined randomly in prediction models. As mentioned earlier, this study has also utilized a random approach to select data in both training and testing phases for building the proposed model. The use of this approach is efficient and effective while limited data is available. However, when dealing with a large amount of data, the use of this method may decrease the model accuracy during some testing phases due to the random selection of data, which may lead to training the model based on some certain data range, and in the testing phase, the model encounters data with a different range from the training data, thereby reducing the model accuracy significantly. Since the proposed MLP-HHO model provided the highest performance compared with the other models in the previous steps, we proposed a more robust model improvement for forecasting the longitudinal dispersion coefficient by adding a preprocess step. For this purpose, we have employed the K-means model, which is arranged as unsupervised machine learning method, to find the data average (the cluster center) based on the W/H ratio. Given the data of dispersion, we initially considered the number of cluster centers equal to 5 and divided all the data based on the cluster centers. Therefore, in the training phase, the model was trained based on an equal number of data from each group, so that, the robustness of the model could be maintained against data dispersion during testing phase. Table 8 shows the cluster center as well as the number of data placed in each cluster according to the W/H ratio.

Table 8 Centroids of data sets in K-means clustering technique
Full size table

After developing the combined model, we tested it by all the data including 164 data series addressed in Sect. 3. Table 9 shows the values of the statistical parameters calculated for the data simulated by the K-means-MLP-HHO model. It is clear that, the use of K-means to cluster the data before modeling has improved the accuracy of the MLP-HHO model during the training and testing phases compared to the random data selection strategy. For example, the RMSE value has decreased from 57.22 to 34.12 m2/s in the training phase and from 24.09 to 17.77 m2/s in the testing phase and overall from 51.16 to 30.99 m2/s. According to the parameter U95, it is clear that the clustering-based model provide the favorable predictions. Also, the lowest uncertainty in prediction of the longitudinal dispersion coefficient (35.687) is observed in the results obtained by the clustering-based model in testing phase.

Table 9 Comparison between the clustering and random-based selection MLP-HHO model for train, test and overall data
Full size table

Moreover, as Fig. 13 shows, the use of k-means in combination with the proposed model improves the robustness in the testing phase as the coefficient of determination (R2) of the predicted and real data in both, training and testing phases is equal.

Fig. 13
figure 13

Cross plots of the implemented K-means-MLP-HHO

Full size image

5.5 Sensitivity analysis

Finally, a sensitivity analysis was performed to evaluate the relative importance of the input parameters (\(W, U, H,U_{*}\)) on the longitudinal dispersion coefficient using the MLP-HHO model. For this purpose, Eq. (25) was utilized

$$r\left( {I_{j} , O} \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {I_{j,i} - \overline{I}_{j} } \right)\left( {O_{i} - \overline{O}} \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {I_{j,i} - \overline{I}_{j} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \overline{O}} \right)^{2} } }}$$
(25)

where I and \(\overline{I}\) are the input parameter, related to the longitudinal dispersion coefficient and its average value, respectively. O and \(\overline{O}\) denote the predicted longitudinal dispersion coefficient output and its average value using K-means-MLP-HHO model, respectively.

The highest value for r by the input \(I_{j}\) indicates the greater impact on the predicted output. Figure 14 shows the sensitivity analysis of the input data on the longitudinal dispersion coefficient by the K-means-MLP-HHO model. As indicated, the width parameter W (\(r = 0.573\)), the average flow velocity \(U\) (\(r = 0.553\)) and the flow depth H (\(r = 0.409\)) by the highest values of the relevancy factor are recognized as the most important factor on the longitudinal dispersion coefficient estimation in rivers.

Fig. 14
figure 14

Sensitivity analysis of the input parameters using K-means-MLP-HHO (all data)

Full size image

6 Conclusion

In this study, a new hybrid model using the artificial intelligence (AI) methods is developed to estimate the rivers' longitudinal dispersion coefficient accurately.

The proposed model consists of a powerful multilayer perceptron neural network and a new metaheuristic optimization algorithm called HHO, inspired by the Harris hawk behavior. Two other well-known algorithms, ICA and PSO, were used to train the MLP in order to illustrate the high accuracy of the developed MLP-HHO. For this purpose, 164 series of measured data gathered from previous studies in two groups based on width-to-depth ratio, \(\frac{W}{H} \le 28\) and \(\frac{W}{H} > 28\), were evaluated. The investigations on the models’ efficiency using the statistical indicators show that the combination of the metaheuristic and MLP algorithms performs better than MLP standalone in solving the complex problem of longitudinal dispersion coefficient in rivers.

According to the results, the MLP-HHO model, with R2 = 0.9587 for \(\frac{W}{H} \le 28\) data and R2 = 0.9761 for \(\frac{W}{H} > 28\) data in the testing phase, is the best proposed AI model for predicting the longitudinal dispersion coefficient in rivers than other models. Finally, to increase the robustness of MLP-HHO model, a classification technique, namely K-means, is coupled with it. Thus, a certain percentage of data was selected for better model learning that includes all data ranges. The performance of K-means-MLP-HHO was compared with MLP-HHO model. The boosting K-means-MLP-HHO model with R2 = 0.97, was the best performing model for estimating the longitudinal dispersion coefficient in rivers. Furthermore, the sensitivity analysis related to the input parameters using the relevancy error factor shows that the flow width (W) and the average flow velocity (\(U\)) have the highest influence on the longitudinal dispersion coefficient. As the relevancy error factor was 0.573 and 0.553, respectively, for these parameters. Furthermore, the shear velocity (\(U_{*}\)) has the least influence on the behavior of longitudinal dispersion coefficient in rivers.

Moreover, the prediction results may be affected by the uncertainty of the input data, it is suggested to develop the probabilistic models in future research and consider the uncertainty of the input data to obtain more reliable results.