Introduction

Water loss is an inevitable problem in almost every WDS, even in those which have been recently installed and the only difference is the amount and the type of loss (Ulanicki et al. 2008). However, these types of losses can be controlled to make economic savings. Managers’ minds have been obsessed with finding leakage management models to attain maximum leakage reduction with the minimum investment that has led to many studies (Mahdavi 2010). After laying the network pipes, the only thing which could affect the leakage amount is the pressure of the pipe that is controllable. From this point of view, reducing the pressure solely or in combination with other methods is a viable, effective, and economical solution for controlling leakage. This pressure reduction has to be conducted to align with supplying the required pressure to meet the consumption requirements throughout the day and night. There are several methods to reduce extra pressure in the network, which one of them is to use PRVs in the WDS. PRVs installation in a WDS could be regarded as an optimization problem. Determination of the optimum number, location, and settings of the valves through optimization methods could be implemented to minimize the leakage (Tabesh and Humehr 2006).

Sterling and Bargiela (1984) proposed a method to minimize leakage through extra pressure reduction in the network by observing the amount of nodes pressure as the goal function using linear programming. To face the non-linear nature of the system, consecutive linearization based on the Newton–Raphson method was utilized. Later, Jowitt and Xu (1990) conducted consecutive linearization of the equations which were dominant on the network. In this method, a decrease of 20% was observed in leakage. Nicolini (2011) formulated the optimal number of locations and settings of the PRVs by taking the minimum required pressure of the nodes for minimizing the number of the valves and considered minimizing the system leakage as the problem objective. He formulated them as the dual-objective optimization problem and utilized the NSGA-II algorithm to solve it. Abdol Magoid (2011) conducted studies on the development and application of several pressure-optimization methods and algorithms at the network level and found out that 60% of leakage could be reduced through proper management. Mutikanga (2012), by effective investigation of the pressure management strategies, revealed that 254–302 L of water loss could be saved daily through reduction of average pressure of the region as 7 m. Nicolini (2011) conducted studies utilizing pressure controlling valves and pumps as turbine (PAT) on the water system of East Napoli, Italy in two separate phases. In the first phase, the PRVs were utilized and in the second phase, some controlling valves were replaced with pumps as a turbine. The results showed that using this method, a large amount of energy is recycled while water losses are greatly reduced. According to the research conducted by Babić et al. (2014) on Kotež, Serbia water network, it was revealed that by reducing the input pressure from 29.5 to 17.5 m using pressure controlling valves, 927 L of water could be saved daily. Saldarriaga and Salcedo (2015), Jafari-Asl (2016) and Jafari-Asl et al. (2018) conducted the studies to ascertain the optimal location and daily settings of the PRVs in WDS to minimize leakage through meta-heuristic methods. The results revealed the proper functioning of the mentioned methods. Latifi et al. (2017) developed a simulation–optimization model based on the Non-Dominated Sorting Genetic Algorithm, version II, (NSGA-II) and EPANET simulation model to find the optimal location of PRVs to maximize the fuzzy reliability index and minimize the excessive pressure in a high-pressure case study WDS.

Creaco and Pezzinga (2018) conducted a comparison between GA and SA algorithms and Linear Programming for the optimal location of control valves for leakage reduction in WDSs. Dini and Asghari (2019) proposed a new efficient method based on PSO to minimize leakage and maximize reliability by finding optimal location and PRVs status in a real large-scale WDS.

The reduction of costs is an important factor to be considered in WDS rule decisions. The use of hydraulic simulations coupled with optimization algorithms has shown to be powerful enough to determine optimal operations (Brentan et al. 2017).

From recent studies which have used artificial intelligence and evolutionary algorithms based methods in the management of water networks, can mention the group method of data handling (GMDH) performance evaluation in predicting the longitudinal distribution coefficient in water networks (Najafzadeh and Sattar 2015), a model based on evolutionary algorithms for conjugate depths of a hydraulic jump in circular pipes (Najafzadeh 2019), and GEP evaluation to describe choke performance in pipeline flow regimes (Kaydany et al. 2014).

Therefore, the main purpose of this study was to investigate the computational efficiency of meta-heuristic methods for optimal locating and optimal daily settings of the PRVs using PSO algorithm to reduce leakage in WDSs. Hence, the organization of manuscript is as: "Introduction", the materials and methods include the explanation of simulation and optimization models; "Application in a case study" represents the application of the proposed model in a case study; "Results and discussion" expresses and discusses the results of the developed model; finally, "Conclusion" concludes the work and discusses possible future researches.

Materials and methods

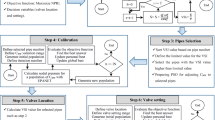
The proposed methodology consists of a simulation–optimization process that aims to select the most appropriate locating and setting of PRV in WDSs. In this research, the EPANET model is employed as a WDS hydraulic simulation model and PSO is utilized as an optimization tool. In this approach, the optimization model (PSO) is coupled with the hydraulic simulation model (EPANET) in an interactive loop.

Optimization model

The PSO algorithm was first introduced by Kennedy and Eberhart (1995). This algorithm is a population-based evolutionary algorithm that was inspired by the simultaneous flight of birds, swarming fish school and their social lives. The PSO algorithm has been a powerful optimization tool and applied in different fields of water engineering such as the optimal operation of reservoir (Kumar and Reddy 2007), optimizing irrigation water allocation (Noory et al. 2012), optimal design of water supply systems (Montalvo et al. 2010), and automatic calibration of water quality model (Afshar et al. 2011).

In the PSO algorithm, every solution could be considered as a bird swarm, which is called a particle. In such structures, the birds have a type of group behavior leads them towards the aims (Shi and Eberhart 1998). Each particle has “s” dimensions, which shows the number of decision variables of the optimization problem. Each particle (i) located by 3 vectors, merely, the current position of the particle (\(x_{i} = (x_{i,1} , x_{i,2} , \ldots ,x_{i,j } , \ldots , x_{i,s} )\)), the best position of the particle (\(b_{i} = (b_{i,1} , b_{i,2} , \ldots ,b_{i,j } , \ldots , b_{i,s} )\)), and the velocity of the particle \((v_{i} = (v_{i,1} , v_{i,2} , \ldots ,v_{i,j } , \ldots , v_{i,s} )).\) In the PSO algorithm, the group particles must be related to each other in a way that the best position of the particle is also determined and illustrated using the\(g_{i} = (g_{1} , g_{2} , \ldots ,g_{j } , \ldots , g_{s} )\). After determining g in each iteration, the location and velocity of every particle of the group will change and it can be implemented according to the Eqs. (1) and (2):

$$x_{i} \left( {t + 1} \right) = x_{i} \left( t \right) + v_{i} \left( {t + 1} \right),$$
(1)
$$v_{i} \left( {t + 1} \right) = v_{i} \left( t \right) + C_{1} \left( {b_{i} - x_{i} \left( t \right)} \right)R_{1} + C_{2} \left( {g - x_{i} \left( t \right)} \right)R_{2} ,$$
(2)

where \(\omega\) is the weight inertia, \(C_{1}\) and \(C_{2}\) are the cognitive and social parameters respectively, \(R_{1}\) and \(R_{2}\) are randomly selected from a uniform distribution in [0, 1], and t is the number of iterations. The initial procedures of PSO go as follows:

  1. 1.

    Randomly initialize population position and velocities.

  2. 2.

    The fitness of each particle is evaluated based on the objective function.

  3. 3.

    If the calculated fitness for each particle (i) is the best value, the position of the particle (i) is stored as (bi).

  4. 4.

    In every iteration among all the particles, the one that owns the best fitness is chosen and the position of the particle is stored as \(g\).

  5. 5.

    The velocities are reformed according to the Eq. (2).

  6. 6.

    The new position of the particles is established according to Eq. (1).

  7. 7.

    If the stopping conditions such as maximum iteration or minimum error occur, the procedures will finish. Otherwise, the procedures will continue again from step 2.

Simulation model

EPANET 2.0 model was developed by Rossman (2000) for an extended period simulation of hydraulic and quality in WDSs. Basic equations governing hydraulic simulation, driven from the mass (Eq. 3) and energy conservation laws (Eq. 6), respectively, are developed in the network nodes and loops:

$$\mathop \sum \limits_{i} Q_{ij,k} - \alpha_{k} Q_{{{\text{req}},i}} - I_{i,k} = 0\quad {\text{for}}\quad i = 1, \ldots N,\quad k = 1, \ldots ,N_{{\text{L}}} ,$$
(3)

where, Qij,k is the flow rate between nodes i and j, \(\alpha_{k}\) is the demand multiplier coefficient, Qreq,i is the average demand at node i, N is the total number of nodes in the system, NL is the total number of load conditions and \(I_{i,k}\) is the leakage at node i that can be defined as follows:

$$I_{i,k} = C_{{\text{L}}} L_{t,i} P_{i,k}^{\gamma } ,$$
(4)

where CL (constant) is coefficient relating the leakage per unit length of pipe to service pressure at node i, Pi,k is the pressure at node i for load condition k, γ is leakage exponent coefficient, and \(L_{{{\text{t}},i}}\) is the total length of pipes tributary to node i. Herein, \(L_{{{\text{t}},i}}\) is considered as:

$$L_{{{\text{t}},i}} = 0.5\mathop \sum \limits_{j} L_{ij} ,$$
(5)

where the sum is again extended to all links connected to node i.

Head loss in every link (conservation of energy), expressed as:

$$H_{i,k} - H_{j,k} = h_{ij,k} ,$$
(6)

where \(H_{i,k}\) and \(H_{j,k}\) are head at nodes i and j, respectively, and \(h_{ij,k}\) is the head loss between nodes i, j, and k representing the load condition. Equations (7) and (8), both based on Hazen–Williams formula in SI units, are adopted for calculation of head losses in network pipes and PRVs, respectively, as follows:

$$h_{ij,k} = 10.668C_{ij}^{ - 1.852} d_{ij}^{ - 4.871} L_{ij} Q_{ij,k}^{1.852} ,$$
(7)
$$h_{ij,k} = 10.668C_{ij}^{ - 1.852} \left( {u_{ij,k} d_{ij} } \right)^{ - 4.871} L_{ij} Q_{ij,k}^{1.852} ,$$
(8)

where Cij is the Hazen–Williams coefficient, di,j pipe is diameter, Lij is length, uij,k is diameter multiplier (in the range 0,…,1), which simulates the presence of a valve in the link connecting nodes i and j, and depends on load condition k.

Equation (9) is adopted to convert the term uij,k into the setting Vij,k (or valve opening), which is defined by previous authors (Jowitt and Xu 1990; Reis et al. 1997; Vairavamoorthy and Lumbers 1998; Nicolini and Zovatto 2009):

$$V_{ij,k} = u_{ij,k}^{4.871/1.852} .$$
(9)

The pressure-driven approach is applied to simulate the hydraulic situation that the available demand is computed as Tabesh et al. (2014):

$$Q_{{{\text{avl}},i}} = \left\{ {\begin{array}{*{20}l} {0 } & {{\text{if}}\quad H_{i} \le H_{i}^{\min } } \\ {Q_{{{\text{req}},i}} \left( {\frac{{H_{i} - H_{i}^{\min } }}{{H_{i}^{{{\text{des}}}} - H_{i}^{\min } }}} \right)} & {{\text{if}}\quad H_{i}^{\min } \le H_{i} \le H_{i}^{{{\text{des}}}} } \\ {Q_{a} + Q_{b} \left( {\frac{{H_{i} - H_{i}^{\min } }}{{H_{i}^{{{\text{des}}}} - H_{i}^{\min } }}} \right)^{\frac{1}{n}} } & {{\text{if}}\quad H_{i}^{{{\text{des}}}} \le H_{i} \le H_{i}^{\max } } \\ {Q_{a} + Q_{b} \left( {\frac{{H_{i}^{\max } - H_{i}^{\min } }}{{H_{i}^{{{\text{des}}}} - H_{i}^{\min } }}} \right)^{\frac{1}{n}} } & {{\text{if}}\quad H_{i} \ge H_{i}^{\max } } \\ \end{array} } \right.,$$
(10)

where \(H_{i}\) is equal to pressure head at node i, \(H_{i}^{\min }\) and \(H_{i}^{\max }\) are the minimum and maximum pressure head at node i, and \(H_{i}^{{{\text{des}}}}\) is desired to head in which the entire demand discharge (\(Q_{{{\text{req}},i}}\)) at node i. \(Q_{a}\) and \(Q_{b}\) are the volumetric and head-dependent portions of the available discharge, respectively. These parameters are calculated as:

$$H_{i}^{\max } = 2H_{i} ,$$
(11)
$$Q_{a} = \alpha \% \times Q_{{{\text{req}},i}} ,$$
(12)
$$Q_{b} = b \cdot \% \times Q_{{{\text{req}},i}} ,$$
(13)
$$\alpha \% + b\% = 100\% .$$
(14)

Equal values of 50% have been proposed for a and b by Tabesh et al. (2014).

Optimization problem

The problem of pressure management in WDSs is presented here as a single objective optimization problem with the objective function of the system total leakage. For three different hydraulic conditions, to each PRV, a vector of random numbers between 0 and 1 is introduced so that, each bit represents valve opening status during a hydraulic condition. It worth to mention that all the links have the potential to use PRV, however, only five links have been selected randomly to use the valves in the optimization process. In what follows, the mathematical formulation of the objective function is presented:

$${\text{Objective}}\,{\text{function}} = \frac{1}{{N_{{\text{L}}} }}\mathop \sum \limits_{k = 1}^{{N_{{\text{L}}} }} \mathop \sum \limits_{i = 1}^{N} W_{k} I_{i,k} = \frac{1}{{N_{{\text{L}}} }}\mathop \sum \limits_{k = 1}^{{N_{{\text{L}}} }} \mathop \sum \limits_{i = 1}^{{\text{N}}} W_{k} C_{{\text{L}}} L_{{{\text{t}},i}} P_{i,k}^{\gamma } ,$$
(15)

where \(N\) represents the number of nodes in the system in which leakages are present and \(W_{k}\) is a weight associated with load condition k.

In general, two types of constraints are imposed on this optimization problem. The first type includes the equations of conservation of mass (Eq. 3) and conservation of energy (Eq. 6). Both mass and energy constraints are automatically considered into the EPANET hydraulic simulation model. The constraint of the minimum required pressure in reference nodes (defined in Eq. 16) is considered in the optimization model by introducing a proper penalty function shown in Eq. (17):

$$H_{i,k} \ge H_{\min ,i} \quad {\text{for}}\,i = 1, \ldots ,N,$$
(16)
$${\text{Penalty}} = \alpha \times \mathop \sum \limits_{i = 1}^{K} \max \left[ {\left( {1 - \frac{{H_{i} }}{{H_{\min } }},0} \right)} \right]^{2} .$$
(17)

In the equations above, \(H_{\min ,i}\) is the minimum required pressure head at node i and \(\alpha\) is the penalty parameter which is chosen by the terial and error. The \(\alpha\) considered here 100,000.

Figure 1 illustrates the described PSO coupled with the EPANET.

Fig. 1
figure 1

The flowchart of PSO coupled with the EPANET

Full size image

Application in a case study

A test WDS from literature (Jowitt and Xu 1990; Nicolini and Zovatto 2009) is considered as a case study. The network includes 25 nodes, 3 reservoirs, and 37 links. The average water consumption of the network is 155 L/s (Fig. 2). Water levels in the reservoirs are constant according to Table 1. The minimum acceptable pressure for reference nodes 19, 22, 21, and 13 have been determined to be30 m. It should be noted that in not-reference nodes or pressure nodes, no minimum pressure constraint is considered. More details about the nodes of the studied network are tabulated in Tables 2 and 3.

Fig. 2
figure 2

Layout of the example network adopted in the analyses

Full size image
Table 1 Reservoir nodes
Full size table
Table 2 Nodal information of case study (Jowitt and Xu 1990)
Full size table
Table 3 Pipe specifications in case study (Jowitt and Xu 1990)
Full size table

Results and discussion

Optimal location of the pressure control valves

The PSO parameters were determined according to trial and error. In the trial and error process, to determine the best values of C1 and C2, the objective function was minimized with different values of these parameters and finally, the values of C1 and C2 were selected as 3 and 2 respectively. In addition, ω was calculated as follows:

$$\omega = 0.5 \times \left( {1 + \frac{1}{\log \left( t \right) + 1}} \right),$$
(18)

where “t” is the number of iterations. To investigate the abilities of the developed model by regulating the parameters corresponding to the above-mentioned values, the model was examined 3 times. All runs converged to the same value of objective function but with different iterations. The iteration of the PSO algorithm loops in each experiment was considered 1000 and the number of the components (group population) was considered 60. Figure 3 represents a schematic diagram of the movement of the best member in each generation toward an optimal solution in trial 2, which has resulted in the best solution. Optimal location and settings of the PRVs for the water requirement conditions of Load 1, Load 2, and Load 3 in problem-solving by optimization model have been presented in Table 4.

Fig. 3
figure 3

Schematic diagram of the movement of the best member in each generation toward optimum answer in trial 2

Full size image
Table 4 Optimal valve locations and setting for three different runs
Full size table

The details of the optimal response obtained from the location and the amount of leakage from the network with optimal placement of the PRVs for water requirement conditions of Load 1, Load 2, and Load 3 in each solution have been given in Table 5. According to these results, it could be observed that the algorithm in trial 2 (optimal run) has chosen links 1, 11, 20, 26, and 27 that were identified as the best links for the existence of five PRVs. It is clear that the average leakage for the first, second, and third load conditions are 29.19, 27.58, and 25.51 without PRVs and It reduced for the tree load conditions, 22.71, 22.09, and 22.92, respectively, for the case study WDS with optimized location and setting PRVs.

Table 5 Leakages I, II, and III refer to total leakage in the system for the first, second, and third load conditions, respectively; average leakage is the second objective function, f
Full size table

In the second step, by considering the optimal location found in step one (1, 11, 20, 26, and 27) for optimization, the valve utilization program in a 24-h period was implemented. Codifying the optimization problem was also considered as it has been presented in the methodology section. PSO algorithm parameters were considered similar to the first step. Group population was considered 40 and maximum iteration was considered 500. The details of the obtained responses have been presented in Fig. 4.

Fig. 4
figure 4

The diagram of regulation rate (opening) of the selected faucets in stage 1

Full size image

Figure 5 shows the leakage diagram during a 24-h utilization period in an uncontrolled and under controlled conditions based on an optimal program by the PSO algorithm. As could be seen, the control program prepared based on the PSO algorithm has caused a significant reduction in leakage level in the network during utilization period in a way that on average, there was 23% leakage reduction in comparison with uncontrolled conditions.

Fig. 5
figure 5

The leakage diagram during a 24-h utilization period in an uncontrolled and under controlled conditions based on an optimal program by the PSO algorithm

Full size image

The diagram of pressure variation in the system during a 24-h utilization period under controlled and uncontrolled circumstances based on optimal program prepared by PSO algorithm is presented in Fig. 6 which shows that the proposed method is successful in regulating pressure level in the network.

Fig. 6
figure 6

The pressure level diagram during a 24-h utilization period in an uncontrolled and under controlled circumstances based on optimal program prepared by PSO algorithm

Full size image

Comparative results based on meta-heuristic algorithms

The best setting parameters of the three types of efficient algorithms determined based on trial and error are represented in Table 6. Also, the comparison between the results of the current study and these algorithms are shown in Table 7. In terms of optimality solutions, the current simulation-optimization model based on PSO has a better performance than the previous works, such as results obtained using the optimization approaches of GA (Nicolini and Zovatto 2009), ABC (Jafari-Asl 2016), and CA (Jafari-Asl et al. 2018). The objective function (the total leakage rate) was 68.85 L/s after solving for 10 times in the best answer by the GA. The ABC and the CA determined the best solution to be 70.15 L/s after 5 trials and 74.05 L/s after 4 trials, respectively. In this study, the best answer was determined after 3 trials using the PSO algorithm which was 67.73 L/s. The number of objective function calculations to obtain the answers is as follows: 100,000 times in GA algorithm, 100,000 times in ABC algorithm, and 60,000 times in PSO algorithm. A comparison of these four methods indicates that the obtained design for the location of pressure-reducing valves using the PSO algorithm led to the maximum reduction of leakage rate in the shortest time has reduced the rate of leakage, which indicates the applicability of this algorithm. In fact, using the PSO algorithm produces the best response with the least amount of objective function calling that in this problem, requires approximately 40,000 times fewer calls than the ABC, GA, and CA algorithms.

Table 6 Setting parameters of algorithms
Full size table
Table 7 Comparison of the results of the present study with previous studies on location optimization of the PRV faucets
Full size table

Conclusion

The control of leakage in water distribution systems (WDSs) is one of the major concerns of water industries for saving water. Leakages from WDSs depend on the nodal pressure, hence reducing the excessive pressure of nodes by installing PRVs is a cheap and effective method for decreasing leakages. Finding the location of valves and their optimal setting are the faced challenges. In this study, an optimization- simulation model was developed to find the optimal location and settings of the PRVs to minimize the leakage rate in WDSs for a 24-h operation period (during a night and day cycle). For this purpose, the PSO algorithm was coupled with the EPANET hydraulic simulation model. The results showed that the total leakage was reduced by 23% in a benchmark WDS during a 24-h operation period after using the proposed model. Generally, the proposed model based on the PSO algorithm was successful in regulating pressure levels to minimize leakage in the WDSs. Future research should focus on how to incorporate the optimization of location and setting of PRVs under demand pattern uncertainty. This is a challenging problem because the uncertainty of demand patterns can change the pressure and demand of the nodes. Other work in this area can be developing a multi-objective optimization model to find the relation between the number of PRVs and total leakage in WDS under uncertainty of demand factor and roughness coefficient.