1 Introduction

Fractional calculus and fractional dynamics started to play an important role in revealing the hidden aspects of the complex systems [1–3] and are undergoing rapid developments with more and more persuasive applications in the real world [4–10].

Fractional calculus has been used widely in classical mechanics as well as in other areas. For example, in his works, Riewe [11, 12] used the fractional calculus to obtain a formalism that can be applied for conservative and non-conservative systems, where one can obtain fractional Lagrangian and fractional Hamiltonian equations of motion these systems. For some other approaches, the readers can see, for example, Refs. [13–16] and the references therein.

Numerical analysis of fractional differential equations appeared in many researches [17–19]. For example, recently, Podlubny [20] and Podlubny et al. [21] introduce how to numerically solve differential equations by using the matrix form representation. In a recent works, we used the decomposition method in studying the fractional Lagrange and Hamilton equations of motion for different physical systems [22–25]. As it is known, the thin elastica model which is under investigation in this work is a flexible cantilevered rod. This name was suggested by Euler [26], who was the first to completely solve the planar, static problem. A detailed mathematical history of the elastica was given by Levien [27]. The importance of this model comes from the fact that it represents nonlinear vibrations which include both torsional and bending modes. We notice that many works have been carried out on this elastic model with different boundaries (see for example Refs. [28–31] and the references therein).

In this line of taught, we believe that the numerical solutions of the fractional Lagrange’s equations of a thin elastica will reveal new aspects of the non-locality of this system.

The fractional variational principle plays an important role in many areas from science and engineering. Fractional Euler-Lagrange equations are new from both mathematical and applied viewpoints. Both exact and numerical solutions contain richer information than the corresponding ones. Therefore, by modeling the classical Lagrangian of thin elastica with fractional derivatives, we have a class of new solutions. After that, we can easily construct a real thin elastica model corresponding to the new fractional Euler-Lagrange equations. Perhaps, this is one of the major advantages of fractional calculus versus the classical one: We can build new real world phenomena by using the non-local fractional differential operators, and we are not violating any existing laws based on classical calculus approach.

This work is organized as follows: In Sect. 2, the basic definitions of fractional derivatives are discussed briefly, and the fractional thin elastica model is presented. In Sect. 3, the numerical analysis of the corresponding fractional Euler-Lagrange’s equations is carried out. The paper closes with concluding remarks.

2 The basic tools and the system

Below, we briefly present the definitions of the left and right derivatives and integrals (see for more details [1, 2, 9, 10]).

The left Riemann–Liouville fractional derivative (LRLFD) reads

$$\begin{aligned} {}_{a}D_{x}^{\alpha } f(x)\!=\!\frac{1}{\Gamma (n\!-\!\alpha )}\left( \frac{\hbox {d}}{\hbox {dx}}\right) ^{n}\int \limits _{a}^{x} \frac{f(\tau )}{(x\!-\!\tau )^{\alpha -n+1}}\hbox {d}\tau \end{aligned}$$
(1)

The expression of the right Riemann–Liouville fractional derivative is given by

$$\begin{aligned} {}_{x}D_x^\alpha f(x)=\frac{1}{\Gamma \left( n-\alpha \right) }\left( -\frac{\hbox {d}}{\hbox {dx}}\right) ^{n}\int \limits _{x}^{b} \frac{f(\tau )}{(\tau -x)^{\alpha -n+1}}\hbox {d}\tau \nonumber \\ \end{aligned}$$
(2)

The left Riemann–Liouville fractional integral (LRLFI) is defined as follows

$$\begin{aligned} {}_{a}I_t^\alpha x(t)=\frac{1}{\Gamma (\alpha )}\int \limits _{a}^{t} (t-\tau )^{\alpha -1}x(\tau )\hbox {d}\tau \end{aligned}$$
(3)

Finally, the right Riemann–Liouville fractional integral (RRLFI) has the form

$$\begin{aligned} {}_{t}I_b^\alpha x(t)=\frac{1}{\Gamma (\alpha )}\int \limits _{t}^{b} (\tau -t)^{\alpha -1}x(\tau )\hbox {d}\tau \end{aligned}$$
(4)

Here, \(\alpha \) is the order of the derivative such that \(n-1\le \alpha \le n\) is not equal to zero. If \(\alpha \) is an integer, these derivatives become the usual ones.

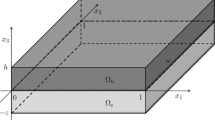
Our physical system (i.e., thin elastic) is shown in Fig. 1 below. The dynamics of this system was studied by Cusumano [26].

Fig. 1
figure 1

Thin elastic: a un-deformed, b bending, c torsional, d non-local (involving both bending and torsional [34])

Full size image

The free vibration of the above linear system involves both bending and torsional modes. As shown in Cusumano [33] work, if non linear effects are included, then complicated dynamics results including chaos are occurred.

The kinetic and potential energies of the system are given as [34]:

$$\begin{aligned} T&= \frac{m}{2}\left[ \left( q_2\right) ^{2}\left( {q}'_1\right) ^{2}+\left( {q}'_2\right) ^{2}\right] + \frac{J}{2}\left( {q}'_1\right) ^{2}.\end{aligned}$$
(5)
$$\begin{aligned} V&= \frac{1}{2} \left[ k_1 \left( q_1 \right) ^{2}+k_2 \left( q_2 \right) ^{2}\right] . \end{aligned}$$
(6)

The prime sign means the differentiation with respect to \(\tau \). Here, \(q_1\) is a generalized coordinate representing the rotational motion which is due to the torsional motion of the elastic, while \(q_2\) is a generalized coordinate representing the rectilinear deflection which is due to the bending motion of the elastica. Now, we make the following notations

$$\begin{aligned} x=\sqrt{\frac{Jk_1 }{m}}q_1 , \quad y=\sqrt{k_1 }q_2 , \quad t=\sqrt{\frac{k_1 }{m}}\tau . \end{aligned}$$
(7)

Thus, the classical Lagrangian equation takes the following form:

$$\begin{aligned} L=\frac{1}{2}\left( 1+\in y^{2}\right) \dot{x}^{2}+\frac{1}{2}\dot{y}^{2}-\frac{1}{2}\left( p^{2}x^{2}+y^{2}\right) . \end{aligned}$$
(8)

where

$$\begin{aligned} \in \,=\frac{m}{Jk_1 }, \end{aligned}$$

and

$$\begin{aligned} p=\sqrt{\frac{k_2 /J}{k_1 /m}}, \end{aligned}$$

the ratio of the frequencies of the torsional \(x- \hbox {mode}\) to the bending \(y- \hbox {mode}\).

The dot means the differentiation with respect to time \(t\). We recall the classical Euler-Lagrange equations of motion as [34]:

$$\begin{aligned}&\left( 1+\in y^{2}\right) \ddot{x}+2\in y\dot{y}\dot{x}+p^{2}x=0.\end{aligned}$$
(9)
$$\begin{aligned}&{\ddot{y}} \,- \in \dot{x}^{2}y+y=0. \end{aligned}$$
(10)

In order to investigate the hidden aspects of the dynamics of this system, we write down the fractional counterpart of the classical Lagrangian given in Eq. (8) as

$$\begin{aligned} L^{F}&= \frac{1}{2}\left( 1+\in y^{2}\right) \left( {}_{a}D_{t}^{\alpha } x\right) ^{2}+\frac{1}{2}\left( {}_{a}D_{t}^{\alpha } y\right) ^{2}\nonumber \\&-\frac{1}{2}\left( p^{2}x^{2}+y^{2}\right) . \end{aligned}$$
(11)

Thus, the corresponding fractional Euler-Lagrange equations read as:

$$\begin{aligned} \frac{\partial L}{\partial q}+{}_{t}D_{b}^{\alpha } \frac{\partial L}{\partial _{a}D_{t}^{\alpha } q}+{}_{a}D_{t}^{\beta } \frac{\partial L}{\partial _{t}D_{b}^{\beta } q}=0, \end{aligned}$$
(12)

where \(q\) is a generalized coordinate.

Applying Eq. (12) to our fractional Lagrangian equation for both \(x\) and \(y\), respectively, we conclude

$$\begin{aligned} -p^{2}x+{}_tD_b^\alpha \left[ \left( 1+\in y^{2}\right) \left( {}_aD_t^\alpha x\right) \right] =0 \end{aligned}$$
(13)

and

$$\begin{aligned} \in y\left( {}_aD_{t}^{\alpha } x\right) ^{2}-y+{}_tD_{b}^{\alpha } {}_aD_{t}^{\alpha } y=0 \end{aligned}$$
(14)

We notice that as \(\alpha \rightarrow 1\), the above two fractional Euler-Lagrange equations reduced to the classical Euler-Lagrange equations of motion.

In the following, we construct the fractional Hamiltonian as it was introduced in [35]. Since our Lagrangian depends on two generalized coordinates, we introduce the following four generalized momenta:

$$\begin{aligned} P_{\alpha ,x}&= \frac{\partial L}{\partial {}_aD_{t}^{\alpha } x}=\left( 1+\in y^{2}\right) \left( {}_aD_{t}^{\alpha } x\right) , \nonumber \\ P_{\alpha ,y}&= \frac{\partial L}{\partial {}_aD_{t}^{\alpha } y}={}_{a}D_{t}^{\alpha } y. \end{aligned}$$
(15)

So, the fractional Hamiltonian function reads:

$$\begin{aligned} H&= P_{\alpha ,x}\, {}_{a}D_{t}^{\alpha } x+P_{\alpha ,y}\, {}_{a}D_{t}^{\alpha } y-L \nonumber \\&= \frac{1}{2}\frac{\left( P_{\alpha ,x} \right) ^{2}}{1+\in y^{2}}+\frac{1}{2}\left( P_{\alpha ,y} \right) ^{2}+\frac{1}{2}\left( p^{2}x^{2}+y^{2}\right) .\nonumber \\ \end{aligned}$$
(16)

As a result, the Hamilton’s equations of motion are obtained as:

$$\begin{aligned} \frac{P_{\alpha ,x} }{1+\in y^{2}}={}_{a}D_{t}^{\alpha } x, \end{aligned}$$

therefore

$$\begin{aligned} P_{\alpha ,y} ={}_{a}D_{t}^{\alpha } y. \end{aligned}$$
(17)

By using

$$\begin{aligned} \frac{\partial H}{\partial x}={}_{t}D_{b}^{\alpha } P_{\alpha ,x} \end{aligned}$$
(18)

we recovered (13).

Using the fact that \(\frac{\partial H}{\partial y}={}_{t}D_{b}^{\alpha } P_{\alpha ,y}\), we get

$$\begin{aligned} y-\frac{\in y}{\left( 1+\in y^{2}\right) ^{2}}\left( P_{\alpha ,x} \right) ^{2}={}_{t}D_{b}^{\alpha } P_{\alpha ,y} \end{aligned}$$
(19)

which reduces to the equation (14).

Again as \(\alpha ,\beta \rightarrow 1\), the fractional Hamilton’s equations reduced to the classical Hamilton’s equations of motion.

3 Numerical method and the simulation results

Our aim, now, is to solve the above fractional Euler-Lagrange’s equations numerically. We recall that Riemann–Liouville fractional derivative is equivalent to the Grünwald–Letnikov derivative for a wide class of the functions if the following condition is satisfied \(f\in C^{(n)}[a,b]\),

$$\begin{aligned} f^{(k)}(a)=0,\,\,(k=0,\ldots ,n-1) \hbox { for } (n-1\!<\!\alpha \!<\!n). \end{aligned}$$

For the numerical solution of the fractional- order Eqs. (13) and (14), we use the decomposition to its canonical form with the substitutions of \(x\equiv x_1\) and \(y\equiv x_2\). We used a set four initial conditions: \(x_1 (0)\equiv x(0)\), \(x_2 (0)\equiv y(0)\) and \(x_3 (0)\equiv \,{}_{a}D_{t}^{\alpha } x(0)\), \(x_4 (0)\equiv \,{}_{a}D_{t}^{\alpha } y(0)\). Instead of left and right side Riemann–Liouville fractional derivatives (1) and (2) in the set of Eqs. (13) and (14), the left and right Grünwald-Letnikov derivatives can be used. This is due to the fact that the left and right Grünwald-Letnikov derivatives are equivalent to the left and right side Riemann–Liouville fractional derivatives for a wide class of functions [10]. Considering this approach, the time interval \([a, b]\) is discretized by \((N + 1)\) equal grid points, where \(N=(b-a)/h\). Thus, we obtain the following formula for discrete equivalents of left and right fractional derivatives:

$$\begin{aligned} {}_{a}D_{t}^{\alpha } x_k&= h^{-\alpha }\sum _{i=0}^k {c_i x_{k-i} ,} \,\,k=0,\ldots ,N, \end{aligned}$$
(20)
$$\begin{aligned} {}_{t}D_{b}^{\alpha } x_k&= h^{-\alpha }\sum _{i=0}^{N-k} {c_i x_{k+i} ,} \,\,k=N,\ldots ,0, \end{aligned}$$
(21)

respectively, where \(x_k \approx x(t_k )\) and \(t_k =kh\). The binomial coefficients \(c_i, i= 1, 2, 3,{\ldots }\) can be calculated according to relation

$$\begin{aligned} c_i =\left( {1-\frac{1+\alpha }{i}} \right) c_{i-1} \end{aligned}$$
(22)

for \(c_0 =1\). Then, the general numerical solution of the fractional nonlinear differential equation with left side derivative (initial value problem) in the form [21–25] becomes

$$\begin{aligned} {}_{a}D_{t}^{\alpha } x(t)=f(x(t),t). \end{aligned}$$
(23)

Under the initial conditions: \(x^{(k)}(0)=x_0 ^{(k)}\), \(k = 0, 1, {\ldots }, n-1\), where \(n-1 < \alpha < n\), it can be expressed for discrete time \(t_k =kh\) in the following form

$$\begin{aligned} x(t_k)=f(x(t_k),t_k)h^{\alpha }-\sum _{i=m}^k {c_i x(t_{k-i})} , \end{aligned}$$
(24)

where \(m=0\) if we do not use a short memory principle, otherwise, it can be related to the memory length. Similarly, it can be derived as a solution for an equation with right side fractional derivative.

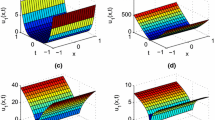
The simulation results are given below. In Fig. 2, \(x\hbox {(t)}\) and \(y\hbox {(t)}\) are plotted for \(\alpha \,=1,\,0.95,\,0.9,\,0.85,\,0.8,0.7,\,0.5\) with \(p = 1, \in \,=\,0.5\) and time 1 second. The Fig. 3 depicts the graphs of \(x(t)\) and \(y(t)\) for \(\alpha =1,0.95,0.9,0.85,0.8, 0.7\) corresponding to \(p = 2, \in \,= 0.2\) and the time 1 s. In the Fig. 4, we show the graphs of \(x(t)\) and \(y(t)\) for \(\alpha =1,0.95,0.9,0.85,0.8, 0.7\) and \(p = 3, \in \,= 0.5\) corresponding to the time of one second. Initial conditions in all simulation experiments were \(x(0)=1\) and \(y(0)=1\).

Fig. 2
figure 2

Simulation result for various order \(\alpha , p = 1,\,\in \,=\,0.5\) and time 1 s

Full size image
Fig. 3
figure 3

Simulation result for various order \(\alpha , p = 2, \in \,=\,0.1\) and time 1 s

Full size image
Fig. 4
figure 4

Simulation result for various order \(\alpha , p = 3, \in \,=\,0.5\) and time 1 s

Full size image

The behaviors of the numerical solution of fractional Euler-Lagrange equations are different from various values of \(\alpha \) and the other parameters \(p\) and \(\in \). One of the most unexpected behavior is the one shown in Fig. 4. As we can see, we may observe the oscillations for variable \(y(t)\).

When we take into account the fractional order of the fractional differential equation, we have one more degree of freedom. In this way, it is possible to have more flexible models and it gives an opportunity to better adjust the dynamical properties of the real system. On the other hand, when we consider fractional order derivative in the model, we deal with the memory of the model because of kernel type in the fractional order derivative and integral.

4 Conclusion

Numerical analysis of fractional differential equations is an efficient tool, especially in real world problem. In this paper, we investigated the numerical solutions of the Euler-Lagrange equations of a mechanical system called thin elastica. The simulation result for various order of \(\alpha , p, \in \) and time one second is shown in Figs. 2, 3 and 4. It is clear from the figures that the behaviors of the fractional Euler-Lagrange equation strongly depend on the order of the fractional derivative. For each graph, we provided the classical solution of the equations \((\alpha = 1)\) in addition to some different cases for \(\alpha \) less than one.

Finally, it is clear from the figures that the numerical solution to the fractional Euler-Lagrange equations is more suitable. It enables us to obtain the classical case (i.e., \(\alpha = 1\)) in addition to fractional order of \(\alpha \). In this way, we demonstrate the main advantages of the fractional order derivative in the model. Besides, we have calculated the corresponding fractional Hamilton equations.