Stepanov-like weighted pseudo almost automorphic solutions to fractional order abstract integro-differential equations

Abstract

In this article, we study the concept of Stepanov-like weighted pseudo almost automorphic solutions to fractional order abstract integro-differential equations. We establish the results with Lipschitz condition and without Lipschitz condition on the forcing term. An interesting example is presented to illustrate the main findings. The results proven are new and complement the existing ones.

1 Introduction

This work is mainly concerned with the existence of Stepanov-like weighted pseudo almost automorphic mild solutions to the following fractional order integro-differential equation

$$\begin{array}{@{}rcl@{}} D_{t}^{\alpha}x(t)\!\!&=&\!\!Ax(t)+D_{t}^{\alpha-1}f(t,x(t),Kx(t)), \\ Kx(t)\!\!&=&\!\!{\int}_{-\infty}^{t}k(t-s)h(s,x(s))\mathrm{d}s, \quad t\in R, \end{array} $$

(1.1)

where 1 < α < 2 and A : D(A)$\subset$ X →X is a linear densely defined operator of sectorial type on a complex Banach space (X,∥.∥). Moreover, the function k satisfies $|k(t)|\le c_{k}\mathrm {e}^{-bt}$ for t≥0 and c _k ,b are positive constants, the function $f:R\times X\times X\rightarrow X$ and $h:R\times X\rightarrow X$ are Stepanov-like weighted pseudo almost automorphic in t for each x,y∈X, satisfying suitable conditions. The fractional derivative $D_{t}^{\alpha }$ is to be understood in the Caputo’s sense. It is well known that integro-differential equations model many situations arising from science and engineering. A particularly rich source is electrical circuit analysis. The activity of interacting inhibitory and excitatory neurons can be described by a system of integro-differential equations. Fractional integro-differential equations can model if the system dynamics is slower and faster. If the ordinary differential system can not explain the dynamics of a process, then fractional order system may explain the dynamics. The problem considered here can be thought of as abstract version of very general form of fractional oscillation/relaxation partial differential equation.

Recent years have witnessed tremendous work flow in the field of fractional differential equations. Many works have been done to prove existence, uniqueness of the solutions of various fractional differential equation of various order. At the same time people have shown applications of fractional calculus in various fields like in the field of viscosity, control, anomalous diffusion etc. It has been claimed in recent investigations that many physical systems can be represented more accurately through fractional derivative formulation [31]. A wonderful book on fractional differential equation is written by Podlubny [36]. The existence and uniqueness of solutions of such kind of differential equations have been shown by many authors, we refer to [1; 2; 4; 10; 13; 14; 24; 25; 30] and references therein. A very natural question in the field of differential equations is to see whether the solution follows the same pattern of forcing term or not. Same question can be asked in the case of fractional differential equations and many people have already worked in this direction ([5; 15] and references therein). In [5], Agarwal et al. have shown the existence of weighted pseudo almost periodic solutions of semilinear fractional differential equations.

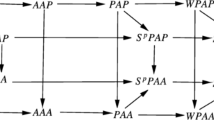
In order to describe the concept of Stepanov-like weighted pseudo almost automorphic, we need to go back to Bohr’s era, who introduced the concept of almost periodic function. Since then there are many important generalizations of this function, the generalization includes pseudo almost periodic functions [42]. These functions are further generalized to weighted pseudo almost periodic function by Diagana [16]. Another important direction of generalization is almost automorphic function, which is introduced by Bochner [8] in the literature. Pseudo almost automorphic functions are natural generalization of almost automorphic functions and introduced by Liang et al. [29]. These functions are further generalized by Blot et al. [6] and was named weighted pseudo almost automorphic. The authors in [6] have proved very important properties of these functions including composition theorem and completeness property. The study of weighted pseudo almost automorphic solutions of various kind of differential equations are very new and an attractive area of research. For more details on theory and a‘pplications of these functions, we refer to [6] and references therein. Stepanov-like pseudo almost periodicity is introduced and studied by Diagana [17; 18; 21], which is a natural generalization of pseudo almost periodicity. Further, Stepanov-like almost automorphy has been introduced by N’Guerekata and Pankov [34]. Diagana and N’Guerekata [22] have shown the existence of almost automorphic solution under the condition that the forcing term is a Stepanov almost automorphic function satisfying Lipschitz condition. Stepanov almost automorphic sequence is studied by Abbas et al. [3]. A very good paper on Stepanov version of Favard theory is discussed by Tarallo [38]. The concept of Stepanov weighted pseudo almost automorphic functions are introduced by Zhang et al. [44]. It is called Stepanov because it uses the norm proposed by Stepanov to define an almost periodic function, which is named as Stepanov almost periodic [37]. In this work, we strengthen many results of Stepanov almost automorphic function. The mathematical topic of interests are the nature of the solutions, stability, periodicity, almost periodicity etc. Stepanov weighted pseudo almost automorphic functions are more general than almost periodic, automorphic functions, and hence it covers wider class of functions. If the observed output of any given system is not showing periodic, almost periodic or almost automorphic behaviour, then one could check whether its behaviour is Stepanov weighted pseudo almost automorphic or not.

The paper is structured as follows. In §2, we give basic definitions and results which are necessary for smooth reading of this paper. Section 3 is devoted to the existence of Stepanov-like weighted pseudo almost automorphic solutions. In §4, we give an example to illustrate our analytical findings.

2 Preliminaries and basic results

In this section, we introduce important notations, definitions, lemmas and preliminary facts which are used throughout this work.

Let (X,∥⋅∥) and (Y,∥⋅∥ _Y ) be two complex Banach spaces. The notation C(R,X), (respectively C(R×Y,X)) denote the collection of all continuous functions from R to X (respectively from R×Y to X). Let B C(R,X) (respectively B C(R×Y,X)) denote the Banach space of bounded continuous functions from R to X (respectively from R×Y to X) with the supremum norm.

The notation L(X,Y) stands for the Banach space of bounded linear operators from X into Y endowed with the operator topology and we abbreviate it as L(X) whenever X=Y. The space L ^p(R,X) denotes the space of all equivalence (with respect to the equality almost everywhere on R) classes of measurable functions $f:R\rightarrow X$ such that ∥f∥∈L ^p(R,R). $L_{loc}^{p}(R,X)$ denotes the space of all equivalence classes of measurable functions $f:R\rightarrow X$ such that the restriction of f to every bounded subinterval of R is in L ^p(R,X).

The Riemann–Liouville fractional integral of order α>0 is defined by

$$I^{\alpha}f(t)=\frac{1}{\Gamma(\alpha)}{{\int}_{0}^{t}}(t-s)^{\alpha-1}f(s)\mathrm{d}s, $$

also, the Caputo fractional derivative of function f of order α>0 is defined by

$$D_{t}^{\alpha}f(t)=\frac{1}{\Gamma(n-\alpha)}{{\int}_{0}^{t}}(t-s)^{n-\alpha-1}\frac{d^{n} f(s)}{\mathrm{d}s^{n}}\mathrm{d}s, $$

where Γ(α) is the gamma function.

DEFINITION 2.1

[7]A function f∈C(R,X) is said to be almost automorphic in Bochner’s sense if for every sequence of real numbers $(s_{n})_{n\in \mathcal {N}}$, there exists a subsequence $(\tau _{n})_{n\in \mathcal {N}}$ such that

$$g(t)=\lim_{n\rightarrow\infty}f(t+\tau_{n}) $$

is well-defined for each t∈R and

$$\lim_{n\rightarrow\infty}g(t-\tau_{n})=f(t) $$

for each t∈R.

Almost automorphic functions (denoted by A A(R,X)) (respectively A A(R×Y,X)) constitute a Banach space when it is endowed with the sup norm. They naturally generalize the concept of (Bochner) almost periodic functions. A typical example [22; 33] of almost automorphic function but not almost periodic is given as

$$\phi(t)=\cos\left(\frac{1}{2+\sin\sqrt{2}t+\sin t}\right),\quad t\in R. $$

Lemma 2.1 [32]. If f,f ₁,f ₂∈A A(R,X),then

(i) f ₁+f ₂∈A A(R,X),

(ii) λ f∈A A(R,X)for every scalar λ,

(iii) f _α ∈A A(R,X)where $f_{\alpha }:R\rightarrow X$ is defined by f _α (⋅)=f(⋅+α), α∈R,

(iv) the range $\mathcal {R}_{f}=\{f(t):t\in R\}$ is relatively compact in X,thus f is bounded in norm ,

(v) if $f_{n}\rightarrow f$ uniformly on R,where each f _n ∈A A(R,X),then f∈A A(R,X)too.

DEFINITION 2.2

[41] A function f∈C(R,X) (respectively C(R×Y,X)) is called pseudo almost automorphic if it can be decomposed as f=g+ϕ, where g∈A A(R,X) (respectively A A(R×Y,X)) and ϕ∈B C(R,X) with

$$\lim_{T\rightarrow\infty}\frac{1}{2T}{\int}_{-T}^{T}\|\phi(s)\|\mathrm{d}s=0 $$

(respectively ϕ∈B C(R×Y,X)) with

$$\lim_{T\rightarrow\infty}\frac{1}{2T}{\int}_{-T}^{T}\|\phi(s,u)\|\mathrm{d}s=0 $$

uniformly for u in any bounded subset of Y).

Denote by P A A(R,X) (respectively P A A(R×Y,X)) the collection of such functions and (P A A(R,X),∥⋅∥ _{P A A} ) (respectively (P A A(R×Y,X),∥⋅∥ _{P A A} )) is a Banach space when endowed with the sup norm. It is not difficult to show that the function defined by

$$f_{\alpha,\beta,\gamma}(t)=\cos\left(\frac{1}{3-\sin t-2\sin \beta t}\right)+\frac{\mathrm{e}^{-|t|^{\gamma}}}{(1+|t|)^{\alpha}}, \quad t\in R $$

is a pseudo almost automorphic function, where $\alpha \in (1,\infty ),\beta \in R/\mathcal {Q}$ and $\gamma \in [0,\infty )$.

Let U be the set of all functions $\rho :R\rightarrow (0,\infty )$ which are positive and locally integrable over R. For a given T>0 and each ρ∈U, set

$$\mu(T,\rho)={\int}_{-T}^{T}\rho(t)\mathrm{d}t. $$

Define

$$\begin{array}{@{}rcl@{}} U_{\infty}\!\!&=&\!\!\left\{\rho\in U:\lim_{T\rightarrow \infty}\mu(T,\rho)=\infty\right\}, \\U_{B}\!\!&=&\!\!\left\{\rho\in U_{\infty}:\rho \, \text {is bounded and} \inf_{x\in R}\rho(x)>0\right\}. \end{array} $$

It is clear that $U_{B}\subset U_{\infty }\subset U$.

DEFINITION 2.3

Let $\rho _{1},\rho _{2}\in U_{\infty }$, ρ ₁ is said to be equivalent to ρ ₂ (i.e., ρ ₁∼ρ ₂) if $\frac {\rho _{1}}{\rho _{2}}\in U_{B}$.

It is trivial to show that ‘ ∼’ is a binary equivalence relation on $U_{\infty }$. The equivalence class of a given weight $\rho \in U_{\infty }$ is denoted by $cl(\rho )=\{\mathbb {Q}\in U_{\infty }:\rho \sim \mathbb {Q}\}$. It is clear that $U_{\infty }=\cup _{\rho \in U_{\infty }}cl(\rho )$.

For $\rho _{1}\in U_{\infty }$, define the weighted ergodic space

$$PAA_{0}(R,X,\rho_{1})\,=\,\left\{\!f\!\in\! BC(R,\!X)\!:\!\lim_{T\rightarrow\infty}\!\frac{1}{\mu(T,\rho_{1})}\!{\int}_{-T}^{T}\!\rho_{1}(s)\|f(s)\|\mathrm{d}s\,=\,0\right\}. $$

Particularly, for $\rho _{1},\rho _{2}\in U_{\infty }$, define ([20]),

$$PAA_{0}(R,X,\rho_{1},\rho_{2})=\left\{f\in BC(R,X):\lim_{T\rightarrow\infty}\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(s)\|f(s)\|\mathrm{d}s=0\right\}, $$

clearly, when ρ ₁ ∼ ρ ₂, this space coincides with the weighted ergodic space PAA ₀(R, X, ρ ₁), that is, PAA ₀(R, X, r h o ₁, ρ ₂) =PAA ₀(R, X, ρ ₂, ρ ₁) =PAA ₀(R, X, ρ ₁) =PAA ₀(R, X, ρ ₂). This fact suggests that the weighted ergodic space PAA ₀(R, X, ρ ₁, ρ ₂) are most interesting when ρ ₁ and ρ ₂ are not necessarily equivalent. So the space PAA ₀(R, X, ρ ₁, ρ ₂) are general and richer than PAA ₀(R, X, ρ ₁) and gives rise to an enlarged space of weighted pseudo almost automorphic functions.

Similarly, define

$$\begin{array}{@{}rcl@{}} &&{\kern-5.1pc}PAA_{0}(R\times X,X,\rho_{1},\rho_{2}) \\ &&{\kern-5.2pc}=\left\{\!f\in BC(R \!\times \! X,X):\lim_{T\rightarrow\infty}\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T} \rho_{2}(s)\|f(s,u)\|\mathrm{d}s\,=\,0 ~\text {uniformly\! in}~ u\in X\vphantom{\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}}\right\} \!\!. \end{array} $$

DEFINITION 2.4

Let $\rho _{1},\rho _{2}\in U_{\infty }$. A function f∈C(R,X) (respectively C(R×Y,X)) is called weighted pseudo almost automorphic if it can be decomposed as f=g+ϕ, where g∈A A(R,X) (respectively A A(R×Y,X)) and ϕ∈P A A ₀(R,X,ρ ₁,ρ ₂) (respectively P A A ₀(R×Y,X,ρ ₁,ρ ₂)). Denote by W P A A(R,X,ρ ₁,ρ ₂) (respectively W P A A(R×Y,X,ρ ₁,ρ ₂)) the set of such functions.

Let p ∈ [1, $\infty$). The space B S ^p(R,X) of all Stepanov bounded functions, with the exponent p, consists of all measurable functions f : R →X such that f ^b ∈L $^{\infty }$(R, L ^p ([0, 1], X)), where f ^b is the Bochner transform of f = defined by f ^b(t, s) =f(t + s), t ∈R, s ∈ [0, 1]. B S ^p(R,X) is a Banach space with the norm

$$\|f\|_{S^{p}}=\|f^{b}\|_{L^{\infty}(R,L^{p})}=\sup_{t\in R}\left({\int}_{t}^{t+1}\|f(\tau)\|^{p}\mathrm{d}\tau\right)^{\frac{1}{p}}. $$

It is obvious that $L^{p}(R,X)\subset BS^{p}(R,X)\subset L_{loc}^{p}(R,X)$ and $BS^{p}(R,X)\subset BS^{q}(R,X)$ for p≥q≥1.

DEFINITION 2.5

[19]The space S ^p AA(R, X) of Stepanov-like almost automorphic functions (or S ^p-almost automorphic functions) consists of all f∈B S ^p(R,X) such that f ^b∈A A(R,L ^p([0,1],X)).

In other words, a function $f\in L_{loc}^{p}(R,X)$ is said to be Stepanov-like almost automorphic if its Bochner transform $f^{b}: R\rightarrow L^{p}([0,1],X)$ is almost automorphic in the sense that for every sequence of real numbers $(s_{n})_{n\in \mathcal {N}}$, there exist a subsequence $(\tau _{n})_{n\in \mathcal {N}}$ and a function $g\in L_{loc}^{p}(R,X)$ such that

$$\begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\left({\int}_{t}^{t+1}\|f(s+\tau_{n})-g(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}=0,\\ \lim_{n\rightarrow\infty}\left({\int}_{t}^{t+1}\|g(s-\tau_{n})-f(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}=0, \end{array} $$

pointwise on R. The collection of all such functions is denoted by S ^p A A(R,X).

From [9], we know that if $1\le p<q<\infty$ and $f\in L_{loc}^{q}(R,X)$ is S ^q-almost automorphic, then f is S ^p-almost automorphic. Also, if f∈A A(R,X), then f is S ^p-almost automorphic for any $1\le p<\infty$, in other words, $AA(R,X)\subset S^{p}AA(R,X)$. An interesting example of f such that f∈S ^p A A(R,X) for p≥1 but f∉A A(R,X) is given in [33].

DEFINITION 2.6

[19]A function $f:R\times Y\rightarrow X, (t,u)\rightarrow f(t,u)$ with $f(\cdot ,u)\in L_{loc}^{p}(R,Y)$ for each u∈Y is said to be S ^p-almost automorphic in t∈R uniformly for u∈Y if for every sequence of real numbers $(s_{n})_{n\in \mathcal {N}}$, there exist a subsequence $(\tau _{n})_{n\in \mathcal {N}}$ and a function $g:R\times Y\rightarrow X$ with $g(\cdot ,u)\in L_{loc}^{p}(R,Y)$ such that

$$\lim_{n\rightarrow\infty}\left({{\int}_{0}^{1}}\|f(t+s+\tau_{n},u)-g(t+s,u)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}=0 $$

and

$$\lim_{n\rightarrow\infty}\left({{\int}_{0}^{1}}\|g(t+s-\tau_{n},u)-f(t+s,u)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}=0, $$

for each t∈R and for each u∈Y. We denote by S ^p A A(R×Y,X) the set of all such functions.

DEFINITION 2.7

[19]A function f∈B S ^p(R,X) is called Stepnaov-like pseudo almost automorphic (or S ^p-pseudo almost automorphic) if it can be decomposed as f=g+ϕ, where g ^b∈A A(R,L ^p([0,1],X)) and ϕ ^b∈P A A ₀(R,L ^p([0,1],X)). Denote by S ^p P A A(R,X) the collection of such functions.

Clearly, a function $f\in L_{loc}^{p}(R,X)$ is said to be S ^p-pseudo almost automorphic if its Bochner transform $f^{b}: R\rightarrow L^{p}([0,1],X)$ is pseudo almost automorphic in the sense that there exist two functions $g,\phi :R\rightarrow X$ such that f=g+ϕ, where g ^b∈A A(R,L ^p([0,1],X)) and ϕ ^b∈P A A ₀(R,L ^p([0,1],X)).

From [19], we know that the space S ^p P A A(R,X) is a Banach space equipped with the norm $\|\cdot \|_{S^{p}}$. If f∈P A A(R,X), then $f\in S^{p}PAA(R,X)$ for each $1\le p<\infty$, in other words, $PAA(R,X)\subset S^{p}PAA(R,X)$. One can find in [19] the example of the function $f\in S^{p}PAA(R,X)$ for p≥1, but f∉P A A(R,X).

DEFINITION 2.8

[19]A function $f:R\times Y\rightarrow X, (t,u)\rightarrow f(t,u)$ with $f(\cdot ,u)\in L_{loc}^{p}(R,X)$ for each u∈Y is said to be S ^p-pseudo almost automorphic if it can be decomposed as f=g+ϕ, where g ^b∈A A(R×Y,L ^p([0,1],X)) and ϕ ^b∈P A A ₀(R×Y,L ^p([0,1],X)). Denote by S ^p P A A(R×Y,X) the collection of such functions.

DEFINITION 2.9

Let $\rho _{1},\rho _{2}\in U_{\infty }$. A function f∈B S ^p(R,X) is said to be weighted Stepanov-like pseudo almost automorphic (or weighted S ^p-pseudo almost automorphic) if it can be decomposed as f=g+ϕ, where g ^b∈A A(R,L ^p([0,1],X)) and ϕ ^b∈P A A ₀(R,L ^p([0,1],X),ρ ₁,ρ ₂). Denote by S ^p W P A A(R,X,ρ ₁,ρ ₂) the collection of such functions.

In other words, a function $f\in L_{loc}^{p}(R,X)$ is said to be weighted S ^p-pseudo almost automorphic if its Bochner transform $f^{b}: R\rightarrow L^{p}([0,1],X)$ is weighted pseudo almost automorphic in the sense that there exist two functions $g,\phi :R\rightarrow X$ such that f=g+ϕ, where g ^b∈A A(R,L ^p([0,1],X)) and ϕ ^b∈P A A ₀(R,L ^p([0,1],X),ρ ₁,ρ ₂), i.e.,

$$\lim_{T\rightarrow\infty}\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\left({\int}_{t}^{t+1}\|\phi(\sigma)\|^{p}\mathrm{d}\sigma\right)^{\frac{1}{p}}=0. $$

DEFINITION 2.10

Let $\rho _{1},\rho _{2}\in U_{\infty }$. A function $f:R\times Y\rightarrow X,(t,u)\rightarrow f(t,u)$ with $f(\cdot ,u)\in L_{loc}^{p}(R,X)$ for each u∈Y is said to be weighted S ^p-pseudo almost automorphic if it can be decomposed as f=g+ϕ, where g ^b∈A A(R×Y,L ^p([0,1],X)) and ϕ ^b∈P A A ₀(R×Y,L ^p([0,1],X),ρ ₁,ρ ₂). The space of such functions is denoted by S ^p W P A A(R×Y,X,ρ ₁,ρ ₂).

Further, let $V_{\infty }$ be the collection of continuous weights $\rho _{1},\rho _{2}\in U_{\infty }$ such that $\lim \sup _{t\rightarrow \infty }\frac {\rho _{2}(t+\tau )}{\rho _{2}(t)}<\infty$ and $\lim \sup _{T\rightarrow \infty }\frac {\mu (T,\rho _{2})}{\mu (T,\rho _{1})}<\infty$ for any τ∈R.

Example 1.

The function defined by $f(t)=\text {signum}(\cos 2\pi \theta t)+e^{-|t|}$ for 𝜃 irrational with the weight functions ρ ₁ (t)=1+t ² ,ρ ₂ (t)=1 is weighted S ^p -pseudo almost automorphic. Also the function f(t) is S ^p -pseudo almost automorphic. Moreover the function $\text {signum}(\cos 2\pi \theta t)$ is S ^p-almost automorphic. The proof for discrete version is given in Abbas et al. [3] , the continuous version follows similarly.

Lemma 2.2.

Let $\rho _{1},\rho _{2}\in V_{\infty },f=g+\phi \in S^{p}WPAA(R,X,\rho _{1},\rho _{2})$ with g ^b ∈AA(R,L ^p ([0,1],X)), ϕ ^b ∈PAA ₀ (R,L ^p ([0,1],X),ρ ₁ ,ρ ₂ ) then $\{g(t+\cdot ):t\in R\}\subset \overline {\{f(t+\cdot ):t\in R\}}$ in L ^p ([0,1],X).

Proof.

We prove this lemma by the contradiction arguments. If the claim is not true, then there exist a t ₀∈R and an 𝜖>0 such that

$$\|g(t_{0}+\cdot)-f(t+\cdot)\|_{p}\ge 2\epsilon, \quad t\in R, $$

where ∥⋅∥ _p denotes the norm of L ^p([0,1],X). Since g ^b∈A A(R,L ^p([0,1],X)), fix t ₀∈R and 𝜖>0 and set B _𝜖 ={τ∈R:∥g(t ₀+τ+⋅)−g(t ₀+⋅)∥ _p <𝜖}, by Lemma 2.1 of [41], there exist s ₁,…,s _m ∈R such that $\cup _{i=1}^{m}(s_{i}+B_{\epsilon })=R$. Let $\hat {s_{i}}=s_{i}-t_{0}(1\le i\le m)$ and $\eta =\max _{1\le i\le m}|\hat {s_{i}}|$. For T∈R with |T|>η and $B_{\epsilon ,T}^{(i)}=[-T+\eta -\hat {s_{i}},T-\eta -\hat {s_{i}}]\cap (t_{0}+B_{\epsilon }),1\le i\le m$, one has $\cup _{i=1}^{m}\left (\hat {s_{i}}+B_{\epsilon ,T}^{(i)}\right )=[-T+\eta ,T-\eta ]$.

Using the fact that $B_{\epsilon ,T}^{(i)}\subset [-T,T]\cap (t_{0}+B_{\epsilon }), i=1,...,m$, we have

$$\begin{array}{@{}rcl@{}} \mu(T-\eta,\rho_{2})\!\!&=&\!\!{\int}_{-T+\eta}^{T-\eta}\rho_{2}(t)\\ &\le&\!\! {\sum}_{i=1}^{m}{\int}_{\hat{s_{i}}+B_{\epsilon,T}^{(i)}}\rho_{2}(t)\mathrm{d}t\\ &\le&\!\! {\sum}_{i=1}^{m}{\int}_{B_{\epsilon,T}^{(i)}}\rho_{2}(t+\hat{s_{i}})\mathrm{d}t\\ &\le&\!\! {\sum}_{i=1}^{m}a_{i}{\int}_{B_{\epsilon,T}^{(i)}}\rho_{2}(t)\mathrm{d}t\\ &\le&\!\!\max_{1\le i\le m}\{a_{i}\}{\sum}_{i=1}^{m}{\int}_{[-T,T]\cap(t_{0}+B_{\epsilon})}\rho_{2}(t)\mathrm{d}t\\ &=&\!\!\max_{1\le i\le m}\{a_{i}\}\cdot m\cdot{\int}_{[-T,T]\cap(t_{0}+B_{\epsilon})}\rho_{2}(t)\mathrm{d}t, \end{array} $$

where $a_{i}=\lim \sup _{t\rightarrow \infty }\frac {\rho _{2}(t+\hat {s_{i}})}{\rho _{2}(t)}<\infty$.

On the other hand, by the Minkowski inequality, for any t∈t ₀+B _𝜖 , one has

$$\begin{array}{@{}rcl@{}} \|\phi(t+\cdot)\|_{p}&=&\|f(t+\cdot)-g(t+\cdot)\|_{p}\\ &\ge& \|g(t_{0}+\cdot)-f(t+\cdot)\|_{p}-\|g(t+\cdot)-g(t_{0}+\cdot)\|_{p}\\ &>&\epsilon. \end{array} $$

Then

$$\begin{array}{@{}rcl@{}} && \frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\left({\int}_{t}^{t+1}\|\phi(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\mathrm{d}s \\ &&=\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\|\phi(t+\cdot)\|_{p}\mathrm{d}t\\ &&\ge \frac{1}{\mu(T,\rho_{1})}{\int}_{[-T,T]\cap(t_{0}+B_{\epsilon})}\rho_{2}(t)\|\phi(t+\cdot)\|_{p}\mathrm{d}t\\ &&>\frac{\epsilon}{\mu(T,\rho_{1})}{\int}_{[-T,T]\cap(t_{0}+B_{\epsilon})}\rho_{2}(t)\mathrm{d}t\\ &&\ge \frac{\epsilon}{\mu(T,\rho_{1})}\cdot\frac{\mu(T-\eta,\rho_{2})}{m\cdot\max_{1\le i\le m}\{a_{i}\}}\\ &&\quad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\rightarrow \frac{\epsilon b}{m\cdot\max_{1\le i\le m}\{a_{i}\}} \quad \text{as}\!\! \quad T\rightarrow\infty, \end{array} $$

□

where $b=\lim \sup _{T\rightarrow \infty }\frac {\mu (T-\eta ,\rho _{2})}{\mu (T,\rho _{1})}<\infty$ since $\rho _{1},\rho _{2}\in V_{\infty }$. This is a contradiction, since ϕ ^b∈P A A ₀(R,L ^p([0,1],X),ρ ₁,ρ ₂). Hence the claim is true.

Theorem 2.1.

For any given $\rho _{1},\rho _{2}\in V_{\infty }$ , the space S ^p WPAA(R,X,ρ ₁ ,ρ ₂ ) is a Banach space endowed with the norm $\|\cdot \|_{S^{p}}$.

Proof.

It suffices to prove that S ^p WPAA(R, X, ρ ₁, ρ ₂) is a closed subspace of B S ^p(R, X). Let f _n =g _n + ϕ _n ∈S ^p WPAA(R, X, ρ ₁, ρ ₂) with ${g_{n}^{b}}$ ∈AA(R, L ^p([0, 1], X)) and ${\phi _{n}^{b}}\in PAA_{0}(R,L^{p}([0,1],X),\rho _{1},\rho _{2})$ such that $\|f_{n}-f\|_{S^{p}}\rightarrow 0$ as $n\rightarrow \infty$. Since f _n =g _n +ϕ _n , by Lemma 2.2, $\{g_{n}(t+\cdot ):t\in R\}\subset \overline {\{f_{n}(t+\cdot ):t\in R\}}$ in L ^p([0,1],X) then ∥g _n (t+⋅)∥ _p ≤∥f _n (t+⋅)∥ _p , whence ∥g _n ∥ _{S p} ≤∥f _n ∥ _{S p} for any n∈N. Therefore, there exists a function g∈S ^p A A(R,X) such that $\|g_{n}-g\|_{S^{p}}\rightarrow 0$ as $n\rightarrow \infty$. Whence $f_{n}-g_{n}=\phi _{n}\rightarrow \phi =f-g$ as $n\rightarrow \infty$.

By writing ϕ=(ϕ−ϕ _n )+ϕ _n , we have

$$\begin{array}{@{}rcl@{}} && \frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\left({\int}_{t}^{t+1}\|\phi(\sigma)\|^{p}\mathrm{d}\sigma\right)^{\frac{1}{p}}\mathrm{d}t \\ &&\qquad\le \frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\left({\int}_{t}^{t+1}\|\phi_{n}(\sigma)-\phi(\sigma)\|^{p}\mathrm{d}\sigma\right)^{\frac{1}{p}}\mathrm{d}t\\ && \qquad\quad+\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\left({\int}_{t}^{t+1}\|\phi_{n}(\sigma)\|^{p}\mathrm{d}\sigma\right)^{\frac{1}{p}}\mathrm{d}t\\ &&\qquad\le\|\phi_{n}-\phi\|_{S^{p}}+\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\left({\int}_{t}^{t+1}\|\phi_{n}(\sigma)\|^{p}\mathrm{d}\sigma\right)^{\frac{1}{p}}\mathrm{d}t. \end{array} $$

□

First taking T →$\infty$ and then n →$\infty$ in the above inequality, we obtain ϕ ^b ∈PAA ₀(R, L ^p([0, 1], X), ρ ₁, ρ ₂), which implies, f =g + ϕ ∈S ^p WPAA(R, X, ρ ₁, ρ ₂). Hence S ^p W P A A(R,X,ρ ₁,ρ ₂) is a Banach space.

DEFINITION 2.11

Assume $\rho \in U_{\infty },\tau \in R$, and define ρ ^τ by ρ ^τ(t)=ρ(t+τ) for t∈R. Define U _T (see [43]) by

$$U_{T}=\{\rho\in U_{\infty}:\rho\sim\rho^{\tau}\ \ \text{for each}\ \tau\in R\}. $$

It is easy to see that U _T contains many weights, such as 1,(1+t ²)/(2+t ²),e ^t and 1+|t|ⁿ with n∈N.

Moreover, it is not difficult to observe that (W P A A(R,X,ρ ₁,ρ ₂),∥⋅∥) (respectively (W P A A(R×Y,X,ρ ₁,ρ ₂),∥⋅∥)), ρ ₁,ρ ₂∈U _T is a Banach space endowed with the sup norm.Lemma 2.3 [39]. Let ρ ₁,ρ ₂∈U _T ,then $PAA_{0}(R,X,\rho _{1},\rho _{2})=PAA_{0}(R,X,\rho _{1}^{\tau },\rho _{2}^{\tau })$ for τ∈R.Lemma 2.4 [39]. Let ρ ₁,ρ ₂∈U _T ,ϕ∈P A A ₀(R,X,ρ ₁,ρ ₂), then ϕ(⋅−τ)∈P A A ₀(R,X,ρ ₁,ρ ₂)for τ ∈ R.

Lemma 2.5.

$WPAA(R,X,\rho _{1},\rho _{2})\subset S^{p}WPAA(R,X,\rho _{1},\rho _{2})$ and S ^q WPAA(R,X, $\rho _{1},\rho _{2})\subset S^{p}WPAA(R,X,\rho _{1},\rho _{2})$ for $1\le p<q<\infty , \rho _{1},\rho _{2}\in U_{\infty }$.

The proof is similar to the proof of Propositions 4.1 and 4.2 in [9]. The details are omitted here.

Theorem 2.2.

Assume that $\rho _{1},\rho _{2}\in U_{\infty },f=f_{1}+f_{2}\in S^{p}WPAA(R\times X\times X,X,\rho _{1},\rho _{2})$ with ${f_{1}^{b}}\in AA(R\times X\times X,L^{p}([0,1],X)),{f_{2}^{b}}\in PAA_{0}(R\times X\times X,L^{p}([0,1],X),\rho _{1},\rho _{2})$ and

(i) there exist constants L _f ,L _f1 >0 such that

$$\begin{array}{@{}rcl@{}} &&\|f(t,x_{1},x_{2})-f(t,y_{1},y_{2})\|\le L_{f}\left(\|x_{1}-y_{1}\|_{X}+\|x_{2}-y_{2}\|_{X}\right),\\ &&\, ~~~~~~~~~~~~~t\in R, x_{i},y_{i}\in X, i=1,2 \end{array} $$

and

$$\begin{array}{@{}rcl@{}} &&\|f_{1}(t,x_{1},x_{2})-f_{1}(t,y_{1},y_{2})\|\le L_{f_{1}}\left(\|x_{1}-y_{1}\|_{X}+\|x_{2}-y_{2}\|_{X}\right), \\ &&~~~~~~~~~~~~~~~t\in R, x_{i},y_{i}\in X, i=1,2. \end{array} $$

(ii) h ₁ =α ₁ +β ₁ ,h ₂ =α ₂ +β ₂ ∈S ^p WPAA(R,X,ρ ₁ ,ρ ₂ ) with ${\alpha _{1}^{b}},{\alpha _{2}^{b}}\in AA(R,L^{p}([0,1],X)),$ ${\beta _{1}^{b}},{\beta _{2}^{b}}\in PAA_{0}(R,L^{p}([0,1],X),\rho _{1},\rho _{2})$ and $\mathbb {K}=\overline {\{\alpha _{1}(t):t\in R\}},\mathbb {M}=\overline {\{\alpha _{2}(t):t\in R\}}$ are compact in X.

Then f(⋅,h ₁ (⋅),h ₂ (⋅))∈S ^p WPAA(R,X,ρ ₁ ,ρ ₂ ).

The proof is similar to the proof of Theorem 3.6 in [40] and hence the details are omitted here.

Lemma 2.6 [23]. Assume that f ∈ S ^p A A(R×X,X)with p > 1and satisfies the following:

(i) there exists a non-negative function L∈S ^r AA(R,R) with $r\ge \max \left \{p,\frac {p}{p-1}\right \}$ such that

$$ \|f(t,u)-f(t,v)\|\le L(t)\|u-v\|, \, u,v\in X, \, t\in R, $$

(ii) x∈S ^p A A(R,X)and $\mathbb {K}=\overline {\{x(t):t\in R\}}$ is compact in X.

Then there exists q∈[1,p)such that f(⋅,x(⋅))∈S ^q A A(R,X).

Theorem 2.3.

Assume that $\rho _{1},\rho _{2}\,{\in }\,U_{\infty },p\,{>}\,1,f\,{=}\,f_{1}+f_{2}\,{\in }\,S^{p}WPAA(R\times X\times X,X,\rho _{1},\rho _{2})$ with ${f_{1}^{b}}\in AA(R\times X\times X,L^{p}([0,1],X)),{f_{2}^{b}}\in PAA_{0}(R\times X\times X,L^{p}([0,1],X),\rho _{1},\rho _{2})$ and

(i) there exist nonnegative functions L _f ,L _f1 ∈S ^r AA(R,R) with $r\ge \max \left \{p,\frac {p}{p-1}\right \}$ such that

$$\begin{array}{@{}rcl@{}} &&\|f(t,x_{1},x_{2})-f(t,y_{1},y_{2})\|\le L_{f}(t)\left(\|x_{1}-y_{1}\|_{X}+\|x_{2}-y_{2}\|_{X}\right),\\ &&~~~~~~~~~~~~~~\, t\in R, x_{i},y_{i}\in X,i=1,2, \end{array} $$

and

$$\begin{array}{@{}rcl@{}} &&\|f_{1}(t,x_{1},x_{2})-f_{1}(t,y_{1},y_{2})\|\le L_{f_{1}}(t)\left(\|x_{1}-y_{1}\|_{X}+\|x_{2}-y_{2}\|_{X}\right),\\ && ~~~~~~~~~~~~~~~~~~~~~~~~~~~t\in R, x_{i},y_{i}\in X,i=1,2. \end{array} $$

h ₁ =α ₁ +β ₁ ,h ₂ =α ₂ +β ₂ ∈S ^p WPAA(R,X,ρ ₁ ,ρ ₂ ) with ${\alpha _{1}^{b}},{\alpha _{2}^{b}}\in AA(R,L^{p}([0,1],X)),$ ${\beta _{1}^{b}},{\beta _{2}^{b}}\in PAA_{0}(R,L^{p}([0,1],X),\rho _{1},\rho _{2})$ and $\mathbb {K}=\overline {\{\alpha _{1}(t):t\in R\}},\mathbb {M}=\overline {\{\alpha _{2}(t):t\in R\}}$ are compact in X.

Then there exists q∈[1,p) such that f(⋅,h ₁ (⋅),h ₂ (⋅))∈S ^q WPAA(R,X,ρ ₁ ,ρ ₂ ).

The proof is similar to the proof of Theorem 3.7 in [40] and hence we omit the details.

Theorem 2.4 [44]. Let $\rho _{1},\rho _{2}\in U_{\infty }$ and $f:R\times X\times X\rightarrow X$ be a S ^p-weighted pseudo almost automorphic function. Suppose that f satisfies the following conditions:

(i) f(t,x,y)is uniformly continuous in any bounded subset $M_{3}\subset X\times X$ uniformly for t∈R,

(ii) g(t,x,y)is uniformly continuous in any bounded subset $M_{3}\subset X\times X$ uniformly for t∈R,

(iii) for every bounded subset $M_{3}\subset X\times X, f(\cdot ,x,y):x,y\in M_{3}$ is bounded in S ^p W P A A(R,X,ρ ₁,ρ ₂).

If h ₁ = α ₁ + β ₁, h ₂ = α ₂ + β ₂ ∈ S ^p WPAA (R ,X ,ρ ₁, ρ ₂),with ${\alpha _{1}^{b}},$ ${\alpha _{2}^{b}}$ ∈AA (R ,L ^p([0,1],X )),${\beta _{1}^{b}},$ ${\beta _{2}^{b}}$ ∈PAA ₀(R, L ^p([0,1],X ),ρ ₁, ρ ₂)and $\mathbb {K}=\overline {\{\alpha _{1}(t):t\in R\}}$, $\mathbb {M}=\overline {\{\alpha _{2}(t):t\in R\}}$ are compact in X,then f(⋅,h ₁(⋅),h ₂(⋅))∈S ^p W P A A(R,X,ρ ₁,ρ ₂).

Now, we recall a useful compactness criterion.

Let $h: R\rightarrow R$ be a continuous function such that h(t)≥1 for all t∈R and $h(t)\rightarrow \infty$ as $|t|\rightarrow \infty$. We consider the space

$$C_{h}(X)=\left\{u\in C(R,X): \lim_{|t|\rightarrow\infty}\frac{u(t)}{h(t)}=0\right\}. $$

The space C _h (X) is a Banach space equipped with the norm $\|u\|_{h}=\sup _{t\in R}\frac {\|u(t)\|}{h(t)}$. (see [11]).

Lemma 2.7 [11]. A subset $K^{{\prime }}\subset C_{h}(X)$ is relatively compact if it satisfies the following conditions:

(c-1) The set $K^{{\prime }}(t)=\{u(t):u\in R\}$ is relatively compact in X for all t∈R.

(c-2) The set R is equicontinuous.

(c-3) For each 𝜖>0, there exists $L^{{\prime }}>0$ such that ∥u(t)∥≤𝜖 h(t)for all u∈R and all $|t|>L^{{\prime }}$.

Lemma 2.8 ([28], Leray–Schauder alternative theorem). Let D be a closed convex subset of a Banach space X such that 0∈D. Let $F:D\rightarrow D$ be a completely continuous map. Then the set {x∈D:x=λ F(x),0<λ<1}is unbounded or the map F has a fixed point in D.

DEFINITION 2.12

[10]A closed linear operator (A,D(A)) with dense domain D(A) in a Banach space X is said to be sectorial of type ω and angle 𝜃 if there are constants $\omega \in R, \, \theta \in (0,\frac {\pi }{2}),\, M>0$, such that its resolvent exists outside the sector

$$\begin{array}{@{}rcl@{}} &&\omega+{\Sigma}_{\theta}:=\{\lambda+\omega:\lambda\in \mathcal{C}, |\arg(-\lambda)|<\theta\}, \end{array} $$

(2.1)

$$\begin{array}{@{}rcl@{}} &&\|(\lambda-A)^{-1}\|\le \frac{M}{|\lambda-\omega|}, \quad \lambda\notin \omega+{\Sigma}_{\theta}. \end{array} $$

(2.2)

DEFINITION 2.13

Let 1<α<2 and A be a closed and linear operator with domain D(A) defined on a Banach space X. The operator A is called the generator of a solution operator if there exist ω∈R and a strongly continuous functions $S_{\alpha }:R_{+}\rightarrow L(X)$, such that $\{\lambda ^{\alpha }:\text {Re}~ \lambda >\omega \}\subset \rho (A)$ and

$$\lambda^{\alpha-1}(\lambda^{\alpha}I-A)^{-1}x={\int}_{0}^{\infty}\mathrm{e}^{-\lambda t}S_{\alpha}(t)x\mathrm{d}t, \quad \text{Re}~\lambda>\omega, \quad x\in X. $$

In [10], Cuesta proved that if A is sectorial of type ω∈R with 0≤𝜃<π(1−α/2), then A is a generator of a solution operator given by

$$S_{\alpha}(t)=\frac{1}{2\pi i}{\int}_{\mathbb{G}}\mathrm{e}^{\lambda t}\lambda^{\alpha-1}(\lambda^{\alpha}-A)^{-1}\mathrm{d}\lambda, \quad t\ge 0, $$

where $\mathbb {G}$ a suitable path lying outside the sector ω+Σ ₀ . Furthermore, he showed that the following lemma holds.

Theorem 2.5 (Theorem 1 of [10]).

Let $A:D(A)\subset X\rightarrow X$ be a sectorial operator in a complex Banach space X, satisfying hypothesis ( 2.1 ) and ( 2.2 ), for some M>0,ω<0 and 0≤𝜃<π(1−α/2). Then there exists C(𝜃,α)>0 depending solely on 𝜃 and α, such that

$$ \|S_{\alpha}(t)\|_{L(X)}\le \frac{C(\theta,\alpha)M}{1+|\omega|t^{\alpha}}, \quad t\ge 0. $$

(2.3)

3 Stepanov-type weighted pseudo almost automorphic solutions

In this section, we first investigate the existence and uniqueness of a weighted pseudo almost automorphic mild solutions for the problem (1.1).

Cuevas and Lizama [12] have shown that the equation of type (1.1) can be thought of as a limiting case of the following equation:

$$\begin{array}{@{}rcl@{}} z^{\prime}(t)&=&{{\int}_{0}^{t}} \frac{(t-s)^{\alpha-2}}{\Gamma(\alpha-1)}Az(s)\mathrm{d}s+f(t,x(t),Kx(t)), \quad t \ge 0, \\ z(s)&=&\phi(s), s\in [-r,0], \end{array} $$

(3.1)

in the sense that the solutions are asymptotic to each other as $t \rightarrow \infty .$ If the operator A is sectorial of type ω with $\theta \in [0,\pi (1-\frac {\alpha }{2}))$, then the problem (3.1) is well posed (see [10]). Thus using variation of parameter formula, one can obtain

$$ z(t)=S_{\alpha}(t)\phi(0)+{{\int}_{0}^{t}}S_{\alpha}(t-s)f(s,x(s),Kx(s))\mathrm{d}s, \quad t \ge 0, $$

(3.2)

where

$$S_{\alpha}(t)=\frac{1}{2\pi i}{\int}_{\gamma} \mathrm{e}^{\lambda t} \lambda^{\alpha-1}(\lambda^{\alpha}I-A)^{-1}\mathrm{d} \lambda, \quad t \ge t_{0}.$$

Here the path γ lies outside the sector ω+S _𝜃 . Further, if S _α (t) is integrable then the solution is given by

$$ x(t)={\int}_{-\infty}^{t} S_{\alpha}(t-s)f(s,x(s),Kx(s))\mathrm{d}s. $$

(3.3)

Subtracting equation (3.3 ) from equation ( 3.2), one obtain

$$z(t)-x(t)=S_{\alpha}(t)x_{0}-{\int}_{t}^{\infty}S_{\alpha}(s)f(t-s,x(t-s),Kx(t-s)).$$

Hence for $f \in L^{p^{\prime }}({\mathbb {R}^{+}\times X,X})$, where $p^{\prime } \in [1,\infty )$, we have $v(t)-u(t) \rightarrow 0$ as $t\rightarrow \infty .$

A mild solution of (1.1) satisfies the following integral equation:

$$ x(t)= S_{\alpha}(t-a)\phi(0) + {{\int}_{a}^{t}}S_{\alpha}(t-s)f(s,x(s),Kx(s))\mathrm{d}s. $$

(3.4)

By taking $a \rightarrow -\infty$, we get the desired form of solution, which motivates the following definition:

DEFINITION 3.1

A continuous function $x:R\rightarrow X$ is called a mild solution of (1.1), if $s\rightarrow$ $S_{\alpha }(t-s)f\left (s,x(s),Kx(s)\right )$ is integrable on $(-\infty ,t)$ for each t∈R and

$$x(t)={\int}_{-\infty}^{t}S_{\alpha}(t-s)f\left(s,x(s),Kx(s)\right)\mathrm{d}s,\, \quad t\in R. $$

In order to prove our results, we need the following assumptions:

(A1) A is a sectorial operator of type ω<0.

(A2) f=f ₁+f ₂∈S ^p W P A A(R×X×X,X,ρ ₁,ρ ₂) with ${f_{1}^{b}}\in AA(R\times X\times X,L^{p}([0,1],X))$, ${f_{2}^{b}}\in PAA_{0}(R\times X\times X,L^{p}([0,1],X),\rho _{1},\rho _{2})$, there exist constants $L_{f},L_{f}^{\prime }$, $L_{f_{1}},L_{f_{1}^{\prime }}>0$ such that

$$\begin{array}{@{}rcl@{}} &&\|f(t,x_{1},x_{2})-f(t,y_{1},y_{2})\|\le L_{f}\|x_{1}-y_{1}\|+L_{f}^{\prime}\|x_{2}-y_{2}\|,\\ &&\, ~~~~~~~~~~~t\in R, x_{i},y_{i}\in X,i=1,2 \end{array} $$

and

$$\begin{array}{@{}rcl@{}} &&\|f_{1}(t,x_{1},x_{2})-f_{1}(t,y_{1},y_{2})\|\le L_{f_{1}}\|x_{1}-y_{1}\|+L_{f_{1}^{\prime}}\|x_{2}-y_{2}\|,\\ && ~~~~~~~~~~~~~t\in R, x_{i},y_{i}\in X,i=1,2. \end{array} $$

(A3) h=h ₁+h ₂∈S ^p W P A A(R×X,X,ρ ₁,ρ ₂) with ${h_{1}^{b}}\in AA(R\times X,L^{p}([0,1]$, $X)),{h_{2}^{b}}\in PAA_{0}(R\times X,L^{p}([0,1],X),\rho _{1},\rho _{2})$, there exist constants L _h ,L _h1>0 such that

$$\|h(t,x)-h(t,y)\|\le L_{h}\|x-y\|, \, t\in R, \, x,y\in X $$

and

$$\vadjust{\vspace*{2pt} } \|h_{1}(t,x)-h_{1}(t,y)\|\le L_{h_{1}}\|x-y\|, \, t\in R, \, x,y\in X. $$

(A4) ρ ₁ ,ρ ₂ ∈U _T and $\sup _{T>0}\frac {\mu (T,\rho _{2})}{\mu (T,\rho _{1})}<\infty$.

Lemma 3.1.

If x ∈ WPAA(R, X, ρ _{1 ,ρ 2} ), and (A1), (A3)–(A4) hold, then Kx∈WPAA(R,X,ρ ₁ ,ρ 2).

Proof.

Since (A3) holds, hence by Theorem 2.2 it is clear that γ(⋅)=h(⋅,x(⋅))∈S ^p W P A A(R×X,X,ρ ₁ ,ρ ₂ ).

Let γ(t)=γ ₁ (t)+γ ₂ (t), where ${\gamma _{1}^{b}}\in AA(R,L^{p}([0,1],X))$ and ${\gamma _{2}^{b}}\in PAA_{0}(R,L^{p}([0,1],X),\rho _{1},\rho _{2})$. Consider the following integrals

$$\begin{array}{@{}rcl@{}} x_{n}(t)&=&{\int}_{t-n}^{t-n+1}k(t-s)\gamma(s)\mathrm{d}s\\ &=&{\int}_{t-n}^{t-n+1}k(t-s)\gamma_{1}(s)\mathrm{d}s+{\int}_{t-n}^{t-n+1}k(t-s)\gamma_{2}(s)\mathrm{d}s\\ &=&u_{n}(t)+v_{n}(t),\quad n\in N, \end{array} $$

where $u_{n}(t)={\int }_{t-n}^{t-n+1}k(t-s)\gamma _{1}(s)\mathrm {d}s$ and $v_{n}(t)={\int }_{t-n}^{t-n+1}k(t-s)\gamma _{2}(s)\mathrm {d}s$.

In order to prove that each x _n is weighted pseudo almost automorphic function, we only need to verify u _n ∈A A(R,X) and v _n ∈P A A ₀ (R,X,ρ ₁ ,ρ ₂ ) for each n=1,2,....

Now, let us show that u _n ∈A A(R,X). For each n∈N, let

$$u_{n}(t)={\int}_{t-n}^{t-n+1}k(t-s)\gamma_{1}(s)\mathrm{d}s={\int}_{n-1}^{n}k(s)\gamma_{1}(t-s)\mathrm{d}s. $$

Fix n∈N and t∈R, we obtain

$$\begin{array}{@{}rcl@{}} \|u_{n}(t+h)-u_{n}(t)\|\!\!&\le&\!\! {\int}_{n-1}^{n}k(s)\|\gamma_{1}(t+h-s)-\gamma_{1}(t-s)\|\mathrm{d}s\\ &\le&\!\! c_{k}{\int}_{n-1}^{n}\mathrm{e}^{-bs}\|\gamma_{1}(t+h-s)-\gamma_{1}(t-s)\|\mathrm{d}s\\ &\le&\!\! c_{k}\left({\int}_{n-1}^{n}\mathrm{e}^{-qbs}\mathrm{d}s\right)^{\frac{1}{q}}\left({\int}_{n-1}^{n}\|\gamma_{1}(t+h-s)-\gamma_{1}(t-s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\\ &\le&\!\! c_{k}e^{-bn}\sqrt[q]{\frac{\mathrm{e}^{qb}-1}{qb}}\left({\int}_{n-1}^{n}\|\gamma_{1}(t+h-s)-\gamma_{1}(t-s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}. \end{array} $$

Since $\gamma _{1}\in L_{loc}^{p}(R,X)$, we get

$$\lim_{h\rightarrow 0}{\int}_{n-1}^{n}\|\gamma_{1}(t+h-s)-\gamma_{1}(t-s)\|^{p}\mathrm{d}s=0, $$

which yields

$$\lim_{h\rightarrow 0}\|u_{n}(t+h)-u_{n}(t)\|=0. $$

The above equality assure the continuity of u _n (t). By Holder inequality, it follows that

$$\begin{array}{@{}rcl@{}} \|u_{n}(t)\|\!\!&\le&\!\!{\int}_{t-n}^{t-n+1}k(t-s)\|\gamma_{1}(s)\|\mathrm{d}s\\ &\le&\!\! c_{k}{\int}_{t-n}^{t-n+1}\mathrm{e}^{-b(t-s)}\|\gamma_{1}(s)\|\mathrm{d}s\\ &\le&\!\! c_{k}\left({\int}_{t-n}^{t-n+1}\mathrm{e}^{-qb(t-s)}\mathrm{d}s\right)^{\frac{1}{q}}\left({\int}_{t-n}^{t-n+1}\|\gamma_{1}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\\ &\le&\!\! c_{k}\left({\int}_{n-1}^{n}\mathrm{e}^{-qbs}\mathrm{d}s\right)^{\frac{1}{p}}\|\gamma_{1}\|_{S^{p}}\\ &\le&\!\! c_{k}e^{-bn}\sqrt[q]{\frac{\mathrm{e}^{qb}-1}{qb}}\|\gamma_{1}\|_{S^{p}}, \end{array} $$

where ∥γ ₁ ∥ _{S p} =$\sup _{t\in R}({\int }_{t}^{t+1}\|\gamma _{1}(s)\|^{p}\mathrm {d}s)^{\frac {1}{p}}$ <$\infty$, thus we have $c_{k}\sqrt [q]{\frac {\mathrm {e}^{qb}-1}{qb}}$ ${\sum }_{n=1}^{\infty }\mathrm {e}^{-bn}<\infty .$ Hence we deduce from the well known Weierstrass theorem that the series ${\sum }_{n=1}^{\infty }u_{n}(t)$ is uniformly convergent on R.

Clearly, u(t)∈C(R,X) and $\|u(t)\|\le {\sum }_{n=1}^{\infty }\|u_{n}(t)\|\le L_{n}(c_{k},b,q)\|\gamma _{1}\|_{S^{p}}$, where L _n (c _k ,b,q)>0 is a constant, which depends only on the parameters c _k ,b and q.

Let $u(t)={\sum }_{n=1}^{\infty }u_{n}(t)$ for each t∈R, then

$$u(t)={\int}_{-\infty}^{t}k(t-s)\gamma_{1}(s)\mathrm{d}s, \quad t\in R. $$

Since ${\gamma _{1}^{b}}\in AA(R,L^{p}([0,1],X))$, then for every sequence of real numbers $\{s_{n}\}_{n\in \mathcal {N}}$ there exist a subsequence $\{s_{m}\}_{m\in \mathcal {N}}$ and a function $\widetilde {\gamma _{1}}(\cdot )\in L_{loc}^{p}(R,X)$ such that for each t∈R,

$$\lim_{m\rightarrow\infty}\left({\int}_{t}^{t+1}\|\gamma_{1}(s+s_{m})-\widetilde{\gamma_{1}}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}=0, $$

and

$$\lim_{m\rightarrow\infty}\left({\int}_{t}^{t+1}\|\widetilde{\gamma_{1}}(s-s_{m})-\gamma_{1}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}=0. $$

Let $\widetilde {u_{n}}(t)={\int }_{n-1}^{n}k(\sigma )\widetilde {\gamma _{1}}(t-\sigma )\mathrm {d}\sigma$, then using the Holder inequality, we obtain

$$\begin{array}{@{}rcl@{}} \|u_{n}(t+s_{m})-\widetilde{u_{n}}(t)\|\!\!&=&\!\!\left\| {\int}_{n-1}^{n}k(\sigma)\left[\gamma_{1}(t+s_{m}-\sigma)-\widetilde{\gamma_{1}}(t-\sigma)\right]\mathrm{d}\sigma\right\|\\ &\le& \!\!c_{k}{\int}_{n-1}^{n}\mathrm{e}^{-b\sigma}\|\gamma_{1}(t+s_{m}-\sigma)-\widetilde{\gamma_{1}}(t-\sigma)\|\mathrm{d}\sigma\\ &\le&\!\! c_{k}\left({\int}_{n-1}^{n}\mathrm{e}^{-qb\sigma}\mathrm{d}\sigma\right)^{\frac{1}{q}}\!\left({\int}_{n-1}^{n}\!\|\gamma_{1}(t\,+\,s_{m}\,-\,\sigma)\,-\,\widetilde{\gamma_{1}}(t\,-\,\sigma)\|^{p}\mathrm{d}\sigma\right)^{\frac{1}{p}}\\ &\le& \!\!c_{k}e^{-bn}\sqrt[q]{\frac{\mathrm{e}^{qb}-1}{qb}}\left({\int}_{n-1}^{n}\|\gamma_{1}(t+s_{m}-\sigma)-\widetilde{\gamma_{1}}(t-\sigma)\|^{p}\mathrm{d}\sigma\right)^{\frac{1}{p}}\\ &&{\kern14.4pc}\rightarrow 0 \quad \text{as} ~ m\rightarrow \infty. \end{array} $$

By a similar argument, we can prove that

$$\lim_{m\rightarrow \infty}\|\widetilde{u_{n}}(t-s_{m})-u_{n}(t)\|=0. $$

Thus, we conclude that u _n ∈A A(R,X) for n∈N, and thus by Lemma 2.1, we have $u(t)={\sum }_{n=1}^{\infty }u_{n}(t)\in AA(R,X)$.

Next, we intend to verify that v _n ∈P A A ₀(R,X,ρ ₁,ρ ₂). For this, we have the following estimates

$$\begin{array}{@{}rcl@{}} \|v_{n}(t)\|\!\!&\le&\!\!{\int}_{t-n}^{t-n+1}k(t-s)\|\gamma_{2}(s)\|\mathrm{d}s\\ &\le&\!\! c_{k}{\int}_{t-n}^{t-n+1}\mathrm{e}^{-b(t-s)}\|\gamma_{2}(s)\|\mathrm{d}s\\ &\le&\!\! c_{k}\left({\int}_{t-n}^{t-n+1}\mathrm{e}^{-qb(t-s)}\mathrm{d}s\right)^{\frac{1}{q}}\left({\int}_{t-n}^{t-n+1}\|\gamma_{2}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\\ &\le&\!\! c_{k}{e}^{-bn}\sqrt[q]{\frac{\mathrm{e}^{qb}-1}{qb}}\left({\int}_{t-n}^{t-n+1}\|\gamma_{2}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}. \end{array} $$

Then for T>0, we get

$$\begin{array}{@{}rcl@{}} &\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\|v_{n}(t)\|\mathrm{d}t\le c_{k}\mathrm{e}^{-bn}\sqrt[q]{\frac{\mathrm{e}^{qb}-1}{qb}}\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\\ &{}\left({\int}_{t-n}^{t-n+1}\|\gamma_{2}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\mathrm{d}t. \end{array} $$

Since ${\gamma _{2}^{b}}\in PAA_{0}(R,L^{p}([0,1],X),\rho _{1},\rho _{2})$, the above inequality gives v _n ∈P A A ₀(R, X,ρ ₁,ρ ₂) for each n=1,2,…. Further, the last estimate leads to

$$\|v_{n}(t)\|\le c_{k}\mathrm{e}^{-bn}\sqrt[q]{\frac{\mathrm{e}^{qb}-1}{qb}}\|\gamma_{2}\|_{S^{p}}. $$

Since $c_{k}\sqrt [q]{\frac {\mathrm {e}^{qb}-1}{qb}}{\sum }_{n=1}^{\infty }\mathrm {e}^{-bn}<\infty$, we deduce from the Weierstrass test that the series ${\sum }_{n=1}^{\infty }v_{n}(t)$ is uniformly convergent on R. Moreover,

$$v(t)={\int}_{-\infty}^{t}k(t-s)\gamma_{2}(s)\mathrm{d}s={\sum}_{n=1}^{\infty}v_{n}(t), $$

and clearly v(t)∈C(R,X) and

$$\|v(t)\|={\sum}_{n=1}^{\infty}\|v_{n}(t)\|\le \mathcal{K}(c_{k},b,q)\|\gamma_{2}\|_{S^{p}}, $$

where $\mathcal {K}(c_{k},b,q)>0$ is a constant that depends only on the constants c _k ,b and q. Using the fact that v _n ∈P A A ₀(R,X,ρ ₁,ρ ₂) and the inequality

$$\begin{array}{@{}rcl@{}} \frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\|v(t)\|\mathrm{d}t&\le& \frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\left\|v(t)-{\sum}_{k=1}^{n}v_{k}(t)\right\|\mathrm{d}t\\ &&+{\sum}_{k=1}^{n}\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\|v_{k}(t)\|\mathrm{d}t, \end{array} $$

□

we deduce that v(⋅) =${\sum }_{n=1}^{\infty }v_{n}(t)$ ∈PAA ₀(R,X,ρ ₁,ρ ₂). Hence Kx ∈WPAA(R, X, ρ ₁, ρ ₂).

Lemma 3.2 [24]. Let $\{E(t)\}_{t\ge 0}\subset \mathcal {B}(X)$ be a strongly continuous family of bounded linear operators such that

$$\|E(t)\|\le \varphi(t), t\in R^{+}, $$

where φ(t)∈L ¹(R ⁺)is nonincreasing. If ψ=ψ ₁+ψ ₂∈S ^p W P A A(R,X,ρ ₁,ρ ₂), with ${\psi _{1}^{b}}\in AA(R,L^{p}([0,1],X))$ and ${\psi _{2}^{b}}\in PAA_{0}(R,L^{p}([0,1],X),\rho _{1},\rho _{2})$ and (A4) holds, then

$$({\Gamma}\psi)(t)={\int}_{-\infty}^{t}E(t-s)\psi(s)\mathrm{d}s,\quad t\in R $$

lies in the space W P A A(R,X,ρ ₁,ρ ₂).

Proof.

For each n ∈N, let $\psi _{n}(t)={\int }_{t-n}^{t-n+1}$ E(t −s) ψ(s)d$s={\int }_{n-1}^{n}E(s)\psi$(t −s)ds, t ∈R.

In addition, for each n ∈N, by the principle of uniform boundedness, M _n =$\sup _{n-1\le s\le n}\|E(s)\|<\infty$.

We first show that Γψ∈B C(R,X). In fact, if ψ∈S ^p W P A A(R,X,ρ ₁,ρ ₂), then $\|\psi \|_{S^{p}}<\infty$, which gives

$$\begin{array}{@{}rcl@{}} \|({\Gamma}\psi)(t)\|\!\!&\le&\!\! {\int}_{-\infty}^{t}\varphi(t-s)\|\psi(s)\|\mathrm{d}s\\ &\le& \!\!{\int}_{0}^{\infty}\varphi(s)\|\psi(t-s)\|\mathrm{d}s\\ &=&\!\!{\sum}_{k=0}^{\infty}{\int}_{k}^{k+1}\varphi(s)\|\psi(t-s)\|\mathrm{d}s\\ &\le& \!\!{\sum}_{k=0}^{\infty}\varphi(k){\int}_{k}^{k+1}\|\psi(t-s)\|\mathrm{d}s\\ &\le&\!\! {\sum}_{k=0}^{\infty}\varphi(k)\left({\int}_{k}^{k+1}\|\psi(t-s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\\ &\le&\!\! {\sum}_{k=0}^{\infty}\varphi(k)\|\psi\|_{S^{p}}\\ &=&\!\!\left[\varphi(0)+\varphi(1)+{\sum}_{k=2}^{\infty}{\int}_{k-2}^{k-1}\varphi(s)\mathrm{d}s\right]\|\psi\|_{S^{p}}\\ &\le& \!\!\left[\varphi(0)+\varphi(1)+\|\varphi\|_{L^{1}(R^{+})}\right]\|\psi\|_{S^{p}}\\ &<&\!\!\infty. \end{array} $$

Let ψ(t) = ψ ₁(t) + ψ ₂(t), where $\psi _{1}^{b}$ ∈AA(R, L ^p([0, 1], X)) and $\psi _{2}^{b}$ ∈PAA ₀(R, L ^p([0, 1], X), ρ ₁, ρ ₂). Consider the following integrals

$$\begin{array}{@{}rcl@{}} x_{n}(t)&=&{\int}_{t-n}^{t-n+1}E(t-s)\psi(s)\mathrm{d}s\\ &=&{\int}_{t-n}^{t-n+1}E(t-s)\psi_{1}(s)\mathrm{d}s+{\int}_{t-n}^{t-n+1}E(t-s)\psi_{2}(s)\mathrm{d}s\\ &=&u_{n}(t)+v_{n}(t),\quad n\in N,\quad t\in R, \end{array} $$

where $u_{n}(t)={\int }_{t-n}^{t-n+1}E(t-s)\psi _{1}(s)\mathrm {d}s$ and $v_{n}(t)={\int }_{t-n}^{t-n+1}E(t-s)\psi _{2}(s)\mathrm {d}s$.

We show that u _n ∈A A(R,X). Fix n∈N and t∈R, we have

$$\begin{array}{@{}rcl@{}} \|u_{n}(t+h)-u_{n}(t)\|\!\!&\le&\!\! {\int}_{n-1}^{n}\varphi(s)\|\psi_{1}(t+h-s)-\psi_{1}(t-s)\|\mathrm{d}s\\ &\le& \!\!M_{n}{\int}_{t-n}^{t-n+1}\|\psi_{1}(s+h)-\psi_{1}(s)\|\mathrm{d}s\\ &\le&\!\! M_{n}\left({\int}_{t-n}^{t-n+1}\|\psi_{1}(s+h)-\psi_{1}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}. \end{array} $$

In view of $\psi _{1}\in L_{loc}^{p}(R,X)$, we get

$$\lim_{h\rightarrow 0}{\int}_{t-n}^{t-n+1}\|\psi_{1}(s+h)-\psi_{1}(s)\|^{p}\mathrm{d}s=0, $$

which yields

$$\lim_{h\rightarrow 0}\|u_{n}(t+h)-u_{n}(t)\|=0. $$

The above relation implies that u _n (t) is continuous.

Since ${\psi _{1}^{b}}\in AA(R,L^{p}([0,1],X))$, then for every sequence of real numbers $\{s_{n}\}_{n\in {\mathcal {N}}}$, there exist a subsequence $\{s_{m}\}_{m\in {\mathcal {N}}}$ and a function $\widetilde {\psi _{1}}\in L_{loc}^{p}(R,X)$ such that for each t∈R,

$$\lim_{m\rightarrow\infty}\left({\int}_{t}^{t+1}\|\psi_{1}(s+s_{m})-\widetilde{\psi_{1}}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}=0, $$

and

$$\lim_{m\rightarrow\infty}\left({\int}_{t}^{t+1}\|\widetilde{\psi_{1}}(s-s_{m})-\psi_{1}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}=0. $$

Let $\widetilde {u_{n}}(t)={\int }_{n-1}^{n}\varphi (\sigma )\widetilde {\psi _{1}}(t-\sigma )\mathrm {d}\sigma$. By using the Holder inequality, we obtain

$$\begin{array}{@{}rcl@{}} \|u_{n}(t+s_{m})-\widetilde{u_{n}}(t)\|\!\!&=&\!\!\left\| {\int}_{n-1}^{n}\varphi(\sigma)\left[\psi_{1}(t+s_{m}-\sigma)-\widetilde{\psi_{1}}(t-\sigma)\right]\mathrm{d}\sigma\right\|\\ &\le& \!\!M_{n}{\int}_{n-1}^{n}\|\psi_{1}(t+s_{m}-\sigma)-\widetilde{\psi_{1}}(t-\sigma)\|\mathrm{d}\sigma\\ &\le& \!\!M_{n}\left({\int}_{t-n}^{t-n+1}\|\psi_{1}(s+s_{m})-\widetilde{\psi_{1}}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\\ &&{\kern9pc}\rightarrow 0 \quad \text{as} ~ m\rightarrow \infty. \end{array} $$

Similarly, we can prove that

$$\lim_{m\rightarrow \infty}\|\widetilde{u_{n}}(t-s_{m})-u_{n}(t)\|=0. $$

Thus, we conclude that u _n ∈A A(R,X) for n∈N.

By Hölder inequality, it follows that

$$\begin{array}{@{}rcl@{}} \|u_{n}(t)\|\!\!&\le&\!\!{\int}_{n-1}^{n}\varphi(s)\|\psi_{1}(t-s)\|\mathrm{d}s\\ &\le&\!\! \varphi(n-1){\int}_{n-1}^{n}\|\psi_{1}(t-s)\|\mathrm{d}s\\ &\le&\!\! \varphi(n-1){\int}_{t-n}^{t-n+1}\|\psi_{1}(s)\|\mathrm{d}s\\ &\le&\!\! \varphi(n-1)\left({\int}_{t-n}^{t-n+1}\|\psi_{1}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\\ &\le&\!\! \varphi(n-1)\|\psi_{1}\|_{S^{p}}, \end{array} $$

where $\|\psi _{1}\|_{S^{p}}=\sup _{t\in R}\left ({\int }_{t}^{t+1}\|\psi _{1}(s)\|^{p}\mathrm {d}s\right )^{\frac {1}{p}}<\infty .$ Hence

$$\begin{array}{@{}rcl@{}} {\sum}_{k=1}^{\infty}\varphi(n-1)\|\psi_{1}\|_{S^{p}}\!\!&\le&\!\! \left(\varphi(0)+{\sum}_{k=2}^{\infty}{\int}_{n-2}^{n-1}\varphi(t)\mathrm{d}t\right)\|\psi_{1}\|_{S^{p}}\\ &\le& \!\!\left(\varphi(0)+\|\varphi\|_{L^{1}(R^{+})}\right)\|\psi_{1}\|_{S^{p}}\\ &<&\!\!\infty, \end{array} $$

which implies that ${\sum }_{n=1}^{\infty }u_{n}(t)$ is uniformly convergent on R.

Let $u(t)={\sum }_{n=1}^{\infty }u_{n}(t)$ for each t∈R, then

$$u(t)={\int}_{-\infty}^{t}E(t-s)\psi_{1}(s)\mathrm{d}s, \quad t\in R. $$

By Lemma 2.1, we have $u(t)={\sum }_{n=1}^{\infty }u_{n}(t)\in AA(R,X)$.

Next, we show that v _n ∈P A A ₀(R,X,ρ ₁,ρ ₂). Indeed

$$\begin{array}{@{}rcl@{}} \|v_{n}(t)\|\!\!&\le&\!\!{\int}_{n-1}^{n}\varphi(s)\|\psi_{2}(t-s)\|\mathrm{d}s\\ \!\!&\le&\!\! \varphi(n-1)\left({\int}_{t-n}^{t-n+1}\|\psi_{2}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}, \end{array} $$

then

$$\begin{array}{@{}rcl@{}} \frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\|v_{n}(t)\|\mathrm{d}t&& \\ && \le \frac{\varphi(n-1)}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t) \left({\int}_{t-n}^{t-n+1}\|\psi_{2}(s)\|^{p}\mathrm{d}s\right)^{\frac{1}{p}}\mathrm{d}t. \end{array} $$

Since ${\psi _{2}^{b}}\in PAA_{0}(R,L^{p}([0,1],X),\rho _{1},\rho _{2})$, the above inequality leads to v _n ∈P A A ₀(R,X,ρ ₁,ρ ₂) for each n=1,2,…. Further, the last estimate leads to

$$\|v_{n}(t)\|\le \varphi(n-1)\|\psi_{2}\|_{S^{p}}. $$

Since

$$\begin{array}{@{}rcl@{}} {\sum}_{n=1}^{\infty}\varphi(n-1)\|\psi_{2}\|_{S^{p}}\!\!&\le& \!\!\left(\varphi(0)+{\sum}_{n=2}^{\infty}{\int}_{n-2}^{n-1}\varphi(t)\mathrm{d}t\right)\|\psi_{2}\|_{S^{p}}\\ &\le& \!\!\left(\varphi(0)+\|\varphi\|_{L^{1}(R^{+})}\right)\|\psi_{2}\|_{S^{p}}\\ &<&\!\!\infty, \end{array} $$

hence we deduce from the Weierstrass test that the series ${\sum }_{n=1}^{\infty }v_{n}(t)$ is uniformly convergent on R. Moreover,

$$v(t)={\int}_{-\infty}^{t}E(t-s)\psi_{2}(s)\mathrm{d}s={\sum}_{n=1}^{\infty}v_{n}(t), $$

which clearly implies v(t)∈C(R,X). Using the fact that v _n ∈P A A ₀(R,X,ρ ₁,ρ ₂) and the inequality

$$\begin{array}{@{}rcl@{}} \frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\|v(t)\|\mathrm{d}t&\le& \frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\left\|v(t)-{\sum}_{k=1}^{n}v_{k}(t)\right\|\mathrm{d}t\\ &&+{\sum}_{k=1}^{n}\frac{1}{\mu(T,\rho_{1})}{\int}_{-T}^{T}\rho_{2}(t)\|v_{k}(t)\|\mathrm{d}t, \end{array} $$

□

we deduce v(⋅) =${\sum }_{n=1}^{\infty }v_{n}$(t) ∈PAA ₀(R, X, ρ ₁, ρ ₂). Thus Γ ψ ∈WPAA(R, X, ρ ₁, ρ ₂).

Theorem 3.1.

Assume that (A1)–(A4) hold. Then problem ( 1.1 ) has a unique weighted pseudo almost automorphic mild solution on R, provided

$$Q=\left[L_{f}+L_{f}^{{\prime}}L_{h}\frac{c_{k}}{b}\right]\frac{C(\theta,\alpha)M|\omega|^{\frac{-1}{\alpha}}\pi}{\alpha\sin(\pi/\alpha)}<1. $$

Proof.

Consider the operator Υ: WPAA(R, X, ρ ₁, ρ ₂) →WPAA(R, X, ρ ₁, ρ ₂) such that

$$ ({\Upsilon} x)(t)={\int}_{-\infty}^{t}S_{\alpha}(t-s)f(s,x(s),Kx(s))\mathrm{d}s,\quad t\in R. $$

(3.5)

□

Let x =x ₁ + x ₂ ∈WPAA(R, X, ρ ₁, ρ ₂), where x ₁ ∈AA(R, X), x ₂ ∈PAA ₀(R, X, ρ ₁, ρ ₂). By Lemma 3.1, Kx ∈WPAA(R, X, ρ ₁, ρ ₂) $\subset$ S ^p WPAA(R, X, ρ ₁, ρ ₂), thus h(⋅) =f(⋅, x(⋅), Kx(⋅)) ∈S ^p WPAA(R, X, ρ ₁, ρ ₂) from Theorem 2.2. By Lemma 3.2, it is not difficult to see that Υ is well defined.

For any x,y∈W P A A(R,X,ρ ₁,ρ ₂), by inequality (2.3), we have

$$\begin{array}{@{}rcl@{}} \|({\Upsilon} x)(t)-({\Upsilon} y)(t)\|\!\!&=&\!\!\left\|{\int}_{-\infty}^{t}S_{\alpha}(t-s) [f(s,x(s),Kx(s))\right.\\ &&\left.-f(s,y(s),Ky(s))]\mathrm{d}s{\vphantom{\int}}\right\|\\ &\le&\!\! {\int}_{-\infty}^{t}\frac{C(\theta,\alpha)M}{1+|\omega|(t-s)^{\alpha}}[L_{f}\|x(s)-y(s)\|\\ &&+L_{f}^{^{\prime}}\|Kx(s)-Ky(s)\|]\mathrm{d}s. \end{array} $$

Consider

$$\begin{array}{@{}rcl@{}} \|Kx(s)-Ky(s)\|\!\!&\le&\!\! {\int}_{-\infty}^{t}|k(t-s)|\|h(s,x(s))-h(s,y(s))\|\mathrm{d}s\\ &\le&\!\! {\int}_{-\infty}^{t}|k(t-s)|L_{h}\|x(s)-y(s)\|\mathrm{d}s\\ &\le&\!\!\sup_{t\in R}\|x(t)-y(t)\|L_{h}\left({\int}_{-\infty}^{t}|k(t-s)|\mathrm{d}s\right)\\ &\le&\!\!\sup_{t\in R}\|x(t)-y(t)\|L_{h}{\int}_{0}^{\infty}|k(s)|\mathrm{d}s\\ &\le&\!\!\sup_{t\in R}\|x(t)-y(t)\|L_{h}{\int}_{0}^{\infty}c_{k}\mathrm{e}^{-bs}\mathrm{d}s\\ &\le&\!\! \frac{c_{k}}{b}L_{h}\sup_{t\in R}\|x(t)-y(t)\|. \end{array} $$

(3.6)

Using (3.2), the last estimate gives

$$\begin{array}{@{}rcl@{}} \|({\Upsilon} x)(t)\,-\,({\Upsilon} y)(t)\|\!\!&\le&\!\!\left[\!L_{f}+L_{f}^{{\prime}}L_{h}\frac{c_{k}}{b}\!\right]\sup_{t\in R}\|x(t)\,-\,y(t)\|{\int}_{0}^{\infty}\frac{C(\theta,\alpha)M}{1+|\omega|s^{\alpha}}\mathrm{d}s\\ &\le&\!\!\left[\!L_{f}+L_{f}^{{\prime}}L_{h}\frac{c_{k}}{b}\right]\frac{C(\theta,\alpha)M|w|^{-1/\alpha}\pi}{\alpha\sin(\pi/\alpha)}\|x-y\|_{WPAA}\\ &\le&\!\!Q\|x-y\|_{WPAA}. \end{array} $$

Hence Υ is a contraction since Q<1. By the Banach contraction principle, Υ has a unique fixed point in W P A A(R,X,ρ ₁,ρ ₂), which is the unique weighted pseudo almost automorphic solution to the problem (1.1).

Theorem 3.2.

Assume that there exist non-negative functions $L_{f},L_{f_{1}}\in S^{r}AA(R,R)$ with $r\ge \max \left \{p,\frac {p}{p-1}\right \}$ , such that

$$\begin{array}{@{}rcl@{}} \|f(t,x_{1},x_{2})-f(t,y_{1},y_{2})\|\!\!&\le&\!\! L_{f}(t)[\|x_{1}-y_{1}\|+\|x_{2}-y_{2}\|],\\ &&{\kern5.5pc}t\in R, \, x_{i},y_{i}\in X, i=1,2, \end{array} $$

and

$$\begin{array}{@{}rcl@{}} \|f_{1}(t,x_{1},x_{2})-f_{1}(t,y_{1},y_{2})\|\!\!&\le&\!\! L_{f_{1}}(t)[\|x_{1}-y_{1}\|+\|x_{2}-y_{2}\|],\\ &&{\kern5.1pc}t\in R, \, x_{i},y_{i}\in X, i=1,2. \end{array} $$

Let (A1), (A3)–(A4) hold , then problem ( 1.1 ) has a unique weighted pseudo almost automorphic solution , provided

$$\|L_{f}\|_{S^{r}}<\frac{b\alpha\sin(\pi/\alpha)}{C(\theta,\alpha)M(b+c_{k}L_{h})[\alpha\sin(\pi/\alpha)+|\omega|^{\frac{-1}{\alpha}}\pi]}. $$

Proof.

Let x =x ₁ + x ₂ ∈WPAA(R, X, ρ ₁ , ρ ₂ ), where x ₁ ∈AA(R, X), x ₂ ∈PAA ₀(R, X, ρ ₁, ρ ₂). By Lemma 2.1, $\mathbb {K}=\overline {\{x_{1}(t):{t}\in R\}}$ and $\mathbb {M}=\overline {\{x_{2}(t):t\in R\}}$ are compact in X. By Lemma 3.1 and Lemma 2.5, $Kx\in WPAA(R,X,\rho _{1},\rho _{2})\subset S^{p}WPAA(R,X,\rho _{1},\rho _{2})$ and $S^{q}WPAA(R,X,\rho _{1},\rho _{2})\subset S^{p}WPAA(R,X,\rho _{1},\rho _{2})$, so by Theorem 2.3, there exists q ∈ [1, p) such that f(⋅,x(⋅),K x(⋅))∈S ^q W P A A(R,X,ρ ₁,ρ ₂).

Define ${\Upsilon }:WPAA(R,X,\rho _{1},\rho _{2})\rightarrow WPAA(R,X,\rho _{1},\rho _{2})$ as in equation (3.1). By Lemma 3.2, Υ maps W P A A(R,X,ρ ₁,ρ ₂) into W P A A(R,X,ρ ₁,ρ ₂).

For any x,y∈W P A A(R,X,ρ ₁,ρ ₂), by inequality (2.3), we have

$$\begin{array}{@{}rcl@{}} \|({\Upsilon} x)(t)-({\Upsilon} y)(t)\|\!\!&=&\!\!\left\|{\int}_{-\infty}^{t}S_{\alpha}(t-s) [f(s,x(s),Kx(s))\right.\\ &&\left.\!\!-f(s,y(s),Ky(s))]\mathrm{d}s{\vphantom{\int}}\right\|\\ &\le&\!\! {\int}_{-\infty}^{t}\frac{C(\theta,\alpha)M}{1+|\omega|(t-s)^{\alpha}}L_{f}(s)[\|x(s)-y(s)\|\\ &&\!\!+\|Kx(s)-Ky(s)\|]\mathrm{d}s. \end{array} $$

Using (3.2), the last estimate leads to

$$\begin{array}{@{}rcl@{}} {}\|({\Upsilon} x)(t)-({\Upsilon} y)(t)\|\!\!&\le&\!\! {\int}_{-\infty}^{t}\frac{C(\theta,\alpha)M}{1+|\omega|(t-s)^{\alpha}}L_{f}(s)\left[1+\frac{c_{k}}{b}L_{h}\right]\|x(s)-y(s)\|\mathrm{d}s\\ &\le&\!\! \left[1+\frac{c_{k}}{b}L_{h}\right]{\int}_{0}^{\infty}\frac{C(\theta,\alpha)M}{1+|\omega|s^{\alpha}}L_{f}(t-s)\mathrm{d}s\|x-y\|_{WPAA}\\ &\le&\!\! \left[1+\frac{c_{k}}{b}L_{h}\right]{\sum}_{k=0}^{\infty}{\int}_{k}^{k+1}\frac{C(\theta,\alpha)M}{1+|\omega|s^{\alpha}}L_{f}(t-s)\mathrm{d}s\|x-y\|_{WPAA}\\ &\le& \!\!\left[1+\frac{c_{k}}{b}L_{h}\right]{\sum}_{k=0}^{\infty}\frac{C(\theta,\alpha)M}{1+|\omega|k^{\alpha}}{\int}_{k}^{k+1}L_{f}(t-s)\mathrm{d}s\|x-y\|_{WPAA}\\ &\le&\!\! \left[1+\frac{c_{k}}{b}L_{h}\right]{\sum}_{k=0}^{\infty}\frac{C(\theta,\alpha)M}{1+|\omega|k^{\alpha}}\|L_{f}\|_{S^{r}}\|x-y\|_{WPAA}\\ &\le& \!\!\left[1+\frac{c_{k}}{b}L_{h}\right]\!\left({\vphantom{{\sum}_{k=1}^{\infty}}}\!C(\theta,\alpha)M\right.\\&&\left.\!\!+{\sum}_{k=1}^{\infty}{\int}_{k-1}^{k}\frac{C(\theta,\alpha)M}{1+|\omega|s^{\alpha}}\mathrm{d}s\!\right)\|L_{f}\|_{S^{r}}\|x-y\|_{WPAA}\\ &\le&\!\! \left[1+\frac{c_{k}}{b}L_{h}\right]\left({\vphantom{\int}}C(\theta,\alpha)M\right.\\&&\left.\!\!+{\int}_{0}^{\infty}\frac{C(\theta,\alpha)M}{1+|\omega|s^{\alpha}}\mathrm{d}s\right)\|L_{f}\|_{S^{r}}\|x-y\|_{WPAA}\\ &=&\!\!C(\theta,\alpha)M\left[1+\frac{c_{k}}{b}L_{h}\right]\left[1+\frac{|\omega|^{\frac{-1}{\alpha}}\pi}{\alpha\sin(\pi/\alpha)}\right]\\ &&\!\!\|L_{f}\|_{S^{r}}\|x-y\|_{WPAA}, \end{array} $$

which gives

$$\|\!({\Upsilon} x)-({\Upsilon} y)\|\!\le \!C(\theta,\alpha)M\!\left[\!1\,+\,\frac{c_{k}}{b}L_{h}\!\right]\!\left[\!\!1\,+\,\frac{|\omega|^{\frac{-1}{\alpha}}\pi}{\alpha\sin(\pi/\alpha)}\!\right]\!\|L_{f}\|_{S^{r}}\|x-y\|_{WPAA}. $$

□

By the Banach contraction principle, Υ has a unique fixed point in W P A A(R,X,ρ ₁,ρ ₂), which is the unique weighted pseudo almost automorphic solution to the problem (1.1).

We next study the existence of weighted pseudo almost automorphic mild solutions of equation (1.1) when the perturbation f is not necessarily Lipschitz continuous. For that, we require the following assumptions:

(A5) The function f =g + ϕ ∈S ^p WPAA(R, X, ρ ₁, ρ ₂), where g ^b ∈AA(R, L ^p([0, 1], X)) is uniformly continuous in any bounded subset $M_{2}\subset X\times X$ uniformly in t∈R and ϕ ^b∈P A A ₀(R,L ^p([0,1],X),ρ ₁,ρ ₂

(A6) f∈S ^p W P A A(R,X,ρ ₁,ρ ₂) and f(t,x,y) is uniformly continuous in any bounded subset $M_{2}\subset X\times X$ uniformly for t∈R, and for every bounded subset $M_{2}\subset X\times X,\{f(\cdot ,x,y):x,y\in M_{2}\}$ is bounded in S ^p W P A A(R,X,ρ ₁,ρ ₂.

(A7) There exists a continuous nondecreasing function $W:[0,\infty )\rightarrow (0,\infty )$ such that

$$\|f(t,x,y)\|\le W(\|x\|+\|y\|) \quad \text{for all} \quad t\in R \,\, \text{and} \quad x\in X. $$

The following existence result is based upon the nonlinear Leray–Schauder alternative theorem.

Theorem 3.3.

Assume that A is sectorial of type ω < 0. Let $f\,{:}\,R\,{\times }\,X\,{\times }\,X\,{\rightarrow }\,X$ be a function which satisfies the assumptions (A5)–(A7) and the following additional conditions :

(i) For each C≥0,

$$\lim_{|t|\rightarrow\infty}{\int}_{-\infty}^{t}\frac{W\left((1+k)Ch(s)\right)}{1+|\omega|(t-s)^{\alpha}}\mathrm{d}s=0, $$

where h is the function given in Lemma 2.7. We set

$$\beta(C):=C(\theta,\alpha)M\left\|{\int}_{-\infty}^{t}\frac{W\left((1+k)Ch(s)\right)}{1+|\omega|(t-s)^{\alpha}}\mathrm{d}s\right\|, $$

where C(𝜃,α) and M are constants given in ( 2.3 ).

(ii) For each 𝜖>0, there is δ>0 such that for every u,v∈C _h (X), ∥u−v∥ _h ≤δ implies that

$$C{}(\theta,{}\alpha)M{}{{\int}_{-\infty}^{t}}{}\frac{\|{}f{}({}s,{}u{}({}s{}),Ku(s))-f(s,v(s),Kv(s))\|}{1+|\omega|(t-s)^{\alpha}}\mathrm{d}s\le \epsilon,{}\quad \text{for all} \,\, t\in R. $$

(iii) $\lim \inf _{\xi \rightarrow \infty }\frac {\xi }{\beta (\xi )}>1$.

(iv) For all a,b∈R, a<b and Λ>0, the set {f(s,h(s)x,K(h(s)x):a≤s≤b, x∈C _h (X), ∥x∥ _h ≤Λ} is relatively compact in X.

Then equation ( 1.1 ) has a weighted pseudo almost automorphic mild solution.

Proof.

We define the operator ${\Gamma }:C_{h}(X)\rightarrow C_{h}(X)$ by

$$({\Gamma} x)(t)={\int}_{-\infty}^{t}S_{\alpha}(t-s)f(s,x(s),Kx(s))\mathrm{d}s, \quad t\in R. $$

We will show that Γ has a fixed point in W P A A(R,X). For the sake of convenience, we divide the proof into several steps.

Step 1: For x∈C _h (X), we have

$$\begin{array}{@{}rcl@{}} \|({\Gamma} x)(t)\|\!\!&\le & \!\!C(\theta,\alpha)M{\int}_{-\infty}^{t}\frac{W(\|x(s)\|+K\|x(s)\|)}{1+|\omega|(t-s)^{\alpha}}\mathrm{d}s\\ &\le & \!\!C(\theta,\alpha)M{\int}_{-\infty}^{t}\frac{W((1+\|K\|)\|x\|_{h}h(s))}{1+|\omega|(t-s)^{\alpha}}\mathrm{d}s \end{array} $$

It follows from condition (i) that Γ is well defined.

Step 2: The operator Γ is continuous.

In fact, for any 𝜖>0, we can choose δ>0 given in condition (ii). If x,y∈C _h (X) and ∥x−y∥ _h ≤δ, then

$$\begin{array}{@{}rcl@{}} &&\|({\Gamma} x)(t)-({\Gamma} y)(t)\|\\&&\le\!C(\theta,\alpha)M{\int}_{-\infty}^{t} \!\frac{\|f{}(s,x(s),Kx(s)){}-{}f{}(s,y(s),Ky(s))\|}{1+|\omega|(t-s)^{\alpha}}\mathrm{d}s \le \epsilon, \end{array} $$

which proves the assertion.

Step 3: In this step, we show that Γ is completely continuous.

Denote B _Λ(X) a closed ball with center at 0 and radius Λ in the space X. Let $V^{{\prime }}(t)={\Gamma }(B_{\Lambda }(C_{h}(X)))$ and $v^{{\prime }}={\Gamma }(x)$ for x∈B _Λ(C _h (X)). First, we prove that $V^{{\prime }}(t)$ is a relatively compact subset of X for each t∈R. It follows form condition (i) that the function $s\rightarrow \frac {C(\theta ,\alpha )MW((1+K){\Lambda } h(t-s))}{1+|\omega |s^{\alpha }}$ is integrable on $[0,\infty )$. Hence, for 𝜖>0, we can choose a≥0 such that $C(\theta ,\alpha )M{\int }_{a}^{\infty }\frac {W((1+K){\Lambda } h(t-s))}{1+|\omega |s^{\alpha }}\mathrm {d}s\le \epsilon$. Since,

$$\begin{array}{@{}rcl@{}} v^{{\prime}}(t)\!\!&=&\!\!{{\int}_{0}^{a}}S_{\alpha}(s)f(t-s,x(t-s),Kx(t-s))\mathrm{d}s\\ &&\!\!+{\int}_{a}^{\infty}S_{\alpha}(s)f(t-s,x(t-s),Kx(t-s))\mathrm{d}s, \end{array} $$

and

$$\begin{array}{@{}rcl@{}} &&\left\|{\int}_{a}^{\infty}S_{\alpha}(s)f(t-s,x(t-s),Kx(t-s))\mathrm{d}s\right\|\\ &&\le C(\theta,\alpha)M{\int}_{a}^{\infty}\frac{W((1+K){\Lambda} h(t-s))}{1+|\omega|s^{\alpha}}\mathrm{d}s\\ &&\le \epsilon, \end{array} $$

we obtain $v^{{\prime }}(t)\in a\overline {c_{0}(N)}+B_{\epsilon }(X)$, where c ₀(N) denotes the convex hull of N and N={S _α (s)f(ξ,h(ξ)x,K(h(ξ)x):0≤s≤a,t−a≤ξ≤t,∥x∥ _h ≤Λ}. Using the strong continuity of S _α (⋅) and property (iv) of f, we can infer that N is a relatively compact set and $V^{{\prime }}(t)\subset a\overline {c_{0}(N)}+B_{\epsilon }(X)$, which establishes our assertion.

Next, we show that the set $V^{{\prime }}$ is equicontinuous. In fact, we can decompose

$$\begin{array}{@{}rcl@{}} v^{{\prime}}(t+s)-v^{{\prime}}(t)&=&{{\int}_{0}^{s}}S_{\alpha}(\sigma)f(t+s-\sigma,x(t+s-\sigma),\\ &&{\kern1pc}Kx(t+s-\sigma))\mathrm{d}\sigma\\ &&+{{\int}_{0}^{a}}[S_{\alpha}(\sigma+s)-S_{\alpha}(\sigma)]f(t-\sigma,x(t-\sigma),\\ &&{\kern1pc}Kx(t-\sigma))\mathrm{d}\sigma\\ &&+{\int}_{a}^{\infty}{}[S_{\alpha}(\sigma{}+{}s){}-{}S_{\alpha}(\sigma)]f(t{}-{}\sigma,x(t{}-{}\sigma),\\\\ &&~~~~~Kx(t-\sigma))\mathrm{d}\sigma. \end{array} $$

For each 𝜖>0, we can choose a>0 and δ ₁>0, such that

$$\begin{array}{@{}rcl@{}} && \left\|{{\int}_{0}^{s}}S_{\alpha}(\sigma)f(t+s-\sigma,x(t+s-\sigma),Kx(t+s-\sigma))\mathrm{d}\sigma\right.\\ &&\quad\left.+{\int}_{a}^{\infty}[S_{\alpha}(\sigma+s)-S_{\alpha}(\sigma)]f(t-\sigma,x(t-\sigma),Kx(t-\sigma))\mathrm{d}\sigma\right\|\\ &&\le C(\theta,\alpha)M\left[{\int}_{0}^{s}\frac{W((1+K){\Lambda} h(t+s-\sigma))}{1+|\omega|\sigma^{\alpha}}\mathrm{d}\sigma\right.\\ &&\quad\left.+{\int}_{a}^{\infty}\frac{W((1+K){\Lambda} h(t-\sigma))}{1+|\omega|\sigma^{\alpha}}\mathrm{d}\sigma\right]\\ &&\le \frac{\epsilon}{2} \end{array} $$

for s≤δ ₁. Moreover, since {f(t−σ,x(t−σ),K x(t−σ)):0≤σ≤a,x∈B _Λ (C _h (X))} is a relatively compact set and S _α (⋅) is strongly continuous, we can choose δ ₂>0 such that $\|[S_{\alpha }(\sigma +s)-S_{\alpha }(\sigma )]f(t-\sigma ,x(t-\sigma ),Kx(t-\sigma ))\|\le \frac {\epsilon }{2a}$ for s≤δ ₂. Combining these estimates, we get $\|v^{{\prime }}(t+s)-v^{{\prime }}(t)\|\le \epsilon$ for 𝜖 small enough and independent of x∈B _Λ(C _h (X)).

Finally, applying condition (i), we obtain

$$\begin{array}{@{}rcl@{}} \frac{\|v^{{\prime}}(t)\|}{h(t)}&\le& \frac{C(\theta,\alpha)M}{h(t)}{\int}_{-\infty}^{t}\frac{W((1+K){\Lambda} h(s)}{1+|\omega|(t-s)^{\alpha}}\mathrm{d}s\\ & &{\kern10pc}\rightarrow 0,\quad |t|\rightarrow\infty, \end{array} $$

and this convergence is independent of x∈B _Λ(C _h (X)). Hence by Lemma 2.7, $V^{{\prime }}$ is a relatively compact set in C _h (X).

Step 4: Let us assume that x ^λ(⋅) is a solution of equation x ^λ=λΓ(x ^λ) for some 0<λ<1. We obtain the following estimate

$$\begin{array}{@{}rcl@{}} \|x^{\lambda}(t)\|&=&\lambda\left\|{\int}_{-\infty}^{t}S_{\alpha}(t-s)f(s,x^{\lambda}(s),Kx^{\lambda}(s))\mathrm{d}s\right\|\\ &\le & C(\theta,\alpha)M{\int}_{-\infty}^{t}\frac{W((1+K)\|x^{\lambda}\|_{h}h(s))}{1+|\omega|(t-s)^{\alpha}}\mathrm{d}s\\ &\le& \beta(\|x^{\lambda}\|_{h}). \end{array} $$

Hence, we get

$$\frac{\|x^{\lambda}\|_{h}}{\beta(\|x^{\lambda}\|_{h})}\le 1. $$

Combining the above relation with condition (iii), we conclude that the set {x ^λ:x ^λ=λΓ(x ^λ),λ∈(0,1)} is bounded.

Step 5: It follows from Lemma 2.5, (A5)–(A6) and Theorem 2.4 that the function $t\rightarrow f(t,x(t),Kx(t))$ belongs to S ^p W P A A(R,X), whenever x∈W P A A(R,X). Hence using Lemma 3.2, we get ${\Gamma }(WPAA(R,X))\subset WPAA(R,X)$ and notice that W P A A(R,X) is a closed subspace of C _h (X). Consequently we can consider the map, ${\Gamma }:WPAA(R,X)\rightarrow WPAA(R,X)$. Using Steps 1–3, we deduce that this map is completely continuous. Applying Lemma 2.8, we infer that Γ has a fixed point x∈W P A A(R,X), which completes the proof. □

4 Example

Fractional partial differential equations have already appeared in several texts on physics and mathematics. Diffusion wave equations of fractional order has been used in many branches of science. These kind of equations represent propagation of mechanical waves in visco-elastic media, charge transport in amorphous semiconductors and many more phenomena. Mathematical aspects of the boundary value problems for these kind of equations and their applications in physics have been considered by many authors (e.g. [31; 36] and reference therein). For example, Mainardi [31] discussed the fractional wave equation governing the propagation of mechanical diffusive waves in viscoelastic media which exhibit a power law creep and Giona et al. [27] have studied the relaxation phenomena in complex viscoelastic material using fractional diffusion equations.

Motivated by the above literature, we consider the following relaxation/oscillation partial differential equation of fractional order as an example of our abstract system,

$$\begin{array}{@{}rcl@{}} \frac{\partial^{\alpha} w(t,x)}{\partial t^{\alpha}}-\frac{\partial^{2} w(t,x)}{\partial x^{2}} & = & \frac{\partial^{\alpha-1}}{\partial t^{\alpha-1}}(f(t,x,w(t,x),Kw(t,x))),\\ &&\quad t\in \mathbb{R}, \quad x\in (0,1) \\ Kw(t,x) & = & {\int}_{-\infty}^{t}k(t-s)h(s,x,w(s,x))\mathrm{d}s, \end{array} $$

(4.1)

$$\begin{array}{@{}rcl@{}} w(t,0)&=& w(t,1)=0, \end{array} $$

(4.2)

where α∈(1,2) and k satisfy $|k(t)| \le c_{k}\mathrm {e}^{-bt}$ for t≥0 and c _k ,b are positive constants, is a real valued function. The function f is defined from $\mathbb {R} \times (0,1) \times \mathbb {R}\times \mathbb {R}$ into $\mathbb {R}$ and h is defined from $\mathbb {R} \times (0,1) \times \mathbb {R}$ into $\mathbb {R}.$ We define an operator A as follows:

$$Au=-u^{\prime \prime},$$

for $u\in D(A)=\{u\in {H_{0}^{1}}(0,1)\cap H^{2}(0,1):u^{\prime \prime } \in H\}.$ The operator A is the infinitesimal generator of an analytic semigroup {T(t):t≥0}, and also self-adjoint [35]. By introducing u(t)x=w(t,x), the above example can be written as

$$D^{\alpha}_{t} u(t)=Au(t)+D^{\alpha-1}_{t} f(t, u(t), Ku(t)), \ u \in X,$$

and $Ku(t)={\int }_{-\infty }^{t}k(t-s)h(s,u(s))\mathrm {d}s.$ If we assume that f satisfy all the assumptions of our result with Lipschitz constant L _f , then the existence of a Stepanov weighted pseudo almost automorphic solution of equation (4.2) is ensured.