1 Introduction

Fractional-order differential equations have been introduced since 300 years ago. In fractional-order calculus theory, non-integer order differentiations and integrations are allowed. In fact, fractional-order differential equations use arbitrary orders of the differentiations and integrations instead of integer ones. In recent years, applications of fractional calculus in real world systems, such as viscoelastic materials [1], energy supply–demand system [2], mechanical systems [3, 4], medical modeling [5], optimization tool [6], and electronic circuit [7], have been successfully reported in the literature. Moreover, applications of fractional-order control techniques in heat diffusion systems [8] and control systems [9–11] have been addressed in the literature. And, it has been shown that the fractional calculus can be applied as an important mathematical tool for exact modeling of practical systems. Therefore, the consideration and analysis of fractional-order dynamical systems are essential in both research and practice.

Chaos is a complex nonlinear phenomenon which is frequently observed in physical, biological, electrical, mechanical, economical, and chemical systems. A chaotic system is a nonlinear deterministic dynamical system that exhibits special attributes including extraordinary sensitivity to system initial conditions, broad band Fourier spectrum, strange attractor, and fractal properties of the motion in phase space. Due to the existence of chaos in real world systems and many valuable applications in engineering and science, synchronization and stabilization of chaotic systems have attracted significant interests among the researchers in the last decades [12–15].

Nowadays, it has been revealed that several fractional-order systems exhibit chaotic behaviors [16–21]. In this regard, some scholars have proposed various control methods for control and synchronization of fractional-order chaotic systems. In [22], the problem of stabilization of fractional-order systems using a finite number of state feedback laws has been addressed. Hamamci [23] has proposed fractional-order PI and PID controllers for stabilization of a given fractional dynamical system. An adaptive controller has been reported in [24] to synchronize chaotic fractional-order systems. In [25], an adaptive sliding mode control schema has been introduced for synchronizing two different uncertain fractional-order chaotic systems. In [26], the problem of decentralized control of fractional-order large-scale nonlinear systems has been solved. The work [27] has used an active control method for anti-synchronization between identical and non-identical fractional-order chaotic systems. Li and Chen [28] have applied traditional Lyapunov theory to synchronize a class of fractional-order chaotic systems via a fractional-order controller approach. Feedback synchronization of the fractional-order reverse butterfly-shaped chaotic system has been studied in [29] and its application to digital cryptography has been demonstrated. Recently, Aghababa [30–38] has used the fractional Lyapunov theorem to design some nonlinear controllers for synchronization and stabilization of fractional chaotic systems.

However, most of the aforementioned papers either have not considered the effects of model uncertainties and external disturbances or they are specific and multi-input. On the other hand, in practical situations, the system uncertainties and external disturbances exist in the chaotic systems’ dynamics. In addition, realizing control of the chaotic systems by designing a single input controller is a significant problem in practical applications, where the single input controller is cheaper and easier to be implemented than a multi-input controller. Thus, it is more valuable to stabilize fractional-order chaotic systems via a single control input. Furthermore, with the discovery of applied non-autonomous fractional-order chaotic systems, such as fractional gyroscope and fractional flywheel governor systems, the stabilization of non-autonomous fractional-order chaotic systems has become as a challenging and open problem to be solved by the control community.

In this paper, we propose an alternative control scheme which utilizes a fractional integral-type sliding surface as well as a single input control law. The proposed fractional sliding mode control is applied for stabilization of uncertain fractional-order autonomous and non-autonomous chaotic systems. First, a novel simple fractional integral-type switching manifold is introduced and it is shown that the resulting sliding mode dynamics is asymptotically stable. Then, using the variable structure control theory, a robust sliding mode switching control law is derived to force the system states to attain the designed fractional sliding manifold in a given finite time and stay on it forever (i.e., to ensure the existence of the sliding motion in a finite time). The finite-time stability of the reaching phase is proved using the fractional Lyapunov stability theorem. Finally, we present two illustrative examples to show the applicability and efficiency of the proposed fractional control technique and to validate the theoretical results of this paper. The main highlights and contributions of this paper are as follows: (1) design of a novel fractional integral-type sliding manifold which is applicable for fractional-order systems; (2) considering the effects of both model uncertainties and external noises in the system dynamics; (3) stabilization of both fractional-order autonomous and non-autonomous chaotic systems; (4) realization of the proposed fractional variable structure control via a single input controller; and (5) guaranteeing the finite-time stability of the reaching phase of the sliding mode controller.

The rest of this paper is organized as follows. In Sect. 2, preliminaries of fractional calculus are included. In Sect. 3, the formulation of the robust control problem of uncertain fractional-order dynamical systems is given. In Sect. 4, the design procedure of the proposed fractional-order variable structure control approach is presented. Some numerical simulations are provided in Sect. 5. At last, Sect. 6 ends this paper with conclusions.

2 Preliminaries of fractional-order differential equations

Up to now, several definitions for the fractional derivatives have been proposed. However, the definition of the fractional-order integration is unique and is given as follows [39]:

Definition 1

The \(\alpha \)th-order Riemann–Liouville fractional integration of function \(f(t)\) is given by

$$\begin{aligned} {}_{t_0 }{I_{t}}^{\alpha } f\left( t \right) =D_t^{-\alpha } f\left( t \right) =\frac{1}{{\Gamma }({\alpha })} \int \nolimits _{t_0 }^t \frac{f(\tau )}{\left( {t-\tau } \right) ^{1-\alpha }}\mathrm{d}\tau , \end{aligned}$$
(1)

where \(\alpha \in R^{+}\), \(\hbox {t}_0 \) is the initial time and \(\Gamma (.)\) is the Gamma function which is defined by \(\Gamma \left( z \right) = \int \nolimits _{t_0 }^\infty t^{z-1}e^{-t}\mathrm{d}t\).

Two important and commonly used definitions of fractional derivatives are listed below [39].

Definition 2

Let \(m-1<\alpha \le m\), \(m\in N\), the Riemann–Liouville fractional derivative of order \(\alpha \) of function \(f(t)\) is defined as follows:

$$\begin{aligned}&_{t_0 }^{RL} D_t^\alpha f\left( t \right) =\frac{\mathrm{d}^{\alpha }f(t)}{\mathrm{d}t^{\alpha }}\nonumber \\&=\frac{1}{{\Gamma }(m-\alpha )}\frac{\mathrm{d}^{m}}{\mathrm{d}t^{m}}\int \nolimits _{t_0 }^t \frac{f(\tau )}{\left( {t-\tau } \right) ^{\alpha -m+1}}\mathrm{d}\tau \end{aligned}$$
(2)

Remark 1

From Definitions 1 and 2 one can see that the relation

$$\begin{aligned} {}_{\quad t_0 }^{RL} {D_{t}^\alpha } \left( {{t_0 }^{{I_{t}^\alpha }} f\left( t \right) } \right) =f\left( t \right) \end{aligned}$$

is satisfied for the Riemann–Liouville fractional integrations and derivatives of order \(\alpha \).

Definition 3

The Caputo fractional derivative of order \(\alpha \) of function \(f(t)\) is defined as follows:

$$\begin{aligned} {_{t_0 }^C}{D_{t}^\alpha } f(t)\!=\!\left\{ \!\! {{\begin{array}{ll} \frac{1}{\Gamma ( {m-\alpha })} \int \nolimits _{t_0 }^t \frac{f^{(m)}( \tau )}{( {t-\tau })^{\alpha -m+1}}\mathrm{d}\tau ,&{}\,\,m\!-\!1\!<\!\alpha \!<\!\!m \\ \frac{\mathrm{d}^{m}}{\mathrm{d}t^{m}}f( t), &{}\,\, \alpha =m \\ \end{array} }} \right. \end{aligned}$$
(3)

where \(m\) is the smallest integer number, larger than \(\alpha \).

Remark 2

It should be noted that the definition of Caputo fractional integration is identical to the definition of Riemann–Liouville fractional integration. Subsequently, from Definitions 1 and 3 one can see that the relation

$$\begin{aligned} {{}_{t_0}^C} {D_t^\alpha } ({{_{t_0}{{I_{t}^\alpha } f( t )}}})=f( t) \end{aligned}$$

is satisfied for the Caputo fractional integrations and derivatives of order \(\upalpha \).

Property 1

The following equality holds for both the Riemann–Liouville and Caputo derivatives [39].

$$\begin{aligned} {{}_{\quad t_0 }^{RL,C}} {D_{t}^\alpha } ( {_{\quad t_0 }^{RL,C} {D_{t}^{-\beta }} f( t )} )=_{\quad t_0 }^{RL,C} {D_{t}^{\alpha -\beta }} f( t ) \end{aligned}$$
(4)

where \(\alpha \ge \beta \ge 0\).

Property 2

[39]. For the Riemann–Liouville derivative, we have

$$\begin{aligned}&{ }_{\quad t_0 }^{RL} D_t^{-\alpha } \left( {{ }_{\quad t_0 }^{RL} D_t^\beta f(t)} \right) ={ }_{\quad t_0 }^{RL} D_t^{\beta -\alpha } f\left( t \right) \nonumber \\&\quad -\sum \nolimits _{j=1}^m \left[ {{ }_{\quad t_0 }^{RL} D_t^{\beta -j} f(t)} \right] _{\left| {t=t_0 } \right. } \frac{\left( {t\!-\!t_0 } \right) ^{\alpha \!-\!j}}{{\Gamma }(1\!+\!\alpha \!-\!j)} , (m-1\!\le \! \beta \! <\!m)\nonumber \\ \end{aligned}$$
(5)

In the rest of this paper, the notation \(D^{\alpha }\) indicates the Riemann–Liouville fractional derivative.

Lemma 1

For an integrable function \(f( t )\), assume that for a nonzero interval \(t\in (0,T)\) the condition \(\left| {f(t)} \right| \ge F_1 \), where \(F_1 >0\) is a constant, is held. Then, there is a positive constant

$$\begin{aligned} L=\frac{F_1 T^{\alpha }}{{\Gamma }\left( {1+\alpha } \right) } \end{aligned}$$

such that the inequality

$$\begin{aligned} { }_0{I_{t_1}^{\alpha }} \left| {f\left( t \right) } \right| \ge L \end{aligned}$$

is hold for \(t\in \left( {0,t_1 } \right) ,t_1 \ge T\).

Proof

It is clear that the equality

$$\begin{aligned} {}_0 {I_{t_1 }}^{\alpha } \left| {f( t )} \right| =\frac{1}{{\Gamma }(\alpha )} \int \nolimits _0^{t_1 } \frac{\left| {f(\tau )} \right| }{\left( {t-\tau } \right) ^{1-\alpha }}\mathrm{d}\tau \end{aligned}$$

can be resulted from the definition of the fractional integration Eq. (1). Now, since there is at least one nonzero interval \(t\in (0,T)\) such that the condition \(\left| {f(t)} \right| \ge F_1 \) is satisfied, we have

$$\begin{aligned} { }_0I_{t_1 }^{\alpha } \left| {f\left( t \right) } \right|&=\frac{1}{{\Gamma }(\alpha )} \int \nolimits _0^{t_1 } \frac{\left| {f(\tau )} \right| }{\left( {t-\tau } \right) ^{1-\alpha }}\mathrm{d}\tau \nonumber \\&\ge \frac{1}{{\Gamma }(\alpha )}\int \nolimits _0^T \frac{\left| {f(\tau )} \right| }{\left( {t-\tau } \right) ^{1-\alpha }}\mathrm{d}\tau \nonumber \\&\ge \frac{F_1 }{{\Gamma }(\alpha )}\int \nolimits _0^T \frac{1}{\left( {t-\tau } \right) ^{1-\alpha }}\mathrm{d}\tau \nonumber \\&=\frac{F_1 T^{\alpha }}{{\Gamma }\left( {1+\alpha } \right) } \end{aligned}$$
(6)

So, it is obvious that the inequality

$$\begin{aligned} {{ }_{0}} I_t^{\alpha } \left| {f\left( t \right) } \right| \ge \frac{F_1 T^{\alpha }}{{\Gamma }\left( {1+\alpha } \right) } \end{aligned}$$

holds for \(f\left( t \right) \). This completes the proof.\(\square \)

Theorem 1

Consider the following autonomous linear fractional-order system

$$\begin{aligned} D^{\alpha }x=Ax,\quad x\left( 0 \right) ={x_0} \end{aligned}$$
(7)

where \(0<\alpha <1\), \(x\in R^{n}\) and \(A\in R^{n\times n}\).

This system is asymptotically stable iff

$$\begin{aligned} \left| {\arg \left( {eigA} \right) } \right| >\alpha \pi /2. \end{aligned}$$

In this case, each component of the states decays toward \(0\) like \(t^{-\alpha }\).

Proof

See [40].\(\square \)

Theorem 2

Let \(x=0\) be an equilibrium point for the non-autonomous fractional-order system

$$\begin{aligned} D^{\alpha }x\left( t \right) =f(x,t), \end{aligned}$$
(8)

where \(f(x,t)\) satisfies the Lipschitz condition with Lipschitz constant \(l>0\) and \(\alpha \in (0,1)\). Assume that there exist a Lyapunov function \(V(t,x(t))\) and class-K functions \(\alpha _1 \), \(\alpha _2 \), and \(\alpha _3 \) satisfying

$$\begin{aligned}&\alpha _1 \left( \Vert x \Vert \right) \le V(t,x)\le \alpha _2 \left( \Vert x \Vert \right) \end{aligned}$$
(9)
$$\begin{aligned}&D^{\beta }V\left( {t,x} \right) \le -\alpha _3 \left( \Vert x \Vert \right) \end{aligned}$$
(10)

where \(\beta \in (0,1)\). Then the equilibrium point of the system (8) is asymptotic stable.

Proof

See [41].\(\square \)

3 Formulation of the robust control of fractional-order uncertain systems

Consider a class of n-dimensional fractional-order chaotic system with model uncertainties, external disturbances, and a single control input as follows:

$$\begin{aligned} \left\{ \! {{\begin{array}{l} {D^{\alpha }x_i =x_{i+1} ,1\le i\le n-1} \\ {D^{\alpha }x_n =f\left( {X,t} \right) +\Delta f\left( {X,t} \right) +d(t)+u(t)}, \\ \end{array} }} \right. \end{aligned}$$
(11)

where \(\alpha \in (0,1)\) is the order of the chaotic system,

$$\begin{aligned} X\left( t \right) =\left[ {x_1 ,x_2 ,\ldots ,x_n } \right] ^{T}\in R^{n} \end{aligned}$$

is the state vector of the chaotic system, \(f(X,t)\in R\) is a given nonlinear function of \(X\) and \(t\), \(\Delta f\left( {X,t} \right) \in R\) represents an unknown model uncertainty term, \(d(t)\in R\) is the external disturbance of the system, and \(u(t)\in R\) is the control input.

Assumption 1

The uncertainty term \(\Delta f\left( {X,t} \right) \) is assumed to be bounded by

$$\begin{aligned} \left| {\Delta f\left( {X,t} \right) } \right| \le \gamma _1, \end{aligned}$$
(12)

where \(\gamma _1 \) is a known positive constant.

Assumption 2

The external disturbance \(d(t)\) is assumed to be bounded by

$$\begin{aligned} \left| {d(t)} \right| \le \gamma _2, \end{aligned}$$
(13)

where \(\gamma _2 \) is a given positive constant.

The control goal of this paper is to design a suitable robust fractional variable structure controller for stabilization of the non-autonomous chaotic system (11) in the presence of system uncertainties and external noises via a single input.

4 The proposed nonlinear variable structure control method

In this section, first a fractional integral-type sliding surface is introduced. Then, a suitable sliding mode control law is proposed to guarantee the occurrence of the sliding motion in a given finite time.

The sliding mode control (SMC) approach [42] is a robust control methodology which is appropriate for high-order nonlinear dynamical systems. The SMC has constructive features such as fast response, low sensitivity to external noises, robustness to the system uncertainties, and easy realization. In the SMC approach, once the system state trajectories approach to the prescribed sliding surface, the system behavior is determined by the sliding mode dynamics. Therefore, the SMC decouples the overall system motion into independent lower dimension components, which decreases the complexity of the controller design. In general, the sliding mode control approach is composed of two phases. The first phase is to select a proper sliding surface with some desired properties. Accordingly, in this paper, we introduce a fractional integral-type sliding surface as follows:

$$\begin{aligned} s\left( t \right) =x_n +D^{-\alpha }\sum \limits _{i=1}^n k_i x_i, \end{aligned}$$
(14)

where \(x_i ,i=1,2,\ldots ,n\) are the system states and \(k_i ,i=1,2,\ldots ,n\) are sliding surface parameters to be introduced later.

Once the system operates in the sliding mode, it satisfies the following Eq. (42).

$$\begin{aligned} s\left( t \right) =0 \end{aligned}$$
(15)

Consequently, Using Eqs. (14) and (15), we have

$$\begin{aligned} s\left( t \right)&= x_n +D^{-\alpha } \sum \limits _{i=1}^n k_i x_i\nonumber \\&= 0\rightarrow x_n =-D^{-\alpha }\sum \limits _{i=1}^n k_i x_i \end{aligned}$$
(16)

Based on the Property 1 and applying the operator \(D^{\alpha }\) to both sides of Eq. (16), we have

$$\begin{aligned} D^{\alpha }x_n =-\sum \limits _{i=1}^n k_i x_i. \end{aligned}$$
(17)

Therefore, using the system dynamics (11) and Eq. (17), the sliding mode dynamics is obtained as follows:

$$\begin{aligned} \left\{ \! {{\begin{array}{l} {D^{\alpha }x_i =x_{i+1} ,\quad 1\le i\le n-1} \\ {D^{\alpha }x_n =- \sum \nolimits _{i=1}^n k_i x_i } \\ \end{array} }} \right. \end{aligned}$$
(18)

Theorem 3

The sliding mode dynamics (18) is asymptotically stable and the states decay toward \(0\) like \(t^{-\alpha }\).

Proof

Rewriting Eq. (18) and rearranging it in a matrix equation form, we have

$$\begin{aligned}&\left\{ \! {{\begin{array}{l} {D^{\alpha }x_1 =x_2 } \\ {D^{\alpha }x_2 =x_3 } \\ \quad \quad \quad {\vdots } \\ {D^{\alpha }x_{n-1} =x_n } \\ {D^{\alpha }x_n =-\sum \nolimits _{i=1}^n k_i x_i } \\ \end{array} }\rightarrow \underbrace{\left[ {{\begin{array}{l} {D^{\alpha }x_1 } \\ {D^{\alpha }x_2 } \\ \vdots \\ {D^{\alpha }x_{n-1} } \\ {D^{\alpha }x_n } \\ \end{array} }} \right] }_{D^{\alpha }X\left( t \right) }} \right. \nonumber \\&= \left[ {{\begin{array}{c} {x_2 } \\ {x_3 } \\ \vdots \\ {x_n } \\ {- \sum \nolimits _{i=1}^n k_i x_i } \\ \end{array} }} \right] \nonumber \\&= {\underbrace{\left[ {{\begin{array}{cccccc} {0}&{} {1}&{} {0}&{}\ldots &{} {\ldots }&{} {0} \\ {0}&{} {0}&{} {1}&{}0&{} {\ldots }&{} {\vdots } \\ \vdots &{} \vdots &{} \vdots &{}\ddots &{} {\ddots }&{} {\vdots } \\ {-k_1 }&{} {-k_2 }&{} \ldots &{} \ldots &{} \ldots &{} {-k_n } \\ \end{array} }} \right] }_A} {\underbrace{\left[ {{\begin{array}{c} {x_1 } \\ {x_2 } \\ \vdots \\ {x_{n-1} } \\ {x_n } \\ \end{array} }} \right] }_{X\left( t \right) }}\nonumber \\&= AX\left( t \right) \end{aligned}$$
(19)

where \(A\) is an \(n\times n\) constant matrix.

The sliding surface parameters \(k_i \) are selected to be positive such that the eigenvalues of matrix \(A\) satisfy the stability condition of Theorem 1, i.e., \(\left| {\arg \left( {eigA} \right) } \right| >\alpha \pi /2\). Therefore, it can be concluded that the sliding mode dynamics (18) is asymptotic stable and if the system states reach it, then they will be converged to the origin. Thus, the proof is completed.

Once an appropriate sliding surface is established, the next step is to determine an input signal \(u(t)\) to guarantee that the system trajectories reach to the sliding surface \(s\left( t \right) =0\) in a given finite time and stay on it forever. In this paper, we propose the following robust sliding mode control law.

$$\begin{aligned} u\left( t \right) =-\left( f( {X,t} )+( {\gamma _1 +\gamma _2 } )sgn( s )\right. \nonumber \\ +\left. \sum \limits _{i=1}^n k_i x_i +\zeta _1 s+\zeta _2 sgn\left( s \right) \right) \end{aligned}$$
(20)

where \(\zeta _1 ,\zeta _2 >0\) are constant scalars.

In what follows, we use the fractional Lyapunov theorem to prove that the sliding motion takes place in a finite time.

Theorem 4

Consider the sliding surface in Eq. (14). If the system (11) with the conditions (12) and (13) is controlled using the control law (20), then the system states will converge to the sliding surface \(s\left( t \right) =0\) in a finite time.

Proof

First, motivated by the work [43], we assume that the following inequality holds.

$$\begin{aligned} \left| { \sum \limits _{i=1}^\infty \frac{{\Gamma }(1+\alpha )}{{\Gamma }(1+i){\Gamma }(1-i+\alpha )}D^{i}sD^{\alpha -i}s} \right| \le \vartheta \left| s \right| \end{aligned}$$
(21)

where \(\vartheta \) is a positive constant.

We choose the following positive definite Lyapunov function candidate

$$\begin{aligned} V\left( t \right) =s^{2}. \end{aligned}$$
(22)

Taking the fractional-order derivative of \(V\left( t \right) \), one has [43]

$$\begin{aligned} D^{\alpha }V\!=\!sD^{\alpha }s+ \sum \limits _{i=1}^\infty \frac{{\Gamma }(1+\alpha )}{{\Gamma }(1+i){\Gamma }(1-i+\alpha )}D^{i}sD^{\alpha -i}s. \end{aligned}$$
(23)

Using the inequality (21), we have

$$\begin{aligned} D^{\alpha }V&\le sD^{\alpha }s +\left| {\sum \limits _{i=1}^\infty \frac{{\Gamma }\left( {1+\alpha } \right) }{{\Gamma }\left( {1+i} \right) {\Gamma }\left( {1-i+\alpha } \right) }D^{i}sD^{\alpha -i}s} \right| \nonumber \\&\le sD^{\alpha }s+\vartheta \left| s \right| . \end{aligned}$$
(24)

Applying \(D^{\alpha }\) to both sides of Eq. (16) and inserting it to the above inequality, we have

$$\begin{aligned} D^{\alpha }V\le s\left( {D^{\alpha }x_n + \sum \nolimits _{i=1}^n k_i x_i } \right) +\vartheta \left| s \right| . \end{aligned}$$
(25)

Based on \(D^{\alpha }x_n =f\left( {X,t} \right) +\Delta f\left( {X,t} \right) +d(t)+u(t)\), one has

$$\begin{aligned} D^{\alpha }V&\le s\left( f\left( {X,t} \right) +\Delta f\left( {X,t} \right) +d(t)+u(t)\right. \nonumber \\&\quad +\left. \sum \limits _{i=1}^n k_i x_i \right) +\vartheta \left| s \right| \end{aligned}$$
(26)

Substituting \(u\left( t \right) \) from (20) into (26), it yields

$$\begin{aligned}&D^{\alpha }V\le s\left( f\left( {X,t} \right) +\Delta f\left( {X,t} \right) +d(t)\right. \nonumber \\&\quad \left. -\left[ f\left( {X,t} \right) +\left( {\gamma _1 +\gamma _2 } \right) sgn\left( s \right) \right. \right. \nonumber \\&\quad +\left. \left. \sum \nolimits _{i=1}^n k_i x_i +\zeta _1 s+\zeta _2 sgn\left( s \right) \right] +\sum \nolimits _{i=1}^n k_i x_i \right) +\vartheta \left| s \right| \nonumber \\ \end{aligned}$$
(27)

It is obvious that

$$\begin{aligned}&D^{\alpha }V\le \left| s \right| \left( {\left| {\Delta f\left( {X,t} \right) } \right| +\left| {d(t)} \right| } \right) \nonumber \\&\quad -\, s\left( {\left( {\gamma _1 \!+\!\gamma _2 } \right) sgn\left( s \right) \!+\!\zeta _1 s\!+\!\zeta _2 sgn\left( s \right) } \right) \!+\!\vartheta \left| s \right| \end{aligned}$$
(28)

Using Assumptions 1 and 2, one has

$$\begin{aligned}&D^{\alpha }V\le \left| s \right| \left( {\gamma _1 +\gamma _2 } \right) \nonumber \\&\quad -\, s\left( {\left( {\gamma _1 +\gamma _2 } \right) sgn\left( s \right) +\zeta _1 s+\zeta _2 sgn\left( s \right) } \right) +\vartheta \left| s \right| \nonumber \\ \end{aligned}$$
(29)

On the basis of \(sgn\left( s \right) s=\left| s \right| \), one obtains

$$\begin{aligned} D^{\alpha }V\le -\zeta _1 s^{2}-\zeta _2 \left| s \right| +\vartheta \left| s \right| \le -\left( {\zeta _2 -\vartheta } \right) \left| s \right| \end{aligned}$$
(30)

where \(\zeta _2 \) is set as \(\zeta _2 >\vartheta \). Consequently, based on Theorem 2, the system states will converge to \(s\left( t \right) =0\) asymptotically.

In order to show that the sliding motion happens in finite time, we have the following statements.

Using Eqs. (24) and (30), we have

$$\begin{aligned} sD^{\alpha }s\le -\zeta _1 s^{2} \end{aligned}$$
(31)

\(\square \)

According to the sign of \(s\), one has the following two cases.

Case 1

\(s>0,s=\left| s \right| \): In this case, dividing both sides of (31) by \(s\), one has

$$\begin{aligned} D^{\alpha }\left| s \right| \le -\zeta _1 \left| s \right| \end{aligned}$$
(32)

Taking the fractional integral of both sides of (32) from \(0\) to the reaching time \(t_r \) and using Property 2, one obtains

$$\begin{aligned} \left| {s\left( {t_r } \right) } \right| -\left| {s(0)} \right| ^{\alpha -1}\frac{t_r^{\alpha -1} }{{\Gamma }(\alpha )}\le -\zeta _1 D^{-\alpha }\left| s \right| \end{aligned}$$
(33)

Based on Lemma 1 and \(D^{-\alpha }\left| {s\left( t \right) } \right| \ge L\), where \(L=\frac{F_1 T^{\alpha }}{{\Gamma }\left( {1+\alpha } \right) }\) is a positive constant, and since \(s\left( {t_r } \right) =0\), we have

$$\begin{aligned} -\left| {s(0)} \right| ^{\alpha -1}\frac{t_r^{\alpha -1} }{{\Gamma }(\alpha )}\le -\zeta _1 L \end{aligned}$$
(34)

After simple manipulations, one has

$$\begin{aligned} t_r \le \left( {\frac{\left| {s(0)} \right| ^{\alpha -1}}{\zeta _1 L}} \right) ^{\frac{1}{1-\alpha }} \end{aligned}$$
(35)

Therefore, in the case of \(s>0\), the states of the system (11) will converge to the sliding surface \(s\left( t \right) =0\) in a finite time.

Case 2

\(s<0,s=-\left| s \right| \): In this case, dividing both sides of (31) by \(s\), one has

$$\begin{aligned} D^{\alpha }s\ge -\zeta _1 s \end{aligned}$$
(36)

Since \(s<0\) is assumed, using \(s=-\left| s \right| \) one obtains

$$\begin{aligned} D^{\alpha }\left| s \right| \le -\zeta _1 \left| s \right| \end{aligned}$$
(37)

Eq. (37) is equal to Eq. (32). Thus, using a same approach applied in Eqs. (33)–(35) the reaching time is obtained as \(t_r \le \left( {\frac{\left| {s(0)} \right| ^{\alpha -1}}{\zeta _1 L}} \right) ^{\frac{1}{1-\alpha }}\). Hence, in the case of \(s<0\), the states of the system (11) will converge to the sliding surface \(s\left( t \right) =0\) in a finite time. This completes the proof.

Remark 3

In Eq. (20), the values of the control parameters can be selected as follows: a) the parameters \(\gamma _1 \) and \(\gamma _2 \) are chosen such that the conditions of Assumption 1 are satisfied; b) the parameters \(k_i ,i=2,3,\ldots ,n\) are chosen to be positive such that the polynomial \(k_n \lambda ^{n-1}+k_{n-1} \lambda ^{n-2}+\cdots +k_2 \lambda +k_1 \) is Hurwitz. In other word, all the roots of the characteristic polynomial \(k_n \lambda ^{n-1}+k_{n-1} \lambda ^{n-2}+\cdots +k_2 \lambda +k_1 \)have negative real parts with desirable pole placement. This selection guarantees the satisfaction of the condition \(\left| {\arg \left( {eigA} \right) } \right| >\alpha \pi /2\).; c) the parameter \(\zeta _1 \) is related to the reaching time expressed in Eq. (35) and affects the control effort. A large value of the parameter \(\zeta _1 \) results in a small reaching time and high control effort. On the other hand, the small value of the parameter \(\zeta _1 \) leads to a large reaching time and low control effort. Therefore, the value of the parameter \(\zeta _1 \)is user and/or problem dependant; d) the parameter \(\zeta _2 \) is the switching gain. It is related to the variable structure inherent of the proposed sliding mode controller. The parameter \(\zeta _2 \) controls the discontinuity of \(u\left( t \right) \). In other word, a large value of \(\zeta _2 \) increases the switching gain and, therefore, the control effort is also decreased. Thus, a small value for the parameter \(\zeta _2 \) is advised.

5 Two illustrative examples

In this section, some numerical simulations are presented to illustrate the effectiveness and efficiency of the proposed fractional sliding mode scheme and to verify the theoretical results of this paper.

5.1 Example 1

This example illustrates the effectiveness of the proposed fractional sliding mode controller in chaos suppression of the following fractional-order uncertain Arneodo chaotic systems [21].

$$\begin{aligned} \left\{ \! {{\begin{array}{l} {D^{\alpha }x_1 =x_2 } \\ {D^{\alpha }x_2 =x_3 } \\ D^{\alpha }x_3 =5.5x_1 -3.5x_2 -x_3 +x_1^3 +\Delta f\left( {x,t} \right) \\ \qquad \qquad \quad +d(t)+u(t). \\ \end{array} }} \right. \end{aligned}$$
(38)

The uncertainty term and external noise of the system are selected as follows:

$$\begin{aligned} \Delta f\left( {X,t} \right) +d(t)=0.1\cos \left( {5t} \right) x_3 -0.1\hbox {sin}(t) \end{aligned}$$
(39)

Initial conditions of the Arneodo system are selected as \(x_1 \left( 0 \right) =0.2\), \(x_2 \left( 0 \right) =-0.1\), and \(x_3 \left( 0 \right) =0.3\). The fractional order \(\alpha \) is also set to \(0.98\) to ensure the existence of chaos for the Arneodo system [21].

We use Eq. (14) and design the following sliding surface.

$$\begin{aligned} s\left( t \right) =D^{-0.98}\left( {40x_1 +15x_2 +x_3 } \right) +x_3 \end{aligned}$$
(40)

Subsequently, according to Eq. (20), the proper control input is designed as follows:

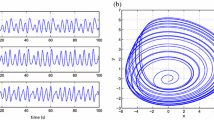
$$\begin{aligned} u\left( t \right)&=-\Big ( 5.5x_1 -3.5x_2 -x_3 +x_1^3 +0.2sgn\left( s \right) \nonumber \\&\quad +40x_1 +15x_2 +x_3 +0.1s+sgn\left( s \right) \Big ) \end{aligned}$$
(41)

The state trajectories of the controlled fractional-order uncertain Arneodo system are shown in Fig. 1. It can be seen that the states converge to zero, which implies that the chaotic behavior of the fractional-order uncertain Arneodo system is successfully suppressed. The time response of the proposed sliding surface (40) is plotted in Fig. 2. It is clear that the sliding surface converges to zero. The time history of the adopted control input (41) is depicted in Fig. 3. Obviously, the control input is feasible in practical applications.

Fig. 1
figure 1

State trajectories of the controlled fractional-order Arneodo system (38)

Full size image
Fig. 2
figure 2

Time response of the applied fractional sliding surface (4)

Full size image
Fig. 3
figure 3

Time history of the adopted sliding control input (41)

Full size image

5.2 Example 2

In this example, the chaotic behavior of the following fractional-order uncertain Genesio chaotic systems [44] is suppressed via the proposed method.

$$\begin{aligned} \left\{ \! {{\begin{array}{l} {D^{\alpha }x_1 =x_2 } \\ {D^{\alpha }x_2 =x_3 } \\ D^{\alpha }x_3 =-6x_1 -2.92x_2 -1.2x_3 +x_1^2\\ \qquad \qquad \quad +\Delta f\left( {X,t} \right) +d(t)+u(t) \\ \end{array} }} \right. \end{aligned}$$
(42)

The uncertainty term and external noise of the system are selected same as those in Eq. (39). Initial conditions of the Genesio system are selected as \(x_1 \left( 0 \right) =3\), \(x_2 \left( 0 \right) =1\), and \(x_3 \left( 0 \right) =1\). The fractional order \(\alpha \) is also set to \(0.98\) to ensure the existence of chaos for the Genesio system [44].

We use Eq. (14) and propose the following sliding surface.

$$\begin{aligned} s\left( t \right) =D^{-0.98}\left( {100x_1 +10x_2 +x_3 } \right) +x_3 \end{aligned}$$
(43)

Subsequently, according to Eq. (20), the proper control input is derived as follows:

$$\begin{aligned} u\left( t \right)&= -\Big ( -6x_1 \!-\!2.92x_2 \!-\!1.2x_3 \!+\! x_1^2 \!+\!0.2sgn\left( s \right) \nonumber \\&\quad +100x_1 +10x_2 +x_3 +s+sgn\left( s \right) \Big ) \end{aligned}$$
(44)

Figure 4 illustrates the state trajectories of the controlled fractional-order uncertain Genesio system. One can see that the system states approach to zero, which indicates that the chaotic behavior of the fractional-order uncertain Genesio system is effectively suppressed. Figure 5 depicts the time response of the applied sliding surface (43). It is seen that the sliding surface attains to zero. The time history of the adopted control input (44) is revealed in Fig. 6. Obviously, the control input is practical.

Fig. 4
figure 4

State trajectories of the controlled fractional-order Genesio system (42)

Full size image
Fig. 5
figure 5

Time response of the applied fractional sliding surface (43)

Full size image
Fig. 6
figure 6

Time history of the adopted sliding control input (44)

Full size image

6 Conclusions

The present paper introduces a novel fractional variable structure controller for stabilization of a class of fractional-order chaotic systems in the presence of both system uncertainties and external disturbances. First, a new fractional integral-type sliding manifold is introduced. It is shown that the proposed sliding manifold is asymptotically stable. Afterwards, based on the variable structure control theory, a robust sliding switching control signal is introduced to ensure the existence of the sliding motion in finite time. We apply the fractional Lyapunov stability theorem to prove the stability of the proposed control scheme. Also, we present some computer simulations to illustrate the effectiveness and applicability of the method for controlling both autonomous and non-autonomous fractional-order uncertain nonlinear dynamical, canonical formed systems.