Abstract
In this paper, first, general dynamic modeling is proposed for multi-input/output nonlinear systems in the form of affine and non-affine systems. Then, an observer barrier function-based adaptive fuzzy scheme is suggested to estimate unknown functions. Briefly, the main contributions of the proposed scheme are: (1) the proposed modeling can be employed in various classes of nonlinear systems, e.g., Single Input–Single Output (SISO), Single Input–Multi Output (SIMO), Multi Input–Single Output (MISO), and Multi Input–Multi Output (MIMO) systems with square or non-square control gain matrix, (2) by combining an observer error signal and the barrier Lyapunov function, the proposed Observer-based Barrier Lyapunov Function (OBLF) method can be employed to solve the problems of output constraint by preventing the output from violating the constraint, and (3) a non-singular robust adaptive fuzzy approach is presented for various classes of nonlinear systems so that the uncertainties are attenuated by a robust bounded \({H}_{\infty }\)-like control term. The proposed scheme guarantees the stability of the closed-loop system based on the Strictly Positive Real (SPR) condition and OBLF theory, but it does not need the SPR conditions to be well known. Finally, to show the usefulness of the proposed technique, the simulation examples are employed for various classes of nonlinear affine and non-affine systems with square or non-square control gains.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Nonlinear dynamical systems can be found in a wide variety of applications, e.g., MIMO, SIMO, MISO, and SISO systems, and also affine and non-affine systems. Stabilization and tracking control are some of the essential parts of these nonlinear systems.
Consider \(\dot{\mathbf{X}}=\mathbf{F} \left(\mathbf{X},\mathbf{U}\right)\) is a non-affine and \(\dot{\mathbf{X}}=\mathbf{F} \left(\mathbf{X}\right)+\mathbf{G}\left(\mathbf{X}\right)\mathbf{U}\) is an affine nonlinear system, where \(\mathbf{X}\) and U are input and output vectors, \(\mathbf{F} \left(\mathbf{X},\mathbf{U}\right)\) and \(\mathbf{F} \left(\mathbf{X}\right)\) are continuous function vectors, and \(\mathbf{G}\left(\mathbf{X}\right)\) is a square or non-square control gain matrix. The majority of control approaches of nonlinear systems are designed for SISO systems and also the MIMO systems with a square control gain matrix. It is yet difficult to employ a proper control strategy for systems with a non-square control gain matrix. In (Gao and Tong 2015), the authors propose a control method for a MIMO affine model of underwater systems with both square and non-square control gain matrices. Also, most of the articles are applied to the control of affine nonlinear systems, because the development of a control technique for non-affine systems is yet a challenge. The authors in (Ghavidel 2018, 2020; Ghavidel and Kalat 2018) develop their control methods for non-affine systems. Furthermore, the authors in (Ghavidel and Kalat 2017a) develop their control method for a class of MIMO systems with non-square control gain matrices. Moreover, in (Ghavidel 2018; Ghavidel and Kalat 2018) a robust method is employed to control both affine and non-affine nonlinear systems. This paper proposes a simple method is proposed to control MIMO systems with square control gain matrices, MIMO systems with non-square control gain matrices, SIMO, MISO, and SISO systems, and also both affine and non-affine nonlinear systems.
Two types of adaptive fuzzy controllers are commonly researched: indirect and direct adaptive fuzzy methods. An important issue in the indirect adaptive fuzzy technique is the possibility of a singularity problem when the inverse of the control gain matrixes is computing. Recently, several stable control approaches have been developed to overcome the singularity problem of SISO systems (Labiod and Guerra 2010; Ghavidel and Kalat 2019; Ghavidel 2020) and MIMO systems (Min et al. 2017). To avoid the singularity problem, in (Lamara et al. 2012) the non-symmetric control gain matrix of the MIMO system is extracted as the sum of a symmetric matrix and a skew-symmetric matrix. Also, a global non-singular terminal sliding mode control method is presented in (Li and Tong 2003). In (Li and Lee 2011), the controller singularity problem is avoided by the decomposition of the control gain matrix into the product of a symmetric positive-definite matrix, a diagonal matrix, and a unity upper triangular matrix. In (Li et al. 2013a), and the estimation of the control gain matrix is decomposed into the product of one diagonal matrix and two orthogonal matrices. The authors in (Li et al. 2013b) presented a symmetric matrix decomposition technique. A regularized inverse of the estimated control gain matrix is employed in (Lin et al. 2012; Li et al. 2015; Min et al. 2017) to avoid the controller singularity problem, and a complex robust control term was proposed to compensate for uncertainties that appear due to using the regular inverse technique. In this paper, based on the proposed OBLF method a non-singular adaptive fuzzy approach is presented for various classes of nonlinear systems.
In practice, all the system states are not available for measurement. To overcome this problem, the authors in (Guo et al. 2020; Li et al. 2020; Tong et al. 2020; Zhang and Dong 2020) developed observer-based adaptive fuzzy control methods. In (Ghavidel and Kalat 2017b; Ghavidel 2018, 2020), the authors employed an observer-based adaptive fuzzy technique with SPR condition which is required for the closed-loop system stability. An important advantage of these schemes is that the proposed approach does not require SPR conditions to be known. This paper develops this observer method for multi-input/output affine and non-affine systems. (Also, the other schemes of observer-based adaptive fuzzy methods with SPR conditions are developed by the authors in Ren et al. 2010; Rigatos 2014.)
Recently, the logarithm barrier functions in Lyapunov theories have been suggested for nonlinear systems (Shaocheng et al. 2005; Schkoda and Crassidis 2007; Shahnazi 2016). By combining the observer error signal and the barrier Lyapunov function, the proposed OBLF control method can be applied to solve the problems of output constraint by preventing the output from violating the constraint. The main purpose of our design consists of modeling a Lyapunov function to guarantee the limitation of the observer error signals.
In many physical systems, input saturation for a limited bound of the control signal is applied. Applying input saturation is a problem to design a stable controller. Some control schemes have been proposed for nonlinear systems in the presence of input saturation (Shi 2014, 2015). These works assume some complicated assumptions and techniques to utilize input saturations. This paper uses a simple and stable strategy employed to design a limited bound of the control signals.
Finally, the main advantages of the proposed method are as follows:
-
1)
Many researchers develop their control methods for affine systems with square control gains. Based on the proposed technique, a general dynamics model is proposed for affine and non-affine forms of SISO, MIMO, SIMO, and MISO systems with non-square control gain matrices (see Sect. 2 for more details).
-
2)
An essential problem of indirect control methods is the possibility of singularity. A non-singular control approach is presented for various classes of nonlinear systems (see Sect. 3.2 for more details).
-
3)
An accurate method is considered for nonlinear systems in the presence of input saturation. This method does not require complex functions, difficult assumptions, and extra robust terms (see Sect. 3.2 for more details).
-
4)
By using a feedback error function instead of the state variables, the number of fuzzy sets and rules can be decreased so that a smaller tracking error is achieved (see Sect. 4.1 for more details).
-
5)
The basic idea of the observer control method is introduced based on an observer scheme in (Ghavidel and Kalat 2017b; Ghavidel 2018, 2020). Note that these approaches are proposed based on the SPR condition. In this paper, it can be extended to SPR condition via the barrier Lyapunov function theory. Hence, although the observer control technique needs proper conditions for SPR, it does not require SPR conditions to be recognized, i.e., the main advantage of the proposed observer\(-\)based scheme is that matrices \({\mathbf{Q}}_{oi}\), \({\mathbf{P}}_{oi}\), \({\mathbf{Q}}_{i}\), \({\mathbf{P}}_{i}\), vector \({\mathbf{B}}_{si}\) and filter \({L}_{i}(s)\) do not require to be known (see Sect. 4.2 for more details).
-
6)
It is an important advantage that the proposed barrier Lyapunov is a function of the observer error signal \(\widetilde{{e_{{{\text{si}}}} }}\), because the selection of the parameter \({k}_{i}\) will not be restricted (see Sect. 4.3 for more details).
-
7)
A bounded robust \({H}_{\infty }\)-like control term is proposed to compensate for uncertainties. The conventional robust \({H}_{\infty }\) terms are presented in (Ghavidel and Kalat 2017c; Ghavidel et al. 2017, 2020) (see Sect. 4.3 for more details).
2 Problem formulation and preliminaries
The general nonlinear systems (Wang 1996) can be more complicated when they are in the form of non-affine systems. In this section, these complicated systems are transformed into the controllable form of non-affine systems.
Therefore, the general model of nonlinear non-affine systems is as follows
where \(\mathbf{Z}={\left[{\mathbf{Z}}_{i},\dots ,{\mathbf{Z}}_{r}\right]}^{T}\) and \({\mathbf{Z}}_{i}\epsilon {\mathcal{R}}^{{p}_{i}}\) is the state vector,\({\mathbf{F}}_{i}\left(\mathbf{Z},\mathbf{U}\right)\epsilon {\mathcal{R}}^{{p}_{i}}\) is the smooth vector, \({p}_{i}\) represents the order of \(i\)-th subsystem of the non-affine system (1),\(\mathbf{U}={[{u}_{1},\dots ,{u}_{m}]}^{T}\epsilon {\mathcal{R}}^{m}\) is the system input vector, \({\mathbf{D}}_{i}\epsilon {\mathcal{R}}^{{p}_{i}}\) is an unknown but bounded external disturbance vector, and \({h}_{i}(\mathbf{Z})\epsilon \mathcal{R}\) is a smooth and known real function for \(i=\mathrm{1,2},\dots , r\) (i.e., subsystems), and \(j=\mathrm{1,2},\dots , m\) (i.e., system inputs). Note that the MIMO Eq. (1) is a general non-affine dynamics model.
It is very important that the general model (1) is not limited only to the control of MIMO systems, it can be easily extended to the SISO, SIMO, and MISO systems. Because MIMO non-affine systems can be transformed into a SISO affine system (\(i=1\) and \(j=1\)), a SIMO affine system (\(i=1,..,r\) and \(j=1\)) and also a MISO affine system (\(i=1\) and \(j=1,..,m\)).
Based on input–output linearization, a diffeomorphism vector \({\mathbf{T}}_{i}={\left[{T}_{1i},\dots ,{T}_{pi}\right]}^{T}\) can be written as \({\mathbf{T}}_{i}={\left[{h}_{i}, L{h}_{i},\dots ,{L}^{{n}_{i}-1}{h}_{i},{T}_{{n}_{i}+1},\dots ,{T}_{{p}_{i}} \right]}^{T}\), so that the control input \({u}_{j}\) appears in the derivation function \({L}^{{n}_{i}-1}{h}_{i}\). The diffeomorphism vector \({\mathbf{T}}_{i}\) can be rewritten as \({\mathbf{T}}_{i}={\left[{x}_{i},\dots ,{{x}_{i}}^{\left({n}_{i}-1\right)},{\zeta }_{1i},\dots ,{\zeta }_{{p}_{i}-{n}_{i}}\right]}^{T}={\left[{\mathbf{X}}_{i};{{\varvec{\upzeta}}}_{i}\right]}^{T}\).
Accordingly, \({\mathbf{X}}_{i}={\left[{x}_{i},\dots ,{{x}_{i}}^{\left({n}_{i}-1\right)}\right]}^{T}\), \({{\varvec{\upzeta}}}_{i}={\left[{\zeta }_{1i},\dots ,{\zeta }_{{p}_{i}-{n}_{i}}\right]}^{T}\), and \({n}_{i}\,\le \,{p}_{i}\). Hence, it transforms the non-affine system (1) to the following controllable form
where the vector \({\mathbf{D}}_{i}(t)\) is transformed into the scalar \({d}_{i}\left(t\right)\). So, if the zero dynamics \({\mathbf{q}}_{i}\left(0,{{\varvec{\upzeta}}}_{1},\dots ,{{\varvec{\upzeta}}}_{r}\right)\) in (2) is asymptotically stable, non-affine system (2) can be transformed into r subsystem of the affine system as
where \(\mathbf{X}={[{\mathbf{X}}_{1},\dots ,{\mathbf{X}}_{r}]}^{T}\).
Assumption 1
The following assumptions are applied for the controllability of the system:
-
1)
Assume that the relative degree of the controllable system (3) is \({n}_{i}\le {p}_{i}\).
-
2)
The function \(\partial {F}_{i}\left(\mathbf{X},\mathbf{U}\right)/\partial \mathbf{U}\) is nonzero so that \(0<\partial {F}_{i}\left(\mathbf{X},\mathbf{U}\right)/\partial \mathbf{U}\le {\overline{F}}_{i}\), for an unknown positive constant \({\overline{F}}_{i}\). Also, external disturbance \({d}_{i}(t)\) is bounded (i.e., \(|{d}_{i}\left(t\right)|\le {\overline{d} }_{i}\)).
Now, it is assumed that \({\mathbf{g}}_{i}\left(\mathbf{X}\right)\) is a bounded and unknown vector; then, system (3) can be transformed into r subsystem of the affine system as
where
By (4), the general dynamic model can be rewritten as
where \(\mathbf{Y}={[{y}_{1},\dots ,{y}_{r}]}^{T}\epsilon {\mathcal{R}}^{r}\) are the output of the system for \(i=\mathrm{1,2},\dots , r\) and \(j=\mathrm{1,2},\dots , m\), respectively, that \(r\) is the number of subsystems and \({n}_{i}\) is the i-th system relative degree where \({n=n}_{1}+{n}_{2}+\dots +{n}_{r}\). Let denote
\(\mathbf{A}=\mathrm{diag}[{\mathbf{A}}_{1},\dots ,\boldsymbol{ }{\mathbf{A}}_{r}]\), \(\mathbf{B}=\mathrm{diag}[{\mathbf{B}}_{1},\dots ,\boldsymbol{ }{\mathbf{B}}_{r}]\), \(\mathbf{C}=\mathrm{diag}[{\mathbf{C}}_{1},\dots ,\boldsymbol{ }{\mathbf{C}}_{r}]\),
\({\mathbf{A}}_{i}=\left[\begin{array}{c}0\\ \begin{array}{c}0\\ \vdots \end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\begin{array}{c} 1\\ \begin{array}{c}0\\ \vdots \end{array}\\ \begin{array}{c} 0\\ 0\end{array}\end{array}\begin{array}{c} 0\\ \begin{array}{c} 1\\ \vdots \end{array}\\ \begin{array}{c} 0\\ 0\end{array}\end{array}\begin{array}{c}\dots \\ \dots \\ \begin{array}{c}\ddots \\ \begin{array}{c}\dots \\ \dots \end{array}\end{array}\end{array}\begin{array}{c}0\\ \begin{array}{c}0\\ \vdots \end{array}\\ \begin{array}{c}1\\ 0\end{array}\end{array}\right]\epsilon { \mathcal{R}}^{{n}_{i}\times {n}_{i}}\), \({\mathbf{B}}_{i}=\left[\begin{array}{c}0\\ 0\\ \begin{array}{c}\vdots \\ 1\end{array}\end{array}\right]\epsilon { \mathcal{R}}^{{n}_{i}\times 1}\), and \({\mathbf{C}}_{i}=\left[\begin{array}{c}1\\ 0\\ \begin{array}{c}\vdots \\ 0\end{array}\end{array}\right]\epsilon { \mathcal{R}}^{{n}_{i}\times 1}\).
Note that, for \(r=m\), the control gain matrix \(\mathbf{G}\left(\mathbf{X}\right){ \mathcal{R}}^{r\times m}\) is a square matrix, and for \(r\ne m\) it can be a non-square matrix. Also, for SISO, MISO, and SIMO systems, it can be defined as:\(1\times 1\) matrix, \(1\times m\) vector, and \(r\times 1\) vector, respectively.
3 Robust and non-singular control of the general dynamic model
In the current section, a general control method is presented for the proposed general dynamic model (5). In this paper, it is assumed that \({\varvec{F}}\left({\varvec{X}}\right)\) and \({\varvec{G}}\left({\varvec{X}}\right)\) are unknown, and \({\varvec{D}}\left(t\right)\ne 0.\) Therefore, the proposed nonsingular controller with control input saturation can be presented by the conception of the ideal controllers and the non-singular control designs.
3.1 The Ideal control design
The control problem is to achieve the state \({\mathbf{X}}_{i}\) for tracking the desired state \({\mathbf{X}}_{di}={\left[{x}_{di},\dots ,{{x}_{di}}^{\left({n}_{i}-1\right)}\right]}^{T}\). The tracking error is defined as
If \(\mathbf{F}\left(\mathbf{X}\right)\) and \(\mathbf{G}\left(\mathbf{X}\right)\) are known and free of external disturbance, i.e., \(\mathbf{D}\left(t\right)=0\), the following ideal control signal \({\mathbf{U}}_{\mathbf{o}}^{\mathbf{*}}\) makes the tracking error in the system (5) becomes stable asymptotically
where \({\varvec{\upbeta}}={\left[{\beta }_{1},\dots ,{\beta }_{r}\right]}^{T}={\left[\left({x}_{d1}^{\left({n}_{1}\right)}+{\mathbf{K}}_{1}^{T}{\mathbf{E}}_{1}\right),\dots ,\left({x}_{dr}^{\left({n}_{r}\right)}+{\mathbf{K}}_{r}^{T}{\mathbf{E}}_{r}\right)\right]}^{T}\). Let \({\mathbf{K}}_{i}\)=\({[{k}_{i1},\dots ,{k}_{i{n}_{i}}]}^{T}\) to be chosen such that the polynomial \({s}^{{n}_{i}}+{k}_{i{n}_{i}}{s}^{{n}_{i}-1}+\dots +{k}_{i1}\) is Hurwitz.
Assumption 2
The control gain matrix \(\mathbf{G}\left(\mathbf{X}\right)\) is assumed to be non-singular, i.e.,\(\mathbf{G}\left(\mathbf{X}\right)\) is an invertible matrix (inverse or pseudo-inverse of \(\mathbf{G}\left(\mathbf{X}\right)\) is available).
Inserting (8) into (4) yields (for \(\mathbf{D}\left(t\right)=0\))
Therefore, if \({\mathbf{G}}^{\#}={\mathbf{I}}_{r\times r}\), (where \({\mathbf{I}}_{r\times r}\) is a unit matrix), then after simple operations we have
indeed, the tracking of the reference command is asymptotically attained from any initial conditions, i.e., \(\underset{\mathrm{t}\to \infty }{\mathrm{lim}}{\mathbf{E}}_{i}=0\). Hence, there exist positive definite matrices \({\mathbf{Q}}_{oi}\) and \({\mathbf{P}}_{oi}\) such that
Definition 1
(Ghavidel and Kalat 2017a): \({\mathbf{G}}^{-}\epsilon {\mathcal{R}}^{m\times r}\) is the “inverse \(/\) pseudo-inverse” of “square \(/\) non-square” matrix \(\mathbf{G}\epsilon {\mathfrak{R}}^{\mathrm{r}\times \mathrm{m}}\); thus, it can be defined as:
Thus, we have
Then, by Definition 1 and by assuming that all matrices are invertible, \({\mathbf{G}}^{\#}\) can be as follows
Therefore, by (14) and the ideal controller (8), (10) can be achieved.
3.2 The non-singular control design in the presence of input saturation
By an unknown vector \({\mathbf{g}}_{i}\left(\mathbf{X}\right)\), non-affine nonlinear systems (3) can be transformed into a nonlinear affine system (4). Thus, it is challenging to determine an accurate function of \(\mathbf{F}(\mathbf{X})\) and \(\mathbf{G}(\mathbf{X})\). Therefore, the controller (8) is unrealizable, because \(\mathbf{F}\left(\mathbf{X}\right)\) and \(\mathbf{G}\left(\mathbf{X}\right)\) are unknown and \(\mathbf{D}\left(t\right)\ne 0.\) To overcome these kinds of problems, an adaptive fuzzy method is used to estimate unknown functions and uncertainties. Thus, it is very important that, although the proposed method needs an accurate function of \(\mathbf{F}\left(\mathbf{X}\right)\) and \(\mathbf{G}\left(\mathbf{X}\right)\), this paper does not require those functions to be known. Let denote:
where \(\hat{\mathbf{G}}\) is the adaptive fuzzy estimation of \(\mathbf{G}\). The adaptive fuzzy controller can be still unrealizable because it is possible that matrices \(\hat{\mathbf{G}}{\hat{\mathbf{G}}}^{-}\), \({\hat{\mathbf{G}}}^{-}\), \(\hat{\mathbf{G}}\), \(\hat{\mathbf{G}}{\hat{\mathbf{G}}}^{T}\) are not invertible.
Definition 2
(Ghavidel and Kalat 2017a): Let \(\mathbf{H}\) be a square matrix and \({\mathbf{H}}^{-1}\) be the inverse of H. So, the regularized inverse of H is defined as \({\mathbf{H}}^{-1}\cong {\mathbf{H}}^{\mathbf{r}}={\mathbf{H}}^{T}[\delta {\mathbf{I}+\mathbf{H}{\mathbf{H}}^{T}]}^{-1}\), where \(\delta \) is a small regularization constant. Using this scheme, it is not necessary to limit the parameter estimations to avoid the singularity problem.
The suggested control scheme is not limited only to the control of MIMO systems; it can be easily extended to the SISO, SIMO, and MISO systems, because MIMO non-affine systems can be transformed into SISO affine systems (\(i=1\) and \(j=1\)), SIMO affine systems (\(i=1,..,r\) and \(j=1\)) and MISO affine systems (\(i=1\) and \(j=1,..,m\)). Note that if \({\mathrm{g}}_{11}^{-1}\) be the inverse of \(\mathbf{G}\left(\mathbf{X}\right)=[{\mathrm{g}}_{11}]\epsilon {\mathcal{R}}^{1\times 1}\), then the regularized inverse of \({\mathrm{g}}_{11}\) is defined as \({\mathrm{g}}_{11}^{-1}\cong {\mathrm{g}}_{11}^{\mathrm{r}}={\mathrm{g}}_{11}[\delta {+{\mathrm{g}}_{11}^{2}]}^{-1}\).
Hence, by Definitions 1 and 2, the estimation of control gains can be proposed as
Indeed, a non-singular robust indirect adaptive fuzzy controller with estimation \({\hat{\mathbf{G}}}^{\mathrm{r}\#}\) is applied to overcome the singularity problem
where \(\hat{\mathbf{F}}\), \(\hat{\mathbf{G},}\) and \(\hat{\mathbf{U}}\) are estimates of \(\mathbf{F}\), \(\mathbf{G},\) and control input \(\mathbf{U}\), respectively, and \({\mathbf{u}}_{\mathbf{r}}\) is a robust control vector to compensate for uncertainties. Let denote:
\({\hat{\mathbf{F}}} = \left[ {\hat{f}_{1} , \ldots ,\hat{f}_{r} } \right]^{T}\), \(\hat{G} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\hat{g}_{11} } & {\hat{g}_{12} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {\hat{g}_{1m} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ \end{array} } & {\begin{array}{*{20}c} \ddots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {\hat{g}_{r1} } & {\hat{g}_{r2} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {\hat{g}_{rm} } \\ \end{array} } \\ \end{array} } \right] \in {\mathcal{R}}^{r \times m}\), \({\mathbf{u}}_{{\mathbf{r}}} = \left[ {u_{r1} , \ldots ,u_{rr} } \right]^{T}\)
To apply the non-singular controller \({\mathbf{U}}_{\mathbf{o}}\), the general dynamic model (5) can be rewritten by adding and then subtracting \(\hat{\mathbf{G}}\mathbf{U}+\left(-\hat{\mathbf{F}}+{\varvec{\upbeta}}+{\mathbf{u}}_{\mathbf{r}}\right)\)
where \(\widetilde{\mathbf{F}}=\hat{\mathbf{F}}-\mathbf{F}\) and \(\widetilde{\mathbf{G}}=\hat{\mathbf{G}}-\mathbf{G}\). After some simple manipulations, we can obtain the tracking error as
where \({\mathbf{D}}_{{\varvec{\upsigma}}}=\mathbf{D}-{\varvec{\upsigma}}={\left[{d}_{\sigma 1},\dots ,{d}_{\sigma r}\right]}^{T}\), and \({\varvec{\upsigma}}\left(\mathbf{X}\right)=\left\{\left(-\hat{\mathbf{F}}+{\varvec{\upbeta}}+{\mathbf{u}}_{\mathbf{r}}\right)-\hat{\mathbf{G}}\mathbf{U}\right\}\) is an uncertainty that appears because of applying the regular inverse technique.
The tracking errors (20) for each subsystem can be rewritten as
where \({\widetilde{f}}_{i}={\hat{f}}_{i}-{f}_{i}\) and \({\widetilde{\mathrm{g}}}_{i}={\hat{\mathrm{g}}}_{i}-{\mathrm{g}}_{i}\).
The controller (17) is still unrealizable because it might not always be available due to the input saturation. We assume that the control input \(\mathbf{U}\) is bounded by upper and lower bounds as
where \({\mathbf{U}}_{\mathbf{o}}={\left[{u}_{o1},\dots ,{u}_{om}\right]}^{T}\) is the controller input to be designed; \({u}_{\mathrm{max}j}\) and \({u}_{\mathrm{min}j}\) are known
upper and lower bound of the controller \({u}_{oj}\). The new ideal controller can be proposed as
where \({\mathbf{U}}^{\mathbf{*}}={\left[{u}_{1}^{*},\dots ,{u}_{m}^{*}\right]}^{T}\). Then, we have
where \(\Delta ={\left[{\Delta }_{1},\dots ,{\Delta }_{m}\right]}^{T}\). It is important to notice that \(\Delta \) is zero in the areas of \({u}_{\mathit{min}j}<{u}_{oj}<{u}_{\mathit{max}j}\) since \(\mathbf{U}={\mathbf{U}}_{\mathbf{o}}\), so that
By substituting the proposed controller (17) into plant (1) and based on (24) and (25), the tracking error for \(u_{\min j} < u_{oj} < u_{\max j}\) (i.e., \(\Delta_{Ij} = 0\)) can be written as
Also, for out of the area \(u_{\min j} < u_{oj} < u_{\max j}\) (i.e., \(\Delta_{Ij} \ne 0\)), we have
By (25)-(27), the tracking error for \(u_{\min j} \le u_{oj} \le u_{\max j}\) can be written as
where
Note that the robust controller \({u}_{ri}\) can play an important role to compensate for these uncertainties.
4 Barrier Lyapunov function-based adaptive fuzzy control
As previously mentioned, it is assumed that \(\mathbf{F}\left(\mathbf{X}\right)\) and \(\mathbf{G}\left(\mathbf{X}\right)\) are unknown. Therefore, we use the fuzzy estimations \(\hat{\mathbf{F}}\) and \(\hat{\mathbf{G}}\) instead. It is very important to note that one of the most important purposes of the article is to design a general nonlinear modeling of multi-input/output affine and non-affine systems. In this study, we suggest the adaptive fuzzy method and develop the proposed controller and general nonlinear modeling by this algorithm. Thus, the adaptive fuzzy method is only one way to estimate unknown functions (we can use other methods, e.g.; neural networks). Furthermore, to improve the performance of the control system, the proposed OBLF approach is employed in this section. Therefore, the first descriptions of the fuzzy logic system and observer models are presented in Sects. 4.1 and 4.2; then, the OBLF method is suggested.
4.1 Description of the fuzzy logic system
To improve the control performance of the adaptive fuzzy scheme and also to reduce the number of fuzzy sets and rules, the authors in (Ghavidel 2018; Ghavidel and Kalat 2018) employed a fuzzy logic system that the feedback error functions as fuzzy inputs are used instead of the state variables. Hence, it can be developed for SISO and MIMO systems.
It is very important that, based on (5), \(\mathbf{F}\) is a function of \(\mathbf{X}\) and \(\mathbf{U}\). Thus, it is a challenging problem for the fuzzy system because the control input \(\mathbf{U}\) is directly fed back into \(\mathbf{F}\). This paper uses a simple method to overcome this problem by applying the following fuzzy input: \(\Xi =\sum_{i=1}^{r}{\Xi }_{i}=\sum_{i=1}^{r}{\mathbf{K}}_{i}^{T}{\mathbf{E}}_{i}\). Note that if the state vector \(\mathbf{X}\) is not directly measurable, hence \(\hat{\Xi }=\sum_{i=1}^{r}{\hat{\Xi }}_{i}=\sum_{i=1}^{r}{\mathbf{K}}_{i}^{T}{\hat{\mathbf{E}}}_{i}\) can be as the input of the fuzzy system, which \( {\hat{\mathbf{E}}}_{i} \) is an estimation error vector of \({\mathbf{E}}_{i}\) (for more details, see Sect. 6).
Thus, the fuzzy logic system is introduced with the following fuzzy IF–THEN rules as
\({F}^{l}\) and \({\overline{y}}^{l}\) are the fuzzy sets, and \({\mu }_{{F}^{l}}\) and \({\mu }_{{y}^{l}}\) are their membership functions, \(\hat{\Xi }\) and \(y \epsilon \mathcal{R}\) are the input and output of the fuzzy system, l = 1,…,\(M\) is the number of fuzzy rules. The output of the proposed fuzzy logic system can be written as
\({\varvec{\uptheta}}={({\overline{y} }^{1},\dots ,{\overline{y} }^{M})}^{T}\) is the output fuzzy membership function. Also, the fuzzy basis functions are defined as
The optimal parameter vectors \({{\varvec{\uptheta}}}^{*}\) are defined as
where || · || represents the Euclidean-norm of a vector. Also, \({\varvec{\Omega}}\) is the compact set defined as \({\varvec{\Omega}}=\left\{{\varvec{\uptheta}} :||{\varvec{\uptheta}}||\le {m}_{y} \right\},\) where \({m}_{y}\) is the positive constant specified by the designer. The minimum approximation error can be written in terms of the optimal parameter estimates as\({\omega }_{o}=y\left(\hat{\Xi }|{{\varvec{\uptheta}}}^{\mathbf{*}}\right)-y\left(\mathbf{X}\right)\).
Remark 1
Note that another method can be applying \({\hat{\Xi }}_{i}\) as the input of the fuzzy logic system. Then, fuzzy IF–THEN rules can be rewritten as: {\({R}^{l}\): IF \({\hat{\Xi }}_{1}\) is \({F}_{1}^{l}\) and … and \({\hat{\Xi }}_{r}\) is \({F}_{r}^{l}\), THEN \(y\) = \({\overline{y}}^{l}\)}, where \({F}_{i}^{l}\) are fuzzy sets. One problem with this method is that increasing the number of fuzzy sets and/or fuzzy IF–THEN rules, compared to the use of fuzzy input \(\hat{\Xi }=\sum_{i=1}^{r}{\hat{\Xi }}_{i}\).
By the above detentions, \({\hat{f}}_{i}\) and \({\hat{\mathrm{g}}}_{ij}\) can be described as follows
Also, \({{\varvec{\uptheta}}}_{i}^{*}\) and \({{\varvec{\uptheta}}}_{ij}^{*}\) are the optimal parameters and can be defined as
where \({\Omega }_{i}=\left\{{{\varvec{\uptheta}}}_{i} :{\underline{m}}_{i}\le ||{{\varvec{\uptheta}}}_{i}||\le {\overline{m}}_{i}\right\}\) and \({\Omega }_{ij}=\left\{{{\varvec{\uptheta}}}_{ij} :{\underline{m}}_{ij}\le ||{{\varvec{\uptheta}}}_{ij}||\le {\overline{m}}_{ij}\right\}\) where \({\overline{m}}_{i}\), \({\underline{m}}_{i}\), \({\overline{m}}_{ij}\) and \({\underline{m}}_{ij}\) are the positive constants specified by the designer. Then, the minimum approximation errors can be written in terms of the optimal parameter estimates as
By fuzzy systems (34) and (35) and the minimum approximation errors (38), the tracking error (28) for each subsystem can be as follows
where \({\omega }_{oi}={d}_{i}+{\omega }_{Ii}\), \({\widetilde{{\varvec{\uptheta}}}}_{i}={{\varvec{\uptheta}}}_{i}-{{\varvec{\uptheta}}}_{i}^{\mathbf{*}}\) and \({\widetilde{{\varvec{\uptheta}}}}_{ij}={{\varvec{\uptheta}}}_{ij}-{{\varvec{\uptheta}}}_{ij}^{\mathbf{*}}\).
This paper suggests the fuzzy input \(\hat{\Xi }\) for the fuzzy approximators; thus, one drawback of utilizing this scheme is that the approximation error \({\omega }_{i}\) maybe increased. Hence, a robust term is required to compensate for the fuzzy approximation errors. Thus, though \({\hat{f}}_{i}\left(\hat{\Xi }|{{\varvec{\uptheta}}}_{i}\right)\) and \({\hat{\mathrm{g}}}_{ij}\left(\hat{\Xi }|{{\varvec{\uptheta}}}_{ij}\right)\) are applied to estimate \({f}_{i}(\mathbf{X})\) and \({\mathrm{g}}_{ij}(\mathbf{X})\), respectively, the controller is still viable.
4.2 Observation of the state vector
The control of the nonlinear system becomes more complicated when the state vector \(\mathbf{X}\) is not directly measurable. Thus, a state observer should be established to approximate the unmeasured states. The following errors are employed.
– error vector \({\mathbf{E}}_{i}={\mathbf{X}}_{di}-{\mathbf{X}}_{i}={\left[{e}_{i},\dots ,{e}_{i}^{({n}_{i}-1)}\right]}^{T}\)
– error of the estimated state vector (error observer) \({\hat{\mathbf{E}}}_{i}={\mathbf{X}}_{di}-{\hat{\mathbf{X}}}_{i}={\left[{\hat{e}}_{i},\dots ,{\hat{e}}_{i}^{({n}_{i}-1)}\right]}^{T}\)
– observation error \({\widetilde{\mathbf{E}}}_{i}={\mathbf{E}}_{i}-{\hat{\mathbf{E}}}_{i}={\hat{\mathbf{X}}}_{i}-{\mathbf{X}}_{i}={\left[{\widetilde{e}}_{i},\dots ,{\widetilde{e}}_{i}^{({n}_{i}-1)}\right]}^{T}\)
When an observer is applied to estimate the state vector \({\mathbf{X}}_{i}\), the suggested control law (17) can be rewritten as
where \(\hat{{\varvec{\upbeta}}}={\left[{\hat{\beta }}_{1},\dots ,{\hat{\beta }}_{r}\right]}^{T}={\left[\left({x}_{d1}^{\left({n}_{1}\right)}+{\mathbf{K}}_{1}^{T}{\hat{\mathbf{E}}}_{1}\right),\dots ,\left({x}_{dr}^{\left({n}_{r}\right)}+{\mathbf{K}}_{r}^{T}{\hat{\mathbf{E}}}_{r}\right)\right]}^{T}\).
By (39), the tracking error (38) for each subsystem can be rewritten as
The observer is designed as follows
where \({\mathbf{K}}_{ci}\)=\({[{k}_{c1i},\dots ,{k}_{c{n}_{i}i}]}^{T}\) is the observer gain vector which guarantees the characteristic polynomial of \({\mathbf{A}}_{si}={\mathbf{A}}_{i}-{\mathbf{K}}_{ci}{\mathbf{C}}_{i}^{T}\) to be Hurwitz. Note that \(-{\mathbf{K}}_{i}^{T}{\hat{\mathbf{E}}}_{i}\) in (42) can be a part of uncertainties as \({\omega }_{1i}={\omega }_{oi}-{\mathbf{K}}_{i}^{T}{\hat{\mathbf{E}}}_{i}\). Otherwise, the matrix \({\mathbf{A}}_{si}\) in observation error dynamics (42) becomes \({\mathbf{A}}_{si}={\mathbf{A}}_{i}-{\mathbf{K}}_{ci}{\mathbf{C}}_{i}^{T}-{\mathbf{B}}_{i}{\mathbf{K}}_{i}^{T}{\hat{\mathbf{E}}}_{i}\). Thus, it is difficult to demonstrate that this matrix \({\mathbf{A}}_{si}\) is Hurwitz, in a high-order system especially.
There exist positive definite matrices \({\mathbf{Q}}_{i}\) and \({\mathbf{P}}_{i}\) such that
where for a given positive definite matrix\({\mathbf{Q}}_{i}\), there exists a positive matrix \({\mathbf{P}}_{i}\) which is the solution of the following equation, and the entries of the vector \({\mathbf{B}}_{si}={\left[{b}_{1i} ,\dots , {b}_{{n}_{i}i}\right]}^{T}\epsilon {\mathcal{R}}^{{n}_{i}}\) which are positive constants.
Because only the observation error \({\widetilde{e}}_{1i}\) can be measured in the observation error dynamics (42), we apply the SPR Lyapunov method to study the stability of the error dynamics (42).
Note that these approaches are proposed based on the Strictly Positive Real (SPR) condition and Lyapunov theory. But in this paper, it can be extended to SPR condition and barrier Lyapunov function theory. Furthermore, by this method, matrices \({{\varvec{Q}}}_{\mathrm{oi}}\), \({{\varvec{P}}}_{\mathrm{oi}}\) \({{\varvec{Q}}}_{i}\), \({{\varvec{P}}}_{i}\), vector\(\boldsymbol{ }{{\varvec{B}}}_{\mathrm{si}}\) and filter \({L}_{i}(s)\) do not require to be known.
The observation error dynamics (42) can be written as
where
and \(H_{i} \left( s \right)\) is a stable transfer function. Hence, (45) can be rewritten as
where filter \({L}_{i}(s)\) is chosen so that \({H}_{i}\left(s\right){L}_{i}(s)\) is an SPR transfer function, and also \({L}_{i}{\left(s\right)}^{-1}\) is an appropriate stable function. Let\({L}_{i}\left(s\right)={b}_{1i}{s}^{{m}_{i}}+{b}_{2i}{s}^{{m}_{i}-1}+\dots +{b}_{{n}_{i}}\), where\({m}_{i}={n}_{i}-1\). If the entries of the vector \(\, {\mathbf{B}}_{si}={\left[{b}_{1i} ,\dots , {b}_{{n}_{i}i}\right]}^{T}\epsilon {\mathcal{R}}^{{n}_{i}}\) are positive constants, all roots of \(\,{L}_{i}\left(s\right)\) are stable. So \({H}_{i}\left(s\right){L}_{i}(s)\) can be an SPR transfer function. The state\(-\)space realization of (46) can be written the following form
where we now have \({\widetilde{\mathbf{E}}}_{si}={\left[{\widetilde{e}}_{i},\dots ,{\widetilde{e}}_{i}^{({n}_{i}-1)}\right]}^{T}\).
It is challenging to determine the entries of the filter\({L}_{i}(s)\), i.e., entries of the vector\({\mathbf{B}}_{s}={\left[{b}_{1} ,\dots , {b}_{{n}_{i}}\right]}^{T}\). To overcome this problem, we can rewrite (47) as
where \(\omega_{i} = \omega_{1i} + \varpi_{i}\) is a lumped uncertainty and \(\varpi_{i} \) can be written as
To achieve the proposed OBLF control method, the error Eq. (45) can be rewritten as
where
4.3 OBLF control approach
The barrier Lyapunov function is an efficient technique to resolve the drawback of output constraint. By confirming the boundedness of the barrier Lyapunov function along the system trajectories, the transgression of constraints is prevented (Shaocheng et al. 2005; Schkoda and Crassidis 2007; Shahnazi 2016). Now, the observer error signal \({\widetilde{e}}_{1i}\) needs the barrier function \({V}_{i}(t)\) to avoid it from reaching the limits \(\pm {k}_{i}\).
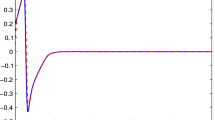
where \(\mathrm{log}(.)\) denotes the natural logarithm of\((.)\), and \({k}_{i}\) the constraint on\({\widetilde{e}}_{si}\), i.e., \(\left|{\widetilde{e}}_{si}\right|<{k}_{i}\). As seen from the schematic illustration of \({V}_{i}\left({\widetilde{e}}_{\mathrm{si}}(t)\right)\) in Fig. 1, the barrier Lyapunov function escapes to infinity at \(\left|{\widetilde{e}}_{\mathrm{si}}\right|={k}_{i}\). It can be shown that \({V}_{i}\) is positive definite, and thus, a valid Lyapunov function candidate in the set\(\left|{\widetilde{e}}_{\mathrm{si}}\right|<{k}_{i}\). From (Schkoda and Crassidis 2007; Shahnazi 2016), if \({V}_{i}\left(t\right)\) is positive definite and\({\dot{V}}_{i}\left(t\right)\,\le 0\), for proper positive constant \({k}_{i}\) we have \(\left|{\widetilde{e}}_{\mathrm{si}}\right|\,<\,{k}_{i}\) so that \({V}_{i}\left(t\right)\to \infty\, \) as\(\left|{\widetilde{e}}_{\mathrm{si}}\right|\to {k}_{i}\). Indeed, \({\widetilde{e}}_{\mathrm{si}}\upepsilon (-{k}_{i},{+k}_{i})\forall t\upepsilon [0,\infty )\).
It is an important advantage that the proposed barrier Lyapunov is a function of the observer error signal \({\widetilde{e}}_{si}={e}_{i}-{ \hat{e}}_{i}={\hat{x}}_{i}-{ x}_{i}\), because the selection of the parameter \({k}_{i}\) will not be complicated. Indeed, we expect \(\widetilde{e}_{{{\text{si}}}} \to 0\) at all times; hence, we always have a limited observer error as \(\left|{\widetilde{e}}_{\mathrm{si}}\right|<{\mathrm{k}}_{\mathrm{i}}\). Therefore, the proposed barrier Lyapunov functions can maintain the observer error \({\widetilde{e}}_{si}\) in a small area. Hence, we can hope that the tracking errors are bounded and converge toward zero, i.e., \({e}_{i},{\hat{e}}_{i}\to 0\), because \({\widetilde{e}}_{\mathrm{si}}={ e}_{i}-{ \hat{e}}_{i}\to 0\). But, the conventional barrier Lyapunov (Shaocheng et al. 2005; Schkoda and Crassidis 2007; Shahnazi 2016) is a function of the trajectory signal error \({e}_{i}={x}_{di}-{x}_{i}\); thus, a selection constraint will occur for parameter \({k}_{i}\) or desired trajectory state \({x}_{di}\), since \({k}_{i}\) directly depends on \({x}_{di}\) as \(|{e}_{i}={x}_{\mathrm{di}}-{x}_{i}|\propto {k}_{i}\). Indeed, even in a good tracking trajectory (e.g., \({e}_{i}={x}_{\mathrm{di}}-{x}_{i}\to 0\)), parameter \({k}_{i}\) may be a large constant. Therefore, the conventional barrier Lyapunov functions can only restrict the tracking error \({e}_{i}\), and it designs a control method that does not drive \({e}_{i}\) out of the interval \(\left|{e}_{i}\right|<{k}_{i}\). In other words, it can't be concluded that the tracking errors asymptotically converge to zero. For more details, see Fig. 2
Now, we define the robust \({H}_{\infty }\)-like control term and the proposed OBLF-Adaptive Fuzzy Laws (OBLF-AFL) as
where \({z}_{i}={\widetilde{e}}_{\mathrm{si}}/({k}_{i}^{2}-{\widetilde{e}}_{\mathrm{si}}^{2})\), and \({\lambda }_{i}\), \({k}_{i}\), \({\gamma }_{i}\), and \({\gamma }_{ij}\) are positive designing constants. Also, the \({H}_{\infty }\)-like tracking performance can be achieved for a prescribed attenuation level \({\lambda }_{i}\).
In the conventional robust \({H}_{\infty }\) control terms, it is assumed that parameter \({\lambda }_{i}\) should be sufficiently small so that the derivative of the Lyapunov function is semi-negative definite, but this condition yields a very high magnitude of control input \({u}_{j}\) which is not practically feasible. An inappropriate adjustment of parameter \({\lambda }_{i}\) may cause bad behavior of the whole system, e.g., a higher frequency of chattering or a higher tracking error may occur. The proposed bounded robust \({H}_{\infty }\) control term can be one probable answer for solving these problems. The main purpose of this technique is to increase the accuracy of the closed-loop stability. In other words, to improve the compensation for uncertainty \({\omega }_{i}\), a strategy is using the proposed bounded robust control term. Now, we propose the bounded robust \({H}_{\infty }\)-like (54) as
where
where \({\overline{w} }_{i}\) and \({\overline{\omega }}_{i}\) are the user-defined bounds as \(\left|{w}_{i}\right|\le {\overline{w} }_{i}\) and \(\left|{\omega }_{i}\right|\le {\overline{\omega }}_{i}\).
Also, to guarantee the fuzzy parameters are bounded, \({{\varvec{\uptheta}}}_{i}\) and \({{\varvec{\uptheta}}}_{\mathrm{ij}}\) can be improved by a simple projection algorithm. Improved adaptive laws with projection can be written as
where \({{\varvec{\uptheta}}}_{i}\) and \({{\varvec{\uptheta}}}_{ij}\) are described as \({\varvec{\uptheta}}\), and \({\overline{m}}_{i}\) and \({\overline{m}}_{ij}\) are defined as \(\overline{m}\), and also \({\underline{m}}_{i}\) and \({\underline{m}}_{ij}\) are described as \(\underline{m}\). The block diagram of the proposed control method is shown in Fig. 3.
Remark 2
Although the suggested observer-based technique requires proper conditions for filter \({L}_{i}\left(s\right)\) to \({H}_{i}\left(s\right){L}_{i}(s)\) be SPR, the filter \({L}_{i}\left(s\right)\) and vector \({\mathbf{B}}_{si}\left(s\right)\) don't need to be known (i.e., in other words, the filter \({L}_{i}\left(s\right)\) is only applied for analysis purposes). In (Tee et al. 2009), the authors employed a filtered version of adaptive fuzzy law. It seems that applying these filtered adaptive fuzzy laws can make the control system design very difficult, while the Lumped uncertainties \({w}_{i}\) and \({\omega }_{i}\) can be compensated by the bounded robust \({H}_{\infty }\)-like (57).
Theorem
Consider the uncertain nonlinear system—in the form of (1), then using the proposed controller (39), the robust control term (57), and the OBLF-AFLs (55) and (56), the tracking error of the closed-loop system will be uniformly ultimately bounded.
Proof
Consider the Lyapunov function.
The derivative of \({V}_{i}\) is obtained as
By substituting the tracking errors (41) and (49) into (60), and after some simple manipulations, we have
Utilizing (11), (44), and the error dynamics (51), the latter results
Based on the vector \({\mathbf{B}}_{si}\) in filter \({L}_{i}(s)\) (Ghavidel and Kalat 2017b, 2018; Ghavidel 2018), define that \({\widetilde{\mathbf{E}}}_{si}^{T}{\mathbf{P}}_{i}{\mathbf{B}}_{si}={\widetilde{\mathbf{E}}}_{si}^{T}{\mathbf{C}}_{i}={\widetilde{e}}_{si}\); now after some manipulations we have
where \({{\varvec{K}}}_{\mathrm{ci}}^{T}{{\varvec{P}}}_{\mathrm{oi}}{\hat{{\varvec{E}}}}_{i}\) can be a part of the uncertainty \({\omega }_{i}\). Then, (63) can be rewritten as
By the fact \({\dot{\widetilde{{\varvec{\uptheta}}}}}_{i}={\dot{{\varvec{\uptheta}}}}_{i}\) and \({\dot{\widetilde{{\varvec{\uptheta}}}}}_{ij}={\dot{{\varvec{\uptheta}}}}_{ij}\), the adaptive laws (55) and (56) we have
By the robust term \({u}_{ri}\), for out of the areas \(|{z}_{i}|<{\overline{w} }_{i}\) and \(|{\widetilde{e}}_{si}|<{\overline{\omega }}_{i}\), we have
Since \(\left|{\omega }_{i}\right||{\widetilde{e}}_{si}|\le {\overline{\omega }}_{i}|{\widetilde{e}}_{si}|\), and \(\left|{w}_{i}\right||{z}_{i}|\le {\overline{w} }_{i}|{z}_{i}|\). For the areas \(|{z}_{i}|<{\overline{w} }_{i}\) and \(|{\widetilde{e}}_{si}|<{\overline{\omega }}_{i}\), we have
Note that
Therefore, the previous relation becomes
Since \(-{\left(\frac{1}{{\lambda }_{i}}{z}_{i}-{\lambda }_{i}{w}_{i}\right)}^{2}\le 0\) and \(-\frac{1}{2}{\left(\frac{1}{{\lambda }_{i}}{\widetilde{e}}_{si}-{\lambda }_{i}{\omega }_{i}\right)}^{2}\le 0\). Also, based on (Ren et al. 2010),\(-{\widetilde{e}}_{si}{z}_{i}<0\)
Thus, from (74) we have \(-\frac{1}{{\lambda }_{i}^{2}}{\widetilde{e}}_{si}{z}_{i}<0\). Finally, (73) can be written as
where \({\mathbb{E}}_{i}={\left[{\hat{\mathbf{E}}}_{i}, {\widetilde{\mathbf{E}}}_{si}\right]}^{T}\)and \({\mathbb{Q}}_{i}=diag\left[{\mathbf{Q}}_{oi},{\mathbf{Q}}_{i}\right]\). Also, \({\mathbf{Q}}_{oi}\) and \({\mathbf{Q}}_{i} \)are positive definite matrices. Therefore, the \({H}_{\infty }\)-like tracking performance can be achieved, and also for \({\lambda }_{i}\) sufficiently small, Eq. (75) will be true and the bounded \({H}_{\infty }\)-like tracking criterion will hold. Then, the integration of \(\dot{{V}_{i}}\) from 0 to \(\mathrm{T}\) gives
It is assumed that there exists a positive constant \({\mathrm{M}}_{i}>0\) such that \({\int }_{0}^{\infty }\left({\Vert {w}_{i}\Vert }^{2}+{\Vert {\omega }_{i}\Vert }^{2}\right)dt\le {\mathrm{M}}_{i}\); then for the integral \({\int }_{0}^{\mathrm{T}}{\Vert {\mathbb{E}}_{i}\Vert }_{{\mathbb{Q}}_{i}}^{2}dt\) one gets \({\int }_{0}^{\infty }{\Vert {\mathbb{E}}_{i}\Vert }_{{\mathbb{Q}}_{i}}^{2}dt\le 2{V}_{i}\left(0\right)+{\lambda }_{i}^{2}{\mathrm{M}}_{i}\). Thus, the integral \({\int }_{0}^{\mathrm{T}}{\Vert {\mathbb{E}}_{i}\Vert }_{{\mathbb{Q}}_{i}}^{2}dt\) is bounded and according to Barbalat’s Lemma; we have
Remark 3
From (73)-(75), and by term \(-\frac{1}{{\lambda }_{i}^{2}}{\widetilde{e}}_{si}{z}_{i}<0\), we can see that the proposed OBLF approach makes the decreasing of the time derivative of the Lyapunov function, because \(\frac{1}{{\lambda }_{i}^{2}}\) is a large constant. Therefore, we showed that the proposed scheme can improve \(\dot{{V}_{i}}(t)\)
Remark 4
If \({z}_{i}=0\), we have a control approach without OBLF-AFL. Therefore, the robust controller with Observer-Adaptive Fuzzy Law (O-AFL).
The stability of the controller with O-AFL is almost similar to the suggested OBLF-AFL method. Consider the Lyapunov function
The derivative of \({V}_{i}\) is as follows
Similar to the proof of the OBLF-AFL method, it is simple to see that the derivative of \({V}_{i}\) is obtained as
4.4 The control approach for semi-known affine and non-affine systems
If we assume that \({f}_{i}\left({\varvec{X}}\right)={f}_{oi}\left({\varvec{X}}\right)+\Delta {f}_{i}\) and \({g}_{ij}\left({\varvec{X}}\right)={g}_{oij}\left({\varvec{X}}\right)+\Delta {g}_{ij}\), where \({f}_{oi}\) and \({g}_{oij}\) are well known, and \(\Delta {f}_{i}\) and \(\Delta {g}_{ij}\) are unknown functions, one useful method is rewriting the affine system (4) as
where \({\Psi }_{i}=\Delta {f}_{i}+\sum_{j=1}^{m}\Delta {\mathrm{g}}_{ij}{u}_{j}\). The new proposed controller can be as
where
Now, we can apply the proposed adaptive fuzzy estimation \({\hat{\Psi }}_{i}={{\varvec{\uptheta}}}_{i}^{T}{{\varvec{\upxi}}}_{i}\left(\hat{\Xi }\right)\) for uncertainties \({\Psi }_{i}\), by adaptive laws (55) and (80); OBLF-AFL: \({\dot{{\varvec{\uptheta}}}}_{i}=-{\gamma }_{i}\left({z}_{i}+{\widetilde{e}}_{si}\right){{\varvec{\upxi}}}_{i}\), and O-AFL: \({\dot{{\varvec{\uptheta}}}}_{i}=-{\gamma }_{i}{\widetilde{e}}_{si}{{\varvec{\upxi}}}_{i}\). The stability of the controller (84) is similar to the previous schemes. Consider the Lyapunov function
The derivative of \({V}_{i}\) for OBLF-AFL and O-AFL methods is as follows, respectively,
It is simple to see that the derivative of \({V}_{i}\) is obtained as \(\dot{{V}_{i}}\le -\frac{1}{2}{\mathbb{E}}_{i}^{T}{\mathbb{Q}}_{i}{\mathbb{E}}_{i}+\frac{1}{2}{\lambda }_{i}^{2}{\omega }_{i}^{2}\).
5 Simulation example
For highlighting the usefulness of the proposed control method with input saturation, it is applied and simulated under different levels of disturbance. In Example 1, the proposed control is simulated for a SISO non-affine system. In Example 2, the proposed control is applied to a SISO compressor system. In Example 3, the proposed control is simulated for a MIMO non-affine system with square control gain. Furthermore, to apply the control method of Sect. 4.5, in Example 4 and 5 we use a semi-known 6-DoF underwater vehicle and a Hybrid Energy Storage System (HESS). Results illustrate the tracking performance for two cases: 1) the control approach with OBLF-AFL and 2) the control approach with O-AFL.
The constraint parameters\({\overline{m}}_{i}\),\({\overline{m}}_{ij}\), \({\underline{m}}_{i}\) and \({\underline{m}}_{ij}\) are deliberately chosen to be large enough (Ghavidel and Kalat 2017a, 2018). For all examples in this paper, we have three fuzzy membership functions \({\mu }_{l}\left(\hat{\Xi }\right)\) which are assumed in the form of \({\mu }_{l}\left(\hat{\Xi }\right)=\mathrm{exp}\left[-{\left((\hat{\Xi }+{c}_{l})/{\sigma }_{l}\right)}^{2}\right]\) where rule \(l\) denotes the \(l\) th fuzzy rule for\(l=\mathrm{1,2},3\), where \({c}_{l}=\{-1, 0 ,1\}\) is the center of,\({\mu }_{l}=\{{\mu }_{1},{\mu }_{2},{\mu }_{3}\}\), respectively. Also, \({\sigma }_{l}=0.3\) is an arbitrary constant value. Moreover, \({{\varvec{\upxi}}}_{i}={{\varvec{\upxi}}}_{ij}={\left[{\xi }_{1},{\xi }_{2},{\xi }_{3}\right]}^{T}\) and \({\xi }_{l}\) is a positive value expressed as (31). The disturbance is\({d}_{i}=\left\{0.5\mathrm{ sin} \left(\pi t\right)\times u\left(t\right)\right\}+\{5 \mathrm{sin} \left(2\pi t\right)\times u\left(t-10\right)\}\), where \(u\left(.\right)\) is a unit step function. The control design parameters for Examples 1–5 are given in Table 1.
Example 1
Model features:
-
SISO
-
Non-affine
-
Linear input–output
-
Unknown model
The dynamic equation of a SISO non-affine system is as follows (Tee et al. 2009)
The initial conditions of fuzzy parameters are chosen randomly in the intervals \({{\varvec{\uptheta}}}_{1}\left(0\right)=[-0.5, 0.5]\) and \({\varvec{\theta}}_{11} \left( 0 \right) = \left[ {2,3} \right]\). Also, the control input is limited between − 50 and + 50, \({{\varvec{A}}}_{o1}=[0 \mathrm{0,1} 0]\), \({{\varvec{K}}}_{c1}={\left[{k}_{c11},{k}_{c21}\right]}^{T}\) and \({{\varvec{C}}}_{1}={\left[\mathrm{1,0}\right]}^{T}\) (note that \(i=1\)). Moreover, the desired value is \({x}_{d1}=\mathrm{sin}(\pi /5).\)
The tracking trajectory \({x}_{1}\) for SISO non-affine system (\(i,j=1\)) is shown in Fig. 4. The tracking performance of the proposed controller with OBLF-AFL is proper; therefore, it can be seen that the proposed technique can guarantee system performance among uncertainties, and for this task, it reduces the amount of chattering. Furthermore, Fig. 5 shows the estimation errors \({\hat{e}}_{1}\) and \({\hat{\dot{e}}}_{1}\). Figure 6 illustrates the control inputs \({u}_{1}\) with input saturation \(\pm 50\). The results of the study obviously show that the proposed approach can achieve suitable performance.
Tracking trajectories: \({x}_{d1}\) (dotted line), \({x}_{1}\) by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 1
Tracking trajectories \({\hat{e}}_{1}\) and \({\hat{e}}_{2}\): by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 1
Control input \({u}_{1}\) by OBLF-AFL (solid line) and by O-AFL (dashed line), for Example 1
Example 2
Model features:
-
SISO
-
Affine
-
Nonlinear input–output
-
Unknown model
Consider a compressor motor of a fuel cell system. The dynamic equation of the compressor system is as follows (Ulrich et al. 2012)
where \(V\), \(I\), \(L\), \(R\), \(\Omega \), P, and \(Q={c}_{p}P\) are the voltage input, the current input, inductance, resistance, the propeller rotational velocity, piston pressure, and shaft torque, respectively. Also \({k}_{t}\), \({k}_{f}\), \({k}_{e}\), \(J\), \({c}_{w}\), \({v}_{w}\), and \({k}_{h}\) are the motor constants. Therefore, non-affine models (85) can be proposed as
where
\({f}_{1}={b}_{1}\Omega +{b}_{2}\dot{\Omega }+{b}_{3}P\),\({\mathrm{g}}_{11}={b}_{4}\), and \({u}_{1}=V\)
The model parameters are follows:
\(b_{1} = - \frac{{R + k_{e} k_{t} + c_{p} v_{m}^{ - 1} c_{w} L}}{L}\), \(b_{2} = - \frac{{k_{f} + RJ}}{L}\), \(b_{3} = \frac{{Rc_{p} + c_{p} v_{m}^{ - 1} k_{h}^{ - 1} L}}{L}\), \(b_{4} = \frac{{k_{t} }}{L}\),
The initial conditions of fuzzy parameters are chosen randomly in the intervals \({{\varvec{\uptheta}}}_{1}\left(0\right)=[-1, 1]\) and \( {{\varvec{\uptheta}}}_{11}\left(0\right)=[1, 3]\). Also, the control input is limited between -8 and +8, \({\mathbf{A}}_{o1}=[0 \mathrm{0,1} 0]\), \({\mathbf{K}}_{c1}={\left[{k}_{c11},{k}_{c21}\right]}^{T}\) and \({\mathbf{C}}_{1}={\left[\mathrm{1,0}\right]}^{T}\). Moreover, the desired value is \({x}_{d1}=5 \mathrm{sin}(\pi /5).\)
The tracking trajectory \({y}_{1}\) for SISO non-affine system (\(i,j=1\)) is shown in Fig. 7. The tracking performance of the proposed controller with OBLF-AFL is proper; therefore, it can be seen that the suggested control design can guarantee system performance among uncertainties, and for this task, it reduces the amount of chattering. Moreover, Fig. 8 shows the estimation errors \({\hat{e}}_{1}\) and \({\hat{\dot{e}}}_{1}\). Figure 9 illustrates the control inputs \({u}_{1}\) with input saturation \(\pm 8\). The results of the study clearly demonstrate that the proposed method can achieve suitable performance.
Tracking trajectories: \({x}_{d1}\) (dotted line), \({x}_{1}\) by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 2
Tracking trajectories \({\hat{e}}_{1}\) and \({\hat{\dot{e}}}_{1}\): by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 2
Control input \({u}_{1}\) by OBLF-AFL (solid line) and by O-AFL (dashed line), for Example 2
Example 3
Model features:
-
MIMO
-
Non-affine
-
Nonlinear input–output
-
Square control gain
-
Unknown model
Consider the following academic MIMO non-affine nonlinear system as
Based on (Ghavidel 2018; Ghavidel and Kalat 2018), the system with output \(y\) has a relative degree of 2 (\(r = 2\)) for each subsystem. The zero dynamics of system are \({\dot{x}}_{31}={x}_{11}-0.8{x}_{31}\) and \({\dot{x}}_{32}={x}_{12}-2{x}_{32}\). This means that system is stable. Thus, it can be modeled as a second-order plant. The realization process includes four states (\({x}_{11}\), \({x}_{21}\), \({x}_{12}\) and \({x}_{22}\)), and the outputs are modeled as \({y}_{1}={x}_{11}\) and \({y}_{2}={x}_{12}\) (states \({x}_{31}\) and \({x}_{32}\) neglected). Therefore, we can show the system without unmodeled dynamic as
We can easily check that \(\partial {F}_{i}\left(\mathbf{X},\mathbf{U}\right)/\partial \mathbf{U}>0\). The initial conditions of fuzzy parameters are chosen randomly in the intervals \({{\varvec{\uptheta}}}_{11}\left(0\right)={{\varvec{\uptheta}}}_{22}\left(0\right)=[-0.5, 0.5]\), \( {{\varvec{\uptheta}}}_{11}\left(0\right)={{\varvec{\uptheta}}}_{22}\left(0\right)=[5, 8]\) and \({{\varvec{\uptheta}}}_{12}\left(0\right)={{\varvec{\uptheta}}}_{21}\left(0\right)=[0.5, 1]\). Also, the control input is limited between − 3 and + 3, \({\mathbf{A}}_{o1}={\mathbf{A}}_{o2}=[0 \mathrm{0,1} 0]\), \({\mathbf{K}}_{c1}={\left[{k}_{c11},\dots ,{k}_{c21}\right]}^{T}\), \({\mathbf{K}}_{c2}={\left[{k}_{c12},\dots ,{k}_{c22}\right]}^{T}\)and \({\mathbf{C}}_{1}={\mathbf{C}}_{2}={\left[\mathrm{1,0}\right]}^{T}\). Moreover, desired values are \({x}_{d1}=\mathrm{sin}(\pi /5) \)and \({x}_{d2}=-\mathrm{sin}(\pi /5)\).
The tracking trajectories \({x}_{i}\) for the MIMO non-affine system (\(i=\mathrm{1,2}\)) are shown in Figs. 10 and 11. Moreover, Figs. 12 and 13 show the trajectories of estimate errors \({\hat{e}}_{i}\) and \({\dot{\hat{e}}}_{i}\). Figures 14 and 15 illustrate the control inputs \({u}_{j}\) with input saturation \(\pm 3\). The results of the study clearly exhibit that the suggested method can achieve proper performance.
Tracking trajectories: \({x}_{d1}\) (dotted line), \({x}_{1}\) by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 3
Tracking trajectories: \({x}_{d2}\) (dotted line), \({x}_{2}\) by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 3
Tracking trajectories \({\hat{e}}_{1}\) and \({\dot{\hat{e}}}_{1}\): by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 3
Tracking trajectories \({\hat{e}}_{2}\) and \({\dot{\hat{e}}}_{2}\): by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 3
Control inputs: \({u}_{1}\) (solid line) and \({u}_{2}\) (dashed line), by OBLF-AFL, for Example 3
Control inputs: \({u}_{1}\) (solid line) and \({u}_{2}\) (dashed line), by O-AFL, for Example 3
Example 4
Model features:
-
MIMO
-
Affine
-
Linear input–output
-
Non-square control gain
-
Semi-known model
To show the usefulness and effectiveness of the proposed method, a physical example is employed. Details on the matrices operated for a model of a 6-DoF underwater vehicle with 8 thrusters can be as (Ghavidel and Kalat 2017a)
where \(\mathbf{F}={\left[{f}_{1},\dots ,{f}_{6}\right]}^{T}\epsilon {\mathfrak{R}}^{6 }\), \(\mathbf{G}=\left[{\mathrm{g}}_{ij}\right] \epsilon {\mathfrak{R}}^{6\times 8 }\), \(\mathbf{D}\)=\({\left[{d}_{1},\dots ,{d}_{6}\right]}^{T}\epsilon {\mathfrak{R}}^{6 }\), \(\mathbf{U}\)=\({\left[{u}_{1},\dots ,{u}_{6}\right]}^{T}\epsilon {\mathfrak{R}}^{6 }\).
Based on section 5.4, we assume that the system is semi-known. The initial conditions of fuzzy parameters are chosen randomly in the intervals \({{\varvec{\uptheta}}}_{i}\left(0\right)=[-1, 1]\). Also, the control input is limited between − 20 and +20, \({\mathbf{A}}_{oi}=[0 \mathrm{0,1} 0]\), \({\mathbf{K}}_{ci}={\left[{k}_{c1i},{k}_{c2i}\right]}^{T}\), and \({\mathbf{C}}_{i}={\left[\mathrm{1,0}\right]}^{T}\). Moreover, desired values are \({x}_{di}=\left\{\mathrm{2,3},4,\frac{\pi }{3},\frac{\pi }{4},\frac{2\pi }{5}\right\}.\)
The tracking trajectories for the 6-DoF underwater vehicle are shown in Fig. 16. The tracking performances of the suggested OBLF-AFL are also proper. So, it can be seen that the proposed controller can guarantee system performance. We can see that the tracking errors are uniformly ultimately bounded and converge to a small region near zero. Moreover, Fig. 17 illustrates the control inputs \({u}_{j}\) with input saturation \(\pm 20\).
Tracking trajectories: \({x}_{di}\) (dotted line), \({x}_{i}\) by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 4
Control input \({u}_{j}\) by OBLF-AFL (solid line) and by O-AFL (dashed line), for Example 4
Example 5
Model features:
-
SISO
-
Affine
-
Nonlinear input–output
-
Semi-known model
The average control models of each part of a HESS with the boost-buck converter (e.g.; battery or supercapacitor) can be expressed as (Ghavidel and Mousavi-G 2022a, b)
where \(V\) and \(I\) are the average voltage and current, \(R\) and \(L\) are the IGBT inductor and resistance, function \({\mathbb{F}}\) is the dynamical model of HESS (e.g.; battery in this study), \({u}_{1}\) is the average value of the switching signal, \(d\) is the external disturbance, and \({V}_{L}=750\) v is the stable voltage of the DC-bus.
The system with output \({y}_{1}=I\) has a relative degree of 1 (\(r = 1\)). Then we have; \({f}_{1}=\left(-\mathrm{RI}+V\right){L}^{-1}\) and \({g}_{1}=-{\mathrm{VL}}^{-1}\). The initial conditions of fuzzy parameters are chosen randomly in the intervals \({{\varvec{\theta}}}_{1}\left(0\right)=0\). Also, the control input is limited between \(\pm 1\), \({{\varvec{A}}}_{o1}=[0 \mathrm{0,1} 0]\), \({{\varvec{K}}}_{c1}={\left[{k}_{c11},{k}_{c21}\right]}^{T}\) and \({{\varvec{C}}}_{1}={\left[\mathrm{1,0}\right]}^{T}\). Moreover, the desired value is \({x}_{d1}=5 \mathrm{sin}(\pi /5).\)
The tracking trajectory \({y}_{1}\) is shown in Fig. 18. The tracking performance of the proposed controller with OBLF-AFL is good, and for this task, it reduces the amount of chattering. Moreover, Fig. 19 shows the estimation error \({\hat{e}}_{1}\). Figure 20 illustrates the control inputs \({u}_{1}\) with input saturation \(\pm 1\). The results of the study clearly demonstrate that the proposed method can achieve suitable performance.
Tracking trajectories: \({x}_{d1}\) (dotted line), \({y}_{1}\) by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 5
Tracking trajectory \({\hat{e}}_{1}\): by OBLF-AFL (solid line) and O-AFL (dashed line), for Example 5
Control input \({u}_{1}\) by OBLF-AFL (solid line) and by O-AFL (dashed line), for Example 5
5.1 The comparing results
By comparing case results, it can be seen that the control performance of the proposed control with the OBLF-AFL method is suitable. Also, we see that the tracking errors can converge to a small neighborhood of zero. Moreover, we can state that the results show the usefulness and effectiveness of the suggested controller and the ability to maintain the system performance amid various uncertainties and disturbances' various amplitude and frequency.
In short, the performance of the proposed method for various classes of nonlinear systems is suitable. The reasons are that the proposed method is based on combining advantages of barrier Lyapunov, fuzzy system, adaptive method, a bounded robust \({H}_{\infty }\)-like control term, and a simple and accurate observer scheme. Also, we do not have an SPR transfer function, and it does not require matrices \({\mathbf{Q}}_{i}\), \({\mathbf{P}}_{i}\),\({\mathbf{Q}}_{oi}\), \({\mathbf{P}}_{oi}\) and vectors \({\mathbf{B}}_{1}\), \({\mathbf{B}}_{2}\) to be known. Furthermore, the fuzzy estimator with the feedback error function \(\hat{\Xi }\) as input in the fuzzy adaptive controller can improve the sensitivity of \({u}_{j}\) to the tracking errors, while the number of fuzzy term sets and rules is decreased. Moreover, the proposed method is computationally simple, effective, robust, and properly behaved in the presence of input saturation. Also, by this technique, the chattering phenomenon can be alleviated.
Remark 5
Some more comparisons were performed for Examples 1–5 without the input saturation. According to these simulation results, it was observed that with input saturation a large overshoot of the control input may be generated in the earliest moments as an impulse signal. These large overshoots may cause bad behavior of the system under control because they may play a destructive role. Hence, simulation studies are neglected for this method. Furthermore, several simulations were carried out for control of various nonlinear systems, e.g., for MIMO maglev bogy (Wen et al. 2011), MISO and SISO affine MLS (Yousfi et al. 2014), MIMO affine robot system (Ghavidel and Kalat 2017c), etc. Simulation studies show the usefulness of the suggested approach. The simulation results were under the fuzzy logic inputs \(\hat{\Xi }\) and \(\hat{\mathbf{X}}\). These simulation studies are neglected for this method. Briefly, from Table 2 we can see the tracking performances of the control approach with OBLF-AFL and O-AFL in the presence of large and sudden disturbances. Also, we want to develop our design method in the next study so it can be applied for intelligent computing approaches (Youssef et al. 2018; Li et al. 2019; Al-Qerem et al. 2020).
6 Conclusion
In this paper, a non-singular control strategy with an OBLF-AFL is applied for various types of nonlinear systems (i.e., for MIMO, MISO, MIMO, and SISO systems). Also, a bounded \({H}_{\infty }-\) like control term is employed to compensate for uncertainties. A stability analysis is introduced to solve the problem of nonlinear systems with input saturation. Moreover, the suggested scheme can be applied to unknown or semi-unknown affine and non-affine systems. Also, the proposed observer controller does not need SPR conditions to be identified. Moreover, a fuzzy estimator with the feedback error function \(\hat{\Xi }\) is used, so that, the number of fuzzy sets and also fuzzy IF–THEN rules is reduced. The suggested approach is robust and accurate with less computing. The simulation results signify obviously that the tracking errors are very small. Finally, the proposed strategy can maintain system performance despite various uncertainties and external disturbances with a proper reduction in chattering. The proposed approach is not limited only to the simulation examples; it can be applied to various class of nonlinear systems, e.g., MIMO, MISO, MIMO, and SISO systems. We want to develop this scheme in the next study, so it can be applied to industrial and practical systems.
Data availability
Enquiries about data availability should be directed to the authors.
References
Al-Qerem A, Alauthman M, Almomani A, Gupta BB (2020) IoT transaction processing through cooperative concurrency control on fog–cloud computing environment. Soft Comput 24:5695–5711
Gao Y, Tong S (2015) Composite adaptive fuzzy output feedback dynamic surface control design for uncertain nonlinear stochastic systems with input quantization. Int J Fuzzy Syst 17:609–622
Ghavidel HF (2018) Robust control of large scale nonlinear systems by a hybrid adaptive fuzzy observer design with input saturation. Soft Comput 22:6473–6487. https://doi.org/10.1007/s00500-017-2699-z
Ghavidel HF (2020) A modeling error-based adaptive fuzzy observer approach with input saturation analysis for robust control of affine and non-affine systems. Soft Comput 24:1717–1735. https://doi.org/10.1007/s00500-019-03999-0
Ghavidel HF, Kalat AA (2017a) Robust control for MIMO hybrid dynamical system of underwater vehicles by composite adaptive fuzzy estimation of uncertainties. Nonlinear Dyn 89:2347–2365. https://doi.org/10.1007/s11071-017-3590-2
Ghavidel HF, Kalat AA (2017b) Observer-based robust composite adaptive fuzzy control by uncertainty estimation for a class of nonlinear systems. Neurocomputing 230:100–109. https://doi.org/10.1016/j.neucom.2016.12.001
Ghavidel HF, Kalat AA (2017c) Robust composite adaptive fuzzy identification control of uncertain MIMO nonlinear systems in the presence of input saturation. Arab J Sci Eng 42:5045–5058. https://doi.org/10.1007/s13369-017-2552-9
Ghavidel HF, Kalat AA (2018) Observer-based hybrid adaptive fuzzy control for affine and nonaffine uncertain nonlinear systems. Neural Comput Appl 30:1187–1202. https://doi.org/10.1007/s00521-016-2732-7
Ghavidel HF, Kalat AA (2019) Synchronization adaptive fuzzy gain scheduling PID controller for a class of mimo nonlinear systems. Int J Uncertain Fuzziness Knowledge-Based Syst 27:515–535
Ghavidel HF, Mousavi-G SM (2022a) Observer-based type-2 fuzzy approach for robust control and energy management strategy of hybrid energy storage systems. Int J Hydrogen Energy 47:14983–15000. https://doi.org/10.1016/j.ijhydene.2022.02.236
Ghavidel HF, Mousavi-G SM (2022b) Modeling analysis, control, and type-2 fuzzy energy management strategy of hybrid fuel cell-battery-supercapacitor systems. J Energy Storage 51:104456. https://doi.org/10.1016/j.est.2022b.104456
Ghavidel HF, Kalat AA, Ghorbani V (2017) Observer-based robust adaptive fuzzy approach for current control of robot manipulators by estimation of uncertainties. Modares Mech Eng 17:286–294
Ghavidel HF, Mousavi Gazafroudi SM, Asad R (2020) Thrust control of BLDC thruster motors by observer-based robust adaptive fuzzy control. J Iran Assoc Electr Electron Eng 17:109–118
Guo X, Liang H, Pan Y (2020) Observer-based adaptive fuzzy tracking control for stochastic nonlinear multi-agent systems with dead-zone input. Appl Math Comput 379:125269
Labiod S, Guerra TM (2010) Indirect adaptive fuzzy control for a class of nonaffine nonlinear systems with unknown control directions. Int J Control Autom Syst 8:903–907. https://doi.org/10.1007/s12555-010-0425-z
Lamara A, Colin G, Lanusse P et al (2012) Decentralized robust control-system for a non-square MIMO system, the air-path of a turbocharged diesel engine. IFAC Proc 45:130–137
Li IH, Lee LW (2011) A hierarchical structure of observer-based adaptive fuzzy-neural controller for MIMO systems. Fuzzy Sets Syst 185:52–82
Li H-X, Tong S (2003) A hybrid adaptive fuzzy control for a class of nonlinear MIMO systems. IEEE Trans Fuzzy Syst 11:24–34
Li Y, Li T, Tong S (2013a) Adaptive fuzzy modular backstepping output feedback control of uncertain nonlinear systems in the presence of input saturation. Int J Mach Learn Cybern 4:527–536
Li Y, Tong S, Li T (2013b) Direct adaptive fuzzy backstepping control of uncertain nonlinear systems in the presence of input saturation. Neural Comput Appl 23:1207–1216
Li Y, Tong S, Li T (2015) Composite adaptive fuzzy output feedback control design for uncertain nonlinear strict-feedback systems with input saturation. IEEE Trans Cybern 45:2299–2308
Li D, Deng L, Gupta BB et al (2019) A novel CNN based security guaranteed image watermarking generation scenario for smart city applications. Inf Sci (NY) 479:432–447
Li Y, Qu F, Tong S (2020) Observer-based fuzzy adaptive finite-time containment control of nonlinear multiagent systems with input delay. IEEE Trans Cybern 51:126
Lin D, Wang X, Yao Y (2012) Fuzzy neural adaptive tracking control of unknown chaotic systems with input saturation. Nonlinear Dyn 67:2889–2897
Min D-J, Kwon S-D, Kwark J-W, Kim M-Y (2017) Gust wind effects on stability and ride quality of actively controlled maglev guideway systems. Shock Vib 2017
Ren B, Ge SS, Tee KP, Lee TH (2010) Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function. IEEE Trans Neural Networks 21:1339–1345
Rigatos GG (2014) A differential flatness theory approach to observer-based adaptive fuzzy control of MIMO nonlinear dynamical systems. Nonlinear Dyn 76:1335–1354
Schkoda R, Crassidis A (2007) Dynamic inversion control for non-square systems with application to aircraft longitudinal control. In: AIAA Atmospheric Flight Me-chanics Conference. South Carolina. pp 1–14
Shahnazi R (2016) Observer-based adaptive interval type-2 fuzzy control of uncertain MIMO nonlinear systems with unknown asymmetric saturation actuators. Neurocomputing 171:1053–1065
Shaocheng T, Bin C, Yongfu W (2005) Fuzzy adaptive output feedback control for MIMO nonlinear systems. Fuzzy Sets Syst 156:285–299
Shi W (2014) Adaptive fuzzy control for MIMO nonlinear systems with nonsymmetric control gain matrix and unknown control direction. IEEE Trans Fuzzy Syst 22:1288–1300
Shi W (2015) Observer-based fuzzy adaptive control for multi-input multi-output nonlinear systems with a nonsymmetric control gain matrix and unknown control direction. Fuzzy Sets Syst 263:1–26
Tee KP, Ge SS, Tay EH (2009) Barrier Lyapunov Functions for the control of output-constrained. Automatica 45:918–927. https://doi.org/10.1016/j.automatica.2008.11.017
Tong S, Min X, Li Y (2020) Observer-based adaptive fuzzy tracking control for strict-feedback nonlinear systems with unknown control gain functions. IEEE Trans Cybern 50:3903
Ulrich S, Sasiadek JZ, Barkana I (2012) Decentralized simple adaptive control for nonsquare Euler-Lagrange systems. In: 2012 American Control Conference (ACC). IEEE, pp 232–237
Wang L-X (1996) A course in fuzzy systems and control. Prentice-Hall, Inc.
Wen C, Zhou J, Liu Z, Su H (2011) Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Trans Automat Contr 56:1672–1678
Yousfi N, Melchior P, Lanusse P et al (2014) Decentralized CRONE control of nonsquare multivariable systems in path-tracking design. Nonlinear Dyn 76:447–457
Youssef F, El Habib BL, Hamza R et al (2018) A new conception of load balancing in cloud computing using tasks classification levels. Int J Cloud Appl Comput 8:118–133
Zhang Q, Dong J (2020) Disturbance-observer-based adaptive fuzzy control for nonlinear state constrained systems with input saturation and input delay. Fuzzy Sets Syst 392:77–92
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The author declares that they have no conflict of interest.
Human participants
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Fallah Ghavidel, H., Mosavi-G, S.M. Barrier Lyapunov function-based adaptive fuzzy control for general dynamic modeling of affine and non-affine systems. Soft Comput 27, 12539–12557 (2023). https://doi.org/10.1007/s00500-023-07904-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-023-07904-8