1 Introduction

Underwater vehicles can be found in many different designs, dimensions, speeds and special abilities, and are built for a wide range of applications, e.g., submarines, autonomous underwater vehicles (AUVs) and remotely operated underwater vehicles (ROVs). Stabilization and tracking control is one of the most essential parts of an underwater vehicle. They are nonlinear systems, and due to the uncertainties and disturbances, their good tracking performance always is an important control task. In the past years, several control techniques have been developed for the underwater vehicles [1,2,3,4,5,6,7,8,9,10,11,12,13].

Majority of control methods of underwater vehicles are based on the conventional torque control [1,2,3, 6, 11, 13]. In this method, the most important problem is that the dynamics of actuators for providing the desired torques are omitted and therefore the control signals cannot be applied directly to the inputs of actuators for driving the underwater vehicles. To resolve this problem, voltage/current-based control input has been presented in this paper, in order to control electrically driven of the underwater vehicles. In fact, since the underwater vehicles are driven by electrical actuators their actuator thrusters must be controlled. The electrical inputs of actuated thrusters are controlled by voltage/current employed on the motor inputs.

Another important issue in the control of the underwater vehicles is the uncertainties. The uncertainty can include parametric uncertainty, external disturbance forces and un-modeled dynamics. By combining an adaptive fuzzy scheme and robust control term, in this study, a novel adaptive fuzzy control scheme is proposed to approximate the uncertainties and also a robust controller is applied to attenuate the effect of fuzzy approximation error in tracking control.

In recent years, fuzzy logic system has been applied in wide application for numerous products and industrial purposes. Wang presented a general analysis of control scheme for a class of nonlinear systems [14]. Combination of the adaptive arrangement and fuzzy system is a powerful control method for designing robust control approach with known/unknown uncertainties and nonlinearities [15].

Two types of adaptive fuzzy controllers are commonly researched: indirect and direct adaptive fuzzy methods. Indirect adaptive fuzzy control scheme is applied to estimate the unknown dynamic functions of the system, so indirect fuzzy controllers are designed by these estimators. Direct adaptive fuzzy controller directly originates to emulate an ideal controller without determining the model of the unknown dynamic functions. Recently, numerous adaptive fuzzy methods have been employed for a class of SISO [14,15,16,17,18,19] and also MIMO [20,21,22,23,24,25,26] nonlinear uncertain systems. In the adaptive fuzzy approaches, the control methods are generally formed of a fuzzy logic system for main adjustment and a usual typical compensator, such as sliding mode control [1, 2]. In these cases, in order to decrease the chattering effect of sliding term some techniques are used such as a boundary layer [20], \(H_\infty \) control [14, 15], using a combination of the two types of sliding mode control and \(H_\infty \) control [22], robust PI control [19], supervisory control [17], tangent hyperbolic robust function [10], two-mode control [16] and fractional-order sliding mode controller [18]. Also, many adaptive fuzzy methods have been utilized for underwater vehicles [1, 2, 10,11,12,13]. In this study by combining a composite adaptive fuzzy (CAF) scheme and a robust control term, a robust controller is suggested for the proposed MHDS of underwater systems to dispel the uncertainties and disturbances.

Robustness and stability of the closed-loop systems are usually guaranteed by robust compensators. Therefore based on [14], it is possible that the robust compensator term becomes main controller and plays an extra role than the adaptive fuzzy controller; hence, the composite adaptation can be applied to solve this problem. The basic aim for use this method is a faster and smoother adaptation technique using both the tracking and prediction errors.

In Ghavidel and Kalat [14], have presented a CAF approach that estimates the system uncertainties very well, also guarantees stability of the closed-loop system and provides a good tracking performance. In [14, 27,28,29], a CAF method has been used for a class of SISO and in [24] for a class of MIMO systems. Also in [30,31,32], a composite adaptive back-stepping has been developed for a class of non-affine MIMO nonlinear systems.

The adaptive fuzzy control approaches are created from some fuzzy IF–THEN rules afforded by human expert knowledge. Then, in the adaptive fuzzy controllers that inputs of fuzzy system are the state variables, the fuzzy controller may not converge to the desired function. In [14, 15], authors have presented an adaptive fuzzy system that uses the feedback error signals instead of the state variables as input in the adaptive fuzzy controller, which provides a good tracking performance. In this paper, a fuzzy logic system is utilized that uses the dynamics of the modeling error instead of the state variables as input in the adaptive fuzzy approximator. Indeed, in order to achieve a good estimation of uncertainties, to achieve a smaller tracking error, and also to decrease the number of fuzzy sets and rules, as the inputs of fuzzy approximator are selected the modeling errors instead of the state variables.

There may be several assumptions in the simplified models for decoupled single-DOF dynamical systems [1,2,3, 7, 9,10,11,12]. In this paper, a more precise MIMO six-DOF model for an accurate control of the underwater system is proposed (i.e., a second-order dynamical model for each DOF). Indeed, by the both underwater vehicles and actuator models, the voltage control input is directly available for control.

Note that the torque control efforts cannot be used directly to the inputs of the actuators for driving the underwater vehicles (e.g., the voltage inputs of the actuators DC motors). In order to control the underwater systems, the control signal must be applied to the actuators. The most important problem of the torque control method is that the dynamics of actuators for providing the desired torques are omitted. In the torque control method, the control problem may become more complicated, since it consists of two steps: first, torque control should be designed and then the estimate of a control signal for the actuator inputs would be proposed. The control of underwater system by the torque methods becomes more complicated when the actuators are in the presence of external disturbances and uncertainties. Furthermore, in order to estimate the control effort of actuators based on the torque methods, there may be several assumptions to find a proper relation between torque and voltage/current inputs, e.g., the motor viscous friction, motor inductance and ambient fluid velocity are considered worthless, vehicle is moving at low speed, all rotational mechanical dynamics and motor electrical dynamics are ignored, etc. To solve this problem, by the proposed MHDS of underwater vehicle and its actuators, in this paper an input control method of actuators can be presented to control electrically driven of the underwater vehicles.

Moreover, by applying adaptive fuzzy method in the proposed MHDS, if we do not use sensor for the actuator thrusters (e.g., speed sensors for measuring the propeller speed of electrical thruster), then we have a sensorless control of the actuator thrusters (e.g., estimation of the vehicle position is independent of the propeller speed sensors).

Briefly, compared with the existed results, the main advantages of the proposed control scheme are as follows:

  1. (1)

    The proposed control scheme is not limited only to control of the underwater vehicles, but can be applied for a class of nonlinear MIMO systems with square/non-square control gain matrices.

  2. (2)

    In the proposed control method, the voltage control input is directly available for control of underwater vehicle. (Note that voltage control design based on the torque control method may become more complicated, since it can consist of two steps).

  3. (3)

    By the proposed MHDS, it is possible to reduce computations complexity, while providing a good and robust tracking performance. In other words, the dynamical effects and uncertainties of the both underwater vehicle and actuators system can be compensated by the proposed control method.

  4. (4)

    By the sensorless control of the actuator thrusters, it seems that the implementation of the proposed method is simpler and production cost is less.

  5. (5)

    In order to improve the approximation of uncertainties by adaptive fuzzy algorithm, and also to reduce the number of fuzzy sets and rules, in this paper we employ a CAF control method that uses the modified modeling error signals instead of the state variables as input in the CAF. Note that the basic idea of the CAF method for a good estimation of uncertainties is introduced by authors in [14].

  6. (6)

    In [20, 25], in order to solve the singularity problem, a complex robust control term is proposed, while in this paper we propose a very simple and efficient robust control term.

This paper is organized as follows: In Sect. 2, the dynamic model of underwater vehicle and its actuators is expressed. In Sect. 3, the MHDS control strategy of the underwater system is described. In Sect. 4, the control system and description of the CAFL scheme is presented. In Sect. 5, simulation examples are provided to demonstrate the performance and feasibility of the proposed scheme. Sect. 6 concludes the main advantages of the proposed method.

2 Dynamic of underwater vehicle and its actuators

2.1 Underwater dynamic model

In this section, the nonlinear underwater system with the presence of uncertainties is described. A general dynamic model for the underwater vehicle is used in [33, 34]. The general motion of the underwater vehicle can be explained by using a body-fixed frame relative to an earth-fixed frame. On this basis, this transformation can be represented by

$$\begin{aligned} {\dot{\mathbf{x}}} = {\mathbf{J}}\left( {\mathbf{x}} \right) {\mathbf{v}} \end{aligned}$$
(1)

where \(\mathbf{v}=\left[ {v_x, v_y , v_z, v_\phi , v_\theta , v_\psi } \right] ^\mathrm{T}\) is the vector of linear and angular velocities in the body-fixed reference frame, \(\mathbf{x}=\left[ {x, y, z, \phi , \theta , \psi } \right] ^\mathrm{T}\) represents the position, and \(\mathbf{J}\left( \mathbf{x} \right) \) is the Jacobian transformation matrix.

The general equation of motion for the underwater vehicle can be written as

$$\begin{aligned} \mathbf{M}{\dot{\mathbf{v}}} + {\mathbf{C}}\left( {\mathbf{v}} \right) {\mathbf{v}} + {\mathbf{D}}\left( {\mathbf{v}} \right) {\mathbf{v}} + {\mathbf{g}}\left( {\mathbf{x}} \right) + {{\varvec{\upeta }}}\left( t \right) = {{{\varvec{\uptau }}}} \end{aligned}$$
(2)

where \(\mathbf{M}\in \mathfrak {R}^{6\times 6}\) is the mass inertia matrix including added mass term and rigid body term, \(\mathbf{C}\left( \mathbf{v} \right) \in \mathfrak {R}^{6\times 6}\) is the centripetal and Coriolis matrix, \(\mathbf{D}\left( \mathbf{v} \right) \in \mathfrak {R}^{6\times 6}\) represents the hydrodynamic quadratic damping, \(\mathbf{g}\left( \mathbf{x} \right) \in \mathfrak {R}^{6}\) is the gravitational and buoyancy vector, \({{\varvec{\upeta }}}\left( t \right) \in \mathfrak {R}^{6}\) is an external disturbance vector and \({{\varvec{\uptau }} } \in \mathfrak {R}^{6}\) is the vector of total thrust input vector consisting of control forces and moments.

Details on the matrices \(\mathbf{J}\left( \mathbf{x} \right) \), \(\mathbf{M}\), \(\mathbf{C}\left( \mathbf{v} \right) \), \(\mathbf{D}\left( \mathbf{v} \right) \) and \(\mathbf{g}\left( \mathbf{x} \right) \) operated for a model of underwater vehicle have been presented in [34].

It is quite difficult to get all the 36 added mass parameters and inertia matrix \(\mathbf{M}\in \mathfrak {R}^{6\times 6}\). In this paper, \(\mathbf{M}\) can be simplified into \( \mathbf{M}=\mathbf{M}_\mathbf{o} +\Delta _\mathrm{M} \), where \(\mathbf{M}_\mathbf{o} \in \mathfrak {R}^{6\times 6}\) is the nominal matrix and \(\Delta _\mathrm{M} \in \mathfrak {R}^{6\times 6}\) is an unknown matrix. Usually, the damping of the underwater vehicles are nonlinear and coupled in nature. In this paper, \(\mathbf{D}\) can be simplified into \(\mathbf{D}\left( \mathbf{v} \right) =\mathbf{D}_{\varvec{o}} +\Delta _\mathrm{D} \), where \(\mathbf{D}_{\varvec{o}} \in \mathfrak {R}^{6\times 6}\) is the nominal matrix, and \(\Delta _\mathrm{D} \in \mathfrak {R}^{6\times 6}\) is an unknown matrix. Also \(\mathbf{C}\left( \mathbf{v} \right) =\mathbf{C}_{{\varvec{o}}} +\Delta _\mathrm{C} \) where \(\mathbf{C}_{{\varvec{o}}} \in \mathfrak {R}^{6\times 6}\) is the nominal matrix, and \(\Delta _\mathrm{C} \in \mathfrak {R}^{6\times 6}\) is an unknown matrix and \(\mathbf{g}\left( \mathbf{x} \right) =\mathbf{g}_{{\varvec{o}}} +\Delta _\mathrm{g} \) where \(\mathbf{g}_{{\varvec{o}}} \in \mathfrak {R}^{6}\) is the nominal vector, and \(\Delta _\mathrm{g} \in \mathfrak {R}^{6}\) is an unknown vector.

Therefore, from the dynamic model (2), the unknown terms of \(\Delta _\mathrm{M} {\dot{\mathbf{v}}}\), \(\Delta _\mathrm{C} \mathbf{v}\), \(\Delta _\mathrm{D} \mathbf{v}\) and \(\Delta _\mathrm{g}\) are incorporated in uncertainty vector \(\Delta \in \mathfrak {R}^{6}\)

$$\begin{aligned} \Delta =\Delta _\mathrm{M} {\dot{\mathbf{v}}} + \Delta _\mathrm{C} \mathbf{v}+ \Delta _\mathrm{D} \mathbf{v}+ \Delta _\mathrm{g} . \end{aligned}$$
(3)

From (1), it can be directly implied that \( \mathbf{v}=\mathbf{J}^{{\varvec{-1}}}\left( \mathbf{x} \right) {\dot{\mathbf{x}}}\) and \({\dot{\mathbf{v}}} = {{\dot{\mathbf{J}}}^{{\varvec{-1}}}}{\dot{\mathbf{x}}} + {{\mathbf{J}}^{{\varvec{-1}}}}{\ddot{\mathbf{x}}}\), [1], then after some simple manipulations, we can obtain the equations of motion for the general Eq. (2) as

$$\begin{aligned}&{{\mathbf{M}}_{\mathbf{J}}}{\ddot{\mathbf{x}}} + {{\mathbf{J}}^\mathrm{T}}{{\mathbf{M}}_{\mathbf{o}}}{{\dot{\mathbf{J}}}^{{\varvec{-1}}}}{\dot{\mathbf{x}}} + {{\mathbf{C}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{D}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{g}}_\mathrm{{J}}}\left( {\mathbf{x}} \right) \nonumber \\&\quad +\,{{{{\varvec{\upeta }}}}_{\mathbf{J}}} + {\Delta _{\mathbf{J}}} = {{{{\varvec{\uptau }}}}_{\mathbf{J}}} \end{aligned}$$
(4)

where \(\mathbf{M}_\mathbf{J} =\mathbf{J}^{-\mathrm{T}}{} \mathbf{M}_\mathbf{o} \mathbf{J}^{-1}\), \(\mathbf{C}_\mathbf{J} =\mathbf{J}^{-\mathrm{T}}{} \mathbf{C}_{\varvec{o}} \mathbf{J}^{-1}\), \(\mathbf{D}_\mathbf{J} =\mathbf{J}^{-\mathrm{T}}{} \mathbf{D}_{\varvec{o}} \mathbf{J}^{-1}\), \(\mathbf{g}_\mathbf{J} =\mathbf{J}^{-\mathrm{T}}{} \mathbf{g}_{\varvec{o}} \), \({{\varvec{\upeta }}}_\mathbf{J} =\mathbf{J}^{-\mathrm{T}}{{\varvec{\upeta }}}\), \(\Delta _\mathbf{J} =\mathbf{J}^{-\mathrm{T}}\Delta \) and \({{\varvec{\uptau }}}_\mathbf{J} =\mathbf{J}^{-\mathrm{T}}{{\varvec{\uptau }}}\). Therefore, the dynamic model for underwater vehicles can be written as

$$\begin{aligned} \mathbf{M}_\mathbf{J}{\ddot{\mathbf{x}}} = \mathbf{f}_\mathbf{k} + {{{{\varvec{\uptau }}}}_\mathbf{J}} \end{aligned}$$
(5)

where \({{\mathbf{f}}_{\mathbf{k}}} = - \left( {{\mathbf{J}}^\mathrm{T}}{{\mathbf{M}}_{\mathbf{o}}}{{{\dot{\mathbf{J}}}}^{{\varvec{-1}}}}{\dot{\mathbf{x}}} + {{\mathbf{C}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{D}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{g}}_\mathrm{{J}}}\left( {\mathbf{x}} \right) + {\varvec{\eta }_{\mathbf{J}}} + {\Delta _{\mathbf{J}}} \right) \). The total thrust input vector can be conveniently represented by

$$\begin{aligned} {{\varvec{\uptau }} }=\mathbf{BT} \end{aligned}$$
(6)

where \(\mathbf{T} \in \mathfrak {R}^{\mathrm{N}}\) is a vector containing the magnitude of thrust exerted by each thruster (the effect on the vehicle through the force produced by each thruster), \(\hbox {N}\) is the number of thrusters and \(\mathbf{B}\in \mathfrak {R}^{6\times N}\) is a mapping matrix which represents the distribution of the thrust forces on the vehicle.

Remark 1

Note that, in [1,2,3, 7, 9,10,11,12] the simplified models for decoupled single-DOF dynamical equations of the underwater vehicles are presented. Although it is not theoretically justified [7], this models are simplified by neglecting off-diagonal entries and coupling terms, tether dynamics, the off-diagonal elements of the added mass matrix, the Coriolis and centripetal kinematics, drag coupling terms, etc. This approximation relies on the fact that the off-diagonal elements of the positive definite matrices are much smaller than their diagonal counterparts and the hydrodynamic damping coupling is negligible at low speeds. In this paper, we apply the more precise MIMO six-DOF model (5) for more accurate control of the underwater system.

2.2 Dynamic model of the actuator thrusters

It is reasonable to assume that the thrust forces are actuated by the actuator inputs. In other words, the thrust forces vector \(\mathbf{T} \in \mathfrak {R}^{N}\) can be related to the actuator input vector \(\mathbf{U}=\left[ {u_1 ,\ldots ,u_M } \right] ^\mathrm{T}\) by a transformation of the form \(\mathbf{T}=\mathbf{f}\left( \mathbf{U} \right) \), where M is the number of actuator inputs. In order to obtain the actuator inputs as the inputs of underwater system, one possible solution for solving the problem is to make a reasonable correlation between the actuator inputs and thrust forces. For example, the transformation from \(\mathbf{T}=\mathbf{f}\left( \mathbf{U} \right) \) can be expressed as

$$\begin{aligned} \mathbf{T}=\mathbf{f}\left( \mathbf{U} \right) ={{\varvec{\upalpha }} \mathbf{U}}+{{\varvec{\upvarphi }}} \end{aligned}$$
(7)

where \({{\varvec{\upalpha }}}\in \mathfrak {R}^{N\times M}\) and \({{\varvec{\upvarphi }} }\in \mathfrak {R}^{N}\), are known/unknown functions, then the control problem is to obtain an accurate and proper estimate of \({\varvec{\alpha }}\) and \({\varvec{\varphi }}\) [for more details, see dynamic model (16)]. The relationship (7) implies that the thrust forces are directly proportional to the actuator inputs. The overall description for this relationship is depicted in Fig. 1, in which thrust input \({{\varvec{\uptau }}}\) is produced by the actuator input \(\mathbf{U}\).

Fig. 1
figure 1

Underwater vehicle with both body-fixed and earth-fixed frames

Full size image

In this paper, we apply the electrical thrusters as the actuators. Electric actuators are common choice for AUVs and ROVs (instead of hydraulic thrusters), even in large underwater vehicles, also most underwater vehicles are using propeller type thruster for their navigation.

The electrical thruster consists of a DC motor connected to a propeller. Since the propeller is attached onto the motor shaft, the DC motor shaft dynamic has to be considered. Most full-ocean depth thrusters are often actuated by the brushless DC (BLDC) electric motors. Based on [8, 34, 35], the simplified dynamic model of the BLDC motors are practically similar to model of the DC motors

$$\begin{aligned} I= & {} k_t^{ - 1}\left( {J\dot{\varOmega } + {k_f}\varOmega + Q} \right) \end{aligned}$$
(8)
$$\begin{aligned} V= & {} L\dot{I} + RI + {k_e}{{\Omega }} \end{aligned}$$
(9)

where V, I, L, R, \({\Omega }\) and Q are the voltage input, the current input, inductance, resistance, the propeller rotational velocity and the shaft torque, respectively. Also \(k_t\), \(k_f\), \(k_e\) and J are the motor viscous friction constant, the motor the viscous friction constant, the back emf constant and the rotor moment of inertia, respectively.

Based on [33,34,35,36], we have

$$\begin{aligned} Q= & {} {c_q}\varOmega \left| \varOmega \right| + {c_{qo}}\dot{\varOmega } \approx {c_q}\varOmega \left| \varOmega \right| \end{aligned}$$
(10)
$$\begin{aligned} T= & {} {c_t}\varOmega \left| \varOmega \right| + {c_{to}}\dot{\varOmega } \approx {c_t}\varOmega \left| \varOmega \right| \end{aligned}$$
(11)
$$\begin{aligned} Q\approx & {} {c_{tq}}T \end{aligned}$$
(12)

where T is thrust force and \(c_t\), \(c_q\) and \(c_{tq}\) are experimentally determined constants and also \(c_{qo}\) and \(c_{to}\) are small constants. A torque control method has been presented in [1, 12], by designing a torque controller. Also from the model (11), the rotational velocities have been estimated for each thruster. But, in this method the propeller rotational velocities are limited, because of the maximal voltage admitted by the thrusters and a saturation rotational velocity is applied. Thus, it seems to be very difficult to perform a high-accuracy control by utilizing this method.

Based on [8], the voltage input of thruster can be written as \(T=c_o V\). Based on [9], by neglecting the motor dynamics, the thrust force can be modeled as \(T=c_V V\left| V \right| \). Also based on [7], thrust force can be modeled as \(I=c_I T\), where \(c_o\), \(c_V\) and \(c_I\) are experimentally determined constants. It can be clearly seen that it is a hard to present a robust reliable controller for these methods. The dynamic of actuators should be neglected to perform these schemes.

In fact, applying the torque control effort is a control problem, because it cannot be used directly to the actuator inputs for driving the underwater vehicles.

Therefore, in order to obtain the thruster voltages as the inputs of the underwater system, by substituting (8) in (9), we have

$$\begin{aligned} V = L\dot{I} + {k_1}\dot{\varOmega } + {k_2}\varOmega + {k_3}Q + {\Delta _o}\left( t \right) \end{aligned}$$
(13)

where \(k_1 =\frac{RJ}{K_t}\), \(k_2 =\frac{R}{K_t }\left( {\frac{k_t k_e }{R}+k_e}\right) \) and \(k_3 =\frac{R}{K_t}\). Also, for more accuracy of the simplified model, we assume that \(\Delta _o \left( t \right) \) is an unknown un-modeled term. By (12), the thruster model (13) can be rewritten as

$$\begin{aligned} V = {k_1}\dot{\varOmega } + {k_2}\varOmega + {k_3}{c_{tq}}T + {\Delta _L}\left( t \right) \end{aligned}$$
(14)

Because the motor inductance L is a sufficiently small parameter, we can treat it as a part of unknown un-modeled term \(\Delta _o\), i.e., \({\Delta _L} = L\dot{I} + {\Delta _o}\).

It is very important to notice that based on [36] and our simulations, models \(T=c_o V\), \(T=c_V V\left| V \right| \), and \(I=c_I T\) are valid and favorable only in long-period wave inputs. Several simulations have been carried out for the dynamic models (8)–(9) and more details are shown in Fig. 2. In this experiment, \(V=10 \,\hbox {sin}\left( t \right) \) and \(V=10\, \hbox {sin}\,\left( 10t \right) \) are applied for long (\(V_l\))- and short (\(V_s\))-period wave inputs, respectively. Also uncertainty \(\Delta _L\) is neglected. However, the control of the thruster system described by (8)–(9) becomes more complicated when \(\Delta _L \ne 0\). Figure 2 shows that, for short period wave inputs we have \(T\ne c_o V\), \(T\ne c_V V\left| V \right| \) and \(I\ne c_I T\).

In order to overcome these problems, in this paper the voltage of thruster model (14) can be applied directly to the inputs of the electrical thrusters for driving the underwater vehicles.

Fig. 2
figure 2

a T versus I, and b T versus V; for short (\(V_s\)) and long (\(V_l\)) period wave inputs

Full size image

Therefore, (14) can be rewritten as

$$\begin{aligned} \alpha V + {\Delta _V}\left( t \right) + \varphi = T \end{aligned}$$
(15)

where \(\alpha =\left( {k_3 c_{tq} } \right) ^{-1}\), \(\varphi = - \alpha \left( {{k_1}\dot{\varOmega } + {k_2}\varOmega }\right) \) and \(\Delta _V =-\alpha \Delta _L\).

The block diagram of the thruster dynamic (14) (the DC motor shaft speed and propeller dynamic) is shown in Fig. 3.

Fig. 3
figure 3

Block diagrams of the thruster dynamic

Full size image

Therefore, based on the proposed technique in (7), thruster dynamic (15) for N numbers of thrusters can be expressed as

$$\begin{aligned} \mathbf{T}={{\varvec{\upalpha }} \mathbf{V}}+{{\varvec{\upvarphi }}}+\underline{\Delta }\left( t \right) \end{aligned}$$
(16)

where \(\mathbf{T}=\left[ {T_1 ,\ldots ,T_N } \right] ^\mathrm{T}\), \({{\varvec{\upalpha }} }={\hbox {diag}}\left( {\alpha _1 ,\ldots ,\alpha _N } \right) \), \({{\varvec{\upvarphi }} }=\left[ {\varphi _1 ,\ldots ,\varphi _N} \right] ^\mathrm{T}\), \(\underline{\Delta }=\left[ {\Delta _{V_1 } ,\ldots ,\Delta _{V_N } } \right] ^\mathrm{T}\) and \(j=1,\ldots , N\).

3 The MHDS system and control design

3.1 The MHDS of underwater vehicle and its actuators

In this section, we design a novel underwater dynamic model via actuator control effort. In order to obtain the actuator inputs of the system, the MHDS is expressed by substituting underwater model (5) into thruster dynamic (16) as follows

$$\begin{aligned} {\ddot{\mathbf{x}}}= & {} {\mathbf{M}}_{\mathbf{J}}^{{\varvec{-1}}}{{\mathbf{f}}_{\mathbf{k}}} + {\mathbf{M}}_{\mathbf{J}}^{{\varvec{-1}}}{{\mathbf{J}}^{ - T}}{\mathbf{B}}\left( {{{\varvec{\upalpha }} \mathbf{V}}} + {{{\varvec{\upvarphi }}}} +\underline{\Delta }\right) \nonumber \\ {\ddot{\mathbf{x}}}= & {} {\mathbf{F}}\left( {{\mathbf{X}},{{{\varvec{\Omega }}}}} \right) + {\mathbf{d}}\left( t \right) + {\mathbf{G}}\left( {\mathbf{X}} \right) {\mathbf{V}} \end{aligned}$$
(17)

where

$$\begin{aligned}&{{{\varvec{\Omega }}}} = {\left[ {{\varOmega _1},{{\dot{\varOmega }}_1}, \ldots ,{\varOmega _N},{{\dot{\varOmega }}_N}} \right] ^\mathrm{T}}\in {\mathfrak {R}^{2N}} \\&{\mathbf{F}}\left( {{\mathbf{X}},{{{\varvec{\Omega }}}}} \right) = - {\mathbf{M}}_{\mathbf{J}}^{ {\varvec{-1}}}\left\{ {{{\mathbf{C}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{D}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{g}}_\mathrm{{J}}}\left( {\mathbf{x}} \right) } \right\} \\&\quad \quad \quad \quad \quad \quad +\,{\mathbf{M}}_{\mathbf{J}}^{{\varvec{-1}}}{{\mathbf{J}}^{{\varvec{-\mathrm{T}}}}}{\mathbf{B}}\,{{{\varvec{\upvarphi }} }} \in {\mathfrak {R}^{6}}\\&{\mathbf{G}}\left( {\mathbf{X}} \right) = {\mathbf{M}}_{\mathbf{J}}^{ {\varvec{-1}}}{{\mathbf{J}}^{{\varvec{-\mathrm{T}}}}}{} \mathbf{B}{\varvec{\upalpha }}\in {\mathfrak {R}^{6 \times N}}\\&{} \mathbf{d}(t)= {\left[ {{d_1}, \ldots ,{d_6}} \right] ^\mathrm{T}} \\&\quad \quad \quad \!\!= {\mathbf{M}}_{\mathbf{J}}^{ {\varvec{-1}}}\left\{ {{\mathbf{J}}^{{\varvec{-\mathrm{T}}}}}{\mathbf{B}}\underline{\Delta } - {{{{\varvec{\upeta }} }}_{\mathbf{J}}} -\,{\Delta _{\mathbf{J}}} - {{\mathbf{J}}^\mathrm{T}}{{\mathbf{M}}_{\mathbf{o}}}{{{\dot{\mathbf{J}}}}^{{\varvec{-1}}}}{\dot{ \mathbf x}} \right\} \end{aligned}$$

Remark 2

Note that because of the presence of term \({\dot{\mathbf{J}}}^{{\varvec{-1}}}\), the vector \(\mathbf{J}^\mathrm{T}{} \mathbf{M}_\mathbf{o} {\dot{\mathbf{J}}}^{{\varvec{-1}}} {\dot{\mathbf{x}}}\) cannot be correctly known; therefore, \(\mathbf{J}^\mathrm{T}{} \mathbf{M}_\mathbf{o} {\dot{\mathbf{J}}}^{{\varvec{-1}}} {\dot{\mathbf{x}}}\) can be considered as a part of the lumped uncertainty vector \(\mathbf{d}\). Also, according to the block diagram of the thruster dynamic Fig. 3, the thruster voltage \(V_j\) (for \(j=1,\ldots ,N\)) is the control input, and the thrust force \(T_j\) and the propeller speed \(\varOmega _j\) are given as the thruster outputs, for each subsystem. Therefore, in the proposed scheme if we do not use speed sensors for measuring the propeller speed \(\varOmega _j\), then we have a speed-sensorless control of the thrusters and in this scheme, estimation of the vehicle position is independent of the propeller speed \(\varOmega _j\). Hence, we have \({\mathbf{F}}\left( {\mathbf{X}} \right) = - {\mathbf{M}}_{\mathbf{J}}^{{\varvec{-1}}}\left\{ {{{\mathbf{C}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{D}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{g}}_\mathrm{{J}}}\left( {\mathbf{x}} \right) } \right\} \), and \({{\varvec{\upvarphi }}} \in \mathfrak {R}^{N}\) is an unknown uncertainty vector, then \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \mathbf{J}^{{\varvec{-\mathrm{T}}}}{} \mathbf{B}\, {{\varvec{\upvarphi }}} \in \mathfrak {R}^{6}\) can be considered as a part of the lumped uncertainty vector \(\mathbf{d}\). Moreover, it seems that the implementation of this method is simpler and production cost is less.

3.2 The control design for MHDS

In order to propose a novel robust voltage control of the MHDS, in this section, we apply a robust composite adaptive fuzzy scheme for control of the thrusters.

If \(\mathbf{x}=\left[ {x, y, z, \phi , \theta , \psi } \right] ^\mathrm{T}=\left[ {x_1 , \ldots ,x_6} \right] ^\mathrm{T}\), then the control problem is to obtain the state \({\varvec{x}}_i =\left[ {x_i , \dot{x}} \right] ^\mathrm{T}\) for tracking a desired state \({\varvec{x}}_{di} =\left[ {x_{di} ,\dot{x}} \right] ^\mathrm{T}\) Then, the tracking error is \(\mathbf{E}_i ={\varvec{x}}_{di} -{\varvec{x}}_i =\left[ {e_i, \dot{e}} \right] ^\mathrm{T}\). Also, we have

$$\begin{aligned} {\mathbf{X}}= & {} \left[ {{\varvec{x}}}_1^\mathrm{T}, \ldots ,\,{{\varvec{x}}}_6^\mathrm{T} \right] ^\mathrm{T}\in {\mathfrak {R}^{12}} \end{aligned}$$
(18)
$$\begin{aligned} {\mathbf{E}}= & {} {\left[ {{\mathbf{E}}_1^\mathrm{T}, \ldots ,{\mathbf{E}}_6^\mathrm{T}} \right] ^\mathrm{T}} \in {\mathfrak {R}^{12}} \end{aligned}$$
(19)

We can rewrite the underwater system (17) as

$$\begin{aligned} {\dot{\mathbf{X}}} = {{\mathbf{A}}_o}{\mathbf{X}} + {\mathbf{B}}\left( {{\mathbf{F}} + {\mathbf{d}}\left( t \right) + {\mathbf{GV}}} \right) \end{aligned}$$
(20)

where \(\mathbf{A}_o ={\hbox {diag}}\left( {\mathbf{A}_{o1} ,\ldots ,\mathbf{A}_{o6}} \right) \) and \(\mathbf{B}={\hbox {diag}}\left( \mathbf{B}_1 ,\ldots ,\mathbf{B}_6 \right) \). Let denote \(\mathbf{A}_{oi} =\left[ {0 \, 1;\, 0 \, 0} \right] \), \(\mathbf{B}_i =\left[ {0,1} \right] ^\mathrm{T}\) and \(\mathbf{K}_i =\left[ {k_{1i} ,k_{2i} } \right] ^\mathrm{T}\) is chosen such that each matrix \(\mathbf{A}_i =\mathbf{A}_{oi} -\mathbf{B}_i \mathbf{K}_i^\mathrm{T}\) is Hurwitz for \(i=1,\ldots ,6\). Also, \(\mathbf{A}={\hbox {diag}}\left( {\mathbf{A}_1 ,\ldots ,\mathbf{A}_6 } \right) \). Hence, there exist positive definite matrices \(\mathbf{Q}_i\) and \(\mathbf{P}_i\) such that

$$\begin{aligned} \mathbf{A}_i^\mathrm{T} \mathbf{P}_i +\mathbf{P}_i \mathbf{A}_i +\mathbf{Q}_i =0 \end{aligned}$$
(21)

The following assumptions are presented for the controllability of the system.

Assumption 1

The reference signals \(x_{d_i}, \dot{x}_{d_i}\) are assumed to be exist and bounded.

Assumption 2

External disturbance \({{\varvec{\upeta }}}_\mathbf{J} \left( t \right) \) is a bounded disturbance vector, also \(\Delta _\mathbf{J} \) and \(\underline{\Delta }\) are bounded uncertainty vectors, then \(\mathbf{d}\left( t \right) \) is a bounded lumped uncertainty vector.

Definition 1

[37]: Let \(\mathbf{G}^{+}\in \mathfrak {R}^{N\times 6 }\) be the “inverse/pseudo- inverse” of “square/non-square” matrix \(\mathbf{G}\in \mathfrak {R}^{6\times \mathrm{N}}\), then \(\mathbf{G}^{+}\) can be as follows

$$\begin{aligned} \mathbf{G}^{+}=\left\{ {{\begin{array}{ll} \left[ {\mathbf{G}^{\mathrm{T}}{} \mathbf{G}} \right] ^{{\varvec{-1}}}{} \mathbf{G}^\mathrm{T} &{} \quad \hbox {if}: \hbox { N}<6 \\ \mathbf{G}^{{\varvec{-1}}} &{} \quad \hbox {if}: \hbox { N}=6 \\ \mathbf{G}^\mathrm{T}\left[ {\mathbf{GG}^\mathrm{T}} \right] ^{{\varvec{-1}}} &{} \quad \hbox {if}: \hbox { N}>6 \\ \end{array}}} \right. \end{aligned}$$
(22)

Based on the dynamic model (17) and Definition 1, we propose a voltage control law for the inputs of thrusters as

$$\begin{aligned} \mathbf{V}=\mathbf{G}^{\# }\left( {-\mathbf{F}-{\hat{\mathbf{d}}}+\mathbf{K}^\mathrm{T}{} \mathbf{E}+{\ddot{\mathbf{x}}}_d+\mathbf{u_\mathbf{r}}} \right) \end{aligned}$$
(23)

where \({\ddot{\mathbf{x}}}_d = {\left[ {{{\ddot{x}}_{d1}}, \ldots ,{{\ddot{x}}_{d6}}} \right] ^\mathrm{T}}\), \({\hat{\mathbf{d}}}\) is an estimate vector of \(\mathbf{d}\) and \(\mathbf{u}_\mathbf{r} =\left[ {u_{r1} ,\ldots u_{r6} } \right] ^\mathrm{T}\) is a robust control term to compensate the uncertainties. Also \(\mathbf{K}={\hbox {diag}}\left( {\mathbf{K}_1 ,\ldots ,\mathbf{K}_6 } \right) \). Moreover, \(\mathbf{G}^{\# }\) can be written as

$$\begin{aligned} \mathbf{G}^{\#}= & {} \mathbf{G}^{+}\left[ {\mathbf{GG}^{+}} \right] ^{{\varvec{-1}}}\nonumber \\= & {} \left\{ {{\begin{array}{ll} \\ \mathbf{G}^{+}\left[ {\mathbf{GG}^{+}} \right] ^{{\varvec{-1}}} &{}\quad \hbox {if}: \hbox { N}<6 \\ \mathbf{G}^{+} &{} \quad \hbox {if}: \hbox { N}\ge 6 \\ \end{array}}} \right. \end{aligned}$$
(24)

Based on definition of “inverse/pseudo-inverse” of “square/non-square” matrices, we have

$$\begin{aligned} \left\{ {{\begin{array}{ll} \mathbf{GG}^{+}\ne \mathbf{I}_{\mathbf{6}\times \mathbf{6}} &{} \quad \hbox {if}: \hbox { N}<6 \\ \mathbf{GG}^{+}=\mathbf{GG}^{{\varvec{-1}}}=\mathbf{I}_{\mathbf{6}\times \mathbf{6}} &{} \quad \hbox {if}: \hbox { N}=6 \\ \mathbf{GG}^{+}=\mathbf{I}_{\mathbf{6}\times \mathbf{6}} &{} \quad \hbox {if}: \hbox { N}>6 \\ \end{array} }} \right. \end{aligned}$$
(25)

Therefore, by substituting the proposed voltage control (23) in (20), we have

$$\begin{aligned} {\dot{\mathbf{X}}}= & {} {{\mathbf{A}}_o}{\mathbf{X}} + {\mathbf{B}}\left( {\mathbf{F}} + {\mathbf{d}}\left( t \right) + {\mathbf{G}}{{\mathbf{G}}^\# }\left\{ - {\mathbf{F}} - {\hat{\mathbf{d}}} \right. \right. \nonumber \\&\left. \left. +\,\, {{\mathbf{K}}^\mathrm{T}}{\mathbf{E}} + {{\ddot{\mathbf{x}}}}_d + {{\mathbf{u}}_{\mathbf{r}}} \right\} \right) \nonumber \\ {\dot{\mathbf{E}}}= & {} {\mathbf{AE}} + {\mathbf{B}}\left\{ {\left( {{\hat{\mathbf{d}}}- {\mathbf{d}}} \right) - {{\mathbf{u}}_{\mathbf{r}}}} \right\} \end{aligned}$$
(26)

For the invertible matrix \(\mathbf{GG}^{+}\), we have \(\mathbf{GG}^{\#}=\mathbf{GG}^{+}\left[ {\mathbf{GG}^{+}} \right] ^{{\varvec{-1}}}= \mathbf{I}_{\mathbf{6}\times \mathbf{6}}\) (for \(\hbox {N}\ge 6\) and also \(\hbox {N}<6\)).

Definition 2

[20, 25]: Let H be a square matrix and \(\mathbf{H}^{{\varvec{-1}}}\) be the inverse of H. Then, the regularized inverse of H is defined as \(\mathbf{H}^{{\varvec{-1}}}\cong \mathbf{H}^{\mathbf{r}}=\mathbf{H}^\mathrm{T}[\delta \mathbf{I}+\mathbf{HH}^\mathrm{T}]^{{\varvec{-1}}}\), where \(\delta \) is a small regularization positive constant.

In this paper, some techniques and assumptions are applied to overcome the singularity problem of the dynamic model (17) and the proposed controller (23):

  1. (1)

    The elements of the Jacobian transformation matrix (2) are selected such that the matrix is always nonsingular, e.g., the Jacobian transformation matrix [34] is undefined for \(\theta =\pm 90^{\circ }\). However, in the vessel operation this problem does not exist because the vehicle is not required to operate at this angle.

  2. (2)

    Matrix \(\mathbf{M}_\mathbf{J}\) is chosen so that it is always nonsingular (e.g., we can propose a diagonal approximation matrix for \(\mathbf{M}_\mathbf{o}\) [1, 34]. The diagonal approximation can be quite good for many applications. Moreover, another way can be applying the regularized inverse).

  3. (3)

    For resolving the singularity problem of matrix \(\mathbf{G}^{\# }=\mathbf{G}^{+}\left[ {\mathbf{GG}^{+}} \right] ^{-1}\), an useful method can be applying regularized inverse of \(\mathbf{G}^{\#}\). Therefore, from (24) and Definition 2 we have

    $$\begin{aligned} \mathbf{G}^{\# }\cong & {} reg\left\{ {\mathbf{G}^{\# }} \right\} \nonumber \\= & {} \left\{ {{\begin{array}{ll} \left[ {\mathbf{G}^\mathrm{T}{} \mathbf{G}} \right] ^{\mathbf{r}}{} \mathbf{G}^\mathrm{T}\times \left[ {\mathbf{G}\left( {\left[ {\mathbf{G}^\mathrm{T}{} \mathbf{G}} \right] ^{\mathbf{r}}{} \mathbf{G}^\mathrm{T}} \right) } \right] ^{\mathbf{r}} &{}\quad \hbox {if}: \hbox { N}<6 \\ \mathbf{G}^{\mathrm{r}} &{} \quad \hbox {if}: \hbox { N}=6 \\ \mathbf{G}^\mathrm{T}\left[ {\mathbf{GG}^\mathrm{T}} \right] ^{\mathbf{r}} &{} \quad \hbox {if}: \hbox { N}>6 \\ \end{array}}} \right. \nonumber \\ \end{aligned}$$
    (27)

Therefore, if we use Definition 2 for the proposed controller (23), then the error dynamic equation (26) can be rewritten as

$$\begin{aligned} {\dot{\mathbf{E}}} = {\mathbf{AE}} + {\mathbf{B}}\left\{ {\left( {{\hat{\mathbf{d}}}} - {\mathbf{d}} \right) - {{\mathbf{u}}_{\mathbf{r}}} + {{{\varvec{\upsigma }}}}} \right\} \end{aligned}$$
(28)

where \({{{\varvec{\upsigma }} }} = \left( {{\mathbf{I}} - {\mathbf{G}} \times reg\left\{ {{{\mathbf{G}}^\# }} \right\} } \right) \left\{ - {\mathbf{F}} - {\hat{\mathbf{d}}}+ {{\mathbf{K}}^\mathrm{T}}{\mathbf{E}} + {{\ddot{\mathbf{x}}}}_d + {{\mathbf{u}}_{\mathbf{r}}} \right\} = {\left[ {{\sigma _1}, \ldots ,{\sigma _6}} \right] ^\mathrm{T}}\). Therefore, after some simple manipulations, the error dynamic equation for each subsystem can be written as

$$\begin{aligned} {\dot{\mathbf{E}}}_i= & {} {{\mathbf{A}}_i}{{\mathbf{E}}_i} + {{\mathbf{B}}_i}\left\{ {\left( {{{\hat{d}}_i} - {d_i}} \right) + {\sigma _i} - {u_{ri}}} \right\} \nonumber \\&\left( {i = 1, \ldots ,6} \right) \end{aligned}$$
(29)

In practice, the estimations of the lumped uncertainty \(d_i\) cannot usually be obtained. In order to overcome the uncertainty, an adaptive fuzzy control scheme is presented to approximate unknown function \(d_i\) and a robust control term is proposed to compensate the fuzzy approximation error.

4 The proposed RCAFc and fuzzy systems

4.1 The series–parallel identification model and modeling error

The series–parallel identification model for the SISO systems has been investigated in [14, 27,28,29]. In this paper, the following series–parallel identification model is defined for the MHDS (17). We define the plant dynamic of the MHDS (17) for each subsystem as follows

$$\begin{aligned} {\ddot{x}_i} = {f_i} + {\mathop {\sum }\limits _{j = 1}^N} {\mathrm{{g}}_{ij}}{u_j} + {d_i}\left( t \right) \end{aligned}$$
(30)

Therefore to achieve the composite adaptation, one defines the filtered modeling error for each subsystem as

$$\begin{aligned} \varepsilon _i ={\dot{\hat{x}}}_i -\dot{x}_i \end{aligned}$$
(31)

where \(\hat{x}_i\) is the estimation of \(x_i\). Then, introduce the following series–parallel identification model with a low-pass filter

$$\begin{aligned} {\ddot{\hat{x}}}_i =-\alpha _i \varepsilon _i +f_i +{\mathop {\sum }\limits _{j=1}^N} \hbox {g}_{ij} u_j +\hat{d}_i -v_i \end{aligned}$$
(32)

where \(\hat{d}_i\) is an estimate of \(d_i \), the estimated state \(\hat{\mathbf{x}}_i =\left[ {\hat{x}_i, {\dot{\hat{x}}}_i} \right] ^\mathrm{T}\) is provided by a series–parallel estimation model of the state vector \(\mathbf{x}_i =\left[ {x_i, \dot{x}_i} \right] ^\mathrm{T}\), \(\alpha _i\) is a positive user-defined filter parameter and \(v_i\) is a modeling compensation term and can be given by the following form

$$\begin{aligned} {v_i} = {\bar{\omega }_i}\,{\mathrm{sign}}\left( {{\varepsilon _i}} \right) \end{aligned}$$
(33)

where \({\bar{\omega }_i} \ge \left| {{\omega _i}} \right| \) is an user-defined finite constant. Using (30) and (32), and \({\dot{\varepsilon }_i} = {\ddot{\hat{x}}}_i - {\ddot{x}_i}\), one gets the modified modeling error dynamic

$$\begin{aligned} {\dot{\varepsilon }_i} = - {\alpha _i}{\varepsilon _i} + {\tilde{d}_i} + {\omega _i} - {v_i} \end{aligned}$$
(34)

where, \(\tilde{d}_i =\hat{d}_i -d_i \).

4.2 Fuzzy logic system and the minimum approximation error

The fuzzy rule base contains of a collection of fuzzy IF–THEN rules as follows

$$\begin{aligned} R^{l}: \hbox { IF } x_1 \hbox { is } F_1^l \hbox { and } {\ldots } \hbox { and } x_n \hbox { is } F_n^l \hbox { THEN } y=\bar{y}^{l}\nonumber \\ \end{aligned}$$
(35)

where \(F_i^l\) are fuzzy sets, \(\bar{y}^{l}\) is a constant, \(l=1,\ldots ,M_\mathbf{X}\) is number of fuzzy rules and \(\mathbf{X}=\left[ {x_1 ,\ldots ,x_n} \right] ^\mathrm{T}\in \, {\mathcal {R}}^{n} \hbox { and } y \in \mathcal{R}\) are the input and output of the fuzzy system, respectively. The above fuzzy system known as zero-order TSK [14] is constructed with a singleton fuzzification, a product inference and a weighted average. Then, the output of fuzzy logic system can be written as

$$\begin{aligned} y\left( \mathbf{X} \right) =\frac{\sum \nolimits _{l=1}^{M_X} \bar{y}^{l}\left[ {\prod \nolimits _{i=1}^n \mu _{F_i^l } \left( {x_i } \right) } \right] }{\sum \nolimits _{l=1}^{M_X } \left[ { \prod \nolimits _{i=1}^n \mu _{F_i^l } \left( {x_i } \right) } \right] }={{\varvec{\uptheta }}}^\mathrm{T}{{\varvec{\upxi }}}\left( \mathbf{X} \right) \end{aligned}$$
(36)

\({{\varvec{\uptheta }}}=\left( {\bar{y}^{1},\ldots , \bar{y}^{M_X }} \right) ^\mathrm{T}=\left[ {\theta _1 ,\ldots , \theta _{M_X}} \right] ^\mathrm{T}\) is the singleton output fuzzy membership functions and \(F_i^l\) is the fuzzy sets with membership functions \(\mu _{F_i^l}\). The fuzzy basis functions are defined as

$$\begin{aligned} \xi ^{l}\left( \mathbf{X} \right) =\frac{\prod \nolimits _{j=1}^n \mu _{F_j^l } \left( {x_i } \right) }{\sum \nolimits _{l=1}^M \left[ {\prod \nolimits _{j=1}^n \mu _{F_j^l } \left( {x_j} \right) } \right] } \end{aligned}$$
(37)

where \({{\varvec{\upxi }}}\left( \mathbf{X} \right) =\left( {\xi ^{1},\ldots ,\xi ^{M_{{\varvec{X}}}}} \right) ^\mathrm{T}\). Then, the optimal parameter vectors \({{\varvec{\uptheta }}}_i^*\) can be defined as

$$\begin{aligned} {{\varvec{\uptheta }}}_i^*=\arg {\hbox {min}}_{{\varvec{\theta }} _i \in {\varOmega } } \left[ {\hbox {sup}}_{{\mathbf{X}\,\in \mathfrak {R}^{n}}} \Vert y\left( {\mathbf{X}{|}{{\varvec{\uptheta }}}_{{\varvec{i}}}} \right) -y\left( \mathbf{X} \right) \Vert \right] \nonumber \\ \end{aligned}$$
(38)

\({{\varvec{\Omega }}}_\mathbf{y}\) is the compact sets defined as \({{\varvec{\Omega }} }_\mathbf{y} =\left\{ {{\varvec{\uptheta }}}_{{\varvec{i}}} :\left| {\left| {{{\varvec{\uptheta }}}_{{\varvec{i}}}} \right| } \right| \le m_y \right\} \), where \(m_y\) is the positive constant specified by the designer. The minimum approximation error can be written in terms of the optimal parameter estimates as \(\omega _{oi} =y\left( {\mathbf{X}|{ {\varvec{\uptheta }}}_i^*} \right) -y\left( \mathbf{X} \right) \).

The important purpose of the adaptive fuzzy controller is to track the reference trajectory. In general, the important drawback of the adaptive fuzzy methods consist in the following question: If \(\mathbf{d}\left( t \right) \) is a full-unknown function, how to design the adaptive fuzzy laws for estimation of the disturbances and the uncertainties using only the state variables? (e.g., estimation of \(\mathbf{d}\left( t \right) \) by state vector \(\mathbf{X}=\left[ {{{\varvec{x}}}_1^\mathrm{T} ,\ldots ,{{\varvec{x}}}_6^\mathrm{T}} \right] ^\mathrm{T}\in \mathfrak {R}^{12})\).

In Ghavidel and Kalat [14, 15], proposed an adaptive fuzzy algorithm that employs the feedback error signals instead of the state variables (e.g., for each subsystem of MHDS, we have \(\varXi _i =\mathbf{K}_i^\mathrm{T} \mathbf{E}_i \in \mathfrak {R}\), where \(\varXi _i\) is used as input in the adaptive fuzzy approximator). The proposed scheme provides a very good tracking performance.

In this paper, a novel adaptive fuzzy logic system is proposed for uncertainty estimation that the modeling error \(\varepsilon _i\) as input of the fuzzy system is used. It is very important to notice that based on the modified modeling error dynamics (34), the modeling error \({\varepsilon _i} = \alpha _i^{ - 1}\left\{ { - {{\dot{\varepsilon } }_i} + {{\tilde{d}}_i} + {\omega _i} - {v_i}} \right\} \) is a function of \(\ddot{x}_i\), \(f_i \left( . \right) \), \(\hbox {g}_i \left( . \right) \) and \(d_i \left( t \right) \). Therefore, it is a proper input of fuzzy approximator instead of the state variables \(\mathbf{X}\). The proposed scheme is not limited only for the estimation of lumped uncertainty \(d_i \left( t \right) \), but can be applied for estimation of all unknown functions of the system (e.g., for \(f_i \left( . \right) \), \(\hbox {g}_i \left( . \right) \) and \(d_i \left( t \right) \)).

It is challenging to determine area of the interval conditions of fuzzy membership functions and also the number of fuzzy sets and/or rules. Therefore, the performance of the control system depends on selecting this fuzzy conditions. As a results, the other benefits of the proposed adaptive fuzzy method are the suggested fuzzy scheme is able to decrease the number of fuzzy sets and/or fuzzy IF–THEN rules. Also, in the proposed method, for the interval conditions of fuzzy membership functions we can choose a small area (since by a proper controller method, it is expected that the modeling errors \(\varepsilon _i\) can be insignificant).

According to above descriptions, the fuzzy logic system for each subsystem is introduced with the following fuzzy IF–THEN rules as

$$\begin{aligned} R^{l}: \hbox { IF } \varepsilon _i \hbox { is } F^{l} \hbox { THEN } \hat{d}_i =\bar{y}^{l}, \left( {l=1,2,\ldots , M_\varepsilon } \right) \nonumber \\ \end{aligned}$$
(39)

and \({{\varvec{\uptheta }} }=\left( \bar{y}^{1},\ldots ,\bar{y}^{M_\varepsilon } \right) ^\mathrm{T}\) is the output fuzzy membership function vector and \(F^{l}\) is the fuzzy sets with membership functions \(\mu _{F^{l}}\). Then, the optimal parameter vectors \({{\varvec{\uptheta }}}_i^*\) for each subsystem can be defined as

$$\begin{aligned} {{\varvec{\uptheta }}}_i^*=\arg {\hbox {min}}_{{{\varvec{\uptheta }}}_i \in {\Omega }} \left[ {{\hbox {sup}}_{\varepsilon _i \in \mathfrak {R},\, \mathbf{X}\in \mathfrak {R}^{n }} \, \Vert d_i \left( {\varepsilon _i |{{\varvec{\uptheta }}}_i } \right) -d_i }\Vert \right] \nonumber \\ \end{aligned}$$
(40)

The minimum approximation error can be written in terms of the optimal parameter estimates as

$$\begin{aligned} \omega _i =\hat{d}_i \left( {\varepsilon _i |{ {\varvec{\uptheta }} }_i^*} \right) -d_i \end{aligned}$$
(41)

4.3 Description of the proposed RCAFc

Note that in this paper we apply the modeling error \(\varepsilon _i\), as input in the fuzzy approximator; thus, one problem of utilizing this method is that the fuzzy approximation error \(\omega _i\) may be increased. Nevertheless, although \(\hat{d}_i \left( {\varepsilon _i | {{\varvec{\uptheta }}}_i } \right) \) is used to estimate the lumped uncertainty \(d_i \left( t \right) \), the proposed controller is still viable, since a robust compensator is used to compensate the influence of the fuzzy approximation error. As a result, high robustness level of robust term may cause saturation of control input, higher frequency of chattering and thus a bad behavior of the whole system. Thus, it is possible that robust term plays a more important role than the adaptive fuzzy term, while a low robustness level of robust term may cause a higher tracking error.

Therefore, to provide a good estimation to the lumped uncertainty vector \(\mathbf{d}\), in [14, 24], a CAF control method is proposed. In this technique, difference between the measured system output and the identification model output is employed on the adaptive fuzzy laws. In other words, the novel adaptive fuzzy estimator with CAFL scheme is more important and the robust term after that, it is the main controller (for more details, see [14, 24]).

Now, the adaptive fuzzy estimator \(\hat{d}\) is as follows

$$\begin{aligned} \hat{d}_i \left( {\varepsilon _i |{{\varvec{\uptheta }}}_i } \right) ={{\varvec{\uptheta }}}_i^\mathrm{T} \varvec{\upxi }_i \left( {\varepsilon _i } \right) \end{aligned}$$
(42)

So the compensation control term \(u_{ri}\) and the CAFL for each subsystem are defined as

$$\begin{aligned}&{u_{ri}} = {\bar{w}_i}~{\mathrm{sign}}\left( {{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}} \right) \end{aligned}$$
(43)
$$\begin{aligned}&{\dot{{{\varvec{\uptheta }}}}}_i =-\gamma _i \left( {\mathbf{E}_i^\mathrm{T} \mathbf{P}_i \mathbf{B}_i +\gamma _{\varepsilon i} \varepsilon _i } \right) {{\varvec{\upxi }}}_i \end{aligned}$$
(44)

where \({\bar{w}_i} \ge \left| {{\omega _i} + {\sigma _i}} \right| \) is an user-defined finite constant, and \(\gamma _i\) and \(\gamma _{\varepsilon i}\) are positive designing constants which determine the rate of the convergence of the fuzzy estimator.

Remark 3

In [20, 25], to solve the singularity problem, a complex robust compensator is proposed. In this paper, the uncertain \(\sigma _i\) can be considered as a part of the fuzzy approximate error \(\omega _i\). Then, the simple robust control term \(u_{ri}\) in (43) can be employed, and \({\bar{w}_i} \ge \left| {{\omega _i} + {\sigma _i}} \right| \) can be attenuated. The proposed scheme in this paper is very simple, efficient and robust.

Theorem

Consider the MHDS in form of (17); then, using the compensation control (33) and CAFL (44) and robust term (43), the tracking error will converge to zero asymptotically.

Proof

Substituting the fuzzy system (42) in the error dynamic equation (29), then by the minimum approximation error (41), we have

$$\begin{aligned} {\dot{\mathbf{E}}}_i = {{\mathbf{A}}_i}{{\mathbf{E}}_i} + {{\mathbf{B}}_i}\left\{ {\tilde{{\varvec{\uptheta }}}}_i^\mathrm{T}{{{\varvec{\upxi }}}} + {w_i} - {u_{ri}} \right\} \end{aligned}$$
(45)

where \(w_i =\omega _i +\sigma _i\). Now, consider the Lyapunov function as

$$\begin{aligned} \dot{\hbox {V}}_i =\frac{1}{2}{} \mathbf{E}_i^\mathrm{T} \mathbf{P}_i \mathbf{E}_i +\frac{\gamma _{\varepsilon i} }{2}\varepsilon _i^2 +\frac{1}{2\gamma _i }\tilde{ {{\varvec{\uptheta }}}}_i^\mathrm{T} {\tilde{ {{\varvec{\uptheta }}}}}_i \end{aligned}$$
(46)

Then, the derivative of \(V_i\) is obtained as

$$\begin{aligned} {{\dot{\hbox {V}}}_i} = \frac{1}{2}\left\{ {\dot{\mathbf{E}}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{E}}_i} + {\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\dot{\mathbf{E}}}}_i \right\} + {\gamma _{\varepsilon i}}{\varepsilon _i}{\dot{\varepsilon }_i} + \frac{1}{{{\gamma _i}}}\tilde{{\varvec{\uptheta }}}_i^\mathrm{T}{\dot{\tilde{{{\varvec{\uptheta }} }}}}_i\nonumber \\ \end{aligned}$$
(47)

Using the error dynamic equation (45) and the modified modeling error dynamic (34), (47) can be rewritten as

$$\begin{aligned} {{\dot{\hbox {V}}}_i}= & {} \frac{1}{2}\left\{ \left[ {{\mathbf{E}}_i^\mathrm{T}{\mathbf{A}}_i^\mathrm{T} + {{{\varvec{\upxi }}}}_i^\mathrm{T}{{\tilde{{{\varvec{\uptheta }} }}}_i}{\mathbf{B}}_i^\mathrm{T} + {{\left( {{w_i} - {u_{ri}}} \right) }^\mathrm{T}}{\mathbf{B}}_i^\mathrm{T}} \right] {{\mathbf{P}}_i}{{\mathbf{E}}_i}\right. \nonumber \\&\left. +\,{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}~\left[ {{{\mathbf{A}}_i}{{\mathbf{E}}_i} + {{\mathbf{B}}_i}\tilde{{{\varvec{\uptheta }}}}_i^\mathrm{T}{{{{\varvec{\upxi }}}}_i} + {{\mathbf{B}}_i}\left( {{w_i} - {u_{ri}}} \right) } \right] \right\} \nonumber \\&+\,{\gamma _{\varepsilon i}}{\varepsilon _i}\left( { - {\alpha _{Fi}}{\varepsilon _i} + \tilde{{{\varvec{\uptheta }} }} _i^\mathrm{T}{{{{\varvec{\upxi }}}}_i} + {\omega _i} - {v_i}} \right) + \frac{1}{{{\gamma _i}}}\tilde{{{\varvec{\uptheta }} }}_i^\mathrm{T}{\dot{\tilde{{{\varvec{\uptheta }}}}}_i}\nonumber \\ \end{aligned}$$
(48)

Then, (48) can be rewritten as

$$\begin{aligned} {{\dot{\hbox {V}}}_i}= & {} \frac{1}{2}{\mathbf{E}}_i^\mathrm{T}\left\{ {{\mathbf{A}}_i^\mathrm{T}{{\mathbf{P}}_i} + {{\mathbf{P}}_i}{{\mathbf{A}}_i}} \right\} {{\mathbf{E}}_i} + {\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}\left( {{w_i} - {u_{ri}}} \right) \nonumber \\&+\,{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}\tilde{\varvec{\uptheta }} _i^\mathrm{T}{{{{\varvec{\upxi }} }}_i} - {\gamma _{\varepsilon i}}{\alpha _i}\varepsilon _{Fi}^2 + {\gamma _{\varepsilon i}}{\varepsilon _i}\tilde{\varvec{\uptheta }} _i^\mathrm{T}{{{{\varvec{\upxi }} }}_i} \nonumber \\&+\,{\gamma _{\varepsilon i}}{\varepsilon _i}\left( {{\omega _i} - {v_i}} \right) + \frac{1}{{{\gamma _i}}}\tilde{\varvec{\uptheta }} _i^\mathrm{T}{\dot{\tilde{{{\varvec{\uptheta }}}}}_i} \end{aligned}$$
(49)

Utilizing Eq. (21), the latter results

$$\begin{aligned} {{\dot{\hbox {V}}}_i}= & {} - \frac{1}{2}{\mathbf{E}}_i^\mathrm{T}{{\mathbf{Q}}_i}{{\mathbf{E}}_i} + {\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}\left( {{w_i} - {u_{ri}}} \right) \nonumber \\&+\,{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}\tilde{{{\varvec{\uptheta }} }}_i^\mathrm{T}{{{{\varvec{\upxi }}}}_i} - {\gamma _{\varepsilon i}}{\alpha _i}\varepsilon _i^2 + {\gamma _{\varepsilon i}}{\varepsilon _i}\tilde{{{\varvec{\uptheta }}}}_i^\mathrm{T}{{{{\varvec{\upxi }}}}_i}\nonumber \\&+\,{\gamma _{\varepsilon i}}{\varepsilon _i}\left( {{\omega _i} - {v_i}} \right) + \frac{1}{{{\gamma _i}}}\tilde{{{\varvec{\uptheta }} }} _i^\mathrm{T}{\dot{\tilde{{{\varvec{\uptheta }}}}}_i} \end{aligned}$$
(50)

Also, (50) can be expressed as

$$\begin{aligned} {{\dot{\hbox {V}}}_i} = - \frac{1}{2}{\mathbf{E}}_i^\mathrm{T}{{\mathbf{Q}}_i}{{\mathbf{E}}_i} + {{\dot{ \hbox {V}}}_{1i}} + {{\dot{\hbox {V}}}_{2i}} \end{aligned}$$
(51)

where

$$\begin{aligned} {{\dot{\hbox {V}}}_{1i}}= & {} {\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}\left( {{w_i} - {u_{ri}}} \right) \end{aligned}$$
(52)
$$\begin{aligned} {{\dot{\hbox {V}}}_{2i}}= & {} - {\gamma _{\varepsilon i}}{\alpha _i}\varepsilon _i^2 + {\gamma _{\varepsilon i}}{\varepsilon _i}\tilde{{{\varvec{\uptheta }}}}_i^\mathrm{T}{{{{\varvec{\upxi }}}}_i} + {\gamma _{\varepsilon i}}{\varepsilon _i}\left( {{\omega _i} - {v_i}} \right) \nonumber \\&+ \,\frac{1}{{{\gamma _i}}}\tilde{{{\varvec{\uptheta }}}} _i^\mathrm{T}{\dot{\tilde{{{\varvec{\uptheta }}}}}_i} \end{aligned}$$
(53)

Substituting robust control term (43) into (52), we have

$$\begin{aligned} {{\dot{\hbox {V}}}_{1i}} = {\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}{w_i} - \left| {{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}} \right| {\bar{w}_i} \le 0 \end{aligned}$$
(54)

Since \(\left| {{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}{w_i}} \right| \le \left| {{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}||{w_i}} \right| \le \left| {{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}} \right| {\bar{w}_i}\)

By the fact \(\dot{\tilde{{\varvec{\uptheta }} }}={\dot{{\varvec{\uptheta }} }}\) and from the compensation term (33), the modified modeling error (34) and the CAFL (44), \(\dot{V}_{2i}\) can be rewritten as

$$\begin{aligned} {{\dot{\hbox {V}}}_{2i}}= & {} - {\gamma _{\varepsilon i}}{\alpha _i}\varepsilon _i^2 + {\gamma _{\varepsilon i}}{\varepsilon _i}\left( {{\omega _i} - {v_i}} \right) \nonumber \\&+\,\tilde{{{\varvec{\uptheta }} }}_i^\mathrm{T}\left( {\left( {{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i} + {\gamma _{\varepsilon i}}{\varepsilon _i}} \right) {{{{\varvec{\upxi }}}}_i} + \frac{1}{{{\gamma _i}}}{{\dot{\tilde{{{\varvec{\uptheta }}}}}}_i}} \right) \end{aligned}$$
(55)
$$\begin{aligned} {{\dot{\hbox {V}}}_{2i}}= & {} - {\gamma _{\varepsilon i}}{\alpha _i}\varepsilon _i^2 + \left( {{\gamma _{\varepsilon i}}{\omega _i}{\varepsilon _i} - {\gamma _{\varepsilon i}}{{\bar{\omega }}_i}\left| {{\varepsilon _i}} \right| } \right) \end{aligned}$$
(56)
$$\begin{aligned} {{\dot{\hbox {V}}}_{2i}}\le & {} - {\gamma _{\varepsilon i}}{\alpha _i}\varepsilon _i^2 \end{aligned}$$
(57)

Since \(\left| {\gamma _{\varepsilon i} \omega _i \varepsilon _i } \right| \le \left| {\gamma _{\varepsilon i} \left| {\left| {\omega _i } \right| } \right| \varepsilon _i } \right| \le \gamma _{\varepsilon i} \left| {\varepsilon _i } \right| \bar{\omega }_{i}\), also \(-\gamma _{\varepsilon i} \alpha _i \varepsilon _i^2 \le 0.\) From the above results, it follows that

$$\begin{aligned} \dot{{{\hbox {V}}_i}}= - \frac{1}{2}{\mathbf{E}}_i^\mathrm{T}{{\mathbf{Q}}_i}{{\mathbf{E}}_i} + {{\dot{ \hbox {V}}}_{1i}} + {{\dot{\hbox {V}}}_{2i}} \le - \frac{1}{2}{\mathbf{E}}_i^\mathrm{T}{{\mathbf{Q}}_i}{{\mathbf{E}}_i} \le 0\nonumber \\ \end{aligned}$$
(58)

Since \(\mathbf{Q}_i\) is positive definite matrix, \(\dot{\hbox {V}}_i\) is negative semi-definite, i.e., \(\hbox {V}_i \left( t \right) \le \hbox {V}_i \left( 0 \right) \). From (58) we have

$$\begin{aligned} \int _0^\mathrm{T} \mathbf{E}_i^\mathrm{T} \mathbf{Q}_i \mathbf{E}_i {\hbox {d}}t\le 2\left( {\hbox {V}_i \left( 0 \right) -\hbox {V}_i \left( t \right) } \right) \end{aligned}$$
(59)

Because \(\hbox {V}_i \left( 0 \right) \) and \(\hbox {V}_i \left( t \right) \) are bounded, the following result is achieved

$$\begin{aligned} \lim \nolimits _{t\rightarrow \infty } \int _0^\mathrm{T} \mathbf{E}_i^\mathrm{T} \mathbf{Q}_i \mathbf{E}_i \, {\hbox {d}}t\le \infty \end{aligned}$$
(60)

Also, it can be shown that \(\ddot{\hbox {{V}}}_{1}\) is bounded and according to Barbalat’s lemma [38], the error vector tends to zero as \(t\rightarrow \infty \). \(\square \)

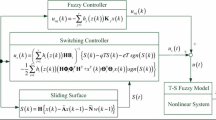
The block diagram of the underwater system and the proposed RCAFc (23) is shown in Fig. 4.

Fig. 4
figure 4

Block diagram of the proposed RCAFc (23)

Full size image

The overall design procedure can be summarized in the following steps:

Step 1::

Specify the positive gain \(k_i\) and feedback gain vector \(\mathbf{K}_i\), such that the characteristic matrices \(\mathbf{A}_{oi} -\mathbf{B}_i \mathbf{K}_i^\mathrm{T}\) is strictly Hurwitz matrices. Then, specify a positive definite matrix \(\mathbf{Q}_i\) and solve the Lyapunov equation (21), to obtain a positive definite symmetric matrix \(\mathbf{P}_i\).

Step2::

Define the series–parallel identification model for the system, to reduce the modeling error.

Step3::

Next, construct the fuzzy system \(\hat{d}_i \left( {\varepsilon _i \hbox {|}{{\varvec{\uptheta }} }_i } \right) \), to estimate the lumped uncertainty, \(d_i\). The CAFL will be obtained by using the prediction error and by the RCAFc scheme, the voltage control vector \(\mathbf{V}\) is generated.

Step4::

Set the design parameters \(\gamma _i\), \(\gamma _{\varepsilon i}\), also \(\bar{w}_{i}\) and \(\bar{\omega }_{i}\). The convergence rate of the tracking error is determined by the range of the design parameters.

Remark 4

In this paper, the modeling error \(\varepsilon _i\) is introduced as additional feedback information to construct the RCAFc, by the CAFL (44). If \(\gamma _{\varepsilon i} =0\), we have a Robust Adaptive Fuzzy control (RAFc), with the following Adaptive Fuzzy Law (AFL) for each subsystem

$$\begin{aligned} {{\dot{{\varvec{\uptheta }}}}_i} = - {\gamma _i}{\mathbf{E}}_i^\mathrm{T}{{\mathbf{P}}_i}{{\mathbf{B}}_i}{{{{\varvec{\upxi }}}}_i} \end{aligned}$$
(61)

In the RAFc, the structure of adaptive fuzzy and stability of the controller based on Lyapunov theory is somewhat similar to the proposed RCAFc method. From (58) and by term \(-\gamma _{\varepsilon i} \alpha _i \varepsilon _i^2\), we see that the proposed RCAFc makes the decreasing of the time derivative of Lyapunov function (i.e., by \(\gamma _{\varepsilon i} >0)\). Therefore, it is obvious that the proposed scheme improves \(\dot{\hbox {{V}}}_{i}(t)\)

Remark 5

In many applications, the function \(\hbox {sign}\left( \cdot \right) \) in robust terms (33) and (43) are replaced by a smooth function \(\tanh \left( {\frac{.}{\emptyset }} \right) \) where \(\emptyset >0\) is a small positive design constant in order to remedy the control chattering.

Fig. 5
figure 5

Control system process for the proposed scheme

Full size image

5 Simulation examples

In this section, for highlighting the usefulness of hybrid combination of the underwater vehicle dynamic model into the actuator dynamic model, we simulate the proposed RCAFc and RAFc, under different level of uncertainties. Therefore in this study, results show the tracking performance for two cases: \(\gamma _{\varepsilon i} >0\) and \(\gamma _{\varepsilon i} =0\), respectively. Also, we let \({\mathbf{F}} = - {\mathbf{M}}_{\mathbf{J}}^{ - 1}\left\{ {{{\mathbf{C}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{D}}_{\mathbf{J}}}\left( {\mathbf{x}} \right) {\dot{\mathbf{x}}} + {{\mathbf{g}}_\mathrm{{J}}}\left( {\mathbf{x}} \right) } \right\} \) if speed-sensorless scheme is required (in other words, \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \mathbf{J}^{{\varvec{-\mathrm{T}}}}{} \mathbf{B}\, {{\varvec{\varphi }}}\) is added to the lumped uncertainty \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \left\{ \mathbf{J}^{{\varvec{-\mathrm{T}}}}{} \mathbf{B}\underline{\Delta } -{{\varvec{\upeta }} }_\mathbf{J} -\Delta _\mathbf{J} -\mathbf{J}^\mathrm{T}\mathbf{M}_\mathbf{o} {\dot{\mathbf{J}}}^{{\varvec{-1}}} \dot{\hbox {x}}\right\} )\); otherwise, \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \mathbf{J}^{{\varvec{-\mathrm{T}}}}\mathbf{B}\,{\varvec{\varphi }} \) is a well-known function when a speed-sensor scheme is chosen (in other words, \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \mathbf{J}^{{\varvec{-\mathrm{T}}}}{} \mathbf{B}\, {{\varvec{\varphi }}}\) is added to \(\mathbf{F}\)). To verify the general control system pattern for the simulation example, Fig. 5 shows control system process for the proposed schemes. For all examples, it is assumed that the lumped uncertainties \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \left\{ \mathbf{J}^{{\varvec{-\mathrm{T}}}}{} \mathbf{B}\underline{\Delta } -{{\varvec{\upeta }} }_\mathbf{J} -\Delta _\mathbf{J} -\mathbf{J}^\mathrm{T}\mathbf{M}_\mathbf{o} {\dot{\mathbf{J}}}^{-1} \dot{\hbox {x}}\right\} \) are presented in Fig. 7 (i.e., the lumped uncertainties with dotted lines).

Also for all examples in this paper, we have three fuzzy membership functions \(\mu _l \left( {\varepsilon _i } \right) \) which are assumed in the form of \( \mu _l \left( {\varepsilon _i } \right) =\exp \left[ {-\left( {\left( {\varepsilon _i +c_l } \right) /\sigma _l } \right) ^{2}} \right] \) for \(l=1,\ldots ,5\), where \(c_l =\) and \(\sigma _l\) are constant values. Also, the initial states and desired positions are \(\mathbf{x}\left( 0 \right) =\left[ {0,0,0,0,0,0} \right] ^\mathrm{T}\) and \(\mathbf{x}_d =\left[ {2, 3 ,4 ,\pi /3 ,\pi /4, 2\pi /5} \right] ^\mathrm{T}\), respectively. The control design parameters of the RCAFc and the RAFc are given in Table 1.

In these simulation examples, it is assumed that the thrust force vector \(\mathbf{T}=\left[ {T_1 ,\ldots ,T_8 } \right] ^\mathrm{T}\in \mathfrak {R}^{8}\) implies the thrust forces that every the thruster DC motor delivers. Also, mapping matrix \(\mathbf{B}\in \mathfrak {R}^{6\times 8}\) is defined as [9]. Furthermore, the control design parameters of the thruster DC motors are given in “Appendix.” Note that all the thruster DC motors \(T_1 \) to \(T_8\) are assumed to be similar. Also, details on the matrices \(\mathbf{J}\left( \mathbf{x} \right) \), \(\mathbf{M}\), \(\mathbf{C}\left( \mathbf{v} \right) \), \(\mathbf{D}\left( \mathbf{v} \right) \) and \(\mathbf{g}\left( \mathbf{x} \right) \) operated for a model of underwater vehicle are presented in [34].

Remark 6

Several simulations have been carried out for estimation of the lumped uncertainty vector \(\mathbf{d}\left( t \right) \) using the state variables, i.e., by \(\hat{d}_i \left( {\mathbf{X}|{{\varvec{\uptheta }} }_i } \right) \). According to the simulation results, this method is not able to hold the system performance in the various uncertainties. Therefore, the simulation studies are neglected for this method.

Table 1 Control design parameters
Full size table
Fig. 6
figure 6

Tracking trajectories \(x_{di}\) (dotted line), state variable \(x_i\) by RCAFc (solid line) and by RAFc (dashed line), for example 1

Full size image
Fig. 7
figure 7

Approximation of lumped uncertainty \(d_i \left( t \right) \) (dotted line), by RCAFc (solid line) and by RAFc (dashed line), for example 1

Full size image
Fig. 8
figure 8

Robust control term \(u_{ri}\), for example 1

Full size image
Fig. 9
figure 9

Control voltage \(V_j\) by RCAFc (solid line) and by RAFc (dashed line), for example 1

Full size image
Fig. 10
figure 10

Tracking trajectories \(x_{di}\) (dotted line), state variable \(x_i\) by RCAFc (solid line), for example 2

Full size image

5.1 Example 1: the proposed controller with speed-sensor scheme

In this case, the lumped uncertainty vector is \(\mathbf{d}\left( t \right) =\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \left\{ \mathbf{J}^{{\varvec{-\mathrm{T}}}}{} \mathbf{B}\underline{\Delta } -{{\varvec{\upeta }} }_\mathbf{J} -\Delta _\mathbf{J} -\mathbf{J}^\mathrm{T}\mathbf{M}_\mathbf{o} \dot{\mathbf{J}}^{{\varvec{-1}}}\dot{\mathbf{x}} \right\} \), and \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \mathbf{J}^{{\varvec{-\mathrm{T}}}}{} \mathbf{B} {\varvec{\upvarphi }}\) is a well-known function (the lumped uncertainties \(d_i \left( t \right) \) are shown in Fig. 7 with dotted line).

The tracking trajectories for the MHDS are shown in Fig. 6. The tracking performances of the both proposed RCAFc and the RAFc are also very good; therefore, it can be seen that the suggested control design can guarantee the system performance among uncertainties, and for this task, it reduces amount of chattering. We can see that the tracking errors are uniformly ultimately bounded and converge to a small region near zero. Figure 7 shows the approximation of lumped uncertainty \(d_i \left( t \right) \). Therefore, the proposed method is able to identify and compensate these lumped uncertainties. Also robust control signals for the proposed RCAFc and the RAFc are shown in Fig. 8. The proposed RCAFc provides a smaller robust term control signal compare to RAFc. In other words, the proposed scheme achieves a better control performance while less robust control effort is spent. The control inputs \(V_j\) for the proposed RCAFc and the RAFc are shown in Fig. 9. The results of the study clearly demonstrate that the proposed RCAFc can achieve the better approximate of the lumped uncertainty \(d_i \left( t \right) \), and the robust control signals of the proposed RCAFc method are much smaller than the RAFc.

5.2 Example 2: the RCAFc with speed-sensorless scheme

In this case, \(\mathbf{d}\left( t \right) =\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \left\{ \mathbf{J}^{{\varvec{-\mathrm{T}}}}\mathbf{B}\underline{\Delta }-{{\varvec{\upeta }} }_\mathbf{J} -\Delta _\mathbf{J} -\mathbf{J}^\mathrm{T}{} \mathbf{M}_\mathbf{o} \dot{\mathbf{J}}^{{\varvec{-1}}}{\mathbf{x}} \right\} \), so that, we assume that \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \left\{ \mathbf{J}^{{\varvec{-\mathrm{T}}}}\mathbf{B}\underline{\Delta }-{{\varvec{\upeta }} }_\mathbf{J} -\Delta _\mathbf{J} -\mathbf{J}^\mathrm{T}{} \mathbf{M}_\mathbf{o} \dot{\mathbf{J}}^{{\varvec{-1}}}{\mathbf{x}} \right\} \) is presented in Fig. 7 with dotted lines, and unknown term \(\mathbf{M}_\mathbf{J}^{{\varvec{-1}}} \mathbf{J}^{{\varvec{-\mathrm{T}}}}{} \mathbf{B}\, {{\varvec{\upvarphi }}}\) can be configured based on the MHDS behavior.

The simulation results of RCAFc for Example 2 are similar to the Example 1. Figure 10 shows the tracking trajectories of the RCAFc. The tracking performances of the proposed method is very good; therefore, it can be seen that the suggested control design can guarantee system performance among uncertainties. Figure 11 indicates the trajectories of the state \(x_i\) and its estimation \(\hat{x}_i\) (the series–parallel state), for the proposed RCAF. From Figs. 10 and 11, we can see that the tracking errors and the state estimation errors are uniformly bounded and small.

Figure 12 shows the approximation of lumped uncertainties. The control input \(u_i\) is shown in Fig. 13.

Several simulations have been carried out for the RAFc. According to simulation results, RAFc method is able to hold system performance for a high robustness level of robust term (e.g., \(\bar{w}_{i}\) is large). Hence, the robust term is more important and the adaptive fuzzy scheme after that, it is a main controller (the adaptive fuzzy estimator term of the RAFc is much smaller than that of the robust term). It can be seen that the proposed RCAFc can guarantee system performance with a small or high robustness level of robust term (for more details, see [14]). Therefore in Example 2, simulation studies are neglected for RAFc method. Simulation results and the performance for the proposed RCAFc method were observed fully robust to these design parameters and initial conditions.

Fig. 11
figure 11

Tracking trajectories state variable \(x_i\) (solid line) and state estimation \(\hat{x}_i\) (dashed line) by RCAFc, for example 2

Full size image
Fig. 12
figure 12

Lumped uncertainty \(d_i \left( t \right) \) (dashed line) and estimate \(\hat{d}_i\) (solid line) by RCAFc, for example 2

Full size image
Fig. 13
figure 13

Control voltage \(V_j\) by RCAFc, for example 2

Full size image

5.3 The simulation results

Comparing two case results, it can be seen that the trajectories performance by the RCAFc is improved. Therefore, we see that the proposed RCAFc method can use the smallest magnitude of the robust term control signal and the tracking error converges to a small neighborhood of zero. It implies that the proposed RCAFc can achieve the better approximate of the lumped uncertainty \(d_i \left( t \right) \), with a smaller robust term control signal compare to RAFc.

Also, the simulation results show clearly that the tracking error of the proposed RCAFc is less than RAFc, i.e., the composed adaptive fuzzy estimator is more important and the robust controller after that the composed adaptive fuzzy scheme is a main controller. Thus, we can state that the results explain the usefulness and effectiveness of the proposed technique together with the proposed RCAFc, and the ability of maintaining the system performance amid the various uncertainties and disturbances which have large amplitude and also high frequency.

Table 2 Comparison of the control performance for the RCAFC and the RAFC, in the presence of large and sudden lumped uncertainties
Full size table

In short, the improved performance of the proposed RCAFc over the RAFc is due to its ability to identify and compensate the lumped uncertainty \(d_i \left( t \right) \), and therefore, utilizing this scheme, the robust control term of the proposed RCAFc is much smaller than the RAFc, whereas in the RAFc, supervisory control signal plays more important role than the adaptive fuzzy controller. Hence, it diminishes the original purpose of using adaptive fuzzy scheme.

Furthermore, the fuzzy approximator with the modeling error \(\varepsilon _i\) as input in the fuzzy adaptive controller is able to improve the sensitivity of \(u_i\) to the tracking errors, while the number of fuzzy term sets and also fuzzy IF–THEN rules are decreased. In other words, \(\hat{d}_i \left( {\varepsilon _i {|}{{\varvec{\uptheta }} }_i } \right) \) represents disturbance and uncertainties as functions of the modeling errors \(\varepsilon _i\).

The proposed method is computationally simple, effective, robust and well behaved with fast response. Simulation results have shown the usefulness of the proposed method. Moreover, using this scheme, the chattering phenomenon in the proposed controller is alleviated. The reason is that the proposed approach is based on combining the advantages of fuzzy system, adaptive method, the series–parallel estimation and robust control with simple and accurate estimation of the large and sudden lumped uncertainty vector \(\mathbf{d}\left( t \right) \) which obtains important benefits, because a novel adaptive fuzzy logic system is proposed for uncertainty estimation that the modeling error \(\varepsilon _i\) as input is used and also, in order to improve the approximation of lumped uncertainty \(d_i\), we employed a modified modeling error in the adaptive fuzzy estimator \(\hat{d}_i \left( {\varepsilon _i |{{\varvec{\uptheta }} }_i } \right) \).

Remark 7

Several simulations were carried out for the control of the MHDS by the RCAFc and the RAFc with uncertainty estimator \(\hat{d}_i \left( {\varepsilon _i {|}{{\varvec{\uptheta }} }_i } \right) \), and also by the RCAFc and the RAFc with uncertainty estimator \(\hat{d}_i \left( {\mathbf{X} |{{\varvec{\uptheta }} }_i } \right) \). It can be seen that performance of the proposed method is fully robust to these design parameters and initial conditions. Briefly, from Table 2 we can see the tracking performances of these methods in the presence of large and sudden lumped uncertainties. (Also several simulations have been carried out for control of various nonlinear systems, e.g., for MIMO magnetic levitation system [39], and SISO inverted pendulum system [16]. Simulation studies display the usefulness and efficiency of the proposed technique).

6 Conclusion

In this paper, a novel control method is applied based on a MHDS (the combination of actuators and underwater vehicle) and by the robust composite adaptive fuzzy controller (RCAFc). The proposed scheme can be a speed-sensorless method for the actuator system; thus, it does not need an accurate mathematical model of the system actuator. Moreover, it seems that implementation of this method is simpler and production cost is less. Therefore, these control laws can be used for the systems that the actuator models are unknown. Using the modeling error between the proposed MHDS system model and the series–parallel identification model with a low-pass filter, the composite adaptation is combined into the RAFc scheme to estimate and compensate the large and sudden uncertainties, i.e., the adaptive fuzzy estimator with the CAFL is more important and the robust controller after that, it is a main controller. The RCAFc is superior to the RAFc in the face of sudden changes in uncertainty. Furthermore, the fuzzy approximator with the modeling error \(\varepsilon _i\) as input indicates which is able to improve the system performance, while number of fuzzy sets and also fuzzy IF–THEN rules are decreased. The proposed method is robust, simple, accurate, with less computing. The simulation results indicate clearly that the tracking errors of the proposed scheme are very small. Furthermore, the proposed controller is able to maintain system performance among various uncertainties with a considerable reduction of chattering. The proposed control technique is not limited only to the control of the underwater vehicles, but can be applied for control of a class of nonlinear MHDS. We want to develop our design method in the next study, so that it can control an observer-based non-affine large-scale MHDS.