A study of a lock fuzzy EPQ model with deterioration and stock and unit selling price-dependent demand using preservation technology

Abstract

This article deals with a deteriorated economic production quantity (EPQ) inventory model where the preservation technology is applied to restore the significant loss of items during production. The demand function is unit selling price and stock sensitive, and the production rate is also stock sensitive. Here we assume that the sum of percentage of deterioration and the rate of preservation is 100%. First of all, we develop a profit function for EPQ model under given assumptions, and then, we split the model into three different submodels by considering the unit selling price, unit cost prices and taking both of them as lock fuzzy numbers, respectively. Numerical illustrations are done with the help of a solution algorithm based on $\alpha -$ cuts of fuzzy numbers, and it has been compared with the results of general fuzzy cases of each of the submodels. Graphical illustrations and sensitivity analysis are made to show the novelty of the new approach. The managerial insights are also discussed followed by a conclusion.

1 Introduction

1.1 Literature review on related inventory model

The word inventory stands not only for stock of goods which may be of three types: raw materials’, semi-finished good and finished good but also its management and operations. Harris (1915) examined the establishment of inventory control problem in field of operation research which was the traditional economic order quantity (EOQ) model. From the improvement in the EOQ model, a great deal of research work has been made on the inventory control problems which also included the economic production quantity (EPQ) model. In practical sense, almost all products loss their utility after certain period which indicates that deterioration is an important factor to study. Ghare and Schrader (1963) were the first who developed an inventory model with constant deterioration. Then, several works (see Li et al. 2010; Tan et al. 2013; Shaikh et al. 2019a, b, Lee et al. 2012; Bhunia et al. 2014; Jaggi et al. 2015) have been reported in this context.

Preservation is an important issue to resist the deterioration of the items. Hsu et al. (2010) first used the concept of preservation technique in the study of inventory control problems. Following this work, more researches (see Pal et al. 2018; Dye and Hsieh 2012; Hsieh and Dye 2013; Dye 2013) had carried out in this direction. Zhang et al. (2014) considered preservation and deterioration for a problem with stock-dependent demand. Also, selling price of items plays a vital role on the demand of product. Mishra et al. (2017) presented a preservation inventory model under the price-dependent demand with shortage. Teng and Chang (2005) proposed a model with stock- and price-dependent demand. Hou and Lin (2006) also introduced a model with the demand related to price and stock of items. Some more research works (see Yang 2012; Yang et al. 2015; Zhang et al. 2016; Pal et al. 2013; Shaikh et al. 2019a, b; Li et al. 2019) are noted in this context. Recently, Rahaman et al. (2020) described a fractional order model with stock- and price-dependent demand and stock-dependent production rate of deteriorated items.

1.2 Recent development of fuzzy decision-making in inventory management problems

Zadeh (1965) introduced the concept of fuzzy set. Subsequently, the concept was utilized by Bellman and Zadeh (1970) in decision-making problems. From that point forward, numerous researches have been occupied by describing the actual nature of the fuzzy set (see Dubois and Prade 1978; Kaufmann and Gupta 1985; Baez-Sancheza et al. 2012; Beg and Ashraf 2014; Deli and Broumi 2015; Kumar 2018). Also, Diamond (1989, 1990) has discussed both k-type fuzzy numbers and star-type fuzzy numbers. A means of finding the membership of general fuzzy numbers was also developed by Chutia et al. (2010). Roychoudhury and Pedrycz (2003) provided the functional relationship among fuzzy complements. In addition, fuzzy control theory was enriched by Bobeylev (1985, 1988) with the help of the Cauchy problem. Buckley (1988) discussed the generalization of fuzzy sets for practical applications. To date, a number of researchers, including Roy and Maji (2010), Molodtsov (1999), Cagman et al. (2011) etc., have studied fuzzy soft sets; fuzzy rough sets were developed by Pawlak (1982), and hesitant fuzzy sets have been improved by Torra (2010), Karmakar et al. (2017a), De and Sana (2015), etc., in real-world final decision-making problems.

Moreover, the concept of integrating the impact of learning experiences into fuzzy sets, namely the triangular dense fuzzy set (TDFS), along with new defuzzification methods, was described by De and Beg (2016a, b), and they also utilized this fuzzy set in philosophical contexts also (see De and Beg 2016a, b). In their observations, the Cauchy sequence was employed, which naturally converges to zero. Using this property, they studied the triangular dense fuzzy set, in which the ambiguity decreases with time. De and Mahata (2016) discussed the cloudy fuzzy set, which is an important extension of the triangular dense fuzzy set using a continuous time variable. Recently, Karmakar et al. (2017b, 2018) studied a pollution control scheme for a sponge iron production plant model utilizing the triangular dense fuzzy rule. Additionally, Rahaman et al. (2021a, b) studied the joint impact of learning and memory on the lot-sizing problem using fuzzy fractional calculus under the dense fuzzy sense. A two-decision-makers single-decision inventory model utilizes the concept of the triangular dense fuzzy lock set. Recently, Rahaman et al. (2021a, b) studied an EOQ model with price-dependent demand rate under memory motivated lock fuzzy scenario.

1.3 Motivation

After brief reviewing the EPQ model, our finding is that (a) stock-, price-dependent demand and production rate, (b) deterioration and preservation technology against deterioration are rarely used in the literature. Focusing this point of view, we develop an EPQ model where (a) demand is a linear function of price and stock; (b) production rate is a linear function of stock; (c) deterioration occurred, (d) preservation technology is applied to prevent deterioration. Again, basic objective of fuzzy theory is to reach the goal under uncertain phenomena. De (2017) introduced the novel idea of lock fuzzy set which enlightens the new aspect of fuzziness. We have used this fact in decision-making for our proposed model which has the capability to give better optimization. Moreover, in a manufacturing farm, if more stock is raised, then it is better to decrease the production rate. Similarly, more selling price of items reduces the interest of customers for certain items. But, the displayed stock in showrooms makes a positive result on demand pattern and some times over stock may reduce the demand. Thus, this is an exceptionally intriguing and needful study relating to the control of stocks of the manufacturing farms.

2 Preliminaries

In this section, some important definitions and known results regarding triangular dense fuzzy set (De and Beg 2016a, b) and triangular dense fuzzy lock set De (2018) are presented here which are needful to describe the fuzzy model.

Definition 2.1

Let $\tilde{A }$ be fuzzy number whose components are elements of the Cartesian product ${\mathbb{R}}\times {\mathbb{N}}$, (where ${\mathbb{R}}$ and ${\mathbb{N}}$ represent the set of real numbers and natural number, respectively) with membership grade satisfying the functional relation $\mu :{\mathbb{R}}\times {\mathbb{N}}\to [\mathrm{0,1}]$. If $\mu (x,n)\to 1$, as $n\to \infty$, for some $x\in {\mathbb{R}}$ and $n\in {\mathbb{N}}$, then $\tilde{A }$ is called dense fuzzy set.

In particular, if $\tilde{A }$ is triangular in the above definition, it is called triangular dense fuzzy set (TDFS). Furthermore, if $\mu (x,n)$ attain the highest membership degree $1$ for some $n\in {\mathbb{N}}$, then it is called the normalized triangular dense fuzzy set (NTDFS).

Example 2.1

Let us take a NTDFS as follows.

$\tilde{A }=<a\left(1-\frac{\rho }{1+n}\right),a, a\left(1+\frac{\sigma }{1+n}\right)>$, where $\rho ,\sigma \in (\mathrm{0,1})$, $a$ be a real number and $n$ be a natural number. Then, its membership function is given by

$$\mu \left(x,n\right)=\left\{\begin{array}{c}0\,,\,\, for\,x<a\left(1-\frac{\rho }{1+n}\right) or\,x>a\left(1+\frac{\sigma }{1+n}\right)\\ \frac{x-a\left(1-\frac{\rho }{1+n}\right)}{\frac{a\rho }{1+n}},\,\, for\,a\left(1-\frac{\rho }{1+n}\right)\le x\le a\\ \frac{a\left(1+\frac{\sigma }{1+n}\right)-x}{\frac{a\sigma }{1+n}},\,\, for\,a\le \mathrm{x}\le a\left(1+\frac{\sigma }{1+n}\right)\end{array}\right.$$

Definition 2.2

Let $\tilde{A }=<a,b,c>$ be a TDFS, and if $\mu (x,n)\nrightarrow 1$, as $n\to \infty$, for some $x\in {\mathbb{R}}$ and $n\in {\mathbb{N}}$ and consequently its index value $I(\tilde{A })\nrightarrow b$, then $\tilde{A }$ is called triangular dense fuzzy lock set (TDFLS).

Definition 2.3

Let $\tilde{A }=<b{t}_{n},b,b{s}_{n}>$ be a sequential form of TDFS, where ${t}_{n}$ and ${s}_{n}$ are two sequence functions. And if ${t}_{n}\to {\delta }_{1}(<1)$ and ${s}_{n}\to {\delta }_{2}$ (> 1) as $n\to \infty$, then $\tilde{A }\nrightarrow \{b\}$ and $\tilde{A }$ is called triangular dense fuzzy lock set (TDFLS).

Definition 2.4

Let the sequential definition of TDFS is $\tilde{A }=<a\left(1-\rho {t}_{n}\right), a,a\left(1+\sigma { s}_{n}\right)>$, where $\rho ,\sigma \in {\mathbb{R}}$ and ${t}_{n}$, ${s}_{n}$ are two Cauchy sequence of functions having the point of convergence $\frac{1}{{k}_{1}}$ and $\frac{1}{{k}_{2}},$ respectively (${k}_{1}$ and ${k}_{2}$ are two nonzero real numbers). Then, $\tilde{A }$ is called triangular dense fuzzy lock set (TDFLS) with double keys ${k}_{1}$ and ${k}_{2},$ respectively, and the keys depend upon $\rho$ and $\sigma$.

The membership function of TDFLS defined above is given by

$$\mu \left(x,n\right)=\left\{\begin{array}{c}0,\,\, for\,x<a\left(1-\rho {t}_{n}\right) or x>a\left(1+\sigma {s}_{n}\right)\\ \frac{x-a\left(1-\rho {t}_{n}\right)}{a\rho {t}_{n}},\, for\, a\left(1-\rho {t}_{n}\right)\le x\le a\\ \frac{a\left(1+\sigma { s}_{n}\right)-x}{a\sigma {s}_{n}}, \,\,for\,a\le \mathrm{x}\le a\left(1+\sigma { s}_{n}\right)\end{array}\right.$$

Example 2.2

Let us take a TDFLS as follows. $\tilde{A }=<a\left(1-\rho (\frac{1}{{k}_{1}}-\frac{1}{1+n})\right),a, a\left(1+\sigma (\frac{1}{{k}_{2}}+\frac{1}{1+n})\right)>$, where $\rho ,\sigma \in (\mathrm{0,1})$, $a$ be a real number and $n$ be a natural number; ${k}_{1}$ and ${k}_{2}$ are two nonzero real numbers. Here, ${k}_{1}$ and ${k}_{2}$ are two keys of the TDFLS. Its membership function is given by

$$\mu \left(x,n\right)=\left\{\begin{array}{c}0,\,\, for\,x<a\left(1-\rho (\frac{1}{{k}_{1}}-\frac{1}{1+n})\right)or\,a\left(1+\sigma (\frac{1}{{k}_{2}}+\frac{1}{1+n})\right)\\ \frac{x-a\left(1-\rho (\frac{1}{{k}_{1}}-\frac{1}{1+n})\right)}{a\rho (\frac{1}{{k}_{1}}-\frac{1}{1+n})},\,\, for\,a\left(1-\rho (\frac{1}{{k}_{1}}-\frac{1}{1+n})\right)\le x\le a\\ \frac{a\left(1+\sigma (\frac{1}{{k}_{2}}+\frac{1}{1+n})\right)-x}{a\sigma (\frac{1}{{k}_{2}}+\frac{1}{1+n})}, \,\, for\,a\le \mathrm{x}\le a\left(1+\sigma (\frac{1}{{k}_{2}}+\frac{1}{1+n})\right)\end{array}\right.$$

3 Notations and assumptions

To describe our proposed problem, we use the following notations with certain units and description given in Table 1.

Table 1 Notations with their units and certain meaning for the proposed model (crisp)

3.1 Assumptions

The following assumptions have been considered to be used in the proposed model:

• i) The production rate $K(t)$ is assumed to be a linear function of stock. Considering the intuitive facts that the production is better to be decreased in the presence of large stock is used here. Thus, $K(t)=\gamma -\delta I(t)$, where $\gamma ,\delta >0$ and $I(t)$ is the on-hand inventory or stock.

• ii) Demand of the production depends on price and stock. Fact is that the demand increases and decreases according as the selling price is decreases and increases, respectively. Also, the presence of the lot of stock may provide positive or negative impact in demand. Sometimes, more displayed stock attracts customer and increases the demand. However, it also quite possible that customer’s interest on products which are much available in the market is gone decreasing. Therefore, $D(t)=\eta -\zeta p+\xi I(t),$ where $\eta ,\zeta$ are positive constant, $\xi$ is any constant and $p$ is the price of the product.

• iii) Deterioration of the product occurs both in the production and non-production period. Also, to decrease the deterioration, preservation technology is applied to the system. The deterioration rate ($\theta$) and preservation rate $(\phi )$ are constants satisfying the relation $\theta +\phi =1$.

• iv) No shortage is allowed.

• v) Replenishment rate is infinite, but lot size is finite.

• vi) The time horizon is infinite.

• vii) Lead time is zero.

4 Defining the EPQ inventory model under several environments

4.1 Formulation of Crisp EPQ model

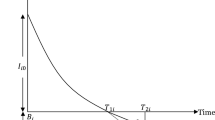
The inventory starts at $t=0$ with the production rate $K.$ During the time interval $0\le t\le {T}_{1}$, the inventory level decreases meeting up the demand at the rate $D$ and facing a deterioration of the rate $\phi$. Also, the fresh production and preservation at the rate $\theta$ make a positive impact on the growth of the inventory level. However, the total combine effect makes a result of decreasing the level of stock during this time interval. At time ${t=T}_{1}$, the production is stopped after reaching the sufficient stock of the product. During the time interval ${T}_{1}\le t\le T$, all the components except the production remain same, and thus, in the second phase (non-productive phase) of the cycle, the stock level decreases gradually, and at the time $t=T$, the inventory cycle is stopped with zero level of stock after fulfilling the demand. Figure 1 describes the change of inventory with respect to time.

Fig. 1

Graphical representation of the EPQ model with preservation

Then, the governing differential equations of the production process are given below:

$$\frac{dI(t)}{dt}+\left(\phi -\theta \right)I\left(t\right)=\{\gamma -\delta I(t)\}-\left\{\eta -\zeta p+\xi I(t)\right\} , 0\le t\le {T}_{1}$$

(1)

$$\frac{dJ(t)}{dt}+\left(\phi -\theta \right)J\left(t\right)=-\left\{\eta -\zeta p+\xi J\left(t\right)\right\}, {T}_{1}\le t\le T$$

(2)

With

$$\left\{\begin{array}{l}I\left(0\right)=0\\ I\left({T}_{1}\right)={I}_{mAX}=J({T}_{1}) \\ J\left(T\right)=0\end{array}\right.$$

(3)

Solving the Eqs. (1) and (2) and by using (3), we get

$$I\left(t\right)=\frac{(\gamma -\eta +\zeta p)}{(\phi -\theta +\delta +\xi )}\left[1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right)t}\right], 0\le t\le {T}_{1}$$

(4)

$$J\left(t\right)=\frac{(-\eta +\zeta p)}{(\phi -\theta +\xi )}\left[1-{{e}}^{\left(\phi -\theta +\xi \right)\left(T-t\right)}\right], {T}_{1}\le t\le T$$

(5)

Also, using the continuity condition at $t={T}_{1}$ in (4) and (5), we have $I\left({T}_{1}\right)=J\left({T}_{1}\right)$

$$\frac{(\gamma -\eta +\zeta p)}{(\phi -\theta +\delta +\xi )}\left[1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right]=\frac{(-\eta +\zeta p)}{(\phi -\theta +\xi )}[1-{{e}}^{\left(\phi -\theta +\xi \right)(T-{T}_{1})}]$$

i.e.,

$$T={T}_{1}+\frac{1}{(\phi -\theta +\xi )}\mathrm{ln}\left[1-\frac{(\gamma -\eta +\zeta p)(\phi -\theta +\xi )}{(\phi -\theta +\delta +\xi )(-\eta +\zeta p)}\{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\}\right]$$

(6)

Also, then

$${I}_{max}=\frac{(\gamma -\eta +\zeta p)}{(\phi -\theta +\delta +\xi )}\left[1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right]$$

(7)

Total sales revenue

$$TSR=p\left[{\int }_{0}^{{T}_{1}}\left\{\eta -\zeta p+\xi I\left(t\right)\right\}dt+{\int }_{{T}_{1}}^{T}\left\{\eta -\zeta p+\xi J\left(t\right)\right\}dt\right]=p\left(\eta -\zeta p\right)T+\xi pX$$

(8)

where $X={\int }_{0}^{{T}_{1}}I(t)dt+{\int }_{{T}_{1}}^{T}J(t)dt$

$$={\int }_{0}^{{T}_{1}}\frac{(\gamma -\eta +\zeta p)}{(\phi -\theta +\delta +\xi )}[1-{{e}}^{-(\phi -\theta +\delta +\xi )t}]dt+{\int }_{{T}_{1}}^{T}\frac{(-\eta +\zeta p)}{(\phi -\theta +\xi )}[1-{{e}}^{\left(\phi -\theta +\xi \right)(T-t)}]dt$$

$$=\frac{(\gamma -\eta +\zeta p)}{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]+\frac{(-\eta +\zeta p)}{(\phi -\theta +\xi )}\left[\left(T-{T}_{1}\right)-\frac{{{e}}^{\left(\phi -\theta +\xi \right){(T-T}_{1})}-1}{\left(\phi -\theta +\xi \right)}\right]$$

$$=A+p\zeta B$$

(9)

and

$$A=\frac{(\gamma -\eta )}{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]-\frac{\eta }{(\phi -\theta +\xi )}\left[\left(T-{T}_{1}\right)-\frac{{{e}}^{\left(\phi -\theta +\xi \right){(T-T}_{1})}-1}{\left(\phi -\theta +\xi \right)}\right]$$

(10)

$$B=\frac{1}{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]+\frac{1}{(\phi -\theta +\xi )}\left[\left(T-{T}_{1}\right)-\frac{{{e}}^{\left(\phi -\theta +\xi \right){(T-T}_{1})}-1}{\left(\phi -\theta +\xi \right)}\right]$$

(11)

Total setup cost ${=c}_{s}$

Total holding cost,

$$THC={c}_{h}\left[{\int }_{0}^{{T}_{1}}I\left(t\right)dt+{\int }_{{T}_{1}}^{T}J\left(t\right)dt\right]={c}_{h}X$$

(12)

Total production cost

$$TPC={c}_{p}{\int }_{0}^{{T}_{1}}\{\gamma -\delta I\left(t\right)\}dt={c}_{p}\gamma {T}_{1}-\frac{(\gamma -\eta +\zeta p){c}_{p}\delta }{(\phi -\theta +\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}-1}{\left(\phi -\theta +\delta +\xi \right)}\right] = M-Np$$

(13)

where

$$M={c}_{p}\gamma {T}_{1}-\frac{(\gamma -\eta ){c}_{p}\delta }{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]={c}_{p}\gamma {T}_{1}-\left(\frac{\gamma -\eta }{\zeta }\right)N$$

(14)

$$N=\frac{\zeta {c}_{p}\delta }{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]$$

(15)

Total deterioration cost

$$TDC={c}_{d}\phi \left[{\int }_{0}^{{T}_{1}}\left\{I\left(t\right)-D(t)\right\}dt+{\int }_{{T}_{1}}^{T}\left\{J\left(t\right)-D(t)\right\}dt\right] ={c}_{d}\phi \left[{\int }_{0}^{{T}_{1}}\{\left(-\eta +\zeta p\right)+\left(1-\xi \right)I(t)\}dt+{\int }_{{T}_{1}}^{T}\{\left(-\eta +\zeta p\right)+\left(1-\xi \right)J(t)\}dt\right] ={c}_{d}\phi \left(-\eta +\zeta p\right)T+{c}_{d}\phi \left(1-\xi \right)X$$

(16)

Total preservation cost

$$TPRC={c}_{pr}\theta \left[{\int }_{0}^{{T}_{1}}\left\{I\left(t\right)-D(t)\right\}dt+{\int }_{{T}_{1}}^{T}\left\{J\left(t\right)-D(t)\right\}dt\right] ={c}_{pr}\theta \left[{\int }_{0}^{{T}_{1}}\{\left(-\eta +\zeta p\right)+\left(1-\xi \right)I(t)\}dt+{\int }_{{T}_{1}}^{T}\{\left(-\eta +\zeta p\right)+\left(1-\xi \right)J(t)\}dt\right] ={c}_{pr}\theta \left(-\eta +\zeta p\right)T+{c}_{pr}\theta \left(1-\xi \right)X$$

(17)

So, the total profit per cycle is given by

$$TP=TSR-({c}_{s}+THC+TPC+TDC+TPRC)=\left(\xi B-T\right)\zeta {p}^{2}+\left(\eta T+\xi A\right)p-[{c}_{s}+{c}_{h}A+{c}_{h}\zeta Bp+M-Np+\left({c}_{d}\phi +{c}_{pr}\theta \right)\left\{A\left(1-\xi \right)-\eta T\right\}+\left({c}_{d}\phi +{c}_{pr}\theta \right)\zeta \{B\left(1-\xi \right)+T\}p] =\left(\xi B-T\right)\zeta {p}^{2}+\left[\left(\eta T+\xi A\right)-{c}_{h}\zeta B+N-\left({c}_{d}\phi +{c}_{pr}\theta \right)\zeta \left\{B\left(1-\xi \right)+T\right\}\right]p-[{c}_{s}+{c}_{h}A+M+\left({c}_{d}\phi +{c}_{pr}\theta \right)\left\{A\left(1-\xi \right)-\eta T\right\}]$$

(18)

And thus, total average profit $TAP=\frac{TP}{T}={F}_{0}{p}^{2}+{F}_{1}p+{F}_{2}$ and the basic problem is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} Maximize\,TAP={F}_{0}{p}^{2}+{F}_{1}p+{F}_{2}\\ Where, \begin{array}{c}where, {F}_{0}=\frac{\left(\xi B-T\right)\zeta }{T}\\ {F}_{1}=\frac{\left(\eta T+\xi A\right)-{c}_{h}\zeta B+N-\left({c}_{d}\phi +{c}_{pr}\theta \right)\zeta \left\{B\left(1-\xi \right)+T\right\}}{T}\\ {F}_{2}=\frac{\left({c}_{d}\phi +{c}_{pr}\theta \right)\left\{\eta T-A\left(1-\xi \right)\right\}-{c}_{s}-{c}_{h}A-M}{T}\end{array}\\ Subject\,to\,{I}_{max}=\frac{1}{(\phi -\theta +\delta +\xi )}\left[1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right](\gamma -\eta +\zeta p),\\ T={T}_{1}+\frac{1}{\left(\phi -\theta +\xi \right)}\mathrm{ln}\left[1+\frac{\left(\gamma -\eta +\zeta p\right)}{\left(\eta -\zeta p\right)}\left\{\frac{\left(\phi -\theta +\xi \right)}{\left(\phi -\theta +\delta +\xi \right)}\right\}\left\{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right\}\right],\\ N=\frac{\zeta {c}_{p}\delta }{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right], M={c}_{p}\gamma {T}_{1}-\left(\frac{\gamma -\eta }{\zeta }\right)N, \theta +\phi =1\end{array}\right. } \end{aligned}$$

(19)

4.2 Particular Cases under crisp problem

Case 1: when deterioration is occurred completely in the absence of preservation.

Let, $\theta \to 0$ then $\phi \to 1$ and then

$$TAP={{F}_{0}}^{^{\prime}}{p}^{2}+{{F}_{1}}^{^{\prime}}p+{{F}_{3}}^{^{\prime}}, {I}_{max}=\frac{1}{(1+\delta +\xi )}\left[1-{{e}}^{-\left(1+\delta +\xi \right){T}_{1}}\right](\gamma -\eta +\zeta p)$$

where ${{F}_{0}}^{\mathrm{^{\prime}}}=\frac{\left(\xi {B}^{\mathrm{^{\prime}}}-T\right)\zeta }{T}$, ${{F}_{1}}^{\mathrm{^{\prime}}}=\frac{\left(\eta T+\xi {A}^{\mathrm{^{\prime}}}\right)-{c}_{h}\zeta {B}^{\mathrm{^{\prime}}}+{N}^{\mathrm{^{\prime}}}-{c}_{d}\zeta \left\{{B}^{\mathrm{^{\prime}}}\left(1-\xi \right)+T\right\}}{T}$, ${{F}_{3}}^{\mathrm{^{\prime}}}=-\frac{{c}_{s}+{c}_{h}{A}^{\mathrm{^{\prime}}}+{M}^{\mathrm{^{\prime}}}+{c}_{d}\left\{{A}^{\mathrm{^{\prime}}}\left(1-\xi \right)-\eta T\right\}}{T},$ ${A}^{\mathrm{^{\prime}}}=\frac{(\gamma -\eta )}{(1+\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(1+\delta +\xi \right){T}_{1}}-1}{\left(1+\delta +\xi \right)}\right]-\frac{\eta }{(1+\xi )}\left[(T-{T}_{1})+\frac{1-{{e}}^{\left(1+\xi \right){(T-T}_{1})}}{\left(1+\xi \right)}\right]$, ${B}^{\mathrm{^{\prime}}}=\frac{1}{(1+\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(1+\delta +\xi \right){T}_{1}}-1}{\left(1+\delta +\xi \right)}\right]+\frac{1}{(1+\xi )}\left[(T-{T}_{1})+\frac{1-{{e}}^{\left(1+\xi \right){(T-T}_{1})}}{\left(1+\xi \right)}\right]$

$${M}^{^{\prime}}={c}_{p}\gamma {T}_{1}-\frac{\left(\gamma -\eta \right){c}_{p}\delta }{\left(1+\delta +\xi \right)}\left[{T}_{1}+\frac{{{e}}^{-\left(1+\delta +\xi \right){T}_{1}}-1}{\left(1+\delta +\xi \right)}\right], {N}^{^{\prime}}=\frac{\zeta {c}_{p}\delta }{(1+\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(1+\delta +\xi \right){T}_{1}}-1}{\left(1+\delta +\xi \right)}\right]$$

Case 2: when the demand is independent of the price.

If, $\zeta \to 0$ then $TAP={{F}_{0}}^{^{\prime}}{p}^{2}+{{F}_{1}}^{^{\prime}}p+{{F}_{3}}^{^{\prime}}, {I}_{max}=\frac{(\gamma -\eta )}{(\phi -\theta +\delta +\xi )}\left[1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right]$

$${{F}_{0}}^{^{\prime}}=0, {{F}_{1}}^{^{\prime}}=\frac{\left(\eta T+\xi {A}^{^{\prime}}\right)+{N}^{^{\prime}}}{T}, {{F}_{3}}^{^{\prime}}=-\frac{{c}_{s}+{c}_{h}{A}^{^{\prime}}+{M}^{^{\prime}}+\left({c}_{d}\phi +{c}_{pr}\theta \right)\left\{{A}^{^{\prime}}\left(1-\xi \right)-\eta T\right\}}{T}$$

$${A}^{^{\prime}}=\frac{(\gamma -\eta )}{(\phi -\theta +\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}-1}{\left(\phi -\theta +\delta +\xi \right)}\right]-\frac{\eta }{(\phi -\theta +\xi )}\left[(T-{T}_{1})+\frac{1-{{e}}^{\left(\phi -\theta +\xi \right){(T-T}_{1})}}{\left(\phi -\theta +\xi \right)}\right]$$

$${B}^{^{\prime}}=\frac{1}{(\phi -\theta +\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}-1}{\left(\phi -\theta +\delta +\xi \right)}\right]+\frac{1}{(\phi -\theta +\xi )}\left[(T-{T}_{1})+\frac{1-{{e}}^{\left(\phi -\theta +\xi \right){(T-T}_{1})}}{\left(\phi -\theta +\xi \right)}\right]$$

$${M}^{^{\prime}}={c}_{p}\gamma {T}_{1}-\frac{\left(\gamma -\eta \right){c}_{p}\delta }{\left(\phi -\theta +\delta +\xi \right)}, {N}^{^{\prime}}=0$$

Case 3: when complete preservation confirms no deterioration.

If, $\phi \to 0$, then $\theta \to 1$ and then $TAP={{F}_{0}}^{^{\prime}}{p}^{2}+{{F}_{1}}^{^{\prime}}p+{{F}_{3}}^{^{\prime}}$, ${I}_{max}=\frac{(\gamma -\eta +\zeta p)}{(-1+\delta +\xi )}\left[1-{{e}}^{-\left(-1+\delta +\xi \right){T}_{1}}\right]$, where ${{F}_{0}}^{^{\prime}}=\frac{\left(\xi {B}^{^{\prime}}-T\right)\zeta }{T}$, ${{F}_{1}}^{^{\prime}}=\frac{\left(\eta T+\xi {A}^{^{\prime}}\right)-{c}_{h}\zeta {B}^{^{\prime}}+{N}^{^{\prime}}-{c}_{pr}\zeta \left\{{B}^{^{\prime}}\left(1-\xi \right)+T\right\}}{T}$, ${{F}_{3}}^{^{\prime}}=-\frac{{c}_{s}+{c}_{h}{A}^{^{\prime}}+{M}^{^{\prime}}+{c}_{pr}\left\{{A}^{^{\prime}}\left(1-\xi \right)-\eta T\right\}}{T}$, ${A}^{^{\prime}}=\frac{(\gamma -\eta )}{(-1+\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(-1+\delta +\xi \right){T}_{1}}-1}{\left(-1+\delta +\xi \right)}\right]-\frac{\eta }{(-1+\xi )}\left[(T-{T}_{1})+\frac{1-{{e}}^{\left(-1+\xi \right){(T-T}_{1})}}{\left(-1+\xi \right)}\right]$, ${B}^{^{\prime}}=\frac{1}{(-1+\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(-1+\delta +\xi \right){T}_{1}}-1}{\left(-1+\delta +\xi \right)}\right]+\frac{1}{(-1+\xi )}\left[(T-{T}_{1})+\frac{1-{{e}}^{\left(-1+\xi \right){(T-T}_{1})}}{\left(-1+\xi \right)}\right]$, ${M}^{^{\prime}}={c}_{p}\gamma {T}_{1}-\frac{(\gamma -\eta ){c}_{p}\delta }{(-1+\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(-1+\delta +\xi \right){T}_{1}}-1}{\left(-1+\delta +\xi \right)}\right]$ and ${N}^{^{\prime}}=\frac{\zeta {c}_{p}\delta }{(-1+\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(-1+\delta +\xi \right){T}_{1}}-1}{\left(-1+\delta +\xi \right)}\right]$

Case 4: when deterioration does not occur, and hence, there is no need of preservation.

If, $\theta , \phi \to 0$ then $TAP={{F}_{0}}^{^{\prime}}{p}^{2}+{{F}_{1}}^{^{\prime}}p+{{F}_{3}}^{^{\prime}}{I}_{max}=\frac{1}{(\delta +\xi )}\left[1-{{e}}^{-\left(\delta +\xi \right){T}_{1}}\right](\gamma -\eta +\zeta p)$

$${{F}_{0}}^{^{\prime}}=\frac{\left(\xi {B}^{^{\prime}}-T\right)\zeta }{T}, {{F}_{1}}^{^{\prime}}=\frac{\left(\eta T+\xi {A}^{^{\prime}}\right)-{c}_{h}\zeta {B}^{^{\prime}}+{N}^{^{\prime}}}{T}, {{F}_{3}}^{^{\prime}}=-\frac{{c}_{s}+{c}_{h}{A}^{^{\prime}}+{M}^{^{\prime}}}{T}, {A}^{^{\prime}}= \frac{(\gamma -\eta )}{(\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(\delta +\xi \right){T}_{1}}-1}{\left(\delta +\xi \right)}\right]-\frac{\eta }{\xi }\left[(T-{T}_{1})+\frac{1-{{e}}^{{\xi (T-T}_{1})}}{\xi }\right], {B}^{^{\prime}}=\frac{1}{(\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(\delta +\xi \right){T}_{1}}-1}{\left(\delta +\xi \right)}\right]+\frac{1}{\xi }\left[(T-{T}_{1})+\frac{1-{{e}}^{{\xi (T-T}_{1})}}{\xi }\right]$$

$${M}^{^{\prime}}={c}_{p}\gamma {T}_{1}-\frac{\left(\gamma -\eta \right){c}_{p}\delta }{\left(\delta +\xi \right)}\left[{T}_{1}+\frac{{{e}}^{-\left(\delta +\xi \right){T}_{1}}-1}{\left(\delta +\xi \right)}\right], {N}^{^{\prime}}=\frac{\zeta {c}_{p}\delta }{(\delta +\xi )}\left[{T}_{1}+\frac{{{e}}^{-\left(\delta +\xi \right){T}_{1}}-1}{\left(\delta +\xi \right)}\right]$$

Case 5: when deterioration does not occur, and hence, there is no need of preservation and neither demand nor production depends on stock.

If, $\phi ,\theta ,\delta ,\xi \to 0$ Then $TAP={{F}_{0}}^{^{\prime}}{p}^{2}+{{F}_{1}}^{^{\prime}}p+{{F}_{3}}^{^{\prime}}$, ${I}_{max}=\underset{\delta \to 0}{\mathrm{lim}}\frac{(\gamma -\eta +\zeta p)}{\delta }\left[1-{{e}}^{-{\delta T}_{1}}\right]=(\gamma -\eta +\zeta p){T}_{1}$, ${{F}_{0}}^{^{\prime}}=-\zeta$, ${{F}_{1}}^{^{\prime}}=\frac{\eta T-{c}_{h}\zeta {B}^{^{\prime}}+{N}^{^{\prime}}}{T}$, ${{F}_{3}}^{^{\prime}}=-\frac{{c}_{s}+{c}_{h}{A}^{^{\prime}}+{M}^{^{\prime}}}{T}$, ${A}^{^{\prime}}=\underset{\delta \to 0}{\mathrm{lim}}\frac{(\gamma -\eta )}{\delta }\left[{T}_{1}+\frac{{{e}}^{-\delta {T}_{1}}-1}{\delta }\right] -\underset{\xi \to 0}{\mathrm{lim}}\frac{\eta }{\xi }\left[(T-{T}_{1})+\frac{1-{{e}}^{{\xi (T-T}_{1})}}{\xi }\right]=\underset{\delta \to 0}{\mathrm{lim}}\frac{(\gamma -\eta )}{{\delta }^{2}}\left[\delta {T}_{1}+{{e}}^{-\delta {T}_{1}}-1\right] -\underset{\xi \to 0}{\mathrm{lim}}\frac{\eta }{{\xi }^{2}}\left[\xi (T-{T}_{1})+1-{{e}}^{{\xi (T-T}_{1})}\right]$, $=\frac{\left(\gamma -\eta \right){{T}_{1}}^{2}+\eta {(T-{T}_{1})}^{2}}{2}$, ${B}^{^{\prime}}=\underset{\delta \to 0}{\mathrm{lim}}\frac{1}{\delta }\left[{T}_{1}+\frac{{{e}}^{-\delta {T}_{1}}-1}{\delta }\right]+\underset{\xi \to 0}{\mathrm{lim}}\frac{1}{\xi }\left[(T-{T}_{1})+\frac{1-{{e}}^{{\xi (T-T}_{1})}}{\xi }\right]=\underset{\delta \to 0}{\mathrm{lim}}\frac{1}{{\delta }^{2}}\left[\delta {T}_{1}+{{e}}^{-\delta {T}_{1}}-1\right]+\underset{\xi \to 0}{\mathrm{lim}}\frac{1}{{\xi }^{2}}\left[\xi (T-{T}_{1})+1-{{e}}^{{\xi (T-T}_{1})}\right]=\frac{{{T}_{1}}^{2}-{(T-{T}_{1})}^{2}}{2}$ , ${M}^{^{\prime}}={c}_{p}\gamma {T}_{1}$, ${N}^{^{\prime}}=0$.

Case 6: when deterioration does not occur, and hence, there is no need of preservation and demand and stock are constant.

If, $\phi ,\theta ,\delta ,\xi ,\zeta \to 0$ Then $TAP={{F}_{0}}^{^{\prime}}{p}^{2}+{{F}_{1}}^{^{\prime}}p+{{F}_{3}}^{^{\prime}}$, ${I}_{max}=\underset{\delta \to 0}{\mathrm{lim}}\frac{(\gamma -\eta p)}{\delta }\left[1-{{e}}^{-{\delta T}_{1}}\right]=(\gamma -\eta ){T}_{1}$, ${{F}_{0}}^{^{\prime}}=0$, ${{F}_{1}}^{^{\prime}}=\frac{\eta T+{N}^{^{\prime}}}{T}$, ${{F}_{3}}^{^{\prime}}=-\frac{{c}_{s}+{c}_{h}{A}^{^{\prime}}+{M}^{^{\prime}}}{T}$, ${A}^{^{\prime}}=\underset{\delta \to 0}{\mathrm{lim}}\frac{(\gamma -\eta )}{\delta }\left[{T}_{1}+\frac{{{e}}^{-\delta {T}_{1}}-1}{\delta }\right] -\underset{\xi \to 0}{\mathrm{lim}}\frac{\eta }{\xi }\left[(T-{T}_{1})+\frac{1-{{e}}^{{\xi (T-T}_{1})}}{\xi }\right]=\underset{\delta \to 0}{\mathrm{lim}}\frac{(\gamma -\eta )}{{\delta }^{2}}\left[\delta {T}_{1}+{{e}}^{-\delta {T}_{1}}-1\right] -\underset{\xi \to 0}{\mathrm{lim}}\frac{\eta }{{\xi }^{2}}\left[\xi (T-{T}_{1})+1-{{e}}^{{\xi (T-T}_{1})}\right]$, $=\frac{\left(\gamma -\eta \right){{T}_{1}}^{2}+\eta {(T-{T}_{1})}^{2}}{2}$, ${B}^{^{\prime}}=\underset{\delta \to 0}{\mathrm{lim}}\frac{1}{\delta }\left[{T}_{1}+\frac{{{e}}^{-\delta {T}_{1}}-1}{\delta }\right]+\underset{\xi \to 0}{\mathrm{lim}}\frac{1}{\xi }\left[(T-{T}_{1})+\frac{1-{{e}}^{{\xi (T-T}_{1})}}{\xi }\right]=\underset{\delta \to 0}{\mathrm{lim}}\frac{1}{{\delta }^{2}}\left[\delta {T}_{1}+{{e}}^{-\delta {T}_{1}}-1\right]+\underset{\xi \to 0}{\mathrm{lim}}\frac{1}{{\xi }^{2}}\left[\xi (T-{T}_{1})+1-{{e}}^{{\xi (T-T}_{1})}\right]=\frac{{{T}_{1}}^{2}-{(T-{T}_{1})}^{2}}{2}$, ${M}^{^{\prime}}={c}_{p}\gamma {T}_{1}$, ${N}^{^{\prime}}=0$

That is, $=\eta p-\{\frac{{c}_{s}}{T}+{c}_{h}\frac{{{\left(\gamma -\eta \right)T}_{1}}^{2}+\eta {\left(T-{T}_{1}\right)}^{2}}{2T}+\frac{{c}_{p}\gamma {T}_{1}}{T}\}$, ${I}_{max}=(\gamma -\eta ){T}_{1}$ and this is the classical EPQ model (the profit maximization sense).

4.3 Formulation of Fuzzy Mathematical Model

In real-life problem, very often it is observed that several cost parameters associated with the problem (19) discussed above are non-randomly uncertain. Thus, we consider selling price and various cost prices as fuzzy parameters. Three types of the fuzzy model may be developed as follows:

• i) Unit selling price of the items assumes R-triangular lock fuzzy number.

• ii) Only cost prices are assumed to be L-triangular lock fuzzy number.

• iii) Selling price of the commodities is assumed to be R-triangular lock fuzzy number, and the cost prices are assumed to be L-triangular lock fuzzy number.

These three models are defined as model-A, model-B and model-C, respectively, and they are describing as follows:

4.4 Model-A

Here, the selling price of the commodities is considered to be the R-triangular lock fuzzy number given $\tilde{p }$ given by its membership functions

$$\mu (\tilde{p })=\left\{\begin{array}{l}0\quad if\; p\le {p}_{0}\\ \frac{{p}_{0}(1+\frac{{\sigma }_{0}}{{k}_{0}})-p}{{p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}}\quad if\; {p}_{0}\le p\le {p}_{0}(1+\frac{{\sigma }_{0}}{{k}_{0}})\\ 1\quad if\; p\ge {p}_{0}(1+\frac{{\sigma }_{0}}{{k}_{0}})\end{array}\right.$$

(20)

where ${k}_{0}$ is the key.

Other parameters of (19) are assumed to be crisps. Then, right $\alpha$-cut of the selling price $\tilde{p }$ is given by

$$p\left(\alpha \right)\le {p}_{0}\left(1+\frac{{\sigma }_{0}}{{k}_{0}}\right)-\alpha {p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}$$

(21)

Then, the fuzzy model is given by

$$\left\{\begin{array}{c}Maximize\, \widetilde{Z}\,\widetilde{=} {\widetilde{F}_{0}}{\widetilde{p }}^{2}+{\widetilde{F}_{1}}\widetilde{p }+\widetilde{{F}_{2}}\\ \begin{array}{c}\widetilde{{F}_{0}}=\frac{\left(\xi \widetilde{B }-\widetilde{T }\right)\zeta }{\widetilde{T }}\\ \widetilde{{F}_{1}}\widetilde{=}\frac{\left(\eta \tilde{T }+\xi \tilde{A }\right)-{c}_{h}\zeta \tilde{B }+N-\left({c}_{d}\phi +{c}_{pr}\theta \right)\zeta \left\{\tilde{B }\left(1-\xi \right)+\tilde{T }\right\}}{\tilde{T }}\\ \widetilde{{F}_{2}}\stackrel{\sim }=\frac{\left({c}_{d}\phi +{c}_{pr}\theta \right)\left\{\eta \tilde{T }-\tilde{A }\left(1-\xi \right)\right\}-{c}_{s}-{c}_{h}\tilde{A }-M}{\tilde{T }}\end{array}\\ \stackrel{\sim }{\mathrm{Q }}\widetilde{=}\frac{1}{\left(\phi -\theta +\delta +\xi \right)}\left[1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right](\gamma -\eta +\zeta \tilde{p } ),\\ \tilde{T }\widetilde{=}{T}_{1}+\frac{1}{\left(\phi -\theta +\xi \right)}\mathrm{ln}\left[1+\frac{\left(\gamma -\eta +\zeta \tilde{p }\right)}{\left(\eta -\zeta \tilde{p }\right)}\left\{\frac{\left(\phi -\theta +\xi \right)}{\left(\phi -\theta +\delta +\xi \right)}\right\}\left\{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right\}\right]\\ \begin{array}{c}\tilde{A }\widetilde{=}\frac{(\gamma -\eta )}{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]-\frac{\eta }{(\phi -\theta +\xi )}\left[\left(\tilde{T }-{T}_{1}\right)-\frac{{{e}}^{\left(\phi -\theta +\xi \right){(\tilde{T }-T}_{1})}-1}{\left(\phi -\theta +\xi \right)}\right]\\ \tilde{B }\widetilde{=}\frac{1}{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]+\frac{1}{(\phi -\theta +\xi )}\left[\left(\tilde{T }-{T}_{1}\right)-\frac{{{e}}^{\left(\phi -\theta +\xi \right){(\tilde{T }-T}_{1})}-1}{\left(\phi -\theta +\xi \right)}\right]\\ \begin{array}{c}M={c}_{p}\gamma {T}_{1}-\left(\frac{\gamma -\eta }{\zeta }\right)N, N=\frac{\zeta {c}_{p}\delta }{(\phi -\theta +\delta +\xi )}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]\\ \theta +\phi =1\end{array}\end{array}\end{array}\right.$$

(22)

Thus, in terms of $\alpha$-cuts our fuzzy problem reduced to equivalent nonlinear problem as

$$ \left\{ {\begin{array}{*{20}c} {Maximize\,\alpha } \\ {Subject\,to\,Z \ge F_{0} \left( \alpha \right)\left\{ {p_{0} \left( {1 + \frac{{\sigma_{0} }}{{k_{0} }}} \right) - \alpha p_{0} \frac{{\sigma_{0} }}{{k_{0} }}} \right\}^{2} + F_{1} \left( \alpha \right)\left\{ {p_{0} \left( {1 + \frac{{\sigma_{0} }}{{k_{0} }}} \right) - \alpha p_{0} \frac{{\sigma_{0} }}{{k_{0} }}} \right\} + F_{2} \left( \alpha \right)} \\ {F_{0} \left( \alpha \right) = \frac{{\left( {\xi B\left( \alpha \right) - T\left( \alpha \right)} \right)\zeta }}{T\left( \alpha \right)},} \\ {F_{1} \left( \alpha \right) = \frac{{\left( {\eta T\left( \alpha \right) + \xi A\left( \alpha \right)} \right) - c_{h} \zeta B\left( \alpha \right) + N - \left( {c_{d} \phi + c_{pr} \left( \alpha \right)\theta } \right)\zeta \left\{ {B\left( \alpha \right)\left( {1 - \xi } \right) + T\left( \alpha \right)} \right\}}}{T\left( \alpha \right)}} \\ {F_{2} \left( \alpha \right) = \frac{{\left( {c_{d} \phi + c_{pr} \theta } \right)\left\{ {\eta T\left( \alpha \right) - A\left( \alpha \right)\left( {1 - \xi } \right)} \right\} - c_{s} - c_{h} A\left( \alpha \right) - M}}{T\left( \alpha \right)}} \\ {Q\left( \alpha \right) = \frac{1}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} } \right]\left( {\gamma - \eta + \zeta \left\{ {p_{0} \left( {1 + \frac{{\sigma_{0} }}{{k_{0} }}} \right) - \alpha p_{0} \frac{{\sigma_{0} }}{{k_{0} }}} \right\}} \right)} \\ {A\left( \alpha \right) = \frac{{\left( {\gamma - \eta } \right)}}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right] - \frac{\eta }{{\left( {\phi - \theta + \xi } \right)}}\left[ {\left( {T\left( \alpha \right) - T_{1} } \right) - \frac{{e^{{\left( {\phi - \theta + \xi } \right)(T\left( \alpha \right) - T_{1} )}} - 1}}{{\left( {\phi - \theta + \xi } \right)}}} \right]} \\ {B\left( \alpha \right) = \frac{1}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right] + \frac{1}{{\left( {\phi - \theta + \xi } \right)}}\left[ {\left( {T\left( \alpha \right) - T_{1} } \right) - \frac{{e^{{\left( {\phi - \theta + \xi } \right)(T\left( \alpha \right) - T_{1} )}} - 1}}{{\left( {\phi - \theta + \xi } \right)}}} \right]} \\ {T\left( \alpha \right) = T_{1} + \frac{1}{{\left( {\phi - \theta + \xi } \right)}}\ln \left[ {1 + \frac{{\left( {\gamma - \eta + \zeta \left\{ {p_{0} \left( {1 + \frac{{\sigma_{0} }}{{k_{0} }}} \right) - \alpha p_{0} \frac{{\sigma_{0} }}{{k_{0} }}} \right\}} \right)}}{{\left( {\eta - \zeta \left\{ {p_{0} \left( {1 + \frac{{\sigma_{0} }}{{k_{0} }}} \right) - \alpha p_{0} \frac{{\sigma_{0} }}{{k_{0} }}} \right\}} \right)}}\left\{ {\frac{{\left( {\phi - \theta + \xi } \right)}}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right\}\left\{ {1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} } \right\}} \right],} \\ {N = \frac{{\zeta c_{p} \delta }}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right], M = c_{p} \gamma T_{1} - \left( {\frac{\gamma - \eta }{\zeta }} \right)N, \theta + \phi = 1} \\ \end{array} } \right. $$

(23)

4.5 Model-B

In this second type of problem, we consider all the cost to be the L-triangular lock fuzzy number. The selling price and other parameters in (19) are considered to crisps. The costs are denoted $\stackrel{\sim }{{c}_{i}}(i=\mathrm{1,2},\mathrm{3,4},5)$, where $\stackrel{\sim }{{c}_{1}}=\stackrel{\sim }{{c}_{p}}$, $\stackrel{\sim }{{c}_{2}}=\stackrel{\sim }{{c}_{d}}$, $\stackrel{\sim }{{c}_{3}}=\stackrel{\sim }{{c}_{h}}$, $\stackrel{\sim }{{c}_{4}}=\stackrel{\sim }{{c}_{s}}$ and $\stackrel{\sim }{{c}_{5}}=\stackrel{\sim }{{c}_{pr}}$ and the membership function is given by

$$\mu (\stackrel{\sim }{{c}_{i}})=\left\{\begin{array}{c}\,0\,if\,{c}_{i}\le {c}_{i0}(1-\frac{{\sigma }_{i}}{{k}_{i}})\\ \frac{{c}_{i}-{c}_{i0}(1-\frac{{\sigma }_{i}}{{k}_{i}})}{{c}_{i0}{\sigma }_{i}{/k}_{i}}\,if\,{c}_{i0}(1-\frac{{\sigma }_{i}}{{k}_{i}})\le {c}_{i}\le {c}_{i0}\,i=\mathrm{1,2},\mathrm{3,4}\,and\,5\\\,1\,if\,{c}_{i}\ge {c}_{i0}\end{array}\right.$$

(24)

The left $\alpha$-cut of the costs $\stackrel{\sim }{{c}_{i}}(i=\mathrm{1,2},\mathrm{3,4},5)$ is given by

$${c}_{i}\left(\alpha \right)={c}_{i0}\left(1-\frac{{\sigma }_{i}}{{k}_{i}}\right)+\alpha {c}_{i0}{\sigma }_{i}{/k}_{i}$$

(25)

where ${k}_{i}(i=1, \mathrm{2,3},\mathrm{4,5})$ are the corresponding keys.

Then, the fuzzy optimization problem will be

$$ \left\{ {\begin{array}{*{20}c} {Maximize\,\widetilde{Z }\widetilde{ = }F_{0} p ^{2} + \widetilde{{F_{1} }}p + \widetilde{{F_{2} }}} \\ {F_{0} = \frac{{\left( {\xi B - T } \right)\zeta }}{T }} \\ {\widetilde{{F_{1} }}\tilde{ = }\frac{{\left( {\eta T + \xi A } \right) - \widetilde{{c_{h} }}\zeta B + \widetilde{N } - \left( {\widetilde{{c_{d} }}\phi + \widetilde{{c_{pr} }}\theta } \right)\zeta \left\{ {B \left( {1 - \xi } \right) + T } \right\}}}{T }} \\ { \widetilde{{F_{2} }}\tilde{ = }\frac{{\left( {\widetilde{{c_{d} }}\phi + \widetilde{{c_{pr} }}\theta } \right)\left\{ {\eta T - A \left( {1 - \xi } \right)} \right\} - \widetilde{{c_{s} }} - \widetilde{{c_{h} }}A {-}\widetilde{M }}}{T } } \\ {Q = \frac{1}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} } \right]\left( {\gamma - \eta + \zeta p } \right),} \\ {T = T_{1} + \frac{1}{{\left( {\phi - \theta + \xi } \right)}}\ln \left[ {1 + \frac{{\left( {\gamma - \eta + \zeta p } \right)}}{{\left( {\eta - \zeta p } \right)}}\left\{ {\frac{{\left( {\phi - \theta + \xi } \right)}}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right\}\left\{ {1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} } \right\}} \right]} \\ {A = \frac{{\left( {\gamma - \eta } \right)}}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right] - \frac{\eta }{{\left( {\phi - \theta + \xi } \right)}}\left[ {\left( {T - T_{1} } \right) - \frac{{e^{{\left( {\phi - \theta + \xi } \right)(T - T_{1} )}} - 1}}{{\left( {\phi - \theta + \xi } \right)}}} \right]} \\ {B = \frac{1}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right] + \frac{1}{{\left( {\phi - \theta + \xi } \right)}}\left[ {\left( {T - T_{1} } \right) - \frac{{e^{{\left( {\phi - \theta + \xi } \right)(T - T_{1} )}} - 1}}{{\left( {\phi - \theta + \xi } \right)}}} \right]} \\ {\tilde{M} = \widetilde{{c_{p} }}\gamma T_{1} - \left( {\frac{\gamma - \eta }{\zeta }} \right)\tilde{N}, \tilde{N} = \frac{{\zeta \widetilde{{c_{p} }}\delta }}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right]} \\ {\theta + \phi = 1} \\ \end{array} } \right. $$

(26)

Thus, using $\alpha$-cuts the fuzzy problem (26) reduces to equivalent nonlinear problem as

$$\left\{\begin{array}{c}Maximize\,\alpha \\ Subject\,to\,Z\ge {F}_{0}{p }^{2}+p{F}_{1}(\alpha )+{F}_{2}(\alpha )\\ \begin{array}{c}\begin{array}{c}{F}_{0}\left(\alpha \right)=\frac{\left(\xi B-T \right)\zeta }{T },{c}_{i}\left(\alpha \right)={c}_{i0}\left(1-\frac{{\sigma }_{i}}{{k}_{i}}\right)+\alpha {\sigma }_{i}, i=\mathrm{1,2},\mathrm{3,4}\,and\,5\\ {F}_{1}(\alpha )=\frac{\left(\eta T+\xi A\right)-{c}_{h}\zeta B+N(\alpha )-\left({c}_{d}(\alpha )\phi +{c}_{pr}(\alpha )\theta \right)\zeta \left\{B\left(1-\xi \right)+T\right\}}{T}\\ {F}_{2}(\alpha )=\frac{\left({c}_{d}(\alpha )\phi +{c}_{pr}(\alpha )\theta \right)\left\{\eta T-A\left(1-\xi \right)\right\}-{c}_{s}(\alpha )-{c}_{h}(\alpha )A-M(\alpha )}{T}\end{array}\\ Q=\frac{1}{\left(\phi -\theta +\delta +\xi \right)}\left[1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right](\gamma -\eta +\zeta p),\\ T={T}_{1}+\frac{1}{\left(\phi -\theta +\xi \right)}\mathrm{ln}\left[1+\frac{\left(\gamma -\eta +\zeta p\right)}{\left(\eta -\zeta p\right)}\left\{\frac{\left(\phi -\theta +\xi \right)}{\left(\phi -\theta +\delta +\xi \right)}\right\}\left\{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right\}\right],\\ N(\alpha )=\frac{\zeta {c}_{p}(\alpha )\delta }{\left(\phi -\theta +\delta +\xi \right)}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right], M(\alpha )={c}_{p}(\alpha )\gamma {T}_{1}-\left(\frac{\gamma -\eta }{\zeta }\right)N(\alpha ), \theta +\phi =1\end{array}\end{array}\right.$$

(27)

4.6 Model-C

In this third type of problem, we consider all the cost to be the L-triangular lock fuzzy number and the selling price to be R-triangular lock fuzzy number and other parameters in (19) are considered to crisps. Then, the fuzzy model will be given by

$$ \left\{ {\begin{array}{*{20}c} {Maximize\,\widetilde{Z }\widetilde{ = }\widetilde{{F_{0} }}\widetilde{p }^{2} + \widetilde{{F_{1} }}\widetilde{p } + \widetilde{{F_{2} }}} \\ {\widetilde{{F_{0} }} = \frac{{\left( {\xi \widetilde{B } - \widetilde{T }} \right)\zeta }}{{\widetilde{T }}}} \\ {\widetilde{{F_{1} }}\tilde{ = }\frac{{\left( {\eta \widetilde{T } + \xi \widetilde{A }} \right) - \widetilde{{c_{h} }}\zeta \widetilde{B } + N - \left( {\widetilde{{c_{d} }}\phi + \widetilde{{c_{pr} }}\theta } \right)\zeta \left\{ {\widetilde{B }\left( {1 - \xi } \right) + \widetilde{T }} \right\}}}{{\widetilde{T }}}} \\ {\widetilde{{F_{2} }}\tilde{ = }\frac{{\left( {\widetilde{{c_{d} }}\phi + \widetilde{{c_{pr} }}\theta } \right)\left\{ {\eta \widetilde{T } - \widetilde{A }\left( {1 - \xi } \right)} \right\} - \widetilde{{c_{s} }} - \widetilde{{c_{h} }}\widetilde{A } - M}}{{\widetilde{T }}}} \\ {\widetilde{Q }\widetilde{ = }\frac{1}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} } \right]\left( {\gamma - \eta + \zeta \widetilde{p } } \right)} \\ {\widetilde{T }\tilde{ = }T_{1} + \frac{1}{{\left( {\phi - \theta + \xi } \right)}}\ln \left[ {1 + \frac{{\left( {\gamma - \eta + \zeta \widetilde{p }} \right)}}{{\left( {\eta - \zeta \widetilde{p }} \right)}}\left\{ {\frac{{\left( {\phi - \theta + \xi } \right)}}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right\}\left\{ {1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} } \right\}} \right]} \\ {\widetilde{A }\tilde{ = }\frac{{\left( {\gamma - \eta } \right)}}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right] - \frac{\eta }{{\left( {\phi - \theta + \xi } \right)}}\left[ {\left( {\widetilde{T } - T_{1} } \right) - \frac{{e^{{\left( {\phi - \theta + \xi } \right)(T - T_{1} )}} - 1}}{{\left( {\phi - \theta + \xi } \right)}}} \right]} \\ {\widetilde{B }\tilde{ = }\frac{1}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right] + \frac{1}{{\left( {\phi - \theta + \xi } \right)}}\left[ {\left( {\widetilde{T } - T_{1} } \right) - \frac{{e^{{\left( {\phi - \theta + \xi } \right)(\widetilde{T } - T_{1} )}} - 1}}{{\left( {\phi - \theta + \xi } \right)}}} \right]} \\ {\tilde{M} = \widetilde{{c_{p} }}\gamma T_{1} - \left( {\frac{\gamma - \eta }{\zeta }} \right)\tilde{N}, \tilde{N} = \frac{{\zeta \widetilde{{c_{p} }}\delta }}{{\left( {\phi - \theta + \delta + \xi } \right)}}\left[ {T_{1} - \frac{{1 - e^{{ - \left( {\phi - \theta + \delta + \xi } \right)T_{1} }} }}{{\left( {\phi - \theta + \delta + \xi } \right)}}} \right]} \\ {\theta + \phi = 1} \\ \end{array} } \right. $$

(28)

Then, $\alpha$-cuts of the fuzzy functions (28) are given by

$$\left\{\begin{array}{c}Z\left(\alpha \right)= {F}_{0}\left(\alpha \right){\left\{{p}_{0}\left(1+\frac{{\sigma }_{0}}{{k}_{0}}\right)-\alpha {p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}\right\}}^{2}+{F}_{1}(\alpha )\left\{{p}_{0}\left(1+\frac{{\sigma }_{0}}{{k}_{0}}\right)-\alpha {p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}\right\}+{F}_{2}(\alpha ) \\ \begin{array}{c}\begin{array}{c}{F}_{0}\left(\alpha \right)=\frac{\left(\xi B(\alpha )-T(\alpha )\right)\zeta }{T(\alpha )} ,{c}_{i}\left(\alpha \right)={c}_{i0}\left(1-\frac{{\sigma }_{i}}{{k}_{i}}\right)+\alpha {\sigma }_{i}, i=\mathrm{1,2},\mathrm{3,4} \,and \,5\\ {F}_{1}(\alpha )=\frac{\left(\eta T(\alpha )+\xi A(\alpha )\right)-{c}_{h}(\alpha )\zeta B(\alpha )+N(\alpha )-\left({c}_{d}(\alpha )\phi +{c}_{pr}(\alpha )\theta \right)\zeta \left\{B(\alpha )\left(1-\xi \right)+T(\alpha )\right\}}{T(\alpha )}\\ {F}_{2}(\alpha )=\frac{\left({c}_{d}(\alpha )\phi +{c}_{pr}(\alpha )\theta \right)\left\{\eta T(\alpha )-A(\alpha )\left(1-\xi \right)\right\}-{c}_{s}(\alpha )-{c}_{h}(\alpha )A(\alpha )-M(\alpha )}{T(\alpha )}\end{array}\\ A\left(\alpha \right)=\frac{\left(\gamma -\eta \right)}{\left(\phi -\theta +\delta +\xi \right)}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]-\frac{\eta }{\left(\phi -\theta +\xi \right)}\left[\left(T(\alpha )-{T}_{1}\right)-\frac{{{e}}^{\left(\phi -\theta +\xi \right){(T(\alpha )-T}_{1})}-1}{\left(\phi -\theta +\xi \right)}\right]\\ B\left(\alpha \right)=\frac{1}{\left(\phi -\theta +\delta +\xi \right)}\left[{T}_{1}-\frac{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]+\frac{1}{\left(\phi -\theta +\xi \right)}\left[\left(T\left(\alpha \right)-{T}_{1}\right)-\frac{{{e}}^{\left(\phi -\theta +\xi \right){(T(\alpha )-T}_{1})}-1}{\left(\phi -\theta +\xi \right)}\right]\\ N(\alpha )=\frac{\zeta {c}_{p}(\alpha )\delta }{\left(\phi -\theta +\delta +\xi \right)}\left[{T}_{1}-\frac{{1-{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}}{\left(\phi -\theta +\delta +\xi \right)}\right]\\ M(\alpha )={c}_{p}(\alpha )\gamma {T}_{1}-\left(\frac{\gamma -\eta }{\zeta }\right)N(\alpha )\\ T\left(\alpha \right)={T}_{1}+\frac{1}{\left(\phi -\theta +\xi \right)}\mathrm{ln}\left[1+\frac{\left(\gamma -\eta +\zeta \left\{{p}_{0}\left(1+\frac{{\sigma }_{0}}{{k}_{0}}\right)-\alpha {p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}\right\}\right)}{\left(\eta -\zeta \left\{{p}_{0}\left(1+\frac{{\sigma }_{0}}{{k}_{0}}\right)-\alpha {p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}\right\}\right)}\left\{\frac{\left(\phi -\theta +\xi \right)}{\left(\phi -\theta +\delta +\xi \right)}\right\}\left\{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right\}\right]\end{array}\end{array}\right.$$

(29)

Thus, using $\alpha$-cuts the fuzzy functions (29) reduces to equivalent nonlinear problem as

$$\left\{\begin{array}{c}Maximize\,\alpha \\ \begin{array}{c}Subject\,to\,Z\ge Z\left(\alpha \right)\\ where \alpha -cut\, are\, is\, given\, by (30)\end{array}\\ \begin{array}{c}Q\left(\alpha \right)=\frac{1}{\left(\phi -\theta +\delta +\xi \right)}\left[1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right]\left[\gamma -\eta +\zeta \left\{{p}_{0}\left(1+\frac{{\sigma }_{0}}{{k}_{0}}\right)-\alpha {p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}\right\}\right]\\ T\left(\alpha \right)={T}_{1}+\frac{1}{\left(\phi -\theta +\xi \right)}\mathrm{ln}\left[1+\frac{\left(\gamma -\eta +\zeta \left\{{p}_{0}\left(1+\frac{{\sigma }_{0}}{{k}_{0}}\right)-\alpha {p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}\right\}\right)}{\left(\eta -\zeta \left\{{p}_{0}\left(1+\frac{{\sigma }_{0}}{{k}_{0}}\right)-\alpha {p}_{0}\frac{{\sigma }_{0}}{{k}_{0}}\right\}\right)}\left\{\frac{\left(\phi -\theta +\xi \right)}{\left(\phi -\theta +\delta +\xi \right)}\right\}\left\{1-{{e}}^{-\left(\phi -\theta +\delta +\xi \right){T}_{1}}\right\}\right]\end{array}\end{array}\right.$$

(30)

4.7 Solution methodology

We solve the optimization problem (crisp, general fuzzy and lock fuzzy) using the following algorithm.

4.8 Solution Algorithm

Step-1 Input the values of the parameters corresponding to the crisp problem.

Step-2 Solve the crisp problem and find the total average profit ${TAP}^{*}$ for the crisp problem.

Step-3 Apply the general fuzzy rule considering the following cases:

• (a) Only $p$ to be R- triangular fuzzy number (Model-A)

• (b) Only ${c}_{i}$($i=\mathrm{1.2,3},\mathrm{4,5}$) to be L-Triangular fuzzy number (Model-B)

• (c) p to be R- triangular fuzzy number and ${c}_{i}$($i=\mathrm{1.2,3},\mathrm{4,5}$) to be L-Triangular fuzzy number (Model-C)

Step-4 Find the total average profits ${{TAP}_{fA}}^{*}$, ${{TAP}_{fB}}^{*}$ and ${{TAP}_{fB}}^{*}$ for the Model-A, Model-B and Model-C, respectively.

Step-5 Find ${{TAP}_{f}}^{*}=\mathrm{max}\left\{{{TAP}_{fA}}^{*},{{TAP}_{fB}}^{*} ,{{TAP}_{fC}}^{*}\right\}.$

Step-6 Check whether ${TAP}^{*}<{{TAP}_{f}}^{*}$. If yes go to Step-7 else go to Step-8.

Step-7 Store ${{TAP}_{opt}}^{*}={{TAP}_{f}}^{*}$. Go to Step-9.

Step-8 Store ${{TAP}_{opt}}^{*}={TAP}^{*}$. Go to Step-15.

Step-9 Apply the lock fuzzy rule considering the following cases:

• i) Only $p$ to be R-triangular lock fuzzy number (Model-A)

• ii) Only ${c}_{i}$($i=\mathrm{1.2,3},\mathrm{4,5}$) to be L-triangular lock fuzzy number (Model-B)

• iii) $p$ to be R- triangular lock fuzzy number and ${c}_{i}$($i=\mathrm{1.2,3},\mathrm{4,5}$) to be L-triangular lock fuzzy numbers (Model-C)

Step-10 Find the total average profits ${{TAP}_{lA}}^{*}$, ${{TAP}_{lB}}^{*}$ and ${{TAP}_{lC}}^{*}$ for the Model-A, Model-B and Model-C, respectively.

Step-11 Find ${{TAP}_{l}}^{*}=\mathrm{max}\left\{{{TAP}_{lA}}^{*},{{TAP}_{lB}}^{*} ,{{TAP}_{lB}}^{*}\right\}.$

Step-12 Check whether ${{TAP}_{opt}}^{*}<{{TAP}_{l}}^{*}$. If yes go to Step-13 else go to Step-14.

Step-13 Store ${{TAP}_{opt}}^{*}={{TAP}_{l}}^{*}$. Go to Step-15.

Step-14 Store ${{TAP}_{opt}}^{*}={{TAP}_{opt}}^{*}$. Go to Step-15.

Step-15 End.

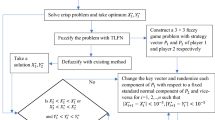
The flow chart of the algorithm mentioned above is presented in Fig. 2.

Fig. 2

Flow chart for solution methodology

5 Numerical simulation

For numerical illustration, we consider the following values of the input parameters:

• (1) For the crisp model, we take ${c}_{h}=3.5$, ${c}_{s}=500$, ${c}_{d}=1.2$, ${c}_{pr}=4.5$, ${c}_{p}=50$, $p=80$, $\phi =0.15$, $\theta =0.85$, $\gamma =200$, $\xi =1.8$, $\zeta =0.001$, $\eta =50$, $\delta =0.2$.

• (2) For the fuzzy model-A, we take${c}_{h}=3.5$, ${c}_{s}=500$, ${c}_{d}=1.2$, ${c}_{pr}=4.5$, ${c}_{p}=50$, ${p}_{0}=80$, $\phi =0.15$, $\theta =0.85$, $\gamma =200$, $\xi =1.8$, $\zeta =0.001$, $\eta =50$, $\delta =0.2,\sigma =0.2$ and the key ${k}_{0}=0.5$ for fuzzy lock values of selling price. Also, taking ${k}_{0}=1$, the model reduces to the corresponding general fuzzy model.

• (3) For the fuzzy model-B, we take${c}_{h0}=3.5$, ${c}_{s0}=500$, ${c}_{d0}=1.2$, ${c}_{pr0}=4.5$, ${c}_{p0}=50$, $p=80$, $\phi =0.15$, $\theta =0.85$, $\gamma =200$, $\xi =1.8$, $\zeta =0.001$, $\eta =50$, $\delta =0.2,\sigma =0.2$ and the key vector as${[{k}_{1}{, k}_{2 }, {k}_{3}, {k}_{4}{,k}_{5}]}^{T}={[0.75, 1, 1.25, 1.5, 1.75]}^{T}$,where ${k}_{i}(i=1, \mathrm{2,3},\mathrm{4,5})$ are the corresponding keys for the fuzzy lock values of production cost, preservation cost, holding cost, set up cost and deterioration cost, respectively. Also, taking ${k}_{1}={k}_{2}={k}_{3}={k}_{4}={k}_{5}=1$ the model is reduced to the corresponding general fuzzy model.

• (4) For the fuzzy model-C, we take ${c}_{h0}=3.5$, ${c}_{s0}=500$, ${c}_{d0}=1.2$, ${c}_{pr0}=4.5$, ${c}_{p0}=50$, ${p}_{0}=80$, $\phi =0.15$, $\theta =0.85$, $\gamma =200$, $\xi =1.8$, $\zeta =0.001$, $\eta =50$, $\delta =0.2,\sigma =0.2$ and the key vector as ${[{k}_{0}{k}_{1}{k}_{2}{k}_{3}{k}_{4}{k}_{5}]}^{T}={[0.5, 0.75, 1, 1.25, 1.5, 1.75]}^{T}$,where ${k}_{i}(i=\mathrm{0,1}, \mathrm{2,3},\mathrm{4,5})$ are the corresponding keys for the fuzzy lock values of selling price, production cost, preservation cost, holding cost, setup cost and deterioration cost, respectively. Also, taking ${k}_{0}={k}_{1}={k}_{2}={k}_{3}={k}_{4}={k}_{5}=1$ the model is reduced to the corresponding general fuzzy model.

The optimum value of the objective function ${TAP}^{*}$ and the values of the decision variables.

${T}_{1}$, $T$, ${I}_{max}$ and $\alpha$ for the above-mentioned models are given in Table 2.

Table 2 Optimal solution for different models under crisp and fuzzy system

Table 2 gives the optimal results of the proposed model under various scenarios. Throughout the whole table, we see the profit value becomes maximum for the model where all the unit costs as well as unit selling prices are assumed to be lock fuzzy parameters. The range of maximum inventory lies within [105.93, 108.78] units with respect to the production time period zone [1.92, 2.14] months and the cycle time interval [3.015, 3.306] months, respectively. The crisp model is much inferior to all other submodels.

6 Sensitivity analysis

For sensitivity analysis, we consider the model-C with lock fuzzy approach which has given maximum total average profit compared to other models discussed in this study. In Table 3, the changes of the optimal value of total average profit along with the decisions variables with respect to the change (− 30% to + 30%) in value of the key vector for optimal solution are presented.

Table 3 Sensitivity analysis for the model-C (% changes in the value of key vector)

Table 3 indicates that whenever a positive change up to + 30% is performed the average profit value increases up to + 16.04% and that decreases up to -30%, then the profit value reaches to + 59.79% more with respect to the crisp optimal solution. The values of the other decision variables like maximum inventory, production run time and cycle time get around 105.95 units, 1.92 months and 3.015 months, respectively.

Also, we perform a sensitivity analysis of the same Model- C by considering the individual change of the keys and it is presented in Table 4.

Table 4 Sensitivity of the objective function with the changes of individual keys

From the sensitivity analysis as shown in Table 4, it is seen that the key vector ${( k}_{0} , {k}_{4} \,and\, {k}_{5} )$ is highly sensitive for the profit function that enhances the range 20.12% to 51.62% exclusively. For the keys${k}_{1}\;and\; {k}_{3}$, no feasible solution is obtained for the changes + 10% to + 30% alone, and whenever the key ${k}_{2}$ assumes a change − 30% to − 20%, the value of the profit function has also no feasible solution; the other cases give high sensitivity of the profit function explicitly. The values of the other decision variables are kept almost same as per Table 3.

However, we may perform a sensitivity analysis for non- fuzzy parameters which is stated in Table 5.

Table 5 Sensitivity analysis for non-fuzzy parameters

In Table 5, we see that all the nonfuzzy parameters have restricted feasible zone for which the profit function has no feasible solutions. For the initial demand parameter $\gamma ,$ no feasible zone is the change + 10%, + 30% and −30%; the parameter $\xi$ has no feasible zone within the change interval (−30% to + 20%); the parameter $\zeta$ has no feasibility at + 10% change;$\eta$ has nonfeasibility in the change range (−30% to −20%); and finally, the parameter $\delta$ has nonfeasibility at −10% and −30%, respectively. The maximum profit in such cases may be hiked from 0.42% to 89.7%; the maximum inventory enhances from 67.76 to 157.76 units; the production run time assumes values within 1.126–2.876 months, and the cycle time gets the value range 1.904–4.239 months, respectively. The overall study indicates that, in most of the cases, the profit function increases around (20–40) %.

7 Graphical illustrations

In this section, we shall discuss several graphical representations.

In Fig. 3, a comparison on the optimal value of the total average profit for different models under crisp and fuzzy (both general and lock) is presented. Here we see that the crisp model has profit value near $7400; for Model -A, the gap between general fuzzy and the lock fuzzy result covers around $ 1200; for Model B, that gap also reaches to $ 400 approximately; and finally for model-C, it becomes around $ 2000 keeping the highest peak over all the graphs.

Fig. 3

Optimal solution or models under crisps and fuzzy system

Figure 4 shows the change of total average profit with respect to the change (−30% to + 30%) of the key vector with respect to the base values. The lower values of the keys give the higher values of the profit function; around the changes (−10% to + 10%) the profit curve has a sudden fall, but after that the curve gets horizontal for further changes of the keys.

Fig. 4

Variation in total average profit ($) with respect to the change of the key vector

From Fig. 5 and Fig. 6, we see the changes of the total average profit and the maximum inventory level with respect to variation in cycle time, respectively.

Fig. 5

Cycle time (T) vs total average profit (TAP)

Fig. 6

Cycle time (T) vs maximum inventory level

In Fig. 5, if we consider the cycle time more than 3.487 months, then the average profit of the model will be always up but within the time span 2.238 to 3.487 months the profit modes around $9500. At 2.069 months of cycle time, the profit decreases to $ 7500 and the time around 2.069 months the profit function gets a ‘V’ shape.

If we see Fig. 6, then we notice that the amount of maximum inventory curve is becoming a monotonic increasing starting from the cycle time 2.069 months with inventory level 70 units on wards. But below that cycle time the inventory level curve gets a decreasing function with bounds (65–80) units exclusively.

Figure 7 expresses a cap like three-dimensional surface representation of the maximum inventory level under the variation in cycle time and the production run time. It is observed that low production run time and high cycle time correspond to the maximum inventory level. But low production run time and low cycle time are associated with low inventory level.

Fig. 7

Maximum inventory level vs cycle time ($T$) and production time (${T}_{1}$)

Figure 8 represents a surface like structure of the average inventory profit over the variation in production run time and cycle time. If the production run time assumes value around 2 months and the cycle time assumes value near 3 months, then the average inventory profit becomes minimum. Lower production run time and lower cycle time are also giving the minimum profit, but all other cases always give higher inventory profit alone.

Fig. 8

Total profit ($) vs cycle time ($T$) and production time (${T}_{1}$)

The relational dependency of the maximum inventory level and the total average profit with respect to the cycle time and aspiration level are shown in Fig. 9 and Fig. 10, respectively. Figure 9 gives a spoon-like surface structure; the higher aspiration level (cases of strong fuzzy numbers) and lower cycle time are becoming a part of higher inventory level. A sudden slope has been occurred if the cycle time assumes value within the range 3–4.5 months.

Fig. 9

Maximum inventory level vs cycle time ($T$) and aspiration level

Fig. 10

Total profit vs cycle time ($T$) and aspiration level

Figure 10 discusses a spoon like surface where the changes of average inventory profit are taken care of with respect to the change of aspiration level and the cycle time. The overall profit due to all strong aspiration level becomes within the range $(13,000–14,000). Taking the cycle time within 1.5–2.5 months, the profit value runs across lower to higher then higher to lower (taking range $7000–11,000) for increasing aspiration levels explicitly.

8 Conclusion

We have studied a deteriorated EPQ model with unit selling price and stock-sensitive demand under the maintenance of preservation technology and fuzzy systems. The novelty of this article is that we have considered a new demand function which is the functions of unit selling price and stock of items and the production rate itself is stock sensitive simultaneously. Then, we extend its basic structures into fuzzy environments. Our findings reveals that the lock fuzzy approach is an intelligent approach with respect to the traditional crisp and fuzzy approaches, respectively, when the unit selling prices and all cost components are assumed to be lock fuzzy numbers. However, the managerial insights are stated as follows:

• a) Higher aspiration level and higher cycle time might give more profit and more stock of the model

• b) More production run time and low cycle time give more profit and more stock.

• c) Lock fuzzy system is the more appropriate approach to follow all the time.

• d) Crisp parameters are highly sensitive. So cares should always be taken.

• e) General fuzzy system is better but not the best with respect to crisp model.

• f) Selling prices and cost prices have to be taken as fuzzy parameters.