1 Introduction

Here, we hall discuss literature study into two different subsections, namely general overview and the motivation and specific study and they are given below.

1.1 General overview

In any production management process, disruption in supply is a natural fact due to machine break downs, labour strikes or quality problems. Also, issues of reliability are an essential part of any production management process. Process reliability and system reliability are two types of reliability which are commonly viewed in any production process. Reliability equation for an inventory problem and its asymptotic solutions was studied by Prekopa (1965). Prekopa and Kelly (1978) discussed a reliability-based inventory model using stochastic programming. Cheng (1989) considered an economic production quantity (EPQ) model with flexibility and reliability. Cheng (1991) discussed an economic production quantity model with process reliability and quality assurance. Tripathy et al. (2003) considered process reliability measure in developing economic order quantity (EOQ) model. Chakraborty et al. (2008) discussed about process deterioration and machine breakdown. He and He (2010) made a production model for deteriorating inventory with production disruptions. A generalized geometric programming problem of an economic production quantity model with flexibility and reliability is considered by Leung (2007). Panda and Maiti (2009) made a geometric programming approach to solve multi-item inventory model with price dependent demand under flexibility, reliability and imprecise space constraint.

However, some eminent researchers like Sana (2010), Tripathy and Pattnaik (2011) etc. worked with EPQ inventory models on reliability in an imperfect production system. Louit et al. (2011) described optimization models for critical spare parts inventories. A study of repairable parts inventory system operating under performance-based contract was discussed by Mirzahosseinian and Piplani (2011). EPQ model for deteriorating inventory with random machine unavailability and shortage was studied by Chung et al. (2011). Glock (2013) analysed machine breakdown random shifts in the production rate with increasing profit. A literature review on inventory modelling with reliability measures was discussed by Ahmed and Sultana (2014). Simultaneous determination of production lot size and process parameters under process deterioration and process breakdown was studied by Jeang (2012). Lin and Chang (2012) developed system reliability of a manufacturing network with reworking action and different failure rates. Wee and Widyadana (2012) worked with various types of EPQ models for deteriorating items with rework and stochastic preventive maintenance time. Widyadana and Wee (2012) discussed an economic production quantity model for deteriorating items with preventive maintenance policy and random machine breakdown. Huang et al. (2017) made an unreliable production system with endogenous reliability and product deterioration.

However, to study with uncertain system we must rely on the fuzzy system developed by Zadeh (1965). A procedure for ordering fuzzy subsets of the unit interval was introduced by Yager (1981). A production inventory model with fuzzy random demand and with flexibility and reliability considerations was made by Bag et al. (2009). Fuzzy parametric geometric programming approaches was considered by Mahapatra et al. (2012) to solve a fuzzy EPQ model under flexibility and reliability. De and Beg (2016) introduced the dense fuzzy sets and its new defuzzification methods to measure the learning experiences of decision maker. De (2017) gave another more significant characterization of the fuzzy sets in the name of triangular dense fuzzy lock sets. After this invention Karmakar et al. (2017) first discussed the robust application of dense fuzzy lock set in pollution sensitive EPQ model. Recently, De and Mahata (2019) developed a production inventory supply chain model with partial backordering and disruption under triangular linguistic dense fuzzy lock set approach.

1.2 Motivation and specific study

Game Theory is another approach of getting decision of any production management problem. We know, in the present scenario, marketing of finished products has become one of the most vital issues in the field of industrial production process and it has not been grown up by the researchers in a deep way. If we look at the competitive market very closely, then we see that the producer usually wants to sell the product to their customers at a higher profit and the customers want to buy more products at the lowest possible price. Customer and producer each apply different strategies for their own benefit. Thus, game theory is one of the best ways to explain this competitive situation in real life through fuzzy mathematical models. A game is defined by a set of players (in this case producer or customers) and their possibilities to play the game according to some rules which are often called the set of strategies. The result of the game for a particular player does not depend only on his own decisions, but also on the behaviour as well as strategies of the other players. Now, the decision maker wants to minimize the annual average cost without perceiving what the customers want to get the actual demand. But the production can be controlled by controlling several cost components of the entire production process. On the other hand, the customers are trying to get more benefit from producers by means of availing quality goods. For these points of view, we have incorporated game theory in our model and applied it for cost optimization in inventory management system.

Although, Fuzzy game theoretic approach is the modern trends to solve a production management problem instead of traditional game theory. Several research articles have been found in these directions. Preda (1989) established the relationship between convex optimization and matrix game equivalence. Arfi (2006) discussed a new part of game theory which is known as Linguistic fuzzy-logic game theory. A new approach for the solution of fuzzy games is developed by eminent researchers like Thirucheran et al. (2017), Krishnaveni and Ganesan (2018). Researchers like Metzger and Rieger (2019), Song and Gao (2018) discussed about non-cooperative games with dominated strategies and solved various types of green supply chain game models. De et al. (2020) solved an EPQ model of defective production process by neutrosophic fuzzy approach using game theory.

On the other hand, environmental pollution is a very important issue in any industrial set up recent times. We know that any industry requires a lot of heat to produce items which in most cases are generated from the combustion of fossil fuels. But, during combustion huge amounts of toxic gases such as Carbon dioxide, Carbon Monoxide, Sulphur dioxide, Nitrogen dioxide etc. release and began to add into the atmosphere. Moreover, industrial wastes are not being recycled due to lack of proper planning. So, they lying free days after day in the environment and are polluting various lands, canals and water bodies. As a result, with the growth of the industrial zone, the surrounding environment is being polluted excessively. Due to this pollution, global warming takes place and consequently various diseases of the human body (lungs, kidneys, heart, etc.) spread easily. Realizing the harmful effect of pollution most of the industries are currently considering pollution reduction measure as an important parameter in their production–transportation models.

Several researchers have worked with the policies of carbon cap taxation or carbon footprint. Wiedmann and Minx (2008) gave a new definition of carbon footprint in environment. Benjaafar et al. (2010) discussed the management of carbon footprint in the light of some different types of inventory models. A noble carbon-constrained EOQ model was developed by Chen et al. (2013). Rao et al. (2014) analysed the amount of air pollution and corrosion from various buildings and historical structures. Xu et al. (2016) discussed about the decision making in the multi staged production house under the effect of carbon tax regulations. Aarthi (2017) reviewed the facts of air pollution in various iron industries extensively. Akten and Akyol (2018) worked on environmental pollution to reduce the amount of carbon. Aljazzar et al. (2018) developed a novel strategy to decrease the carbon emissions in supply chains using delay-in-payment method. Ciardiello et al. (2018) analysed pollution responsible-based allocations in a supply network with the help of game theory. Chunhai et al. (2020) solved a useful inventory problem for the deteriorating items under the effect of carbon emissions. Bhattacharya and De (2020) developed a two-layer pollution-based SC model by fuzzy game theory. De et al. (2021) solved a pollution-based SC model under the effect of fuzzy approximate reasoning. Beyond this, some major literature reviews of the related domain have been presented in Table 1 given below.

Table 1 Some major literature reviews on related domain
Full size table

From the above study, it is seen that none of the researchers have been studied with the EPQ model for process reliability in machine breakdown under lock fuzzy environment. In this article, we show the role of key vectors whose proper application may change the average expenditure of a production management system. The schematic diagram of the proposed model is given in Fig. 1. This article is organised as follow: Sect. 1 includes introduction that splits into two subsections namely general overview and specific study, Sect. 2 discusses preliminary concepts. Section 3 explains some notations and assumptions, Sect. 4 includes a real case study and research problem, Sect. 5 develops crisp mathematical modelling, Sect. 6 discusses lock fuzzy game problem. Section 7 corresponds a numerical illustration, Sect. 8 analyses the graphical illustrations and finally Sect. 9 makes a concluding remark followed by scope of future work.

Fig. 1
figure 1

Schematic diagram of the proposed model

Full size image

2 Preliminaries

Here, we present the formation of pollution function, concepts of game theory, triangular fuzzy lock set and Gaussian normality in different subsections which will be used in developing the proposed model.

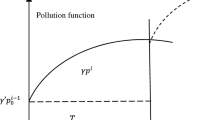
2.1 Pollution function (extension of Karmakar et al. (2017))

From the analysis of the modified Lotka-Volterra predator–prey model [by Doust and Gholizade (2014)] we see that if coexistence of predator and prey is not possible then both the predator and prey will extinct from the world. In this model, there are two basic assumptions which are as follows: one is the prey will extinct if and only if these are eaten by predator and the another is the predator will continue to decrease due to natural causes. Now inspiring from Karmakar et al. (2017) we want to extend the idea of predator–prey model to pollution-production relationship in production inventory system. If we look closely at the reality, we can see that there are many similarities between the predator–prey model and the pollution-production model. We consider the environmental pollution arising from production as predator and the production system as prey. Some factors are responsible for this consideration and they are as follow:

  1. (i)

    In absence of environmental pollution, the rate of production will decrease exponentially with the maximum consuming capacity of the customers.

  2. (ii)

    The production rate will drop slowly due to the unavailability of raw materials from the putrefying environmental resources or pollutant environment.

  3. (iii)

    In the absence of production, the pollution rate decreases proportionally and increases exponentially with the presence of production itself.

Combining these factors assuming the production rate (per month) be P and the pollution rate be Y, we can construct the governing differential equation of pollution-production rate as follow:

$$ \left\{ \begin{gathered} \dot{P} = aP - rP^{2} - \alpha PY,\;a,\;r,\;\alpha > 0 \hfill \\ \dot{Y} = - cY + \gamma PY,\;c,\;\gamma > 0 \hfill \\ \end{gathered} \right. $$
(1)

where it is assumed that, the production rate will decrease slowly for shortage of raw materials that are coming from exhaustion of natural resources. Also, without production, the pollution level decreases proportionally.

Now, to solve (1), utilizing the theories of differential equations, we obtain the critical points \(\left(\mathrm{0,0}\right), \left(\frac{{a}^{^{\prime}}}{r},0\right)\;and\;\left(\frac{c}{\gamma },\frac{{a}^{^{\prime}}\gamma -cr}{\alpha \gamma }\right),\) respectively, with the associated Jacobian \(J\left[P,Y\right]=\left[\begin{array}{cc}{a}^{^{\prime}}-2rP-\alpha Y& -\alpha P\\ \gamma Y& -c+\gamma P\end{array}\right]\). Here, the Jacobian \(J[\mathrm{0,0}]\) is unstable. \(J[\frac{{a}^{^{\prime}}}{r},0]\) is stable if\(\frac{\alpha }{c}<\frac{r}{\gamma }\). The Jacobian \(J\left[\frac{c}{\gamma },\frac{{a}^{^{\prime}}\gamma -cr}{\alpha \gamma }\right]\) is stable as it has two imaginary eigen values with negative real parts. Since our motive is to minimize pollution with optimal production, so we select the critical point\(\left(\frac{{a}^{^{\prime}}}{r},0\right)\). At the point\(\left(\frac{{a}^{^{\prime}}}{r},0\right)\), \(p=\frac{{a}^{^{\prime}}}{r},Y=0.\) The two equations in (1) can be combined as \( \left( {\frac{{a^{\prime } }}{P} - r} \right)\dot{P} + \dot{Y} = \left( {a^{\prime } - rP} \right)\left( {a^{\prime } - \dot{r}\dot{P} - \alpha Y} \right) + \left( { - cY + \gamma PY} \right) \)

Putting \(P=\frac{{a}^{^{\prime}}}{r}, Y=0\), the above equation becomes \(\left(\frac{{a}^{^{\prime}}}{P}-r\right)\dot{P}+\dot{Y} = 0\)

Integrating we get \({a}^{^{\prime}}\mathrm{log}P-rP+Y={c}^{^{\prime}}(constant)\)

However, we reset \({a}^{^{\prime}}, r\) and \({c}^{^{\prime}}\) in such a way that our study data satisfies the above equation and the pollution rate gets values near permissible limit under maximum production rate. This is only possible when we take \({a}^{^{\prime}}=0.45, r=0.01,{ c}^{^{\prime}}=0.25\) and get the functional dependence of amount of pollution Y (%) with the production rate P in metric tonnes (MT) per time under pollution control measures and it is given by

$$Y = 0.45 + 0.01\;P - 0.25\;{\text{log}}\left( P \right)$$
(2)

2.2 Concept of game theory

Definition 1

A game \(G\) consists of a set of players (leaders/agents) \(M=\left\{1, 2,...,m\right\},\) an action set denoted by \({\Omega }_{i}\) (also referred to as a set of strategies\({S}_{i}\)) available for each player i and an individual payoff (utility) \({U}_{i}\) or cost function \({T}_{i}\) for each player\(i\in M\). Here, each player individually takes an optimal action which optimizes its own objective function and each player’s success in making decisions depends on the decisions of the others. We define a non-co-operative game \(G\) as an object specified by\((M, S, \Omega , T)\), where \(S={S}_{1}\times {S}_{2}\times ....\times {S}_{m}\) is known as the strategy space, \(\Omega ={\Omega }_{1}\times {\Omega }_{2}\times ....\times {\Omega }_{m}\) is the action space, and\(T: \Omega \to {\mathbb{R}}^{m}\), defined as \(T(u)={\left[{T}_{1}(u), {T}_{2}(u), ..., {T}_{m}(u)\right]}^{T}, u\in \Omega \) is the vector of objective functions associated to each of the m players, or agents participating in the game. In some cases, a graph notation might be more appropriate than the set M notation. Conventionally T represents a vector of cost functions to be minimized by the agents.

Definition 2

Let the strategies of player 1 be \(S=({s}_{1},{s}_{2},\dots .,{s}_{m})\) and that of player 2 be \(T=({t}_{1},{t}_{2},\dots .,{t}_{n})\) having the payoff matrix \(A=\left(\begin{array}{c}\begin{array}{ccc}{a}_{11}& {a}_{12}& \begin{array}{cc}\dots & {a}_{1n}\end{array}\end{array}\\ \begin{array}{ccc}{a}_{21}& {a}_{22}& \begin{array}{cc}\dots & {a}_{2n}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{ccc}\vdots & \vdots & \begin{array}{cc}\vdots & \vdots \end{array}\end{array}\\ \begin{array}{ccc}{a}_{m1}& {a}_{m2}& \begin{array}{cc}\dots & {a}_{mn}\end{array}\end{array}\end{array}\end{array}\right)\) with probability space \((p, q)\) such that \(p=({p}_{1},{p}_{2},....,{p}_{m}); {p}_{i}\ge 0, {p}_{1}+{p}_{2}+....+{p}_{m}=1\) and \(q=({q}_{1},{q}_{2},....,{q}_{n}); {q}_{i}\ge 0, {q}_{1}+{q}_{2}+....+{q}_{n}=1\). Here, \({p}_{j}({q}_{j})\) expresses the probability of choosing the j-th strategy from the strategy space S(T). Then, the expected payoff is defined by the relation: \(\pi (p,q)=\sum_{i=1}^{m}\sum_{j=1}^{n}{p}_{j}{q}_{j}{a}_{ij}\).

2.3 Triangular fuzzy lock set (De 2017)

Definition 3

Let the triangular fuzzy number \(\widetilde{A}=\langle a\left\{1-\rho {f}_{n}\right\},a,a\left\{1+\sigma {g}_{n}\right\}\rangle \) for \(0<\rho , \sigma \in {\mathbb{R}}\) and\({f}_{n}\), \({g}_{n}\) are two Cauchy sequences of functions having converging points \(\frac{1}{{k}_{1}}\) and \(\frac{1}{{k}_{2}}\),\(0\ne {k}_{1},{k}_{2}\in {\mathbb{R}}\), respectively, then the fuzzy set \(\widetilde{A}\) is called triangular fuzzy lock set with double keys \({k}_{1}\) and\({k}_{2}\), and they depend upon \(\rho \) and\(\sigma \), respectively. The corresponding membership function of \(\widetilde{A}\) is defined by.

$$ \mu (x,n) = \left\{ {\begin{array}{*{20}c} {0\;{\text{if}}\;x < a\left\{ {1 - \rho f_{n} } \right\}{\text{or}}\;x > a\left\{ {1 + \sigma g_{n} } \right\}} \\ {\frac{{x - a\left\{ {1 - \rho f_{n} } \right\}}}{{a\rho f_{n} }}{\text{if}}\;a\left\{ {1 - \rho f_{n} } \right\} \le x \le a} \\ {\frac{{x - a\left\{ {1 - \rho f_{n} } \right\}}}{{a\rho f_{n} }}{\text{if}}\;a \le x \le a\left\{ {1 + \sigma g_{n} } \right\}} \\ \end{array} } \right. $$
(3)

2.4 Gaussian normality

We know that most of the physical phenomenon follow the Gaussian distribution. So, we assume the strategic probability of game players follow Gaussian probability curve of the form

$$y(x)=\frac{1}{\sqrt{2\pi }}{e}^{\frac{-{x}^{2}}{2}}$$
(4)

We generally take the first, second, third quartiles of \(y(x)\) as \({p}_{1}, {p}_{2}, {p}_{3}\) for player 1 and \({p}_{1}^{\prime}, {p}_{2}^{\prime}, {p}_{3}^{\prime}\) for player 2, respectively. The graphical illustration is shown in Fig. 2.

Fig. 2
figure 2

Gaussian Normality

Full size image

3 Notation and assumptions

3.1 Notations

We define the following notations:

\(D\) :

Demand rate per unit time.

K :

Fixed production rate for zero pollution.

P :

Initial production rate (P > K).

T :

Production time.

s :

Breaking time point.

\({T}_{m}\) :

The time when inventory level drops to zero.

h :

Inventory holding cost per unit item per unit time.

A :

Fixed set up cost per cycle

\({c}_{d}\) :

Deterioration cost per unit item per unit time.

\({c}_{R}\) :

Risk cost per unit item per cycle.

\(\alpha \) :

Restoration rate of production process, so failure rate becomes \((1-\alpha )\)

\({M}_{0}\) :

The maximum restoration cost per cycle.

M :

Restoration cost per cycle (the cost requires to recover the system failure); so, we define \(M={M}_{0}(1-\alpha )\).

\({\lambda }_{0}\) :

The initial reliability parameter.

\({\lambda }_{1}\) :

The final reliability parameter.

\(\lambda \) :

Unit time investment cost ($) to increase reliability parameter.

\(\theta \) :

Deterioration rate per unit time per unit item.

\(\delta \) :

Scale parameter.

Y :

Pollution rate (%).

Q :

Maximum order quantity.

3.2 Basic assumptions

  1. (i)

    Let us consider a single-product production system in which the production process drops to a lower level.

  2. (ii)

    By investment, the expected shifting time can be prolonged, so as to increase the reliability of the system. Let us assume the unit time investment cost (\(\lambda \)) function to increase the process reliability from \({\lambda }_{0}\) to \({\lambda }_{1}\) as \({\lambda }_{1}={\lambda }_{0}+\frac{\delta \lambda }{\lambda +1}\) which gives \(\lambda =\frac{{\lambda }_{1}-{\lambda }_{0}}{\delta -{\lambda }_{1}+{\lambda }_{0}}\) ,\({\lambda }_{1}\in [{\lambda }_{0},\infty )\).

  3. (iii)

    In control state, the production line is reliable with a constant production rate P. In the out-of-control state, the production rate drops to \(\alpha P (D>\alpha P)\). The breaking time point \(s\) is a finite number.

  4. (iv)

    Demand rate D is constant per unit time.

  5. (v)

    Initial production rate P(> D) is constant per unit time.

  6. (vi)

    Production line cannot be restored during the production run.

  7. (vii)

    When production run ends, a fixed cost is paid to restore the production system.

  8. (viii)

    The restoration time is zero so that the damage of the production line has no effect to the production of the next period.

  9. (ix)

    The parameters like production rate (P), demand rate (D) and all the cost components are assumed to be lock fuzzy numbers.

4 Case study and problem definition

We visited a Semi-Government controlled spinning factory who are producing yarn for regional needs, situated at Midnapore town, West Bengal, India [(Latitude, Longitude) = (22.415280, 87.325320), GPS Co-ordinates (22° 24′ 55.008'' N, 87° 19′ 31.152'' E)]. After long discussions with the manager, we came to know that the factory is running with a marginal profit and the management is trying to minimize their monthly expenditure. The produced items are packed and is being exhausted due to demand and deterioration. From the past experience, it is observed that few products get deteriorated with a constant rate. However, two scenarios may come where with and without system failures occur during the production run time. For without system failure (in-control-state) the production rate is always greater than the normal demand rate. But, in out-of- control state the demand rate exceeds the production rate. Indeed, the possibility of having greater production rate than normal demand rate in out-of-control state of the production process has not appeared yet because of production sustainability. We also notice that there are six kinds of costs, namely holding cost, fixed set up cost, restoration cost, deterioration cost, reliability investment cost and risk cost due to pollution on over production involved in the process (shown in Table 2). The monthly needs of yarn are 1400 packets. The monthly production of yarn is more or less 1500 packets.

Table 2 Values of system parameters
Full size table

Moreover, after talking with the manager, we also came to know that this factory requires the burning of fossil fuels to regulate the production of the factory and for over production they carry some pollution cost in the name of risk cost. Therefore, the following research problem may be put over here. Also, the data obtained from this study has been put in Table 2.

  1. (i)

    What will be the optimum production run /breaking time and optimum cycle time so as to minimize the system cost?

  2. (ii)

    How much amount of quantity to be produced such that the average inventory cost will be minimum?

  3. (iii)

    How much pollution can be controlled by applying best strategy?

  4. (iv)

    How much production failure rate (process reliability) can be controlled?

  5. (v)

    What is the best strategy for which the system cost can be reduced?

5 Formulation of crisp mathematical model

Here, we shall formulate the mathematical model in two different scenarios.

5.1 Scenario 1. No failure during the production run.

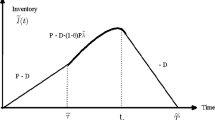
Let the production process starts with zero stock and production rate P. During the production run time \(T\), the inventory level gradually increases at a rate P and it reaches its maximum value at the end of time \(T\) and the production stops. The inventory depletes due to normal demand rate D and the deterioration \(\theta \) throughout the cycle time \({T}_{m}\). The graphical representation of the model is given in Fig. 3 and the governing differential equation of the problem is given below.

Fig. 3
figure 3

Production run without failure

Full size image
$$ \left\{ \begin{gathered} \frac{{d(I(t))}}{{dt}} = \left\{ {\begin{array}{*{20}c} {P - D - \theta I(t),0 < t < T} \\ { - D - \theta I(t),T < t < T_{m} } \\ \end{array} } \right. \hfill \\ {\text{subject\;to}},\;I(0) = I(T_{m} ) = 0 \hfill \\ \end{gathered} \right. $$
(5)

Now, solving the Eq. (5) we can get the inventory level at any time t as follows.

$$I(t)=\left\{\begin{array}{c}\frac{P-D }{\theta }\left(1-{e}^{-\theta t}\right), 0<t<T\\ \frac{D }{\theta }\left({e}^{\theta \left({T}_{m}-t\right)}-1\right), T<t<{T}_{m}\end{array}\right.$$
(6)

The total inventory cost (\({TC}_{1}(T)\)) for the cycle time \({T}_{m}\) consists of inventory holding cost, set up cost, deterioration cost, reliability investment cost and risk cost due to pollution by over production and it is given by.

\({TC}_{1}(T)=\) Inventory holding cost + Set up cost + Deterioration (total production-total demand) cost + Reliability investment + Risk cost due to pollution

$$ \begin{gathered} = \left\{ {h\mathop \int\limits_{0}^{T} I\left( t \right)dt + h\mathop \int \limits_{T}^{{T_{m} }} I\left( t \right)dt} \right\} + \left\{ A \right\} + \left\{ {c_{d} \left( {PT - DT_{m} } \right)} \right\} + \left\{ {\lambda T_{m} } \right\} + \left\{ {c_{R} \left( {1 - \frac{K}{P}} \right)} \right\} \hfill \\ = h\mathop \int \limits_{0}^{T} \frac{P - D }{\theta }\left( {1 - e^{ - \theta t} } \right)dt + h\mathop \int \limits_{T}^{{T_{m} }} \frac{D }{\theta }\left( {e^{{\theta \left( {T_{m} - t} \right)}} - 1} \right)dt + A + \left( {PT - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ = h\frac{P - D }{\theta }\left[ {t + \frac{{e^{ - \theta t} }}{\theta }} \right]_{0}^{T} + h\frac{D }{\theta }\left[ {\frac{{e^{{\theta \left( {T_{m} - t} \right)}} }}{ - \theta } - t} \right]_{T}^{{T_{m} }} + A + c_{d} \left( {PT - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ = h\frac{P - D }{\theta }\left[ {T + \frac{{e^{ - \theta T} }}{\theta } - \frac{1 }{\theta }} \right] + h\frac{D }{\theta }\left[ { - \frac{1}{\theta } - T_{m} + \frac{{e^{{\theta \left( {T_{m} - T} \right)}} }}{\theta } + T} \right] + A + c_{d} \left( {PT - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ = \frac{{h\left( {P - D} \right)}}{{\theta^{2} }}\left[ {\theta T + e^{ - \theta T} - 1} \right] + \frac{hD}{{\theta^{2} }}\left[ {e^{{\theta \left( {T_{m} - T} \right)}} - \theta \left( {T_{m} - T} \right) - 1} \right] + A + c_{d} \left( {PT - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ \end{gathered} $$
(7)

and from the continuity of \(I(t)\) at \(t=T\) we can find the cycle time \({T}_{m}\) as

$$ T_{m} = \frac{1}{\theta }\ln \left[ {\frac{{P - D}}{D}\left( {1 - e^{{ - \theta T}} } \right) + 1} \right] + T $$
(8)

Therefore, the total average inventory cost is

$$w=\frac{{TC}_{1}(T)}{{T}_{m}}$$
(9)

Hence, the problem of optimization is given by

$$\left\{\begin{array}{l}\mathrm{Minimize}\, w=\frac{{TC}_{1}\left(T\right)}{{T}_{m}}\\ \begin{array}{l}\mathrm{Subject\, to}, {T}_{m}=\frac{1}{\theta }\mathit{ln}\left[\frac{P-D}{D}\left(1-{e}^{-\theta T}\right)+1\right]+T \\ {TC}_{1}= h\left\{\frac{P-D}{{\theta }^{2}}\left[\theta T+{e}^{-\theta T}-1\right]+\frac{D}{{\theta }^{2}}\left[{e}^{\theta \left({T}_{m}-T\right)}-\theta \left({T}_{m}-T\right)-1\right]\right\}\\ \quad +A+{c}_{d}\left(PT-D{T}_{m}\right)+\lambda {T}_{m}+{c}_{R}\left(1-\frac{K}{P}\right) \end{array} \\ \begin{array}{l}Y=0.45+0.01P-0.25\mathit{ln}P, {T}_{m}>\mathrm{T}\\ Q=\frac{D\left({e}^{\theta \left({T}_{m}-T\right)}-1\right)}{\theta }\end{array}\end{array}\right.$$
(10)

5.2 Scenario 2. Failure occurs during production run

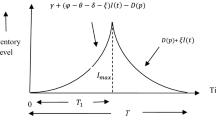
Let the production process starts with zero inventories with production rate P. The production run time is . Production rate in the time interval [0,\(s\)] is P, and that for time interval [\(s, T\)] is \(\alpha P\), where \(\alpha \) is the restoration rate of production process. Inventory level gradually increases and it reaches its maximum value at the end of time\(s\). After the time T, the production stops. The inventory depletes due to normal demand rate D and deterioration \(\theta \) throughout the cycle time\({T}_{m}\). The graphical representation of the problem is shown in Fig. 4 and the governing differential equation of the problem is given below.

Fig. 4
figure 4

Production run with failure

Full size image
$$ \left| {\left\{ \begin{gathered} \frac{{d(I(t))}}{{dt}} = \left\{ {\begin{array}{*{20}c} {P - D - \theta I(t),0 \le t \le s} \\ {\alpha P - D - \theta I(t),s \le t \le T} \\ { - D - \theta I(t),T \le t \le T_{m} } \\ \end{array} } \right. \hfill \\ {\text{subject}}\;to,\;I(0) = I(T_{m} ) = 0 \hfill \\ \end{gathered} \right.} \right. $$
(11)

Now, solving the Eq. (11) we can find the expression of the inventory level at any time t as

$$ I\left( t \right) = \left\{ \begin{gathered} \frac{{P - D}}{\theta }\left( {1 - e^{{ - \theta t}} } \right),0 \le t \le s \hfill \\ \frac{{\alpha P - D}}{\theta } + \left[ {\frac{{\left( {1 - \alpha } \right)P}}{\theta }e^{{\theta s}} - \frac{{P - D}}{\theta }} \right]e^{{ - \theta t}} ,s \le t \le T \hfill \\ \frac{D}{\theta }\left( {e^{{\theta \left( {T_{m} - t} \right)}} - 1} \right),T \le t \le T_{m} \hfill \\ \end{gathered} \right. $$
(12)

The total inventory cost (\({TC}_{2}(T,s)\)) consists of holding cost, set up cost, deterioration cost, restoration cost, reliability investment cost and risk cost due to over production and it is given by.

\({TC}_{2}(T,s)=\) Inventory holding cost + Set up cost + Restoration cost + Deterioration (Total production-total demand) cost + Reliability investment + Risk cost due to pollution

$$ \begin{gathered} = \left\{ {h\mathop \int \limits_{0}^{s} I\left( t \right)dt + h\mathop \int \limits_{s}^{T} I\left( t \right)dt + h\mathop \int \limits_{T}^{{T_{m} }} I\left( t \right)dt} \right\} + \left\{ A \right\} + \left\{ M \right\} \hfill \\ \;\;\; + \left\{ {c_{d} \left( {Ps + \alpha P\left( {T - s} \right) - DT_{m} } \right)} \right\} + \left\{ {\lambda T_{m} } \right\} + \left\{ {c_{R} \left( {1 - \frac{K}{P}} \right)} \right\} \hfill \\ = h\mathop \int \limits_{0}^{s} \frac{{P - D~}}{\theta }\left( {1 - e^{{ - \theta t}} } \right)dt + h\mathop \int \limits_{s}^{T} \left\{ {\frac{{\alpha P - D}}{\theta } + \left[ {\frac{{\left( {1 - \alpha } \right)P}}{\theta }e^{{\theta s}} - \frac{{P - D~}}{\theta }} \right]e^{{ - \theta t}} } \right\}dt \hfill \\ \;\;\; + h\mathop \int \limits_{T}^{{T_{m} }} \frac{D}{\theta }\left( {e^{{\theta \left( {T_{m} - t} \right)}} - 1} \right)dt + A + M + c_{d} \left( {Ps + \alpha P\left( {T - s} \right) - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ = h\frac{{P - D~}}{\theta }\left[ {t + \frac{{e^{{ - \theta t}} }}{\theta }} \right]_{0}^{s} + h\left[ {\frac{{\alpha P - D}}{\theta }t + \left\{ {\frac{{\left( {1 - \alpha } \right)P}}{\theta }e^{{\theta s}} - \frac{{P - D~}}{\theta }} \right\}\frac{{e^{{ - \theta t}} }}{{ - \theta }}} \right]_{s}^{T} \hfill \\ \;\;\; + h\frac{D}{\theta }\left[ {\frac{{e^{{\theta \left( {T_{m} - t} \right)}} }}{{ - \theta }} - t} \right]_{T}^{{T_{m} }} + A + M + c_{d} \left( {Ps + \alpha P\left( {T - s} \right) - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ = h\frac{{P - D~}}{\theta }\left[ {s + \frac{{e^{{ - \theta s}} }}{\theta } - \frac{1}{\theta }} \right] + h\left[ {\frac{{\alpha P - D}}{\theta }T + \left\{ {\frac{{\left( {1 - \alpha } \right)P}}{\theta }e^{{\theta s}} - \frac{{P - D~}}{\theta }} \right\}\frac{{e^{{ - \theta T}} }}{{ - \theta }} - \frac{{\alpha P - D}}{\theta }s} \right. \hfill \\ \left. {\;\;\; - \left\{ {\frac{{\left( {1 - \alpha } \right)P}}{\theta }e^{{\theta s}} - \frac{{P - D~}}{\theta }} \right\}\frac{{e^{{ - \theta s}} }}{{ - \theta }}} \right] + h\frac{D}{\theta }\left[ { - \frac{1}{\theta } - T_{m} + \frac{{e^{{\theta \left( {T_{m} - T} \right)}} }}{\theta } + T} \right] \hfill \\ \;\;\; + A + M + c_{d} \left( {Ps + \alpha P\left( {T - s} \right) - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ = h\frac{{P - D~}}{{\theta ^{2} }}\left[ {\theta s + e^{{ - \theta s}} - 1} \right] + h\left[ {\frac{{\alpha P - D}}{\theta }\left( {T - s} \right) - \left\{ {\frac{{\left( {1 - \alpha } \right)Pe^{{\theta s}} - P + D}}{{\theta ^{2} }}} \right\}\left( {e^{{ - \theta T}} - e^{{ - \theta s}} } \right)} \right] \hfill \\ \;\;\; + h\frac{D}{{\theta ^{2} }}\left[ {e^{{\theta \left( {T_{m} - T} \right)}} - \theta \left( {T_{m} - T} \right) - 1} \right] + A + M + c_{d} \left( {Ps + \alpha P\left( {T - s} \right) - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ = ~h\left[ {\frac{{P - D}}{{\theta ^{2} }}\left\{ {\theta s + e^{{ - \theta s}} - 1} \right\} + \frac{{\alpha P - D}}{\theta }\left( {T - s} \right) - \frac{{\left( {1 - \alpha } \right)Pe^{{\theta s}} - P + D}}{{\theta ^{2} }}\left( {e^{{ - \theta T}} - e^{{ - \theta s}} } \right)} \right. \hfill \\ \left. {\;\;\; + \frac{D}{{\theta ^{2} }}\left\{ {e^{{\theta \left( {T_{m} - T} \right)}} - \theta \left( {T_{m} - T} \right) - 1} \right\}} \right] + A + M_{0} \left( {1 - \alpha } \right) + c_{d} \left( {Ps + \alpha P\left( {T - s} \right) - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ \end{gathered} $$
(13)

and from the continuity of \(I(t)\) at \(t=s, t=T\) we can find the cycle time \({T}_{m}\) as

$${T}_{m}=\frac{1}{\theta }\mathit{ln}\left[\frac{\alpha P-D}{D}+\frac{(1-\alpha )P}{D}{e}^{\theta (s-T)}-\frac{P-D}{D}{e}^{-\theta T}+1\right]+T$$
(14)

Thus, the total average inventory cost is

$$Z=\frac{{TC}_{2}(T,s)}{{T}_{m}}$$
(15)

Therefore, our optimization problem is given by

$$ \left\{ \begin{gathered} {\text{Minimize}}\;Z = \frac{{TC_{2} \left( {T,s} \right)}}{{T_{m} }} \hfill \\ {\text{Subject}}\;{\text{to}},T_{m} = \frac{1}{\theta }\ln \left[ {\frac{{\alpha P - D}}{D} + \frac{{(1 - \alpha )P}}{D}e^{{\theta (s - T)}} - \frac{{P - D}}{D}e^{{ - \theta T}} + 1} \right] + T \hfill \\ TC_{2} = h\left\{ {\frac{{P - D}}{{\theta ^{2} }}\left[ {\theta s + e^{{ - \theta s}} - 1} \right] + \frac{{\alpha P - D}}{\theta }\left( {T - s} \right)} \right. \hfill \\ \left. { - \frac{{(1 - \alpha )Pe^{{\theta s}} - P + D}}{{\theta ^{2} }}\left( {e^{{ - \theta T}} - e^{{ - \theta s}} } \right) + \frac{D}{{\theta ^{2} }}\left[ {e^{{\theta \left( {T_{m} - T} \right)}} - \theta \left( {T_{m} - T} \right) - 1} \right]} \right\} \hfill \\ + A + M_{0} \left( {1 - \alpha } \right) + c_{d} \left( {Ps + \alpha P\left( {T - s} \right) - DT_{m} } \right) + \lambda T_{m} + c_{R} \left( {1 - \frac{K}{P}} \right) \hfill \\ Y = 0.45 + 0.01P - 0.25\ln P,T_{m} > T,T > s \hfill \\ Q = \frac{{\left( {P - D} \right)\left( {1 - e^{{ - \theta s}} } \right)}}{\theta } \hfill \\ \end{gathered} \right. $$
(16)

6 Formulation of game problem using triangular lock fuzzy set

Here, we consider the production inventory process in Scenario 2. Let the decision maker wants to minimize his average inventory cost without knowing the demand pattern of his customers. On the other hand, the customers are trying to get more benefit from this inventory by means of availing quality of goods/items. Now, the average inventory cost can be written as \(Z=f\left(P, D,{C}_{1}, {C}_{2}, {C}_{3}, {C}_{4}, {C}_{5}, {C}_{6}, T, {T}_{m}\right)\), where \(\left({C}_{1}, {C}_{2}, {C}_{3}, {C}_{4}, {C}_{5}, {C}_{6}\right)=\left(h, A, {M}_{0}, {c}_{d}, \lambda , {c}_{R}\right)\). Let us consider all the parameters associated to the production process are fuzzy numbers. Let the cost parameters \(\left({C}_{1}, {C}_{2}, {C}_{3}, {C}_{4}, {C}_{5}, {C}_{6}\right)=\left(h, A, {M}_{0}, {c}_{d}, {c}_{I}, {c}_{R}\right)\), the production rate (P) and demand rate (D) follow triangular lock fuzzy numbers. Now the cost matrix and the equivalent matrix game can be written as

where

$$ \left\{ \begin{gathered} \widetilde{D} = \left\langle {D_{1} ,D_{2} ,D_{3} } \right\rangle \equiv \left\langle {D_{2} \left( {1 - \frac{{\rho _{D} }}{{k_{D}^{L} }}} \right),D_{2} ,D_{2} \left( {1 + \frac{{\sigma _{D} }}{{k_{D}^{R} }}} \right)} \right\rangle \hfill \\ \widetilde{P} = \left\langle {P_{1} ,P_{2} ,P_{3} } \right\rangle \equiv \left\langle {P_{2} \left( {1 - \frac{{\rho _{P} }}{{k_{P}^{L} }}} \right),P_{2} ,P_{2} \left( {1 + \frac{{\sigma _{P} }}{{k_{P}^{R} }}} \right)} \right\rangle \hfill \\ \widetilde{C}_{i} = \left\langle {C_{{i1}} ,C_{{i2}} ,C_{{i3}} } \right\rangle \equiv \left\langle {C_{{i2}} \left( {1 - \frac{{\rho _{{C_{i} }} }}{{k_{{C_{i} }}^{L} }}} \right),C_{{i2}} ,C_{{i2}} \left( {1 + \frac{{\sigma _{{C_{i} }} }}{{k_{{C_{i} }}^{R} }}} \right)} \right\rangle ,\;i = {\text{1}},{\text{2}},..,6 \hfill \\ Z_{{11}} = f\left( {P_{1} ,D_{1} ,C_{{11}} ,C_{{21}} ,C_{{31}} ,C_{{41}} ,C_{{51}} ,C_{{61}} ,T,T_{m} } \right) \hfill \\ Z_{{12}} = f\left( {P_{2} ,D_{1} ,C_{{12}} ,C_{{22}} ,C_{{32}} ,C_{{42}} ,C_{{52}} ,C_{{62}} ,T,T_{m} } \right) \hfill \\ Z_{{13}} = f\left( {P_{3} ,D_{1} ,C_{{13}} ,C_{{23}} ,C_{{33}} ,C_{{43}} ,C_{{53}} ,C_{{63}} ,T,T_{m} } \right) \hfill \\ Z_{{21}} = f\left( {P_{1} ,D_{2} ,C_{{11}} ,C_{{21}} ,C_{{31}} ,C_{{41}} ,C_{{51}} ,C_{{61}} ,T,T_{m} } \right) \hfill \\ Z_{{22}} = f\left( {P_{2} ,D_{2} ,C_{{12}} ,C_{{22}} ,C_{{32}} ,C_{{42}} ,C_{{52}} ,C_{{62}} ,T,T_{m} } \right) \hfill \\ Z_{{23}} = f\left( {P_{3} ,D_{2} ,C_{{13}} ,C_{{23}} ,C_{{33}} ,C_{{43}} ,C_{{53}} ,C_{{63}} ,T,T_{m} } \right) \hfill \\ Z_{{31}} = f\left( {P_{1} ,D_{3} ,C_{{11}} ,C_{{21}} ,C_{{31}} ,C_{{41}} ,C_{{51}} ,C_{{61}} ,T,T_{m} } \right) \hfill \\ Z_{{32}} = f\left( {P_{2} ,D_{3} ,C_{{12}} ,C_{{22}} ,C_{{32}} ,C_{{42}} ,C_{{52}} ,C_{{62}} ,T,T_{m} } \right) \hfill \\ Z_{{33}} = f\left( {P_{3} ,D_{3} ,C_{{13}} ,C_{{23}} ,C_{{33}} ,C_{{43}} ,C_{{53}} ,C_{{63}} ,T,T_{m} } \right) \hfill \\ \end{gathered} \right. $$
(17)

Now, letting probability strategies of Player 1 as \(\left({p}_{1},{p}_{2},{p}_{3}\right)\) and that for Player 2 is \(\left({p}_{1}^{^{\prime}},{p}_{2}^{^{\prime}},{p}_{3}^{^{\prime}}\right)\). Then the game matrix becomes \(\begin{array}{c}\begin{array}{c}\mathrm{ Producer}\\ \begin{array}{ccc}{p}_{1}^{^{\prime}}& {p}_{2}^{^{\prime}}& {p}_{3}^{^{\prime}}\end{array}\end{array}\\ \begin{array}{cc}\mathrm{Customer}& \begin{array}{c}{p}_{1}\\ {p}_{2}\\ {p}_{3}\end{array}\end{array} \left[\begin{array}{ccc}{Z}_{11}& {Z}_{12}& {Z}_{13}\\ {Z}_{21}& {Z}_{22}& {Z}_{23}\\ {Z}_{31}& {Z}_{32}& {Z}_{33}\end{array}\right]\end{array}\)

Now as per Sect. 2.2, the inventory problem reduces to

$$ \left\{ \begin{gathered} {\text{Minimize}}\;\pi = Z_{{11}} p_{1} p_{1}^{'} + Z_{{12}} p_{1} p_{2}^{'} + Z_{{13}} p_{1} p_{3}^{'} + \hfill \\ Z_{{21}} p_{2} p_{1}^{'} + Z_{{22}} p_{2} p_{2}^{'} + Z_{{23}} p_{2} p_{3}^{'} + Z_{{31}} p_{3} p_{1}^{'} + Z_{{32}} p_{3} p_{2}^{'} + Z_{{33}} p_{3} p_{3}^{'} \hfill \\ {\text{Subject}}\;{\text{to}},~p_{1} + p_{2} + p_{3} = 1,~p_{1}^{'} + p_{2}^{'} + p_{3}^{'} = 1, \hfill \\ I\left( {\widetilde{P}} \right) = \frac{{\left( {P_{1} + 2P_{2} + P_{3} } \right)}}{4},I\left( {\widetilde{D}} \right) = \frac{{\left( {D_{1} + ~2D_{2} + ~D_{3} } \right)}}{4} \hfill \\ T_{m} = \frac{1}{\theta }\ln \left[ {\frac{{\alpha I\left( {\widetilde{P}} \right) - I\left( {\widetilde{D}} \right)}}{{I\left( {\widetilde{D}} \right)}} + \frac{{\left( {1 - \alpha } \right)I\left( {\widetilde{P}} \right)}}{{I\left( {\widetilde{D}} \right)}}e^{{\theta \left( {s - T} \right)}} - \frac{{I\left( {\widetilde{P}} \right) - I\left( {\widetilde{D}} \right)}}{{I\left( {\widetilde{D}} \right)}}e^{{ - \theta T}} + 1} \right] + T \hfill \\ Q = \frac{{\left( {I\left( {\widetilde{P}} \right) - I\left( {\widetilde{D}} \right)} \right)\left( {1 - e^{{ - \theta s}} } \right)}}{\theta } \hfill \\ Y = 0.45 + 0.01 \times I\left( {\widetilde{P}} \right) - 0.25\ln \left( {I\left( {\widetilde{P}} \right)} \right),~T_{m} > T \hfill \\ \end{gathered} \right. $$
(18)

7 Numerical examples

Here, we take the data set obtained from the case study in Table 2 and using LINGO software, we solve the problem (10) and (16), then the optimal results are listed in Table 3. However, solving (18) we get the optimal result and it is shown in Table 4.

Table 3 Crisp optimal solutions in different scenarios
Full size table
Table 4 Optimal solution of game problem under general fuzzy environment in scenario 2
Full size table

Table 3 shows that the optimum results of production run time, cycle time, pollution rate, order quantity and the average inventory cost in both scenarios. From the Scenario 1, we see that the average inventory cost is $ 1529.00 with respect to the optimum order quantity 609.20 units and the cycle time 6.56 months. Also, the production run time assumes 6.13 months while the pollution contribution to the environment due to production is 13.62%. However, from the Scenario 2, we see that the average inventory cost is $ 2110.75 which is 38.05% higher than the first scenario. But the optimum order quantity reduces to 49.97 units with respect to cycle time 1.8 months, production run time 1.3 months and the same pollution contribution 13.62% explicitly. Also, from this scenario we get the restoration rate 0.92 and the optimum breaking time 0.5 months of the production system. The variation of deterioration rate did not give any significant variation of average inventory cost as a whole.

Table 4 shows the solution of the game problem under general fuzzy system. From this table we see that how the average inventory cost is decreasing with the increasing machine breakdown time. We see that at the cycle time 0.4 months and the production run time 0.20 months, the average inventory cost takes a large value $ 11,186.51 with respect to the optimum order quantity 65.49 units, pollution contribution is 13.26%, restoration rate is 0.93 and the breaking time is 0.2 month, respectively. Indeed, the average inventory cost becomes minimum $ 2526.17 with respect to the optimum order quantity 229.09 units and the pollution contribution is 13.26% due to the breaking time 0.7 months, production run time 0.93 months and cycle time 1.40 months exclusively.

Here, we also compute the optimal inventory cost for the case of scenario 2 whenever we wish to use increasing order (\(\uparrow \)) and decreasing order (\(\downarrow \)) of the components of the key vectors associated to all the lock fuzzy parameters and they are put in Table 5.

Table 5 Solution of game problem under lock fuzzy environment in scenario 2
Full size table

Table 5 shows the solution of the game problem under lock fuzzy environment. We see that the optimum values of the decision variables like breaking time (0.5 months), production run time (1.3 months) and the cycle time (1.8 months) are fixed throughout the whole table. Here the proper choice of key parameters can change the average inventory cost, order quantity and the pollution contribution significantly. If the decision maker (DM) applies the keys/strategies like L1, L3, L4 or L7 then the average inventory cost is getting lesser (the range of cost reduction becomes 1.05% to 3.19%) than the crisp average inventory cost. In fact, the minimum average inventory cost becomes $ 2043.46 which has 3.19% reduction with respect to the crisp solution by the application of L1 key only. Also, the DM can minimize the pollution index up to 13.27% using the key parameters L2 or L5 alone and in that case the compromise cost will be increased within the range (1.79%, 5.23%). Although, the minimum restoration rate and order quantity for the whole study are 0.92 and 64 units respectively, but the maximum restoration rate and maximum order quantity are 0.99 and 138.96 units, respectively, for the changes of several key vectors and in these cases the range of excess system cost compromise is (-3.19%, 6.86%) with respect to the crisp optimal.

Now, we shall present the optimal solution in Table 6 for the varying breaking time (s) of the proposed model keeping L1 as threshold key vector.

Table 6 Solution of game problem for lock fuzzy environment under various breaking times in scenario 2
Full size table

Table 6 shows the variation of the average inventory cost under different breaking times using the base key vector L1 for lock fuzzy environment with fuzzy system parameter (\(\rho , \sigma \)) (= (0.4, 0.3)). In the entire table we see, the optimum restoration rate and the pollution contribution are same taking the values 0.95 and 13.81%, respectively. Also, it is seen that when the breaking time of the machinery process becomes 0.2 months, production run time and cycle time assume values 1.0 months and 1.2 months respectively, then the average inventory cost reaches its maximum value $ 3692.07 which is almost 75% higher than the crisp value and the order quantity assumes minimum value 25.61 units. However, at the breaking time 0.8 months, production run time 1.6 months and cycle time 2.4 months, the average inventory cost becomes lowest amounting with $ 1357.57 which is 36% lesser than that of crisp value. Although, this table reveals the system cost is going to minimize with the increase of duration of machinery process break down time within the time span 0.2–0.8 months exclusively.

8 Graphical illustrations

Here, we draw several graphs related to the data set obtained in Tables 4, 5 and 6.

Figure 5 expresses a line graph of zigzag path of the average inventory cost function with the variation of cycle time. It is seen that the average inventory cost takes the minimum value $ 2526.27 at the cycle time 1.4 months. At the cycle time 0.4 months the average inventory cost is getting very high (near $ 11,186), but as the cycle time increases up to 1.4 months the average inventory cost goes down monotonously and beyond that the results are something different.

Fig. 5
figure 5

Variation of average inventory cost with respect to cycle time

Full size image

Figure 6 shows that the fluctuation of the objective value with respect to different key vectors under lock fuzzy environment. The orange line is showing the crisp value of the average inventory cost. Moreover, it is seen that the average inventory cost curve is getting lower value from the crisp cost curve with the application of the key vectors L1, L3, L4 and L7 respectively, whereas it takes higher value with the application of key vectors L2, L5 and L6 explicitly. However, the average inventory cost curve is showing two peaks at $ 2221.08 and $ 2255.64 under the change of key vectors L2 and L6, respectively, and four valleys at $ 2043.46, $ 2082.37, $ 2057.64 and $ 2088.50, respectively, under the changes of key vectors L1, L3, L4 and L7, respectively. But the minimum cost ($ 2043.46) occurs at the initial key vector L1 explicitly.

Fig. 6
figure 6

Variation of average inventory cost with respect to different cost vectors

Full size image

Figure 7 shows the variation of pollution rate (in %) under the variation of process reliability. Here, we see that within a certain restoration rate (α = 0.93), the pollution rate remains more or less constant. But after this value, the percentage of pollution rate curve began to increase monotonically. In other words, when the production system is more reliable then over production might happen and hence, the pollution rate (%) increases in a faster rate.

Fig. 7
figure 7

Variation of pollution rate with respect to restoration rate

Full size image

Figure 8 gives a zigzag type line graph for the average inventory cost function with respect to the increase of process reliability (restoration rate). In this figure, we see that there are three peaks that take values with $3003, $ 2526 and $ 2256 for the process reliability 0.87, 0.93 and 0.99, respectively, and four valleys that assume values with $2562, $2149, $2043 and $2089 for the process reliability 0.71, 0.92, 0.95 and 0.97, respectively. The graph also shows that the average inventory cost curve assumes minimum when the process reliability reaches the value α = 0.95 as a whole.

Fig. 8
figure 8

Variation of average inventory cost with respect to restoration rate

Full size image

Figure 9 expresses the three-dimensional surface like curve of average inventory cost with the variation of process reliability (restoration rate) as well as breaking time point. This U-shaped surface shows the minimum average inventory cost (close to $ 2000) occurs at the breaking point 0.8 months and the process reliability 0.85. Also, we see that at the minimum breaking time 0.2 months and minimum process reliability 0.7, the average inventory cost is getting very high $ 11,186. But, at the breaking time 0.9 month and process reliability 0.99, the average inventory cost takes a higher value which is nearly $ 8000 exclusively.

Fig. 9
figure 9

Variation of average inventory cost with respect to shifting time and restoration rate

Full size image

9 Conclusion

In this article, we have studied a pollution sensitive production inventory model by taking instant restoration rate and deterioration under two different scenarios. The game theory and the lock fuzzy system have also been employed to optimize the model. We performed a real case study in a spinning factory followed by research problems. At first, we develop a crisp model then we convert this model into a game problem with the help of lock fuzzy numbers. Basically, we have fuzzified all the cost components, the demand and the production rate all at a time. Gaussian probabilistic strategies are considered during the construction of expected pay offs of the proposed game matrix. Our findings reveal that the lock fuzzy game theoretic approach gives minimum cost $ 2043.46 with respect to the optimum order quantity 64.00 units, the optimal cycle time 1.8 months, the optimum production run time 1.3 months and the optimum breaking time 0.5 months under the application of the key vector L1. In this case, the process reliability takes the value 0.95. But if the manager/decision maker wishes to minimize pollution level in the production system (s)he has to apply the key vector L5 to get minimum pollution (13.27%) with compromise minimum average inventory cost is $ 2148.61 with respect to the order quantity 79.49 units and the process reliability 0.92. Therefore, from this study some useful managerial insights may be drawn which are listed below:

  1. (i)

    All the decisions are traditional in scenario 1 because no failure is occurred.

  2. (ii)

    Scenario 2 consists of failure based deteriorating items and pollution sensitive model which gives minimum optimum solution under game theoretic lock fuzzy environment with respect to the crisp and general fuzzy environments.

  3. (iii)

    The decision maker can choose any one of the key vectors from a set of several keys available in the system and obtain the best optimal solution as (s)he would like to wish.

By this model, in one side we are able to get higher inventory cost where the key vectors are wrongly applied, in another side the average inventory cost assumes lowest value where the key vectors are applied intelligently.

However, the limitation of this work is that leakage of key vectors’ information might be harmful to the model. Also applying some other fuzzy membership of the fuzzy parameters one can get different results.

10 Scope of future work

Taking different types of fuzzy sets over various types of stochastic parameters in production inventory models some other research articles can be developed. Also, anybody can study this model under the application of hesitant fuzzy set, intuitionistic fuzzy set and neutrosophic set. With several probability density functions in some other complex models, numerous research articles can be developed in future.