1 Introduction

To solve complex optimization problems with a limited time in engineering optimization area is a challenge and hot research topic. How to design some simple and effective methods to adapt and overcome more and more real-world engineering optimization problems are value to study and discussing. Many optimization problems come from real life and industrial production, and they through principle logic, mathematical thinking and planning modeling method evolved into mathematical optimization problems. Although the conventional methods can often find a solution, it has become more and more tedious and time consuming. Moreover, the conventional methods cannot guarantee finding the optimal solution effectively in a very short time. Therefore, many advanced metaheuristic optimization algorithms are being developed. These new optimization algorithms are capable of achieving the global or near global optimum solution with less information about the problems. Compared to the conventional method, the metaheuristic optimization algorithms have some advantages and they play an important role in science and engineering field.

During the past several decades, many well-known metaheuristic optimization algorithms have been developed to solve optimization problems, such as genetic algorithm (GA) (Deb et al. 2002), harmony search(HS) (Geem et al. 2001; Papa et al. 2016), particles swarm optimization (PSO) (Eberhart and Kennedy 1995), artificial bee colony (ABC) (Akay and Karaboga 2012), differential evolution (DE) (Storn and Price 1997), gravitational search algorithm (GSA) (Rashedi et al. 2009) and teaching–learning-based optimization (TLBO) (Rao et al. 2011). These algorithms attracted much attention and aroused many scholars interesting. Jaya algorithm is a relatively new algorithm (Rao and Waghmare 2016) based on the principle to move the solution closer to the best solution and further away from the worst solution at the same time. This principle ensures that Jaya algorithm has good exploitation ability. However, its exploration capability is not better. Therefore, it is important to find a strategy to enhance the exploration capability of Jaya algorithm. To improve the performance of the Jaya algorithm, researchers have proposed various Jaya variants in the past decades (Azizi et al. 2019; Degertekin et al. 2019; Yu et al. 2017; Zhang et al. 2018; Wang et al. 2018a). Warid et al. (2018) proposed a modified Jaya algorithm based on novel quasi-oppositional strategy, and it is applied to the multi-objective optimal power flow problem. Yu et al. (2019) employed a performance-guided Jaya algorithm to solve the parameter identification problem of photovoltaic cell and module. Rao (2019) summarized the application of Jaya algorithm and its variants on constrained and unconstrained benchmark functions. Ocłoń et al. (2018) presented a modified Jaya algorithm to solve the thermal performance optimization of the underground power cable system. Rao and Saroj (2018a) designed an elitism-based self-adaptive multi-population Jaya algorithm, which was used to solve some engineering optimization problems. Jaya algorithm faces a few problems like other metaheuristic optimization algorithms such as TLBO algorithm and HS algorithm. For example, it easily gets stuck in local space for some optimization problems and its exploitation and exploration capability need to be balanced and adjusted. Based on this observation, our aim is to improve the performance of Jaya algorithm and to make it more applicable.

To improve the performance of Jaya algorithm, some main contributions are summarized as follows:

  1. (1)

    A commensal learning strategy is used to increase the probability of finding the global optimum, in which the person history best and worst information is used to explore new solution area.

  2. (2)

    A multi-populations strategy based on Gaussian distribution scheme and learning dictionary is utilized to enhance the exploration capability, meanwhile every subpopulation employed three Gaussian distributions at each generation, roulette wheel selection is employed to choose a scheme based on learning dictionary.

  3. (3)

    The performance of Jaya-SCLMP is evaluated based on 28 CEC 2013 unconstrained benchmark problems and reliability problems, i.e., complex (bridge) system, series system and series–parallel system. Compared with several Jaya variants and several state-of-the-art other algorithms, the experimental results reveal that Jaya-SCLMP can obtain some competitive results.

The remainder of this paper is organized as follows. The related work on the Jaya algorithm is reviewed in Sect. 2. Section 3 describes the original Jaya algorithm. The proposed Jaya-SCLMP is proposed in Sect. 4. In Sect. 5, Jaya-SCLMP is compared with several EAs based on 28 CEC 2013 unconstrained benchmark problems and three example reliability problems. The experimental results and discussions are also reported. Finally, Sect. 6 draws the conclusions.

2 Related work

To improve the performance of Jaya algorithm, researchers have proposed many Jaya algorithm variants in recent years. The improvements in Jaya algorithm have been active and rapid with many successful applications to various real-world optimization problems.

To improve the Jaya algorithm, researchers are focusing on parameter adjustment, operator design, hybrid algorithm, etc. To increase the probability of finding the global optimum, Ocłon et al. (2018) proposed a modified Jaya algorithm (MJaya) with a novel candidate update scheme. Farah and Belazi (2018) proposed a novel chaotic Jaya algorithm for unconstrained numerical optimization, in which chaotic theory and strategy are integrated into search operation. Rao et al. (2017) introduced a quasi-oppositional based Jaya algorithm (QO-Jaya). In QO-Jaya, a quasi-opposite population is generated at each generation to achieve a better performance (Rao and Rai 2017). Rao et al. (2017) presented a self-adaptive multi-population-based Jaya algorithm for engineering optimization problems, called SAMP-Jaya. SAMP-Jaya divides the population into a number of groups based on the quality of the solution (Rao and Saroj 2017a). One year later, Rao and Saroj (2018b) incorporated an elitism strategy into SAMP-Jaya to improve the performance of SAMP-Jaya. Rao and More (2017) proposed a self-adaptive Jaya algorithm to optimize and analyze the selected thermal devices. Some improved Jaya algorithms are summarized in Table 1.

Table 1 Several Jaya variants and their improvements
Full size table

Application study is another research aspect of Jaya algorithm. Rao et al. (2016) used the Jaya algorithm to solve micro-channel heat sink dimensional optimization, compared to other related algorithm, Jaya algorithm has some merits in optimization performance. Moreover, (2017b) further considered the constrained economic optimization of shell-and-tube heat exchangers and provided a modified Jaya algorithm based on differential strategies such as elitist mechanism, and the simulation shows that the modified Jaya algorithms perform better. Wang et al. (2018b) combined wavelet Renyi entropy with three-segment encoded Jaya algorithm to solve alcoholism identification. Azizi et al. (2019) used hybrid ant lion optimizer and Jaya algorithm to solve fuzzy controller optimum design. In 2018, Rao et al. employed elitist-Jaya algorithm to solve heat exchangers multi-objective optimization problem (Rao and Saroj 2018c) and proposed a multi-team perturbation guiding Jaya algorithm for wind farm layout optimization problem (Rao and Keesari 2018). Grzywinski employed Jaya algorithm with frequency constraints for the optimization of the braced dome structures (Grzywinski et al. 2019). Degertekin proposed a Jaya algorithm to solve sizing, layout and topology design optimization of truss structures (Degertekin et al. 2018). Huang proposed a novel model-free solution algorithm, the natural cubic-spline-guided Jaya algorithm (S-Jaya), for efficiently solving the maximum power point tracking (MPPT) problem of PV systems under partial shading conditions (Huang et al. 2018). Wang designed a novel elite opposition-based Jaya algorithm for parameter estimation of photovoltaic cell models (Wang and Huang 2018). In 2019, Gao et al. (2019) proposed a discrete Jaya algorithm for solving a flexible job-shop rescheduling problem (FJRP), in which five objective-oriented local search operators and four ensembles of them are proposed to improve the performance of DJaya algorithm.

In sum, Jaya algorithm has many advantages. However, like other algorithms, it suffers from some weaknesses while it is used to solve real-world complex and large-scale optimization problems. It is valuable and important to enhance the exploration capability of Jaya algorithm. Our paper focuses on the improvement of the Jaya algorithm and some applications with some new ideas.

3 Jaya algorithm

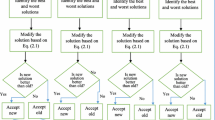
Jaya algorithm is a relatively new algorithm. The core of Jaya algorithm lies in the principle of moving the solution closer to the best solution and further away from the worst solution at the same time. The details of Jaya algorithm can be described as below.

Let f(x) be the objective function to be optimized. Assume that at any iteration i, there are D design variables and NP candidate solutions (i.e., population size, i = 1, 2, …, NP). If xti,j is the value of the jth variable for the ith candidate during the tth iteration, then this value is modified as follows:

$$ X\begin{array}{*{20}c} {{\text{t}} + {1}} \\ {i,j} \\ \end{array} = X\begin{array}{*{20}c} t \\ {i,j} \\ \end{array} + r\begin{array}{*{20}c} {} \\ {1,i,j} \\ \end{array} \times \left( {X\begin{array}{*{20}c} {\text{t}} \\ {best,j} \\ \end{array} - \left| {X\begin{array}{*{20}c} t \\ {i,j} \\ \end{array} } \right|} \right) - r\begin{array}{*{20}c} {} \\ {2,i,j} \\ \end{array} \times \left( {X\begin{array}{*{20}c} {\text{t}} \\ {worst,j} \\ \end{array} - \left| {X\begin{array}{*{20}c} t \\ {i,j} \\ \end{array} } \right|} \right) $$
(1)

where Xtbest,j is the value of the variable j for the best candidate and Xtworst,j is the value of the variable j for the worst candidate in the population. Xti,+j1 is the updated value of Xti,j and r1,i,j and r2,i,j are the two random numbers for the jth variable during the tth iteration in the range [0,1]. The term r1,i,j × (Xtbest,j−|Xti,j|) indicates the tendency of the solution to move closer to the best solution, and the term r2,i,j × (Xtworst,j−|Xti,j|) indicates the tendency of the solution to avoid the worst solution (Rao and Waghmare 2016). Xti,+j1 is accepted if it gives a better fitness value. Figure 1 shows the flowchart of the Jaya algorithm.

Fig. 1
figure 1

The flowchart of the Jaya algorithm

Full size image

4 Jaya-SCLMP algorithm

In this section, we propose a self-adaptively commensal learning-based multi-population Jaya algorithm, namely Jaya-SCLMP. In Jaya-SCLMP, we modify the candidate update scheme of Jaya algorithm. Moreover, the commensal learning strategy and multi-population strategy are incorporated into Jaya-SCLMP to increase the probability of finding the global optimum.

4.1 Commensal learning strategy

In 2017, Peng et al. (2017) proposed the conception of commensal learning, and the primary idea is the mutation strategies and parameter settings adaptively adjust together under the same criteria and multiple combinations of the two parts commensal evolution for each individual. In Peng et al. (2017), the results show that the commensal learning can enhance the performance of differential evolution algorithm. We analyze the characteristic of Jaya algorithm and consider to use the commensal learning to amend the performance of Jaya algorithm. Jaya algorithm was proposed as an algorithm with less algorithm-specific parameters, but it can easily be trapped in local optima. To the best of our knowledge, using a number of subpopulations distributes the solutions over the search space rather than concentrating on a particular region. This multi-population strategy can enhance the population diversity of the algorithm. Therefore, the candidate solutions can escape from the local optima. How to use the commensal learning to improve the performance of Jaya algorithm is a challenge? We realized the random uniform distribution random number maybe affect the optimization process of Jaya algorithm. To adjust the random number under the same condition for balancing the search space, so the idea of commensal learning is integrated. In Jaya algorithm, new candidate solutions are generated through Eq. (1), but in Jaya-SCLMP, new candidates are produced by following Eq. (2):

$$ X\begin{array}{*{20}c} {{\text{t}} + {1}} \\ {i,{\text{j}}} \\ \end{array} = X\begin{array}{*{20}c} t \\ {i,j} \\ \end{array} + N\left( {\mu ,\sigma^{2} } \right) \times \left( {X\begin{array}{*{20}c} {\text{t}} \\ {best({\text{p}}),j} \\ \end{array} - \left| {X\begin{array}{*{20}c} t \\ {i,j} \\ \end{array} } \right|} \right) - N(\mu ,\sigma^{2} ) \times \left( {X\begin{array}{*{20}c} {\text{t}} \\ {worst(p),j} \\ \end{array} - \left| {X\begin{array}{*{20}c} t \\ {i,j} \\ \end{array} } \right|} \right) $$
(2)

where X tbest(p),j is the value of the jth variable for the person best candidate and X tworst(p),j is the value of the jth variable for the person worst candidate in pth subpopulation at tth generation. N(μ,σ2) is a random real number Gaussian distribution µ = 0.3, 06, 0.9; σ2 = 0.025. We use Gaussian distribution with different average value take the place of uniform distribution which is used in Jaya algorithm. The idea is to maximize the likelihood of generating new solutions along appropriate directions and accelerate the convergence speed. To enhance the population diversity of the algorithm, the commensal learning is proposed in this paper. The primary idea is to balance the search space based on the best solution and the worst solution under the same criteria. Further, it uses multiple combinations of the two parts of the commensal evolution for each individual.

4.2 Multi-population strategy

In order to improve the diversity of the Jaya algorithm, we consider to design multi-population strategy based on different Gaussian distribution. At first, combine with the commensal learning to analyze the setting of Gaussian distribution parameter values and the number of group. The number of groups is set 2, 3, 4, 5, 6, the value of µ set in (0, 1), the value of σ2 set in stochastic value, a great many of simulation test shown that if we use four groups to this algorithm, it has better results. Meanwhile, we find the value of µ and σ2 have effect for the performance, so we fixed four groups and discuss the value of µ and σ2. We all know if each groups contain different schemes, maybe the diversity is better, but too many will reduce the search accuracy, so we try to use three schemes, in fact, too many times tests also show the three schemes are effect. Therefore, we should use 12 schemes because each group has three schemes. Although the simulation results may not show the only one conditions, we obtain a relative better situation. Due to space limitation, the data and charts of specific parameter simulation will not be added. We elaborate how to choose the best solution and the worst solution of four subpopulations combined with three Gaussian distribution parameter settings to form twelve subpopulation update schemes. The twelve subpopulation update schemes are shown as follows:

Scheme 1: Xtbest(1), Xtworst(1), N(0.3, 0.025).

Scheme 2: Xtbest(1), Xtworst(1), N(0.6, 0.025).

Scheme 3: Xtbest(1), Xtworst(1), N(0.9, 0.025).

Scheme 4: Xtbest(2), Xtworst(2), N(0.3, 0.025).

Scheme 5: Xtbest(2), Xtworst(2), N(0.6, 0.025).

Scheme 6: Xtbest(2), Xtworst(2), N(0.9, 0.025).

Scheme 7: Xtbest(3), Xtworst(3), N(0.3, 0.025).

Scheme 8: Xtbest(3), Xtworst(3), N(0.6, 0.025).

Scheme 9: Xtbest(3), Xtworst(3), N(0.9, 0.025).

Scheme 10: Xtbest(4), Xtworst(4), N(0.3, 0.025).

Scheme 11: Xtbest(4), Xtworst(4), N(0.6, 0.025).

Scheme 12: Xtbest(4), Xtworst(4), N(0.9, 0.025).

For every subpopulation at each generation, roulette wheel selection is employed to choose a scheme based on learning dictionary to evolve. Learning dictionary is an assessment table of evolution effectiveness. After selection operation in pth subpopulation, the times of successful update (stp,s) and the times of tried update (ttp,s) on the sth scheme are recorded. As shown in Table 2, the row and column of the learning dictionary represent four subpopulations and the twelve update schemes, respectively. In the learning dictionary, the cell(s,p) records the twelve update schemes and the success rate (srp,s) for pth subpopulation on sth scheme, and srp,s is obtained by dividing stp,s by ttp,s. Subpopulations will select an update scheme according to the success rate (srp,s) to update its individuals.

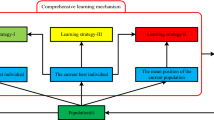
Table 2 Illustration of the learning dictionary
Full size table

4.3 Framework of Jaya-SCLMP

Step 1: Initialization four subpopulations.

1.1 Randomly initialize the individuals of four subpopulations within the upper and lower limits;

1.2 Evaluate fitness of each individual of four subpopulations;

Step 2: Evolutionary phase.

2.1 Find the best and worst individual of each subpopulation.

2.2 For each subpopulation, select a scheme according to learning dictionary for each subpopulation to update its individuals;

2.3 If Xti,+j1 is better than Xti,j, accept Xti,+j1.

Step 3: If the termination criteria is satisfied, stop; otherwise go to Step 2.

Like the traditional Jaya algorithm, Jaya-SCLMP also consists of a very simple framework. At the first, Jaya-SCLMP initializes four subpopulations. In the evolutionary process, Jaya-SCLMP first finds the best solutions and the worst solutions of the subpopulations. Then, for each subpopulation, an update scheme according to the success rate is chosen and then its individuals are updated. The steps of the Jaya-SCLMP algorithm are described in Fig. 2.

Fig. 2
figure 2

The flowchart of the Jaya-SCLMP algorithm

Full size image

4.4 Computational complexity

For simplicity we compute the running time of an algorithm purely as a function of the length of the string representing the input. In the worst-case analysis, the form we consider the longest running time of all inputs of a particular length. The time complexity of an algorithm is commonly expressed using the big O notation, which excludes coefficients and lower-order terms. In this subsection, the computational complexity of the proposed algorithm was briefly analyzed based on the computation procedure of the proposed algorithm. Based on the flowchart of the Jaya algorithm (Fig. 1) and the flowchart of the Jaya-SCLMP algorithm (Fig. 2), we can know that the difference is Jaya-SCLMP algorithm need select a scheme according to learning dictionary for each subpopulation to update their individuals. Assume the population size is NP, the dimension is D, to find the best and worst solution need time is TB, Ft is the objective function computational time, initialize each decision variables need time is TI, the implement iteration is K, £ denotes the updating time, then the computation time of the Jaya as follows:

$$ {\text{TQ}} = {\text{TI}} + {\text{K}} \times ({\text{TB}} + {\text{NP}} \times ({\text{D}} + {\text{F}}_{t} + \pounds)) $$
(3)
$$ {\text{T}}1 = \mathop {\lim }\limits_{K \to \infty } \frac{TQ}{K} = {\text{TB}} + {\text{NP}} \times \left( {{\text{D}} + {\text{ Ft}} + {\text{\pounds}}} \right) $$
(4)

Obviously, assume the same condition, the selection operation needs W time, then the computation time of the Jaya-SCLMP algorithm as follows:

$$ {\text{TP}} = {\text{TI}} + K \times ({\text{TB}} + 4 \times (W + {\text{NP}}/4 \times (D + F_{t} + \pounds))) $$
(5)
$$ T2 = \mathop {\lim }\limits_{K \to \infty } \frac{{{\text{TP}}}}{K} = {\text{TB}} + 4 \times \left( {W + {\text{NP}}/4 \times \left( {D + Ft + \pounds} \right)} \right) $$
(6)
$$ T2 - T1 = 4W $$
(7)

Baes on the above analysis, we realized that the proposed algorithm needs more time compared to the original algorithm, but it not relative to the iteration times, if the search mechanism is better, it can obtain a good solution in a few time. The experiment results are shown in Table 10. Under the same optimization accuracy, the computation effort of SCLMP-Jaya is better than the other compared algorithms.

5 Experiment results and analysis

5.1 Experimental settings

To test the performance of the proposed Jaya-SCLMP algorithm, the CEC 2013 and CEC 2015 unconstrained benchmark problems are considered in the experiment. Twenty-eight unconstrained benchmark problems with different characteristics including unimodal, multimodal and composition are selected from CEC 2013 test suite. These benchmark problems are briefly described in Table 3. The detailed description of these unconstrained benchmark problems can be found in Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization (Liang et al. 2013). The size of dimension D of these unconstrained benchmark problems is set to 30. In our experiments, Jaya-SCLMP is compared with Jaya algorithm (Rao and Waghmare 2016), MJaya (Ocłoń et al. 2018), QO-Jaya (Rao and Rai 2017), SAMP-Jaya (Rao and Saroj 2017a), GOTLBO (Chen et al. 2016) and GOPSO (Wang et al. 2011) in the experiments. GOTLBO and GOPSO use generalized oppositional teaching learning-based optimization to enhance the performance of basic algorithms. The subpopulation size of SCLMP-Jaya is 25. The other parameters of Jaya, MJaya, QO-Jaya, SAMP-Jaya, GOPSO and GOTLBO are set as the same as in their original papers. Due to the stochastic characteristics of EAs, we conduct 30 independent runs for each algorithm and each benchmark problem with 300,000 function evaluations (FEs) as the termination criterion. Moreover, we record the mean and standard deviation of the optimization error values (f(X’) − f(X*)) for evaluating the efficiency of the comparison algorithms, where X’ is the best individual gained by the algorithm in a run and X* is the global optimum of the benchmark problem.

Table 3 Summary of the 28 CEC 2013 Test Functions (search range [− 100,100])
Full size table

In addition to 28 unconstrained benchmark problems, three example problems are selected to test the performance of the Jaya-SCLMP algorithm for reliability problems. Reliability problem is a kind of constrained optimization problems. According to the definition of the Advisory Group on the Reliability of Electronic Equipment, reliability indicates the probability implementing specific performance or function of products and achieving successfully the objectives within a time schedule under a certain environment. The reliability problem is usually formulated as a nonlinear programming problem, which is subject to several resource constraints such as cost, weight and volume. Various complex systems come out with the development of industrial engineering, and the reliability designing of these systems is very important. Thus, more accurate and efficient methods are needed in finding the optimal system reliability. Otherwise, the safety and efficiency of a system cannot be guaranteed. The three problems are a series system, series–parallel system and complex (bridge) system. Three reliability problems are described as in Wu et al. (2011), Ouyang et al. (2015).


P1. Complex (bridge) system ( Fig.  3 ).

Fig. 3
figure 3

The schematic diagram of complex (bridge) system (P1)

Full size image

P1 is a nonlinear mixed integer programming problem for a complex (bridge) system with five subsystems, and this example is used to demonstrate the efficiency of Jaya-SCLMP algorithm. The complex (bridge) system optimization problem (Ouyang et al. 2015) is as follows:

$$ \begin{aligned} {\text{max }}f({\mathbf{r}},{\mathbf{n}}) & = R_{1} R_{2} + R_{3} R_{4} + R_{1} R_{4} R_{5} + R_{2} R_{3} R_{5} - R_{1} R_{2} R_{3} R_{4} - R_{1} R_{2} R_{3} R_{5} \\ & - R_{1} R_{2} R_{4} R_{5} - R_{1} R_{3} R_{4} R_{5} - R_{2} R_{3} R_{4} R_{5} + 2R_{1} R_{2} R_{3} R_{4} R_{5} \\ s.t.g_{1} ({\mathbf{r}},{\mathbf{n}}) = & \sum\limits_{i = 1}^{m} {w_{i} v_{i}^{2} n_{i}^{2} } - V \le 0, \\ g_{2} ({\mathbf{r}},{\mathbf{n}}) = & \sum\limits_{i = 1}^{m} {\alpha_{i} \left( - \frac{1000}{{\ln (r_{i} )}}\right)^{{\beta_{i} }} [n_{i} + \exp (0.25n_{i} )]} - C \le 0, \\ g_{3} ({\mathbf{r}},{\mathbf{n}}) = & \sum\limits_{i = 1}^{m} {w_{i} n_{i} \exp (0.5n_{i} )} - W \le 0, \\ 0 \le & r_{i} \le 1, \, n_{i} \in Z^{ + } ,\;\;1 \le i \le m. \\ \end{aligned} $$
(8)

Here, m is the number of subsystems in the system; ni is the number of components in subsystem i, (1 ≤ i ≤ m); ri is the reliability of each component in subsystem i; qi = 1 − ri is the failure probability of each component in subsystem i; Ri(ni) = 1 − qnii is the reliability of subsystem i; f(r, n) is the system reliability. wi is the weight of each component in subsystem i, and vi is the volume of each component in subsystem i; furthermore, V is the upper limit on the sum of the subsystems’ products of volume and weight; C is the upper limit on the cost of the system; W is the upper limit on the weight of the system. The parameters βi and αi are physical features of system components. Constraint g1(r, n) is a combination of weight, redundancy allocation and volume; g2(r, n) is a cost constraint, while g3(r, n) is a weight constraint. The input parameters of the complex (bridge) system are shown in Table 4.

Table 4 Data used in complex (bridge) system (P1) and series system (P2)
Full size table

P2. Series system ( Fig.  4 ).

Fig. 4
figure 4

Series system (P2)

Full size image

P2 is a nonlinear mixed integer programming problem for a series system with five subsystems, and the problem formulation is as follows (Ouyang et al. 2018):

$$ \begin{aligned} & {\text{max }}f({\mathbf{r}},{\mathbf{n}}) = \prod\limits_{i = 1}^{m} {R_{i} (n_{i} )} \\ & s.t. \\ & g_{1} ({\mathbf{r}},{\mathbf{n}}) = \sum\limits_{i = 1}^{m} {w_{i} v_{i}^{2} n_{i}^{2} } - V \le 0, \\ & g_{2} ({\mathbf{r}},{\mathbf{n}}) = \sum\limits_{i = 1}^{m} {\alpha_{i} \left( { - \frac{1000}{{\ln (r_{i} )}}} \right)^{{\beta_{i} }} [n_{i} + \exp (0.25n_{i} )]} - C \le 0, \\ & g_{3} ({\mathbf{r}},{\mathbf{n}}) = \sum\limits_{i = 1}^{m} {w_{i} n_{i} \exp (0.5n_{i} )} - W \le 0, \\ & 0 \le r_{i} \le 1, \, n_{i} \in Z^{ + } , \, 1 \le i \le m. \\ \end{aligned} $$
(9)

P2 has three nonlinear constraints, and they are the same as P1. In addition, the input parameters of series system are also the same as those of the complex (bridge) system, and they are also shown in Table 4.


P3. Series–parallel system ( Fig.  5 ).

Fig. 5
figure 5

Series–parallel system (P3)

Full size image

P3 is a nonlinear mixed integer programming problem for a series–parallel system with five subsystems. The problem formulation is as follows:

$$ \begin{aligned} & {\text{Max}}\;f \, (r, \, n) \, = 1 - (1 - R_{1} R_{2} )(1 - (R_{3} + R_{4} - R_{3} R_{4} )R_{5} ) \\ & s.t. \\ & g1(r,n) = \sum\limits_{i = 1}^{m} {w_{i}^{{}} } v_{i}^{2} n_{i}^{2} - V \le 0 \\ & g2(r,n) = \sum\limits_{i = 1}^{m} {\alpha_{i} } \left( { - \frac{1000}{{\ln (r_{i} )}}} \right)^{{\beta_{i} }} \left[ {n_{i} + \exp (0.25n_{i} )} \right] - C \le 0 \\ & g3(r,n) = \sum\limits_{i = 1}^{m} {w_{i} n_{i} } \exp (0.25n_{i} ) - W \le 0 \\ & 0 \le r_{1} \le 1,n_{i} \in Z^{ + } ,\;\;1 \le i \le m \\ \end{aligned} $$
(10)

P3 has the same nonlinear constraints as P1, but there are some differences in input parameters. The input parameters of P3 are shown in Table 5.

Table 5 Data used in series–parallel system (P3)
Full size table

To demonstrate the superiority of the Jaya_SCLMP algorithm in solving the reliability problems, we select the other five algorithms for comparison, and they are the Jaya algorithm, the SAMP_Jaya, the QO_Jaya, the GOPSO and the GOTLBO. The above three problems are used to compare performance of six algorithms on solving reliability problems. The parameters of the six algorithms are set as follows: For GOTLBO, population size NP = 50, jumping rate Jr = 1, teaching factor TF = 1; For GOPSO, NP = 40, cognitive parameter c1 = 1.49618, social parameter c2 = 1.49618, inertia weight w = 0.72984, Jr = 0.3; For Jaya, NP = 10; For QO_Jaya, NP = 20; For SAMP_Jaya, NP = 300, the minimal number of subpopulations is 2, the maximal number of subpopulations is 10; For Jaya_SCLMP, subpopulations size sNP = 25. In addition, we adopt a penalty function method to handle constraints. It is well known that the maximization of f (r, n) can be transformed into the minimization of − f (r, n); thus, the penalty function is described as:

$$ \min F(r,n) = - f(r,n) + \lambda \sum\limits_{j = 1}^{ng} {[\max (0,g_{i} (r,n))]}^{2} $$
(11)

where λ represents penalty coefficient and it is set to 1010 in this paper. Due to the stochastic characteristics of EAs, we conduct 30 independent runs for each algorithm and each test problem with 15,000 function evaluations (FEs) as the termination criterion.

5.2 Results discussion and analysis

The mean and standard deviation of the optimization error values achieved by each algorithm for 28 unconstraint benchmark problems CO1 ~ CO28 are shown in Tables 6 and 7. For convergence, the best results among all algorithms are highlighted in overstriking. In order to obtain statistically sound conclusions, the two-tailed t test at a 0.05 significance level is performed on the experimental results (Wang et al. 2011; Yao et al. 1999). The summary of the comparison results is shown in the last three rows of Tables 6 and 7. “Mean” and “SD” represent the mean and standard deviation of the optimization error values achieved by 30 independent runs, respectively. The symbols “ + ”, “ − ”, and “≈” denote that Jaya-SCLMP achieves better, worse and similar results, respectively, than the corresponding algorithms according to the two-tailed t test.

Table 6 Experimental results of Jaya, MJaya, QO-Jaya and Jaya-SCLMP over 30 independent runs for the 28 unconstraint benchmark problems
Full size table
Table 7 Experimental results of SAMP-Jaya, GOPSO, GOTLBO and Jaya-SCLMP over 30 independent runs for the 28 unconstraint benchmark problems
Full size table

Based on the experimental results in Tables 6 and 7, we can see that Jaya-SCLMP is significantly better than Jaya, MJaya, QO-Jaya, SAMP-Jaya algorithms for the majority of the benchmark problems. Specifically, Jaya-SCLMP achieves better results than Jaya on 20 out of 28 benchmark problems. For the remaining eight benchmark problems, Jaya-SCLMP performs similarly to Jaya on benchmark problems CO8, CO14, CO16, CO22 and CO26 while Jaya performs better than Jaya-SCLMP on benchmark problems CO15, CO20 and CO23. MJaya outperforms Jaya-SCLMP on 4 benchmark problems (namely CO15, CO20, CO23 and CO26), while SCLMP-Jaya achieves better results than MJaya on 19 benchmark problems. Both Jaya-SCLMP and MJaya exhibit almost similar performance on 5 benchmark problems. For QO-Jaya, it performs similarly to Jaya-SCLMP on 7 benchmark problems. In addition, QO-Jaya is better than Jaya-SCLMP on CO15 and CO26, while Jaya-SCLMP outperforms QO-Jaya on 19 benchmark problems. Moreover, SAMP-Jaya surpasses Jaya-SCLMP on CO26. In contrast, Jaya-SCLMP is better than SAMP-Jaya on 26 out of 28 benchmark problems. Both SAMP-Jaya and Jaya-SCLMP demonstrate similar performance on benchmark problems CO20. From the comparison results among Jaya-SCLMP, Jaya, MJaya, QO-Jaya and SAMP-Jaya, it is known that the multi-population strategy and the commensal learning strategy work together to improve the performance of Jaya-SCLMP. It can be known that Jaya-SCLMP outperforms GOPSO and GOTLBO 25 and 24 out of 28 benchmark problems, respectively. GOPSO is better than Jaya-SCLMP on 1 benchmark problem. GOTLBO cannot be better than Jaya-SCLMP on any benchmark problems. In addition, Jaya-SCLMP is similar to GOPSO and GOTLBO on 2 and 4 benchmark problems. Thus, Jaya-SCLMP is significantly better than many algorithms on the majority of the benchmark problems.

Figure 6 shows the convergence curves of Jaya-SCLMP, MJaya,QO-Jaya, SAMP-Jaya, GOPSO and GOTLBO for some typical benchmark problems. It can be seen from Fig. 6 that Jaya-SCLMP exhibits faster convergence speed than Jaya, MJaya, QO-Jaya, SAMP-Jaya, GOPSO and GOTLBO. The outstanding convergence performance of Jaya-SCLMP should be due to the incorporated multi-populations and commensal learning strategy, which can enhance the search ability. In order to compare the total performance of multiple algorithms on all benchmark problems, the Friedman test is conducted on the experimental results following (Yao et al. 1999). The average rankings of the seven algorithms for all benchmark problems are shown in Table 8. The best average ranking among the comparison algorithms is shown in italics. The seven algorithms can be sorted by the average ranking into the following order: Jaya-SCLMP, MJaya, Jaya, QO-Jaya, GOPSO, SAMP-Jaya and GOTLBO. Jaya-SCLMP rank first, which exhibits better total performance than MJaya, Jaya, QO-Jaya, GOPSO, SAMP-Jaya and GOTLBO on all benchmark problems. The better performance of Jaya-SCLMP can be because both the multi-population scheme and the commensal learning strategy work together to improve the performance of Jaya-SCLMP.

Fig. 6
figure 6figure 6

Convergence curves of Jaya, MJaya, QO-Jaya, SAMP-Jaya, Jaya_SCLMP, GOPSO and GOTLBO for some typical benchmark functions

Full size image
Table 8 Average rankings of the seven algorithms for 28 unconstraint benchmark problems gained by the Friedman test
Full size table

In order to further show the performance of the proposed algorithm, according to the literature (Rao and Saroj 2017a), the summary of the CEC 2015 expensive optimization test problem is used in our paper. The detail of the 15 CEC 2015 test functions can be seen in the literature (Rao and Saroj 2017a) (Appendix A2). Based on the reference (Rao and Saroj 2017a), maximum function evaluations (MFE) of 500 and 1500 are considered as one of the stopping criteria for 10-dimensional and 30-dimensional problems, respectively. All the experiment conditions are same to the reference (Rao and Saroj 2017a). The results obtained by our proposed algorithm are compared with cooperative PSO with stochastic movements (EPSO), DE, (μ + λ)-evolutionary strategy (ES), specialized and generalized parameters experiments of covariance matrix adaption evolution strategy (CMAES-S and CMAES-G). The comparison of the computational results is presented in Table 9.

Table 9 Comparative results for mean error obtained by different approaches for CEC’ 15 problems
Full size table

From Table 9, it can be seen that the performance of the proposed algorithm is superior to DE algorithm in 12 problems. Only 3 functions, DE algorithm achieves better results for all the functions with 10 and 30 dimensions. Therefore, the proposed algorithm has better performance than DE algorithm. In contrast to Jaya algorithm, our proposed algorithm performs significantly better in 11 problems. Besides the rest of 4 functions, the proposed algorithm achieves similar results as Jaya algorithm. Compared to (µ + λ)ES algorithm, the proposed algorithm have better results in 11 functions. The proposed algorithm also get 11 better results compared to CMAES-S and CMAES-G algorithm. Compared to our proposed algorithm, EPSO have better results only 3 functions in 15 functions. SAMP-Jaya perform better in 5 functions, and similar in 2 functions, but worse in 8 cases. According to the experimental results, it can be observed that the proposed algorithm performs better on the more complex shifted and rotated problems. In all, the proposed algorithm has some advantages compared to all the compared algorithms.

The comparison of three example problems between the optimization results of the Jaya_SCLMP and those of the five other algorithms are presented in Table 10. NFOS represents the number of feasible “optima” solution found out of 30 runs and SD represents standard deviation. For convenience, the best results among all algorithms are highlighted in overstriking. Based on the experimental results in Table 10, we can see that for P1 and P3, the best, worst, mean results obtained by the Jaya_SCLMP are all very close to each other in each case, and the standard deviations are 9.42711E−05 and 7.58188E−05, respectively. From Figs. 7, 8 and 9, it can be seen that the Jaya_SCLMP has strong convergence and stability than five other algorithms. In addition, the mean results for P1 and P3 using Jaya_SCLMP algorithm are 0.9997974871 and 0.9999210543, respectively, and both mean results are better than those obtained by five other algorithms. For P2, the best result obtained by QO_Jaya is better than the best result obtained by Jaya_SCLMP, but the mean result obtained by Jaya_SCLMP is better than those obtained by five other algorithms. In addition, for P2, we can see that Jaya, QO_Jaya and SAMP_Jaya are easy to be trapped in local optima. For P1 and P3, the Jaya_SCLMP obtains larger NFOS than the SAMP_Jaya. For P2, the Jaya_SCLMP obtains larger NFOS than Jaya, QO_Jaya and SAMP_Jaya, and the same NFOS is obtained by Jaya_SCLMP, GOPSO and GOTLBO for P1–P3. On the whole, the Jaya_SCLMP has demonstrated a higher efficiency in finding an “optima” solution (or near “optima” solution) when compared to the other three Jaya variants.

Table 10 Results of the three examples using six algorithms
Full size table
Fig. 7
figure 7

The result of P1 using six algorithms

Full size image
Fig. 8
figure 8

The result of P2 using six algorithms

Full size image
Fig. 9
figure 9

The result of P3 using six algorithms

Full size image

In order to compare the search efficiency and running time of the proposed algorithm and the other different algorithms, we select a threshold value for each benchmark problems. To give a fair chance to all the metaheuristics compared. We run each algorithm on a function and stop as soon as the best value determined by the algorithm falls below the predefined threshold or a maximum number of OFEs is exceeded. Here, the threshold is 102, the maximum number of objective function evaluations (OFE) is fixed as 1 × 105. The experiment results are recorded in Table 11.

Table 11 Comparison of the number of objective function evaluations
Full size table

From Table 11, it can be obviously seen that SCLMP-Jaya take less number of objective function evaluations for the same predefined threshold compared to all the other algorithms, which is demonstrated that the SCLMP-Jaya has better search efficiency. In other words, under the same optimization accuracy, the computation effort of SCLMP-Jaya is better than the other compared algorithms.

6 Conclusion

Jaya algorithm has gained great success in science and engineering field. In order to enhance the performance of the Jaya algorithm, a self-adaptively commensal learning-based multi-populations Jaya algorithm, called Jaya-SCLMP, is proposed in this study. On the one hand, Jaya-SCLMP employs commensal learning strategy to accelerate the convergence speed. On the other hand, Jaya-SCLMP uses multi-populations scheme to increase the probability of finding the global optimum. In the numerical experiments, 28 benchmark test functions and three example problems of reliability problems are utilized to evaluate the performance of Jaya-SCLMP. Moreover, Jaya-SCLMP is compared with six algorithms, namely MJaya, Jaya, QO-Jaya, SAMP-Jaya, GOPSO and GOTLBO. The experimental results reveal that Jaya-SCLMP can exhibit better performance than these algorithms on the majority of the test functions and that the Jaya-SCLMP is superior to the other five algorithms in finding the maximal reliability for the three example problems. In the future research, we will utilize the proposed Jaya-SCLMP to solve other real-world optimization problems, such as constraint and multi-objective optimization problems.