Improved grey wolf optimization based on the two-stage search of hybrid CMA-ES

Abstract

Hybrid algorithms with different features are an important trend in algorithm improvement. In this paper, an improved grey wolf optimization based on the two-stage search of hybrid covariance matrix adaptation-evolution strategy (CMA-ES) is proposed to overcome the shortcomings of the original grey wolf optimization that easily falls into the local minima when solving complex optimization problems. First, the improved algorithm divides the whole search process into two stages. In the first stage, the improved algorithm makes full use of the global search ability of grey wolf optimization on a large scale and thoroughly explores the location of the optimal solution. In the second stage, due to CMA-ES having a strong local search capability, the three CMA-ES instances use the α wolf, β wolf and δ wolf as the starting points. In addition, these instances have different step size for parallel local exploitations. Second, in order to make full use of the global search ability of the grey wolf algorithm, the Beta distribution is used to generate as much of an initial population as possible in the non-edge region of the solution space. Third, the new algorithm improves the hunting formula of the grey wolf algorithm, which increases the diversity of the population through the interference of other individuals and reduces the use of the head wolf’s guidance to the population. Finally, the new algorithm is quantitatively evaluated by fifteen standard benchmark functions, five test functions of CEC 2014 suite and two engineering design cases. The results show that the improved algorithm significantly improves the convergence, robustness and efficiency for solving complex optimization problems compared with other six well-known optimization algorithms.

1 Introduction

For many complex optimization problems, the traditional methods based on calculus (such as the Newton method and conjugate gradient method) have difficulty finding the optimal solution because of the lack of differentiability. Intelligent optimization methods, such as particle swarm optimization (PSO) (Eberhart and Kennedy 2002), the differential evolution algorithm (DE) (Storn and Price 1997), the fruit fly algorithm (FOA) (Pan 2012), the multi-verse optimizer (MVO) (Mirjalili et al. 2015), the whale optimization algorithm (WOA) (Mirjalili and Lewis 2016) and other intelligent optimization methods, have significant advantages in solving complex optimization problems. These intelligent optimization algorithms are based on natural heuristics and do not have any special requirements for the differentiability, continuity or convexity of the problem. Therefore, these intelligent optimization algorithms have been widely used (Peng et al. 2013; Chen et al. 2018).

The common goal of these algorithms is to find the best quality solutions and better convergence performance. To do this, intelligent optimization algorithms should be equipped with exploration and exploitation to ensure that they find the global optimum (Mirjalili et al. 2012; Chakri et al. 2017). Intelligent optimization algorithms can be broadly classified into three categories: constructive algorithms, improvement algorithms and hybrid algorithms (Nagano and Moccellin 2002). Although many research achievements have been achieved for the intelligent optimization algorithm, it still easily falls into the local optimal and has low precision in solving complex problems.

Considering the restrictiveness of the constructive algorithms and the improvement algorithms, recently, the research concentration has expanded to hybrid algorithms instead of a sole intelligent algorithm. The purpose of hybrid algorithms is to synthesize the advantages of different algorithms (Aydilek 2018). The no free lunch theorem has shown that all optimization algorithms have the same average performance in the mathematical sense (Wolpert and Macready 1997). Therefore, each algorithm has its scope of application. An important purpose of the hybrid algorithm is to make use of the unique features and advantages of each algorithm and to obtain the best solution in the largest problem domain. It has become evident that the hybrid of two or more intelligent algorithms is the most efficient approach and can have good application in dealing with the real-world engineering problems (Qiu et al. 2017; Chi et al. 2017; Anand and Suganthi 2018; Lin and Chiu 2018). The evolutionary computing and hybrid algorithm research expert, Raidl, believes that (Raidl 2006) choosing an appropriate hybrid algorithm is necessary to solve the most complex problems efficiently.

Grey wolf optimization (GWO), proposed by Mirjalili et al. (2014) in 2014, is a new intelligent optimization algorithm, which simulates the social hierarchy and hunting behaviors of grey wolves. In numerical optimization, the GWO algorithm (Mirjalili et al. 2014) and its variants (Saxena et al. 2018; Gupta and Deep 2018a, b, c; Gupta and Deep 2019) have been proven to be superior to the particle swarm optimization, the differential evolution algorithm and the gravitational search algorithm, etc., and has been successfully applied to solving economic dispatch problems (Kamboj et al. 2016; Pradhan et al. 2016; Venkatakrishnan et al. 2018), feature selection (Emary et al. 2015; Yamany et al. 2016; Medjahed et al. 2016; Daniel et al. 2017) and wireless sensor networks (Sujitha and Baskaran 2017). However, similar to other intelligent optimization algorithms, the GWO algorithm overemphasizes the global search. Therefore, it has lower search precision when optimizing some complex functions.

The covariance matrix adaptation-evolution strategy (CMA-ES) (Hansen 2006) is an excellent stochastic method for the continuous domain of nonlinear, non-convex functions. During the exploitation of the parameter space, CMA-ES attempts to learn a second-order model of the underlying objective function. However, the CMA-ES algorithm is a local search algorithm in essence that has a strong local search capability but is relatively weak in global search capability (Preuss 2010; Melo and Iacca 2014; Xu et al. 2017).

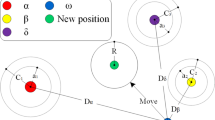
Along with the developmental trend of the hybrid algorithms discussed above, this paper proposes an improved grey wolf optimization based on the two-stage search of the hybrid CMA-ES (CMAGWO). The CMAGWO algorithm is divided into two stages in order to make up for the disadvantage of the slow convergence speed of GWO and the weak global search ability of the CMA-ES. In the first stage, the GWO algorithm, with a strong global search capability, conducts a large-scale search in as many possible locations of the region of optimal solution. In the second stage, three CMA-ES instances are generated for the local fine exploitation in parallel. The α wolf, β wolf and δ wolf, which are obtained in the first stage, are used as the starting point of the CMA-ES. In addition, each CMA-ES instance concurrently explores different regions of the search space and exchanges information about its status. Furthermore, in order to use the global search ability of the grey wolf algorithm, the population of GWO uses the Beta distribution in the initialization process. This allows the initial solution to be thoroughly generated in the non-edge region of the solution space. In the new algorithm, the process of wolves hunting in the original GWO is improved. The diversity of the population is increased by the interference of other individuals, and the absolute guidance of the head wolves to each individual is reduced.

The quantification evaluations of the algorithm are performed with fifteen standard benchmark functions, five test functions of CEC 2014 suite and two engineering design cases. The results show that the convergence accuracy, convergence speed and search robustness of CMAGWO have been significantly improved in solving complex problems over other approaches.

The rest of the paper is organized as follows. Section 2 briefly reviews the fundamentals of GWO and CMA-ES. The proposed CMAGWO algorithm is explained in Sect. 3. The experimental results are demonstrated in Sect. 4, comparing the performance of CMAGWO with other algorithms. Section 5 solves the two engineering optimization cases. Finally, Sect. 6 concludes the paper.

2 The original GWO and original CMA-ES

In this section, the features of the original GWO and the original CMA-ES are discussed.

2.1 The original grey wolf optimization

Grey wolves are considered apex predators, meaning that they are at the top of the food chain. They have a very strict social hierarchy. Grey wolf optimization is inspired by the grey wolf’s social hierarchy and hunting behavior. Compared with other evolutionary algorithms, GWO improves the optimization efficiency of the algorithm using swarm intelligence, which is based on the behavior of grey wolves within a social hierarchy when hunting prey. To mathematically model the social hierarchy of wolves, we consider the fittest solution as the $\alpha$. Consequently, the second and third best solutions are named $\beta$ and $\delta$, respectively. The rest of the candidate solutions are assumed to be $\zeta$. In the original GWO, the hunting is guided by $\alpha$, $\beta$ and $\delta$. The $\zeta$ wolves follow these three wolves.

When grey wolf optimization is used to solve the continuous problem, it is assumed that the population of grey wolves is $m$ and the dimension of each grey wolf is $n$. The position $x_{i}$ of wolf $i$ in the n-dimensional space can be expressed as follows:

$$ x_{i} = (x_{i1} ,x_{i2} , \ldots ,x_{in} ),\quad i = 1, \ldots ,m $$

(1)

The position $x_{\text{p}}$ of the prey is the global optimal solution. During the hunting process, grey wolves encircle the prey according to the following formula:

$$ D = \left| {\xi \cdot x_{\text{p}} (g) - x(g)} \right| $$

(2)

In the formula, $g$ is the current number of iterations. $x_{\text{p}} (g)$ indicates the position of the prey when the algorithm iterates to the $g$ th iteration, and $x(g)$ represents the position of the wolf in the $g$th iteration. $\xi$ is the coefficient:

$$ \xi = 2r_{1} $$

(3)

where $r_{1}$ is a random number in the range [0, 1].

When the grey wolves chase the prey, the positions of the grey wolves are updated according to Eq. (4).

$$ x(g + 1) = x_{\text{p}} (g) - A \cdot D $$

(4)

$$ A = 2a \cdot r_{2} - a $$

(5)

where $A$ is the convergence factor and $r_{2}$ is a random number in the range [0, 1].

According to Eq. (6), $a$ decreases linearly from 2 to 0 with the increase in the iterations. ${\text{Max}}\_{\text{iter}}$ is the maximum number of iterations.

$$ a = 2 - \frac{2g}{{{\text{Max}}\_{\text{iter}}}} $$

(6)

Grey wolves have the ability to recognize the location of prey and encircle them, but in the optimization process, the position $x_{\text{p}}$ of prey is unknown. To mathematically simulate the hunting behavior of grey wolves, we suppose that the $\alpha$ wolf, $\beta$ wolf and $\delta$ wolf have better knowledge about the potential location of prey. Therefore, we save the first three best solutions obtained so far and oblige the other search agents to update their positions according to the position of the best search agents. The hunting formula follows Eqs. (7)–(13):

$$ D_{\alpha } = \left| {\xi_{1} \cdot x_{\alpha } (g) - x(g)} \right| $$

(7)

$$ D_{\beta } = \left| {\xi_{2} \cdot x_{\beta } (g) - x(g)} \right| $$

(8)

$$ D_{\delta } = \left| {\xi_{3} \cdot x_{\delta } (g) - x(g)} \right| $$

(9)

$$ x_{1} (g) = x_{\alpha } (g) - A_{1} \cdot D_{\alpha } $$

(10)

$$ x_{2} (g) = x_{\beta } (g) - A_{2} \cdot D_{\beta } $$

(11)

$$ x_{3} (g) = x_{\delta } (g) - A_{3} \cdot D_{\delta } $$

(12)

$$ x(g + 1) = \frac{{x_{1} (g) + x_{2} (g) + x_{3} (g)}}{3} $$

(13)

According to Eqs. (7)–(12), we can calculate the distance between the grey wolf and the positions $x_{\alpha }$, $x_{\beta }$ and $x_{\delta }$ of the $\alpha$ wolf, $\beta$ wolf and $\delta$ wolf, respectively. According to Eq. (13), the direction of the individual moving toward the prey can be determined.

2.2 The original CMA-ES

Here, we consider a standard CMA-ES with a weighted intermediate recombination, step-size adaptation, and a combination of rank-μ update and rank-one update (Hansen 2006). At each iteration of the algorithm, the members of the new population are sampled from a multivariate normal distribution with the mean (${\text{mean}} \in R^{n}$) and covariance ($C \in R^{n \times n}$). $n$ is the dimension. The sampling radius is controlled by the overall standard deviation (step size) $\theta$. Let $x(g)$ represent the individual at generation $g$.

The CMA-ES optimization algorithm is approaching the optimal solution by repeatedly performing sampling, selection and recombination, updating parameters and so on. The algorithm stops and outputs the result when the maximum number of iterations is reached or the precision is met. The main operators of the CMA-ES algorithm are as follows:

• 1. Sampling

  In the CMA-ES, the population of the new search is generated by a multivariate normal distribution. The sampling formula is as follows:

  $$ x(g + 1) = {\text{mean}}^{g} + \theta^{g} \cdot N(0,C^{g} ) $$

  (14)

  where $N(0,C^{g} )$ is a multivariate normal distribution with zero mean and the covariance matrix ($C^{g}$). $g$ is the current number of iterations. ${\text{mean}}^{g}$ is the center point of the population, and $\theta^{g}$ is the step size.

• 2. Selection and recombination The new mean (${\text{mean}}^{g + 1}$) of the search distribution is a weighted average of the selected points $\mu$.

  $$ {\text{mean}}^{g + 1} = \sum\limits_{i = 1}^{\mu } {\omega_{i} x_{i;m}^{{}} (g + 1)} $$

  (15)

  where $\omega_{i}$ is the weight value, $\sum\nolimits_{i = 1}^{\mu } {\omega_{i} = 1}$, and $\omega_{1} \ge \omega_{2} \ge \cdots \ge \omega_{\mu } > 0$. The optimal individual assigns a larger weight value. $x_{i;m}^{{}} (g + 1)$ is the individual ($i$) after the sorting of the population ($m$) in the $g$ th iteration.

• 3. Updating parameters

  • 1. Adapting the covariance matrix

    $$ C^{g + 1} = (1 - c_{1} - c_{\mu } )C^{g} + c_{1} p_{\text{c}}^{g + 1} (p_{\text{c}}^{g + 1} )^{T} + c_{\mu } \sum\limits_{i = 1}^{\mu } {\omega_{i} } y_{i;m}^{{}} (g + 1)(y_{i;m}^{{}} (g + 1))^{T} $$

    (16)

    where $p_{\text{c}}^{g + 1}$ is the evolution path of covariance matrix ($C^{g + 1}$) in the $g + 1$th iteration. $c_{1}$ is the learning rate for the rank-one update. $c_{\mu }$ is the learning rate for the rank-$\mu$ update.

    $$ p_{\text{c}}^{g + 1} = (1 - c_{\text{c}} )p_{\text{c}}^{g} + \sqrt {c_{\text{c}} (2 - c_{\text{c}} )\mu_{\text{eff}} } \frac{{{\text{mean}}^{g + 1} - {\text{mean}}^{g} }}{{\theta^{g} }} $$

    (17)
    $$ y_{i;m}^{{}} (g + 1) = \frac{{x_{i;m}^{{}} (g + 1) - {\text{mean}}^{g} }}{{\theta^{g} }} $$

    (18)

    where $c_{\text{c}}$ is decay rate for the evolution path ($p_{\text{c}}^{g + 1}$). $\mu_{\text{eff}}$ is the variance effective selection mass, and $1 \le \mu_{\text{eff}} \le \mu$.

  • 2. Step-size adaptation

    $$ \theta^{g + 1} = \theta^{g} \exp \left( {\frac{{c_{\theta } }}{{d_{\theta } }}\left( {\frac{{\left\| {p_{\theta }^{g + 1} } \right\|}}{{E\left\| {N(0,I)} \right\|}} - 1} \right)} \right) $$

    (19)

    where $p_{\theta }^{g + 1}$ is the evolution path of step size ($\theta^{g + 1}$) in the $g + 1$th iteration. $E\left\| {N(0,I)} \right\|$ is the expectation of the Euclidean norm of $N(0,I)$. $I$ is the unit matrix. $c_{\theta }$ is the decay rate of the evolutionary path $p_{\theta }^{g + 1}$. $d_{\theta } \approx 1$ is the damping parameter.

    $$ p_{\theta }^{g + 1} = (1 - c_{\text{c}} )p_{\theta }^{g} + \sqrt {c_{\theta } (2 - c_{\theta } )\mu_{\text{eff}} } C^{ - \sqrt g } \frac{{{\text{mean}}^{g + 1} - {\text{mean}}^{g} }}{{\theta^{g} }} $$

    (20)

The CMA-ES algorithm completes the optimization process through the above steps. The initial search point is given or randomly generated and then randomly generates the next-generation population centered on the initial point of a certain probability density. Then, the evolutionary strategy parameters are updated to adjust the evolutionary direction, and finally, the optimal solution is achieved.

3 Improved GWO based on the two-stage search of hybrid CMA-ES

3.1 Population initialization

The advantage of the intelligent optimization algorithm is that the group members cooperate with each other and use the guidance of a certain mechanism to approach the optimal solution from the initial position. Therefore, the initial distribution of the population affects the search efficiency of the algorithm. The method of randomly generating the initial individual based on uniform distribution has the advantage of simplicity. However, in actual cases, the optimal solution is less located on the edge of the search space. It is more desirable to generate as many individuals as possible in the non-edge region and generate fewer individuals at the edge of the solution space. The ${\text{Beta}}$ distribution in the stochastic process reflects this distributional characteristic very well (Klein et al. 2016).

$$ {\text{Beta}}(x) = \frac{{x^{u - 1} (1 - x)^{v - 1} }}{B(u,v)},0 < x < 1 $$

(21)

where the denominator is the ${\text{Beta}}$ function, which can be defined as follows:

$$ B(u,v) = \int_{0}^{1} {t^{u - 1} (1 - t)^{v - 1} {\text{d}}t} $$

(22)

when $u = v = 1.2$, the graph of the ${\text{Beta}}$ distribution is as follows:

Figure 1 shows that the initial individuals generated by the ${\text{Beta}}$ distribution are mainly distributed in the non-edge regions. The population generated by this distribution can appear near the target area with a greater probability. Thus, the search efficiency is improved. The ${\text{Beta}}$ distribution conforms to the desired initial distribution of the population.

Fig. 1

The graph of the ${\text{Beta}}$ distribution

3.2 Global guidance of the GWO for hunting

Over the course of the iterations, the $\alpha$ wolf, the $\beta$ wolf and the $\delta$ wolf of the original GWO estimate the probable position of the prey. Each candidate solution updates its distance from the prey.

In the improved algorithm of the hybrid CMA-ES with the two-stage search, the GWO algorithm mainly plays the role of global search ability. Therefore, during the execution of the algorithm, the hunting process of the original grey wolf algorithm is improved. The overall guidance ability is increased to improve the diversity of the population by reducing the use of the head wolf’s guidance to each individual.

$$ D_{\alpha } = \left| {\xi_{1} \cdot x_{\alpha } (g) - x(g)} \right| $$

(23)

$$ D_{\beta } = \left| {\xi_{2} \cdot x_{\beta } (g) - x(g)} \right| $$

(24)

$$ D_{\delta } = \left| {\xi_{3} \cdot x_{\delta } (g) - x(g)} \right| $$

(25)

In the hunting formula of the original GWO, the positions of wolves are guided by the positions $x_{\alpha }$, $x_{\beta }$ and $x_{\delta }$ of the $\alpha$ wolf, $\beta$ wolf and $\delta$ wolf, respectively. In the new algorithm, the hunting formula is improved to guide the population optimization according to the distance between the grey wolves and the head wolf, thus improving the global generalization ability of the algorithm.

$$ x_{1} (g) = a \cdot x^{\prime}_{1} (g) - A_{1} \cdot \left| {\xi_{1} \cdot x_{\alpha } (g) - x(g)} \right| $$

(26)

$$ x_{2} (g) = a \cdot x^{\prime}_{2} (g) - A_{2} \cdot \left| {\xi_{2} \cdot x_{\beta } (g) - x(g)} \right| $$

(27)

$$ x_{3} (g) = a \cdot x^{\prime}_{3} (g) - A_{3} \cdot \left| {\xi_{3} \cdot x_{\delta } (g) - x(g)} \right| $$

(28)

$$ x(g + 1) = \frac{{x_{1} (g) + x_{2} (g) + x_{3} (g)}}{3} $$

(29)

where $x^{\prime}_{1} (g)$, $x^{\prime}_{2} (g)$ and $x^{\prime}_{3} (g)$ are the grey wolf individuals, which are different from $x(g)$ in the population. As the number of iterations increases, $a$ decreases linearly from 2 to 0. In the early stage of searching, $x^{\prime}_{1} (g)$, $x^{\prime}_{2} (g)$ and $x^{\prime}_{3} (g)$ play major roles in the generation of new individuals. $a$ gradually changes to 0 in the search process in Eq. (6). Therefore, the weights of $x^{\prime}_{1} (g)$, $x^{\prime}_{2} (g)$ and $x^{\prime}_{3} (g)$ are gradually reduced.

3.3 The hybrid CMAGWO procedure

CMA-ES is suitable for strong nonlinear and non-convex problems in continuous domains and has a strong local search capability (Wang et al. 2016). By improving the initial distribution of the original grey wolf algorithm and the global guidance of the hunting process, the improved grey wolf optimization can better realize the global search.

Therefore, the CMAGWO algorithm obtained by the hybrid design in the first stage uses the improved GWO algorithm for global search, guides the entire population to optimize it and detects as many new solutions as possible within the global scope. With the algorithm running, the search performance of the improved GWO algorithm is reduced to a certain threshold value. The CMAGWO algorithm transforms from the global detection as the main target to the local refined mining search. In the local refined search stage, the head wolf’s guidance ability is exploited. The positions $x_{\alpha }$, $x_{\beta }$ and $x_{\delta }$ of the three head wolves $\alpha$, $\beta$ and $\delta$ obtained from the improved GWO algorithm are used as the starting points of this stage. The CMAGWO algorithm generates three CMA-ES instances by performing a parallel search (instance CMA-ES-α, instance CMA-ES-β and instance CMA-ES-δ) in this stage. The starting points of the three instances of CMA-ES (instance CMA-ES-α, instance CMA-ES-β and instance CMA-ES-δ) can be described as follows:

Instance CMA-ES-α:

$$ {\text{mean\_}}\alpha = x_{\alpha } $$

(30)

Instance CMA-ES-β:

$$ {\text{mean\_}}\beta = x_{\beta } $$

(31)

Instance CMA-ES-δ:

$$ {\text{mean\_}}\delta = x_{\delta } $$

(32)

The initial step size is the ratio of the Euclidean distance between the instance center and the population center to the Euclidean distance of all individual and population center.

Instance CMA-ES-α:

$$ \theta \_\alpha = \frac{{d\left| {x_{\alpha } ,\bar{x}} \right|}}{{d\left| {x_{1} ,\bar{x}} \right| + d\left| {x_{2} ,\bar{x}} \right| + \cdots + d\left| {x_{i} ,\bar{x}} \right| + \cdots + d\left| {x_{m} ,\bar{x}} \right|}} $$

(33)

Instance CMA-ES-β:

$$ \theta \_\beta = \frac{{d\left| {x_{\beta } ,\bar{x}} \right|}}{{d\left| {x_{1} ,\bar{x}} \right| + d\left| {x_{2} ,\bar{x}} \right| + \cdots + d\left| {x_{i} ,\bar{x}} \right| + \cdots + d\left| {x_{m} ,\bar{x}} \right|}} $$

(34)

Instance CMA-ES-δ:

$$ \theta \_\delta = \frac{{d\left| {x_{\delta } ,\bar{x}} \right|}}{{d\left| {x_{1} ,\bar{x}} \right| + d\left| {x_{2} ,\bar{x}} \right| + \cdots + d\left| {x_{i} ,\bar{x}} \right| + \cdots + d\left| {x_{m} ,\bar{x}} \right|}} $$

(35)

where

$$ d\left| {x_{i} ,\bar{x}} \right| = \sqrt {\sum\limits_{j = 1}^{n} {\left( {x_{ij} - \bar{x}_{j} } \right)^{2} } } $$

(36)

$$ \bar{x} = (\bar{x}_{1} ,\bar{x}_{2} , \ldots ,\bar{x}_{j} , \ldots ,\bar{x}_{n} ),\quad 1 \le j \le n $$

(37)

$$ \bar{x}_{j} = \frac{1}{m}\left( {x_{1j} + x_{2j} + \cdots + x_{ij} + \cdots + x_{mj} } \right),\quad 1 \le j \le n $$

(38)

The CMAGWO algorithm sorts the population of each instance and generates the instances’ center points of the next generation using the weighted average of the previous $\mu$ individuals. In the second stage, the search coverage of instance CMA-ES-α, instance CMA-ES-β and instance CMA-ES-δ is as far as possible to avoid overlapping. Therefore, different scaling factors are used on the three instances: 1, 0.1 and 0.01. The CMAGWO algorithm obtains the new generation in the second stage according to Eqs. (39)–(41).

$$ x\_\alpha (g + 1) = {\text{mean\_}}\alpha^{g} + 1.0*\theta \_\alpha^{g} \cdot N(0,C\_\alpha^{g} ) $$

(39)

$$ x\_\beta (g + 1) = {\text{mean\_}}\beta^{g} + 0.1*\theta \_\beta^{g} \cdot N(0,C\_\beta^{g} ) $$

(40)

$$ x\_\delta (g + 1) = {\text{mean\_}}\delta^{g} + 0.01*\theta \_\delta^{g} \cdot N(0,C\_\delta^{g} ) $$

(41)

The value of the means (${\text{mean\_}}\alpha^{g + 1} ,\;{\text{mean\_}}\beta^{g + 1} ,\;{\text{and}}\;{\text{mean\_}}\delta^{g + 1}$), the covariance matrixes ($C\_\alpha^{g + 1}$, $C\_\beta^{g + 1}$, and $C\_\delta^{g + 1}$) and the step sizes ($\theta \_\alpha^{g + 1}$, $\theta \_\beta^{g + 1}$, and $\theta \_\delta^{g + 1}$) are updated according to Eqs. (15)–(20). Each instance independently searches the solution space from the starting point in parallel. In the CMAGWO, the population uses the data exchange mechanism to exchange information and shares the excellent individuals. Individuals evolve in the different environments for the three instances and perform fine mining in their respective local areas.

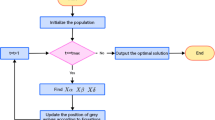
3.4 Pseudo-code of the proposed algorithm

The proposed CMAGWO can be given as follows:

• Step 1 Initializing the algorithm parameters.

  The maximum number of iterations is ${\text{Max\_iter}}$. a, A, $\xi$, $c_{\theta }$, $d_{\theta }$, $c_{c}$, $\mu_{\text{eff}}$ and other parameters are generated. Let g = 1.

• Step 2 In the search space, the grey wolf’s $m$ individuals are generated using the ${\text{Beta}}$ distribution to form the initial population.

• Step 3 Calculate the objective function value of each grey wolf and denote the positions as $x_{\alpha }$, $x_{\beta }$, and $x_{\delta }$ for the best three grey wolves.

• Step 4 Calculate the distance between the position of the grey wolf and the positions $x_{\alpha }$, $x_{\beta }$ and $x_{\delta }$ according to Eqs. (23)–(25).

• Step 5 Update the position of each grey wolf according to Eqs. (26)–(29).

• Step 6 When the performance of the improved GWO is reduced to a certain threshold, instance CMA-ES-α, instance CMA-ES-β and instance CMA-ES-δ are generated centered on $x_{\alpha }$, $x_{\beta }$ and $x_{\delta }$ according to Eqs. (30)–(32). The initial step size is generated by Eqs. (33)–(35). Otherwise, go to Step 3.

• Step 7 The three CMA-ES instances are sampled according to Eqs. (39)–(41).

• Step 8 Instance CMA-ES-α, instance CMA-ES-β and instance CMA-ES-δ perform the selection and recombination operations.

• Step 9 Update the mean (${\text{mean}}^{g + 1}$), covariance matrix ($C^{g + 1}$) and step size ($\theta^{g + 1}$) according to Eqs. (15)–(20).

• Step 10 If the accuracy is met or the maximum number of iterations is reached, the algorithm ends and the optimal solution is output; otherwise, Step 11 is performed.

• Step 11 g = g + 1, and return to Step 7.

3.5 Computational complexity

The computational complexity of an optimization algorithm is a key metric for evaluating the run time of an algorithm. The computational complexity of GWO and CMAGWO depends on the number of wolves $m$ in pack, dimensions of the problem $n$ and maximum number of iterations ${\text{Max\_iter}}$. By analyzing the steps of algorithms, the computational complexity of the CMAGWO and original GWO is defined as follows according to Eqs. (42), (43):

$$ O({\text{GWO}}) = O({\text{Max\_iter}} \times m \times n) $$

(42)

$$ \begin{aligned} O({\text{CMAGWO}}) & = O({\text{iter}}1 \times m \times n + 3 \times ({\text{Max\_iter}} - {\text{iter}}1) \times n) \\ & = O({\text{iter}}1 \times m \times n) + O(({\text{Max}}\_{\text{iter}} - {\text{iter}}1) \times n) \\ \end{aligned} $$

(43)

where ${\text{iter}}1$ represents the iteration numbers of CMAGWO in the first stage. The computational complexity of CMA-ES is $O(n)$ of each iteration (Hansen 2006).

4 Experimental verification and analysis

To verify the performance of the CMAGWO algorithm, fifteen standard benchmark functions and five test functions of CEC 2014 suite are used to test it. These functions are typical complex test functions. Moreover, the traditional methods based on calculus are difficult to obtain better results. All computational experiences for the test functions are implemented using MATLAB R2016b on a PC with an Intel core i5-2410 4.0 GHz processor and 8.0 GB memory.

The mathematical definitions and other relevant details of fifteen standard benchmark functions such as domains of variable and dimensions of the function are given in Table 1. Generally speaking, the standard benchmark functions are minimization functions and include three types: unimodal (F₁, F₇, F₈, F₉, F₁₀), multimodal (F₂, F₃, F₅, F₆, F₁₅) and fixed-dimension multimodal (F₄, F₁₁, F₁₂, F₁₃, F₁₄).

Table 1 The standard benchmark functions

4.1 The diversity measure of GWO and CMAGWO

The exploration and exploitation are the two important diversity characteristics of population. A large value of diversity implies more exploration while low implies more exploitation. The average distance is defined as the average of distances of all individuals from the population center. This diversity measure is given in Olorunda and Engelbrecht (2008). Three standard benchmark functions (unimodal function F₁, multimodal function F₂ and fixed-dimension multimodal function F₄) are taken into consideration for the average distance to quantify the diversity measure of individuals in the GWO and CMAGWO.

In all experiments, the values of the common parameters used in each algorithm, such as the population size and the total iteration number, are chosen to be the same. For all algorithms, the population size is set as m = 50 and the total number of iterations is set as ${\text{Max\_iter}} = 300$. To reduce the random error of the simulation, all experiments on each test function are repeated 15 runs.

A low value of the average distance shows population convergence around the population center, while a high value shows large dispersion of individuals from the population center. Figure 2 shows that the average distance of CMAGWO is large than GWO before 46th iteration. The average distance of CMAGWO is less than GWO after 46th iteration due to hybrid three CMA-ES instances. Figure 3 shows that the turning point of evolutionary iterations is 22th iteration. The turning point is 17th iteration in Fig. 4. The CMAGWO retains high diversity in early stage of the search process and proportionally decreases diversity as search progresses. It is observed that the average distance is decreased gradually over the course of iteration, two-stage search that guarantees transition between exploration and exploitation. It is clear from the results of average distance that the exploration ability and exploitation ability of the CMAGWO based on the two-stage search of hybrid CMA-ES are better than the GWO.

Fig. 2

The average distance for the unimodal function $F_{1}$

Fig. 3

The average distance for the multimodal function $F_{2}$

Fig. 4

The average distance for the fixed-dimension multimodal function $F_{4}$

4.2 Performance on the standard benchmark functions

In order to analyze the convergence speed and accuracy, the CMAGWO algorithm is compared with GWO, CMA-ES, MVO, WOA, PSOGWO (which is the hybrid of GWO and PSO) (Singh and Singh 2017), and DEGWO (which is the hybrid of GWO and DE) (Zhu et al. 2015). The algorithms and other specific parameter settings are given as follows: The GWO algorithm is the same as the parameter setting in reference (Mirjalili et al. 2014), CMA-ES refers to (Hansen 2006), MVO refers to (Mirjalili et al. 2015), WOA refers to Mirjalili and Lewis (2016), PSOGWO refers to Singh and Singh (2017), and DEGWO refers to Zhu et al. (2015). The experimental environment and the iteration numbers of algorithms are the same as above.

In practical applications, the efficiency of the algorithm is given more attention while the convergence is ensured. To compare the convergence efficiency of these algorithms, Table 2 shows the convergence algebra of each algorithm on the standard benchmark functions. (The iteration number is recorded as the convergence algebra when the MEAN value is less than 10E−3.)

Table 2 The convergence algebra on the standard benchmark functions

The CMA-ES performs well on some functions. The results show that the CMAGWO algorithm is excellent on unimodal (F₁, F₇, F₉, F₁₀), multimodal (F₂, F₃, F₅, F₆, F₁₅) and fixed-dimension multimodal (F₄, F₁₁, F₁₂, F₁₄), converges to the global optimal solution at a faster speed, and has good optimization efficiency. Even for function $F_{8}$ and function $F_{13}$, the CMAGWO algorithm is better than other algorithms.

The detailed computational data of all test functions for these algorithms will be presented. The best objective function value (BEST), the worst objective function value (WORST), the mean value (MEAN) and the standard deviation (STD) of all algorithms are given. These indices are used to evaluate the accuracy of the algorithm (the ability to jump out of the local optimum) and the robustness. Tables 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17 show the BEST, the WORST, the MEAN and the STD of seven algorithms on each standard benchmark function. To maintain a fair competitive environment, the stopping criterion for all the algorithms is maximum iteration. Tables 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17 and Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19 show the performance results of the algorithms.

Table 3 Optimal results for the function $F_{1}$

Table 4 Optimal results for the function $F_{2}$

Table 5 Optimal results for the function $F_{3}$

Table 6 Optimal results for the function $F_{4}$

Table 7 Optimal results for the function $F_{5}$

Table 8 Optimal results for the function $F_{6}$

Table 9 Optimal results for the function $F_{7}$

Table 10 Optimal results for the function $F_{8}$

Table 11 Optimal results for the function $F_{9}$

Table 12 Optimal results for the function $F_{10}$

Table 13 Optimal results for the function $F_{11}$

Table 14 Optimal results for the function $F_{12}$

Table 15 Optimal results for the function $F_{13}$

Table 16 Optimal results for the function $F_{14}$

Table 17 Optimal results for the function $F_{15}$

Fig. 5

The convergence curve on the function $F_{1}$

Fig. 6

The convergence curve on the function $F_{2}$

Fig. 7

The convergence curve on the function $F_{3}$

Fig. 8

The convergence curve on the function $F_{4}$

Fig. 9

The convergence curve on the function $F_{5}$

Fig. 10

The convergence curve on the function $F_{6}$

Fig. 11

The convergence curve on the function $F_{7}$

Fig. 12

The convergence curve on the function $F_{8}$

Fig. 13

The convergence curve on the function $F_{9}$

Fig. 14

The convergence curve on the function $F_{10}$

Fig. 15

The convergence curve on the function $F_{11}$

Fig. 16

The convergence curve on the function $F_{12}$

Fig. 17

The convergence curve on the function $F_{13}$

Fig. 18

The convergence curve on the function $F_{14}$

Fig. 19

The convergence curve on the function $F_{15}$

From the results (Tables 3, 9, 10, 11, 12) of unimodal functions (F₁, F₇, F₈, F₉, F₁₀), it can be concluded that the CMAGWO algorithm has higher BEST values and MEAN values than the other algorithms. It is worth mentioning here that the values of the STD for unimodal functions are also competitive for CMAGWO. These low values are indicator of better solution quality obtained from independent runs. Similarly, for multimodal functions (F₂, F₃, F₅, F₆, F₁₅), fixed-dimension multimodal functions (F₄, F₁₁, F₁₂, F₁₃, F₁₄), the results of CMAGWO are competitive for these functions too. For unimodal function $F_{8}$ and fixed-dimension multimodal function $F_{13}$, the MEAN value of the CMAGWO algorithm is large than 10E−3, but also better than other algorithms. Therefore, the CMAGWO algorithm proposed in this paper has better robustness and accuracy on these standard benchmark functions.

To give a visualized and detailed comparison, Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19 give the convergence curves of the proposed CMAGWO algorithm, GWO, MVO, WOA, CMA-ES, PSOGWO and DEGWO on fifteen standard benchmark functions. In these figures, convergence curves are plotted corresponding to the MEAN value of the objective functions obtain in 15 runs. In these graphs, the horizontal axis represents the number of iterations and the vertical axis represents the objective function value. The initialization points of each algorithm are same.

According to the results of Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19, CMAGWO is able to provide very competitive results. It is noted that the unimodal functions (F₁, F₇, F₈, F₉ and F₁₀) are suitable for benchmarking exploitation. Therefore, these results (Figs. 5, 11, 12, 13 and 14) show the superior performance of CMAGWO based on the two-stage search in terms of exploiting the optimum. This is due to the proposed exploitation operators previously discussed. Therefore, these results evidence high exploitation capability of the CMAGWO algorithm. In contrast to the unimodal functions, multimodal functions (F₂, F₃, F₅, F₆ and F₁₅) and fixed-dimension multimodal functions (F₄, F₁₁, F₁₂, F₁₃, and F₁₄) have many local optima with the number increasing exponentially with dimension. This makes them suitable for benchmarking the exploration ability of an algorithm. Due to global search ability of CMAGWO with the Beta distribution and the improved hunting formula, the convergence graphs of fixed-dimension multimodal functions (Figs. 8, 15, 16, 17, 18) show the higher diversity in early stage of the search process and better concentration as search progresses. According to Figs. 6, 7, 9, 10 and 19, CMAGWO also provides very competitive results on the multimodal functions (F₂, F₃, F₅, F₆, F₁₅) as well. It can be observed that the proposed algorithm CMAGWO narrates a more efficient performance compared to GWO, MVO, WOA, CMA-ES, PSOGWO and DEGWO with superior convergence speed and higher precision.

4.3 Performance on the five CEC 2014 benchmark functions

The next experimental study is designed on the five numerical optimization problems considered from CEC 2014 special session and competition on single objective real-parameter numerical optimization (Liang et al. 2013). These five test functions of CEC 2014 suite are especially equipped with various novel characteristics such as novel basic problems and functions are shifted, rotated, expanded, and combined variants of the most complicated mathematical optimization problems presented in the literature. The details of these five test functions such as the search domains and dimensions are described in Table 18. For all algorithms (GWO, MVO, WOA, CMA-ES, DEGWO, PSOGWO and CMAGWO), the population size is set as m = 50 and the total number of iterations is set as ${\text{Max\_iter}} = 2000$. All experiments on each CEC 2014 suite are iterated over 15 independent runs. The termination criteria in all the algorithms are taken same for a fair comparison between algorithms to avoid the biasedness in performance.

Table 18 The brief description of CEC 2014 benchmark functions

From Table 18, the comparative analysis of the performance of proposed algorithms is studied. The detailed computational data of all test functions for these algorithms are presented in Tables 19, 20, 21, 22 and 23 and Figs. 20, 21, 22, 23 and 24.

Table 19 Optimal results for the function $F_{16}$

Table 20 Optimal results for the function $F_{17}$

Table 21 Optimal results for the function $F_{18}$

Table 22 Optimal results for the function $F_{19}$

Table 23 Optimal results for the function $F_{20}$

Fig. 20

The convergence curve on the function $F_{16}$

Fig. 21

The convergence curve on the function $F_{17}$

Fig. 22

The convergence curve on the function $F_{18}$

Fig. 23

The convergence curve on the function $F_{19}$

Fig. 24

The convergence curve on the function $F_{20}$

The BEST, the WORST, the MEAN and the STD of all algorithms are given in Tables 19, 20, 21, 22 and 23. Inspecting the MEAN values of these functions, it is observed that MEAN values are optimal for CMAGWO as compared with the other algorithms. It is worth mentioning here that in some cases, especially for function $F_{16}$ Rotated High Conditioned Elliptic Function (CEC1) and $F_{18}$ Shifted and Rotated Katsuura Function (CEC12), the CMAGWO finds the Minimum value. From the STD values obtained from experiments, it is also observed that the performance of CMAGWO is competitive. These indices evaluate the accuracy, and the robustness of the CMAGWO is better than that of other six algorithms.

Convergence curves of this experiment are shown in Fig. 20 for $F_{16}$ Rotated High Conditioned Elliptic Function (CEC1), in Fig. 21 for $F_{17}$ Shifted and Rotated Rastrigin’s Function (CEC9), in Fig. 22 for $F_{18}$ Shifted and Rotated Katsuura Function (CEC12), in Fig. 23 for $F_{19}$ Hybrid Function 5 (N = 5) (CEC21), and in Fig. 24 for $F_{20}$ Composition Function 5 (N = 5) (CEC27). The results of these CEC2014 functions strongly prove that high exploration of the CMAGWO algorithm is fruitful for avoiding local solutions. By inspecting the convergence curves of these functions, it is empirical to state that a significant improvement has been observed in convergence characteristics by the proposed the two-stage search compared to GWO, MVO, WOA, CMA-ES, PSOGWO and DEGWO.

Based on the observations reported in this section, it can be concluded that the CMAGWO algorithm provides very competitive results on these test functions. This superior capability is due to the hybrid mechanism. As mentioned above, some iterations are devoted to exploration (the first stage) and the rest to exploitation (the second stage). Moreover, by embedding Beta distribution in the initialization process and the process of wolves hunting changed, the exploration ability is accelerated. High local optima avoidance of this algorithm is finding that is inferred from above results. The five test functions of CEC 2014 suite have very difficult search spaces, so the accurate approximation of their global optima needs high exploration and exploitation combined. The results again evidence that the CMAGWO algorithm properly balances these two conflicting milestones. In the following section, the applications of proposed algorithm on real engineering problems are investigated.

5 Application studies on two engineering cases

In this section, to validate the accuracy and effectiveness of the proposed CMAGWO, we use two engineering cases as applications.

5.1 Optimization design of linkage mechanism

The movement of the linkage mechanism (such as the trajectory of a moving point) can be described as the function derived from the relationship of the mechanism’s geometric parameters. Suppose that $F\theta_{i}$ is the desired output angle and $S\theta$ is the actual output angle of the linkage mechanism. $F\theta_{0}$ is the initial angle for the linkage mechanism.

According to the mechanism’s kinematics, the actual output angle of the linkage is obtained as follows:

$$ S\theta = \left\{ {\begin{array}{*{20}c} {\pi - \arccos \frac{{r_{i}^{2} - x_{2}^{2} + x_{1}^{2} }}{{2r_{1} x_{2} }} - \arccos \frac{{r_{i} + 24}}{{10r_{1} }}\begin{array}{*{20}c} {} & {0 < \varphi_{i} \le \pi } \\ \end{array} } \\ {\pi - \arccos \frac{{r_{i}^{2} - x_{2}^{2} + x_{1}^{2} }}{{2r_{1} x_{2} }} + \arccos \frac{{r_{i} + 24}}{{10r_{1} }}\begin{array}{*{20}c} {} & {\pi < \varphi_{i} \le 2\pi } \\ \end{array} } \\ \end{array} } \right. $$

(44)

where $r_{i}$ is the connection parameter, $r_{i} = \sqrt {26 - 10\cos \varphi_{i} }$, $i$ is the sequence number after angle division, and $i = 0,1,2, \ldots ,30$, $\varphi_{i}$ is the actual position angle of the crank, $\varphi_{i} = \varphi_{0} + \frac{i}{30} \times \frac{\pi }{2}$, and $\varphi_{0}$ is the initial angle for the crank.

The desired output angle of the linkage mechanism can be described as follows:

$$ F\theta_{i} = F\theta_{0} + \frac{2}{3\pi }(\varphi_{i} - \varphi_{0} )^{2} $$

(45)

Within the given range (in order to make the mechanism have the best transfer performance, the transmission angle of the mechanism required is the minimum value or the maximum value), the optimal design of the linkage mechanism should minimize the error between the actual output angle and the desired output angle. Therefore, the mathematical model for the optimization problem minimizes the least square error between the expected value and the actual value of the output angle of the linkage mechanism.

$$ f(x) = \sum\limits_{i = 0}^{30} {(F\theta_{i} - S\theta )^{2} } $$

(46)

The given range of motion can be described as a constraint condition:

$$ - x_{1}^{2} - x_{2}^{2} + \sqrt 2 x_{1} x_{2} + 16 \ge 0 $$

(47)

$$ x_{1}^{2} + x_{2}^{2} + \sqrt 2 x_{1} x_{2} - 36 \ge 0 $$

(48)

where $0 \le x_{1} \le 5.0$ and $0 \le x_{2} \le 5.0$.

For the constraint conditions, this paper uses the penalty function method to transform the constraint problem into an unconstrained one by introducing a penalty factor.

In this work, the proposed CMAGWO algorithm and other six referred algorithms: GWO, MVO, WOA, CMA-ES, PSOGWO and DEGWO, are all employed to solve the optimization problem of the linkage mechanism. The parameters of these algorithms for this problem are set as the same as in Sect. 4. To solve this optimization problem, results are averaged over 15 independent runs. Figure 25 along with Table 24 shows the results of the CMAGWO with other six algorithms.

Fig. 25

The convergence curve on the optimization problem of linkage mechanism

Table 24 Optimal results for the problem of linkage mechanism

Figure 25 shows that compared with GWO, MVO, WOA, CMA-ES, PSOGWO and DEGWO, the CMAGWO algorithm has a faster convergence speed, which is more satisfactory with the requirements of the actual engineering efficiency. The results of MEAN value and BEST value in Table 24 show that the CMAGWO algorithm can approach the expected value of the linkage mechanism with higher precision. The CMAGWO has the smallest STD between the seven algorithms. Therefore, the CMAGWO algorithm has stronger robustness and adaptability.

5.2 Position optimization of the robotic arm

The robotic arm is composed of the rotating joints and the moving joints. Thus, the robotic arm model can be simplified to the joints that are connected end to end. The first joint is connected to the base of the robotic arm, and the ends are connected with an effector such as a manipulator, welding gun or spray gun. The end effector position that we want to achieve is finally realized by the movement of the joints of the robotic arm.

Therefore, according to the forward kinematics equation of the robotic arm, the relationship between the position of the end effector and the angle of each joint is established. To realize the end effector to complete the work task in the operation space, the actual position ${\text{PE}} = ({\text{PE}}_{1} ,{\text{PE}}_{2} ,{\text{PE}}_{3} )$ of the arm end can be calculated by the following:

$$ \begin{aligned} {\text{PE}}_{1} & = l_{1} - l_{4} *\cos (x_{1} )*\sin x_{2} *\sin x_{3} - \cos x_{1} \cos x_{2} \cos x_{3} - l_{2} *\sin x_{1} - l*\sin x_{1} *\sin x_{4} \\ & \quad + \cos x_{4} *\cos x_{1} *sinx_{2} *\sin x_{3} - \cos x_{1} *\cos x_{2} *\cos x_{3} + l_{3} *\cos x_{1} *\cos x_{2} \\ \end{aligned} $$

(49)

$$ \begin{aligned} {\text{PE}}_{2} & = l_{2} \cos x_{1} - l_{4} *\sin x_{1} *\sin x_{2} *\sin x_{3} - \cos x_{2} \cos x_{3} \sin x_{1} - l*\cos x_{1} *\sin x_{4} \\ & \quad - \cos x_{4} *\sin x_{1} *\sin x_{2} *\sin x_{3} - \cos x_{2} *\cos x_{3} *\sin x_{1} + l_{3} *\cos x_{2} *\sin x_{1} \\ \end{aligned} $$

(50)

$$ \begin{aligned} {\text{PE}}_{3} & = - l_{4} *\cos x_{2} *\sin x_{3} + \cos x_{3} \sin x_{2} + l_{3} *\sin x_{2} - l*\cos x_{4} *\cos x_{2} *\sin x_{3} \\ & \quad + \cos x_{3} *\sin x_{2} \\ \end{aligned} $$

(51)

where the D–H parameters of the arm are the length of the end ($l = 0.085$) and the lengths of the common vertical line between one joint and the next joint ($l_{1} = 0.175$, $l_{2} = 0.082$, $l_{3} = 0.38$ and $l_{4} = 0.26$).

The desired position of the arm end is known. Based on the model that requires the highest accuracy to reach the target point and moves the joint angle as small as possible, the objective function is established as follows:

$$ \begin{aligned} f(x) & = \sqrt {\left( {{\text{PF}}_{1} - {\text{PE}}_{1} } \right)^{2} + \left( {{\text{PF}}_{2} - {\text{PE}}_{2} } \right)^{2} + \left( {{\text{PF}}_{3} - {\text{PE}}_{3} } \right)^{2} } \\ & \quad + 10^{ - 5} *((x_{1} - q0_{1} )^{2} + 0.5*(x_{2} - q0_{2} )^{2} + 0.5*(x_{3} - q0_{3} )^{2} + 0.1*(x_{4} - q0_{4} )^{2} ) \\ \end{aligned} $$

(52)

where the initial angle of each joint of the robotic arm is $q0 = ( - \frac{\pi }{2},\frac{\pi }{2}, - \frac{\pi }{2},0)$, and the constraint condition of each joint is $- \;2.62 \le x_{1} \le - \;0.52$, $0.52 \le x_{2} \le 2.62$, $- \;2.35 \le x_{3} \le - \;0.79$ and $- \;1 \le x_{4} \le 1$.

Taking the desired target position ${\text{PF}} = ( - \;0.0516, - \;0.4006, - \;0.4135)$ of the arm end as an example, CMAGWO is used for position optimization and compared with the other algorithms.

Figure 26 shows the convergence curves of the seven algorithms for the position optimization of the robotic arm. The parameters of these algorithms for this problem are set as the same as in Sect. 4. Figure 26 shows that compared with GWO, MVO, WOA, CMA-ES, PSOGWO and DEGWO, the CMAGWO algorithm can approach the desired target position at a faster convergence speed.

Fig. 26

The convergence curve on the position optimization of robotic arm

The results obtained by the proposed CMAGWO are compared with those gained by other six algorithms, and the comparisons are presented in Table 25. The experimental results in Table 25 show that the CMAGWO algorithm has a higher BEST value and MEAN value in the optimization position of robotic arm. Moreover, the STD of CMAGWO is also the smallest in these algorithms. Table 25 shows that CMAGWO has stronger robustness and accuracy of robotic arm position optimization and verifies the effectiveness of the CMAGWO algorithm.

Table 25 Optimal results for the end position of robotic arm

The results of the design optimization of linkage mechanism and position optimization of the robotic arm demonstrate the performance of the CMAGWO algorithm in terms of exploration, exploitation, local optima avoidance and convergence. This is again due to the two-stage search of hybrid CMA-ES. Furthermore, in order to give full global search ability of the grey wolf optimization, the initial population is thoroughly generated in the non-edge region of the solution space by the Beta distribution. The new algorithm improves the hunting formula of the original GWO, increases the diversity of the population through the interference of other individuals and reduces the absolute guidance of the head wolf to each individual. The results show a good balance between exploration and exploitation. This comprehensive study shows that the proposed CMAGWO algorithm has merit among the GWO, MVO, WOA, CMA-ES, PSOGWO and DEGWO.

6 Conclusion

To break through the limitations of the sole algorithm, this paper proposes an improved grey wolf optimization based on the two-stage search of hybrid CMA-ES, which is combined with the global search ability of the GWO algorithm and the strong local search ability of the CMA-ES algorithm. In the first stage, the CMAGWO algorithm mainly uses the global ability of the grey wolf algorithm to explore the entire search space. At this stage, the approximate location of the optimal solution is located as much as possible. When a certain search threshold is reached, the local parallel refinement search is switched. In the second stage, three instances are used to exploit the key areas. During the search process, data exchange and information sharing between instances are carried out. The purposes of the two stages are different, and the operators and operation strategies are different.

Finally, the improved algorithm is validated by fifteen standard benchmark functions and five test functions of CEC 2014 suite. The CMAGWO has been compared with other six popular meta heuristic algorithms. The results show that the CMAGWO algorithm proposed in this paper effectively improves the performance and overcomes the disadvantages of the GWO algorithm, which easily falls into the local optimum in solving complex functions. Moreover, the applicability of the CMAGWO has been demonstrated on two engineering design cases. Through the analysis of the optimal results and the convergence curve, it is observed that the CMAGWO is more satisfactory with the requirements of the actual engineering efficiency. Application of the proposed CMAGWO on more practical challenging problems will be investigated in future.