A novel chaotic Jaya algorithm for unconstrained numerical optimization

Abstract

Jaya algorithm is one of the recent algorithms developed to solve optimization problems. The basic concept of this algorithm consists in moving the obtained solution, for a given problem, toward the best solution and avoiding the worst one. However, it severely suffers from premature convergence problem and therefore can be easily trapped in local optimums. This study aimed to alleviate these drawbacks and improve the performance of the original Jaya algorithm. Here, three new mutation strategies were implemented in the original Jaya to improve both its global and local search abilities. Chaotic maps were proved to be able to boost the search capabilities of meta-heuristic algorithms. Therefore, after demonstrating its chaotic behavior through the sensitivity to initial conditions, topological transitivity and the density of periodic points, we proposed a new 2D cross chaotic map. The chaotic sequences provided by the proposed chaotic map were embedded into the original Jaya algorithm to generate the initial population and control the search equations. It is worth mentioning that the modifications incorporated in the original algorithm did not affect its two essential characteristics, i.e., simplicity and nonrequirement of additional control parameters. As case studies, sixteen benchmark functions were used to evaluate the performance of the proposed chaotic Jaya algorithm (C-Jaya) regarding solution accuracy and convergence speed. Comparisons with some other meta-heuristic algorithms for low-, middle- and high-dimensional benchmark functions show that the proposed C-Jaya algorithm enhances the performance of original Jaya significantly. Moreover, it offers the fastest global convergence, the highest solution quality and it is the most robust on almost all the test functions among all the algorithms. Nonparametric statistical procedures, i.e., Friedman test, Friedman aligned ranks test and Quade test, conducted to analyze the obtained results, show the superiority of the proposed algorithm.

1 Introduction

1.1 Research background

Several problems in various engineering domains can be formulated as optimization problems. Thus, the achievement of optimal solutions requires better optimization algorithms. Traditional optimization algorithms like dynamic programming, linear programming, steepest descent usually fail to reach optimal solutions for large-scale problems particularly with nondifferentiable, epistasis, i.e., correlated parameter, nonconvex and nonlinear objective function. Moreover, previous techniques fail to handle multimodal optimization problems. To overcome the aforementioned problems, heuristic algorithms have emerged as a robust method for finding optimum solutions for a given problem. Several classification criteria have been considered in the literature, such as deterministic, iterative-based, stochastic, population-based. The search process of population-based algorithms is initiated with the generation of random candidate solutions. The initial population is enhanced over time until a termination condition is satisfied. This kind of algorithms can be classified into two main groups: swarm intelligence-based algorithms and evolutionary algorithms (EA). Recently, some inventive techniques have been involved in improving the efficiency of the heuristic methods and the obtained algorithms are called meta-heuristic. The main advantages of these algorithms compared to conventional techniques are simplicity, better local optimum avoidance, gradient-free mechanism and flexibility. Researchers have made enormous efforts in this field, and nature-inspired meta-heuristic optimization algorithms have proved their efficiency in several optimization problems and thereby are extensively used.

1.2 Related works

Over the last three decades, well-known nature-inspired optimization algorithms have been developed: genetic algorithm (GA) [23] based on simulating living beings evolution and the survival of the fittest stated in Darwinian theory; particle swarm optimization (PSO) [32] based on the social behavior of fish schooling or bird flocking; artificial immune algorithm (AIA) [17] which is inspired by the behavior of the human being’s immune system; ant colony optimization (ACO) [14] which imitates the ant colonies foraging behavior; biogeography-based optimization (BBO) [54] which simulates the island species migration behavior; shuffled frog Leaping (SFL) [15] which imitates the collaborative behavior of the frogs; artificial bee colony (ABC) [31] which is inspired by the honey bee foraging behavior; gravitational search algorithm (GSA) [51] which works on Newton gravity law; Grenade Explosion Method (GEM) [2] which is inspired by the explosion of a grenade; and teaching-learning algorithm (TLA) [48, 49] which imitates the teaching and learning processes.

All the aforementioned algorithms presented some limitations in their evolution process. The main weakness consists in the fact that the effectiveness of these algorithms is profoundly affected by the fixed control parameters [49]. In other words, the excellent selection of the parameters is crucial for the evolution process toward the optimum solution. For example, genetic algorithm provides near-optimal solutions owing to the difficulty to adjust the adequate controlling settings, such as mutation rate and crossover rate. The same applies to PSO, which uses cognitive and social parameters and inertia weight [28]. Similar to these two algorithms, ABC needs some control parameters, for instance, number of bees, limit. Similarly, BBO requires the probability of the habitat modification, mutation probability, habitat elitism parameter and population size. The design of an optimization algorithm that does not require control parameters has challenged researchers. This property was taken into account in this research.

Recently, there has been a surge of interest in the use of hybridization which is the combination of optimization algorithms to improve their quality [6,7,8, 21, 64]. The performance of the obtained algorithm is almost always superior to the original. Chaos is among the newest techniques applied in various engineering fields. Chaos theory concerns the study of chaotic dynamical systems which can be defined as nonlinear dynamical systems characterized by a high sensitivity to their initial conditions [38, 42]. In other words, the outcome of the system is substantially affected by small changes in the initial conditions. Moreover, it can be recognized as pseudo-random behavior produced by a deterministic nonlinear system. Due to dynamic characteristics and ergodicity, chaos search emerges as a powerful technique for hybridization. The incorporation of chaos in a meta-heuristic algorithm can be divided into three classes; in the first class, the chaotic sequences generated by chaotic maps are used to substitute random numbers. In the second, local search approaches are implemented via chaotic map function, whereas the control parameters of algorithms are generated chaotically in the third one [30].

Being fascinated by the potential of chaos, many researchers have demonstrated that the introduction of chaos in optimization algorithms contributes to improving their original version, such as chaotic differential evolution [27, 43], chaotic genetic algorithms [37, 61], chaotic simulated annealing [24, 39], chaotic firefly algorithm [19, 22], chaotic-bat swarm optimization [18] and chaotic biogeography-based optimization [52, 53, 59]. In 2010, Alatas embedded seven chaotic maps into harmony search (HS) algorithms [4]. He proved that chaos could improve their solution quality. In another work, Alatas demonstrated the benefit of introducing chaos in the ABC algorithm [3]. A chaos-improved version of the imperialist competitive algorithm (ICA) was proposed in 2012 by Talatahari et al. [57]. Mirjalili and Gandomi [40] pinpointed the problem of trapping in local optimum in gravitational search algorithm (GSA) and proposed a chaos-enhanced version of GSA. Also, Gao et al. [20] introduced chaos in GSA in two different manners. The first approach can be summarized in substituting random sequences by chaotic sequences generated by the chaotic map, while the second one uses chaos like a local search method. In [29], Jordehi developed three different versions of chaotic-bat swarm optimization (BSO) algorithm using eleven chaotic maps, and the best one was retained as the proposed BSO algorithm. Huang et al. [25] proposed a new chaotic cuckoo search (CCS) optimization algorithm by embedding chaotic approach into cuckoo search (CS) algorithm. In [16], Farah et al. proposed a new chaotic teaching-learning algorithm and applied it to a real-life problem. All the above studies prove the successful applicability of chaos approach in meta-heuristic algorithms.

1.3 Our contribution

The objective of the present work was to establish an efficient chaotic-based C-Jaya algorithm that alleviates premature convergence problem and outperforms the performance of its original version as well as those of the existing well-established meta-heuristic algorithms. Three new search equations were implemented for modifying the search process of the original Jaya algorithm which increases its search capabilities, improves the global convergence abilities and prevents the search process from sticking on a local optimum. Furthermore, a new 2D cross chaotic map was proposed and its characteristics were proved by Devaney definition. This chaotic map was firstly used to generate the initial population and secondly integrated into the search equations. By doing so, the chaotic search would directly enhance the current solutions obtained by Jaya algorithm, lead to a satisfactory convergence speed and possibly allow a higher probability to escape from local solution.

1.4 Structure of the paper

The remainder of this paper is organized as follows. The proposed 2D cross chaotic map and its impact on Jaya algorithm are given in Sect. 2. Section 3 presents a brief description of the Jaya algorithm. Section 4 discusses the integration of the proposed chaotic map into the original Jaya algorithm to develop the proposed C-Jaya algorithm. Section 5 is devoted to testing the proposed approach through benchmark problems by comparing the results achieved by the proposed algorithm with those obtained via well-known meta-heuristic algorithms. Finally, a summary of our paper based on the comparison analysis is presented in Sect. 6.

2 The proposed 2D cross chaotic map and its impact on Jaya algorithm

2.1 The new 2D cross chaotic map

The proposed 2D cross chaotic map is defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{i+1}=\cos \left( k\arccos (y_i)\right) \\ y_{i+1}=16x_i^5-20x_i^3+5x_i \end{array}\right. } \end{aligned}$$

(1)

where $x_i$, $y_i\in \left[ -\,1,1\right]$, $k>1$ and $(x_0,y_0)$ are the initial conditions. However, Chebyshev map $x_{i+1}=\cos \left( k\arccos (y_i)\right)$ has been proven chaotic in [33]. The chaos proof of $G(x)=16x^5-20x^3+5x$ based on Devaney definition [12] is given in “Appendix A.”

Fig. 1

The evaluated solutions by 2000 FEs of Jaya algorithm when solving $f_6$ and $f_7$ problems a $f_6$ Ackley, b $f_7$ Rastrigin

2.2 The impact of the 2D cross map on Jaya algorithm

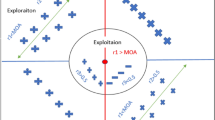
Before explaining the role of the new 2D cross map in the improvement of Jaya algorithm, two concepts must be defined: exploitation and exploration. The former consists in focusing more on a thoroughly narrow—but promising—area of the search space to improve the initial solution. This process allows to refine the solution and avoid big jumps in the search space. Therefore, exploitation is linked to local search as it improves the present solution by searching in its vicinity with a tiny perturbation. The latter deals with covering the whole search space to find other good solutions that can be enhanced. Indeed, it is linked with global search, i.e., search in diverse regions of the whole space, to gain new promising solutions and avoid being trapped in local optimums. A good optimization algorithm should strike a balance between exploitation and exploration [9, 13, 56, 58]. In fact, escaping local optimums requires a high level of diversification at the beginning of the algorithm and a lower one at its end. At the same time, the improvement of the current solution(s) requires a high level of intensification (refining) at the end of the algorithm and a lower one in its beginning. In short, the algorithm should favor global search in the beginning and local search at the end.

Recently, chaos has been extensively studied in the optimization field due to its dynamic properties, which support the algorithm to overcome local optimums [62, 63]. These properties include sensitivity to initial conditions, quasi-stochastic property and ergodicity [34]. They produce a high level of diversification in the algorithm that helps to explore the search space properly and then escape from any potential local optimum.

Fig. 2

Convergence visualization of solutions (for the first five generations) when solving $f_6$ and $f_7$ problems using Jaya algorithm a $f_{6}$ Ackley, b $f_{7}$ Rastrigin

Fig. 3

The evaluated solutions by 2000 FEs of C-Jaya algorithm when solving $f_6$ and $f_7$ problems a $f_6$ Ackley, b $f_7$ Rastrigin

Fig. 4

Convergence visualization of solutions (for the first five generations) when solving $f_6$ and $f_7$ problems using C-Jaya algorithm a $f_{6}$ Ackley, b $f_{7}$ Rastrigin

Moreover, the main idea of Jaya defined by Eq. (2) is as follows: A promising solution derived from a specific problem should approach the best solution and escape the worst one concurrently. This fact intensifies the local search and accelerates the convergence rate of the algorithm. So, Jaya favors exploitation over exploration, which affects the population diversity and the capability of the algorithm to avoid local optimums. The evaluated solutions of 2000 function evaluations (FEs), of $f_6$ and $f_7$ 10-dimensional functions (see Table 1), using the standard Jaya algorithm, in the scenario of minimization problems are shown in Fig. 1. It is clear that the algorithm was unable to escape local minima and then fails to converge to the best solution. The former effect transposes the main idea of Jaya (Eq. (2)), which favors exploitation rather than exploration. Moreover, the convergence visualizations of $f_6$ and $f_7$ 10-dimensional functions are illustrated in Fig. 2 for the first five generations. One can note the weakness of Jaya algorithm to reach the best solution (here, the global minima, i.e., the (0, 0) pair.) Therefore, a balance between exploitation and exploration should be established. In this context, an improvement of Jaya algorithm based on the new 2D cross chaotic map was proposed. In fact, to maintain in equilibrium the exploration and exploitation capabilities of the search process, three mutation equations (Eqs. (3)–(5)) were used randomly for each solution in the improved algorithm. The first mutation (Eq. (3)) serves to enhance the population diversity as well as the global search capability. The individuals were guided by the best solution with the hope of finding other promising areas in the search space. Therefore, the algorithm becomes suitable for problems characterized by many local optimums. The second mutation (Eq. (4)) allows further increase in population diversity and an improvement in the current solution by avoiding the worst one. The third mutation (Eq. (5)) favors local search around the best solution that implies a fast convergence speed. Additionally, each mutation was supported by the use of other solutions to improve the population diversity and then the exploration ability of the algorithm. The chaotic values derived from the 2D cross map have a dual task. First, a balance between the local and global search was achieved by using them to substitute the random mutation strategy. Second, the chaotic mutation further improves the capability to avoid being trapped in local optimums. The evaluated solutions of 2000 FEs, of $f_6$ and $f_7$ 10-dimensional functions, using the chaotic Jaya (C-Jaya), in minimizing problems are shown in Fig. 3. It is observed that C-Jaya can escape local minima and achieve a satisfactory success level in leading to the best solution. In addition, the convergence visualizations of $f_6$ and $f_7$ 10-dimensional functions are illustrated in Fig. 4 for the first five generations. It is clear that C-Jaya reaches the best solution. Thus, it presents an appropriate balance between local and global search. All the above results ensure that the 2D cross map plays a crucial role in enhancing the standard Jaya algorithm.

3 Traditional Jaya algorithm

The Jaya algorithm was first introduced by Rao [44]. It was designed for handling both unconstrained and constrained optimization problems. The basic idea behind this algorithm is that the obtained solution for the optimization problem should avoid the worst solution and go toward the best one [46, 50]. Compared to other algorithms, Jaya algorithm does not require any additional control parameters except the common control parameters, i.e., the number of population and the number of function evaluations [1]. The details of Jaya algorithm performance are reported in [47].

Fig. 5

Flowchart of the original Jaya algorithm

Fig. 6

Flowchart of the proposed chaotic Jaya algorithm

Let $f\left( X\right)$ be the function to be optimized (i.e., objective function). The dimension of decision vector is m, and the population size is k. Let $f\left( Xbest\right)$ be the best value of the objective function produced by the best candidate. In the same manner, the worst candidate can be defined as the decision vector which produces the worst objective value (i.e., $f\left( Xworst\right)$). The solution is updated according to the difference between the best candidate and the existing solution as well as the worst candidate and the existing solution as follows [45, 55, 60]:

$$\begin{aligned} Xnew_{i,j}= & {} X_{i,j}+ r_{1i,j}\left( Xbest_{j}- \left| X_{i,j}\right| \right) \nonumber \\&- r_{2i,j}\left( Xworst_{j}- \left| X_{i,j} \right| \right) \end{aligned}$$

(2)

where $Xbest_{j}$ and $Xworst_{j}$ are the values of the jth element of, respectively, the best and the worst candidate, $Xnew_{i,j}$ is the update value of $X_{i,j}$, $r_{1i,j}$ and $r_{2i,j}$ are two different random numbers in the range $\left[ 0,1\right]$. The term $r_{1i,j}\left( Xbest_{j}- \left| X_{i,j}\right| \right)$ reveals the tendency of the solution to move toward the best solution, whereas the term $- r_{2i,j}\left( Xworst_{j}- \left| X_{i,j} \right| \right)$ reveals the tendency of the solution to escape from the worst solution. The acceptance criterion of the solutions is the improvement of the objective function. All the accepted function values at the end of the iteration are transferred to the next iteration. The name of the Jaya algorithm (i.e., victory) comes from the fact that this algorithm can achieve victories by attaining the best solution. The flowchart of the traditional Jaya algorithm is given in Fig. 5.

Table 1 Details of test functions used

Table 2 Statistical results of 30 runs on 10-dimensional functions obtained by PSO, DE, HS, ABC, TLBO, Jaya and C-Jaya algorithms

Table 3 Mean number of function evaluations, time consumed and success rate by comparative algorithms for 10-dimensional functions over 30 independent runs

Table 4 Statistical results of 30 runs on 30-dimensional functions obtained by PSO, DE, HS, ABC, TLBO, Jaya and C-Jaya algorithms

Table 5 Mean number of function evaluations, time consumed and success rate by comparative algorithms for 30-dimensional functions over 30 independent runs

Table 6 Statistical results of 30 runs on 100-dimensional functions obtained by PSO, DE, HS, ABC, TLBO, Jaya and C-Jaya algorithms

Table 7 Mean number of function evaluations, time consumed and success rate by comparative algorithms for 100-dimensional functions over 30 independent runs

4 Chaotic Jaya algorithm (C-Jaya)

The population of the original Jaya algorithm suffers from the lack of diversity and premature convergence which may occur when the objective function converges to a local optimum. Therefore, to surmount the drawbacks of the original Jaya algorithm, the diversity of the population must be increased.

In addition, an efficient optimization algorithm needs a balance between exploitation and exploration [5, 26, 35, 41]. The former refers to the ability of a population to converge as fast as possible to optimal solutions, whereas the latter can be defined as the ability of the algorithm to explore different regions in a search space. Excessive exploitation will lead to local search only, whereas excessive exploration will result in a random search. To overcome the search, balance and convergence problems, we proposed three search equations for the original Jaya algorithm. The trial vectors $X_{new}$ were generated using a random solution Xrand, and the best and worst solutions (Xbest and Xworst) are, respectively, given as follows:

$$\begin{aligned} Xnew_{i,j}= & {} chaos_{i,j} Xrand_{i,j}\nonumber \\&+\,chaos_{i,j} \left( X_{i,j}- chaos_{i,j} Xrand_{i,j}\right) \nonumber \\&+\,chaos_{i,j} \left( Xbest_{j}- chaos_{i,j} Xrand_{i,j}\right) \end{aligned}$$

(3)

$$\begin{aligned} Xnew_{i,j}= & {} chaos_{i,j} Xrand_{i,j}\nonumber \\&+\,chaos_{i,j}\left( X_{i,j}-chaos_{i,j} Xrand_{i,j}\right) \nonumber \\&+\,chaos_{i,j} \left( Xworst_{j}- chaos_{i,j} Xrand_{i,j}\right) \nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned} Xnew_{i,j}= & {} chaos_{i,j} Xbest_{j}\nonumber \\&+\,chaos_{i,j} \left( Xrand_{i,j}-S_{F} Xbest_{j}\right) \end{aligned}$$

(5)

where $chaos_{i,j}$ is the absolute value of a chaotic variable generated by the 2D cross chaotic map. The scaling factor (SF) can take two values (1 or 2) chaotically. When SF is equal to 1, Eq. (5) allows a search around the best solution, which favors local search ability and then reduces implementation time. However, a premature convergence is usually encountered when multimodal optimization problems are considered. Therefore, even if the local search is applied, global optimum cannot be reached, whereas, when SF equals 2, an important perturbation to current solutions is introduced. Consequently, premature convergence to the local optimum is avoided and the searching behavior is improved. The scaling factor is defined as follows: $S_{F}= round \left[ 1 + chaos_{i}\right]$.

In traditional Jaya algorithm, the candidate solutions are updated by involving the worst and the best solution simultaneously. This procedure can improve the convergence rate and the exploitation capability of the optimization algorithm. However, the prompt convergence rate may degrade the exploration ability and the population diversity of the algorithm. To maintain the balance between the exploitation and the exploration abilities, a new search strategy based on three mutually exclusive equations is introduced. In fact, the equations are selected randomly according to chaotic values $chaos_{i,j}$ and random numbers a and b at each iteration. These random numbers are generated by a Gaussian distribution. It can be seen that the introduced random numbers allow the choice between the three search equations which modulate the degree of avoiding the worst solution and approaching the best one. As a result, this modulation enables the increase of convergence speed and the improvement of the current solution. Besides, a chaotic sequence is introduced to boost the quality of the best solution which attracts the candidate solutions to its region.

The first mutation (Eq. (3)) allowed an improvement of solutions for large-scale problems and increased the global search capabilities and the population diversity. The best solution was used as an attractor to guide the individuals to the most promising areas in a feasible search space. Unfortunately, in problems characterized by enormous local optimum, premature convergence may be encountered. The second mutation (Eq. (4)) further increased the population diversity and improved the global solution by avoiding the worst one. The third mutation (Eq. (5)) has a powerful local search around the best solution and provides a fast convergence speed. It is worth mentioning that the mutation strategy was selected randomly.

4.1 Steps of the proposed C-Jaya

Based on the aforementioned formulation, the steps involved in the proposed C-Jaya algorithm can be encapsulated as follows:

• Step 1 Initialization.

  • Step 1.1 Initialize the value of chaos using the proposed 2D cross chaotic map $(x_{0}=0.2,y_{0}=0.3)$.

  • Step 1.2 Set FEsMAX and SN the maximum number of function evaluations and the population size, respectively.

• Step 2 Generate chaotic sequences.

• Step 3 Generate SN solutions chaotically, with length D (dimension of problems), to form an initial population as follows:

  $$\begin{aligned} X_{i,j}=XL_{i}+chaos_{i,j}(XU_{i}-XL_{i}) \end{aligned}$$

  where $1\le i\le SN$ and $1\le j\le D$. $XL_{i}$ and $XU_{i}$ are the lowest and highest bounds of decision vector, respectively.

• Step 4 Evaluate the objective function of the initial population and set FEs= SN, where FEs are the number of function evaluations.

• Step 5 Update population: Let a and b be two random integers with $a<b$, and let $chaos_{i,j}$ be a chaotic value related to solution in the ith row and jth column. Herein, $1\le i\le SN$ and $1\le j\le D$.

  • Step 5.1 Identify the worst and the best solutions in the population.

    If $chaos_{i,j} < a$

  • Step 5.2 Calculate the new solution $Xnew_{i,j}$ using Eq. (3).

    If $a< chaos_{i,j}< b$

  • Step 5.3 Generate the new solution $Xnew_{i,j}$ using Eq. (4).

    If $chaos_{i,j} >b$

  • Step 5.4 Generate the new solution $Xnew_{i,j}$ using Eq. (5).

• Step 6 Evaluate the new fitness for the new decision vector $Xnew_{i}$ and set $FEs=FEs+1$.

• Step 7 Accept $Xnew_{i}$ if the objective function value is improved.

• Step 8 If $FEs<FEsMAX$ go to Step 5, else stop and output the best solution so far.

The flowchart of the proposed C-Jaya is given in Fig. 6.

5 Experiments and comparisons

In this section, the accuracy and the performance of the proposed algorithm were investigated. In fact, it was applied in the optimization of 16 benchmark functions. The obtained results were compared with those of PSO, DE, HS, ABC, TLBO and Jaya algorithms. In what follows, we will present the characteristics of the benchmark functions and the set of the obtained results.

5.1 Test functions

The effectiveness of C-Jaya for numerical optimization problems was proven by minimizing 16 benchmark functions. Besides, a comparison with traditional Jaya algorithm and other algorithms was performed. These functions belong to three different groups, namely: unimodal ($f_{1}$–$f_{5}$), multimodal ($f_{6}$–$f_{9}$) and rotated versions of $f_{3}$–$f_{9}$ ($f_{10}$–$f_{16}$). Table 1 illustrates the specifications of these functions. The global optimum of all benchmark functions is equal to zero. The set of test functions were evaluated in 10, 30 and 100 dimensions.

5.2 Parameter settings

All experiments were carried out using an i7-1.80 GHz CPU, 8-GB RAM and Windows XP with MATLAB 2017a. With the aim of mitigating statistical errors, all experiments were repeated 30 times. For all algorithms, the population size was set to 20 in 10-dimensional problems and 40 for 30-dimensional and 100-dimensional problems. The number of function evaluations (FEs) is considered as a stopping criterion for population-based algorithms. In our experiments, for the 10-dimensional problems, the maximum number of function evaluations was set as 20,000, whereas FEs were set to 80,000 for 30-dimensional and 100-dimensional functions.

P.S In Tables 3, 5 and 7 “NaN” denotes that the algorithm cannot produce an acceptable solution during 30 independent runs, whereas boldface in Tables 2, 3, 4, 5, 6 and 7 indicates the best solutions.

5.3 Results for 10-dimensional problems

5.3.1 Comparison of solution accuracy

The performances of the PSO, DE, HS, ABC and C-Jaya algorithms on a large set of benchmark functions for 10D in 30 independent runs are given in Table 2.

The results for the unimodal functions $f_{1}$–$f_{4}$ show that C-Jaya outperforms all the comparative algorithms regarding the best mean values, the standard deviations and the standard errors of means and succeeds to reach the global optimum. It is worth mentioning that the unimodal benchmark functions $f_{1}$–$f_{4}$ present one global optimum without any local optimum; thus, they are obviously adequate for investigating the exploitation of algorithms. Therefore, these results prove that our proposed approach enhances, remarkably, the “exploitation” in Jaya algorithm.

For $f_{5}$, all algorithms failed to attain the global optimum, and the Jaya algorithm produced the best result.

For $f_{6}$, the proposed algorithm obtained the best mean, StdDev and SEM than other ones. However, PSO, DE, ABC and TLBO reached competitive results. Only C-Jaya, DE and ABC algorithms attained good results for $f_{7}$, and in particular, C-Jaya attained the global optimum value.

DE, TLBO and C-Jaya produced better results than other algorithms for $f_{8}$. Each of these algorithms has reached the global optimum value. Thus, DE, ABC and C-Jaya outperform the other algorithms in solving $f_{8}$ problem. For $f_{9}$, only C-Jaya reached the global optimum value and the rest of the algorithms performed similarly.

The multimodal benchmark functions ($f_{6}$ to $f_{9}$), unlike the unimodal functions, have many local optimums. As a result, they are suitable for testing the exploration of a given algorithm. Meanwhile, with the increase of the local minima number of multimodal functions, the problem becomes very difficult to solve. According to the obtained results, C-Jaya significantly provides a good solution accuracy and a higher probability to escape from local optimums as well.

In rotated problems $f_{10}$, $f_{11}$, $f_{14}$ and $f_{16}$ only the proposed algorithm attained the global optimum value. Furthermore, TLBO algorithm produced the most competitive results compared to other ones. The Jaya algorithm has the best mean for $f_{12}$, whereas C-Jaya is the best one for solving $f_{13}$ problem. However, all algorithms, expect TLBO and C-Jaya, failed to reach the minimum value of $f_{15}$. We can conclude that the C-Jaya achieves good results regarding solutions quality for low-dimensional problems.

Fig. 7

Convergence performance of different algorithms on the $f_1-f_4$ 10-dimensional functions a $f_1$ sphere, b $f_2$ quadric, c $f_3$ sum square, d $f_4$ Zakharov

Fig. 8

Convergence performance of different algorithms on the $f_5-f_8$ 10-dimensional functions a $f_5$ Rosenbrock, b $f_6$ Ackley, c $f_7$ Rastrigin, d $f_8$ Weierstrass

Fig. 9

Convergence performance of different algorithms on the $f_9-f_{12}$ 10-dimensional functions a $f_9$ Griewank, b $f_{10}$ rotated sum square, c $f_{11}$ rotated Zakharov, d $f_{12}$ rotated Rosenbrock

Fig. 10

Convergence performance of different on the $f_9-f_{16}$ 10-dimensional functions a $f_{13}$ rotated Ackley, b $f_{14}$ rotated Rastrigin, c $f_{15}$ rotated Weierstrass, d $f_{16}$ rotated Griewank

5.3.2 Comparison of convergence

The speed of attaining global optimum is an important criterion in judging the performance of a given optimization algorithm. The effectiveness of the proposed algorithm was demonstrated via the computational effort expressed by the mean number of function evaluations (FEs), the CPU time and the success rate (SR) provided in Table 3. The proposed algorithm presents the highest success rate and the fewest number of FEs required to attain the global optimum. To further evaluate the exploitation property of C-Jaya algorithm compared to other ones, the convergence graphs of all used functions are illustrated in Figs. 7, 8, 9 and 10. It is worth mentioning that we shifted the values of the objective function by a gap of $10^{-3}$, due to the existence of some zero values. Thus, we can plot them in semi-log scale. These figures show that the C-Jaya algorithm presents not only a good overall performance regarding the quality of the obtained optimal solution but also faster convergence rates in most test problems. It is also clear that the C-Jaya algorithm outperforms other algorithms concerning the ultimate result similarly. As far as the convergence characteristic is concerned, the proposed algorithm converges very fast in most of the test functions compared to the other algorithms. Overall, the performance of C-Jaya is significantly superior to the other comparative algorithms, except for Rosenbrock function in which the ABC algorithm is the most effective.

To further validate the convergence performance of the proposed algorithm, a comparison of the computational time spent by all used algorithms to reach the first acceptable solution was made (Table 3). These CPU times allow a fair comparison of speed convergence among all algorithms. It is clear that the C-Jaya requires less CPU time to reach the first acceptable solution than other algorithms for all test functions. Despite the fact that the proposed algorithm uses additional sequences compared with the original algorithm, C-Jaya ranks first among all the algorithms. In fact, it requires a minimum number of FEs to attain an acceptable solution.

In conclusion, C-Jaya is a powerful algorithm for solving complex optimization problems.

5.3.3 Statistical tests

We applied the Friedman test which is a well-known procedure for testing the differences between more than two algorithms [10, 11, 36]. To achieve this goal, we also used its two advanced versions which are the Friedman aligned ranks test and the Quade test. Figures 11 and 12 illustrate the ranking of algorithms used in the experiments based on the standard errors of means. As can be seen from these figures, C-Jaya obtained the best ranking, followed by TLBO algorithm. We can conclude that the proposed algorithm evidently outperforms the comparative algorithms.

Fig. 11

Average ranking of comparative algorithms by Friedman test (a) and Friedman aligned test (b) for 10-dimensional problems

5.4 Results for 30-dimensional problems

5.4.1 Comparison of solution accuracy

Table 4 indicates that C-Jaya reaches the global optimum for the unimodal functions $f_{1}$–$f_{4}$ and the TLBO algorithm gives the best results among the other comparative algorithms. All the other algorithms, except HS algorithm, obtained acceptable solutions for the test function $f_{5}$. Nevertheless, all algorithms failed to reach the global optimum for the same function. For the test function $f_{6}$, DE, TLBO and C-Jaya obtained better results than other algorithms. The proposed algorithm gives the same output for the test functions $f_{7}$–$f_{11}$ and $f_{14}$–$f_{16}$. The obtained solutions for the previous test problems are equal to the theoretical optimum. For the test function $f_{12}$ all algorithms produced similar results, except ABC which does not reach an acceptable solution. Moreover, C-Jaya and TLBO again produce the best solution for $f_{13}$ test function.

It should be noted that the modifications incorporated in the original Jaya algorithm improve its performance regarding solutions accuracy substantially.

5.4.2 Comparison of convergence

Table 5 shows the mean number of FEs, the CPU time and the success rate obtained in 30 independent runs. The success rates were calculated during each run by counting the number of fitness values less than the acceptable level (shown in Table 1), after the completion of 80,000 FEs.

As can be seen from this table, C-Jaya produces the highest success rate compared to other algorithms for all test functions. Also, the smallest number of FEs required by C-Jaya to reach an acceptable solution, demonstrates its high speed of convergence in all test problems.

To further assess the convergence performance of the proposed C-Jaya, the CPU required to attain the first acceptable solution was calculated (Table 5). The obtained results for C-Jaya algorithm were compared with other algorithms. We can conclude that C-Jaya requires less CPU time for all test functions except for $f_2$ function which is ranked second best. In a first analysis, C-Jaya required the generation of chaotic sequences and may need more CPU time than the original one. However, the additional CPU time introduced by the added operations in C-Jaya was compensated by the improvement of diversity characteristic.

Fig. 12

Average ranking of comparative algorithms by Quade test for 10-dimensional problems

Fig. 13

Average ranking of comparative algorithms by Friedman test (a) and Friedman aligned test (b) for 30-dimensional problems

5.4.3 Statistical tests

To prove the efficiency of the proposed algorithm in comparison with the other ones, we performed Friedman, Friedman aligned and Quade tests. Figures 13 and 14 show that C-Jaya is the best performing algorithm, for all tests, among all other algorithms. Thus, it is ranked first among all comparative algorithms. Therefore, C-Jaya can be considered as a very efficient algorithm for overcoming complex optimization problems.

5.5 Results for 100-dimensional problems

5.5.1 Comparison of solution accuracy

The performances of the proposed C-Jaya, in high-dimensional problems, were evaluated by considering the aforementioned benchmark functions in 100 dimensions. The results presented in Table 6 give the means of the best solutions, the standard deviations and the standard errors of means obtained from 30 independent runs.

It can be seen that C-Jaya outperforms the comparative algorithms. We can again conclude that the TLBO produces the most competitive results among all other algorithms. It is worth noting that all comparative algorithms failed to attain the global optimum, except the TLBO which succeeded to reach the theoretical optimum in only four test functions. Thus, the C-Jaya is a very efficient algorithm for solving optimization problems.

Fig. 14

Average ranking of comparative algorithms by Quade test for 30-dimensional problems

Fig. 15

Average ranking of comparative algorithms by Friedman test (a) and Friedman aligned test (b) for 100-dimensional problems

5.5.2 Comparison of convergence

In this section, the computational effort and the success rate produced by all algorithms, in solving the considered problems, were studied. Indeed, experiments were conducted to obtain the FEs required by each algorithm to reach the optimal solution. The algorithms are terminated, if the global optimum is attained or if the FEs is completed. Table 7 shows results of all algorithms regarding the mean number of FEs, the CPU time and the success rate obtained in 30 independent runs.

In all test functions, the C-Jaya algorithm required the fewest number of FEs and as a consequence the least computational effort. Equally, the proposed algorithm reached 100% success rate for fourteen test functions, whereas the best among the other algorithms, i.e., TLBO algorithm, obtained the same result for twelve benchmark functions. Moreover, C-Jaya requires less CPU time for all test functions except for $f_1$, $f_3$, $f_6$ and $f_9$ functions which is ranked second best. It is worth noting here that the original Jaya algorithm failed in all test problems, which reflects its weakness in global search. Thanks to the modifications introduced in Jaya, the obtained algorithm presents high efficiency and robustness.

To get a deep insight into the convergence performance of the C-Jaya algorithm and to make a fair comparison for high-dimensional problems, CPU times required by the studied algorithms were computed to achieve the first acceptable solution (Table 7). Regarding CPU time, C-Jaya algorithm is the most effective at finding the first acceptable solution for 14 from 16 benchmark functions. Moreover, TLBO algorithm is the second most effective, in attaining the first acceptable solution for 13 from 16 benchmark functions. Besides, the proposed algorithm is the best performing regarding CPU time in almost all test functions. Furthermore, it is observed from results that PSO, HS and Jaya algorithms fail to attain an acceptable solution for all test functions. Moreover, DE and ABC algorithms reach an acceptable solution for only one benchmark function.

Fig. 16

Average ranking of comparative algorithms by Quade test for 100-dimensional problems

5.5.3 Statistical analysis

To statistically quantify the performance of the algorithms used in the experiments, Friedman, Friedman aligned and Quade tests were performed based on standard errors of means. Figures 15 and 16 present the ranking of considered algorithms according to these tests. It is obvious from these histograms that C-Jaya is ranked first among all comparative algorithms. These results confirm the ability of the proposed algorithm for solving optimization problems.

We can, therefore, conclude that the proposed C-Jaya has better-searching ability, robustness and efficiency for handling engineering design problems and that its performance surpasses all comparative algorithms.

6 Conclusion

In this work, we proposed a new chaotic Jaya algorithm that mitigates premature convergence problem of the original Jaya algorithm. Three new search equations were implemented to enhance the search abilities of the Jaya algorithm. Moreover, after investigating its chaotic behavior, the proposed 2D cross chaotic map was embedded in the original Jaya algorithm with the aim of improving both its exploration and exploitation abilities. It is worth mentioning that the modifications incorporated in Jaya algorithm maintained its simplicity and control parameter-free property. Experimental results based on unimodal and multimodal benchmark functions prove that the proposed chaotic Jaya algorithm (C-Jaya) outperforms the original one. Also, comparing the results with other well-known optimization algorithms, i.e., PSO, DE, HS, ABC and TLBO, proves the predominance of the proposed C-Jaya concerning solution accuracy and speed convergence as well as nonparametric statistical tests.

Appendix A: The proof of chaos for G(x)

Definition 1

(Discrete chaos of Devaney) Consider a discrete dynamical system in the following form:

$$\begin{aligned} y_{i+1}=g(y_i),\quad g: J\rightarrow J,\quad y_0\in J \end{aligned}$$

(6)

g(x) is chaotic if the following conditions are satisfied [12].

• (1) Sensitive to initial conditions

  $$\begin{aligned}&\exists ~ \Omega>0,\quad \forall ~ y_0\in J,\quad \omega>0,\quad \exists ~ n\in N,\quad z_0\in J \nonumber \\&\left| y_0-z_0\right| <\omega \Rightarrow \left| g^n(y_0)-g^n(z_0)\right| >\Omega . \end{aligned}$$

  (7)

• (2) Topological transitivity

  $$\begin{aligned} \forall ~ J_1,\,\, J_2\in J,\quad \exists ~ y_0\in J_1,\quad n\in N,\quad g^n(y_0)\in J_2. \end{aligned}$$

  (8)

• (3) Density of periodic points in J Let $K=\{k\in J|\exists n\in N:\,\, g^n(k)=k\}$ be the set of periodic points of g. Therefore, K is dense in $J:\overline{K}=J$.

Definition 2

Let $f: I\rightarrow I$ and $g: J\rightarrow J$ be maps. f and g are topologically conjugated if there exists a homeomorphism $h: I\rightarrow J$ that makes $h\circ f=g\circ h$.

Theorem

Let $f:I\rightarrow I$ and $g: J\rightarrow J$ be conjugate via h. If f is chaotic on I, then g is chaotic on J.

Proof

• (1) (Sensitive to initial conditions) Let f have sensitivity constant $\alpha$. Let $I=\left[ \omega _0,\omega _1\right]$. Assume $\alpha <\omega _1-\omega _0$. Consider the function $|h(x+\alpha )-h(x)|$ where $x\in \left[ \omega _0,\omega _1-\alpha \right]$. This function has minimum value $\lambda$ as it is continuous and positive. So, h maps intervals of length $\alpha$ to intervals of length at least $\lambda$. We assume that g has sensitivity constant $\lambda$. Let $x_0\in J$ and B be an open interval about $x_0$. Therefore, $h^{-1}(B)$ is an open interval about $h^{-1}(x_0)$. By sensitive to initial conditions, there is $y_0\in h^{-1}(B)$ and $m>0$ which satisfy $\left| f^m\left( h^{-1}(x_0)\right) -f^m(y_0)\right| >\alpha$. Then,

  $$\begin{aligned}&\left| h\left( f^m\left( h^{-1}(x_0)\right) \right) -h\left( f^m(y_0)\right) \right| \\&\quad =\left| g^m(x_0)-g^m\left( h(y_0)\right) \right| >\lambda . \end{aligned}$$

• (2) (Topological transitivity) Let A and B be open subintervals of J. So, $h^{-1}(A)$ and $h^{-1}(B)$ are open subintervals of I (h is a continuous function). As f is topologically transitive, there is $x_0\in h^{-1}(A)$ that fulfills $f^n(x_0)\in h^{-1}(B)$ for some n. Therefore, $h(x_0)\in A$ and $g^n\left( h(x_0)\right) =h\left( f^n(x_0)\right) \in B$.

• (3) (Density of periodic points) Let A be an open subinterval of J and consider $h^{-1}(A)\subset I$. Since periodic points of f are dense in I, there is a periodic point $x\in h^{-1}(A)$ of period m. We have $g\circ h=h\circ f$, so $g^m\left( h(x)\right) =h\left( f^m(x)\right) =h(x)$. Therefore, h(x) is a periodic point of period m in A and periodic points are dense in J. According to the definition of chaos Devaney [12], g is chaotic on J.

$\square$

It is known that $\phi (\theta )=5\theta$ is chaotic [12] under the unit circle mapping $S^1\rightarrow S^1$, so $\phi$ is sensitive to initial value, topologically transitive and dense in $S^1$.

Considering $h(\theta )=\cos \theta$, we have $G\circ h=16\cos ^5\theta -20\cos ^3\theta +5\cos \theta =\cos (5\theta )=h\circ \phi$. So G is conjugated to $\phi$ in $y\in J=\left[ -1,1\right]$. Thus, as $\phi$ is chaotic on $S^1$, then G is chaotic on $J=\left[ -1,1\right]$.

1.1 The randomness proof of G(x)

Because function $G(x)=16x^5-20x^3+5x$ is a Chebyshev polynomial of degree 5 $(T_5(x)=\cos (5\theta ), x=\cos \theta )$, so its invariant density is

$$\begin{aligned} \rho _G(x)=\frac{1}{\pi \sqrt{1-x^2}},\quad -1<x<1 \end{aligned}$$

(9)

1.1.1 The auto-correlation proof

It is known that

$$\begin{aligned} \bar{x}&=\int _{-1}^{1}x\rho _G(x)\mathrm{d}x\\&\overset{x=\sin u}{=}\int _{\frac{-\pi }{2}}^{\frac{\pi }{2}}\sin u\frac{1}{\sqrt{1-\sin ^2 u}}\cos u \mathrm{d}u=0. \end{aligned}$$

Considering $x=\cos u$ and $\tau$ is the iterative times of G(x). We have $G^\tau (x)=\cos (5^\tau u)$. When $\tau \ne 0$,

$$\begin{aligned} \begin{aligned} C_G(\tau )&= \int _{-1}^{1}x\rho _G(x)G^\tau (x)\mathrm{d}x-\bar{x}^2 \\&= \int _{-1}^{1}x\frac{1}{\pi \sqrt{1-x^2}}G^\tau (x)\mathrm{d}x-\bar{x}^2=0. \end{aligned} \end{aligned}$$

When $\tau =0$,

$$\begin{aligned} \begin{aligned} C_G(0) =&\int _{-1}^{1}x\rho _G(x)G^0(x)\mathrm{d}x-\bar{x}^2 \\ =&\int _{-1}^{1}x^2\frac{1}{\pi \sqrt{1-x^2}}\mathrm{d}x-\bar{x}^2\\ \overset{x=\cos u}{=}&\int _{\pi }^{0}\cos ^2u\frac{1}{\pi \sqrt{1-\cos ^2u}}\\&\times (-\sin u) \mathrm{d}u\\ =&\frac{1}{\pi }\int _{0}^{\pi }\frac{1+\cos (2u)}{2}\mathrm{d}u=0.5. \end{aligned} \end{aligned}$$

Therefore, auto-correlation function of G(x) is:

$$\begin{aligned} C_G(\tau )={\left\{ \begin{array}{ll} 0.5 &{} \quad \text {if } \tau =0\\ 0 &{} \quad \text {if } \tau \ne 0\\ \end{array}\right. } \end{aligned}$$

(10)

The auto-correlation function of G(x) shows that when the iterative times $\tau \ne 0$, the time sequences generated by G(x) are independent.

1.1.2 The cross-correlation proof

Considering $x=\cos u$ and $\tau$ is the iterative times of G(x). We have $G^\tau (x)=\cos (5^\tau u)$.

Therefore, the cross-correlation function is given by

$$\begin{aligned} rr_G(\tau )=0 \end{aligned}$$

(11)

The result given in Eq. (11) shows that time sequences produced by G(x) with different initial values have no relation to each other at any time. According to the above characteristics, the average value of G(x) and the cross-correlation are 0, so the probability statistical characteristic is the same as the white noise and thus G(x) function can be used as an ideal chaotic sequence generator.

1.2 The proof of the equal probability of the pseudo-random sequence

When G(x) is iterated, a chaotic sequence is produced as follows: $g_0,g_1,\ldots ,g_p=G(x_{p-1})$ where p is an integer. The chaotic range $V=\left[ -1,1\right]$ is divided into M subdomains $v_i$, $i=0,1,2,\ldots ,M-1$. With $v_i=(t_i,t_{i+1})$ for $i=0,1,\ldots ,M-1$. Here, $t_i$ is defined by Eq. (12)

$$\begin{aligned} t_i=-\cos \left( \frac{i}{M}\pi \right) , \quad i=0,1,2,\ldots ,M-1 \end{aligned}$$

(12)

The initial conditions $(x_0,y_0)$ of the cross chaotic map are used to generate a value of chaotic sequence $\left\{ g_p\right\} _{p=1}^{\infty }$.

Definition 3

Mapping $S:V\rightarrow {0,1,\ldots ,M-1}$, $x_p\rightarrow i=s_k$, $x_p\in v_i$, $p=0,1,\ldots$, where $s_p$ is described as Eq. (13), so the N phase pseudo-random sequence $\left\{ s_p\right\} _{p=0}^{\infty }$ distributes in the N subdomains proportionally.

$$\begin{aligned} s_p={\left\{ \begin{array}{ll} \left\lfloor (1-\arccos (g_p)/\pi )\times M\right\rfloor , &{} \text {if} g_p\in \left[ -1,1\right] ,\\ M-1, &{} \text {if } g_p=1\\ \end{array}\right. } \end{aligned}$$

(13)

Proof

According to Eqs. (9) and (13), the probability of element i appearing in $\left\{ s_p\right\} _{p=0}^{\infty }$ is:

$$\begin{aligned} Prob(i)=\int _{t_i}^{t_{i+1}} \rho (x)dx=\frac{1}{M} \end{aligned}$$

$\square$

Obviously $\left\{ s_p\right\} _{p=0}^{\infty }$ obeys uniform distribution.