Uncertain portfolio adjusting model using semiabsolute deviation

Abstract

Since the financial markets are complex, sometimes the future security returns are represented mainly based on experts’ judgments. This paper discusses a portfolio adjusting problem with risky assets in which security returns are given subject to experts’ estimations. Here, we propose uncertain mean-semiabsolute deviation adjusting models for portfolio optimization problem in the trade-off between risk and return on investment. Various uncertainty distributions of the security returns based on experts’ evaluations are used to convert the proposed models into equivalent deterministic forms. Finally, numerical examples with synthetic uncertain returns are illustrated to demonstrate the effectiveness of the proposed models and the influence of transaction cost in portfolio selection.

1 Introduction

One of the most well-known portfolio selection models in contemporary finance is the mean-variance model developed by Markowitz (1952). However, it is not extensively used to construct large-scale portfolio problems in its original form. The reason for this is the computational difficulty associated with solving a large-scale quadratic programming problem with a dense covariance matrix. To overcome the problem, many methods have been used to transform the problem into a linear programming. Most of the literatures in portfolio optimization, variance and absolute deviation are used to measure the risk. But in case of asymmetric return distribution, the risk measure maybe have to sacrifice too much expected return in eliminating both low and high return extremes. To measure real investment risk in financial market, semi-variance (Markowitz 1993) and semiabsolute deviation (Speranza 1993) have been employed. Konno and Yamazaki (1991) used the absolute deviation risk function to replace the variance in Markowitz’s model and formulated as a linear programming model. Simaan (1997) provided a detailed comparison of the mean-variance and the mean-absolute deviation models. In particular, Speranza (1993) first formulated a semiabsolute deviation portfolio selection model in stochastic environment.

In real situations, historical data may be insufficient to estimate probability distributions of security returns. Another feasible way is to estimate returns by experts based on their subjective evaluations. To deal with this subjective uncertainty, Liu (2007) founded the concept of uncertainty measure and further developed it as uncertain theory in Liu (2010). Furthermore, Liu (2010) also proposed uncertain programming for solving optimization problems involving uncertain variables. In this area, there are many works to be done, for example, vehicle routing and project scheduling problems (Liu 2010), shortest path problem (Gao 2011), single period inventory problem (Qin and Kar 2013), finance problem (Chen et al. 2013; Li et al. 2013), production planning problem (Ning et al. 2013), facility location-allocation problem (Wen et al. 2014) and data envelopment analysis (Wen et al. in press).

In particular, Qin et al. (2009) and Huang (2011) applied uncertainty theory to model portfolio optimization problem. Zhu (2010) applied uncertain optimal control to model continuous-time portfolio selection problem. As extensions, Huang and Qiao (2012) presented a risk index model for multi-period case and then employed the risk index to study the portfolio adjusting problem Huang and Ying (2013) subject to experts’ evaluations. Yao and Ji (2014) introduced a portfolio selection model based on the idea of uncertain decision-making. In the framework of uncertainty theory, the variance of an uncertain variable cannot be exactly calculated using its uncertain distribution. Therefore, Liu (2010) have to use a stipulation to handle this situation. Liu and Qin (2012) further introduced the concept of semiabsolute deviation to measure downside risk in the case of asymmetrical uncertain returns. Li and Qin (2014) followed the concept and formulated a mean-semiabsolute deviation model by considering the security returns with interval expected returns as uncertain variables. The main advantage is that the semiabsolute deviation of an uncertain return is exactly determined by its uncertainty distribution. Thus, it provides an exact measurement of risk or downside risk in an uncertain environment.

Due to the rapidly changing situations in the financial markets, an existing portfolio may not be efficient after a certain period of time. Again changing the financial data in the market has a great impact on the investor’s holdings. Therefore, portfolio adjustment is necessary in response to the changed situation in financial markets and investor’s capital. The cost associated with buying or selling of a risky asset, known as transaction cost, is one of the main concerns for portfolio managers. Arnott and Wagner (1990) first suggested that ignoring transaction costs would result in an inefficient portfolio; whereas, adding transaction costs would assist decision makers to better understanding of an efficient frontier. Some researchers like Patel and Subrahmanyam (1982), Morton and Pliska (1995), Yoshimoto (1996), Choi et al. (2007), Lobo et al. (2007), Bertsimas and Pachamanova (2002), Baule (2010), Wen et al. (2014), etc. extended the works on portfolio selection problems with transaction costs. In the portfolio adjusting problem, investors always update their existing portfolios by buying or selling risk assets to hedge the fluctuations of financial markets. Some researchers such as Fang et al. (2006), Glen (2011), Lee and Yu (2011) and Zhang et al. (2011) studied the portfolio adjusting problems in the framework of return-risk trade-off.

Up to now, there is no paper considering the portfolio adjusting problem in the assumption of uncertain variable returns by using semiabsolute deviation to measure risk. The purpose of this paper is to develop the uncertain portfolio adjustment problem according to the expert’s evaluations of future return of the security. Similar to Markowitz’s mean-variance idea, here we use the expected value and semiabsolute deviation of the uncertain return on portfolios as the investment return and risk measurements, respectively. Equivalent deterministic models are obtained by further providing various uncertainty distributions. The rest of the paper is organized as follows. In Sect. 2, we review some fundamentals of uncertainty theory. Section 3 formulates the mean-semiabsolute deviation portfolio adjustment model when the returns of assets are uncertain variables. Section 4 provides some equivalent deterministic forms of mean-semiabsolute deviation models. In Sect. 5, numerical examples are given to illustrate the effectiveness of the proposed model. Some concluding remarks are given in Sect. 6. Finally, all the proofs are placed in the appendix to preserve the continuity of the presentation.

2 Preliminaries

In 2007, Liu proposed the concept of uncertain measure and founded uncertainty theory. In this part, we recall some basic definitions and properties about uncertain measure and uncertain variable, which will be used in the whole paper.

Let $\Gamma$ be a non-empty set, and let $\mathcal {L}$ be a $\sigma$-algebra over $\Gamma$. Each element $\Lambda \in \mathcal {L}$ is called an event. It is necessary to assign to each event $\Lambda$ a number $\mathcal {M}\{\Lambda \}$ which indicates the chance that $\Lambda$ will occur. Liu (2007) proposed three axioms to ensure that the number $\mathcal {M}\{\Lambda \}$ satisfying certain mathematical properties, (1) $\mathcal {M}\{\Gamma \}=1$; (2) $\mathcal {M}\{\Lambda \}+\mathcal {M}\{\Lambda ^{c}\}=1$ for any event $\Lambda$; (3) For every countable sequence of events $\{\Lambda _i\}$, we have

$$\begin{aligned} \mathcal {M}\left\{ \bigcup _{i=1}^{\infty }\Lambda _i\right\} \le \sum _{i=1}^{\infty }\mathcal {M}\{\Lambda _i\}. \end{aligned}$$

(1)

The triplet $(\Gamma ,\mathcal {L},\mathcal {M})$ is called an uncertainty space. Furthermore, Liu (2010) provided the product axiom as follows. If $(\Gamma _k,\mathcal {L}_k,\mathcal {M}_k)$ are uncertainty spaces for $k=1,2,\ldots$, then the product uncertain measure $\mathcal {M}$ is an uncertain measure satisfying

$$\begin{aligned} \mathcal {M}\left\{ \prod _{k=1}^{\infty }\Lambda _k\right\} =\bigwedge _{k=1}^{\infty }\mathcal {M}_k\{\Lambda _k\}, \end{aligned}$$

where $\Lambda _k$ are arbitrarily chosen events from $\mathcal {L}_k$ for $k=1,2,\ldots$, respectively.

An uncertain variable $\xi$ is defined by Liu (2007) as a measurable function from an uncertainty space $(\Gamma ,{\mathcal {L}},\mathcal {M})$ to the set of real numbers, i.e., for any Borel set $B$ of real numbers, the set $\{\xi \in B\}=\{\gamma \in \Gamma |\xi (\gamma )\in B\}$ is an event. It can be characterized by an uncertainty distribution which is a function $\Phi : {\mathfrak {R}} \rightarrow [0,1]$ defined by Liu (2007) as $\Phi (t)=\mathcal {M}\{\xi \le t\}$. For example, by a linear uncertain variable, we mean that the variable has the following linear uncertainty distribution

$$\begin{aligned} \Phi (r)=\left\{ \begin{array}{ll} 0, &{} \quad \mathrm{if\ } r\le a,\\ (r-a)/(b-a),&{} \quad \mathrm{if\ }a\le r\le b,\\ 1, &{} \quad \mathrm{if\ } r\ge b. \end{array}\right. \end{aligned}$$

The linear uncertain variable is denoted by $\mathcal {L}(a,b)$ where $a$ and $b$ are real numbers with $a<b$. By a zigzag uncertain variable, we mean that the variable has the following zigzag uncertainty distribution

$$\begin{aligned} \Phi (r)=\left\{ \begin{array}{cl} 0, &{} \quad \mathrm{if\ } r\le a,\\ (r-a)/2(b-a),&{} \quad \mathrm{if\ }a\le r\le b,\\ (x+c-2b)/2(c-b), &{} \quad \mathrm{if\ } b\le r\le c, \\ 1, &{} \quad \mathrm{if}\ r\ge c. \end{array}\right. \end{aligned}$$

The zigzag uncertain variable is denoted by ${\mathcal {Z}}(a,b,c)$ where $a, b, c$ are real numbers with $a < b < c$. By a normal uncertain variable, we mean that the variable has the following normal uncertainty distribution

$$\begin{aligned} \Phi (r)=\left( 1+\exp \left( \frac{\pi (e-r)}{\sqrt{3}\sigma }\right) \right) ^{-1},\ r\in \mathfrak {R}. \end{aligned}$$

The normal uncertain variable is denoted by $\mathcal {N}(e,\sigma )$ where $e$ and $\sigma$ are real numbers with $\sigma >0$.

The uncertain variables $\xi _1,\xi _2,\ldots ,\xi _m$ are said by Liu (2007) to be independent if

$$\begin{aligned} \mathcal {M}\left\{ \bigcap _{i=1}^{m}\{\xi _i\in B_i\}\right\} =\min \limits _{1\le i\le m}\mathcal {M}\left\{ \xi _i\in B_i\right\} \end{aligned}$$

(2)

for any Borel sets $B_1,B_2,\ldots ,B_m$ of real numbers. To rank uncertain variables, the expected value of $\xi$ was proposed by Liu (2007) as

$$\begin{aligned} E[\xi ]=\int _{0}^{+\infty }\mathcal {M}\{\xi \ge r\}\hbox {d}r-\int _{-\infty }^{0}\mathcal {M}\{\xi \le r\}\hbox {d}r \end{aligned}$$

(3)

provided that at least one of the two integrals is finite. For example, the linear uncertain variable $\xi \sim \mathcal {L}(a,b)$ has an expected value $E[\xi ]=(a+b)/2$; the zigzag uncertain variable $\xi \sim \mathcal {Z}(a,b,c)$ has an expected value $E[\xi ]=(a+2b+c)/4$; the normal uncertain variable $\xi \sim \mathcal {N}(e,\sigma )$ has an expected value $e$, i.e., $E[\xi ] =e$.

Lemma 1

(Liu 2010) Let $a$ and $b$ be two real numbers, and $\xi$ and $\eta$ two uncertain variables. Then we have $E[a\xi +b]=aE[\xi ]+b$. Further, if $\xi$ and $\eta$ are independent, then $E[a\xi +b\eta ]=aE[\xi ]+bE[\eta ]$.

Definition 1

(Liu and Qin 2012) Let $\xi$ be an uncertain variable with finite expected value $e$. Then, the semiabsolute deviation of $\xi$ is defined as

$$\begin{aligned} Sa[\xi ]=E\left[ |(\xi -e)^-|\right] , \end{aligned}$$

(4)

where $(\xi -e)^-=\min (\xi -e,0)$.

Lemma 2

(Liu and Qin 2012) Let $\xi$ be an uncertain variable with finite expected value $e$, and $\Phi (\cdot )$ its uncertainty distribution. Then, we have $Sa[\xi ]=\int _{-\infty }^e\Phi (r)\mathrm{d}r.$

Lemma 3

(Liu and Qin 2012) Let $\xi$ be an uncertain variable with finite expected value. Then for any real numbers $a$ and $b$, we have

$$\begin{aligned} Sa[a\xi +b]=|a|\cdot Sa[\xi ]. \end{aligned}$$

(5)

3 Uncertain mean-semiabsolute deviation adjusting model

In this section, we formulate the problem of finding the desirable portfolio by rebalancing the existing portfolio. Suppose that an investor has an existing portfolio $x^0=(x_1^0,x_2^0,\ldots ,x_n^0)$ in which $x_i^0$ is the current holding of risk security $i~(i=1,2,\ldots ,n)$. Due to the changes of situation in financial market, the investor decides to adjust his/her portfolio to maximize the return and/or minimize the risk.

Let $x^+ =(x_1^+,x_2^+,\ldots ,x_n^+)$ and $x^- =(x_1^-,x_2^-,\ldots ,x_n^-)$, where $x_i^+$ and $x_i^-$ are, respectively, the proportion of the $i$-th security brought and sold by the investor. It is evident that $x_i^+$ and $x_i^-$ are both non-negative. After adjusting, the holding amount of the $i$-th risk security can be expressed as

$$\begin{aligned} x_i=x_i^0+x_i^+-x_i^-,~i=1,2,\ldots ,n. \end{aligned}$$

Let $b_i$ and $s_i$ are, respectively, the unit transaction cost for purchasing and selling the risk security $i~(i=1,2,\ldots ,n)$. Without loss of generality, we assume that $b_i,s_i>0$ for $i=1,2,\ldots ,n$. Then, the total transaction cost incurred by adjusting the existing portfolio is $\sum _{i=1}^n(b_ix_i^++s_ix_i^-)$. Let $\xi _i$ be the future return of security $i~(i=1,2,\ldots ,n)$. Then, the net return of the portfolio $x=(x_1,x_2,\ldots ,x_n)$ after rebalancing is

$$\begin{aligned} r(x_1,x_2,\ldots ,x_n)=\sum \limits _{i=1}^n\xi _ix_i-\sum \limits _{i=1}^n\left( b_ix_i^++s_ix_i^-\right) . \end{aligned}$$

(6)

Analogous to the framework of mean-risk model, the expected value of $r(x_1,x_2,\ldots ,x_n)$ is considered as the investment return. If the investor accepts semiabsolute deviation as risk measure, then the investment risk of the portfolio $(x_1,x_2,\ldots ,x_n)$ is measured by $Sa[r(x_1,x_2,\ldots ,x_n)]$. By trading off return and risk, we establish the following mean-semiabsolute deviation adjusting model

$$\begin{aligned} \left\{ \begin{array}{ll}\min &{} Sa\left[ r(x_1,x_2,\ldots ,x_n)\right] \\ \max &{} E\left[ r(x_1,x_2,\ldots ,x_n)\right] \\ \hbox {s.t.} &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,n\\ &{} x_i,x_i^+,x_i^- \ge 0,\ i=1,2,\ldots ,n. \\ \end{array}\right. \end{aligned}$$

(7)

Definition 2

A feasible solution $(\hat{x}_1^+,\ldots ,\hat{x}_n^+,\hat{x}_1^-,\ldots ,\hat{x}_n^-)$ is said to be a Pareto optimal solution of Model (7) if there is no feasible solution $(x_1^+,\ldots ,x_n^+,x_1^-,\ldots ,x_n^-)$ such that

$$\begin{aligned}&E[r(\hat{x}_1^+,\ldots ,\hat{x}_n^+,\hat{x}_1^-,\ldots ,\hat{x}_n^-)]\\&\quad \le E[r(x_1^+,\ldots ,x_n^+,x_1^-,\ldots ,x_n^-)],\\&Sa[r(\hat{x}_1^+,\ldots ,\hat{x}_n^+,\hat{x}_1^-,\ldots ,\hat{x}_n^-)]\\&\quad \ge Sa[r(x_1^+,\ldots ,x_n^+,x_1^-,\ldots ,x_n^-)] \end{aligned}$$

and at least one of these two inequalities strictly holds.

Theorem 1

Model (7) is equivalent to the following one,

$$\begin{aligned} \left\{ \begin{array}{ll}\min &{} Sa\left[ \sum _{i=1}^n\xi _ix_i\right] \\ \max &{} E\left[ \sum _{i=1}^n\xi _ix_i\right] -\sum _{i=1}^n(b_ix_i^++s_ix_i^-)\\ \hbox {s.t.} &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,n\\ &{} x_i,x_i^+,x_i^- \ge 0,\ i=1,2,\ldots ,n. \end{array}\right. \end{aligned}$$

(8)

Theorem 2

If $(\hat{x}_1^+,\ldots ,\hat{x}_n^+,\hat{x}_1^-,\ldots ,\hat{x}_n^-)$ is the Pareto optimal solution of Model (8), then we have $\hat{x}_i^+\cdot \hat{x}_i^-=0$ for $i=1,2,\ldots ,n$.

If the investment is self-financing, i.e., no new fund is added and no fund is taken out of the existing portfolio, then we have

$$\begin{aligned} \sum _{i=1}^nx_i^0-\sum _{i=1}^n\left( b_ix_i^++s_ix_i^-\right) =\sum _{i=1}^nx_i. \end{aligned}$$

Let $l_i$ and $u_i$ be the lower bound and the upper bound of holding on risk security $i$ after adjusting for $i=1,2,\ldots ,n$. Then, we reformulate the mean-semiabsolute deviation model as follows:

$$\begin{aligned} \left\{ \begin{array}{ll}\min &{} Sa\left[ \sum _{i=1}^n\xi _ix_i\right] \\ \max &{} E\left[ \sum _{i=1}^n\xi _ix_i\right] -\sum _{i=1}^n(b_ix_i^++s_ix_i^-)\\ \hbox {s.t.} &{}\sum _{i=1}^nx_i^0-\sum _{i=1}^n(b_ix_i^++s_ix_i^-)=\sum _{i=1}^nx_i\\ &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,n\\ &{} x_i^+\cdot x_i^-=0,\ i=1,2,\ldots ,n\\ &{} x_i^+,x_i^- \ge 0,\ i=1,2,\ldots ,n, \\ &{} l_i\le x_i\le u_i,\ i=1,2,\ldots ,n. \end{array}\right. \end{aligned}$$

(9)

We introduce a risk-averse factor $\phi$ to convert Model (9) into a single-objective programming

$$\begin{aligned} \left\{ \begin{array}{ll} \max &{} E\left[ \sum _{i=1}^n\xi _ix_i\right] -\sum _{i=1}^n(b_ix_i^++s_ix_i^-)-\phi Sa\left[ \sum _{i=1}^n\xi _ix_i\right] \\ \hbox {s.t.} &{}\sum _{i=1}^nx_i^0-\sum _{i=1}^n(b_ix_i^++s_ix_i^-)=\sum _{i=1}^nx_i\\ &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,n\\ &{} x_i^+\cdot x_i^-=0,\ i=1,2,\ldots ,n\\ &{} x_i^+,x_i^- \ge 0,\ i=1,2,\ldots ,n, \\ &{} l_i\le x_i\le u_i,\ i=1,2,\ldots ,n. \end{array}\right. \end{aligned}$$

(10)

The greater the factor $\phi$, the more conservative is the investor.

4 Equivalents of mean-semiabsolute deviation adjusting models

To simplify the proposed models, this section will consider several special situations in which deterministic models are obtained. We first assume that uncertain returns $\xi _1,\xi _2,\ldots ,\xi _n$ are independent in the sense of uncertain measure, which implies that $E[\xi _1x_1+\xi _2x_2\cdots +\xi _nx_n]=x_1E[\xi _1]+x_2E[\xi _2]+\cdots +x_nE[\xi _n]$.

Theorem 3

Suppose that security returns $\xi _1,\xi _2,\ldots ,\xi _n$ are all linear uncertain variables. Denote by $\xi _i=(c_i,d_i)$ for $i=1,2,\ldots ,n$. Then, model (9) is converted into the following deterministic model 11,

$$\begin{aligned} \left\{ \begin{array}{ll}\min &{} \sum _{i=1}^nx_i(d_i-c_i)\\ \max &{} \sum _{i=1}^nx_i(d_i+c_i)-2\sum _{i=1}^n(b_ix_i^++s_ix_i^-)\\ \hbox {s.t.} &{}\sum _{i=1}^nx_i^0-\sum _{i=1}^n(b_ix_i^++s_ix_i^-)=\sum _{i=1}^nx_i\\ &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,n\\ &{} x_i^+\cdot x_i^-=0,\ i=1,2,\ldots ,n\\ &{} x_i^+,x_i^- \ge 0,\ i=1,2,\ldots ,n, \\ &{} l_i\le x_i\le u_i,\ i=1,2,\ldots ,n \end{array}\right. \end{aligned}$$

(11)

which is a bi-objective linear programming model.

Theorem 4

Suppose that security returns $\xi _1,\xi _2,\ldots ,\xi _n$ are all zigzag uncertain variables. Denote by $\xi _i=(a_i-\alpha _i,a_i,a_i+\beta _i)$ for $i=1,2,\ldots ,n$. Then model (9) is converted into the following deterministic model,

$$\begin{aligned} \left\{ \begin{array}{ll}\min &{} \displaystyle \frac{\left( \sum _{i=1}^n2x_i(\alpha _i+\beta _i)+\left| \sum _{i=1}^nx_i(\alpha _i-\beta _i)\right| \right) ^2}{\sum _{i=1}^nx_i(\alpha _i+\beta _i)+\left| \sum _{i=1}^nx_i(\alpha _i-\beta _i)\right| }\\ \max &{} \sum _{i=1}^nx_i(4a_i+\beta _i-\alpha _i)-4\sum _{i=1}^n(b_ix_i^++s_ix_i^-)\\ \hbox {s.t.} &{}\sum _{i=1}^nx_i^0-\sum _{i=1}^n(b_ix_i^++s_ix_i^-)=\sum _{i=1}^nx_i\\ &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,n\\ &{} x_i^+\cdot x_i^-=0,\ i=1,2,\ldots ,n\\ &{} x_i^+,x_i^- \ge 0,\ i=1,2,\ldots ,n, \\ &{} l_i\le x_i\le u_i,\ i=1,2,\ldots ,n. \end{array}\right. \end{aligned}$$

(12)

Remark 1

If $\alpha _i< \beta _i$ for $i=1,2,\ldots ,n$, then we have

$$\begin{aligned} Sa\left[ \sum _{i=1}^n\xi _ix_i\right] =\frac{\left[ \sum _{i=1}^nx_i(\alpha _i+3\beta _i)\right] ^2}{2\sum _{i=1}^n\beta _ix_i}. \end{aligned}$$

If $\alpha _i=\beta _i$ for $i=1,2,\ldots ,n$, then we have $Sa[\sum _{i=1}^n\xi _ix_i]=4\sum _{i=1}^nx_i(\alpha _i+\beta _i).$ If $\alpha _i>\beta _i$ for $i=1,2,\ldots ,n$, then we have

$$\begin{aligned} Sa\left[ \sum _{i=1}^n\xi _ix_i\right] =\frac{\left[ \sum _{i=1}^nx_i(3\alpha _i+\beta _i)\right] ^2}{2\sum _{i=1}^n\alpha _ix_i}. \end{aligned}$$

Theorem 5

In these special situations, the first objective function of Model (12) has a relatively simple expression.

$$\begin{aligned} \left\{ \begin{array}{ll}\min &{} \sum _{i=1}^n\sigma _ix_i\\ \max &{} \sum _{i=1}^ne_ix_i-\sum _{i=1}^n(b_ix_i^++s_ix_i^-)\\ \hbox {s.t.} &{} \sum _{i=1}^nx_i^0-\sum _{i=1}^n(b_ix_i^++s_ix_i^-)=\sum _{i=1}^nx_i\\ &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,n\\ &{} x_i^+\cdot x_i^-=0,\ i=1,2,\ldots ,n\\ &{} x_i^+,x_i^- \ge 0,\ i=1,2,\ldots ,n, \\ &{} l_i\le x_i\le u_i,\ i=1,2,\ldots ,n \end{array}\right. \end{aligned}$$

(13)

which is also a bi-objective linear programming.

Theorem 6

Suppose that security returns $\xi _1,\xi _2,\ldots ,\xi _n$ are uncertain variables with regular uncertainty distributions $\Phi _1,\Phi _2,\ldots ,\Phi _n$. Denote by $\Phi _1^{-1},\Phi _2^{-1},\ldots ,\Phi _n^{-1}$ the inverse uncertainty distributions of $\Phi _1,\Phi _2,\ldots ,\Phi _n$. Then, model (9) is converted into the following deterministic model (14),

$$\begin{aligned} \left\{ \begin{array}{ll}\min &{} \displaystyle \int _{-\infty }^{\sum _{i=1}^nx_i\int _0^1\Phi _i^{-1}(\alpha )\mathrm{d}\alpha } \alpha (r)\mathrm{d}r\\ \max &{} \sum _{i=1}^nx_i\int _0^1\Phi _i^{-1}(\alpha )\mathrm{d}\alpha -\sum _{i=1}^n(b_ix_i^++s_ix_i^-)\\ \hbox {s.t.} &{} \sum _{i=1}^nx_i^0-\sum _{i=1}^n(b_ix_i^++s_ix_i^-)=\sum _{i=1}^nx_i\\ &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,n\\ &{} x_i^+\cdot x_i^-=0,\ i=1,2,\ldots ,n\\ &{} x_i^+,x_i^- \ge 0,\ i=1,2,\ldots ,n, \\ &{} l_i\le x_i\le u_i,\ i=1,2,\ldots ,n \end{array}\right. \end{aligned}$$

(14)

in which $\alpha (r)$ is just the root of the equation $x_1\Phi _1^{-1}(\alpha )+\cdots +x_n\Phi _n^{-1}(\alpha )=r$.

Remark 2

Similar to Theorems 3–6, we can also translate Model (10) into deterministic ones when the security returns have the same type of uncertainty distributions.

Table 1 Zigzag uncertain returns of ten securities in Example 1

5 Numerical examples

This section will present two numerical examples to illustrate our proposed model.

Example 1

In this example, we consider a case with ten securities with zigzag uncertain returns shown in Table 1.

Assume that unit purchasing cost $b_i$ is $0.01$ and unit selling cost $s_i$ is $0.02$ for $i=1,2,\ldots ,10$. Further, assume that the holding quantity after adjusting is no more than $0.3$ and short selling is not allowed. That is to say, $l_i=0$ and $u_i=0.3$ for $i=1,2,\ldots ,10$. Model (10) is employed to seek the optimal portfolio, which is rewritten as follows:

$$\begin{aligned} \left\{ \begin{array}{ll}\max &{} \displaystyle \frac{1}{4}\sum _{i=1}^{10}[x_i(4a_i+\beta _i-\alpha _i)-4(b_ix_i^++s_ix_i^-)]\\ &{}\quad -\phi \frac{\left( \sum _{i=1}^{10}2x_i(\alpha _i+\beta _i)+\left| \sum _{i=1}^{10}x_i(\alpha _i-\beta _i)\right| \right) ^2}{\sum _{i=1}^{10}x_i(\alpha _i+\beta _i)+\left| \sum _{i=1}^{10}x_i(\alpha _i-\beta _i)\right| }\\ \hbox {s.t.} &{}\sum _{i=1}^{10}x_i^0-\sum _{i=1}^{10}(b_ix_i^++s_ix_i^-)=\sum _{i=1}^{10}x_i\\ &{} x_i=x_i^0+x_i^+-x_i^-,\ i=1,2,\ldots ,10\\ &{} x_i^+\cdot x_i^-=0,\ i=1,2,\ldots ,10\\ &{} 0\le x_i\le 0.3,\ i=1,2,\ldots ,10 \end{array}\right. \end{aligned}$$

(15)

which is a deterministic mathematical programming with linear constraints.

Assume that the investor’s current existing portfolio before adjusting is

$$\begin{aligned}&(x_1^0,x_2^0,x_3^0,x_4^0,x_5^0,x_6^0,x_7^0,x_8^0,x_9^0,x_{10}^0)\\&\quad =(0.10, 0.10, 0.10, 0.10, 0.10, 0.10, 0.10, 0.10, 0.10, 0.10). \end{aligned}$$

The function “fmincon” in Matlab is employed to solve the model, and the computational results are shown in Table 2 for different risk-averse factors $\phi$.

Table 2 The optimal adjusting strategies for ten securities for different values of $\phi$

Example 2

We consider another problem with ten securities with different types of uncertain returns. The first five securities have zigzag uncertain returns denoted by $\xi _1=\mathcal {Z}(-0.4,0.1,0.6)$, $\xi _2=\mathcal {Z}(-0.8,-0.2,0.4)$, $\xi _3=\mathcal {Z}(-0.5,-0.1,0.3)$, $\xi _4=\mathcal {Z}(-0.6,0.1,0.8)$ and $\xi _5=\mathcal {Z}(-0.6,0.2,1.0)$, respectively, and the other five securities have normal uncertain returns denoted by $\xi _6=\mathcal {N}(-0.10,0.05), \xi _7=\mathcal {N}(0.10,0.24), \xi _8=\mathcal {N}(-0.05, 0.12), \xi _9=\mathcal {N}(0.15, 0.15), \xi _{10}=\mathcal {N}(0.05, 0.16)$, respectively. First, we can obtain their inverse uncertainty distributions as follows:

$$\begin{aligned}&Phi_1^{-1}(\alpha )=\alpha -0.4\\&\Phi _2^{-1}(\alpha )=1.2\alpha -0.8\\&\Phi _3^{-1}(\alpha )=0.8\alpha -0.5\\&\Phi _4^{-1}(\alpha )=1.4\alpha -0.6\\&\Phi _5^{-1}(\alpha )=1.6\alpha -0.6\\&\Phi _6^{-1}(\alpha )=-0.10+0.123\ln (\alpha /(1-\alpha ))\\&\Phi _7^{-1}(\alpha )=0.10+0.270\ln (\alpha /(1-\alpha ))\\&\Phi _8^{-1}(\alpha )=-0.05+0.191\ln (\alpha /(1-\alpha ))\\&\Phi _9^{-1}(\alpha )=0.15+0.214\ln (\alpha /(1-\alpha ))\\&\Phi _{10}^{-1}(\alpha )=0.05+0.221\ln (\alpha /(1-\alpha )) \end{aligned}$$

Let $(x_1,x_2,\ldots ,x_{10})$ be the portfolio after adjusting. Then we have

$$\begin{aligned}&x_1\Phi _1^{-1}(\alpha )+x_2\Phi _2^{-1}(\alpha )+\cdots +x_{10}\Phi _{10}^{-1}(\alpha )\\&\quad =(x_1+1.2x_2+0.8x_3+1.4x_4+1.6x_5)\alpha \\&\qquad +(0.123x_6+0.270x_7+0.191x_8+0.214x_9\\&\quad +0.221x_{10})\ln (\alpha /(1-\alpha ))\\&\qquad -0.4x_1-0.8x_2-0.5x_3-0.6x_4-0.6x_5\\&\qquad -0.10x_6+0.10x_7-0.05x_8+0.15x_9+0.05x_{10}. \end{aligned}$$

If the short-selling is not allowed, then $x_1,\ldots ,x_{10}$ are all non-negative. Consequently, $x_1\Phi _1^{-1}(\alpha )+x_2\Phi _2^{-1}(\alpha )+\cdots +x_{10}\Phi _{10}^{-1}(\alpha )$ is an increasing function of $\alpha$ which implies that the equation

$$\begin{aligned} x_1\Phi _1^{-1}(\alpha )+x_2\Phi _2^{-1}(\alpha )+\cdots +x_{10}\Phi _{10}^{-1}(\alpha )=r \end{aligned}$$

has only one root, denoted by $\alpha (r)$. The function “fzero” in Matlab can be used to find the root of the above equation.

Assume that the investor’s current holding on security $i$ is $x_i^0=0.10$, and $b_i=0.01, s_i=0.02$ for $i=1,2,\ldots ,10$. In addition, we assume that the holding quantity is no more than 0.3 after adjusting. If the investor wishes to minimize the semiabsolute deviation (risk) when the expected return is no less than the return level $r_0$, then the corresponding mean-semiabsolute deviation adjusting model is reformulated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll}\min &{} \displaystyle \int _{-\infty }^{\tau }\alpha (r)\mathrm{d}r\\ \hbox {s.t.} &{} 0.025+0.1x_1^+-0.2x_2^+-0.1x_3^++0.1x_4^++0.2x_5^+-0.1x_6^+\\ &{} +0.1x_7^+-0.05x_8^++0.15x_9^++0.05x_{10}^+-0.1x_1^-+0.2x_2^-\\ &{}+0.1x_3^{-}0.1x_4^--0.2x_5^-+0.1x_6^--0.1x_7^-+0.05x_8^{-}-0.15x_9^{-}\\ &{} -0.05x_{10}^-=\tau 0.025+0.09x_1^+-0.21x_2^+-0.11x_3^++0.09x_4^+\\ &{} +0.19x_5^{+}-0.11x_6^{+}+0.09x_7^+-0.06x_8^++0.14x_9^++0.04x_{10}^+\\ &{}-0.12x_1^{-}+0.18x_2^-+0.08x_3^{-}-0.12x_4^--0.22x_5^-+0.08x_6^-\\ &{}-0.12x_7^-+0.03x_8^--0.17x_9^--0.07x_{10}^-\ge r_0\\ &{} \sum \nolimits _{i=1}^{10}x_i^+-0.9703\sum \nolimits _{i=1}^{10}x_i^-=0\\ &{} x_i^+\cdot x_i^-=0,\ i=1,2,\ldots ,10\\ &{} 0\le x_i^+\le 0.2,\ i=1,2,\ldots ,10\\ &{} 0\le x_i^-\le 0.1,\ i=1,2,\ldots ,10, \end{array}\right. \nonumber \\ \end{aligned}$$

(16)

where $\alpha (r)$ is the root of

$$\begin{aligned}&(0.6+x_1^++1.2x_2^++0.8x_3^++1.4x_4^++1.6x_5^+-x_1^-\\&\quad -1.2x_2^--0.8x_3^--1.4x_4^--1.6x_5^-)\alpha \\&\quad +(0.1019+0.123x_6^++0.270x_7^++0.191x_8^++0.214x_9^+\\&\quad +0.221x_{10}^+-0.123x_6^--0.270x_7^-\\&\quad -0.191x_8^--0.214x_9^--0.221x_{10}^-)\ln (\alpha /(1-\alpha ))-0.275\\&\quad -0.4x_1^+-0.8x_2^+-0.5x_3^+-0.6x_4^+-0.6x_5^+-0.10x_6^+\\&\quad +0.10x_7^+-0.05x_8^++0.15x_9^++0.05x_{10}^+\\&\quad +0.4x_1^-+0.8x_2^-+0.5x_3^-+0.6x_4^-+0.6x_5^-+0.10x_6^-\\&\quad -0.10x_7^-+0.05x_8^--0.15x_9^--0.05x_{10}^-=r \end{aligned}$$

in which $r\le \tau$.

Fig. 1

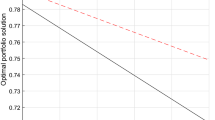
The efficient frontier of Example 2

The function “fmincon” in Matlab is again employed to solve the above model, in which the objective is calculated based on numerical integral and the function “fzero” is called. The obtained results are shown in Table 3. The last row shows the corresponding semiabsolute deviations of optimal portfolios. It can be observed that the semiabsolute deviation will increase with the desired return levels $r_0$ increases. To see intuitively this point, the efficient frontier is shown in Fig. 1 in which the vertical axis is the return levels and the horizontal axis is the corresponding minimum semiabsolute deviations.

Table 3 The optimal adjusting strategies for ten securities for different return levels $r_0$

6 Conclusions

In this paper, we have considered the problem of unbalancing an existing portfolio in response to changed financial markets. The returns of risk securities are given by the expert’s evaluation and treated as uncertain variables. We used the expected value and semiabsolute deviation of uncertain variables to measure the return and risk of the securities, respectively. Considering the return of risky securities are linear, zigzag and normal uncertain variables, we converted the optimization models into corresponding crisp mathematical programming. Two numerical examples were presented to show the effectiveness of the proposed approach. The modeling methods provide alternatives to solve portfolio selection and are also applied to other fields.

Appendix

Proof of Theorem 1

Note that $\sum _{i=1}^n\xi _ix_i$ is also an uncertain variable. It immediately follows from Lemmas 1 and 3 of Sect. 2 that the theorem holds.

Proof of Theorem 2

Assume that there exists $k\in \{1,2,\ldots ,n\}$ such that $\hat{x}_k^+>0$ and $\hat{x}_k^->0$. Without loss of generality, it is assumed that $\hat{x}_k^+ > \hat{x}_k^-$. The optimal holding quantity of security $i$ after adjusting is $\hat{x}_k=x_k^0+\hat{x}_k^+-\hat{x}_k^-$. We set $\tilde{x}_k^+=\hat{x}_k^+-\hat{x}_k^-$ and $\tilde{x}_k^-=0$. It is evident that $\tilde{x}_k^+\cdot \tilde{x}_k^-=0$, $\tilde{x}_k^+,\tilde{x}_k^-\ge 0$ and $\tilde{x}_k=x_k^0+\tilde{x}_k^+-\tilde{x}_k^-=\hat{x}_k$ which implies that $(\hat{x}_1^+,\ldots ,\hat{x}_{k-1}^+,\tilde{x}_k^+,\hat{x}_{k+1}^+,\ldots ,\hat{x}_n^+, \hat{x}_1^-,\ldots ,\hat{x}_{k-1}^-,\tilde{x}_k^-,\hat{x}_{k+1}^-,\ldots ,\hat{x}_n^-)$ is a feasible solution of Model (8). Note that

$$\begin{aligned}&r(\hat{x}_1,\ldots ,\hat{x}_{k-1},\tilde{x}_k,\hat{x}_{k+1},\ldots ,\hat{x}_n)\\&\qquad -r(\hat{x}_1,\ldots ,\hat{x}_{k-1},\hat{x}_k,\hat{x}_{k+1},\ldots ,\hat{x}_n)\\&\quad =(b_k+s_k)\hat{x}_k^->0 \end{aligned}$$

which means that $E[r(\hat{x}_1,\ldots ,\hat{x}_{k-1},\tilde{x}_k,\hat{x}_{k+1},\ldots ,\hat{x}_n)] >E[r(\hat{x}_1,\ldots ,\hat{x}_{k-1},\hat{x}_k,\hat{x}_{k+1},\ldots ,\hat{x}_n)]$. In addition, since $\tilde{x}_k=\hat{x}_k$, the return on the portfolio $(\hat{x}_1,\ldots ,\hat{x}_{k-1},\tilde{x}_k,\hat{x}_{k+1},\ldots ,\hat{x}_n)$ has the same semiabsolute deviation as that on the portfolio $(\hat{x}_1,\ldots ,\hat{x}_{k-1},\hat{x}_k,\hat{x}_{k+1},\ldots ,\hat{x}_n)$. Therefore, it is in contradiction to that $(\hat{x}_1^+,\ldots ,\hat{x}_n^+,\hat{x}_1^-,\ldots ,\hat{x}_n^-)$ is Pareto optimal. The theorem is completed.

Proof of Theorem 3

It follows from the operational law of uncertain variables that the portfolio return $\sum _{i=1}^n\xi _ix_i =(\sum _{i=1}^nx_ic_i,\sum _{i=1}^nx_id_i)$ is also a linear uncertain variable with expected value $\sum _{i=1}^nx_i(d_i+c_i)/2$. Further, we have

$$\begin{aligned}&E\left[ \sum _{i=1}^n\xi _ix_i\right] -\sum _{i=1}^n(b_ix_i^++s_ix_i^-)\\&\qquad =\frac{1}{2}\left( \sum _{i=1}^nx_i(d_i+c_i)-2\sum _{i=1}^n(b_ix_i^++s_ix_i^-)\right) . \end{aligned}$$

Therefore, the second objective is equivalent to maximize the term in parentheses on the right-hand side of the above equation. In addition, it follows from Liu and Qin (2012) that

$$\begin{aligned} Sa\left[ \sum _{i=1}^n\xi _ix_i\right] =\frac{1}{8}\sum _{i=1}^nx_i(d_i-c_i). \end{aligned}$$

Note that since $x_i\ge 0$ and $d_i>c_i$ for $i=1,2,\ldots ,n$, we have $\sum _{i=1}^nx_i(d_i-c_i)\ge 0$ which implies that the first objective is equivalent to minimize it. The theorem is proved.

Proof of Theorem 4

It follows that the portfolio return

$$\begin{aligned} \sum _{i=1}^n\xi _ix_i =\left( \sum _{i=1}^nx_i(a_i-\alpha _i),\sum _{i=1}^nx_ia_i,\sum _{i=1}^nx_i(a_i+\beta _i)\right) \end{aligned}$$

is also a zigzag uncertain variable. According to the definition of expected value, we have $E[\sum _{i=1}^n\xi _ix_i]=\sum _{i=1}^nx_i(4a_i+\beta _i-\alpha _i)/4$ which implies that the second objective is equivalent to maximize $\sum _{i=1}^nx_i(4a_i+\beta _i-\alpha _i)-4\sum _{i=1}^n(b_ix_i^++s_ix_i^-)$. Further, by the definition of semiabsolute deviation of uncertain variable, it is obtained that

$$\begin{aligned} Sa\left[ \sum _{i=1}^n\xi _ix_i\right] \!=\!\frac{\left[ \sum _{i=1}^n2x_i(\alpha _i\!+\!\beta _i)\!+\!\left| \sum _{i=1}^nx_i(\alpha _i\!-\!\beta _i)\right| \right] ^2}{\sum _{i=1}^nx_i(\alpha _i\!+\!\beta _i)\!+\!\left| \sum _{i=1}^nx_i(\alpha _i\!-\!\beta _i)\right| }. \end{aligned}$$

Substituting the semiabsolute deviation of the portfolio return into the first objective, the theorem is proved.

Proof of Theorem 5

It follows from the operational law of normal uncertain variables that the portfolio return $\sum _{i=1}^n\xi _ix_i\sim \mathcal {N}(\sum _{i=1}^nx_ie_i,$ $\sum _{i=1}^nx_i\sigma _i)$ is also a normal uncertain variable. Further, it follows from the definitions of expected value and semiabsolute deviation of uncertain variables that

$$\begin{aligned}&E\left[ \sum _{i=1}^n\xi _ix_i\right] =\sum \limits _{i=1}^ne_ix_i\ge 0,\\&Sa\left[ \sum _{i=1}^n\xi _ix_i\right] =\frac{\sqrt{3}\ln 2}{\pi }\sum \limits _{i=1}^n\sigma _ix_i\ge 0 \end{aligned}$$

in which non-negativity holds due to non-negativity of $x_i,e_i$ and $\sigma _i$ for $i=1,2,\ldots ,n$. Substituting them into the two objective functions in Model (9), the theorem is proved.

Proof of Theorem 6

The second objective holds since $E[\xi _i]=\int _0^1\Phi _i^{-1}(\alpha )\mathrm{d}\alpha$ for $i=1,2,\ldots ,n$ by Lemma 1. According to the definition of semiabsolute deviation of uncertain variable, we have

$$\begin{aligned} Sa\left[ \sum _{i=1}^n\xi _ix_i\right]&= \int _0^{+\infty }\mathcal {M}\left\{ \min \left\{ \sum _{i=1}^n\xi _ix_i\right. \right. \\&\left. \left. -\sum _{i=1}^nx_i\int _0^1\Phi _i^{-1}(\alpha )\mathrm{d}\alpha ,0\right\} \ge r\right\} \mathrm{d}r\\&= \int _{-\infty }^{\sum _{i=1}^nx_i\int _0^1\Phi _i^{-1}(\alpha )\mathrm{d}\alpha }\mathcal {M}\left\{ \sum _{i=1}^n\xi _ix_i{\le } r\right\} \mathrm{d}r. \end{aligned}$$

Note that since $x_i\ge 0$ for $i=1,2,\ldots ,n$, it follows from the operational law (Liu 2010) that $\xi _1x_1+\xi _2x_2\cdots +\xi _nx_n$ has an inverse uncertainty distribution $\Psi _1^{-1}(\alpha ) = x_1\Phi _1^{-1}(\alpha )+x_2\Phi _2^{-1}(\alpha )\cdots +x_n\Phi _n^{-1}(\alpha )$. For any given r, the value of $\Psi (r)=M\{\xi _1x_1+\cdots +\xi _nx_n\le r\}$ is just the root of the equation $\Psi _1^{-1}(\alpha ) = r$, i.e., $x_1\Phi _1^{-1}(\alpha )+\cdots +x_n\Phi _n^{-1}(\alpha )=r$. Substituting it into the expression of $Sa[\xi _1x_1+\xi _2x_2\cdots +\xi _nx_n]$, the first objective function is obtained. The theorem is proved.