Abstract
We present an open-source software RKPM2D for solving PDEs under the reproducing kernel particle method (RKPM)-based meshfree computational framework. Compared to conventional mesh-based methods, RKPM provides many attractive features, such as arbitrary order of continuity and discontinuity, relaxed tie between the quality of the discretization and the quality of approximation, simple h-adaptive refinement, and ability to embed physics-based enrichment functions, among others, which make RKPM promising for solving challenging engineering problems. The aim of the present software package is to support reproducible research and serve as an efficient test platform for further development of meshfree methods. The RKPM2D software consists of a set of data structures and subroutines for discretizing two-dimensional domains, nodal representative domain creation by Voronoi diagram partitioning, boundary condition specification, reproducing kernel shape function generation, domain integrations with stabilization, a complete meshfree solver, and visualization tools for post-processing. In this paper, a brief overview that covers the key theoretical aspects of RKPM is given, such as the reproducing kernel approximation, weak form using Nitsche’s method for boundary condition enforcement, various domain integration schemes (Gauss quadrature and stabilized nodal integration methods), as well as the fully discrete equations. In addition, the computer implementation aspects employed in RKPM2D are discussed in detail. Benchmark problems solved by RKPM2D are presented to demonstrate the convergence, efficiency, and robustness of the RKPM implementation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, the reproducing kernel particle method (RKPM) [1,2,3] has been recognized as an effective numerical method for solving partial differential equations (PDEs). Compared to conventional mesh-based numerical methods such as the finite element method (FEM), the reproducing kernel (RK) approximation in RKPM is constructed based on a set of scattered points without any mesh connectivity, and thus, the strong tie between the quality of the discretization and the quality of approximation in conventional mesh-based methods is relaxed. This “meshfree” feature makes RKPM well-suited for solving large deformation and multiphysics problems where FEM suffers from mesh distortion or mesh entanglement [1, 4, 5]. In addition, RKPM provides controllable orders of continuity and completeness, independent from one another, which enables effective solutions of PDEs involving high-order smoothness or discontinuities, and accordingly, implementation of h- and p-adaptive refinement becomes straightforward [6,7,8,9,10]. Furthermore, the wavelet-like multi-resolution properties can be obtained in the RK approximation, making it suitable for multi-resolution and multi-scale modeling [6,7,8]. Recently, accelerated and convergent RKPM formulations have been developed with the employment of variationally consistent and stabilized nodal integration techniques [11, 12]. With above-mentioned advantages, RKPM has been successfully applied to a number of challenging engineering problems, including thin shell structural mechanics [13, 14], manufacturing processes [15,16,17], image-based biomechanics [18], geomechanics and natural disasters [19, 20], fracture/damage mechanics [21,22,23], shock dynamics [24,25,26] and penetration/fragmentation phenomena [27,28,29], to name a few. Interested readers can refer to [2, 30] for a comprehensive review of RKPM and its applications.
While the overall programing structure of meshfree Galerkin methods using Gauss integration have been discussed in [31, 32], and efficient neighbor searching algorithms and associated data structures for meshfree methods have been developed in [33,34,35,36], a public domain RKPM-based source code is in high demand. In this paper, we present an RKPM-based open-source computational software called RKPM2D [37] that can effectively solve PDEs in a 2D domain with an arbitrary geometry. Nitsche’s method [38, 39] is adopted for imposition of essential boundary conditions in the meshfree Galerkin equations. For domain integration, the variationally consistent and stabilized nodal integration methods [11, 40], Modified Stabilized Conforming Nodal Integration (MSCNI) [41], and Naturally Stabilized Nodal Integration (NSNI) [12] are implemented in RKPM2D in addition to the conventional Gauss quadrature scheme. The program consists of a set of data structures and subroutines for two-dimensional domain discretization, nodal representative domain creation by Voronoi diagram partitioning, reproducing kernel shape function generation, a meshfree Galerkin equation solver, and visualization tools for post-processing. For demonstration purposes, linear elastostatics is chosen as the model problem, and extensions of the RKPM open-source software for solving other types of PDEs are straightforward. The RKPM2D code is implemented under a MATLAB environment [42] with pre-process, solver, and post-process functions fully integrated.
This paper is organized as follows. A brief review of the basic equations of RKPM for linear elasticity is given in Sect. 2, where various domain integration techniques such as Gauss integration, direct nodal integration, and stabilized nodal integration are introduced. In Sect. 3, the computer implementation aspects are presented, including neighbor search processes, RK shape function construction, and domain integration procedures. Benchmark problems are presented in Sect. 4 to demonstrate the capabilities of RKPM2D. Conclusions are then given in Sect. 5.
2 Overview of the reproducing kernel particle method
2.1 Reproducing kernel approximation
In RKPM, the numerical approximation is constructed based upon a set of scattered points or nodes [43]. The domain \( \varOmega \) is discretized by a set of nodes \( \left\{ {\varvec{x}_{1} ,\varvec{x}_{2} ,\ldots \varvec{x}_{\text{NP}} } \right\} \) as shown in Fig. 1, where \( \varvec{x}_{I} \) is the position vector of node \( I \) and \( {\text{NP}} \) is the total number of nodes. The RK approximation of a function \( u \) is expressed as
Illustration of a 2D RK discretization: support coverage and nodal shape function with circular kernel
where \( \varvec{x} \) is the spatial coordinates, \( u_{I} \) is the associated nodal coefficient to be determined, and \( \varPsi_{I} \left( \varvec{x} \right) \) is the reproducing kernel (RK) shape function of node \( I \) expressed as:
where the basis vector \( \varvec{H}\left( {\varvec{x} - \varvec{x}_{I} } \right) \) is defined as
and \( \varvec{ M}\left( \varvec{x} \right) \) is the so-called moment matrix:
The set \( G_{\varvec{x}} = \left\{ {I|\varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) \ne 0 } \right\} \) shown in Eqs. (1) and (4) contains the nodal indexes of point \( \varvec{x} \)’s neighbors, and \( \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) \) is the kernel function centered at \( \varvec{x}_{I} \) with compact support size \( a_{I} \) defined as
In the above equation, \( \tilde{c} \) is the normalized support size, and \( h_{I} \) is the nodal spacing associated with nodal point \( \varvec{x}_{I} \) defined as:
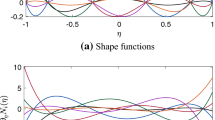
in which the set \( B_{I} \) contains the four nodes that are closest to point \( \varvec{x}_{I} \) for 2D problems. The kernel function controls the smoothness of the approximation as shown in Fig. 2, where the \( C^{0} \) tent kernel function is compared with the following \( C^{2} \) cubic B-spline kernel function:
in which \( z_{I} \) is defined as \( z_{I} = \frac{{\varvec{x} - \varvec{x}_{I} }}{{a_{I} }} \). In addition, shape functions with different normalized support sizes are plotted in Fig. 3, which clearly illustrates that the locality of the approximation is controlled by the kernel support size.
Kernel function and corresponding RK shape function with linear basis and normalized support size \( \tilde{c} = 1.5 \): a tent kernel and b corresponding RK shape function. c cubic B-spline kernel and d corresponding RK shape function
a Cubic B-spline kernel and b corresponding RK shape function (right) with linear basis and normalized support size \( \tilde{c} = 1.5, \,2.5,\, {\text{and}} \,\, 3.5 \)
By construction, the RK shape functions satisfy the following \( n \)th order reproducing conditions:
where \( n \) is the specified order of completeness, which determines the order of consistency in the solution of PDEs. When linear basis is employed, both the zero-th and first-order reproducing conditions are satisfied for uniform and arbitrary point distribution as shown in Fig. 4.
Errors in the zero-th- and first-order reproducing conditions for the RK shape function with linear basis and normalized support size \( \tilde{c} = 1.5 \), where a uniform point distribution are used in a and b and an arbitrary point distribution is used in c and d
2.2 Galerkin formulation
Consider the following linear elasticity problem:
where \( u_{i} \) is the displacement, \( \sigma_{ij} = C_{ijkl} \varepsilon_{kl} \) is the Cauchy stress, \( C_{ijkl} \) is the elasticity tensor, \( \varepsilon_{ij} = \left( {u_{i,j} + u_{j,i} } \right)/2 \) is the strain, \( n_{j} \) is the surface normal on \( \partial \varOmega \), \( b_{i} \) is the body force, and \( t_{i} \) and \( g_{i} \) denote the prescribed traction and displacement on \( \partial \varOmega_{t} \) and \( \partial \varOmega_{g} \), respectively. Using Nitsche’s method [44] for the enforcement of essential boundary conditions, the weak form of Eq. (9) can be written as follows
where \( \lambda_{i} \) is the Lagrange multiplier, and in Nitsche’s method, it is taken as the surface traction for elasticity problems, i.e., \( \lambda_{i} = \sigma_{ij} n_{j} \), and \( \beta = \beta_{\text{nor}} E/\bar{h} \) with \( \beta_{\text{nor}} \) the normalized penalty parameter, \( E \) the Young’s modulus, and \( \bar{h} \) the average of nodal spacing. Considering the following RK approximation for \( \varvec{u} \) and \( \delta \varvec{u} \):
Equation (10) yields the following matrix equation:
where
in which each matrix and vector for two-dimensional elasticity are expressed as
where \( n_{i} \) is the component of the surface unit normal on the essential boundary and \( s_{i} = 0\, {\text{or}}\, 1 \) serves as a switch for imposing each component of the boundary displacement.
2.3 Domain integration
Domain integration plays an important role in accuracy, stability, and convergence of meshfree methods. Unlike FEM which utilizes the element topology for integration, quadrature domains for meshfree methods can be chosen either as background cells that are independent from the point locations, or associated with the nodal representative domains. The former scheme is commonly adopted in conjunction with the Gauss quadrature scheme, and the latter is used for nodal integration schemes; both have been implemented in RKPM2D as discussed in this section.
2.3.1 Gauss integration
When Gauss quadrature is adopted, quadrature points are generated based upon background cells [45, 46] as shown in Fig. 5, where only the quadrature points inside the physical domain are considered for domain integration. Gauss points for contour integrals are generated along the natural and essential boundaries, also shown in Fig. 5.
Meshfree points and background Gauss quadrature points in arbitrary two-dimensional domain \( \varOmega \)
The domain and boundary integrations in (15)–(21) are computed as follows:
where \( \varvec{P}\left( \varvec{x} \right) \) and \( \varvec{Q}\left( \varvec{x} \right) \) denote integrands in the domain and boundary integrals in (15)–(21); \( \varvec{x}_{N} \varvec{ } \), \( W_{N} \), and \( {\text{NG}} \) are the domain Gauss points, weights, and the number of domain Gauss points, respectively, and \( \hat{\varvec{x}}_{N} \), \( \hat{W}_{N} \), and \( {\text{NG}}g \) are essential boundary Gauss points, weights, and the number of essential boundary Gauss points, respectively. The same integration rules are used for the natural boundary integration. Since RK shape functions are rational functions and their supports overlap with each other, the misalignment of Gauss integration cells and shape function supports lead to large quadrature errors unless high-order integration schemes are adopted, as shown in [11, 45]. Nonetheless, Gauss integration is chosen as a reference quadrature scheme herein.
2.3.2 First-order variational consistent nodal integration with gradient smoothing
The simplest nodal integration method is direct nodal integration (DNI), where shape functions and their derivatives are evaluated directly at nodes.
The domain and boundary integrations in (15)–(21) are computed as follows:
where \( \varvec{x}_{N} \), \( A_{N} \), and \( {\text{NP}} \) are the RK node locations, nodal representative domain areas, and the number of RK nodes, respectively, and \( \hat{\varvec{x}}_{N} \), \( L_{N} \), and \( {\text{NP}}g \) are essential boundary RK nodes, length of the nodal representative domain, and the number of RK nodes on the essential boundary, respectively. The same integration rules are used for the natural boundary integration.
DNI is notorious for spurious zero-energy modes and non-convergent numerical solutions. To ensure linear variational consistency, i.e., the ability of numerical methods to pass the linear patch test, Chen et al. [40] showed that the quadrature rules need to meet the following first-order integration constraint for the shape function gradient:
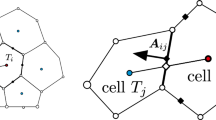
In (28), \( \wedge \) over the integral symbols denotes numerical integration. For nodal integration as the quadrature rule for the domain integration on the left hand side of Eq. (28), Chen et al. [40] introduced the following nodally smoothed gradient \( \tilde{\varPsi }_{I,i} \) at the nodal point \( \varvec{x}_{N} \):
where AN denotes the area of the nodal representative domain \( \varOmega_{N} \) associated with node N, and ni denotes the i-th component of the outward unit normal vector to the smoothing domain boundary as shown in Fig. 6. It was shown in [1] that integrating Eq. (28) with nodal integration with the smoothed gradient of shape function in Eq. (29), the first-order integration constraint in Eq. (28) is exactly satisfied as long as the same boundary integral quadrature rules are used for the right hand side of both Eqs. (28) and (29). As discussed in [11], in order to maintain linear consistency of the smoothed gradient of a linearly consistent shape function, a simple one-point Gauss integration rule can be used for the contour integral in Eq. (29):
Voronoi cell diagram in two-dimensional domain \( \varOmega \)
where \( S_{N} = \left\{ {K |\tilde{\varvec{x}}_{N}^{K} \in \partial \varOmega_{N} } \right\} \) contains all center points of each boundary segment associated with node \( \varvec{x}_{N} \), and the integration weight \( L_{K} \) is the length of the \( K\)th segment of the smoothing cell boundary. By employing smoothed shape function gradients, the stiffness matrix and the force vectors are re-formulated as follows:
where \( \tilde{\varvec{B}}_{I} \left( {\varvec{x}_{N} } \right) \) is defined as
Remark
For the smoothed gradients in Eq. (29), conforming nodal representative domains as shown in Fig. 6 are employed here by following the SCNI approach [40]. On the other hand, non-conforming nodal representative domains can also be employed, which leads to the so-called stabilized non-conforming nodal integration (SNNI) approach [41]. While SNNI violates the first-order integration constraint (Eq. (28)), it can be corrected by the variational consistent integration (VCI) [11] to recover the optimal rates of convergence. VCI can also be used to achieve higher rates of convergence in RKPM with higher-order bases in the RK approximation.
2.3.3 Stabilized nodal integration schemes
Spurious oscillatory modes can be triggered in nodal integration methods. Therefore, additional stabilization techniques are needed to eliminate these low-energy modes, which will be described in this subsection.
2.3.3.1 Modified stabilized nodal integration
The first stabilization technique employed here for eliminating spurious low-energy modes is called modified stabilized nodal integration [41, 47], where a least-squares type stabilization term is introduced into the stiffness matrix:
where \( {\text{NS}} \) denotes the number of sub-cells associated with each nodal integration cell (as shown in Fig. 7), \( \hat{\varvec{x}}_{N}^{S} \) denotes the centroid of the \( S \)th sub-cell, \( \tilde{\varvec{B}}_{J} ( {\hat{\varvec{x}}_{N}^{S} }) \) is the smoothed gradient evaluated by Eqs. (30) and (34) for the \( S\)th sub-cell, and \( A_{N}^{S} \) denotes the area of the \( S \)th sub-cell of the \( N \) th nodal cell. Here, \( 0 \le c_{\text{stab}} \le 1 \) is a stabilization parameter, which is chosen to be \( c_{\text{stab}} = 1 \) based on the study of Puso et al. [47] for elasticity. If the direct gradient \( \varvec{B}_{I} ( {\varvec{x}_{N} }) \) and \( \varvec{B}_{I} ( {\hat{\varvec{x}}_{N}^{S} } ) \) are used for nodal integration and stabilization terms in Eq. (35), the stiffness matrix is formulated as:
Illustration of nodal integration cells of the modified stabilized nodal integration
which is a modified stabilization for the DNI method. For comparison purposes, in the rest of this paper we will refer the modified formulations (35) based on SCNI as Modified SCNI (MSCNI), and (36) based on DNI as modified DNI (MDNI), respectively. The least-squares-type stabilization term in (35) enhances the coercivity of the discrete formulation and suppresses spurious low-energy modes in nodal integrations, but meanwhile, a number of additional shape function evaluations are required.
2.3.3.2 Naturally stabilized nodal integration
The other stabilized integration technique employed here is the naturally stabilized nodal integration (NSNI) proposed in [12], where an implicit gradient expansion of the strain field is introduced as:
where \( \hat{\varvec{u}}_{,i}^{h} \left( {{\varvec{x}}_{N} } \right) = \sum\nolimits_{I = 1}^{\text{NP}} {\varPsi_{Ii}^{\nabla } \left( {\varvec{x}_{N} } \right)\varvec{u}_{I} } \) is the implicit gradient of the displacement with \( \varPsi_{Ii}^{\nabla } \) the implicit gradient of the RK shape function [22]:
where \( \varvec{H } = \left[ {\begin{array}{*{20}c} 1, & {x_{1} - x_{I1} }, & {x_{2} - x_{I2} } \\ \end{array} } \right]^{\text{T}} \) and the vector \( \varvec{H}_{i} \) takes on the following values for linear basis:
Introducing the gradient expansion terms (37) into the variational equations, the stiffness matrix is obtained as
and \( \varvec{ B}_{I1}^{\nabla } \left( {\varvec{x}_{N} } \right) \) and \( \varvec{B}_{I2}^{\nabla } \left( {\varvec{x}_{N} } \right) \) are defined as follows:
Here, the derivatives of the RK implicit gradients \( \varPsi_{Ii,j}^{\nabla } \) in Eq. (41) are obtained by the direct differentiation of the first-order implicit gradient \( \varPsi_{Ii}^{\nabla } \) in Eq. (38) with respect to \( x_{j} \) [12]. Alternatively, one can also approximate \( \varPsi_{Ii,j}^{\nabla } \) by taking the smoothed derivative of \( \varPsi_{Ii}^{\nabla } \) in Eq. (29). In the present RKPM2D implementation, we adopt the former approach in computing \( \varPsi_{Ii,j}^{\nabla } \) by the direct differentiation of \( \varPsi_{Ii}^{\nabla } \) at nodal points by following [12]. The terms \( M_{1} \left( {\varvec{x}_{N} } \right), M_{2} \left( {\varvec{x}_{N} } \right) \) in Eq. (41) are the second moments of inertia in each nodal integration domain:
From Eqs. (40)–(42), no subdivision of integration cells is required in the stabilization. Similar to the discussion in the previous section, this stabilization technique can also be employed in conjunction with DNI by replacing the smoothed gradients in Eq. (40) with direct gradients:
Accordingly, the DNI- and SCNI-based naturally stabilized formulations in Eq. (43) and in Eq. (40) are denoted as NSDNI and NSCNI, respectively, which will be examined and compared in detail in Sect. 4.
3 Computer implementation aspects
In this section, the basic data structures and main functions of RKPM2D will be explained, which cover domain discretization, RK shape functions and gradients, domain integration, assembly of stiffness matrices and force vectors, and visualization of the numerical results. Also, the key differences between RKPM and FEM programs are discussed. The source codes (.m files) of RKPM2D are publicly available online [37].
3.1 Overall program structure
The general flowchart of RKPM2D is given in Fig. 8. Unlike in the FEM procedures where the element type is tied with mesh/nodes generation, the order of basis and smoothness is independent of the domain discretization in RKPM, while the general program functionalities (such as matrix assembly and solver) of a meshfree Galerkin method are similar to that of FEM.
Flowchart of the RKPM procedure
As shown in Fig. 8, the numerical procedures for the model problem described in Eqs. (9)–(22) consist of input file generation, domain discretization, quadrature rule definition, shape function construction, matrix assembly, solver, and post-processing. The corresponding main subroutine names of RKPM2D are also shown in Fig. 8.
3.2 Input file generation
To illustrate the functionality of each main subroutine shown in Fig. 8, let us consider a linear elasticity problem (Eq. (9)) with a manufactured solution of
which can be considered as a linear patch test and is defined here over the 2D circular domain \( \varOmega \subset {\mathbb{R}}^{2} \) shown in Fig. 9.
Domain discretization for model problem in 2D circular domain \( \varOmega \)
The traction \( \varvec{t} \), body force \( \varvec{b} \), and displacement \( \varvec{g} \) are prescribed based on the exact solution \( \varvec{u}^{\text{exact}} \) in Eq. (44):
where \( \varvec{\varepsilon}^{\text{exact}} \) and \( \varvec{\sigma}^{\text{exact}} \) are exact strain and stress defined as:
where \( \varvec{\eta} \) is the matrix of outward unit normal vector of the boundary, \( \varvec{C} \) is the matrix of elastic tensor with Young’s modulus \( E = 2.1 \times 10^{11} \) and Poisson’s ratio \( \nu = 0.3 \). The traction \( \varvec{t} \) is imposed on \( \partial \varOmega_{t} :\left( {x_{1} ,x_{2} } \right) \in \partial \varOmega ,\, x_{2} > 0.5 \), essential boundary conditions \( \varvec{g} \) are enforced on \( \partial \varOmega_{g} :\left( {x_{1} ,x_{2} } \right) \in \partial \varOmega , \,x_{2} \le 0.5 \), and the body force is \( \varvec{b} = 0 \) in this case. Accordingly, the input file for this problem is created by the function getInput with three data structures: RK, Quadrature, and Model, which define the RK shape functions, quadrature rules, numerical parameters (such as penalty parameters, elastic modulus, and Poisson ratio), respectively. A sample input file for the above-mentioned linear patch test is given in Listing 1, where RK contains the following fields:
KernelFunction: kernel functions with different levels of continuity.
KernelGeometry: the nodal support shape where “CIR” and “REC” represent circular and rectangular supports, respectively.
NormalizedSupportSize: normalized support size \( \tilde{c} \).
Order: the order of basis (constant, linear, or quadratic).
Note that the RK shape functions are computed at the beginning of the simulation based on the information in the structure RK. The variable names for kernel functions with different levels of continuity are listed in Table 1, and the corresponding mathematical expressions of each kernel function are given in Appendix A
In Listing 1, Quadrature contains the following fields:
Integration: basic quadrature rules, where “DNI,” “SCNI,” and “GAUSS” options are provided.
Stabilization: types of stabilization for nodal integration, where symbol “N” represents naturally stabilized nodal integration and symbol “M” represents modified nodal integration as described in Sect. 2.3.3.
Option_BCintegration: quadrature rules for boundary integrals, including “NODAL” and “GAUSS” options.
nGaussPoints: the number of Gauss points \( N_{\text{g}} \in {\mathbb{N}} \) in each background integration cell. For example, \( N_{\text{g}} = 6 \) denotes \( 6 \times 6 \) Gauss points in each cell
nGaussCells: the parameter determines the number of background integration cells along \( x_{1} \) or \( x_{2} \) direction of the problem domain, depending on the problem domain dimension.
Note that the nGaussPoints and nGaussCells are used only for Gauss integration. In addition, Model contains the following fields:
E, nu: Young’s modulus \( E \), Poisson ratio \( \nu \).
DOFu: the number of nodal degrees of freedom, DOFu=2 for 2D elasticity.
BetaNormalized: normalized penalty parameter.
xVertices: physical coordinates of integration cells.
CriteriaEBC: function handle to define the essential boundaries.
CriteriaNBC: function handle to define the natural boundaries.
To implement the traction \( \varvec{t} \), body force \( \varvec{b} \), displacement \( \varvec{g} \) based on the exact solution \( \varvec{u}^{\text{exact}} \) in Eqs. (45)–(49), and the switch matrix \( \varvec{S} \), the symbolic computation in MATLAB is employed to obtain the expression of \( \varvec{t} \), \( \varvec{b} \), \( \varvec{g} \), and \( \varvec{S} \). As shown in Listing 2, for any given exact displacement field \( \varvec{u}^{\text{exact}} \left( \varvec{x} \right) \) in the symbolic form, \( \varvec{t } \), \( \varvec{b} \), \( \varvec{g} \), and \( \varvec{S} \) based on Eqs. (45)–(49) are obtained from the function Pre_GenerateBoundaryConditions with \( \varvec{u}^{\text{exact}} \) as an input variable, as shown in Listing 3. Then, these variables are saved as function handles under the structure Model.ExactSolution by matlabFunction command (note: a function handle is a data type in MATLAB to store an association with a function). Alternatively, if the exact solution \( \varvec{u}^{\text{exact}} \) is not specified, then one can define traction \( \varvec{t} \), body force \( \varvec{b} \), displacement \( \varvec{g} \), and switch matrix \( \varvec{S} \) in individual functions, as shown in Listing 4. The structure Model.ExactSolution contains the following fields:
t: return the traction \( \varvec{t} \).
b: return the body force vector \( \varvec{b} \).
g: return the imposed displacement \( \varvec{g} \).
S: return the switch matrix \( \varvec{S} \).
3.3 Domain discretization
After the definition of basic model input parameters (RK, Quadrature, Model), the function Pre_GenerateDiscretization(Model) is called for domain discretization. Pre_GenerateDiscretization will return the structure Discretization which consists of the following fields:
xI_Boundary: coordinates of the boundary RK nodes
xI_Interior: coordinates of the interior RK nodes
nP: the total number of discretized RK nodes, \( {\text{NP}} \).
As shown in the command lines in Listing 5, the MATLAB built-in functions geometryFromEdges and generateMesh are employed to decompose the domain into conforming sub-domains (that can be considered as an FEM mesh), and the resulting vertices are directly employed as meshfree nodes.
Alternatively, users of RKPM2D can also define the meshfree nodes manually or importing an FEM mesh from CAD/FEM software instead of using the MATLAB built-in meshing function. Such a subroutine, sub_ReadNeutralInputFiles, is given in Listing 6 which reads in nodal coordinates from a PATRAN neutral file.
3.4 Quadrature point generation
The quadrature points are generated in the function Pre_GenerateQuadraturePoints which support the following two domain integration schemes:
Nodal integration, where the Voronoi cells are defined.
Gauss integration, where the background integration cells are defined.
Standard Gauss integration cell and the corresponding coordinates and weights of Gauss points are employed for Gauss integration. As for nodal integration, the quadrature points and weights are based on Voronoi cells. The construction of Voronoi diagram is achieved by employing the function getVoronoiDiagram, which is modified from the open-source code sub_VoronoiLimit [48]. By calling getVoronoiDiagram, the structure VoronoiDiagram which contains the following fields will be returned:
VerticeCoordinates: all vertices’ coordinates of Voronoi cells.
VoronoiCell: indexes of vertices within each Voronoi cell.
The VoronoiDiagram structure defines the quadrature rules required for nodal integration as described in Eqs. (26) and (27). By looping over the Voronoi cells, the following two classes are added by Pre_GenerateQuadraturePoints into the structure Quadrature which defines the quadrature rules to compute the RK shape functions for domain and boundary integration:
Domain: class that defines the variables required for domain integration.
nQuad: the total number of quadrature points.
xQuad: the coordinates of quadrature points.
Weight: quadrature weights for domain integral.
BC: class that defines the variables required for boundary integration.
nQuad_onBoundary: the number of quadrature points on the boundary.
xQuad_onBoundary: coordinates of quadrature points on the boundary.
Weight_onBoundary: quadrature weights for contour integral.
Normal_onBoundary: outward unit normal vectors at quadrature points along the boundary.
3.5 RK shape function generation
In FE programing, double loops are required to evaluate the stiffness matrix and force vector, including one loop over all elements and another loop over all quadrature points within each element. In RKPM, only one loop over all quadrature points is required if a nodal integration method is used. As shown in Fig. 10, at each quadrature point, the RK shape functions and their derivatives \( \varPsi_{I} \left( {\varvec{x}_{N} } \right) \), \( \varPsi_{I,1} \left( {\varvec{x}_{N} } \right) \), and \( \varPsi_{I,2} \left( {\varvec{x}_{N} } \right) \) [and/or smooth and implicit gradients given in Eqs. (29) and (38)] are evaluated in the physical domain. In contrast, FEM shape functions and derivatives constructed in the parametric domain and require an isoparametric mapping process which may introduce large errors when the elements are severely distorted.
Flowchart of the algorithm in a RK and b FE shape function generation
Another difference in computing RK and FE shape functions is the determination of nodal neighbors. FEM relies on the use of an element mesh to define the shape functions, and thus, the neighbors for a given evaluation point are simply the nodes defining the element. In contrast, in RKPM the shape functions are defined directly at nodes without the element connectivity. Consequently, a neighbor search is necessary to determine the neighbors of a given evaluation point in RKPM. The neighbor search algorithm could be CPU intensive, especially for 3D simulations, so efficient spatial search algorithms such as KD-Tree [49], DESS [50], among others [33,34,35,36] have been employed. In this study, the efficient search algorithms KDTreeSearcher [51] and rangesearch function under KDTreeSearcher are employed. The command line for constructing the neighbor list is:
Here the inputs of rangesearch are explained as follows
xI: coordinates of RK nodes \( \varvec{x}_{I} \).
x: coordinates of evaluation points \( \varvec{x} \).
SupportSize: the support size \( a_{I} \).
Evaluation of RK shape functions with respect to RK nodes \( \varvec{x}_{I} \) at an evaluation point \( \varvec{x} \) is performed in getRKShapeFunction, for which the program structure is illustrated in Algorithm 1 to Algorithm 4. Note that, in the evaluation of the derivatives of kernel functions in Algorithm 3, the derivative of the distance \( z_{I,i} = \frac{{\left( {x_{i} - x_{iI} } \right)}}{{\left( {z_{I} a_{I}^{2} } \right)}} \) becomes singular when the evaluation point \( \varvec{x} \) approaches node \( \varvec{x}_{I} \) (i.e., \( z_{I} = ||\varvec{x} - \varvec{x}_{I}||\, \approx 0 \)). This is avoided by setting \( z_{I} = 0, {\varvec{\nabla}} z_{I} = {\varvec{0}} \) if \( ||\varvec{x} - \varvec{x}_{I}||\, < {\text{eps}} \), where \( {\text{eps}} \) is the default positive machine precision number in MATLAB, which works well for symmetric and smooth kernels. Alternatively, we can set \( z_{I,1} = \frac{{\left( {x_{1} - x_{1I} } \right)}}{{\left( {z_{I} a_{I}^{2} + {\text{eps}}} \right)}} \), to keep the denominator of \( z_{I,1} \) positive (as with \( z_{I,2} \)). The latter approach is implemented in RKPM2D.
The evaluations of direct derivatives \( \varPsi_{I,1} \left( {\varvec{x}_{N} } \right) \) and \( \varPsi_{I,2} \left( {\varvec{x}_{N} } \right) \) for DNI and GI at quadrature points \( \varvec{x}_{N} \) are straightforward as the direct derivatives can be computed by Algorithm 1 to Algorithm 4. In SCNI, the direct derivatives are replaced with smoothed derivatives \( \tilde{\varPsi }_{I,1} \left( {\varvec{x}_{N} } \right) \) and \( \tilde{\varPsi }_{I,2} \left( {\varvec{x}_{N} } \right) \), for which the smoothing procedure is given in Algorithm 5. \( {\mathbf{VoronoiCell}}\left\{ I \right\}\left( K \right) \) denotes a cell structure for Voronoi cells to define the \( K \)th index of cell vertices for the \( I \)th Voronoi cell, and \( {\mathbf{Vertices}} \) is a vector that defines the Cartesian coordinates of Voronoi cell vertices. The smoothing process in Algorithm 5 is computed by the function getSmoothedDerivative as given in Listing 7. For given inputs of a smoothing cell vertices’ coordinates \( \left\{ {\varvec{x}_{v} } \right\}_{1}^{\text{NV }} \) (denoted as “xV” in Listing 7) and nodal coordinates \( \varvec{x}_{I} \) (denoted as “xI” in Listing 7), the function getSmoothedDerivative gives the corresponding smoothed derivatives \( \tilde{\varPsi }_{I,1} \left( {\varvec{x}_{N} } \right) \), \( \tilde{\varPsi }_{I,2} \left( {\varvec{x}_{N} } \right) \) and the smoothing domain area \( A_{N} \).
The computed shape functions and their derivatives are stored in the structure Quadrature as:
SHP: matrix of size nQuad×nP that stores the shape functions \( \varPsi_{I} \left( {\varvec{x}_{N} } \right) \) of all nodes.
nQuad: number of quadrature points for domain integration, the value \( = {\text{NG}} \) for Gauss integration and \( = {\text{NP}} \) for nodal integration
SHPDX1: matrix of size nQuad\( \times \)nP that stores the shape function derivatives \( \varPsi_{I,1} \left( {\varvec{x}_{N} } \right) \) or \( \tilde{\varPsi }_{I,1} \left( {\varvec{x}_{N} } \right) \) of all nodes.
SHPDX2: matrix of size nQuad\( \times \)nP that stores the shape function derivatives \( \varPsi_{I,2} \left( {\varvec{x}_{N} } \right) \) or \( \tilde{\varPsi }_{I,2} \left( {\varvec{x}_{N} } \right) \) of all nodes.
The shape functions can be evaluated at the boundary in a similar manner as described in Algorithm 5.
3.6 Stabilization methods
The stabilization terms associated with M- and N-type stabilization methods are computed under the function Pre_GenerateShapeFunction where RK shape functions and direct/smoothed gradients are also evaluated. For the M-type stabilization method discussed in Sect. 2.3.3.1, the nodal representative domain is divided into sub-cells by using the MATLAB built-in function delaunayTriangulation, which divides the polygon Voronoi domain into several triangular sub-cells. The procedures for generating the sub-cells and associated evaluation points for the additional stabilization terms are shown in Listing 8. By looping over each sub-cell, the shape function gradients with associated integration weights (i.e., the area of each sub-cell) are computed. At each sub-cell, the function getSmoothedDerivative in Listing 7 is employed to evaluate the smoothed gradient to construct the M-type stabilization terms in [Eq. (35)]. An alternative way is to evaluate direct shape function gradient [Eq. (36)] by Algorithm 1 to Algorithm 4 at the centroid of each sub-cell for the M-type stabilization, which is adopted in Sect. 4 for DNI-based methods.
Once all stabilization terms are computed, they are stored under the structure Quadrature.MtypeStabilization with the following fields:
nS: number of sub-cells \( {\text{NS}} \) for the \( N \)-th Voronoi cell.
SHPDX1_Is: cell structure contains matrix of size nS\( \times \)nP that stores the shape function derivatives \( \varPsi_{I,1} \left( {\hat{\varvec{x}}_{N}^{S} } \right) \) or \( \tilde{\varPsi }_{I,1} \left( {\hat{\varvec{x}}_{N}^{S} } \right) \) in the \( N \)-th Voronoi cell
SHPDX2_Is: cell structure contains matrix of size nS\( \times \)nP that stores the shape function derivatives \( \varPsi_{I,2} \left( {\hat{\varvec{x}}_{N}^{S} } \right) \) or \( \tilde{\varPsi }_{I,2} \left( {\hat{\varvec{x}}_{N}^{S} } \right) \) in the \( N \)-th Voronoi cell
AREA_Is: cell structure that stores area of the \( s \)th sub-cell associated with the \( N \)-th Voronoi cell
Unlike the M-type stabilization method, the subdivision of the Voronoi diagrams is not required in the N-type stabilization method discussed in Sect. 2.3.3.2. The second-order shape function derivatives are achieved by taking direct derivatives of the first-order implicit gradients, which can be easily achieved by replacing the \( \varvec{H}_{0}^{\text{T}} \) in Algorithm 1 with \( \varvec{H}_{1}^{\text{T}} \) and \( \varvec{H}_{2}^{\text{T}} \) shown in Eq. (39). The corresponding output \( \varPsi_{I,1} \left( \varvec{x} \right) \) and \( \varPsi_{I,2} \left( \varvec{x} \right) \) would become \( \varPsi_{I1,1}^{\nabla } \) and \( \varPsi_{I1,2}^{\nabla } \) when \( \varvec{H}_{1}^{\text{T}} \) is used (or \( \varPsi_{I2,1}^{\nabla } \) and \( \varPsi_{I2,2}^{\nabla } \) when \( \varvec{H}_{2}^{\text{T}} \) is used). The second moments of inertia \( M_{1} \left( {\varvec{x}_{N} } \right) \), \( M_{2} \left( {\varvec{x}_{N} } \right) \) in each nodal integration domain are computed straightforwardly by the formula in [52] from the Voronoi vertices’ coordinates as shown in Listing 9.
Once all stabilization terms are computed, they are stored under the structure Quadrature.NtypeStabilization with the following fields:
SHPDX1X1: matrix of size nP\( \times \)nP that stores the shape function second derivatives \( \varPsi_{I1,1}^{\nabla } \) of all nodes.
SHPDX1X2: matrix of size nP\( \times \)nP that stores the shape function second derivatives \( \varPsi_{I1,2}^{\nabla } \) of all nodes.
SHPDX2X2: matrix of size nP\( \times \)nP that stores the shape function second derivatives \( \varPsi_{I2,2}^{\nabla } \) of all nodes.
M: second moments of inertia \( M_{1} \left( {\varvec{x}_{N} } \right), M_{2} \left( {\varvec{x}_{N} } \right) \) in each nodal integration domain.
3.7 Matrix evaluation and assembly
Once RK shape functions are computed, the function MatrixAssmebly is called to evaluate and assemble the stiffness matrix and force vector.
The \( 2 \times 2 \) matrix \( \varvec{K}_{IJ}^{c} \) in Eq. (15) denotes a block of entries corresponding to nodes \( I \) and \( J \), which can be evaluated at a quadrature point as follows:
To obtain the \( 2{\text{NP}} \times 2{\text{NP }} \) matrix \( \varvec{K}^{c} \), one can assemble the sub-block \( \varvec{K}_{IJ}^{c} \) into the total matrix \( \varvec{K}^{c} \) based on the nodal indexes \( I \) and \( J \), as described in Algorithm 7
The above algorithm can be conveniently implemented in C/C++/FORTRAN in a highly efficient manner. However, it becomes time-consuming when the involved “for” loops over quadrature points and neighbor nodal lists are executed in the MATLAB environment. To enhance the computational efficiency of RKPM2D, we explore the capability of MATLAB in sparse matrix multiplication and assembly and directly compute the total matrix \( \varvec{K}^{c} \):
where \( \varvec{B}\left( \varvec{x} \right) \) is defined as
The domain integration of Eq. (50) can be done by either Gauss integration in Eq. (24) or nodal integration in Eq. (26). In a similar manner, we can directly compute the total body force vector \( \varvec{F}^{\text{b}} \), the total traction vector \( \varvec{F}^{\text{t}} \), and the Nitsche’s terms \( \varvec{K}^{\beta } ,\varvec{K}^{g} ,\varvec{F}^{\beta } ,\varvec{F}^{g} \), where an array \( \varvec{\varPsi}\left( \varvec{x} \right) \) that stores all the shape functions is defined:
Once all these matrices and vectors are obtained, the total stiffness matrix \( \varvec{K} \) and total force vector \( \varvec{F} \) can be calculated as follows
The procedure described by Eqs. (50)–(54) is adopted in the implementation of RKPM2D, and the associated program structure of MatrixAssmebly is given in Algorithm 8.
Accordingly, the MATLAB command lines for the assembly of the stiffness matrix \( \varvec{K}^{c} \) and body force vector \( \varvec{F}^{\text{b}} \) are given in Listing 10.
Note that the MATLAB built-in sparse matrix data structure [53] is adopted, so only nonzero components of shape functions and shape function gradients are computed and stored, which significantly reduces the memory requirements. In Listing 11, the command lines for the assembly of the traction force \( \varvec{F}^{\text{t}} \) and the Nitsche’s terms, \( \varvec{K}^{\beta } ,\varvec{K}^{g} ,\varvec{F}^{\beta } ,\varvec{F}^{g} \) are given.
As seen from Algorithm 8, Listing 10 and Listing 11, the function MatrixAssembly only involves shape functions and quadrature rules under the data structure Quadrature, whereas the material parameters and evaluation of traction \( \varvec{t} \), body force \( \varvec{b} \), essential boundary conditions \( \varvec{g} \), and switch \( \varvec{S} \) are obtained under the data structure Model. After the assembly, the resultant system of linear equations is obtained:
which can be solved by either direct methods such as LU factorization, Gauss elimination, or non-stationary iterative methods such as PCG, GMRES, and BICGSTAB [54]. Many of these solvers are available in the public domain and can be readily integrated into RKPM2D. Here, the MATLAB built-in function mldivide is adopted, which takes advantage of matrix symmetries and automatically assign an appropriate matrix solver.
Remark
Marginal changes in the inputs from Quadrature and Model and slight modifications in Listing 10 and Listing 11 can be performed to convert the code to solve a different type of equation. For demonstration, an example of modifying the routine in Algorithm 8 to solve a diffusion equation is given in Appendix B.
3.8 Post-processing
The final step of the program is to compute and visualize the computed displacement, strain and stress fields with the use of the routine PostProcess. The following fields are computed and returned:
uhI: matrix of size \( {\text{NP}} \times 2 \) that defines the displacements at RK nodes \( \varvec{u}^{h} \left( {\varvec{x}_{I} } \right) \).
Strain: double vector of size \( {\text{NP}} \times 3 \) that defines the strain at RK nodes \( \varvec{\varepsilon}\left( {\varvec{x}_{I} } \right) = \left[ {\varepsilon_{11} \left( {\varvec{x}_{I} } \right),\varepsilon_{22} \left( {\varvec{x}_{I} } \right),2\varepsilon_{12} \left( {\varvec{x}_{I} } \right)} \right] \).
Stress: double vector of size \( {\text{NP}} \times 3 \) that defines the stress at RK nodes \( \varvec{\sigma}\left( {\varvec{x}_{I} } \right) = \left[ {\sigma_{11} \left( {\varvec{x}_{I} } \right),\sigma_{22} \left( {\varvec{x}_{I} } \right),2\sigma_{12} \left( {\varvec{x}_{I} } \right)} \right] \).
For simplicity, the continuous fields of displacement, strain, and stress are plotted based on Delaunay triangulation of the whole domain by using the MATALB built-in functions delaunayTriangulation and trisurf as shown in Listing 12.
4 Numerical examples
In this section, benchmark numerical examples are analyzed to examine the performance of the open-source code RKPM2D. The reproducing kernel approximation with linear basis and cubic B-spline kernel is adopted, for which circular support with a normalized support size \( \tilde{c} = 2.0 \) is employed. The normalized penalty parameter for Nitsche’s method is chosen to be \( \beta_{\text{nor}} = 100 \). In the examples, the following domain integration methods are analyzed and compared:
- 1.
GI: Gauss integration in Eqs. (24)–(25), where different integration orders are considered.
- 2.
- 3.
MDNI: modified DNI formulation in Eq. (36)
- 4.
NDNI: naturally stabilized DNI formulation in Eq. (43)
- 5.
SCNI: stabilized conforming nodal integration in Eqs. (31)–(33)
- 6.
MSCNI: modified SCNI formulation in Eq. (35)
- 7.
NSCNI: naturally stabilized SCNI in Eq. (40)
To access the accuracy of different numerical schemes, the following normalized displacement and energy norms are employed:
in which the superscript “\( h \)” and “exact” denote the numerical and exact solutions, respectively.
For domain integration involved in Eqs. (56) and (57), a high-order Gauss integration is employed
where \( \varvec{u}_{N}^{h} = \varvec{u}^{h} \left( {\varvec{x}_{N} } \right) \), \( \varvec{u}_{N}^{\text{exact}} = \varvec{u}^{\text{exact}} \left( {\varvec{x}_{N} } \right) \), \( {\text{NG}}g \) is the total number of Gauss points, and \( W_{N} \) is the weight for the Gauss points. The number of integration cells for error evaluation is set equal to the total number of nodes, and \( 10 \times 10 \) Gauss points per integration cell is used, so the total number of quadrature points for error norm calculation is \( {\text{NG}}g = 100 \times {\text{NP}} \) in Eqs. (58) and (59). The convergence rate for each formulation is calculated by averaging the rates at different refinement levels.
4.1 Patch test
In the first example, the linear patch test is analyzed to verify the accuracy of RKPM2D using linear basis in the RK approximation. The elasticity equation in (9) is considered with the exact solution defined as a linear polynomial function:
Accordingly, the traction \( \varvec{t} =\varvec{\eta}^{\text{T}} \varvec{C\varepsilon }^{\text{exact}} \) is imposed on \( \partial \varOmega_{t} :\left( {x_{1} ,x_{2} } \right) \in \partial \varOmega , \quad x_{2} > 0.5 \), where \( \varvec{\eta} \) is the collection of outward unit normal vector of the boundary surface, \( \varvec{C} \) is the matrix of elastic moduli with Young’s modulus \( E = 2.1 \times 10^{11} \) and Poisson’s ratio \( \nu = 0.3 \), \( \varvec{\varepsilon}^{\text{exact}} \) is the exact strain with \( \varvec{\varepsilon}^{\text{exact}} = \left[ {0.1, 0.1, 0.35} \right]^{\text{T}} \); \( \varvec{g} = \varvec{u}^{\text{exact}} \) is enforced on \( \partial \varOmega_{g} :\left( {x_{1} ,x_{2} } \right) \in \partial \varOmega , \quad x_{2} \le 0.5 \), and the body force is set to \( \varvec{b} = 0. \) Four geometries are considered, and their nodal discretizations are shown in Fig. 11.
a Geometry 1, b geometry 2, c geometry 3, and d geometry 4 considered in the patch test
When Gauss integration (GI) is employed, uniform background integration cells with \( 1 \times 1 \), \( 2 \times 2 \), \( 4 \times 4 \), or \( 6 \times 6 \) Gauss points per cell is considered. The displacement and energy error norms (Eqs. (58) and (59)) using GI, DNI, and SCNI are given in Tables 2 and 3, respectively. As can be seen, while low-order GI diverges, high-order GI (\( 6 \times 6 \) integration points per cell) can achieve the \( L_{2} \) errors around \( 10^{ - 4} \) but is computationally expensive, as will be shown later. For nodal integrations, DNI leads to very large errors, whereas SCNI exactly passes the patch test for all geometries.
Next, the solution accuracy with model discretization refinement under both uniform and non-uniform discretizations is examined. As shown in Fig. 12, non-uniform discretizations are generated by introducing random numbers between \( \pm 0.5h \) into the uniform discretizations, where \( h \) is the nodal distance in the uniform discretizations of a unit square. For GI, \( 4 \times 4 \), \( 9 \times 9 \), \( 14 \times 14 \), and \( 19 \times 19 \) background integration cells are constructed based on uniform discretizations with \( 5 \times 5 \), \( 10 \times 10 \), \( 15 \times 15 \), and \( 20 \times 20 \) nodes, respectively. As shown in Tables 4, 5, 6, and 7, SCNI-based methods pass the patch test independent of the type of discretizations, whereas DNI-based methods and GI yield large errors. For instance, the displacement error norm is around \( 10^{ - 3} \) in DNI and \( 10^{ - 6} \) in GI \( 6 \times 6 \) under uniform discretizations in Table 4, and under non-uniform discretizations in Table 6 the error norms increase up to \( 10^{ - 2} \) and around \( 10^{ - 5} \sim10^{ - 6} \) in DNI and GI \( 6 \times 6 \), respectively. Also, as shown in Table 5, the energy norm in uniform discretizations is around \( 10^{ - 2} \) in DNI and \( 10^{ - 5} \) in GI \( 6 \times 6 \) and the error further increases in the non-uniform cases as shown in Table 7. On the other hand, the error norms in SCNI are always less than \( 10^{ - 12} \). Furthermore, for nodal integrations with additional stabilizations (N-type and M-type), all SCNI-based formulations (MSCNI and NSCNI) pass the linear patch test, while all DNI-based formulations fail even with the employment of additional stabilization techniques due to the violation of variational consistency conditions. To restore the variational consistency for DNI-based methods, the VCI approach [11] can be used, but is considered out of the scope of this paper since conforming smoothing (SCNI-based methods) can be employed to satisfy the conditions.
Uniform and non-uniform discretizations of a square domain with a\( 5 \times 5 \), b\( 10 \times 10 \), c\( 15 \times 15 \), and d\( 20 \times 20 \) nodes, where the non-uniform discretizations from e to h consist of randomized nodal distributions that correspond to the uniform nodal distributions from a to d, respectively
4.2 Cantilever beam problem
A cantilever beam problem shown in Fig. 13 is considered next. The exact displacement solution to this problem is:
Problem setting of a cantilever beam under a shear force
in which the Young’s modulus \( E = 1 \) and Poisson ratio \( \nu = 0.3 \) is selected, and the geometry is shown in Fig. 13. The exact displacement solution is prescribed on the left wall as the essential boundary condition, i.e., \( \varvec{g} = \varvec{u}^{\text{exact}} \), and the corresponding traction is imposed on the right-side surface as the natural boundary condition.
Uniform and non-uniform nodal discretizations of the beam are shown in Fig. 14. For GI, equally spaced \( 12 \times 3 \), \( 24 \times 6 \), \( 36 \times 9 \), and \( 48 \times 12 \) background Gauss integration cells are adopted, which correspond to four different levels of refinement. The convergence of DNI and SCNI is compared in Fig. 15, which shows that MSCNI and NSCNI have the optimal convergence rate compared to SCNI- and other DNI-based methods. In the cases of non-uniform discretizations, the DNI-based schemes yield poor convergence.
Uniform and non-uniform discretizations for the accuracy and efficiency study in the cantilever beam problem. a\( 13 \times 4 \), b\( 25 \times 7 \), c\( 37 \times 10 \), and d\( 49 \times 13 \) nodes, where the non-uniform discretizations from e to h consist of randomized nodal distributions that correspond to the uniform nodal distributions from a to d, respectively
Accuracy of DNI- and SCNI-based nodal integration methods for the cantilever beam problem. The numbers in the legends denote the convergence rates
The stabilized nodal integrations MSCNI and NSCNI are compared with various orders of Gauss integration as shown in Fig. 16. It can be seen that only high-order Gauss integration, GI \( 4 \times 4 \) and GI \( 6 \times 6 \), converges under uniform and non-uniform nodal distributions in both the \( L_{2} \) norm and energy norm. For the stabilized nodal integration methods, MSCNI is found to be less accurate in displacement error norm but is as accurate as GI \( 6 \times 6 \) in the energy norm. On the other hand, NSCNI shows the same level of accuracy in both displacement and energy norms as GI \( 6 \times 6 \) under non-uniform nodal distributions. Figure 17 shows the stress distribution of DNI, NSCNI, and MSCNI under non-uniform discretizations. As can be seen, DNI leads to severe oscillations, while NSCNI and MSCNI demonstrate accurate solutions compared to the exact solution.
Accuracy of MSCNI, NSCNI, and Gauss integration (GI) for the cantilever beam problem. The numbers in the legends denote the convergence rates
Stress fields of the cantilever beam problem under non-uniform discretization in the case of Fig. 14h
In Fig. 18, the efficiency of nodal integration methods is compared to that of various orders of Gauss integration. For both uniform and non-uniform cases, the computational cost of the nodal integration method is similar to that of GI \( 2 \times 2 \). Among the nodal integration methods, NSCNI is found to achieve the same accuracy as the high-order GI with much lower computational cost, and in addition, NSCNI is more effective than SCNI and MSCNI with both accuracy and CPU time considered.
Computational efficiency of various orders Gauss integrations (GI), DNI-based methods, and SCNI-based methods for the cantilever beam problem, where the same nodal discretizations as described in Fig. 14 are employed
4.3 Plate with a hole problem under highly distorted discretizations
The problem of a plate with a circular hole is considered to assess the performance of RKPM2D under highly distorted discretizations. The plate is subjected to far-field traction \( T_{1} \) in the \( x_{1} \) direction, and due to symmetry, only a quarter of the plate is modeled as illustrated in Fig. 19, where the length \( L = 4 \) and inner radius \( R = 1 \) are chosen. There is no body force, i.e., \( \varvec{b} = 0 \), and the traction imposed on the finite domain boundary is defined as \( \varvec{t} = \varvec{n} \cdot\varvec{\sigma}^{\text{exact}} \), where \( \varvec{n} \) is the surface normal on the boundary and \( \varvec{\sigma}^{\text{exact}} \) is the exact stress field given below as well as the exact displacement field \( \varvec{u}^{\text{exact}} \):
Problem settings for plate with a hole under far-field traction
where (\( r, \theta \)) denote polar coordinates, \( T_{1} = 10 \), \( \mu = \frac{E}{{2\left( {1 + \nu } \right)}} \), \( \kappa = \frac{3 - \nu }{1 + \nu } \), in which Young’s modulus and Poisson ratio are taken as \( E = 2.1 \times 10^{11} \) and \( \nu = 0.3 \), respectively.
To examine the influence of non-uniform discretizations on the performance of RKPM, domain discretizations with highly distorted nodal distributions are generated using Shestakov’s algorithm [55]. In the discretization process, given the coordinates \( \varvec{x}_{1\sim4} \) of four corner nodes of a quadrilateral domain, a new node is created with its position \( \varvec{x} \) determined by Eq. (64):
where
In this algorithm, the following control parameters need to be defined:
\( n_{c} \in {\mathbb{N}} \): a constant parameter that controls the discretization refinement level;
\( 0 < \gamma_{\text{d}} \le 0.5 \): a constant parameter that controls the discretization distortion level;
\( {\text{rand}}_{1} ,{\text{rand}}_{2} \in \left[ {0,1} \right] \): random numbers that randomly perturb the nodal positions.
After generating the new nodal point \( \varvec{x} \) by Eq. (64), the quadrilateral domain can be divided into four quadrilateral sub-domains, and within each sub-domain, the above procedure can be repeatedly applied to create more nodal points and sub-domains until the total number of nodes equals \( \left( {2^{{n_{c} }} + 1} \right) \times \left( {2^{{n_{c} }} + 1} \right) \), i.e., when the desired refinement level controlled by \( n_{c} \) is achieved.
Note that when the distortion parameter is chosen as \( \gamma_{\text{d}} = 0.5 \), a uniform nodal discretization is obtained, whereas decreasing \( \gamma_{\text{d}} \) will result in a more distorted nodal distribution, for which poorly shaped elements are yielded if FEM is used. On the other hand, varying the random numbers \( {\text{rand}}_{1} \) and \( {\text{rand}}_{2} \) can lead to different nodal distributions, but the associated distortion levels will remain the same as long as the distortion parameter \( \gamma_{\text{d}} \) is unchanged.
In the present study, the plate domain is firstly divided into two sub-domains as illustrated in red color in Fig. 20, and each sub-domain is discretized with \( \left( {2^{{n_{c} }} + 1} \right) \times \left( {2^{{n_{c} }} + 1} \right) \) nodes using the above-mentioned Shestakov’s algorithm. Nodes located on the domain boundaries are generated in a similar fashion. Interested readers can refer to [55] for more details of the Shestakov’s algorithm. Three levels of discretization refinement are adopted with the refinement parameter \( n_{c} = \) 2, 3, 4, respectively. Further, at each refinement level, 15 tests are performed with a different set of random numbers [\( {\text{rand}}_{1} ,{\text{rand}}_{2} \) in Eq. (65)] for each test, as illustrated in Fig. 20. It is noteworthy to mention that since a constant distortion parameter \( \gamma_{\text{d}} = 0.1 \) is adopted, the distortion levels of all 45 discretizations are considered identical and highly distorted.
Highly distorted nodal discretizations at three refinement levels for the plate, where 15 randomly perturbed discretizations (from test 1 to test 15) at each refinement level are generated. (Color figure online)
To study the convergence properties of RKPM, we define the nodal spacing as \( \tilde{h} = \sqrt {A/{\text{NP}}} \), where \( A \) is the area of the whole domain and \( {\text{NP}} \) is the total number of nodes. In order to evaluate the numerical accuracy, we compute the mean values of \( L_{2} \) and energy norms for the 15 discretizations employed at each refinement level and plot them in Fig. 21 for comparison of different numerical schemes. The results show that DNI and high-order GI do not converge under the highly distorted discretizations, where \( 2^{{n_{c} }} \times 2^{{n_{c} }} \) uniformly distributed background integration cells are adopted for the GI scheme. On the other hand, all SCNI-based nodal integration schemes show satisfactory performance. In particular, both NSCNI and MSCNI achieve optimal convergence and good accuracy.
Convergence under highly distorted discretizations for the plate problem, where the mean error norms of 15 randomly perturbed discretizations at each refinement level are plotted. The numbers in the legends denote the convergence rates
To assess the sensitivity of each numerical scheme on randomly perturbed nodal positions, the following standard deviations in numerical error norms are defined:
where \( {\text{NT}} = 15 \) denotes the total number of test cases at each refinement level, \( e_{i}^{{L_{2} }} = \varvec{u} - \varvec{u}^{h}_{{L_{2} }} \) and \( e_{i}^{E} = \varvec{u} - \varvec{u}^{h}_{E} \) denote the \( L_{2} \) and energy error norms for the i-th test, and \( \bar{e}^{{L_{2} }} \) and \( \bar{e}^{\text{E}} \) are the mean values of the \( L_{2} \) and energy error norms, respectively. Tables 8 and 9 give the calculated standard deviations in \( L_{2} \) and energy error norms, which show that SCNI-based schemes yield similar deviations with the high-order GI, whereas DNI-based methods result in very large deviations. The results clearly indicate that DNI-based methods are very sensitive to the nodal positions, whereas SCNI-based methods are more robust and perform well even when the highly distorted nodal discretizations are perturbed.
Finally, the computational efficiency of high-order GI and different nodal integrations is compared in Fig. 22, where the mean values of error norms at each refinement level are plotted. Compared to DNI-based methods and the high-order GI, both MSCNI and NSCNI show superior performance, and NSCNI achieves the best efficiency among all schemes under the highly distorted nodal discretizations.
Efficiency under highly distorted discretizations for the plate problem, where the mean error norms of 15 randomly perturbed discretizations at each refinement level are plotted, where the same nodal discretizations as described in Fig. 20 are employed
5 Conclusion
We have developed an open-source software called RKPM2D for meshfree analysis. The program is developed based on the reproducing kernel particle method (RKPM) and consists of a set of data structures and routines for discretizing two-dimensional domains, imposition of boundary conditions, nodal representative domain creation by Voronoi diagram partitioning, reproducing kernel shape function generation, domain integration using Gauss integration and various stabilized nodal integration methods, meshfree Galerkin matrix assembly and solver, and visualization tools for post-processing. Benchmark problems are presented to verify the convergence, efficiency, and robustness properties of the RK approximation in conjunction with stabilized nodal integrations implemented in RKPM2D, under both uniform and highly non-uniform nodal distributions.
The open source code can serve as an entry point for researchers who are interested in the computer implementation of RKPM, as well as other related meshfree methods, and the code can also be adopted as a rapid prototyping and testing tool for further development of advanced meshfree algorithms. Although the linear elasticity problem is chosen as the model problem, the flexibility of the code allows the extension to solve different PDEs for various scientific and engineering problems.
References
Chen J-S, Pan C, Wu C-T, Liu WK (1996) Reproducing kernel particle methods for large deformation analysis of non-linear structures. Comput Methods Appl Mech Eng 139(1–4):195–227
Chen J-S, Hillman M, Chi S-W (2017) Meshfree methods: progress made after 20 years. J Eng Mech 143(4):04017001
Liu WK, Jun S, Zhang YF (1995) Reproducing kernel particle methods. Int J Numer Methods Fluids 20(8–9):1081–1106
Liu WK, Hao S, Belytschko T, Li S, Chang CT (1999) Multiple scale meshfree methods for damage fracture and localization. Comput Mater Sci 16(1–4):197–205
Li S, Hao W, Liu WK (2000) Mesh-free simulations of shear banding in large deformation. Int J Solids Struct 37(48–50):7185–7206
Liu WK, Jun S, Sihling DT, Chen Y, Hao W (1997) Multiresolution reproducing kernel particle method for computational fluid dynamics. Int J Numer Methods Fluids 24(12):1391–1415
Liu WK, Chen Y (1995) Wavelet and multiple scale reproducing kernel methods. Int J Numer Methods Fluids 21(10):901–931
Liu WK, Chen Y, Uras RA, Chang CT (1996) Generalized multiple scale reproducing kernel particle methods. Comput Methods Appl Mech Eng 139(1–4):91–157
Ruter MO, Chen J-S (2017) An enhanced-strain error estimator for Galerkin meshfree methods based on stabilized conforming nodal integration. Comput Math Appl 74(9):2144–2171
You Y, Chen J-S, Lu H (2003) Filters, reproducing kernel, and adaptive meshfree method. Comput Mech 31(3–4):316–326
Chen J-S, Hillman M, Ruter M (2013) An arbitrary order variationally consistent integration for Galerkin meshfree methods. Int J Numer Methods Eng 95(5):387–418
Hillman M, Chen J-S (2016) An accelerated, convergent, and stable nodal integration in Galerkin meshfree methods for linear and nonlinear mechanics. Int J Numer Methods Eng 107(7):603–630
Chen J-S, Wang D (2006) A constrained reproducing kernel particle formulation for shear deformable shell in Cartesian coordinates. Int J Numer Methods Eng 68(2):151–172
Kim NH, Choi KK, Chen J-S, Botkin ME (2002) Meshfree analysis and design sensitivity analysis for shell structures. Int J Numer Methods Eng 53(9):2087–2116
Chen J-S, Pan C, Roque C, Wang H-P (1998) A Lagrangian reproducing kernel particle method for metal forming analysis. Comput Mech 22(3):289–307
Chen J-S, Wang H-P, Yoon S, You Y (2000) Some recent improvements in meshfree methods for incompressible finite elasticity boundary value problems with contact. Comput Mech 25(2–3):137–156
Wang H-P, Wu C-T, Chen J-S (2014) A reproducing kernel smooth contact formulation for metal forming simulations. Comput Mech 54(1):151–169
Chen J-S, Basava RR, Zhang Y, Csapo R, Malis V, Sinha U, Hodgson J, Sinha S (2016) Pixel-based meshfree modelling of skeletal muscles. Comput Methods Biomech Biomed Eng Imaging Vis 4(2):73–85
Wei H, Chen J-S, Hillman M (2016) A stabilized nodally integrated meshfree formulation for fully coupled hydro-mechanical analysis of fluid-saturated porous media. Comput Fluids 141:105–115
Wei H, Chen J-S, Beckwith F, Baek J (2019) A naturally stabilized semi-Lagrangian meshfree formulation for multiphase porous media with application to landslide modeling. J Eng Mech. https://doi.org/10.1061/(ASCE)EM.1943-7889.0001729
Chen J-S, Wu C-T, Belytschko T (2000) Regularization of material instabilities by meshfree approximations with intrinsic length scales. Int J Numer Methods Eng 47(7):1303–1322
Chen J-S, Zhang X, Belytschko T (2004) An implicit gradient model by a reproducing kernel strain regularization in strain localization problems. Comput Methods Appl Mech Eng 193(27–29):2827–2844
Wei H, Chen J-S (2018) A damage particle method for smeared modeling of brittle fracture. Int J Multiscale Comput Eng 16(4):303–324
Roth MJ, Chen J-S, Slawson TR, Danielson KT (2016) Stable and flux-conserved meshfree formulation to model shocks. Comput Mech 57(5):773–792
Roth MJ, Chen J-S, Danielson KT, Slawson TR (2016) Hydrodynamic meshfree method for high-rate solid dynamics using a Rankine–Hugoniot enhancement in a Riemann-SCNI framework. Int J Numer Methods Eng 108(12):1525–1549
Huang T-H, Chen J-S, Wei H, Roth MJ, Sherburn JA, Bishop JE, Tupek MR, Fang EH (2019) A MUSCL-SCNI approach for meshfree modeling of shock waves in fluids. Comput Part Mech. https://doi.org/10.1007/s40571-019-00248-x
Guan P-C, Chi S-W, Chen J-S, Slawson T, Roth MJ (2011) Semi-Lagrangian reproducing kernel particle method for fragment-impact problems. Int J Impact Eng 38(12):1033–1047
Sherburn JA, Roth MJ, Chen J, Hillman M (2015) Meshfree modeling of concrete slab perforation using a reproducing kernel particle impact and penetration formulation. Int J Impact Eng 86:96–110
Chi S-W, Lee C-H, Chen J-S, Guan P-C (2015) A level set enhanced natural kernel contact algorithm for impact and penetration modeling. Int J Numer Methods Eng 102(34):839–866
Chen J-S, Liu WK, Hillman M, Chi S-W, Lian Y, Bessa M (2017) Reproducing kernel particle method for solving partial differential equations. In: Stein E, De Borst R, Hughes TJR (eds) Encyclopedia of computational mechanics, 2nd edn. Wiley, Chichester, pp 1–44
Hardee E, Chang K-H, Yoon S, Kaneko M, Grindeanu I, Chen J-S (1999) A structural nonlinear analysis workspace (SNAW) based on meshless methods. Adv Eng Softw 30(30):153–175
Hsieh Y-M, Pan M-S (2014) ESFM: an essential software framework for meshfree methods. Adv Eng Softw 76:133–147
Barbieri E, Meo M (2012) A fast object-oriented Matlab implementation of the reproducing kernel particle method. Comput Mech 49(5):581–602
Cartwright C, Oliveira S, Stewart DE (2006) Parallel support set searches for meshfree methods. SIAM J Sci Comput 28(4):1318–1334
Parreira GF, Fonseca AR, Lisboa AC, Silva EJ, Mesquita RC (2006) Efficient algorithms and data structures for element-free Galerkin method. IEEE Trans Magn 42(4):659–662
Olliff J, Alford B, Simkins DC (2018) Efficient searching in meshfree methods. Comput Mech 62(6):1461–1483
Chen J-S, Hillman M, Huang T-H, Wei H (2019) RKPM2D: an open-source implementation of nodally integrated reproducing kernel particle method for solving partial differential equations. Mendeley Data. https://doi.org/10.17632/prfxg9cbrx
Nitsche J (1970–1971) Uber ein Variationsprinzip zur Losung von Dirichlet-Problemen bei Verwendung von Teilraumen, die keinen Randbedingungen unterworfen sind. Abh Math Sem Univ Hamburg 36: 9–15
Fernandez-Mendez S, Huerta A (2004) Imposing essential boundary conditions in mesh-free methods. Comput Methods Appl Mech Eng 193(12–14):1257–1275
Chen J-S, Wu C-T, Yoon S, You Y (2001) A stabilized conforming nodal integration for Galerkin mesh-free methods. Int J Numer Methods Eng 50(2):435–466
Chen J-S, Hu W, Puso M, Wu Y, Zhang X (2007) Strain smoothing for stabilization and regularization of Galerkin meshfree methods. In: Schweitzer MA (ed) Meshfree methods for partial differential equations III. Springer, Berlin, pp 57–75
MATLAB Release 2019a (2019) The MathWorks Inc., Natick
Li S, Liu WK (2007) Meshfree particle methods. Springer, Berlin
Chen J-S, Wang H-P (2000) New boundary condition treatments in meshfree computation of contact problems. Comput Methods Appl Mech Eng 187(3–4):441–468
Dolbow J, Belytschko T (1999) Numerical integration of the Galerkin weak form in meshfree methods. Comput Mech 23(3):219–230
Lu Y, Belytschko T, Gu L (1994) A new implementation of the element free Galerkin method. Comput Methods Appl Mech Eng 113(3–4):397–414
Puso MA, Zywicz E, Chen J (2007) A new stabilized nodal integration approach. In: Schweitzer MA (ed) Meshfree methods for partial differential equations III. Springer, Berlin, pp 207–217
Sievers J (2016) Constrain the vertices of a Voronoi decomposition to the domain of the input data. MathWorks, 31th October 2016. http://se.mathworks.com/matlabcentral/fileexchange/34428-voronoilimit. Accessed 1st Sept 2018
Bentley JL (1975) Multidimensional binary search trees used for associative searching. Commun ACM 18(9):509–517
Perkins E, Williams JR (2001) A fast contact detection algorithm insensitive to object sizes. Eng Comput 18(1/2):48–62
Friedman JH, Bentley JL, Finkel RA (1976) An algorithm for finding best matches in logarithmic time. ACM Trans Math Softw 3(SLAC-PUB-1549-REV. 2):209–226
Steger C (1996) On the calculation of arbitrary moments of polygons. Munchen University, Technical Report FGBV-96-05, Munchen, Germany
Gilbert JR, Moler C, Schreiber R (1992) Sparse matrices in MATLAB: design and implementation. SIAM J Matrix Anal Appl 13(1):333–356
Saad Y (2003) Iterative methods for sparse linear systems. SIAM, Minneapolis
Shestakov A, Kershaw D, Zimmerman G (1990) Test problems in radiative transfer calculations. Nucl Sci Eng 105(1):88–104
Acknowledgements
The support from Sandia National Laboratories under the Contract 1655264 to the University of California, San Diego, is greatly appreciated.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
In RKPM2D, six kernel functions with different levels of continuity are implemented, as described in Table 1, and the corresponding mathematical expressions of these kernel functions are given as follows.
- 1.
The Heaviside kernel function:
$$ \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\text{for}} \\ {\text{for}} \\ \end{array} } & {\begin{array}{*{20}c} {0 \le z_{I} \le 1,} \\ {z_{I} > 1} \\ \end{array} } \\ \end{array} } \right. $$(68) - 2.
The linear B-spline (tent) kernel function:
$$ \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {1 - z_{I} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}l} {\text{for}} \\ {\text{for}} \\ \end{array} } & {\begin{array}{*{20}l} {0 \le z_{I} \le 1,} \\ {z_{I} > 1} \\ \end{array} } \\ \end{array} } \right. $$(69) - 3.
The quadratic B-spline kernel function:
$$ \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) = \left\{ {\begin{array}{*{20}l} {1 - 3z_{I}^{2} } \\ {3/2 - 3z_{I} + 3/2z_{I}^{2} } \\ 0 \\ \end{array} } \right.\begin{array}{*{20}l} {\text{for}} \\ {\text{for}} \\ {\text{for}} \\ \end{array} \begin{array}{*{20}l} {0 \le z_{I} \le 1/3,} \\ {1/3 \le z_{I} \le 1,} \\ {z_{I} > 1} \\ \end{array} $$(70) - 4.
The cubic B-spline kernel function:
$$ \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) = \left\{ {\begin{array}{*{20}l} {2/3 - 4z_{I}^{2} + 4z_{I}^{3} } \\ {4/3 - 4z_{I} + 4z_{I}^{2} - 4/3z_{I}^{3} } \\ 0 \\ \end{array} } \right.\begin{array}{*{20}l} \quad{\text{for}} \\ \quad {\text{for}} \\ \quad{\text{for}} \\ \end{array} \begin{array}{*{20}l} \quad {0 \le z_{I} \le 1/2,} \\ \quad {1/2 \le z_{I} \le 1,} \\ \quad{z_{I} > 1} \\ \end{array} $$(71) - 5.
The quartic B-spline kernel function:
$$ \begin{aligned} & \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) = \\ & \left\{ {\begin{array}{*{20}l} {1 - \frac{150}{23}z_{I}^{2} + \frac{375}{23}z_{I}^{4} } \hfill & { {\text{for}} 0 \le z_{I} \le \frac{1}{5},} \hfill \\ {\frac{22}{23} + \frac{20}{23}z_{I} - \frac{300}{23}z_{I}^{2} + \frac{500}{23}z_{I}^{3} - \frac{250}{23}z_{I}^{4} } \hfill & {{\text{for}} \frac{1}{5} \le z_{I} \le \frac{3}{5},} \hfill \\ {\frac{125}{46} - \frac{250}{23} z_{I} + \frac{375}{23}z_{I}^{2} - \frac{250}{23}z_{I}^{3} + \frac{125}{46}z_{I}^{4} } \hfill & {{\text{for}} \frac{3}{5} \le z_{I} \le 1,} \hfill \\ 0 \hfill & { {\text{for}} z_{I} > 1} \hfill \\ \end{array} } \right. \\ \end{aligned} $$(72) - 6.
The quintic B-spline kernel function:
$$ \begin{aligned} & \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) = \\ & \left\{ {\begin{array}{*{20}l} {1 - \frac{90}{11}z_{I}^{2} + \frac{405}{11}z_{I}^{4} - \frac{405}{11}z_{I}^{5} } \hfill & {{\text{for}}\,\, 0 \le z_{I} \le \frac{1}{3},} \hfill \\ {\frac{17}{22} + \frac{75}{22} z_{I} - \frac{315}{11}z_{I}^{2} + \frac{674}{11}z_{I}^{3} - \frac{1215}{22}z_{I}^{4} + \frac{405}{22}z_{I}^{5} } \hfill & {{\text{for}}\,\, \frac{1}{3} \le z_{I} \le \frac{2}{3},} \hfill \\ {\frac{81}{22} - \frac{405}{22} z_{I} + \frac{405}{11}z_{I}^{2} - \frac{405}{11}z_{I}^{3} + \frac{405}{22}z_{I}^{4} - \frac{81}{22}z_{I}^{5} } \hfill & {{\text{for}}\,\, \frac{2}{3} \le z_{I} \le 1,} \hfill \\ 0 \hfill & {{\text{for}}\,\, z_{I} > 1} \hfill \\ \end{array} } \right. \\ \end{aligned} $$(73)
Appendix B
In this section, a diffusion problem is used as example to illustrate how to modify RKPM2D for the solution of different types of PDEs. A diffusion equation is considered as follows:
where \( u \) is a scalar field, \( D_{ij} \) is the diffusivity, \( b \) is the source term, and \( t \) and \( g \) are the prescribed boundary flux and boundary values of \( u \) on \( \partial \varOmega_{t} \) and \( \partial \varOmega_{g} \), respectively. By introducing the RK approximation in Eq. (11), (74) can be recast into the following matrix equations for isotropic scalar diffusivity:
where
in which the matrices and vectors in nodal integration are expressed as
where \( \varvec{D} \) is the diffusivity tensor, \( d \) is the diffusion coefficient, and \( \varvec{\eta} \) is a collection of components of the surface unit normal on the boundary, and \( S = 1 \) is set for the convenience of keeping a unified coding structure in RKPM2D. Let us consider a diffusion problem [Eq. (74)] with a manufactured solution:
in a circular domain \( \varOmega \subset {\mathbb{R}}^{2} \) shown in Fig. 9 from Sect. 3.2. The flux \( t = 0.1n_{1} + 0.2n_{2} \) is imposed on \( \partial \varOmega_{t} :\left( {x_{1} ,x_{2} } \right) \in \partial \varOmega , \quad x_{2} > 0.5 \) where \( n_{1} {\text{ and }}n_{2} \) are the normal vector components. \( g = u^{\text{exact}} \) is enforced on \( \partial \varOmega_{g} :\left( {x_{1} ,x_{2} } \right) \in \partial \varOmega ,\quad x_{2} \le 0.5 \), and the body source is \( b = 0. \)
The input file for this problem is generated in the function getInput. Compared to Listing 1, the following changes need to be made:
Remove Model.nu and Model.Condition, as Poisson ratio and plane-stress/strain condition are not required for diffusion problem.
Replace Model.E with Model.d (i.e., change the definition of Young’s modulus \( E \) to be the diffusion coefficient \( d \)).
Replace Model.ElasticTensor with Model.DiffusiveTensor (i.e., change the definition of elastic tensor \( \varvec{C} \) to be the diffusive tensor \( \varvec{D} \)).
Set Model.DiffusiveTensor=diag([Model.d,Model.d])to define the diffusive tensor \( \varvec{D} = \left[ {\begin{array}{*{20}l} d & 0 \\ 0 & d \\ \end{array} } \right] \).
Set Model.DOFu=1 to change the nodal degrees of freedom DOFu from 2 to 1.
Set u_exact=0.1+0.1*x1+0.2*x2 to define the exact solution \( u^{\text{exact}} \).
In addition, we also need to modify the subroutine getBoundaryConditions to generate the exact boundary flux \( t =\varvec{\eta}^{\text{T}} \varvec{D}{\varvec{\nabla}} u^{\text{exact}} \), source term \( b = {\varvec{\nabla}} \cdot \left( {\varvec{D}{\varvec{\nabla}} u^{\text{exact}} } \right) \), essential boundary conditions \( g = u^{\text{exact}} \), and switch matrix \( S = 1 \) based on a given expression of the exact solution \( u^{\text{exact}} \) in a symbolic form, as shown in Listing 13.
Listing 13 shows command lines of function to generate exact heat flux \( t \), heat source \( b \), imposed scalar field \( g \), and switch matrix \( S \) for diffusion problems.
Due to the change of dimensionality in the \( \varvec{B} \) and \( \varvec{\varPsi} \) matrices compared to the elasticity problem, modifications are made to MatrixAssmebly (Listing 10) as follows
Set d=Model.d to define the diffusivity coefficient.
Set D=Model.DiffusiveTensor to define the diffusivity from input files.
Replace E with d (i.e., replace the Young’s modulus E with diffusion coefficient d).
Replace C with D (i.e., replace elastic tensor C with diffusive tensor D).
Set B=sparse(2,nP*DOFu).
Set PSI=sparse(1,nP*DOFu).
Modify the allocation of the B and PSI from shape function SHP and derivative SHPDX1, SHPDX2 as:
PSI=SHP(idx_nQuad,:);
B(1,:)=SHPDX1(idx_nQuad,:);
B(2,:)=SHPDX2(idx_nQuad,:);
Set ETA=[n1; n2;]to define the surface normal \( \varvec{\eta} \).
With the above-mentioned modifications, RKPM2D is converted to a program for solving diffusion problems. By comparing the original code for elasticity problems with the modified code for diffusion problems, one can see that only minimal code modifications are required. This capability of easy code extension is a unique feature of RKPM2D [37].
Rights and permissions
About this article
Cite this article
Huang, TH., Wei, H., Chen, JS. et al. RKPM2D: an open-source implementation of nodally integrated reproducing kernel particle method for solving partial differential equations. Comp. Part. Mech. 7, 393–433 (2020). https://doi.org/10.1007/s40571-019-00272-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40571-019-00272-x