Abstract
Phase-field crack approximation relies on the proper definition of the crack driving strain energy density to govern the crack evolution and a realistic model for the modified stresses on the crack surface. A novel approach, the directional split, is introduced, analyzed and compared to the two commonly used formulations, which are the spectral split and the volumetric–deviatoric split. The directional split is based on the decomposition of the stress tensor with respect to the crack orientation, specified by a local crack coordinate system, into crack driving and persistent components. Accordingly, a modified stress strain relation is proposed to model fundamental crack characteristics properly, and a thermodynamically consistent crack driving strain energy density is postulated. The split is applied to numerical examples of initially cracked specimens and compared to results obtained by the two standard approaches.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The occurrence of cracks is one of the most severe failure mechanisms within any kind of structure due to the fact, that the structural system undergoes fundamental changes involving dramatical reduction of the load bearing capacity and, at the worst, even a total loss of stability. While a standard structural design covers typical load cases, there are extraordinary events, e.g. earthquakes or impacts, accompanied by an inevitable excess of the ultimate loads, which have to be considered additionally during the design phase. In case of critical infrastructure or vital structures being affected, e.g. power plants or passengers cells, respectively, the simulation and investigation of catastrophic events may be the key to topology optimization and meaningful reinforcement of existing structures. Beside the identification of critical components and the prediction of crack evolution itself, proper tools and methods to simulate the post fracture behaviour and an according evaluation of the residual load bearing capacity are the focus of this paper.
The continuous crack approximation by a phase-field method is advantageous both from the theoretical as well as the implementation point of view. In contrast to discrete crack representations, the emerging crack does not require mesh manipulation, due to its introduction as an additional degree of freedom for the same discretization and shape functions as used for the displacement field (see e.g. [31]). On the other hand, crack initiation and all kinds of crack evolution (propagation, kinking, merging, branching, arrest) are governed by the competition between fracture energy and potential energy within a strongly coupled system of partial differential equations containing the balance of linear momentum and the evolution equation of the phase-field. For the case of brittle fracture, this relates directly to the postulates of Griffith [15]. Complex post-processing evaluations, e.g. by use of material forces as well as additional criteria, e.g. a branching threshold or velocity dependent fracture toughness, are not necessary at all to obtain a crack path prediction close to experimental evidence, see e.g. [6, 31]. Extensions to ductile fracture are published, see e.g. [1,2,3, 8, 24], as well as cohesive approaches, see e.g. [12, 22, 35, 36]. Furthermore, anisotropic fracture toughness is investigated e.g. in [11, 20, 29, 33, 34].
A basic feature of every phase-field model is the so-called split of the strain energy density into crack driving and persistent components. Up to date, two fundamental approaches are available. The first is strongly related to damage mechanics and has been introduced by Amor et al. in [5]. Essentially, the strain tensor is split into volumetric and deviatoric components and the crack is assumed to be driven by volumetric expansion and deviatoric strains. Accordingly, volumetric tensile and deviatoric stresses are degraded. This kind of split, subsequently denoted as the volumetric–deviatoric split, is used e.g. in [4, 18, 30, 39] among others. The second approach was introduced by Miehe et al. in [26, 27]. Here, the strain tensor is decomposed into its principal components. Based on the assumption, that only tensile components may drive a crack, an according crack driving strain energy density is postulated. This concept is more related to actual fracture mechanics, as there are similar concepts evaluating principal strains or stresses for the driving of crack evolution in analytical approaches. The split has been applied e.g. in [7, 17, 31] and among others.
Both approaches are developed as an enhancement of the phase-field model initially proposed by Francfort and Marigo in [13]. In the original model, the crack is driven by the whole strain energy density. Accordingly, the whole stress tensor is degraded, which, on the one hand, results in crack propagation due to compressive loading, while, on the other hand, existing cracks exhibit interpenetration of the crack surfaces under compressive loading. Although, both the spectral and the volumetric–deviatoric split resolve the unrealistic behaviour of crack evolution under compressive loading, additional features are to be addressed in order to accomplish a realistic model for crack approximation by a phase-field approach. It is Strobl and Seelig in [32] to note for the first time, that both splits violated basic crack boundary conditions and the only way to remedy this, is to include an information about the crack orientation into the phase-field model. They proposed to retrieve this information from an evaluation of the gradient of the phase-field for existing cracks. While this is shown to work well for an initially cracked specimen with a simple phase-field profile, it leads to an unrealistic crack orientation both at the crack tip and within fully degraded elements. Furthermore, an according procedure to obtain crack evolution has not been presented. In the paper at hand, an alternative approach, the directional split, is introduced. The model is designed to obtain a phase-field crack approximation, that fulfills basic crack characteristics defined for ideal plane and friction-less crack surfaces. Again, it is based on the additional information of the crack orientation, which enables a decomposition of strains and stresses with respect to a local crack coordinate system into normal and shear components, that are categorized into crack driving and persistent components. Furthermore, an according procedure for crack evolution is proposed.
In Sect. 2, the theoretical basis of the directional split is presented. Section 3 is focused on the finite element implementation of the model and Sect. 4 shows its application to numerical examples in order to contrast the results with those obtained by the spectral and the volumetric–deviatoric split. Finally, concluding remarks and comments close the paper.
2 A directional phase-field approach to dynamic fracture
2.1 Numerical approximation of the topology and orientation of existing cracks within the framework of the phase-field method
The numerical approximation of the topology of a crack in the directional phase-field approach is based on the second order crack density functional
with the regularization length l, the phase-field order parameter p and the gradient operator \(\nabla \). Any sharp crack \({\varGamma }\) inside a domain \({\varOmega }\) can be represented by the regularized and continuous approximation
that includes both a representation of the cracked parts of the domain with \(p=1\) as well as a transition zone to intact regions where \(p=0\). The width of the transition zone is governed by the regularization length l, see Fig. 1. According to the theory of \({\varGamma }\)-convergence, discussed in [10], the sharp crack is approximated for the limiting case of \(l\rightarrow 0\). Furthermore, there is an important link to the discretization of the structure by a number of N finite elements. According to [17], the most accurate approximation of the crack topology in a 2D setup is achieved by \(l=2~\text {min}(h_e\vert e\in N)\) with \(h_e\) being the characteristic element size of element e, i.e. the smallest distance between two nodes within that element. However, based on the discussion in [21] considering a one-dimensional investigation of \({\varGamma }\)-convergence in a numerical setup with uniform mesh size h, the most accurate solution is obtained for \(l=32\, h\).
Regularized crack approximation \({\varGamma }_l\) of the sharp crack \({\varGamma }\) in domain \({\varOmega }\) and phase-field p across \({\varGamma }_l\)
The continuous approximation of the topology of a crack by \({\varGamma }_l\) is beneficial because of the mesh-independent representation of the crack within the finite element method (FEM) and the exploitation of \({\varGamma }_l\) as a measurement for the surface of the crack. On the other hand, this introduces difficulties when it is necessary to track the path of a crack, e.g. obtaining the position of the crack tip, the location of branching or the angle of kinking, which is discussed and partially resolved in [31]. A common strategy to visualize the crack surfaces is their representation by isosurfaces at a predefined critical phase-field value \(p_c\), e.g. \(p_c=0.95\), combined with the blanking out of elements where \(p> p_c\).
Crack orientation vector \({\mathbf {r}}\) and decomposition of a stress tensor in the orthonormal crack reference coordinate system (CCS)
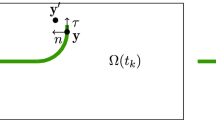
In order to describe the orientation of a crack, a vector \({\mathbf {r}}\) is defined such, that it is perpendicular to the crack surface. Based on the crack orientation vector \({\mathbf {r}}\) and two additional vectors \({\mathbf {s}}\) and \({\mathbf {t}}\), the crack coordinate system, shown in Fig. 2, is defined. The vectors \({\mathbf {r}}\), \({\mathbf {s}}\) and \({\mathbf {t}}\) constitute an orthonormal crack reference coordinate system (CCS). Within the CCS, any strain or stress tensor can be decomposed into components with respect to the crack orientation. In terms of stresses, it is possible to define quantities on the crack surface, i.e. the normal component \(\varvec{\sigma }_{rr}\) and the pairwise shear components \(\varvec{\sigma }_{rs}\), \(\varvec{\sigma }_{sr}\) and \(\varvec{\sigma }_{rt}\), \(\varvec{\sigma }_{tr}\) as well as quantities in the plane of the crack, i.e. the normal components \(\varvec{\sigma }_{ss}\) and \(\varvec{\sigma }_{tt}\) and the shear components \(\varvec{\sigma }_{st}\), \(\varvec{\sigma }_{ts}\).
Based on the CCS, a set of second order crack orientation projection tensors (CPT) is defined as
For brief notation, a projection tensor for shear components \((a\ne b\)) is introduced as
The contraction of the stress tensor with a CPT yields the scalar magnitude of the correspondent stress component as
Characteristics of an ideal planar and frictionless crack
The orientation of a magnitude in space is defined also by the correspondent CPT, which yields the tensors for the stress components, shown in Fig. 2, by
The original stress tensor is obtained as a summation of all components by
The same procedure is applicable to strain tensors.
2.2 Crack characteristics and categories of stress
Consider an idealized crack as a pair of two surfaces within a domain, which are perfectly planar and friction-less. For the closed crack without external loads, both surfaces have force-free contact. Then, three fundamental crack characteristics are identified and visualized in Fig. 3:
-
(a)
force-free crack surface separation,
-
(b)
transmission of compressive forces perpendicular to the crack surface via contact and
-
(c)
resistance-free sliding of the crack surfaces in the plane of the crack.
Considering both, the decomposition of the stress tensor based on the CCS, and as well, the crack characteristics identified and illustrated in Fig. 3, a modified stress tensors within the framework of the phase-field method is defined as
with a degradation function g(p), where \(g(p=0)=1\) and \(g(p=1)=0\), and the crack-driving stress tensor
and the persistent stress tensor
with the bracket operator \(\langle \bullet \rangle _\pm =\frac{1}{2}\left( \bullet \pm \vert \bullet \vert \right) \). The crack-driving stress tensor contains all components, that are directly affected by a crack, i.e. degraded according to a degradation function depending on the phase-field value, while the components of the persistent stress tensor are unaffected by the crack. At this point, the separation into crack-driving and persistent components is completely independent of the constitutive relation between stresses and strains, i.e. the behaviour of cracks can be applied to any material behaviour described by an according constitutive relation between the tensors of strains and stresses.
2.3 Evolution of cracks within a directional phase-field method
In the following, the evolution for the directional phase-field model is derived for the case of brittle fracture in a linear elastic material considering transient effects. The derivation of the governing partial differential equations (PDE) of a dynamic phase-field model for brittle fracture from an according Hamiltonian principle can be found e.g. in [30]. The procedure results in the balance of linear momentum
with the density \(\rho \), the vector of acceleration \(\ddot{{\mathbf {u}}}\) and the divergence operator \(\text {div}(\bullet )\), and an evolution equation for the phase-field
with the crack driving part of the strain energy density \(\psi ^+\). Most of the phase-field approaches available are based on either a volumetric–deviatoric or a spectral decomposition of the strain tensor \(\varvec{\varepsilon }\), that have been introduced by [5] and [26], respectively. The volumetric–deviatoric decomposition yields a crack driving part of the strain energy density of
with the compression modulus K, the second order identity tensor \({\mathbf {1}}\), the shear modulus \(\mu \) and the deviatoric part of the strain tensor \(\varvec{\varepsilon }_D = \varvec{\varepsilon } - \frac{\varvec{\varepsilon }:{\mathbf {1}}}{3}{\mathbf {1}}\). The crack driving part of the strain energy density based on a spectral decomposition reads
where
is the tensile part of the strain tensor \(\varvec{\varepsilon }\), which has been decomposed into its principal values \({{\hat{\varepsilon }}}_i\) and according eigenvectors \({\mathbf {n}}_i\). Furthermore, \(\lambda \) is the first Lamé coefficient. Both approaches are motivated by the observation, that the initial assumption of Francfort and Marigo in [13], i.e.
considering the whole strain energy density to drive the phase-field evolution, resulted in cracks due to compressive loading and subsequent interpenetration of the crack surfaces.
Based on the definition of a crack driving stress category \(\varvec{\sigma }^+\), given in the previous section, a thermodynamically consistent ansatz for an according crack driving part of the strain energy density is
establishing a relation between the stresses \(\varvec{\sigma }^+\) affected by the crack and the energetic complement \(\psi ^+\) to drive the crack’s evolution.
Due to the continuous description of the crack in the phase-field method, material points in the vicinity of a crack can have phase-field values between 0 and 1. In contrast to damage mechanics, where material is partially damaged and a value of e.g. 0.6 is meaningful in a certain sense, this transition is of mere numerical meaning for the phase-field, i.e. in a phase-field model, it is supposed to be either a crack (\(p=1\)) or sound material (\(p=0\)) and the continuous change only fulfills the function of a proper representation of the discrete crack within a continuous approximation. Nevertheless, at every point inside this transition zone, a crack orientation vector \({\mathbf {r}}\) exists as a consequence of either the initialisation of the problem or the previous step of the simulation. A crack driving strain energy density based on the existing crack orientation employs Eq. (9), i.e. the orientation is assumed to be constant and the evolution of the crack is driven by the strain energy density related to the crack driving stress category in this specific CCS. In such a way, an existing crack may propagate further with the same orientation. Additionally, the approach presented here also considers the change of the crack orientation based on an assumption related to the principal stress hypothesis known from fracture mechanics. In contrast to the original idea of a limiting stress value, here, only the direction of the largest principal stress is considered in order to realign the crack’s orientation. It is assumed, that a crack propagates in any direction on a plane, that is perpendicular to the direction of the largest principal stress and, hence, this direction is identical to the crack orientation vector \({\mathbf {r}}\) at this point. In such a case, the crack driving stress tensor reads
with the magnitude of the largest principal stress \({\hat{\sigma }}_1\) and its eigenvector \({\mathbf {n}}_1\).
The choice, whether the original orientation is kept or the crack needs to reorientate according to the direction of the largest principal stress, is made based on the evaluation of the magnitudes of crack driving strain energy densities. In a first step, the state of load, i.e. loading or unloading, has to be determined. To this end, it is checked whether both crack driving strain energy densities, obtained by either Eqs. (9) or (18) within Eq. (17), have a lower value than the largest, previously existing strain energy density at the point, that resulted in the current phase-field. In such a case, the crack undergoes a local unloading, i.e. the existing crack (orientation) is decisive for the relation between stresses and strains and the Eqs. (9) and (10) have to be employed within the constitutive formulation Eq. (8) to calculate the final stress tensors. Otherwise, the crack is in a loading state and the crack orientation may be changing. Yet, this is only the case, when the crack driving strain energy density obtained by Eq. (18) is larger than the one obtained by Eq. (9). Such an assumption is comparable to the well known principle of maximum plastic dissipation stated by Von Mises in [38], i.e. the formation of a crack is the result of a maximum dissipation of potential energy.
2.4 Modified categories of stress according to a stress-free separation of directional phase-field cracks
According to the crack characteristics for tensile loading perpendicular to the crack surface illustrated in Fig. 3a), the separation of the crack faces or opening of the crack results in no reaction forces that act against this movement, i.e. there is no resistance against the opening of a crack. Furthermore, a discrete separation as shown in Fig. 3a) is not affecting the lateral deformation of both bodies. Due to the continuous description of a crack within the phase-field framework, the open space between the crack surfaces is actually occupied by fully degraded elements. On the one hand, an arbitrary amount of crack opening given by a strain \(\varvec{\varepsilon }^{rr}\) for these elements should result in zero stresses \(\varvec{\sigma }^{rr}\) in that direction. On the other hand, the lateral deformation or necking of the elastic material, that is caused by Poisson’s effect, should release completely until the separated bodies have neither strain nor stresses in the plane of the crack. This feature of the crack is illustrated in Fig. 4, where the initial linear elastic deformation of a body under tensile loading on the left side of the picture results in the two separated objects on the right hand side of the figure, which have no constriction, once the crack is present. Within the phase-field method, the grey shaded region is occupied by fully degraded elements. As the crack evolves, these elements have to release both their stresses perpendicular to the crack surface \(\varvec{\sigma }^{rr}\) as well as their strains within the plane of the crack \(\varvec{\varepsilon }^{ss}\) and \(\varvec{\varepsilon }^{tt}\).
Elastic deformation of a specimen before (left) and after (right) the formation of a crack, where the grey shaded region is occupied by fully degraded elements within the phase-field method
Assuming a finite amount of crack opening related to \(\varvec{\varepsilon }^{rr} \ne 0\), a released state of strain is given by the magnitudes \({\hat{\varepsilon }}^{ss}={\hat{\varepsilon }}^{tt}={\hat{\varepsilon }}^{rs}={\hat{\varepsilon }}^{rt}={\hat{\varepsilon }}^{st}=0\) with the symmetry \({\hat{\varepsilon }}^{sr}={\hat{\varepsilon }}^{rs}\), \({\hat{\varepsilon }}^{tr}={\hat{\varepsilon }}^{rt}\) and \({\hat{\varepsilon }}^{ts}={\hat{\varepsilon }}^{st}\). Based on the assumption of a linear elastic material behaviour, i.e.
the corresponding non-zero magnitudes of stress components are
Consequently, a specific magnitude of stress due to crack opening is related to the corresponding magnitude of lateral stresses by
According to Eq. (9), only tensile stresses perpendicular to the crack surface are degraded, thus, the appearance of lateral stresses due to the strain state of crack opening is neglected and leads to an unrealistic behaviour of the model. Therefore, the category of crack driving stresses with a constant crack orientation needs to be modified to read
It should be noted, that the additional components depend on the magnitude of the tensile stresses perpendicular to the crack surface \(\langle {\hat{\sigma }}^{rr}\rangle _+\) modified by the scaling factor \(\frac{\lambda }{\lambda +2\mu }\) and act in the direction of the normal stresses in the plane of the crack \({\varvec{M}}^\text {ss}\) and \({\varvec{M}}^\text {tt}\). The additional components are considered in a similar manner, but with different sign, for the category of persistent stresses by
which results in recovering the original linear-elastic behaviour for \(p=0\).
In the case of a modified crack orientation, an according modification yields the crack driving stress tensor
and the persistent stress tensor
3 Finite element implementation
3.1 Enhanced degradation function for the directional phase-field method
The choice of the degradation function g(p) in Eq. (8) is a crucial part of the crack approximation approach with the phase-field method, as it establishes and defines the relation between the amount of elastic energy released during the evolution of fracture and the counterpart of crack surface energy. Basic requirements are the undegraded state for sound material (\(g(p=0)=1\)) and the total degradation for broken material (\(g(p=1)=0\)). Within the range of \(0\le p\le 1\), the function needs to be continuous, differentiable and monotonically decreasing. Furthermore, in order to restrict the phase-field evolution to a maximum value of \(p=1\), the first derivative of the degradation function with respect to the phase-field has to be zero for this value, i.e. \(\left. \partial _p\, g(p)\right| _{p=1}=0\). Common choice is the quadratic function
that is traced back to the pioneering work of Bourdin in [9]. Furthermore, the cubic function
and the quartic function
are discussed in [19]. While both alternatives result in a more brittle behaviour of the fracture process, they suffer the necessity of a numerical perturbation of the phase-field, which is needed in order to accomplish a transition from the uncracked state at \(p=0\). Without such a perturbation, which is required for the whole phase-field at every first step of the Newton iteration of each load step, the phase-field is, regardless the applied load, not evolving at all. This is caused by the fact, that the according first derivative of the degradation function with respect to the phase-field, \(\partial _p\, g(p)=\frac{\partial \, g(p)}{\partial \, p}\), is zero for the initial state of sound material at \(p=0\). Therefore, the driving force of the phase-field evolution within the PDE for the phase-field evolution, Eq. (12), is multiplied with 0 and no evolution of p is possible.
Due to the sensitivity of the directional phase-field approach to the value of p, a different type of degradation function is proposed. In addition to the aforementioned requirements, the value of \(\partial _p\, g(p)\) needs to be nonzero and monotonically increasing. On the one hand, this ensures the onset of fracture without any additional requirements of perturbation. On the other hand, a similar shift to a more brittle behaviour can be achieved. The function proposed here is a superposition of the linear function \(m\cdot p+n\) and the exponential function \(a\cdot \text {exp}(b\cdot p)\) by
Based on the choice of \(b>0\), the other variables a, m and n may be obtained by fullfilling the requirements \(g_e(0,b)=1\), \(g_e(1,b)=0\) and \(\partial _p g_e(p,b)\vert _{p=1}=0\), which results in
The graph in Fig. 5 illustrates the shape of the degradation functions discussed. The first and second derivative with respect to p are given in Figs. 6 and 7, respectively.
Degradation function g(p)
The degradation function, employed within Eq. (8), defines the degradation of the crack driving component of stresses \(\varvec{\sigma }^+\). The very basic requirements \(g(0)=1\) and \(g(1)=0\) ensure an unchanged material behaviour for unbroken material at \(p=0\) and the total degradation of \(\varvec{\sigma }^+\) at \(p=1\), respectively. The continuous reduction of g(p) for increasing p guarantees, that no unrealistic values of \(g(p)>1\) or \(g(p)<0\) are obtained within the permissible range of \(0\le p\le 1\). These requirements are fulfilled by all functions mentioned above.
First derivative of the degradation function \(\partial _p\;g(p)\)
The first derivative of the degradation function \(\partial _p\;g(p)\) with respect to p is employed in Eq. (12) as a multiplier to the crack driving strain energy density, where this product is in fact the driving force of the phase-field evolution. Here, the requirement \(\partial _p g_d(p;b)\vert _{p=1}=0\) becomes clear, as this renders the driving force to be zero, as soon as \(p=1\). Therefore, no further development of p is enforced. Another interesting feature of the first derivative is its role to scale the crack driving strain energy density. Within \(0<p<1\), all degradation functions discussed have negative values for its first derivate, which results in increasing p for increasing \(\psi ^+\). However, the value of multiplication or scaling factor is changing with respect to p. While the quadratic degradation functions scales \(\psi ^+\) by a maximum factor of \(-2\) for the unbroken material, the cubic and the quartic functions have their maxima \(-1.5\) at \(p=0.5\) and \(-1.778\) at \(p=0.333\). The linear-exponential approaches have a quite constant scaling factor of \(\approx -1\) for small values of p. For larger values of b, the value of the initially constant scaling factor decreases, however, at \(p=1\) it is zero for every b, as required previously. It is shown in the simulations, that this fact leads to a more brittle behaviour of the models with increasing b, as the evolution of p is enforced or accelerated for higher values of p. Furthermore, here again, the numerical problem with \(g_b(p)\) and \(g_c(p)\) becomes evident, as both of them have \(\partial _p g_d(p;b)\vert _{p=0}=0\). Hence, the initial scaling factor for the crack driving strain energy density in Eq. (12) is zero, which results in zero driving forces for the phase-field evolution, regardless the state of strain present. Although, this is overcome by the introduction of a numerical perturbation of the phase-field in every first step of the Newton iteration of each load step, as discussed in [19], both approaches are not implemented and analyzed further in this paper.
Second derivative of the degradation function \(\partial ^2_p\;g(p)\)
The second derivative of the degradation function \(\partial ^2_p\;g(p)=\frac{\partial ^2\;g(p)}{\partial \,p\,\partial \,p}\) with respect to p is employed in Eq. (49) for the computation of a part of the stiffness for the phase-field degree of freedom, that relates to the crack driving strain energy density. The other two parts are related to the bulk and the gradient term of the crack density functional in Eq. (1). As already stated, the cubic and quartic degradation functions are not discussed further, however, the change of sign of \(\partial ^2_p\;g(p)\) within \(0<p<1\) is in fact changing the impact of the crack driving strain energy density on the tangent. As they are not implemented and tested in this paper, it remains unclear, how this affects the stability of the solution. For the quadratic degradation function \(g_a(p)\), the factor is constant for all p and, therefore, the stiffness always depends on the value of the crack driving strain energy density present. The linear-exponential functions have a constant factor of \(\approx 0\) for small values of p, which results in a constant stiffness for the phase-field degree of freedom for this range of p and an improvement of the numerical stability, as this results in a linear equation for the phase-field degree of freedom.
3.2 Irreversibility
Within fracture of brittle material, a macroscopic crack is considered to be irreversible in nature. Considering the evolution equation for the phase-field, Eq. (12), the driving force for the phase-field \(\psi ^+\) is directly connected to the mechanical loading, thus, a decrease in load yields a decrease in phase-field values. Therefore, an irreversibility constraint needs to be introduced.
Two basic approaches are available. There is a procedure related to damage mechanics, introduced by Miehe et al. in [26], where the driving force is replaced by a history variable. This step ensures the local constraint \(\dot{p}>0\). Furthermore, this approach is easy to implement. The other approach is introduced by Bourdin et al. in [9]. They recommend to impose additional boundary conditions on the phase-field, once it reaches a critical value. Although, this results in a local recovery of the phase-field for fully developed cracks and the possibility of a full recovery, if the phase-field did not exceed this value during the loading. Nevertheless, it has been shown in [21], that the damage-like history variable approach yields a significant error in the profile of a fully evolved crack and overestimates the numerically obtained amount of crack surface up to a factor of 2.
In this work, a combination of both approaches is applied, in order to benefit from the elegant simplicity of a formulation with a damage-like history while obtaining a proper profile for fully evolved cracks. A critical value for the phase-field \(p_c\) is defined. Based on this value, a history variable \({\mathcal {H}}(t)\) is introduced, that depends on the current solution time \(t_n\) as well as on a previous step of the simulation at time \(t_{n-1}\). The history variable reads
and is used in the modified evolution equation for the phase-field
Based on the history variable, local loading and unloading can be distinguished.
3.3 Pre-existing cracks
It is quite common to analyze new phase-field approaches by their application to structures with initial cracks, e.g. Mode I, Mode II and Mode III fracture or generally prenotched structures like beams, shells or plates. In the past, most researches focused on a discrete way to discretize initial cracks rather than their representation by an initial phase-field. While this is partially due to the shortcomings of the existing splits for the phase-field models available, the paper at hand is focused on the representation of initial cracks by the phase-field approach. To this end, an initial crack within a structure has to be represented by an initial phase-field profile.
The initial phase-field profile is obtained by solving the evolution equation Eq. (32) subjected to Dirichlet boundary conditions for the phase-field \(p=1\) at a set of given nodal points within the discretization. During this solution, the mechanical field is frozen and no mechanical loads are involved, which results in a proper phase-field profile. However, for the directional split, an initial crack orientation has to be specified in addition. Furthermore, this orientation may change in the subsequent loading for the mechanical field, while the decision, whether the orientation is changing, depends on the local value of the crack driving strain energy density. As the phase-field profile results out of the Dirichlet boundary conditions and no mechanical load has been involved in obtaining the profile, also the local value of the initial crack driving part of strain energy density has to be set according to the existing phase-field profile. This is achieved by a subsequent modification of the history variable \({\mathcal {H}}(t_0)\) according to the local value of p by
3.4 Finite element setup
According to the standard procedure of the FEM, the domain \({\varOmega }\) is decomposed into finite elements 
with n nodes and the global equation system
is assembled by nodewise contributions for the vectors of acceleration and displacement,
respectively, and elementwise vectors of residuum and matrices of mass and stiffness,
respectively. For the phase-field method, the nodal vector of displacements 
is generalized in order to contain further the phase-field degree of freedom, thus
8-node brick elements with linear shape functions within the small strain assumption are applied in all subsequent simulations. Accordingly, the displacement, the strain, the phase-field and the spatial gradient of the phase-field are approximated inside an element by
respectively, where \(i=\{1,2,3\}\) denotes a coordinate direction x, y or z, I is the number of the node, \(N^I\) is the node specific shape function according to [40], \({\hat{u}}^I_i\) and \({\hat{p}}^I\) are the nodal values of the displacements and the phase-field, respectively, and \((\bullet )_{,j}\) denotes the partial derivative of (\(\bullet \)) with respect to the jth coordinate direction. Furthermore, the vector of the element residuum reads
where
is the vector of the nodal residuum, which can be split in three mechanical and one phase-field related part. The residuum for the ith mechanical degree of freedom reads
and the residuum for phase degree of freedom is given by
where the summation convention is applied at identical indices. Furthermore, the element stiffness reads
where the specific stiffness matrix, related to nodes I and J, reads
There, four components are specified, i.e.
The partial derivative of the modified stress tensor \(\varvec{\sigma }^d\) with respect to the strain tensor \(\varvec{\varepsilon }\) yields the fourth order material tensor \({\mathfrak {C}}\), that may be split into crack driving and persistent components by
Within a constant crack orientation, the crack driving material tensor reads
and the persistent material tensor is given by
Within the change of the crack orientation, the eigenvectors of the strain tensor are involved. Therefore, the procedure described in [23] has to be applied in order to obtain the partial derivatives of the eigenvectors with respect to the strain tensor. Here, the principal directions 1, 2 and 3 are replaced by the directions r, s and t, respectively, yet, these directions still correspond to the accompanying eigenvectors and eigenvalues. After some manipulations, one writes
and
In the case of two identical eigenvalues \({\hat{\varepsilon }}_a\) and \({\hat{\varepsilon }}_b\) or if both values are zero, the expression \(\frac{1}{{\hat{\varepsilon }}_a-{\hat{\varepsilon }}_b}\) is replaced by zero. Furthermore, the tensor, that results from the derivative of the history variable \({\mathcal {H}}\) with respect to the strain tensor \(\varvec{\varepsilon }\), depends on the local determination between loading and unloading, thus
which results in an unsymmetric element stiffness matrix for local unloading cases.
The elemental mass matrix 
depends on components 
related to nodes, similar to the definition of the stiffness in Eq. (46). Yet, the only non-zero entries here are on the diagonal for the mechanical degrees of freedom, i.e.
Thus, a consistent mass matrix is used.
3.5 Solution of the equation system
The subsequent Sect. 4 contains numerical examples, both for transient and static cases having initial cracks and no crack propagation as well as those with initial cracks and subsequent crack propagation. Beside the prescription of values for specific degrees of freedom of nodes by Dirichlet boundary conditions, external nodal loads are given by \({\mathbf {F}}_{ext}\), that are considered within Eq. (34). The response of the system to given constraints and external loads is obtained by the solution of the global equation system
where the change in the field variables from time \(t_n\) to \(t_{n+1}\) is given by the solution vector \({\varDelta }{\mathbf {u}}\) with the right hand side \({\varDelta }{\mathbf {R}}\), containing both internal contributions and external loads, and the global tangent \({\mathbf {S}}\). While the incremental right hand side is given by
the global tangent consists of contributions from the stiffness and the mass, i.e.
The above equation enables the decoupling of space and time by exploitation of scalar multipliers \(c_1\) and \(c_3\), which only depend on the choice of the time integration method. Based on the discussions on proper time integration for transient phase-field simulations in [7, 31], the HHT time integration method, described in [16], is used. This time integration scheme basically damps out spurious frequency responses and is controlled by a single parameter \(\alpha \), which is set to \(\alpha =0.667\) in the following. Thus, we have
Furthermore, this scheme is universal to static and dynamic problems, as the static problem description can be obtained out of the transient setting by simply setting \(c_1=1\) and \(\rho =0~\text {kg/m}^3\) in the computation of the mass matrix. The solution of the equation system (59) involves a number of Newton iterations to resolve the non-linear problem and is obtained on a HPC environment with the Bi-CGSTAB solver [37] applied.
The degradation of parts of the stiffness results in numerical problems during the solution of Eq. (59) in case of a static simulation, which is a known issue for the phase-field model and is discussed in detail in [14]. Two approaches are available to overcome the challenge. The first approach is using a staggered solution for the problem, i.e. there are alternating steps solving for the increments of the displacement field and the phase-field, while the respective other field is fixed for that step. The staggered solution scheme is a robust approach, that yields stable results for phase-field crack evolution both in static and dynamic simulations. In the contribution at hand, the scheme is specifically realised such, that at the beginning of each load step, the mechanical field is solved once, setting the tolerance values for the subsequent staggered iterations. Then, within a loop, the phase-field and the mechanical field are solved in an alternated manner. The loop is finished, as soon as both fields are not changing any more or a maximum number of 50 cycles has been performed. The second approach is known as the monolithic solution scheme, i.e. the increments for both field quantites are computed simultaneously from the equation system containing both the mechanical and the phase-field related components as well as all the coupling terms. Considering static simulations, where only the stiffness matrix is relevant, the degradation of specific parts of the stiffness leads to the fact, that the equation system is no longer well-posed and no convergence may be obtained. It should be noted, that even for static cases, a monolithic solution is possible as long as p is small. However, the second approach can be applied in transient simulations. Here, although the stiffness is totally degraded at a certain point, there is the constant contribution of the mass in Eq. (61), rendering the simulation stable and convergent even for the case of propagating phase-field cracks and high values of p. However, in order to obtain reasonable results, basic requirements of transient simulations have to be fulfilled, e.g. proper mesh and size of the time step.
4 Numerical examples
4.1 Two-piece Bar
The first example is a benchmark simulation fabricated to demonstrate the behaviour of the proposed model applied to initial cracks. A static simulation is analyzed in order to demonstrate the impact of lateral stresses on the opening of a crack. Two transient simulations are investigated to point out the differences between the directional, the volumetric/deviatoric and the spectral split for both, normal and shear loading on the crack surface.
Setup of the precracked bar benchmark simulation
A cylindrical bar of length \(L=0.25~\text {m}\) and diameter \(D=0.01~\text {m}\) with an initial crack at half of the length, as depicted in Fig. 8, is considered. The load is applied at the front edge of the specimen A. The material parameters are \(\lambda =8.9~\text {GPa}\), \(\mu =13.3~\text {GPa}\) and \(\rho =2300~\text {kg/m}^3\). The bar is discretized by 8-node brick elements of uniform shape close to cubes and the largest element dimension is \({h\approx 1~\text {mm}}\), therefore, the length scale is set to \(l=2~\text {mm}\).
Profile of initial phase-field crack
The initial step in each simulation, both for the static and the transient case, is a staggered phase-field solution step in order to resolve the boundary conditions of \(p=1\) at no mechanical loading. The boundary condition is applied as a prescribed value to the phase-field degree of freedom at all nodes with coordinates \(0.125~\text {m}\le z\le 0.126~\text {m}\) in order to obtain a slice of fully degraded elements. This step results in the phase-field profile shown in Fig. 9. Furthermore, within this step, the initial crack orientation is set to be \(r=[0,0,1]^\text {T}\).
In the static simulation, additional boundary conditions are introduced. First of all, the longitudinal displacements (in z-direction) are restrained at the rear end of the bar B. Furthermore, the lateral displacements (x- and y-directions) on both ends A and B are fixed, too. The displacement u(t) increases linearly in order to apply tensile loading on the crack and results in an opening of the crack. Without the modifications concerning lateral stresses specified in Eqs. (22) and (23), i.e. making use of the initial assumptions given in Eqs. (9) and (10), the opening of the crack is accompanied by a lateral deformation of the elements, see Fig. 10a). Taking the modified equations into account, the necking can be eliminated and a realistic behaviour of a crack under tension is obtained, see Fig. 10b).
In the first transient simulation, the original bar with the initial crack and no additional boundary conditions as depicted in Fig. 8 is considered. Furthermore, the displacement loading at edge A is replaced by a force loading in the opposite direction in order to introduce and study the propagation of a compressive wave in the longitudinal direction of the bar. The time dependency of the load is half sinusoidal with an amplitude of \(1~\text {MPa}\) and a period of \(10~\mu \text {s}\). The magnitude of the stresses in longitudinal direction \(\sigma _{zz}\) is recorded at positions C1 and C2 (see Fig. 8) and evaluated for the application of the spectral, the volumetric/deviatoric and the directional split.
Stress signal in longitudinal direction \(\sigma _{zz}\) at points C1 and C2 for longitudinal load on the spectral split
Stress signal in longitudinal direction \(\sigma _{zz}\) at points C1 and C2 for longitudinal load on the volumetric/deviatoric split
Considering a load on a crack acting perpendicular to the surface of the crack as given in this first transient example and, as well, the crack characteristics specified in Sect. 2.2, the result depends on the inner direction of the load itself. For a compressive loading, the crack is able to transmit forces via contact of its faces, whereas, for a tensile loading, the faces separate and no force can be transmitted. Furthermore, stress waves are reflected at a free edge of a body, inverting both their direction and the sign of the magnitude. Therefore, the expected result of this benchmark is characterized by 4 features. At first, the wave is propagating in longitudinal direction approaching the crack. The initially sinusoidally shaped compressive wave induces lateral expansion that leads to an oscillation in that direction and creates a number of smaller longitudinal waves following the original pulse (F1). As the main wave is compressive, it passes the crack without significant interaction (F2). At the free end, the wave is reflected and approaches the crack again, this time as a tensile wave (F3). The tensile wave is reflected at the crack in a similar manner as happened before at the free edge, which leads to the wave being trapped in the rear part of the cylinder bouncing back and forth as a tensile and compressive wave, respectively (F4).
Stress signal in longitudinal direction \(\sigma _{zz}\) at points C1 and C2 for longitudinal load on the directional split
The results of the first transient simulation are shown in Figs. 11, 12 and 13, for the spectral, the volumetric/deviatoric and the directional split, respectively. The most important aspect shown is the failure of the volumetric/deviatoric split, when it comes to a correct transmission of the compressive forces over the crack (F2). Instead of the correct behaviour shown in Figs. 11 and 13, the compressive wave splits into a reflected and a transmitted portion, as depicted in Fig. 12. In the subsequent simulation, all three splits are able to model the reflection of the tensile wave correctly (F4). It should be noted, that the amplitude decay obtained in all the simulations is directly related to the lateral expansion of the cylinder cross-section due to the longitudinal compression by the wave passing by. In such a way, a considerable amount of the energy introduced by the load is transferred to the following wave (F1). Nevertheless, the important observations with respect to the characteristics of a crack under loading perpendicular to its surface are possible.
Stress signal in shear direction \(\sigma _{zx}\) at points C1 and C2 for torsional load on the spectral split
In the second transient simulation, the original bar with the initial crack and no additional boundary conditions as depicted in Fig. 8 are considered. Furthermore, the displacement loading perpendicular to the edge A is replaced by a rotational displacement loading of this edge around the z-axis in order to introduce and study the propagation of a shear wave in the bar. The time dependency of the rotation is linearly increasing for \(30~\mu \text {s}\) up to a rotation of \(\approx 11^\circ \) and then held constant. The magnitude of the shear stresses in circumferential direction \(\sigma _{xz}\) at positions C1 and C2 (see Fig. 8) are recorded and evaluated for the application of the spectral, the volumetric/deviatoric and the directional split.
Stress signal in shear direction \(\sigma _{zx}\) at points C1 and C2 for torsional load on the volumetric/deviatoric split
Considering a shear load approaching a crack as given in this second transient example and, as well, the crack characteristics specified in Sect. 2.2, i.e. a perfect plane and friction-less crack surface, no shear can be transmitted. Therefore, the crack has to appear like a free surface to the shear loading, i.e. it is reflected and reverted both in sign and direction (F3). Therefore, the load is trapped inside the first part of the cylinder from the beginning of the simulation and no stress signal should be measured at point C2. As the reflected load reaches again the edge A, it is repeatedly reflected. However, this time, it is not a reflection at a free edge, as this edge is fixed in order to apply the rotational load. Therefore, the sign of the shear loading after the reflection is constant and only the direction is inverted (F5).
Stress signal in shear direction \(\sigma _{zx}\) at points C1 and C2 for torsional load on the directional split
The results of the second transient simulation are shown in Figs. 14, 15 and 16, for the spectral, the volumetric/deviatoric and the directional split, respectively. The most important aspect shown is the failure of the spectral split, when it comes to a correct modelling of not transmitting shear load over the crack (F3). Instead of the correct behaviour, shown in Figs. 15 and 16, a considerable amount of the shear passes the crack and can be measured at point C2, see Fig. 14. With both, the volumetric/deviatoric as well as the directional split, it is possible to obtain a correct result in principle, i.e. a major amount of the shear loading is reflected at the crack in a way similar to the reflection at a free edge, see Figs. 15 and 16. Nevertheless, minor numerical noise is recorded at position C2 for both simulations and its explanation is not clear yet. There may be a relation to the second aspect of the reflection at the crack, which is a dramatical change in the profile of the shear loading. Although, both models show a good agreement to the expectations in general, these two points require further investigation.
Finally, it should be recapitulated, that with the proposed directional split, it is possible to obtain the characteristics of an ideal plane and friction-less crack considering loads normal and tangential to the crack surface, while the spectral and volumetric/deviatoric approaches fail on the one or other aspect, respectively.
4.2 Realigned crack orientation vector
The second example is a study on the division of the strain energy density for a given state of strain into persistent and crack driving parts with respect to the orientation of a crack. The study is restricted to two-dimensional states of strain, because the involved complexity is reduced while the essential features are revealed more easily. Considering the crack driving portion \(\psi ^+\) of the total strain energy density \(\psi _0\) for a linear elastic material, according to Eqs. (17) and (16), respectively, the persistent counterpart \(\psi ^-\) may be obtained by
Furthermore, based on the assumption of linear elasticity and the given state of strain, a similar decomposition into persistent and crack driving categories is available for the stress tensors \(\varvec{\sigma }^+\) and \(\varvec{\sigma }^-\). The decomposition for the stresses is illustrated in Fig. 17, where the influence of the choice of the crack orientation \({\mathbf {r}}\) is visualized. In a two-dimensional setting, the crack orientation is thoroughly defined by the angle \(0^\circ \le \phi < 180^\circ \) spanned between the x-axis and the crack orientation vector itself. In the subsequent study, the impact of the choice of \(\phi \) is demonstrated on a number of given states of strain and the according split of the strain energy density is discussed. As every possible two-dimensional state of strain can be represented by a set of two principal strains, \(\varepsilon _\text {xy}=\varepsilon _\text {yx}=0\) is assumed in the following.
Stress categories in two dimensions with respect to the crack orientation \({\mathbf {r}}\)
Considering uniaxial tension, e.g. \(\varepsilon _\text {xx}=0\) and \(\varepsilon _\text {yy}=0.02\), a decomposition of the strain energy density is shown in Fig. 18. As expected, the largest amount of crack driving energy density \(\psi ^+\) is obtained for the crack orientation coinciding with the direction of the uniaxial strain \(\varepsilon _\text {yy}\), i.e. \(\phi =90^\circ \), confirming the quality of the assumption to align the crack orientation with the largest principal tensile stress in such a case. A deviation of \({\mathbf {r}}\) from that direction reduces the crack driving energy density available until there is no crack driving energy density at all for the direction perpendicular to the direction of the uniaxial strain, i.e. \(\phi =0^\circ \).
Decomposition of the strain energy density according to the crack orientation for uniaxial tension
Extension of the previously analyzed state of strain by a second, smaller principal strain, i.e. \(\varepsilon _\text {xx}=0.01\) and \(\varepsilon _\text {yy}=0.02\), results in the decomposition of the strain energy density as shown in Fig. 19. Again, the crack orientation aligned with the largest principal strain yields the largest crack driving strain energy density. Nevertheless, for all possible crack orientations, there is always a finite amount of crack driving strain energy density available. Allthough it is trivial, it should be noted, that in the case of two equal tensile principle strains, the amount of crack driving strain energy density is constant for every crack orientation.
Decomposition of the strain energy density according to the crack orientation for biaxial tension
A similar observation holds for a state of volumetric compression. However, in such a case, the constant value of the crack driving strain energy density remains zero regardless of the crack orientation. An interesting observation can be made for a biaxial compressive state of strain, e.g. \(\varepsilon _\text {xx}=-\,0.01\) and \(\varepsilon _\text {yy}=-\,0.02\), see Fig. 20. A natural assumption would be that with two compressive principle strains, no crack evolution should be possible at all. Nevertheless, the directional split proposed considers shear to be crack driving. As the crack orientation maximizes the shear components \(\sigma _\text {rs}\) and \(\sigma _\text {sr}\) at \(\phi =45^\circ \) and \(\phi =135^\circ \), a finite amount of crack driving strain energy density is available. However, this finding is not considered for a modified crack orientation, yet. Unless the larger, shear related strain energy density is not obtained due to a previously existing crack orientation, cracks will always align along the direction of the largest principal stress. Furthermore, beside the probably costly computation of the energetically maximization of \(\psi ^+\) in a three-dimensional setup, another fundamental difficulty is the choice between \(\phi =45^\circ \) and \(\phi =135^\circ \). As the energetic level considering crack evolution is identical for both directions, it seems that the introduction of multiple crack orientations at a single point is necessary. The development of such a split remains an open issue for further research. Nevertheless, it is worth considering these energetically identical directions \(\phi =45^\circ \) and \(\phi =135^\circ \) to be a first step of a novel approach to the phenomenom of crack branching based on energetical evaluations.
Decomposition of the strain energy density according to the crack orientation for biaxial compression
It has to be noted, that, due to the phenomenon discussed in the previous strain state, the proposed directional split underestimates the crack driving strain energy density dramatically for quite a range of mixed strain states, e.g. \(\varepsilon _\text {xx}=0.01\) and \(\varepsilon _\text {yy}=-\,0.02\). As visualized in Fig. 21, the crack driving strain energy density for the crack orientation aligned with the direction of the largest principal strain is only 12.5% of \(\psi _0\), whereas the maximum crack driving strain energy density rises up to \(\approx 84.4\%\) of \(\psi _0\) for crack orientations \(\phi =45^\circ \) and \(\phi =135^\circ \) respectively.
Decomposition of the strain energy density according to the crack orientation for a mixed strain state with dominant compression
Another example is analyzed in order to demonstrate, that indeed, the angle of branching may be energetically determined. Consider the strain state \(\varepsilon _\text {xx}=-\,0.01\) and \(\varepsilon _\text {yy}=0.02\) and its evaluation in Fig. 22. Here, an energetically motivated angle of the crack orientation is either \(\phi =55^\circ \) or \(\phi =125^\circ \).
Decomposition of the strain energy density according to the crack orientation for a mixed strain state with dominant tension
Furthermore, this example is used to show another approach to the modification of the crack driving and persistent stress components according to Eqs. (22) and (23), respectively. Figure 23 shows the range of \(50^\circ<\phi <65^\circ \) considering \(\psi ^+\) according to Eqs. (9), (10), (22) and (23). Without modification, a negative amount of persistent strain energy density \(\psi ^-\) is obtained for the range of \(55^\circ<\phi <62^\circ \), while the counterpart \(\psi ^+\) exceeds the amount of total strain energy density \(\psi _0\) available. While the sum of both energies still yields the correct value of \(\psi _0\), it is physically meaningless to split the strain energy density in such a way and the corrections according to Eqs. (22) and (23) are absolutely mandatory.
Close up view on the extreme values of the original and modified decomposition of the strain energy density according to the crack orientation for a mixed strain state with dominant tension
The alignement of the crack orientation with the direction of the largest principle stress value is a meaningful and robust approach to obtain a modified crack orientation in a large number of possible states of strain. However, there are certain mixed mode states, where a different crack orientation would lead to a larger amount of dissipated energy, which should be preferred. It has been shown, that already in a two-dimensional setup, there are two energetically identical crack orientations and, thus, the model would have to be extended such, that multiple crack orientations are possible at a single point. As a first step, the investigation should be extended to three-dimensional strain states. Furthermore, a study of the impact of Poisson’s ratio on the branching angle and the maximum crack driving strain energy density should be carried out. At this point, it would be interesting to incorporate the approach presented in [39], i.e. to specify different toughnesses for Mode I and Mode II fracture, as this has been observed in concrete to be the case.
4.3 Mode I
In the third example, the application of the spectral, the volumetric–deviatoric and the directional split on a Mode I fracture test are investigated in a static simulation. The three splits are contrasted with each other in order to illustrate their characteristics. Furthermore, the enhanced degradation function is evaluated with respect to the relation between load and displacement as well as the enhanced convergence of the solution. Finally, the crack orientation due to Mode I fracture is investigated and compared for static and dynamic simulations. A subsequent simulation demonstrates the agreement of the behaviour of the proposed directional split with the crack characteristics specified in Sect. 2.2.
Setup of the Mode I benchmark simulation
The geometry investigated is shown in Fig. 24a), where \(H=1~\text {m}\), \(W=1~\text {m}\) and \(T=0.1~\text {m}\). The material parameters are \(\lambda =7.15~\text {GPa}\), \(\mu =12.71~\text {GPa}\), \(\rho =2600~\text {kg/m}^3\) and \(G_c=500~\text {J/m}^2\). The geometry is discretized by \(100\times 100\times 10\) 8-node brick elements and the length scale parameter is set to \(l=2~\text {cm}\). The initial crack is modeled by a row of fully degraded elements. The initial profile of the phase-field, shown in Fig. 24b), is obtained by an initial simulation step without mechanical loading with the boundary condition \(p=1\) at the nodes at \(0.50~\text {m}\le y\le 1.00~\text {m}\), each for \(x= 0.50~\text {m}\) and \(x= 0.51~\text {m}\). The initial crack orientation is \({\mathbf {r}}=[1,0,0]^\text {T}\).
Load specification function for the static Mode I fracture test
The displacement boundary at the top and bottom edges are actually a constraint in x- and y-direction in order to apply additional compression and shear loading, after the Mode I fracture evolved. For the static simulations, the pseudo time \({\bar{t}}\) is applied to manage the consecutive loading cases. The displacements are defined by \(u_x({\bar{t}})={\hat{u}}\cdot f_x({\bar{t}})\) and \(u_y({\bar{t}})={\hat{u}}\cdot f_y({\bar{t}})\), where \({\hat{u}}=1~\text {mm}\) and \(f_x({\bar{t}})\) and \(f_y({\bar{t}})\) according to Fig. 25. The specimen is subjected to tensile loading according to Mode I fracture within \(0\le {\bar{t}}\le 1.0\), where the load is large enough to result in a crack opening after full evolution of the phase-field crack. The crack is closed and subsequently compressed within \(1.0\le {\bar{t}}\le 3.0\). After unloading until \({\bar{t}}=4.0\), a shear load is applied until the end of simulation at \({\bar{t}}=6.0\).
Crack propagation for the Mode I benchmark simulation: a Typical widening of crack tip during propagation and b fully broken state
The static simulation of the standard Mode I loading (\(0\le \bar{t}\le 1\)) results in a horizontal crack through the whole specimen, which is identical for all three split applied, see Fig. 26b). However, the intermediate steps of crack propagation with the typical widened and round out profile, see Fig. 26a), are obtained for different times with respect to the split applied. It is due to the fact, that the different splits have different times for the onset of fracture and different values for the peak load and the accompanying displacement as well. A relation between load and displacement at the upper edge of the specimen (\(x=1\,\text {m}\)) is shown in Fig. 27, where the abbreviations S, VD, D0, D1 and D2 stand for spectral split, volumetric–deviatoric split, directional split with \(g_a(p)\), directional split with \(g_d(p;10)\) and directional split with \(g_d(p;100)\), respectively. The static simulation results are obtained by a combination of a monolithic and a staggered solution in order to speed up the solution of the equation system. At the beginning, monolithic steps with large time increments of \({\varDelta }{\bar{t}}=0.01\) are performed, which are followed by monolithic steps with small time increments of \({\varDelta }\bar{t}=0.0001\), which again are followed by staggered solution steps with the small time increments of \({\varDelta }{\bar{t}}=0.0001\). The spectral and the directional split results are obtained for 20 monolithic steps with large time increments, 20 monolithic steps with small time increments and subsequent staggered steps until the end of the crack propagation. For the volumetric–deviatoric split, the onset of fracture is earlier and, therefore, only 19 monolithic steps with large time increments have been performed. The spectral split, the volumetric deviatoric split and the directional split with the quadratic degradation function \(g_a(p)\) exhibit approximately similar peak values \(295.7~\text {kN}\) at \({\bar{t}}=0.2\), \(297.3~\text {kN}\) at \({\bar{t}}=0.1951\) and \(298.1~\text {kN}\) at \(\bar{t}=0.2017\), respectively. The directional split results with the linear-exponential degradation function, D1 and D2, exhibit a more brittle behaviour compared to the previously discussed results, i.e. the deviation from the linear-elastic slope is smaller due to a smaller amount of softening before the peak load and a more abrupt degradation of the system’s load bearing capacity is displayed. Moreover, the peak loads are significantly larger, that is \(329.6~\text {kN}\) at \({\bar{t}}=0.2032\) and \(346.9~\text {kN}\) at \(\bar{t}=0.2085\) for D1 and D2, respectively. Furthermore, D2 reveals a saw tooth behaviour, i.e. there is an initial, short crack propagation at \({\bar{t}}=0.2085\) that stabilizes at the very next step for a reaction force of \(341.8~\text {kN}\), followed by another increase up to \(345.2~\text {kN}\) at \({\bar{t}}=0.2113\) and a subsequent instable crack propagation to the point of the completely fractured state (Fig. 26b)) with a totally degraded load bearing capacity.
Load displacement relation at the upper edge (\(x=1~\text {m}\)) of the specimen
It should be noted, that the totally degraded state, i.e. \(p=1\), is not obtained for any model applied here for the standard Mode I fracture loading (\(0\le {\bar{t}}\le 1\)). Rather, a value very close, e.g. \(p=0.999\), can be achieved for the apparent total degradation, see Fig. 27, at \(u_x>0.25~\text {mm}\). As the displacement is increased up to a value of \(u_x=1~\text {mm}\) at \({\bar{t}}=1\), also the value of p is increasing, too, however, \(p<1\) holds for all simulations performed.
Failure of the volumetric–deviatoric split at compression loading at \({\bar{t}}=2.28\), mesh, phase-field and scaled deformation (scale factor 500): a volumetric–deviatoric split and b directional split
After the unloading for \(1<{\bar{t}}\le 2\), the direction of the displacement is inverted and the crack is compressed. Again, a staggered solution scheme with large time increments of \({\varDelta }\bar{t}=0.01\) is applied to obtain the solution. While the spectral and the directional split resemble in the behaviour of an uncracked linear elastic specimen, i.e. transmit the load properly with a deformation state, the volumetric–deviatoric split encouters diverged results at \({\bar{t}}=2.29\). This is already indicated by the results at time \({\bar{t}}=2.28\), see Fig. 28a), where the deformation is scaled by a factor of 500 in order visualize the problem. Due to the total degradation of the stiffness related to the deviatoric components of the stress tensor in this model, the lateral expansion of the side edges is not confined at all in the fully degraded elements. The proper behaviour, similar to an uncracked linear elastic specimen, is obtained both for the spectral and the directional split, see Fig. 28b).
Failure of the spectral split at shear loading at \({\bar{t}}=5.0\), mesh, phase-field and scaled deformation (scale factor 100): a spectral split and b directional split
For \(4<{\bar{t}}\), shear loading is applied, both, in order to demonstrate the ability of the directional split to show a plausible behaviour in such situation, and to reveal a fundamental problem of the spectral split in such cases. The deformation of the specimen at \({\bar{t}}=5\) is shown in Fig. 29, scaled by a factor of 100. The directional split is not transmitting shear stresses of the crack, as they are part of the degraded component \(\varvec{\sigma }^+\). Therefore, the fully degraded elements are sheared without any resistance. It should be noted, that the volumetric–deviatoric split exhibits a similary behaviour in this loading case. However, within the spectral split, the shear stress is decomposed into a tensile and a compressive principle component, where only the tensile component is degraded. Therefore, shearing induces a resistance in the fully degraded elements resulting in tensile forces on the upper left and the lower right corner. This leads to the initiation of additional cracks at these locations, which propagate along the bounded edges as shown in Fig. 29a).
Crack orientation vector \({\mathbf {r}}\) of the directional split at \({\bar{t}}=0.2030\): a phase-field p and b stress perpendicular to the crack surface \(\varvec{\sigma }_{xx}\)
Crack orientation vector \({\mathbf {r}}\) of the directional split at \({\bar{t}}=0.2067\): a phase-field p and b stress perpendicular to the crack surface \(\varvec{\sigma }_{xx}\)
Crack orientation vector \({\mathbf {r}}\) of the directional split at \({\bar{t}}=1.0\): a phase-field p and b stress perpendicular to the crack surface \(\varvec{\sigma }_{xx}\)
An important aspect of the directional split is the crack orientation, that is specified at each integration point of each element by means of a history variable (e.g. Figs. 30, 31). As a matter of easy visualization, the crack orientation is averaged within one element and displayed as a vector with its midpoint at the center of the elements face. With increasing local \(\psi ^+\), the crack orientation is aligned with the direction of the largest principle strain at this point. Note, that within the initial phase-field profile, the initially set local history field of \(\psi ^+\) according to Eq. (33) is decisive for that decision. Furthermore, the direction is only modified, when the crack driving strain energy density with respect to the new orientation is larger than the value of \(\psi ^+\) within the old orientation. However, due to the typical stress distribution in front of the crack tip at Mode I loading, see e.g. Fig. 30b), a crack orientation according to Fig. 30a) is obtained. The orientation is preserved up to the moment of a fully cracked specimen, shown in Fig. 31a, b). It has been noted before, that for the locally evolved phase-field values \(p<1\) holds, i.e. there are no fully degraded elements and a small, finite amount of stress perpendicular to the crack surface can still be transmitted, see e.g. Fig. 32b). However, the value of these stresses is several magnitudes below the stresses endured in the sound material. Furthermore, due to the typical crack orientation obtained, there are stress inclusions along the crack surfaces (locally restricted areas of high stresses). As the tensile load is increased, also the linear elastic reference energy according to Eq. (17) is increasing and as the deformation for the opening of the crack results in a uniaxial state of strain, also the crack orientation is aligned uniformly in the direction of the x-axis, see Fig. 32a). In consequence, the stress inclusions are reduced. Furthermore, the phase-field values are increased slightly, which results in a further degradation of the transmitted stresses by another magnitude, see Fig. 32b).
Number of Newton iterations at each load step
The staggered part of the static solution is very expensive during crack propagation. The diagram in Fig. 33 illustrates the cost for the solution in terms of Newton iterations per load step. It is clearly visible, that the directional split with the quadratic degradation function is comparable to the spectral, abbreviated by D0 and S, respectively. It is not possible to obtain a good convergence for the volumetric–deviatoric split, abbreviated by VD, as the majority of the solutions during crack evolution are a result of an aborted staggered iteration due to excess of the given maximum number of 50 iteration for a staggered iteration. Nevertheless, the changes in the field variables are small at that time and both the load displacement relation and the crack path are reasonable. It has not been investigated, if convergence can be obtained by a larger maximum number of staggered iterations. Furthermore, the linear-exponential degradation function is clearly superior, as the number of load steps with a large number of Newton iterations is reduced clearly. The total number of Newton iterations necessary to reach load step 160 is \(17\,114\) for the directional split with the quadratic degradation function, which is reduced to \(10\,804\) and \(7\,794\) for the directional split D1 and D2 with \(g_d(p,10)\) and \(g_d(p,100)\), respectively.
Load specification function for the transient Mode I fracture test
Another improvement of the number of Newton iterations necessary per load step can be achieved by a monolithic solution of the problem via a transient simulation during the crack propagation. In contrast to the static simulations, convergence is obtained in a maximum of 7 steps at each loading step, when the crack is propagating, while linear elastic behaviour without considerable phase-field evolution requires only 2 iterations. Here, a physically meaningful time \(t~\text {[s]}\) has to be applied. Furthermore, the time step for the transient simulations depends on the material properties and the element size, in order to resolve the wave propagation and account for transient effects properly. For the material and discretization given here, \({\varDelta }t=3~\mu \text {s}\) holds. Another aspect of the transient simulation is the realistic approximation of crack propagation velocities and branching behaviour of the crack, as discussed in [31]. The modified load specification functions with respect to time t are shown in Fig. 34.
Crack orientation vector \({\mathbf {r}}\) of the directional split for the first static step at \(t=13~\text {ms}\) after the transient crack propagation: a phase-field p and b stress perpendicular to the crack surface \(\varvec{\sigma }_{xx}\)
The transient simulation is carried out for the same geometry, material and discretization as analyzed for the static simulation. The inertia effects are considered for \(1\,000\) steps with \({\varDelta }t=3~\mu \text {s}\). After this, a subsequent static simulation is performed, i.e. \(c_3=0\) and \({\varDelta }t=10~\text {ms}\), in order to test the characteristics of the crack for tension. Given the slow loading specified as \(f_1(t)\) in Fig. 34, a straight crack, similar to the one shown in Fig. 26b), is obtained. However, due to the transient propagation, the resultant crack orientation is slightly different, see Fig. 35a). In the transient simulation, the typical stress concentration in front of the crack tip is obtain for the tip of the initial crack at \(0.50~\text {m}\le y\le 0.45~\text {m}\), too, which results in a crack orientation at these points. However, the further the crack propagated, the more the crack orientation aligned perpendicular to the crack path. This results in a comparably large stress inclusion at the position of the initial crack tip, see Fig. 35b). Nevertheless, the magnitude of the inclusion of \(\approx 380~\text {Pa}\) is small compared to magnitude of the stress of \(\approx 120~\text {kPa}\), that is obtained for the onset of crack propagation.
Branched configuration of the directional split after fast Mode I loading: a phase-field p and b phase-field p at a close up on the branching point and crack orientation vector \({\mathbf {r}}\)
The application of the fast loading specified as \(f_2(t)\) in Fig. 34 results in the branched configuration shown in Fig. 36a). As shown in Fig. 36b), the model is able to predict branching and yields a reasonable crack orientation in that case. Nevertheless, the broadening of the phase-field profile for the branching point and the subsequent propagation are significant and remain an open issue to be investigated and resolved. One probable reason may be the fact, that it is almost impossible to obtain fully degraded elements in the phase-field model, especially for the transient simulation, where the crack opening is small. Furthermore, the propagation of the crack at an angle to the regular meshing may cause additional problems known as the mesh bias discussed in [28].
4.4 Mode II
In the fourth example, the application of the spectral, the volumetric–deviatoric and the directional split on a Mode II fracture test are investigated in a static simulation. The three splits are contrasted with each other in order to illustrate their characteristics. Furthermore, the enhanced degradation function is evaluated with respect to the relation between load and displacement. Finally, the crack orientation due to Mode II fracture is investigated and compared for static and dynamic simulations.
Setup of the Mode II benchmark simulation: a load and boundary in x-y-plane, b plane strain boundary and c initial phase-field profile
The geometry, boundary conditions and the initial phase-field are shown in Fig. 37, where \(H=1~\text {m}\), \(W=1~\text {m}\) and \(T=0.01~\text {m}\). The material parameters are \(\lambda =7.15~\text {GPa}\), \(\mu =12.71~\text {GPa}\), \(\rho =2600~\text {kg/m}^3\) and \(G_c=500~\text {J/m}^2\). The geometry is discretized by \(100\times 100\times 10\) 8 node brick elements and the length scale parameter is set to \(l=2~\text {cm}\). The initial crack is modeled by a row of fully degraded elements. The initial profile of the phase-field, shown in Fig. 37c), is obtained by an initial simulation step without mechanical loading with the boundary condition \(p=1\) at the nodes at \(0~\text {m}\le x\le 0.5~\text {m}\), each for \(y= 0.5~\text {m}\) and \(y= 0.51~\text {m}\). The initial crack orientation is \({\mathbf {r}}=[1,0,0]^\text {T}\).
Load displacement relation at the upper edge (\(x=1~\text {m}\)) of the specimen for the y-direction
The displacement boundary at the top edge imposes a displacement in y-direction in combination with a restricted movement in x-direction in order to apply simple shear loading according to a Mode II test. For the static simulations, the pseudo time \({\bar{t}}\) is applied. The displacements are defined by \(u_y({\bar{t}})={\hat{u}}\cdot f_{x}({\bar{t}})\), where \({\hat{u}}=-\,2~\text {mm}\) and \(f_x({\bar{t}})\) according to Fig. 25, i.e. a shearing displacement in negative y-direction is applied.
Final crack path at \({\bar{t}}=0.3\): a spectral split, b volumetric–deviatoric split and c directional split with quadratic degradation function \(g_a(p)\)
The static simulation of the simple shear loading according to Mode II fracture results in different phase-field profiles for each split applied, see Fig. 39. The failure of the spectral split is demonstrated by the unrealistic reaction forces shown in Fig. 38 and the crack pattern obtained, shown in Fig. 39a). The explanation for this behaviour is similar to the reason discussed for the subsequent loading in the previous example, i.e. a significant amount of the shear is transmitted over the crack, which leads to an overestimation of the reaction force and the crack evolution in the corner of the specimen. Note, that the situation changes fundamentally, when the initial crack is approximated in a discrete manner, i.e. separating the elements along the edge of the initial crack. Then, the result would be more like the result obtained for the volumetric–deviatoric split, which shows a typical crack propagation at an angle compared to the initial crack, see Fig. 39b). Also, the directional split shows a fundamentally different behaviour than the spectral and the volumetric–deviatoric split. Instead of a kinking of the crack, a straight crack propagation is obtained, which is naturally obtained based on energetic consideration, i.e. a local comparison between the energies dissipated by fracture according to shear components in the initial crack orientation and fracture due to large principal tensile strain in a modified crack orientation yields the result, that the fracture due to the shear dissipates more energy, as the resultant crack orientation vectors around the initial crack tip region indicate, see Fig. 40. While this is in perfect agreement with the findings in Sect. 4.2, it raises the question, how to obtain the energetically defined crack orientation, when neither the initial nor the crack orientation according to tensile principal stress assumptions should be used. This remains an open issue in this paper. The relation between the shear displacement and the reaction force at the upper edge of the specimen at \(x=1\,\text {m}\) is plotted in Fig. 38. Again, the failure of the spectral split is obvious and it is interesting to note, that the more stiff response originates out of the shear transmission behaviour of the initial crack with this split. Furthermore, the directional split shows a very brittle response compared to the volumetric–deviatoric results, which resembles more to a damage-like softening and a later abrupt failure at \({\bar{t}}=0.243\). However, it has to be noted, that for the Mode II loading, the quadratic degradation function shows a more abrupt drop in the reaction force than the results obtained with linear-exponential degradation function. Yet, the results obtained with the linear-exponential degradation functions remain closer to a linear elastic material, i.e. again a more brittle behaviour is obtained with this kind of degradation function (Fig. 38).
Crack orientation vector \({\mathbf {r}}\) of the directional split at \({\bar{t}}=0.3\) with the quadratic degradation function \(g_a(p)\)
All simulations are obtained with a constant pseudo time step of \({\varDelta }{\bar{t}}=0.001\) in a staggered simulation. It is worth to note, that for this simulation, the quadratic degradation function (D0) shows the better performance with respect to the number of Newton iterations necessary to obtain the solution, see Fig. 41. Here, the results of the spectral split are not included, due to its failure to display a plausible Mode II crack propagation result. The total number of Newton iterations performed to reach the load step 300 are \(32\,557\), \(3\,624\), \(4\,832\) and \(4\,904\) for the volumetric–deviatoric split (VD), the directional split with \(g_a(p)\) (D0), \(g_e(p,10)\) (D1) and \(g_e(p,100)\) (D2), respectively.
Number of Newton iterations at each load step
Result of the directional split for shear in negative y-direction at \(t=6~\text {ms}\): a phase-field p and b close up view on the crack orientation vector \({\mathbf {r}}\) at the kinking point
Result of the directional split for shear in positive y-direction at \(t=6~\text {ms}\): a phase-field p and b close up view on the crack orientation vector \({\mathbf {r}}\) at the kinking point
The transient simulations are obtained in a similar manner as the transient simulations for Mode I loading, i.e. a constant time step of \({\varDelta }t=3~\mu \text {s}\) is applied. Furthermore, the magnitude of the displacement is increased to \({\hat{u}}=-\,120~\text {mm}\) in order to trigger crack evolution within a reasonable number of simulation steps. In addition, both shear in positive and negative y-direction are considered by a change in the sign of the magnitude. The results of the simulations are shown in Figs. 42 and 43 for the shear in negative and positive y-direction, respectively. For the transient simulation with the modified magnitude of the displacement, kinking can be observed. Furthermore, for the shear in negative y-direction, branching after \(0.2~\text {m}\) of straight crack propagation is observed with a horizontal branch and a branch at the typical angle for the shear failure, see Fig. 42. While the horizontal branch is frustrated after a short distance, the kinked branch propagates further. However, due to the increased dissipation by the branching and widening, the kinked branch is not propagating as far as the branch observed in shear in positive y-direction, see Fig. 43. Furthermore, considering the close up on the crack orientation vector \({\mathbf {r}}\) in Figs. 42b) and 43b) for shear in negative and positive y-direction, respectively, the crack seems to be reasonably aligned to the kinked branch, but shows some obscure crack orientation vectors at the branching point. Although this is a result of the principal strain evaluation during the crack evolution, the dramatical change in the orientation between two neighboring elements may lead to strong inclusions of stress for a subsequent loading of the crack. It may be necessary to develop an approach to smooth and reorientate the cracks in such regions, in order to obtain realistic behaviour. This is a topic for future research on the directional split.
4.5 Mode III
The fifth example is a proof of concept for the directional split in a Mode III loading situation. In contrast to the previous simulations, the mesh is very coarse in order to reduce the computational cost of the simulation and have a better visibility of the crack orientation vector results in the setup, where the third dimension is significant to understand the behaviour. The spectral split, the volumetric–deviatoric split and the directional split are applied and the results of static simulations are contrasted against each other. Furthermore, the modified degradation function is evaluated with respect to the relation between load and displacement as well as the convergence of the solution.
Setup of the Mode III benchmark simulation: a geometry and load and b initial phase-field profile with deformation according to Mode III loading
The geometry and the loading are shown in Fig. 44a), where \(T=1~\text {m}\), \(H=1~\text {m}\) and \(W=1~\text {m}\). In order to obtain a proper shearing of the initial crack, additional boundary conditions are introduced. Each surface of the cube is restricted in its displacement in x-direction. Furthermore, the surfaces at \(x=0~\text {m}\), \(x=1~\text {m}\), \(y=0~\text {m}\), \(z=0~\text {m}\) and \(z=1~\text {m}\) are constrained in their movement in the x-direction. Finally, the movement in z-direction is bounded on the surface at \(y=1~\text {m}\), where the load is applied on the half of the surface with \(0~\text {m}\le x\le 0.50~\text {m}\). The material parameters are \(\lambda =7.15~\text {GPa}\), \(\mu =12.71~\text {GPa}\), \(G_c=500~\text {J/m}^2\) and the length scale parameter is set to \(l=10~\text {cm}\). The cube is discretized by \(20\times 20\times 20\) elements and the mesh, the initial phase-field and a Mode III deformation of \(10~\mu \text {m}\) scaled by a factor of \(10^4\) are shown in Fig. 44b). The initial profile of the phase-field is obtained by an initial simulation step without mechanical loading with the boundary condition \(p=1\) at the nodes at \(0.5~\text {m}\le y\le 1.0~\text {m}\), each for \(x= 0.5~\text {m}\) and \(x= 0.51~\text {m}\).
The displacement boundary at the edge \(y=1~\text {m}\) imposes a displacement in z-direction \(u_z({\bar{t}})\) in order to induce a shear loading according to a Mode III fracture, see Fig. 44b). The static simulations use the pseudo time \({\bar{t}}\) and a constant time step of \({\varDelta }{\bar{t}}=0.01\). The displacement values are defined by \(u_z({\bar{t}})={\hat{u}}\cdot f_{x}({\bar{t}})\), where \({\hat{u}}=1~\text {mm}\) and \(f_x({\bar{t}})\) according to Fig. 25. Fracture occurs within \(\bar{t}<1.0\) for all three splits applied. The phase-field profiles obtained together with the scaled displacements (scale factor 100) at \({\bar{t}}=1.0\) are shown in Fig. 45 and the reaction forces are plotted in Fig. 46. The phase-field profiles obtained for both the spectral split and the volumetric–deviatoric split are not as expected. While the failure along the support is at least reasonable for the volumetric–deviatoric split, the wrong treatment of shear loading in the spectral split results in an unplausible behaviour both considering the phase-field evolution as well as the reaction forces obtained.
Final phase-field profile at a deformation of \(u_z=1 ~\text {mm}\) (scale factor 100): a spectral split, b volumetric–deviatoric split and c directional split
Load displacement relation at the upper edge (\(x=1~\text {m}\)) of the specimen for the y-direction
Shear stress \(\varvec{\sigma }_{yz}\) with the directional split: a before onset of crack propagation \(\bar{t}=0.45\) and b for fully developed crack at \(\bar{t}=1.00\)
The directional split models a straight crack propagation along a constant crack orientation similar to the one specified for the initial crack, see Fig. 45c). The reaction forces are typical for a brittle failure with an abrupt drop in reaction force as soon as the crack evolves. It should be noted, that the correct modeling of the transmission of shear forces over the initial crack with the directional split results in a softer behaviour than for the spectral split and a stiffer response than for the volumetric–deviatoric split. Again, the linear-exponential degradation function models a more brittle behaviour, i.e. there is a shorter softening region, a higher peak reaction force and a larger displacement to obtain a fully cracked specimen. However, it is not possible to obtain convergence for the simulation with \(g_e(p,100)\) after the onset of the first crack propagation.
Stress perpendicular to the crack surface \(\varvec{\sigma }_{xx}\) and crack orientation vector \({\mathbf {r}}\) for the directional split with the quadratic degradation function \(g_a(p)\) at \({{\bar{t}}=1.00}\)
Again, there are minor stress inclusions around the location of the initial crack tip, see Fig. 47. These inclusions are directly related to the direction of the set of the crack orientation vectors \({\mathbf {r}}\) around the crack tip, shown in Fig. 48, that are artefacts of the strain state at the initial crack tip at the beginning of the simulation. Moreover, they are several magnitudes smaller than the stresses in the linear elastic material response at the onset of crack propagation. It should be noted, that the orientation is reasonable at fully cracked elements with \(p=1\), which results in a realistic behaviour of the fully cracked specimen from the global point of view. Nevertheless, the inclusions itself are a mere numerical phenomenon of the model and, although they may be small, it cannot be assumed that they are negligible considering numerical precision. The behaviour and interaction of these inclusions should be studied further in more complex crack propagation scenarios.
Number of Newton iterations at each load step
The results for the convergence of the simulations differs from the ones observed in the previous simulation. The spectral split results are ignored due to the total failure to model realistic results in this case. The volumetric–deviatoric split, although the phase-field profile is not as expected, display a very stable behaviour with a very small amount of steps necessary to obtain the solution. As already stated, it has been impossible to obtain convergence for the linear-exponential degradation function \(g_e(p,100)\). Actually, for the Mode III fracture example, the quadratic degradation function shows a much more stable result than \(g_e(p,10)\) for obtaining a similar final phase-field profile, see Fig. 49).
5 Conclusions
In this paper, an alternative split for the strain energy density is presented. Based on the definition of fundamental crack characteristics and a phase-field crack approximation including the orientation of the crack by a vector field, the stress categorization into crack driving and persistent components is outlined. Accordingly, the modified stress strain relation with a degradation function and the computation of the crack driving part of the strain energy density is proposed and included into the framework of phase-field crack approximation. An approach for the modification of the crack orientation based on energetic considerations is presented. Furthermore, a novel type of degradation function is introduced, that leads to a more brittle behaviour of the model. While convergence can be enhanced in some cases, examples are found, where the convergence of the standard quadratic degradation function is superior.
The directional split introduced here is tested and compared to the spectral split and the volumetric–deviatoric split for various examples. The first example considers the transient transmission of forces over an initial crack of the cross-section of a cylindrical specimen. It is shown, that the directional split, in contrast to the spectral and the volumetric–deviatoric split, models the characteristic transmission of compressive stress waves and the reflection of tensile and shear stress waves correctly.
In a two-dimensional setup, the relation between the crack driving strain energy density and the orientation of the crack orientation vector \({\mathbf {r}}\) is investigated. The alignment of the crack orientation to the direction of the largest principle, tensile strain is a reasonable approach in most of the cases. However, there are strain states, where the maximum crack driving strain energy density is related to a crack orientation, where the shear on the crack surface is dominant. However, in the proposed model, the crack orientation can only change according to the principal strain criteria or remain in the direction specified by the previous step. In order to actually use the largest crack driving strain energy density in all cases, two aspects have to be considered. At first, the crack orientation, where the crack driving strain energy density is at its maximum, has to be found numerically. Furthermore, in a two-dimensional setup, there are already two energetically equivalent crack orientations available. The angle between these orientations could be assumed as the energetically determined branching angle at this point. However, it still is an open task to develop a decomposition of the strain or stress tensor considering more than a single crack orientation vector. Furthermore, the expansion to a three-dimensional problem may yield additional challenges.
The three fundamental modes of fracture (Mode I, II and III) are investigated by using the directional split, the spectral split and the volumetric–deviatoric split. The initial crack is always modelled by an initial phase-field. Mode I fracture can be simulated by all three approaches, resulting in reasonable crack path prediction and realistic reaction forces. However, a subsequent compression and shearing of the existing cracks reveals the defect of the spectral split for shear loading and the defect of the volumetric–deviatoric split in compressive loading, while the directional split models the behaviour realistically. Considering inertia in a transient simulation, a fast Mode I loading results in a branched phase-field profile with a reasonable crack orientation for the directional split. However, there is widening of the phase-field profile that may be partially related to the mesh bias. The static Mode II fracture simulation results in a straight phase-field crack, which is in contradiction to the results obtained with the spectral split and the volumetric–deviatoric split, when a discrete initial crack is used. However, the straight path is motiviated and explained by the increased energy dissipation by considering shear on the crack surface to be crack driving in this case. Furthermore, transient shearing of the initial crack results in a kinked crack also for the directional split. Finally, Mode III is investigated by a relatively coarse mesh to proof the concept of the directional split. Again, it is possible to obtain a straight crack and a brittle result for the reaction forces. Nevertheless, there is no comparison to the other results possible, as both the spectral split and the volumetric–deviatoric split fail totally for this example.
Generally, the algorithm to determine the crack orientation by either the previous crack orientation or the direction of the largest principal, tensile strain is robust and based on energetic considerations. Meaningful crack orientations are always obtained for fully degraded elements, however, in the transition zone, the crack orientations based on the principal strain assumption lead to a finite amount of stress inclusions. It remains an open question, how to resolve this problem.
The directional split proposed and analyzed in this paper is an enhancement of the existing approaches of phase-field crack approximation considering the realistic simulation of normal and shear loads on ideal plane and friction-less crack surfaces. The approach is incorporated into the framework of the phase-field method in order to simulate crack propagation and a realistic post fracture behaviour. Further work is necessary in order to include friction effects on the crack surfaces and the interlocking phenomenon for rough crack surfaces. An incorporation of mode dependent fracture toughnesses, as observed e.g. in concrete, is possible and straight forward due to the identification of normal and shear stress components in the local crack coordinate system.
The application of this approach to inelastic material behaviour, including plasticity, viscoelasticity and large strains in general, is a challenging task. A fundamental issue is the impact of the geometry change due to large strains to the definition of the crack orientation vector and the decomposition of the stresses by the crack orientation projection tensors. Furthermore, while the additive decomposition is the key to separate crack driving and persistent stress components here, an analogous additive decomposition has to be applied to the large strain framework, e.g. a logarithmic strain measure, see [25]. Considering plasticity, additional considerations on the definition of the crack orientation during crack evolution are necessary, i.e. whether the alignment of the crack orientation vector to the vector of the largest principal strain is still valid. A different approach, e.g. a restriction of the spectral decomposition to the elastic part of the strain tensor, would lead to a much higher complexity of the consistent linearization and implementation of the approach.
References
Aldakheel F (2016) Mechanics of nonlocal dissipative solids: gradient plasticity and phase field modeling of ductile fracture. Ph.D. thesis, Universität Stuttgart
Aldakheel F, Wriggers P, Miehe C (2017) A modified gurson-type plasticity model at finite strains: formulation, numerical analysis and phase-field coupling. Comput Mech. https://doi.org/10.1007/s00466-017-1530-0
Ambati M, Gerasimov T, Lorenzis LD (2015) Phase-field modeling of ductile fracture. Comput. Mech 55:1017–1040
Ambati M, Gerasimov T, Lorenzis LD (2015) A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput Mech 55:383–405
Amor H, Marigo JJ, Maurini C (2009) Regularized formulation of the variational brittle fracture with unilateral contact: numerical experiments. J Mech Phys Solids 57:1209–1229
Bleyer J, Roux-Langlois C, Molinari JF (2017) Dynamic crack propagation with a variational phase-field model: limiting speed, crack branching and velocity-toughening mechanisms. Int J Fract 204:79–100
Borden M (2012) Isogeometric analysis of phase-field mmodel for dynamic brittle and ductile fracture. Ph.D. thesis, The University of Texas at Austin
Borden MJ, Hughes TJ, Landis CM, Anvari A, Lee IJ (2016) A phase-field formulation for fracture in ductile materials: finite deformation balance law derivation, plastic degradation, and stress triaxiality effects. Comput Methods Appl Mech Eng 312:130–166
Bourdin B, Francfort G, Marigo JJ (2000) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48:797–826
Braides A (2002) Gamma-convergence for beginners. Oxford University Press, Oxford
Clayton J, Knap J (2011) A phase field model of deformation twinning: nonlinear theory and numerical simulations. Physica D 240:841–858
Contia S, Focardic M, Iurlano F (2016) Phase field approximation of cohesive fracture models. Ann Inst H Poincare (C) Nonlinear Anal 33:1033–1067
Francfort GA, Marigo JJ (1998) Revisiting brittle fracture as an energy minimization problem. J Mech Phys Solids 46:1319–1342
Gerasimov T, Lorenzis LD (2015) A line search assisted monolithic approach for phase-field computing of brittle fracture. Comput Methods Appl Mech Eng 312:276–303
Griffith AA (1921) The phenomena of rupture and flow in solids. Philos Trans R Soc Lond Ser A 221:163–198
Hilber H, Hughes T, Taylor R (1977) Improved numerical dissipation for the time intergration algorithms in structural dynamics. Earthq Eng Struct Dyn 5:283–292
Hofacker M (2013) A thermodynamically consistent phase field approach to fracture. Ph.D. thesis, Universität Stuttgart
Kuhn C, Müller R (2011) A new finite element technique for a phase field model of brittle fracture. J Theor Appl Mech 49:1115–1133
Kuhn C, Schlüter A, Müller R (2015) On degradation functions in phase field fracture models. Comput Mater Sci 108:374–384
Li B, Peco C, Millán D, Arias I, Arroyo M (2015) Phase-field modeling and simulation of fracture in brittle materials with strongly anisotropic surface energy. Int J Numer Methods Eng 102:711–727
Linse T, Hennig P, Kästner M, de Borst R (2017) A convergence study of phase-field models for brittle fracture. Eng Fract Mech 184:307–318
May S, Vignollet J, de Borst R (2015) A numerical assessment of phase-field models for brittle and cohesive fracture: gamma-convergence and stress oscillations. Eur J Mech A/Solids 52:72–84
Miehe C (1993) Computation of isotropic tensor functions. Commun Numer Methods Eng 9:889–896
Miehe C, Aldakheel F, Raina A (2016) Phase field modeling of ductile fracture at finite strains: a variational gradient-extended plasticity-damage theory. Int J Plast 84:1–32
Miehe C, Apel N, Lambrecht M (2002) Anisotropic additive plasticity in the logarithmic strain space: modular kinematic formulation and implementation based on incremental minimization principles for standard materials. Comput Methods Appl Mech Eng 191:5383–5425
Miehe C, Hofacker M, Welschinger F (2010) A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput Methods Appl Mech Eng 199:2765–2778
Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field FE implementations. Int J Numer Methods Eng 83:1273–1311
Negri M (2007) Convergence analysis for a smeared crack approach in brittle fracture. Interfaces and Free Boundaries 9:307–330
Nguyen TT, Baietto JRMC (2017) Phase field modelling of anisotropic crack propagation. Eur J Mech A/Solids 65:279–288
Schlüter A (2013) FE-Implementierung eines dynamischen Phasenfeldmodells für Bruchvorgänge. Master’s thesis, Technische Universität Kaiserslautern
Steinke C, Özenç K, Chinaryan G, Kaliske M (2016) A comparative study of the r-adaptive material force approach and the phase-field method in dynamic fracture. Int J Fract 201:97–118
Strobl M, Seelig T (2015) A novel treatment of crack boundary conditions in phase field models of fracture. Proc Appl Math Mech 15:155–156
Teichtmeister S, Kienle D, Aldakheel F, Keip MA (2017) Phase field modeling of fracture in anisotropic brittle solids. Int J Non-linear Mech 97:1–21
Teichtmeister S, Miehe C (2015) Phase-field modeling of fracture in anisotropic media. Proc Appl Math Mech 15:159–160
Verhoosel CV, de Borst R (2013) A phase-field model for cohesive fracture. Int J Numer Methods Eng 96:43–62
Vignollet J, May S, de Borst R, Verhoosel CV (2014) Phase-field models for brittle and cohesive fracture. Meccanica 49:2587–2601
van der Vorst HA (1992) Bi-CGSTAB: a fast and smoothly converging variant of bi-cg for the solution of nonsymmetric linear systems. SIAM J Sci Stat Comput 13:631–644
von Mises R (1928) Mechanik der plastischen Formänderung von Kristallen. Z Angew Math Mec 8:161–185
Zhang X, Sloan SW, Vignes C, Sheng D (2017) A modification of the phase-field model for mixed mode crack propagation in rock-like materials. Comput Methods Appl Mech Eng 322:123–136
Zienkiewicz OC (1977) The finite element method. Methode der finiten Elemente, 2nd edn. Carl Hanser, München
Acknowledgements
The authors would like to acknowledge the financial support of “German Research Foundation“ under Grant KA 1163/19 and as well the technical support of the centre for information services and high performance computing of TU Dresden for providing access to the Bull HPC-Cluster.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Steinke, C., Kaliske, M. A phase-field crack model based on directional stress decomposition. Comput Mech 63, 1019–1046 (2019). https://doi.org/10.1007/s00466-018-1635-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-018-1635-0